Improved Low-Complexity, Pilot-Based Channel Estimation for Large Intelligent Surface Systems

Abstract

In Large Intelligent Surface (LIS) systems, achieving accurate channel estimation is essential for enhancing communication quality and system efficiency. The main focus of this study is on using the Least Squares (LS) method to estimate pilot-based channels. It also looks at more advanced methods, like using low-density parity-check (LDPC) codes, antenna selection, and optimized pilot design, to make the method more accurate and effective. We employ orthogonal pilot sequences to reduce signal interference and improve pilot power to enhance estimation performance. Additionally, LDPC codes play a crucial role in eliminating noise and interference effects, thereby improving system reliability. We also propose selective configurations of LIS antennas to balance high performance with reduced computational costs. Collectively, these strategies lead to a significant reduction in the Bit Error Rate (BER) and a remarkable improvement in the overall system performance, offering a practical solution for complex LIS deployments.

1. Introduction

1.1. Motivation

The development of next-generation wireless communication systems has positioned Large Intelligent Surfaces (LISs) as a revolutionary technology to meet the increasing demands for higher data rates, better connectivity, and extended network coverage [1]. LIS systems, designed to improve signal transmission and minimize interference, employ a vast network of low-cost active antennas, making them particularly suitable for the promoting requirements of 5G-and-beyond networks [2]. However, achieving optimal performance in LISs heavily depends on precise Channel State Information (CSI), which is a critical component for advanced signal processing and reliable data transfer [3].

One of the crucial technical challenges in LIS systems is channel estimation, a process that involves accurately determining channel characteristics from the received signals. This domain widely adopts pilot-based techniques due to their simplicity and effectiveness [4]. These methods utilize predefined pilot symbols sent through the channel, enabling the receiver to estimate its characteristics. Several methods are employed for channel estimation, including the following:

• Pilot-based techniques: these include methods such as Least Squares (LS) and Minimum Mean Square Error (MMSE).
• Machine learning-based methods: these leverage data-driven approaches for enhanced accuracy.
• Compressed sensing: this approach exploits the channel’s sparsity to estimate its parameters efficiently.

Among various techniques, the LS method stands out for its ease of implementation and minimal computational complexity [5]. Despite its advantages, the LS method is highly sensitive to noise and interference, which can lead to significant inaccuracies in large-scale systems with numerous antennas [6].

1.2. Pilot-Based Estimation

Accurate channel estimation plays a crucial role in ensuring optimal performance in LIS systems. One of the primary challenges in these systems is channel estimation, especially in complex scenarios. Conventional pilot-based methods, especially the LS algorithm, have gained widespread adoption due to their simplicity and efficiency [7]. In this approach, the base station transmits predefined pilot symbols, which the receiver uses to estimate the channel characteristics. In LIS systems, pilot signals travel through both direct and reflected paths. The intelligent surface’s reflective properties help the signals travel further [8].

Although LS-based estimation offers advantages such as an improved Signal-to-Noise Ratio (SNR), spectral efficiency, and data throughput, it faces challenges in low SNR conditions. In such cases, the accuracy of estimation diminishes, which negatively impacts metrics such as the Bit Error Rate (BER) and throughput. To achieve optimal performance in these systems, it is crucial to meticulously design pilot sequences, adjust spacing, and allocate power appropriately. Only by addressing these factors can LIS systems achieve higher reliability, improved spectral efficiency, and effectively meet the demands of next-generation networks [9].

1.3. Novelty and Contribution

Our work presents a new hybrid method for LS-based channel estimation in LIS systems. It overcomes key limitations of previous studies and introduces practical improvements. We compare different channel estimation techniques and thoroughly evaluate their accuracy, complexity, and energy efficiency. Below, we clearly explain how our innovations go beyond past research.

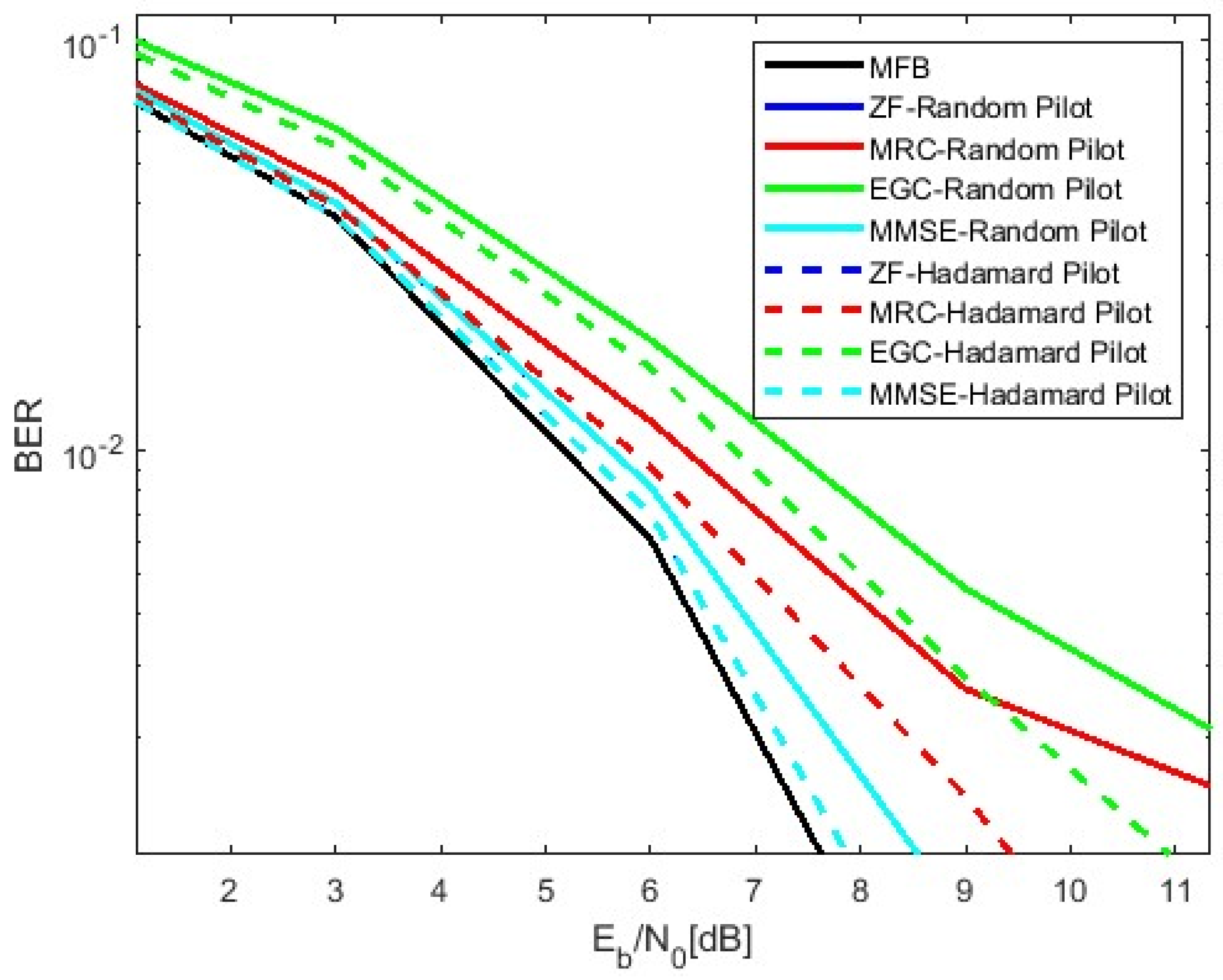
1.3.1. Enhanced Pilot-Based Channel Estimation with Hadamard Sequences

• Unlike traditional pilot sequences used in LIS systems [10], our method employs structured Hadamard sequences that are specifically optimized for low-SNR conditions, reducing cross-interference and improving channel estimation accuracy.
• Unlike conventional pilots, Hadamard sequences enable perfect orthogonality even under multipath fading, leading to more stable channel estimation.

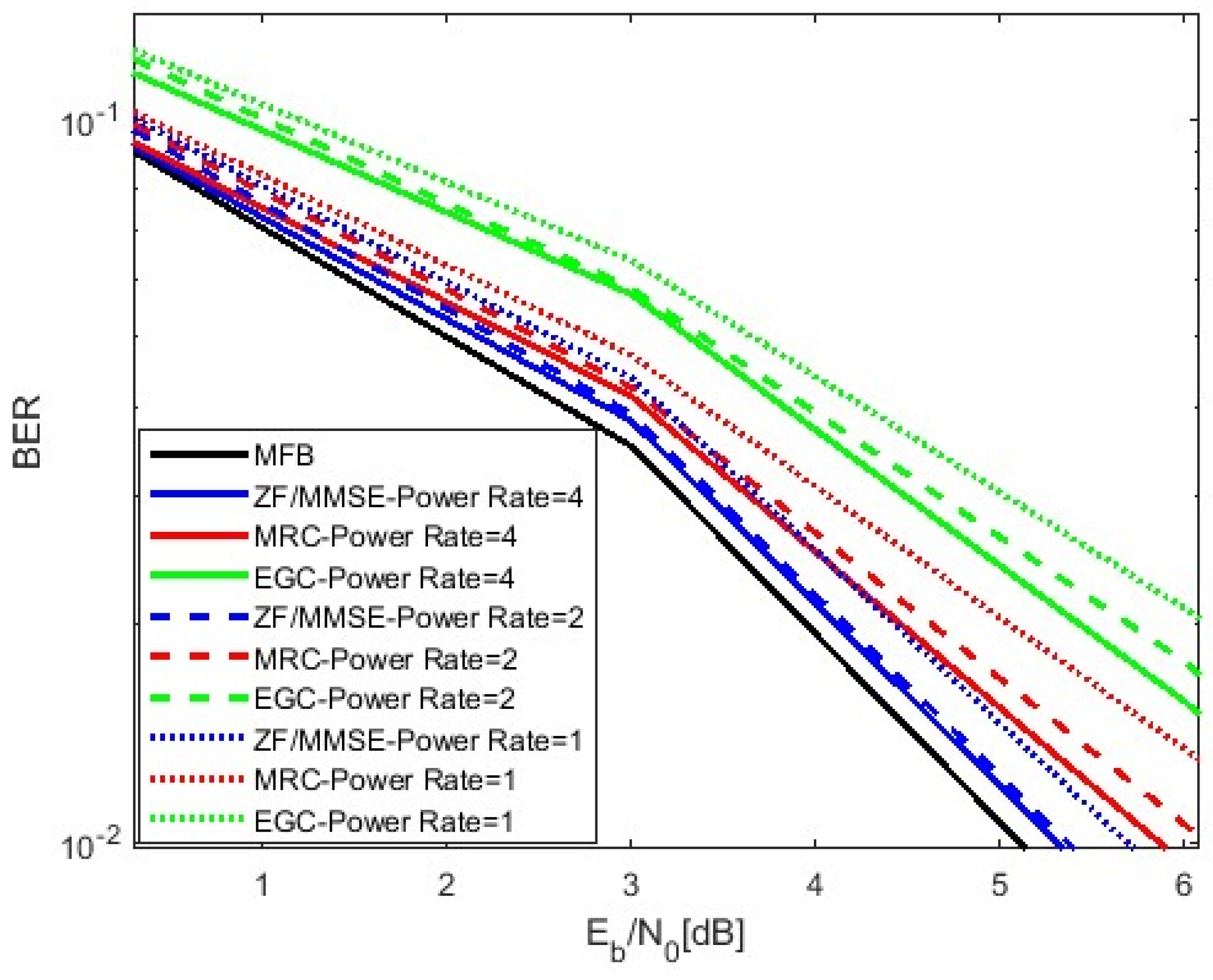
1.3.2. Adaptive Pilot Power Optimization for Dynamic Channel Conditions

• Prior methods such as [11] use fixed pilot power, which does not account for varying noise conditions. Our approach introduces real-time adaptive power scaling, ensuring an optimal SNR while maintaining spectral efficiency.
• Our simulations show that adaptive power optimization reduces the BER more effectively than static power allocation, especially when the signal is weak.

1.3.3. Dynamic Pilot Number Adjustment to Reduce Overhead

• Traditional LIS estimation methods [12] rely on a fixed number of pilots, leading to inefficiencies. Our method uses adaptive pilot clustering, where pilot density increases only when needed.
• Our simulations show that adaptive power optimization helps lower the BER in changing environments better than static power allocation.

1.3.4. Iterative Channel Estimation for Progressive Accuracy Refinement

• Conventional LS estimation [13] relies on single-pass estimation, which can introduce high residual errors. We implement iterative refinement, where channel estimates improve progressively across iterations.
• Our approach gradually improves channel estimation over multiple iterations, making it more effective in noisy LIS environments.

1.3.5. Selective LIS Antenna Activation for Computational Efficiency

• Previous LIS systems [14] activate all antennas, increasing computational complexity. We propose intelligent antenna selection, activating only the most effective elements.
• This technique lowers computational effort by selecting only the most effective antennas while keeping channel estimation accuracy high.

1.3.6. LDPC-Assisted LS Estimation for Noise-Resilient Performance

• While LDPC codes have been used for error correction [15], their integration with LS-based LIS channel estimation has not been fully explored. We introduce a joint LS-LDPC decoding framework, which significantly improves channel robustness.
• Our method enhances channel robustness by combining LS estimation with LDPC decoding, improving the performance in high-noise conditions.

This framework significantly outperforms conventional LS estimation methods by reducing the BER while optimizing complexity and energy efficiency. Monte Carlo simulations confirm that our approach provides a practical, scalable, and high-performance solution for LIS systems.

As a unique idea, our study introduces Hadamard-based pilot assignment with adaptive power control to improve channel estimation and reduce interference. We optimize pilot allocation and LIS antenna selection to lower the complexity while keeping the accuracy high. Additionally, our iterative LS refinement enhances estimation over multiple steps, and the first LS-LDPC integration in LIS systems improves noise resistance and stability.

Table 1 highlights how our proposed method improves upon previous research across six key aspects of LS-based channel estimation in LIS systems.

Table 1. Comparison of our work with previous studies.

Aspect	Previous Methods	Our Improvement
Enhanced pilot-based channel estimation	Conventional methods use fixed orthogonal pilots, leading to interference and limited spectral efficiency.	We introduce Hadamard-based dynamic pilot assignment, which significantly reduces interference and improves channel estimation accuracy under varying SNR conditions.
Pilot power optimization	Previous works rely on fixed pilot power allocation, which does not adapt to fluctuating channel conditions.	Our method dynamically adjusts pilot power based on real-time channel variations, ensuring an optimal SNR while maintaining spectral efficiency.
Adaptive pilot symbol allocation	Previous works rely on fixed pilot traditional approaches use a fixed number of pilot symbols, leading to inefficient estimation in low-SNR scenarios.	We propose adaptive pilot clustering, where the system selectively increases pilot symbols only when necessary, reducing unnecessary overhead.
Iterative channel estimation	Conventional LS estimation performs single-pass estimation, often leaving residual errors.	Our iterative refinement process progressively updates channel estimates over multiple iterations, leading to significantly improved accuracy, particularly in noisy environments.
Selective LIS antenna activation	Previous LIS systems activate all antennas, increasing complexity and computational burden.	We introduce intelligent antenna selection, where only the most effective antennas are used, reducing complexity without sacrificing accuracy.
LDPC-assisted LS estimation	LDPC codes have been used for error correction but were not integrated with LS estimation in LIS systems.	We develop a joint LS-LDPC decoding framework, which significantly enhances noise resilience and system stability in high-interference conditions.

1.4. Characteristics of LIS Systems

A LIS is a promising near-field wireless communications, remote sensing, and positioning technology. A LIS is composed of a variety of tiny panels, each of which generates a number of baseband outputs and may be turned on or off. The proposed LIS system is efficient for urban environments, reducing computational complexity and power consumption by selectively activating antennas. LIS systems differ from traditional wireless communication setups in several fundamental ways [16,17]:

• Large surface for signal reflection and transmission: unlike conventional MIMO systems with separate antennas, a LIS is a Large Intelligent Surface with many small antennas that control radio waves.
• More flexibility in selecting the signal path: a LIS improves signal quality and reduces interference, leading to improving spectral efficiency and coverage.
• Reconfigurable electromagnetic properties: unlike traditional base stations, a LIS can change wave properties for better transmission and lower energy consumption.
• Reduced hardware complexity: instead of complex and powerful equipment, a LIS uses simple and low-energy components for sending and receiving signals [14].
• Compatible with 6G networks: a LIS can match with 6G systems easily, providing ultra-reliable, low-latency communication (URLLC) and massive machine-type communication (m-MTC) through intelligent signal manipulation [18].

1.5. Objective and Organization of This Article

The previous work considered was “A Low Complexity Channel Estimation using superimposed pilots and Detection for Massive MIMO Using SC-FDE”. On the other hand, this article provides improved low-complexity LS channel estimation for LIS systems with regard to traditional and random pilot-based methods [19].

This article is structured as follows: Section 2 provides an in-depth overview of the system model receiver techniques and the LS channel estimation process. Section 3 outlines the proposed enhancements, including the pilot design, pilot power optimization, and antenna selection. Section 4 details the simulation setup, specifying the parameters and performance metrics used for evaluation. Section 5 presents the simulation results and discusses their implications for system performance. Finally, the article’s conclusions and some future study offerings are discussed in Section 6.

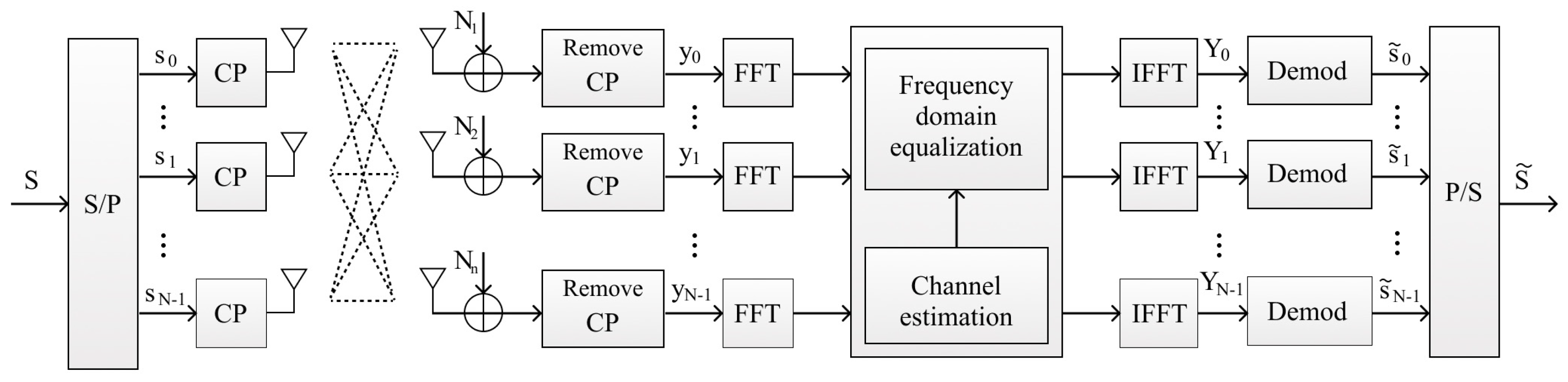
2. System Characterization

This study explores the design of receiver architectures for LIS systems. In such systems, the number of parallel data streams is determined by the count of T transmitting antennas, while the diversity order is characterized by the number of R receiving antennas (uplink is considered). The analysis assumes that the Single-Carrier Frequency Domain Equalization (SC-FDE) signals employ Quadrature Phase-Shift Keying (QPSK) modulation [20].

2.1. Channel Model

As depicted in Figure 1, the $n$-th transmitted block of $N$ data symbols, sent by the $t$-th UE (User Equipment), is denoted as ${\mathit{s}}_n^{\left(t\right)}$, while the received block at the $r$-th antenna of the LIS system is represented as ${\mathit{y}}_n^{\left(r\right)}$. The mapping between the time-domain signal and the frequency-domain signal for the $k$-th subcarrier (assumed to remain invariant during the transmission of a given block) is defined by the Discrete Fourier Transform $DFT\left\{{\mathit{s}}_n^{\left(t\right)};n=\mathrm{0,1},...,N-1\right\}=\left\{{\mathit{S}}_k^{\left(t\right)};k=\mathrm{0,1},...,N-1\right\}$, (a similar process applies, mutatis mutandis, to the received signal block, the channel, and the noise).

Figure 1. Block diagram of LIS system with SC-FDE signals.

The received frequency-domain signal, in matrix–vector representation, is expressed as [21]:

$${\mathit{Y}}_k=\left[Y_k^{\left(1\right)},\dots ,Y_k^{\left(R\right)}\right]={\mathit{S}}_k{\mathit{H}}_k+{\mathit{N}}_k$$

(1)

where ${\mathit{S}}_k={\left[{\mathit{S}}_k^{\left(1\right)},...,{\mathit{S}}_k^{\left(T\right)}\right]}^T$ represents the frequency-domain transmitted data symbols. ${\mathit{H}}_k$ denotes the $T\times R$ channel frequency response for the $k$-th subcarrier, assumed invariant during the transmission of a given block. The $\left(r,t\right)$-th element of ${\mathit{H}}_k$ is represented as ${\mathit{H}}_k^{(t,r)}$.${\mathit{N}}_k$ corresponds to the frequency-domain noise block for the same subcarrier [22].

2.2. Receiver Algorithms

Four receivers’ algorithms, such as Zero Forcing (ZF), MMSE, Equal Gain Combining (EGC), and Maximum Ratio Combining (MRC), are used to process the received signal after channel estimation [23]. ZF and MMSE receivers are computationally intensive, with ZF suffering from noise amplification at high noise levels. In contrast, MRC and EGC are simpler but introduce interference, requiring iterative suppression.

Assuming a non-iterative receiver, the estimated frequency domain data symbols ${\tilde{\mathit{S}}}_k={\left[{\tilde{\mathit{S}}}_k^{\left(1\right)},\dots ,{\tilde{\mathit{S}}}_k^{\left(R\right)}\right]}^T$ become

$${\tilde{\mathit{S}}}_k={\mathit{B}}_k{\mathit{Y}}_k$$

(2)

Depending on the algorithm, ${\mathit{B}}_k$ can be computed as the following:

• ZF: this linear receiver inverts the channel matrix to cancel interference:

$${\mathit{B}}_k={\left[{\mathit{H}}_k^H{\mathit{H}}_k\right]}^{-1}{\mathit{H}}_k^H$$

(3)

• MMSE: balances interference suppression and noise amplification by minimizing the mean square error:

  $${\mathit{B}}_k={\left[{\mathit{H}}_k^H{\mathit{H}}_k+\beta \mathit{I}\right]}^{-1}{\mathit{H}}_k^H$$

  (4)

  where $\beta ={\sigma }_N^2/{\sigma }_S^2={\displaystyle \frac{E\left[{\left|{\mathit{N}}_k\right|}^2\right]/2}{E\left[{\left|{\mathit{S}}_k\right|}^2\right]/2}}$ and where $\mathit{I}$ is an $R\times R$ identity matrix.
• MRC: this receiver combines the received signals based on the channel gains, improving the SNR:

  $${\mathit{B}}_k={\mathit{H}}_k^H$$

  (5)
• EGC: combines signals from multiple antennas with equal weights but adjusts phase to maximize received power:

  $${\mathit{B}}_k=\mathrm{e}\mathrm{x}\mathrm{p}\left\{j\cdot \mathrm{a}\mathrm{r}\mathrm{g}\left({\mathit{H}}_k^H\right)\right\}$$

  (6)
• Iterative Block Decision Feedback Equalization (IB-DFE) is an advanced equalization technique used in communication systems to improve the performance in multipath or interference-limited environments. It iteratively refines the received signal by leveraging feedback from previously detected data, combining concepts from block-based processing and decision feedback. ${\mathit{C}}_k$ is a feedback filter matrix, ${\mathit{B}}_k$ stands for the forward filter matrix, and ${\overline{\mathit{S}}}_k$ represents the detected signal from the previous iteration.

$${\tilde{\mathit{S}}}_k={\mathit{B}}_k^H{\mathit{Y}}_k-{\mathit{C}}_k{\overline{\mathit{S}}}_k$$

(7)

The interference cancellation matrix ${\mathit{C}}_k$ can be computed as:

$${\mathit{C}}_k={\mathit{A}}_k^H{\mathit{H}}_k-\mathit{I}$$

(8)

where $\mathit{I}$ is an $R\times R$ identity matrix, and ${\mathit{A}}_k^H={\left[{\displaystyle \frac{{\mathit{H}}_{k,(r,t)}}{\left|{\mathit{H}}_{k,(r,t)}\right|}}\right]}_{N_R\times N_T}$.

2.3. LS Channel Estimation

For an optimal system, accurate channel estimation is essential. One of adopted methodologies for LIS channel estimation involves the utilization of pilot signals, commonly known as training sequences, followed by channel estimation based on the received data and the understanding of training symbols, in a LIS system with T transmitting antennas and R receiving antennas. The received signal can be represented by (1). The matrix $\mathit{H}$ is considered to be random. Simultaneously, it is expected that any estimator of $\mathit{H}$ will provide an estimate of a specific realization of the random matrix that corresponds to the current block of the received data.

To estimate the channel matrix $\mathit{H}$, it is necessary to broadcast $N\ge T$ training signal vectors ${\mathit{S}}_1,{\mathit{S}}_2,...{\mathit{S}}_N$.

According to the least squares algorithm $\mathit{S}$ and received data, the realization of channel matrix can be estimate using the LS:

$${\mathit{H}}_{LS}=\mathit{Y}\widehat{\mathit{S}}$$

(9)

where ${\mathit{H}}_{LS}={\mathit{S}}^H{\left(\mathit{S} {\mathit{S}}^H\right)}^{-1}\mathit{Y}$ is the pseudoinverse of $\mathit{S}$ [24]. ${\mathit{S}}^H$ is the Hermitian (conjugate transpose) of $\mathit{S}$.

3. Receiver Design Considerations for LIS: Proposed Improvements in Channel Estimation

We propose several methods to address the challenges associated with pilot-based channel estimation and improve it in LIS systems, which can enhance the accuracy of the estimation process and, consequently, the system’s performance. To overcome the limitations of conventional LS channel estimation in LIS systems, this section introduces four enhancements: (1) optimized pilot design with orthogonal pilot sequences; (2) increased channel estimation accuracy through pilot power optimization; (3) an increased number of pilots and selective LIS antenna configurations; and (4) decreased error with increasing iteration and the impact of LDPC codes on channel estimation. These improvements aim to reduce pilot contamination, enhance estimation accuracy, and strike a balance between performance and computational efficiency.

3.1. Optimized Pilot Design and Enhancing the Quality of Pilot Data

3.1.1. Orthogonal Pilot Sequences

Orthogonal pilot sequences are fundamental in wireless communication systems for accurate channel estimation. By utilizing orthogonal pilot sequences, we aim to reduce pilot contamination and interference, thereby improving the accuracy of the channel estimate. Hadamard sequences fulfill these requirements effectively. This article uses Hadamard sequences to ensure minimal cross-correlation. In mathematical terms, for the two pilot sequences ${\mathit{S}}_i$ and ${\mathit{S}}_j$, orthogonal means [25]:

$${\mathit{S}}_i^H{\mathit{S}}_j=0 \mathrm{for} i\ne j$$

(10)

where ${\mathit{S}}_i^H$ is the Hermitian (conjugate transpose) of ${\mathit{S}}_i$.

Orthogonality ensures that when these sequences are transmitted simultaneously, their cross-interference is minimized, allowing for the accurate separation and estimation of multiple channels at the receiver.

A.

Hadamard as Orthogonal Pilot Sequences

Orthogonal pilot sequences are employed to minimize interference and pilot contamination. Orthogonal sequences such as Hadamard matrices ensure minimal cross-correlation between pilots transmitted by different terminals. For a system with $T$ terminals and $N$ pilot symbols, the pilot matrix ${\mathit{S}}_k$ is constructed as $Hadamard\left(N\right)$, where rows are assigned to terminals in a mutually orthogonal manner. This design ensures that the channel estimates for different users are independent, even under multi-user interference [26].

To generate Hadamard sequences, one should create a Hadamard matrix, where each different row represents a complete orthogonal Hadamard sequence. A Hadamard matrix is an $n\times n$ matrix $\mathit{S}$, with entries of either +1 or −1, and its rows are mutually orthogonal.

Let $\mathit{H}$ be a Hadamard matrix of order $n$. The transpose of $\mathit{H}$ is closely related to its inverse

$$\mathit{H} {\mathit{H}}^T=n{\mathit{I}}_n$$

(11)

where ${\mathit{I}}_n$ is the $n\times n$ identity matrix, and ${\mathit{H}}^T$ is the transpose of $\mathit{H}$.

Algorithm 1 provides the initial LS estimation of the channel response matrix based on received pilot symbols.

Algorithm 1: Hadamard Orthogonal Pilot-Based Channel Estimation

Input: Define system parameters: - $\mathrm{Hadamard} \mathrm{matrix} \mathit{H}$ $\mathrm{of} \mathrm{size} M$, used for pilot sequences; - $\mathrm{Received} \mathrm{signal} \mathrm{matrix} \mathit{Y}$ $\mathrm{of} \mathrm{size} N$; - $\mathrm{Noise} \mathrm{variance} {\sigma }^2$; - LIS configuration parameters: number of LIS antennas. Preprocessing: 2. $\mathrm{Extract} \mathrm{the} \mathrm{pilot} \mathrm{sequence} \mathrm{matrix} \mathit{S}$$, \mathrm{which} \mathrm{corresponds} \mathrm{to} \mathrm{the} \mathrm{first} M$$\mathrm{rows} \mathrm{of} \mathrm{the} \mathrm{Hadamard} \mathrm{matrix} \mathit{H}$. 3. $\mathrm{Initialize} \mathrm{the} \mathrm{channel} \mathrm{estimate} \widehat{\mathit{H}}$ to zero. Repeat: $\mathrm{For} \mathrm{each} \mathrm{subcarrier} \mathrm{or} \mathrm{time} \mathrm{slot} t$: 4. Step 1$: \mathrm{extract} \mathrm{the} \mathrm{received} \mathrm{signal} {\mathit{Y}}_t$$\mathrm{for} \mathrm{the} \mathrm{current} \mathrm{time} \mathrm{slot} t$$\mathrm{from} \mathrm{the} \mathrm{received} \mathrm{matrix} Y$. 5. Step 2$: \mathrm{separate} \mathrm{the} \mathrm{pilot} \mathrm{signals} \mathrm{by} \mathrm{applying} \mathrm{the} \mathrm{Hadamard} \mathrm{inverse} \mathrm{transform} {\mathit{S}}^{-1}$$\mathrm{to} {\mathit{Y}}_t$. 6. Step 3:$\mathrm{estimate} \mathrm{the} \mathrm{channel} \mathrm{matrix} {\widehat{\mathit{H}}}_t$ using the LS method: $${\widehat{\mathit{H}}}_t={\mathit{S}}^H{\left(\mathit{S} {\mathit{S}}^H\right)}^{-1}{\mathit{Y}}_t$$ where ${\mathit{S}}^H$$\mathrm{is} \mathrm{the} \mathrm{Hermitian} \mathrm{transpose} \mathrm{of} \mathrm{the} \mathrm{pilot} \mathrm{matrix} \mathit{S}$. 7. Step 4$: \mathrm{update} \mathrm{the} \mathrm{overall} \mathrm{channel} \mathrm{estimate} \widehat{\mathit{H} }$ by averaging over time slots or subcarriers: $$\widehat{\mathit{H}}\to \widehat{\mathit{H}}+{\displaystyle \frac{{\widehat{\mathit{H}}}_t}{T}}$$ where $T$ is the total number of time slots or subcarriers. until: 8. The convergence criteria are met, or all subcarriers/time slots are processed. Output: 9. $\mathrm{The} \mathrm{estimated} \mathrm{channel} \mathrm{matrix} \widehat{\mathit{H}}$.

B.

Properties of Hadamard Pilots:

• Orthogonality: each pilot sequence is orthogonal to others, allowing easy separation at the receiver [27].
• Low complexity: Hadamard sequences are computationally efficient to generate and process.
• Binary nature: They are simple to implement in hardware or software with $+1/-1$ entries.

3.1.2. Pilot Power Optimization [19]

The pilot power is scaled to improve the SNR of the received pilot signals, resulting in more accurate channel estimation. When the pilot signals are stronger relative to noise, the effect of noise on the estimation process is reduced, leading to more reliable estimates of the channel coefficients [28].

Higher pilot power helps in mitigating the high-dimensional complexity of estimating channels for a massive number of antennas or surface elements.

Improved estimation leads to better beamforming and higher energy efficiency, which are crucial for LIS systems.

The power allocated to pilot symbols is scaled to enhance the SNR of the received pilot signals. The channel estimation process becomes more robust to noise, at the cost of slightly reduced data throughput [29].

Increasing pilot power improves estimation accuracy and the SNR, but it also raises the computational complexity, energy consumption, and potential interference. Balancing pilot power is essential to maintain spectral efficiency and avoid excessive overhead [30].

Algorithm 2 improves LS estimation by using more pilot symbols power than Algorithm 1. This helps to make channel estimation more accurate, especially at a low SNR. According to the algorithm, after estimating the channel at pilot subcarriers, the next step involves interpolating these estimates to obtain the full channel response across all subcarriers. This step is essential for accurate signal reconstruction and optimal receiver performance [31].

• Interpolation process: the estimated pilot-based channel matrix is interpolated across all subcarriers using a suitable interpolation function, which represents the chosen interpolation technique.
• Interpolation methods: commonly used interpolation techniques include the following:
  • Linear interpolation: a simple method that connects pilot estimates with straight-line approximations;
  • Spline interpolation: a more accurate approach that ensures smooth transitions between estimated points.
• Low-pass filtering: this mitigates noise effects and provides a smoother channel response by eliminating high-frequency artifacts.

A.

Defining the Optimization Problem

To optimize pilot power, we need to define a function to minimize channel estimation error or reduce the BER. The proposed model is formulated as [24]:

$$\underset{P}{min} E\left[{‖\widehat{\mathit{H}}-\mathit{H}‖}^2\right]$$

(12)

where $H$ is the actual channel matrix, $\widehat{H}$ defines the estimated channel matrix using LSand, and $P=\left[P_1, P_2, \dots ,P_N\right]$ shows the pilot power allocation vector.

The sum of all allocated pilot powers must not exceed the available power budget $P_{max}$ [32]:

$$\sum _{i=1}^N{\mathit{P}}_i\le {\mathit{P}}_{max}$$

(13)

where $N$ is the number of pilot subcarriers. Each pilot subcarrier must achieve a minimum SNR for reliable estimation [33]:

$${\displaystyle \frac{{\mathit{P}}_i{\left|{\mathit{H}}_i\right|}^2}{{\sigma }^2}}\ge {\gamma }_{min},{\forall }_i\in \left\{1, 2, \dots ,N\right\}$$

(14)

where ${\mathit{H}}_i$ is the channel coefficient for the $i$th pilot subcarrier. ${\sigma }^2$ is the noise variance (as defined in Algorithm 2). ${\gamma }_{\mathit{m}\mathit{i}\mathit{n}}$ shows the minimum required SNR.

A simple adaptive pilot power allocation strategy based on the estimated channel quality can be:

$${\mathit{P}}_i\le {\displaystyle \frac{{\mathit{P}}_{max}}{N}}\cdot {\displaystyle \frac{{\left|{\mathit{H}}_i\right|}^2}{\sum _{j=1}^N{\left|{\mathit{H}}_i\right|}^2}}$$

(15)

Pilots with stronger channel conditions receive higher power. The total allocated power remains within ${\mathit{P}}_{max}$.

Algorithm 2: Improved LS Channel Estimation with Increased Pilot Power

Input: Define system parameters: - $\mathrm{Define} N$$\mathrm{subcarriers}, P$$\mathrm{pilot} \mathrm{subcarriers}, \mathrm{and} \rho$ used for pilot power scaling; - ${\mathit{S}}_p$ as pilots; - $\mathrm{Received} \mathrm{signal} \mathrm{matrix} {\mathit{Y}}_p$; - $\mathrm{Noise} \mathrm{variance} {\sigma }^2$; - $\mathrm{Scale} \mathrm{pilot} \mathrm{power}: {\mathit{S}}_p^{scaled}=\rho .{\mathit{S}}_p$. Pilot symbol insertion: 2. Step 1: spread pilots over subcarriers. 3. Step 2: define new pilot symbols. LS estimation: 4. Step 1: compute received scaled pilots. 5. Step 2$: \mathrm{estimate} \mathrm{channel} \mathrm{on} \mathrm{pilots}: {\widehat{\mathit{H}}}_p={\mathit{S}}^H{\left(\mathit{S} {\mathit{S}}^H\right)}^{-1}{\mathit{Y}}_p$. Interpolation: 6. $\mathrm{Interpolate} \mathrm{over} \mathrm{all} \mathrm{subcarriers}: {\widehat{\mathit{H}}}_{Total}=Interp\left({\widehat{\mathit{H}}}_p\right)$. 7. Apply low-pass filtering in frequency domain. Output: 8. $\mathrm{Estimated} \mathrm{channel} \mathrm{response}\widehat{\mathit{H}}=\left\{{\widehat{\mathit{H}}}_{Total}\right\}$.

3.1.3. Increasing the Number of Pilots [19]

Increasing the number of pilots in channel estimation involves transmitting a greater quantity of known pilot signals during the training phase. This approach enhances the accuracy of channel estimation by providing more reference data, reducing the impact of noise and interference. However, it comes with trade-offs such as increased overhead and reduced spectral efficiency, which should be balanced to optimize system performance [34]. Algorithm 3 shows LS Channel Estimation with increased Pilot Number.

Algorithm 3: Improved LS Channel Estimation with Increased Pilot Number

Input: Define system parameters: - $N$$\mathrm{subcarriers} \mathrm{and} P$ initial pilot subcarriers; - ${\mathit{S}}_p$ pilots; - ${\mathit{Y}}_p$ received signal matrix; - $\mathrm{Select} \mathrm{new} \mathrm{increased} \mathrm{number} \mathrm{of} \mathrm{pilots} {\mathit{H}}_p^{\left(i\right)}$. Pilot symbol insertion: 2. Step 1$: \mathrm{spread} \mathrm{pilots} \mathrm{over} P_n$ subcarriers. 3. Step 2$: \mathrm{define} \mathrm{new} \mathrm{pilot} \mathrm{symbols} {\mathit{S}}_p^n$. LS estimation: 4. Step 1$: \mathrm{compute} \mathrm{received} \mathrm{pilots} Y_p^n$. 5. Step 2$: \mathrm{estimate} \mathrm{channel} \mathrm{on} \mathrm{pilots}: {\widehat{\mathit{H}}}_p^n={\displaystyle \frac{{\mathit{Y}}_p^n}{{\mathit{S}}_p^n}}= {{\mathit{S}}_p^n}^H{\left({\mathit{S}}_p^n {{\mathit{S}}_p^n}^H\right)}^{-1}{\mathit{Y}}_p^n$. Improved interpolation: 6. $\mathrm{Interpolate} \mathrm{over} \mathrm{all} \mathrm{subcarriers}: {\widehat{\mathit{H}}}_{Total}=Interp\left({\widehat{\mathit{H}}}_p^n\right)$. 7. Low-pass filtering in frequency domain. Output: 8. $\mathrm{Estimated} \mathrm{channel} \mathrm{response} \widehat{\mathit{H}}=\left\{{\widehat{\mathit{H}}}_{Total}\right\}$.

A.

Optimization Problem for Number of Pilots $N_p$

To optimize the number of pilot symbols, we formulate a minimization problem that balances channel estimation accuracy and pilot overhead while ensuring SNR constraints are met, as given below.

Subject to:

$$N_{min}\le N_p\le N_{max}$$

(16)

$${\displaystyle \frac{1}{N_p}}\sum _{i=1}^{N_p}{\displaystyle \frac{{\mathit{P}}_{\mathit{i}}{\left|{\mathit{H}}_{\mathit{i}}\right|}^2}{{\sigma }^2}}\ge {\gamma }_{min}$$

(17)

Optimal solution [24]:

$$N_p^{*}=\arg \underset{N_p}{min}\left[{\displaystyle \frac{1}{N_p}}\sum _{i=1}^{N_p}{\displaystyle \frac{{\mathit{P}}_{\mathit{i}}{\left|{\mathit{H}}_{\mathit{i}}\right|}^2}{{\sigma }^2}}\right]$$

(18)

$N_p$ represents the number of pilot symbols, constrained between $N_{min}$ and $N_{max}$. The objective is to minimize channel estimation error while ensuring that the received pilot SNR meets a required threshold ${\gamma }_{min}$. The optimal number of pilots, $N_p^{*}$, is determined by balancing pilot overhead and estimation accuracy.

3.1.4. Adding Pilot Iteration to Channel Estimation [10]

In LIS systems, iterative pilot-based channel estimation techniques can significantly enhance estimation accuracy, especially in complex or interference-prone environments. We can use the identified data to improve channel estimation in subsequent iterations. In iterative channel estimation, the channel estimate is updated over several iterations using the estimated channel from the previous iteration. This technique is particularly useful when the channel is subject to noise, interference, and fading, which makes single-pass estimation insufficient. After the first pass, we can use the output of the initial estimation to refine the channel estimate. This can be achieved by applying the data symbols in the next iteration to further improve the estimation [35].

Applying pilot iteration improves the estimation accuracy and interference mitigation but increases the computational complexity and energy consumption. Proper tuning ensures spectral efficiency gains while minimizing processing overhead.

Algorithm 4 improves LS estimation by using an iterative process. It repeats the estimation steps multiple times, making each iteration’s channel estimation more accurate.

A.

Optimization Problem for Number of Pilot Iterations $N_{iter}$

To optimize the number of pilot symbols, we formulate a minimization problem that balances channel estimation accuracy and pilot overhead while ensuring SNR constraints are met, as given below.

Subject to:

The number of iterations does not exceed a predefined limit.

$$N_{iter}\le N_{iter,max}$$

$${\displaystyle \frac{1}{N_p}}\sum _{i=1}^{N_p}{‖{\widehat{\mathit{H}}}^{\left(k\right)}-{\widehat{\mathit{H}}}^{(k-1)}‖}^2\le ϵ$$

(19)

The iterative refinements stop when the channel estimate improvement is below the threshold $\mathit{ϵ}$.

Optimal solution [24]:

$$N_{iter}^{*}=\min \left\{N_{iter}|{\displaystyle \frac{1}{N_p}}{\sum }_{i=1}^{N_p}{‖{\widehat{\mathit{H}}}^{\left(\mathit{k}\right)}-{\widehat{\mathit{H}}}^{(\mathit{k}-1)}‖}^2\le ϵ\right\}$$

(20)

The minimum number of iterations is found when the channel estimate change is very small. This helps avoid unnecessary computations. As the number of pilots $N_p$ increases, the initial channel estimate improves, leading to fewer required iterations $N_{iter}^{*}$, since the algorithm converges faster.

Algorithm 4: Improved LS Channel Estimation with Increased Pilot Iteration

Input: 1. Define system parameters: - $N$$\mathrm{subcarriers} \mathrm{and} P$ initial pilot subcarriers; - ${\mathit{S}}_p$ pilots; - ${\mathit{Y}}_p$ received signal matrix; - $I_m\to$ maximum number of iterations; - $\epsilon \to$ refinement threshold. Initial LS estimation: 2. $\mathrm{Perform} \mathrm{LS} \mathrm{estimation} \mathrm{on} \mathrm{initial} \mathrm{pilots}: {\widehat{\mathit{H}}}_p^{\left(0\right)}={\displaystyle \frac{{\mathit{Y}}_p}{{\mathit{S}}_p}}$. Iterative refinement: For $i$ $=1 \mathrm{to} I_m$: 3. Step 1$: \mathrm{transmit} \mathrm{new} \mathrm{pilots} {\mathit{S}}_p^{\left(i\right)}$$\mathrm{and} \mathrm{receive} {\mathit{Y}}_p^{\left(i\right)}$. 4. Step 2$: \mathrm{create} \mathrm{a} \mathrm{new} \mathrm{estimate} \mathrm{channel} \mathrm{on} \mathrm{pilots}: {\widehat{\mathit{H}}}^{\left(i\right)}.$ $${{\widehat{\mathit{H}}}^{\left(i\right)}}_p={\displaystyle \frac{{\mathit{Y}}_p^{\left(i\right)}}{{\mathit{S}}_p^{\left(i\right)}}}= {{\mathit{S}}_p^{\left(i\right)}}^H{\left({\mathit{S}}_p^{\left(i\right)} {{\mathit{S}}_p^{\left(i\right)}}^H\right)}^{-1}{\mathit{Y}}_p^{\left(i\right)}$$ 5. Step 3$: \mathrm{Check} \mathrm{convergence}: \mathrm{if} ‖{\widehat{\mathit{H}}}_p^{\left(\mathrm{i}\right)}-{\widehat{\mathit{H}}}_p^{(\mathrm{i}-1)}‖\le \epsilon$$\to$ stop iteration. Improved interpolation: 6. $\mathrm{Interpolate} \mathrm{the} \mathrm{final} \mathrm{pilot}\text{-}\mathrm{based} \mathrm{channel} \mathrm{estimate} H_p^{\left(i\right)}$ to all subcarriers: $${\widehat{H}}_{Total}=Interp\left({{\widehat{H}}^n}_p\right).$$ Output: 7. $\mathrm{Estimated} \mathrm{channel} \mathrm{response} \widehat{\mathit{H}}=\left\{{\widehat{\mathit{H}}}_{Total}\right\}$.

3.2. Selective LIS Antenna Configurations and Increasing Channel Estimation Accuracy

This section concentrates on improving LS channel estimation through the selection of ideal antenna configurations from a LIS and improving the overall accuracy of the channel estimation procedure.

Optimized Antenna Configurations and LIS Technology for Improved Channel Estimation

In LIS systems, not all antennas contribute equally to the received signal quality. Antennas closer to the transmitter or those experiencing stronger signal conditions have a more significant impact on the channel estimation process. By focusing on these relevant antennas, the system can:

• Reduce computational complexity: focusing on fewer, high-impact antennas reduces the size of the matrices involved in channel estimation and subsequent signal processing, leading to faster computations [36].
• Maintain estimation accuracy: selecting the most relevant antennas ensures that the accuracy of channel estimation remains high, as only the antennas that contribute most to the signal quality are used.
• Enhance scalability: this approach is particularly beneficial for LIS systems with hundreds or thousands of antennas, where reducing the number of active antennas directly impacts the system’s computational efficiency.
• Energy efficiency: selective activation conserves power by disabling less effective antennas, improving overall efficiency.
• Interference: by focusing transmission and reception on high-quality antennas, the approach reduces multi-user interference.

By strategically selecting the most effective antennas, the accuracy of channel estimation in LIS systems is significantly enhanced. This selective approach ensures that the key antennas contributing to the highest SNR are prioritized, leading to more precise channel estimation. As a result, the BER is reduced, the system capacity increases, and the overall performance of the LIS-based wireless communication system improves [37].

3.3. LDPC Codes in Mitigating the Effects of Channel Estimation Errors

LDPC codes are very effective because they enable reliable data transmission close to Shannon’s channel capacity. They are widely used in modern communication systems due to their high error correction ability and low-complexity decoding in noisy channels. Compared to other error-correcting codes, LDPC codes handle errors better and are more efficient to encode and decode.

3.3.1. Reducing Sensitivity to Channel Estimation Errors

LDPC codes provide robust error correction capabilities, helping reduce the system’s sensitivity to inaccuracies in channel estimation. This ensures that the system maintains performance even when noise or interference leads to erroneous channel estimates [38].

3.3.2. Improving Performance in Sparse Channels

In large-scale LIS systems, where channels are often sparse and nonlinear, LDPC codes can enhance efficiency by managing the complexity of channel estimation while offering superior error correction [39].

3.3.3. Enhancing Spectral Efficiency and Energy Savings

LDPC codes help LIS systems save power while keeping signals strong. They reduce repeated transmissions, improving data efficiency. They also adapt to channel changes, making LIS networks more energy efficient and better for high data loads [40].

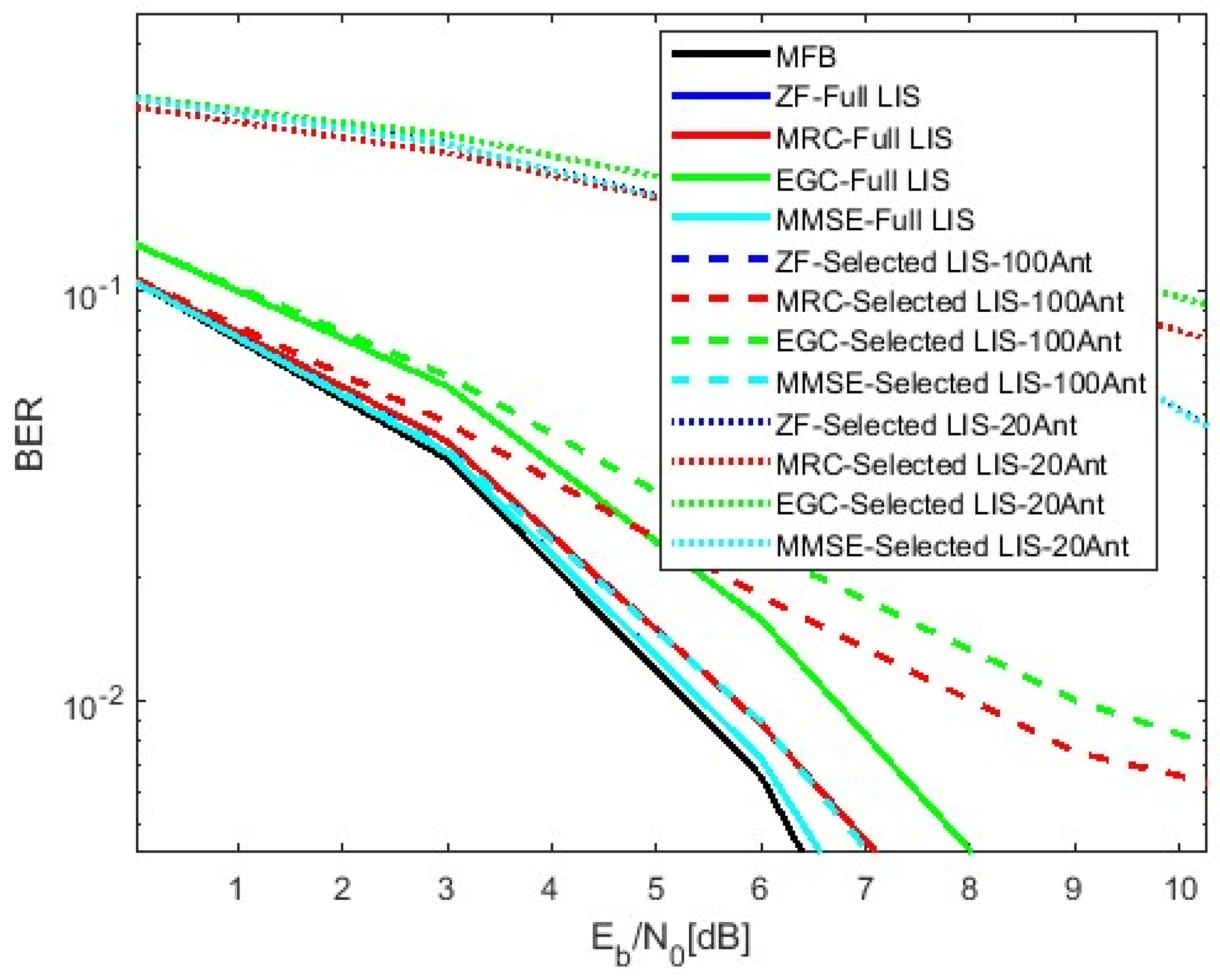
4. Simulation Performance Results

This section presents performance evaluations of the proposed LIS scheme optimized for mm-wave frequencies with SC-FDE signals. The BER performance is analyzed as a function of $E_b/N_0$, where $N_0$ is the one-sided noise power spectral density, and $E_b$ is the transmitted bit energy. The effects of cyclic prefix power overhead were not considered. Monte Carlo simulations assessed the system performance using QPSK modulation, with a block length of $N$ = 256 symbols (the results were consistent for other $N$ values, as long as $N\gg 1$). A Rayleigh fading channel with 16 uncorrelated equal-power paths was used. The Rayleigh model is used due to the dense multipath propagation in LIS systems, the absence of a Line-of-Sight (NLoS) path in many scenarios, and its standard adoption in MIMO research for performance evaluation under multipath conditions. Each block spans 1 s, while the cyclic prefix lasts 0.125 s. In the results for this paper, we considered a carrier frequency of 2 GHz. However, we would like to point out that our technique and main conclusions remain valid for other carrier frequencies with similar propagation characteristics, provided that we achieve the proper scaling (say, doubling the carrier frequency and reducing to half the LIS and scenario dimensions). For MIMO spatial multiplexing, multi-layer transmission was applied, achieving a $T$-times symbol rate increase with $T$ transmitting and $R$ receiving antennas, in the uplink direction. Feasibility requires $T\times R$ for the proper detection of $T$ concurrent symbol streams.

The MATLAB code simulates a LIS system using a Uniform Rectangular Array (URA) model. Here is a simple breakdown of its details and feasibility:

• LIS channel modeling:
  • The receiver is assumed to be in the near field of the LIS.
  • The beam focuses on both angle and distance, unlike traditional far-field beamforming, which only considers direction.
  • The simulation includes multipath reflections and time delays ($\mathsf{\tau }$) to make it more realistic.
• Radio and environmental parameters:
  • Carrier frequency: 2G Hz;
  • Antenna spacing: $\mathsf{\lambda }/2$;
  • User locations: randomly placed inside a room;
  • Number of antennas: 4 × $400$ LISs (LIS antenna consist of four panels and each panel has 100 antennas; in total 4 × 100 = 400).
• Practical feasibility of LIS:
  • LIS is modeled as an active antenna system, where each element has independent gain and phase control.
  • Near-field beamforming is used to focus signals on users.
  • Power adjustments are applied to keep the system practical.
  • Real-world feasibility depends on hardware challenges, the real-time processing of many antennas, and precise phase/gain calibration.

Also, the MATLAB code includes LDPC encoding and decoding to improve communication reliability. Here is a basic overview of its details and practicality:

• LDPC encoding and decoding:
  • The LDPC encoder converts input bits into a longer coded sequence to improve error correction.
  • The LDPC decoder uses a hard-decision method with a maximum of 20 iterations to decode the received data.
  • The decoder stops early if the parity check is satisfied.
• LDPC integration with LIS:
  • LDPC is applied to 4PSK modulation before transmission.
  • After LIS-based transmission and reception, LDPC decoding is used to recover the original data.
  • The simulation includes different equalization and interference cancellation methods (MRC, EGC, ZF, and MMSE).

Table 2 compares various methods for improving channel estimation in LIS systems based on metrics such as complexity, energy efficiency, interference reduction, estimation accuracy, and spectral efficiency.

• Pilot power optimization increases the strength of the pilot signals, improving the channel estimation accuracy but slightly reducing the spectral efficiency because it takes up more transmission power.
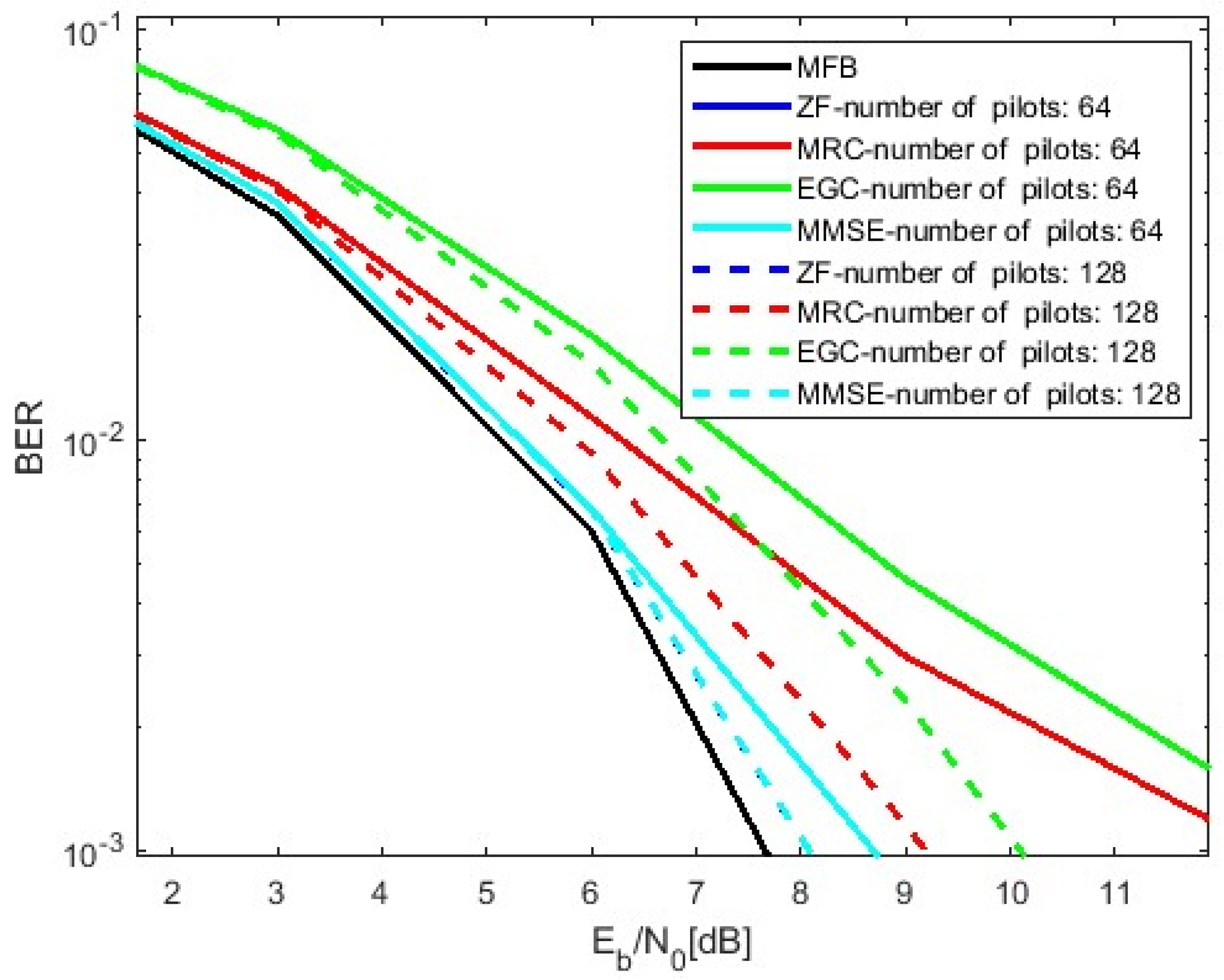
• Increasing the number of pilots helps achieve better accuracy but comes with a trade-off: higher complexity and reduced spectral efficiency due to the extra pilot overhead.
• Iterative estimation improves the accuracy over multiple iterations, but it requires more processing power, making it computationally expensive.
• Channel selection focuses only on the most useful LIS antennas, reducing the complexity while still maintaining good accuracy and efficiency.
• Hadamard orthogonal pilot sequences minimize interference between pilots, improving both the accuracy and spectral efficiency while keeping the complexity low.

Table 2. Comparison of channel estimation improvement methods across key performance metrics.

Improvement Method	Complexity	Energy Efficiency	Interference Reduction	Estimation Accuracy	Spectral Efficiency
Pilot power optimization	Moderate	Improves with careful scaling	Minimal impact on interference	Improves SNR for pilots	Moderate (trade-off with data throughput)
Increasing number of pilots	High (due to increased overhead)	Decreases due to higher overhead	No direct impact	Improves with increased reference data	Decreases due to increased pilot overhead
Iterative estimation	High (due to iterations)	Improves with better estimation accuracy	Moderate (depends on feedback accuracy)	Significantly improves after iterations	Improves by refining estimates
Channel selection	Low (reduces processing load)	Improves by focusing resources on high-impact antennas	High (reduces inter-user interference)	Moderate (focuses on relevant antennas)	Improves by reducing unnecessary overhead
Hadamard orthogonal sequences	Low (efficient generation)	Moderate (no direct impact on energy efficiency)	High (minimizes pilot contamination)	High (ensures minimal cross-correlation)	High (reduces pilot interference)

Table 2. Comparison of channel estimation improvement methods across key performance metrics.

Improvement Method	Complexity	Energy Efficiency	Interference Reduction	Estimation Accuracy	Spectral Efficiency
Pilot power optimization	Moderate	Improves with careful scaling	Minimal impact on interference	Improves SNR for pilots	Moderate (trade-off with data throughput)
Increasing number of pilots	High (due to increased overhead)	Decreases due to higher overhead	No direct impact	Improves with increased reference data	Decreases due to increased pilot overhead
Iterative estimation	High (due to iterations)	Improves with better estimation accuracy	Moderate (depends on feedback accuracy)	Significantly improves after iterations	Improves by refining estimates
Channel selection	Low (reduces processing load)	Improves by focusing resources on high-impact antennas	High (reduces inter-user interference)	Moderate (focuses on relevant antennas)	Improves by reducing unnecessary overhead
Hadamard orthogonal sequences	Low (efficient generation)	Moderate (no direct impact on energy efficiency)	High (minimizes pilot contamination)	High (ensures minimal cross-correlation)	High (reduces pilot interference)

Figure 2 investigates the performance results without LDPC codes in LIS systems with 4 transmitting antennas and 400 receiver antennas (4 × 400). Hadamard pilots offer better BER performance than random pilots due to their orthogonality, which enhances channel estimation accuracy. The improvement is most significant for MMSE and ZF, especially at a high SNR ($E_b/N_0>6$ dB). MMSE and MRC with Hadamard pilots provide better channel estimation accuracy, reducing interference and improving spectral efficiency. ZF with Hadamard pilots performs better than with random pilots but still has lower accuracy than MMSE. More complex methods like MMSE require higher computational power and energy but achieve a lower BER and better spectral efficiency. The MFB curve provides a benchmark for evaluating the performance of a channel, which is modeled as the sum of delayed and independent Rayleigh-fading rays.

Figure 2. BER results for comparing Hadamard pilot vs. random pilot 4 × 400 LIS system.

Figure 3 highlights the significant impact of pilot power rates on BER performance in LIS systems with 4 transmitting antennas and 400 receiver antennas (4 × 400) without LDPC codes under channel estimation scenarios. The simulation results demonstrate that BER performance improves with increasing power rates (Rate = 1 (0 dB), 2 (−3 dB), and 4 (−6 dB)), underscoring the role of accurate channel estimation. Higher pilot power (e.g., power rate = 4) achieves near-optimal performance, particularly in low $E_b/N_0$ conditions, while MMSE performs best overall. ZF’s sensitivity to noise leads to degraded performance at a lower $E_b/N_0$, whereas MRC and EGC show consistent reliability. These findings emphasize the importance of pilot power optimization in mitigating channel estimation errors, balancing improved BER performance with the trade-off in spectral efficiency. Moreover, this chart shows that higher power rates (−6 dB) improve energy efficiency by reducing the BER at a lower $E_b/N_0$. ZF/MMSE has higher complexity but better interference handling, while MRC and EGC are simpler but more sensitive to interference.

Figure 3. BER results for power rate [1, 2, and 4] effect on channel estimation.

Figure 4 compares the performance results of the BER as a function of $E_b/N_0$ for various channel estimation techniques under different pilot configurations. The simulation results demonstrate that increasing the number of pilot symbols from 64 to 128 significantly improves the BER performance across all channel estimation techniques. In this simulation, 64 pilots were used for 128 antennas by employing antenna clustering, compressed sensing, and adaptive pilot allocation (Table 3). Instead of assigning one pilot per antenna, 128 antennas were grouped into 64 clusters, with each cluster sharing a pilot, reducing overhead while maintaining estimation accuracy. The results show at a high $E_b/N_0$, methods like MMSE and MRC approach the MFB, achieving a lower BER. In low-$E_b/N_0$ conditions, the use of 64 pilots provides a notable advantage, particularly for MMSE, due to enhanced channel estimation accuracy. These findings highlight the trade-off between pilot overhead and improved performance. Overall, increasing the number of pilots reduces the BER but increases the energy consumption and complexity. MMSE and ZF handle interference better, while MRC and EGC are simpler but more sensitive to noise.

Figure 4. BER results on the impact of changing the number of pilots on the 4 × 400 LIS system.

Table 3. Comparison of the number of 64 and 128 pilots.

Number of Pilots	Channel Estimation Accuracy	Spectral Efficiency	Pilot Overhead	Recommendation
64	Moderate	Medium	Medium	Best trade-off between accuracy and overhead
128	High	Low	High	Suitable for systems with limited antennas

Figure 5 demonstrates the impact of iterative channel estimation on BER performance across different receiver configurations (ZF, MRC, EGC, and MMSE). As the number of iterations increases from iteration 1 to iteration 3, the BER improves significantly for all methods. Among the configurations, MMSE and ZF show the most substantial improvements, approaching the theoretical MFB performance with additional iterations. MRC and EGC also benefit from iterations but exhibit comparatively moderate gains. These results highlight that iterative techniques effectively enhance channel estimation accuracy, albeit at the cost of increased computational complexity. Conducting three iterations typically achieves a balance between accuracy and computational complexity, providing substantial improvements without overburdening the system. This graph shows how different detection and combining methods affect the BER. More iteration improves the accuracy but increases the complexity and energy consumption.

Figure 5. BER results on the effects of iterative channel estimation on BER performance.

Figure 6 compares the BER performance versus $E_b/N_{0 }$ for various receivers (ZF, MRC, EGC, and MMSE) with Full LIS (400 antennas) and Selected LIS configurations (100 and 20 antennas). A Full LIS achieves the best performance due to maximum spatial diversity, particularly with MMSE and ZF receivers at a higher $E_b/N_{0 }$ due to their robustness to interference and noise. Reducing antennas to 100 or 20 degrades the BER, especially for ZF and EGC, due to reduced diversity and weaker channel estimation. MMSE and MRC are more robust under these constraints. A Full LIS offers optimal performance and improves the accuracy but increases the complexity and energy consumption: 100 antennas balance performance and complexity, while 20 antennas suit low-cost systems with acceptable performance trade-offs.

Figure 6. BER results on comparison between “Full-LIS” and “Selected LIS” for different receivers.

Figure 7 shows the impact of LDPC coding on the BER performance for various channel estimation techniques. Solid lines (with LDPC) exhibit significantly lower BERs than dashed lines (without LDPC), highlighting LDPC’s error-correction benefits. LDPC improves the performances of ZF, MRC, EGC, and MMSE, bringing them closer to the ideal MFB benchmark. Among these, MMSE with LDPC achieve the best BERs, followed by MRC and EGC. Overall, LDPC coding greatly enhances the reliability across different $E_b/N_{0 }$ values.

Figure 7. BER results on the effect of LDPC codes on channel estimates on the 4 × 32 LIS configuration with 2 users.

Table 4 highlights the key design principles and performance characteristics of ZF, MMSE, MRC, and EGC receiver architectures, illustrating their relative strengths and weaknesses across various metrics base on the BER performance, complexity, energy efficiency, interference reduction, spectral efficiency, and accuracy.

Table 4. Comparison of receiver architectures based on design and performance metrics.

Receiver Architecture	BER Performance	Complexity	Energy Efficiency	Interference	Spectral Efficiency	Accuracy
ZF	High	High	Moderate	Low	High	Moderate
MMSE	High	Moderate	Moderate	Good	Moderate	High
MRC	Moderate	Moderate	High	Moderate	High	High
EGC	Moderate	Low	High	Low	Moderate	Moderate

1.

BER Performance (Figure 2 and Figure 3)

MMSE and MRC have better performances because they optimize the signal strength and reduce noise, and ZF has a moderate BER because it removes interference but amplifies noise. EGC has the worst BER because it does not consider signal strength differences.

2.

Computational Complexity (Figure 6)

MMSE and ZF require matrix operations, making them more computationally expensive. MRC and EGC are simpler because they do not perform matrix inversions.

3.

Energy Efficiency (Figure 4)

MMSE and ZF use more energy due to complex calculations, while MRC and EGC are more energy efficient, since they use simpler operations.

4.

Interference Reduction (Figure 5)

ZF removes interference completely but may increase noise. MMSE balances noise and interference, making it the most effective. MRC reduces interference but is not as effective as MMSE. EGC does not actively reduce interference.

5.

Spectral Efficiency (Figure 7)

MMSE and MRC use the available bandwidth more effectively. ZF performs well but can suffer under high noise. EGC is the least efficient. Therefore, MMSE and MRC achieve better spectral efficiency, while EGC is the least efficient.

6.

Accuracy (Figure 2 and Figure 3)

MMSE and MRC estimate the channel more accurately. ZF is accurate but affected by noise. EGC has poor channel estimation. Overall MMSE and MRC give the most accurate results, while EGC is the least accurate.

5. Conclusions

This study demonstrated that pilot-based channel estimation, combined with techniques such as optimized pilot design, data-aided refinement, selective LIS antenna configurations, and the utilization of LDPC codes, significantly enhances the performance of LIS systems. These methods achieved notable improvements, including a reduction in the BER. MATLAB-based simulations validated the effectiveness of these techniques, confirming their suitability for next-generation communication systems.

6. Future Research

Future research will focus on the practical implementation of these methods in real-world LIS systems and on optimizing their performance under various and specific channel conditions. Future work may also focus on extending the proposed methods to time-varying channels and incorporating advanced estimation techniques, such as MMSE and deep learning-based approaches, for further performance gains.