Featured Application
This paper proposes a novel approach to examine the rationality of the current exit design (width) on typical high-speed railway platforms in China to improve passenger safety. The empirical analysis based on real data offers valuable insights and practical suggestions to redesign and improve the features of high-speed railway platforms.
Abstract
There are several accidents in China’s high-speed railways where passengers fall off the platform every year. In response to the risks of falling off high-speed railway platforms associated with passenger overcrowding, this study explores the platform exit width range in determining how to reduce the risk. In order to quantify the risk, we first define the risk probability to measure the likelihood of passengers falling off the platform. Then, we propose an integrated model that combines the passenger flow assignment with a dynamic calculation of passenger flow. This methodology addresses the passenger flow assignment through modeling passenger choices based on path utilities and determines an interpretable exit width range that ensures safe, non-congested evacuation within the designated timeframe. Empirical analysis reveals that the ranges of exit width and achieving different aims of risk probabilities are negatively correlated. The current exit width of 6 m on high-speed railway platforms is insufficient. Our results recommend expanding this width to between 6.43 and 7.01 m to facilitate more efficient passenger exits under normal operating conditions (risk probability of 10%). This adjustment potentially reduces the required investment in surveillance equipment by 77.7% and halves the monetary costs, thereby encouraging railway managers to implement these recommendations. Due to being restricted by a fixed platform width of 10 m, the limitation of optimizing the exit width aims to allow about 2770 passengers at most to leave the platform within the specified travel time.
1. Introduction
1.1. Background
High-speed railways provide swift and comfortable travel experiences that are highly valued by passengers. Nonetheless, when passengers arrive at their destination and disembark, it is the most stressful time for station managers. Based on the feedback from these station managers with years of operational experience, we believe that the limited platforms and narrow exits necessitate that passengers efficiently navigate the station within a specified timeframe, resulting in a buildup of congestion on the platform. This congestion heightens the risk of passengers falling from the platform; the denser the crowd, the greater the likelihood of such incidents [,]. Therefore, the aim of our research question is to address the issue by optimizing the current exit width to reduce congestion and the risk of falling off the platform. The optimized exit width range can ensure that the disembarking passengers complete their exit process within the designated timeframe, which means safe, non-congested evacuation.
As illustrated in Figure 1, which depicts a typical high-speed rail platform layout, the exit process unfolds as follows: Upon the train’s arrival, passengers get off the train and proceed from points A1, A2, B1, B2, C1, and C2 in the direction of the red arrows, converging at the designated purple points A, B, and C. Subsequently, passengers move from points A, B, and C along the red arrows to eventually go through exits D or E, thus completing their disembarkation. In this process, the unidirectional nature of the exits requires passengers from points A and C to first reach point B before they can continue towards exits D or E.
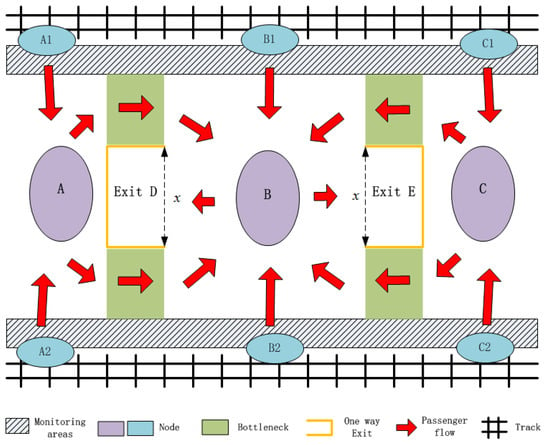
Figure 1.
A diagram of the passenger exit process (drawn based on actual data of the platform configuration by Microsoft Visio 2010).
Due to the monitoring areas in Figure 1 being adjacent to the tracks, the likelihood of passengers falling onto the tracks is significantly increased upon entry. Thus, the monitored areas are the hazardous zones. Generally, out of instinct to avoid danger, passengers are aware that the monitored zones are hazardous and tend to avoid them deliberately. However, during peak travel times, the narrow exits can lead to congestion at point B, potentially forcing passengers into the monitored areas and thus increasing the risk of falls. Consequently, surveillance cameras are essential in these areas to ascertain when passengers cross into them. Relying solely on video surveillance as a preventative measure against falls is very costly, and reducing this cost is a primary concern for station managers.
In addition, it can be found that simply widening the exits will shrink the bottleneck areas. These narrow bottlenecks can also cause congestion that forces passengers to fall down onto the tracks from bottleneck areas. Therefore, blindly expanding exits is not feasible (infinitely increasing the exit width is not allowed). On the basis of the above introductions, we believe that a feasible key point to improving passenger safety on the platforms in a real application is to redesign the defective exit configurations, especially the width. In other words, we should determine a fully demonstrated width for exits on a typical platform.
The process of passengers exiting the platform can be viewed as a problem of passenger flow assignment on paths based on individual microscopic choices, while the goal of completing the non-emergency evacuation within the designated timeframe to alleviate congestion requires estimating the travel time under combinations of paths and periods. Thus, determining how to identify the characteristics of passenger flow assignment on the platforms and construct a mathematical function with density, speed, and flow to accurately calculate the total travel time are the major challenges in this paper.
This paper proceeds as follows: Section 1 lists the research background and research aim, highlighting our contributions through a literature comparison. Section 2 constructs the mathematical model formulation. Section 3 provides the algorithms to solve the model. Section 4 shows the numerical experiments. Section 5 concludes this paper.
1.2. Literature Review
For a railway platform, exit width, exit location, and bottleneck size are considered the three major features affecting the total travel time of passengers (pedestrians) [,] and indirectly determining their safety. On the other hand, pedestrian dynamics is a major paradigm to address issues such as path choice and passenger flow assignment. Hence, we mainly conduct a literature review based on these two aspects.
1.2.1. Exit Width, Exit Location, and Bottleneck
Discussions on exit width and exit location regularly appear in the form of its influence on evacuation time in emergency evacuation issues. The authors of [] emphasized that four influencing factors, that is, total evacuation distance, evacuation speed, width of exits, and personnel density, could heavily impact the total spending time. The authors of [] considered factors including the spatial distance, occupant density, and exit width to solve the problem of multiple exit choices for pedestrians. Some scholars have provided a similar conclusion in that modifying individual speeds and the average minimum width of the stairs could potentially reduce the overall evacuation time by 50% [].
Furthermore, some works have investigated how to obtain the optimal exit width under a given constraint of evacuation time. The authors of [] presented a method of computing the optimal width of exits to improve the safety of pedestrian evacuation and the utilization efficiency of emergency exits in pedestrian walking facilities. The authors of [] paid attention to the phenomenon called the faster-is-slower (FIS) effect though implementing experiments. They found that the FIS effect could be effectively prevented when the width of an exit is twice the size of the particles. The authors of [] proposed a two-dimensional Cellular Automata (CA) model to simulate the exit evacuation dynamics and state that the total flux of an exit is an increasing nonlinear function of exit width, which can be used to calculate the optimal exit width. The authors of [] considered the issue of exit width in scenarios with obstacles. The sensitivity analysis of various variables indicates that the distance between the obstacle and the exit, the obstacle size, and the exit width are three key factors. The evacuation effect is optimal when they equal to 1.25:1:1 under the 30-degree corner exit. The authors of [] discussed different exit widths and found that the evacuation time decreases with an increase in exit width, and it tends to be stable when all exits have a width of 2.5 m. The authors of [] analyzed four size-related parameters of convex exit, namely, the width of the bottleneck at passage, the passage size, the passage length, and the exit width, to determine the optimum design of the convex exit.
Additionally, the exit location can also affect the total evacuation (travel) time. The authors of [] aimed to present new software that provides all possible combinations of optimization for the exit door location. The authors of [] believed that the number of evacuees differs for different functional spaces, resulting in uneven distributions of evacuees in the building plan. Thus, they proposed a design optimization method for exit locations based on BIM and ontology to provide exit location redesign plans to make the evacuation time shorter. The authors of [] established an Artificial Bee Colony (ABC) optimization algorithm based on the stochastic method to find the optimal locations of the exit doors. This method overcomes the main limitation of the tedious process of handling multi-room problems and more complex room arrangements. The authors of [] emphasized the relationship between the optimal value of f and building size to improve the performance-based design of building exits.
The area near the exit often becomes a bottleneck that is crucial for emergency evacuation. Moreover, the design of the exit will directly affect the bottleneck size []. The authors of [] carried out experimental research to analyze the influence of emergency signage and crowded bottleneck areas. The authors of [] introduced an emergency evacuation model for limited spaces to examine the evacuation efficiency, density of the bottleneck area, escape route, and other important factors based on different exit widths.
1.2.2. Pedestrian Dynamics and Passenger Decision Making
The ultimate goal of analyzing the exit width, exit location, and bottleneck area is to identify the behaviors of passengers and simulate their decision-making process, which dominantly determine the path selection, passenger flow on paths or links, and total travel time in platform navigation. Pedestrian dynamics is the main paradigm used to investigate the aforementioned issues, and it can be roughly divided into a macroscopic model and microscopic model [].
The macroscopic model views pedestrians as a whole, moving in a manner similar to liquid. Thus, concepts such as density, speed, and flow are introduced into the simulation and prediction of the status of pedestrians’ movements [,,,]. The relationship between speed, density, and flow determines the optimal dimensions of facilities []. Scholars empirically measure and estimate this relationship through experiments under different circumstances. Unfortunately, the significant differences between various research results [] imply that there are no fixed and precise functional relations among them, requiring the fitted model to be correct based on observed data. Additionally, the macroscopic model ignores individual choice behaviors and has poor performance in application scenarios for small-scale pedestrians.
Conversely, microscopic models focus on each pedestrian’s choice behavior to describe their movements on links, paths, and key locations. This type of model mainly includes Cellular Automata, the social force model, the game-theoretic model, and the mathematical optimization model. The Cellular Automata (CA) model was used to divide the layout of a place into cells and to represent each cell as a pedestrian []. Thus, a pedestrian makes decisions relying on the adjacent cells in a predefined set of rules. The authors of [] further developed a new model that allows several pedestrians in one cell or a single pedestrian to occupy multiple cells for more detailed information.
The social force (SF) model has received the most attention and was adopted in the description of pedestrian reactions to the surroundings in recent years. The authors of [] introduced the SF model to stimulate pedestrian movement on stairs. To conduct a more in-depth study on exit selection, the authors of [] categorized pedestrians into different groups with the SF model, which can be summarized as the modified social force (MSF) model. The authors of [] introduced the utility function to the SF model and formulated the results of exit choices by calculating the utility value.
Game theory originates from economics and has also been applied to pedestrian dynamics. When considering game theory, it often means treating pedestrians as smart individuals with rational expectations so that their choices can be more accurately predicted. An early study [] adopted game theory to predict the walking behavior of pedestrians. Subsequently, several works continued to extend game theory to investigate pedestrian behaviors based on equilibrium principles [].
Mathematical programming methods are also widely used for modeling individual behaviors. In order to evacuate people through exits with the goal of the shortest time, the authors of [] developed a fast dynamic programming evacuation approach to assign the optimal number of evacuees to each possible path. The authors of [] focused on the problem of facilitating the final exit assignment and proposed an integer programming model to minimize the average evacuation time in a complex building when an emergency event occurs. The authors of [] established a simulation-optimization model, which combines the Genetic Algorithm (GA) with the microscopic traveler assignment model, aiming to help evacuees find the optimal exit gates and start times in a large-scale evacuation problem with multiple exits.
Pedestrian dynamics provides an important perspective for modeling passenger decision making. The ability to collect comprehensive information and decision-making mechanisms are two core factors that diversely shape passenger choice behaviors and determine the adopting theory and model under different scenarios []. There are broad theoretical paradigms for understanding and predicting passenger choice. One is called “utility theory” [] and the other is known as “heuristics” []. It is generally believed that passengers can perceive useful information in their choice processes, while enclosed spaces, such as subway stations, buildings, and interior spaces, which degrade passengers’ visibility, make them only able to access limited information []. In these circumstances, passengers can only perceive information selectively and purposely to make self-perceived optimal choices [].
1.3. Motivations and Contributions
(1) Methodology. Passenger gatherings, responding to and deciding upon information, varies according to different circumstances. Studies should be conducted based on the characteristics of scenarios to model passenger decision-making processes [,]. As analyzed earlier, microscopic models adequately consider the individual choice behaviors based on the integration of environmental information into mental representations, leading to interpretable results. However, in a large-scale problem with numerous objects, accurately characterizing the behaviors of each individual and formulating their interplay are almost impossible, bringing exponential computational complexities [,,,,,,,,,,,]. On the other hand, adopting a macroscopic model [,,,,,,] is beneficial for solving large-scale problems, while it heavily relies on repeated simulation experiments based on giving appropriate parameters. In order to meet the requirements of the application scenario and eliminate the shortcomings of the models mentioned above, we address the issue of passenger flow assignment by the micro-individual passenger choice model and calculate total passenger flow based on the macro-traffic flow model (Table 1).

Table 1.
Comparison of modeling techniques (summary based on the above literature).
(2) Problem Circumstance. The above literature showed that the evacuation problem generally implies two assumptions: One is that the evacuation occurs in an enclosed place with complex internal structures, such as subway stations, buildings, etc., that obstruct pedestrians’ vision. The other is that evacuation is an emergency scenario and pedestrians are in a hurry and panic, which causes pedestrians to leave or escape at an abnormal speed [,,,,,,]. These situations force pedestrians to subconsciously make decisions and choose the nearest exit or the least crowded route within their vision. However, a typical high-speed railway platform is open without any obstruction, expanding passengers’ visibility to collect information comprehensively, resulting in accurate and reasonable choices, such as selecting the shortest paths or the least crowded exits, and achieving the maximum utilities.
Therefore, the contributions of this paper are threefold:
- In order to quantify the risk of passengers falling off the platform, we propose a new concept of risk probability. We apply a normal distribution to fit the probability distribution of the number of disembarking passengers. The risk probability is defined using the gap of cumulative probability corresponding to the number of passengers completing the exit under the maximum allowable travel time.
- We propose a novel integrated approach that combines passenger flow assignment based on choices of individual passenger path utility with a dynamic calculation of passenger flow. This methodology determines a fully demonstrated range of exit widths that reduce the risk probability to 10%.
- We prove that the optimal solution of the passenger flow assignment model with minimum generalized cost is equivalent to the number of passengers based on path utility choices, thereby simplifying this problem.
- We identify the bottleneck areas on a typical platform of a Chinese high-speed railway. The bottlenecks have opposite effects on the exit width on different travel paths (links), which suggests that the exit cannot be expanded infinitely to reduce congestion.
2. Model Formulation
2.1. Assumptions and Notations
- Passengers have ample time to make decisions that maximize their own utilities [].
- Due to the limited platform area, passengers can accurately assess the number of people on each path by observation (experience and common sense).
- Platform exits are unidirectional [].
2.2. Platform Exit Width Range
2.2.1. Passenger Flow Assignment Based on Path Utility
In Figure 1, passengers disembarking within will gather at node A, that is, moving from nodes A1 and A2 to node A. Similarly, passengers getting off within will arrive at node B. Due to the unidirectional platform exits, passengers at node A as well as node C will first move to node B, and then from node B to exit D or exit E. Passengers disembarking from nodes B1 and B2 can choose exits D or E directly.
The above can be illustrated in Figure 2. Considering the sequential order of passengers from different initial nodes arriving at node B, the passenger choice process is depicted in Figure 3, which simplifies the process into two periods. In period 1 (), passengers from nodes A1(C1) and A2(C2) go through the bottleneck to node A and then to node B. At the same time, passengers from nodes B1 and B2 move directly to node B and then proceed to exit D or exit E. In period 2 (), passengers who have already departed from nodes A(C) and are arriving at node B then travel to exit D or E.
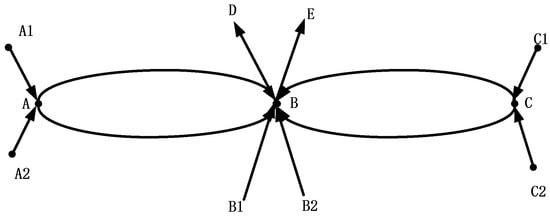
Figure 2.
A diagram of passenger paths on the platform (abbreviated according to Figure 1 by Microsoft Visio).
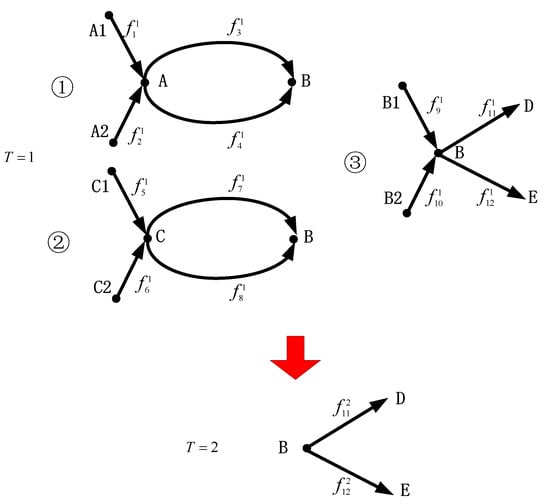
Figure 3.
The path selection of passengers (considering the travel order of passengers on the platform based on Figure 2 by Microsoft Visio).
Figure 3 describes a time–space path network on a high-speed railway platform. represents a set of nodes and represents a set of paths. Passengers make choices based on path utility, which is negatively correlated with travel time. The utility of path linking two adjacent nodes is with a random error that follows the Gamble probability distribution.
According to the utility theory [] and MNL model [], the probability of passengers choosing path between node pair is computed by Equation (2).
where utility can be seen as the opposite of generalized cost. We take the minimized generalized cost of all passengers as the objective function to propose a passenger flow assignment model on a high-speed railway platform.
where is the penalty entropy, which represents the congestion caused by an increase in passenger flow. This congestion exacerbates the generalized cost in the entire network. At the same time, the penalty entropy ensures that all passenger flows are not concentrated on the path with the lowest cost to achieve equilibrium. Thus, all paths being selected by passengers guarantees consistency with the actual circumstances. is the maximum allowable passenger flow, resulting from the limited space on the platform. Constraint (4) requires that the total passenger flow of a node pair must be equal to the sum of passenger flows on all related paths. Inequality (5) regulates the threshold of passenger flow on a link.
Theorem 1.
The optimal solution of the passenger flow assignment model proposed in this study is equivalent to the passenger selection based on path utility.
Proof of Theorem 1.
Model (3) is a convex optimization problem with linear constraints, transforming constraints (4) and (5) into Lagrange multipliers and incorporating them into model (3) to construct model (6) [].
For any ,
Let ; then,
Because , , and , Equation (8) is just the KKT (Karush–Kuhn–Tucker) condition of model (3). Meanwhile, it is notable that the probability of passenger selection can be expressed as
□
It is obvious that Formulas (2) and (9) are equivalent. Therefore, Theorem 1 has been proven. By using Theorem 1, we can directly solve the passenger flow assignment problem through calculating the path utilities to simplify solving the original problem.
Constraints (11)–(17) ensure that the proposed model conforms to the application scenario in this paper, where represents the number of passengers disembarking from the train on track , which follows a normal distribution, . The gap between the cumulative probability of passenger flow that satisfies a normal distribution and 100% is defined as the risk probability. Thus, means the number of passengers corresponding to the cumulative probability of 90%, and the risk probability is 10%. The risk probability quantifies the risk of passengers falling off the platform from a probabilistic perspective.
For period 2 (), only passengers at node B proceed to exit D or E. Constraint (17) indicates that the passengers departing from node B in the second period are equal to the arrived passengers from nodes A and C in the first period.
2.2.2. Exit Width Range
To improve passenger safety, it is necessary to scientifically and reasonably determine the width of the exits. Specific parameters on a platform are marked in Figure 4. As shown, a high-speed rail platform typically contains two exits with the same length and width. The exits are symmetrically designed with platform width and platform length . refers to the width of the bottleneck. When the exit is excessively large, passengers can quickly pass through them from node B to D or E. However, the shrinkage of the bottleneck is likely to cause passengers to be unable to reach node B from nodes A or C within the stipulated time, resulting in congestion in the bottleneck. Conversely, a small exit may ensure passengers successfully pass though the bottleneck and reach node B within the stipulated time while causing congestion on node B. The above two situations all increase the risk of falling off the platform. Next, we provide the following discussions about these two scenarios, respectively.
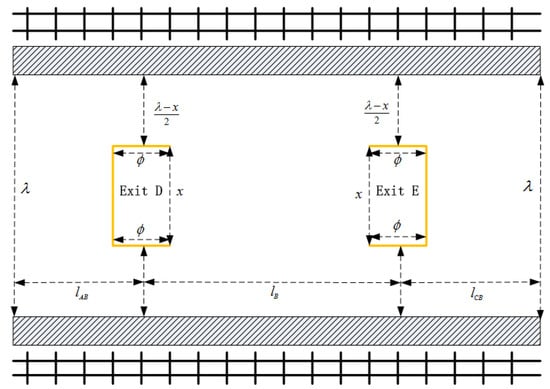
Figure 4.
Parameters for typical platform (platform plan with main parameter based on actual data by Microsoft Visio).
(1) When , it corresponds to passengers traveling from node A or C to node B, passing through the bottleneck area. According to classic flow-density theory [], the relationship between speed and density is described by Equation (18).
where is the maximum passenger flow density and is the occupied area by each passenger.
In Figure 5, initially, due to fewer passengers entering the bottleneck, the area occupied by each passenger is extensive, resulting in a lower passenger flow density. As more passengers go through the bottleneck, the occupied area gradually drops, which means the passenger flow density increases. It remains stable once reaching the maximum passenger flow density (the minimum area occupied). As the number of passengers decreases, the occupied area increases, approaching the end. Therefore, the occupied area is a function of decision variable travel time .
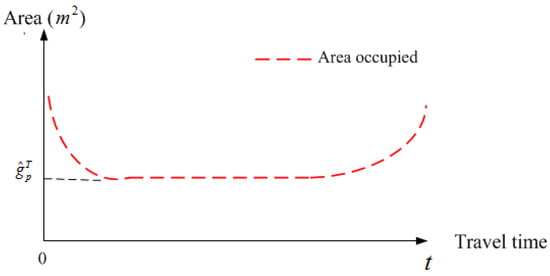
Figure 5.
Curve of change in occupied area (diagram of changes in passenger-occupied area over time by Microsoft Visio).
Every link is constrained by the maximum allowable travel time, thus obtaining the passenger flow passing through link under the maximum allowable travel time .
The range of exit widths must ensure that meets Equation (21).
Because , , and the passenger flow decreases monotonically as the exit width increases. Thus, the boundary value of the exit width is .
The exit width range is .
(2) When , this describes the process of passengers traveling from node B to exits D or E. The width of the exit directly determines the time taken by passengers to pass through the exits. The density of passenger flow is given as below.
The total volume of passenger flow can be calculated as
The first and second derivatives of are found as follows:
Obviously, because of and , there exists that satisfies . Note that , so it can be known that as the exit expands, the passenger flow first increases and then decreases with as the dividing point. Therefore, when the passenger flow meets the minimum value limited by constraints, the corresponding boundary value of minimum exit width is .
The exit width range is generated as follows:
Finally, the exit width range that conforms to all links is found, where means the intersection for all elements :
3. Solution Process
Step 1: Estimate the values of parameters in the path utility function. Thus, obtain the passenger flow on each path. Complete passenger flow assignment based on Formulas (9) and (10) to output the passenger flow on each link . Due to the fact that the travel path of passengers on the platform is axisymmetric with the exit as the reference, the values of parameters in the path utility function linking two adjacent nodes are the same. This further simplifies the passenger assignment problem.
Step 2: Consider the extreme case where the total travel time equals the maximum allowable time. Then, randomly output the set of maximum allowable travel times for each link in period . satisfies the below constraints.
Step 3: Solve for the boundary values of exit width for passengers traveling through the bottleneck.
Begin the loop
Let , begin the loop.
For in list (3,4,7,8):
(1) Sample the average occupied area at each time point .
(2) Estimate function using linear function approximation based on sample data at each time point.
(3) Solve the boundary value of exit width based on (19)–(22).
(4) Obtain the exit width range .
End the loop.
Step 4: Solve for the boundary values of exit width for passengers passing through the exit.
Begin the loop.
For in list (1,2):
For in list (11,12):
(1) Sampling the average occupied area at each time point and estimate function using linear functions approximation based on sample data at each time point by Equation (34).
(2) Solve boundary value of exit width based on (23)–(27).
(3) Obtain the exit width range by Formula (28).
End the loop.
Step 5: Determine the exit width range for all situations by Equation (29).
4. Case Studies Based on Real Data
4.1. Numerical Results
We have collected the data of Nanjing South railway station in China’s high-speed railway, from 1 March 2024 to 31 May 2024, as an example. These data are used to estimate parameters in the following texts. According to the actual situation, a typical platform has a length of 450 m and two exits. The length parameters of each segment are as follows: m, m, and m. Due to the complexity of the investment plan and approval involved in the renovation of the platform, the width of the exit will remain unchanged at 10 m in the short term. Thus, the entire platform width is m and the length of the exit is m. The current exit width is 6 m.
Passenger flow sample data from 1 March 2024 to 31 May 2024 show that the number of disembarking passengers for trains stopping at track 1 follows a normal distribution , and for track 2, it also follows a normal distribution , as shown in Table 2. The risk probability is set as 10%. All these are shown in Table 2 and Table 3.

Table 2.
Mean and standard deviation of the number of passengers getting off the trains (calculated from sample data).

Table 3.
Values of main parameters (actual data).
According to Figure 1, since the width, length, and positions of the two exits on the platform are symmetrically distributed, the path utility obtained by passengers facing multiple paths between the same adjacent node pair is equal. Therefore, the assigned passenger flow for all paths and links is shown in Table 4 and Table 5.

Table 4.
Passenger flow of node pairs (intermediate results under passenger flow assignment).

Table 5.
Passenger flow of links with different periods (intermediate results under passenger flow assignment).
The minimum interval time for adjacent trains to stop on the same track is 5 min (300 s, ; high-speed railway operation regulations) []. This indicates that passengers getting off the previous high-speed train need to exit within 5 min; otherwise, the next high-speed train will arrive, bringing more passengers and exceeding the designed threshold capacity of the platform, significantly weakening passenger safety. The time it takes for passengers to reach the node from the train is related to the distance. According to the samples, the maximum allowable travel time on each link is estimated in Table 6.

Table 6.
Maximum allowable travel time for links with different periods (intermediate results).
Based on actual operational experience, a passenger’s speed is limited when carrying luggage, with a maximum flow speed of m/s. The minimum area occupied by a moving passenger is 0.5 square meters, i.e., . All instances of congestion resulting from passengers failing to pass though the links during the maximum allowable travel time are taken as the scenario objects to sample the average occupied area data. Then, the average of all samples is calculated to fit linear functions at sample point .
All linear functions are connected to approximate the curve of the change in average occupied area during the maximum allowable travel time ; the range of exit widths for each link is obtained and shown in Table 7.

Table 7.
The range of widths of the high-speed railway platform exit (final results).
Finally, the reasonable exit width is between 6.43 m and 7.01 m (Table 8).

Table 8.
The reasonable width of the high-speed railway platform exit (final results).
Table 8 shows that the reasonable exit width range is from 6.43 m to 7.01 m, which is 0.43 m larger than the actual exit width of 6 m. The width of 6 m meets the maximum allowable time constraint on relevant paths for passengers traveling from nodes A and C to node B through the bottleneck (6 < 7.01 < 7.67). However, considering the situation where passengers travel from node B to exits D and E (), 6 m still cannot ensure that passengers complete their exit within the maximum allowable travel time during period 1 (T = 1). This demonstrates that the current exit width of 6 m on Chinese high-speed railway platforms is insufficient and will inevitably lead to passenger congestion around the area near node B in extreme cases. As the number of congested passengers increases, the risk of falling from the platform at the location is exacerbated. According to our calculation results, the platform exit should be increased from 6 m to 6.43 m at least. This ensures that passengers can successfully leave the platform within the maximum allowable travel time in 90% of cases, and improves the safety of passengers on the platform.
4.2. Influence of Extremely Large Passenger Flow on Exit Width Range
Risks are always hidden in extreme scenarios. Consider the extreme situation of an oversized passenger flow (disembarking passengers) that may occur in the operation of a high-speed railway. The risk probability of passengers falling off the platform resulting from congestion is equivalent to the cumulative distribution probability of the number of passengers that can leave the platform within the maximum allowable travel time by optimizing the exit width. Section 4.1 discusses the width range of the platform exit corresponding to a 90% percentile cumulative probability of passenger flow. While this still means that there is still a 10% probability that cannot guarantee that passengers exit within the maximum allowable travel time, it results in accidents of falling off the platform when the exit width is between 6.43 m and 7.01 m.
In order to study the interplay between passenger flow and exit width range, we set risk probabilities of 5% and 2%, respectively, to explore the impact of an extremely oversized passenger flow on exit width. Keeping the other parameters constant, the results of the platform exit width range under risk probabilities of 5% and 2% are shown in Table 9. It can be concluded that as the disembarking passengers increase, the exit width range shrinks. Because the exit width is limited by the total platform width of 10 m, there is no solution for optimization of the exit width under a 2% risk probability. At this time, the platform should be widened instead of expanding the exit. Finally, we determine that the current optimal exit width can only reduce the risk probability by about 3.1% at most.

Table 9.
The width of a high-speed railway platform exit under different risk probabilities (detailed results under different risk coefficients).
We further expand the scenarios of passenger flow to compute the range of exit widths. As shown in Figure 6, under the current maximum allowable travel time of 300 s, the exit width range is roughly inversely proportional to the number of passengers getting off the trains. When the number of disembarking passengers exceeds 2720, changing the exit width is no longer effective and the platform width needs to be redesigned.
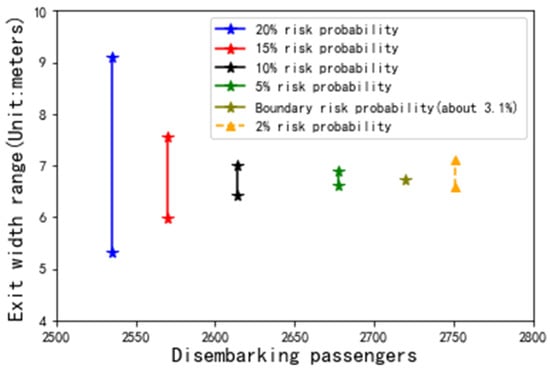
Figure 6.
The exit width with different risk probabilities (based on Table 9 using Python 3.7).
4.3. The Influence of Widening the Exit on Economic Cost
Figure 7a shows the current video surveillance footage, with blue boxes representing the monitoring area (dangerous area). As seen, as the camera devices are affected by factors such as camera resolution and lighting, a set of surveillance equipment can only effectively recognize within a distance of about 50 m, which requires installing a set of monitoring equipment at regular intervals and incurs high costs (red boxes in Figure 7b). According to the proposal in this paper to define part of the platform outside the bottleneck area as the monitoring area, monitoring and warning this area can effectively achieve the goal of preventing passengers from falling from the platform.

Figure 7.
The current monitored area and surveillance devices (red boxes) (actual operational pictures provided by the station): (a) A passengers entering dangerous areas; (b) surveillance camera.
By alleviating congestion, the frequency of passengers entering the monitored (danger) area is correspondingly reduced. The remaining risk area that passengers still enter is redefined as the new monitoring area. Therefore, we narrow the monitoring area and redefine part of the platform outside the bottleneck (Figure 8) as the danger area for video surveillance (monitoring area). Passengers entering this area will be monitored in real-time, and an alarm will be triggered if they remain there for more than 3 s (red boxes in Figure 7a and Figure 8). A comparison in Figure 8 and Figure 9 shows that the monitoring area is significantly reduced. The reduced monitoring area cuts down the number of required monitoring devices (cameras), thereby lowering the monetary costs.

Figure 8.
The narrowing of the monitored area of the platform in reality (actual operational pictures provided by the station): (a) The current monitored area; (b) The new monitored area after optimizing the exit width.
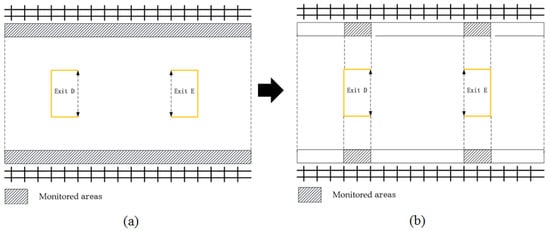
Figure 9.
A schematic of the narrowing of the monitored area on the platform (a diagram of the changes in the monitoring area, drawn by Microsoft Visio): (a) The size of current monitored (risk) area; (b) The size of new monitored (risk) area after optimizing the exit width.
Obviously, the new monitoring area is significantly smaller than the current one, resulting in less required surveillance equipment and lower economic costs. Table 9 shows that the new monitoring area is only 80 m2, cutting down the area by 91% compared to the current one. According to the information provided by the station managers, the cost of a set of monitoring equipment is approximately CNY 50,000. All monitoring equipment needs a server system support, which is valued at CNY 500,000. Correspondingly, the required surveillance equipment is compressed to 4 sets from 18 sets, leading to a reduction of 50% in terms of economic cost (Table 10).

Table 10.
A comparison of economic cost (calculated from actual data).
5. Discussion and Conclusions
This study explores a range of platform exit widths to determine how to reduce the risk of falling off the platform. In order to quantify this risk, we first use the gap of cumulative probability corresponding to the number of passengers completing the exit under the maximum allowable travel time to define the risk probability to measure the likelihood of passengers falling off the platform. Then, we propose an integrated model that combines passenger flow assignment with the dynamic calculation of passenger flow.
- (1)
- We found that the current exit width of 6 m is insufficient in ensuring congestion-free passenger flow, contributing to the annual platform fall incidents in China. We recommend increasing the platform exit width to a range of 6.43 to 7.01 m to reduce the risk probability to 10%. This adjustment also decreases the likelihood of passengers entering hazardous zones, allowing for a redefinition of monitoring areas outside the bottleneck.
- (2)
- Compared to the previous design, the newly defined monitored areas are reduced by 91%, resulting in a 77.7% decrease in the required surveillance equipment and a 50% reduction in monetary investment.
- (3)
- Due to the restriction of a typical platform width of 10 m, the limit of redesigning the exit width aims to allow 2770 passengers to leave the platform within the maximum specified travel time. At this time, the risk probability is still 3.1%.
- (4)
- Based on actual operational constraints, it is necessary to set a minimum risk tolerance (risk probability) for station managers. The ranges of exit widths required to achieve different aims of risk probabilities vary.
- (5)
- Our recommendations provide theoretical guidance for redesigning the platform (exit). However, due to the complexity of the investment plan and approval involved in the renovation of the platform, the width of the exit will remain unchanged in the short term. It is recommended to add managers in bottleneck areas to assist passengers in safely exiting the platform and prevent them from falling down onto the tracks during extreme passenger flows.
Fortunately, the suggested expansion of the exit width to 6.43 m has at least been implemented in several high-speed railway stations in China, receiving positive feedback from station managers.
However, the interplay between passenger flow density and speed under specific exit widths has not been further theorized. In addition, the exit location will also affect the results within the maximum allowable passage time. Future work will focus on incorporating exit width and location into a joint optimization model, making the outcomes more realistic and enhancing their practical applicability.
At the same time, in the next in-depth study, we will add considerations such as increasing the platform width (removing the limitation of 10 m for platforms) and introducing multi-directional exits, increase the depth of analysis, and improve the clarity, robustness, and practicality of the research results.
Author Contributions
Conceptualization, F.L.; methodology, F.L. and D.W.; software, F.L. and Z.W.; writing—original draft preparation, F.L. and Z.W. writing—review and editing, D.W. and Z.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China under Grant No. U21A201646.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts to interest.
Abbreviations
| Variables | Meanings |
| Node | |
| Track included in platform | |
| Link | |
| path | |
| ; otherwise, it equals 0 | |
| Period | |
| . | |
| Travel time on platform | |
| Parameters | Meanings |
| Maximum passenger flow speed | |
| Exit length | |
| Platform width | |
| Length of platform | |
| , estimated from samples | |
| Decision Variables | Meanings |
| Exit width range |
References
- Jiang, Z.; Fan, W.; Liu, W.; Zhu, B.; Gu, J. Reinforcement learning approach for coordinated passenger inflow control of urban rail transit in peak hours. Transp. Res. Part C Emerg. Technol. 2018, 88, 1–16. [Google Scholar] [CrossRef]
- Wang, H.; Li, L.; Pan, P.; Wang, Y.; Jin, Y. Early warning of burst passenger flow in public transportation system. Transp. Res. Part C Emerg. Technol. 2019, 105, 580–598. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, C.; Yap, J.; Li, H.; Zhang, S. Emergency evacuation simulation at starting connection of cross-sea bridge: Case study on Haicang Avenue Subway Station in Xiamen Rail transit line. J. Build. Eng. 2020, 29, 101163. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, G.; Yuan, G.; Wang, Y. Quantitative risk assessment methods of evacuation safety for collapse of large steel structure gymnasium caused by localized fire. Saf. Sci. 2016, 87, 234–242. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, M.; Wu, X.; AbouRizk, S. Simulation-based route planning for pedestrian evacuation in metro stations: A case study. Autom. Constr. 2016, 71, 430–442. [Google Scholar] [CrossRef]
- Bianca, C.; Mogno, C. A thermostatted kinetic theory model for event-driven pedestrian dynamics. Eur. Phys. J. Plus 2018, 133, 213–215. [Google Scholar] [CrossRef]
- Jiang, C.; Yuan, F.; Chow, W. Effect of varying two key parameters in simulating evacuation for subway stations in China. Saf. Sci. 2010, 48, 445–451. [Google Scholar] [CrossRef]
- Wang, S.; Yue, H.; Zhang, B.; Li, J. Setting the Width of Emergency Exit in Pedestrian Walking Facilities. In Proceedings of the 9th International Conference on Traffic and Transportation Studies (ICTTS 2014), Shaoxing, China, 1–2 August 2014; Volume 38, pp. 233–240. [Google Scholar]
- Zhang, Y.; Ma, J.; Si, Y.; Ran, T.; Wu, F.; Wang, G.; Lin, P. Required width of exit to avoid the faster-is-slower effect in highly competitive evacuation. Chin. Phys. B 2017, 8, 084504. [Google Scholar]
- Zhao, D.L.; Yang, L.Z.; Li, J. Exit dynamics of occupant evacuation in an emergency. Phys. A-Stat. Mech. Its Appl. 2006, 2, 501–551. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.C.; Li, J.; Feng, J.; Xu, S.; Liu, J.; Wang, Y. Performance optimization of the obstacle to corner bottleneck under emergency evacuation. J. Build. Eng. 2022, 45, 103658. [Google Scholar] [CrossRef]
- Cai, Z.; Zhou, R.; Cui, Y.; Wang, Y.; Jiang, J. Influencing factors for exit selection in subway station evacuation. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. 2022, 125, 104498. [Google Scholar] [CrossRef]
- Li, J.; Wan, J.; Li, J.; Wang, Z.; Wang, Y. Research on the influence of building convex exit on crowd evacuation and its design optimization. In Building Simulation; Tsinghua University Press: Beijing, China, 2022. [Google Scholar]
- Kallianiotis, A.; Kaliampakos, D. Optimization of exit location in underground spaces. Tunn. Undergr. Space Technol. 2016, 60, 96–110. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, L.; Sun, Z.; Fan, X.; Zhang, M. Design Optimization of Building Exit Locations Based on Building Information Model and Ontology. Sustainability 2023, 15, 12922. [Google Scholar] [CrossRef]
- Khamis, N.; Selamat, H.; Ismail, F.S.; Lutfy, O.F.; Haniff, M.F.; Nordin, I.N.A.M. Optimized exit door locations for a safer emergency evacuation using crowd evacuation model and artificial bee colony optimization. Chaos Solitons Fractals 2020, 131, 109505. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, L.; Li, J.; Zhu, Y.; Zhou, L. Relationship between performance-based design of building exits and state transition of pedestrian flow during occupant evacuation. J. Fire Prot. Eng. 2006, 4, 269–281. [Google Scholar]
- Sun, L.; Luo, W.; Yao, L.; Qiu, S.; Rong, J. A comparative study of funnel shape bottlenecks in subway stations. Transp. Res. Part A Policy Pract. 2017, 98, 14–27. [Google Scholar] [CrossRef]
- Kretz, T.; Grünebohm, A.; Schreckenberg, M. Experimental study of pedestrian flow through a bottleneck. J. Stat. Mech Theory Exp. 2006, P10014. [Google Scholar] [CrossRef]
- Li, Z.; Xu, W. Pedestrian evacuation within limited-space buildings based on different exit design scheme. Saf. Sci. 2020, 124, 104575. [Google Scholar] [CrossRef]
- Wei, X.; Wei, Z. Research progress on pedestrian dynamics. Chin. J. Ergon. 2008, 2, 68–71. [Google Scholar]
- Gao, Z.; Qu, Y.; Li, X.; Long, J.; Huang, H. Simulating the Dynamic Escape Process in Large Public Places. Oper. Res. 2014, 62, 1344–1357. [Google Scholar] [CrossRef]
- Zhou, X.; Mahmassani, H. A structural state space model for real-time traffic origin–destination demand estimation and prediction in a day-to-day learning framework. Transp. Res. Part B Methodol. 2007, 41, 823–840. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, Y.; Guo, J.; Cao, Z.; Jia, L. Multi-point short-term prediction of station passenger flow based on temporal multi-graph convolutional network. Phys. A Stat. Mech. Its Appl. 2022, 604, 127959. [Google Scholar] [CrossRef]
- Schadschneider, A.; Seyfried, A. Empirical results for pedestrian dynamics and their implications for cellular automata models. In Pedestrian Behavior; Emerald Group Publishing Limited: Leeds, UK, 2009; pp. 27–43. [Google Scholar] [CrossRef]
- Vermuyten, H.; Beliën, J.; Boeck, L.; Reniers, G.; Wauters, T. A review of optimisation models for pedestrian evacuation and design problems. Saf. Sci. 2016, 87, 167–178. [Google Scholar] [CrossRef]
- Blue, V.J.; Adler, J.L. Cellular automata microsimulation for modeling bi-directional pedestrian walkways. Transp. Res. Part B Methodol. 2001, 35, 293–312. [Google Scholar] [CrossRef]
- Guo, R.; Huang, H.; Wong, S. Route choice in pedestrian evacuation under conditions of good and zero visibility: Experimental and simulation results. Transp. Res. Part B Methodol. 2012, 46, 669–686. [Google Scholar] [CrossRef]
- Qu, Y.; Gao, Z.; Xiao, Y.; Li, X. Modeling the pedestrian’s movement and simulating evacuation dynamics on stairs. Saf. Sci. 2014, 70, 189–201. [Google Scholar] [CrossRef]
- Zhou, R.; Cui, Y.; Wang, Y.; Jiang, J. A modified social force model with different categories of pedestrians for subway station evacuation. Tunn. Undergr. Space Technol. 2021, 110, 103837. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, J.; Zhang, X.; Zhang, J.; Wang, Q.; Zhang, Q. Pedestrians’ behavior in emergency evacuation: Modeling and simulation. Chin. Phys. B 2016, 25, 118901. [Google Scholar]
- Hoogendoorn, S.; Bovy, P. Simulation of pedestrian flows by optimal control and differential games. Optim. Control Appl. Methods 2003, 24, 153–172. [Google Scholar] [CrossRef]
- Huang, L.; Wong, S.; Zhang, M.; Shu, C.; Lam, W.H. Revisiting Hughes dynamic continuum model for pedestrian flow and the development of an efficient solution algorithm. Transp. Res. Part B Methodol. 2009, 43, 127–141. [Google Scholar] [CrossRef]
- Chen, P.; Feng, F. A fast flow control algorithm for real-time emergency evacuation in large indoor areas. Fire Saf. J. 2009, 44, 732–740. [Google Scholar] [CrossRef]
- Kang, J.; Jeong, I.; Kwun, J. Optimal facility-final exit assignment algorithm for building complex evacuation. Comput. Ind. Eng. 2015, 85, 169–176. [Google Scholar] [CrossRef]
- Abdelghany, A.; Abdelghany, K.; Mahmassani, H.; Alhalabi, W. Modeling framework for optimal evacuation of large-scale crowded pedestrian facilities. Eur. J. Oper. Res. 2014, 3, 1105–1118. [Google Scholar] [CrossRef]
- Tong, Y.; Bode, N.W.F. The principles of pedestrian route choice. J. R. Soc. Interface 2022, 19, 20220061. [Google Scholar] [CrossRef]
- Fishburn, P.C. Utility theory. Manag. Sci. 1968, 14, 335–378. [Google Scholar] [CrossRef]
- Gigerenzer, G.; Gaissmaier, W. Heuristic decision making. Annu. Rev. Psychol. 2011, 62, 451–482. [Google Scholar] [CrossRef]
- MacEachren, A.M. Application of environmental learning theory to spatial knowledge acquisition from maps. Ann. Assoc. Am. Geogr. 1992, 2, 245–274. [Google Scholar] [CrossRef]
- GB50157-2013; Code for Design of Metro. Ministry of Housing and Urban-Rural Development (MOHURD): Beijing, China, 2013. (In Chinese)
- Mcfadden, D. Conditional Logit Analysis of Qualitative Choice Behavior; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Chen, X.; Yang, Z.H.; Sheng, Y.; Qiu, R. Passenger flow equilibrium distribution for the multi-airport system considering passenger delay. Math. Pract. Theory 2024, 54, 108–118. [Google Scholar]
- Daganzo, C. Fundamentals of Transportation and Traffic Operations; Pergamon: Oxford, UK, 1997. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).