An In-Depth Analysis of the Seismic Performance Characteristics of Steel–Concrete Composite Structures
Abstract
1. Introduction
- The fundamental principles of steel–concrete composite action under seismic loading
- Experimental studies on the seismic performance of composite elements and systems
- Analytical and numerical modeling techniques for predicting composite behavior
- Current design codes and standards for seismic design of composite structures
- Emerging technologies and novel composite systems for enhanced earthquake resistance
- Case studies of notable composite structures in seismic regions
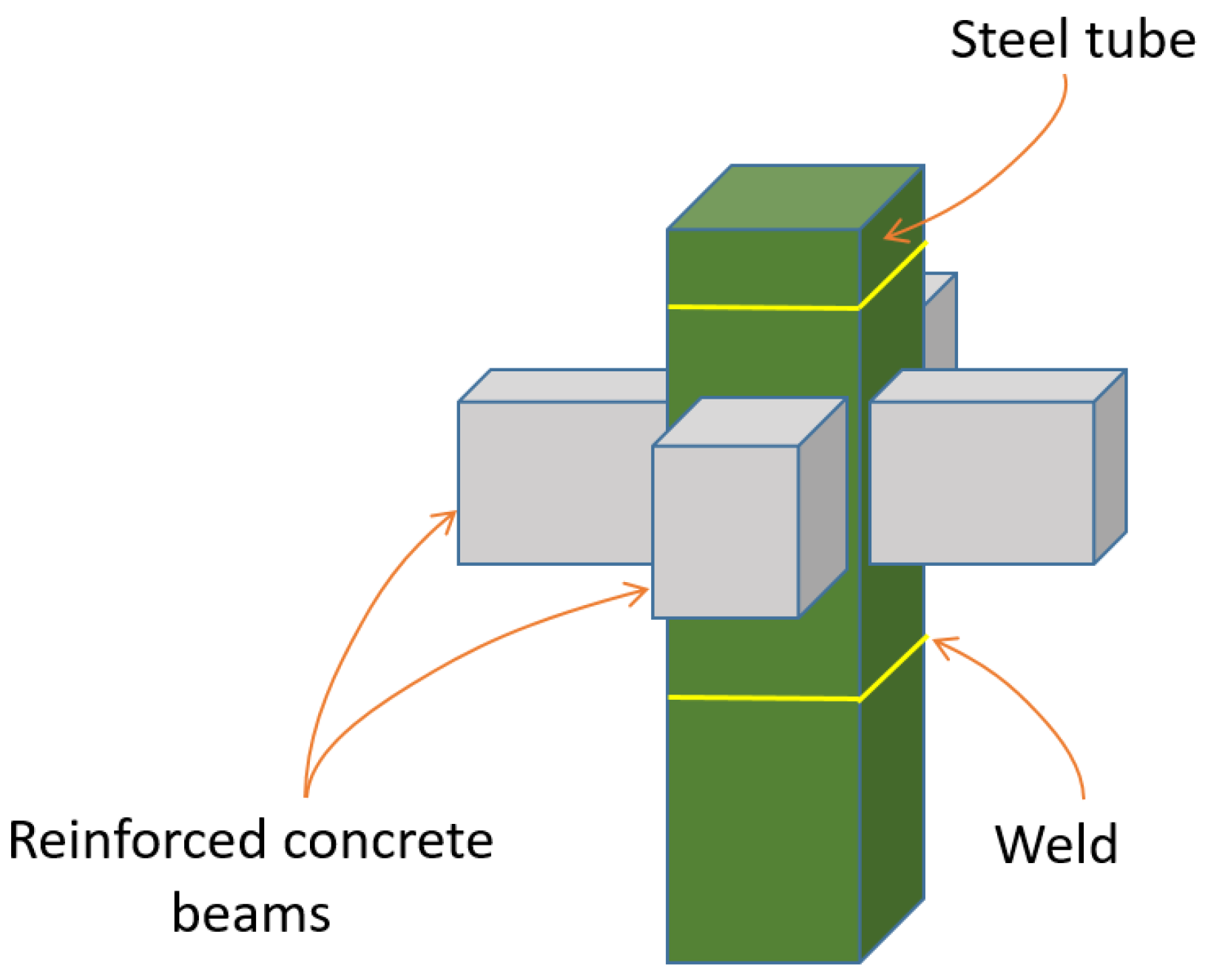
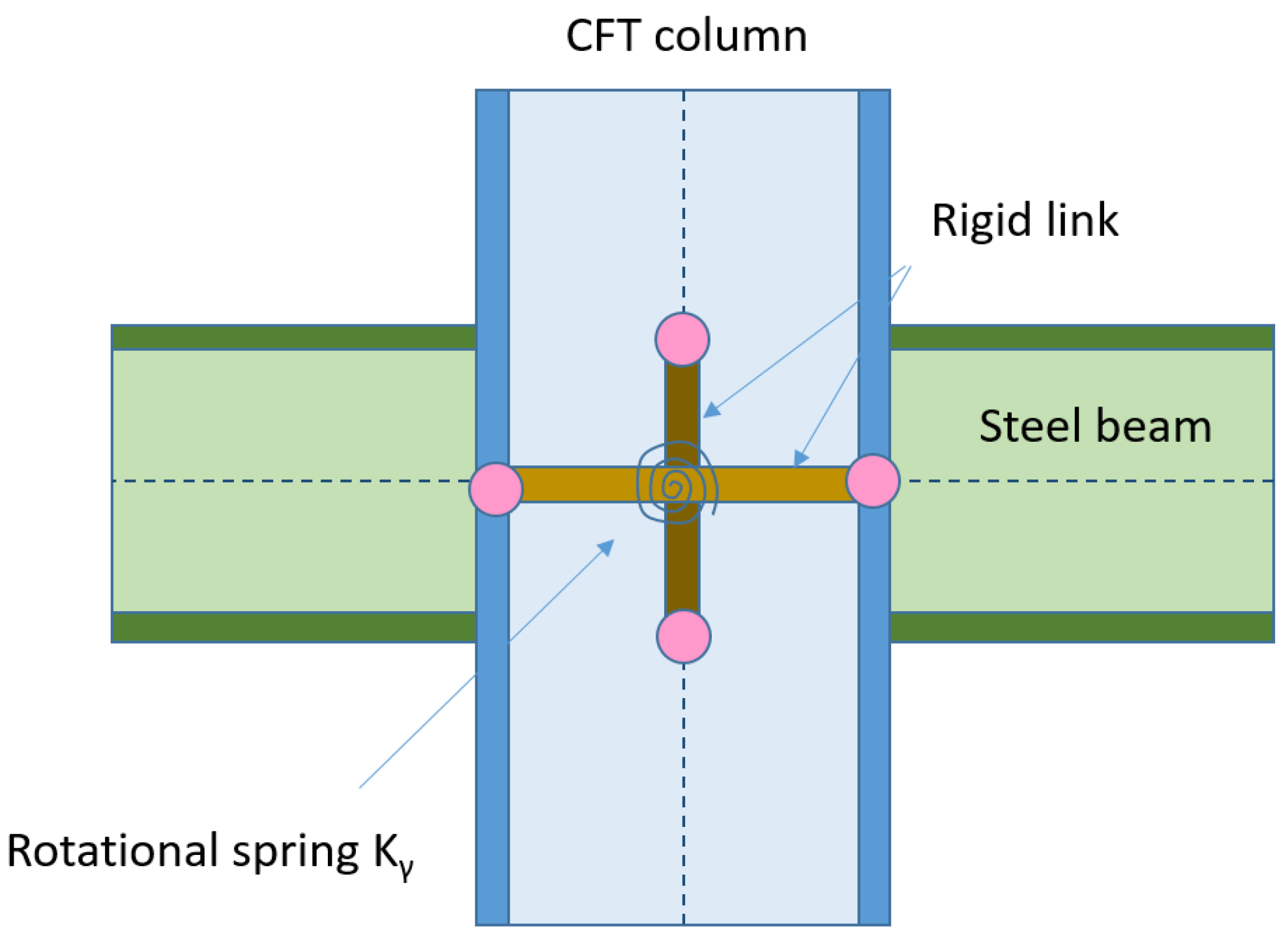
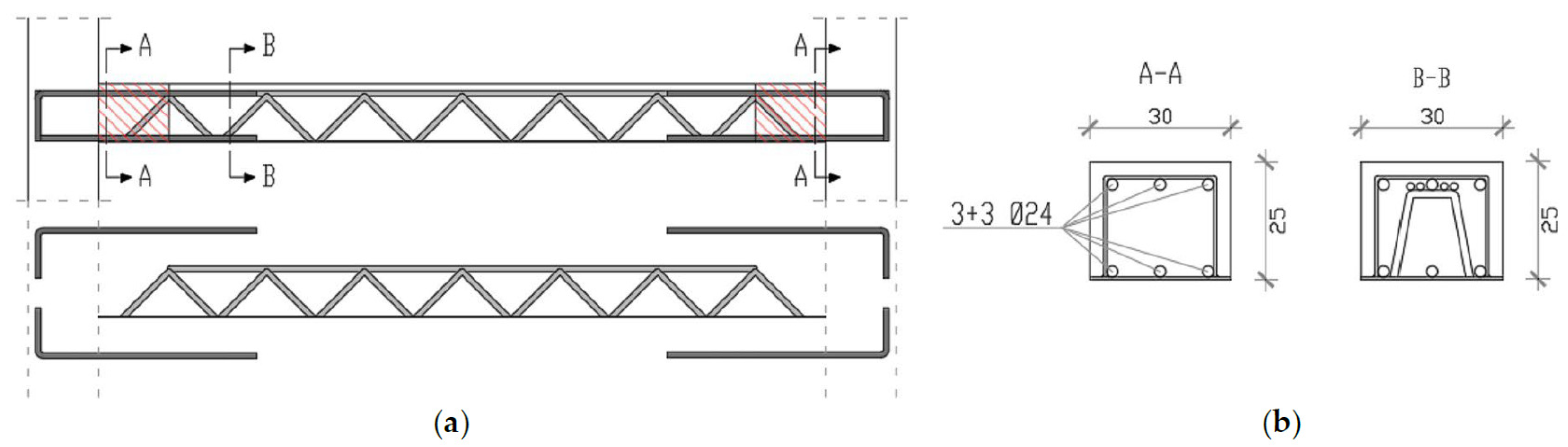
- Beam–column joints of composite frames under seismic loads: the behavior of composite beam–column connections under seismic loading is examined, including moment-resisting frames and various joint configurations. Research on load transfer mechanisms and failure modes is discussed.
- The seismic behavior of steel–concrete composite shear walls: composite concrete/steel shear wall systems, including steel-plate shear walls with concrete infill and composite coupling beams, are reviewed. Their effectiveness in lateral load resistance and energy dissipation is analyzed.
- Modeling techniques for composite members and structures under earthquake excitation: advanced numerical modeling techniques for composite structures, including finite element analysis, multi-scale modeling approaches, and the challenges in accurately representing composite behavior are discussed.
- The behavior of composite beams under cyclic loads: the hysteretic response of composite beams under repeated loading, including local buckling phenomena and the influence of concrete encasement on steel beam performance, is investigated.
- The behavior of composite beam-columns under cyclic loads: the performance of composite columns under cyclic loading, considering various cross-section types (e.g., concrete-filled steel tubes, encased steel sections) and their impact on ductility and energy dissipation is analyzed.
- The seismic performance of composite buildings: the advances in the seismic design of composite building structures are analyzed. The review focuses on the inelastic behavior of composite buildings where the evaluation of inelasticity at various levels of seismic intensity is significantly enhanced by seismic design approaches that allow for the control of structural deterioration at both the elemental scale (for instance, crucial structural parts) and the overall building scale (such as individual floors).
- Composite construction and foundation seismic design: seismic design considerations for foundations supporting composite structures, including pile-to-pile cap connections and soil–structure interaction effects, are discussed.
- Seismic isolation and energy dissipation devices for composite structures: the integration of base isolation systems with composite structures, focusing on their effectiveness in reducing seismic demands and improving overall structural performance, is examined. Additionally, the implementation of various damping devices (e.g., viscous dampers and friction dampers) in composite structures and their contribution to energy dissipation during seismic events is reviewed.
- The progressive collapse resistance of composite structures: the resistance of composite structures to progressive collapse under extreme loading conditions, including the role of composite action in enhancing structural robustness, is evaluated.
- Optimal design strategies for earthquake-resistant composite buildings: optimization strategies for composite structural systems, considering both material usage and seismic performance objectives is explored.
- The seismic performance of steel–concrete composite bridges: the application of composite construction in bridge engineering, focusing on the seismic performance of composite deck systems, piers, and abutments, is explored.
- Smart materials and sensors: new smart materials and sensors enhance the seismic performance of steel–concrete structures, offering self-centering and real-time monitoring capabilities.
2. Beam–Column Joints of Composite Frames Under Seismic Loads
2.1. Beam–Column Joints of Composite Frames Under Seismic Loads: State-of-the-Art
2.2. Beam–Column Joints of Composite Frames Under Seismic Loads: Key Findings
- Composite action enhances the strength and stiffness of joints when compared to bare steel joints.
- Proper reinforcement detailing in the joint area is essential for achieving ductile behavior.
- The presence of a concrete slab significantly affects the moment capacity and failure mode of the joint.
- Panel zone deformation has a noteworthy role in the overall rotation of the joint.
- Under cyclic loading, concrete crushing and bond deterioration of reinforcement can occur.
- The shear strength of joints is affected by the depth of the beam and the axial load on the column.
- Incorporating through-beam details can enhance joint performance in comparison to external beam–column connections.
- Composite joints generally demonstrate good energy dissipation capacity when subjected to seismic loading.
3. Seismic Behavior of Steel–Concrete Composite Shear Walls
3.1. Seismic Behavior of Steel–Concrete Composite Shear Walls: State-of-the-Art
3.2. Seismic Behavior of Steel–Concrete Composite Shear Walls: Key Findings
- Composite shear walls typically demonstrate enhanced strength and stiffness when compared to conventional reinforced concrete or steel-plate shear walls alone. This is due to the combination of materials, such as steel and concrete, which work together to provide increased structural integrity.
- Furthermore, the use of steel and concrete in composite shear walls often results in improved ductility. This means that the structure is able to endure larger displacements without failure during seismic events. This is crucial for ensuring the safety and resilience of the composite building structures during earthquakes.
- Another advantage of composite shear walls is their ability to dissipate energy. This enhanced energy dissipation capability is essential for seismic resistance, as it helps to absorb and dissolve the energy generated by earthquake forces, plummeting the potential for damage.
- Composite designs also offer the advantage of reduced wall thickness. Compared to traditional reinforced concrete walls, composite designs can often achieve the same level of strength and stiffness with thinner wall sections. This not only saves space but also reduces the amount of material required for construction.
- Additionally, the use of steel elements in composite shear walls can contribute to faster construction. Compared to conventional reinforced concrete systems, the incorporation of steel elements can expedite the construction process, resulting in time and cost savings.
- The presence of steel elements in composite shear walls also improves crack control. Steel helps to control crack formation and propagation in the concrete, enhancing the overall durability and longevity of the structure.
- Composite shear walls generally exhibit improved cyclic performance under cyclic loading conditions, which are representative of seismic actions. This means that they are better able to withstand repeated loading and unloading cycles without significant damage or failure.
- Proper design of composite shear walls can also lead to more predictable and desirable failure modes during extreme seismic events. By carefully considering the design and configuration of the walls, engineers can ensure that the structure behaves in a controlled manner, minimizing the risk of catastrophic failure.
- Furthermore, composite shear walls offer versatility in design. They provide various configuration options, allowing designers to optimize the performance of the walls for specific seismic demands. This flexibility enables engineers to tailor the design to meet the specific requirements of each project.
4. Modeling Techniques for Composite Members and Structures Under Earthquake Excitation
4.1. Modeling Techniques for Composite Members and Structures Under Earthquake Excitation: State-of-the-Art
4.2. Modeling Techniques for Composite Members and Structures Under Earthquake Excitation: Key Findings
- The seismic response of composite buildings is significantly influenced by the modeling of composite action, which alters the stiffness, strength, and energy dissipation capacity of the structure compared to non-composite systems.
- Accurate modeling of interfaces, such as the steel–concrete interface behavior, is crucial for overall structural performance, including slip and partial interactions.
- Nonlinear behavior, including inelastic deformations in steel and concrete components, as well as their composite action, must be taken into account for realistic seismic analysis.
- The performance of beam–column joints, especially in moment-resisting frames, is greatly influenced by connection details, affecting energy dissipation and overall ductility.
- The modeling of floor diaphragms is important, as composite floor systems affect load distribution and structural dynamics, requiring careful consideration in the modeling process.
- Material degradation due to cyclic loading should be considered, as it can lead to strength and stiffness degradation in both steel and concrete, affecting the seismic response.
- Three-dimensional modeling is often necessary to capture effects, such as torsion and bidirectional loading, which can be significant in composite structures.
- Utilizing sophisticated numerical techniques, like finite element analysis incorporating intricate material models, has the potential to offer precise assessment of the local and global performance of composite structures.
- Future research should focus on creating standardized protocols for assessing the durability of composite structures under different seismic intensities and frequencies.
5. Behavior of Composite Beams Under Cyclic Loads
5.1. Behavior of Composite Beams Under Cyclic Loads: State-of-the-Art
5.2. Behavior of Composite Beams Under Cyclic Loads: Key Findings
- The beam–column connection performance is essential in composite structures under seismic loads, as these are often critical points for energy dissipation and load transfer.
- Composite beams generally possess excellent energy dissipation capacity under cyclic loading, a crucial factor for seismic performance. This behavior is attributed to the interaction between steel and concrete components.
- Composite beams typically exhibit high ductility when properly designed, allowing for significant deformation without sudden failure. This characteristic is essential for maintaining structural integrity during earthquakes.
- Composite beams may experience stiffness degradation under repeated cyclic loading, often due to concrete cracking, steel yielding, and slip at the steel–concrete interface.
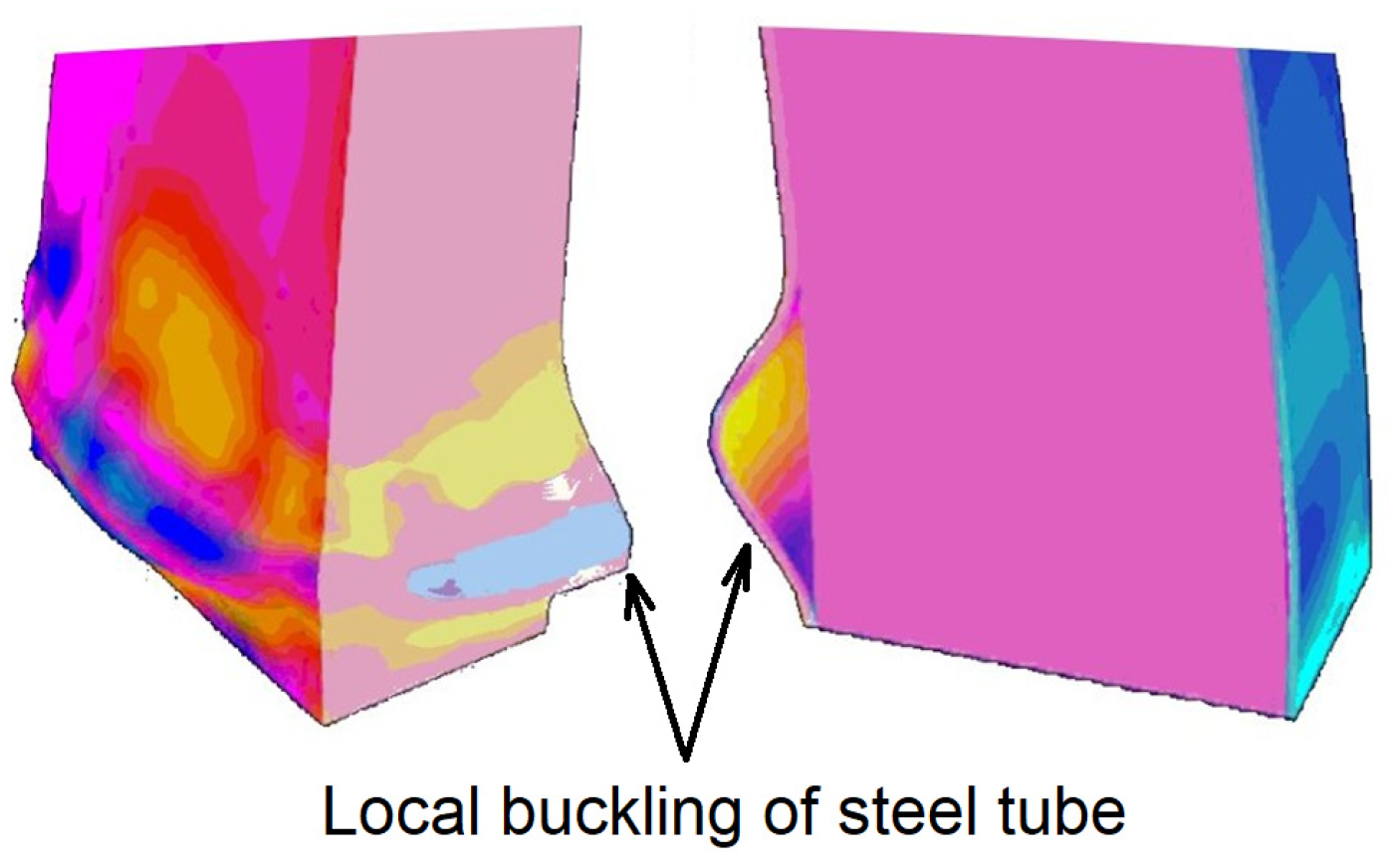
- The strength of composite beams can deteriorate with increasing load cycles, primarily due to local buckling of steel components and concrete crushing.
- The performance of shear connectors, such as headed studs, is critical in composite action. Inadequate shear connection may result in heightened slippage and diminished composite behavior when subjected to cyclic loading.
- Steel components in composite beams, particularly in the beam flanges and web, may experience local buckling under high cyclic loads, affecting the overall performance of the composite beam.
- The concrete slab significantly influences the behavior of composite beams, providing additional stiffness and strength. However, concrete damage and cracking can occur under severe cyclic loading.
- Composite beams may accumulate residual deformations after cyclic loading, which can affect the post-earthquake serviceability of the structure.
- Maintaining composite action throughout cyclic loading is essential for optimal seismic performance. The proper detailing and design of shear connectors are crucial to achieve this.
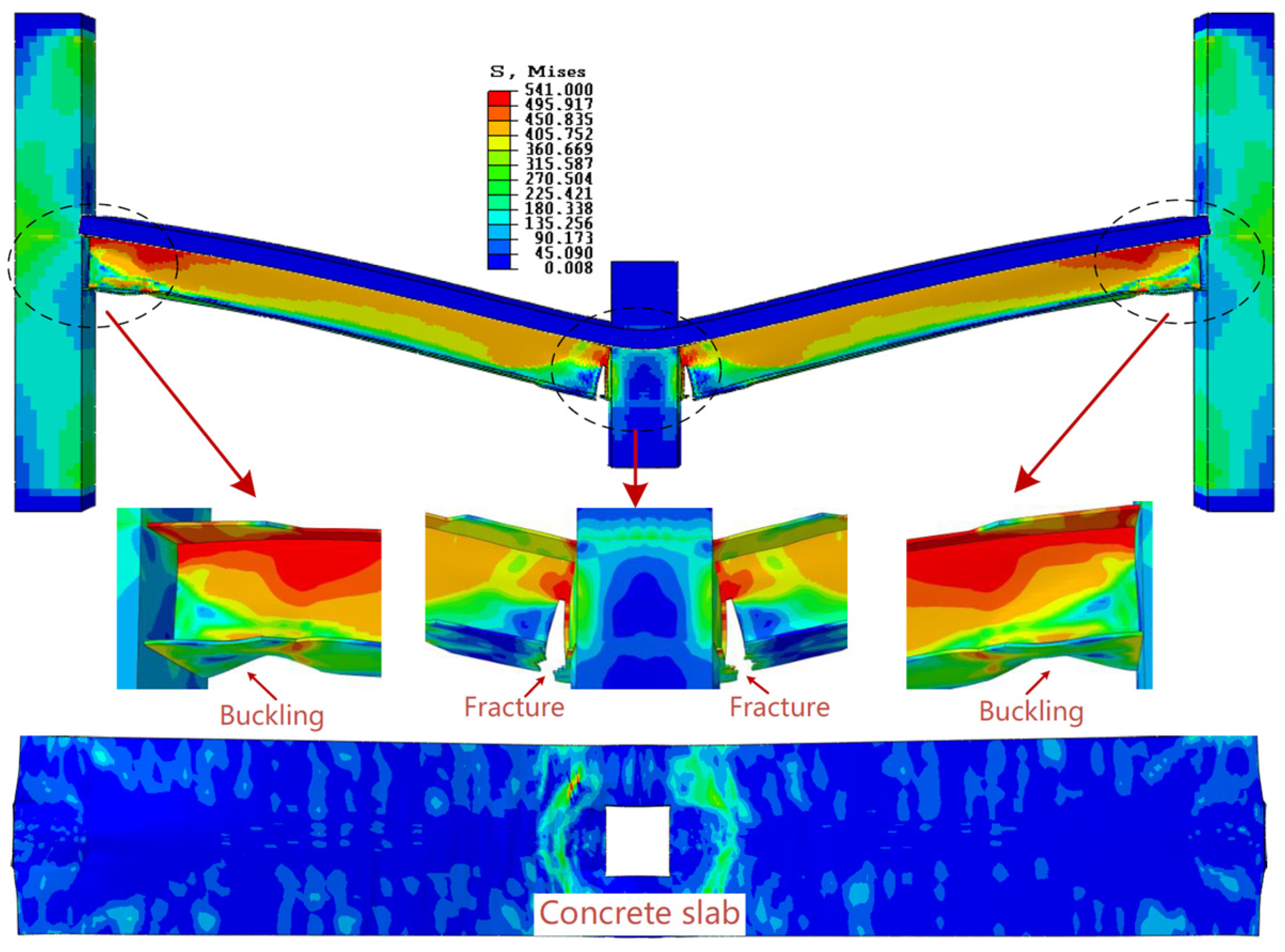
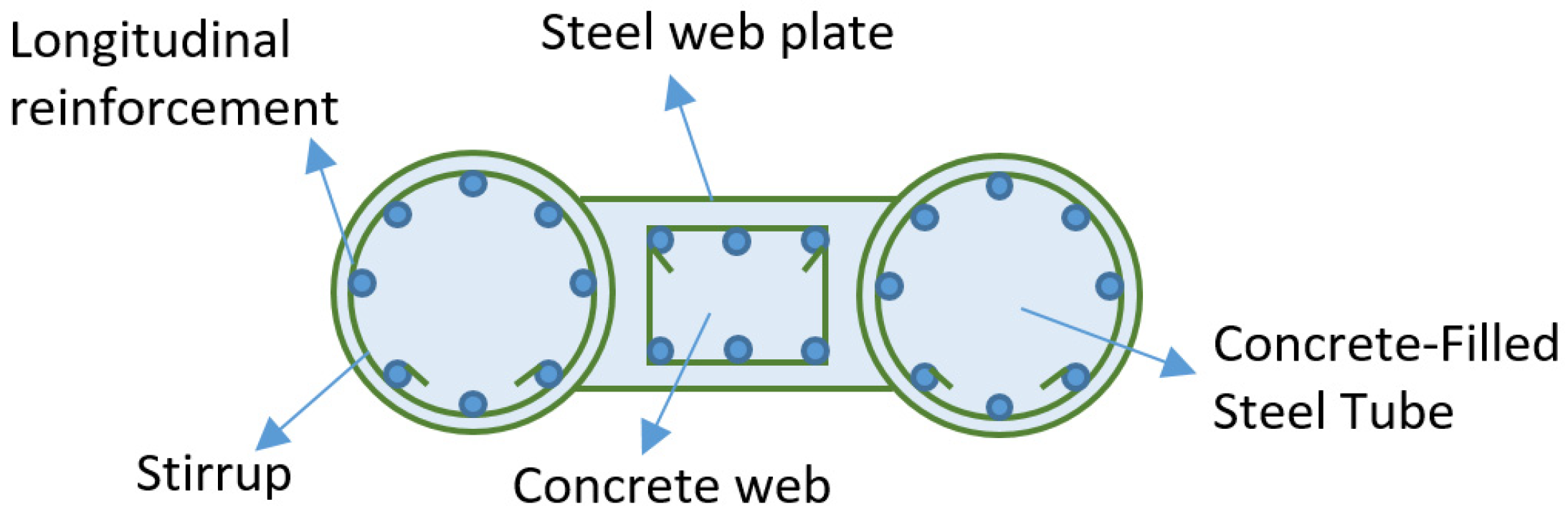
6. Behavior of Composite Beam-Columns Under Cyclic Loads
6.1. Behavior of Composite Beam-Columns Under Cyclic Loads: State-of-the-Art
6.2. Behavior of Composite Beam-Columns Under Cyclic Loads: Key Findings
7. Seismic Performance of Composite Building Structures
7.1. Seismic Performance of Composite Buildings: State-of-the-Art
7.2. Seismic Performance of Composite Buildings: Key Findings
7.3. Contextual Variability in the Seismic Performance of Composite Structures
8. Composite Construction and Foundation Seismic Design
8.1. Composite Construction and Foundation Seismic Design: State-of-the-Art
8.2. Composite Construction and Foundation Seismic Design: Key Findings
9. Seismic Isolation and Energy Dissipation Devices for Composite Structures
9.1. Seismic Isolation and Energy Dissipation Devices for Composite Structures: State-of-the-Art
9.2. Seismic Isolation and Energy Dissipation Devices for Composite Structures: Key Findings
10. Progressive Collapse Resistance of Composite Structures
10.1. Progressive Collapse Resistance of Composite Structures: State-of-the-Art
10.2. Progressive Collapse Resistance of Composite Structures: Key Findings
11. Optimal Design Strategies for Earthquake-Resistant Composite Buildings
11.1. Optimal Design Strategies for Earthquake-Resistant Composite Buildings: State-of-the-Art
11.2. Optimal Design Strategies for Earthquake-Resistant Composite Buildings: Key Findings
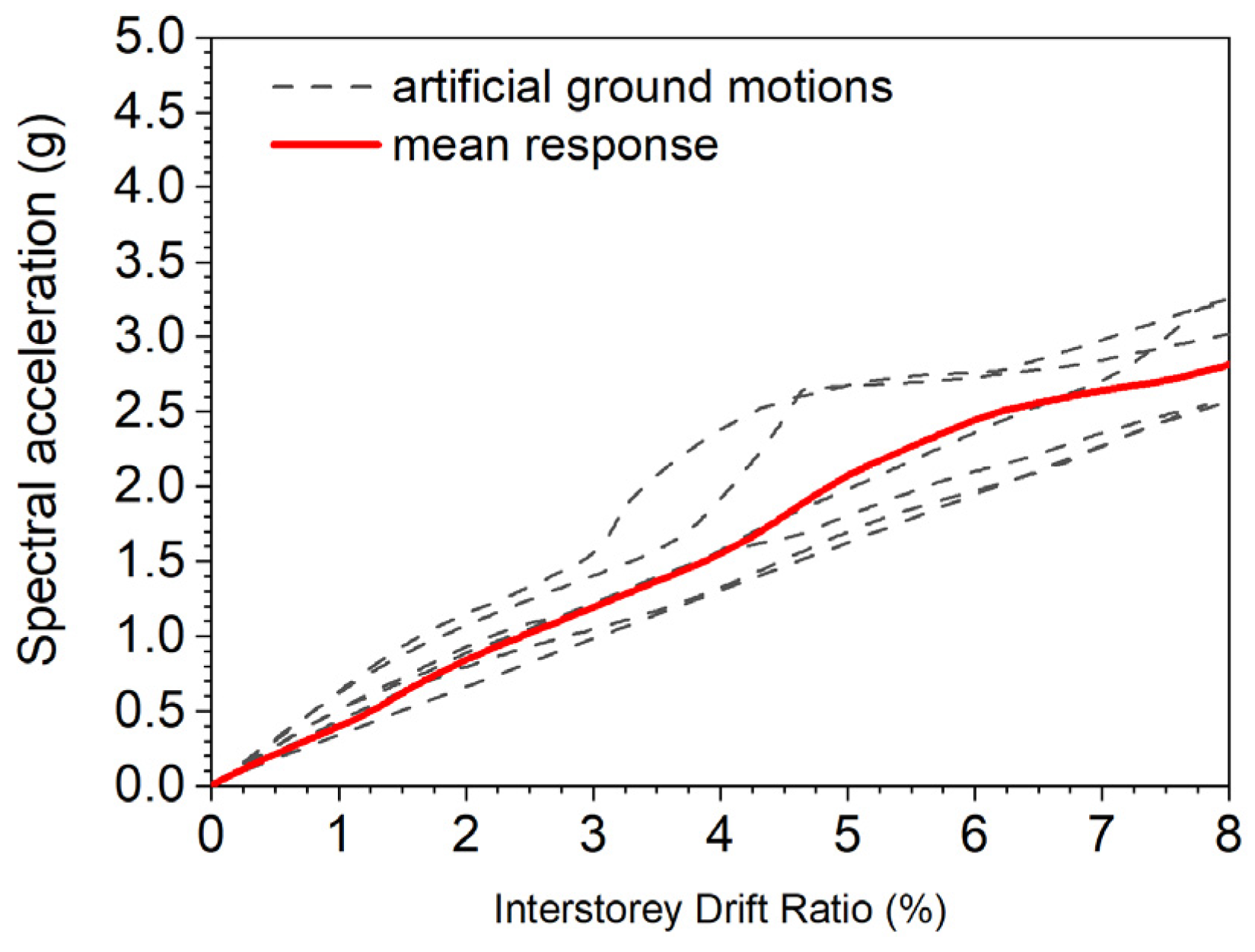
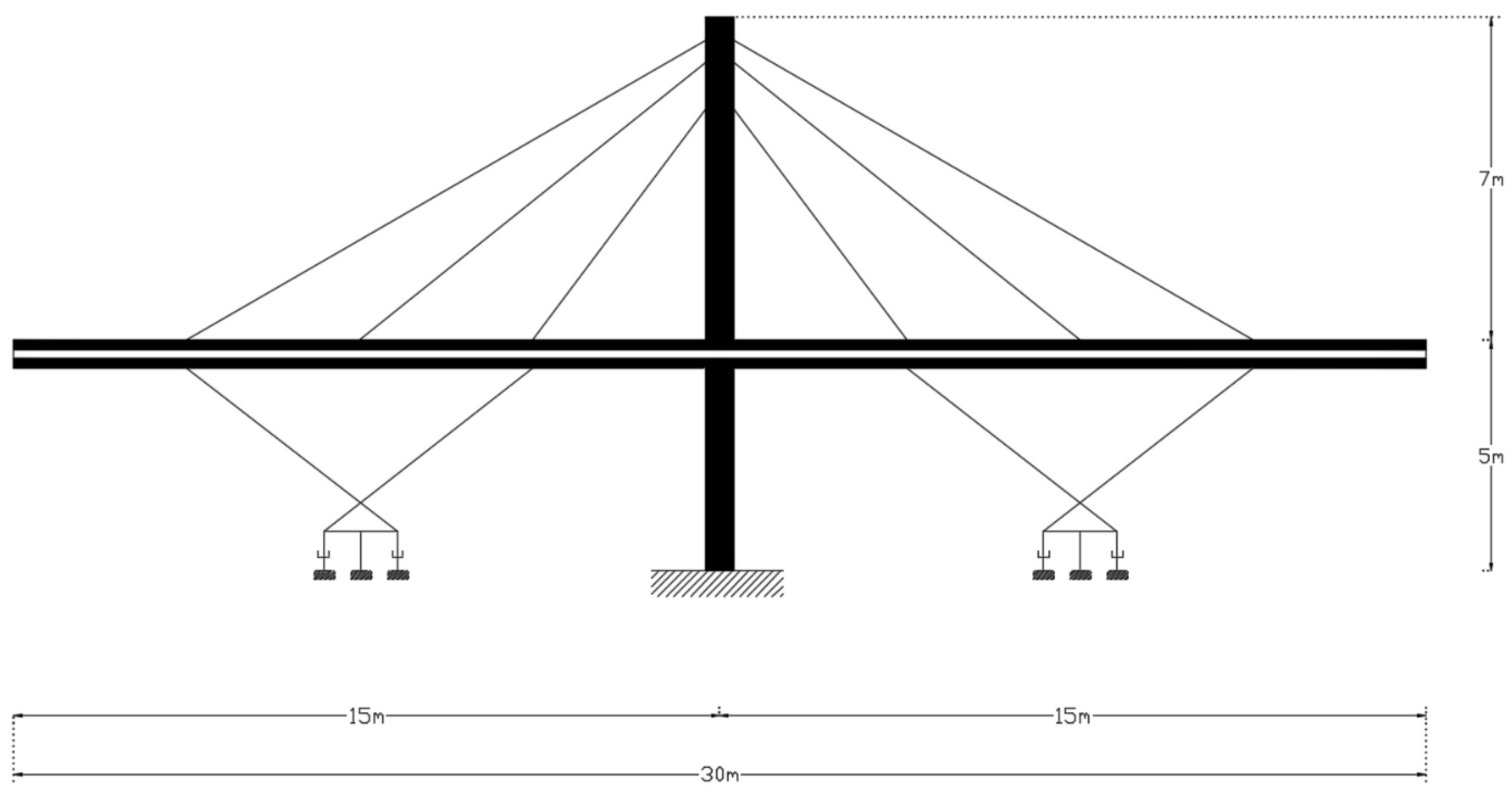
12. Seismic Performance of Steel–Concrete Composite Bridges
12.1. Seismic Performance of Steel–Concrete Composite Bridges: State-of-the-Art
12.2. Seismic Performance of Steel–Concrete Composite Bridges: Key Findings
13. Smart Materials and Sensors
14. Towards Next-Generation Composite Structural Systems: Research Perspectives
14.1. Emerging Vibration Protection Strategies
14.2. 3D Printing Techniques
14.3. Self-Healing Material Technologies
14.4. Machine Learning-Based Models
15. Conclusions and Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ataei, A.; Bradford, M.A.; Liu, X. Computational modelling of the moment-rotation relationship for decon-structable flush end plate beam-to-column composite joints. J. Constr. Steel Res. 2017, 129, 75–92. [Google Scholar]
- Van-Long, H.; Jean-Pierre, J.; Jean-François, D. Extended end-plate to concrete-filled rectangular column joint using long bolts. J. Constr. Steel Res. 2015, 113, 156–168. [Google Scholar]
- Wang, J.; Pan, X.; Peng, X. Pseudo-dynamic tests of assembly blind bolted composite frames to CFST columns. J. Constr. Steel Res. 2017, 139, 83–100. [Google Scholar]
- Peng, Z.; Dai, S.B.; Pi, Y.L.; Li, D.; Zhang, Y.C.; Huang, J. Seismic behaviour of innovative ring-bar rein-forced connections composed of T-shaped CFST columns and RC beams with slabs. Thin-Walled Struct. 2018, 127, 1–16. [Google Scholar]
- Peng, Z.; Dai, S.B.; Pi, Y.L.; Zhang, Y.C.; Huang, J. Seismic performance of end-plate connections between T-shaped CFST columns and RC beams. J. Constr. Steel Res. 2018, 145, 167–183. [Google Scholar]
- Peng, S.; Xiong, Z.; Xu, C.X.; Fei, J.; Chen, X. Research on shear strength of CFSST column and H-section with beam composite joint of unequal depth. J. Constr. Steel Res. 2021, 180, 106575. [Google Scholar]
- Mou, B.; Liu, X.; Sun, Z. Seismic behavior of a novel beam to reinforced concrete-filled steel tube column joint. J. Constr. Steel Res. 2021, 187, 106931. [Google Scholar] [CrossRef]
- Yu, Y.; Luo, Y.; Lin, S.; Wei, B.; Jiang, L.; Liu, Q. Experimental seismic behaviors of different connections to CFST end-columns in shear walls. J. Constr. Steel Res. 2022, 196, 107385. [Google Scholar]
- Cheng, Y.; Yang, Y.; Teng, Y.; Yu, Y.; Chen, Y.F. Seismic performance of T-shaped CFST column to U-shaped steel-concrete composite beam joint. J. Constr. Steel Res. 2022, 199, 107564. [Google Scholar]
- Li, J.; Mou, B.; Wang, Z. Cyclic behavior of column-to-column connections in novel prefabricated H-shaped steel beam to CFST column joint. J. Constr. Steel Res. 2023, 200, 107657. [Google Scholar]
- Chen, Q.J.; Cai, J.; Bradford, M.A.; Liu, X.; Zuo, Z.L. Seismic behaviour of a through-beam connection be-tween concrete-filled steel tubular columns and reinforced concrete beams. Eng. Struct. 2014, 80, 24–39. [Google Scholar] [CrossRef]
- Jeddi, M.Z.; Sulong, N.R.; Khanouki, M.A. Seismic performance of a new through rib stiffener beam connection to concrete-filled steel tubular columns: An experimental study. Eng. Struct. 2017, 131, 477–491. [Google Scholar] [CrossRef]
- Amadio, C.; Bedon, C.; Fasan, M.; Pecce, M.R. Refined numerical modelling for the structural assessment of steel-concrete composite beam-to-column joints under seismic loads. Eng. Struct. 2017, 138, 394–409. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Liu, J.; Zhou, X. Experimental investigation of special-shaped concrete-filled steel tubular column to steel beam connections under cyclic loading. Eng. Struct. 2017, 151, 68–84. [Google Scholar] [CrossRef]
- Li, W.; Xu, L.F.; Qian, W.W. Seismic performance of 3-D steel beam to concrete-encased CFST column joints: Tests. Eng. Struct. 2021, 232, 111793. [Google Scholar] [CrossRef]
- Wu, C.; Liu, J.; Tan, W.; Wang, P. Seismic behavior of composite interior joints of prefabricated H-shaped steel reinforced concrete column-steel beam. In Structures; Elsevier: Amsterdam, The Netherlands, 2020; Volume 23, pp. 558–572. [Google Scholar]
- Wang, J.; Zhang, H.; Jiang, Z. Seismic behavior of blind bolted end plate composite joints to CFTST columns. Thin-Walled Struct. 2016, 108, 256–269. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D. Development and testing of precast concrete-filled square steel tube column-to-RC beam connections under cyclic loading. Constr. Build. Mater. 2021, 280, 122540. [Google Scholar] [CrossRef]
- Wang, J.X.; Yang, Y.; Xian, W.; Li, Q.Y. Progressive collapse mechanism analysis of concrete-filled square steel tubular column to steel beam joint with bolted–welded hybrid connection. Int. J. Steel Struct. 2020, 20, 1618–1635. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, W.; Tang, X.; Cheng, Y. Seismic behavior of plane frame with special-shaped CFST columns, H-shaped steel beams and vertical rib connections. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 31, pp. 721–739. [Google Scholar]
- Xu, X.; Cheng, R.; Yang, P.; Chen, K.; Li, J. Behavior of T-shaped CFST column and U-shaped steel-concrete composite beam joints. J. Build. Eng. 2021, 43, 103157. [Google Scholar] [CrossRef]
- Duan, L.; Nie, X.; Su, H.; Tan, J. Seismic Response Analysis of Steel–Concrete Composite Frame Structures with URSP Connectors. Materials 2022, 15, 8655. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Guo, L. Seismic tests and nonlinear model of beam-CFDST column joints with blind fasteners. J. Build. Eng. 2022, 45, 103415. [Google Scholar]
- Zhou, J.; Chen, Z.; Xu, W.; Liao, H.; Wang, N. Seismic behavior of 3-D beam to L-shaped concrete encased steel composite column joint: An experimental study. J. Build. Eng. 2022, 52, 104437. [Google Scholar]
- Chen, L.; Feng, J.; Xue, Y.; Liang, C. Seismic behavior of an innovative prefabricated steel-concrete composite beam-column joint. J. Build. Eng. 2023, 76, 107211. [Google Scholar]
- Gan, D.; Zhou, Z.; Zhou, X.; Hai Tan, K. Seismic behavior tests of square reinforced concrete–filled steel tube columns connected to RC beam joints. J. Struct. Eng. 2019, 145, 04018267. [Google Scholar]
- Lai, Z.; Fischer, E.C.; Varma, A.H. Database and review of beam-to-column connections for seismic design of composite special moment frames. J. Struct. Eng. 2019, 145, 04019023. [Google Scholar]
- Fan, J.; Li, Q.; Nie, J.; Zhou, H. Experimental study on the seismic performance of 3D joints between concrete-filled square steel tubular columns and composite beams. J. Struct. Eng. 2014, 140, 04014094. [Google Scholar]
- Wu, C.; Liu, J.; Shi, W. Seismic performance of composite joints between prefabricated steel-reinforced concrete columns and steel beams: Experimental study. Bull. Earthq. Eng. 2020, 18, 3817–3841. [Google Scholar]
- Liu, J.; He, W.; Cheng, G.; Chen, Y.F. Seismic behavior of large-diameter CFTST column to steel beam connections. J. Constr. Steel Res. 2020, 175, 106338. [Google Scholar]
- Amadio, C.; Bedon, C.; Fasan, M. Numerical assessment of slab-interaction effects on the behaviour of steel-concrete composite joints. J. Constr. Steel Res. 2017, 139, 397–410. [Google Scholar]
- Demonceau, J.F.; Ciutina, A. Characterisation of beam-to-column steel-concrete composite joints beyond current Eurocode provisions. In Structures; Elsevier: Amsterdam, The Netherlands, 2019; Volume 21, pp. 167–175. [Google Scholar]
- Mo, J.; Uy, B.; Li, D.; Thai, H.T.; Tran, H. A review of the behaviour and design of steel–concrete composite shear walls. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 31, pp. 1230–1253. [Google Scholar]
- Lan, T.; Wang, X.; Cui, Y.; Liu, X.; You, Y. Analysis and application of double steel plate concrete composite shear wall in the R&D Building of Zhanjiang Bay Laboratory. Buildings 2023, 13, 3055. [Google Scholar] [CrossRef]
- Todea, V.; Dan, D.; Florut, S.C.; Stoian, V. Experimental investigations on the seismic behavior of composite steel concrete coupled shear walls with central openings. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 33, pp. 878–896. [Google Scholar]
- Qiao, Q.Y.; Cao, W.L.; Li, X.Y.; Dong, H.Y.; Zhang, W.W.; Yin, F. Seismic behavior of shear walls with boundary CFST columns and embedded multiple steel plates: Experimental investigation. Eng. Struct. 2018, 160, 243–256. [Google Scholar]
- Najm, H.M.; Ibrahim, A.M.; Sabri, M.M.; Hassan, A.; Morkhade, S.; Mashaan, N.S.; Eldirderi, M.M.A.; Khedher, K.M. Modelling of cyclic load behaviour of smart composite steel-concrete shear wall using finite element analysis. Buildings 2022, 12, 850. [Google Scholar] [CrossRef]
- Rahnavard, R.; Hassanipour, A.; Mounesi, A. Numerical study on important parameters of composite steel-concrete shear walls. J. Constr. Steel Res. 2016, 121, 441–456. [Google Scholar]
- Zhang, X.; Qin, Y.; Chen, Z. Experimental seismic behavior of innovative composite shear walls. J. Constr. Steel Res. 2016, 116, 218–232. [Google Scholar]
- Hossain, K.M.; Rafiei, S.; Lachemi, M.; Behdinan, K. Structural performance of profiled composite wall under in-plane cyclic loading. Eng. Struct. 2016, 110, 88–104. [Google Scholar]
- Polat, E.; Bruneau, M. Modeling cyclic inelastic in-plane flexural behavior of concrete filled sandwich steel panel walls. Eng. Struct. 2017, 148, 63–80. [Google Scholar]
- Zhao, W.; Guo, Q.; Huang, Z.; Tan, L.; Chen, J.; Ye, Y. Hysteretic model for steel–concrete composite shear walls subjected to in-plane cyclic loading. Eng. Struct. 2016, 106, 461–470. [Google Scholar]
- Wang, M.Z.; Guo, Y.L.; Zhu, J.S.; Yang, X.; Tong, J.Z. Sectional strength design of concrete-infilled double steel corrugated-plate walls with T-section. J. Constr. Steel Res. 2019, 160, 23–44. [Google Scholar]
- Luo, Q.; Wang, W.; Sun, Z.; Xu, S.; Wang, B. Seismic performance analysis of corrugated-steel-plate composite shear wall based on corner failure. J. Constr. Steel Res. 2021, 180, 106606. [Google Scholar]
- Haghi, N.; Epackachi, S.; Kazemi, M.T. Macro modeling of steel-concrete composite shear walls. In Structures; Elsevier: Amsterdam, The Netherlands, 2020; Volume 23, pp. 383–406. [Google Scholar]
- Shafaei, S.; Varma, A.H.; Broberg, M.; Klemencic, R. Modeling the cyclic behavior of composite plate shear walls/concrete filled (C-PSW/CF). J. Constr. Steel Res. 2021, 184, 106810. [Google Scholar]
- Chen, L.; Mahmoud, H.; Tong, S.M.; Zhou, Y. Seismic behavior of double steel plate–HSC composite walls. Eng. Struct. 2015, 102, 1–12. [Google Scholar] [CrossRef]
- Epackachi, S.; Whittaker, A.S.; Varma, A.H.; Kurt, E.G. Finite element modeling of steel-plate concrete composite wall piers. Eng. Struct. 2015, 100, 369–384. [Google Scholar] [CrossRef]
- Huang, Z.; Liew, J.R. Compressive resistance of steel-concrete-steel sandwich composite walls with J-hook connectors. J. Constr. Steel Res. 2016, 124, 142–162. [Google Scholar] [CrossRef]
- Hu, H.S.; Nie, J.G.; Eatherton, M.R. Deformation capacity of concrete-filled steel plate composite shear walls. J. Constr. Steel Res. 2014, 103, 148–158. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, S.; Guo, L. Cyclic behavior of low shear-span ratio dovetailed profiled steel–concrete composite shear walls. J. Build. Eng. 2022, 59, 105094. [Google Scholar] [CrossRef]
- Wang, S.; Wang, W.; Chen, Y.; Hou, H.; Xie, S. Seismic performance of double skin composite wall under maximum considered far-field earthquake loading protocol. J. Build. Eng. 2022, 55, 104705. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, H.; Jiang, L.; Zhang, Y.; Yuan, Z.; Zhang, Z.; Chu, X.; Li, B. Seismic Behaviors of Novel Steel-Reinforced Concrete Composite Frames Prestressed with Bonding Tendons. Buildings 2023, 13, 2124. [Google Scholar] [CrossRef]
- Kenarangi, H.; Kizilarslan, E.; Bruneau, M. Cyclic behavior of c-shaped composite plate shear walls–concrete filled. Eng. Struct. 2021, 226, 111306. [Google Scholar]
- Serras, D.N.; Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Modeling of circular concrete-filled steel tubes subjected to cyclic lateral loading. In Structures; Elsevier: Amsterdam, The Netherlands, 2016; Volume 8, pp. 75–93. [Google Scholar]
- Sahin, B.; Bravo-Haro, M.A.; Elghazouli, A.Y. Assessment of cyclic degradation effects in composite steel-concrete members. J. Constr. Steel Res. 2022, 192, 107231. [Google Scholar]
- Liu, X.; Bradford, M.A.; Chen, Q.J.; Ban, H. Finite element modelling of steel–concrete composite beams with high-strength friction-grip bolt shear connectors. Finite Elem. Anal. Des. 2016, 108, 54–65. [Google Scholar]
- Katwal, U.; Tao, Z.; Hassan, M.K. Finite element modelling of steel-concrete composite beams with profiled steel sheeting. J. Constr. Steel Res. 2018, 146, 1–15. [Google Scholar] [CrossRef]
- Peng, S.; Wang, J.; Yao, Y.; Min, T.; Li, C.; Luo, L.; Zhu, Y.; Wen, X.; Zhou, M. A modified Park-Ang model for seismic damage assessment of recycled aggregate concrete-filled square steel tube columns. Case Stud. Constr. Mater. 2022, 17, e01692. [Google Scholar] [CrossRef]
- Sahin, B.; Bravo-Haro, M.A.; Elghazouli, A.Y. Modelling and response of composite steel-concrete members under cyclic loading. Ce/Papers 2023, 6, 160–166. [Google Scholar] [CrossRef]
- El Jisr, H.; Kohrangi, M.; Lignos, D.G. Proposed nonlinear macro-model for seismic risk assessment of compo-site-steel moment resisting frames. Earthq. Eng. Struct. Dyn. 2022, 51, 1180–1200. [Google Scholar] [CrossRef]
- Papavasileiou, G. Analytical framework for the substitution of steel-concrete composite columns with equivalent steel columns in structural design. ESR J. 2017, 2. [Google Scholar]
- Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Modeling level selection for seismic analysis of concrete-filled steel tube/moment-resisting frames by using fragility curves. Earthq. Eng. Struct. Dyn. 2015, 44, 199–220. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, X. The slab effect of composite frames: From modified fiber modeling to seismic fragility assessment. J. Constr. Steel Res. 2021, 186, 106877. [Google Scholar] [CrossRef]
- Fa-xing, D.; Jing, L.; Xue-mei, L.; Zhi-wu, Y.; Yong-suo, L. Experimental investigation on hysteretic behavior of simply supported steel-concrete composite beam. J. Constr. Steel Res. 2018, 144, 153–165. [Google Scholar] [CrossRef]
- Han, L.H.; An, Y.F.; Roeder, C.; Ren, Q.X. Performance of concrete-encased CFST box members under bending. J. Constr. Steel Res. 2015, 106, 138–153. [Google Scholar] [CrossRef]
- Suzuki, A.; Kimura, Y. Cyclic behavior of component model of composite beam subjected to fully reversed cyclic loading. J. Struct. Eng. 2019, 145, 04019015. [Google Scholar] [CrossRef]
- Zhu, L.; Ning, Q.; Han, W.; Zhao, C. Seismic performance of self-centering concrete-filled square steel tubular column-to-steel beam connection equipped with SMA bolts. Thin-Walled Struct. 2023, 183, 110351. [Google Scholar]
- Huang, Y.; Yi, W.; Zhang, R.; Xu, M. Behavior and design modification of RBS moment connections with composite beams. Eng. Struct. 2014, 59, 39–48. [Google Scholar]
- Di Cesare, A.; Belviso, P.; Ponzo, F.C.; Vitone, G. Seismic Behavior and Modeling of Ductile Composite Steel-Trussed Concrete Beam to Column Joints. Appl. Sci. 2023, 13, 11139. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Fang, C. Performance of partially encased composite beams under static and cyclic bending. In Structures; Elsevier: Amsterdam, The Netherlands, 2017; Volume 9, pp. 29–40. [Google Scholar]
- El Jisr, H.; Elkady, A.; Lignos, D.G. Composite steel beam database for seismic design and performance assessment of composite-steel moment-resisting frame systems. Bull. Earthq. Eng. 2019, 17, 3015–3039. [Google Scholar]
- Suzuki, A.; Kimura, Y. Mechanical performance of stud connection in steel-concrete composite beam under reversed stress. Eng. Struct. 2021, 249, 113338. [Google Scholar] [CrossRef]
- Suzuki, A.; Hiraga, K.; Kimura, Y. Cyclic behavior of steel-concrete composite dowel by clothoid-shaped shear connectors under fully reversed cyclic stress. J. Adv. Concr. Technol. 2023, 21, 76–91. [Google Scholar]
- Montuori, R.; Nastri, E.; Piluso, V.; Todisco, P. Experimental and analytical study on the behaviour of circular concrete filled steel tubes in cyclic bending. Eng. Struct. 2024, 304, 117610. [Google Scholar]
- Kim, S.B.; Lee, E.T.; Kim, J.R.; Kim, S.S. Experimental study on bending behavior and seismic performance of hybrid composite beam with new shape. Int. J. Steel Struct. 2016, 16, 477–488. [Google Scholar]
- Wang, J.T.; Wu, X.H.; Yang, B.; Sun, Q. Bearing capacity and damage behavior of hcftst columns under cyclic loading. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 32, pp. 1492–1506. [Google Scholar]
- Qian, W.W.; Li, W.; Han, L.H.; Zhao, X.L. Analytical behavior of concrete-encased CFST columns under cyclic lateral loading. J. Constr. Steel Res. 2016, 120, 206–220. [Google Scholar]
- Tang, Y.C.; Li, L.J.; Feng, W.X.; Liu, F.; Liao, B. Seismic performance of recycled aggregate concrete–filled steel tube columns. J. Constr. Steel Res. 2017, 133, 112–124. [Google Scholar]
- Ma, H.; Qiang, J.; Xi, J.; Zhao, Y. Cyclic loading tests and horizontal bearing capacity of recycled concrete filled circular steel tube and profile steel composite columns. J. Constr. Steel Res. 2022, 199, 107572. [Google Scholar] [CrossRef]
- Ma, H.; Liu, F.; Fang, L.; Zhao, Y.; Gan, X. Cyclic loading tests and seismic behaviors of steel-reinforced recycled aggregate concrete filled square steel tube composite columns. J. Constr. Steel Res. 2024, 212, 108270. [Google Scholar] [CrossRef]
- Luo, C.; Wang, F.; Chen, H.; Qi, A.; Chen, Y. Study on the hysteretic behavior of recycled aggregate concrete-filled steel tube columns containing ferronickel slag. J. Build. Eng. 2022, 46, 103695. [Google Scholar] [CrossRef]
- Zeng, L.; Li, L.; Xiao, P.; Zeng, J.; Liu, F. Experimental study of seismic performance of full-scale basalt FRP-recycled aggregate concrete-steel tubular columns. Thin-Walled Struct. 2020, 151, 106185. [Google Scholar] [CrossRef]
- Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Parameter identification of three hysteretic models for the simulation of the response of CFT columns to cyclic loading. Eng. Struct. 2014, 61, 44–60. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Cao, W.; Yu, C. Cyclic behavior of steel tube-reinforced high-strength concrete composite columns with high-strength steel bars. Eng. Struct. 2019, 189, 565–579. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, S.; Lai, P. Hysteretic behavior of multi-cell L-shaped concrete-filled steel tubular columns at different loading angles. Eng. Struct. 2020, 202, 109887. [Google Scholar] [CrossRef]
- Kim, H.J.; Park, H.G.; Hwang, H.J. Cyclic lateral loading test for composite columns with high-strength steel angle cage. Eng. Struct. 2022, 250, 113463. [Google Scholar] [CrossRef]
- Xiong, J.; Ren, F.; Li, S.; Tian, S.; Li, Y.; Mo, J. A study on low-frequency vibration mitigation by using the metamaterial-tailored composite concrete-filled steel tube column. Eng. Struct. 2024, 305, 117673. [Google Scholar] [CrossRef]
- Hassan, W.M.; Farag, M. Seismic performance of steel-reinforced concrete composite columns in existing and modern construction. Soil Dyn. Earthq. Eng. 2021, 151, 106945. [Google Scholar] [CrossRef]
- Mostafa, M.M.; Wu, T.; Liu, X.; Fu, B. The composite steel reinforced concrete column under axial and seismic loads: A review. Int. J. Steel Struct. 2019, 19, 1969–1987. [Google Scholar] [CrossRef]
- Hassan, W.M.; Reyes, J.C.; González, C.; Pallarés, F.J.; Spinel, J.S. Seismic vulnerability and resilience of steel-reinforced concrete (SRC) composite column buildings with non-seismic details. Eng. Struct. 2021, 244, 112810. [Google Scholar] [CrossRef]
- Campian, C.; Nagy, Z.; Pop, M. Behavior of fully encased steel-concrete composite columns subjected to monotonic and cyclic loading. Procedia Eng. 2015, 117, 439–451. [Google Scholar] [CrossRef]
- Chen, C.; Wang, C.; Sun, H. Experimental study on seismic behavior of full encased steel-concrete composite columns. J. Struct. Eng. 2014, 140, 04014024. [Google Scholar] [CrossRef]
- Chen, Z.; Dong, S.; Du, Y. Experimental study and numerical analysis on seismic performance of FRP confined high-strength rectangular concrete-filled steel tube columns. Thin-Walled Struct. 2021, 162, 107560. [Google Scholar] [CrossRef]
- Gautham, A.S.D.R.; Sahoo, D.R. Behavior of steel-reinforced composite concrete columns under combined axial and lateral cyclic loading. J. Build. Eng. 2021, 39, 102305. [Google Scholar] [CrossRef]
- Serras, D.N.; Skalomenos, K.A.; Hatzigeorgiou, G.D. A displacement/damage controlled seismic design method for MRFs with concrete-filled steel tubular columns and composite beams. Soil Dyn. Earthq. Eng. 2021, 143, 106608. [Google Scholar] [CrossRef]
- Serras, D.N.; Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Inelastic behavior of circular concrete-filled steel tubes: Monotonic versus cyclic response. Bull. Earthq. Eng. 2017, 15, 5413–5434. [Google Scholar] [CrossRef]
- Bai, Y.; Ma, X.; Wang, B.; Cao, G.; Beer, M. Cumulative Component Damages on Collapse Capacity of Ductile Steel and CFT Moment Resisting Frames under Over-design Ground Motions. J. Earthq. Eng. 2022, 26, 3012–3033. [Google Scholar] [CrossRef]
- Wu, Z.; Nie, X.; Zhao, J.; Wang, W.; Duan, L. Numerical Study on the Seismic Behavior of Steel–Concrete Composite Frame with Uplift-Restricted and Slip-Permitted (URSP) Connectors. Buildings 2023, 13, 2598. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Chen, C.; Cui, M. Seismic Performance Assessment of Composite Frame–High-Strength Steel Plate Wall Core Tube Resilient Structural System. Buildings 2024, 14, 301. [Google Scholar] [CrossRef]
- Zhao, H.; Tao, M.X.; Ding, R. Experimental study on seismic behaviour of composite frames with wide floor slabs considering the effect of floor loads. Eng. Struct. 2020, 220, 111024. [Google Scholar]
- Tondini, N.; Zanon, G.; Pucinotti, R.; Di Filippo, R.; Bursi, O.S. Seismic performance and fragility functions of a 3D steel-concrete composite structure made of high-strength steel. Eng. Struct. 2018, 174, 373–383. [Google Scholar]
- Braconi, A.; Caprili, S.I.L.V.I.A.; Degee, H.; Guendel, M.; Hjiaj, M.; Hoffmeister, B.; Karamanos, S.A.; Rinaldi, V.; Salvatore, W.A.L.T.E.R.; Somja, H. Efficiency of Eurocode 8 design rules for steel and steel-concrete composite structures. J. Constr. Steel Res. 2015, 112, 108–129. [Google Scholar]
- Badalassi, M.; Braconi, A.; Cajot, L.G.; Caprili, S.; Degee, H.; Gündel, M.; Hjiaj, M.; Hoffmeister, B.; Karamanos, S.A.; Salvatore, W.; et al. Influence of variability of material mechanical properties on seismic performance of steel and steel–concrete composite structures. Bull. Earthq. Eng. 2017, 15, 1559–1607. [Google Scholar]
- Etli, S. Parametric Analysis of the Performance of Steel-Concrete Composite Structures Designed with TBDY 2018. Int. J. Innov. Eng. Appl. 2022, 6, 7–16. [Google Scholar]
- Etli, S. Performance evaluation of steel-concrete composite structures designed in poorly graded soils. Rev. Constr. 2023, 22, 259–276. [Google Scholar]
- Denavit, M.D.; Hajjar, J.F.; Perea, T.; Leon, R.T. Seismic performance factors for moment frames with steel-concrete composite columns and steel beams. Earthq. Eng. Struct. Dyn. 2016, 45, 1685–1703. [Google Scholar]
- Zhao, H.; Qian, X.Y.; Zhu, Y.J. Seismic behaviour of post-earthquake composite frame structures with different damage levels. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 58, p. 105482. [Google Scholar]
- Ding, F.X.; Yin, G.A.; Jiang, L.Z.; Bai, Y. Composite frame of circular CFST column to steel-concrete composite beam under lateral cyclic loading. Thin-Walled Struct. 2018, 122, 137–146. [Google Scholar]
- Etli, S.; Güneyisi, E.M. Assessment of seismic behavior factor of code-designed steel–concrete composite buildings. Arab. J. Sci. Eng. 2021, 46, 4271–4292. [Google Scholar]
- Zhao, H. Analysis of seismic behavior of composite frame structures. Steel Compos. Struct. 2016, 20, 719–729. [Google Scholar] [CrossRef]
- Wang, K.; Lu, X.F.; Yuan, S.F.; Cao, D.F.; Chen, Z.X. Analysis on hysteretic behavior of composite frames with concrete-encased CFST columns. J. Constr. Steel Res. 2017, 135, 176–186. [Google Scholar] [CrossRef]
- Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Seismic behavior of composite steel/concrete MRFs: Deformation assessment and behavior factors. Bull. Earthq. Eng. 2015, 13, 3871–3896. [Google Scholar] [CrossRef]
- Karthiga, S.N.; Santhosh, R.; Kannan, V. Comparison of seismic performance of reinforced concrete frame structure and composite frame structure using response spectrum analysis. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 764, p. 012057. [Google Scholar]
- Andreotti, R.; Giuliani, G.; Tondini, N.; Bursi, O.S. Hybrid simulation of a partial-strength steel–concrete composite moment-resisting frame endowed with hysteretic replaceable beam splices. Earthq. Eng. Struct. Dyn. 2023, 52, 51–70. [Google Scholar] [CrossRef]
- Li, J.; Xu, L. Seismic performance improvement of continuous rigid-frame bridges with hybrid control system under near-fault ground motions. Soil Dyn. Earthq. Eng. 2023, 168, 107858. [Google Scholar] [CrossRef]
- Hüsem, M.; Nasery, M.M.; Okur, F.Y.; Altunişik, A.C. Experimental evaluation of damage effect on dynamic characteristics of concrete encased composite column-beam connections. Eng. Fail. Anal. 2018, 91, 129–150. [Google Scholar] [CrossRef]
- Kanyilmaz, A.; Muhaxheri, M.; Castiglioni, C.A. Influence of repairable bolted dissipative beam splices (structural fuses) on reducing the seismic vulnerability of steel-concrete composite frames. Soil Dyn. Earthq. Eng. 2019, 119, 281–298. [Google Scholar] [CrossRef]
- Nasery, M.M.; Hüsem, M.; Okur, F.Y.; Altunişik, A.C. Damage effect on experimental modal parameters of haunch strengthened concrete-encased composite column–beam connections. Int. J. Damage Mech. 2020, 29, 297–334. [Google Scholar] [CrossRef]
- Qi, L.; Xue, J.; Zhai, L.; Zhao, X.; Leon, R.T. Experimental and numerical studies on seismic performance of traditional style steel-concrete composite frame. Compos. Struct. 2018, 201, 514–527. [Google Scholar] [CrossRef]
- Xue, J.; Ma, L.; Zhao, X.; Zhang, X.; Zhai, L.; Zhao, X. Investigation on steel-concrete composite frame in Chinese traditional style buildings by pseudo-dynamic test. J. Constr. Steel Res. 2019, 157, 282–296. [Google Scholar] [CrossRef]
- Rashidi, M.; Sharafi, P.; Alembagheri, M.; Bigdeli, A.; Samali, B. Operational modal analysis, testing and modelling of prefabricated steel modules with different LSF composite walls. Materials 2020, 13, 5816. [Google Scholar] [CrossRef]
- Zeng, L.; Xiao, Y.; Chen, Y.; Jin, S.; Xie, W.; Li, X. Seismic damage evaluation of concrete-encased steel frame-reinforced concrete core tube buildings based on dynamic characteristics. Appl. Sci. 2017, 7, 314. [Google Scholar] [CrossRef]
- Reena, G.C.; Gurupatham BG, A.; Tsavdaridis, K.D. Column link behavior in eccentrically braced composite 3-dimensional frames. Buildings 2023, 13, 2970. [Google Scholar] [CrossRef]
- Liang, Q.Q. Analysis and Design of Steel and Composite Structures; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Application of the hybrid force/displacement (HFD) seismic design method to composite steel/concrete plane frames. J. Constr. Steel Res. 2015, 115, 179–190. [Google Scholar] [CrossRef]
- Gajbhiye, P.D.; Mashaan, N.S.; Bhaiya, V.; Wankhade, R.L.; Vishnu, S.P. Inelastic Behavior of Steel and Composite Frame Structure Subjected to Earthquake Loading. Appl. Mech. 2023, 4, 899–926. [Google Scholar] [CrossRef]
- Johnson, R.P. Composite Structures of Steel and Concrete: Beams, Slabs, Columns and Frames for Buildings; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Abbas, H.; Siddiqui, N.A.; Khateeb, B.M.; Almusallam, T.H.; Al-Salloum, Y.A. Performance of new CFST square column-to-foundation connections for cyclic loads. J. Constr. Steel Res. 2021, 185, 106868. [Google Scholar] [CrossRef]
- Khateeb, B.M.; Siddiqui, N.A.; Almusallam, T.H.; Abbas, H.; Al-Salloum, Y.A. Behavior of novel CFST circular column-to-foundation connections under cyclic loading. Eng. Struct. 2020, 221, 111051. [Google Scholar] [CrossRef]
- Serras, D.N.; Panagaki, S.D.; Skalomenos, K.A.; Hatzigeorgiou, G.D. Inelastic lateral and seismic behaviour of concrete-filled steel tubular pile foundations. Soil Dyn. Earthq. Eng. 2021, 143, 106657. [Google Scholar] [CrossRef]
- Zhou, M.; Yuan, W.; Zhang, Y. Seismic material properties of reinforced concrete and steel casing composite concrete in elevated pile-group foundation. Pol. Marit. Res. 2015, 22, 141–148. [Google Scholar] [CrossRef][Green Version]
- Wang, N.; Zhou, F.; Xu, H.; Xu, Z. Experimental study on steel-plate composite wall-to-foundation connections subjected to combined axial compression and cyclic lateral-force. Eng. Struct. 2020, 207, 110205. [Google Scholar] [CrossRef]
- Vakili Sadeghi, H.; Mirghaderi, S.R.; Epackachi, S.; Asgarpoor, M.; Gharavi, A. Numerical study on split base plate connection with concentric anchors between steel-plate composite wall and concrete basemat. Struct. Des. Tall Spec. Build. 2022, 31, e1937. [Google Scholar]
- Kurt, E.G.; Varma, A.H.; Sohn, Y.M. Direct shear strength of rebar-coupler anchor systems for steel-plate composite (SC) walls. Int. J. Steel Struct. 2016, 16, 1397–1409. [Google Scholar]
- Siddiqui, N.A.; Abbas, H.; Khateeb, B.M.; Almusallam, T.H.; Al-Salloum, Y. Optimum embedment depths for CFST column-to-foundation connections: Analytical and reliability-based approach. J. Build. Eng. 2024, 91, 109628. [Google Scholar]
- Feng, M.; Liu, B.; Zhang, L.; Wang, Y.; Sun, H. Seismic behavior of embedded rubberized concrete-filled corrugated steel tube column-to-foundation connections: Experimental, numerical modelling, and design. Soil Dyn. Earthq. Eng. 2024, 176, 108285. [Google Scholar]
- Li, X.; Xiao, Y.; Xu, Y.M.; Lu, J.; Ding, B.D.; Zhou, T. Structural behavior of double-CFT-pile foundations under cyclic loads. Soil Dyn. Earthq. Eng. 2020, 128, 105863. [Google Scholar]
- Won, D.; Lee, J.; Seo, J.; Kang, Y.J.; Kim, S. Hysteretic performance of column-footing joints with steel composite hollow RC columns under cyclic load. J. Build. Eng. 2020, 29, 101165. [Google Scholar]
- Thusoo, S.; Obara, T.; Kono, S.; Miyahara, K. Design models for steel-encased high-strength precast concrete piles under axial-flexural loads. Eng. Struct. 2021, 228, 111465. [Google Scholar]
- Stephens, M.T.; Lehman, D.E.; Roeder, C.W. Design of CFST column-to-foundation/cap beam connections for moderate and high seismic regions. Eng. Struct. 2016, 122, 323–337. [Google Scholar]
- Wang, W.; Lyu, X.; Zheng, J.; Yi, S.; Li, J.; Yu, Y. Post-Fire Seismic Performance of Concrete-Filled Steel Tube Frame Structures Considering Soil-Structure Interaction (SSI). Buildings 2024, 14, 555. [Google Scholar] [CrossRef]
- Darwish, A.Q.; Bhandari, M. Seismic response reduction of high rise steel-concrete composite buildings equipped with base isolation system. Mater. Today Proc. 2022, 59, 516–524. [Google Scholar]
- Darwish, A.Q.; Bhandari, M. Vibration response reduction of seismic forces using lead rubber bearing isolators in composite buildings. J. Vib. Eng. Technol. 2022, 10, 1309–1324. [Google Scholar] [CrossRef]
- Li, K.; Fa, G. The structural design and earthquake resistance assessment of composite steel–concrete frame structures with welded dissipative fuses. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 53, pp. 742–748. [Google Scholar]
- Li, C.; Liu, Y.; Li, H.N. Fragility assessment and optimum design of a steel–concrete frame structure with hybrid energy-dissipated devices under multi-hazards of earthquake and wind. Eng. Struct. 2021, 245, 112878. [Google Scholar] [CrossRef]
- Zhuang, L.; Wang, J.; Nie, X.; Wu, Z. Experimental study on seismic behaviour of eccentrically braced compo-site frame with vertical LYP steel shear link. Eng. Struct. 2022, 255, 113957. [Google Scholar] [CrossRef]
- Javaid, K.; Verma, N. Seismic performance of irregular composite buildings: A comparative study of the effectiveness of buckling restrained braces and viscous dampers. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Guo, L.; Wang, J. Hysteretic energy distribution model of CFDST composite frame with metallic dampers using coupled shear-flexural beam model. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 57, p. 104971. [Google Scholar]
- Zhuang, L.D.; Zhao, J.Z. Numerical Study on the Seismic Behavior of Eccentrically Braced Composite Frames with a Vertical Low-Yield-Point Steel Shear Link. Buildings 2022, 12, 1359. [Google Scholar] [CrossRef]
- Thakur, R.; Tiwary, A.K. Comparative study on the effectiveness of fluid viscous dampers and base isolation: An approach toward enhancing seismic performance of composite structures. Innov. Infrastruct. Solut. 2023, 8, 267. [Google Scholar] [CrossRef]
- Zhao, J.Z.; Tao, M.X.; Zhuang, L.D. Development of bent shear panel dampers for eccentrically braced composite frames. J. Constr. Steel Res. 2022, 193, 107292. [Google Scholar]
- Li, B.; Wang, J.; Yang, J.; Pan, X.; Baniotopoulos, C.C. Pseudo-dynamic response and analytical evaluation of blind bolted CFT frames with BRBs. J. Constr. Steel Res. 2020, 166, 105744. [Google Scholar] [CrossRef]
- Katsimpini, P.; Papagiannopoulos, G.; Hatzigeorgiou, G. Seismic Response of a Cable-Stayed Bridge with Concrete-Filled Steel Tube (CFST) Pylons Equipped with the Seesaw System. GeoHazards 2024, 5, 1074–1092. [Google Scholar] [CrossRef]
- Katsimpini, P. On the Seismic Response of Composite Structures Equipped with Wall Dampers Under Multiple Earthquakes. Modelling 2024, 6, 1. [Google Scholar] [CrossRef]
- Katsimpini, P.; Papagiannopoulos, G.; Hatzigeorgiou, G. A Simple Method to Evaluate the Bearing Capacity of Concrete-Filled Steel Tubes with Rectangular and Circular Sections: Beams, Columns, and Beam–Columns. Appl. Sci. 2024, 14, 8995. [Google Scholar] [CrossRef]
- Chorafa, E.; Skrapalliou, E.; Katsimpini, P. On the Nonlinear Behavior of Composite Structures under Multiple Earthquakes Considering Soil–Structure Interaction. CivilEng 2024, 5, 673–693. [Google Scholar] [CrossRef]
- Javaid, K.; Verma, N. Vibration control of seismic forces using viscous dampers and buckling restrained braces in irregular composite buildings. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2023; Volume 1110, p. 012052. [Google Scholar]
- Zandonini, R.; Baldassino, N.; Freddi, F.; Roverso, G. Steel-concrete frames under the column loss scenario: An experimental study. J. Constr. Steel Res. 2019, 162, 105527. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, W.D.; Li, H.W. Progressive collapse resistance of composite frame with concrete-filled steel tubular column under a penultimate column removal scenario. J. Constr. Steel Res. 2022, 189, 107085. [Google Scholar] [CrossRef]
- Zheng, Y.H.; Zhong, W.H.; Tan, Z.; Meng, B.; Duan, S.C. A novel modeling method for fiber-based progressive collapse analysis of composite frames. Eng. Fail. Anal. 2022, 140, 106519. [Google Scholar] [CrossRef]
- Wang, W.; Li, H.; Wang, J. Progressive collapse analysis of concrete-filled steel tubular column to steel beam connections using multi-scale model. In Structures; Elsevier: Amsterdam, The Netherlands, 2017; Volume 9, pp. 123–133. [Google Scholar]
- Papavasileiou, G.; Pnevmatikos, N. The cost of retrofitting steel-concrete composite buildings against progressive collapse with steel cables. Int. J. Progress. Sci. Technol. (IJPSAT) 2017, 6, 103–115. [Google Scholar]
- Wang, J.; Li, Y. Collapse Resistance of Composite Structures with Various Optimized Beam–Column Connection Forms. J. Compos. Sci. 2023, 7, 477. [Google Scholar] [CrossRef]
- Bai, Y.; Hu, H.; Wang, J.; Sun, Q. Modeling on collapse behaviour of high-rise concrete-filled steel composite frames under over-design seismic excitations. Struct. Infrastruct. Eng. 2017, 13, 1563–1575. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, W.D. Multi-scale numerical simulation analysis of CFST column-composite beam frame un-der a column-loss scenario. J. Constr. Steel Res. 2022, 190, 107151. [Google Scholar] [CrossRef]
- Wang, K.; Luo, H.; Guo, K.; Zhou, J.; Ma, H. Seismic collapse resistance performance on out-jacketing frames with concrete-encased CFST columns for adding storeys. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 33, pp. 41–53. [Google Scholar]
- Papavasileiou, G.S.; Charmpis, D.C.; Lagaros, N.D. Optimized seismic retrofit of steel-concrete composite buildings. Eng. Struct. 2020, 213, 110573. [Google Scholar] [CrossRef]
- Papavasileiou, G.S.; Charmpis, D.C. Earthquake-resistant buildings with steel or composite columns: Comparative assessment using structural optimization. J. Build. Eng. 2020, 27, 100988. [Google Scholar]
- Papavasileiou, G.S.; Charmpis, D.C. Seismic design optimization of multi–storey steel–concrete composite buildings. Comput. Struct. 2016, 170, 49–61. [Google Scholar]
- Lin, Y.; Zhang, X. Life-cycle cost-oriented multiobjective optimization of composite frames considering the slab effect. Struct. Des. Tall Spec. Build. 2023, 32, e2008. [Google Scholar]
- Kamaris, G.S.; Skalomenos, K.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Seismic damage estimation of in-plane regular steel/concrete composite moment resisting frames. Eng. Struct. 2016, 115, 67–77. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdipour Moghanni, R.; Javadi, S.M. Chaotic optimization algorithm for performance-based optimization design of composite moment frames. Eng. Comput. 2022, 38, 2729–2741. [Google Scholar]
- Lin, Y.; Bi, K.; Zong, Z.; Hao, H.; Lin, J.; Chen, Y. Seismic performance of steel-concrete composite rigid-frame bridge: Shake table test and numerical simulation. J. Bridge Eng. 2020, 25, 04020032. [Google Scholar]
- Paolacci, F.; Giannini, R.; Alessandri, S.; Corritore, D. On the cyclic behaviour of new pier-to-deck connections for short-medium span composite I-girder bridges. J. Traffic Transp. Eng. 2018, 5, 439–453. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, H.; Wang, X.; Liu, J. Seismic behavior of dumb-bell steel tube confined reinforced concrete piers. Eng. Struct. 2020, 206, 110126. [Google Scholar]
- Zhou, X.; Xu, T.; Liu, J.; Wang, X.; Chen, Y.F. Seismic performance of concrete-encased column connections for concrete filled thin-walled steel tube piers. Eng. Struct. 2022, 269, 114803. [Google Scholar] [CrossRef]
- Du, C.; Li, Z.X.; Liang, X.; Zhang, H.; Zhao, B. Shaking table test on seismic behavior of posttensioned precast segmental Concrete-Filled double skin steel tubular piers. Eng. Struct. 2023, 294, 116752. [Google Scholar] [CrossRef]
- Gu, C.; Wang, X.; Zhou, X.; Huang, C. Performance-based assessment of the novel prefabricated CFST bridge pier by numerical approach. Eng. Struct. 2024, 314, 118362. [Google Scholar] [CrossRef]
- Xiang, N.; Feng, Y.; Chen, X. Novel fiber-based seismic response modelling and design method of partially CFST bridge piers considering local buckling effect. Soil Dyn. Earthq. Eng. 2023, 170, 107911. [Google Scholar] [CrossRef]
- Fu, T.; Ren, X.; Wang, K.; Zhu, Z. Seismic performance of prefabricated steel tube-confined concrete circular pier. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 43, pp. 910–925. [Google Scholar]
- Li, Z.X.; Du, C.; Liu, D.; Liang, X.; Zhao, B. Comparative study on seismic performance of concrete-filled double skin tubular piers and hollow concrete piers: Experimental and analytical. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 49, pp. 1078–1092. [Google Scholar]
- Li, Z.X.; Du, C.; Liang, X.; Zhang, H.; Zhao, B. Experimental and numerical investigation on hysteretic behavior of posttensioned precast segmental Concrete-filled double skin steel tubular piers. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 54, pp. 1772–1787. [Google Scholar]
- Lin, Y.; Li, Y.; Zong, Z.; Bi, K.; Xing, K.; Li, Y. Numerical study of seismic performance of steel-concrete composite rigid-frame bridge with precast segmental CFDST piers crossing fault-rupture zones. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 56, p. 105039. [Google Scholar]
- Yan, J.; Yang, J.; Zheng, J.; Jiang, K.; Jiang, A.; Ning, X.; Han, X.; Li, H. Experimental study on GFRP-steel double-skin rubber concrete composite piers under mixed loading. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; Volume 64, p. 106493. [Google Scholar]
- Zeng, X.; Zhu, S.; Deng, K.; Pang, L.; Zhao, C. Design method and seismic vulnerability of bridges using UHPC-NSC composite pier. Eng. Struct. 2024, 312, 118265. [Google Scholar] [CrossRef]
- Zeng, X.; Zhu, S.; Deng, K.; Zhao, C.; Zhou, Y. Experimental and numerical study on cyclic behavior of a UHPC-RC composite pier. Earthq. Eng. Eng. Vib. 2023, 22, 731–745. [Google Scholar]
- Wu, Y.; Zhang, N.; Li, J.; Gao, M.; Chen, J.; Sha, X. A research on the shear capacity of column pier embedded steel tube. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 397, p. 012038. [Google Scholar]
- Younesi, A.; Rezaeifar, O.; Gholhaki, M.; Esfandiari, A. Damage detection in concrete filled tube columns based on experimental modal data and wavelet technique. Mech. Adv. Compos. Struct. 2020, 7, 245–254. [Google Scholar]
- Yue, J.; Fang, H.; Xia, Y.; Wang, H.; Wu, K. Damage Evolutions and AE Characteristics for Square Concrete-Filled Steel Tubular Columns Under Axial Load. Int. J. Steel Struct. 2020, 20, 1904–1915. [Google Scholar] [CrossRef]
- Shen, Q.; Li, K.; Wang, J.; Wang, F.; Hu, Z.; Li, G. Cyclic behaviour of circular CFT-SG columns under axial tension-compression: Novel FE modelling and design methods. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; Volume 62, p. 106148. [Google Scholar]
- Zhang, J.; Li, Y.; Du, G.; Song, G. Damage detection of L-shaped concrete filled steel tube (L-CFST) columns under cyclic loading using embedded piezoceramic transducers. Sensors 2018, 18, 2171. [Google Scholar] [CrossRef]
- Chen, D.; Montano, V.; Huo, L.; Fan, S.; Song, G. Detection of subsurface voids in concrete-filled steel tubular (CFST) structure using percussion approach. Constr. Build. Mater. 2020, 262, 119761. [Google Scholar]
- Hu, J.W. Smart Connection Systems: Design and Seismic Analysis; Taylor and Francis: London, UK, 2015. [Google Scholar]
- Zhang, J.; Xu, J.; Guan, W.; Du, G. Damage detection of concrete-filled square steel tube (CFSST) column joints under cyclic loading using piezoceramic transducers. Sensors 2018, 18, 3266. [Google Scholar] [CrossRef]
- Zhang, D.; Li, N.; Zhang, S. Energy dissipation and resilience of precast segmented concrete-filled steel tube self-centering column: Parameter study and design methodology. Eng. Struct. 2021, 244, 112747. [Google Scholar]
- Chen, Z.; Qin, Y.; Wang, X. Development of connections to concrete-filled rectangular tubular columns. Adv. Steel Constr. 2015, 11, 408–426. [Google Scholar]
- Hayashi, K.; Skalomenos, K.A.; Inamasu, H.; Luo, Y.B. Self-centering rocking composite frame using double-skin concrete-filled steel tube columns and energy-dissipating fuses in multiple locations. J. Struct. Eng. 2018, 144, 04018146. [Google Scholar]
- Zhong, C. Self-Centering, Shear-Controlling Rocking-Isolation Podium System for Enhanced Resilience of Tall Buildings. Doctoral Dissertation, University of Toronto, ON, Canada, 2023. [Google Scholar]
- Zhang, Y.; Guo, J.; Yang, J.; Li, X. Recent structural developments and applications of magnetorheological dampers (mrd): A review. Magnetochemistry 2023, 9, 90. [Google Scholar] [CrossRef]
- Zhai, Q.; Zhang, J.; Xiao, J.; Du, G.; Huang, Y. Feasibility of piezoceramic transducer-enabled active sensing for the monitoring cross-shaped concrete filled steel tubular (CCFST) columns under cyclic loading. Measurement 2021, 182, 109646. [Google Scholar]
- Velychkovych, A.; Mykhailiuk, V.; Andrusyak, A. Numerical Model for Studying the Properties of a New Friction Damper Developed Based on the Shell with a Helical Cut. Appl. Mech. 2025, 6, 1. [Google Scholar] [CrossRef]
- Landar, S.; Velychkovych, A.; Ropyak, L.; Andrusyak, A. A method for applying the use of a smart 4 controller for the assessment of drill string bottom-part vibrations and shock loads. Vibration 2024, 7, 802–828. [Google Scholar] [CrossRef]
- Shatskyi, I.; Velychkovych, A. Analytical model of structural damping in friction module of shell shock absorber connected to spring. Shock Vib. 2023, 2023, 4140583. [Google Scholar]
- Dutkiewicz, M.; Velychkovych, A.; Shatskyi, I.; Shopa, V. Efficient model of the interaction of elastomeric filler with an open shell and a chrome-plated shaft in a dry friction damper. Materials 2022, 15, 4671. [Google Scholar] [CrossRef]
- Ng, W.L.; Goh, G.L.; Goh, G.D.; Ten, J.S.J.; Yeong, W.Y. Progress and opportunities for machine learning in materials and processes of additive manufacturing. Adv. Mater. 2024, 36, 2310006. [Google Scholar]
- Mohanty, S.; Gokuldoss Prashanth, K. Metallic coatings through additive manufacturing: A review. Materials 2023, 16, 2325. [Google Scholar] [CrossRef]
- Farid, M.I.; Wu, W.; Guiwei, L.; Yu, Z. Research on imminent enlargements of smart materials and structures towards novel 4D printing (4DP: SMs-SSs). Int. J. Adv. Manuf. Technol. 2023, 126, 2803–2823. [Google Scholar]
- Hassan, A.; Alomayri, T.; Noaman, M.F.; Zhang, C. 3D Printed Concrete for Sustainable Construction: A Review of Mechanical Properties and Environmental Impact. Arch. Comput. Methods Eng. 2025, 1–31. [Google Scholar] [CrossRef]
- Baktheer, A.; Classen, M. A review of recent trends and challenges in numerical modeling of the anisotropic behavior of hardened 3D printed concrete. Addit. Manuf. 2024, 89, 104309. [Google Scholar]
- Tahmasebinia, F.; Jabbari, A.A.; Skrzypkowski, K. The Application of Finite Element Simulation and 3D Printing in Structural Design within Construction Industry 4.0. Appl. Sci. 2023, 13, 3929. [Google Scholar] [CrossRef]
- Raphael, B.; Senthilnathan, S.; Patel, A.; Bhat, S. A review of concrete 3D printed structural members. Front. Built Environ. 2023, 8, 1034020. [Google Scholar]
- Shufrin, I.; Pasternak, E.; Dyskin, A. Environmentally friendly smart construction—Review of recent developments and opportunities. Appl. Sci. 2023, 13, 12891. [Google Scholar] [CrossRef]
- Wu, Z.; Memari, A.M.; Duarte, J.P. State of the art review of reinforcement strategies and technologies for 3D printing of concrete. Energies 2022, 15, 360. [Google Scholar] [CrossRef]
- Cao, X.; Wu, S.; Cui, H. Experimental study on in-situ mesh fabrication for reinforcing 3D-printed concrete. Autom. Constr. 2025, 170, 105923. [Google Scholar]
- Menna, C.; Mata-Falcón, J.; Bos, F.P.; Vantyghem, G.; Ferrara, L.; Asprone, D.; Salet, T.; Kaufmann, W. Opportunities and challenges for structural engineering of digitally fabricated concrete. Cem. Concr. Res. 2020, 133, 106079. [Google Scholar]
- Tian, Q.; Zhou, J.; Hou, J.; Zhou, Z.; Liang, Z.; Sun, M.; Hu, J.; Huang, J. Building the future: Smart concrete as a key element in next-generation construction. Constr. Build. Mater. 2024, 429, 136364. [Google Scholar]
- De Schutter, G.; Lesage, K.; Mechtcherine, V.; Nerella, V.N.; Habert, G.; Agusti-Juan, I. Vision of 3D printing with concrete—Technical, economic and environmental potentials. Cem. Concr. Res. 2018, 112, 25–36. [Google Scholar] [CrossRef]
- Amran, M.; Onaizi, A.M.; Fediuk, R.; Vatin, N.I.; Muhammad Rashid, R.S.; Abdelgader, H.; Ozbakkaloglu, T. Self-healing concrete as a prospective construction material: A review. Materials 2022, 15, 3214. [Google Scholar] [CrossRef]
- Qian, H.; Umar, M.; Khan, M.N.A.; Shi, Y.; Manan, A.; Raza, A.; Li, F.; Li, Z.; Chen, G. A state-of-the-art review on shape memory alloys (SMA) in concrete: Mechanical properties, self-healing capabilities, and hybrid composite fabrication. Mater. Today Commun. 2024, 40, 109738. [Google Scholar]
- Albuhairi, D.; Di Sarno, L. Low-carbon self-healing concrete: State-of-the-art, challenges and opportunities. Buildings 2022, 12, 1196. [Google Scholar] [CrossRef]
- Fernandez, C.A.; Correa, M.; Nguyen, M.T.; Rod, K.A.; Dai, G.L.; Cosimbescu, L.; Rousseau, R.; Glezakou, V.A. Progress and challenges in self-healing cementitious materials. J. Mater. Sci. 2021, 56, 201–230. [Google Scholar]
- Luhar, S.; Luhar, I.; Shaikh, F.U.A. A review on the performance evaluation of autonomous self-healing bacterial concrete: Mechanisms, strength, durability, and microstructural properties. J. Compos. Sci. 2022, 6, 23. [Google Scholar] [CrossRef]
- Huseien, G.F.; Nehdi, M.L.; Faridmehr, I.; Ghoshal, S.K.; Hamzah, H.K.; Benjeddou, O.; Alrshoudi, F. Smart bio-agents-activated sustainable self-healing cementitious materials: An all-inclusive overview on progress, benefits and challenges. Sustainability 2022, 14, 1980. [Google Scholar] [CrossRef]
- Nodehi, M.; Ozbakkaloglu, T.; Gholampour, A. A systematic review of bacteria-based self-healing concrete: Biomineralization, mechanical, and durability properties. J. Build. Eng. 2022, 49, 104038. [Google Scholar] [CrossRef]
- Anjali, R.; Kumar, S.A.; Gangolu, J.; Abiraami, R. Experimental study on self-healing of micro-cracks in concrete with combination of environmentally friendly bacteria. Sustain. Struct. Build. 2024, 95, 109. [Google Scholar]
- Hermawan, H.; Wiktor, V.; Gruyaert, E.; Serna, P. Experimental investigation on the bond behaviour of steel reinforcement in self-healing concrete. Constr. Build. Mater. 2023, 383, 131378. [Google Scholar]
- Elmenshawy, Y.; Elmahdy, M.A.; Moawad, M.; Elshami, A.A.; Ahmad, S.S.; Nagai, K. Investigating the bacterial sustainable self-healing capabilities of cracks in structural concrete at different temperatures. Case Stud. Constr. Mater. 2024, 20, e03188. [Google Scholar]
- Al-Obaidi, S.; He, S.; Schlangen, E.; Ferrara, L. Effect of matrix self-healing on the bond-slip behavior of micro steel fibers in ultra-high-performance concrete. Mater. Struct. 2023, 56, 161. [Google Scholar] [CrossRef]
- Şimşek, B. Investigation of self-healing ability of hydroxyapatite blended cement paste modified with graphene oxide and silver nanoparticles. Constr. Build. Mater. 2022, 320, 126250. [Google Scholar]
- VS, S.; Xavier, J.R. Effects of nanomaterials on mechanical properties in cementitious construction materials for high-strength concrete applications: A review. J. Adhes. Sci. Technol. 2024, 38, 3737–3768. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katsimpini, P.; Papagiannopoulos, G.; Hatzigeorgiou, G. An In-Depth Analysis of the Seismic Performance Characteristics of Steel–Concrete Composite Structures. Appl. Sci. 2025, 15, 3715. https://doi.org/10.3390/app15073715
Katsimpini P, Papagiannopoulos G, Hatzigeorgiou G. An In-Depth Analysis of the Seismic Performance Characteristics of Steel–Concrete Composite Structures. Applied Sciences. 2025; 15(7):3715. https://doi.org/10.3390/app15073715
Chicago/Turabian StyleKatsimpini, Panagiota, George Papagiannopoulos, and George Hatzigeorgiou. 2025. "An In-Depth Analysis of the Seismic Performance Characteristics of Steel–Concrete Composite Structures" Applied Sciences 15, no. 7: 3715. https://doi.org/10.3390/app15073715
APA StyleKatsimpini, P., Papagiannopoulos, G., & Hatzigeorgiou, G. (2025). An In-Depth Analysis of the Seismic Performance Characteristics of Steel–Concrete Composite Structures. Applied Sciences, 15(7), 3715. https://doi.org/10.3390/app15073715







