MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems
Abstract
:1. Introduction
Key Contributions
- This is the first publicly available data set specifically designed for bearing fault diagnosis in independent cart systems.
- A comprehensive system description is given, including experimental setup, experimental configurations, sensor configurations, and fault injection methodology.
- It is a multisensor data set capturing vibration signals and system variables under varied operating conditions.
- The data set is structured to support future research in condition monitoring, feature extraction, and predictive maintenance.
2. Description of the Experimental Setup
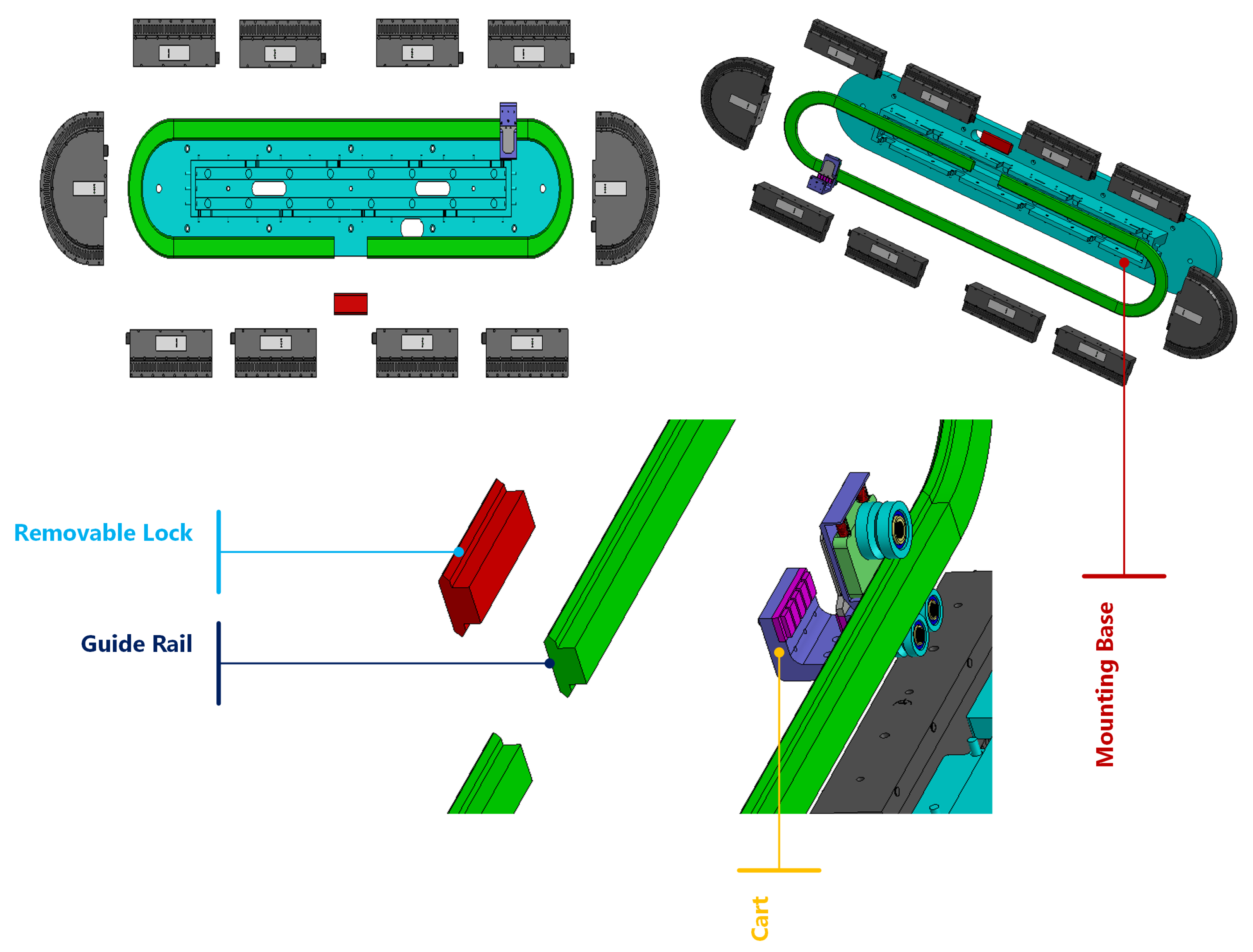
2.1. Linear Motor Modules
2.1.1. Upper Straight Modules Section
2.1.2. Curved Modules
2.1.3. Lower Straight Modules Section
2.2. Cart/Mover
- Magnetic Plates: Each cart has a pair of magnetic plates, with five magnets on each plate. These magnets define the cart’s length along the track as 50 mm and interact with the linear motor’s magnetic field to enable controlled motion.
- Encoder Flag: The cart is equipped with an encoder flag that provides real-time feedback on its actual position along the track. This ensures precise tracking and synchronization of the cart movement with the overall system.
- Rolling Element Bearings: The cart is supported by three rolling element bearings arranged to maintain stability and proper alignment with the guide rail. The configuration includes two smaller, identical bearings positioned on the top and one larger bearing at the bottom. This arrangement secures the cart to the guide rail, ensuring smooth and stable movement. All bearings share the same design characteristics: they feature two rows of deep grooves on the inside and a V-shaped groove on the outer race that matches the profile of the guide rail. In this setup, the bearing’s outer race rotates while the inner race remains stationary. The dimensions and parameters of the bearings used in the experimental setup are detailed in Table 1, providing essential information to understand the mechanical characteristics of the system. The bearings used in this study are part of the GFX Hepco guidance systems for Beckhoff XTS. Detailed specifications regarding the bearing materials, including the types of materials in contact (e.g., steel-on-steel), are provided in the manufacturer’s documentation [35]. This information is critical for understanding the material interactions and operational conditions of the bearings during the experiments.
- Preloading Mechanism: A spring-like preload mechanism is incorporated to adjust grip and evenly distribute forces across the top and bottom bearings. This mechanism improves stability and provides the necessary radial forces for the bearings, ensuring consistent contact with the guide rail under varying load conditions.
| Bearing Type | Number of Rows | Number of Balls | Ball Diameter (mm) | OR Diameter (mm) | IR Diameter (mm) | Pitch Diameter (mm) |
|---|---|---|---|---|---|---|
| Top Bearing | 2 | 7, 7 | 3.95 | 25 | 10.75 | 14.70 |
| Bottom Bearing | 2 | 7, 7 | 5.55 | 34 | 14.60 | 20.15 |
2.3. Accelerometers
2.4. Acquisition System
2.5. Motion Control and System Programming
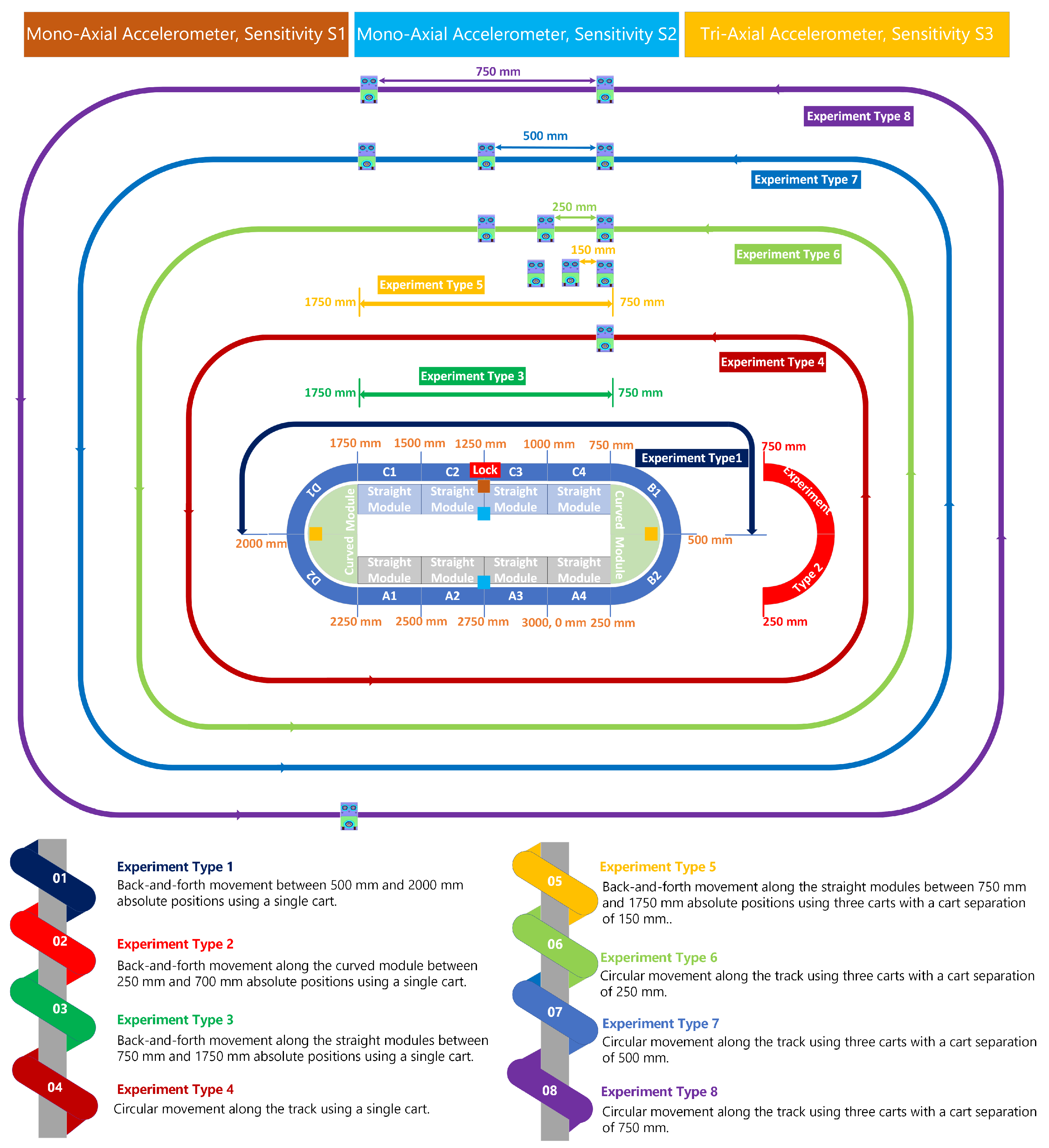
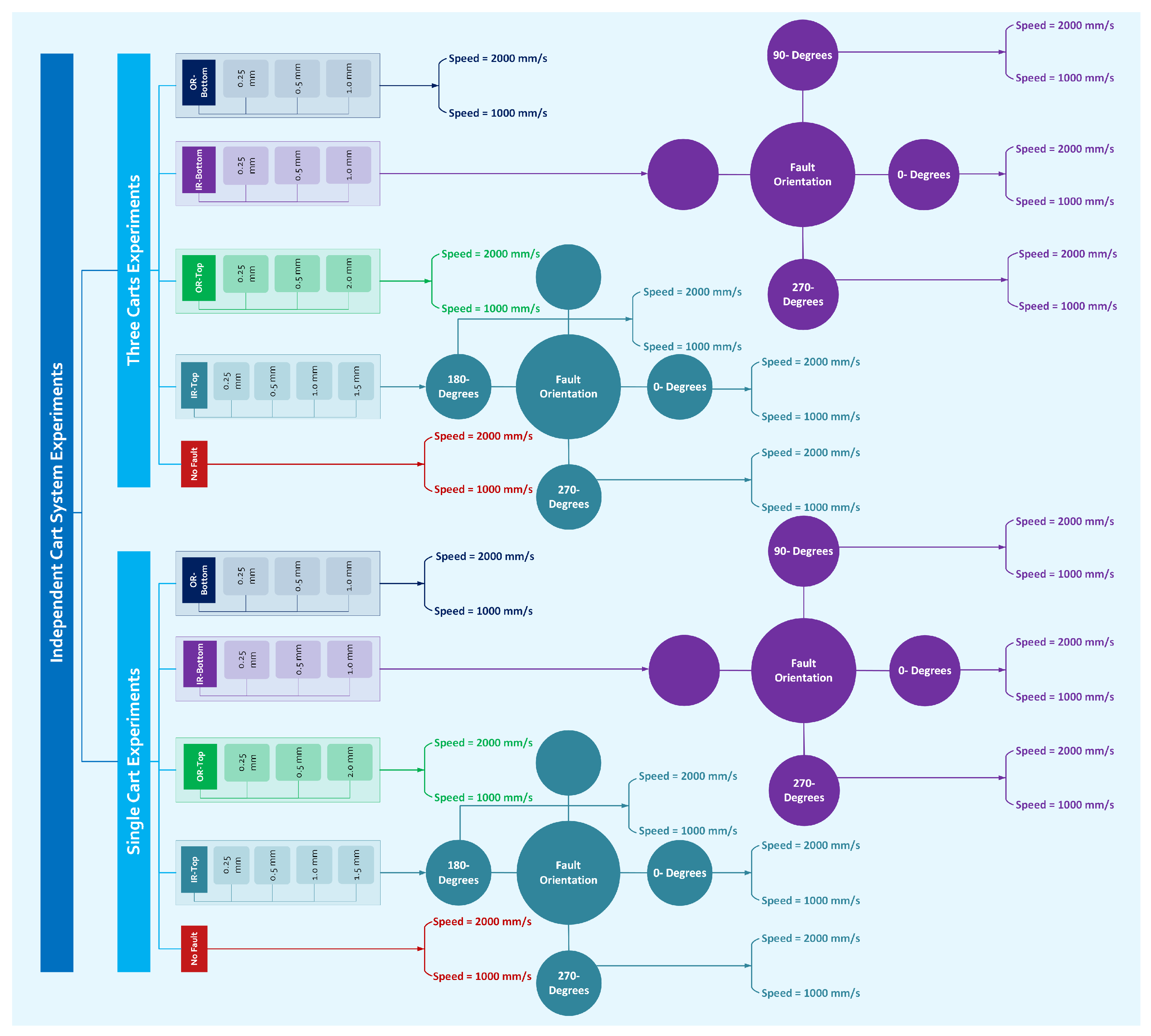
3. Experimental Campaign
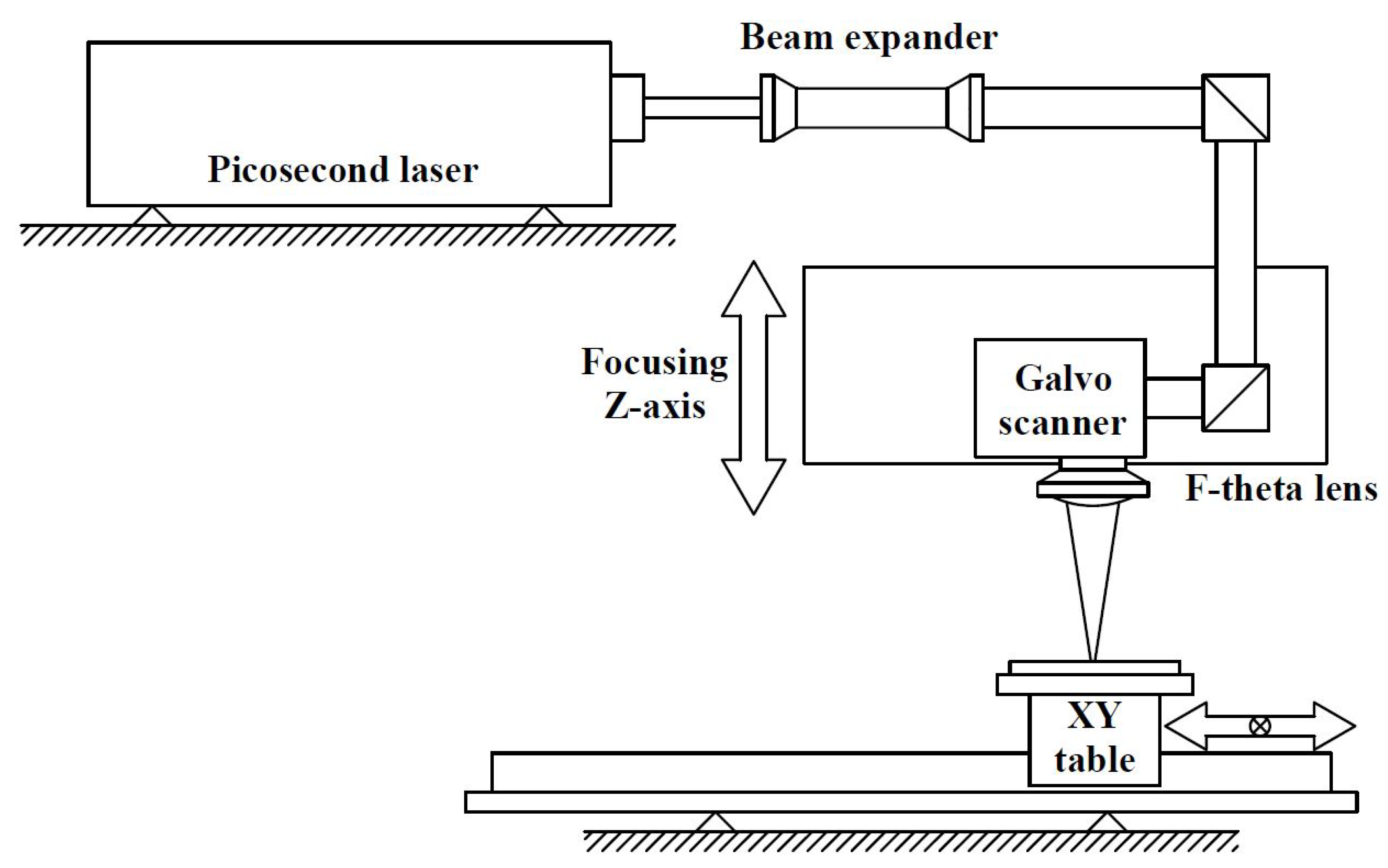
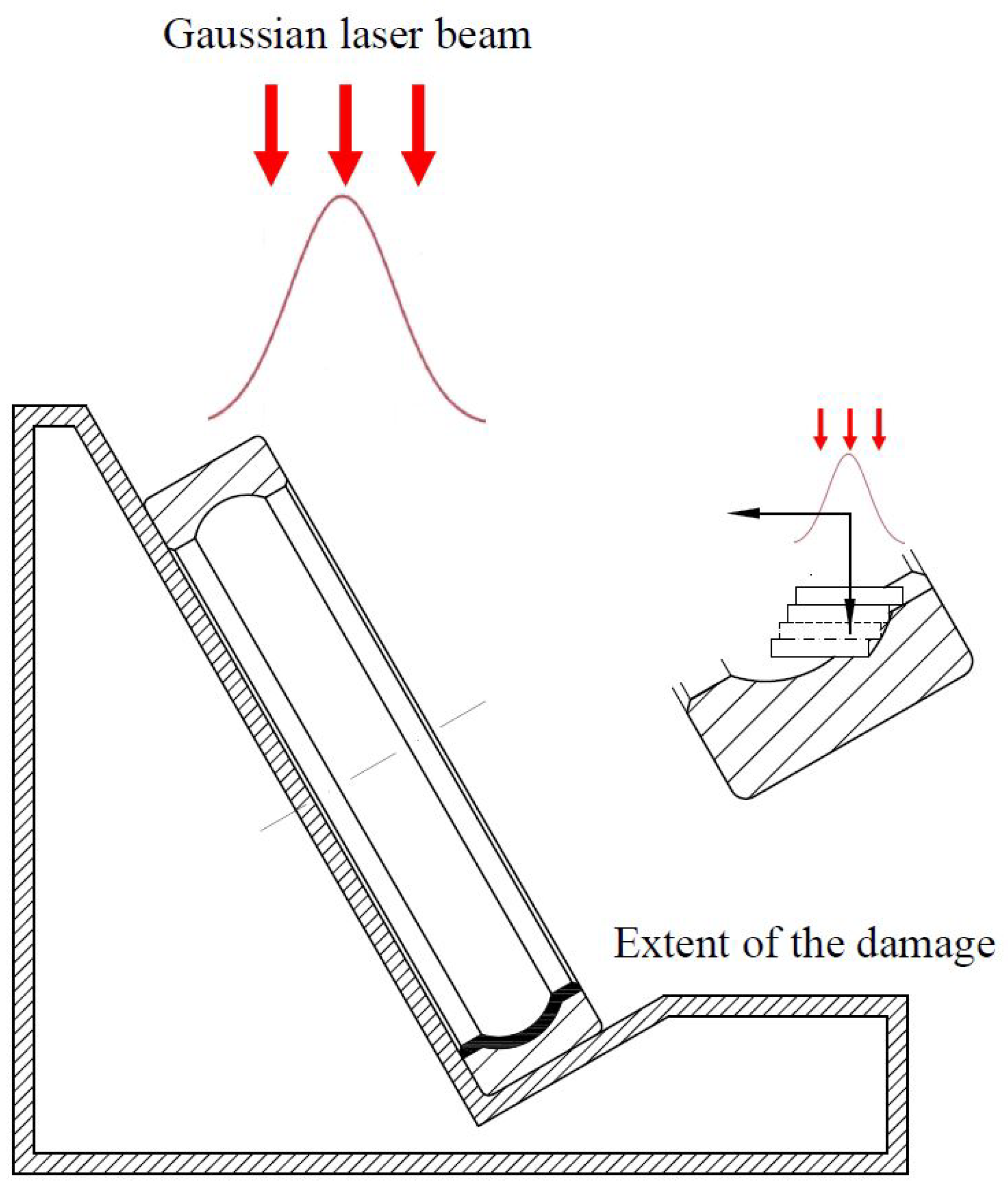
4. Fault Injection Methodology
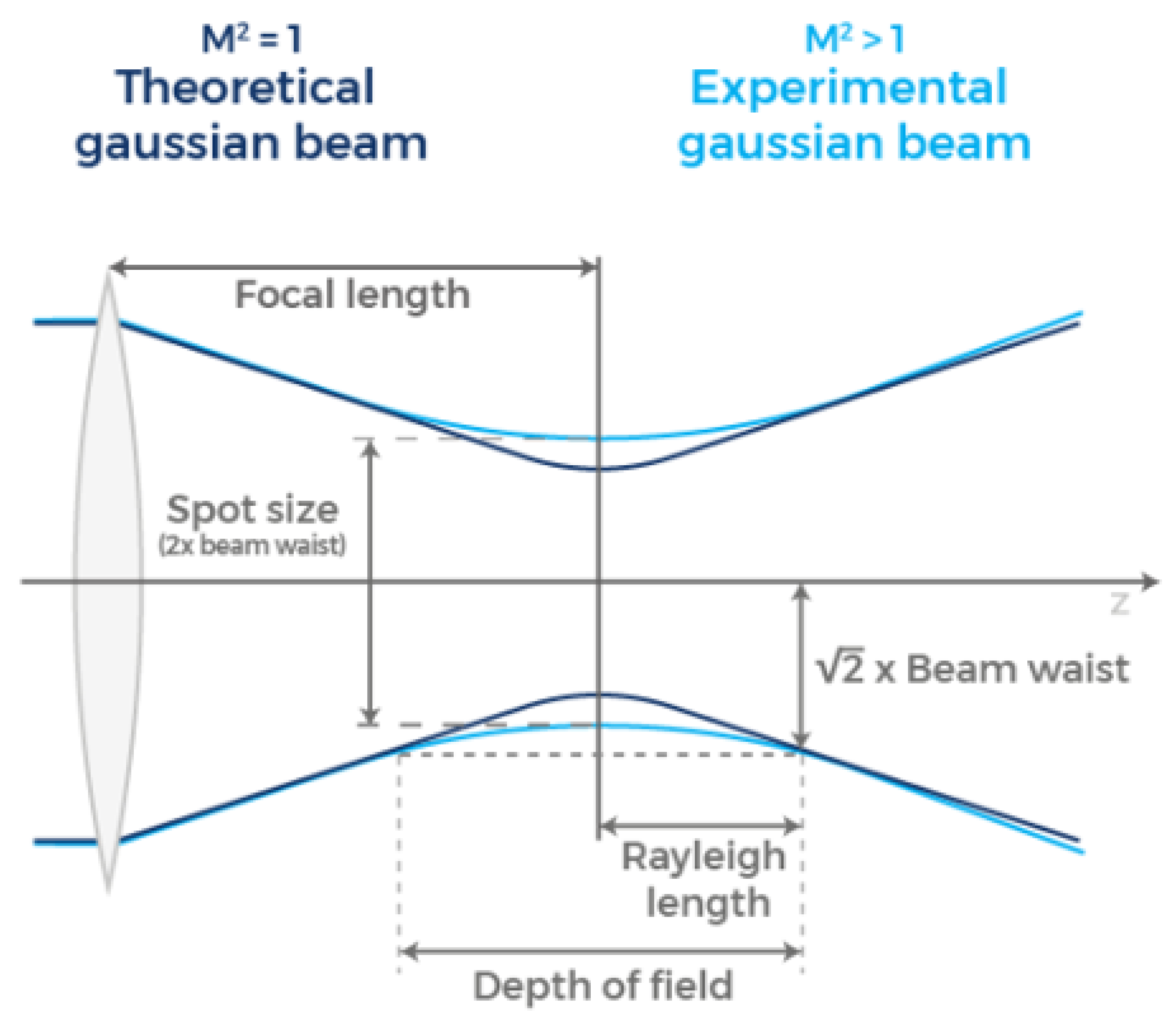
- Rayleigh length , as the distance from the beam waist, where the beam radius is increased by a factor of the :
- Depth of field (D.O.F.) as the distance on either side of the beam waist, , over which the beam diameter grows by 5%
5. Experimental Data Acquisition
5.1. Single-Cart Experiments
5.2. Three-Cart Fleet Experiments
5.3. Bearing Defects
6. Data Set Repository
7. Preprocessing Methodology
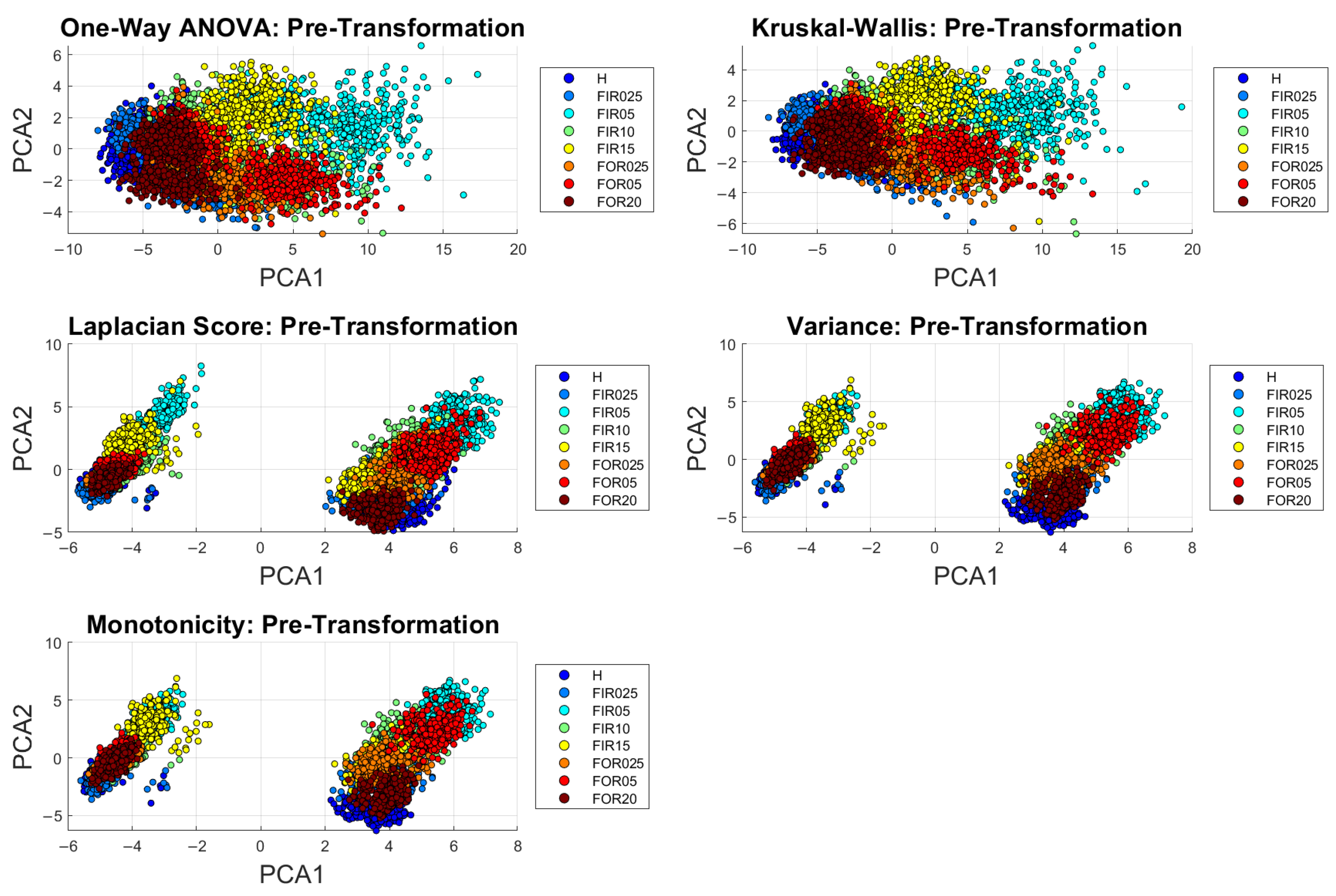
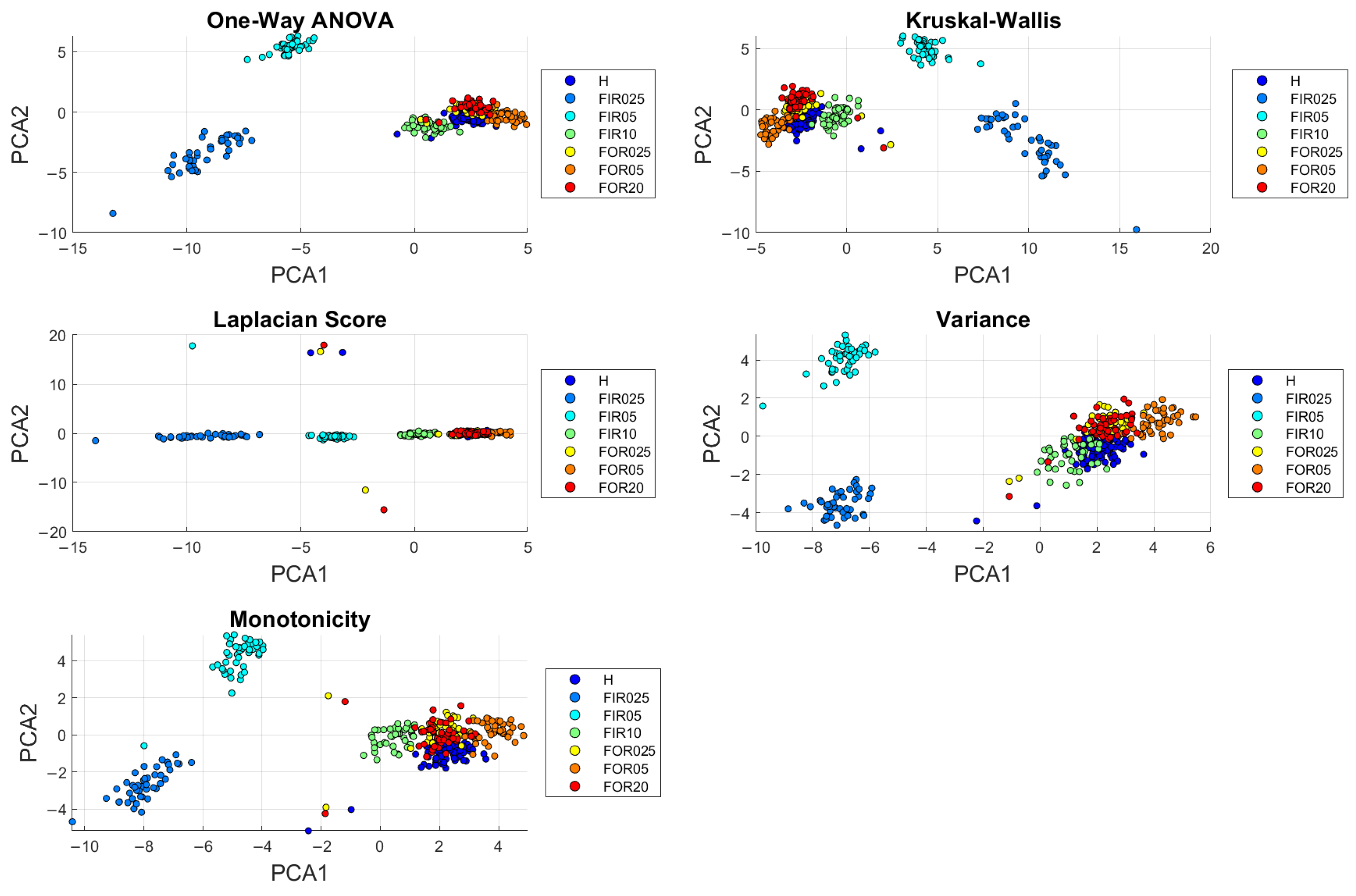
7.1. Feature Ranking Methods
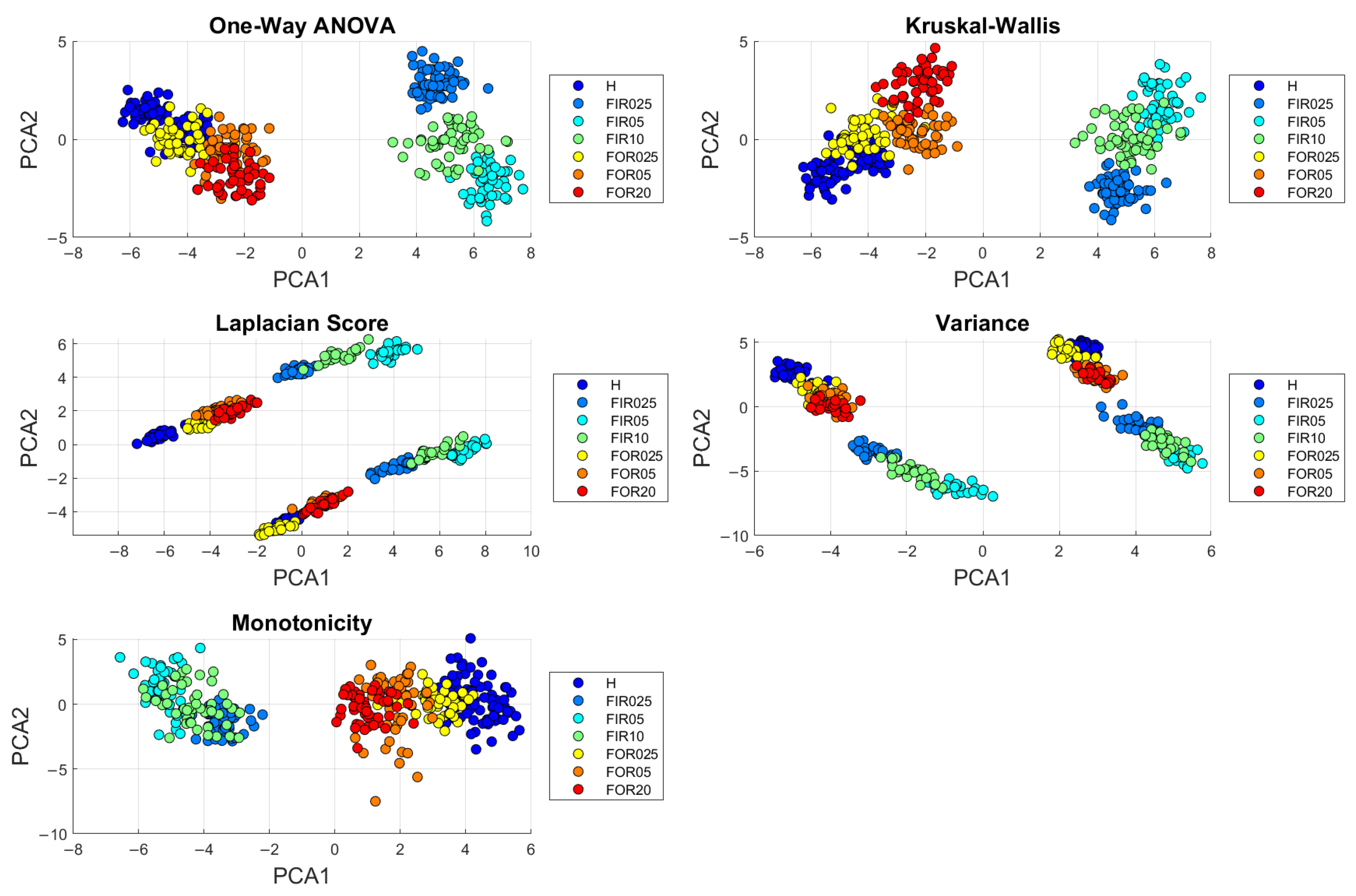
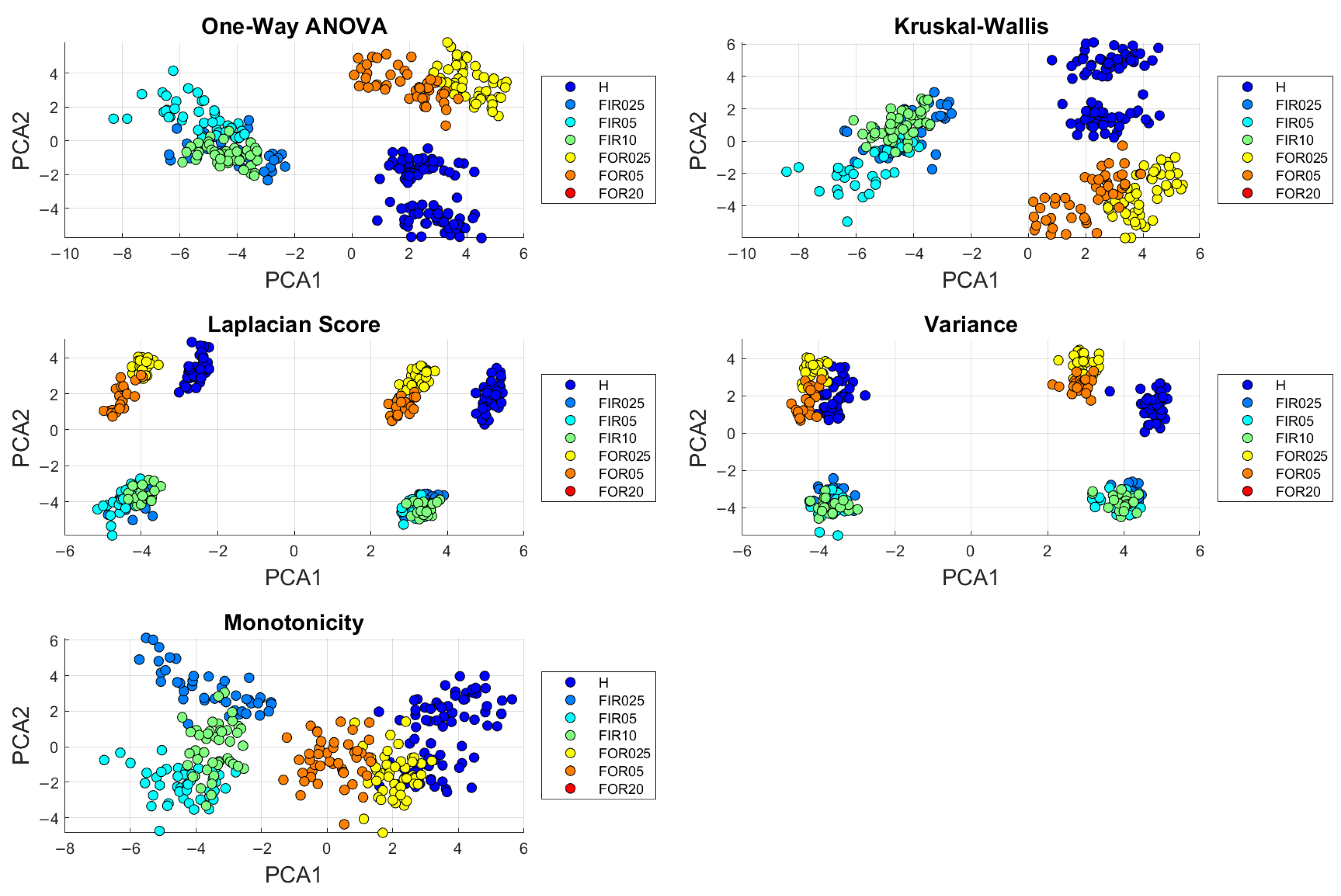
7.1.1. One-Way ANOVA
7.1.2. Kruskal–Wallis
7.1.3. Laplacian Score
7.1.4. Variance
7.1.5. Monotonicity
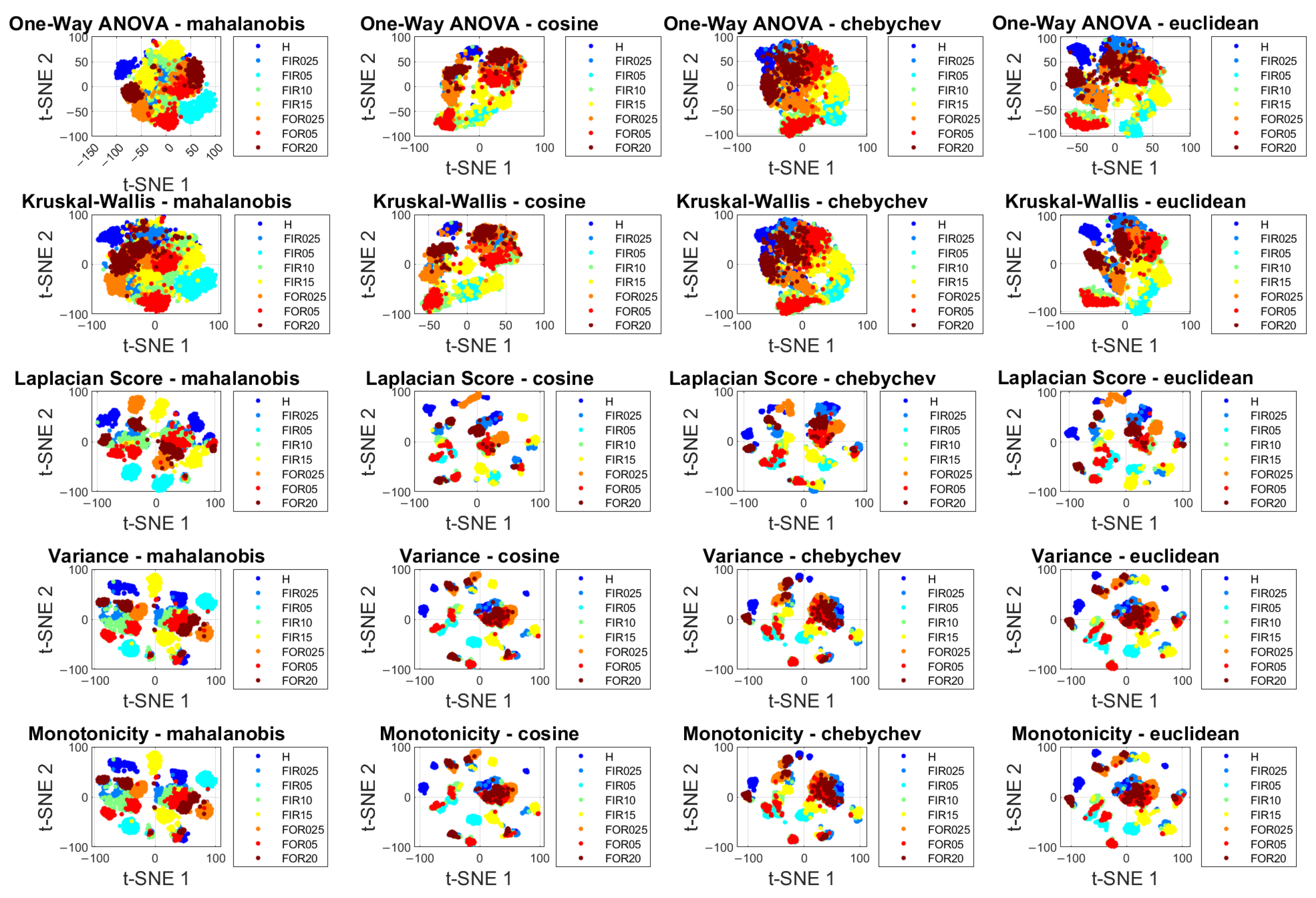
7.2. Dimensionality Reduction
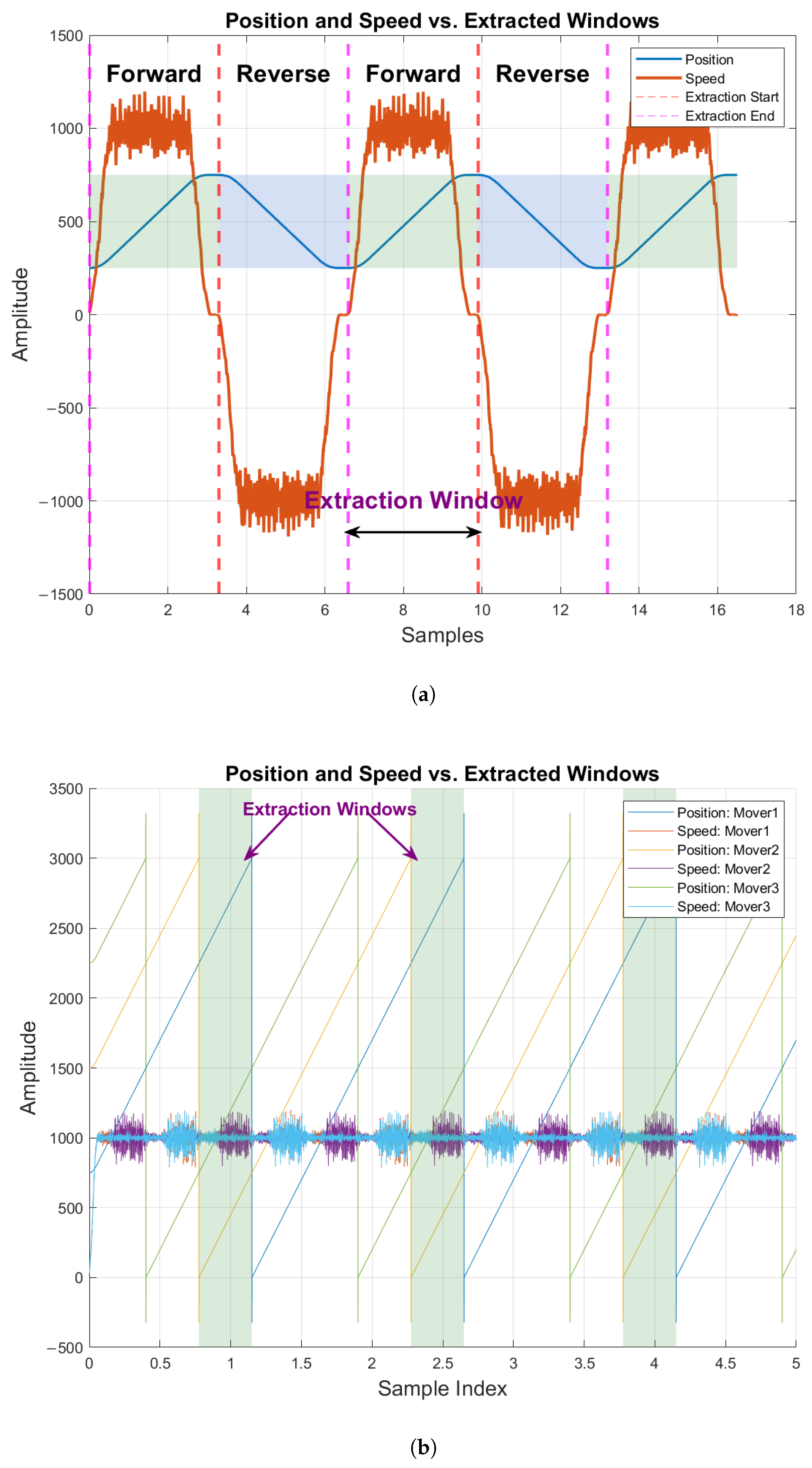
7.3. Speed Profiles
8. Data Visualization and Analysis
8.1. Single Cart Experiments
8.2. Three Cart Experiments
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Data Variables Naming Conventions
Appendix A.1.1. System Variables
- For single-cart experiments, variables are not suffixed with cart numbers.
- For three-cart experiments, the variables are suffixed with _M1, _M2, and _M3 to denote individual carts.
Appendix A.1.2. Vibration Channels
Mono-Axial Accelerometers
- mono_PCB_Top: PCB-manufactured accelerometer mounted on the top section of the guide rail, positioned halfway along the track.
- mono_ifm_Top: ifm-manufactured accelerometer, also near the top section of the guide rail on an aluminum rod, positioned halfway along the track.
- mono_PCB_Bottom: PCB-manufactured accelerometer mounted on the bottom section of the guide rail, positioned halfway along the track.
Tri-Axial Accelerometers
- Sensors capturing vibrations in the X, Y, and Z directions, mounted on the left and right sides of the guide.
| Category | Variable Type | Single-Cart Experiments | Three-Cart Experiments |
|---|---|---|---|
| System Variables | Position | ActHwPos | ActHwPos_M1 ActHwPos_M2 ActHwPos_M3 |
| Following Error | ActFollowingError | ActFollowingError_M1 ActFollowingError_M2 ActFollowingError_M3 | |
| Velocity | ActVelo | ActVelo_M1 ActVelo_M2 ActVelo_M3 | |
| Velocity Error | ActVeloError | ActVeloError_M1 ActVeloError_M2 ActVeloError_M3 | |
| Set Current | SetCurr | SetCurr_M1 SetCurr_M2 SetCurr_M3 | |
| Vibration Channels | Mono-Axial | mono_PCB_Top mono_ifm_Top mono_PCB_Bottom | mono_PCB_Top mono_ifm_Top mono_PCB_Bottom |
| Tri-Axial | X_Guide_Left Y_Guide_Left Z_Guide_Left X_Guide_Right Y_Guide_Right Z_Guide_Right | X_Guide_Left Y_Guide_Left Z_Guide_Left X_Guide_Right Y_Guide_Right Z_Guide_Right |
Appendix A.2. File Naming Conventions for Experimental Data
Appendix A.2.1. Experiment Type 1–4
Appendix A.2.2. Experiment Type 5–8
Appendix A.3. Description of File Names
Fault Condition
- H: No Fault (Healthy).
- F: Bearing Fault.
Experiment Category
- SingleMover: Single-cart experiments.
- 3Movers: Three-cart experiments.
Experiment Description
- StraightTop: Straight path back-and-forth movement along the upper section of the guide rail.
- Curved: Back-and-forth movement limited to the curved module only.
- CompleteRotation: Circular movement along the track.
Separation Details
- 150mmSeparation: The relative distance between two carts is150 mm.
- 250mmSeparation: The relative distance between two carts is 250 mm.
- 500mmSeparation: The relative distance between two carts is 500 mm.
- 750mmSeparation: The relative distance between two carts is 750 mm.
Speed
- 1000: Nominal cart speed profile of 1000 mm/s.
- 2000: Nominal cart speed profile of 2000 mm/s.
Fault Details
- Fault Type: IR (Inner Race), OR (Outer Race).
- Fault Severity: Fault width, 025 (0.25 mm), 05 (0.5 mm), 10 (1.0 mm), 15 (1.5 mm) and 20 (2.0 mm).
Fault Location
- Top: Top bearing.
- Bottom: Bottom bearing.
Trial Number
- Denotes the trial or realization number for the specific experiment (e.g., Real1).
Appendix A.4. Creating and Exporting a YT Scope Project in TwinCAT XAE Shell

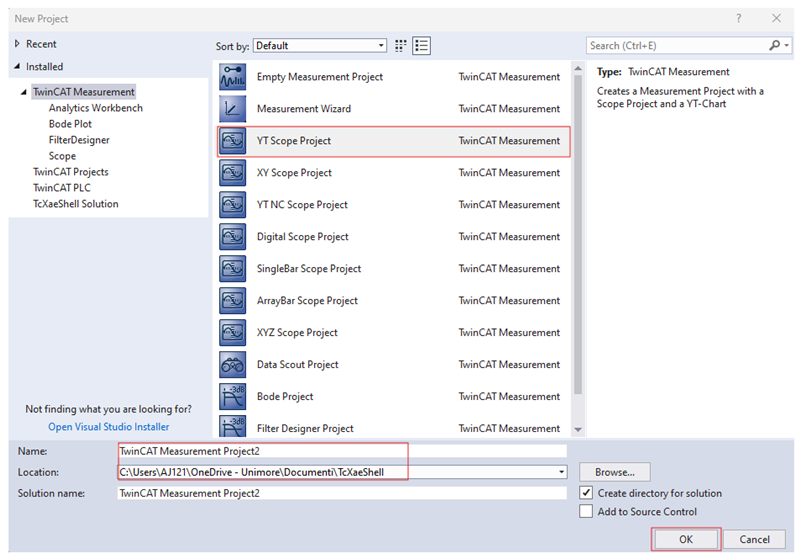
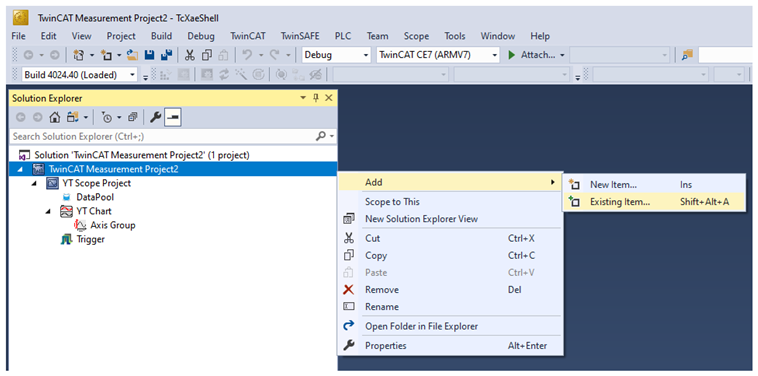
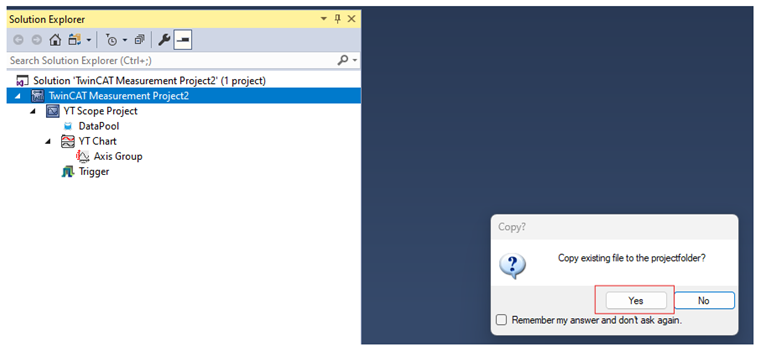
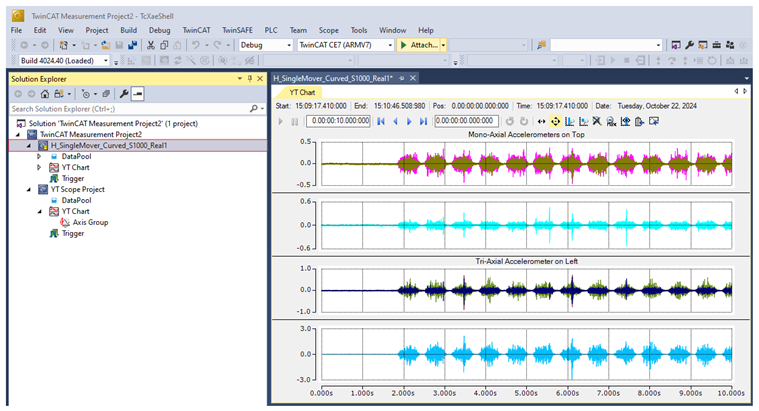

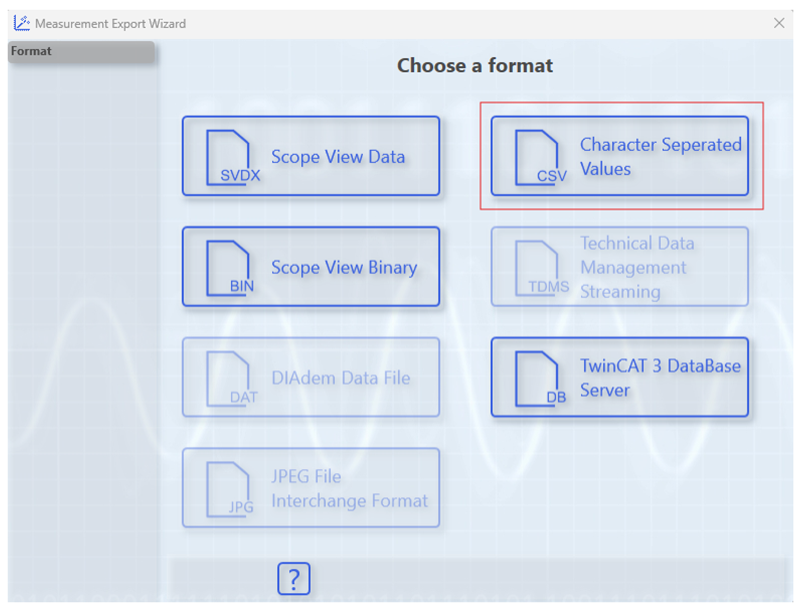
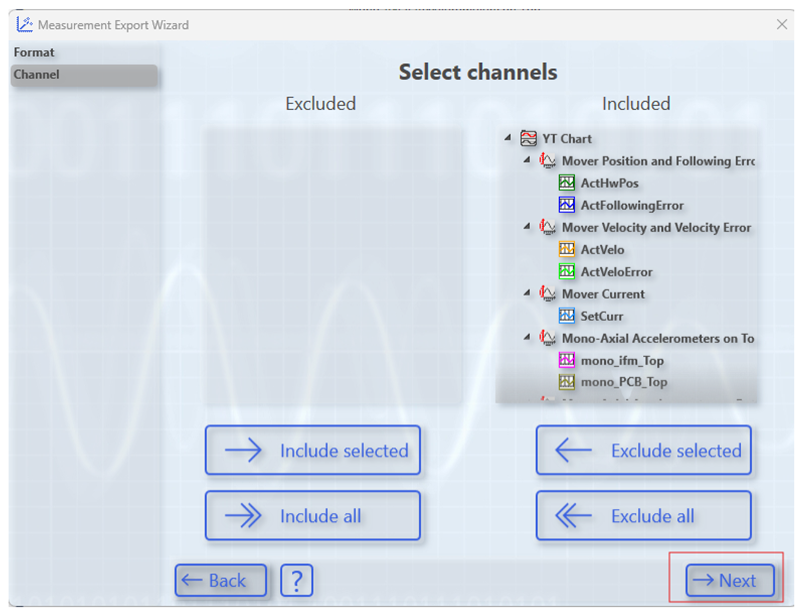
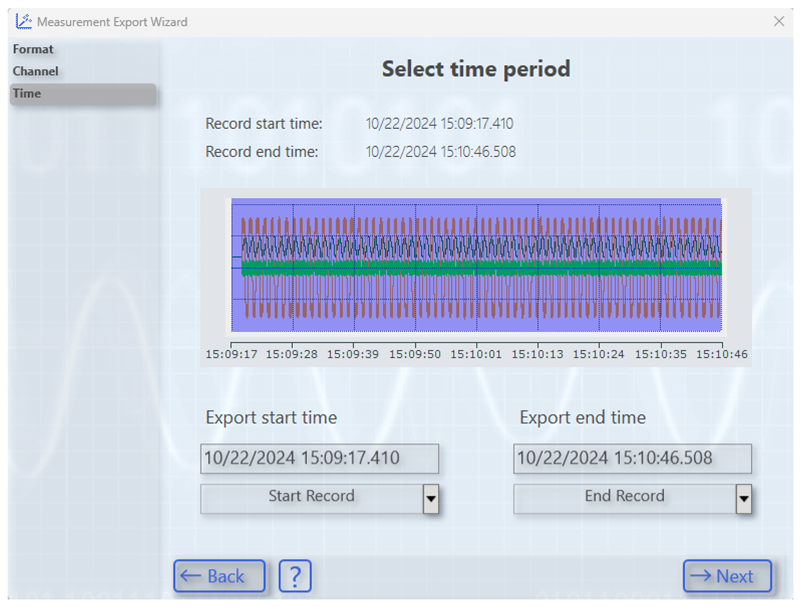
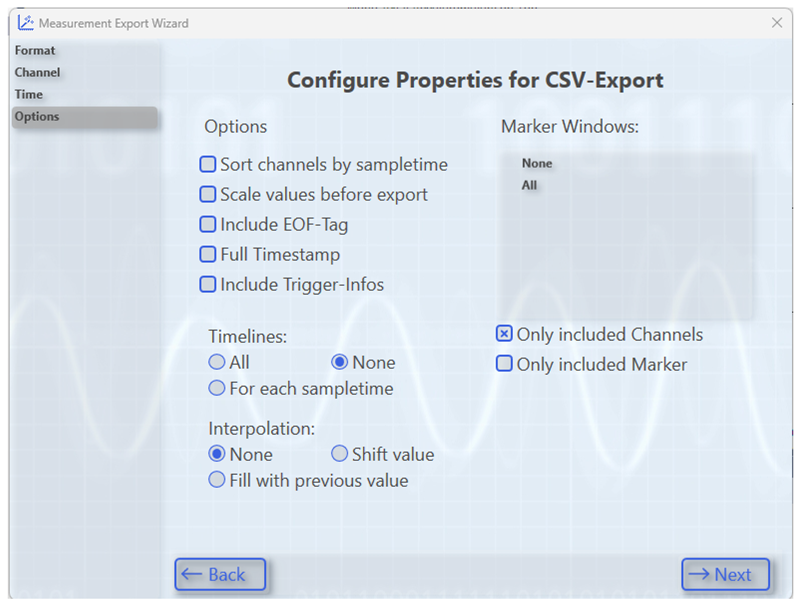
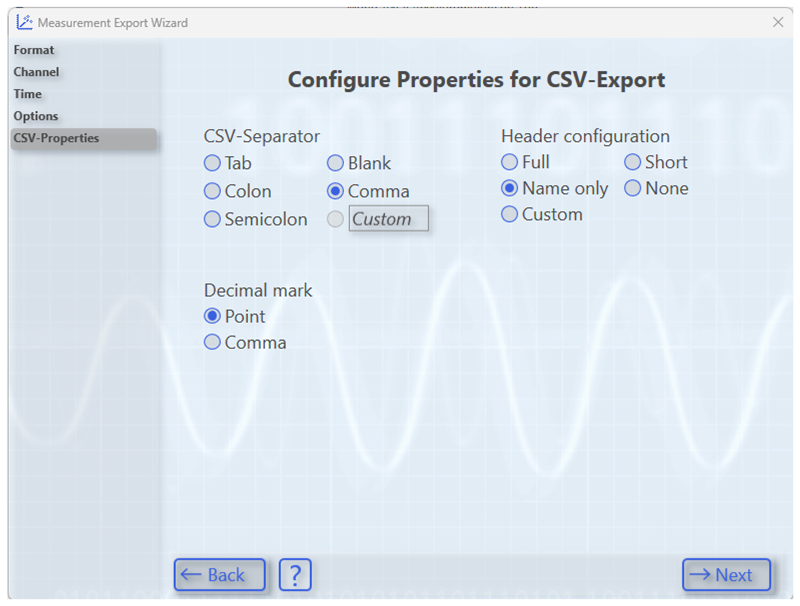
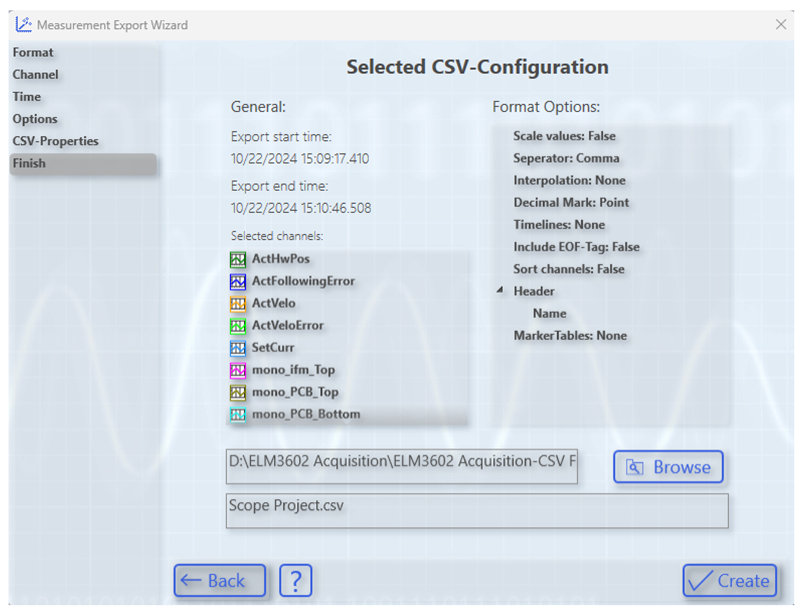
References
- Beckhoff Automation. Extended Transport Systems (XTS). Available online: https://www.beckhoff.com/en-en/products/motion/xts-linear-product-transport/?msclkid=fd69f89dec35190c45d89f054681eef2 (accessed on 20 January 2025).
- Rockwell Automation. Independent Cart Technology. Available online: https://www.rockwellautomation.com/en-us/products/hardware/independent-cart-technology.html (accessed on 20 January 2025).
- Jabbar, A.; D’Elia, G.; Cocconcelli, M. Experimental Setup for Non-stationary Condition Monitoring of Independent Cart Systems. In International Congress and Workshop on Industrial AI and eMaintenance; Kumar, U., Karim, R., Galar, D., Kour, R., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 517–530. [Google Scholar] [CrossRef]
- Jabbar, A.; Cocconcelli, M.; d’Elia, G.; Strozzi, M.; Rubini, R. Results on Experimental Data Analysis of Independent Cart Systems in Non-Stationary Conditions. In Surveillance, Vibrations, Shock and Noise; Institut Supérieur de l’Aéronautique et de l’Espace [ISAE-SUPAERO]: Toulouse, France, 2023; hal-04165905. [Google Scholar]
- Xu, J.; Zhao, L.; Ren, Y.; Li, Z.; Abbas, Z.; Zhang, L.; Islam, M.S. LightYOLO: Lightweight model based on YOLOv8n for defect detection of ultrasonically welded wire terminations. Eng. Sci. Technol. Int. J. 2024, 60, 101896. [Google Scholar] [CrossRef]
- Lazović, T.; Marinković, A.; Atanasovska, I.; Sedak, M.; Stojanović, B. From Innovation to Standardization—A Century of Rolling Bearing Life Formula. Machines 2024, 12, 444. [Google Scholar] [CrossRef]
- Pastukhov, A.; Timashov, E. Procedure for Simulation of Stable Thermal Conductivity of Bearing Assemblies. Adv. Eng. Lett. 2023, 2, 58–63. [Google Scholar] [CrossRef]
- Kamat, P.; Kumar, S.; Sugandhi, R. Vibration-based anomaly pattern mining for remaining useful life (RUL) prediction in bearings. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 290. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, R.; Jin, W.; Deng, L.; He, T.; Ma, S. Rolling Bearing Fault Diagnosis Using a Deep Convolutional Autoencoding Network and Improved Gustafson-Kessel Clustering. Shock Vib. 2020, 2020, 8846589. [Google Scholar] [CrossRef]
- Barcelos, A.S.; Cardoso, A.J.M. Current-based bearing fault diagnosis using deep learning algorithms. Energies 2021, 14, 2509. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, H.; Yang, S.; Jiang, J.; Li, G. An Improved Robust Sparse Convex Clustering. Tsinghua Sci. Technol. 2023, 28, 989–998. [Google Scholar] [CrossRef]
- Chen, J.; Wang, G.; Lv, J.; He, Z.; Yang, T.; Tang, C. Open-Set Classification for Signal Diagnosis of Machinery Sensor in Industrial Environment. IEEE Trans. Ind. Inform. 2023, 19, 2574–2584. [Google Scholar] [CrossRef]
- He, D.; Zhao, J.; Jin, Z.; Huang, C.; Zhang, F.; Wu, J. Prediction of bearing remaining useful life based on a two-stage updated digital twin. Adv. Eng. Inform. 2025, 65, 103123. [Google Scholar] [CrossRef]
- Sun, Y.; Tao, H.; Stojanovic, V. Pseudo-label guided dual classifier domain adversarial network for unsupervised cross-domain fault diagnosis with small samples. Adv. Eng. Inform. 2025, 64, 102986. [Google Scholar] [CrossRef]
- Chang, Q.; Fang, C.; Zhou, W.; Meng, X. A multi-order moment matching-based unsupervised domain adaptation with application to cross-working condition fault diagnosis of rolling bearings. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]
- Xu, H.; Peng, X.; Wang, J.; Liu, J.; He, C. Adaptive graph-guided joint soft clustering and distribution alignment for cross-load and cross-device rotating machinery fault transfer diagnosis. Meas. Sci. Technol. 2024, 35, 045009. [Google Scholar] [CrossRef]
- Wang, G.; Huang, J.; Zhang, F. Ensemble clustering-based fault diagnosis method incorporating traditional and deep representation features. Meas. Sci. Technol. 2021, 32, 095110. [Google Scholar] [CrossRef]
- Wu, J.; Lin, M.; Lv, Y.; Cheng, Y. Intelligent fault diagnosis of rolling bearings based on clustering algorithm of fast search and find of density peaks. Qual. Eng. 2023, 35, 399–412. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Z.; Zhu, D.; Gao, Q.; Sun, D. Bearing Fault Diagnosis Based on Clustering and Sparse Representation in Frequency Domain. IEEE Trans. Instrum. Meas. 2021, 70, 3513914. [Google Scholar] [CrossRef]
- Xu, F.; Fang, Y.J.; Wang, D.; Liang, J.Q.; Tsui, K.L. Combining DBN and FCM for Fault Diagnosis of Roller Element Bearings without Using Data Labels. Shock Vib. 2018, 2018, 3059230. [Google Scholar] [CrossRef]
- Xu, F.; Tse, P.W. Combined deep belief network in deep learning with affinity propagation clustering algorithm for roller bearings fault diagnosis without data label. JVC/J. Vib. Control 2019, 25, 473–482. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, M. A novel deep fuzzy clustering neural network model and its application in rolling bearing fault recognition. Meas. Sci. Technol. 2018, 29, 125005. [Google Scholar] [CrossRef]
- Wen, H.; Guo, W.; Li, X. A novel deep clustering network using multi-representation autoencoder and adversarial learning for large cross-domain fault diagnosis of rolling bearings. Expert Syst. Appl. 2023, 225, 120066. [Google Scholar] [CrossRef]
- Wei, J.; Huang, H.; Yao, L.; Hu, Y.; Fan, Q.; Huang, D. New imbalanced fault diagnosis framework based on Cluster-MWMOTE and MFO-optimized LS-SVM using limited and complex bearing data. Eng. Appl. Artif. Intell. 2020, 96, 103966. [Google Scholar] [CrossRef]
- Hang, Q.; Yang, J.; Xing, L. Diagnosis of rolling bearing based on classification for high dimensional unbalanced data. IEEE Access 2019, 7, 79159–79172. [Google Scholar] [CrossRef]
- Mamun, A.A.; Bappy, M.M.; Mudiyanselage, A.S.; Li, J.; Jiang, Z.; Tian, Z.; Fuller, S.; Falls, T.C.; Bian, L.; Tian, W. Multi-channel sensor fusion for real-time bearing fault diagnosis by frequency-domain multilinear principal component analysis. Int. J. Adv. Manuf. Technol. 2023, 124, 1321–1334. [Google Scholar] [CrossRef]
- Wang, C.; Nie, J.; Yin, P.; Xu, J.; Yu, S.; Ding, X. Unknown fault detection of rolling bearings guided by global–local feature coupling. Mech. Syst. Signal Process. 2024, 213, 111331. [Google Scholar] [CrossRef]
- Hu, B. Bearing data set. IEEE Dataport 2023. [Google Scholar] [CrossRef]
- Lee, J.; Qiu, H.; Yu, G.; Lin, J.; Rexnord Technical Services. IMS, University of Cincinnati. “Bearing Data Set”; NASA Prognostics Data Repository, NASA Ames Research Center: Moffett Field, CA, USA, 2007.
- Daga, A.P.; Fasana, A.; Marchesiello, S.; Garibaldi, L. The Politecnico di Torino rolling bearing test rig: Description and analysis of open access data. Mech. Syst. Signal Process. 2019, 120, 252–273. [Google Scholar] [CrossRef]
- Case Western Reserve University CWRU) Bearing Data Center. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 20 January 2025).
- Wang, B.; Lei, Y.; Li, N.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2020, 69, 401–412. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly Accurate Machine Fault Diagnosis Using Deep Transfer Learning. IEEE Trans. Ind. Inform. 2018, 15, 2446–2455. [Google Scholar]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An Experimental Platform for Bearings Accelerated Life Test. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012. [Google Scholar]
- Hepco Motion. GFX- Guidance System for Backhoff XTS Linear Transport System. Available online: https://www.hepcomotion.com/product/driven-track-systems/gfx-guidance-system-for-beckhoff-xts-linear-transport-system (accessed on 20 January 2025).
- Jabbar, A.; Mazzonetto, M.; Orazi, L.; Cocconcelli, M. Ultrafast laser damaging of ball bearings for the condition monitoring of a fleet of linear motors. In Proceedings of the PHM Society European Conference 2024, Prague, Czech Republic, 3–5 July 2024; Volume 8, p. 10. [Google Scholar] [CrossRef]
- MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems—Experiment Type 1 and 2. Available online: https://zenodo.org/records/14753683 (accessed on 29 January 2025).
- MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems—Experiment Type 3 and 4. Available online: https://zenodo.org/records/14755761 (accessed on 29 January 2025).
- MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems—Experiment Type 5 and 6. Available online: https://zenodo.org/records/14761243 (accessed on 29 January 2025).
- MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems—Experiment Type 7. Available online: https://zenodo.org/records/14764717 (accessed on 29 January 2025).
- MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems—Experiment Type 8. Available online: https://zenodo.org/records/14765815 (accessed on 29 January 2025).
- Fisher, R.A. Statistical Methods for Research Workers; Oliver and Boyd: Edinburgh, UK, 1925. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models, 4th ed.; Irwin Press: Chicago, IL, USA, 1996. [Google Scholar]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Sheskin, D.J. Handbook of Parametric and Nonparametric Statistical Procedures; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- He, X.; Cai, D.; Niyogi, P. Laplacian Score for Feature Selection. Adv. Neural Inf. Process. Syst. 2005, 18, 507–514. [Google Scholar]
- Coble, J.; Hines, J.W. Identifying Optimal Prognostic Parameters from Data: A Genetic Algorithms Approach. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, CA, USA, 28 September–1 October 2009. [Google Scholar]
- Pořízka, P.; Klus, J.; Képeš, E.; Prochazka, D.; Hahn, D.W.; Kaiser, J. On the utilization of principal component analysis in laser-induced breakdown spectroscopy data analysis, a review. Spectrochim. Acta Part At. Spectrosc. 2018, 148, 65–82. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Phil. Trans. R. Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Kitao, A. Principal Component Analysis and Related Methods for Investigating the Dynamics of Biological Macromolecules. J 2022, 5, 298–317. [Google Scholar] [CrossRef]
- Jung, S.; Dagobert, T.; Morel, J.; Facciolo, G. A Review of t-SNE. Image Process. Line 2024, 14, 250–270. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Gove, R.; Cadalzo, L.; Leiby, N.; Singer, J.M.; Zaitzeff, A. New guidance for using t-SNE: Alternative defaults, hyperparameter selection automation, and comparative evaluation. Vis. Inform. 2022, 6, 87–97. [Google Scholar] [CrossRef]
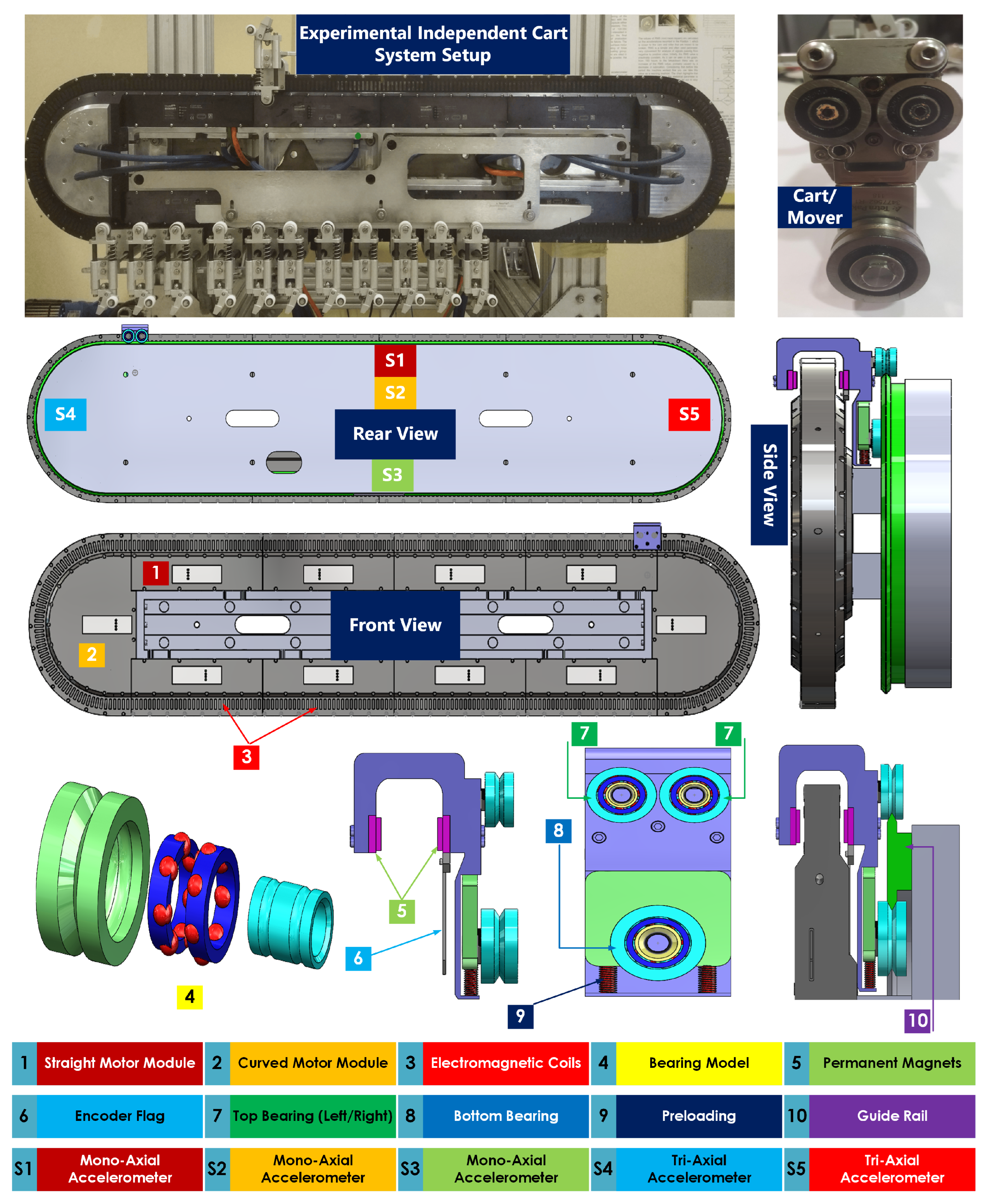



| Part Number | Manufacturer | Type | Location | Description |
|---|---|---|---|---|
| 356B21 | PCB Piezotronics. Depew, NY, USA | Tri-Axial | Left curved module | Mounted on the left curved module of the guide rail |
| 356A02 | PCB Piezotronics. Depew, NY, USA | Tri-Axial | Right curved module | Mounted on the right curved module of the guide rail |
| 353B18 | PCB Piezotronics. Depew, NY, USA | Mono-Axial | Upper straight section | Mounted midway along the upper straight section of the guide rail |
| 353B18 | PCB Piezotronics. Depew, NY, USA | Mono-Axial | Lower straight section | Mounted midway along the lower straight section of the guide rail |
| VSP001 | ifm efector, inc. Malvern, PA, USA | Mono-Axial | Aluminum rod on the upper straight section | Mounted on an aluminum rod attached to the guide rail, midway along the upper straight section |
| Phase | Description | Issues Encountered | Improvements Implemented |
|---|---|---|---|
| Initial Experiments | Faults injected manually; data collected with early acquisition system | Poor fault injection; low-resolution data; low sampling frequency | Baseline experiments with initial setup |
| Refined Experiments | Different cart numbers and loading mechanisms tested | Variability in results due to inconsistent loads and cart configurations | Standardized loading mechanisms |
| Data Acquisition Upgrade | Upgraded to 24-bit resolution with 50 kHz sampling | Improved resolution, but inconsistent manual fault sizes | Laser Fault Injection |
| Laser Fault Injection | Laser fault injection without dismantling the bearings | Result variability due to partial fault coverage from inner-outer race proximity | Bearings were disassembled |
| Final Experiments | Laser-based fault injection with bearing disassembly | None | Final data set used for analysis |
| Parameter | Unit of Measure | Value |
|---|---|---|
| Wavelength, | nm | 1064 |
| Average Output Power, P | W | 13.32 |
| Pulse Frequency, f | kHz | 300 |
| Pulse energy, E | µJ | 44.4 |
| Pulse duration, | ps | 10 |
| Pulse fluence, F | J/cm2 | 56.56 |
| Line spacing, s | µm | 5 |
| Marking speed, | m/s | 1 |
| Number of passes on each groove, p | 150 |
| Experiment Class | Speed Profile | Fault Type | Fault Size (mm) | Fault Orientation | Experiment Type | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (mm/s) | 0.25 | 0.5 | 1.0 | 1.5 | 2.0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||
| Single Cart | 1000 | IR-Top | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ |
| OR-Top | ✓ | ✓ | ✗ | ✗ | ✓ | Not Applicable | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | |||||
| IR-Bottom | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ||
| OR-Bottom | ✓ | ✓ | ✓ | ✗ | ✗ | Not Applicable | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | |||||
| 2000 | IR-Top | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | |
| OR-Top | ✓ | ✓ | ✗ | ✗ | ✓ | Not Applicable | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | |||||
| IR-Bottom | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ||
| OR-Bottom | ✓ | ✓ | ✓ | ✗ | ✗ | Not Applicable | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | |||||
| Three Carts | 1000 | IR-Top | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ |
| OR-Top | ✓ | ✓ | ✗ | ✗ | ✓ | Not Applicable | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | |||||
| IR-Bottom | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ||
| OR-Bottom | ✓ | ✓ | ✓ | ✗ | ✗ | Not Applicable | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | |||||
| 2000 | IR-Top | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | |
| OR-Top | ✓ | ✓ | ✗ | ✗ | ✓ | Not Applicable | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | |||||
| IR-Bottom | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ||
| OR-Bottom | ✓ | ✓ | ✓ | ✗ | ✗ | Not Applicable | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | |||||
| Statistical Parameter | Mathematical Expression |
|---|---|
| Mean | |
| RMS | |
| Standard Deviation | |
| Shape Factor | |
| Kurtosis | |
| Skewness | |
| Peak Value | |
| Impulse Factor | |
| Crest Factor | |
| Clearance Factor | |
| Signal-to-Noise Ratio | |
| Total Harmonic Distortion | |
| Signal-to-Noise And Distortion Ratio |
| Label | Defect | Dimension (mm) |
|---|---|---|
| H | No Fault | – |
| FIR025 | Inner Race Fault | 0.25 |
| FIR05 | Inner Race Fault | 0.5 |
| FIR10 | Inner Race Fault | 1.0 |
| FIR15 | Inner Race Fault | 1.5 |
| FOR025 | Outer Race Fault | 0.25 |
| FOR05 | Outer Race Fault | 0.5 |
| FOR10 | Outer Race Fault | 1.0 |
| FOR20 | Outer Race Fault | 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabbar, A.; Cocconcelli, M.; D’Elia, G.; Borghi, D.; Capelli, L.; Cavalaglio Camargo Molano, J.; Strozzi, M.; Rubini, R. MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems. Appl. Sci. 2025, 15, 3691. https://doi.org/10.3390/app15073691
Jabbar A, Cocconcelli M, D’Elia G, Borghi D, Capelli L, Cavalaglio Camargo Molano J, Strozzi M, Rubini R. MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems. Applied Sciences. 2025; 15(7):3691. https://doi.org/10.3390/app15073691
Chicago/Turabian StyleJabbar, Abdul, Marco Cocconcelli, Gianluca D’Elia, Davide Borghi, Luca Capelli, Jacopo Cavalaglio Camargo Molano, Matteo Strozzi, and Riccardo Rubini. 2025. "MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems" Applied Sciences 15, no. 7: 3691. https://doi.org/10.3390/app15073691
APA StyleJabbar, A., Cocconcelli, M., D’Elia, G., Borghi, D., Capelli, L., Cavalaglio Camargo Molano, J., Strozzi, M., & Rubini, R. (2025). MOIRA-UNIMORE Bearing Data Set for Independent Cart Systems. Applied Sciences, 15(7), 3691. https://doi.org/10.3390/app15073691








