Rotor Unbalanced Vibration Control of Active Magnetic Bearing High-Speed Motor via Adaptive Fuzzy Controller Based on Switching Notch Filter
Abstract
1. Introduction
2. Dynamical Mode of AMB Rigid Rotor System During Accelerated Motion
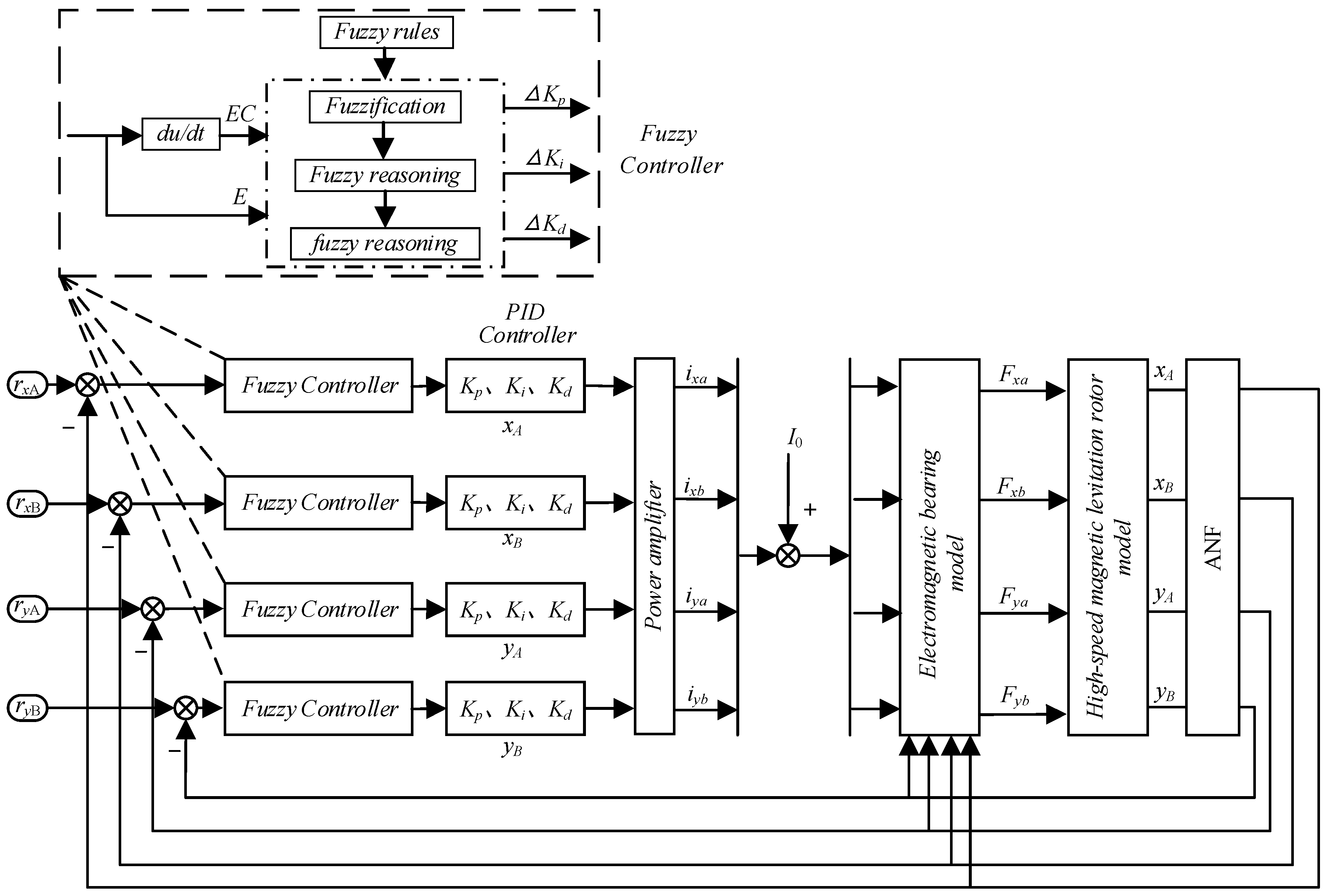
3. AMB Rigid Rotor System Based on Fuzzy Control Strategy
3.1. Defining the Input and Output Variables of the Fuzzy Controller
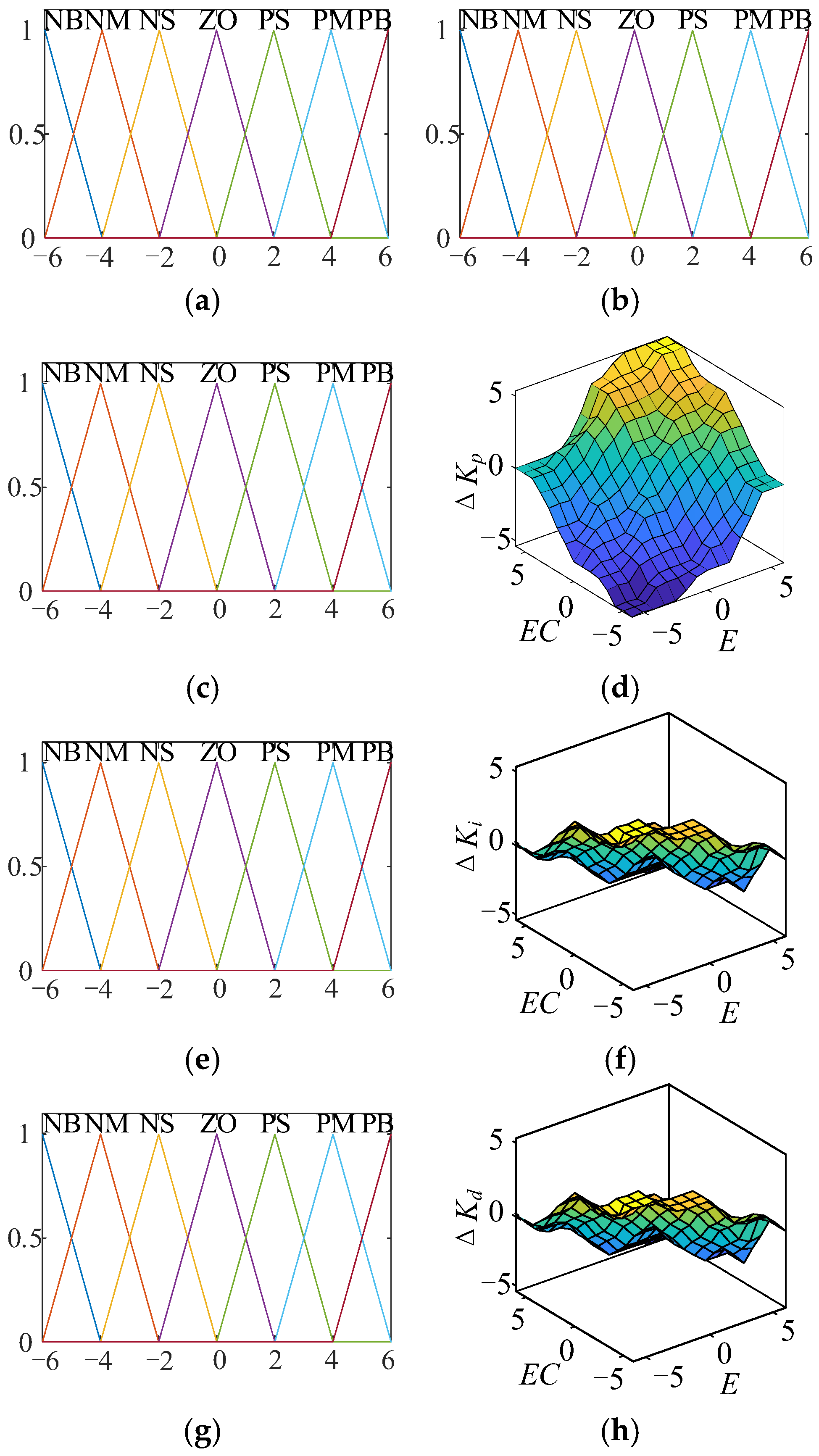
3.2. Defining the Fuzzy Controller Affiliation Function
3.3. Defining a Fuzzy Knowledge Base for Fuzzy Controllers
3.4. Fuzzy Inference and Defuzzification of Fuzzy Controllers
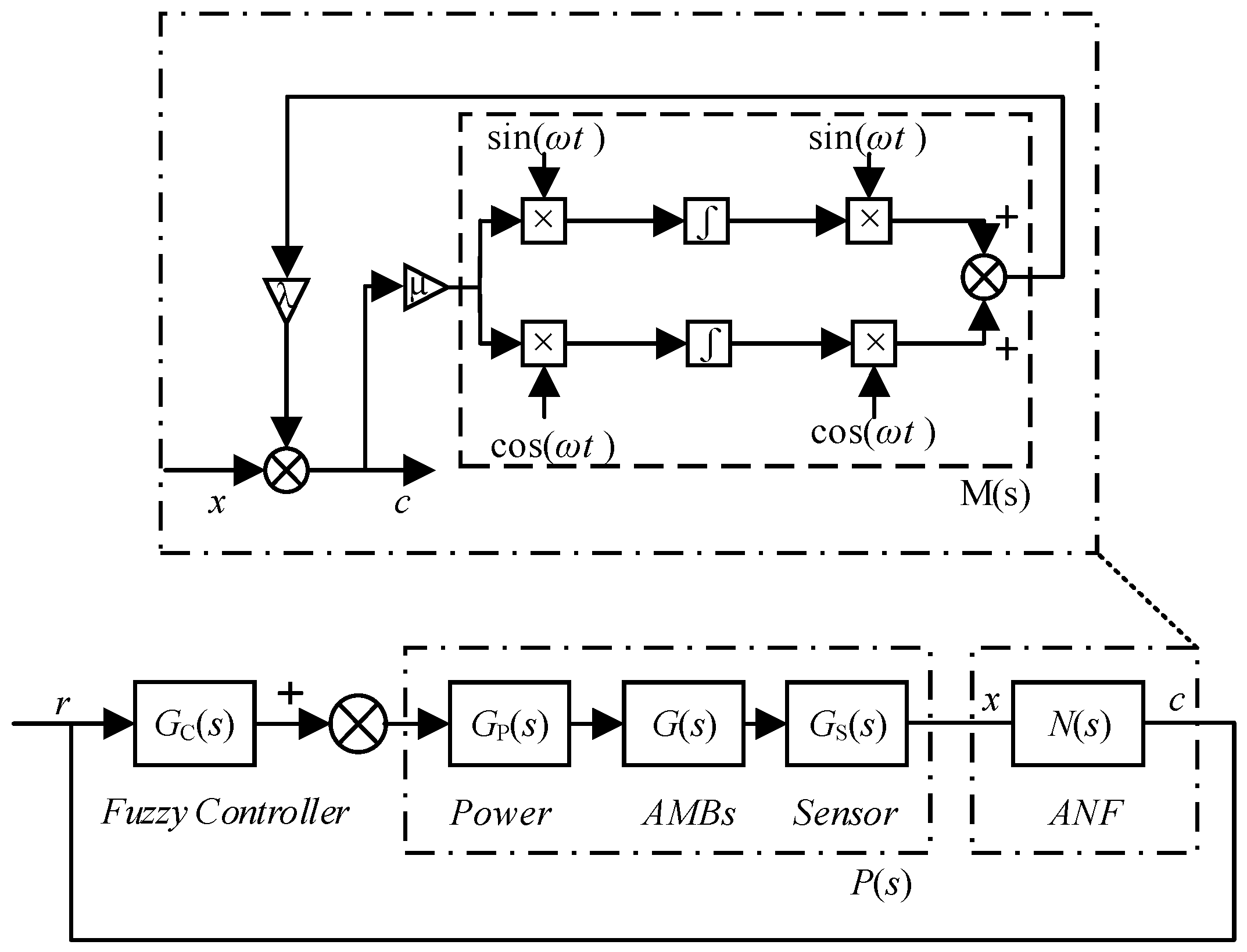
4. Switching Adaptive Notch Filter Vibration Control Strategy Based on Fuzzy Control
4.1. Bipolar Filter
4.2. Fuzzy Control Based on Adaptive ANF
- (1)
- It is possible to simultaneously take into account the rotor unbalanced vibration control of AMB rigid rotor systems in the presence of rigid body translational modes and rigid body conical modes;
- (2)
- By avoiding the design of an interference observer and controlling the polarity switching, transient vibrations produced during the switching instant can be effectively reduced.
4.3. Stability Analysis of AFC-ANF
5. Simulation Results
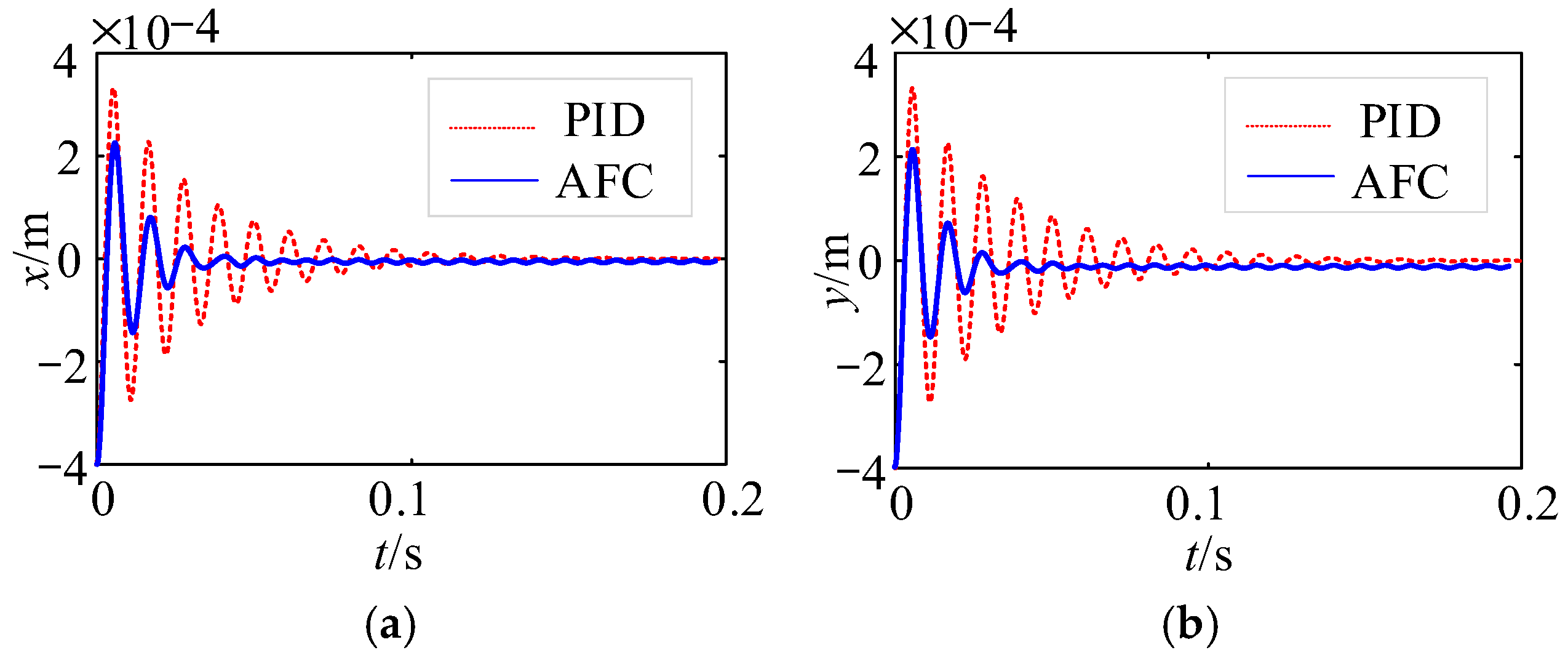
5.1. Suspension Control of the AMBs Rigid Rotor System
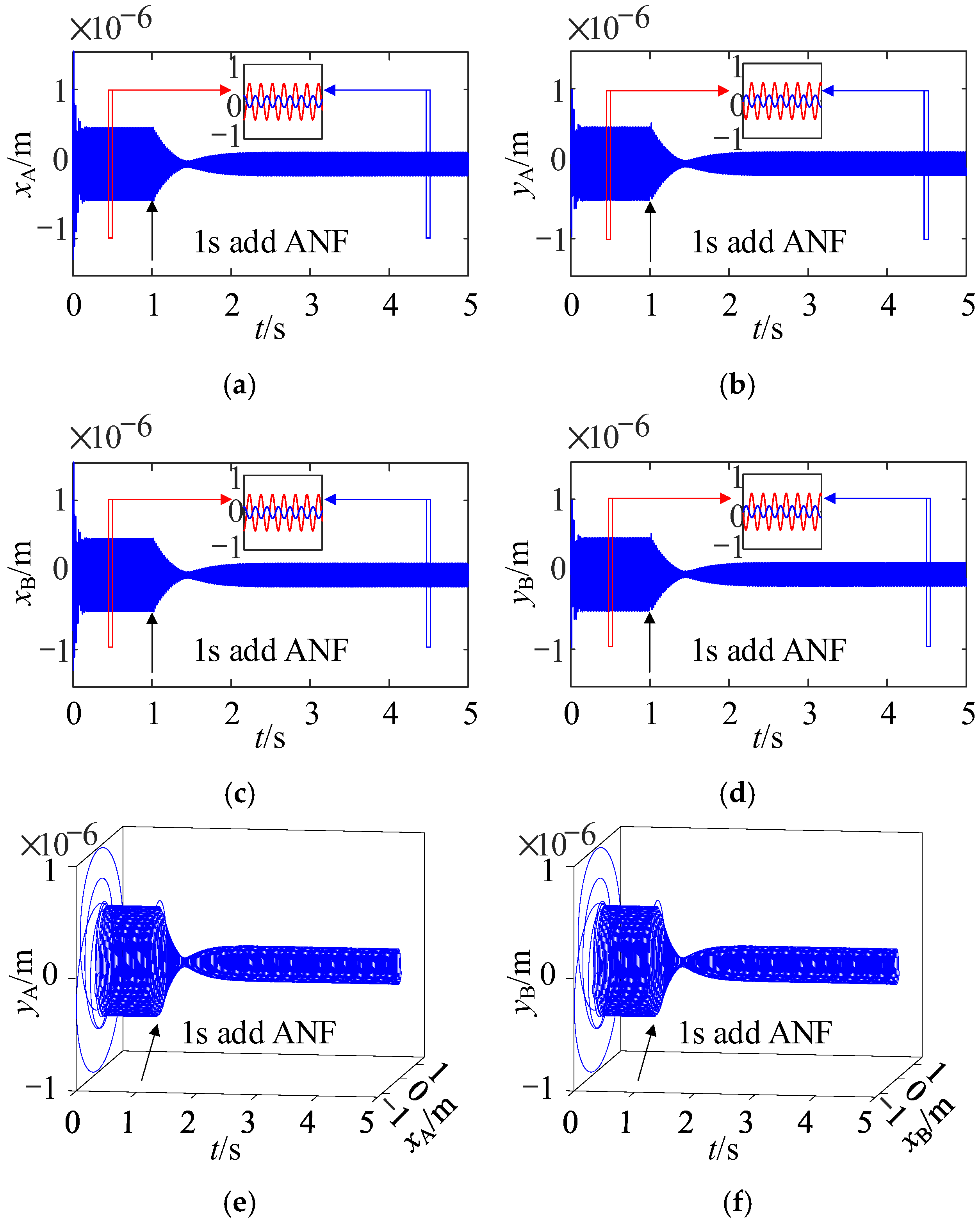
5.2. The Correctness Verification of AFC-ANF When the Rotor Runs at a Constant Speed
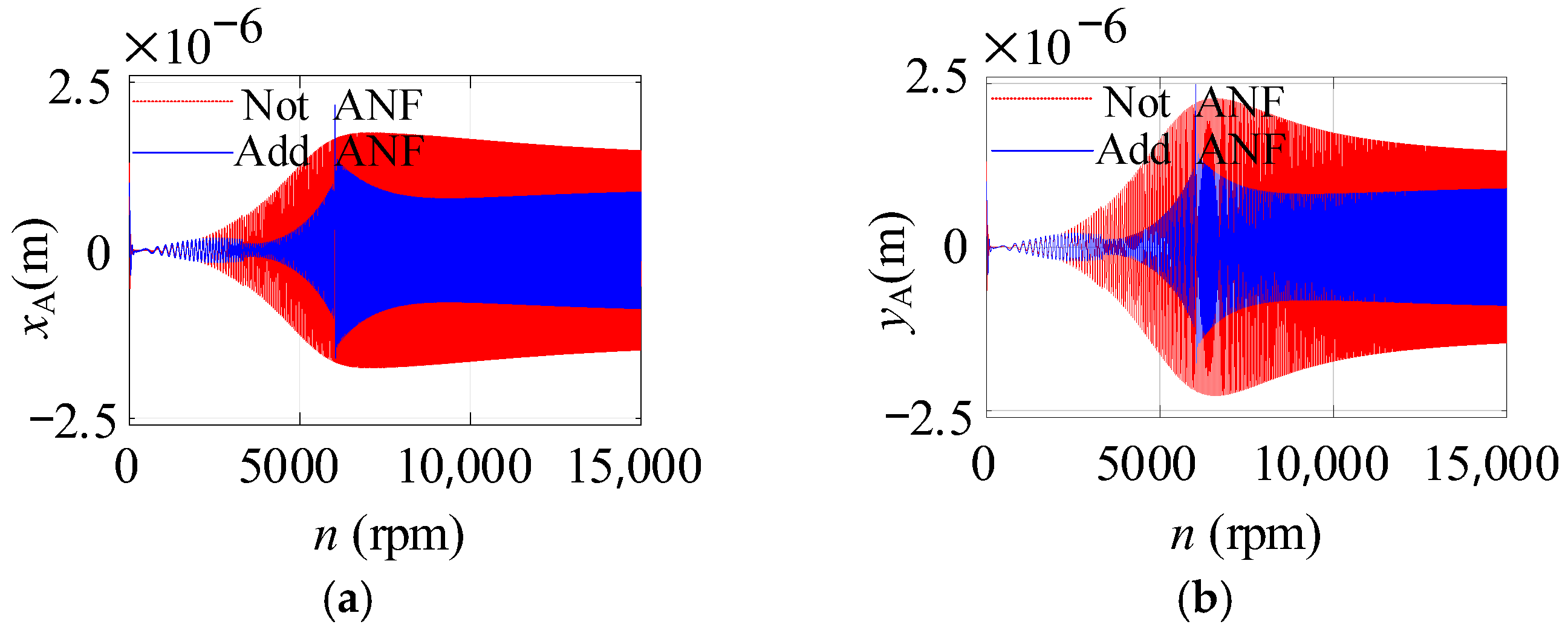
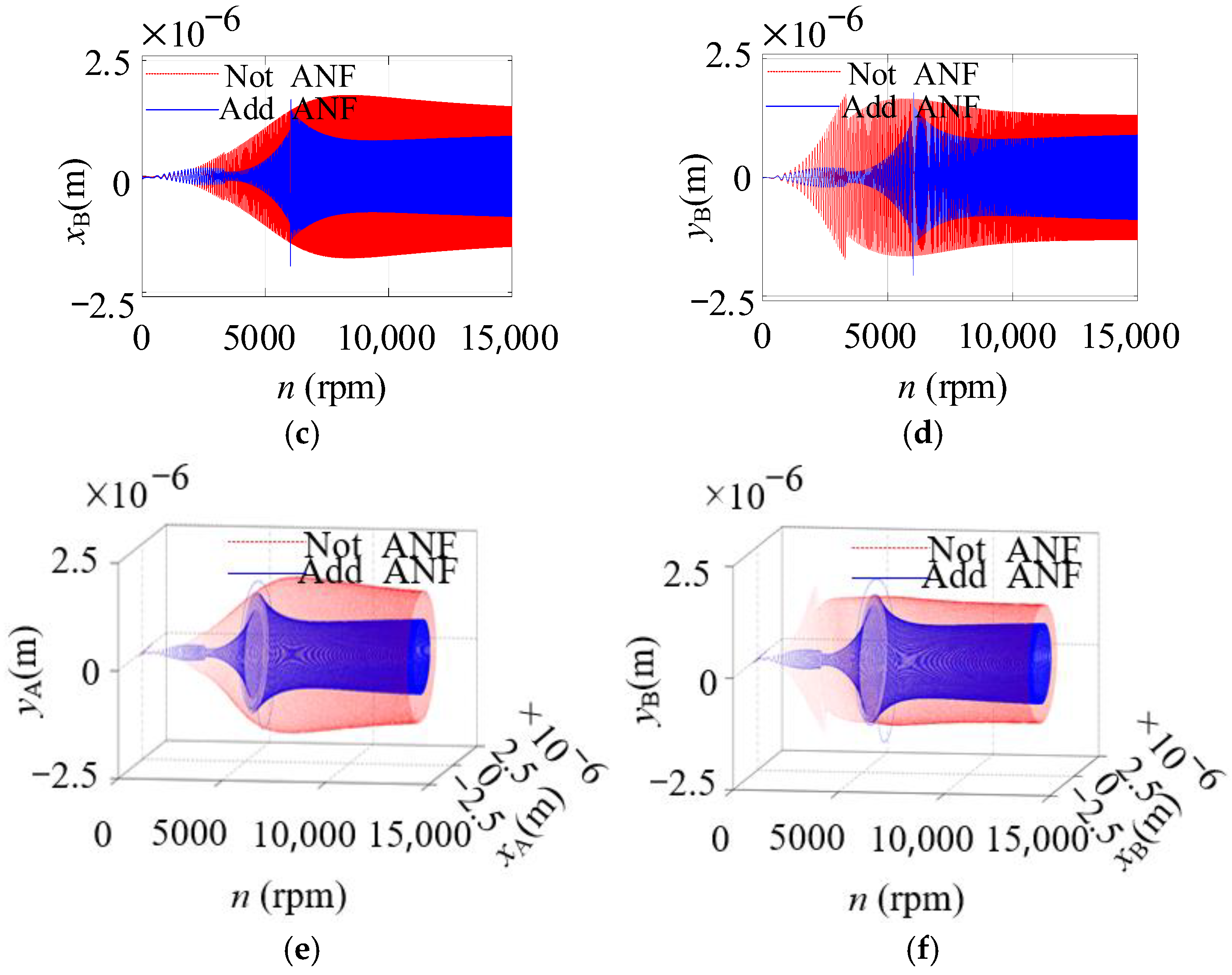
5.3. The Correctness Verification of AFC-ANF When the Rotor Is Under Acceleration
6. Experimental Results
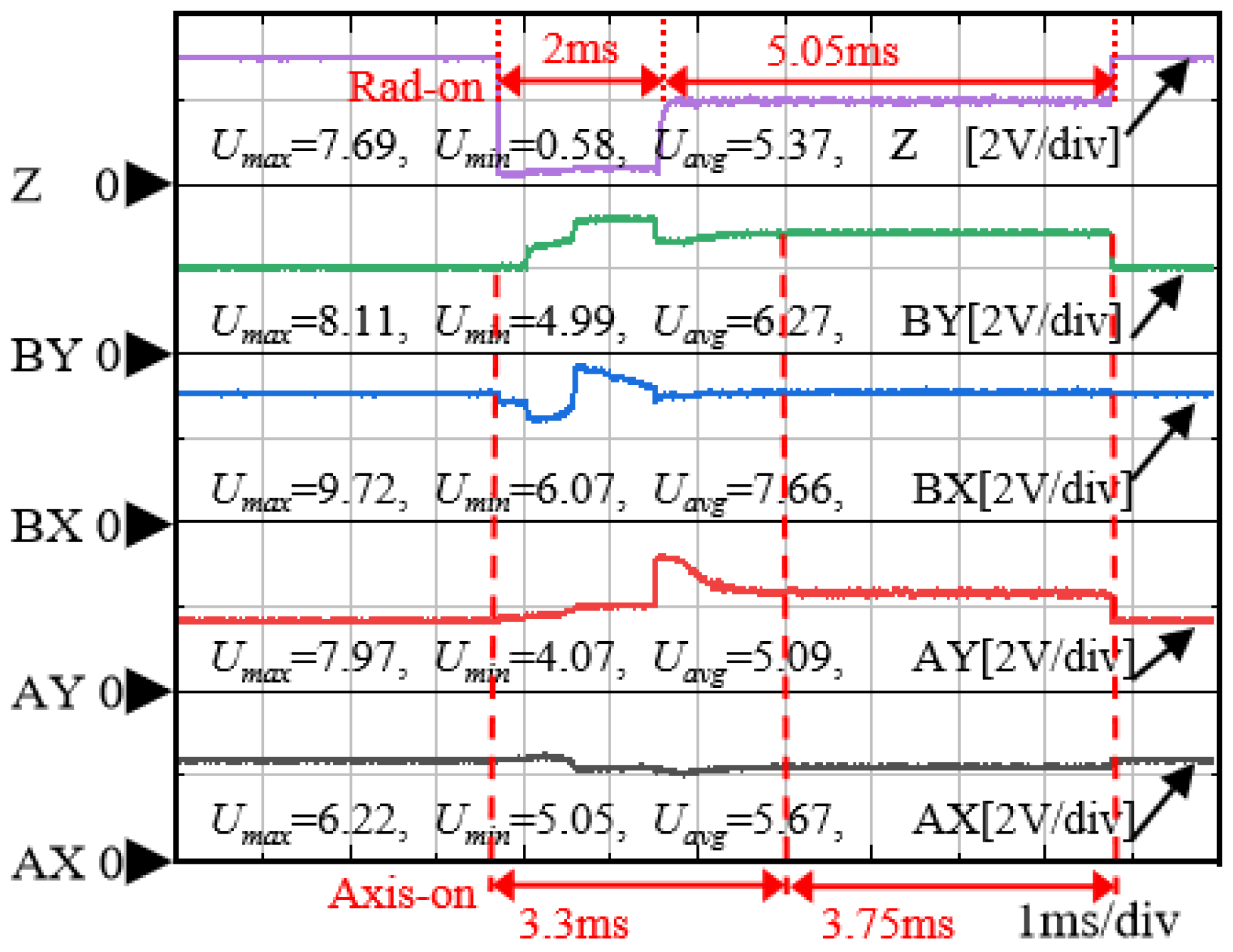
6.1. Experimental Results of Suspension Control of the AMB Rigid Rotor System
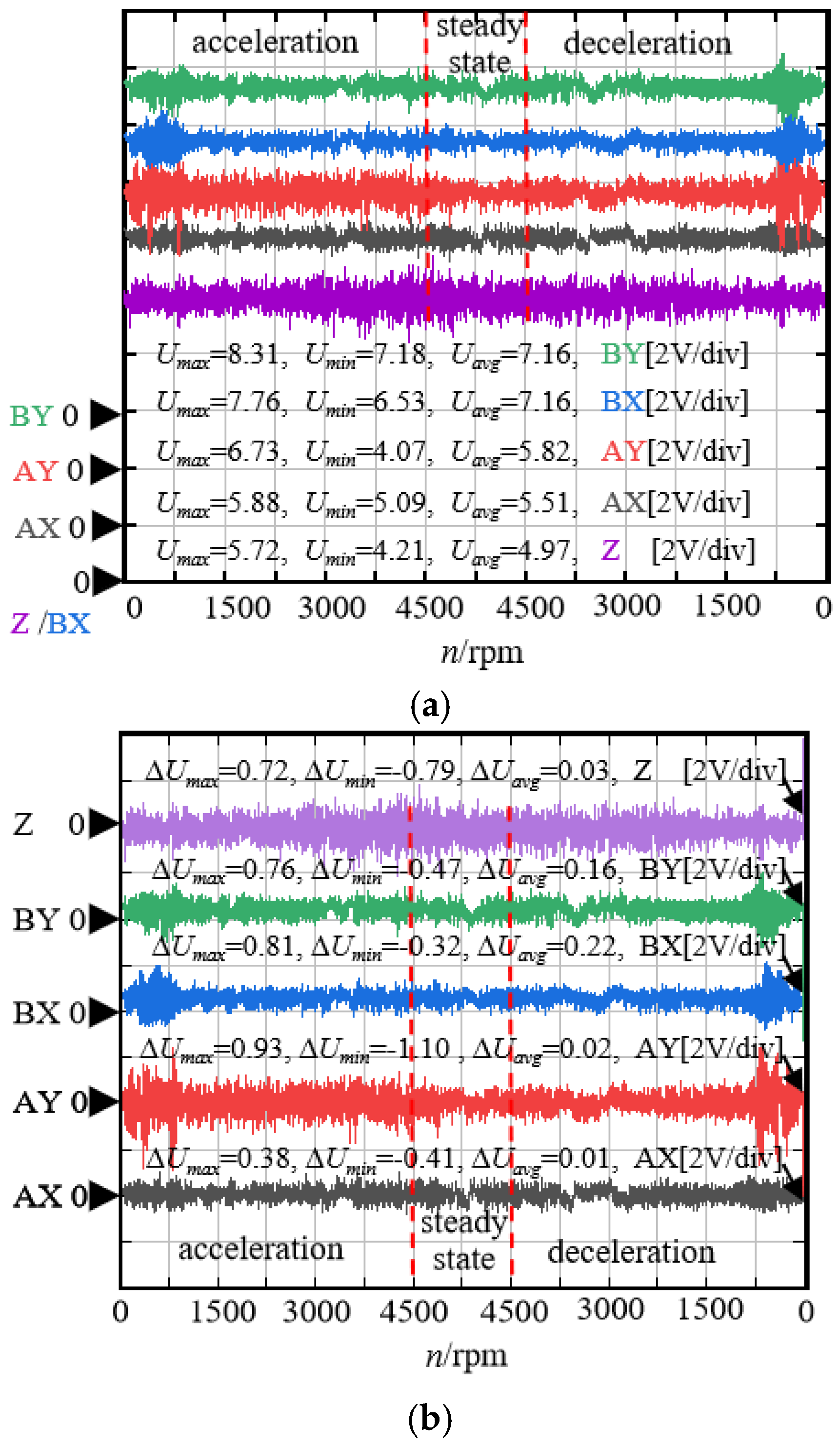
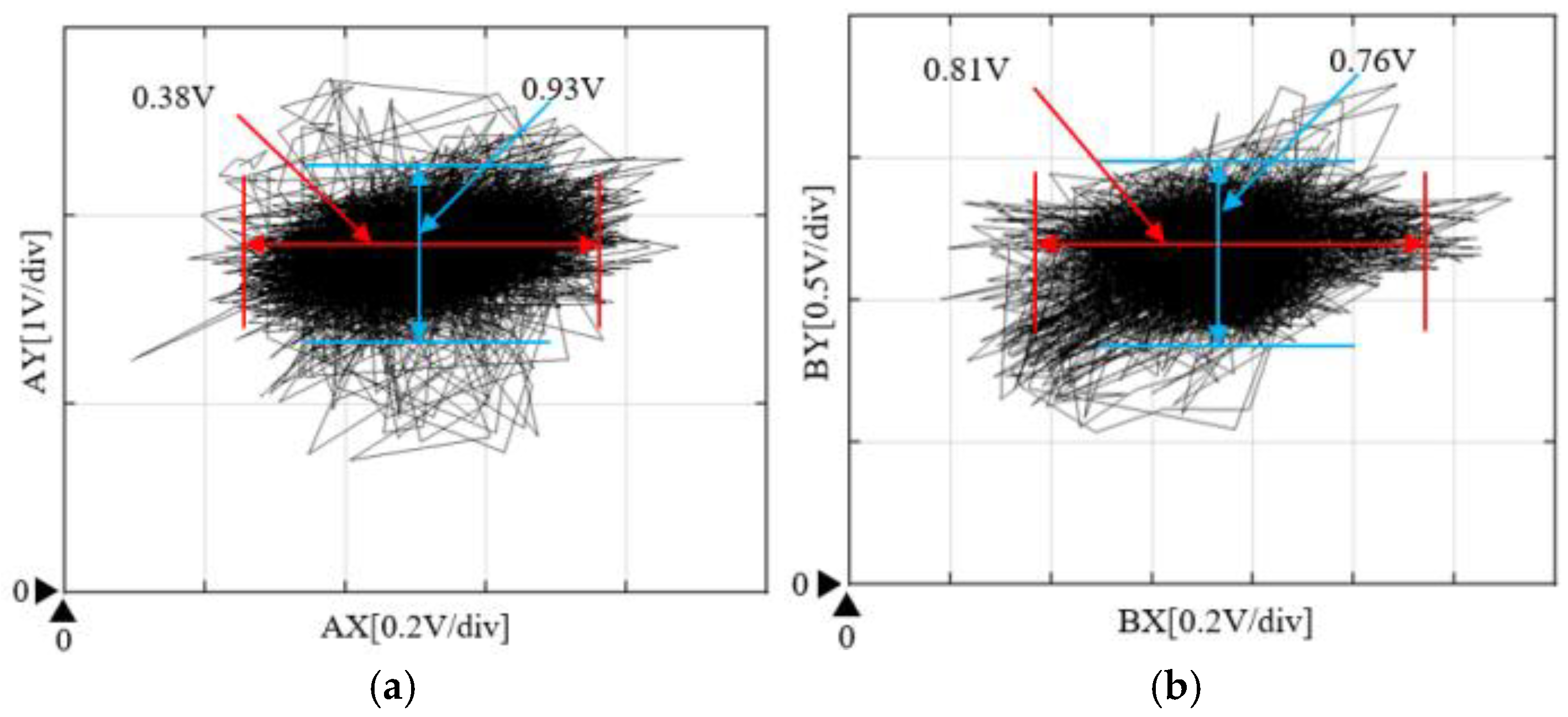
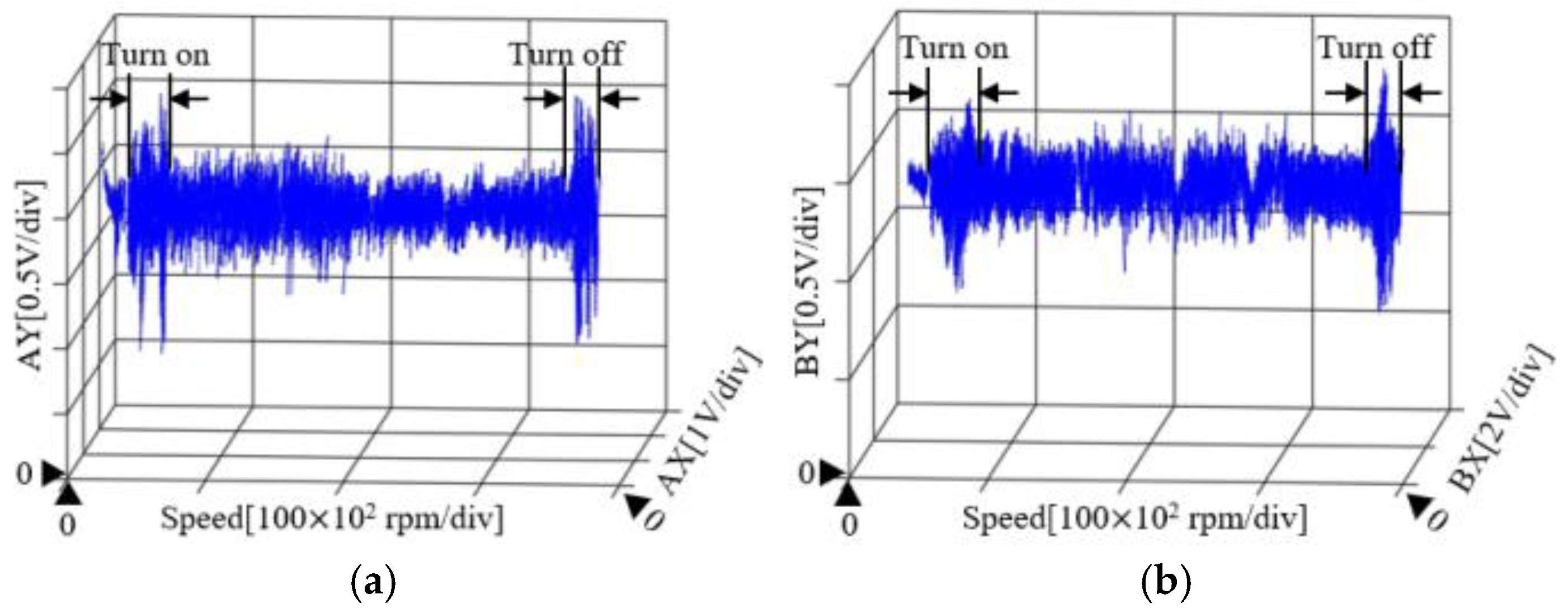
6.2. Acceleration Control of the AMB Rigid Rotor System
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMBs | Active magnetic bearings. |
| ANF | Adaptive notch filter. |
| AFC | Adaptive fuzzy controller. |
Appendix A
| EC | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| E | ||||||||
| NB | PB/PS/NB | PB/NS/NB | PM/NB/NM | PM/NB/NM | PS/NB/NS | ZO/NM/ZO | ZO/PS/ZO | |
| NM | PB/PS/NB | PB/NS/NB | PM/NB/NM | PS/NM/NS | PS/NM/NS | ZN/SO/ZO | NS/ZO/ZO | |
| NS | PM/ZO/NB | PM/NS/NM | PM/NM/NS | PS/NM/NS | ZO/NS/ZO | NS/NS/PS | NS/ZO/PS | |
| ZO | PM/ZO/NM | PM/NS/NM | PS/NS/NS | ZO/NS/ZO | NS/NS/PS | NM/NS/PM | NM/ZO/PM | |
| PS | PS/ZO/ZM | PS/ZO/NS | ZO/ZO/ZO | NS/ZO/PS | NS/ZO/PS | NM/ZO/PM | NM/ZO/PB | |
| PM | PS/PB/ZO | ZO/NS/ZO | ZS/PS/PS | NM/PS/PS | NM/PS/PM | NM/PS/PB | NB/PB/PB | |
| PB | ZO/PB/ZO | ZO/PM/ZO | NM/PM/PS | NM/PM/PM | NM/PS/PM | NB/PS/PB | NB/PB/PB | |
References
- Hutterer, M.; Wimme, D.; Schrödl, M. Stabilization of a Magnetically Levitated Rotor in the Case of a Defective Radial Actuator. IEEE/ASME Trans. Mechatron. 2020, 25, 2599–2609. [Google Scholar]
- Zheng, S.; Wang, C. Rotor Balancing for Magnetically Levitated TMPs Integrated with Vibration Self-Sensing of Magnetic Bearings. IEEE/ASME Trans. Mechatron. 2021, 26, 3031–3039. [Google Scholar]
- Zhou, M.; Shuai, Y.; Jiang, D.; Liu, Z. Active Magnetic Bearing PID Tuning with Model-Free Time-Domain Analysis Based Heuristic Algorithm. IEEE Trans. Ind. Inform. 2024, 20, 12157–12167. [Google Scholar]
- Yu, Y.; Yang, Z.; Han, C.; Liu, H. Fuzzy Adaptive Back-Stepping Sliding Mode Controller for High-Precision Deflection Control of the Magnetically Suspended Momentum Wheel. IEEE Trans. Ind. Electron. 2018, 65, 3530–3538. [Google Scholar]
- Xu, G.; Fu, Y.; Zhan, Y.; Wang, Z.; Zhao, H.; Zhang, Y. Influence of Different Rotor Damping Structures on Dynamic Characteristic of Dual-Excited Synchronous Generator with Excitation Control. IEEE Trans. Ind. Appl. 2023, 59, 6634–6644. [Google Scholar]
- Fang, L.; Ding, S.; Park, J.H.; Ma, L. Adaptive Fuzzy Control for Stochastic High-Order Nonlinear Systems with Output Constraints. IEEE Trans. Fuzzy Syst. 2021, 29, 2635–2646. [Google Scholar]
- Han, B.; Chen, Y.; Li, M.; Zheng, S.; Zhang, X. Stable Control of Nutation and Precession for the Radial Four-Degree-of-Freedom AMB-Rotor System Considering Strong Gyroscopic Effects. IEEE Trans. Ind. Electron. 2021, 68, 11369–11378. [Google Scholar]
- Ma, P.; Yu, J.; Wang, Q.G.; Liu, J. Filter- and Observer-Based Finite-Time Adaptive Fuzzy Control for Induction Motors Systems Considering Stochastic Disturbance and Load Variation. IEEE Trans. Power Electron. 2023, 38, 1599–1609. [Google Scholar]
- Chen, Y.; Du, L.; Sun, Q.; Bai, J.; Li, H.; Shi, Y. Self-Calibration Method of Displacement Sensor in AMB-Rotor System Based on Magnetic Bearing Current Control. IEEE Trans. Ind. Electron. 2024, 71, 5148–5156. [Google Scholar]
- Chen, S.Y.; Chiang, H.H.; Liu, T.S.; Chang, C.H. Precision Motion Control of Permanent Magnet Linear Synchronous Motors Using Adaptive Fuzzy Fractional-Order Sliding-Mode Control. IEEE/ASME Trans. Mechatron. 2019, 24, 741–752. [Google Scholar]
- Ren, G.P.; Chen, Z.; Zhang, H.T.; Wu, Y.; Meng, H.; Wu, D.; Ding, H. Design of Interval Type-2 Fuzzy Controllers for Active Magnetic Bearing Systems. IEEE/ASME Trans. Mechatron. 2020, 5, 2449–2459. [Google Scholar]
- Tang, Y.; Yang, P.; Yang, Y.; Zhao, Z.; Lai, L.L. Fuzzy Adaptive Frequency Support Control Strategy for Wind Turbines With Improved Rotor Speed Recovery. IEEE Trans. Sustain. Energy 2024, 115, 1351–1364. [Google Scholar] [CrossRef]
- Jing, Y.Z.; Feng, W.; Wang, S.; Ma, S.; Hao, J.; Dong, J. Levitation Control Strategy Based on Adaptive Non-singular Terminal Sliding Mode. J. Southwest Jiaotong Univ. 2022, 57, 566–573. [Google Scholar]
- Zuo, Y.; Ge, X.; Zhang, S.; Cao, H.; Wang, H.; Wang, Y.; Lee, C.H. Sensorless Control of IPMSM Drives Based on Extended State Observer with Enhanced Position Estimation Accuracy. IEEE Trans. Power Electron. 2025, 40, 787–800. [Google Scholar]
- Ye, J.H.; Shi, D.; Qi, Y.S.; Gao, J.H.; Shen, J.X. Vibration Suppression for Active Magnetic Bearings Using Adaptive Filter with Iterative Search Algorithm. CES Trans. Electr. Mach. Syst. 2024, 8, 61–71. [Google Scholar]
- Gong, L.; Zhu, C. Synchronous Vibration Control for Magnetically Suspended Rotor System Using a Variable Angle Compensation Algorithm. IEEE Trans. Ind. Electron. 2021, 68, 6547–6559. [Google Scholar]
- Yu, Y.; Shao, Y.; Chai, F.; Cui, M. Static-Errorless Position Estimation for Sensorless PMSM Drives with Enhanced Robustness Against the Full-Frequency Domain Disturbance. IEEE Trans. Power Electron. 2022, 37, 5884–5897. [Google Scholar]
- Zhang, Y.; Zheng, S.; Chen, Q.; Fang, J. Surge Detection Approach for Magnetically Suspended Centrifugal Compressors Using Adaptive Frequency Estimator. IEEE Trans. Ind. Electron. 2018, 65, 5733–5742. [Google Scholar]
- Ma, W.; Liu, G.; Zhou, J.; Han, X.; Zheng, S. Surge Detection of AMB-Supported Centrifugal Compressors Using a Normalized Adaptive Notch Filter. IEEE Trans. Instrum. Meas. 2024, 67, 480–489. [Google Scholar]
- Peng, C.; Zhu, M.; Wang, K.; Ren, Y.; Deng, Z. A Two-Stage Synchronous Vibration Control for Magnetically Suspended Rotor System in the Full Speed Range. IEEE Trans. Ind. Electron. 2020, 67, 480–489. [Google Scholar]
- Borque Gallego, G.; Rossini, L.; Achtnich, T.; Araujo, D.M.; Perriard, Y. Novel Generalized Notch Filter for Harmonic Vibration Suppression in Magnetic Bearing Systems. IEEE Trans. Ind. Appl. 2021, 57, 6977–6987. [Google Scholar]
- Gong, L.; Zhu, C. Vibration Suppression for Magnetically Levitated High-Speed Motors Based on Polarity Switching Tracking Filter and Disturbance Observer. IEEE Trans. Ind. Electron. 2021, 68, 4667–4678. [Google Scholar]
- Zhong, Y.; Zhou, J.; Zhang, Y.; Zhou, Y.; Xu, Y. Modelling and vibration response of a magnetically suspended flexible rotor considering base motion. Appl. Math. Model. 2023, 118, 518–540. [Google Scholar] [CrossRef]
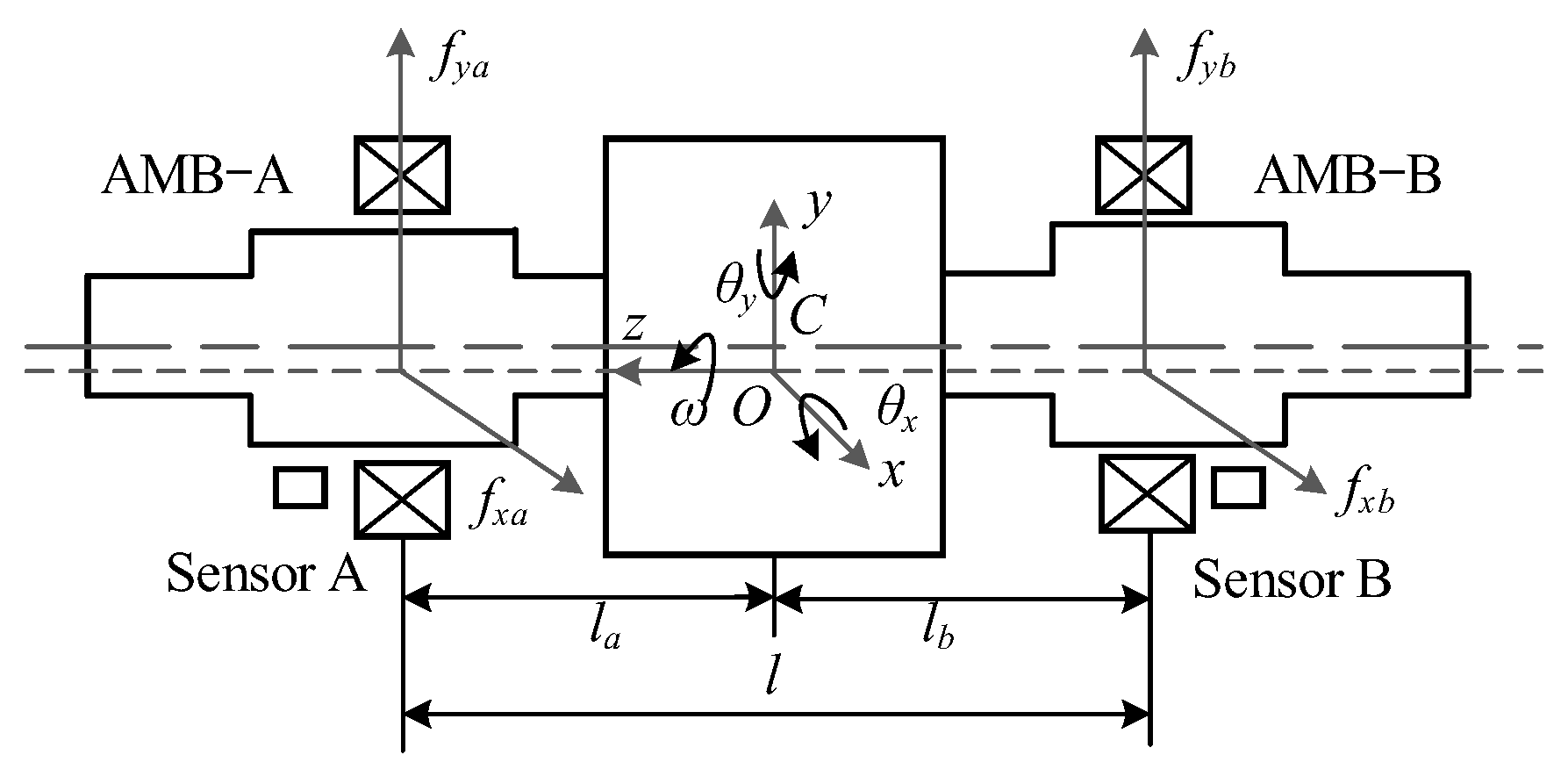




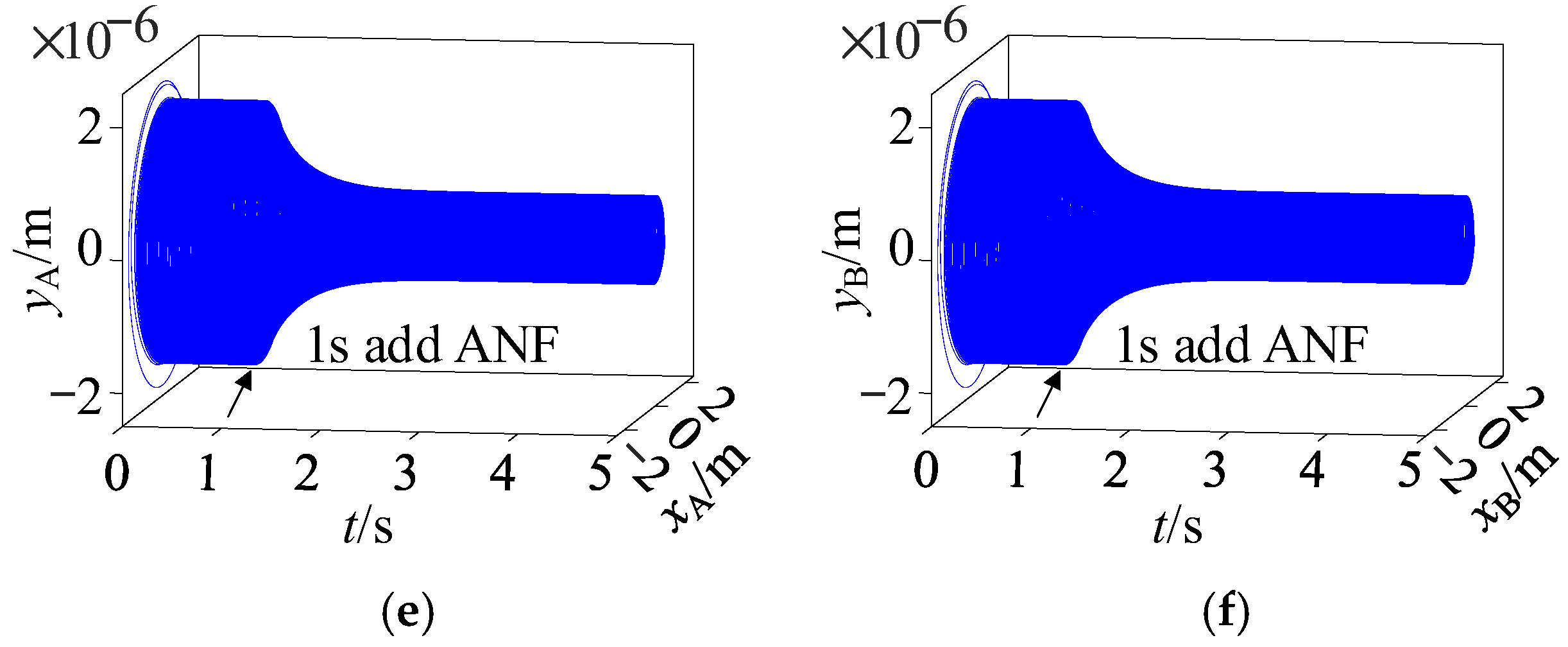

| Symbol | Meaning | Value |
|---|---|---|
| m | Rotor mass (kg) | 18.09 |
| J | Moment of inertia about x and y axes (kg·m2) | 0.2 |
| la and lb | Distance from ends A and B to the central plane (m) | 0.13 |
| ki | Current stiffness coefficient (N/A) | 577.96 |
| kh | Displacement stiffness coefficient (N/m) | 2.75 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, L.; Luo, W.; Li, Y.; Chen, J.; Hua, Z. Rotor Unbalanced Vibration Control of Active Magnetic Bearing High-Speed Motor via Adaptive Fuzzy Controller Based on Switching Notch Filter. Appl. Sci. 2025, 15, 3681. https://doi.org/10.3390/app15073681
Gong L, Luo W, Li Y, Chen J, Hua Z. Rotor Unbalanced Vibration Control of Active Magnetic Bearing High-Speed Motor via Adaptive Fuzzy Controller Based on Switching Notch Filter. Applied Sciences. 2025; 15(7):3681. https://doi.org/10.3390/app15073681
Chicago/Turabian StyleGong, Lei, Wenjuan Luo, Yu Li, Jingwen Chen, and Zhiguang Hua. 2025. "Rotor Unbalanced Vibration Control of Active Magnetic Bearing High-Speed Motor via Adaptive Fuzzy Controller Based on Switching Notch Filter" Applied Sciences 15, no. 7: 3681. https://doi.org/10.3390/app15073681
APA StyleGong, L., Luo, W., Li, Y., Chen, J., & Hua, Z. (2025). Rotor Unbalanced Vibration Control of Active Magnetic Bearing High-Speed Motor via Adaptive Fuzzy Controller Based on Switching Notch Filter. Applied Sciences, 15(7), 3681. https://doi.org/10.3390/app15073681






