Performance and Effectiveness of the Passive-Compliant Citrus-Picking Manipulator

Abstract

The application of citrus-picking robotic hands in orchard environments is constrained by the diversity in fruit size and shape, as well as the need to control fruit damage during harvesting. To address this issue, this study proposes a passively compliant citrus-picking robotic hand and experimentally evaluates its performance. The robotic hand employs a spring-assisted grasping mechanism, optimizing the gripping force range and adjusting spring parameters to achieve passive, compliant encapsulation of citrus fruits of varying sizes while preventing damage. Furthermore, to accommodate citrus fruits with varying ellipticity, the robotic hand incorporates a floating linkage mechanism, enabling each finger to move independently under the control of a single stepper motor, thereby enhancing adaptability to morphological variations. Experimental results indicate that the robotic hand can reliably grasp citrus fruits of various sizes and ellipticities, and complete the harvesting process by rotating four times without applying tensile force, with a damage rate of only 2.6%. The proposed passively compliant robotic hand features a simple structure and strong adaptability, offering a reference for enhancing the applicability of citrus-picking robots in complex orchard environments. Future research will focus on further optimizing the robotic hand’s structure, improving harvesting efficiency, and exploring its adaptability in various operational environments.

1. Introduction

Citrus is a widely cultivated economic crop in China, and its production has been increasing yearly [1]. Currently, citrus harvesting is mainly done manually [2]. However, due to the increasingly serious aging population and labor shortage in China, the cost of manual harvesting has risen significantly [3,4,5]. The demand for replacing manual labor with machines for harvesting has become more urgent [6,7,8,9]. The harvesting manipulator, as a key component of the fruit-and-vegetable-harvesting robot, greatly affects the harvesting rate and damage rate of the robot. Therefore, research on harvesting manipulators is of vital importance [10,11,12,13].

In recent years, scholars—both domestically and internationally—have conducted extensive research on end-effectors for fruit-and-vegetable harvesting [14,15,16,17,18], which can be mainly divided into two categories: the first category is cutting-type end-effectors [19], which detach the fruit from the tree by cutting the fruit stem [20,21,22]. Wang Yi [23] from Chongqing University designed a snake-mouth-inspired gripping end-effector based on biomimetic principles, which can cut the citrus stem without knowing the exact orientation of the stem in space. However, when picking a citrus from a cluster, it is difficult to cut the stem. Xu Liming [24] from China Agricultural University designed an end-effector for navel orange harvesting, which consists of an adsorption device, a gripping mechanism, and a cutting mechanism. The suction cup picks the fruit surface through a lower cylinder, the gripping mechanism secures the fruit, and an upper cylinder cuts the stem. However, when the stem is out of the cutting mechanism’s range, stem-cutting may fail. The second category is twisting-type end-effectors [25], which detach the fruit by grasping or adsorbing the fruit and applying a twisting force to break the stem [25,26,27]. Wei Bo [28] from the Chongqing University of Posts and Telecommunications designed an underactuated citrus harvesting end-effector, using a fusion control of three-finger grasping and deflection to harvest citrus fruits of various sizes and ellipsoidal shapes. Yu Lang [29] from Zhejiang Agricultural and Forestry University designed an underactuated joint-type harvesting end-effector, capable of harvesting spherical fruits of different diameters. However, the above-mentioned end-effectors are complex in structure, with multiple transmission mechanisms, leading to poor stability. He Jingquan et al. [30] designed a two-finger end-effector for spherical fruits, incorporating biomimetic fingerprint textures to enhance friction and prevent fruit from slipping. This design showed good adaptability in flexible grasping tests. However, the stability of these methods under different operating conditions still requires further improvement. In addition, some studies have adopted vacuum adsorption technology to improve harvesting adaptability. Hu et al. [31] proposed an apple harvesting end-effector based on vacuum suction cups, replacing traditional funnel-shaped suction inlets with smaller suction cups, making it easier to pass through the tree canopy. However, this method is highly dependent on the adsorption force, and when the robotic arm tilts, the adsorption force decreases, causing the fruit to slip off.

In summary, although existing research has made progress in improving the harvesting success rate and reducing fruit damage, there are still several limitations: (1) the adaptability of cutting-type end-effectors is poor in complex fruit stem environments; (2) the harvesting stability of twisting-type end-effectors [32] needs optimization due to the complexity of the transmission mechanisms; (3) vacuum suction end-effectors experience reduced suction capability when the robotic arm tilts, affecting harvesting success. Therefore, this paper proposes a new passive-compliant four-finger robotic hand for harvesting citrus fruits of different sizes and elliptical shapes. The structure is simple, providing a certain level of adaptability and stability, which improves upon the complex structures of existing end-effectors. A prototype was created, and citrus harvesting tests were conducted to validate the reasonableness of the end-effector mechanism. This provides technical support for the overall design of future citrus harvesting robots to improve harvesting efficiency and reduce fruit damage.

2. Methods

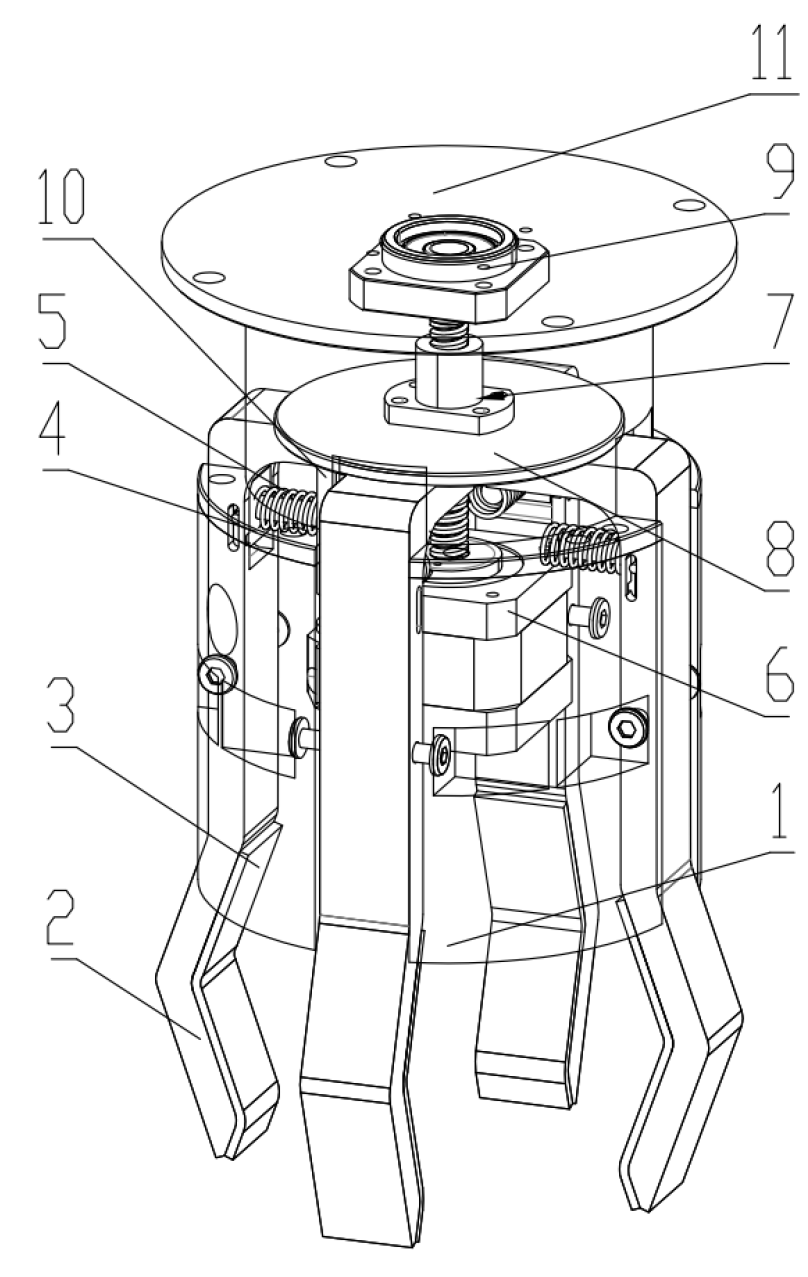
2.1. Overall Structure Scheme

This paper proposes a passive-compliant harvesting robotic hand, which uses a stepper motor as the power output for compressing the spring, with the spring serving as the source of the gripping force. Assisted by the spring, the gripping force adjusts according to the size of the citrus—the larger the citrus, the greater the gripping force, but it must not exceed the limit pressure that could damage the citrus flesh; conversely, the smaller the citrus, the lower the gripping force, ensuring stable grasping. As shown in Figure 1, the actuator consists of (1) a mounting housing, (2) gripping components, (3) cushioning material, (4) a rotating base, (5) a spring, (6) a stepper motor screw mechanism, (7) a ball, (8) a nut seat, (9) a support base, (10) an inductive proximity switch, and (11) a mounting base. The gripper components are four in number, and they grasp the citrus using the gripping force provided by the spring, giving the harvesting robotic hand a certain degree of compliance during the picking process. In addition, with the design of a floating connection between the nut seat and the gripper components, the harvesting robotic hand achieves independent motion of each gripper component using a single stepper motor as the driving element, making it capable of harvesting citrus fruits of different elliptical shapes, reducing the total number of motors and thus simplifying the structure.

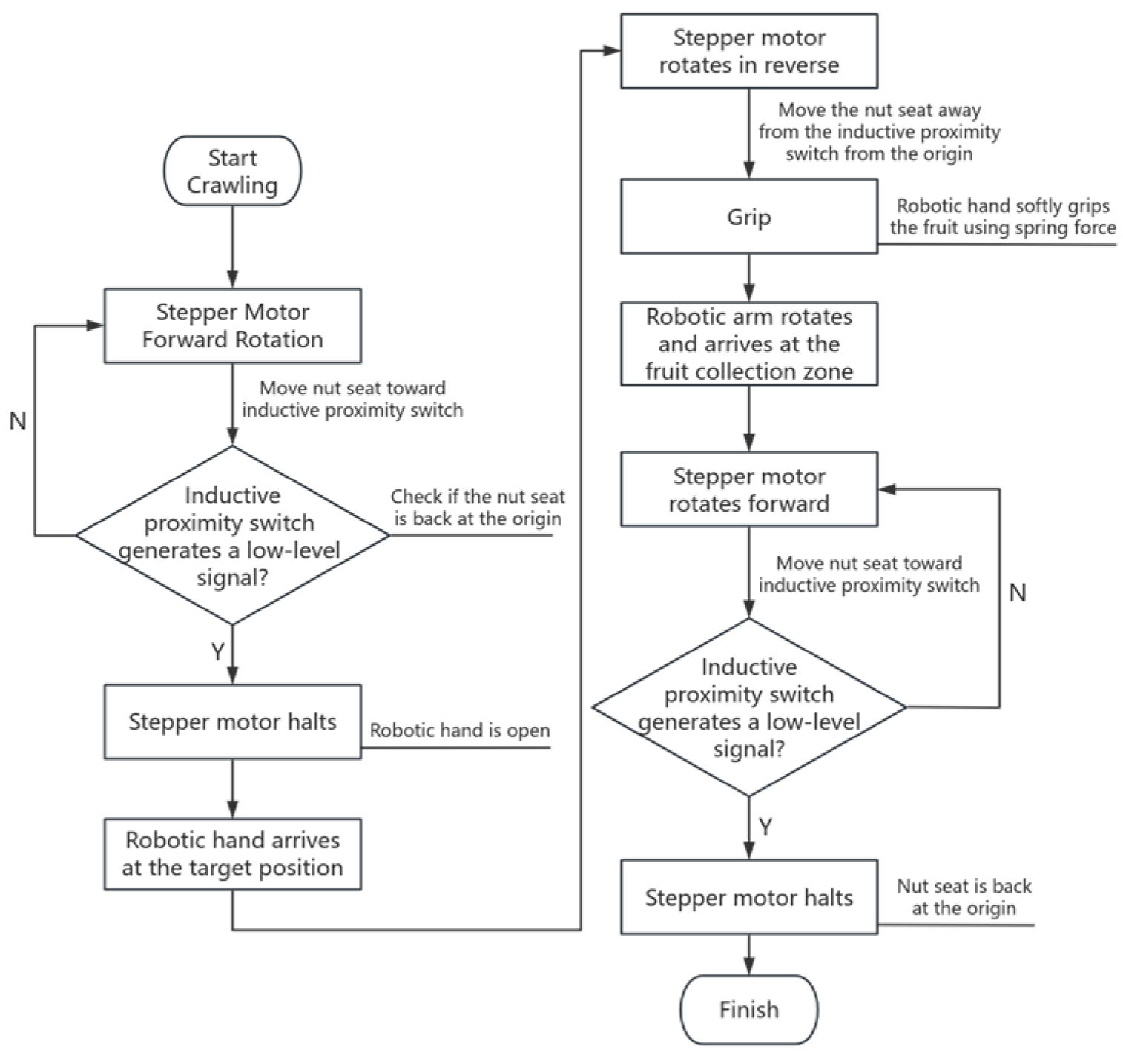
2.2. Working Principle of the Picking Manipulator

In the initial stage, the stepper motor rotates to drive the ball screw, moving the nut seat toward the motor, and pushing the gripper components to overcome the spring force and open the jaws. When the nut seat contacts the inductive proximity switch, it reaches the origin position, and the stepper motor stops rotating. At this point, the spring on each gripper component is compressed, and the gripper components are in an open state. During the gripping phase, the stepper motor reverses to drive the ball screw, moving the nut seat from the origin position toward the direction away from the motor. The gripper components, under the action of the spring force, gently grasp the fruit, and the gripper components envelope and clamp the surface of the fruit. Finally, the citrus is twisted off through the rotational motion of the robotic arm’s wrist joint and delivered to the fruit collection area. The nut seat returns to the origin position through the stepper motor’s forward rotation, releasing the citrus and completing the harvesting operation. The harvesting process is shown in Figure 2.

3. Parameter Optimization of Picking Manipulator

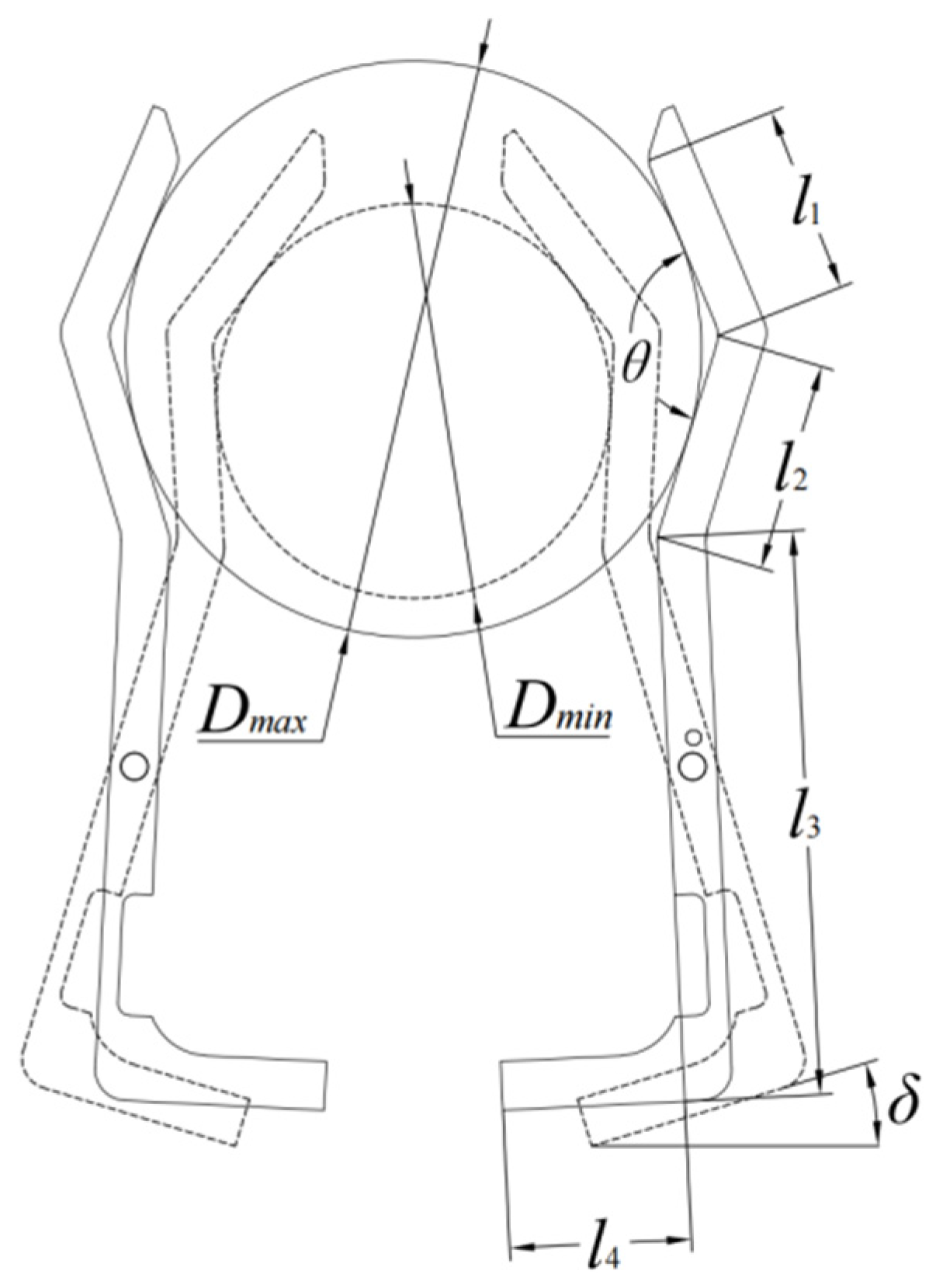
3.1. Citrus Mathematical Model and Grasping Component Optimization

There are many varieties of citrus, including varieties such as thick-skinned citrus, oranges, grapefruits, and lemons. This study primarily focuses on Navel oranges from the Hubei province, with fruits that are round or oval in shape. The fruits are usually fairly uniform in shape, with moderate thickness and fragile stems, but they are tightly wrapped and not easily peeled.

A mathematical expression for the size and shape of the citrus is established. Since each gripper component of the harvesting robotic arm has an independent compliance characteristic, it is assumed that the citrus can be modeled as a sphere for analysis. The coordinates (x, y, z) of any point on the surface of the citrus satisfy Equation (1).

$${\displaystyle \frac{x^2}{r^2}}+{\displaystyle \frac{y^2}{r^2}}+{\displaystyle \frac{z^2}{r^2}}=1$$

(1)

In the equation, r represents the horizontal diameter of the citrus, in millimeters.

Using the range of horizontal diameters of the citrus as the criterion, the citrus is modeled for gripping in SolidWorks 2021. To ensure that the inner surface of the gripping components maintains contact points with citrus fruits of any size, CAD was employed to simulate and optimize the relevant finger parameters, resulting in the determination of the gripping component dimensions and two gripping postures, as shown in Figure 3. l₁ is the length of the distal phalanx, in mm; l₂ is the length of the middle phalanx, in mm; l₃ is the length of the proximal phalanx, in mm; l₄ is the length of the base, in mm; O is the pivot point; δ is the angle of rotation of the gripper component relative to the pivot point O, in °; θ is the angle between the distal and middle phalanges, in °; D_max is the maximum gripping diameter, in mm; and D_min is the minimum gripping diameter, in mm. The optimal parameters were determined as follows: the length of the distal phalanx of the gripper component, l₁, is 31 mm, the length of the middle phalanx, l₂, is 35 mm, and the angle between them, θ, is 140°. Considering the overall structure of the end-effector, the proximal phalanx length, l₃, is set to 93 mm, and the length of the gripper base, l₄, is set to 30 mm, as shown in Figure 3. When the gripper base is in a horizontal position, the gripping range is maximized, with the gripping diameter, D_max, approximately 100 mm. When the gripper component rotates relative to the pivot point O by an angle δ of 16.83°, the gripping diameter, D_min, is 65 mm.

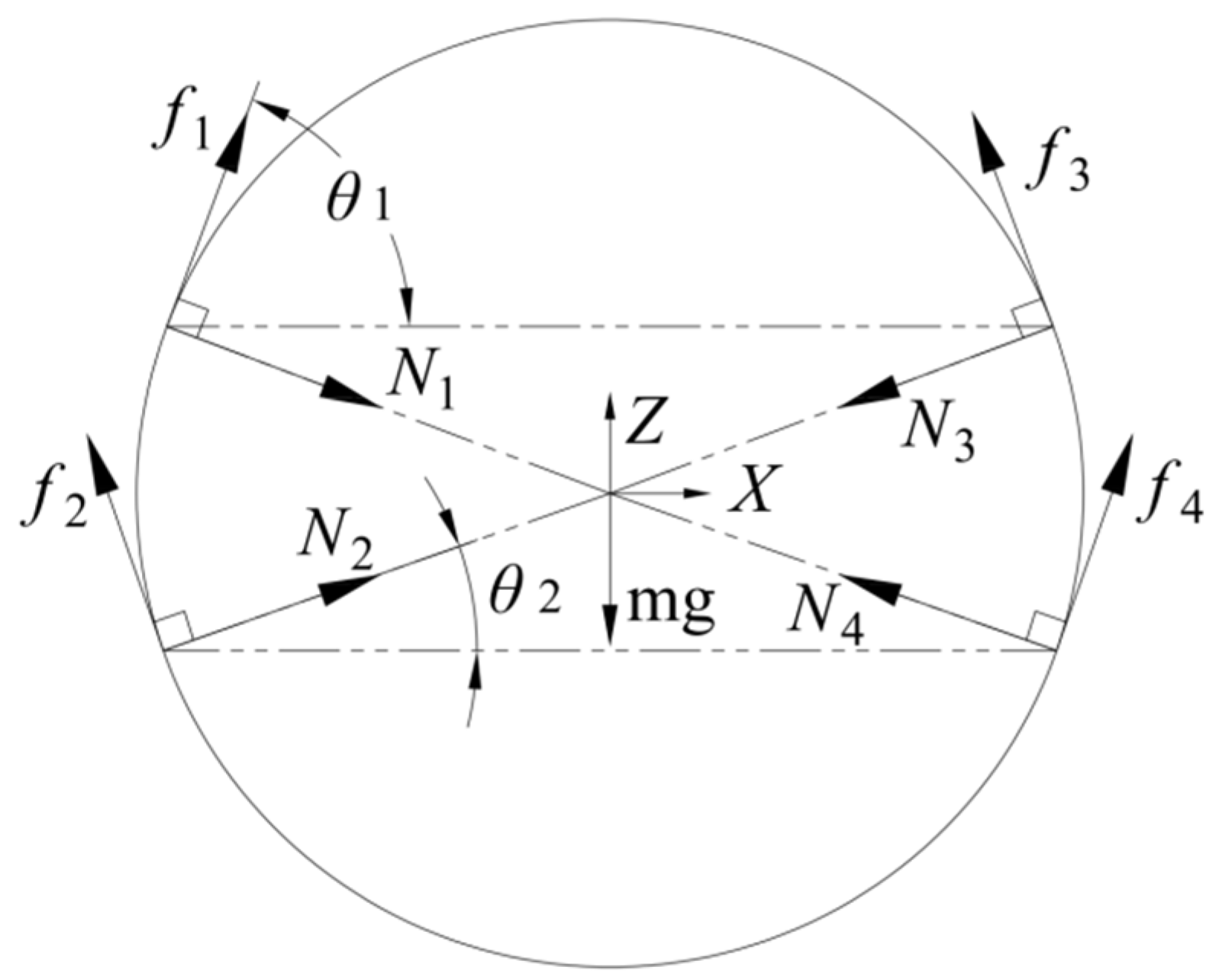
3.2. Stress Analysis of Citrus

Due to the 4 V-shaped gripping components having a total of 8 contact points with the citrus, the force on the i-th contact point mainly consists of the normal force N_i, the frictional force f_i, and the gravitational force of the citrus mg. When grasping the citrus with a D_min of 65 mm, the force on the citrus is simulated using CAD 2022 software, resulting in an angle θ₁ of 53.17°and an angle θ₂ of 3.17°. The main force analysis is shown in Figure 4. f_i represents the static friction force along the gripping surface at the i-th contact point (N); N_i represents the normal force at the i-th contact point (N); θ₁ is the angle between f₁, f₃, f₅ and f₇ and the horizontal plane (°); θ₂ is the angle between N₂, N₄, N₆, and N₈ and the horizontal plane (°); mg is the gravitational force of the citrus fruit (N). The 4 V-shaped gripping components of the harvesting robotic hand are evenly distributed on the surface of the citrus, and the normal force, N_i, on each contact point is equal, satisfying Equation (2). The forces in the horizontal direction satisfy Equations (3)–(6), so the resultant force on the citrus in the horizontal direction is 0. To ensure that the smallest size of citrus is stably gripped without slipping, the citrus force balance equation should satisfy Equation (7). Under this condition, when the maximum static friction between the gripper component and the fruit is reached, Equation (8) is satisfied. At this point, the normal force on each contact point is minimized, with the minimum normal force denoted as N_min, satisfying the condition in Equation (9).

$$N_i=N_1=N_2=N_3\cdots N_8$$

(2)

$$f_1\cos {\theta }_1-f_3\cos {\theta }_1=0$$

(3)

$$f_4\sin {\theta }_2-f_2\sin {\theta }_2=0$$

(4)

$$f_5\cos {\theta }_1-f_7\cos {\theta }_1=0$$

(5)

$$f_8\sin {\theta }_2-f_6\sin {\theta }_2=0$$

(6)

$$\left(\begin{array}{l}{f}_1+f_3+\\ f_5+f_7\end{array}\right)\sin {\theta }_1+\left(\begin{array}{l}{f}_2+f_4+\\ f_6+f_8\end{array}\right)\cos {\theta }_2+\left(\begin{array}{l}{N}_2+N_4\\ +N_6+N_8\end{array}\right)\sin {\theta }_2-\left(\begin{array}{l}{N}_1+N_3+\\ N_5+N_7\end{array}\right)\cos {\theta }_1-mg=0$$

(7)

$$f_i=\mu N_i$$

(8)

$$N_{\min }\ge N_i$$

(9)

In the equation, m represents the mass of the citrus fruit (kg), g is the gravitational acceleration (taken as 9.8 m/s²), and μ is the coefficient of friction between the citrus peel and the cushioning material.

Attaching a certain amount of cushioning material to the surface of the V-shaped gripping components can increase the friction coefficient, improve the compliance of the finger surface, reduce the required normal force, and reduce potential mechanical damage during the gripping process. Different cushioning materials have varying friction coefficients with the citrus peel, and there are three common types: rubber, silicone, and pearl cotton. In this study, silicone is chosen as the cushioning material, with μ taken as 0.68 [19]. The citrus with a minimum diameter, D_min, of 65 mm has a mass of approximately 140 g. By increasing the margin coefficient by 10%, the fruit mass is taken as 154 g, and solving Equations (7) to (9) results in a minimum normal force of 0.56 N. Additionally, because the larger the citrus, the greater the gripping force provided by the harvesting manipulator, the excessive normal force could damage the citrus’ biological tissue. Therefore, when considering the citrus with a maximum diameter, D_max of 100 mm, the maximum normal force that the citrus can withstand, denoted as N_max, must be considered. The longitudinal elastic modulus of the citrus peel and flesh are 11.408 MPa and 0.277 MPa, respectively, with ultimate stresses of 1.250 MPa and 0.048 MPa. When the gripping force is 12 N, the maximum equivalent stresses in the citrus peel and flesh are 1.091 MPa and 0.035 MPa, both of which are lower than their respective ultimate stresses, meaning no mechanical damage will occur to the citrus [24,33]. When the load on the citrus is less than 10 N, the citrus remains within the elastic range, and the elastic deformation is minimal, with deformation being less than 6 mm. Therefore, it can be considered safe for the citrus when the harvesting manipulator exerts a force of less than 10 N during robotic harvesting [19]. Therefore, the normal force range can be determined as 0.56 to 10 N.

To ensure stable grasping and prevent slipping of the maximum-sized citrus, the minimum normal force required at each contact point is N_min. At this point, θ₁ is 69.38° and θ₂ is 19.38°, with the primary force analysis shown in Figure 5. f_i represents the static friction force along the finger surface of the i-th contact point, in N; N_i represents the normal force at the i-th contact point, in N; θ₁ represents the angles between f₁, f₃, f₅, f₇ and the horizontal plane, in °; θ₂ represents the angles between N₂, N₄, N₆, N₈ and the horizontal plane, in °; mg represents the gravitational force of the citrus, in N. The citrus with a maximum diameter, D_max, of 100mm has a mass of approximately 340 g. By increasing the margin coefficient by 10%, the fruit mass is taken as 374 g, and solving Equations (7) to (9) yields a minimum normal force N_min of 0.92 N. Thus, the load borne by the citrus during stable grasping is between 0.92 and 10 N. The contact between the harvesting manipulator and the citrus surface is not a simple point-to-surface contact, but a complex multi-point contact problem. The surface of the citrus has a certain curvature and is not smooth, and its surface characteristics affect the distribution and contact area. Therefore, the contact relationship should be considered as a combination of multiple contact points, rather than simple point or surface contact. Additionally, as citrus is a flexible body, it undergoes local deformation when subjected to force, and the degree of deformation may vary with changes in external forces. Different contact areas experience varying degrees of pressure, leading to differences in the deformation of the peel and the stress distribution in the flesh. Therefore, deformation factors need to be introduced in the force analysis to more accurately describe the mechanism of contact and force transmission. This force analysis does not account for these complex nonlinear behaviors. Future research should consider contact forces, friction forces, and the deformation response of the fruit to more comprehensively simulate the force conditions during the harvesting process. Therefore, this study selects a safe load range from 4 to 9 N.

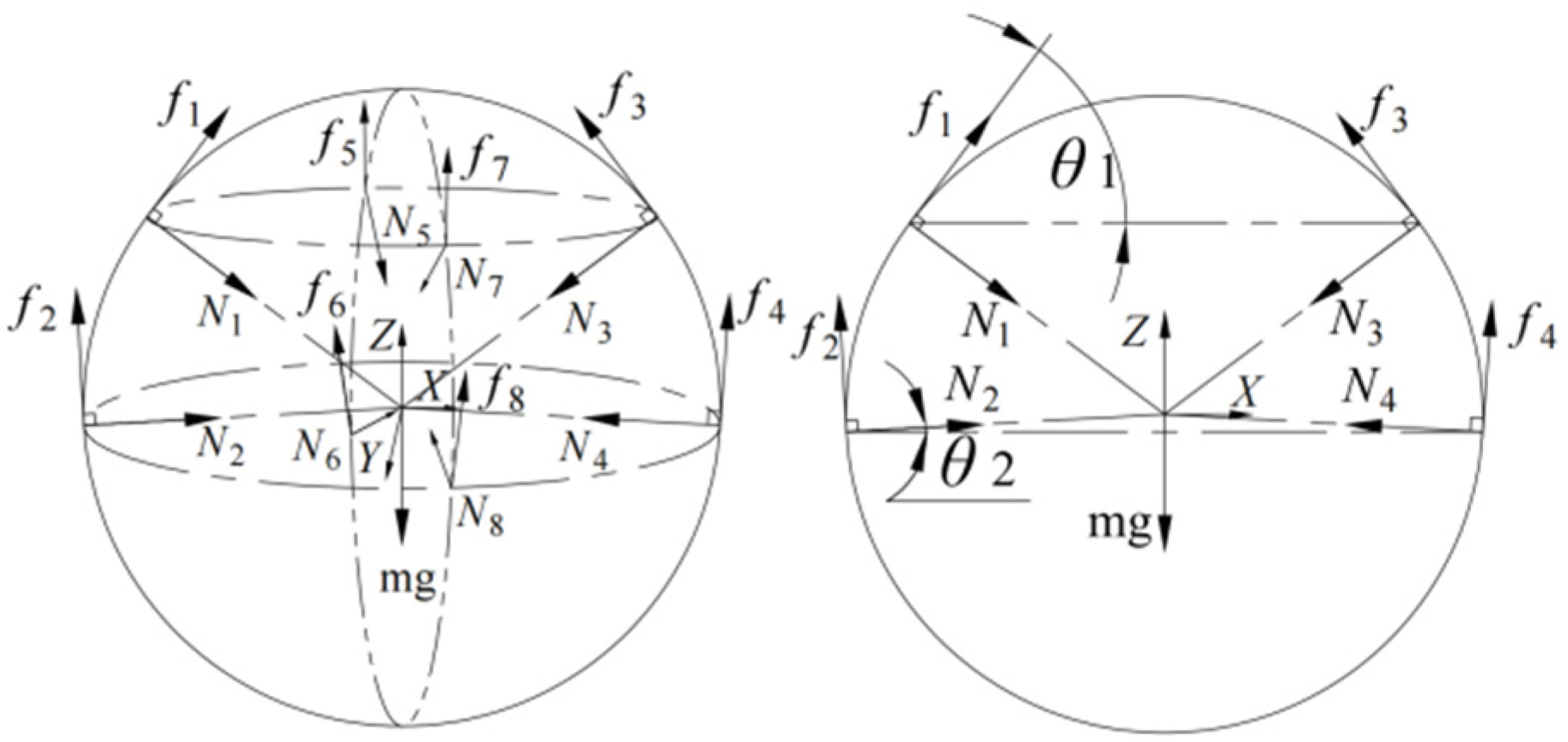
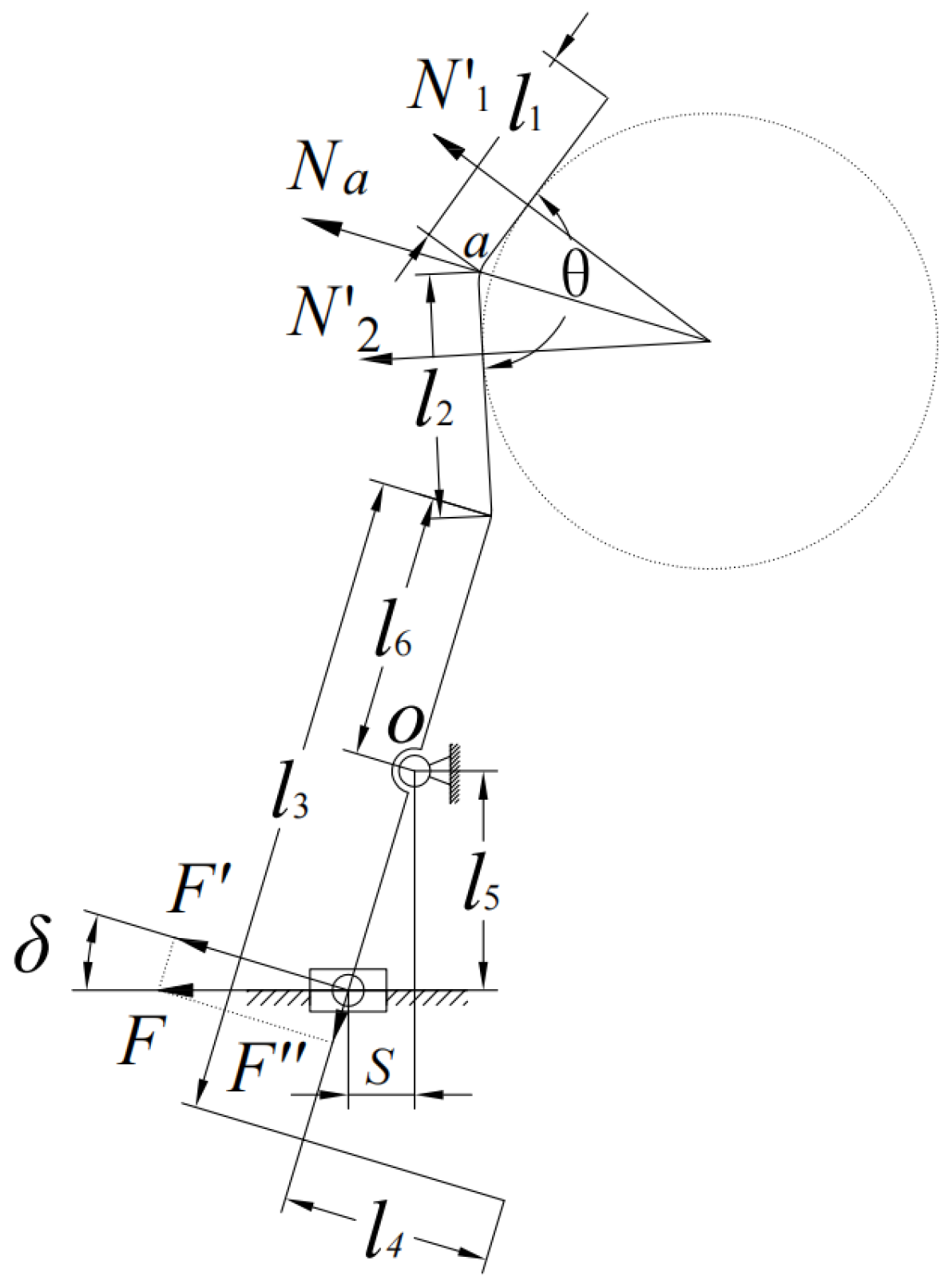
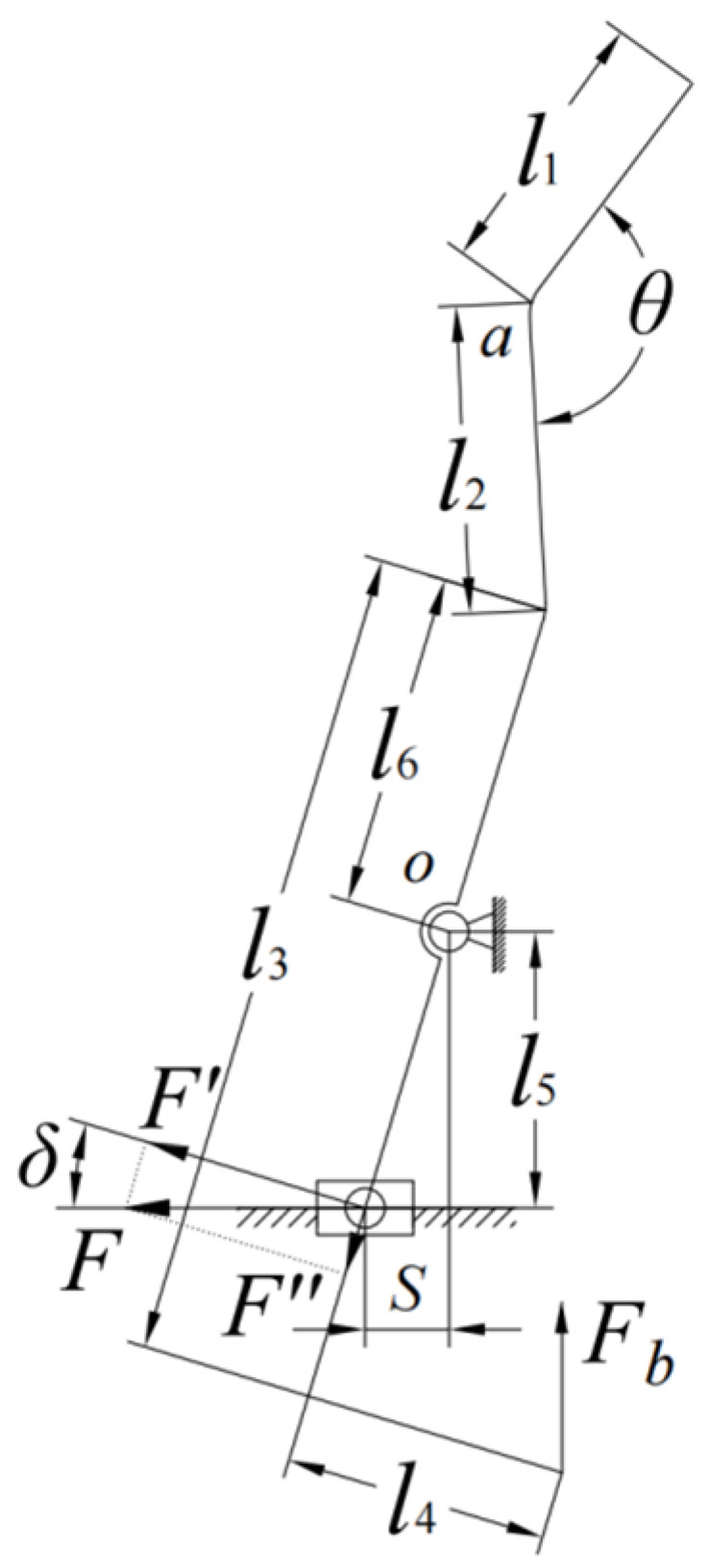
3.3. Grasping Component Force Analysis and Component Selection

3.3.1. Force Analysis of Grasping Member

Since the four gripping components are evenly distributed on the surface of the citrus, force analysis is performed on one side, as shown in Figure 6. Point O is the pivot point of the gripping component; $N_1^{\prime }$is the normal force at the first contact point, in N; $N_2^{\prime }$is the normal force at the second contact point, in N; N_a is the resultant force of $N_1^{\prime }$and $N_2^{\prime }$, in N; l₅ is the perpendicular distance from the pivot point O to the sliding block movement surface, in mm; l₆ is the distance from the pivot point O to the proximal end of the middle finger, in mm; S is the stroke of the sliding block, in mm; $F^{\prime }$ and $F^{″}$ are the components of force F in two directions, in N; δ is the rotational angle of the gripper relative to the pivot point O, in °; θ is the angle between the distal and middle phalanges, in °. The distance from point O to the spring force F is l₅ = 31.3 mm, and the distance from point O to the proximal end of the middle finger segment is l₆ = 38 mm. $N_1^{\prime }$ and $N_2^{\prime }$ represent the normal forces acting on the gripping components, and their resultant force is N_a, with the action line passing through point a. Since $N_1^{\prime }$ and $N_2^{\prime }$ are equal in magnitude and symmetric about point a, the resultant moment M_a is 0, meaning that point a only experiences the resultant force N_a. Assuming the gripping component is an ideal mechanism (i.e., ignoring friction), the forces on the gripping component are simplified to point O. Based on the force moment equilibrium equation, as shown in Equation (10), the required spring force F is derived.

$${\displaystyle \sum _{i=1}^n{M}_i}=M_q+M_p=0$$

(10)

In the equation, n = 2; M_q is the resultant moment of the force N_a about point O, in N·m; M_p is the resultant moment of the spring force F about point O, in N·m. The equations are as follows:

$$M_q=N_a\left(l_2\sin {\displaystyle \frac{\theta }{2}}+l_6\right)$$

(11)

$$N_a=2N_1^{\prime }\sin {\displaystyle \frac{\theta }{2}}$$

(12)

$$M_p=-F^{\prime }{\displaystyle \frac{l_5}{\cos \delta }}$$

(13)

$$F={\displaystyle \frac{F^{\prime }}{\cos \delta }}$$

(14)

By solving Equations (10) to (14) simultaneously, we obtain the following:

$$F={\displaystyle \frac{2N_1^{\prime }\sin \frac{\theta }{2}\left(l_2\sin \frac{\theta }{2}+l_6\right)}{l_5}}$$

(15)

From Equation (15), it can be seen that l₂, l₅, l₆, and θ are inherent parameters of the gripper, and the spring force F depends only on the normal force $N_1^{\prime }$exerted on the gripper, since $N_1^{\prime }$ is the reaction force of N₁, equal in magnitude and opposite in direction. The citrus fruit bears a safe load of 4 to 9 N, so the required spring force range is from 17.1 to 38.4 N.

3.3.2. Parts Selection

When grasping a citrus with the maximum diameter, D_max, the spring force is 38.4 N, and the citrus load is 9 N; when grasping a citrus with the minimum diameter, D_min, the spring force is 17.1 N, and the citrus load is 4 N. Let the spring stiffness be k, satisfying Equations (16) and (17):

$$F_1=k{x}_1$$

(16)

$$F_2=k{x}_2$$

(17)

$$s=x_1-x_2$$

(18)

$$s=l_5\tan \delta$$

(19)

In the equation, F₁ is the spring force provided when grasping a citrus with D_max, in N; x₁ is the compression of the spring, in mm; F₂ is the spring force provided when grasping a citrus with Dmin, in N; x₂ is the compression of the spring, in mm; s is the change in spring compression, in mm.

By solving Equations (16) to (19), the spring stiffness k is calculated to be 2.25. When grasping a citrus with the maximum diameter, D_max, the spring compression x₁ is 17.1 mm, and when grasping a citrus with the minimum diameter, D_min, the spring compression x₂ is 7.6 mm. Therefore, a spring with a length of 38 mm and a stiffness of 2.25 can be selected.

When the stepper motor rotates, the ball screw converts the torque into thrust, which causes the gripping component to overcome the spring force and compress the spring, thereby opening the gripping component. At this moment, the force analysis of the gripping component is shown in Figure 7. l₅ is the vertical distance from the pivot point O to the sliding block’s motion surface, in mm; l₆ is the length from pivot point O to the proximal end of the middle phalanx, in mm; s is the stroke of the sliding block, in mm; $F^{\prime }$ and $F^{″}$ are the components of force F in two directions, in N; F_b is the thrust applied to the gripper component by the ball screw, in N; δ is the rotation angle of the gripper component relative to pivot point O, in °. The forces acting on the gripping mechanism are simplified to the point O. Based on the equilibrium of the resultant moment, as shown in Equation (20), the thrust F_b exerted by the ball screw on a single gripping component is derived:

$${\displaystyle \sum M_o}={\displaystyle \sum M_b}+{\displaystyle \sum M_p}=0$$

(20)

In the equation, M_b represents the resultant moment of F_b about point O, in N·m. The equations are as follows:

$${\displaystyle \sum M_b}=F_b\left[l_4\cos \delta -\left(l_3-l_6\right)\sin \delta \right]$$

(21)

$${\displaystyle \sum M_p}=-F{l}_5$$

(22)

$$F=k\left(x_1-l_5\tan \delta \right)$$

(23)

By solving Equations (20) to (23) simultaneously, we obtain the following:

$$F_b={\displaystyle \frac{k{l}_5\left(x_1-l_5\tan \delta \right)}{l_4\cos \delta -\left(l_3-l_6\right)\sin \delta }}$$

(24)

$$F_b^{\prime }={\displaystyle \frac{k{l}_5^2{\sec }^2\delta }{l_4\sin \delta +\left(l_3-l_6\right)\cos \delta }}$$

(25)

The parameters x₁, l₃, l₄, l₅, l₆, and k are known design parameters. By differentiating Equation (24) and using Equation (25), it can be seen that Equation (24) is monotonically increasing for δ ∈ [0,16.83], and when the angle δ is 16.83°, the maximum F_b is 42 N.

The ball screw mechanism selected is the 0802 model, with a diameter of 8 mm and a lead of 2 mm. The screw has no load in the vertical direction, and the transmission efficiency is assumed to be 0.95. According to Equation (26), the required motor torque is calculated to be 0.056 N·m. Therefore, a 42-stepper motor with two phases, four wires, and no brake is chosen, with a rated torque of 0.25 N·m, which is 4.4 times the calculated torque, meeting the requirements.

$$T={\displaystyle \frac{4F_{b}I}{2\pi n}}$$

(26)

In the equation, T represents the torque of the stepper motor in N·m; F_b represents the axial thrust exerted on a single gripper component by the ball screw in N; I is the lead of the screw in mm; n is the transmission efficiency of the screw.

4. Results

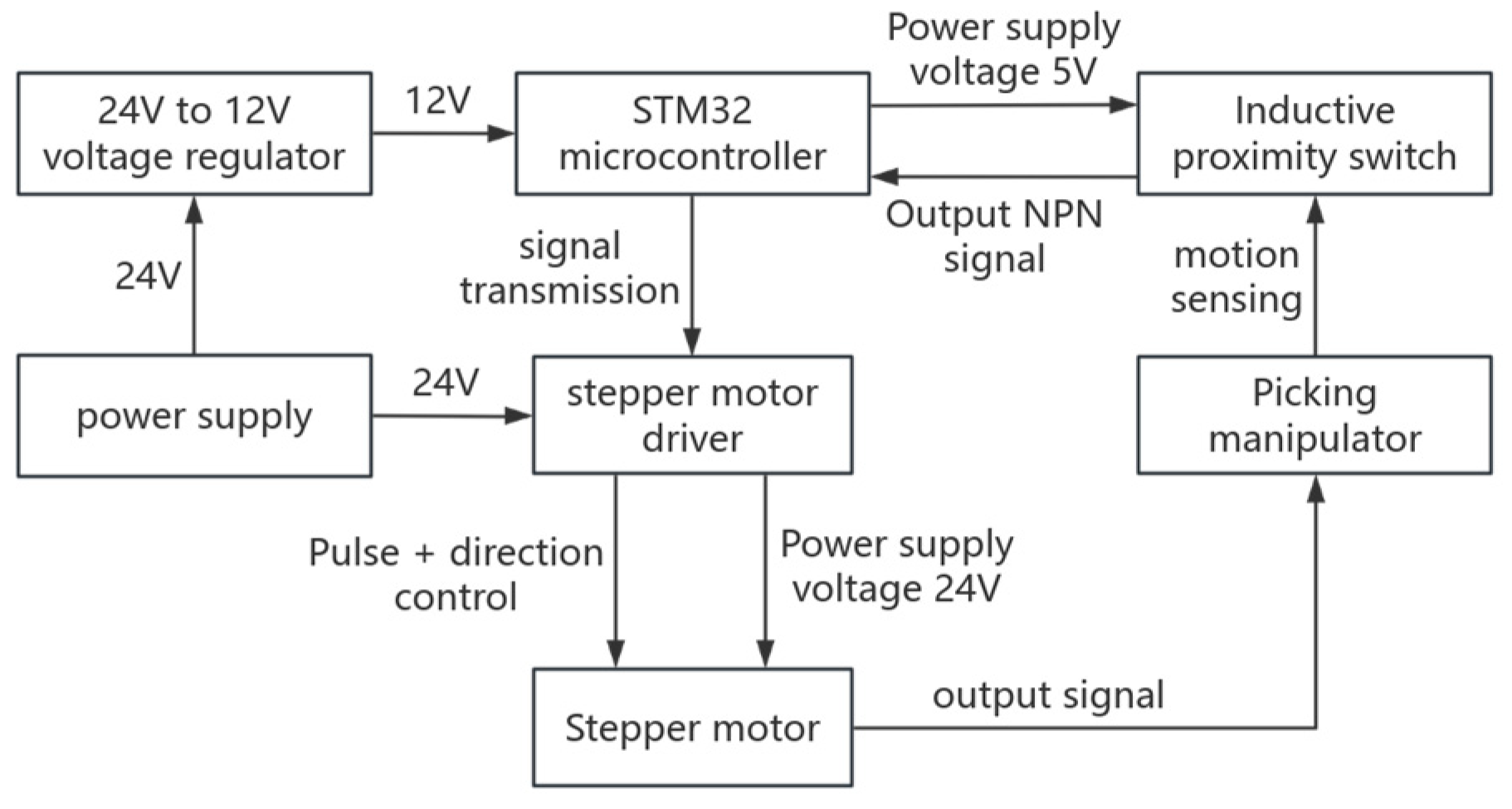
4.1. Control System Constitution

The hardware system of the harvesting robotic arm includes a DC24V power supply, a 24 V to 12 V voltage regulator, an STM32 microcontroller (model STM32F103C8T6, power supply voltage 12 V), a stepper motor driver (model DM420), and an inductive proximity switch with an NPN normally open type (brand: Omron, model: E2E-X1C1). The software is programmed in C++ 14. The overall system architecture is shown in Figure 8.

The entire control system adopts the end control principle. Initially, the microcontroller sends a reverse command to the driver, which controls the stepper motor to continuously rotate in reverse until the nut seat approaches the inductive proximity switch. The proximity switch outputs a low-level signal, indicating that the nut seat has returned to the home position (gripping component open state), and the stepper motor stops rotating. After the citrus enters the grabbing range, the microcontroller sends forward rotation, pulse count, and pulse frequency commands to the driver. The driver controls the stepper motor to rotate forward at a speed of 2r/s for four cycles. At this point, the nut seat gradually stops contacting the grabbing component, and the grabbing component slowly grips the fruit under the action of spring force. Finally, the citrus is twisted off by rotating and then delivered to the fruit collection area. The microcontroller sends a reverse command to the driver, which controls the stepper motor to rotate in reverse until the inductive proximity switch outputs a low-level signal, stopping the stepper motor and completing the return to the home position while unloading the fruit.

To verify the shape adaptability of the citrus-picking robot designed in this paper and its final picking performance, envelope tests were conducted in a laboratory environment, followed by picking tests in an orchard environment.

4.2. Envelope Test in Laboratory Environment

The picking robot’s stepper motor lacks a braking function, so the actuator begins in a closed state. First, the stepper motor reverses, and the nut seat reaches the origin position, opening the gripper. After initialization, the enveloping process is shown in Figure 9. The stepper motor then rotates forward, and the nut seat moves away from the origin position. Under the spring’s force, the gripper envelopes the citrus. Figure 10a shows the enveloping of citrus with a diameter of 65~100 mm, while Figure 10b shows the enveloping of elliptical citrus. It can be seen that the picking robot demonstrates good adaptability to different sizes and elliptical-shaped citrus fruits, with the grippers automatically conforming to the citrus surface to complete the enveloping and grasping. The weight of citrus fruits with different diameters is recorded during grasping. While in the grasped state, the citrus fruit is fixed to one end of a force gauge. Both the manipulator and the force gauge are placed horizontally, and the force gauge is used to pull the citrus fruit horizontally. The force exerted by the gauge is recorded when the gripping components begin to rotate. This recorded force represents the maximum weight that the manipulator can securely grasp for citrus fruits of varying diameters. The experimental results are presented in

Table 1. Gripping test results.

Citrus Diameter/mm	Citrus Weight/kg	Maximum Gripping Weight/kg
65	0.131	0.8
75	0.201	1.7
85	0.292	2.3
95	0.408	2.9

.

The gripping test results indicate that the larger the diameter of the citrus fruit, the greater the gripping force exerted by the manipulator. Moreover, the maximum grasped weight exceeds the weight of the citrus fruit in all cases. Therefore, the harvesting robotic arm can stably grip fruits of different diameters.

4.3. Picking Experiment in Orchard Environment

In the experiment on the cutting force of citrus stems, Fu Shun [34] found that the maximum cutting resistance required to cut stems of different thicknesses varies significantly, with the maximum cutting force reaching 136.94 N. This makes cutting the stem for citrus-picking a relatively difficult operation. In comparison, the force separation method [25] is simple and easy to operate. Research shows that Navel oranges in Hubei Province begin to mature in November and can be harvested until March of the following year. Late-season Navel oranges begin to mature in March and can be harvested until June. The skin of Navel oranges is tightly wrapped, and the stems are relatively brittle. When manually rotating and picking, adding a pulling force makes it easy to pick the oranges. Even after the stem completely detaches, the calyx still stays tightly against the fruit’s skin. Therefore, the citrus-picking robot in this paper adopts the force separation method. The gripper component of the robot grabs the fruit and breaks the stem by rotating multiple times to pick the fruit. To verify the practical feasibility of the optimized picking robot in an orchard environment, a field picking test of Navel oranges was conducted in an orchard in Wuhan in January 2024, as shown in Figure 11. Based on the field orchard test, the fruit diameter range for picking was 65~100 mm, with a total of 420 samples picked. The citrus numbers and fruit damage rates were recorded for different rotation ranges, (0,1), (1,2), (2,3), and (3,4), where the number of rotation cycles refers to the number of rotations required by the picking robot to successfully twist and detach the stem. The test results are shown in

Table 2. Capture test results.

Fruit Diameter Range/mm		65~75	75~85	85~95	Mean Value
Number of rotations	(0,1)	52	21	25	32.7
	(1,2)	60	63	35	53.7
	(2,3)	20	40	55	38.3
	(3,4)	8	16	25	16.3
Picking quantity		140	140	140	140
Damage quantity		4	2	5	3
Fruit damage rate/%		2.9	1.4	3.6	2.6

.

The picking results show that the number of rotations required to break the citrus stem varies with the size of the fruit. Without applying pulling force, the fruit can be fully detached after four rotations, with a damage rate of 2.6%. During the picking process, branches were found to contact the fruit skin, and when twisted, the branches were inserted into the skin, causing fruit damage. Furthermore, after bringing the harvested citrus back to the lab, no visible damage was observed at the stem connection, as shown in Figure 12. Upon cutting the fruit for an internal examination, no damage to the flesh was found. Therefore, in the absence of external pulling force, the main cause of fruit damage can be attributed to physical interference from branches during the twisting process.

5. Discussion and Conclusions

This study designed a passive-compliant citrus harvesting robotic hand, utilizing a spring-assisted gripping structure that allows it to adapt to citrus fruits of different sizes without the need for pressure sensors. Additionally, the floating connection structure of the nut seat enables each gripping component to move independently under the drive of a single motor, allowing the gripping components to automatically conform to the citrus surface. This improves the adaptability to the fruit shape without requiring complex feedback control, thereby simplifying the system structure. Based on static analysis, the relationship between the gripping force of the harvesting hand and the spring force was derived, providing a theoretical basis for determining spring parameters for the harvesting of different spherical fruits. A physical prototype of the harvesting hand was constructed, and citrus harvesting tests were conducted both in the laboratory and orchards. The experimental results show that the harvesting hand has good adaptability to citrus fruits of varying sizes and ellipsoid shapes. Each gripping component automatically conforms to the citrus surface, and after rotating four turns without applying pulling force, the fruit detaches completely with a damage rate of 2.6%. Currently, rigid robotic hands [35] typically rely on multiple motors to drive independent joints, combined with force sensors for precise control to ensure stable fruit grasping. However, this approach increases system cost and heavily depends on sensors. Underactuated robotic hands [29], on the other hand, achieve multi-degree-of-freedom motion with fewer driving units, often using flexible joints or adaptive structures to improve grasping capability. Nevertheless, most underactuated robotic hands still require external sensors or precise mechanical modeling to adjust the gripping force and avoid fruit damage or slipping. The passive-compliant robotic hand in this study outperforms rigid robotic hands in terms of harvesting adaptability, structural simplification, and gripping stability. Additionally, it achieves an adaptive grasping ability similar to that of underactuated robotic hands without requiring complex sensor control. Experimental results show that this robotic hand is suitable for orchard environments and effectively reduces the risk of fruit damage. However, future research will need to optimize the rotation harvesting angle to reduce fruit damage caused by branch interference and extend testing to different fruit varieties to enhance its generalizability.