Featured Application
This study offers practical applications for enhancing the safety and efficiency of urban underground roads. By analyzing vehicle operating characteristics and risks at curves in urban underground roads, the results provide valuable references for traffic management authorities to implement effective safety measures and accident prevention strategies. For instance, safety measures and accident prevention should focus particularly on the circular curve sections of the curves. Additionally, the results can guide the selection of geometric indicators in the future construction of urban underground road curves.
Abstract
To clarify the operational characteristics and driving risks of urban underground road curves, a real vehicle driving experiment involving 20 subjects was conducted at the Jiefangbei Underground Ring Road in Chongqing. High-precision instruments were utilized to collect driving data, including vehicle speed, lateral acceleration, and longitudinal acceleration. Significance tests were performed on lateral acceleration, longitudinal acceleration, entering curve deceleration, and exiting curve acceleration. The driver behavior risk at curves was evaluated using G-G diagrams, and the distribution characteristics of curve danger points were determined. Subsequently, models were established for the relationships between lateral acceleration, entering curve deceleration, exiting curve acceleration, and curve geometric parameters. The results show that: (1) significant differences exist in lateral and longitudinal acceleration under different radius ranges; (2) the sections with the highest curve danger levels in urban underground road curves primarily concentrate within the circular curve sections of curves; (3) the number of driving risk points per unit length (m) is not correlated with curve type, but significantly related to curve radius range; (4) the relationship models between entering curve deceleration, exiting curve acceleration, and curve parameters are upward-opening quadratic functions, whereas the relationship model between lateral acceleration and curve parameters comprises two quadratic functions with different orientations.
1. Introduction
With increasing population and residential car ownership, urban road spaces are facing challenges to meet the demands of urban transportation and social development. Therefore, developing underground space resources has been considered as a solution to this problem. China is currently at the forefront of urban underground space development in terms of the quantity of urban underground space, subway construction, complex underground development, and related industries [1]. Furthermore, to improve urban transportation and overcome the limitations posed by natural and artificial barriers, such as rivers, lakes, bays, mountains, roads, and buildings, an increasing number of cities are investing in tunnel and underground road construction. The aim is to create broader spaces for the economic and social growth of cities. By the end of 2021, 406 urban road tunnels had been built in 82 of China’s 661 cities [2]. These urban tunnels have reduced travel distances and improved transportation efficiency, thereby alleviating urban traffic congestion.
Curves are relatively dangerous sections of road networks [3]. In 2017, approximately 17.1% of road traffic accidents in China occurred on curves, and curved road accidents caused 22.6% of deaths and 18.4% of injuries [4]. When facing the safety challenges posed by curve risks on ground roads, horizontal curve signs and markings are used to enhance safety in curve driving [5,6]. Symbolic road signs can effectively improve drivers’ estimations of the curvature of dangerous curves [7]. However, for urban underground roads, their limited building space restricts the development of curves, resulting in some curves having too small radii. This, and the dim and monotonous internal environments of subterranean roads, can cause drivers to experience velocity and curvature illusions. Moreover, the lateral walls of curves can obstruct the line of sight, restricting the visual field of the driver and further increasing the complexity and risk associated with driving. Meanwhile, as a semi-enclosed structure, the narrow and dark environment of tunnels can also cause tension and anxiety in drivers. Driving in a monotonous environment can lead to driver boredom and fatigue [8]. Furthermore, the current design standard for urban underground roads in China mainly refer to the Urban Underground Road Engineering Design Specification CJJ221-2015 [9]. However, this specification does not explicitly define the safety range for a curve radius, nor provide a definition for small-radius curves. In actual construction, due to the constraints of terrain and architectural space, the radius of underground road curves is often relatively small, resulting in the high safety risks in the design and construction of curves. Therefore, it is necessary to assess the risks of curves on urban underground roads. Based on the above discussion, in order to explore the operating characteristics and driving risks of vehicles on underground road curves, identify the locations with higher curve risks, and propose reference values for the geometric indicators of underground road curves. In this study, a real vehicle test was employed to acquire continuous-driving data, including the vehicle’s operating speed, lateral acceleration, and longitudinal acceleration. The distribution characteristics of acceleration on curved urban underground roads were analyzed, and the safety and risk of driver behavior were evaluated based on the acceleration driving risk model (G-G diagram). Finally, the correlation between the geometric curvature parameters and the driving acceleration of the vehicle was explored. The findings are instructive for reducing the number of accidents on urban underground roads and for improving the driving safety of their curved sections. The main contributions of this study are as follows.
- (1)
- The acceleration cumulative frequency distribution characteristics of curves on urban underground roads and the comfort and stability of driving on each curve were obtained based on the collected continuous vehicle operation data (lateral and longitudinal accelerations).
- (2)
- The driving behavior risk of curves on urban underground roads was analyzed based on the acceleration data and driver risk model, and the areas with the highest driving risk on these curves were identified. Meanwhile, the safety improvement methods on risk curves were discussed. The findings provide valuable insights for traffic management authorities to develop safety improvement measures, and they serve as a reference for accident prevention efforts.
- (3)
- The correlations and sensitivities between the lateral acceleration, entering curve deceleration, exiting curve acceleration, and curve geometry parameters were obtained separately based on the acceleration and curve geometry parameter data. The findings provide a reference for selecting geometric indicators for future construction of underground road curves.
2. Literature Review
The unique visual environment of urban underground roadways can impact drivers’ visual and psychological states, thereby influencing their driving behavior. Therefore, examining the effects of underground road environments on driver behavior from the perspectives of driver vision, psychology, and more plays a crucial role in enhancing underground road safety. Among them, the tunnel environment has a significant impact on visual perception. Huang et al. proposed four traffic visual guidance schemes for the diversion and convergence zones of urban underground roads, and studied their impact on driving behavior through simulated driving experiments [10]. He et al. investigated the influence of the sidewall effect on drivers in urban tunnels and found significant differences in the distribution of driver attention and vehicle stability among different lanes, with the left side being the most significant [11]. Moreover, the geometric design of underground roads can affect driving stability. Therefore, Diao proposed an optimal value for the alignment design index of an underground road access ramp based on the driver’s physiological index through a driving simulation test [12]. Additionally, changes in the geometric shapes of underground roadways can affect drivers’ psychological states, visual load, driving speeds, and acceleration. Jiao et al. found that the saccadic angle dispersion of drivers in ultralong urban underwater tunnels increased with the radius [13]. Fang et al. also discovered that the longer the urban tunnel, the more dispersed the distribution of driver gaze points [14]. In addition, researchers have found that the geometric indicators of urban underground roads affect vehicle speed and driver heart rate. For instance, Feng et al. conducted on-road experiments and found that the longitudinal slope had a significant impact on the growth rate of driver heart rate, with a higher increase observed for downhill sections than for uphill sections [15]. Liu et al. found that the lane width and shoulder width of three-lane underground urban highways significantly affected the driving speed, with lane width having a greater impact than shoulder width [16]. Furthermore, tunnel lighting and illumination also have a certain impact on tunnel driving safety. Ge et al. [17] found that at lower speeds, the at least four times stopping sight distance (4SSD) of advanced vehicle lighting systems (AVLL) is crucial for improving driver speed consistency and control feel within curves, helping to reduce sudden speed adjustments. Feng et al. [18] found through experimental analysis that in road tunnels where vehicle speed limits are less than 60 km per hour, under vehicle headlight illumination, human visibility of obstacles exceeds stopping distance. However, analyzing the visual characteristics and psychological load of the driver does not directly reflect the risk level of driving behavior. It primarily reflects the driver’s cognitive and psychological states. Therefore, one must analyze the driving characteristics and risks of vehicles based on lateral and longitudinal acceleration data.
Acceleration is an important indicator of vehicle driving characteristics. It is also a core indicator for analyzing the stability, safety, comfort, and driving behavior of a vehicle. The driving characteristics of a car are primarily influenced by the longitudinal, lateral, and vertical accelerations. Lateral acceleration is generated by the centrifugal force when the vehicle is turning and is the main indicator for describing the cornering state, driving stability, and comfort of the car. Many previous studies have established statistical models to study lateral acceleration. For example, Fan et al. used lateral acceleration as an indicator to evaluate the safety level of curves and analyzed the correlation between driving behavior factors and road curvature using a linear regression model [19]. Pothukuchi et al. collected continuous lateral acceleration data from 83 drivers and developed a model supported by support vector regression to assess the lateral acceleration of vehicles on interchange ramps [20]. Vaiana et al. developed the Driving Style Diagram (DSD) model by overlapping the driving experience zone with the friction circle under constraints to obtain the G-G diagram [21], which is used to assess the safety of driving behavior. Longitudinal acceleration is the rate of change in vehicle speed in the longitudinal direction and reflects vehicle speed variation and driving performance. Many studies have combined analyses of vehicle lateral and longitudinal acceleration data to provide a more comprehensive evaluation and quantification of acceleration characteristics and their relationships. Liu et al. quantified the variations in the instantaneous longitudinal and lateral accelerations in basic safety messages [22]. Ali et al. analyzed and quantified the impact of driver age, sex, vehicle class, and location on longitudinal and lateral acceleration [23]. Eboli et al. proposed a method to describe the relationship between lateral acceleration, longitudinal acceleration, and speed, and used it to assess driving behavior safety [24]. A model for the rate of change in lateral acceleration considering the horizontal, vertical, and lateral directions was established by Gu, and the comfort and safety of vehicles were analyzed [25]. Ding et al. analyzed the operational characteristics and driving risks of interchange ramps based on vehicle lateral and longitudinal acceleration data [26]. In the distinctive environment of underground roadways, acceleration also exhibits certain characteristics. Zheng et al. [27] analyzed the operating characteristics of vehicles on urban underground spiral ramps based on vehicle acceleration value, and found that drivers’ deceleration value during cornering on continuous downhill sections is higher than acceleration. Xu et al. [28] found that lateral acceleration at curves in underground roadways increases during the entry phase of a curve, remains relatively stable in the middle of the curve, and decreases during the exit phase.
When vehicles travel on curved roads, they are subject to lateral forces. These forces, combined with limited visibility for the driver, cause the stability of the vehicle during driving to be inferior to that on straight roads. Consequently, the incidence of traffic accidents on curved roads is generally higher than that on straight roads [29]. Investigating the characteristics and influencing factors of accidents on curved roads helps improve the safety of these curves. Crisma et al. explored the relationship between the radii of horizontal curves and accident rates and found an inverse relationship between radius size and accident rate [30]. Zhu et al. analyzed the severity of accidents on curved roads using Bayesian networks [31]. Many researchers have also developed statistical models related to curve acceleration and speed. Khanjari et al. proposed a reverse horizontal curve lateral acceleration model using vehicle dynamics modeling and multivariate modeling methods [32]. Eboli et al. analyzed the relationship between vehicle speed and curve radius on curved roads and developed a predictive model for the speed–radius relationship [33]. Considering the relationship between the geometric alignment of curves and the driver speed, Dias et al. assessed the impact of the horizontal geometry and desired travel speed on driver speed and acceleration behavior on curved highways [34]. Semeida et al. found that the curve radius has the greatest influence on V85 speed [35]. Bassan et al. discovered that the horizontal curve radius in highway tunnels is significantly lower than that on open roads, and the difference increases with higher design speeds [36].
3. Materials and Methods
3.1. Research Object
The experimental site was situated on the Jiefangbei Underground Ring Road in Yuzhong District, Chongqing, China. The large number of curves on the ring road provided a rich research object for this study. Therefore, fourteen curves with small radii and poor alignment on the underground ring road were studied (Figure 1). The technical indicators of the 14 curves are listed in Table 1. Meanwhile, the Jiefangbei Underground Ring Road has a design speed of 30 km/h, with a lane width of 3.5 m and a shoulder width of 0.5 m. The loop is a two-lane road, and the tunnel end walls feature a vertical design. The specific real structural characteristics are shown in Figure 2. The entire underground road is not equipped with any guardrail facilities. Additionally, the road and curve in the study exhibit directional characteristics, with both sharing the same operational direction. The specific direction is indicated by the arrow in Figure 1.
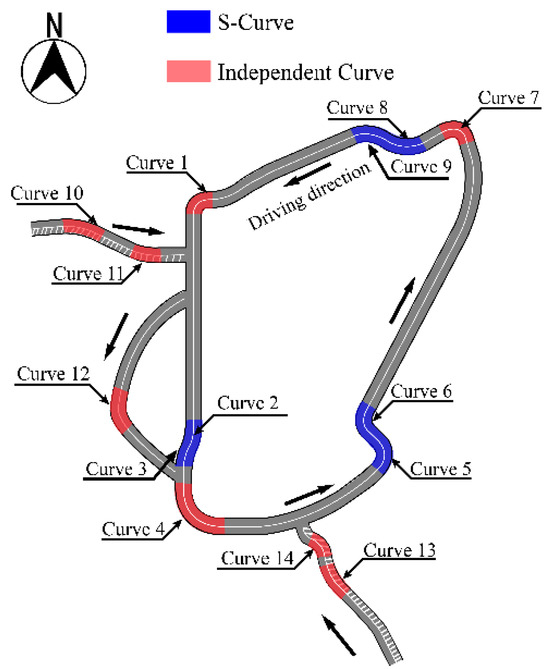
Figure 1.
Curve schematic diagram.

Figure 2.
Realistic view of tunnel structural features.
According to the Urban Road Engineering Design Specification CJJ37-2012 [9], the minimum radius for setting superelevation at a design speed of 30 km/h is generally 85 m, and the minimum radius without setting superelevation is 150 m. Therefore, for urban underground roads, we consider curves with R ≤ 85 m as extreme small radius curves, curves with 85 m < R ≤ 150 m as general small radius curves, and curves with R > 150 m as ordinary radius curves.

Table 1.
Main technical indicators of research object.
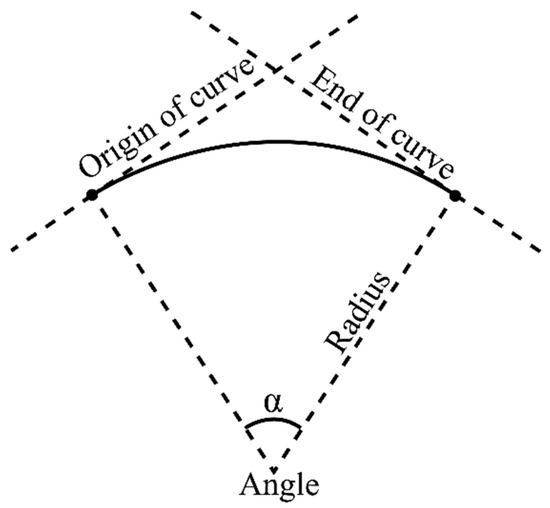
Figure 3.
Angle schematic diagram.
Table 1.
Main technical indicators of research object.
| Curve Numbers | Radius (m) | Slope (%) | Angle (°) | (km·h−1) | Illuminance (Lux) | |
|---|---|---|---|---|---|---|
| Extreme small radius curves | Curve 1 | 35 | 5.90% | 90 | 20.52 | 127.3 |
| Curve 5 | 45 | 3.60% | 89 | 34.30 | 118.5 | |
| Curve 6 | 48 | 3.60% | 75 | 30.94 | 121.3 | |
| Curve 7 | 30 | 3.90% | 85 | 21.51 | 118.9 | |
| Curve 9 | 60 | 5.90% | 46 | 23.27 | 133.1 | |
| Curve 14 | 50 | 5.90% | 54 | 34.90 | 122.4 | |
| General small radius curves | Curve 4 | 85 | −3.00% | 82 | 38.53 | 125.9 |
| Curve 8 | 115 | −2.70% | 50 | 26.34 | 108.9 | |
| Curve 12 | 85 | −3.20% | 69 | 44.26 | 106.3 | |
| Curve 13 | 120 | 5.90% | 40 | 41.41 | 108.3 | |
| Ordinary radius curves | Curve 2 | 200 | 1.00% | 38 | 34.76 | 114.8 |
| Curve 3 | 200 | −0.90% | 38 | 35.24 | 113.6 | |
| Curve 10 | 175 | 4.20% | 35 | 39.25 | 115.4 | |
| Curve 11 | 200 | 2.85% | 24 | 42.63 | 112.2 |
Angle of curve, as shown in Figure 3. : average speed of all subjects across curve, subjects refers to the 20 drivers who participated in the on-road driving experiment.
3.2. Test Vehicles and Instruments
Considering the adaptability of the test instrument and vehicle, the Honda Accord (SUV) was chosen as the test vehicle. In this experiment, an inertial measurement unit (IMU) was employed to collect the vehicle’s longitudinal and lateral acceleration data at a fixed sampling frequency of 10 Hz, which is inherent to the instrument and cannot be adjusted. The forward collision warning system Mobileye630 (from Mobileye company, headquartered in Jerusalem, Israel) was used to obtain data, such as vehicle speed and obstacle information, with a sampling frequency of 10 Hz. These two sets of equipment can collect vehicle speed, lateral acceleration, longitudinal acceleration, and other data. To facilitate data postprocessing and interception, a driving recorder was installed in front of the test vehicle to record the vehicle driving situation and test video during the test. The test vehicle and instruments are shown in Figure 4.

Figure 4.
Experimental vehicle and instruments.
3.3. Experimental Driver
A total of 14 male and 6 female drivers were selected based on the gender ratio of drivers in China, which is approximately 7:3 [37,38]. The age distribution of the drivers ranged from 20 to 50 years old, with an average age of 39 years and an average driving experience of 13 years.
The experiment was conducted on the Jiefangbei Underground Ring Road in Yuzhong District, Chongqing. The experiment was conducted between 8:00 a.m. and 7:00 p.m. Regarding the situation of road traffic flow, since the road had not yet been officially opened to the public, unauthorized access by social vehicles was prohibited during the test period. As a result, the experiments were conducted under free-flow traffic conditions. Before the start of the experiment, the participating drivers were familiarized with the vehicle driving interface and conditions and were instructed to drive according to their regular driving style. Meanwhile, all drivers in this experiment followed the same driving route. Additionally, the cornering performance characteristics were analyzed based on the most adverse visibility conditions; thus, all drivers kept driving in the inner lane to maintain consistent driving conditions. Regarding the arrangement of experimental personnel, there were three personnel involved in the experiment: two operated the Mobileye 630 and IMU inertial sensors (from Jiangsu Chaoke Electronics Technology Co., Ltd., headquartered in Changzhou, China), and one was responsible for recording the timing of the drivers through the designated area.
3.4. Interpretation and Collection of Data
The research focuses on the actual operational characteristics and driving risks of vehicles at curves. According to the Specifications for Safety Audit of Highway Projects (JTG B05-2015) [39], the analysis of road conditions should consider the actual forces acting on the vehicle, including the components of gravitational acceleration. Therefore, the acceleration referred to in this study is the total acceleration. A schematic diagram of this acceleration is shown in Figure 5, and the calculation formula is provided in Equation (1):

Figure 5.
Schematic diagram of acceleration defined in this study.
To ensure better comparability of the data across different curves, all curve data were collected during a single, continuous driving session, and the sample sizes for each curve were consistent. During the driving process, due to the constraints of the route, drivers may repeatedly pass through certain curves (e.g., Curve 4). Therefore, when extracting curve data, this portion of the data was directly excluded.
Before starting the experiment, the IMU was calibrated. The calibration of the IMU primarily involved adjusting the spiral knob on the IMU device to center the bubble on the right side of the IMU, while ensuring that the horizontal and vertical pointers on the IMU computer software (CH Center V1.2.5) aligned with the horizontal and vertical lines, respectively. The specific calibration process is illustrated in Figure 6.
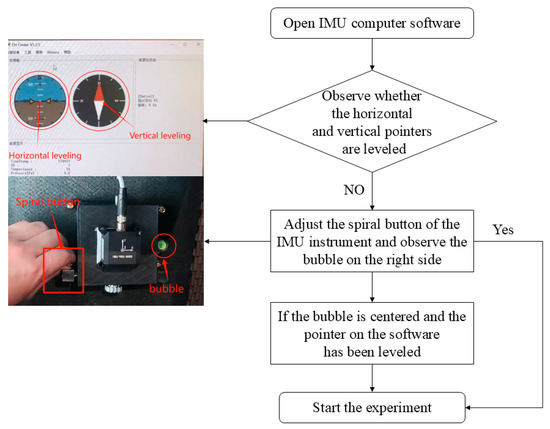
Figure 6.
Flowchart of the calibration process.
The data extraction start and end points in this paper were determined based on the times when the vehicle passed the start and end points of the curve. These points were the tangent points between the straight section and the curve, and the times of passage were specifically recorded by the test personnel. The calculation process for the curve distance S is shown in Figure 7 and Equation (2):
In the formula, S: the distance traveled from the start point to the end point of the curve; Vi: the speed corresponding to the i-th 0.1 s; 0.1 s: the time for Mobileye to collect a speed data; n: the n 0.1 s required for the vehicle to travel from the start point to the end point of a curve.
Figure 7.
Schematic diagram of curve distance calculation.
Owing to the high sampling frequency of the experimental instruments, the lateral and longitudinal acceleration curves can exhibit significant fluctuations when subjected to external disturbances. In this manuscript, data filtering is conducted using the Savitzky–Golay filtering method. Figure 8 shows a comparison of partial data before and after filtering in this article.
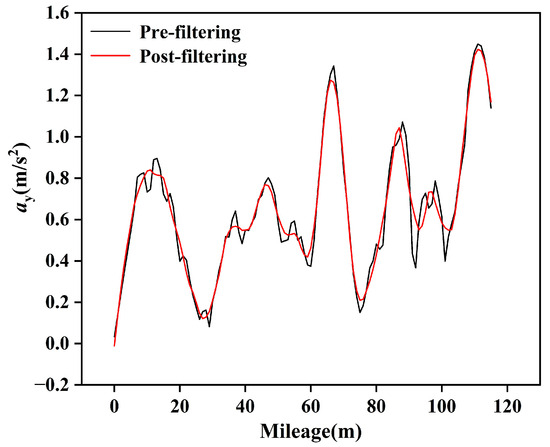
Figure 8.
Comparison before and after data filtering.
4. Results
4.1. Significant Test for Acceleration Difference
To investigate the relationship between lateral acceleration, longitudinal acceleration, and types of curves and radii in underground urban roadways, the Mann–Whitney method is used to test the significance in this study. The results are shown in Table 2. It can be found that the lateral acceleration of the independent curve is significantly greater than that of the S-curve at the 0.05 level (p = 0.02881), and the longitudinal acceleration of the independent curve is not significantly smaller than that of the S-curve (p = 0.21329).

Table 2.
Results of Mann–Whitney test for accelerations in different types of curves.
Further exploring the influence of different radius ranges on vehicle accelerations at curves, since the data does not obey the normal distribution, this paper uses the Kruskal–Wallis H test of the nonparametric test method to analyze the vehicle acceleration under different curve types. The test results are shown in Table 3. It can be seen from Table 3 that there are significant differences in the acceleration of vehicles driving at the curves of urban underground roads in three different radius ranges. For curves with an extreme radius (R ≤ 85 m), the lateral acceleration is significantly greater than general small radius curves (85 m < R ≤ 150 m) and ordinary radius curves (R > 150 m). This could be due to the small radius of the curves, subjecting vehicles to significant centrifugal force, resulting in increased lateral acceleration. Moreover, the lateral acceleration in general small radius curves is significantly higher than those in ordinary radius curves. Regarding longitudinal acceleration, the ordinary radius curves’ are significantly greater than those of extreme small radius curves and general small radius curves. This might be because ordinary radius curves have larger radii and better alignment, reducing driving pressure on the driver, hence making drivers more inclined to utilize higher speeds and accelerations when navigating the curves.

Table 3.
Results of one-way ANOVA for accelerations in different radius range of curves (m/s2).
4.2. Driving Risk Model
4.2.1. Driving Risk Model and Its Distribution Characteristics
Vehicle acceleration, deceleration, and angle are the main factors influencing driving behavior. The variation in longitudinal acceleration is related to the application of the brake and accelerator pedals. Changes in lateral acceleration are influenced by the amplitude and speed of steering. When driving on curves on urban underground roads, drivers assess the risks of upcoming curves based on their experience and perform different driving maneuvers to maintain vehicle stability.
In this study, the risk of driver behavior on different curves of urban underground roads was evaluated using G-G diagrams, referring to the methodology proposed by Vaiana [21] for constructing a driving-style graph model. The abscissa in the figure represents the lateral acceleration Ay, where Ay > 0 in the first and fourth quadrants and Ay < 0 in the second and third quadrants. An Ay of “+” indicates a right turn, and an Ay of “−” indicates a left turn. The ordinate represents the longitudinal acceleration Ax, where Ax > 0 in the first and second quadrants and Ax < 0 in the third and fourth quadrants. An Ax is “+” when the driver takes acceleration measures, and it is “−” when the driver takes braking measures.
In Figure 9, the enclosed area within the closed curve represents safe driving behavior, whereas the area outside the curve represents dangerous driving behavior. Therefore, whether the current driving behavior is risky was determined based on the position of the vehicle lateral and longitudinal accelerations in the graph at a given moment. In addition, owing to the complex alignment of urban underground roads, the characteristics of more entrances and exits, and the radical driving styles of some drivers, vehicles still face driving risks, even if they are being driven within the safety limits defined by the G-G diagram. Therefore, an indicator Ms can be introduced to evaluate the level of aggressiveness in the driving behaviors of drivers within the safe range. This indicator is defined as:
Ms = |OE/OF|
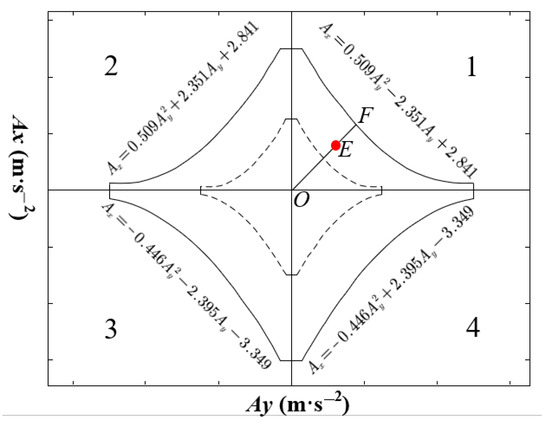
Figure 9.
G-G graph of driving behavior.
The formulas defining the safe boundaries for quadrants one and two are as follows:
The formulas defining the safe boundaries for quadrants one and two are as follows:
To differentiate the different driving behaviors, a new dashed region can be added to the G-G diagram (Figure 9). This region can be defined with Ms = 0.5, serving as a boundary to delineate the various driving behaviors. When 0 ≤ Ms ≤ 0.5, it represents driving behavior safety. When 0.5 < Ms ≤ 1, it indicates dangerous driving behavior.
Figure 10 shows the G-G diagram representing the driving behavior of each driver on curves of urban underground roads (partial G-G diagrams). Figure 10a reveals that in the extreme small radius curves, when driving on independent curves 1, 7, and 14, most of driver behavior points fall into the driving danger zone, indicating the presence of risky behaviors on these three curves. Among them, curve 1 has the most points falling in the danger zone, and these points are distributed far from the closed curve, indicating the highest level of safety risk. When driving on continuous curves 5 and 6, curve 5 has more behavior points falling in the danger zone than curve 6, indicating that curve 5 has a significantly higher driving risk than curve 6.
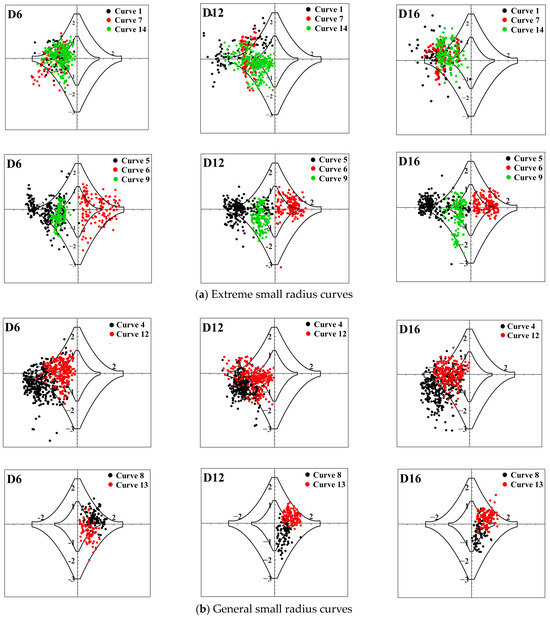

Figure 10.
The G-G graph of curves.
Figure 10b reveals that general small radius curve 4 has more behavior points falling in the danger zone compared to curve 12, and these points are also farther away from the enveloping curve, indicating a higher level of driving danger for curve 4. A few behavior points fall into the danger zone on curves 8 and 13, indicating better driving behavior.
Figure 10c reveals that ordinary radius curve 3 has many driving behavior points falling in the danger zone, while curves 2, 10, and 11 have only a few behavior points in the danger zone, indicating good driving behavior on curves 2, 10, and 11.
4.2.2. Significant Difference Test of Driving Risk Points
In order to further analyze the safety risk of driving in three types of curves, the significance analysis of the number of driving risk behavior points of vehicles in urban underground road curves under different types of curves and different radius ranges is carried out. The data do not obey the normal distribution, the non-parametric test analysis was adopted. The results are shown in Table 4. It can be found that at the 0.05 level, the number of driving risk points per unit length (m) of the independent curve is not significantly greater than that of the S curve (p = 0.96513).

Table 4.
Analysis results of driving risk points variance.
In addition, it can be observed that there are only two significant differences in the number of driving risk points per unit length of the curve under different radius ranges at the 0.05 level. Specifically, the average number of risk points per unit length in extreme small radius curves is significantly higher than that in general small radius curves, and both are significantly higher than in ordinary radius curves. Therefore, the safety risk of driving on the three types of curves is ranked as follows: extreme small radius curves > general small radius curves > ordinary radius curves.
4.2.3. Curve Distribution Characteristics of Risky Driving Behavior
The curves for plotting according to the range of curve radius and length were grouped, and the number of dangerous driving behavior points corresponding to curve mileage to explore the distribution characteristics of hazardous driving behavior points on curves were organized, as shown in Figure 11. It can be found that the number of dangerous points on curves increases with the increase in curve mileage. In the entry phase, the number of hazardous points starts to grow until it reaches a relatively high level and then maintains a high numerical level within a certain mileage range, indicating higher driving risks for vehicles at this point. Subsequently, the number of dangerous points decreases until the vehicle exits the curve. By observing the fluctuation range in hazardous points on each curve, it can be found that curves with higher driving danger risk levels, such as curves 1, 2, 3, 4, 5, 6, 7, and 14, have a larger fluctuation range of the number of dangerous behavior points. In addition, curves with lower driving risk levels, such as curves 8, 9, 10, 11, 12, and 13, have a smaller fluctuation range of the number of dangerous behavior points.
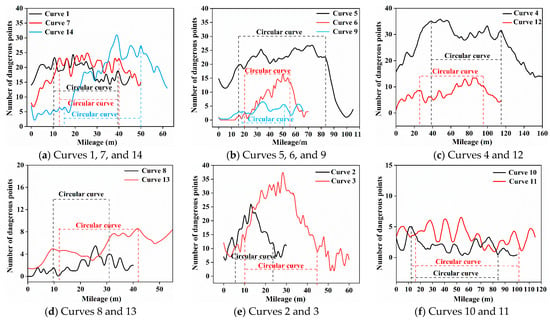
Figure 11.
Distribution characteristics of risk points in curves.
The mileage range corresponding to the section with the highest number of danger points for each curve was identified based on the observed number of danger points corresponding to each mileage in Figure 11, and then represent the obtained mileage ranges on the geometric diagram of the curves, as shown in Table 5. It can be found that the high-risk sections of the curves are mainly concentrated in the circular curve sections of the curves.

Table 5.
Distribution characteristics of dangerous driving behavior in curves.
Table 5 reveals that the high-risk section mileage accounts for 20–60% of the entire curve on extreme small radius curves 1, 5, 6, 7, 9, 14; the high-risk section mileage accounts for 20–50% of the entire curve on general small radius curves 4, 8, 12, 13; the high-risk section mileage accounts for 5–30% of the entire curve on ordinary radius curves 2, 3, 10, 11. Meanwhile, the high-risk section mileage of curves 1, 4, 5, 7 in the circular curve sections of the curves exceeding 90%. Vehicles traveling on these circular curve segments of the curves are in a high-risk state for an extended period. These curves share a common characteristic of having a small radius with a large turning angle.
Observing the geometric distribution of high risk curve sections on curves 2, 6, 8, 9, 11, 12, 13, and 14, it can be seen that they are mostly in the latter half of circular curves.
4.3. Sensitivity of Acceleration to Curve Parameters
4.3.1. Influence of Curve Radius on Acceleration
The radius of a curve is an important parameter that describes the geometric characteristics of the curve. Its magnitude affects the centrifugal force acting on the vehicle and the choice of speed by the driver, thereby influencing the changes in the lateral and longitudinal accelerations of the vehicle. Because vehicle stability is worst when the lateral acceleration reaches its peak, the peak lateral acceleration of each participant was extracted while the driver navigated through different curves. The collected data were organized to create a scatter plot of lateral acceleration versus radius, as shown in Figure 12a, along with the corresponding model.
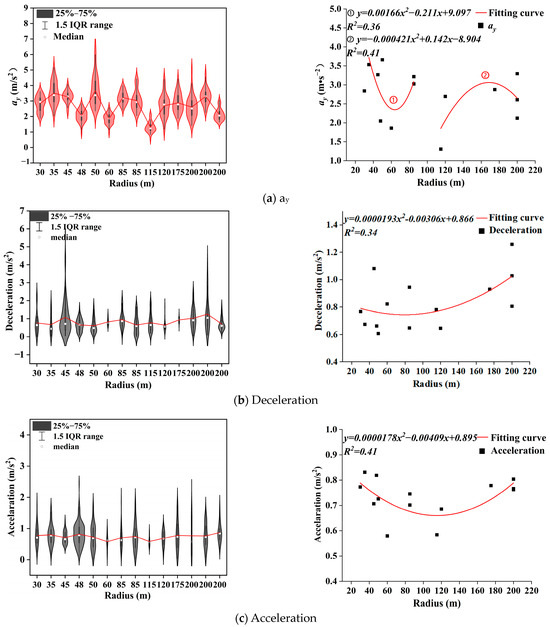
Figure 12.
Scatter plot and model of lateral and longitudinal acceleration-radius.
Figure 12a describes the relationship between lateral acceleration at the curve of an underground road and the radius of the curve. As can be seen from Figure 12a, the lateral acceleration is minimal at a radius of 115 m and maximal at a radius of 50 m. When R ≤ 50 m, the overall distribution of lateral acceleration is higher. The relationship model between lateral acceleration and curve radius consists of two quadratic functions with opposite openings, represented by fitting curves 1 and 2. Fitting curve 1 shows that when R ≤ 80 m, lateral acceleration decreases first and then increases with increasing radius. Fitting curve 2 shows that when R > 80 m, lateral acceleration increases first and then decreases with increasing radius. These two changing trends are the result of the combined effects of curve radius and vehicle speed.
Figure 12b,c, respectively, describe the relationships between entering curve deceleration and radius, exiting curve acceleration, and radius. Figure 12b reveals that drivers perform deceleration more frequently at the entry point of curve 5 (R = 45 m), and less frequently at the entries of curve 9 (R = 60 m) and curve 10 (R = 175 m). Figure 12c shows that drivers accelerate more frequently at the exit of curve 6 (R = 48 m), and less frequently at the exits of curve 2 (R = 200 m) and curve 8 (R = 115 m). It can be found that drivers frequently decelerate during the entry phase of the curve before an S-curve, with fewer instances of acceleration during the exit phase. Conversely, during the entry phase of the curve after the S-curve, there are fewer instances of deceleration, with more frequent instances of acceleration during the exit phase.
The changing trend of the fitting curve between deceleration radius and acceleration radius is as follows: with the increase in radius, the deceleration (acceleration) tends to decrease first and then increase. The reason for this changing trend may be that when the curve radius is less than 120 m, the larger the radius, the higher the critical safe speed of the curve, and the smaller the speed reduction required by the driver. Therefore, the deceleration into the curve decreases. However, when the radius is greater than 120 m, the larger the radius and the later the driver reduces speed, leading to an increase in deceleration into the curve. For urban underground road curves, when the radius is small (R < 60 m) or large (R > 160 m), the entering curve deceleration and exiting curve acceleration will be large. The driver’s risk model indicates that the smaller the curve radius, the greater the driving risk. Therefore, when it is inevitable to design small radius curves in urban underground roads, it is recommended to ensure that the radius is greater than 60 m as much as possible.
Table 6 presents the results of the Kruskal–Wallis test for the deceleration during the entry phase and the acceleration during the exit phase of vehicles at urban underground road curves with different radius ranges. Table 6 shows that there is a significant difference in entering curve deceleration between the extreme small radius curve and the ordinary radius curve at the level of 0.05, and there is no significant difference between the other groups. There is a significant difference in exiting curve acceleration between the ordinary small radius curve and the ordinary radius curve at the level of 0.05, and there is no significant difference in the other groups.

Table 6.
Kruskal–Wallis results of entering curve deceleration and exiting curve acceleration with different radius ranges.
4.3.2. Influence of Curve Angle on Acceleration
The curve angle is another important parameter that describes the geometric characteristics of a curve. The size of the curve angle has an influence on the vehicle driving characteristics, driver line of sight, and operational requirements. At larger curve angles, drivers must start steering and decelerating earlier to maintain vehicle stability and safety. Therefore, the size of the curve angle affects the magnitude of the longitudinal acceleration of the vehicle. Simultaneously, drivers must use a larger steering angle to control the steering wheel and maintain stable circular motion, thereby influencing vehicle lateral acceleration.
Figure 13a describes the relationship between lateral acceleration at the curve of an underground road and the curve angle. The figure shows that the lateral acceleration is at its minimum when the angle is 50° and at its maximum when the angle is 54°. When the angle is less than or equal to 50°, the overall distribution of lateral acceleration is relatively high. The model of the relationship between lateral acceleration and the curve angle is composed of two quadratic functions with opposite openings, represented by fitting curves 1 and 2. Fitting curve 1 shows that when the angle is less than 50°, lateral acceleration tends to increase and then decrease with the increase in the curve angle. Fitting curve 2 shows that when the curve angle is greater than 50°, lateral acceleration tends to decrease and then increase with the increase in the curve angle.
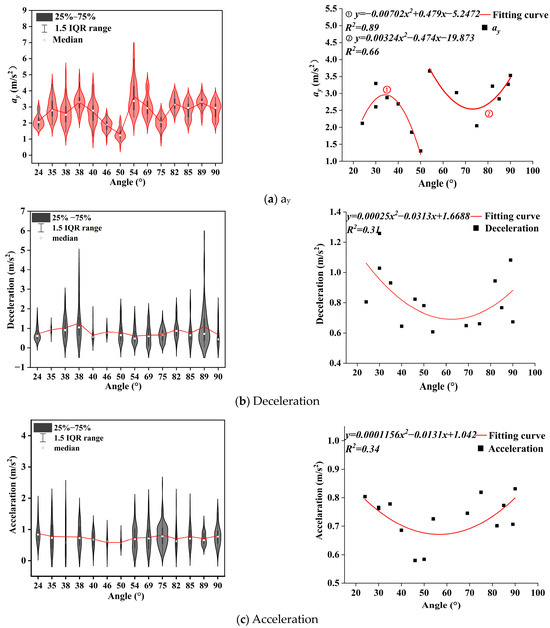
Figure 13.
Scatter plot and model of lateral and longitudinal acceleration-angle.
Figure 13b,c, respectively, describe the relationships between entering curve deceleration and curve angle and exiting curve acceleration and curve angle. The figures show that the longitudinal acceleration and deceleration change similarly with the curve angle and the radius, showing a trend of decreasing first and then increasing with the increase in angle.
For urban underground road curves, when the angle is small (α < 40°) or large (α > 70°), the entering curve deceleration and exiting curve acceleration will be high. Driver risk models indicate lower driving risks on curves with small angles; hence, for urban underground road curve designs, it is recommended to keep the curve angle α < 70°.
Table 7 provides the results of the Kruskal–Wallis test for vehicle deceleration during the entry phase and acceleration during the exit phase of curves in urban underground roads across different angle ranges. As shown in Table 7, there is a significant difference between the entering curve deceleration of the small angle curve and the large angle curve. There is a significant difference between the entering curve deceleration of the medium angle curve and the large angle curve. Meanwhile, it can be observed that there is a significant difference between the exiting curve acceleration of the small angle curve and the medium angle curve. There is a significant difference between the exiting curve acceleration of the medium angle curve and the large angle curve.

Table 7.
Kruskal–Wallis results of entering curve deceleration and exiting curve acceleration with different angle ranges.
5. Discussion
According to the risk characterization of driving behavior represented by the G-G diagram, the proportion of driving behavior points on city underground road curves that fall within the safety limits is relatively small. This indicates that the safety risk of curves on urban underground roads is high. A small curve radius increases the risk of driving on curves and the probability of accidents. This finding is consistent with those of a previous study [40]. In addition, higher vehicle operating speeds increase the risk of driving on curves because inappropriate curve speeds are the main cause of collisions, skidding, and rollovers [29,41]. Regarding the distribution characteristics of risky driving behavior on curves, it was found that the number of dangerous points on the curves increases during the entry phase, remains relatively high during the middle section of the curve, and decreases during the exit phase. This indicates that driving behavior on the horizontal curves of urban underground roads poses the highest risk. However, Kempa et al. found the curve entry is the most dangerous location on a curve, followed by the middle section [42]. The possible reasons for this difference are as follows. The curves on urban underground roads are constrained by space, generally resulting in a smaller radius, and the circular curve sections of the curves have the maximum curvature, leading to the highest lateral acceleration. The speed limit on urban underground roads also results in a smaller speed difference between straight sections and curve entries compared with surface roads. As a result, the deceleration during the entry phase of the curve is not too abrupt. Therefore, the driving risk is highest in the circular curve sections of the curves on urban underground roads.
In terms of improving curve safety, enhancing the safety performance of critical sections of underground roads can significantly enhance overall driving safety [43]. Therefore, safety improvement measures are proposed based on signage, road markings, and safety facilities, considering the distinct characteristics of risky curves. First, for Curves 1, 5, 7, and 14, which have small radii and poor alignment, the following measures can be implemented to enhance driving safety. (1) The setting of longitudinal deceleration markings and alignment guidance signs can help drivers achieve a smooth transition in curved sections with small radii [44]. Therefore, longitudinal deceleration markings and chevron alignment signs can be set along horizontal curves to improve driving stability. (2) Installing colored antiskid pavement on slopes, curves, tunnel entrances and exits, etc., where accidents are more likely can serve as a good colorful warning and have an antiskid effect [45]. Therefore, a colored antiskid pavement can be set at the curve to improve driving safety. (3) A convex lens can be set in the middle of the curve to improve the poor sight of a small-radius curve.
For Curves 2, 3, 5, and 6, which are S-curves, it is recommended to increase the lengths of the straight sections between consecutive curves to enable drivers to adapt better to the transitions between curves. On Curves 4, 12, and 13, vehicle travel data reveal that drivers tend to operate at higher speeds. Specific warning signs can significantly reduce vehicle speed [46]; thus, speed-reducing signs can be set up at the entrances of curves to warn drivers to slow down. Chevron alignment signs can affect speed control by providing a warning [47]; thus, chevron alignment signs can be laid along the horizontal curve. In terms of the visual improvement of underground roads, the setting of retroreflective rings can enable drivers to maintain good direction perception and reduce reaction time, which improves driving safety [48]. Therefore, an appropriate number of retroreflective rings can be installed on curves.
Regarding the sensitivity of acceleration to curve parameters, although the fitted functions obtained in this study have a relatively low R2 value, we only discuss the potential relationship between acceleration and curve radius or curvature based on the graphical representation of the fitted functions. Regarding the relationship between lateral acceleration and curve radius, Xu et al.’s research has concluded that there is a negative correlation between lateral acceleration and curve radius [49]. However, on urban underground roads, when the curve radius is less than 80 m, the lateral acceleration initially decreases and then increases as the radius increases. Conversely, when the radius is greater than 80 m, the lateral acceleration initially increases and then decreases as the radius increases. The reason for the difference between aboveground curves and urban underground curves may be that, as the radius of the curve increases, the linear conditions gradually improve, and the impact of the tunnel environment on the driver’s sight distance and vision gradually decreases.
In addition, road superelevation also has a certain impact on vehicle acceleration. The distribution characteristics of lateral acceleration of vehicles under different road superelevations are shown in Figure 14. It can be observed that the lateral acceleration of curves with a superelevation of 2% is generally higher than that of curves with a superelevation of 1.5%. Meanwhile, under the same ultra-high conditions, a larger-radius curve has a smaller lateral acceleration. The distribution characteristics of longitudinal acceleration of vehicles under different road superelevations are shown in Figure 15. Figure 15 reveals that under different superelevation conditions, the deceleration of vehicles entering curves and the acceleration of vehicles exiting curves show little overall difference. This indicates that the impact of superelevation on longitudinal acceleration is relatively small. The main factors affecting longitudinal acceleration are still the radius and angle of the curves.
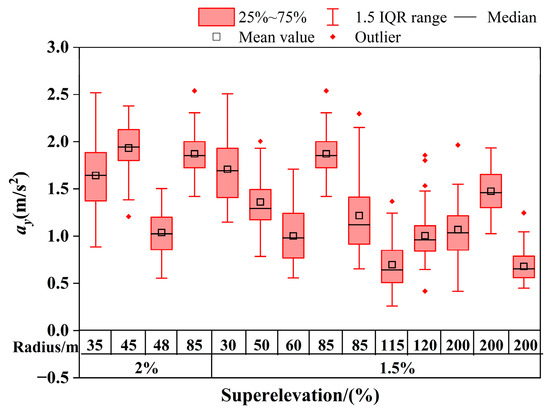
Figure 14.
Lateral accelerations at different superelevation.
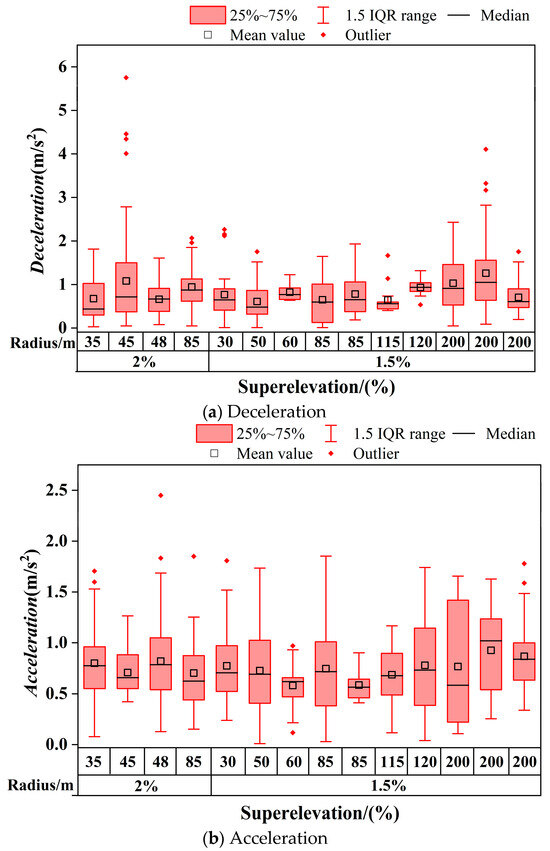
Figure 15.
Accelerations at different superelevations.
Regarding the relationship between acceleration and deceleration and the curve radius and angle, it has been found that the acceleration and deceleration rates decrease with an increase in the curve radius and increase with an increase in the curve angle [50]. However, we found that acceleration and deceleration first decreased and then increased with an increase in the curve radius and angle of rotation on underground road curves. The reason for this difference may be that a curve with a larger radius and a smaller curve angle on underground road would provide the driver with a safe signal, as the choice of speed is higher. The amplitude of the vehicle speed reduction is greater and the vehicle turning speed increases. When a curve presents less driving risk, the driver also chooses a greater acceleration to drive out of the curve as quickly as possible. This study proposes radius and angle value ranges for small-radius curves as R > 60 m and α < 70° based on the analysis results of the driving risk model and the model correlating acceleration with curve radius and angle.
6. Conclusions
This study obtained driving data including vehicle speed, lateral acceleration, and longitudinal acceleration through real vehicle experiments, and explored the significance of the relationship between acceleration and curve types, radius, and angles through data analysis. It evaluated the risk and distribution characteristics of drivers’ driving behaviors on curves based on the acceleration driving risk model, and conducted a significant test on the differences in driving risk points. Finally, it discussed the correlation between curve radius, angle, vehicle lateral acceleration, entering curve deceleration, and exiting curve acceleration. The main conclusions are as follows:
- (1)
- Significant differences exist in lateral acceleration and longitudinal acceleration under different radius ranges when driving at curves in urban underground roads. There is a significant difference in the lateral acceleration between the independent curves and the S-curves, and the longitudinal acceleration does not exist. There are significant differences between some groups in the entering curve deceleration and exiting curve acceleration for curves with different radius ranges and different angle ranges.
- (2)
- The number of driving risk points per unit length (m) under different curve types does not show significant differences. The number of driving risk points per unit length (m) of the extreme small radius curve and the general small radius curve is significantly larger than that of the ordinary radius curve.
- (3)
- The number of danger points at curves increases initially with mileage, then stabilizes with fluctuations for a distance, and finally decreases. The road sections with the highest level of danger points are mainly concentrated within the circular curve sections of the curves, especially in the latter half of the circular curve section in the direction of travel.
- (4)
- The lateral acceleration of vehicles at curves in urban underground roads shows the following relationships with curve radius and angle: when the curve radius is less than 80 m, the lateral acceleration decreases initially with increasing radius and then increases; when the radius is greater than 80 m, it initially increases and then decreases. When the curve angle is less than 50°, the lateral acceleration increases initially with the angle and then decreases as the angle increases; when the angle is greater than 50°, it decreases initially and then increases. The entering curve deceleration and exiting curve acceleration of vehicles at curves in urban underground roads both show a trend of initially decreasing and then increasing with increasing curve radius and angle. Additionally, R > 60 m and α < 70° are the recommended value ranges for small radius curves.
In some situations, drivers can enter urban underground roads in a fatigued state, and the duration of driving and fatigue will to some extent influence a driver’s choice of speed, thereby affecting acceleration [51]. However, in this study, the subjects were in good condition at the start of the experiment, it does not account for the initial impact of driving experience, curve direction, or psychophysiological factors. Therefore, future research should incorporate additional parameters such as driver eye movements and electrocardiograms to provide a more comprehensive assessment of driver behavior from a psychophysiological perspective. Furthermore, special attention should be given to the construction of measurement systems to ensure the construction of a correct mathematical apparatus. Meanwhile, experiments could be expanded to include different underground roadways, varying traffic densities, illuminance levels, and vehicle models as variables to validate and extend the conclusions. Finally, comparative analyses with aboveground roads could be conducted to further enrich the study’s insights.
Author Contributions
Z.Z.: methodology, project administration, writing—review and editing. Y.X.: investigation, visualization, writing—original draft. Z.W.: investigation. J.R.: formal analysis. H.Z.: data curation. J.X.: conceptualization, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 52202407); China Postdoctoral Science Foundation (No. 2022M710547); and Natural Science Foundation of Chongqing, China (CSTB2022NSCQ-BHX0731); The Innovative Plan of the Department of Housing and Urban-Rural Development of Guangdong Province (2024-K35-205016).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, Z.L.; Chen, J.Y.; Liu, H.; Zhang, Z.F. Present status and development trends of underground space in Chinese cities: Evaluation and analysis. Tunn. Undergr. Space Technol. 2018, 71, 253–270. [Google Scholar]
- Xu, F.; Du, Z.; Chen, C. Distribution and development characteristics of urban road tunnels in China. Mod. Tunn. Technol. 2022, 59, 35–41. [Google Scholar]
- Hummer, J.E.; Rasdorf, W.; Findley, D.J.; Zegeer, C.V.; Sundstrom, C.A. Curve collisions: Road and collision charac-teristics and countermeasures. J. Transp. Saf. Secur. 2010, 2, 203–220. [Google Scholar]
- Chen, Y.; Shi, T.; Yu, S.; Shi, Q.; He, J.; Bian, Y. Setting the speed limit for highway horizontal curves: A revision of inferred design speed based on vehicle system dynamics. Saf. Sci. 2022, 151, 105729. [Google Scholar]
- Jurewicz, C.; Chau, T.; Mihailidis, P.; Bui, B. From research to practice-development of a rural mass curve treatment program. J. Australas. Coll. Road Saf. 2015, 26, 11–19. [Google Scholar]
- Cafiso, S.; D’Agostino, C.; Kiec, M. Investigating safety performance of the SAFESTAR system for route-based curve treatment. Reliab. Eng. Syst. Saf. 2019, 188, 125–132. [Google Scholar]
- Milleville-Pennel, I.; Jean-Michel, H.; Elise, J. The use of hazard road signs to improve the perception of severe bends. Accid. Anal. Prev. 2007, 39, 721–730. [Google Scholar] [CrossRef]
- Liu, J.; Ye, F.; Zhu, W.; Su, E.; Peng, W.; Han, X.; Wen, X. Evaluation of the impact of landscape zone on driver distraction and visual comfort in road tunnels. Tunn. Undergr. Space Technol. 2025, 156, 106248. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Urban Underground Road Engineering (CJJ 221-2015); China Architecture & Building Press: Beijing, China, 2015; ISBN 1511226448. [Google Scholar]
- Huang, Y.; Chen, F.; Song, M.; Pan, X.; You, K. Effect evaluation of traffic guidance in urban underground road diverging and merging areas: A simulator study. Accid. Anal. Prev. 2023, 186, 107036. [Google Scholar]
- He, S.; Du, Z.; Han, L.; Wang, S.; Chen, Y. Impact of urban tunnel sidewall effect on drivers: Examining visual charac-teristics and driving behavior across different lanes. Tunn. Undergr. Space Technol. 2024, 143, 105476. [Google Scholar] [CrossRef]
- Diao, Z. Research on Safety Optimization Design Technology of Tunnel Ramp. Master’s Thesis, Southeast University, Nanjing, China, 2019. [Google Scholar]
- Jiao, F.; Du, Z.; Wang, S.; Ni, Y.; He, R. Drivers’ saccade characteristics in curves of extra-long urban underwater tunnels. Transp. Res. Rec. 2020, 2674, 102–111. [Google Scholar]
- Fang, S.; Ma, J. Experimental analysis of driver visual characteristics in urban tunnels. Appl. Sci. 2021, 11, 4274. [Google Scholar] [CrossRef]
- Feng, Z.; Yang, M.; Zhang, W.; Du, Y.; Bai, H. Effect of longitudinal slope of urban underpass tunnels on drivers’ heart rate and speed: A study based on a real vehicle experiment. Tunn. Undergr. Space Technol. 2018, 81, 525–533. [Google Scholar]
- Liu, S.; Wang, J.; Fu, T. Effects of lane width, lane position and edge shoulder width on driving behavior in underground urban expressways: A driving simulator study. Int. J. Environ. Res. Public Health 2016, 13, 1010. [Google Scholar] [CrossRef]
- Ge, H.; Song, C.; Jing, D.; Li, W.; Shi, Z.; Guo, Z.; Zhang, F. Analysis of the effect of highway extra-long tunnel Accompanying vehicle lighting on driving behavior in horizontal curve—A driving simulation study. Tunn. Undergr. Space Technol. 2025, 157, 106286. [Google Scholar]
- Feng, S.; Gao, W.; Zhou, L.; Li, J.; Mao, W.; Liu, X. Experimental study on obstacle visibility and driving safety in lighting environment of road tunnel interior zone. Tunn. Undergr. Space Technol. 2024, 146, 105641. [Google Scholar]
- Fan, L.; Lu, L.; Deng, W.; Lu, J.J. Role of vehicle trajectory and lateral acceleration in designing horizontal curve radius of off-ramp: A driving simulator based study. Adv. Transp. Stud. 2015, 36, 119. [Google Scholar]
- Pothukuchi, S.; Pawar, D.S. Modeling Lateral Acceleration on Ramp Curves of Service Interchanges in India: An In-strumented-Vehicle Study. J. Transp. Eng. Part A Syst. 2021, 147, 04021089. [Google Scholar]
- Vaiana, R.; Iuele, T.; Astarita, V.; Caruso, M.V.; Tassitani, A.; Zaffino, C.; Giofrè, V.P. Driving behavior and traffic safety: An acceleration-based safety evaluation procedure for smartphones. Mod. Appl. Sci. 2014, 8, 88. [Google Scholar]
- Liu, J.; Khattak, A.J. Delivering improved alerts, warnings, and control assistance using basic safety messages transmitted between connected vehicles. Transp. Res. C Emerg. Technol. 2016, 68, 83–100. [Google Scholar]
- Ali, G.; McLaughlin, S.; Ahmadian, M. Quantifying the effect of roadway, driver, vehicle, and location characteristics on the frequency of longitudinal and lateral accelerations. Accid. Anal. Prev. 2021, 161, 106356. [Google Scholar] [PubMed]
- Eboli, L.; Mazzulla, G.; Pungillo, G. Combining speed and acceleration to define car users’safe or unsafe driving behaviour. Transp. Res. C Emerg. Technol. 2016, 68, 113–125. [Google Scholar]
- Gu, H. The Study of Highway Alignment Comfortableness Evaluation Method Based on the Lateral Acceleration Rate. Master’s Thesis, South China University of Technology, Guangzhou, China, 2010. [Google Scholar]
- Ding, R.; Liu, j.; Jiang, Y. Driving risks of interchange ramp based on vehicle acceleration data. J. Transp. Inf. Saf. 2021, 39, 17–25. [Google Scholar]
- Zheng, Z.; Zheng, L.; Xu, Y.; Rao, J.; Zhang, H.; Xu, J. Study on the operating characteristics of passenger cars on urban underground spiral ramps based on real vehicle data. Chin. J. Highw. Transp. 2024, 37, 273–288. [Google Scholar]
- Xu, Y.; Wang, Z.; Zheng, Z.; Rao, J.; Xu, J. Research on the Lateral Acceleration Characteristics of Vehicles in Urban Underground Road Curves. In Proceedings of the 24th COTA International Conference of Transportation Professionals, Shenzhen, China, 23–26 July 2024; pp. 2518–2528. [Google Scholar]
- Deng, Z.; Chu, D.; Wu, C.; He, Y.; Cui, J. Curve safe speed model considering driving style based on driver behaviour questionnaire. Transp. Res. F Traffic Psychol. Behav. 2019, 65, 536–547. [Google Scholar]
- Crisman, B.; Marchionna, A.; Perco, P.; Roberti, R. Operating speed prediction model for two-lane rural roads. In Proceedings of the 3rd International Symposium on Highway Geometric Design, Chicago, IL, USA, 29 June–2 July 2005. [Google Scholar]
- Zhu, L.; Lu, L.; Zhang, W.; Zhao, Y.; Song, M. Analysis of accident severity for curved roadways based on bayesian networks. Sustainability 2019, 11, 2223. [Google Scholar] [CrossRef]
- Khanjari, M.; Abdi Kordani, A.; Zarei, M. Simulation and modelling of safety of roadways in reverse horizontal curves (RHCs): With focus on lateral acceleration. Adv. Civ. Eng. 2022, 2022, 1952323. [Google Scholar]
- Eboli, L.; Guido, G.; Mazzulla, G.; Pungillo, G. Experimental relationships between operating speeds of successive road design elements in two-lane rural highways. Transport 2017, 32, 138–145. [Google Scholar]
- Dias, C.; Oguchi, T.; Wimalasena, K. Drivers’ speeding behavior on expressway curves: Exploring the effect of curve radius and desired speed. Transp. Res. Rec. 2018, 2672, 48–60. [Google Scholar]
- Semeida, A.M. Application of artificial neural networks for operating speed prediction at horizontal curves: A case study in Egypt. J. Mod. Transp. 2014, 22, 20–29. [Google Scholar]
- Bassan, S. Sight distance and horizontal curve aspects in the design of road tunnels vs. highways. Tunn. Undergr. Space Technol. 2015, 45, 214–226. [Google Scholar]
- Zheng, Z.; Du, Z.; Li, P. On the visual environment rhythmic design for the vehicle drivers to travel through the long highway tunnels. J. Saf. Environ. 2017, 17, 1800–1805. [Google Scholar]
- Zheng, Z.; Du, Z.; Yan, Q.; Xiang, Q.; Chen, G. The impact of rhythm-based visual reference system in long highway tunnels. Saf. Sci. 2017, 95, 75–82. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Specifications for Highway Safety Audit (JTG B05-2015); People’s Communications Press: Beijing, China, 2015. [Google Scholar]
- Choudhari, T.; Maji, A. Risk assessment of horizontal curves based on lateral acceleration index: A driving simulator-based study. Transp. Dev. Econ. 2021, 7, 2. [Google Scholar]
- Aguil-Éra, V.; Glaser, S. Data requirements for enhanced digital maps in an advanced curve-speed warning system. Transp. Res. Rec. 2004, 1886, 109–118. [Google Scholar]
- Othman, S.; Thomson, R.; Lannér, G. Safety analysis of horizontal curves using real traffic data. J. Transp. Eng. 2014, 140, 04014005. [Google Scholar]
- Kirytopoulos, K.; Kazaras, K.; Papapavlou, P.; Ntzeremes, P.; Tatsiopoulos, I. Exploring driving habits and safety critical behavioural intentions among road tunnel users: A questionnaire survey in Greece. Tunn. Undergr. Space Technol. 2017, 63, 244–251. [Google Scholar]
- Zhao, X.; Wu, Y.; Rong, J.; Ma, J. The effect of chevron alignment signs on driver performance on horizontal curves with different roadway geometries. Accid. Anal. Prev. 2015, 75, 226–235. [Google Scholar]
- Liu, H.; Zhang, Z.; Guo, D.; Peng, L.; Bao, Z.; Han, W. Research progress and prospect of application technology of thin-layer antiskid colored pavement at home and abroad. In Proceedings of the 2011 International Conference on Electric Technology and Civil Engineering (ICETCE), Lushan, China, 22–24 April 2011; pp. 2557–2560. [Google Scholar]
- Van Houten, R.; Van Huten, F. The effects of a specific prompting sign on speed reduction. Accid. Anal. Prev. 1987, 19, 115–117. [Google Scholar]
- Wu, Y.; Zhao, X.; Rong, J.; Ma, J. Influence analysis of chevron alignment signs on drivers’ speed choices at horizontal curves on highways. J. Southeast Univ. (Nat. Sci. Ed.) 2015, 31, 412–417. [Google Scholar]
- Du, Z.; Wang, S.; Yang, L.; Ni, Y.; Jiao, F. Experimental study on the efficacy of retroreflective rings in the curved freeways tunnels. Tunn. Undergr. Space Technol. 2021, 110, 103813. [Google Scholar] [CrossRef]
- Xu, J.; Yang, K.; Shao, Y.; Lu, G. An experimental study on lateral acceleration of cars indifferent environments in Sichuan, Southwest China. Discrete Dyn. Nat. Soc. 2015, 2015, 494130. [Google Scholar]
- Xu, J.; Yang, K.; Zhou, J.; Wang, X.; Shao, Y.M. Longitudinal acceleration of vehicles on complex mountain roads. Proc. Inst. Civ. Eng. Transp. 2019, 172, 249–263. [Google Scholar] [CrossRef]
- Gershon, P.; Ronen, A.; Oron-Gilad, T.; Shinar, D. The effects of an interactive cognitive task (ICT) in suppressing fatigue symptoms in driving. Transp. Res. Part F Traffic Psychol. Behav. 2009, 12, 21–28. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).