Observer-Based Prescribed-Time Bipartite Output Consensus of Nonlinear Multi-Agent Systems with Exogenous Disturbances

Abstract

In this study, we developed a framework for achieving prescribed-time bipartite output consensus in nonlinear multi-agent systems by introducing a distributed observer approach. We propose a novel control protocol that utilizes a bipartite projective parameter and allows the settling time to be predetermined within a physically feasible range, independent of the system parameters and initial conditions. By using a time-varying scaling function ($\mu (t)$), the prescribed time may not depend on initial conditions and system parameters and covers more complex, nonlinear multi-agent systems. State and disturbance observers are co-designed to estimate unmeasurable states and reject external perturbations. Sufficient conditions for scenarios regarding the presence of exogenous disturbances are established by using algebraic graph theory, nonlinear system theory, Lyapunov stability, and matrix theory. Finally, numerical simulations verify the effectiveness of the designed protocol and the correctness of the proposed theorem.

1. Introduction

Multi-agent systems comprise multiple autonomous agents that collaborate to perform complex tasks through local information exchange and interaction. In recent years, with the rapid development of fields such as information communication and artificial intelligence, multi-agent systems have been widely applied in many areas, such as vehicle technology [1,2], formation control [3,4], satellite constellations [5], and robotics [6]. Consensus [7,8,9,10,11], as one of the fundamental topics in coordinated control, has been extensively studied by numerous scholars, primarily focusing on multi-agent systems of different orders. However, achieving consensus among agents is a fundamental challenge in MASs, particularly in ensuring safety and coordination while enabling information sharing and collective decision making.

The abovementioned works focus on agents that have cooperative relationships, and interactions among agents are described through communication topologies. In this case, cooperative relationships are marked with non-negative weights. However, in practical applications, there may also exist competitive relationships among agents, in which case the communication between agents is described by using signed graphs with both positive and negative edges [12,13,14,15]. The authors of [16] studied the first-order integrator and introduced the concept of bipartite consistency. Bipartite consensus is a specific form of the consensus matters within multi-agent systems where all the agents are divided into two distinct, non-overlapping subsets. The agents in each group should reach an agreement about their states by sharing information exclusively with agents from the other group. The bipartite consensus theory presented in [17] was utilized to develop a novel multi-agent secure image communication system. The leading agents and following agents responsible for image transmission can produce consistent encryption and decryption keystreams. The experimental results demonstrate that the newly constructed multi-agent secure image communication system exhibits outstanding performance in terms of statistical properties, correlation, key sensitivity, resistance to differential attacks, and information entropy analysis.

In the early stages of research on consensus in multi-agent systems, more attention was paid to the asymptotic stability of consensus. With the advancement of contemporary society, scholars have increasingly focused on finite-time consensus in MASs due to its potential to achieve rapid convergence within a specified time frame [18,19,20,21]. Nevertheless, the finite-time consensus presented in the abovementioned literature studies exhibits certain limitations, as the designated finite times are intricately dependent on the initial conditions and parameter configurations of the multi-agent system. In response to these limitations, the concept of fixed-time consensus, which operates independently of initial conditions, thereby enabling the system to reach consensus within a predetermined fixed time, was introduced [22,23,24]. However, it is essential to recognize that fixed time is still constrained by the influence of system parameters and, consequently, may not always be set arbitrarily. To address the aforementioned shortcomings, the concept of arbitrary prescribed time has been proposed. This framework offers the advantage of allowing the convergence time of MASs to be explicitly predetermined, independently of both the initial conditions and system parameters [25]. Furthermore, the authors of [25] introduced a novel time-varying scalar function designed for control systems that ensures that system stability can be achieved within the designated preset time.

The measurement of system state information is largely influenced by the precision of instruments and external interference. There may be significant errors between the measured data and the actual state. Thus, designing a proper observer-based protocol is a promising approach to solve the formation control problem. The observer-based method has been successfully applied across various fields [26], and numerous researchers have utilized observers for linear systems, yielding favorable results. However, more in-depth research is needed in the area of nonlinear systems.

The operation of multi-agent system is inevitably affected by the external environment. Interference signals generated by external systems can significantly impact the consensus of multi-agent systems [27]. Therefore, it is essential to consider the effects of exogenous disturbances when addressing the consensus issues of multi-agent systems. That is to say that in practical applications, systems may be subject to exogenous disturbances [28], which can lead to unavoidable instability. Consequently, the consensus problem of multi-agent systems with exogenous disturbances has garnered considerable attention. Investigating such issues enhances the practical relevance of this research study.

Building on the aforementioned ideas, we concentrate on the issue of observer-based prescribed-time bipartite output consensus for nonlinear multi-agent systems in both the absence and presence of exogenous disturbances. The most important contributions and innovation points of this study are described as follows:

• In contrast to previous studies on bipartite consensus, which necessitate a network topology to achieve a balanced state [29], in this study, we demonstrate that the implementation of cooperation and competition does not require such a topology to attain a balanced condition.
• Compared with [30,31], this study broadens the discussion to encompass more complex nonlinear multi-agent systems, which is more practical. Furthermore, it places particular emphasis on scenarios involving exogenous disturbances, thereby enhancing the generality of the model.
• With reference to [32], state observers and disturbance observers are designed to effectively estimate their actual values, allowing for the extension of consensus from the previously established fixed- and finite-time frameworks to a prescribed-time consensus approach.

The paper is organized as follows: In Section 2, we present some preparatory knowledge on notations and graph theory. In Section 3, we expound upon the main theorem. Next, an example is provided in Section 4 to validate the effectiveness of the results. Finally, in Section 5, we present the conclusions of the study and propose future research directions.

2. Preliminaries

2.1. Notations

In this study, we adopt the following notations: $R^n$ represents the n-dimensional Euclidean space; ${\mathbf{1}}_N$ denotes the N-dimensional all-ones column vector; the set of $n\times m$ real matrices is defined as $R^{n\times m}$, where $I_n\in R^{n\times n}$ denotes the identity matrix; ${\lambda }_{max}(P)$ and ${\lambda }_{min}(P)$ denote the maximal and minimum eigenvalues of matrix P, respectively; $Diag\{·\}$ refers to the diagonal matrix; and ⊗ is the Kronecker product. The Euclidean norm for vectors or the induced norm for matrices is defined as $\Vert ·\Vert$.

2.2. Graph Theory

Let a topology graph contain $B+P$ agents; its communication topology can be modeled as an undirected graph ($\mathcal{G}(\mathcal{V},ϵ,\mathcal{A})$, where $\mathcal{V}=\{1,2,\dots ,B,B+1,\dots ,B+P\}$ represents a set of nodes, $ϵ\subset \mathcal{V}\times \mathcal{V}=\{(k,s)|k,s\in \mathcal{V}\}$ is another set of nodes, and $\mathcal{A}=(a_{ij})\in R^{(B+P)\times (B+P)}$ is the adjacency matrix). The set of neighbors of agent i is defined as $N_i=\{j\in \mathcal{V}|(i,j)\in \epsilon ,i\ne j\}$. $L=(l_{ij})\in R^{(B+P)\times (N+M)}$ stands for the Laplacian matrix, with $l_{ii}={\sum }_{s=1}^{B+P}{a}_{is}$, $l_{ij}=-a_{ij}$, and $i\ne j$. Provided that an undirected graph ($\mathcal{G}$) has a path between any two nodes, then $\mathcal{G}$ is considered to be connected.

2.3. Model Description

In this study, we consider a multi-agent system consisting of $B+P$ agents in which the dynamics of the agents are designed as

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_i(t)& =f(x_i(t))+u_i(t)+\sigma {\omega }_i(t),\hfill \\ \hfill y_i(t)& =C{x}_i(t),\hfill \end{array}\right.$$

(1)

for $i=1,2,\dots ,B,B+1,\dots ,B+P$, where $x_i(t)\in R^n$, $u_i(t)\in R^n$, ${\omega }_i(t)\in R^n$, and $y_i(t)\in R^m$ are the system state, control protocol, bounded exogenous disturbance, and output of agent i, respectively. Matrix $C\in R^{m\times n}$ is a constant matrix. $\sigma$ is a detective mechanism that can be used to detect whether the system is affected by exogenous disturbances and is defined as follows:

$$\sigma =\left\{\begin{array}{cc}1,\hfill & \hfill {\omega }_i(t)exists\\ 0,\hfill & \hfill otherwise.\end{array}\right.$$

(2)

Let us suppose that a disturbance (${\omega }_i(t),i=1,2,\dots ,B,B+1,\dots ,B+P$) is generated by the following linear exogenous system [33]:

$$\left\{\begin{array}{c}\hfill {\dot{d}}_i(t)=Q{d}_i(t),\\ \hfill {\omega }_i(t)=K{d}_i(t),\end{array}\right.$$

(3)

where $d_i(t)\in R^l$ denotes the state of the exogenous disturbance and $Q\in R^{l\times l}$ and $K\in R^{n\times l}$ are known constant matrices of the exogenous system.

The continuously vector-valued function ($f:R^n\to R^n$) represents a nonlinear term satisfying the following Lipschitz conditions.

Assumption 1.

For a known nonlinear function (f), there exists a non-negative constant (ρ) such that

$$\begin{array}{c}\hfill \Vert f(a)-f(b)\Vert ⩽\rho \Vert a-b\Vert ,\forall a,b\in R^n.\end{array}$$

(4)

It should be noted that ρ does not need to be given or known exactly, and an upper bound of ρ should be estimated in this study.

We define ${\mathcal{V}}_1=\{1,2,\dots ,B\}$ as group 1 and ${\mathcal{V}}_2=\{B+1,B+2,\dots ,B+P\}$ as group 2. This clearly satisfies $\mathcal{V}={\mathcal{V}}_1\cup {\mathcal{V}}_2$ and ${\mathcal{V}}_1\cap {\mathcal{V}}_2=\varnothing$.

In this study, the state information of each agent is supposed to be unavailable, which is common in many scenarios and adds to the complexity of control.

For the purpose of designing a prescribed-time bipartite output control protocol, we introduce a time-varying scaling function [25] as

$$\mu (t)=\left\{\begin{array}{cc}{\displaystyle \frac{T^h}{{(T+t_0-t)}^h}},\hfill & \hfill t\in [t_0,t_0+T)\\ 1,\hfill & \hfill t\in [t_0+T,\infty )\end{array}\right.$$

(5)

where $T>0$ is the prescribed time and $h>2$.

We define the right-hand derivative of $\mu (t)$ at $t=t_0+T$ as $\dot{\mu }(t_0+T)$. Then,

$$\dot{\mu }(t)=\left\{\begin{array}{cc}{\displaystyle \frac{h}{T}}{\mu }^{1+{\displaystyle \frac{1}{h}}},\hfill & \hfill t\in [t_0,t_0+T)\\ 0,\hfill & \hfill t\in [t_0+T,\infty ).\end{array}\right.$$

(6)

Remark 1.

The core role of $\mu (t)$ is to ensure that the multi-agent system achieves bipartite output consensus within a user-defined time (T) by dynamically adjusting the gain of the control protocol. Its design guarantees accelerated convergence during $t\in [t_0,t_0+T)$ and maintains a stability of $\mu (t)=1$ for $t\in [t_0,t_0+T)$. Compared with traditional finite-time or fixed-time control frameworks, this mechanism eliminates the dependence on initial conditions or system parameters, allowing the convergence time to be fully specified by the user. As t approaches $t_0+T$, the denominator ($T+t_0-t$) approaches zero, causing $\mu (t)$ to grow rapidly. This amplifies the gain term in the control protocol, accelerating system convergence. For $t>t_0+T$, $\mu (t)\equiv 1$, ensuring the system remains stable after consensus is achieved. The condition of $h>2$ ensures that $\mu (t)$ becomes sufficiently steep near $t=t_0+T$, enhancing control over convergence speed and avoiding overshoot or delays caused by insufficient gain.

Lemma 1

([34]). Let us consider a non-negative continuously differentiable function ($V(t)$). If it satisfies the condition that

$$\begin{array}{c}\hfill \dot{V}(t)⩽-{\beta }_{1}V(t)-{\beta }_2{\displaystyle \frac{\dot{\mu }(t)}{\mu (t)}}V(t),\end{array}$$

(7)

where ${\beta }_1⩾0$ and ${\beta }_2>0$ are two constants. Then, for $t\in [t_0,t_0+T)$, it yields

$$\begin{array}{c}\hfill V(t)⩽{\mu }^{-{\beta }_2}(t){\mathrm{e}}^{-{\beta }_1(t-t_0)}V(t_0).\end{array}$$

(8)

Additionally, for $t\in [t_0+T,+\infty )$, it satisfies $V(t)\equiv 0$.

Assumption 2.

Undirected graph $\mathcal{G}$ is connected.

Lemma 2

([35]). For undirected graph $\mathcal{G}$, the eigenvalues of L are allowed to be organized as $0={\lambda }_1(L)<{\lambda }_2(L)⩽\cdots ⩽{\lambda }_{B+P}(L)$.

Definition 1.

Multi-agent system (1) is considered to achieve prescribed-time (T) bipartite output consensus if

$$\begin{array}{cc}\hfill (1)& \underset{t\to t_0+T}{\lim }\parallel y_i(t)-s_{ij}{y}_j(t)\parallel =0,\hfill \\ \hfill (2)& \parallel y_i(t)-s_{ij}{y}_j(t)\parallel \equiv 0,fort\in [t_0+T,+\infty ),\hfill \end{array}$$

where

$$\begin{array}{c}\hfill s_{ij}=\left\{\begin{array}{cc}1,\hfill & \hfill i,j\in {\mathcal{V}}_{1}ori,j\in {\mathcal{V}}_2\\ -1,\hfill & \hfill i\in {\mathcal{V}}_{1}andj\in {\mathcal{V}}_{2}orj\in {\mathcal{V}}_{1}andi\in {\mathcal{V}}_2\end{array}\right..\end{array}$$

(9)

3. Control Protocol Design and Stability Analysis

In this section, we discuss the situation where we have consensus with exogenous disturbance, which means that $\sigma =1$. In order to realize the prescribed-time bipartite output consensus of multi-agent systems of the undirected topology (1) with state and disturbance observers, the control protocol is proposed as

$$\begin{array}{cc}\hfill u_i(t)=& -\alpha (k_1+k_2{\displaystyle \frac{\dot{\mu }(t)}{\mu (t)}})\sum _{j\in N_i}{a}_{ij}({\widehat{x}}_i(t)-s_{ij}{\widehat{x}}_j(t))-{\widehat{\omega }}_i(t),\hfill \end{array}$$

(10)

with the state observer expressed as

$$\begin{array}{c}\hfill \dot{{\widehat{x}}_i}(t)=u_i(t)+f({\widehat{x}}_i(t))+{\widehat{\omega }}_i(t)-G_1(y_i(t)-C{\widehat{x}}_i(t)),\end{array}$$

(11)

and the disturbance observer expressed as

$$\begin{array}{c}\hfill \dot{{\widehat{d}}_i}(t)=H{\widehat{d}}_i(t)-G_2({\omega }_i(t)-K{\widehat{d}}_i(t)),\end{array}$$

(12)

where $k_1>{\displaystyle \frac{2+{\rho }^2}{{\lambda }_{min}(C{C}^{\mathrm{T}})}}$; $k_2>0$; ${\widehat{\omega }}_i(t)=K{\widehat{d}}_i(t)$ denotes the estimated value of ${\omega }_i(t)$; ${\widehat{d}}_i(t)$ is the estimated value of $d_i(t)$; and $G_1$ and $G_2$ are observer gain matrices to be designed, respectively.

Remark 2.

The design of protocol (10) can achieve bipartite consensus including cooperation and competition without requiring a topological graph to be a balanced graph. Traditional bipartite consensus protocols typically require the communication topology to be a balanced graph (i.e., the in degree equals the out degree for each node) [29] to counteract the sign effects of competitive relationships. Here, by introducing the sign matrix as $S=\mathit{diag}\{1,\dots ,1,-1,\dots ,-1\}$, this study directly encodes competitive interactions into the control protocol, eliminating the need for a balanced topology.

Theorem 1.

Under Assumptions 1 and 2, for any predefined $T>0$, a prescribed-time bipartite output consensus can be achieved for multi-agent system (1) with $\sigma =1$ under distributed control protocol (10) if the following apply:

(1) 

Control parameter $\alpha ⩾{\displaystyle \frac{{\lambda }_{max}(C{C}^{\mathrm{T}})+{\lambda }_{min}(C{C}^{\mathrm{T}})}{2{\lambda }_2(L)}}$;

(2) 

$K^{\mathrm{T}}KH+H^{\mathrm{T}}{K}^{\mathrm{T}}K⩽K^{\mathrm{T}}K$;

(3) 

Observer gain matrix $G_1=-(k_1+k_2{\displaystyle \frac{\dot{\mu }(t)}{\mu (t)}})C^{\mathrm{T}}$;

(4) 

Observer gain matrix

$G_2=-{\displaystyle \frac{(k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)}){\lambda }_{min}(C{C}^{\mathrm{T}})+{\lambda }_{max}^2(L){\lambda }_{max}(C^{\mathrm{T}}C)}{2{\lambda }_{min}(K{K}^{\mathrm{T}})}}{K}^{\mathrm{T}}$.

Proof. 

We convert system (1) into the following compact forms under control protocol (10) with state observer (11):

$$\left\{\begin{array}{cc}\hfill \dot{X}(t)=& -\alpha (k_1+k_2{\displaystyle \frac{\dot{\mu }(t)}{\mu (t)}})(S^{-1}LS\otimes I_n)\widehat{X}(t)\hfill \\ \hfill & +(I_{B+P}\otimes K)(d(t)-\widehat{d}(t))+F,\hfill \\ \hfill Y(t)=& (I_{B+P}\otimes C)X(t),\hfill \end{array}\right.$$

(13)

with

$$\begin{array}{cc}\hfill \dot{\widehat{X}}(t)=& -\alpha (k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)})(S^{-1}LS\otimes I_n)\widehat{X}(t)+\widehat{F}\hfill \\ \hfill & -(I_{B+P}\otimes G_{1}C)(X(t)-\widehat{X}(t)).\hfill \end{array}$$

(14)

Above, $S=diag\{1,1,\dots ,1,-1,\dots ,-1\}$, $d(t)={(d_1^{\mathrm{T}}(t),d_2^{\mathrm{T}}(t),\dots ,d_{N+M}^{\mathrm{T}}(t))}^{\mathrm{T}}$, $\widehat{d}(t)={({\widehat{d}}_1^{\mathrm{T}}(t),{\widehat{d}}_2^{\mathrm{T}}(t),\dots ,{\widehat{d}}_{N+M}^{\mathrm{T}}(t))}^{\mathrm{T}}$, $F=(f^{\mathrm{T}}(x_1(t)),f^{\mathrm{T}}(x_2(t)),\cdots ,f^{\mathrm{T}}(x_{N+M}$${(t)))}^{\mathrm{T}}$, and $\widehat{F}=(f^{\mathrm{T}}{\widehat{x}}_1(t),f^{\mathrm{T}}{\widehat{x}}_2(t),\cdots ,f^{\mathrm{T}}{\widehat{x}}_{N+M}{(t)}^{\mathrm{T}})$.

We define the bipartite output error vectors as ${\zeta }_i(t)={\sum }_{j\in N_i}{a}_{ij}(y_i(t)-s_{ij}{y}_j(t))$ and $\widehat{{\zeta }_i}(t)={\sum }_{j\in N_i}{a}_{ij}(\widehat{y_i}(t)-s_{ij}\widehat{y_j}(t)),i=1,2,\dots ,B,B+1,\dots ,B+P$, i.e.,

$$\begin{array}{c}\hfill \zeta (t)=(S^{-1}LS\otimes I_m)Y(t),\end{array}$$

(15)

and

$$\begin{array}{c}\hfill \widehat{\zeta }(t)=(S^{-1}LS\otimes I_m)\widehat{Y}(t),\end{array}$$

(16)

where $\zeta (t)={({\zeta }_1^{\mathrm{T}}(t),{\zeta }_2^{\mathrm{T}}(t),\dots ,{\zeta }_B^{\mathrm{T}}(t),{\zeta }_{B+1}^{\mathrm{T}}(t),\dots ,{\zeta }_{B+P}^{\mathrm{T}}(t))}^{\mathrm{T}}$ and $\widehat{\zeta }(t)=({\widehat{\zeta }}_1^{\mathrm{T}}(t)$, ${\widehat{\zeta }}_2^{\mathrm{T}}(t),\dots ,{\widehat{\zeta }}_B^{\mathrm{T}}(t),{\widehat{\zeta }}_{B+1}^{\mathrm{T}}(t),\dots ,{\widehat{\zeta }}_{B+P}^{\mathrm{T}}{(t))}^{\mathrm{T}}$.

We denote the output observer error vectors as ${\overline{\zeta }}_i(t)={\zeta }_i(t)-\widehat{{\zeta }_i}(t),i=1,2,\dots ,B$, $B+1,\dots ,B+P$. Then,

$$\begin{array}{c}\hfill \overline{\zeta }(t)=(S^{-1}LS\otimes I_m)(Y(t)-\widehat{Y}(t)).\end{array}$$

(17)

We denote the exogenous disturbance observer error vectors as $e_i(t)={\omega }_i(t)-{\widehat{\omega }}_i(t)$, which indicates that

$$\begin{array}{c}\hfill e(t)=(I_{B+P}\otimes K)(d(t)-\widehat{d}(t)),\end{array}$$

(18)

and

$$\begin{array}{c}\hfill \dot{\widehat{d}}(t)=(I_{B+P}\otimes H)\widehat{d}(t)-(I_{B+P}\otimes G_2)e(t),\end{array}$$

(19)

where $e(t)={(e_1^{\mathrm{T}}(t),e_2^{\mathrm{T}}(t),\dots ,e_{B+P}^{\mathrm{T}}(t))}^{\mathrm{T}}$.

Hence, we consider the Lyapunov function candidate as

$$\begin{array}{c}\hfill V(t)={\widehat{\zeta }}^{\mathrm{T}}(t)\widehat{\zeta }(t)+{\overline{\zeta }}^{\mathrm{T}}(t)\overline{\zeta }(t)+e^{\mathrm{T}}(t)e(t),\end{array}$$

(20)

and we take the time derivative of $V(t)$ with $\widehat{\zeta }(t)$, $\overline{\zeta }(t)$, and $e(t)$ along the trajectories of (13), (14), and (19), respectively, as

$$\begin{array}{cc}\hfill \dot{V}(t)=& 2{\widehat{\zeta }}^{\mathrm{T}}(t)(S^{-1}LS\otimes C)[-\alpha (k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)})(S^{-1}LS\otimes I_n)\widehat{X}(t)+\widehat{F}\hfill \\ \hfill & -(I_{B+P}\otimes G_{1}C)(X(t)-\widehat{X}(t))]\hfill \\ \hfill & +2{\overline{\zeta }}^{\mathrm{T}}(t)(S^{-1}LS\otimes C)[(F-\widehat{F})+e(t)+(I_{B+P}\otimes G_{1}C)(X(t)-\widehat{X}(t))]\hfill \\ \hfill & +2e^{\mathrm{T}}(t)(I_{B+P}\otimes K)[(I_{B+P}\otimes Q)(d(t)-\widehat{d}(t))+(I_{B+P}\otimes G_2)e(t)]\hfill \\ \hfill ⩽& -2\alpha (k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)}){\widehat{\zeta }}^{\mathrm{T}}(t)(S^{-1}LS\otimes I_m)\widehat{\zeta }(t)+(1+{\rho }^2){\widehat{\zeta }}^{\mathrm{T}}(t)\widehat{\zeta }(t)\hfill \\ \hfill & +2(k_1+k_2{\displaystyle \frac{\dot{\mu }(t)}{\mu (t)}}){\widehat{\zeta }}^{\mathrm{T}}(t)(I_{B+P}\otimes C{C}^{\mathrm{T}})\overline{\zeta }(t)+(1+{\rho }^2){\overline{\zeta }}^{\mathrm{T}}(t)\overline{\zeta }(t)\hfill \\ \hfill & +{\overline{\zeta }}^{\mathrm{T}}(t)\overline{\zeta }(t)+{\lambda }_{max}^2(L){\lambda }_{max}(C^{\mathrm{T}}C)e^{\mathrm{T}}(t)e(t)\hfill \\ \hfill & -2(k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)}){\overline{\zeta }}^{\mathrm{T}}(t)(I_{B+P}\otimes C{C}^{\mathrm{T}})\overline{\zeta }(t)+e^{\mathrm{T}}(t)e(t)\hfill \\ \hfill & -[(k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)}){\lambda }_{min}(C{C}^{\mathrm{T}})+{\lambda }_{max}^2(L){\lambda }_{max}(C^{\mathrm{T}}C)]e^{\mathrm{T}}(t)e(t)\hfill \\ \hfill ⩽& -{\lambda }_{min}(C{C}^{\mathrm{T}})(k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)}){\widehat{\zeta }}^{\mathrm{T}}(t)\widehat{\zeta }(t)+(1+{\rho }^2){\widehat{\zeta }}^{\mathrm{T}}(t)\widehat{\zeta }(t)\hfill \\ \hfill & -{\lambda }_{min}(C{C}^{\mathrm{T}})(k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)}){\overline{\zeta }}^{\mathrm{T}}(t)\overline{\zeta }(t)+(2+{\rho }^2){\overline{\zeta }}^{\mathrm{T}}(t)\overline{\zeta }(t)\hfill \\ \hfill & -{\lambda }_{min}(C{C}^{\mathrm{T}})(k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)})e^{\mathrm{T}}(t)e(t)+e^{\mathrm{T}}(t)e(t)\hfill \\ \hfill ⩽& -[({\lambda }_{min}(C{C}^{\mathrm{T}})k_1-2-{\rho }^2)+{\lambda }_{min}(C{C}^{\mathrm{T}})k_2\frac{\dot{\mu }(t)}{\mu (t)}]V(t).\hfill \end{array}$$

(21)

Above, the following inequality is utilized:

$$\begin{array}{cc}\hfill & 2e^{\mathrm{T}}(t)(I_{B+P}\otimes KQ)(d(t)-\widehat{d}(t))\hfill \\ \hfill =& 2{(d(t)-\widehat{d}(t))}^{\mathrm{T}}(I_{B+P}\otimes K^{\mathrm{T}}KQ)(d(t)-\widehat{d}(t))\hfill \\ \hfill ⩽& {(d(t)-\widehat{d}(t))}^{\mathrm{T}}[I_{B+P}\otimes K^{\mathrm{T}}K](d(t)-\widehat{d}(t))\hfill \\ \hfill =& e^{\mathrm{T}}(t)e(t).\hfill \end{array}$$

(22)

According to (20)–(22), one has

$$\begin{array}{c}\hfill \dot{V}(t)⩽-{\beta }_{1}V(t)-{\beta }_2{\displaystyle \frac{\dot{\mu }(t)}{\mu (t)}}V(t),\end{array}$$

(23)

where ${\beta }_1={\lambda }_{min}(C{C}^{\mathrm{T}})k_1-2-{\rho }^2$ and ${\beta }_2={\lambda }_{min}(C{C}^{\mathrm{T}})k_2$.

According to Lemma 1, we have $V(t)⩽{\mu }^{-{\beta }_2}(t){\mathrm{e}}^{-{\beta }_1(t-t_0)}V(t_0)$ for $t\in [t_0,t_0+T)$, which signifies that $\underset{t\to t_0+T}{\lim }V(t)=0$, and $V(t)\equiv 0$ for $t\in [t_0+T,+\infty )$. We can infer that for each i, $\underset{t\to t_0+T}{\lim }\widehat{{\zeta }_i}(t)=0$, $\underset{t\to t_0+T}{\lim }({\zeta }_i(t)-\widehat{{\zeta }_i}(t))=0$, and $\widehat{{\zeta }_i}(t)\equiv 0$ under the definition of $V(t)$ in (20), and ${\zeta }_i(t)-\widehat{{\zeta }_i}(t)\equiv 0$ for $t\in [t_0+T,+\infty )$, which means that $\underset{t\to t_0+T}{\lim }{y}_i(t)=s_{ij}{y}_j(t)$ and $y_i(t)\equiv s_{ij}{y}_j(t)$ for $t\in [t_0+T,+\infty )$. Therefore, system (1) is said to realize prescribed-time bipartite output consensus under distributed control protocol (10). □

Remark 3.

Compared with existing observer-based prescribed-time consensus studies such as [36,37], which have divided the proof into three different parts, i.e., $[t_0,t_0+T_1]$, $[t_0+T_1,t_0+T_1+T_2]$, and $[t_0+T_1+T_2,\infty ]$, the current study requires $T_1<T_2$ [36] and the construction of different Lyapunov functions for different parts [37]. In this paper, the unified Lyapunov function is constructed to consider the above three different time intervals at the same time within a unified time (T).

Let us suppose the situation where we have consensus in the absence of external disturbances, specifically when $\sigma =0$. In order to realize the prescribed-time bipartite output consensus of multi-agent systems (1) of the undirected topology with state observers, the following control protocol is proposed:

$$\begin{array}{c}\hfill u_i(t)=-\alpha (k_1+k_2{\displaystyle \frac{\dot{\mu }(t)}{\mu (t)}})\sum _{j\in N_i}{a}_{ij}(\widehat{x_i}(t)-s_{ij}\widehat{x_j}(t)),\end{array}$$

(24)

with state observer expressed as

$$\begin{array}{cc}\hfill \dot{\widehat{x_i}}(t)& =u_i(t)+f(\widehat{x_i}(t))-G_1(y_i(t)-C\widehat{x_i}(t)),\hfill \end{array}$$

(25)

where $\alpha$ is a constant that is yet to be specified, $k_1>{\displaystyle \frac{1+{\rho }^2}{{\lambda }_{min}(C{C}^{\mathrm{T}})}}$, $k_2>0$, $\mu (t)$ is designed in (5), $\widehat{x_i}(t)$ is the estimation of state $x_i$, and $G_1$ is an observer gain matrix to be determined.

Corollary 1.

Under Assumptions 1 and 2, for any predefined $T>0$, prescribed-time group output consensus can be achieved for a multi-agent system (1) with $\sigma =0$ under a distributed control protocol (24) if the following apply:

(1) 

Control parameter $\alpha ⩾\frac{{\lambda }_{max}(C{C}^{\mathrm{T}})+{\lambda }_{min}(C{C}^{\mathrm{T}})}{2{\lambda }_2(L)}$;

(2) 

Observer gain matrix $G_1=-(k_1+k_2\frac{\dot{\mu }(t)}{\mu (t)})C^{\mathrm{T}}$.

The proof of the corollary is a simplification of the process for Theorem 1.

4. Numerical Simulation

A simulation example is listed in the present section to demonstrate the results of the theoretical analysis conducted in this study. The simulation was conducted in MATLAB R2021b on a workstation equipped with an Intel Core i5-12500K CPU, 16 GB RAM, and an NVIDIA RTX 3050 GPU.

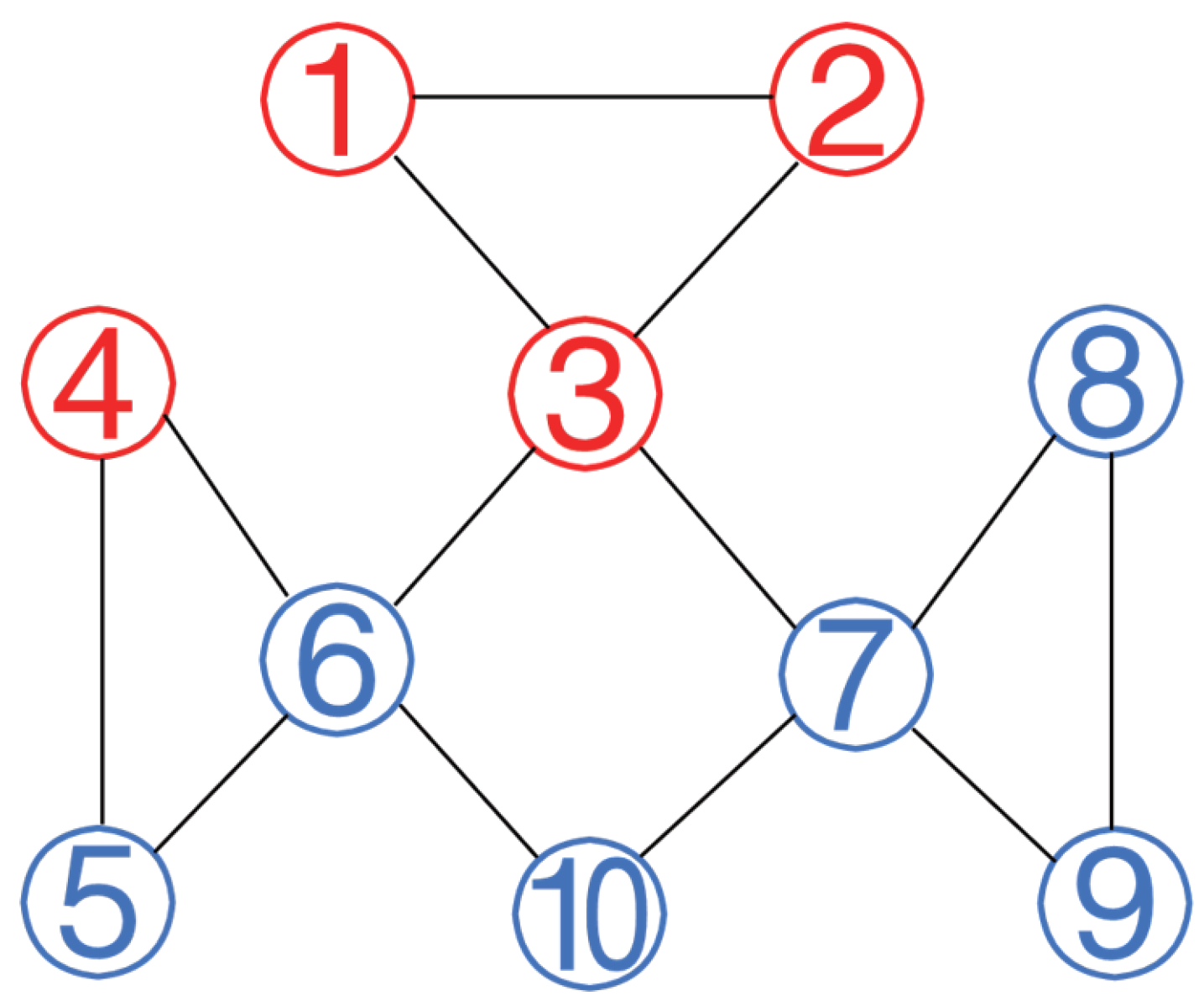
Example 1.

Figure 1 shows the communication topology denoting that a multi-agent system with 10 agents was divided into two groups, ${\mathcal{V}}_1=\{1,2,3,4\}$ and ${\mathcal{V}}_2=\{5,6,7,8,9,10\}$; let $f(x_i(t))=[0.5sin(x_{i2}(t)),0.2cos(x_{i3}(t)),$$2sin(2x_{i1}(t)){]}^{\mathrm{T}}\in R^3$. Thus, the nonlinear dynamics of the agents are presented as follows:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_{i1}(t)& =0.5sin(x_{i2}(t))+u_{i1}(t)+\sigma {\omega }_{i1}(t),\hfill \\ \hfill {\dot{x}}_{i2}(t)& =0.2cos(x_{i3}(t))+u_{i2}(t)+\sigma {\omega }_{i2}(t),\hfill \\ \hfill {\dot{x}}_{i3}(t)& =2sin(2x_{i1}(t))+u_{i3}(t)+\sigma {\omega }_{i3}(t),\hfill \end{array}\right.$$

(26)

where $x_i(t)={(x_{i1}(t),x_{i2}(t),x_{i3}(t))}^{\mathrm{T}}$, $u_i(t)={(u_{i1}(t),u_{i2}(t),u_{i3}(t))}^{\mathrm{T}}$, and ${\omega }_i(t)={({\omega }_{i1}(t),{\omega }_{i2}(t),{\omega }_{i3}(t))}^{\mathrm{T}}$. The constant matrices of the system are given as

$$\begin{array}{c}\hfill Q=\left[\begin{array}{cccc}-0.4& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& -1.4& 0\\ 0& 0& 0& 0\end{array}\right];K=\left[\begin{array}{cccc}-0.6& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1.2& 0\end{array}\right];\end{array}$$

$$\begin{array}{c}\hfill C=\left[\begin{array}{ccc}1.4& 0& 0\\ 0& 0.8& 0\end{array}\right].\end{array}$$

The initial states of agents ($x_{ij}(0)$, $j=1,2,3$) are randomly selected within the range of $[-10,10]$. The prescribed time is $T=3$ s.

For the case of consensus with exogenous disturbance, i.e., $\sigma =1$, we set $k_1=3.4$, $k_2=0.8$, and $h=3$. The initial states of disturbances ($d_{ij}(0)$, $j=1,2,3,4$) are randomly selected within the range of $[-10,10]$. According to the design of C, one has ${\lambda }_{min}(C{C}^{\mathrm{T}})=0.64$ and ${\lambda }_{max}(C{C}^{\mathrm{T}})=1.96$. Thus, we choose $\alpha =2.97$. The conditions of Theorem 1 are all satisfied.

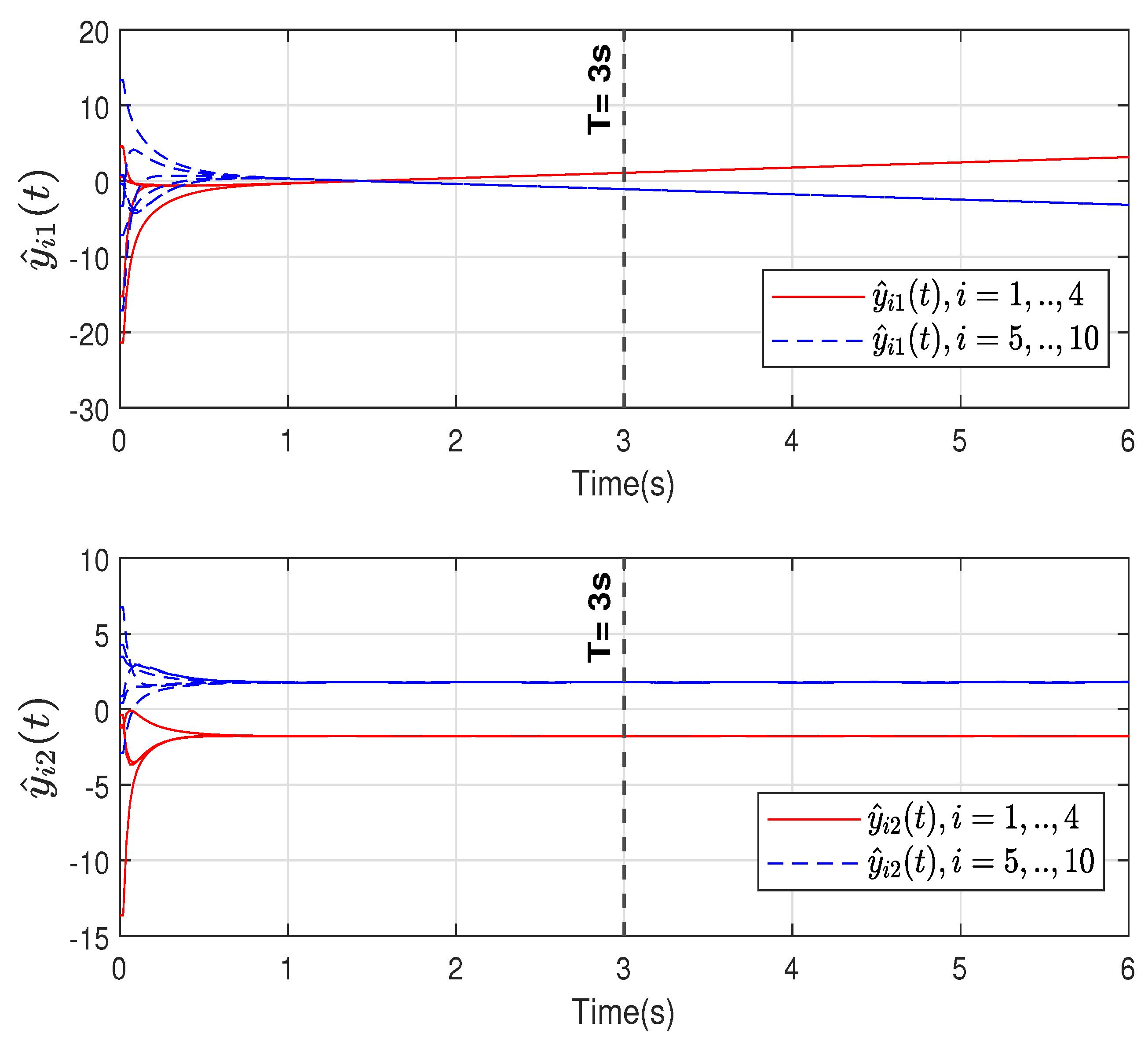
Figure 2 and Figure 3 compare the states of two groups of observers with and without prescribed-time control, respectively. Figure 2 shows that bipartite output consensus can be achieved at T = 3 s under the prescribed-time control protocol (10). Figure 3 indicates that without prescribed-time control ($u_i(t)=-\alpha {\sum }_{j\in N_i}{a}_{ij}({\widehat{x}}_i(t)-s_{ij}{\widehat{x}}_j(t))-{\widehat{\omega }}_i(t)$), bipartite output consensus is achieved at T = 8 s. Figure 4a describes the error between the output states ($y_i(t)$) and their observers (${\widehat{y}}_i(t)$), i.e., ${\widehat{e}}_i(t)=\Vert {\widehat{y}}_i(t)-y_i(t)\Vert$, $i=1,2,\cdots ,10$. Figure 4b describes the error between the disturbances (${\omega }_i(t)$) and their observers ${\widehat{\omega }}_i(t)$, i.e., $e_i(t)=\Vert {\widehat{\omega }}_i(t)-{\omega }_i(t)\Vert$, $i=1,2,\cdots ,10$. Figure 4c describes the error of bipartite output consensus as $E(t)={\sum }_{j=2}^n\Vert \widehat{y_1}(t)-s_{1j}\widehat{y_j}(t)\Vert$. Figure 4 indicates that two types of observers can converge to the actual output state and achieve bipartite output consensus at a prescribed time of T = 3 s. 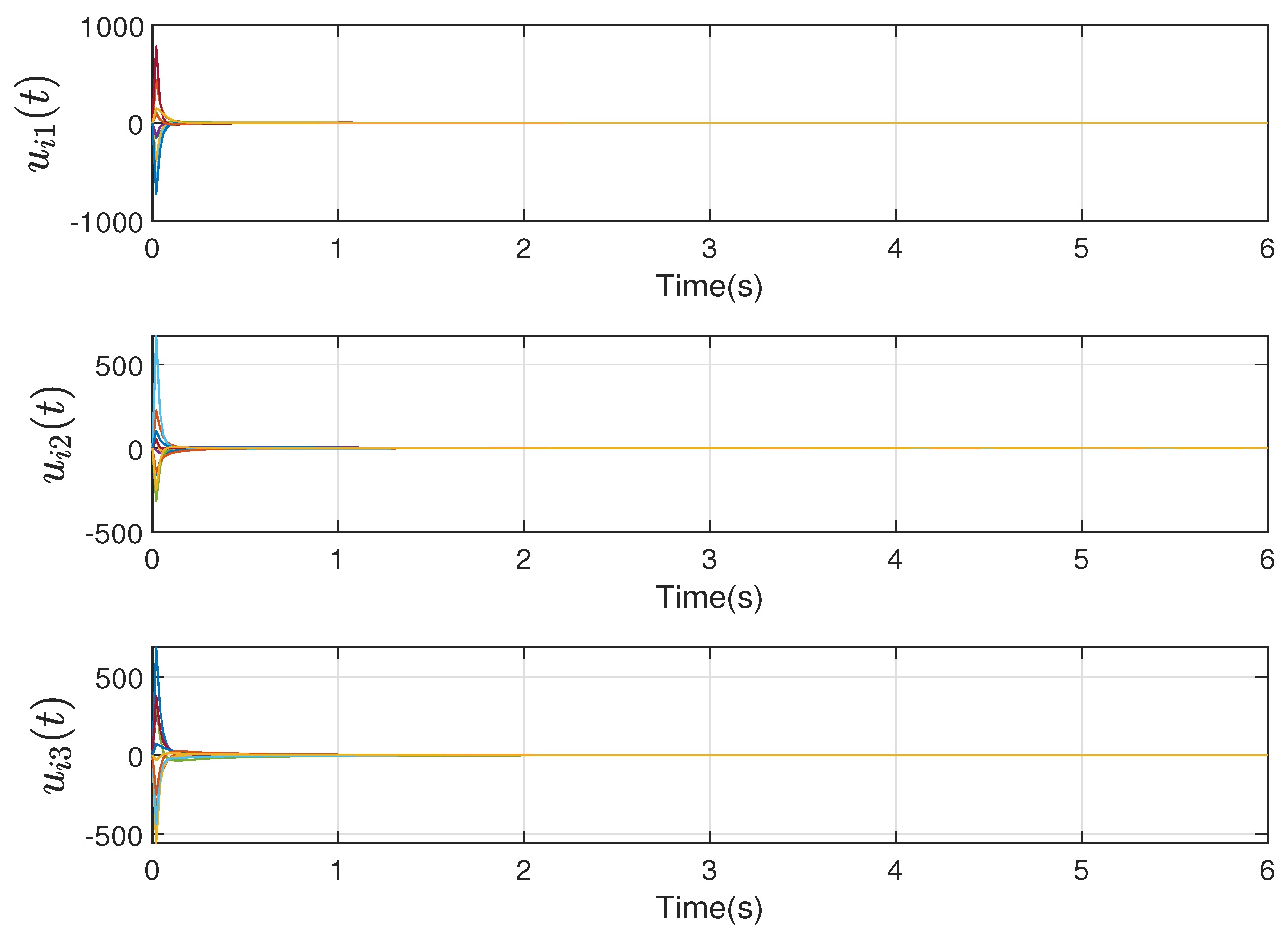Figure 5 illustrates that the control inputs ($u_i(t)$, $i=1,2,\cdots ,10$) are relatively large in the beginning; however, $u_i(t)$ can converge to 0 at T = 3 s.

Therefore, the prescribed-time bipartite output consensus of nonlinear multi-agent systems with exogenous disturbances can be achieved under the conditions of Theorem 1.

Remark 4.

As shown in Figure 3, the multi-agent system without prescribed-time control needs 8 s to achieve consensus. Similarly, the multi-agent systems discussed in [38], with four followers still, need 15 s to achieve consensus. Therefore, the prescribed-time control protocols provide a better solution to ensure that the multi-agent system achieves consensus within a shorter prescribed time (T).

Remark 5.

To verify system robustness, additional experiments were conducted with initial states ($x_{ij}(0)$) randomly distributed within the range of $[-20,20]$, initial states of disturbances ($d_{ij}(0)$) randomly distributed within the range of $[-20,20]$ and parameter perturbations—for example, increasing the nonlinear term coefficient by 10%. Results demonstrate that even with enlarged initial errors or parameter deviations from nominal values, the system still achieves convergence within $T=3s$.

5. Conclusions

A framework for observer-based prescribed-time bipartite output consensus for nonlinear multi-agent systems subject to external disturbances has been presented. The designed protocol provides a more effective method of ensuring that multi-agent systems realize consensus within a specified time frame while mitigating the effects of initial conditions and system parameters. Observers are employed to precisely estimate the actual states of the agents and the external disturbances within the predefined time. The proposed framework holds significant potential for real-world applications, such as enabling dynamic coordination of cooperative and competitive relationships in multi-vehicle collision avoidance within intelligent transportation systems, facilitating rapid task allocation for heterogeneous satellite clusters under external disturbances in space-based formation control, and achieving synchronized operations of industrial robotic arms in complex disturbance-prone environments like automated assembly lines. These scenarios demonstrate the protocol’s adaptability to both collaborative and adversarial interactions while ensuring robustness against uncertainties. Future research can further explore applications in complex scenarios such as dynamic topologies, heterogeneous agents, and high-order multi-agent systems. In particular, designing robust and efficient control strategies will be an important research direction when dealing with communication delays, bandwidth limitations, and security and privacy protection requirements. Moreover, fourth-order dynamics can be applied in UAV models. However, adjustments to the observer gain matrices ($G1$ and $G2$) are required to accommodate higher-order dynamics. Future research will focus on adaptive parameter tuning based on Lyapunov functions to enhance compatibility with complex system architectures while maintaining prescribed-time convergence guarantees.