Variation in Electron Radiation Properties Under the Action of Chirped Pulses in Nonlinear Thomson Scattering
Abstract
1. Introduction
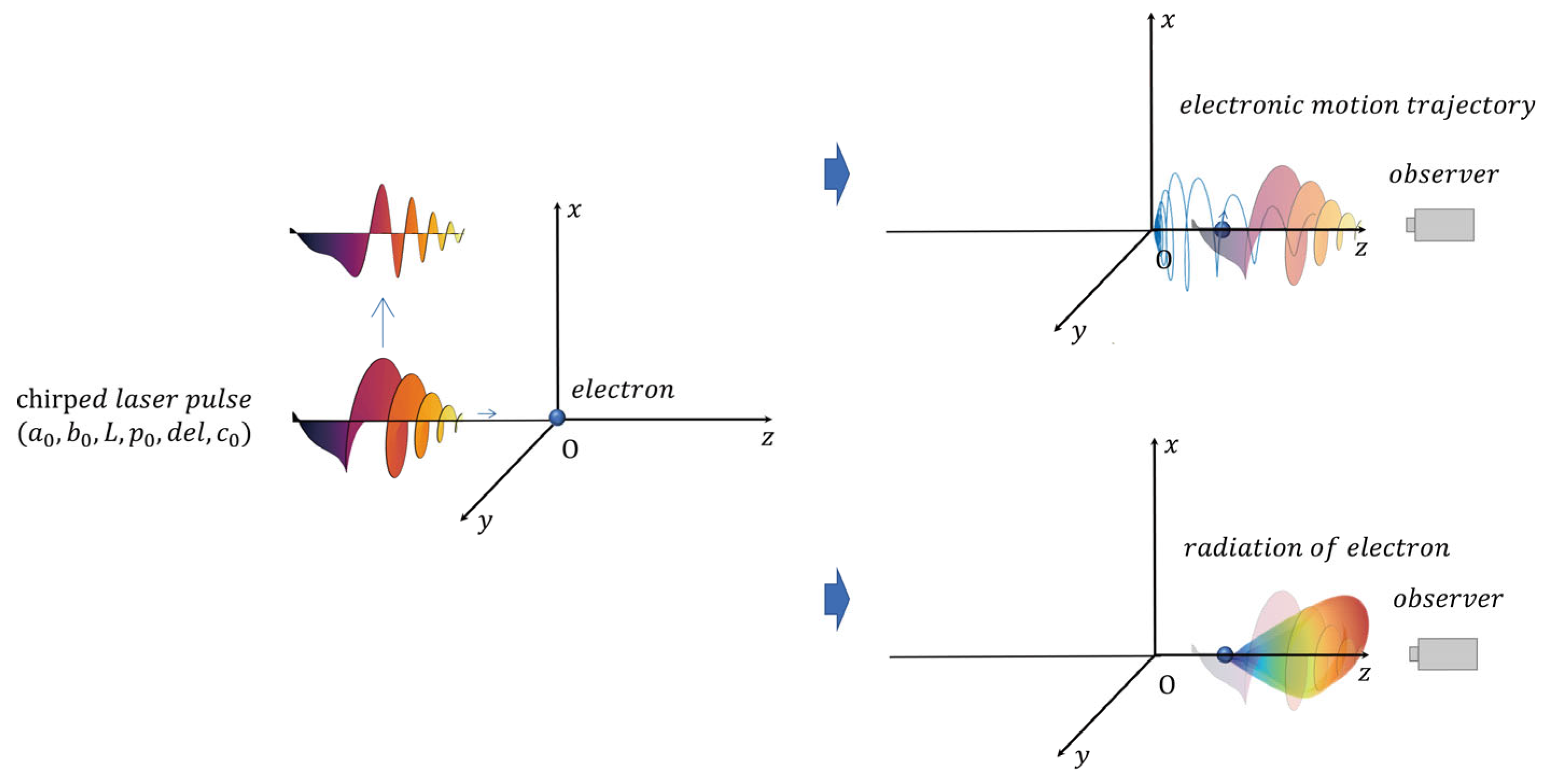
2. Materials and Methods
3. Results
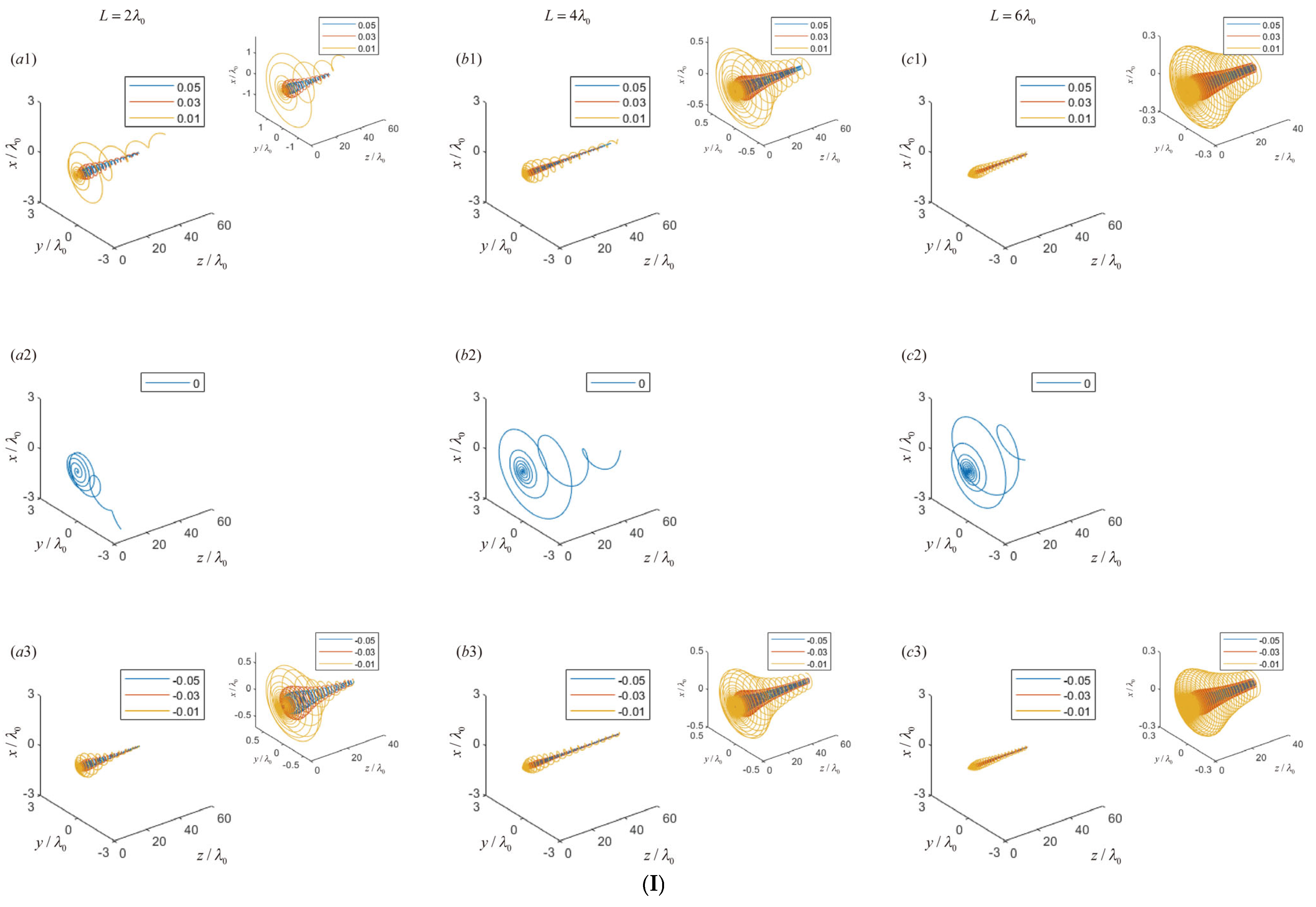
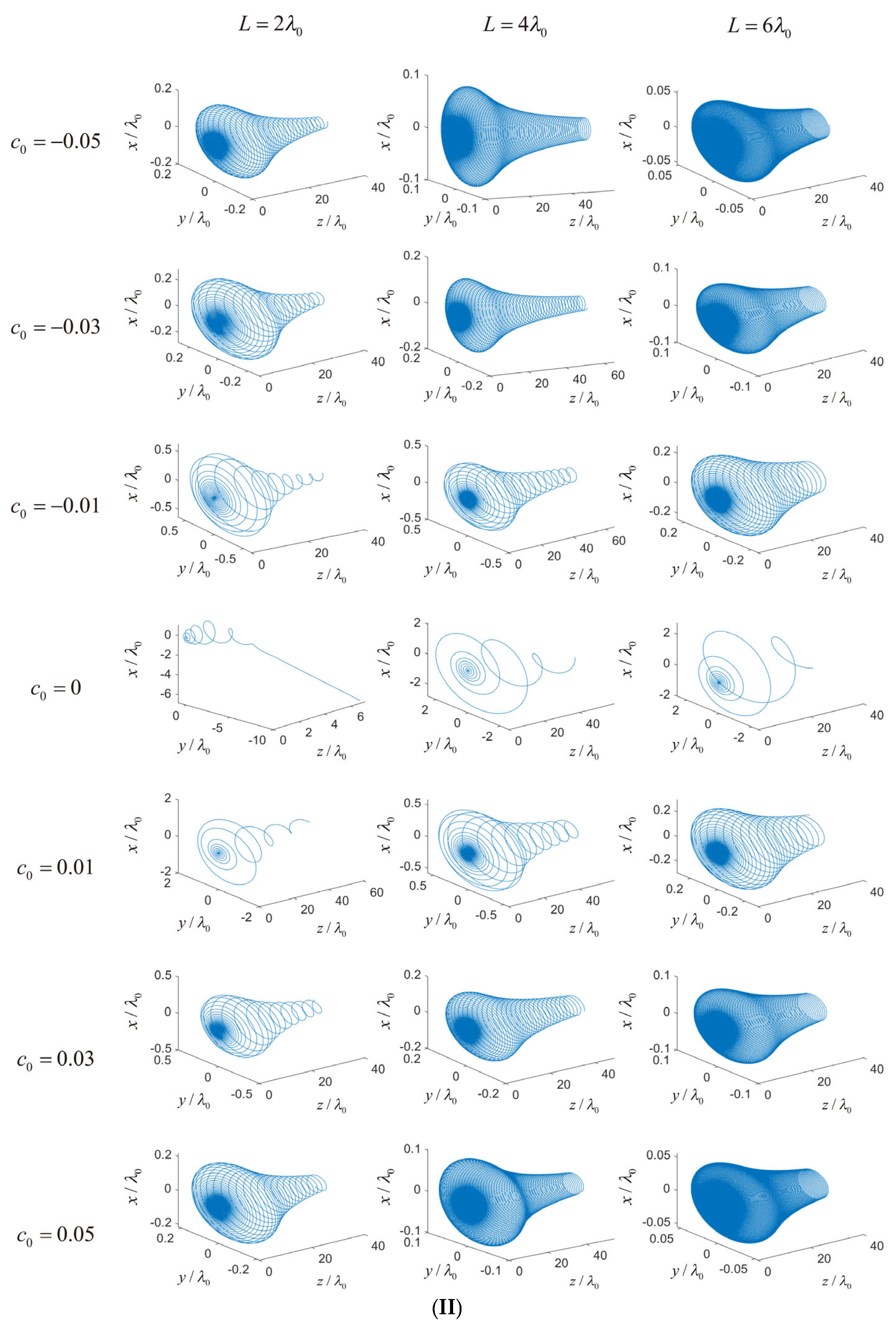
3.1. Motion Trajectory Analysis
3.2. Spatial Distribution of Radiation
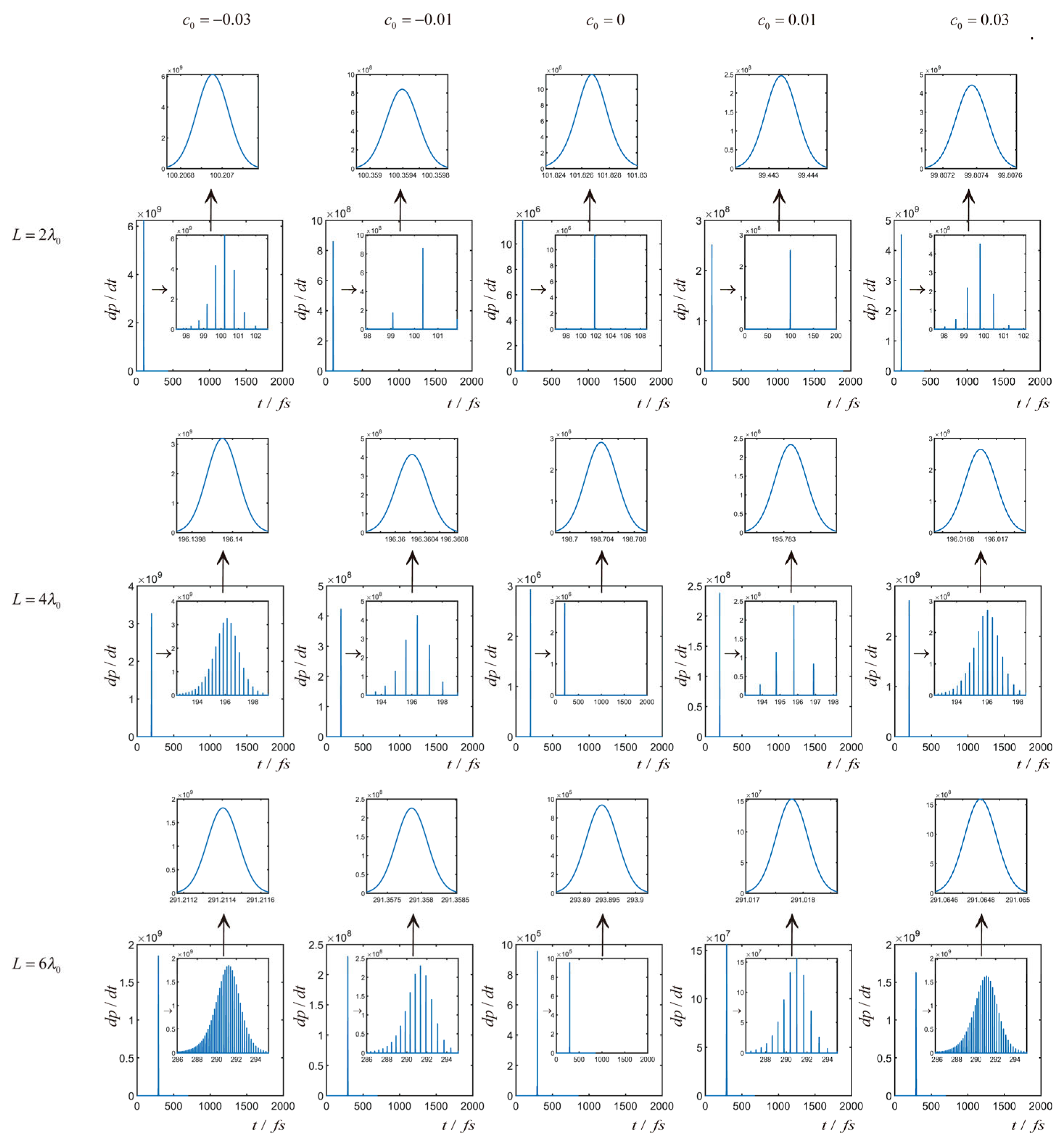
3.3. Time Spectrum Analysis
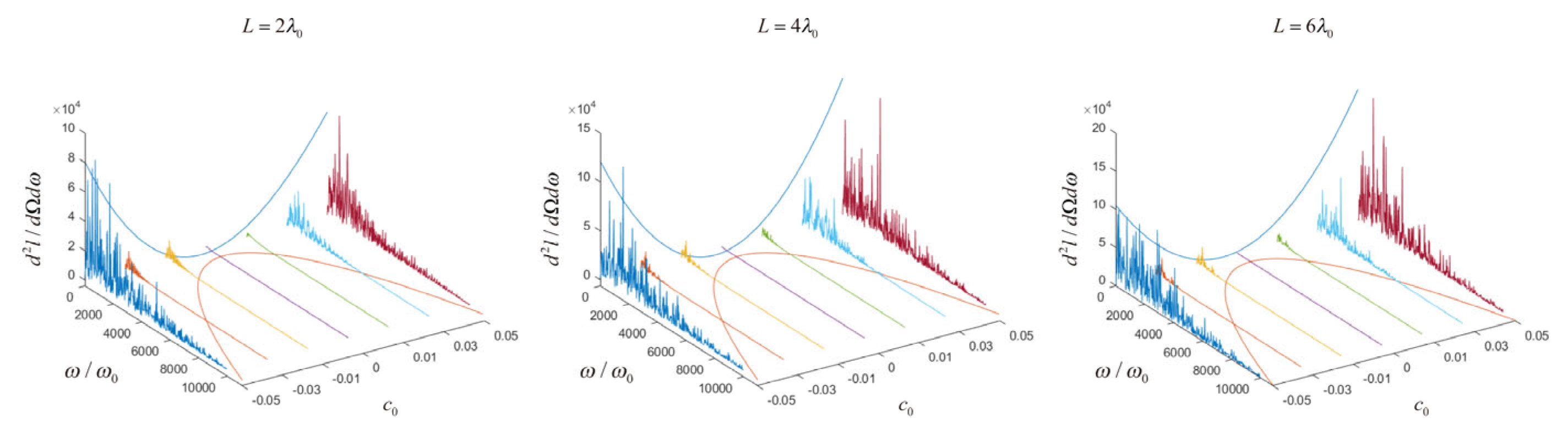
3.4. Frequency Spectrum Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Sohbatzadeh, F.; Mirzanejhad, S.; Ghasemi, M. Electron acceleration by a chirped Gaussian laser pulse in vacuum. Phys. Plasmas 2006, 13, 123108. [Google Scholar]
- Sun, J.; Wang, S.; Zhu, W.; Li, X.; Jiang, L. Simulation of femtosecond laser-induced periodic surface structures on fused silica by considering intrapulse and interpulse feedback. J. Appl. Phys. 2024, 136, 013103. [Google Scholar]
- Chi, Z.; Du, Y.; Huang, W.; Tang, C. Focal spot characteristics of Thomson scattering X-ray sources. J. Appl. Phys. 2018, 124, 124901. [Google Scholar] [CrossRef]
- Rykovanov, S.G.; Geddes, C.G.R.; Schroeder, C.B.; Esarey, E.; Leemans, W.P. Controlling the spectral shape of nonlinear Thomson scattering with proper laser chirping. Phys. Rev. Accel. Beams 2016, 19, 030701. [Google Scholar]
- Mahreen; Prakash, G.V.; Kar, S.; Sahu, D.; Ganguli, A. Influence of pulse modulation frequency on helium RF atmospheric pressure plasma jet characteristics. Contrib. Plasma Phys. 2022, 62, e202200007. [Google Scholar] [CrossRef]
- Aumann, S.; Donner, S.; Fischer, J.; Müller, F. Optical coherence tomography (OCT): Principle and technical realization. In High Resolution Imaging in Microscopy and Ophthalmology: New Frontiers in Biomedical Optics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 59–85. [Google Scholar]
- Galvanauskas, A. Mode-scalable fiber-based chirped pulse amplification systems. IEEE J. Sel. Top. Quantum Electron. 2001, 7, 504–517. [Google Scholar]
- Zaouter, Y.; Guichard, F.; Daniault, L.; Hanna, M.; Morin, F.; Hönninger, C.; Mottay, E.; Druon, F.; Georges, P. Femtosecond fiber chirped-and divided-pulse amplification system. Opt. Lett. 2013, 38, 106–108. [Google Scholar] [CrossRef]
- Yu, L.-H.; Chu, Y.-X.; Gan, Z.-B.; Liang, X.-Y.; Li, R.-X.; Xu, Z.-Z. Trends in ultrashort and ultrahigh power laser pulses based on optical parametric chirped pulse amplification. Chin. Phys. B 2015, 24, 018704. [Google Scholar]
- Hu, Y.-H.; Wang, Y.-W.; Wen, S.-C.; Fan, D.-Y. Nonlinear images of scatterers in chirped pulsed laser beams. Chin. Phys. B 2010, 19, 114207. [Google Scholar]
- Maher-McWilliams, C.; Douglas, P.; Barker, P.F. Laser-driven acceleration of neutral particles. Nat. Photon. 2012, 6, 386–390. [Google Scholar]
- Singh, K.P. Electron acceleration by a chirped short intense laser pulse in vacuum. Appl. Phys. Lett. 2005, 87, 254102. [Google Scholar]
- Wong, L.J.; Kärtner, F.X. Direct acceleration of an electron in infinite vacuum by a pulsed radially-polarized laser beam. Opt. Express 2010, 18, 25035–25051. [Google Scholar]
- Zhang, Y.; Yang, Q.; Wang, J.; Gong, X.; Tian, Y. Zeptosecond-Yoctosecond Pulses Generated by Nonlinear Inverse Thomson Scattering: Modulation and Spatiotemporal Properties. Appl. Sci. 2024, 14, 7038. [Google Scholar] [CrossRef]
- Hartemann, F.V.; Landahl, E.C.; Troha, A.L.; Van Meter, J.R.; Baldis, H.A.; Freeman, R.R.; Luhmann, N.C.; Song, L.; Kerman, A.K.; Yu, D.U.L. The chirped-pulse inverse free-electron laser: A high-gradient vacuum laser accelerator. Phys. Plasmas 1999, 6, 4104–4110. [Google Scholar]
- Terzić, B.; McKaig, J.; Johnson, E.; Dharanikota, T.; Krafft, G.A. Laser chirping in inverse Compton sources at high electron beam energies and high laser intensities. Phys. Rev. Accel. Beams 2021, 24, 094401. [Google Scholar]
- Feng, C.; Shen, L.; Zhang, M.; Wang, D.; Zhao, Z.; Xiang, D. Chirped pulse amplification in a seeded free-electron laser for generating high-power ultra-short radiation. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2013, 712, 113–119. [Google Scholar]
- Zeng, L.; Wang, X.; Liang, Y.; Yi, H.; Zhang, W.; Yang, X. Chirped-Pulse Amplification in an Echo-Enabled Harmonic-Generation Free-Electron Laser. Appl. Sci. 2023, 13, 10292. [Google Scholar] [CrossRef]
- Gupta, D.N.; Kumar, S.; Yoon, M.; Hur, M.S.; Suk, H. Electron acceleration by a short laser beam in the presence of a long-wavelength electromagnetic wave. J. Appl. Phys. 2007, 102, 056106. [Google Scholar]
- Hu, Y.N.; Cheng, L.H.; Yao, Z.W.; Zhang, X.B.; Zhang, A.X.; Xue, J.K. Direct electron acceleration by chirped laser pulse in a cylindrical plasma channel. Chin. Phys. B 2020, 29, 084103. [Google Scholar]
- Fang, T.; Liang-You, P.; Qi-Huang, G. Ionization of atoms by chirped attosecond pulses. Chin. Phys. B 2009, 18, 4807–4814. [Google Scholar]
- Jie, W.; Zhen, Z.; Xue-Shen, L. Extension of high-order harmonics and generation of an isolated attosecond pulse in the chirped laser field. Chin. Phys. B 2010, 19, 093201. [Google Scholar]
- Wang, H.-L.; Yang, A.-J.; Leng, Y.-X.; Wang, C.; Xu, Z.-Z.; Hou, L.-T. Optical parametric chirped pulse amplification based on photonic crystal fibre. Chin. Phys. B 2011, 20, 084208. [Google Scholar]
- Jisrawi, N.M.; Galow, B.J.; Salamin, Y.I. Simulation of the relativistic electron dynamics and acceleration in a linearly-chirped laser pulse. Laser Part. Beams 2014, 32, 671–680. [Google Scholar]
- Li, J.-X.; Zang, W.-P.; Tian, J.-G. Electron acceleration in vacuum induced by a tightly focused chirped laser pulse. Appl. Phys. Lett. 2010, 96, 031103. [Google Scholar]
- Kumar, S.; Yoon, M. Electron acceleration by a chirped circularly polarized laser pulse in vacuum in the presence of a planar magnetic wiggler. Phys. Scr. 2008, 77, 025404. [Google Scholar]
- Koga, J.; Esirkepov, T.Z.; Bulanov, S.V. Nonlinear Thomson scattering in the strong radiation damping regime. Phys. Plasmas 2005, 12, 093106. [Google Scholar]
- Lee, K.; Chung, S.Y.; Kim, D.E. Relativistic Nonlinear Thomson Scattering: Toward Intense Attosecond Pulse. In Advances in Solid State Lasers Development and Applications; IntechOpen: London, UK, 2010. [Google Scholar]
- Glushkov, A.V. Multiphoton spectroscopy of atoms and nuclei in a laser field: Relativistic energy approach and radiation atomic lines moments method. In Advances in Quantum Chemistry; Academic Press: New York, NY, USA, 2019; Volume 78, pp. 253–285. [Google Scholar]
- Wang, Y.; Yang, Q.; Chang, Y.; Lin, Z.; Tian, Y. Collision off-axis position dependence of relativistic nonlinear Thomson inverse scattering of an excited electron in a tightly focused circular polarized laser pulse. Chin. Phys. B 2023, 33, 013301. [Google Scholar]
- Barton, J.P.; Alexander, D.R.; Barton, J.P.; Alexander, D.R. Fifth-order corrected electromagnetic field components for a fundamental Gaussian beam. J. Appl. Phys. 1989, 66, 2800–2802. [Google Scholar]
- Salamin, Y.I.; Keitel, C.H. Electron acceleration by a tightly focused laser beam. Phys. Rev. Lett. 2002, 88, 095005. [Google Scholar]
- Zhang, S.Y. Accurate correction field of circularly polarized laser and its acceleration effect. J. At. Mol. Sci. 2010, 1, 308–317. [Google Scholar]
- Greiner, W. Classical Electrodynamics. John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Shampine, L.F.; Watts, H.A. Practical Solution of Ordinary Differential Equations by Runge—Kutta Methods [Writing a High-Quality Code Description of RKF45, in FORTRAN for CDC 6600 Computer]; No. SAND-76-0585; Sandia Labs.: Albuquerque, NM, USA, 1976. [Google Scholar]
- Nishidate, Y. A Ray Equation for Optically Anisotropic Inhomogeneous Media and Its Closed-Form Solutions for Estimating Ray-Trajectories. Available online: https://www.researchgate.net/publication/298887528_A_ray_equation_for_optically_anisotropic_inhomogeneous_media_and_its_closed-form_solutions_for_estimating_ray-trajectories (accessed on 13 January 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Xu, J.; Wang, Z.; Zheng, Q.; Yan, J.; Tian, Y. Variation in Electron Radiation Properties Under the Action of Chirped Pulses in Nonlinear Thomson Scattering. Appl. Sci. 2025, 15, 3619. https://doi.org/10.3390/app15073619
Li J, Xu J, Wang Z, Zheng Q, Yan J, Tian Y. Variation in Electron Radiation Properties Under the Action of Chirped Pulses in Nonlinear Thomson Scattering. Applied Sciences. 2025; 15(7):3619. https://doi.org/10.3390/app15073619
Chicago/Turabian StyleLi, Jiachen, Junyuan Xu, Zi Wang, Qianmin Zheng, Juncheng Yan, and Youwei Tian. 2025. "Variation in Electron Radiation Properties Under the Action of Chirped Pulses in Nonlinear Thomson Scattering" Applied Sciences 15, no. 7: 3619. https://doi.org/10.3390/app15073619
APA StyleLi, J., Xu, J., Wang, Z., Zheng, Q., Yan, J., & Tian, Y. (2025). Variation in Electron Radiation Properties Under the Action of Chirped Pulses in Nonlinear Thomson Scattering. Applied Sciences, 15(7), 3619. https://doi.org/10.3390/app15073619





