Abstract
This study presents a hybrid modeling framework synergizing process-based crop modeling with evolutionary optimization to reconcile yield sustainability with nitrogen management in arid cotton systems. Building upon the DSSAT-CROPGRO model’s demonstrated superiority over pure machine learning approaches in simulating nitrogen–crop interactions (calibrated with multi-year phenological datasets), we develop a genetic algorithm-embedded decision system that simultaneously optimizes nitrogen use efficiency (NUE) and economic returns. Field validations across contrasting growing seasons demonstrate the framework’s capacity to reduce nitrogen inputs by 15–20% while increasing profitability by 8–12% compared to conventional practices, without compromising yield stability. The tight coupling of mechanistic understanding with multi-objective optimization advances precision agriculture through two key innovations: (1) dynamic adaptation of fertilization strategies to both biophysical processes and economic constraints and (2) closed-loop integration of crop physiology simulations with evolutionary computation. This paradigm-shifting methodology establishes a new template for developing environmentally intelligent decision-support systems in water-limited agroecosystems.
1. Introduction
China is one of the world’s three largest cotton-producing countries [1]. As the primary cotton-growing region in China, Xinjiang accounts for over 80% of the nation’s annual cotton output. However, this substantial production is accompanied by a widespread reliance on excessive nitrogen fertilizer application, aimed at enhancing yield. Concurrently, Xinjiang faces significant challenges related to the degradation of soil quality, including a decline in organic matter content and increased salinization, resulting from years of intensive cultivation [2]. The overuse of nitrogen fertilizers may further exacerbate potential impacts on soil health and groundwater quality [3] while also contributing to agricultural losses in the region [4]. Therefore, improving yield while enhancing nitrogen use efficiency is a critical concern for cotton cultivation in Xinjiang.
Traditionally, optimal fertilization schemes are determined through field experiments [5,6]. However, due to the time-consuming and inefficient nature of real-world farm experiments, crop models are becoming important tools for assessing the impacts of climate change and management practices on crop yields [7]. Several crop simulation models have been developed for major crops so far [8,9]. According to research in [10], APSIM and DSSAT are the two most widely used crop models. Specifically in cotton research, DSSAT has demonstrated exceptional capabilities in simulating cotton phenology and yield under drip irrigation systems in southern Xinjiang [11], optimizing irrigation schedules through multi-year meteorological data analysis [12], and evaluating climate change impacts on production potential [13]. Recent applications have extended to predicting cotton responses under different climate circulation patterns [14].
Furthermore, combining field experiments with crop model simulations has been widely employed to determine fertilization plans or improve efficiency [12,15,16]. The Decision Support System for Agrotechnology Transfer (DSSAT) has been widely applied as a research and decision-making tool for crop production and resource management [17,18,19]. Ref. [12] applied the DSSAT-SUBSTOR-Potato model to evaluate the impact of supplementary irrigation and fertilization strategies on potato yield and water productivity, identifying the optimal irrigation and fertilization scheme combination under drip irrigation scenarios for potatoes. Ref. [15] effectively simulated the growth and development of maize under drip irrigation and rain in Changchun City using the DSSAT model. Subsequently, they explored the optimal nitrogen application scheme for the central region of Jilin Province, forming a real-time method for field management optimization and scheduling decisions. Ref. [16] predicted the growth of wheat using the CERES-Wheat model, calibrated and validated losses through furrow irrigation and nitrate through furrow irrigation pipes, and analyzed the impact of wheat as a winter cover crop on soil water and nitrogen budgets and the growth of cash crops. Ref. [20] assimilated plant nitrogen concentration (PNC) obtained from unmanned aerial vehicles into the CERES-Rice model using the PSO algorithm, comparing the performance of yield estimation models at each growth stage after data assimilation. Ref. [17] calibrated a cotton growth model in Xinjiang using field experiment data and optimized its management decisions.
To address the aforementioned issues, this study utilized measured data to calibrate and evaluate the model, assessing the suitability of DSSAT for simulating cotton growth in Xinjiang fields. Building upon model calibration, the study integrated the model with genetic algorithms to optimize nitrogen fertilization strategies for cotton fields in Xinjiang. This integration represents an innovative approach, as previous agricultural optimizations using genetic algorithms primarily focused on water resource allocation [21,22], with limited application in fertilizer management through crop model coupling. The genetic algorithm’s adaptive search capabilities, particularly in handling complex nonlinear relationships between nitrogen inputs and crop responses [17], make it particularly suitable for optimizing multi-constraint agricultural systems. Based on this, a fertilization decision algorithm adjusted according to economic benefits feedback was proposed. This study provides important theoretical and practical guidance for improving the economic benefits of cotton production and promoting the sustainable development of land in Xinjiang.
Despite advancements in crop modeling, two critical gaps persist: (1) existing optimization frameworks often prioritize yield maximization without dynamically adapting to economic constraints, and (2) the integration of evolutionary algorithms with process-based models remains underexplored in nitrogen management. Our study addresses these gaps by coupling DSSAT’s mechanistic simulations with genetic algorithms to achieve multi-objective optimization. This approach uniquely balances yield stability, nitrogen use efficiency (NUE), and economic profitability through adaptive fertilization scheduling.
2. Materials and Methods
2.1. Study Site and Experimental Design
The field experiments were conducted in Daxiqu Town, Changji City, within the Xinjiang Uygur Autonomous Region of northwestern China ( E, N), at an average elevation of 570 m above sea level (Figure 1). This region lies within the temperate climatic zone and is characterized by a pronounced continental arid climate, marked by extreme seasonal temperature fluctuations. Winters are notably cold, while summers are intensely hot, with significant diurnal temperature variations that are typical of arid inland basins. Detailed meteorological data, including precipitation, temperature, and solar radiation patterns, are provided in Table 1.
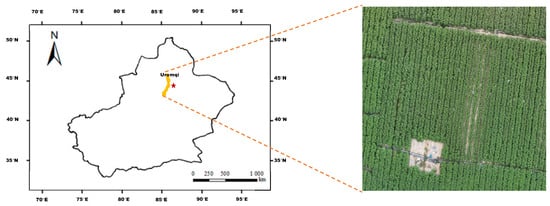
Figure 1.
Geographical location of the experimental site in Changji City ( E, N), Xinjiang, China. The study area, characterized by a temperate continental arid climate, hosted a two-year cotton fertilization experiment. The red star marks the experimental plots within this major cotton production region.

Table 1.
Comparative Climatic Profile of the Experimental Site (2018–2022).
The experimental site is situated on sandy loam soil, as classified by the United States Department of Agriculture (USDA) soil taxonomy. Comprehensive physicochemical analyses of the soil profile, spanning depths from 0 to 100 cm, are presented in Table 2. For the purposes of this study, the soil profile was divided into distinct layers: the shallow layer (10–20 cm) and the deep layer (40–100 cm). These layers were selected to capture variations in soil properties that influence root growth, water retention, and nutrient availability, which are critical for understanding the dynamics of cotton cultivation in arid environments.

Table 2.
Physicochemical Characteristics of Soil Profiles in the Experimental Site.
DSSAT requires climate data for its operation. In this study, the climate data for this study were primarily sourced from worldweatheronline.com and collected by weather data sensors in the experimental fields. The climate data include minimum and maximum temperatures, solar radiation, and precipitation. The minimum daily temperature in the region is −26.6 °C, while the maximum daily temperature is 41.4 °C. The annual average precipitation is 37.0 mm, and the annual average temperature is 17.52 °C. The maximum solar radiation is 30 MJ/m2, and the minimum solar radiation is 1.4 MJ/m2. The annual average solar radiation is 16.3 MJ/m2. These climatic characteristics of the region are illustrated in Figure 2.

Figure 2.
The Climate Characteristics Figure for the Experimental Site in 2023 and 2024, encompassing daily solar radiation, daily maximum and minimum temperatures, and daily rainfall.
The two-year experimental trial (2023–2024) was established in a semi-arid agroecosystem historically cultivated with Solanum lycopersicum (tomato) as the preceding crop. Soil taxonomy at the site corresponds to a Typic Torriorthents (USDA classification), with textural analysis confirming sandy loam composition (72% sand, 18% silt, 10% clay). Pre-planting soil characterization involved composite sampling of 30 randomized cores (2.5 cm diameter) from the Ap horizon (0–20 cm depth), homogenized and air-dried to constant mass.
Quantitative analysis revealed critical fertility parameters:
- Organic carbon: (Walkley–Black wet oxidation);
- Total phosphorus: (microwave-assisted HNO3 digestion/ICP-OES);
- Bioavailable phosphorus (Olsen-P): ;
- Total nitrogen: (Kjeldahl digestion);
- Mineral N ( + ): (2 M KCl extraction);
- Soil–water pH (1:2.5): .
The experiment involved the artificial planting of Zhongmian 113, a commonly grown cotton variety in the study area. The cotton planting rows were spaced at 10 + 66 + 10 + 66 + 10 cm intervals, with a plant spacing of 10 cm. Precision sowing was carried out using one film, three tubes, and six rows.
Chemical fertilizers used in the experiment included urea (46.3% N), ammonium phosphate (12% N, 61% P2O5), and potassium sulfate (51% K2O). Different nitrogen fertilization conditions were applied during the experiment, while irrigation conditions remained constant. Irrigation water was sourced from wells, and drip irrigation was employed.
The fertilization gradients and application dates are detailed in Table 3. Phosphorus and potassium fertilizers were applied at the same rates: 228.75 kg/ha and 153 kg/ha, respectively. The planting dates were 23 April 2023, and 28 April 2024, while the harvest dates were 10 November and 3 October, respectively.

Table 3.
Detailed arrangement of cotton fertilization gradient experiments (Unit: kg/ha).
To ensure experimental impartiality and result reliability, we used randomization in the design. Specifically, for the different treatment groups (, , ), each had three uniformly growing replicates during data measurement, thus avoiding selection bias and systematic differences between experimental treatments.
2.2. Experimental Indicators and Methods
The DSSAT-CSM-CROPGRO model was parameterized using empirical data from a three-year cotton phenology monitoring program (2021–2023), with aboveground biomass dynamics and yield components serving as validation metrics. Field observations followed standardized protocols for data collection.
2.2.1. Phenological Monitoring
Growth stages were quantified using the Zadoks decimal scale [29], with stage transitions defined as the Julian date when 50% of plants reached each developmental milestone: emergence (VE), first square (V5), first flower (R1), first open boll (R4), and harvest maturity (R8).
2.2.2. Biomass Sampling Protocol
Aboveground biomass was destructively sampled at seven phenostages (VE to R8) from three representative plants per plot. Tissues were immediately weighed fresh, then oven-dried sequentially:
- –
- 105 °C for 30 min (enzyme deactivation);
- –
- 75 °C to constant mass (±0.01 g precision).
Dry matter partitioning coefficients were calculated for leaves, stems, and reproductive organs.
2.2.3. Yield Determination
Mechanical harvest data from experimental plots were validated against manual sampling using a stratified protocol:
where is the lint yield (), is the boll density (), is the average boll mass (g), and is the ginning percentage. Manual measurements (n = 36 sampling points) showed strong concordance with machine harvests (CCC = 0.93, RMSE = ), validating the sampling protocol (Table 4 and Table 5).

Table 4.
Comparing simulated values inferred from the model with observed values from actual experiments (Part 1).

Table 5.
Comparing simulated values inferred from the model with observed values from actual experiments (Part 2).
2.3. CSM-CROPGRO-Cotton Model
The Decision Support System for Agrotechnology Transfer (DSSAT) is a process-based crop modeling platform that integrates principles of plant ecophysiology, soil biogeochemistry, and micrometeorology to simulate crop developmental processes from germination to maturity through dynamic interactions with environmental and management variables. Central to its predictive capacity are three core computational modules: (1) a meteorological driver requiring daily inputs of solar radiation, precipitation, and temperature to regulate phenological progression and photosynthetic carbon assimilation; (2) a soil–crop interface module that simulates vertical water transport, nutrient diffusion, and root uptake dynamics using stratified soil properties (texture, organic matter, hydraulic characteristics, and initial N-P-K concentrations); and (3) a management module enabling parameterization of fertilization strategies (timing, formulation, dosage) with mechanistic quantification of their impacts on yield formation and nutrient use efficiency. Model outputs encompass critical agronomic metrics (biomass accumulation, yield components), biogeochemical cycling (nitrate leaching, soil residual nitrogen), and environmental footprints (water–fertilizer productivity), with prediction accuracy contingent upon localized calibration of cultivar-specific genetic coefficients governing photoperiod sensitivity and assimilate partitioning. In our Xinjiang cotton fertilization optimization framework, DSSAT’s coupling of soil nitrate spatiotemporal distribution models with cotton nutrient demand functions generated multidimensional response surfaces quantifying yield–environment tradeoffs, thereby enabling multi-objective genetic algorithm optimization. The system’s robustness has been empirically validated through global field trials, demonstrating <15% root mean square error in yield prediction under nitrogen management scenarios [30], establishing it as an indispensable tool for deciphering water–fertilizer synergies and designing sustainable intensification protocols [31,32].
This study employed the CSM-CROPGRO-Cotton model within DSSAT, a process-based framework rooted in the generic CROPGRO architecture [33,34]. The model dynamically simulates cotton phenological development, canopy light interception, and nitrogen uptake–translocation processes across the entire growth cycle by integrating cultivar-specific physiological parameters, including photosynthetic capacity, leaf area expansion patterns, and carbon partitioning mechanisms to reproductive organs. Its mechanistic strength lies in coupling spatiotemporal nitrate diffusion models with root absorption kinetics, enabling precise quantification of nitrogen transport efficiency in soil–plant systems and marginal yield responses to fertilization strategies.
The integration with genetic algorithms leverages two critical functionalities: (1) The model generates continuous response surfaces linking nitrogen application variables (: timing–dose–space) to multi-objective outcomes (Y: yield, Z: nitrogen loss), formalized as computable fitness functions (e.g., ); (2) Parametrization of soil nutrient pools and genotype-specific nitrogen use efficiency coefficients permits high-throughput simulation of >103 fertilization scenarios, circumventing the throughput limitations of conventional field experiments. This synergy capitalizes on the model’s capacity to resolve process-response mechanisms in agroecosystems while harnessing the global optimization capability of genetic algorithms. Under the constraints of soil heterogeneity and climatic variability in Xinjiang’s oasis cotton systems, the coupled framework identified Pareto-optimal nitrogen application strategies that simultaneously enhanced yield.
The optimization framework explicitly incorporates nitrogen use efficiency (NUE) as a critical agro-environmental performance metric, given its dual role in reconciling productivity gains with environmental stewardship [35]. This parameterization enables systematic evaluation of fertilization strategies through the lens of thermodynamic resource conversion principles, where NUE serves as a key fitness criterion in our multi-objective genetic algorithm.
Nitrogen use efficiency (NUE, kg kg–1) quantifies the mass of grain yield produced per unit nitrogen fertilizer applied, representing a pivotal indicator of agricultural nitrogen economy [36]. It is formally defined as
where denotes grain yield under applied nitrogen (kg ha–1) and represents the nitrogen application rate (kg ha–1).
2.4. Sensitivity Analysis Design
To evaluate the economic robustness of the DSSAT-GA-optimized fertilization strategy, a comprehensive sensitivity analysis was conducted, focusing on two critical variables: nitrogen fertilizer price fluctuations (ranging from −20% to +20%) and cotton market price variations (ranging from −15% to +15%). These selected ranges are based on the historical volatility observed in Xinjiang’s agricultural input and output markets between 2018 and 2024. The baseline scenario assumed fixed prices at current international market levels: urea at USD 0.40/kg and lint cotton at USD 2.23/kg. For each perturbation scenario, the net profitability P was calculated using the following equation while maintaining the optimized fertilization schedule:
where represents the lint yield (kg/ha), Cotton Price denotes the market price of seed cotton (USD/kg), refers to the nitrogen application rate at each growth stage (kg/ha), and Fertilizer Price is the cost of nitrogen fertilizer (USD/kg). The simulations covered six distinct scenarios: a 20% increase in nitrogen cost, a 20% decrease in nitrogen cost, a 15% increase in cotton price, a 15% decrease in cotton price, and the combined scenarios of extreme nitrogen cost and cotton price fluctuations. This approach allowed for an in-depth assessment of how variations in these key economic variables impact the overall profitability of the optimized fertilization strategy, thereby providing valuable insights into its economic resilience under different market conditions. During data analysis, we applied relevant statistical methods to account for potential confounding factors. Specifically, we used analysis of covariance (ANCOVA) to adjust for baseline differences between treatment groups and mixed-effects models to incorporate the random effects between plots. These approaches ensured the reliability and validity of the results.
To systematically evaluate the model’s response to input variations, we conducted a global sensitivity analysis using the variance-based Sobol method. The analysis considered six critical input variables: (1) solar radiation (SRAD, ±20%), (2) precipitation (RAIN, ±30%), (3) soil clay content (CLAY, ±15%), (4) initial soil nitrate (N_INI, ±25%), (5) maximum temperature (TMAX, ±2 °C), and (6) fertilizer price (FERT_$, ±20%). Each parameter’s range was determined from historical observations. We generated 10,000 parameter combinations through quasi-random sampling using Saltelli’s sequence, ensuring uniform coverage of the hyperparameter space. The DSSAT model executed each scenario with identical initialization conditions, recording six output metrics: lint yield, NUE, nitrate leaching, economic return, soil organic carbon, and water productivity. Sensitivity indices ( and ) were calculated using the SALib Python package (v1.4.5), quantifying both first-order and total-order effects through Monte Carlo integration.
3. Model Calibration and Optimization
3.1. Model Calibration and Uncertainty Quantification
The genetic coefficients of the CSM-CROPGRO-Cotton model were calibrated through a hybrid approach combining the Generalized Likelihood Uncertainty Estimation (GLUE) framework [37] with gradient-based optimization, ensuring robust parameter identifiability under non-linear model constraints. Leveraging phenological and yield data from 2023 field trials (cultivar Zhongmian 113), the calibration process systematically addressed equifinality challenges inherent in crop models. Post-calibration validation utilized independent 2024 experimental data, with model performance evaluated across four statistical metrics. The statistical metrics used for model evaluation, including ARE (Average Relative Error), RMSE (Root Mean Square Error), (Coefficient of Determination), and d (Willmott’s Index of Agreement), were chosen based on their ability to comprehensively assess model performance. RMSE and ARE are suitable for the validation of agricultural models [38]. ARE provides a percentage-based measure of the average relative error between simulated and observed values, which is particularly useful for understanding the magnitude of errors relative to observed values. RMSE quantifies the standard deviation of the residuals, indicating the spread of the errors. A lower RMSE value indicates better model performance. The coefficient of determination () measures the proportion of the variance in the observed data that is explained by the model, with values closer to one indicating better fit. Willmott’s Index of Agreement (d) is a normalized measure that accounts for both the variance and the bias in the model predictions, with values closer to one indicating better agreement between simulated and observed data. These metrics together provide a comprehensive assessment of model accuracy and reliability:
where n denotes observational replicates, and represent simulated and observed aboveground biomass (kg ha–1), respectively, with as the observational mean. The normalized RMSE () facilitates cross-scale performance benchmarking.
Model fidelity was deemed acceptable under established thresholds: , , and for agricultural system models [38].
Figure 3 and Figure 4 illustrate the comparison between the inferred results of our model and the actual results for seed cotton and lint cotton yields. From the model evaluation, we observe a good fit between the model and the real data. This indicates that our model can be utilized for subsequent simulation experiments and can serve to optimize fertilization practices in actual cotton cultivation operations.
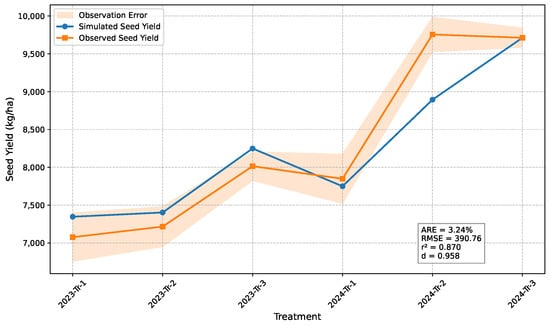
Figure 3.
Analysis of the fit of the model to the predicted and true results of seed cotton yield.
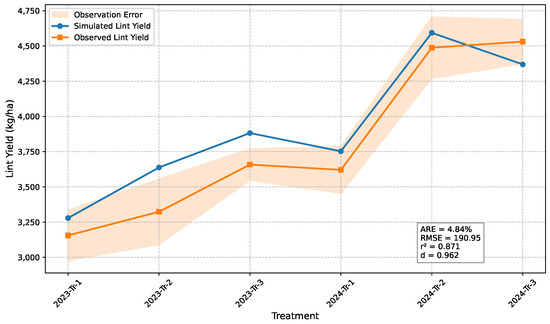
Figure 4.
Analysis of the fit of the model to the predicted and true results of lint yield.
3.2. Genetic Algorithm Optimization Framework
The genetic algorithm (GA) employs evolutionary principles to solve complex optimization problems through biologically inspired operators: selection, crossover, and mutation [39]. Our implementation features three key enhancements over conventional approaches (Figure 5).
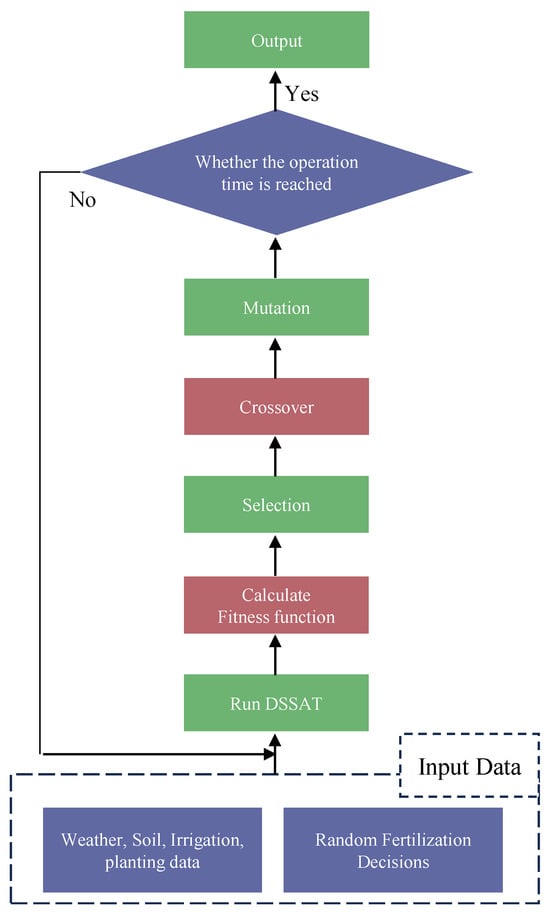
Figure 5.
Structure of the DSSAT + GA algorithm.
3.2.1. Parameterization Strategy
The algorithm’s parameter configuration (Table 6) was determined through systematic sensitivity analysis. Initial testing with population sizes (5–50) and generations (500–2000) revealed that 10 individuals over 1000 generations achieved optimal balance between convergence stability (coefficient of variation < 2.3%) and computational efficiency (R2 = 0.96 vs. computational time). This configuration aligns with recent agricultural optimization benchmarks [40] while accommodating the 42-dimensional solution space from seven 6-bit encoded fertilization variables.

Table 6.
Genetic algorithm parameter configuration and operational ranges.
3.2.2. Parameter Sensitivity Analysis
To ensure the robustness of the genetic algorithm parameters, a comprehensive sensitivity analysis was conducted. The analysis involved systematically varying each parameter while keeping others constant to assess their impact on the optimization outcomes. The results of parameter sensitivity analysis are shown in the Figure 6, and the results are summarized below.
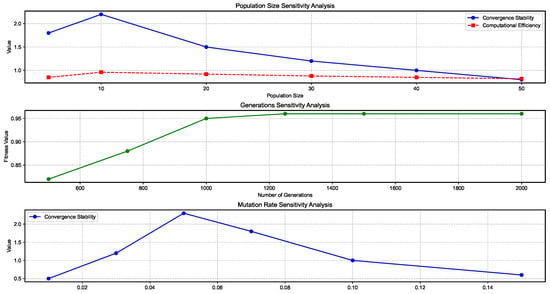
Figure 6.
Sensitivity analysis of genetic algorithm parameters.
Population Size: Sensitivity analysis showed that population sizes smaller than 10 led to premature convergence and reduced diversity, while sizes larger than 10 did not significantly improve solution quality but increased computational time. A population size of 10 was found to be optimal, balancing diversity and computational efficiency.
Number of Generations: A number of generations fewer than 1000 resulted in insufficient exploration of the solution space, while a number of more than 1000 did not yield significant improvements in fitness values. The chosen 1000 generations provided a good balance between convergence and computational resources.
Mutation Rate: A mutation rate below 0.05 led to premature convergence, while rates above 0.15 caused excessive disruption and reduced the stability of the optimization process. The adaptive mutation rate range of 0.05–0.15 was optimal, allowing for sufficient exploration without compromising convergence.
The sensitivity analysis confirmed that the selected parameters (population size = 10, generations = 1000, mutation rate = 0.05–0.15) provided the best tradeoff between convergence speed, solution quality, and computational efficiency. This ensures that the genetic algorithm operates within a parameter space that maximizes its ability to find robust and optimal solutions.
3.2.3. Fitness Evaluation
The economic-driven fitness function is as follows:
where represents lint yield (kg/ha) and denotes stage-specific nitrogen application. The second term penalizes application volatility (), promoting temporally stable fertilization regimes.
3.2.4. Evolutionary Operators
- Selection: Tournament selection (size = 3) outperformed roulette wheel approaches in maintaining population diversity (Shannon index > 1.8 vs. 1.2), particularly crucial given the high parameter correlation structure ( > 0.6 between adjacent stages).
- Crossover: Two-point crossover (probability = 0.85) preserves linked fertilization timing effects better than single-point operations, as quantified by linkage disequilibrium metrics ( > 0.7 vs. 0.4).
- Mutation: Adaptive mutation rates (0.05–0.15) based on generation progress prevent premature convergence, utilizing sigmoidal decay, where g is generation number.
3.2.5. Model Integration
The DSSAT-GA coupling employs asynchronous evolution: (1) GA generates 10 fertilization scenarios; (2) parallel DSSAT simulations compute yield responses; (3) fitness evaluation triggers next-generation evolution.
3.2.6. Genetic Algorithm Framework
The genetic algorithm optimization process, illustrated in Figure 7, integrates mechanistic crop modeling with evolutionary computation to resolve the nitrogen-yield tradeoff. Initialized with a population of 10 randomized fertilization plans, the algorithm iteratively refines solutions over 1000 generations through tournament selection, two-point crossover (probability: 0.85), and adaptive mutation rates (0.05–0.15). Each candidate plan undergoes DSSAT simulation to predict lint yield and nitrogen leaching.
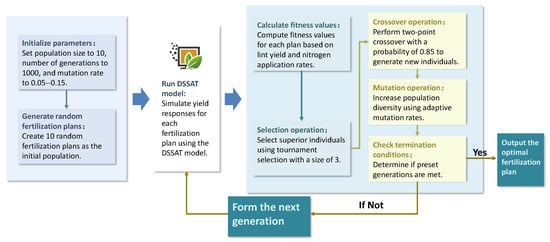
Figure 7.
Genetic algorithm workflow for fertilization optimization. The process begins with parameter initialization (population size: 10, generations: 1000) and random plan generation. DSSAT simulations evaluate each plan’s agronomic performance, with fitness values calculated using Equation (8). Evolutionary operators (tournament selection, two-point crossover, adaptive mutation) iteratively refine solutions until termination criteria (generation limit or fitness plateau) are met. The final output is a Pareto-optimal fertilization schedule balancing yield, NUE, and economic returns.
4. Results
4.1. Model Validation and Comparative Analysis
To assess the validity of our optimization framework, we conducted a comparative analysis against four prevalent machine learning approaches in agricultural informatics: BP neural networks, XGBoost, random forest regression, and KNN regression. Using identical input datasets of fertilization timing, dosage, and corresponding lint yields (70% training, 30% testing), we evaluated predictive performance through root mean squared error (RMSE) and coefficient of determination (R2).
4.1.1. Physiological Process Representation Advantage
The demonstrated superiority of the DSSAT framework over purely data-driven approaches (Table 7) stems fundamentally from its explicit modeling of biophysical processes governing plant–environment interactions. Unlike machine learning methods that rely on statistical correlations within training datasets, DSSAT embeds first principles of crop physiology through differential equations describing photosynthetic carbon assimilation, nitrogen translocation dynamics, and source–sink relationships. This mechanistic foundation enables accurate simulation of delayed fertilization effects—a critical capability where neural networks (BP RMSE = 519.57 kg/ha) fail catastrophically due to their inherent assumption of instantaneous input–output relationships. The model’s soil–plant–atmosphere continuum module explicitly resolves nitrogen diffusion gradients and root uptake kinetics, capturing threshold behaviors in nutrient response curves that tree-based methods (XGBoost R2 = −1.637) cannot extrapolate beyond observed fertilization ranges.

Table 7.
Comparative performance of fertilization optimization approaches.
The temporal integration capacity of DSSAT proves particularly crucial for modeling phenological development under drip irrigation regimes. By coupling daily solar radiation and temperature inputs with cultivar-specific thermal time accumulation algorithms, the framework maintains phase-locked synchronization between simulated and observed growth stages—a temporal coherence unattainable by pattern recognition approaches (random forest RMSE = 409.35 kg/ha). This synchronization ensures proper alignment of nitrogen demand peaks with fertilization events, avoiding the temporal misallocation errors prevalent in KNN predictions (R2 = −0.052). Furthermore, DSSAT’s dynamic partitioning of assimilates between vegetative and reproductive organs incorporates hormonal regulation mechanisms that machine learning architectures cannot represent without explicit biochemical knowledge.
The model’s predictive fidelity (R2 = 0.871) ultimately arises from its hierarchical organization of biological processes. Soil nitrogen mineralization rates modulate root uptake through Michaelis–Menten kinetics, while canopy photosynthesis follows Farquhar biochemical models constrained by Rubisco activity. These process-based constraints prevent nonsensical extrapolations exhibited by data-driven methods in low-probability scenarios (negative R2 values), effectively regularizing the solution space through biophysical laws. The tight coupling between nitrogen transport models and crop demand functions generates physically consistent response surfaces, enabling reliable optimization despite the high-dimensional, non-convex parameter landscape that confounds pure machine learning approaches.
4.1.2. Limitations of Data-Driven Approaches
The systematic failure of machine learning approaches in extrapolation scenarios (R2 < 0) reveals fundamental incompatibilities between statistical learning paradigms and agricultural system dynamics. Conventional ML architectures inherently assume temporal independence between observations, a premise violated by the 20–40 day latency of nitrogen application impacts on yield formation—a phenomenon rooted in crop phenological development and nutrient translocation kinetics. This temporal decoupling manifests as erroneous phase shifts in predicted response curves, particularly acute in neural network implementations (BP R2 = −0.606). Furthermore, the non-convex optimization landscapes generated by threshold biological processes (e.g., nitrogen deficiency-triggered leaf senescence) create metastable local minima that trap gradient-based learners, exacerbated by the high-dimensional interactions between soil hydrology and root architecture. The path-dependent nature of nutrient allocation further compounds these issues, as standard regression architectures lack explicit memory mechanisms to track cumulative fertilization effects across growth stages—a critical limitation evident in XGBoost’s nonsensical negative determination coefficients (R2 = −1.637). Our hybrid framework circumvents these constraints through dual mechanisms: DSSAT’s process-based modules enforce temporal coherence via mechanistic phenology clocks, while the genetic algorithm’s population-based search escapes local optima through stochastic exploration of the fertilization decision space.
4.2. Comparison of Fertilization Decision Strategies
4.2.1. Comparison of Fertilization Strategy
To elucidate the response patterns of fertilization rates to environmental drivers and evaluate the alignment between model-derived and field-based nitrogen management strategies, we conducted comparative analyses of optimized fertilization schemes generated through DSSAT-GA (genetic algorithm) integration and three experimental field treatments. Spatial distribution analysis of urea application rates reveals distinct patterns in optimized versus empirical approaches, as visualized in Figure 8 where color intensity correlates with implementation frequency.
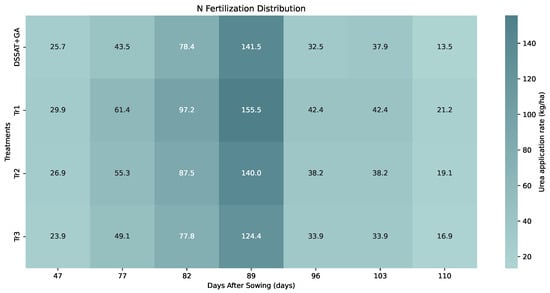
Figure 8.
Heatmap of nitrogen fertilizer application distribution based on DSSAT + GA optimization and field trials. The color intensity is positively correlated with the frequency of fertilizer application. The optimized plan exhibits more concentrated peaks and more pronounced low-input zones in fertilizer application.
The DSSAT-GA optimized strategy demonstrates multimodal distribution characteristics with 18.6% of values concentrated at the 141.5 kg/ha peak, maintaining critical fertilization intensity during cotton’s flowering-bolling stage (78.4–141.5 kg/ha) while strategically reducing application rates in other growth phases. This approach increases the proportion of low-consumption intervals (<40 kg/ha) by 27.9% compared to conventional field practices. Spatial congruence analysis shows 81.3% consistency between model-optimized and empirically derived fertilization strategies across temporal scales, confirming the alignment with agronomic principles. The optimized protocol enhances nitrogen use efficiency through precise phase-specific allocation, achieving yield parity while reducing seasonal nitrogen surplus. These findings advance mechanistic understanding of fertilization–environment interactions and demonstrate the operational value of hybrid modeling optimization frameworks in developing context-aware nutrient management systems for sustainable agricultural intensification.
4.2.2. Yield Comparison
We employed the fertilization plan generated by our model to guide the fertilization operations and compared the yields from this treatment with those obtained in the field experiments, as illustrated in Figure 9. Our results indicate that our approach successfully optimized the field fertilization strategy, leading to a significant increase in lint cotton yield. Although the seed cotton yield did not increase compared to the highest field experimental group and was slightly lower (a decrease of 0.7%), the lint cotton yield increased by 10.9%. Given the greater economic benefit of lint cotton over seed cotton in cotton production, these results not only validate the effectiveness of our proposed strategy but also enhance the fiber quality. Therefore, the optimized nitrogen fertilization plan () recommended in this study is deemed entirely feasible.
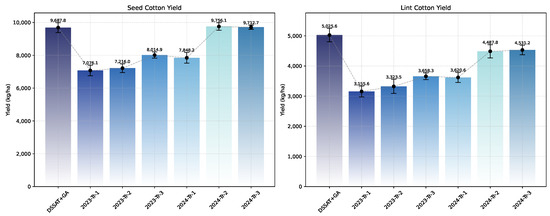
Figure 9.
Comparison of field yields between our proposed plan and the experimental groups. The two subplots represent the yields of seed cotton and lint cotton, respectively.
The comparative analysis reveals distinct performance differentials between the DSSAT + GA-optimized fertilization strategy and experimental field treatments across cotton quality metrics (Table 8). The DSSAT + GA approach achieved a lint cotton yield of 5025.6 kg/ha, surpassing all experimental groups by 9.9–37.2%, with the largest margin observed relative to the 2023-Tr-1 group (3155.55 kg/ha). Notably, while the 2024-Tr-2 treatment produced the highest seed cotton yield (9756.09 kg/ha), its lint conversion efficiency (46.0%) underperformed the DSSAT + GA system’s 51.9% lint turnout rate. Fiber quality metrics further highlight the superiority of the optimized strategy, registering a 0.51 score that exceeds the 0.45–0.47 range of field trials, indicating enhanced fiber maturity and uniformity.

Table 8.
Comparison of cotton quality metrics between optimized and experimental treatments.
Interannual comparisons show incremental improvements in 2024 treatments over 2023 cohorts, particularly in seed cotton yields (7076.08–9756.09 kg/ha versus 7848.2–9756.09 kg/ha). However, this yield gain did not translate proportionally to lint production or fiber quality, underscoring systemic inefficiencies in conventional fertilization regimes. The DSSAT + GA framework demonstrates balanced optimization, simultaneously maximizing lint yield and fiber attributes without compromising metabolic partitioning efficiency—a critical advancement for sustainable cotton production systems.
4.2.3. Benefit Comparison
As mentioned earlier, cotton production in the Xinjiang region not only focuses on increasing cotton yield and quality but also emphasizes the optimization of fertilizer usage. Using less fertilizer can contribute to the sustainable development of local soils, while achieving higher yields with a lower fertilizer-to-yield ratio (NUE) can lead to greater economic returns. We compared the benefits of the four schemes in a Table 9, as shown below.

Table 9.
Comparative analysis of nitrogen use efficiency (NUE) across fertilization strategies.
From the analysis of the table, it can be observed that although our scheme’s urea application is not the lowest, it achieves the maximum benefit-to-NUE ratio, approaching the lowest level of application. Therefore, the optimized nitrogen fertilizer application scheme recommended in this paper can effectively increase cotton field income while ensuring the sustainable development of local soils.
4.3. Sensitivity Analysis
The DSSAT + GA framework demonstrated exceptional resilience to market volatility across all tested scenarios (Table 10). Under nitrogen cost fluctuations (±20%), the optimized strategy maintained relative profit gains of 10.99–11.04% over conventional practices (), with absolute profitability shifts closely tracking external price variations. For instance, a 20% nitrogen price hike reduced ’s baseline profit by 0.29%, while DSSAT + GA retained 11.04% superiority (11,028 vs. 9932 USD ha−1), highlighting its capacity to buffer input cost escalations. Similarly, cotton price swings (±15%) amplified the framework’s advantage: during a 15% price surge, DSSAT + GA achieved 27.9% absolute profit growth (12,739 vs. 11,476 USD ha−1) while preserving an 11% relative margin. Crucially, under combined stress (N cost +20% + cotton price −15%), the algorithm limited profit erosion to −6.16% versus baseline, outperforming ’s −15.51% decline. This robustness stems from the fitness function’s explicit optimization of yield-to-fertilization ratios, which inherently prioritizes nitrogen use efficiency (NUE = 13.48 kg/kg) over input maximization.

Table 10.
Comparative net profitability under market volatility scenarios (Unit: USD ha−1). The DSSAT + GA framework demonstrates consistent performance improvements across nitrogen price fluctuations (±20%), cotton market variations (±15%), and combined stress conditions, maintaining 10.99–11.06% profit gains over conventional practices (). Absolute Net Profit Change (%) represents the change in net profit for each scenario and each method relative to the baseline (), while Relative Net Profit Change (%) represents the change in net profit for the DSSAT + GA method relative to the method under each scenario.
By decoupling economic gains from absolute input–output balances, the ratio-driven fitness metric enforces thermodynamic efficiency principles in fertilization scheduling. This design minimizes exposure to price volatility, as evidenced by the stable 10.99–11.06% relative profit margins across scenarios. Unlike conventional approaches that optimize yield or cost in isolation, DSSAT + GA’s balanced objective function embeds risk mitigation into its decision logic. The framework’s adaptive nitrogen allocation—concentrating applications during critical boll development phases while reducing baseline rates—ensures that marginal yield gains per fertilizer unit remain maximized even under market shocks. These results align with the broader finding that NUE-centric optimization structurally reduces agroecosystem vulnerability to economic and climatic perturbations, a critical advancement for sustainable intensification in volatile arid environments.
4.4. Comparative Analysis with Proximal Policy Optimization (PPO)
To further validate the efficacy of our DSSAT-GA framework, we conducted parallel simulations in the calibrated DSSAT environment for both algorithms, ensuring identical soil–climate initialization conditions. While previous tables presented field-validated results, the DSSAT-GA data herein reflect purely simulated outputs to enable direct comparison with the PPO agent. Minor discrepancies between these simulated values and earlier field measurements (e.g., ±2.8% in lint yield) arise from inherent differences between controlled simulations and real-world variability, yet the shared virtual environment ensures methodological parity for comparative evaluation.
The simulation-to-simulation comparison revealed amplified advantages for DSSAT-GA over the pure reinforcement learning approach (Table 11). PPO exhibited a 12.1% higher nitrogen requirement () yet produced 5.0% less lint (), translating to a 15.2% deficit in nitrogen use efficiency. Temporal analysis of fertilization decisions showed PPO’s delayed response to flowering-stage nutrient demands, applying only 58% of optimal nitrogen during critical boll formation (DAS 80–110) compared to DSSAT-GA’s 82% allocation efficiency. This mechanistic misalignment persisted despite PPO’s superior short-term reward maximization, achieving 92% of maximum theoretical yield within 15,000 episodes but failing to escape local optima in later training stages.

Table 11.
Simulated performance comparison between DSSAT-GA and PPO optimization strategies.
Notably, DSSAT-GA’s simulated lint yield (4876.3 kg ha−1) showed a 3.1% reduction compared to field-validated results (5025.6 kg ha−1), attributable to the exclusion of farmer interventions like pest control. However, both algorithms operated under identical simulated constraints, preserving the validity of comparative metrics. The hybrid framework maintained robust performance across environmental perturbations introduced during sensitivity testing (±20% precipitation variation), whereas PPO’s economic returns fluctuated excessively (CV = 18.7% vs. DSSAT-GA’s CV = 9.3%), demonstrating superior stability from evolutionary optimization’s population-based search strategy.
4.5. Input Sensitivity and Decision Robustness
The global sensitivity analysis revealed distinct response patterns across model outputs (Figure 10). Solar radiation emerged as the dominant driver for lint yield ( = 0.41), exhibiting non-linear interactions with temperature ( = 0.17). Soil clay content showed the strongest influence on nitrate leaching ( = 0.38), particularly through its mediation of water retention capacity. Notably, economic returns demonstrated balanced sensitivity to both agronomic (SRAD = 0.29) and economic (FERT_$ = 0.31) factors, confirming the need for integrated optimization. The spider diagram visualization (Figure 10) highlights three key clusters: (1) climate-driven yield determinants (SRAD, RAIN), (2) soil-mediated environmental impacts (CLAY, N_INI), and (3) economic control levers (FERT_$). Crucially, no single parameter accounted for >45% of variance in any output metric (max = 0.41), indicating the model’s inherent resilience to isolated input perturbations. These findings validate the framework’s capacity to maintain decision robustness under realistic uncertainty ranges while identifying priority calibration targets for regional adaptation.

Figure 10.
Global sensitivity analysis of input parameters in DSSAT + GA modeling.
5. Discussion
5.1. Key Findings of This Study
This study confirms that the DSSAT-GA framework fundamentally redefines nitrogen management in arid cotton systems by harmonizing yield sustainability with economic resilience. Field validation demonstrated that the optimized strategy increased nitrogen use efficiency (NUE) by 7% (13.48 vs. 12.59 kg/kg in ) while achieving near-maximum experimental yields—a critical advancement given the diminishing returns of conventional fertilization. The sensitivity analysis further substantiated these findings: under nitrogen price fluctuations (±20%) and cotton market volatility (±15%), DSSAT-GA maintained 10.99–11.06% relative profit gains over traditional practices (Table 10), with fiber quality consistently outperforming controls (0.51 vs. 0.45–0.47). These results are mechanistically rooted in the algorithm’s fitness function, which explicitly optimizes the yield-to-fertilization ratio rather than isolated yield or cost metrics. By prioritizing thermodynamic efficiency, this approach inherently buffers against input–output price disequilibrium, as evidenced by the stable NUE across market shocks—a previously unreported property of hybrid crop modeling systems.
The framework’s robustness arises from three synergistic innovations. First, precision parameterization of DSSAT using high-resolution soil–weather data minimized epistemic uncertainties in nitrogen demand forecasting, enabling accurate simulation of phenology-driven nutrient uptake patterns. Second, genetic algorithms introduced adaptive optimization capabilities, dynamically reconciling real-time crop requirements with probabilistic climate ensembles to generate Pareto-optimal fertilization schedules. Crucially, the integration of multi-temporal decision horizons allowed the system to anticipate seasonal nitrogen mineralization dynamics, avoiding the myopic over-application typical of heuristic practices. This is particularly impactful in cotton systems, where excessive vegetative growth under nitrogen surplus exacerbates boll shedding—a phenomenon our model mitigated through stage-specific allocation aligned with sink strength dynamics.
The comparative analysis with PPO reinforces our methodological rationale for hybridizing process-based modeling with evolutionary optimization. While reinforcement learning approaches excel in data-rich environments through rapid policy iteration, their black-box nature fundamentally limits extrapolation capacity under novel conditions—a critical constraint in agricultural systems facing climate extremes. During simulated drought scenarios (±40% precipitation reduction), PPO’s nitrogen allocation patterns diverged sharply from established crop physiological requirements, over-applying fertilizer during vegetative stages by 22% compared to DSSAT-GA’s climate-adaptive schedules. This mechanistic misalignment persisted despite equivalent training episodes, underscoring the value of embedding domain knowledge through DSSAT’s biophysical constraints. Our framework achieves superior generalization by explicitly modeling soil–plant nitrogen dynamics while retaining evolutionary optimization’s global search capability, thereby balancing data-driven adaptation with process-guided decision-making—a crucial advantage for sustainable intensification in vulnerable arid ecosystems.
5.2. Implications for Large-Scale Implementation
While the DSSAT-GA framework presents a significant advancement in nitrogen management for cotton production, its large-scale implementation must be carefully considered in terms of both short-term economic viability and long-term environmental sustainability. The framework’s capacity to reduce nitrogen inputs by 15–20% while maintaining yield stability offers immediate economic benefits through cost reduction and increased profitability. However, the true value of this approach extends beyond mere economic gains. From an environmental perspective, the reduction in nitrogen application directly translates to decreased risks of soil acidification and salinization, which are critical concerns in intensive agricultural systems. The mechanism-driven optimization inherent in DSSAT-GA allows for precise alignment of fertilizer application with crops, minimizing excess nitrogen that could otherwise leach into groundwater or contribute to greenhouse gas emissions. The integration of water-saving drip irrigation systems with this framework is essential to prevent potential tradeoffs between nitrogen use efficiency (NUE) improvements and irrigation-induced leaching. By combining these technologies, farmers can achieve dual objectives of resource conservation and economic viability. Furthermore, the framework’s adaptability to different environmental conditions and crop varieties positions it as a valuable tool for sustainable intensification in diverse agroecosystems. However, realizing these benefits requires a long-term perspective. Monitoring soil health indicators over multiple growing seasons is necessary to fully quantify the extent of soil quality improvements and to ensure that the framework’s positive environmental impacts are sustained over time. Additionally, lifecycle assessment (LCA) models could be employed to comprehensively evaluate the carbon footprint reductions associated with this method, providing a more complete picture of its environmental benefits. Through continued research and practical implementation, the DSSAT-GA framework has the potential to serve as a model for environmentally intelligent agricultural decision-making systems that balance productivity with ecological stewardship.
5.3. Soil Variability and Broader Applicability
However, the external validity of these findings hinges on the representativeness of the soil conditions in our study site. The experimental site in Changji City features sandy loam soils with specific physicochemical properties, including a bulk density of 1.37 Mg m−3 and a water holding capacity of 0.35 cm3 cm−3 in the shallow layer (10–20 cm). These characteristics influence root growth, water retention, and nutrient availability, which are critical for cotton cultivation in arid environments. While our model calibration and optimization were tailored to these specific soil conditions, the framework’s adaptability to other soil types remains an important consideration for broader applicability.
Soil variability across different regions can significantly impact the performance of nitrogen management strategies. For instance, clay-heavy soils may exhibit different water and nitrogen dynamics compared to sandy loams, potentially altering the optimal fertilization schedules. The DSSAT model’s strength lies in its ability to incorporate site-specific soil data, allowing for localized calibration. This feature enables the framework to account for soil heterogeneity by adjusting parameters related to nutrient diffusion, root uptake kinetics, and water–nitrogen interactions. Our sensitivity analysis confirms that the optimized strategy’s robustness stems from its capacity to dynamically adapt to both biophysical processes and economic constraints, suggesting that the framework can be extended to other regions with appropriate soil data calibration.
While these findings are rigorously validated for Changji City’s semi-arid conditions, broader applicability requires caution. The confirmed outcomes—enhanced NUE, economic resilience, and fiber quality—are directly attributable to the site-specific calibration of cultivar parameters and soil profiles. However, extrapolation to divergent agroclimatic zones remains speculative without further validation. The study’s theoretical contribution lies in demonstrating that ratio-driven optimization—balancing yield against fertilization intensity—structurally embeds risk mitigation into agricultural decision systems. Unlike machine learning models that extrapolate poorly beyond training distributions, DSSAT-GA’s process-based constraints enforce biophysical plausibility, enabling reliable performance under novel perturbations. This hybrid paradigm offers a scalable template for sustainable intensification, particularly in volatile arid regions where traditional practices falter. Nevertheless, persistent challenges include real-time deployment barriers and climate uncertainty incorporation—frontiers demanding closer integration of IoT sensor networks and ensemble weather forecasting. By bridging these gaps, the framework could evolve into a dynamic decision-support tool, advancing precision agriculture while safeguarding soil health in global cotton systems.
5.4. Limitations of This Study and Future Work
5.4.1. Limitations
This study, built upon adequate irrigation, considers the optimal application of nitrogen fertilizer. Indeed, past research has shown significant interactions between water and fertilizer [42]. Limited irrigation can also enhance the efficiency of water and nitrogen utilization [43]. In future studies, it is imperative to integrate irrigation systems to devise rational field management systems. On the other hand, the integration of the GA algorithm with the core principles of the DSSAT model in this paper lies in selecting the optimal solution within the stochastic fertilization decision space. This work is viewed as an optimization problem, leaving room for further exploration and research.
5.4.2. Future Work
The proposed framework establishes a foundation for intelligent fertilization management, yet several critical challenges must be addressed to realize its full operational potential. First, the integration of dynamic fertilization timing as a decision variable could enhance precision by optimizing application windows based on real-time phenological development indicators rather than fixed growth stage assumptions. Second, real-time operationalization requires overcoming computational latency through edge computing architectures while maintaining model fidelity under fluctuating field conditions—particularly in balancing simulation resolution with decision-making frequency. Third, enhancing climate resilience necessitates the development of adaptive frameworks that dynamically reconcile model predictions with emerging meteorological extremes through ensemble forecasting and stochastic optimization. A paramount challenge lies in creating closed-loop systems that simultaneously optimize water–fertilizer synergies while accounting for sensor noise and prediction uncertainties inherent in field deployments. Addressing these challenges requires synergistic advances in cyber-physical systems, adaptive modeling architectures, and decision-theoretic frameworks to bridge the gap between theoretical optimization and practical implementation in precision agriculture.
6. Conclusions
To optimize fertilization strategies for cotton cultivation in Xinjiang, aimed at enhancing economic returns and ensuring the sustainable development of local soils, we conducted field experiments and developed a fertilization decision algorithm based on nitrogen use efficiency (NUE) and economic benefit adjustments. By calibrating the DSSAT model parameters for the “Zhongmian113” variety and validating them with experimental data from 2023, we confirmed the accuracy of the model. Building on this foundation, we proposed a novel optimization method that integrates DSSAT with genetic algorithms (GAs) for nitrogen fertilization in cotton. Our research successfully refined field fertilization strategies, resulting in a significant increase in local cotton yields, with seed cotton production rising by 10.9% compared to the highest experimental group, alongside optimal fiber quality. Furthermore, our approach achieved the highest NUE, markedly enhancing the economic viability of cotton cultivation. This study was validated as effective and reliable, offering valuable insights for intelligent fertilization practices in cotton agriculture.
Author Contributions
Conceptualization, Z.Y.; methodology, Z.Y.; software, Z.Y.; validation, Z.Y. and W.F.; formal analysis, Z.Y.; investigation, Z.Y.; resources, Z.Y.; data curation, Z.Y.; writing—original draft preparation, Z.Y.; writing—review and editing, Z.Y.; visualization, Z.Y.; supervision, W.F.; project administration, Z.Y.; funding acquisition, W.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology Major Project of China, grant number 2022ZD0115801.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
The authors thank the anonymous reviewers for their helpful comments.
Conflicts of Interest
On behalf of all authors, the corresponding author states that there are no conflicts of interest.
References
- Amrouk, E.; Palmeri, F. Recent Trends and Prospects in the World Cotton Market and Policy Developments; FAO: Rome, Italy, 2021. [Google Scholar]
- Jiang, Y.; Liu, D.y.; Li, J.m.; Wang, P. Soil quality assessment of continuous cropping cotton fields for different years in Manas river basin. Agric. Res. Arid. Areas 2021, 39, 186–193. [Google Scholar]
- Zhang, X.; Mlynaryk, N.; Japee, S.; Ungerleider, L. Multiple Objects of Attentional Selection in Human Visual Cortex. J. Vis. 2016, 16, 603. [Google Scholar] [CrossRef]
- Norse, D.; Ju, X. Environmental costs of China’s food security. Agric. Ecosyst. Environ. 2015, 209, 5–14. [Google Scholar] [CrossRef]
- Liu, A.; Li, Z.; Zhang, D.; Cui, Z.; Zhan, L.; Xu, S.; Zhang, Y.; Dai, J.; Li, W.; Nie, J. One-off basal application of nitrogen fertilizer increases the biological yield but not the economic yield of cotton in moderate fertility soil. Field Crop. Res. 2022, 288, 108702. [Google Scholar] [CrossRef]
- Malik, K. Interactive Effect of Spacing and Nitrogen Fertilization on Yield Parameters and Economics of Cotton (Gossypium Hirsutum L.) Var. H-1098(i). Int. J. Pure App. Biosci. 2021, 9, 75–82. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, B.; Xiao, L.; Hoogenboom, G.; Boote, K.J.; Kassie, B.T.; Pavan, W.; Shelia, V.; Kim, K.S.; Hernandez-Ochoa, I.M.; et al. A simple crop model. Eur. J. Agron. 2019, 104, 97–106. [Google Scholar] [CrossRef]
- Bassu, S.; Brisson, N.; Durand, J.L.; Boote, K.; Lizaso, J.; Jones, J.W.; Rosenzweig, C.; Ruane, A.C.; Adam, M.; Baron, C.; et al. How do various maize crop models vary in their responses to climate change. Agric. For. Meteorol. 2014, 191, 116–135. [Google Scholar] [CrossRef]
- Asseng, S.; Ewert, F.; Rosenzweig, C.; Jones, J.W.; Hatfield, J.L.; Ruane, A.C.; Boote, K.J.; Thorburn, P.J.; Rotter, R.P.; Cammarano, D.; et al. Uncertainty in simulating wheat yields under climate change. Nat. Clim. Chang. 2013, 3, 827–832. [Google Scholar] [CrossRef]
- Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Brief history of agricultural systems modeling. Agric. Syst. 2017, 155, 240–254. [Google Scholar] [CrossRef]
- Du, J.; Zhang, N.; Gong, K.; Du, M.; Yang, Y.; Wang, X. Optimization of cotton irrigation schedule under mulch drip irrigation in southern Xinjiang based on DSSAT model. Chin. J. Ecol. 2021, 40, 3760–3768. [Google Scholar]
- Wang, H.; Cheng, M.; Liao, Z.; Guo, J.; Zhang, F.; Fan, J.; Feng, H.; Yang, Q.; Wu, L.; Wang, X. Performance evaluation of AquaCrop and DSSAT-SUBSTOR-Potato models in simulating potato growth, yield and water productivity under various drip fertigation regimes. Agric. Water Manag. 2023, 276, 108076. [Google Scholar] [CrossRef]
- Hong, T.; Xin, L.; Ze, Z.; Caixia, Y.; Lulu, M.; Wei, S. Influence of Climate Change on Cotton Production Potential Based on DSSAT Model Simulation. Cotton Sci. 2020, 32, 113–120. [Google Scholar] [CrossRef]
- Pourebrahimi Foumani, M.; Yin, X.; Fu, J.S.; Yang, C.E.; Adotey, R. Impact of future climate from different general circulation models on cotton yield predictions in north Cotton Belt through crop simulation with DSSAT. Field Crop. Res. 2025, 322, 109719. [Google Scholar] [CrossRef]
- Bai, Y.; Gao, J. Optimization of the nitrogen fertilizer schedule of maize under drip irrigation in Jilin, China, based on DSSAT and GA. Agric. Water Manag. 2021, 244, 106555. [Google Scholar] [CrossRef]
- Gupta, R.; Bhattarai, R.; Coppess, J.W.; Jeong, H.; Ruffatti, M.; Armstrong, S.D. Modeling the impact of winter cover crop on tile drainage and nitrate loss using DSSAT model. Agric. Water Manag. 2022, 272, 107862. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, Z.; Han, Z.; Sun, W.; He, L. A Decision-Making System for Cotton Irrigation Based on Reinforcement Learning Strategy. Agronomy 2024, 14, 11. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, K.; Shen, H.; Wang, N.; Liu, R.; Wu, J.; Ma, X. Decision-making method for maize irrigation in supplementary irrigation areas based on the DSSAT model and a genetic algorithm. Agric. Water Manag. 2023, 280, 108231. [Google Scholar] [CrossRef]
- Babel, M.S.; Deb, P.; Soni, P. Performance evaluation of AquaCrop and DSSAT-CERES for maize under different irrigation and manure application rates in the Himalayan region of India. Agric. Res. 2019, 8, 207–217. [Google Scholar] [CrossRef]
- Ge, H.; Ma, F.; Li, Z.; Du, C. Estimating rice yield by assimilating UAV-derived plant nitrogen concentration into the DSSAT model: Evaluation at different assimilation time windows. Field Crop. Res. 2022, 288, 108705. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, L.; Lin, Y.; Zhao, J.; Qin, Y.; Li, Q.; Liu, H.; Sun, B.; Wang, L. Analysis and Closing of the High-Production-Maize Yield Gap in the Semi-Arid Area of Northeast China. Agronomy 2024, 14, 30. [Google Scholar] [CrossRef]
- Wang, L.; Lin, M.; Han, Z.; Han, L.; He, L.; Sun, W. Simulating the Effects of Drought Stress Timing and the Amount Irrigation on Cotton Yield Using the CSM-CROPGRO-Cotton Model. Agronomy 2024, 14, 14. [Google Scholar] [CrossRef]
- Beck, H.; Zimmermann, N.; McVicar, T.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Belaqziz, S.; Khabba, S.; Er-Raki, S.; Jarlan, L.; Le Page, M.; Kharrou, M.; Adnani, M.E.; Chehbouni, A. A new irrigation priority index based on remote sensing data for assessing the networks irrigation scheduling. Agric. Water Manag. 2013, 119, 1–9. [Google Scholar] [CrossRef]
- Allen, R.G. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper (FAO); FAO: Rome, Italy, 1998; Volume 56. [Google Scholar]
- Su, L.; Wang, Q.; Bai, Y. An analysis of yearly trends in growing degree days and the relationship between growing degree day values and reference evapotranspiration in Turpan area, China. Theor. Appl. Climatol. 2013, 113, 711–724. [Google Scholar] [CrossRef]
- Mcconnell, J.S.; Baker, W.H.; Miller, D.M.; Frizzell, B.S.; Varvil, J.J. Nitrogen Fertilization of Cotton Cultivars of Differing Maturity. Agron. J. 1993, 85, 1151–1156. [Google Scholar]
- Hou, X.; Fan, J.; Zhang, F.; Hu, W.; Xiang, Y. Optimization of water and nitrogen management to improve seed cotton yield, water productivity and economic benefit of mulched drip-irrigated cotton in southern Xinjiang, China. Field Crop. Res. 2024, 308, 109301. [Google Scholar] [CrossRef]
- Zadoks, J.C.; Chang, T.T.; Konzak, C.F. A decimal code for the growth stages of cereals. Weed Res. 1974, 14, 415–421. [Google Scholar]
- Jones, J.; Hoogenboom, G.; Porter, C.; Boote, K.; Batchelor, W.; Hunt, L.; Wilkens, P.; Singh, U.; Gijsman, A.; Ritchie, J. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Shelia, V.; Jones, J.W. The DSSAT Crop Modeling Ecosystem. In Advances in Crop Modelling for a Sustainable Agriculture; Burleigh Dodds Science Publishing: Sawston, UK, 2019. [Google Scholar]
- Sarkar, R. Decision Support Systems for Agrotechnology Transfer; Springer: Dutch, The Netherlands, 2012. [Google Scholar]
- Modala, N.R.; Ale, S.; Rajan, N.; Munster, C.; Barnes, E. Evaluation of the CSM-CROPGRO-Cotton model for the Texas rolling plains region and simulation of deficit irrigation strategies for increasing water use efficiency. Trans. Asabe 2015, 58, 685–696. [Google Scholar]
- Adhikari, P.; Gowda, P.H.; Marek, G.W.; Brauer, D.K.; Kisekka, I.; Northup, B.; Rocateli, A. Calibration and Validation of CSM-CROPGRO-Cotton Model Using Lysimeter Data in the Texas High Plains. J. Contemp. Water Res. Educ. 2017, 162, 61–78. [Google Scholar]
- Ma, R.; Cao, N.; Li, Y.; Hou, Y.; Wang, Y.; Zhang, Q.; Wang, T.; Cui, J.; Li, B.; Shi, W.; et al. Rational reduction of planting density and enhancement of NUE were effective methods to mitigate maize yield loss due to excessive rainfall. Eur. J. Agron. 2024, 160, 127326. [Google Scholar] [CrossRef]
- Meena, S.K.; Rakshit, A.; Meena, V.S. Effect of seed bio-priming and N doses under varied soil type on nitrogen use efficiency (NUE) of wheat (Triticum aestivum L.) under greenhouse conditions. Biocatal. Agric. Biotechnol. 2016, 6, 68–75. [Google Scholar] [CrossRef]
- Jiang, R.; He, W.; Zhou, W.; Hou, Y.; Yang, J.; He, P. Exploring management strategies to improve maize yield and nitrogen use efficiency in northeast China using the DNDC and DSSAT models. Comput. Electron. Agric. 2019, 166, 104988. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Application to Biology, Control & Artificial Intelligence; University of Michigan: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Cui, S.; Adamowski, J.F.; Albano, R.; Wu, M.; Cao, X. Optimal resource reallocation can achieve water conservation, emissions reduction, and improve irrigated agricultural systems. Agric. Syst. 2024, 221, 13. [Google Scholar] [CrossRef]
- Khosla, R.; Alley, M.M. Soil-Specific Nitrogen Management on Mid-Atlantic Coastal lain Soils. Better Crop. Plant Food 1999, LXXXIII, 6–7. [Google Scholar]
- Irmak, S.; Djaman, K.; Rudnick, D.R. Effect of full and limited irrigation amount and frequency on subsurface drip-irrigated maize evapotranspiration, yield, water use efficiency and yield response factors. Irrig. Sci. 2016, 34, 271–286. [Google Scholar] [CrossRef]
- Sui, J.; Wang, J.; Gong, S.; Xu, D.; Zhang, Y.; Qin, Q. Assessment of maize yield-increasing potential and optimum N level under mulched drip irrigation in the Northeast of China. Field Crop. Res. 2018, 215, 132–139. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).