An Unmanned Delivery Vehicle Path-Planning Method Based on Point-Graph Joint Embedding and Dual Decoders
Abstract
1. Introduction
- 1.
- We design a fuzzy time window model based on customer satisfaction for the distribution path-planning problem of UDVs with fuzzy time windows in urban peripheral areas, which includes a new method to calculate the customer satisfaction function and penalty function. This method improves the practicality of cost calculation, enhances the versatility of the method, and enhances its practical application.
- 2.
- We propose an enhanced deep reinforcement-learning algorithm model based on attention mechanisms combining point-graph joint embedding and a pseudo-label learning strategy to solve the real-life unmanned vehicle distribution problem. Concurrently, the model uses an end-to-end method to calculate the delivery path.
- 3.
- Extensive experiments indicate that the suggested approach outperforms competing algorithms with regard to accuracy, standard deviation, and other indicators. At the same time, the model allows training on data sets of various sizes, can solve problems of different sizes, and has better output results. This makes our method very valuable for practical applications.
2. Related Work
2.1. Heuristics Algorithms for Route Planning Problem
2.2. DRL-Based Methods for Route Planning Problem
2.3. Attention Mechanism in Route Planning Problem
3. The UDVRP Model
3.1. Problem Description
3.2. Basic Assumptions
- 1.
- The precise whereabouts of the distribution center are known, and the distribution center has sufficient charging facilities.
- 2.
- The location, demand, and best service time window of each distribution point are known.
- 3.
- All unmanned vehicles have the same attributes and have maximum load capacity and maximum driving distance limits;
- 4.
- While the autonomous vehicle is traveling, the weight of the battery does not change.
- 5.
- The unmanned vehicle maintains a consistent velocity, with a constant coefficient of battery power consumption, the power consumed has a linear relationship with the driving distance, and the unmanned vehicle has sufficient power to meet the delivery process.
- 6.
- The time spent by an autonomous vehicle at a demand point does not exceed a fixed value.
- 7.
- Only the energy consumption of autonomous vehicles under ideal conditions is considered, and the influence of factors such as weather is not considered.
- 8.
- It is assumed that each demand point can only be delivered by one unmanned vehicle, but one unmanned vehicle can serve multiple demand points.
3.3. Kinematic Model
3.4. Energy Consumption Function
3.5. Customer Satisfaction Function
3.6. Model Formulation
- 1.
- Route optimization constraints:where means served, means not served. If vehicle k travels directly from distribution point i to j, , otherwise . The Equation (4) signifies that the driving distance of each vehicle must not surpass the maximum distance driven. The constraint Equations (5)–(7) mean that each distribution point is only served by one vehicle; Equation (8) means that the number of unmanned delivery vehicles arriving and leaving any distribution node is the same; Equation (9) ensures that the driving trajectory of each vehicle must be It is a closed loop.
- 2.
- Time optimization constraints:If vehicle k selects the route from node i to j, the total time at node i (arrival time plus service time) cannot exceed M; otherwise, if the vehicle k does not choose this path, it considers only the arrival time at node j.Equation (11) sums up the contributions of arrival time, service time, and travel time from all nodes i to j where (indicating the route is selected). The chosen paths have a direct impact on the arrival time to node j.
- 3.
- Load optimization constraints:Equation (12) ensures that the load capacity of each vehicle cannot surpass the maximum load; Equation (13) demonstrates that the initial load capacity of the vehicle when leaving the distribution center is equal to the sum of the cargo volume at the service distribution point; Equation (14) indicates the sequence of vehicles The cargo capacity of serving two distribution points changes; Equation (15) indicates that the vehicle’s cargo capacity is always between 0 and Q.
- 4.
- Penalty cost optimization:Equation (16) represents the penalty cost generated by customer satisfaction.
4. Proposed Method
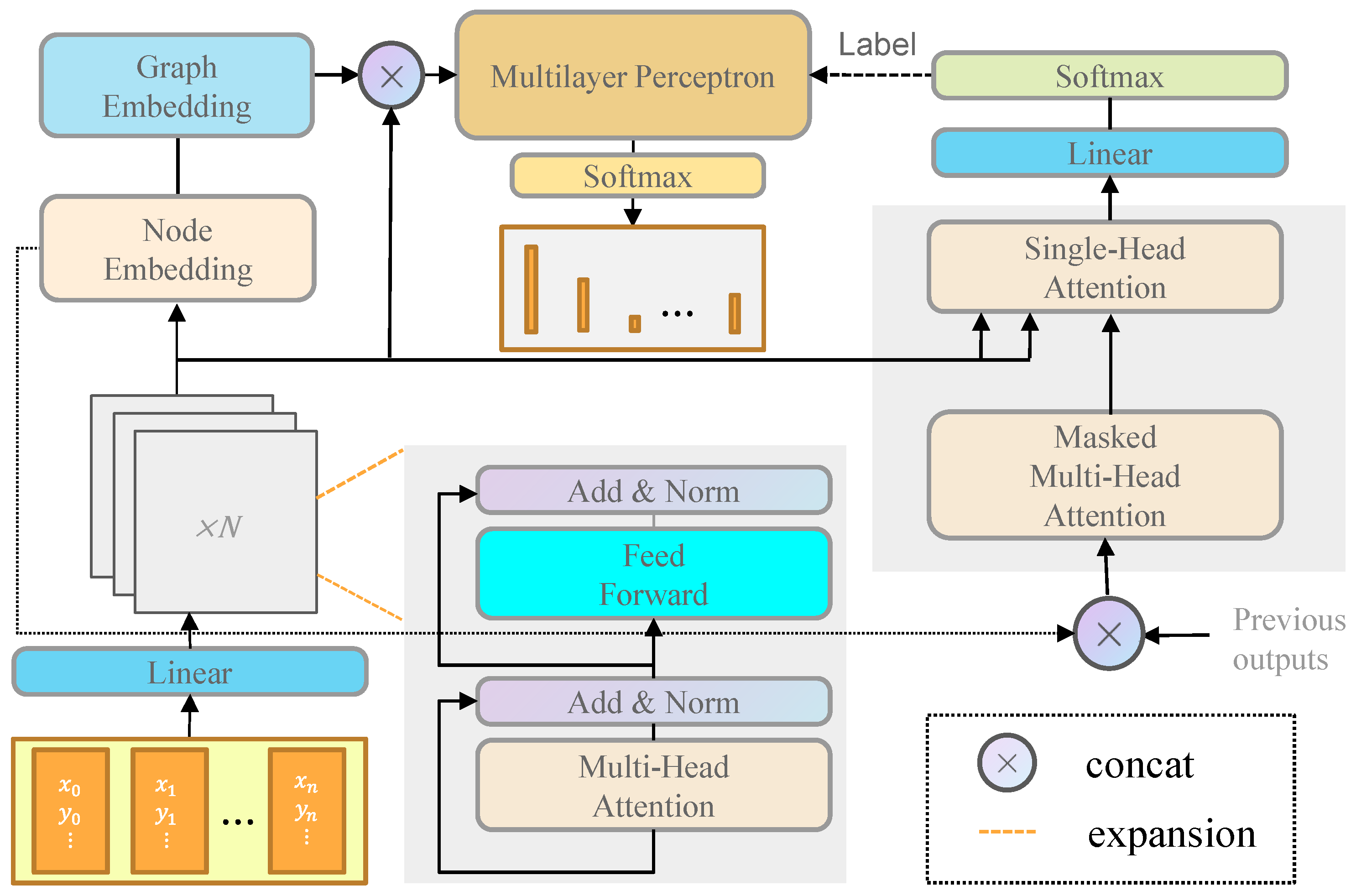
4.1. Overview of Method
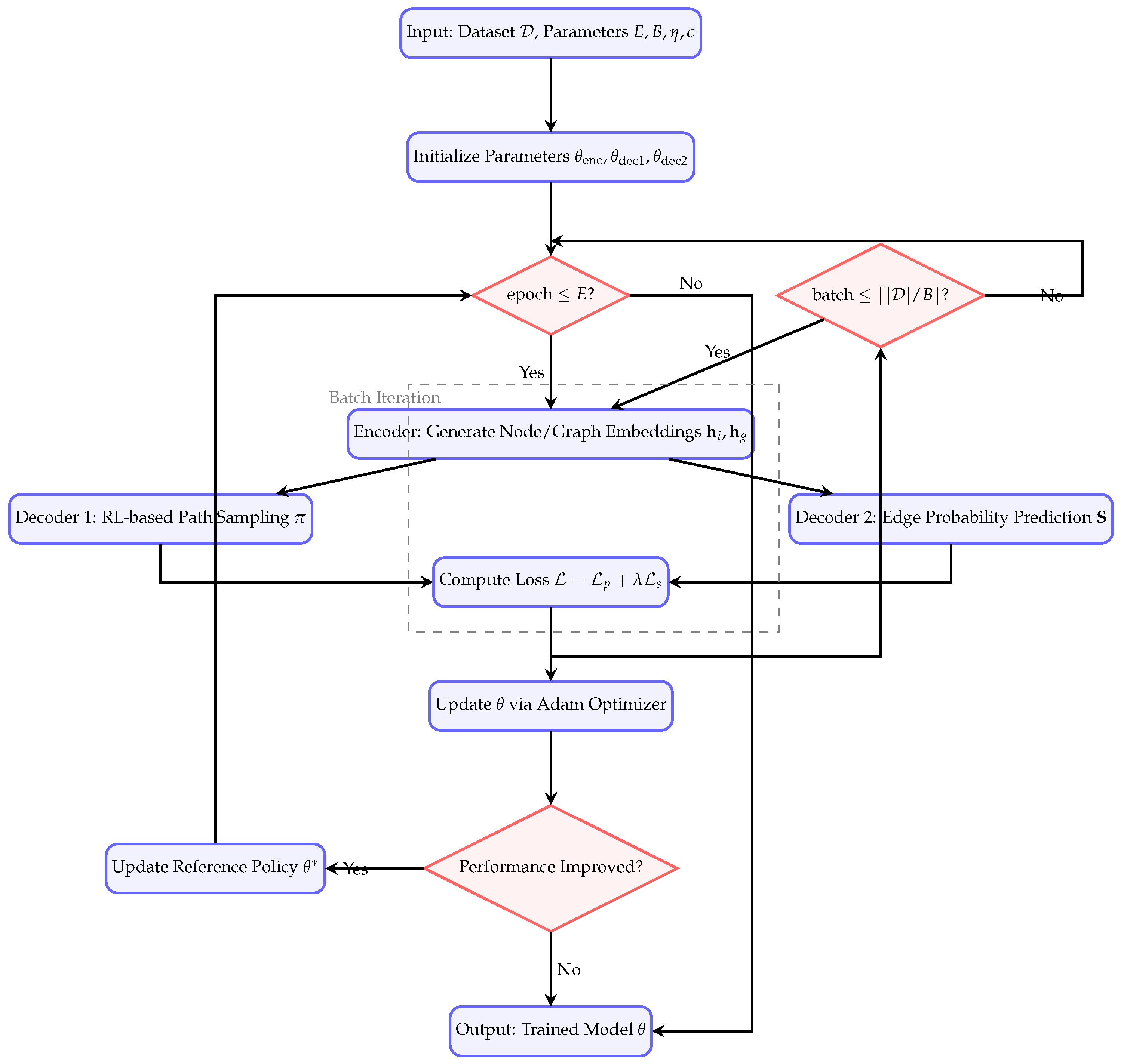
| Algorithm 1:PGDD Training Algorithm |
Require: Training dataset with N nodes per instance Number of epochs E, batch size B, learning rate Exploration rate , pseudo-label confidence threshold Ensure: Trained PGDD model parameters Initialize: Encoder parameters , decoder parameters Reference policy parameters for epoch to E do for batch to do Sample batch from Encoder: Generate node embeddings Compute graph embedding Decoder 1 (Pseudo-Label Generation): Use RL to sample path Compute policy loss Decoder 2 (Sequential Outcome): Predict edge probabilities Generate pseudo-labels ▹ Convert path to adjacency matrix Compute cross-entropy loss Update Parameters: Total loss () Update if then Update reference policy end if end for end for |
4.2. Node and Edge Representation
- : Spatial coordinates.
- : Demand at node i.
- : Ideal delivery time window.
- : Tolerance window for customer satisfaction.
- : Euclidean distance between nodes.
- : Travel time, with m/s.
- , : Penalty coefficients.
| Parameter | Symbol | Description |
|---|---|---|
| Node Coordinates | Spatial position | |
| Node Demand | Cargo volume (kg) | |
| Ideal Time Window | Optimal delivery interval | |
| Tolerance Window | Extended acceptable time range | |
| Edge Distance | Euclidean distance (km) | |
| Travel Time | (h) |
4.3. Node Feature Extraction Module
4.4. Path Generation Module
4.4.1. Pseudo-Label Generation Decoder
4.4.2. Sequential Outcome Decoder
- Cross-Decoder Supervision: Pseudo-labels from Decoder 1 supervise Decoder 2 via cross-entropy loss.
- Dynamic Thresholding: Low-confidence edges () are masked to prevent noise propagation.
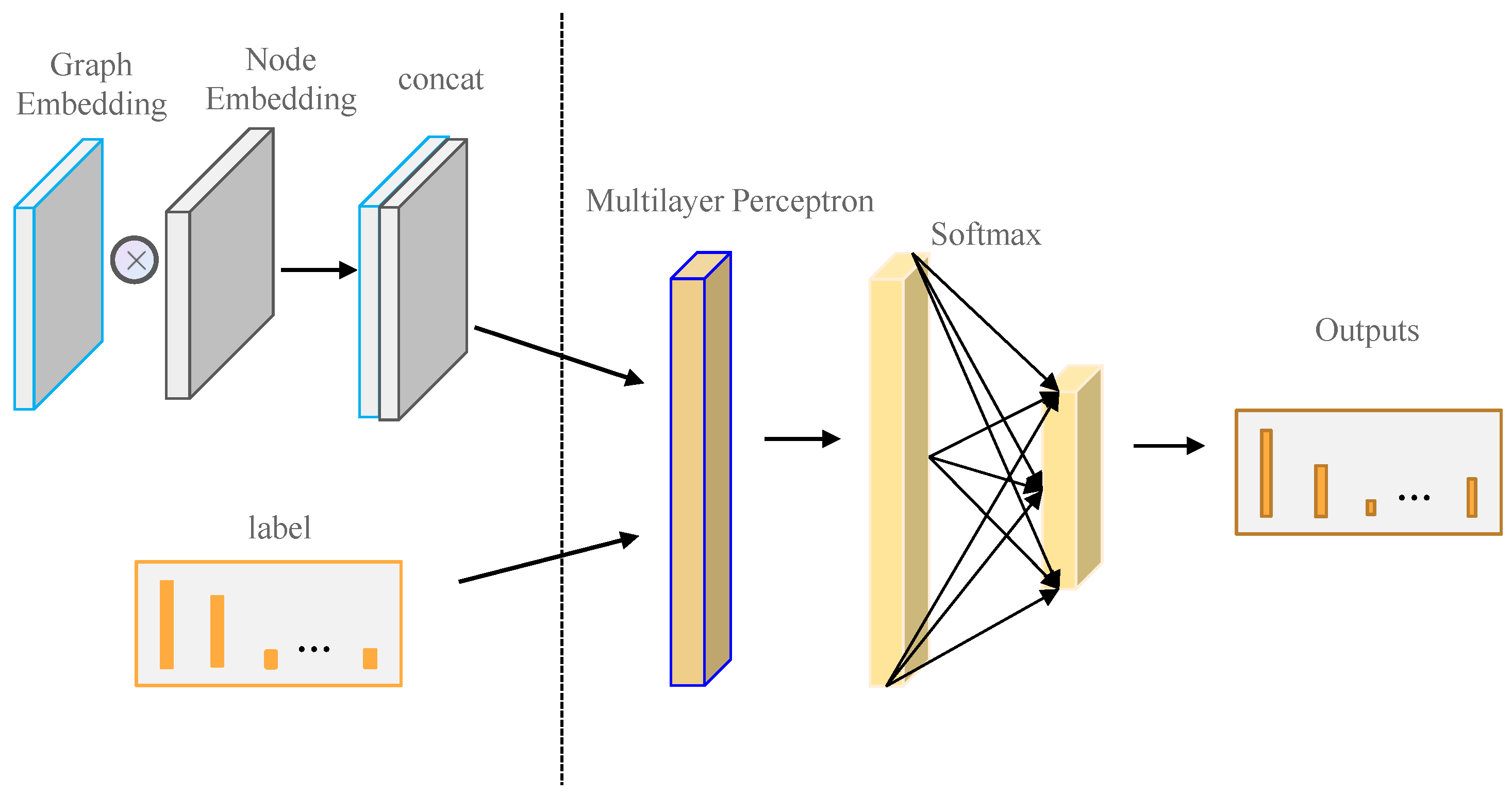
4.5. Overall Loss Function
4.5.1. Reinforcement-Learning Training Strategies
- : Energy consumption cost.
- : Penalty cost for violating customer time windows.
4.5.2. Loss of Pseudo-Label Generation Decoder
4.5.3. Loss of Sequential Outcome Decoder
- : Node embeddings (dimension ).
- : Graph embedding derived from average pooling of all node embeddings.
- : Trainable parameters of Decoder 2.
4.6. Path Execution
5. Experiments
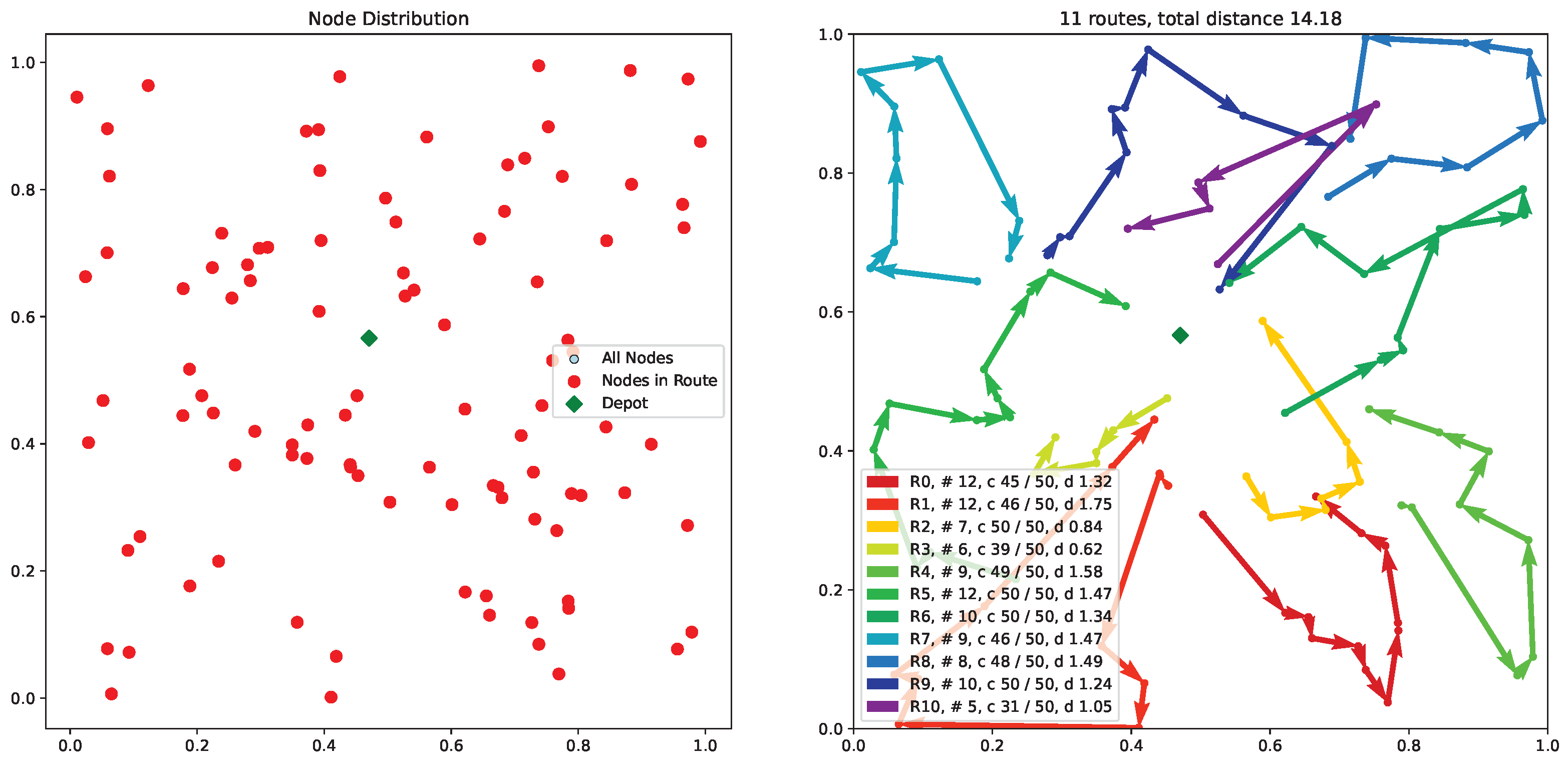
5.1. Dataset and Experimental Setting
- PN: a learning model proposed in [20], which presents pointer attention networks for generating permutations of input elements.
- DRL: a learning model proposed in [16], which integrates the Twin Delayed Deep Deterministic Policy Gradients (TD3) method from Deep Reinforcement Learning (DRL) with the Probabilistic Roadmap (PRM) algorithm, resulting in a novel path planner.
- AM: a learning model proposed in [24], which is based on the attention model with coordination embeddings. It is shown to outperform some well-known methods for the vehicle route planning problem (VRP).
- DRLPP: an advanced Deep Reinforcement-Learning algorithm for Path-Planning proposed in [36], which is designed to rectify the shortcomings inherent in existing path-planning techniques.
- DQL: a deep Q-Learning algorithm proposed in [37], which learns the initial paths using a topological map of the environment.
5.2. Implementation Details
- LiDAR: 50 m detection range for obstacle avoidance and environment mapping.
- RTK-GPS: Localization accuracy of for precise navigation.
- IMU: Inertial measurement unit for real-time attitude estimation.
- Onboard Computing Unit: NVIDIA Jetson AGX Xavier for edge-based inference, achieving a latency of .
5.3. Encoder and Decoder Architecture in Experiments
5.3.1. Encoder
- Multihead Attention (MHA);
- Feed-Forward Network (FFN):
- -
- Hidden dim: .
- -
- Activation: ReLU.
- Residual Connections + Batch Normalization: Applied after each sublayer.
5.3.2. Decoders
- Layers: 1 MHA layer (same as encoder).
- Output: Path sequence via policy gradient.
- Activation: Softmax for probability calculation.
- Layers: 2-layer MLP.
- Hidden Layer: , ReLU activated.
- Output: Edge probabilities via softmax.
5.4. Attention Mechanism in PGDD
5.4.1. Architecture
- parallel attention heads.
- Encoder depth layers.
- Query/key/value dimensions: .
- Hidden dimension: .
5.4.2. Scoring Function
5.4.3. Dynamic Weight Adjustment
5.5. Experimental Result
- Small-Scale Superiority: PGDD achieves near-perfect success (98.7%) in 100-node tasks by balancing cost and satisfaction.
- Path Smoothness: Measured by steering angle change rate . PGDD reduces this rate by 15% compared to baselines.
- Scalability: Maintains >92% success rate in 400-node scenarios despite increased complexity.
- Robustness: Fuzzy time-window penalties reduce late deliveries by 15.2% compared to fixed penalties.
5.6. Robustness Under Disturbances
- Introduce Gaussian noise () in the measurement of vehicle position and velocity v.
- Simulate the disturbance of energy consumption coefficient e due to rainy/snowy weather by increasing it by 20%.
- Model the linear degradation of battery capacity over time, with a 10% reduction per year.
5.7. Ablation Experiment
5.7.1. Effect of the Number of Attention Heads in PGDD
5.7.2. Effect of the Number of Attention Layers in PGDD
5.7.3. Effect of Whether to Consider Customer Satisfaction
5.8. Discussion of the PGDD and Interpretation of the Results
6. Conclusions and Future Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haboucha, C.J.; Ishaq, R.; Shiftan, Y. User preferences regarding autonomous vehicles. Transp. Res. Part C Emerg. Technol. 2017, 78, 37–49. [Google Scholar]
- Liu, D.; Yan, P.; Pu, Z.; Wang, Y.; Kaisar, E.I. Hybrid artificial immune algorithm for optimizing a Van-Robot E-grocery delivery system. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102466. [Google Scholar]
- Li, J.; Zhang, Y.; Meng, K. Joint-Optimization Planning of Electrified Logistic System considering Charging Facility Locations and Electric Logistic Vehicle Routing. In Proceedings of the 2023 IEEE International Conference on Energy Technologies for Future Grids (ETFG), Wollongong, Australia, 3–6 December 2023; pp. 1–5. [Google Scholar]
- Simoni, M.D.; Kutanoglu, E.; Claudel, C.G. Optimization and analysis of a robot-assisted last mile delivery system. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102049. [Google Scholar]
- Yazici, A.; Kirlik, G.; Parlaktuna, O.; Sipahioglu, A. A dynamic path planning approach for multirobot sensor-based coverage considering energy constraints. IEEE Trans. Cybern. 2013, 44, 305–314. [Google Scholar]
- Zhang, C.; Zhou, W.; Qin, W.; Tang, W. A novel UAV path planning approach: Heuristic crossing search and rescue optimization algorithm. Expert Syst. Appl. 2023, 215, 119243. [Google Scholar] [CrossRef]
- Jeong, I.; Jang, Y.; Park, J.; Cho, Y.K. Motion planning of mobile robots for autonomous navigation on uneven ground surfaces. J. Comput. Civ. Eng. 2021, 35, 04021001. [Google Scholar]
- Ma, Q.; Ge, S.; He, D.; Thaker, D.; Drori, I. Combinatorial Optimization by Graph Pointer Networks and Hierarchical Reinforcement Learning. arXiv 2019, arXiv:1911.04936. [Google Scholar]
- Liu, X.; Zhang, D.; Zhang, J.; Zhang, T.; Zhu, H. A path planning method based on the particle swarm optimization trained fuzzy neural network algorithm. Clust. Comput. 2021, 24, 1901–1915. [Google Scholar] [CrossRef]
- Li, T.; Feng, S. Order picking robot with simulation completion time constraint. Comput. Simul. 2021, 38, 348–354. [Google Scholar]
- Honglin, Z.; Yaohua, W.; Chang, H.; Wang, Y. Collaborative optimization of task scheduling and multi-agent path planning in automated warehouses. Complex Intell. Syst. 2023, 9, 5937–5948. [Google Scholar]
- Wang, X.; Liu, X.; Wang, Y. Research on task scheduling and path optimization of warehouse logistics mobile robot based on improved A * algorithm. Ind. Eng. 2019, 22, 34–39. [Google Scholar]
- Wu, Z.C.; Su, W.Z.; Li, J.H. Multi-robot path planning based on improved artificial potential field and B-spline curve optimization. In Proceedings of the Chinese Control Conference, Guangzhou, China, 27–30 July 2019; pp. 4691–4696. [Google Scholar]
- Wang, T.; Huang, P.; Dong, G. Modeling and Path Planning for Persistent Surveillance by Unmanned Ground Vehicle. IEEE Trans. Autom. Sci. Eng. 2021, 18, 1615–1625. [Google Scholar]
- Sabar, N.R.; Goh, S.L.; Turky, A.; Kendall, G. Population-Based Iterated Local Search Approach for Dynamic Vehicle Routing Problems. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2933–2943. [Google Scholar]
- Gao, J.; Ye, W.; Guo, J.; Li, Z. Deep Reinforcement Learning for Indoor Mobile Robot Path Planning. Sensors 2020, 20, 5493. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Liu, Z.; Li, Q.; Prorok, A. Mobile Robot Path Planning in Dynamic Environments Through Globally Guided Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 6932–6939. [Google Scholar]
- Cruz, D.L.; Yu, W. Path planning of multi-agent systems in unknown environment with neural kernel smoothing and reinforcement learning. Neurocomputing 2017, 233, 34–42. [Google Scholar]
- Ye, Y.; Zhang, X.; Sun, J. Automated vehicle’s behavior decision making using deep reinforcement learning and high-fidelity simulation environment. Transp. Res. Part C Emerg. Technol. 2019, 107, 155–170. [Google Scholar]
- Vinyals, O.; Fortunato, M.; Jaitly, N. Pointer networks. Adv. Neural Inf. Process. Syst. 2015, 28, 2692–2700. [Google Scholar]
- Johnson, M.; Schuster, M.; Le, Q.V.; Krikun, M.; Wu, Y.; Chen, Z.; Thorat, N.; Viégas, F.; Wattenberg, M.; Corrado, G.; et al. Google’s multilingual neural machine translation system: Enabling zero-shot translation. Trans. Assoc. Comput. Linguist. 2017, 5, 339–351. [Google Scholar]
- Bello, I.; Pham, H.; Le, Q.V.; Norouzi, M.; Bengio, S. Neural Combinatorial Optimization with Reinforcement Learning. arXiv 2016, arXiv:1611.09940. [Google Scholar]
- Konda, V.R.; Tsitsiklis, J.N. Actor-critic algorithms. Adv. Neural Inf. Process. Syst. 2000, 12, 1008–1014. [Google Scholar]
- Kool, W.; Hoof, H.V.; Welling, M. Attention, learn to solve routing problems! In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zou, Y.; Wu, H.; Yin, Y.; Dhamotharan, L.; Chen, D.; Tiwari, A.K. An improved transformer model with multi-head attention and attention to attention for low-carbon multi-depot vehicle routing problem. Ann. Oper. Res. 2022, 339, 517–536. [Google Scholar]
- Chen, Y.; Chen, M.; Chen, Z.; Cheng, L.; Yang, Y.; Li, H. Delivery path planning of heterogeneous robot system under road network constraints. Comput. Electr. Eng. 2021, 92, 107197. [Google Scholar]
- Liu, W.; Dridi, M.; Ren, J.; Hassani, A.H.E.; Li, S. A double-adaptive general variable neighborhood search for an unmanned electric vehicle routing and scheduling problem in green manufacturing systems. Eng. Appl. Artif. Intell. 2023, 126, 107113. [Google Scholar]
- Chi, S.; Du, P.; Huang, J. Research On Multi-destination Delivery Route Optimization Of Unmanned Express Vehicles. In Proceedings of the 2019 6th International Conference on Systems and Informatics (ICSAI), Shanghai, China, 2–4 November 2019; pp. 655–659. [Google Scholar]
- Keskin, M.; Laporte, G.; Çatay, B. Electric vehicle routing problem with time-dependent waiting times at recharging stations. Comput. Oper. Res. 2019, 107, 77–94. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Oyedotun, O.K.; Ismaeil, K.A.; Aouada, D. Why is everyone training very deep neural network with skip connections? IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 5961–5975. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Lei, K.; Guo, P.; Wang, Y.; Wu, X.; Zhao, W. Solve routing problems with a residual edge-graph attention neural network. Neurocomputing 2022, 508, 79–98. [Google Scholar]
- Li, J.; Xin, L.; Cao, Z.; Lim, A.; Song, W.; Zhang, J. Heterogeneous attentions for solving pickup and delivery problem via deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 2306–2315. [Google Scholar]
- Hazem, Z.B. Study of Q-learning and deep Q-network learning control for a rotary inverted pendulum system. Discov. Appl. Sci. 2024, 6, 49. [Google Scholar]
- Yang, K.; Liu, L. An Improved Deep Reinforcement Learning Algorithm for Path Planning in Unmanned Driving. IEEE Access 2024, 12, 67935–67944. [Google Scholar] [CrossRef]
- Kumaar, A.A.N.; Kochuvila, S. Mobile Service Robot Path Planning Using Deep Reinforcement Learning. IEEE Access 2023, 11, 100083–100096. [Google Scholar] [CrossRef]
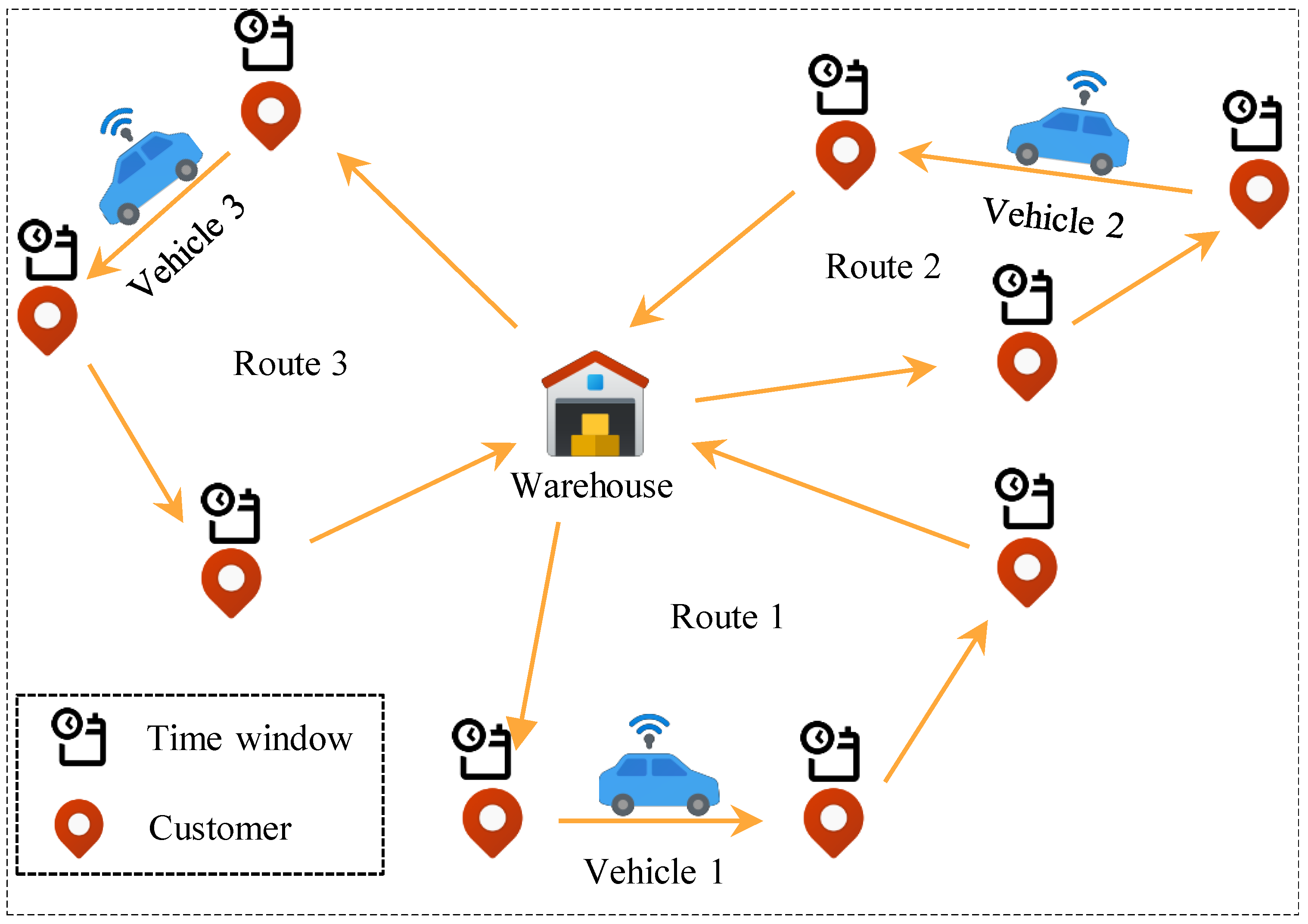
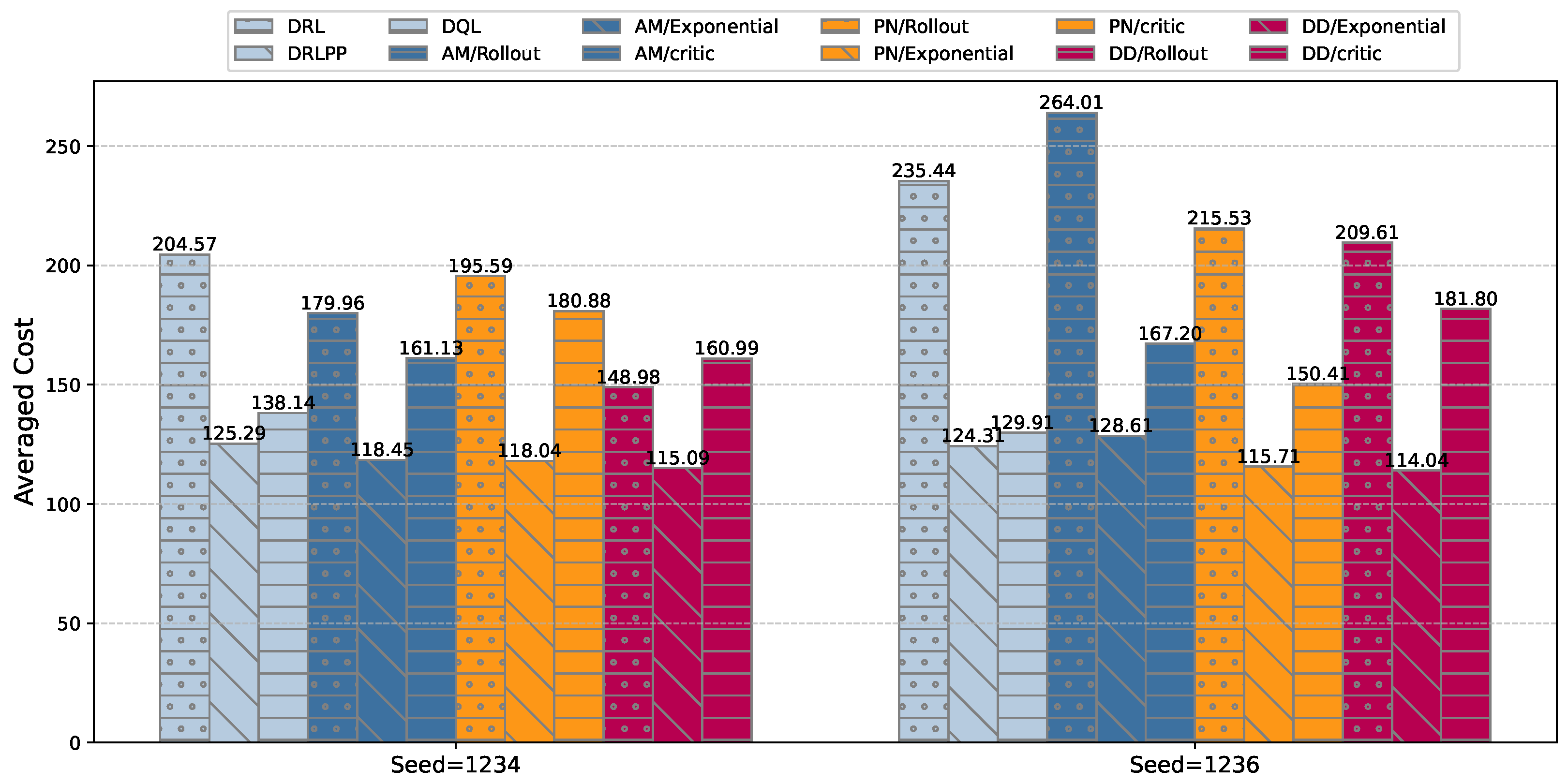
| Method | Key Features & Applications | Limitations |
|---|---|---|
| Scheduling Model for Robot Waiting Time [10] | Optimizes warehousing costs via decision-variable allocation. | Not scalable for complex environments. |
| Improved HEFT-based Task Scheduling [11] | Employs MAPF/TS-MAPF for task scheduling. | Struggles with large-scale networks. |
| Warehouse Space Model [12] | Solves shortest path assignment for warehousing robots. | Effective only for small-scale scenarios. |
| Gain Limits and B-spline Techniques [13] | Enhances path smoothness using potential field repulsion. | Computationally intensive as node count increases. |
| Fuzzy Neural Network via PSO [9] | Merges neural networks with PSO for autonomous routing. | High training complexity and risk of overfitting. |
| Incremental DRL Training [16] | Uses DRL with incremental training for path-planning. | Limited generalization in constrained settings. |
| Dynamic-Window Algorithm [26] | Implements dynamic priority for routing in dynamic environments. | Ignores customer satisfaction constraints. |
| Charging Dispatching Model [27] | Optimizes charging dispatch under capacity constraints. | Focuses solely on charging, neglecting customer factors. |
| Hybrid PSO-GA Approach [28] | Integrates PSO with GA for efficient path optimization. | Neglects compensation costs for unsatisfactory deliveries. |
| Multihead Attention Mechanisms [24] | Improves path optimization via multihead attention. | Prone to overfitting; label reliability issues. |
| Enhanced Attention Transformer [25] | Advanced attention for multi-site vehicle routing. | Insufficient generalization to unseen environments. |
| Genetic Algorithm with Best-First Search [3] | Uses genetic search for joint logistics optimization. | Limited to small-scale problems; scalability issues. |
| Heuristic Path-Planning System [14] | Provides simulation-validated heuristic routing. | Inefficient for large-scale applications. |
| Population-based Strategy with ILS [15] | Combines evolutionary operators with ILS for dynamic routing. | Time-intensive for numerous nodes. |
| Parameter | Description | Value |
|---|---|---|
| L | Wheelbase (distance between front and rear axles) | |
| Maximum linear velocity | ||
| Maximum steering angle | ||
| Maximum acceleration | ||
| Maximum angular velocity | ||
| p | Vehicle curb weight (unloaded) | |
| Q | Maximum payload capacity | |
| e | Energy consumption coefficient | |
| Battery capacity |
| Parameters | Descriptions |
|---|---|
| N | Distribution point collection, |
| s | The distribution center |
| K | Collection of unmanned distribution vehicles, |
| D | Maximum driving distance of unmanned delivery vehicles |
| Q | The maximal load capacity of unmanned delivery vehicles |
| The quantity demanded at distribution point i | |
| The distance from distribution point i to j | |
| c | Fixed costs of unmanned delivery vehicles |
| w | Unit transportation cost of unmanned delivery vehicles |
| e | Specific energy consumption of unmanned delivery vehicles |
| h | Unit energy consumption cost |
| Service duration at distribution point i | |
| The actual time when the vehicle arrives at the distribution point i | |
| The duration of the vehicle from distribution point i to distribution point j | |
| The loading quantity of distribution point i | |
| The discharge quantity of distribution point i | |
| The load of vehicle k when it leaves the distribution point i | |
| Indicates whether the distribution point i is served by vehicle k, binary variable | |
| Indicates whether the vehicle k travels immediately from distribution point i to j, binary variable | |
| Penalty coefficient | |
| Constant, equal to 1.316 |
| Problem Set | Problem Size | Epoch Size | Batch Size | Vehicle Capacity |
|---|---|---|---|---|
| UDVRP100 | 100 | 128,000 | 512 | 50 |
| UDVRP200 | 200 | 128,000 | 512 | 60 |
| UDVRP400 | 400 | 12,800 | 32 | 80 |
| Component | Layers | Hidden Dim | Heads | Activation |
|---|---|---|---|---|
| Encoder | 3 | 128 | 8 | ReLU |
| Decoder 1 | 1 | 128 | 8 | Softmax |
| Decoder 2 | 2 | 256 | - | ReLU/Softmax |
| Parameter | Symbol | Value |
|---|---|---|
| Attention Heads | h | 8 |
| Encoder Layers | L | 3 |
| Query/Key Dimension | 16 | |
| Value Dimension | 16 | |
| Hidden Dimension | 128 | |
| Penalty Coefficients | 0.8, 1.316 |
| Method | n = 100 | n = 200 | n = 400 | |||
|---|---|---|---|---|---|---|
| Seed = 1234 | Seed = 1236 | Seed = 1234 | Seed = 1236 | Seed = 1234 | Seed = 1236 | |
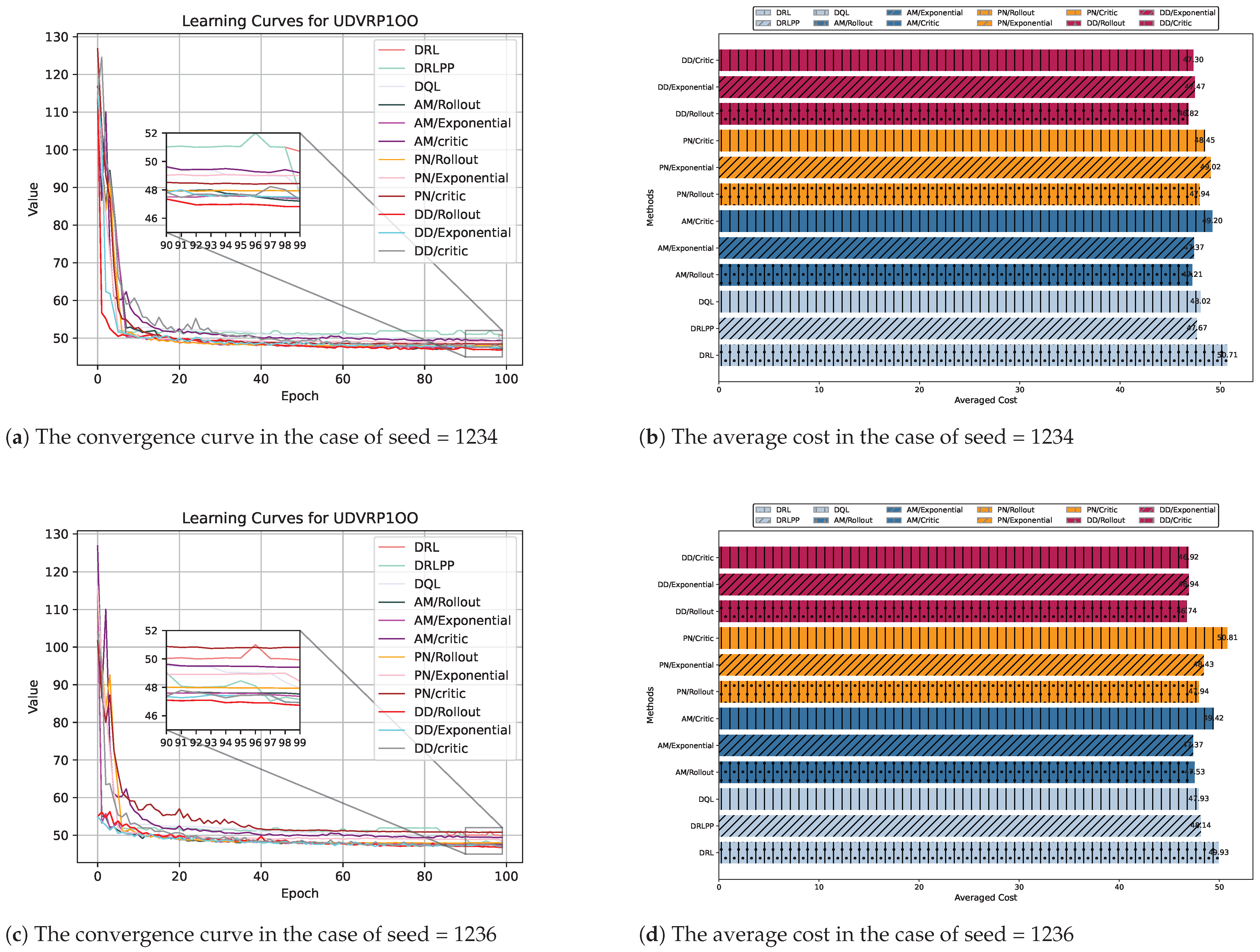
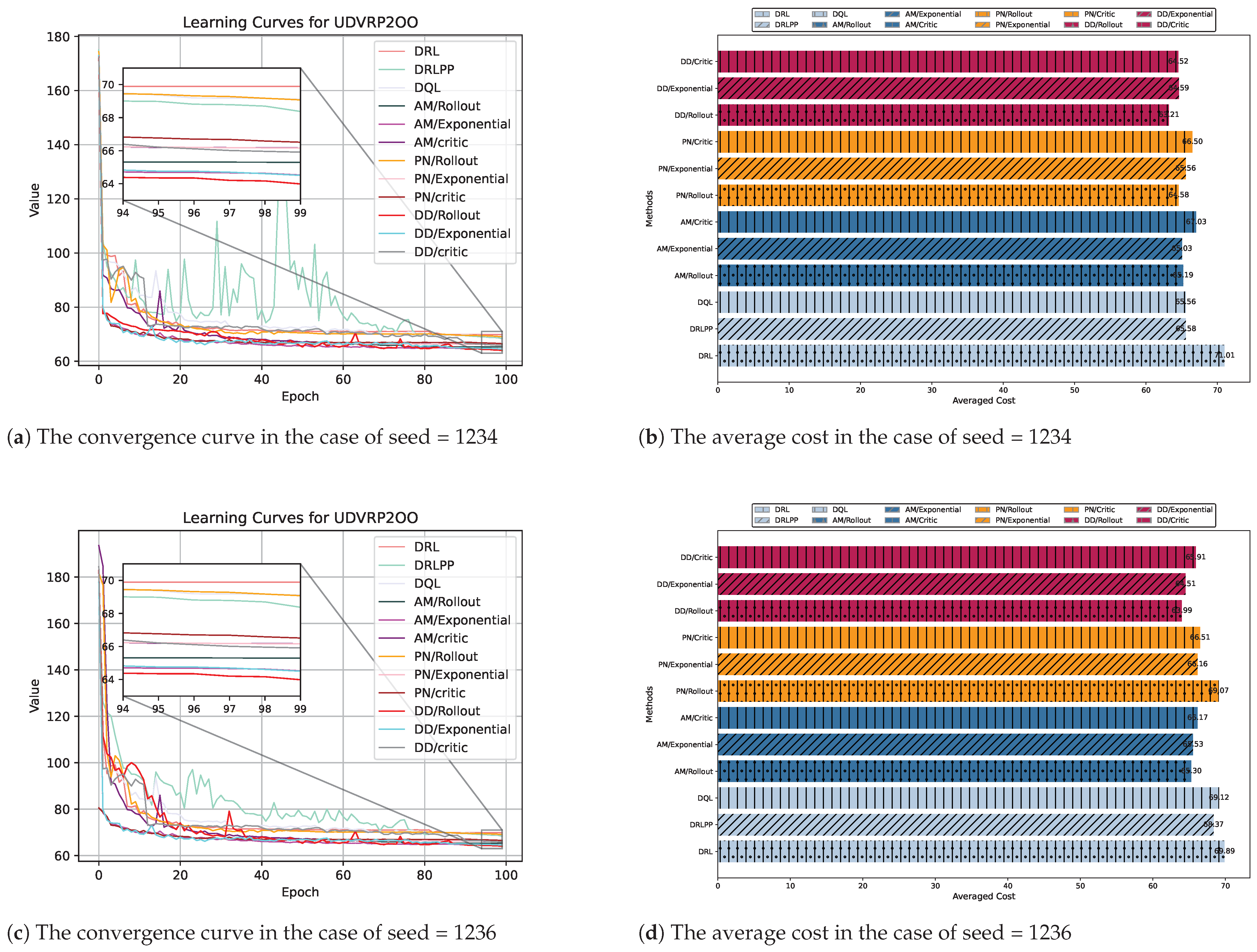
| DRL [16] | 50.71 | 49.93 | 71.01 | 69.89 | 204.57 | 235.44 |
| DRLPP [36] | 47.67 (−5.99%) | 48.14 (−3.61%) | 65.58 (−7.73%) | 68.37 (−2.17%) | 125.29 (−38.75%) | 124.31 (−47.32%) |
| DQL [37] | 48.02 (−5.50%) | 47.93 (−4.01%) | 65.56 (−7.68%) | 69.12 (−1.10%) | 138.14 (−32.47%) | 129.91 (−44.79%) |
| PN/Rollout [20] | 47.94 (−5.46%) | 47.94 (−3.99%) | 64.58 (−9.05%) | 69.07 (−1.17%) | 195.59 (−4.40%) | 264.01 (12.11%) |
| PN/Exponential [20] | 49.02 (−3.33%) | 48.43 (−3.00%) | 65.56 (−7.67%) | 66.16 (−5.34%) | 118.04 (−42.27%) | 128.61 (−45.33%) |
| PN/Critic [20] | 48.45 (−4.45%) | 50.81 (1.76%) | 66.50 (−6.37%) | 66.51 (−4.85%) | 180.88 (−11.60%) | 181.80 (−22.77%) |
| AM/Rollout [24] | 47.21 (−6.89%) | 47.53 (−4.81%) | 65.19 (−8.18%) | 65.30 (−6.53%) | 179.96 (−12.04%) | 215.53 (−8.46%) |
| AM/Exponential [24] | 47.37 (−6.59%) | 47.37 (−5.13%) | 65.03 (−8.43%) | 64.53 (−7.63%) | 118.45 (−42.03%) | 115.71 (−50.84%) |
| AM/Critic [24] | 49.20 (−2.98%) | 49.42 (−1.02%) | 67.03 (−5.62%) | 66.17 (−5.32%) | 161.13 (−21.22%) | 167.20 (−29.00%) |
| Ours/Rollout | 46.82 (−7.66%) | 46.74 (−6.39%) | 63.21 (−10.97%) | 63.99 (−8.44%) | 148.98 (−27.17%) | 209.61 (−10.97%) |
| Ours/Exponential | 47.47 (−6.39%) | 46.94 (−6.00%) | 64.59 (−9.06%) | 64.51 (−7.69%) | 115.09 (−43.80%) | 114.04 (−51.60%) |
| Ours/Critic | 47.30 (−6.71%) | 46.92 (−6.02%) | 64.52 (−9.16%) | 65.91 (−5.68%) | 160.99 (−21.29%) | 150.41 (−36.08%) |
| Method | Mean ± Std | Eval Time (ms) |
|---|---|---|
| DRL [16] | 235.44 ± 0.9367 | 68 |
| DRLPP [36] | 124.31 ± 0.4674 | 79 |
| DQL [37] | 129.91 ± 0.8394 | 66 |
| PN/Rollout [20] | 264.01 ± 1.4585 | 44 |
| PN/Exponential [20] | 128.61 ± 0.9889 | 35 |
| PN/Critic [20] | 181.80 ± 0.6994 | 39 |
| AM/Rollout [24] | 215.53 ± 0.4063 | 34 |
| AM/Exponential [24] | 115.71 ± 0.6744 | 43 |
| AM/Critic [24] | 167.20 ± 0.5045 | 37 |
| Ours/Rollout | 209.61±0.4295 | 74 |
| Ours/Exponential | 114.04 ± 0.0371 | 59 |
| Ours/Critic | 150.41 ± 0.3243 | 81 |
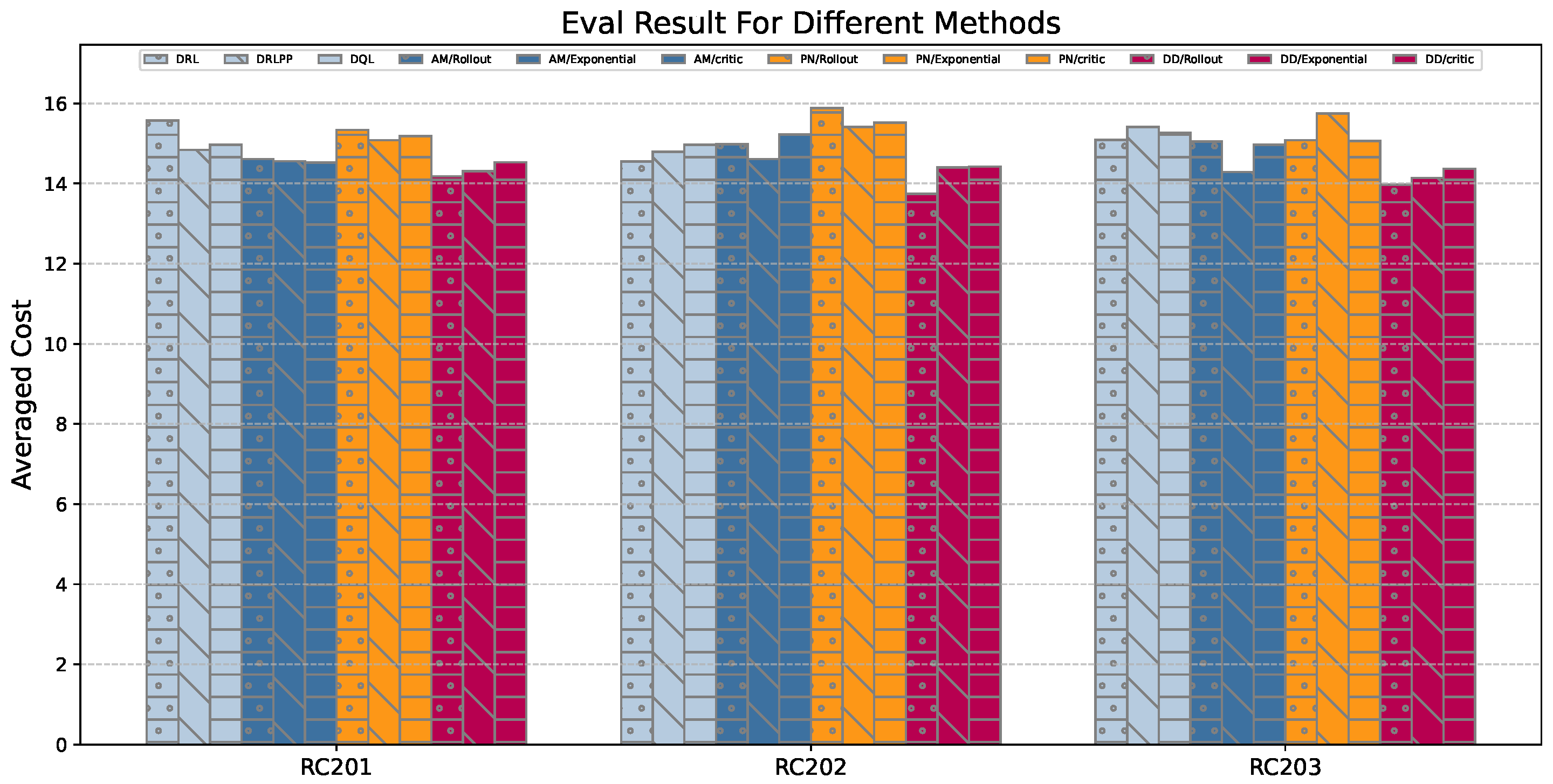
| Method | RC201 | RC202 | RC203 |
|---|---|---|---|
| DRL [16] | 15.57 | 14.55 | 15.09 |
| DRLPP [36] | 14.84 | 14.79 | 15.41 |
| DQL [37] | 14.97 | 14.97 | 15.26 |
| PN/Rollout [20] | 15.34 | 15.88 | 15.08 |
| PN/Exponential [20] | 15.08 | 15.41 | 15.75 |
| PN/Critic [20] | 15.18 | 15.52 | 15.06 |
| AM/Rollout [24] | 14.61 | 14.98 | 15.05 |
| AM/Exponential [24] | 14.56 | 14.61 | 14.29 |
| AM/Critic [24] | 14.52 | 15.23 | 14.97 |
| PGDD/Rollout | 14.18 | 13.74 | 13.97 |
| PGDD/Exponential | 14.31 | 14.40 | 14.14 |
| PGDD/Critic | 14.53 | 14.42 | 14.37 |
| Algorithm | n = 100 | n = 200 | n = 400 |
|---|---|---|---|
| PGDD | 98.7% | 96.5% | 92.3% |
| AM [24] | 94.2% | 91.8% | 87.4% |
| Disturbance Type | Metric | PGDD | AM Baseline [24] |
|---|---|---|---|
| Rainy Weather | Cost Increase | 4.8% | 12.3% |
| Sensor Noise () | Path Deviation Rate | 2.3% | 8.7% |
| Battery Degradation | Task Success Rate | 98.0% | 89.5% |
| Parameters | Seed = 1234 | Seed = 1236 | Epoch Time (s) |
|---|---|---|---|
| H = 1 | 47.59 | 48.91 | 488 |
| H = 2 | 47.02 | 46.77 | 512 |
| H = 4 | 47.48 | 47.18 | 515 |
| H = 8 | 46.82 | 46.74 | 565 |
| H=16 | 47.10 | 47.53 | 627 |
| N = 1 | 47.66 | 47.15 | 478 |
| N = 2 | 47.10 | 47.33 | 496 |
| N = 3 | 46.82 | 46.74 | 565 |
| N = 4 | 47.13 | 47.03 | 585 |
| N = 5 | 48.47 | 47.43 | 594 |
| Parameters | Seed = 1234 | Seed = 1236 | Seed = 1238 |
|---|---|---|---|
| Satisfaction | 46.82 | 46.74 | 48.68 |
| No Satisfaction | 55.43 | 56.77 | 50.22 |
| tanh_function | 46.82 | 46.74 | 48.68 |
| sigmoid_function | 48.25 | 49.13 | 49.32 |
| gaussian_function | 54.51 | 53.68 | 55.38 |
| linear_function | 51.94 | 50.92 | 51.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Ni, Z.; Liu, W.; Chen, Q.; Yan, R. An Unmanned Delivery Vehicle Path-Planning Method Based on Point-Graph Joint Embedding and Dual Decoders. Appl. Sci. 2025, 15, 3556. https://doi.org/10.3390/app15073556
Cheng J, Ni Z, Liu W, Chen Q, Yan R. An Unmanned Delivery Vehicle Path-Planning Method Based on Point-Graph Joint Embedding and Dual Decoders. Applied Sciences. 2025; 15(7):3556. https://doi.org/10.3390/app15073556
Chicago/Turabian StyleCheng, Jiale, Zhiwei Ni, Wentao Liu, Qian Chen, and Rui Yan. 2025. "An Unmanned Delivery Vehicle Path-Planning Method Based on Point-Graph Joint Embedding and Dual Decoders" Applied Sciences 15, no. 7: 3556. https://doi.org/10.3390/app15073556
APA StyleCheng, J., Ni, Z., Liu, W., Chen, Q., & Yan, R. (2025). An Unmanned Delivery Vehicle Path-Planning Method Based on Point-Graph Joint Embedding and Dual Decoders. Applied Sciences, 15(7), 3556. https://doi.org/10.3390/app15073556






