Transforming Wind Data into Insights: A Comparative Study of Stochastic and Machine Learning Models in Wind Speed Forecasting
Abstract
1. Introduction
2. Methodology
2.1. Study Area and Dataset
2.2. Feature Selection
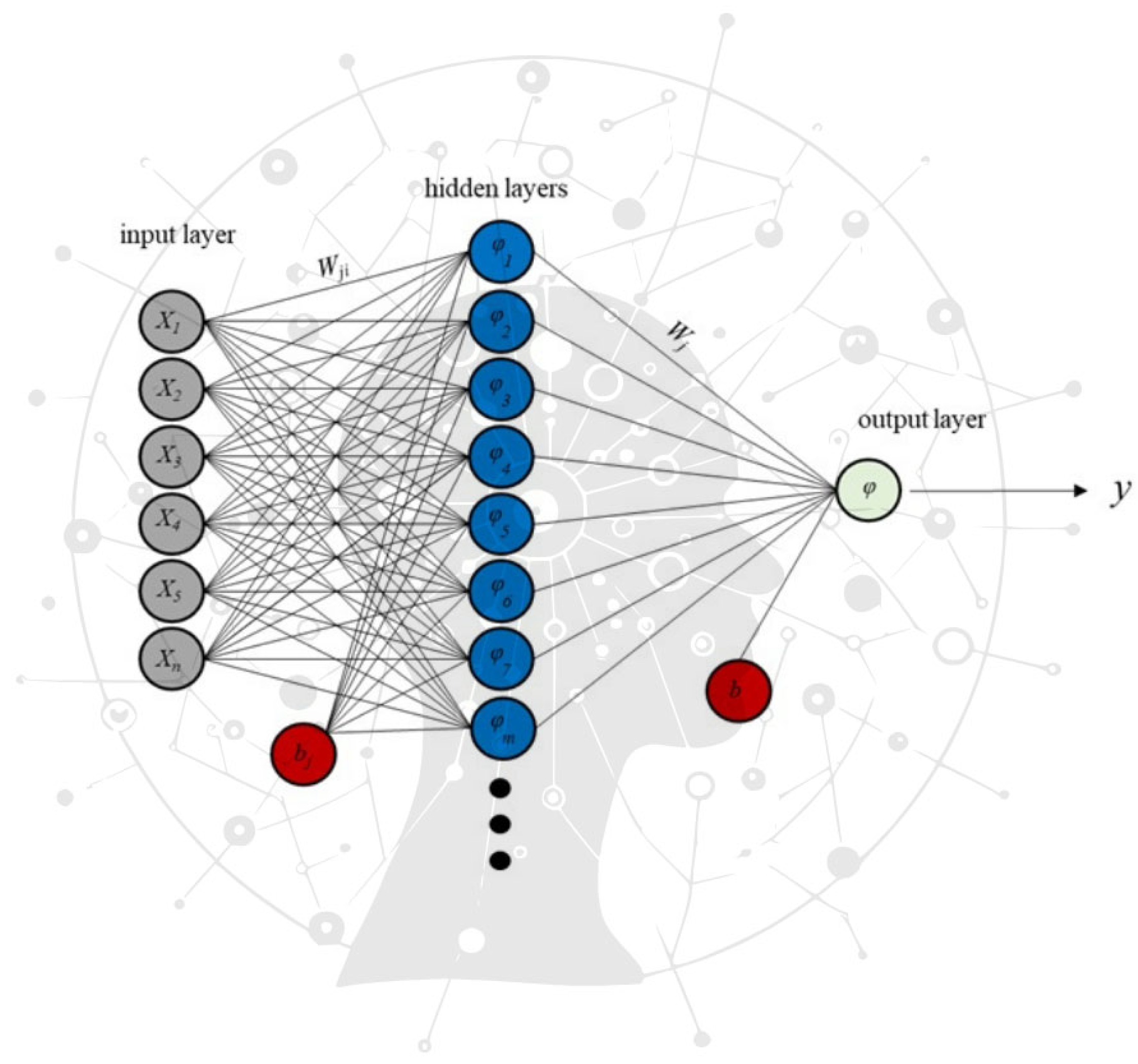
2.3. Artificial Neural Network (ANN)
- m: Number of neurons in the hidden layer.
- N: Number of samples in the input data.
- xi: The ith input variable at time step t.
- wji: Weight connecting the ith neuron in the input layer to the ith neuron in the hidden layer.
- bj: Bias term for the ith hidden neuron.
- ϕj: Activation function applied to the hidden neuron.
- wj: Weight connecting the ith neuron in the hidden layer to the kth neuron in the output layer.
- b: Bias term for the kth output neuron.
- ϕ: Activation function applied to the output neuron.
- y: The predicted kth output at time step t.
2.4. Support Vector Machine (SVM)
2.5. Long-Short Term Memory (LSTM)
2.6. Seasonal Autoregressive Integrated Moving Average (SARIMA)
- P denotes the order of the seasonal autoregressive (AR) model.
- D refers to the number of seasonal differencing required to achieve stationarity.
- Q indicates the order of the seasonal moving average (MA) component.
- S represents the length of the seasonal cycle or periodicity.
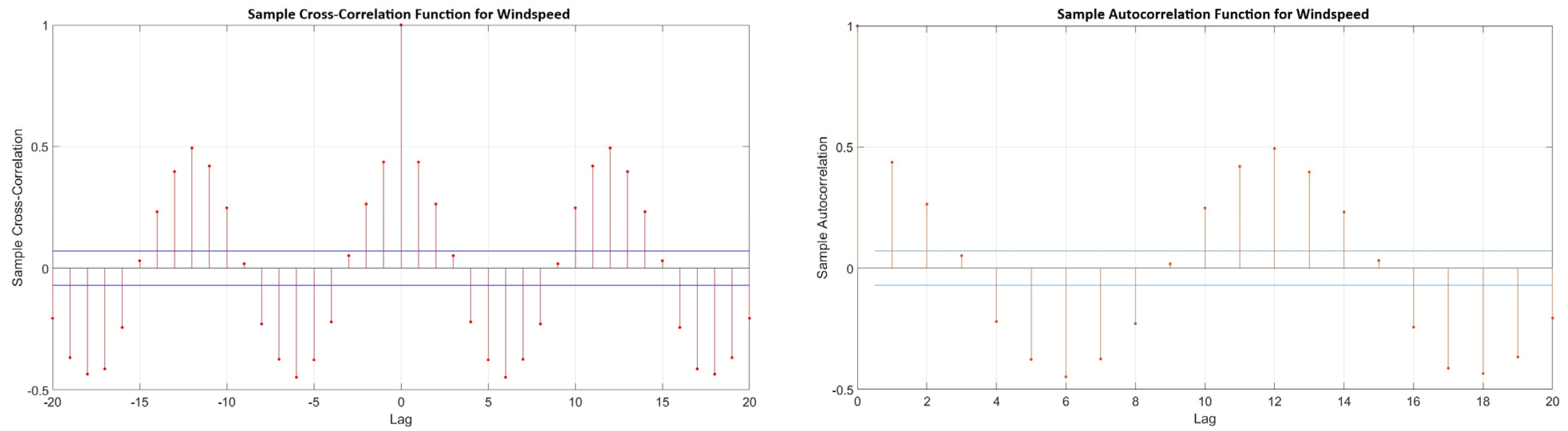
- Identification: This stage focuses on selecting the appropriate level of differencing to transform the time series into a stationary form. It also involves determining the desired order of the model and analyzing the autocorrelation function (ACF) and the partial autocorrelation function (PACF). These functions help to uncover the temporal correlation structure of the transformed data. Specifically:
- The ACF is used to assess whether past values have a significant association with the current values.
- The PACF quantifies the correlation between the variable and its time-lagged values, while controlling for intermediate lags.
- Model Selection: The Akaike information criterion (AIC) and the Bayesian information criterion (BIC) (also referred to as Schwarz’s BIC) are commonly employed to identify the optimal model. These criteria are defined mathematically in Equations (6) and (7), respectively, and provide a trade-off between model complexity and goodness-of-fit.
- Parameter Estimation and Diagnostic Testing: Once the model structure is identified, parameters are estimated, and diagnostic testing is performed to ensure the model adequately fits the data.
2.7. Wavelet Transformation (WT)
- s0 represents the precision step for the signal’s expansion.
- τ0 denotes the localization parameter for handling discrete time series data (), where the data are sampled at discrete intervals (i).
2.8. Performance Metrics
3. Results
4. Discussion
5. Conclusions
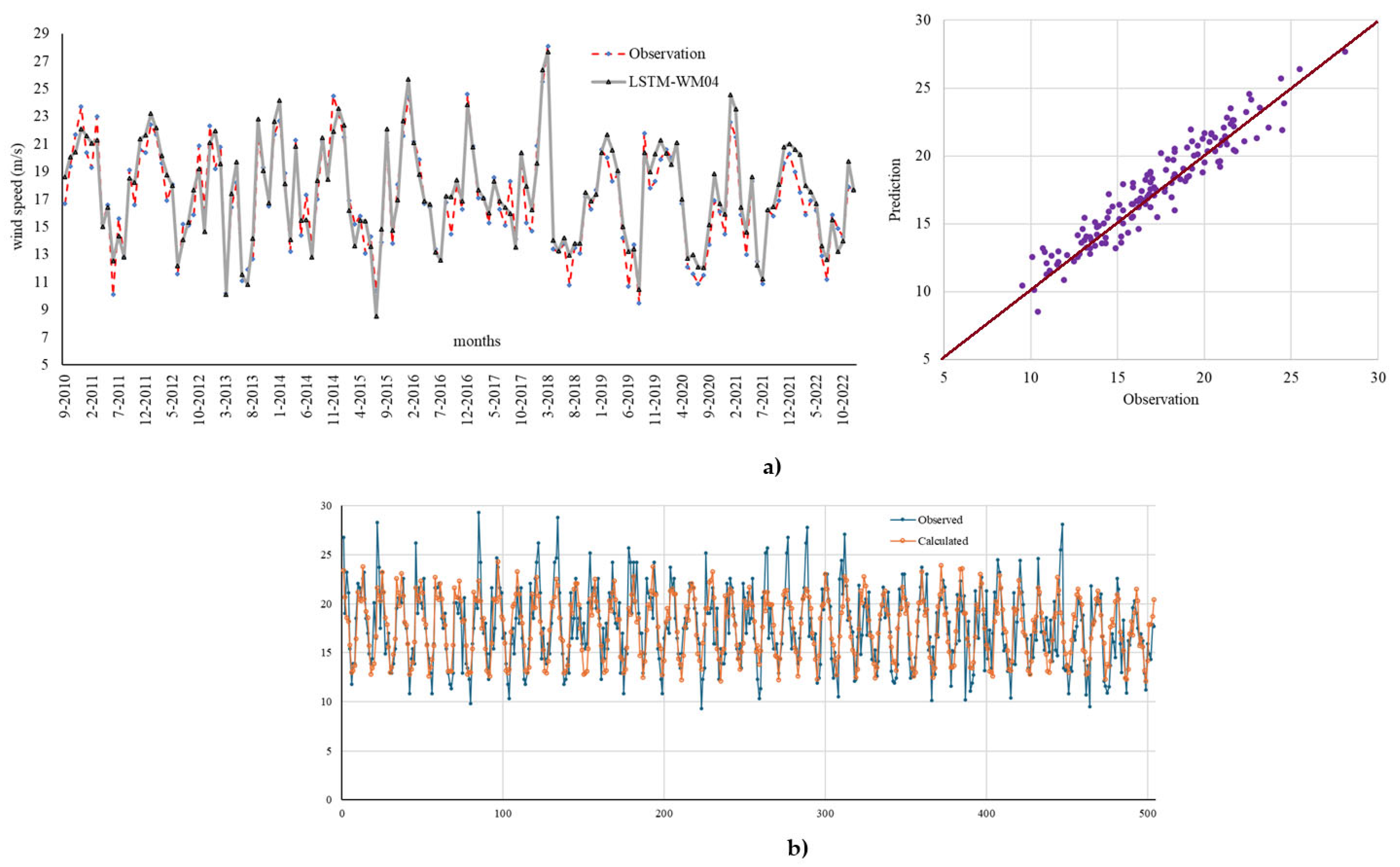
- Based on statistical analysis and visual comparison results, the most successful algorithm was LSTM with WT, and the most successful model was M04. This model’s input structure should be used for wind speed forecasting in this region. Additionally, the input variables should be kept at an optimal level. The input structure for this model was created using lagged data at t-1, t-2, t-11, and t-12.
- In the analysis performed without WT, the most successful algorithm was SARIMA-MR1. Therefore, stochastic methods should be preferred in analyses that do not incorporate WT.
- In the ANN analyses using WT, negative values were found in all models, indicating that WT had an adverse effect on ANN. Consequently, ANN should not be used with WT for wind speed prediction models in this region.
- In SVM analysis incorporating WT, the M05 model yielded the most successful results. However, in terms of performance, this model still lagged behind LSTM models with WT. Nevertheless, WT led to performance improvements in all SVM models.
- Among machine learning methods, the best results were obtained with LSTM in model M04. Compared to other models, the input structure of M04 is the most suitable for wind speed prediction in this region.
- In LSTM analyses with WT, the most successful model was M04, while the least successful was M01. The input structure of M01 consisted of a single lagged t-12 wind data point. The results indicate that model performance varies depending on both the algorithm and the input structure. Therefore, selecting the appropriate algorithm and optimizing the input structure are critical for achieving accurate forecasts.
- In SARIMA analyses, the most successful model parameters were found in MR1. If stochastic methods are used for wind speed forecasting in this region, the MR1 model parameters should be applied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, B.; Yang, K.; Francis, J.A. Summer Arctic dipole wind pattern affects the winter Siberian High. Int. J. Climatol. 2016, 36, 4187–4201. [Google Scholar]
- Crawford, A.D.; Krumhardt, K.M.; Lovenduski, N.S.; van Dijken, G.L.; Arrigo, K.R. Summer high-wind events and phytoplankton productivity in the Arctic Ocean. J. Geophys. Res. Ocean. 2020, 125, e2020JC016565. [Google Scholar]
- Day, J.J.; Hodges, K.I. Growing land-sea temperature contrast and the intensification of Arctic cyclones. Geophys. Res. Lett. 2018, 45, 3673–3681. [Google Scholar]
- Oliver, J. Norway’s Climate Odyssey: Assessing Impacts, Mitigation Strategies, and Policy Responses in a Warming Arctic. Endless Int. J. Future Stud. 2023, 6, 29–43. [Google Scholar] [CrossRef]
- Jaison, A.; Michel, C.; Sorteberg, A.; Breivik, Ø. Projections of windstorms damages under changing climate and demography for Norway. Environ. Res. Clim. 2024, 3, 045006. [Google Scholar]
- Little, A.S.; Priestley, M.D.; Catto, J.L. Future increased risk from extratropical windstorms in northern Europe. Nat. Commun. 2023, 14, 4434. [Google Scholar]
- Momberg, M.; Hedding, D.W.; Luoto, M.; le Roux, P.C. Exposing wind stress as a driver of fine-scale variation in plant communities. J. Ecol. 2021, 109, 2121–2136. [Google Scholar]
- Kim, J.; Lee, K. Unscented Kalman filter-aided long short-term memory approach for wind nowcasting. Aerospace 2021, 8, 236. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, G. A Short-Term Wind Speed Forecasting Hybrid Model Based on Empirical Mode Decomposition and Multiple Kernel Learning. Complexity 2020, 2020, 8811407. [Google Scholar]
- Haque, A.U.; Mandal, P.; Meng, J.; Negnevitsky, M. Wind speed forecast model for wind farm based on a hybrid machine learning algorithm. Int. J. Sustain. Energy 2015, 34, 38–51. [Google Scholar]
- Valsaraj, P.; Thumba, D.A.; Kumar, S. Machine learning-based simplified methods using shorter wind measuring masts for the time ahead wind forecasting at higher altitude for wind energy applications. Renew. Energy Environ. Sustain. 2022, 7, 24. [Google Scholar]
- Fang, S.; Chiang, H.D. Improving supervised wind power forecasting models using extended numerical weather variables and unlabelled data. IET Renew. Power Gener. 2016, 10, 1616–1624. [Google Scholar]
- Demolli, H.; Dokuz, A.S.; Ecemis, A.; Gokcek, M. Wind power forecasting based on daily wind speed data using machine learning algorithms. Energy Convers. Manag. 2019, 198, 111823. [Google Scholar]
- Khosravi, A.; Machado, L.; Nunes, R. Time-series prediction of wind speed using machine learning algorithms: A case study Osorio wind farm, Brazil. Appl. Energy 2018, 224, 550–566. [Google Scholar]
- Feng, C.; Cui, M.; Hodge, B.-M.; Zhang, J. A data-driven multi-model methodology with deep feature selection for short-term wind forecasting. Appl. Energy 2017, 190, 1245–1257. [Google Scholar]
- Yao, F.; Liu, W.; Zhao, X.; Song, L. Integrated Machine Learning and Enhanced Statistical Approach-Based Wind Power Forecasting in Australian Tasmania Wind Farm. Complexity 2020, 2020, 9250937. [Google Scholar]
- Zhang, Y.H.; Wang, H.; Hu, Z.J.; Wang, K.; Li, Y.; Huang, D.S.; Ning, W.H.; Zhang, C.X. A hybrid short-term wind speed forecasting model based on wavelet decomposition and extreme learning machine. Adv. Mater. Res. 2014, 860, 361–367. [Google Scholar]
- Alkesaiberi, A.; Harrou, F.; Sun, Y. Efficient wind power prediction using machine learning methods: A comparative study. Energies 2022, 15, 2327. [Google Scholar] [CrossRef]
- Lee, J.; Wang, W.; Harrou, F.; Sun, Y. Wind power prediction using ensemble learning-based models. IEEE Access 2020, 8, 61517–61527. [Google Scholar]
- Park, S.; Jung, S.; Lee, J.; Hur, J. A short-term forecasting of wind power outputs based on gradient boosting regression tree algorithms. Energies 2023, 16, 1132. [Google Scholar] [CrossRef]
- Heinermann, J.; Kramer, O. Machine learning ensembles for wind power prediction. Renew. Energy 2016, 89, 671–679. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H.; Chong, Z.R. Long-term forecasting of climatic parameters using parametric and non-parametric stochastic modelling. E3S Web Conf. 2022, 34, 05013. [Google Scholar]
- Liu, X.; Lin, Z.; Feng, Z. Short-term offshore wind speed forecast by seasonal ARIMA-A comparison against GRU and LSTM. Energy 2021, 227, 120492. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, J.; Zhang, W.; Wang, J. A corrected hybrid approach for wind speed prediction in Hexi Corridor of China. Energy 2011, 36, 1668–1679. [Google Scholar]
- Tyass, I.; Khalili, T.; Mohamed, R.; Abdelouahed, B.; Raihani, A.; Mansouri, K. Wind speed prediction based on statistical and deep learning models. Int. J. Renew. Energy Dev. 2023, 12, 288. [Google Scholar]
- Islam, M.; Hassan, N.; Rasul, M.; Emami, K.; Chowdhury, A.A. Forecasting of solar and wind resources for power generation. Energies 2023, 16, 6247. [Google Scholar] [CrossRef]
- Wang, H.; Tian, C.; Wang, W.; Luo, X. Time-series analysis of tuberculosis from 2005 to 2017 in China. Epidemiol. Infect. 2018, 146, 935–939. [Google Scholar]
- Rizwan, M.; Hong, L.; Waseem, M.; Ahmad, S.; Sharaf, M.; Shafiq, M. A robust adaptive overcurrent relay coordination scheme for wind-farm-integrated power systems based on forecasting the wind dynamics for smart energy systems. Appl. Sci. 2020, 10, 6318. [Google Scholar] [CrossRef]
- Alencar, D.B.; Affonso, C.M.; Oliveira, R.C.; Jose Filho, C. Hybrid approach combining SARIMA and neural networks for multi-step ahead wind speed forecasting in Brazil. IEEE Access 2018, 6, 55986–55994. [Google Scholar]
- Parasyris, A.; Alexandrakis, G.; Kozyrakis, G.V.; Spanoudaki, K.; Kampanis, N.A. Predicting meteorological variables on local level with SARIMA, LSTM and hybrid techniques. Atmosphere 2022, 13, 878. [Google Scholar] [CrossRef]
- Myklebust, L.H.; Sørgaard, K.; Wynn, R. Local inpatient units may increase patients’ utilization of outpatient services: A comparative cohort-study in Nordland County, Norway. Psychol. Res. Behav. Manag. 2015, 8, 251–257. [Google Scholar] [PubMed]
- Iversen, E.C.; Burningham, H. Relationship between NAO and wind climate over Norway. Clim. Res. 2015, 63, 115–134. [Google Scholar] [CrossRef]
- Jonassen, M.O.; Ólafsson, H.; Reuder, J.; Olseth, J. Multi-scale variability of winds in the complex topography of southwestern Norway. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 11962. [Google Scholar] [CrossRef]
- Díaz-Yáñez, O.; Mola-Yudego, B.; Eriksen, R.; González-Olabarria, J.R. Assessment of the main natural disturbances on Norwegian forest based on 20 years of national inventory. PLoS ONE 2016, 11, e0161361. [Google Scholar] [CrossRef]
- Michel, C.; Sorteberg, A. Future projections of EURO-CORDEX raw and bias-corrected daily maximum wind speeds over Scandinavia. J. Geophys. Res. Atmos. 2023, 128, e2022JD037953. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Hoboken, NJ, USA, 1998. [Google Scholar]
- Demuth, H.; Beale, M. Neural Network Toolbox for Use with MATLAB: User’s Guide; Computation, Visualization, Programming; MathWorks Incorporated: Natick, MA, USA, 1998. [Google Scholar]
- Piri, J.; Amin, S.; Moghaddamnia, A.; Keshavarz, A.; Han, D.; Remesan, R. Daily pan evaporation modeling in a hot and dry climate. J. Hydrol. Eng. 2009, 14, 803–811. [Google Scholar] [CrossRef]
- Kim, T.-W.; Valdés, J.B. Nonlinear model for drought forecasting based on a conjunction of wavelet transforms and neural networks. J. Hydrol. Eng. 2003, 8, 319–328. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Temporal hydrological drought index forecasting for New South Wales, Australia using machine learning approaches. Atmosphere 2020, 11, 585. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Cortes, C. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Oruc, S.; Tugrul, T.; Hinis, M.A. Beyond Traditional Metrics: Exploring the potential of Hybrid algorithms for Drought characterization and prediction in the Tromso Region, Norway. Appl. Sci. 2024, 14, 7813. [Google Scholar] [CrossRef]
- Shabani, E.; Ghorbani, M.A.; Inyurt, S. The power of the GP-ARX model in CO2 emission forecasting. In Risk, Reliability and Sustainable Remediation in the Field of Civil and Environmental Engineering; Elsevier: Amsterdam, The Netherlands, 2022; pp. 79–91. [Google Scholar]
- Buyukyildiz, M.; Kumcu, S.Y. An estimation of the suspended sediment load using adaptive network based fuzzy inference system, support vector machine and artificial neural network models. Water Resour. Manag. 2017, 31, 1343–1359. [Google Scholar]
- Katipoğlu, O.M.; Yeşilyurt, S.N.; Dalkılıç, H.Y.; Akar, F. Application of empirical mode decomposition, particle swarm optimization, and support vector machine methods to predict stream flows. Environ. Monit. Assess. 2023, 195, 1108. [Google Scholar] [PubMed]
- Saha, S.; Saha, A.; Hembram, T.K.; Kundu, B.; Sarkar, R. Novel ensemble of deep learning neural network and support vector machine for landslide susceptibility mapping in Tehri region, Garhwal Himalaya. Geocarto Int. 2022, 37, 17018–17043. [Google Scholar]
- Müller, K.-R.; Mika, S.; Tsuda, K.; Schölkopf, K. An introduction to kernel-based learning algorithms. In Handbook of Neural Network Signal Processing; CRC Press: Boca Raton, FL, USA, 2018; p. 4-1-4-40. [Google Scholar]
- Abumohsen, M.; Owda, A.Y.; Owda, M.; Abumihsan, A. Hybrid machine learning model combining of CNN-LSTM-RF for time series forecasting of Solar Power Generation. e-Prime-Adv. Electr. Eng. Electron. Energy 2024, 9, 100636. [Google Scholar]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural network and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar]
- Gunn, S.R. Support Vector Machines for Classification and Regression; Citeseer: Princeton, NJ, USA, 1997. [Google Scholar]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of groundwater potential mapping based on convolutional neural network (CNN) and support vector regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar]
- Hochreiter, S. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Anshuka, A.; Chandra, R.; Buzacott, A.J.; Sanderson, D.; van Ogtrop, F.F. Spatio temporal hydrological extreme forecasting framework using LSTM deep learning model. Stoch. Environ. Res. Risk Assess. 2022, 36, 3467–3485. [Google Scholar]
- Ham, Y.-S.; Sonu, K.-B.; Paek, U.-S.; Om, K.-C.; Jong, S.-I.; Jo, K.-R. Comparison of LSTM network, neural network and support vector regression coupled with wavelet decomposition for drought forecasting in the western area of the DPRK. Nat. Hazards 2023, 116, 2619–2643. [Google Scholar]
- Zhang, K.; Chao, W.-L.; Sha, F.; Grauman, K. Video summarization with long short-term memory. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part VII 14. pp. 766–782. [Google Scholar]
- Tai, T.-M.; Jhang, Y.-J.; Liao, Z.-W.; Teng, K.-C.; Hwang, W.-J. Sensor-based continuous hand gesture recognition by long short-term memory. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar]
- Hu, X.; Zhang, B.; Tang, G. Research on ship motion prediction algorithm based on dual-pass long short-term memory neural network. IEEE Access 2021, 9, 28429–28438. [Google Scholar]
- Venugopalan, S.; Xu, H.; Donahue, J.; Rohrbach, M.; Mooney, R.; Saenko, K. Translating videos to natural language using deep recurrent neural networks. arXiv 2014, arXiv:1412.4729. [Google Scholar]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar]
- Wang, F.; Gao, G. Optimization of short-term wind power prediction of Multi-kernel Extreme Learning Machine based on Sparrow Search Algorithm. J. Phys. Conf. Ser. 2023, 2527, 012075. [Google Scholar]
- Chen, Q.; Zhao, H.; Qiu, H.; Wang, Q.; Zeng, D.; Ye, M. Time series analysis of rubella incidence in Chongqing, China using SARIMA and BPNN mathematical models. J. Infect. Dev. Ctries. 2022, 16, 1343–1350. [Google Scholar]
- Xu, Q.; Li, R.; Liu, Y.; Luo, C.; Xu, A.; Xue, F.; Xu, Q.; Li, X. Forecasting the incidence of mumps in Zibo City based on a SARIMA model. Int. J. Environ. Res. Public Health 2017, 14, 925. [Google Scholar] [CrossRef]
- Zou, J.-J.; Jiang, G.-F.; Xie, X.-X.; Huang, J.; Yang, X.-B. Application of a combined model with seasonal autoregressive integrated moving average and support vector regression in forecasting hand-foot-mouth disease incidence in Wuhan, China. Medicine 2019, 98, e14195. [Google Scholar]
- Wang, Z.D.; Yang, C.X.; Zhang, S.K.; Wang, Y.B.; Xu, Z.; Feng, Z.J. Analysis and forecasting of syphilis trends in mainland China based on hybrid time series models. Epidemiol. Infect. 2024, 152, e93. [Google Scholar] [PubMed]
- Peirano, R.; Kristjanpoller, W.; Minutolo, M.C. Forecasting inflation in Latin American countries using a SARIMA–LSTM combination. Soft Comput. 2021, 25, 10851–10862. [Google Scholar]
- Maarof, M.Z.M.; Ismail, Z.; Fadzli, M. Optimization of SARIMA model using genetic algorithm method in forecasting Singapore tourist arrivals to Malaysia. Appl. Math. Sci 2014, 8, 8481–8491. [Google Scholar]
- Zhou, L.; Zhao, P.; Wu, D.; Cheng, C.; Huang, H. Time series model for forecasting the number of new admission inpatients. BMC Med. Inform. Decis. Mak. 2018, 18, 1–11. [Google Scholar]
- Yu, G.; Feng, H.; Feng, S.; Zhao, J.; Xu, J. Forecasting hand-foot-and-mouth disease cases using wavelet-based SARIMA–NNAR hybrid model. PLoS ONE 2021, 16, e0246673. [Google Scholar]
- Duangchaemkarn, K.; Boonchieng, W.; Wiwatanadate, P.; Chouvatut, V. SARIMA model forecasting performance of the COVID-19 daily statistics in Thailand during the Omicron variant epidemic. Healthcare 2022, 10, 1310. [Google Scholar] [CrossRef]
- ArunKumar, K.; Kalaga, D.V.; Kumar, C.M.S.; Chilkoor, G.; Kawaji, M.; Brenza, T.M. Forecasting the dynamics of cumulative COVID-19 cases (confirmed, recovered and deaths) for top-16 countries using statistical machine learning models: Auto-Regressive Integrated Moving Average (ARIMA) and Seasonal Auto-Regressive Integrated Moving Average (SARIMA). Appl. Soft Comput. 2021, 103, 107161. [Google Scholar]
- Noor, T.H.; Almars, A.M.; Alwateer, M.; Almaliki, M.; Gad, I.; Atlam, E.-S. Sarima: A seasonal autoregressive integrated moving average model for crime analysis in Saudi Arabia. Electronics 2022, 11, 3986. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Maheswaran, R.; Khosa, R. Comparative study of different wavelets for hydrologic forecasting. Comput. Geosci. 2012, 46, 284–295. [Google Scholar]
- Sang, Y.-F. A review on the applications of wavelet transform in hydrology time series analysis. Atmos. Res. 2013, 122, 8–15. [Google Scholar]
- Wang, H.; Cao, J.Z.; Tang, L.N.; Zhou, Z.F. A Joint Method Based on Wavelet and Curvelet Transform for Image Denoising. Adv. Mater. Res. 2012, 532, 758–762. [Google Scholar]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar]
- Yilmaz, V.; Koycegiz, C.; Buyukyildiz, M. Performance of data-driven models based on seasonal-trend decomposition for streamflow forecasting in different climate regions of Türkiye. Phys. Chem. Earth Parts A/B/C 2024, 136, 103696. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar]
- Karaman, Ö.A. Prediction of Wind Power with Machine Learning Models. Appl. Sci. 2023, 13, 11455. [Google Scholar] [CrossRef]
- Demirtop, A.; Sevli, O. Wind speed prediction using LSTM and ARIMA time series analysis models: A case study of Gelibolu. Turk. J. Eng. 2024, 8, 524–536. [Google Scholar]
- Oruc, S.; Hinis, M.A.; Tugrul, T. Evaluating Performances of LSTM, SVM, GPR, and RF for Drought Prediction in Norway: A Wavelet Decomposition Approach on Regional Forecasting. Water 2024, 16, 3465. [Google Scholar] [CrossRef]
- Taoussi, B.; Damani, M.A.; Boudia, S.M. Seasonal ARIMA and LSTM Models for Wind Speed Prediction at El-Oued Region, Algeria. In Proceedings of the 2024 6th International Conference on Pattern Analysis and Intelligent Systems (PAIS), El Oued, Algeria, 24–25 April 2024. [Google Scholar] [CrossRef]
- Tuğrul, T.; Hınıs, M.A.; Oruç, S. Comparison of LSTM and SVM methods through wavelet decomposition in drought forecasting. Earth Sci. Inform. 2025, 18, 139. [Google Scholar] [CrossRef]
- Tuğrul, T.; Hinis, M.A. Improvement of drought forecasting by means of various machine learning algorithms and wavelet transformation. Acta Geophys. 2024, 73, 855–874. [Google Scholar] [CrossRef]
- Vidyarthi, V.K.; Jain, A. Knowledge extraction from trained ANN drought classification model. J. Hydrol. 2020, 585, 124804. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B. Short-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet transforms and machine learning methods. Sustain. Water Resour. Manag. 2016, 2, 87–101. [Google Scholar] [CrossRef]



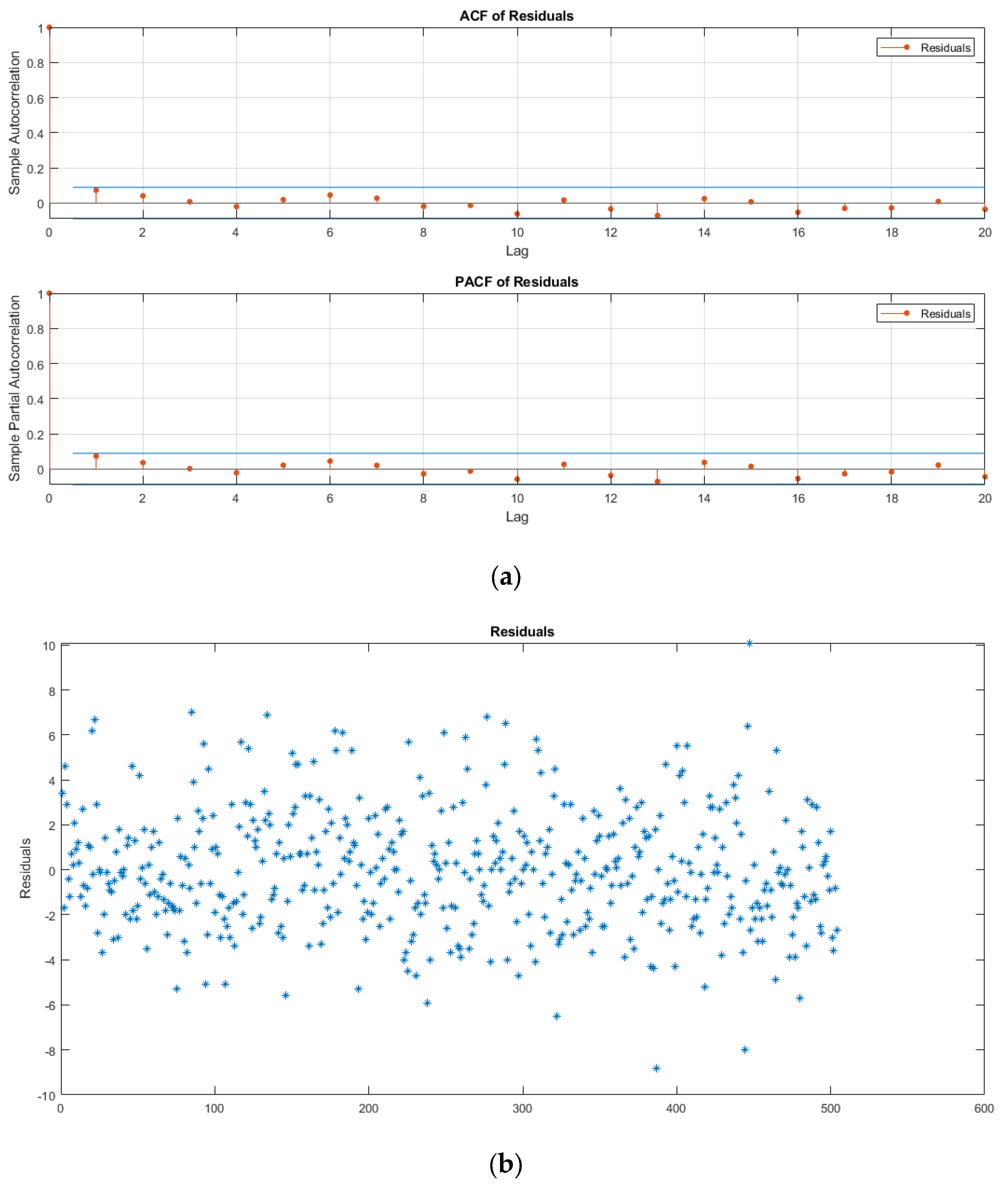
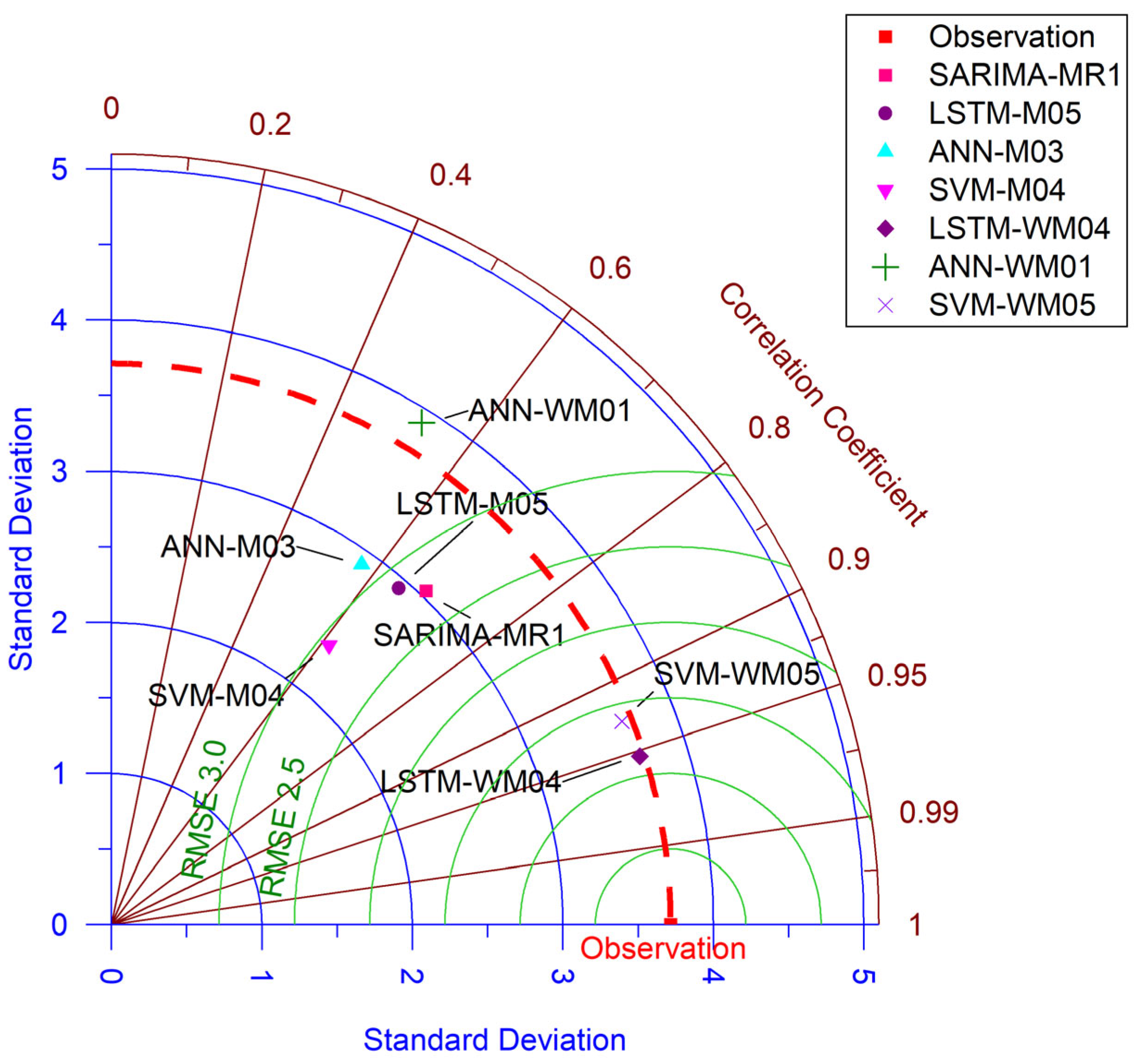
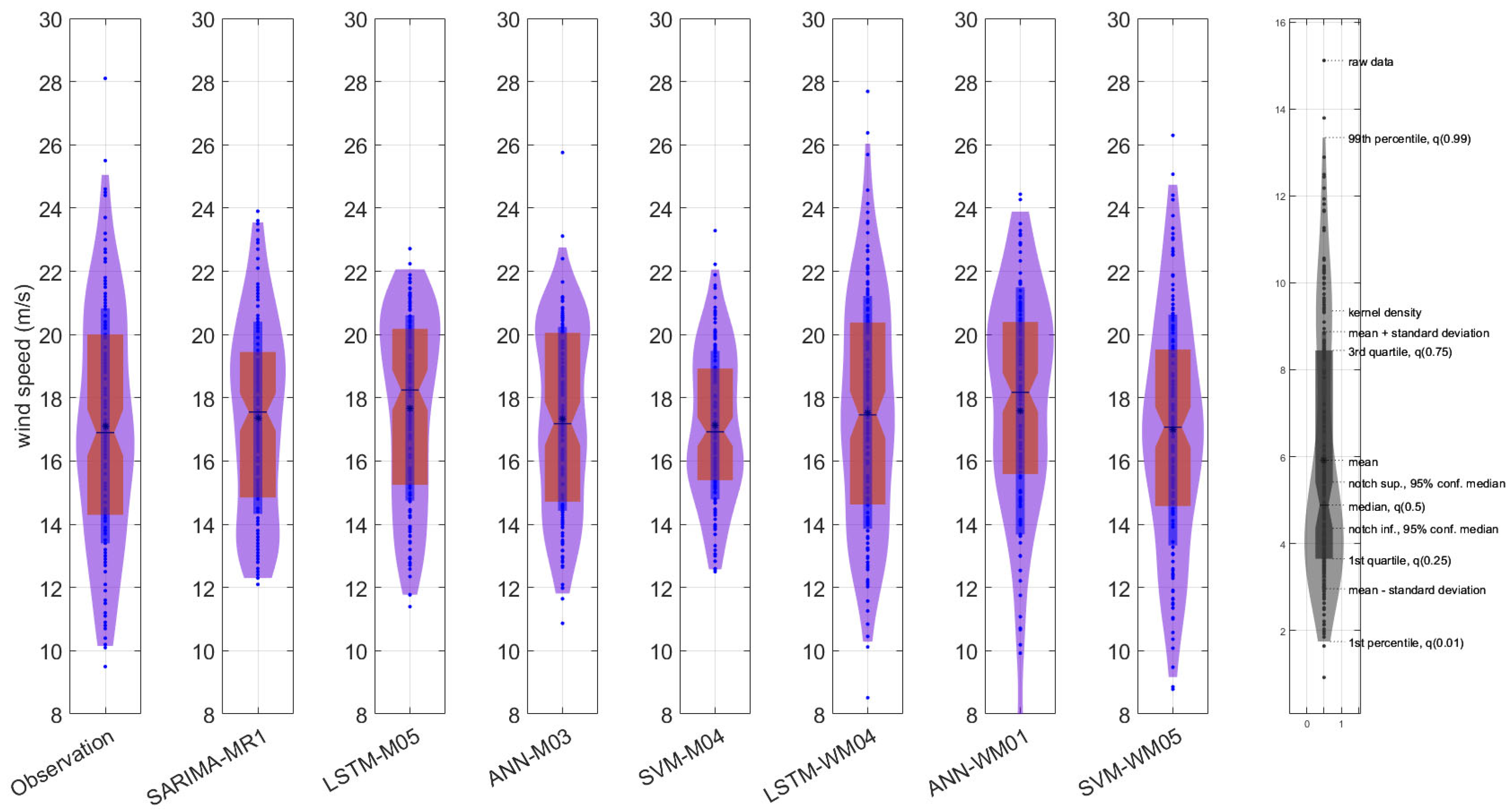

| Data | Number of Data | Initial Data | End of Data | Mean | Min. (m/s) | Max. (m/s) | Standard Deviation | Skewness |
|---|---|---|---|---|---|---|---|---|
| Maximum Monthly Wind Speed | 492 | January 1983 | December 2023 | 17.66 | 9.3 | 29.3 | 3.25 | 1.15 |
| Model | Inputs | Output | ||||
|---|---|---|---|---|---|---|
| M01 | Wt-12 | Wt | ||||
| M02 | Wt-11 | Wt-12 | Wt | |||
| M03 | Wt-1 | Wt-11 | Wt-12 | Wt | ||
| M04 | Wt-2 | Wt-1 | Wt-11 | Wt-12 | Wt | |
| M05 | Wt-10 | Wt-2 | Wt-1 | Wt-11 | Wt-12 | Wt |
| LSTM | ANN | SVM | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | NSE | KGE | PI | RSR | RMSE | R | NSE | KGE | PI | RSR | RMSE | R | NSE | KGE | PI | RSR | RMSE | |
| M01 | 0.6087 | 0.2715 | 0.5612 | 0.1148 | 0.2289 | 0.8506 | 0.5161 | 0.2016 | 0.4562 | 0.1275 | 0.8905 | 3.3086 | 0.5451 | 0.2932 | 0.3992 | 0.1177 | 0.2255 | 0.8378 |
| M02 | 0.6461 | 0.3678 | 0.5519 | 0.1045 | 0.2133 | 0.7924 | 0.5568 | 0.2617 | 0.4810 | 0.1194 | 0.8564 | 3.1816 | 0.5818 | 0.3340 | 0.4434 | 0.1116 | 0.2189 | 0.8133 |
| M03 | 0.6511 | 0.3784 | 0.5466 | 0.1033 | 0.2115 | 0.7858 | 0.5717 | 0.2788 | 0.5195 | 0.1169 | 0.8464 | 3.1446 | 0.6120 | 0.3743 | 0.4613 | 0.1062 | 0.2122 | 0.7883 |
| M04 | 0.4971 | 0.1613 | 0.1391 | 0.1323 | 0.2457 | 0.9127 | 0.5663 | 0.2021 | 0.5544 | 0.1234 | 0.8902 | 3.3075 | 0.6160 | 0.3792 | 0.4683 | 0.1055 | 0.2114 | 0.7853 |
| M05 | 0.6511 | 0.3818 | 0.5910 | 0.1030 | 0.2109 | 0.7836 | 0.2182 | −1.9460 | 0.0029 | 0.3048 | 1.7106 | 6.3554 | 0.6167 | 0.3787 | 0.4678 | 0.1055 | 0.2114 | 0.7856 |
| LSTM-W | ANN-W | SVM-W | ||||||||||||||||
| R | NSE | KGE | PI | RSR | RMSE | R | NSE | KGE | PI | RSR | RMSE | R | NSE | KGE | PI | RSR | RMSE | |
| M01 | 0.6709 | 0.4055 | 0.5991 | 0.0998 | 0.2068 | 0.7684 | 0.5274 | −0.0131 | 0.5238 | 0.1426 | 1.0031 | 3.7270 | 0.6754 | 0.4516 | 0.5858 | 0.0956 | 0.1987 | 0.7381 |
| M02 | 0.6457 | 0.3305 | 0.6260 | 0.1076 | 0.2195 | 0.8155 | 0.1137 | −0.5921 | 0.1034 | 0.2451 | 1.2575 | 4.6720 | 0.6775 | 0.4513 | 0.5976 | 0.0955 | 0.1987 | 0.7383 |
| M03 | 0.9400 | 0.8646 | 0.9282 | 0.0410 | 0.0987 | 0.3667 | 0.4148 | −1.5852 | 0.0588 | 0.2459 | 1.6024 | 5.9534 | 0.8453 | 0.7133 | 0.7745 | 0.0628 | 0.1436 | 0.5336 |
| M04 | 0.9532 | 0.8938 | 0.9463 | 0.0361 | 0.0870 | 0.3248 | 0.2851 | −1.0483 | 0.2104 | 0.2409 | 1.4263 | 5.2993 | 0.9289 | 0.8593 | 0.9276 | 0.0421 | 0.1006 | 0.3739 |
| M05 | 0.9502 | 0.8820 | 0.9421 | 0.0381 | 0.0921 | 0.3423 | 0.4374 | −1.0264 | 0.2224 | 0.2143 | 1.4187 | 5.2710 | 0.9296 | 0.8601 | 0.9270 | 0.0419 | 0.1003 | 0.3728 |
| SARIMA | ||||||||||||||||||
| R | NSE | KGE | PI | RSR | RMSE | |||||||||||||
| MR1 | 0.7411 | 0.5455 | 0.6745 | 0.0856 | 0.6735 | 2.6348 | ||||||||||||
| MR2 | 0.7153 | 0.5013 | 0.6543 | 0.0910 | 0.7055 | 2.7598 | ||||||||||||
| MR3 | 0.7186 | 0.4954 | 0.6859 | 0.0913 | 0.7096 | 2.7761 | ||||||||||||
| MR1: | (0,0,0)(8,1,0)12 | |||||||||||||||||
| MR2: | (1,1,1)(6,1,0)12 | |||||||||||||||||
| MR3: | (6,1,0)(8,1,0)12 | |||||||||||||||||
| (a) | ||||||||
| Model | AIC | BIC | Log Likelihood | |||||
| SARIMA (0,0,0)(8,1,0)12 (MR1) | 992.5600 | 1026.3410 | −488.2800 | |||||
| SARIMA (1,1,1)(6,1,0)12 (MR2) | 1039.2921 | 1073.0730 | −511.6460 | |||||
| SARIMA (6,1,0)(8,1,0)12 (MR3) | 1057.2203 | 1116.3360 | −514.6102 | |||||
| (b) | ||||||||
| Model Estimation Section | ||||||||
| Parameter | Parameter Estimate | Standard Error | T-Value | Prob Level | ||||
| SAR (1) | −0.8007 | 0.0446 | −17.9386 | 0.0000 | ||||
| SAR (2) | −0.7161 | 0.0543 | −13.1831 | 0.0000 | ||||
| SAR (3) | −0.6014 | 0.0604 | −9.9501 | 0.0000 | ||||
| SAR (4) | −0.5319 | 0.0611 | −8.7065 | 0.0000 | ||||
| SAR (5) | −0.4948 | 0.0610 | −8.1042 | 0.0000 | ||||
| SAR (6) | −0.4185 | 0.0592 | −7.0708 | 0.0000 | ||||
| SAR (7) | −0.3718 | 0.0538 | −6.9135 | 0.0000 | ||||
| SAR (8) | −0.1595 | 0.0449 | −3.5508 | 0.0004 | ||||
| (c) | ||||||||
| SAR (1) | SAR (2) | SAR (3) | SAR (4) | SAR (5) | SAR (6) | SAR (7) | SAR (8) | |
| SAR (1) | 1.0000 | 0.6202 | 0.5012 | 0.3906 | 0.3343 | 0.3099 | 0.2599 | 0.2580 |
| SAR (2) | 0.6202 | 1.0000 | 0.7035 | 0.5497 | 0.4252 | 0.3553 | 0.2990 | 0.2431 |
| SAR (3) | 0.5012 | 0.7035 | 1.0000 | 0.7262 | 0.5755 | 0.4437 | 0.3573 | 0.3007 |
| SAR (4) | 0.3906 | 0.5497 | 0.7262 | 1.0000 | 0.7151 | 0.5455 | 0.3914 | 0.2916 |
| SAR (5) | 0.3343 | 0.4252 | 0.5755 | 0.7151 | 1.0000 | 0.6995 | 0.5216 | 0.3538 |
| SAR (6) | 0.3099 | 0.3553 | 0.4437 | 0.5455 | 0.6995 | 1.0000 | 0.6715 | 0.4741 |
| SAR (7) | 0.2599 | 0.2990 | 0.3573 | 0.3914 | 0.5216 | 0.6715 | 1.0000 | 0.6022 |
| SAR (8) | 0.2580 | 0.2431 | 0.3007 | 0.2916 | 0.3538 | 0.4741 | 0.6022 | 1.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuğrul, T.; Oruç, S.; Hınıs, M.A. Transforming Wind Data into Insights: A Comparative Study of Stochastic and Machine Learning Models in Wind Speed Forecasting. Appl. Sci. 2025, 15, 3543. https://doi.org/10.3390/app15073543
Tuğrul T, Oruç S, Hınıs MA. Transforming Wind Data into Insights: A Comparative Study of Stochastic and Machine Learning Models in Wind Speed Forecasting. Applied Sciences. 2025; 15(7):3543. https://doi.org/10.3390/app15073543
Chicago/Turabian StyleTuğrul, Türker, Sertaç Oruç, and Mehmet Ali Hınıs. 2025. "Transforming Wind Data into Insights: A Comparative Study of Stochastic and Machine Learning Models in Wind Speed Forecasting" Applied Sciences 15, no. 7: 3543. https://doi.org/10.3390/app15073543
APA StyleTuğrul, T., Oruç, S., & Hınıs, M. A. (2025). Transforming Wind Data into Insights: A Comparative Study of Stochastic and Machine Learning Models in Wind Speed Forecasting. Applied Sciences, 15(7), 3543. https://doi.org/10.3390/app15073543







