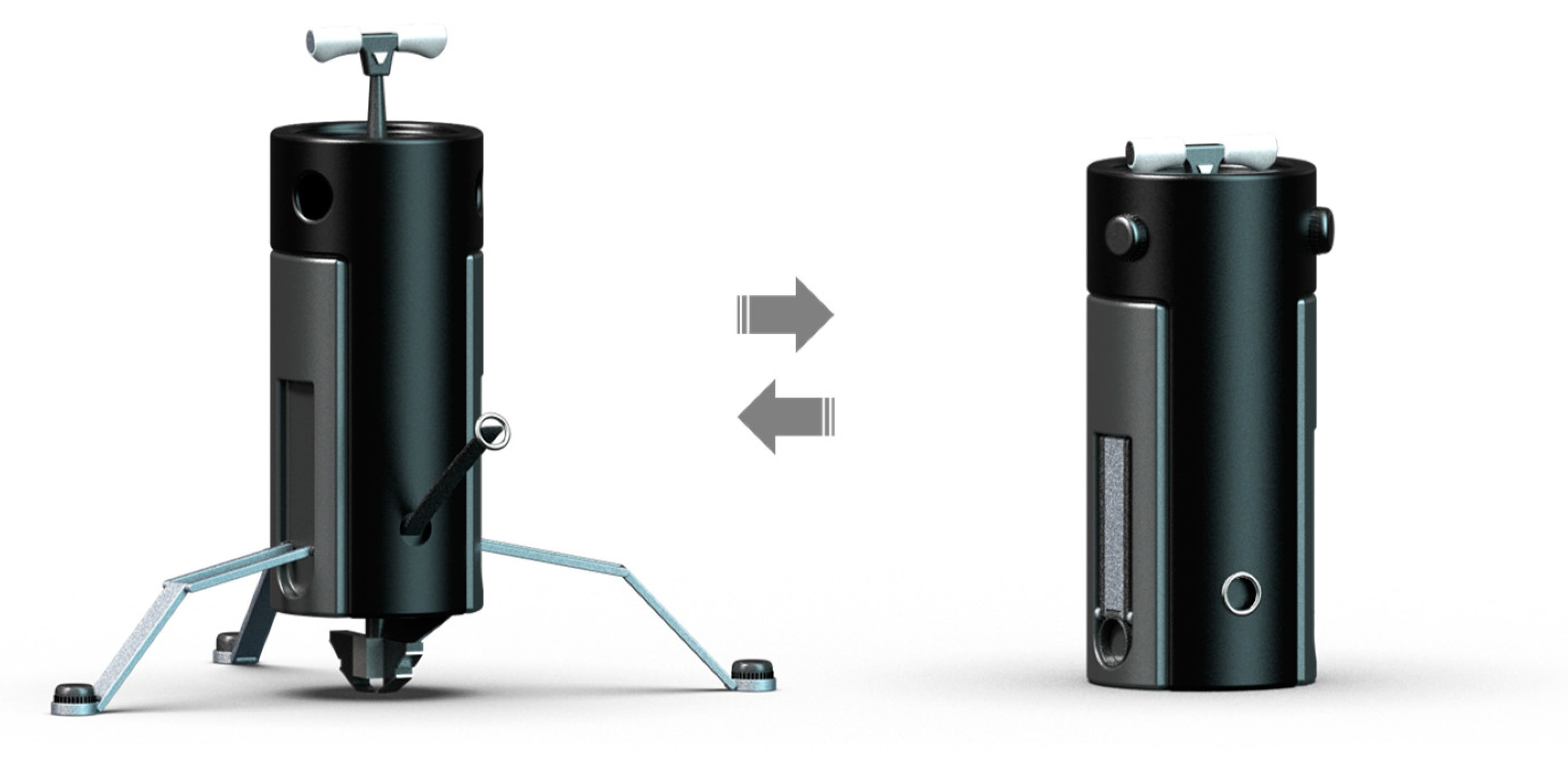
3.2. Solution Based on Axiomatic Design
Axiomatic design is a design decision-making theory based on logical and rational thinking processes, proposed by Professor Suh N.P. [
14]. In axiomatic design, the design space is divided into four domains: the customer domain, functional domain, physical domain, and process domain. Each domain represents a set of data, namely customer attributes (CAs), functional requirements (FRs), design parameters (DPs), and process variables (PVs), respectively [
15]. The mapping between the functional, physical, and process domains follows a hierarchical “zigzag mapping” from higher to lower levels. In adjacent domains, the left domain represents the objectives to be achieved, while the right domain represents the means to achieve these objectives, ensuring the independence of functions and structures at each level. However, the mapping in axiomatic design only reflects the relationships between domains and does not indicate the means by which the objectives in the left domain are achieved. The mapping relationships among the domains in axiomatic design are illustrated in
Figure 2.
Axiomatic design is primarily based on two core axioms: the Independence Axiom and the Information Axiom. The Independence Axiom mandates that functional requirements (FRS) remain mutually independent in the design process to reduce coupling and complexity. The Information Axiom focuses on minimizing the information content in the design, ensuring simplicity and system stability [
16]. The mapping relationship between the functional domain and the physical domain can be expressed as follows:
where
represents the vector of functional requirements, with elements denoted as
;
denotes the vector of design parameters; and
is the design matrix that maps
to
. The specific design expression is given in Equation (4), where
and
represent the number of functional requirements and design parameters, respectively.
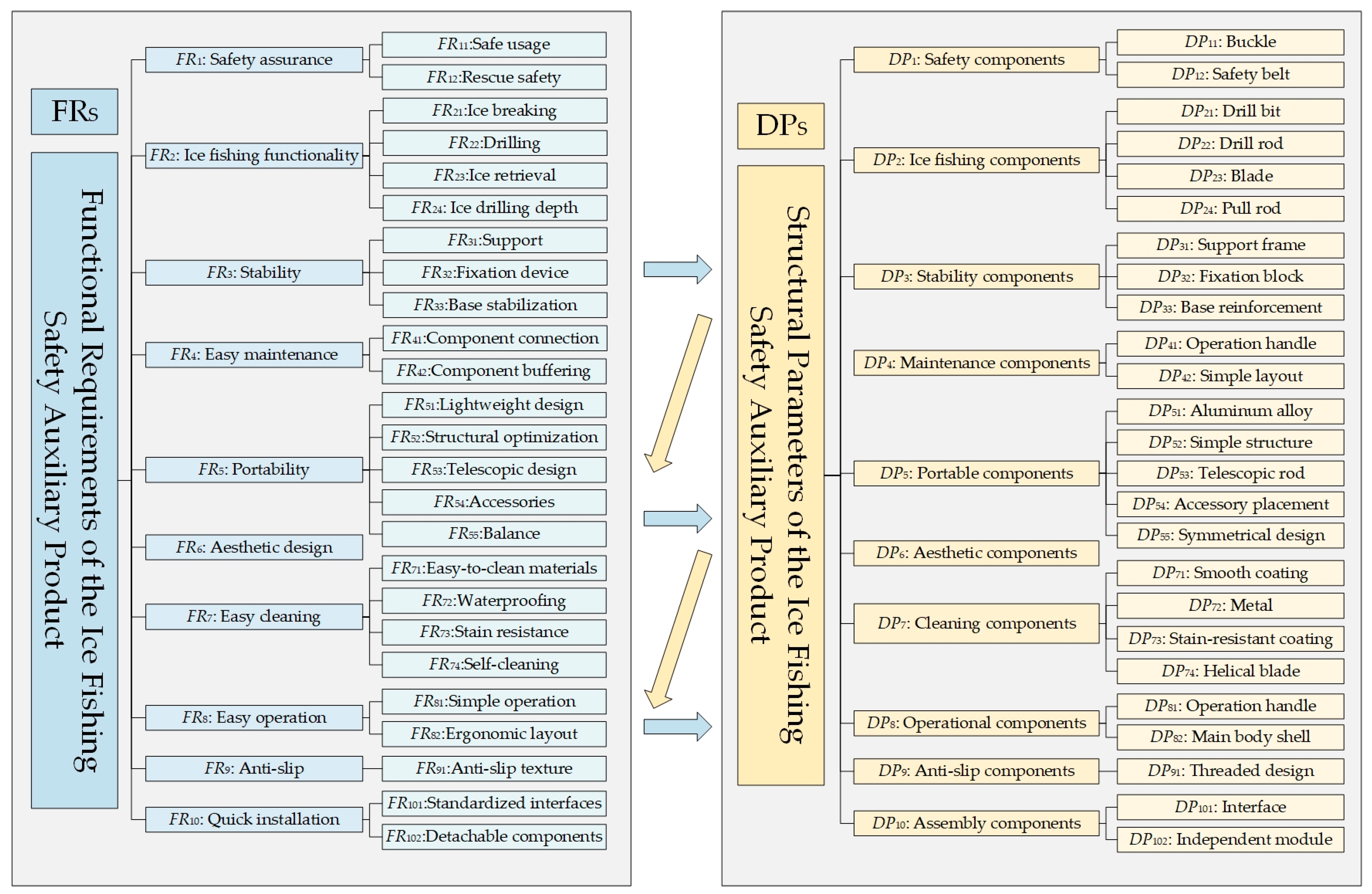
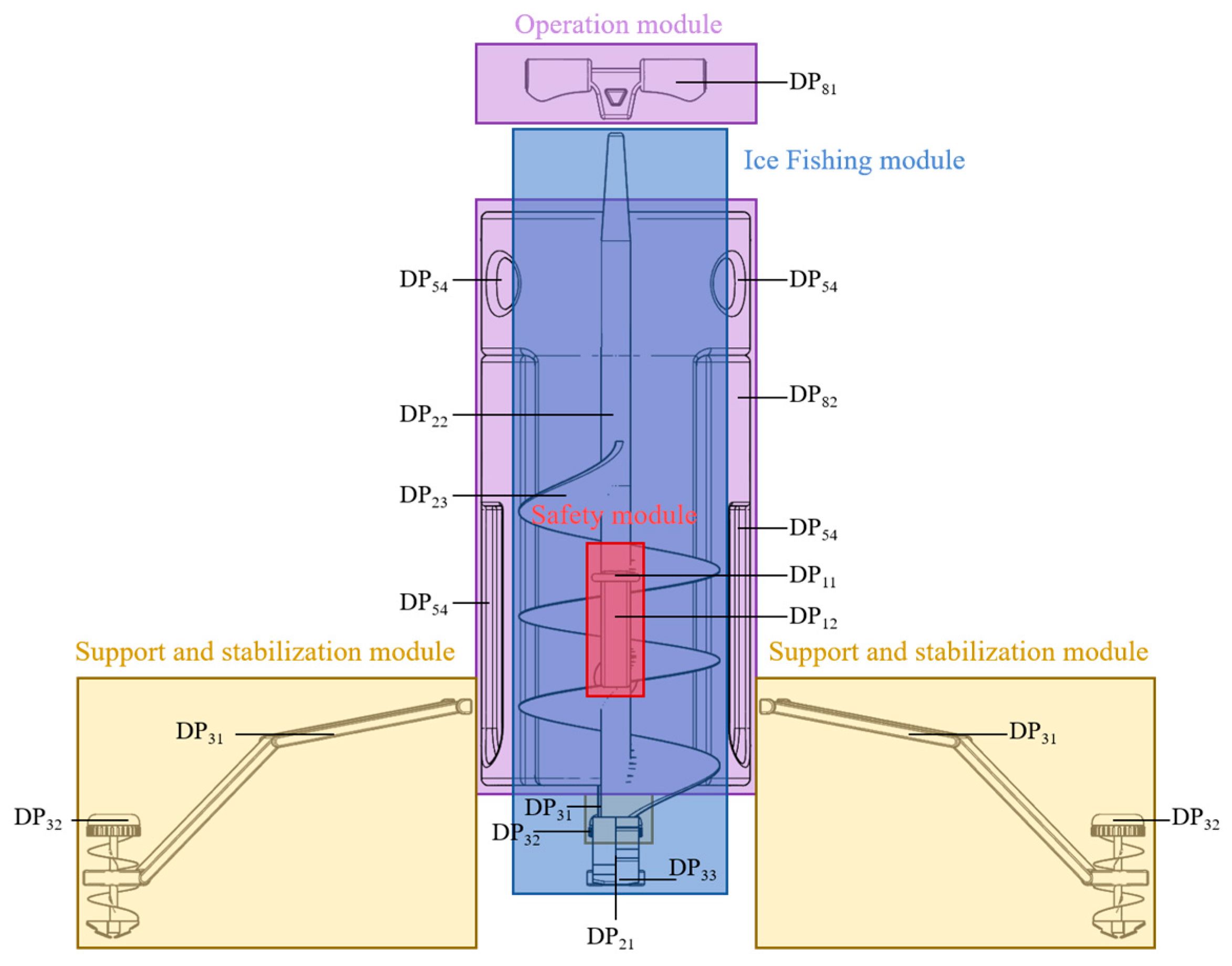
The design requirements obtained through qualitative and quantitative analysis using the Kano model are integrated into the axiomatic design process. Using the “Z-shaped mapping” mechanism between the functional domain and the physical domain, user requirements are progressively decomposed. For example, the requirements for ice fishing can be broken down into functional needs such as ice breaking, ice drilling, and drilling depth. Corresponding structural design parameters are then selected based on these requirements. Specifically, the ice-breaking requirement corresponds to the structural parameter of the drill bit. This process results in the functional decomposition diagram of the ice fishing safety auxiliary product, as shown in
Figure 3.
3.3. Solution with DSM
The design structure matrix (DSM) is an N-order matrix introduced by Donald Steward in 1981 for analyzing information flow [
17]. The core of the DSM lies in its ability to visually represent and analyze the dependencies among the components or activities of a system in matrix form, thereby optimizing processes and reducing unnecessary complexity. Ice fishing safety auxiliary products are complex systems with multiple elements, and the DSM can effectively identify and optimize the dependencies among their components, simplifying the structural layout and improving design efficiency and product performance.
When axiomatic design (AD) is employed as the guiding framework for designing ice fishing safety auxiliary products, requirement analysis and functional decomposition of the device are required to establish the axiomatic design matrix. However, traditional AD matrices only reflect the mapping relationships between functional requirements (FRs) and design parameters (DPs) but fail to capture the interdependencies among design parameters. The DSM offers an intuitive representation of the coupling relationships between design parameters. Hence, the AD-DSM can more comprehensively reflect the mapping and coupling relationships between design parameters for ice fishing safety auxiliary products.
The DSM facilitates modular division based on the coupling relationships within the product structure [
18,
19,
20], but it does not explicitly detail the specific correlations among design parameters. By incorporating geometric correlations, the design matrix can be transformed into a DSM to more accurately display the specific correlations and interrelationships among design parameters, optimizing the product’s modular design [
21]. The specific construction process is as follows:
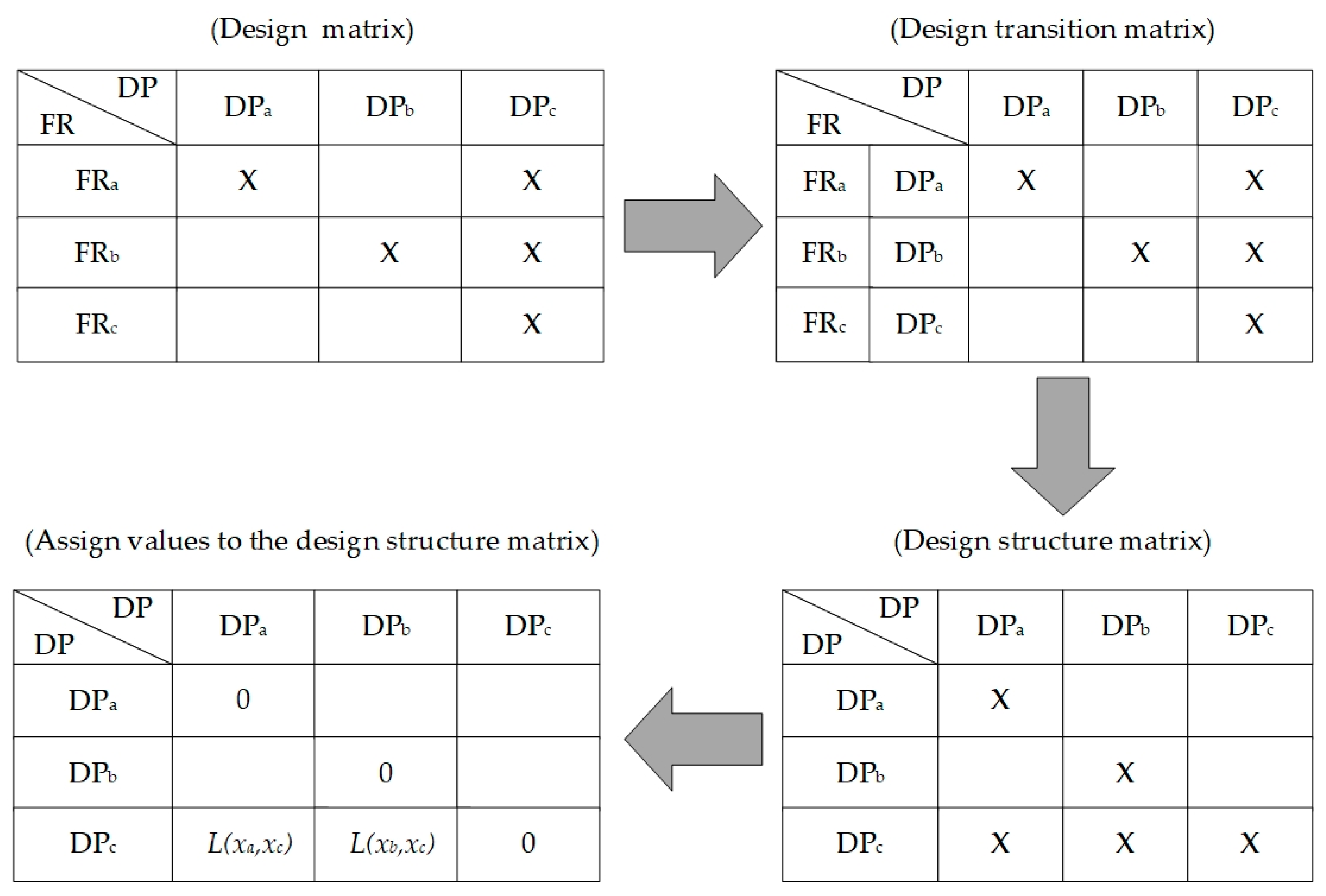
- (1)
Develop an axiom-based design for ice fishing safety auxiliary products based on user needs.
- (2)
Replace the DPS with the highest correlation to the FRS in each row of the axiom design matrix with the corresponding functional items, resulting in the design transition matrix for the ice fishing safety auxiliary product.
- (3)
Perform appropriate transformations on the rows and columns of the design transition matrix, so that elements corresponding to the same design parameters are placed on the diagonal. Adjust the same design parameters to the lower triangular part of the matrix, thereby converting the feedback information into feedforward information, resulting in the DSM for the ice fishing safety auxiliary product.
- (4)
Set the design parameter correlation evaluation criteria and assign values to the DSM for ice fishing safety auxiliary products based on geometric correlation.
The construction process is illustrated in
Figure 4.
Considering the product design requirements and recognizing that general connecting components such as bolts and nuts have minimal impact on the study of detachable design for ice fishing safety auxiliary products, these components were excluded from the analysis. As a result, 23 structural parameters were retained. This study therefore focuses on these 23 structural parameters as the research objects and constructs a design matrix to map the functional–structural requirements of ice fishing safety auxiliary products, as shown in
Table 3.
According to design step (2), the design parameters in the design matrix are adjusted to obtain the design transition matrix, as shown in
Table 4.
According to design step (3), the design transition matrix is converted into the design structure matrix. Since the design structure matrix is a symmetric matrix, the dependency values of the design parameters on the diagonal are the same as those of the corresponding parameter pairs. Therefore, either the upper or lower triangular part of the matrix can be used to represent the entire matrix, resulting in an upgraded and simplified design structure matrix, as shown in
Table 5.
After decoupling the design matrix for ice fishing safety auxiliary products and establishing the DSM following the process in
Figure 4, values are assigned based on geometric correlation [
22]. The physical relationships between design parameters in terms of spatial and geometric connections are referred to as geometric correlation, which includes physical connections, perpendicularity, assembly processes, dimensions, and other physical relationships. Based on reference [
23], the correlation evaluation criteria for the design parameters of the ice fishing safety auxiliary product are established from the perspectives of structural correlation, geometric relationship, functional relevance, and evolutionary correlation degree. Quantitative constraints are applied to the correlated design parameters, and the evaluation criteria are shown in
Table 6,
Table 7,
Table 8 and
Table 9. Specifically, the score α1 in
Table 6 reflects the connection strength between components, ranging from non-dismountable connections (highest score) to no connection (lowest score). These scores are obtained through a qualitative assessment of connection methods such as welding, interference fit, or threading, considering their impact on the product’s performance. The score α2 in
Table 7 represents the geometric relationship between components, with a score of 10 indicating a strict geometric relationship (e.g., parallelism), and lower scores indicating weaker or no geometric relationship. These scores are determined through a geometric analysis of the relative positions and orientations of the components. The score α3 in
Table 8 is used to evaluate the contribution of each component to achieving the overall function of the product. The scores are determined by analyzing the system’s functions and considering how the performance of each component affects the overall functionality, with higher scores indicating a stronger functional relationship. The score α4 in
Table 9 is used to evaluate the impact of upgrading one component on the potential for upgrading other components. A score of 10 indicates that upgrading one component requires upgrading another, while lower scores reflect weaker dependencies between components. The specific scores are determined through an analysis of the component lifecycle and the interdependencies during the upgrade process.
According to the above evaluation criteria, the comprehensive correlation among design parameters of the ice fishing safety auxiliary products can be calculated as follows:
- (1)
Let
C represent the comprehensive correlation among the product components in the four aforementioned aspects. The formula for calculating the comprehensive correlation of the design parameters of the ice fishing safety auxiliary products is as follows:
- (2)
Define the weights of structural correlation, geometrical relationships, functional relevance, and evolutionary correlation for ice fishing safety auxiliary products as
,
,
, and
, respectively. In the modularization of ice fishing safety auxiliary products, structural correlation has the greatest impact on module division. When two components are permanently connected (such as welding or interference fit), they cannot be separated and must belong to the same module. Therefore,
Q1 is assigned the highest weight. Geometrical relationships reflect the geometric constraints between components (such as parallelism or precise alignment), which significantly influence the overall integrity of the module. However, compared to structural connections, geometrical constraints allow some flexibility. Hence,
Q2 is assigned a weight lower than
Q1. Functional relevance evaluates the synergistic effect between components, but not all functionally related components must be tightly connected structurally. Therefore,
Q3 is assigned a moderate weight. Evolutionary correlation measures whether the upgrade of one component requires synchronous adjustments of other components. While important for long-term adaptability, it has less impact on the initial module division. Therefore,
Q4 is assigned the lowest weight. Based on the above, it can be concluded that
Q1 >
Q2 >
Q3 >
Q4. Considering expert consultations and engineering practice, the final weight set is determined as follows:
- (3)
Define the rating set for ice fishing safety auxiliary products as
, where
represent the evaluation values of the four criteria, such as structural tightness. The correlation under each individual criterion can thus be calculated using the following formula:
- (4)
In summary, the formula for calculating the comprehensive correlation
C among the components of ice fishing safety auxiliary products is as follows:
According to the scoring criteria outlined in
Table 6,
Table 7,
Table 8 and
Table 9, the theoretical maximum score for a single evaluation criterion is 10, while the minimum score is 0. Based on this scoring range, a threshold of 5 is established as the benchmark for determining the strength of the correlation between design parameters. When the total correlation value between two design parameters exceeds 5, it indicates a high degree of correlation between them. Such a high level of correlation suggests that the two parameters exhibit strong interdependence in the design process and require synchronized adjustments or optimizations. For instance, when two parameters demonstrate high correlation, they can be considered for inclusion in the same module, or their interdependent effects can be prioritized during design optimization. Conversely, when the total correlation value is less than or equal to 5, it reflects a low degree of correlation, implying minimal mutual influence between the two parameters. In such cases, the parameters can be optimized independently or assigned to different modules for management. Therefore, setting the threshold of the design parameter correlation value at 5 ensures a more scientific and systematic evaluation of the correlation between the design parameters of ice fishing safety auxiliary products.
Based on the transformation method outlined in
Figure 4, the matrix decoupling is performed to obtain the design structure matrix (DSM) for ice fishing safety auxiliary products. The design parameters in the DSM are then assigned values using the correlation evaluation criteria from
Table 6,
Table 7,
Table 8 and
Table 9. For example, for DP11 and DP12, which involve the use of buckles and safety belts, the structural relationship is a threaded connection, which is relatively difficult to disassemble. Therefore, the value of
Q1 is 6. In terms of geometric and positional relationships, the two parameters exhibit a direct relationship, so
Q2 is set to 10. The functional relationship between them is strong, as both parameters jointly ensure safety, so
Q3 is set to 10. Regarding evolutionary correlation, when the safety belt is upgraded, it is recommended that the buckle also be upgraded, so
Q4 is set to 6. Therefore, according to Equation (7), the correlation C(11,12) between design parameters DP11 and DP12 is calculated as follows:
This process is repeated for all parameter pairs, resulting in the design structure matrix for the ice fishing safety auxiliary product with correlation values assigned, as shown in
Table 10.