Recent Advances in Efficient Dynamic Graph Processing

Abstract

Graph as one of the most fundamental and representative data structures has found a wide spectrum of emerging application domains such as social media, financial transactions, biology science, and road networks. Recently, with the proliferation of graph applications, graph processing has attracted much attention in both industry and academia. Among them, most existing works focus on the static graphs in which the vertices and edges are immutable. However, in the real world, graphs are constantly and dynamically changing, bringing tricky challenges to process such dynamic graphs. This paper surveys the recent advances in dynamic graph processing, including centrality, graph coloring, cohesive subgraph, path traversal, and graph separation. We summarize the computational complexity models for dynamic algorithm analysis, theoretically compare the efficiency of algorithms among different research topics. Moreover, we also explore the research opportunities for the future.

1. Introduction

A graph is a mathematical structure consisting of vertices and edges connecting certain pairs of them. Graphs have been widely used to represent the relationships of entities in real-world applications such as: social networks, in which a vertex represents a person and an edge between two vertices means two persons know each other [1]; World Wide Web, in which a vertex represents a web page and an edge stands for the hyperlink between two web pages [2]; collaborations networks, in which a vertex represents an author and an edge indicates the co-author relationship between two authors [3]; and protein–protein interaction of biology, in which a vertex indicates a protein and an edge means physical contacts of high specificity established between proteins [4]. With the proliferation of graph applications, research efforts have been devoted to many fundamental problems in managing and analyzing graph data [5].

Traditionally, researchers mainly focus on static graphs where vertices and edges are fixed and do not change over time [6,7,8,9,10]. However, real-world graphs change their topology over time. In a typical dynamic graph problem, one would like to answer queries on graphs that are undergoing a sequence of updates. The goal of a dynamic graph algorithm is to efficiently update the solution of the problem after dynamic changes, rather than having to recompute it from scratch each time. In the last decades, there has been a growing interest in such dynamically changing graphs [11,12,13]. It is not surprising that dynamic algorithms and dynamic data structures are often more difficult to design and analyze [14,15,16].

• Applications. Specifically, dynamic graph processing has many real applications including:

  -

  Social network analysis. In a social network, users are connected by social relationships, such as friendships, professional collaborations, or online interactions. We can identify influential users through betweenness/closeness centrality [17,18], which is crucial for targeted advertising and information diffusion. Besides, in platforms such as Facebook, Twitter, and Instagram, there are applications for community detection, aiming to find cohesive and tightly connected user groups [19,20,21]. The shortest path can also be used to measure the close relationship between users [22,23]. Moreover, dynamic graph partitioning is an effective technique in social networks for balancing server workloads [24].

  -

  Biology science. A biological network is a graph-based representation of interactions between biological entities, such as genes, proteins, cells, or organisms. In biological network analysis, centrality can pinpoint essential proteins/genes in Protein–Protein Interaction (PPI) networks [17,25,26,27]. Moreover, cohesive subgraphs also play an important role in biological networks such as k-core/truss/clique. For example, they can be used to identify groups of genes with similar expression patterns, which may indicate shared functions between genes [28].

  -

  Transportation network. A transportation network is a system of interconnected routes (roads, railways, airways, etc.) and nodes (intersections, stations, airports) that enable the movement of people and goods. In transportation networks, centrality can be used to identify critical transport hubs for infrastructure planning [26]. Besides, dynamic shortest path algorithms enable real-time navigation updates [29].

  -

  Financial data analysis. A financial graph is a network representation of financial relationships, transactions, and dependencies between entities such as banks, companies, individuals, and assets. Dynamic centrality can identify suspicious transaction patterns [30]. Evolving community detection can reveal money laundering networks [31,32]. Moreover, time-dependent financial graphs have risk. For risk assessment, dynamic cohesive subgraph or community can detect tightly coupled risky assets.For market analysis, dynamic graph clustering can be used to track evolving stock correlations [33].

• Challenges. Specifically, the challenges of dynamic graph processing can be listed as follows:

  -

  High frequency of updates. For instance, in online social networks, the graphs are typically large and continually evolving. As of 2023, Facebook has approximately 2.9 billion monthly active users. On average, there are over 50 million posts, comments, and likes per minute. This translates to about 72 billion interactions per day [34]. Twitter has around 461 million monthly active users as of 2023, about 6,000 tweets are posted every second, which amounts to approximately 500 million tweets per day [35].

  -

  High requirement of efficiency. Many applications that rely on dynamic graph processing require real-time or near-real-time response. For instance, fraud detection in financial services or targeted advertising in social media platforms demand immediate analysis of new connections or patterns within the graphs [36].

  -

  High time complexity of update computation. Graphs are inherently complex structures, and performing graph analysis such as path traversal, community detection, or centrality measures can be computationally intensive. For instance, searching many community models, such as clique and biclique, is proven to be an NP-hard problem [16]. As the graph changes, these operations need to be updated efficiently without recalculating from scratch, especially in large-scale scenarios.

In order to cover the above challenges of dynamic graph processing, we survey papers published in recent years, as shown in

Table 1. Classification of recent works in dynamic graphs.

Problem		Fully Dynamic	Incremental Dynamic	Decremental Dynamic	Streaming Dynamic	Single Update	Batch Update
Centrality	Betweenness Centrality	[17,25,26,37,38,39]	[17,18,25,26,38,39,40,41]	[17,25,26,37,38,39]	[18,26,42]	[17,26,38,39,43]	[25,37,41]
	Closeness Centrality	[37,44,45,46,47]	[37,44,45,46,47]	[37,44,45,46,47]	[45]	[44,45,46,47]	[37]
	Eccentricity	[48]	[48]	[48]	-	[48]	-
Graph Coloring	Vertex Coloring	[49,50,51]	[49,50,51,52,53]	[49,50,51,52,53]	-	[49,52,53,54]	[50,51]
	Edge Coloring	[55]	[54,55,56,57,58,59,60,61]	[54,55,56,59,60,61]	-	[54,55,56,57,58,61]	[59,60]
Cohesive Subgraph	Clique	[62]	[16,62,63,64,65]	[62,63,65]	-	[65]	[16,62,63,64]
	Biclique	-	[66,67]	-	-	[67]	[66]
	k-core	-	[19,20,68,69,70,71,72,73,74,75,76]	[19,20,68,69,70,71,72,73,74,75,76]	-	[70,74]	[19,20,68,69,71,72,73,75,76]
	k-truss	-	[21,77,78,79,80,81,82]	[21,77,78,79,81,82]	-	[21,79,80,82]	[77,78,79,81]
	Community	[83]	[83,84,85,86,87,88]	[83,84,87]	[89]	[84,89]	[83,85,86,87,88]
Path Traversal	DFS	[90,91,92,93,94]	[90,91,92,93,94,95,96,97]	[90,91,92,93,94,98]	-	[90,91,92]	[91,92,93,94,95,96,98]
	Shortest Distance	[99,100,101]	[99,100,101,102,103,104,105,106,107,108]	[99,100,101,102,103,104,107,108,109]	-	[100,103,105,106,109]	[99,101,102,104,106,107,108]
	Reachability	-	[110]	-	-	[110]	-
Graph Separation	Graph Partition	[111,112,113,114]	[24,111,112,113,114,115]	[111,112,113,114]	[111,116,117]	[111]	[112,113,115]
	Clustering	[118]	[118,119,120]	[118]	-	[118,120]	[119]
Systems	Systems	-	[121]	-	[122,123,124]	-	-

. The problems addressed in the existing research on dynamic graphs can be categorized into the following main topics:

-

Centrality. Measure the importance of vertices in graphs. Typical definitions of centrality include betweenness centrality, closeness centrality, and eccentricity. They can be utilized in several application domains such as social media, advertising push, and online search engines.

-

Graph Coloring. Assign a color to each vertex such that no two adjacent vertices share the same color. Graph coloring has many practical applications including register allocation, making schedule, and map coloring, and can also be an optimized technique for other graph problems such as clique enumeration and graph partitioning.

-

Cohesive Subgraph. Discover dense groups of vertices in graphs. Typical cohesive subgraph models include clique, biclique, k-core, k-truss, their diverse variants, and community models. They are widely applied in community detection, recommendation systems, and anomaly detection.

-

Path Traversal. Path traversal is a foundational graph computation problem, including depth-first search, shortest distance queries, and reachability queries, and is known to have direct applications in various fields, especially in road networks, such as path planning, navigation, and traffic control.

-

Graph Separation. Graph separation aims to separate the graph into many partitions or clusters. One is to divide the whole graph into several partitions which is important in distributed graph computing systems. Another is to find dense clusters in graphs, for instance, SCAN is the most representative algorithm for clustering.

Existing related surveys focus either on dynamic graph representation and embedding in the field of machine learning [11,12] or on particular dynamic graph problems such as pattern mining [13], anomaly detection [125], and GPU based processing [126]. For other surveys, they do not focus on dynamic graphs. Among them, [127] is the most similar with our survey which also focuses on dynamic graph algorithms. However, Ref. [127] only focuses on the algorithms on fully dynamic graphs, ignoring not only massive partial dynamic algorithms but also the parallel and distributed algorithms. Motivated by this, to fill the gap in the existing reviews, we cover a broader range by surveying papers for dynamic graphs in different graph problem categories, including fully dynamic algorithms, incremental dynamic algorithms, decremental dynamic algorithms, and streaming dynamic algorithms. Moreover, we detail how each algorithm handles updates, distinguishing among serial update, parallel update and distributed update. Additionally, for each class of algorithms, we analyze the advances of existing works and offer a clear comparison of the theoretical complexity across them.

• General analysis. Dynamic graph algorithms have made significant progress in efficiently handling dynamic networks, leveraging incremental updates (e.g., localized re-computation in k-core maintenance or betweenness centrality) and parallel/distributed processing (e.g., parallel betweenness updates). These techniques drastically reduce re-computation overhead compared to static approaches. Many algorithms, such as those for dynamic DFS and shortest paths, achieve linear or near-optimal update times by exploiting structural properties or incremental label propagation. However, when handling highly dynamic and large-scale graphs, some algorithms (e.g., exact clique enumeration) remain impractical due to NP-hardness or excessive memory usage. Efficiency is heavily influenced by factors such as update rate and frequency (e.g., the number of updates), graph size and structure (e.g., arboricity in coloring or core-truss hierarchies). While recent work has improved scalability via parallelism and approximation, challenges remain in streaming graph support, tight theoretical bounds, and handling complex graph types.
• Contributions. In summary, our main contributions are the following:

  (a)

  First, we provide a systematic classification of existing research on dynamic graph processing. For each class of works, we review the State-of-the-Art and representative works.

  (b)

  Second, we summarize three computational complexity models, including boundedness, semi-boundedness and relative boundedness. Specifically, we theoretically analyze the efficiency of algorithms among different research topics on dynamic graphs.

  (c)

  Third, we make discussions on the potential directions of future works, which will promote the development of dynamic graph processing.

The organization of this survey is shown in Figure 1. Section 2 introduces the concepts and common terminology used in this paper. Section 3 extensively discusses the computational complexity model for evaluating the computational complexity of algorithms. Section 4 reviews and analyzes recent existing works for different categories of algorithms on dynamic graphs. Section 5 presents recent system works aiming at managing dynamic graphs. Section 6 provides a discussion on future research directions. Section 7 concludes this survey.

2. Preliminaries

A general and undirected graph $G(V,E)$ contains a set of vertices V and a set of edges E. The degree of a vertex v in G is the number of its neighbors in G. In other words, based on different application scenarios, graphs can have more specific definitions as follows.

-

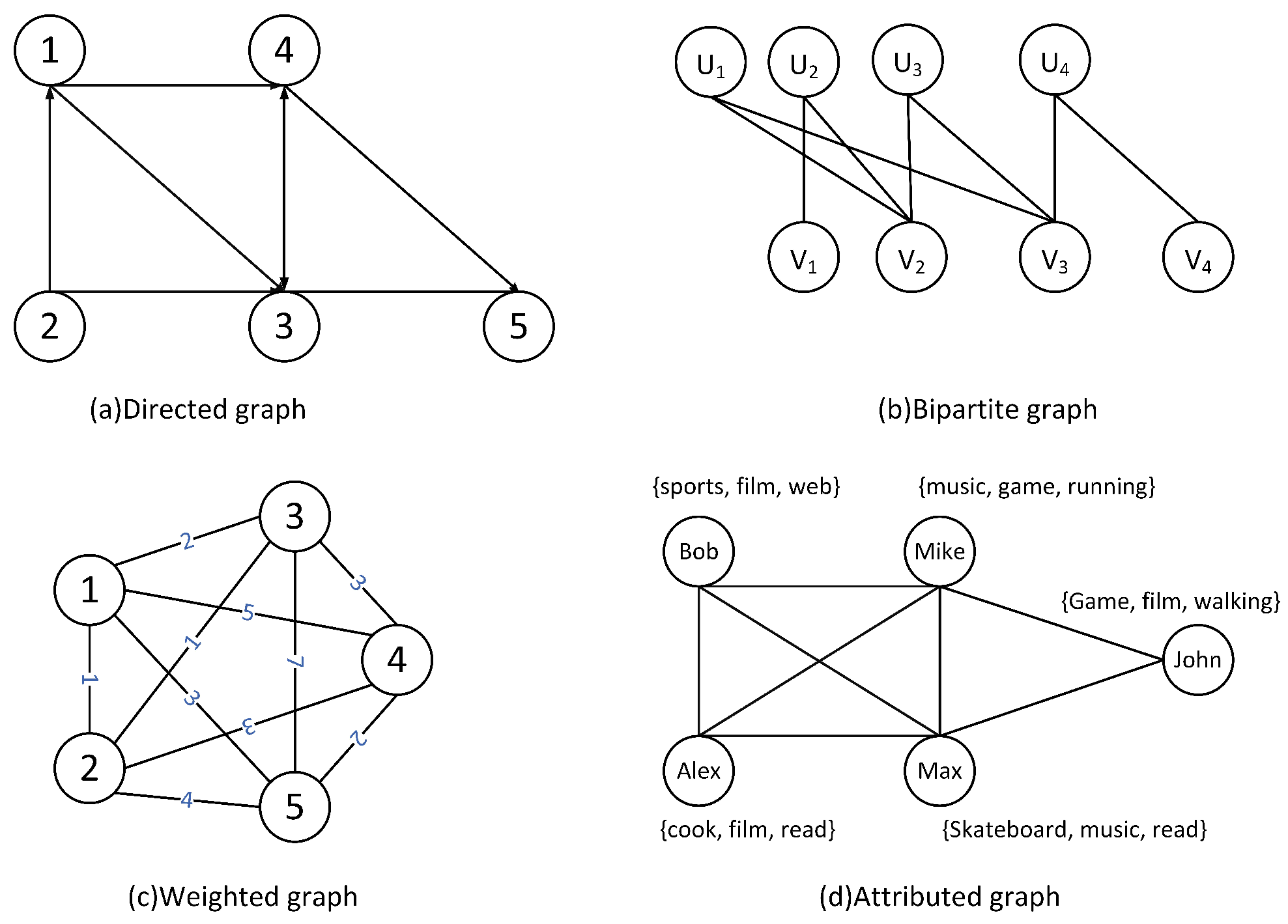
Directed Graph. For a directed graph $G(V,E)$, each edge $e(u,v)$ of G means a direct relationship between u and v, denoted as $u\to v$. In addition, a directed acyclic graph (DAG) is a directed graph that has no cycles. Figure 2a depicts a directed graph with five nodes.

-

Bipartite Graph—a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets, U and V, denoted as $G(U,V,E)$, such that every edge connects a vertex in U to one in V. Figure 2b depicts a bipartite graph.

-

Weighted Graph—a weighted graph has a number assigned to each of its edges, called its weight. The weight can be used to represent distances, influence or capacities. Figure 2c depicts a weighted graph where each edge has a weight.

-

Attributed Graph—an attributed graph is defined as $G=(V,E,A)$, where $V\left(E\right)$ is the node (edge) set and A is the set of attributes associated with nodes. For each node $v\in V$, it has a set of attributes $A\left(v\right)=\{a_0,\dots ,a_m\}$. Figure 2d illustrates an attributed graph, in which each vertex represents a user in a social network, and the associated keywords capture the user’s interests.

A dynamic graph is characterized by changes performed on the set of nodes and/or the set of edges. These changes may correspond to insertions or deletions of vertices or edges. The dynamic types of graphs can be summarized into four cases:

-

Incremental Dynamic—a dynamic graph is incremental dynamic if only vertices or edges are inserted into G.

-

Decremental Dynamic—a dynamic graph is decremental dynamic if only vertices or edges are deleted into G.

-

Fully Dynamic—fully dynamic graphs match the scenarios such that there are not only vertices or edges additions but also vertices or edges deletions.

-

Streaming Dynamic—the graph evolves over time through a continuous stream of updates, where nodes and edges are added or removed incrementally.

In this survey, we review papers regarding to several kinds of graphs under different update types.

3. Computational Complexity Model

In the literature, asymptotic worst-case analysis serves as a standard method for assessing algorithm complexity, representing computational cost as a function of input size. In the case of dynamic graph algorithms, if runtime is measured as a function of input size, many such algorithms exhibit worst-case complexity that is often no more efficient than simply recomputing the solution from scratch. Clearly, assessing the computational complexity of dynamic graph algorithms in this way provides little meaningful insight. As a result, the literature examines various computational complexity frameworks, such as boundedness, relative boundedness, and semi-boundedness.

Definition 1

(Boundedness [128]). A dynamic algorithm is considered bounded if its cost is a polynomial in $\left|\mathsf{CHANGED}\right|$ and $\left|Q\right|$.

The concept of boundedness is first introduced in [129] to address limitations of worst-case analysis, and later adapted for graph problems in [128]. In [128], the authors propose $\left|\mathsf{CHANGED}\right|$ as an adaptive metric for quantifying input and output modifications. For a given query class $\mathcal{Q}$, when applying update $\Delta \left(G\right)$ to graph G and computing $Q(G\oplus \Delta (G\left)\right)$, the output changes $\Delta \left(O\right)$ must satisfy $Q(G\oplus \Delta (G\left)\right)$ = $Q\left(G\right)\oplus \Delta \left(O\right)$. The study [128] establishes two key terms: $\mathsf{MODIFIED}$ captures graph input change $\Delta \left(G\right)$, while $\mathsf{AFFECTED}$ describes query output change $\Delta \left(O\right)$. The combined change $\mathsf{CHANGED}$ is defined as $\mathsf{MODIFIED}\cup \mathsf{AFFECTED}$ to measure total system changes. $\left|\mathsf{CHANGED}\right|$ measures the size of $\mathsf{CHANGED}$. Based on $\left|\mathsf{CHANGED}\right|$, a dynamic algorithm exhibits bounded if the time taken for the update is a function of the parameter of $\left|\mathsf{CHANGED}\right|$. In contrast, it demonstrates unbounded if the computational time grows without bound even when $\left|\mathsf{CHANGED}\right|$ remains constant.

Definition 2

(Relative Boundedness [130]). A dynamic algorithm is called bounded relative if its cost can be expressed as a polynomial function in the sizes of $\left|\mathsf{AFF}\right|$, $|\Delta (G\left)\right|$, and $\left|Q\right|$.

Building upon the concept of boundedness, Ref. [130] puts forward two alternative approaches to assess computational complexity: localizable computations and relative boundedness. Ref. [130] proposes that the dynamic problem for Q is deemed localizable if there exists an incremental algorithm ${\mathcal{T}}_{\Delta }$ such that for $Q\in \mathcal{Q}$, G and $\Delta G$, its computational cost is solely determined by $\left|Q\right|$ and the $d_Q$-neighbors of nodes in $\Delta G$, where $d_Q$ is exclusively dependent on $\left|Q\right|$ only. Consider a query $Q\in \mathcal{Q}$ and a graph G, Ref. [130] defines $G_{\mathcal{T},Q}$ as part of the data of G examined by algorithm $\mathcal{T}$ when evaluating $Q\left(G\right)$. Given updates $\Delta G$ to G, $\mathsf{AFF}$ measures the variation between the inspected data before and after updates (i.e., ${(G\oplus \Delta G)}_{(\mathcal{T},Q)}$ and $G_{(\mathcal{T},Q)}$). A dynamic algorithm ${\mathcal{T}}_{\Delta }$ for $\mathcal{Q}$ is bounded relative to $\mathcal{T}$ if its execution cost scales polynomially with $\left|\mathsf{AFF}\right|$, $|\Delta G|$, and $\left|Q\right|$.

Definition 3

(Semi-Boundedness [131]). A dynamic algorithm is said to be semi-bounded if: (a) its computational cost is a polynomial in $|{\mathsf{AFF}}^{\forall }|$, $|\Delta G|$, and $\left|Q\right|$; and (b) the size of the auxiliary structure is bounded by a polynomial function of $\left|G\right|$.

The metric $\left|\mathsf{CHANGED}\right|$, while accurately reflecting the inherent update costs in dynamic graph problems, imposes such stringent conditions that most practical dynamic graph algorithms cannot achieve bounded complexity under this framework. Consequently, Ref. [131] proposes a more relaxed metric centered on the concept of affected area ${\mathsf{AFF}}^{\forall }$. This measure encompasses not only the direct output changes $\Delta O$, but also includes all data that must be examined by any dynamic algorithm solving the given graph problem to identify these changes. A dynamic algorithm is semi-bounded if its computational complexity remains polynomial in three key parameters: $|{\mathsf{AFF}}^{\forall }|$, $\left|Q\right|$, and $|\Delta G|$. These parameters represent the necessary computations any dynamic algorithm must perform to solve a specific problem.

Theory analysis. The complexity analysis of dynamic algorithms often depends on the number of updates in dynamic graphs. The three models are defined in relation to the size of either $\Delta \left(G\right)$ (the number of updates applied to graph G) or $\left|\mathsf{CHANGED}\right|$(a set that includes $\Delta \left(G\right)$). The difference between $\mathsf{AFF}$ and ${\mathsf{AFF}}^{\forall }$ is that the relative boundedness is defined in terms of the affected area $\mathsf{AFF}$, relative to a specific algorithm $\mathcal{T}$, while $|{\mathsf{AFF}}^{\forall }|$ is for all dynamic algorithms for query $\mathcal{Q}$. Therefore, we have $|{\mathsf{AFF}}^{\forall }|>|\mathsf{AFF}|$. Consequently, the tightness of the above three computational complexity models can be sorted as boundedness > relative boundedness > semi-boundedness. As the boundedness of algorithms is demanding, only few dynamic algorithms can be totally bounded, such like shortest path problems with single-source or all pairs under positive lengths [128,132]. In addition, graph simulation is known as semi-bounded [131]. Ref. [130] proves that regular path queries and strongly connected components computation are relative bounded.

4. Algorithms

In this section, we explore and evaluate dynamic algorithms across various domains of graph computing. We begin by providing definitions and showing recent advancements in dynamic algorithms for each specific graph problem. Subsequently, we conduct a theoretical analysis and compare the time complexities of these algorithms to highlight their efficiency and performance.

4.1. Centrality

Centrality measures the importance of various vertices in a graph. It can be used in the applications such as identifying the most influential persons in a social network, key infrastructure nodes in the internet, and super-spreaders of disease. Since the “importance” of a vertex can be characterized from different perspectives, many different definitions of centrality are investigated in the literature. Typical definitions of centrality include betweenness centrality, closeness centrality, and eccentricity.

4.1.1. Betweenness Centrality

Definition 4

(Betweenness Centrality [133]). Given a graph G, the betweenness centrality of a vertex $v\in V\left(G\right)$ is:

$$bc\left(v\right)=\sum _{s,t\in V\left(G\right)}{\displaystyle \frac{\delta (s,t|v)}{\delta (s,t)}},$$

where $\delta (s,t|v)$ is the number of shortest paths between s and t that include v, and $\delta (s,t)$ is the number of shortest paths between s and t.

For betweenness centrality, the fastest static algorithm to compute exact betweenness centralities for all the vertices is proposed in [133] and it requires $O\left(nm\right)$ and $O(nm+n^{2}logn)$ time on weighted and unweighted graphs, respectively. Regarding the dynamic setting, Ref. [17] is the first work that proposes an efficient algorithm, QUBE, to handle the update of the betweenness centralities of vertices in a graph. QUBE decomposes the input graph into independent components using minimum union cycles, such that the change in one component does not affect the betweenness centrality of nodes in other components. After a graph update, QUBE recomputes the betweenness centrality for the vertices in the affected component. Compared with recomputing from scratch, QUBE significantly reduces the number of explored vertices. Therefore, QUBE achieves great speedup practically.

After [17], Ref. [18] devises an incremental algorithm for betweenness centrality by maintaining the BFS trees for each vertex in the streaming graph. Ref. [40] maintains the betweenness centralities by updating the all-pairs shortest paths. It keeps a directed acyclic subgraph for each vertex containing all the edges that belong to at least one shortest path from the vertex and updates the shortest paths by a Dijkstra-like algorithm. Based on QUBE, Ref. [43] proposes a dynamic algorithm supporting vertex insertion/deletion. Ref. [25] further extends QUBE to support the insertion and deletion of bridge edges. Ref. [26] parallelizes [18] by introducing a novel multi-level data structure and providing an efficient workload estimation strategy. Ref. [39] proposes a parallel incremental algorithm, named iCentral, for the betweenness centrality computation. Different from QUBE, iCentral decomposes the input graph into biconnected components such that the betweenness centrality values of vertices not belonging to the affected biconnected components do not change after the update. Following iCentral, Ref. [37] further explores the opportunities to reduce unnecessary computation for the batch update case. In addition, Refs. [38,41] discuss the approximating betweenness centrality computation in dynamic graphs. Recently, Ref. [42] further improves the performance of the betweenness centrality maintenance on streaming graphs, where edges arrive over time.

4.1.2. Closeness Centrality

Definition 5

(Closeness Centrality [134]). Given a graph G, the closeness centrality of a vertex $v\in V\left(G\right)$ is:

$$cc\left(v\right)={\displaystyle \frac{n-1}{{\displaystyle \sum _{u\in V\left(G\right)}}dist(v,u)}},$$

where $dist(v,u)$ is the shortest distance between v and u.

For the closeness centrality over static and unweighted graphs, it takes $O\left(n\right(m+n\left)\right)$ to compute the closeness centrality of each vertex by using the BFS. In weighted graphs, the time complexity is $O(mn+n^{2}logn)$ if Dijstra’s algorithm with Fabonacci heap is used [135] or $O\left(n^3\right)$ if the Floyd–Warshall algorithm is used [136]. In dynamic graphs, Ref. [44] borrows the idea of maintaining dynamic shortest paths from [137] and proposes fully dynamic algorithms for the closeness centrality computation. Ref. [45] presents a framework named Streamer to parallelize the incremental closeness centrality computation on high-performance clusters. In [46], an algorithm named CENDY is proposed to update the closeness centrality when the edges are inserted/deleted but the vertices are fixed. Based on the observation that if the difference between the shortest distances from a vertex v to both end vertices of the edge to be inserted/deleted is greater than 1, then the shortest path from v to some vertices must change after an update, CENDY derives theoretical properties to quickly identify a set of vertices whose closeness centralities will change after an edge is inserted/deleted and updates the closeness centralities accordingly. Ref. [37] considers the batch update scenario to maintain the closeness centrality and shows a parallel approach to achieve the goal. Ref. [47] leverages the biconnected component and reserves key intermediate results to boost the closeness centrality maintenance.

4.1.3. Eccentricity

Definition 6

(Eccentricity [138]). Given a graph G, the eccentricity of a vertex $v\in V\left(G\right)$ is :

$$ecc\left(v\right)=\underset{u\in V\left(G\right)}{max}dist(v,u).$$

For the eccentricity centrality, Ref. [139] is the State-of-the-Art approach to compute eccentricity centrality for static graphs by non-trivially utilizing the upper and lower bounds of a vertex. Regarding the dynamic graphs, Ref. [48] provides the first algorithm on maintaining the eccentricities upon each edge update. It first scopes the possibly affected nodes and then facilitates a more targeted eccentricity re-computation algorithm to improve the efficiency of maintaining the eccentricities.

Algorithm analysis. We analyze different centrality algorithms over various aspects including graph type, update mode and supported graph change type. As shown in

Table 2. Comparison of time complexity for dynamic betweenness centrality algorithms.

Problem	Algorithm	Graph Type	Update Mode	Fully Dynamic	Incremental Dynamic	Decremental Dynamic	Streaming Dynamic
Betweenness centrality	QUBE [17]	General	Single	✓	✓	✓	✗
Betweenness centrality	Green [18]	General	Single	✗	✓	✗	$O\left(\right|V{|}^2+\left|V\right|\left|E\right|)$
Betweenness centrality	Lee [25]	Weighted	Batch	$O\left(\right|V^{T^{\prime }}\left|\right|E^{T^{\prime }}|+|V|+|E\left|\right)$	✓	✓	✗
Betweenness centrality	Lee [25]	General	Batch	$O\left(\right|V^{T^{\prime }}\left|\right|E^{T^{\prime }}|+|V^{T^{\prime }}\left|2log\right|V^{T^{\prime }}|+|V|+|E\left|\right)$	✓	✓	✗
Betweenness centrality	Green+ [26]	General	Single (parallel)	✓	✓	✓	✓
Betweenness centrality	iCentral [39]	General	Single (parallel)	✓	$O\left(\right|V\left|\right|E|/T)$	✓	✗
B&C centrality	Shukla [37]	General	Batch (parallel)	$O\left(\right|L\left(B\right)|·(\left|V\right|+\left|E\right|\left)\right)$	✓	✓	✗
Closeness centrality	Kas [44]	Directed & weighted	Single	✓	$O\left(\right|\mathsf{Affected}\left|\right)$	$O\left(\right|\mathsf{Affected}{|}_2+\left|\mathsf{Affected}\right|log\left|\mathsf{Affected}\right|)$	✗
Closeness centrality	STREAMER  [45]	General	Single (distributed)	✓	✓	✓	✓
Closeness centrality	CENDY  [46]	General	Single	$O\left(min\right\{|{\acute{V}}_a|,|{\acute{V}}_b\left|\right\}·\left(\right|V|+\left|E\right|\left)\right)$	✓	✓	✗
Closeness centrality	IUA [47]	General	Single	$O\left(\right|V\left|\right)+O\left(\right|{\acute{V}}_a\left|\right(|V_{\mathsf{affect}}|+|E_{\mathsf{affect}}\left)\right)$	✓	✓	✗
Eccentricity	ECC-DY [48]	General	Single	✓	$O\left(\right|E|·\left(\right|C^a|+|C^{b^{\prime }}\left|\right))$	✓	✗

, we list representative works and recent works published within the past three years. Most algorithms support fully dynamic graphs with both edge/vertex insertion/deletion. For the time complexity, Ref. [25] proposes an algorithm whose worst-time complexity is bounded by a polynomial in $|V^{T^{\prime }}|$,$|E^{T^{\prime }}|$,$\left|V\right|$ and $\left|E\right|$ where $|V^{T^{\prime }}|\le |V|$ and $|E^{T^{\prime }}|\le |E|$. In [39], T is the number of threads. $L\left(B\right)$ denotes the set of nodes affected due to all the edges in batch B [37]. In [44], $\left|\mathsf{Affected}\right|$ is used to denote the sum of the number of edges and the nodes in the subgraph formed by AffectedSource and AffectedSink nodes’ neighborhoods. Besides, for the complexity of closeness centrality, $min\left\{\right|{\acute{V}}_a|,|{\acute{V}}_b\left|\right\}$ is very small in real-world networks, $V_{\mathsf{affect}}$ and $E_{\mathsf{affect}}$ are much smaller than the original graph [46,47]. Regarding eccentricity, in [48], the empirical study indicates that the size of $|C^{b^{\prime }}|$ is reduced to a level which is no more than ${10}^2$, achieving high efficiency of eccentricity maintenance.

4.2. Graph Coloring

Graph coloring is a fundamental graph problem that is widely applied in a variety of applications such as nucleic acid sequence design in biochemical networks, air traffic flow management, channel assignment in wireless networks, and community detection in social networks. Classic graph coloring includes vertex coloring and edge coloring.

4.2.1. Vertex Coloring

Definition 7

(Vertex Coloring). Given a graph G, vertex coloring assigns each vertex in G a color such that no two incident vertices (connected by an edge) have the same color.

Vertex coloring seeks to determine an optimal coloring of a graph G, where the chromatic number represents the smallest number of colors required for a valid coloring [140]. This optimization problem is known to be NP-hard for static graphs, as established in [8]. In [141], the computational complexity of optimal graph coloring is established, proving that no polynomial-time algorithm can achieve an $n^{1-ϵ}$ approximation ratio for any $ϵ>0$, unless NP = ZPP. Given this fundamental limitation, researchers have developed numerous approximation approaches for static graph coloring. Ref. [142] presents a systematic survey of existing algorithmic approaches for solving the static graph coloring problem.

In addressing the dynamic vertex coloring problem, Ref. [52] proposes two complementary algorithmic frameworks that establish distinct performance trade-offs between recoloring frequency and color minimization. For any $d>0$, the first algorithm guarantees a proper coloring using $O\left(\mathcal{C}d{N}^{1/d}\right)$ colors while recoloring at most $O\left(d\right)$ vertices per update. Conversely, the second algorithm maintains $O\left(\mathcal{C}d\right)$ colors but requires recoloring $O\left(d{N}^{1/d}\right)$ per update, where $\mathcal{C}$ represents the maximum chromatic number and N denotes the vertex count. Furthermore, Ref. [52] establishes a lower bound showing that for any 2-colorable graph with N vertices, maintaining a proper coloring with c colors(where $c\ge 2$ is constant) must require at least $\Omega \left(N^{2/c(c-1)}\right)$ recolorings per update operation. Ref. [54] studies dynamic graph coloring in the context of bounded-degree graphs. Their work introduces a randomized approach that maintains a proper $(\Delta +1)$-coloring with an amortized expected update time of $O(log\Delta )$, It also presents a deterministic method that achieves a $\Delta (1+o(1\left)\right)$-coloring with an amortized $O(polylog\Delta )$ update time, where $\Delta$ represents the maximum vertex degree. Ref. [49] presents a novel algorithm applicable to general graphs that guarantees a proper $O\left(\alpha {log}^{2}n\right)$-coloring while achieving an amortized time complexity of $\widehat{O}\left(polylog\alpha \right)$, where $\alpha$ denotes the graph’s arboricity. Although the graph coloring problem is NP-complete in general, polynomial-time solutions exist for specific dynamic graph classes, including chordal graphs and biconvex bipartite graphs as demonstrated in [143].

From an application-oriented standpoint, dynamic vertex coloring has been investigated in [51], which introduces an algorithmic approach that performs localized updates to the colors of vertices adjacent to modified edges during insertion/deletion operations. Ref. [50] investigates the dynamic graph coloring problem through an edge-centric coloring approach implemented in a distributed graph processing framework. Ref. [53] introduces the most advanced practical solution for sequential dynamic graph coloring. The algorithm proposed in [53] addresses two key requirements: maintaining stable coloring across updates (effectiveness) and limiting computation to affected neighborhoods (efficiency). The solution employs a propagation mechanism indexed by color, which tracks essential color data per vertex, and naturally restricts processing to adjacent vertices of color-changed nodes.

Algorithm analysis. We analyze different dynamic vertex coloring algorithms over dynamic graphs. As shown in

Table 3. Comparison of time complexity for dynamic vertex coloring algorithms.

Problem	Algorithm	Graph Type	Update Mode	Fully Dynamic	Incremental Dynamic	Decremental Dynamic	Streaming Dynamic
Vertex coloring	Barba [52]	General	Batch	✓	✓	✓	✗
$(\Delta +1)$-coloring	Bhattacharya [54]	General	Single	$O(log\Delta )$	✓	✓	✗
($1+o\left(1\right)$)$\Delta$-coloring	Bhattacharya [54]	General	Single	$O(polylog\Delta )$	✓	✓	✗
$O\left(\alpha {log}^{2}n\right)$-coloring	Solomon [49]	General	Single	$\widehat{O}\left(polylog\alpha \right)$	✓	✓	✗
Vertex coloring	ACODYGRA [51]	General	Batch	✓	✓	✓	✗
Vertex coloring	Sallinen [50]	General	Batch (distributed)	✓	✓	✓	✗
Vertex coloring	Yuan [53]	General	Single	✓	✓	✓	✗

, most vertex coloring algorithms are designed to support fully dynamic graphs. However, research on streaming graphs remains limited and represents an area that requires further exploration and development. For the time complexity, in [54], $\Delta$ denotes the maximum degree of vertices in the graph. In [49], the worst-time complexity with $O\left(\alpha {log}^{2}n\right)$ colors is bounded by a polynomial in $\alpha$ where $\alpha$ is an arboricity value. Refs. [50,51,53] primarily focus on heuristics and experimental results.

4.2.2. Edge Coloring

Definition 8

(Edge Coloring). Edge coloring of a graph is an assignment of colors to the edges of the graph so that no two incident edges have the same color.

Ref. [56] introduces the OHEColoring algorithm, an ordering heuristic-based static edge coloring approach with $O(m·d_{max})$ time complexity (where m represents edge count and $d_{max}$ denotes maximum degree). For dynamic maintenance, the work develops: (1) a propagation mechanism that handles edge recoloring triggered by graph updates, and (2) an edge-priority recoloring algorithm that guarantees single recoloring per edge to optimize computational efficiency.

For dynamic graphs undergoing continuous edge modifications, Refs. [54,55] present efficient solutions to maintain proper edge coloring. Their approaches ensure a proper coloring using at most $(2\Delta -1)$ colors while requiring only $O(log\Delta )$ time complexity per update operation, where $\Delta$ represents the maximum vertex degree. Ref. [57] demonstrates the maintenance of $(1+ϵ)\Delta$-coloring with an amortized update time of $O({log}^{8}n/{ϵ}^4)$ for graphs satisfying $\Delta \ge \Omega ({log}^{2}n/{ϵ}^2)$. This result is later improved by [59], which achieves the same coloring quality with an update time of $O({log}^4(1/ϵ)/{ϵ}^9)$, under the relaxed condition $\Delta \ge {(logn/ϵ)}^{\Theta \left(\right(1/ϵ)log(1/ϵ\left)\right)}$. Ref. [60] establishes an efficient algorithm for maintaining a $(\Delta +O(\alpha \left)\right)$-edge coloring in dynamic graphs, achieving a constant amortized update time $\tilde{O}\left(1\right)$, where $\alpha$ denotes the graph’s arboricity, $\Delta$ represents its maximum degree, and $ϵ$ is a given parameter.

Recent advances in $(1+ϵ)\Delta$-coloring algorithms demonstrate significant progress: Ref. [57] achieves an update time of $O({log}^{8}n/{ϵ}^4)$ when $\Delta =\Omega \left({\displaystyle \frac{{log}^{2}n}{{ϵ}^2}}\right)$, while Ref. [58] removes the degree restriction with $O({log}^{9}n{log}^6\Delta /{ϵ}^6)$ complexity. The algorithm in [59] further reduces the update time to $2^{\tilde{O}log{ϵ}^{-1}\left(\sqrt{logn}\right)}$ under certain parameter conditions on $\Delta$ and $ϵ$.

Algorithm analysis. We compare different edge coloring algorithms over dynamic graphs. Most edge coloring algorithms support incremental/decremental dynamic graphs. For the time complexity of existing works, the worst-time complexity of most algorithms depends on $\Delta$, such as [54,55] where $\Delta$ is the maximum degree. Refs. [57,58,59,61] all studies $(1+ϵ)\Delta$-coloring problem. The worst-time complexity of [57,59,61] is bounded by a polynomial in $ϵ$ and n, where $ϵ>0$ is an arbitrarily small constant and n is the number of vertices. However, there is a noticeable gap in research concerning streaming dynamic algorithms and parallel or distributed algorithms, highlighting an area that demands further investigation and advancement.

4.3. Cohesive Subgraph Search

Cohesive subgraph search is an important and fundamental research problem in graph analysis with many practical applications, including community detection and friend recommendation in social networks, production recommendation and commercial advertising in shopping networks, complex protein detection in PPI networks, etc. [28,144]. Based on different criteria for cohesiveness, multiple cohesive subgraph models are proposed.

4.3.1. Clique Model

Definition 9

(Clique). Given a graph G, a clique C is a maximal subgraph in G, s.t., each pair of vertices in C are neighbors. A k-clique is a clique with k vertices.

As illustrated in Figure 3, subgraph $C_1$ is a 6-clique, while $C_2$ constitutes a 5-clique.

The clique model represents a fundamental and well-studied cohesive subgraph structure in network analysis [7]. The primary computational challenge of this model lies in exhaustively identifying all cliques within a graph G which is a task proven to be NP-hard and admits no known polynomial-time approximation algorithm [141]. Given the dynamic nature of real-world networks undergoing constant edge modifications, efficient clique maintenance algorithms have become increasingly crucial for supporting various practical applications.

Initial research in [62] pioneered maximal clique enumeration (MCE) for dynamic graphs handling single-edge updates. Given a graph G, the approach in [62] processes an edge insertion $(u,v)$ by examining all maximal cliques $\mathcal{A}$ containing u and $\mathcal{B}$ containing v. For each pair of cliques $(A,B)\in \mathcal{A}\times \mathcal{B}$, it generates candidate cliques as $(A\cap B)\cup (u,v)$, achieving a time complexity of O($W^2{n}^2$), where W represents the number of maximal cliques and n is the number of vertices. Subsequent work [65] improves this through an innovative local construction strategy using linear scans, reducing the candidate set size to O(W) and overall complexity to O($W{n}^2$). The framework in [65] also supports edge deletion by inverting the insertion process when edges are removed.

In addition, the research in [63] tackles the challenge of maintaining maximal cliques in dynamic graphs undergoing batch edge updates. The work makes two fundamental contributions: first, it establishes near-optimal bounds quantifying how the set of maximal cliques evolves when edges are added to the graph. Second, it introduces a novel change-sensitive algorithm for incremental clique maintenance whose computational complexity scales linearly with the actual changes in the maximal clique set—particularly effective for small edge additions. Specifically, the algorithm achieves time complexity of $O\left({\Delta }^3\rho \right|{\Lambda }^{new}(G,G^{\prime })\left|\right)$ for enumerating newly formed cliques (where $\Delta$ represents the maximum vertex degree in the updated graph $G^{\prime }$ and $\rho$ denotes the number of added edges), where $O\left(2^{\rho }\right|{\Lambda }^{new}(G,G^{\prime })\left|\right)$ is used for detecting removed cliques. Notably, the proposed method can also be applied to the decremental case. Moreover, Ref. [16] develops a parallelized version of the approach in [63], implementing a shared-memory architecture where multiple threads concurrently process clique enumeration while accessing a globally shared graph structure.

The work in [64] investigates incremental maximal clique enumeration for dynamic graph maintenance, introducing the SOMEi data structure, a space-efficient index for storing intermediate maximal cliques during construction that enables the efficient retrieval of scope-constrained cliques.

4.3.2. Biclique Model

Definition 10

(Biclique). Given a bipartite graph $G=(U\cup V,E)$ where U,V is vertices on different sides of G, and E is edges between U and V, a biclique C is a maximal subgraph in G, s.t., each vertex in $C\cap U$ is connected to each vertex in $C\cap V$.

Figure 4 shows a bipartite graph G with $U\left(G\right)=\left\{U_1,U_2,\dots ,U_7\right\}$, $V\left(G\right)=\left\{V_1,V_2,\dots ,V_6\right\}$. As the maximum biclique C, we have $U\left(C\right)=\left\{U_3,U_4,U_5,U_6\right\}$, $V\left(C\right)=\left\{V_2,V_3,V_4,V_5\right\}$.

On dynamic bipartite graph with adding batch edges over time, Ref. [66] solves the problem of incremental maintenance for maximal bicliques(MBE). Following the key idea for clique maintenance of [63,65], Ref. [66] proposes a change-sensitive incremental maintenance algorithm i.e., its time complexity is proportional to the magnitude of change in the set of maximal bicliques. In other words, all bicliques enumerated are exactly the newly added bicliques or removed bicliques. Ref. [67] proposes a novel algorithm for enumerating maximal bicliques in a dynamically changed graph, focusing only on newly created or reduced maximal bicliques rather than re-searching the entire graph. This approach leverages previously enumerated results to efficiently update the biclique enumeration after each graph modification.

Algorithm analysis. We compare the maximal clique enumeration (MCE) and maximal biclique enumeration (MBE) algorithms over dynamic graphs, respectively. As shown in

Table 4. Comparison of time complexity for dynamic clique and biclique algorithms.

Problem	Algorithm	Graph Type	Update Mode	Fully Dynamic	Incremental Dynamic	Decremental Dynamic	Streaming Dynamic
MCE	Stix [62]	General	Batch	$O\left(W^2{n}^2\right)$	✓	✓	✗
MCE	Sun [65]	General	Single	✗	$O\left(W{n}^2\right)$	$O\left(W{n}^2\right)$	✗
MCE	Das [63]	General	Batch	✗	$O\left({\Delta }^3\rho \right|{\Lambda }^{new}\left|\right)$	✓	✗
MCE	SOMEi [64]	General	Batch	✓	✓	✓	✗
MCE	ParIMCE [16]	General	Batch (parallel)	✗	✓	✗	✗
MBE	DynamicBC [66]	Bipartited	Batch	✗	$O\left({\Delta }^2\rho \right|{\Lambda }^{new}|+2^{\rho }|{\Lambda }^{new}\left|\right)$	✗	✗
MBE	IMBS [67]	Bipartited	Single	✗	✓	✗	✗

, most algorithms can handle incremental dynamic graphs with edge/vertex insertion. For the time complexity, Refs. [62,65] propose algorithms whose worst-time time complexity is bounded by a polynomial in W and n where W represents the number of cliques and n represents the number of vertices. In [63,66], the time complexity depends on several factors including the maximum degree, the size of update edge set and the new formed clique or biclique on the updated graph. In addition, existing works demonstrate limitations when applied to fully dynamic graphs and streaming graphs, as most algorithms are memory-based and rely on single-threaded execution, restricting their scalability and efficiency in more complex and dynamic scenarios.

4.3.3. Core Model

Definition 11

($\mathit{k}$-core). Given a graph G and an integer k, a k-core is a maximal subgraph in G, s.t., the degree of each vertex v in it is not less than k.

As illustrated in Figure 5, the graph exhibits a hierarchical k-core structure comprising 1-core, 2-core, and 3-core layers. The visualization employs progressively darker shading for vertices with higher core numbers, which effectively demonstrates the nested nature of the k-core decomposition model.

The core maintenance problem in dynamic graphs involves efficiently updating vertex core numbers after the insertion/deletion of vertices/edges.

Modern distributed computing platforms have inspired various parallel approaches for k-core index construction and maintenance, designed to maximize resource utilization through scalable distributed architectures [68]. Specifically, Ref. [73] investigates distributed core maintenance under multi-edge updates, demonstrating that only a constant number of vertices require core number reevaluation when the original graph is updated through single or multiple edge insertions/deletions.

In addition, parallel computing approaches have emerged as powerful solutions for core maintenance, leveraging multi-threading and shared-memory architectures to boost performance. Ref. [69] is a pioneering work in this direction with its joint edge set structure and corresponding parallel algorithms. Subsequent work [71,72] develops parallel methods for batch edge processing, establishing the important theoretical result that each edge operation affects vertex core numbers by at most 1. Notably, Ref. [72] proves that edge changes forming a matching can be processed in parallel. Meanwhile, Ref. [19] takes a hierarchical perspective, analyzing the structural properties of k-core hierarchies in dynamic graphs and developing efficient local update strategies for edge modifications.

Building upon the superior edge set framework, Ref. [20] develops unified algorithms for incremental and decremental core maintenance for batch edge operations. These algorithms enable parallel execution by distributing edges sharing common core numbers across threads. Subsequent work in [75] enhances parallelism through the theory of k-insertion/removal graph. While traditional parallel approaches relying on traversal algorithms face sequential bottlenecks when processing uniform-core graphs, Ref. [76] overcomes this limitation by adapting the order algorithm to maintain parallelism regardless of core number distribution.

Algorithm analysis. We compare difference core maintenance algorithms over dynamic graph. As shown in

Table 5. Comparison of time complexity for dynamic core algorithms.

Problem	Algorithm	Graph Type	Update Mode	Fully Dynamic	Incremental Dynamic	Decremental Dynamic	Streaming Dynamic
Core maintenance	Aksu [68]	General	Batch (distributed)	✓	✓	✓	✗
Core maintenance	Hua [69]	General	Batch (parallel)	✓	$O({\Delta }_I·{max}_{S\subseteq E_I}\{m_{S,k}+L_{S,k}·n_{S,k}\})$	$O({\Delta }_I·{max}_{S\subseteq E_D}\{m_{S,k}+L_{S,k}·n_{S,k}\})$	✗
Core maintenance	Aridhi [73]	General	Batch (distributed)	✓	✓	✓	✗
Core maintenance	Wang [71]	General	Batch (parallel)	✓	$O(\Delta I·{max}_{S\subseteq E^{\prime }}\left\{m_S+L_S·n_S\right\})$	$O(\Delta D·{max}_{R\subseteq E^{\prime }}\{m_R+F_R·n_R\})$	✗
Core maintenance	Jin [72]	General	Batch (parallel)	✓	$O\left(\right|E_I|·|V_I|+{\Delta }_I·{max}_{S\subseteq E_I}\{m_S+L_S·n_S\})$	$O\left(\right|E_D|·|V_D|+{\Delta }_D·{max}_{R\subseteq E_D}\{m_R+F_S·n_S\})$	✗
Core maintenance	Li [74]	General	Single	$O\left(\right|V_c\left|{\sum }_{u\in V_c}{D}_u\right)$	✓	✓	✗
Core maintenance	TRAVERSAL [70]	General	Single	$O\left(\right|E\left|\right)$	✓	✓	✗
Core maintenance	Lin [19]	General	Batch	✓	$O(\sum |V^{*}|+x·k_{max}+|T_0\left|\right)$	$O\left({\sum }_{v\in V_{n^{\prime }}}\right|N(V,G\ast )|+|T^{\prime }\left(n^{\prime }\right)\left|\right)$	✗
Core maintenance	Yu [20]	General	Batch	✓	$O({\Delta }_I·|E\left|\right)$	$O({\Delta }_D·|E\left|\right)$	✗
Core maintenance	Yu [20]	General	Batch (parallel)	✓	$O({\Delta }_I·{max}_{S\subseteq E_I}\{m_S+L_S·n_S\})$	$O({\Delta }_D·{max}_{R\subseteq E_D}\{m_R+F_S·n_S\})$	✗
Core maintenance	Bai [75]	General	Batch (parallel)	✓	$O({\varphi }_G·|G^{\prime }\left|\right)$	$O({\varphi }_G·|G_k\left|\right)$	✗
Core maintenance	Guo [76]	General	Batch (parallel)	✓	$O\left(E_I\right|E^{+}|log|E^{+}\left|\right)$	$O\left(E_D\right|E^{*}\left|\right)$	✗

, all core maintenance algorithms support fully dynamic graphs. Existing works have explored a variety of efficient approaches, including single-threaded, parallel, and distributed methods. However, the problem of core maintenance on streaming graphs remains largely unexplored and presents a significant area for future research. For the time complexity, Refs. [20,71] propose parallel core maintenance algorithms in incremental dynamic graphs whose worst-time complexity for both are bounded by a polynomial in $\Delta I$, $m_S$, $L_S$ and $n_S$, where $\Delta I$ is used to represent the maximum number of edges inserted to each vertex in the origin graph, $L_S$ is the max times that a vertex u can be visited by negative DFS procedures in the algorithm execution, and $m_S$ represents the max number of edges traversed when Ref. [20] computes superior degree and Ref. [71] computes constraint superior degree in the case of inserting edges. The worst-time complexity of [69] has the same structure as that of [20,71], with the only differences being $n_S\left(k\right)=\left|V_S\left(k\right)\right|$ and $m_S\left(k\right)=\left|E_S\left(k\right)\right|$. In [75], ${\varphi }_G$ represents the largest core number of vertices in G, $|G^{\prime }|$ denotes the size of updated graph and $|G_k|$ is used to denote the number of k-core. The time complexity of [76] is superior to that of other listed parallel algorithms. Here, $|E^{+}|$ is the largest number of adjacent edges for all vertices in $|V_{+}|$ among each inserted edge where $|V_{+}|$ is a larger set of vertices that is traversed to determine which vertices the core needs to update. For single edge/vertex update, Ref. [70] proposed a linear algorithm named TRAVERSAL whose worst-time complexity is bounded by the number of edges. Moreover, based on the finding that the order algorithm [69] significantly outperforms the traversal algorithm [74] across various real-world graphs, Ref. [76] further performs better than [69]. Ref. [76] improves the existing parallel core maintenance methods [71,72] because the prepossessing of $\Delta E$ is not required so that edges can be inserted or removed on-the-fly.

4.3.4. Truss Model

Definition 12

($\mathit{k}$-truss). Given a graph $G=(V,E)$ and an integer k, a k-truss C is a maximal subgraph of G, s.t., for each edge $e=(u,v)$ in C, vertex u and v form at least $k-2$ triangles in G. Further, the truss number of an edge is defined as the largest k value among all k-trusses containing this edge.

The k-truss decomposition illustrated in Figure 6 reveals a clear structural pattern, where edges possessing higher truss numbers consistently concentrate within more densely interconnected regions of the graph.

The k-truss model, originally introduced by [145], represents a significant cohesive subgraph structure with diverse applications. Given a graph G, truss decomposition computes the trussness $\tau \left(e\right)$ for each edge e in G, where $\tau \left(e\right)$ indicates the maximal k-truss containing e. In dynamic settings, researchers have investigated bounded truss maintenance algorithms where for some polynomial function f and some positive integer c, update cost is polynomial in ${O\left(f\right(\left|\right|\mathsf{CHANGED}\left|\right|}_c\left)\right)$ with ${\left|\right|\mathsf{CHANGED}\left|\right|}_c$ is the size of c-hop neighborhood of $\mathsf{CHANGED}$. Ref. [21] establishes that while edge removals permit bounded maintenance under locally persistent algorithms, edge insertions do not.

The study in [82] examines truss maintenance under single-edge updates by first identifying the scope of potentially affected edges. There are two scenarios for affected edges when inserting or deleting an edge $e_0$. (1) Insertion scenario—for any $e\in E\left(G\right)\cup \left\{e_0\right\}$ with $\tau \left(e\right)<\overline{\widehat{\tau }\left(e_0\right)}$, if e and $e_0$ form a new triangle with weight $\tau \left(e\right)$, or e is connected with $e_0$ through a series of adjacent triangles each with weight $\tau \left(e\right)$, then e may have $\widehat{\tau }\left(e\right)=\tau \left(e\right)+1$, where $\widehat{\tau }\left(e\right)$ denotes the new trussness of e, $\overline{\widehat{\tau }\left(e_0\right)}$ denotes the upper bound of $\widehat{\tau }\left(e_0\right)$. (2) Deletion scenario—this is similar to the insertion scenario. Building upon the affected edge scope identification, Ref. [82] develops a update algorithm using a modified truss decomposition approach. Subsequent work in [80] extends this to vertex insertion scenarios. The State-of-the-Art [21] introduces ${\mathsf{AFF}}^{\le }$ as a practical bounded alternative to $\mathsf{CHANGED}$ for edge insertions, while maintaining removal efficiency. Their insertion algorithm achieves $O\left(f\right(\left|\right|{\mathsf{AFF}}^{\le }{\left|\right|}_c\left)\right)$ for some polynomial function f and some positive integer c with $\left|\right|{\mathsf{AFF}}^{\le }{\left|\right|}_c$ being the size of the c-hop neighborhood of ${\mathsf{AFF}}^{\le }$, demonstrating up to three orders over [82] in experimental evaluations.

While the above works focus only on single edge/vertex insertion/deletion, Ref. [77] pioneers batch processing for truss maintenance with multiple edge operations. To tackle the difficulty in quantifying the trussness changes of the edges in batch processing, The work introduces two novel metrics: sustained support and pivotal support, which can efficiently identify edges likely to change trussness, significantly narrowing the search space.

Ref. [81] further investigates the truss maintenance problem and develops the superior triangle edge set concept, guaranteeing that the truss number of any affected edge changes by at most 1. The proposed parallel algorithms leverage this structure to process batch updates efficiently through iterative processing of multiple edges.

Ref. [79] proposes an incremental community search solution using D-truss in dynamic directed graphs. [78] proposes truss maintenance algorithms capable of handling concurrent edge/vertex insertions and deletions in fully dynamic graphs. Compared with the approach in [77], these algorithms demonstrate superior efficiency and substantially reduce the required iteration count for processing graph updates. Furthermore, the proposed methods in [78] admit efficient parallel implementations that further optimize the iteration complexity of truss maintenance operations.

Algorithm analysis. We analyze different truss maintenance algorithms. As shown in

Table 6. Comparison of time complexity for dynamic truss algorithms.

Problem	Algorithm	Graph Type	Update Mode	Fully Dynamic	Incremental Dynamic	Decremental Dynamic	Streaming Dynamic
Truss maintenance	Zhang [21]	General	Single	✓	✓	✓	✗
Truss maintenance	Luo [77]	General	Batch	✓	$O({ϵ}_I{\left(\right|\Delta E|}^2+{\mathcal{A}}_{max}·(d_{max}^2+{\mathcal{P}}_{max})\left)\right)$	$O({ϵ}_D{\left(\right|\Delta E|}^2+{\mathcal{B}}_{max}·(d_{max}^2+{\mathcal{Q}}_{max})\left)\right)$	✗
Truss maintenance	Li [81]	General	Batch (parallel)	✓	$O(I_G^{\Delta E}{\left(\right|\Delta E|}_{S_{G^{\prime }}}+|E_t^I\left|\right)S_{G^{\prime }})$	$O(R_G^{\Delta E}\left(\right|\Delta E|+|E^{-}\left|\right)S_G^2)$	✗
Truss maintenance	Luo [78]	General	Batch (parallel)	✓	$O(R_{+}·(d_{max}^2\left(\right|\Delta E|+|\Delta V|)+{\mathcal{A}}_{max}·(d_{max}^2+{\mathcal{P}}_{max})\left)\right)$	$O(R_{-}·(d_{max}^2\left(\right|\Delta E|+|\Delta V|)+{\mathcal{B}}_{max}·(d_{max}^2+{\mathcal{Q}}_{max})\left)\right)$	✗
Truss maintenance	Ebadian [80]	General	Single	✗	✓	✗	✗

, most truss maintenance algorithms support fully dynamic graphs. For the time complexity, in [81], worst-time complexity of incremental and decremental algorithms is bounded by the same factors, the only difference is that the increment algorithm is constrained by $|E_t^I|$, while the decremental algorithm is constrained by $|E^{-}|$. Here, $|E_t^I|$ denotes the edge set traversed, and $|E^{-}|$ denotes the set of the edges with truss numbers decreasing. In [78], the worst-time complexity of incremental algorithm is bounded to the polynomial function of $R_{+}$, $d_{max}$, $|\Delta E|$, $|\Delta V|$, ${\mathcal{A}}_{max}$ and ${\mathcal{P}}_{max}$. Here, given a graph $G_T$, where $T\subseteq H=\{\Delta V,\Delta E\}$, $R_{+}={max}_{\begin{array}{c}T\subseteq H\end{array}}{max}_{\begin{array}{c}v\in \Delta V,e\in \Delta E\end{array}}\left\{\right|V_{\Delta }^v\left(T\right)|+|E_{\Delta }^e\left(T\right)\left|\right\}$, ${\mathcal{A}}_{max}={max}_{\begin{array}{c}T\subseteq \Delta H,T^{\prime }\subseteq \Delta H\setminus T\end{array}}\left|A_{T^{\prime }}^T\right|$, ${\mathcal{P}}_{max}={max}_{\begin{array}{c}T\subseteq \Delta H,T^{\prime }\subseteq \Delta H\setminus T,e\in G_{T^{\prime }}\end{array}}{P}_{T^{\prime }}^T\left(e\right)$. For an edge $e\in G_{T^{\prime }}$, let $P_{T^{\prime }}^T\left(e\right)=S\left(e\right)-{\tau }_{G_{T^{\prime }}}\left(e\right)+2$ where $S\left(e\right)$ is the k-triangle support of e in $G_{T^{\prime }}$. Ref. [78] proposes truss maintenance algorithms in fully dynamic graphs for both multiple vertex/edge insertions/deletions. In contrast, the approach in [77] only processes multiple edge insertions/deletions without considering vertex insertions/deletions. The approach in [78] can significantly reduce the iterations needed for processing both inserted/deleted edges and vertices, especially for the cases where inserted/deleted vertices are connected to numerous edges. Therefore, in terms of performance, Ref. [78] offers a superior approach. Ref. [80] extends the algorithms in [82] and proposes the maintenance algorithms to handle single vertex.

4.3.5. Community Search

Community search involves identifying dense subgroups in a given graph and aims to find the best local community for a given set of seed vertices. For dynamic environments, Refs. [88,146] investigate evolving community structures, while Ref. [89] introduces Local Weighted-Edge-based Pattern Summary to characterize homogeneous regions in weighted graph streams which aims to tackle the problem of discovering dynamic communities in weighted graph streams. And then, Ref. [84] presents an algorithm for dynamic seed set expansion, which incrementally updates the community as the underlying graph changes.

The study in [85] proposes Agglomerate, an innovative algorithm for dynamic graphs that adapts the parallel CNM approach [147] from [10]. This method utilizes a greedy static strategy to maximize modularity while maintaining a merge history for backtracking capabilities. The most relevant comparative work is [148], which similarly develops two dynamic algorithms for updating CNM-based clusterings.

Advances in community detection include three distinct approaches: Ref. [87] utilizes personalized centrality measures for local community identification and seed set expansion, while Ref. [86] develops a fine-grained incremental algorithm tracking community evolution through modularity optimization. Complementing these, Ref. [149] introduces an adaptive multi-centrality aggregation method specifically targeting influential nodes and overlapping community structures in dynamic networks.

Recently, The work in [83] introduces a parallel dynamic frontier algorithm that efficiently identifies an approximate set of impacted vertices during batch edge updates (insertions/deletions) with minimal computational overhead.

4.4. Path Traversal

Path traversal in graph theory involves exploring a graph by following paths with many practical applications such as optimizing routes for delivery, public transit, or flight paths on transportation networks. There are three traditional problems in path traversal, i.e., Depth-first search, shortest distance queries, reachability queries.

4.4.1. Depth-First Search

Depth-first search (DFS) is a fundamental graph traversal technique. Starting from a root node, the algorithm exhaustively traverses each branch to its maximum depth before backtracking its steps. After Tarjan’s groundbreaking contributions [150], DFS has become indispensable in solving core graph theory challenges, serving as the foundation for numerous algorithmic solutions such as strongly connected components [150], bipartite matching [151], biconnected components [152], and dominators in directed graphs [153].

Definition 13

(Depth-first Search [154]). Given a directed graph G, a depth-first search (DFS) traverses G in a particular order: starting from an initial vertex, it systematically visits unvisited out-neighbors until reaching a dead-end, then retraces its path to explore alternative branches.

Definition 14

(DFS-Tree [154]). Given a graph G, a DFS-Tree of G is a spanning tree formed by the process of DFS.

Given a directed graph G and any search spanning tree of G, edges can be categorized as either tree edges or non-tree edges. The edges appearing in the tree are called tree edges. The remaining edges $(u,v)$ are non-tree edges that can be further classified into one of the following four types: (1) Forward edge: if u is an ancestor of v in the spanning tree. (2) Backward edge: if u is a descendant of v in the spanning tree. (3) Forward-cross edge: if u and v are unrelated in the tree, and u is visited before v. (4) Backward-cross edge: if u and v are unrelated in the tree, and u is visited after v. Figure 7 illustrates these edge classifications, which are fundamental to analyzing DFS-tree properties.

Lemma 1.

Given a directed graph G, a searching spanning tree of G is a DFS-Tree if and only if there is no forward-cross edge in G under this tree [155].

For a graph G with n vertices and m edges, constructing a DFS-tree via depth-first search requires $O(n+m)$ [154]. While DFS-tree computation is well-understood for static graphs, its dynamic maintenance remained largely unexplored until recent years. Early research focused on the ordered DFS-tree variant, with [156] establishing its P-completeness. Subsequent works [157,158] demonstrate that such P-complete problems inherently resist efficient dynamic solutions. Specifically, Ref. [158] proves that any $O\left(t\right(m,n\left)\right)$-time maintenance algorithm for ordered DFS-trees would imply that all problems in P could be maintained in $\tilde{O}\left(t(m,n)\right)$ time.

Regarding the general DFS-Tree, initial progress includes [95]’s $O\left(mn\right)$-time incremental algorithm for DAGs and [98]’s expected $O(mnlogn)$-time decremental solution for DAGs. For undirected graphs, Ref. [96] achieves $O\left(n^2\right)$ total time for incremental updates. Despite these advances, all existing approaches remain limited to partially dynamic settings and fail to achieve sublinear $o\left(m\right)$ worst-case update time, meaning they may degenerate to static recomputation complexity in worst-case scenarios.

Ref. [94] presents the first fully dynamic DFS algorithm achieving sublinear $O\left(m\right)$ update time. The algorithm leverages pre-update DFS-trees to construct reduced adjacency lists. Their approach achieves a worst-case update time of $O\left(\sqrt{mn}{log}^{2.5}n\right)$ for undirected graphs. Moreover, Ref. [94] also provides an incremental algorithm with an improved $O\left(n{log}^{3}n\right)$ bound for incremental cases. Building on this foundation, Ref. [91] further optimized these results to $O\left(\sqrt{mn}{log}^{2.5}n\right)$ for fully dynamic and $O\left(n\right)$ for incremental settings.

Building upon the framework in [94], Ref. [92] develops an enhanced algorithm achieving $O\left(\sqrt{mn}{log}^{0.75+ϵ}n\right)$ update time for fully dynamic graphs and $O\left(n\sqrt{logn}\right)$ for incremental cases, using $O(mlogn)$ space. In [92], further optimizations reduce space to $O\left(\right(3m+o\left(m\right))logn)$ while maintaining a worst-case update time of $O\left(\sqrt{mn}{log}^{1.25}n\right)$ for thee fully dynamic setting and $O(nlogn)$ for the incremental setting. Ref. [93] introduces a distinct approach through DFS-tree path decomposition, yielding $O\left(\sqrt{mnlogn}\right)$ space. Note that all mentioned algorithms specifically address undirected graph scenarios.

Regarding the fully dynamic DFS-Tree maintenance algorithms in directed graph, Ref. [90] first proposes efficient algorithms from the perspective of practical implementation. According to Lemma 1, the DFS-Tree maintenance problem is essentially to eliminate the forward-cross edges. To efficiently check the edge type in constant time, Ref. [90] attaches the discovery timestamp and finish timestamp of each vertex during the DFS-Tress search. Based on the attached timestamps, the proposed algorithms first identify a candidate time interval such that the DFS-subtree induced by the vertices whose attached timestamps in the candidate time interval may be changed and the other part of the DFS-Tree remains unchanged. By performing the DFS following the vertices whose attached timestamps in the candidate time interval, the correct DFS-Tree can be obtained. Ref. [90] further explores opportunities by refining the candidate time interval and transforming the graph search to tree search to improve the efficiency. Although the algorithms proposed in [90] do not have tight theoretical guarantees, their practical performance is impressive as verified by the experiments on large datasets.

Algorithm analysis. We analyze DFS-Tree algorithm over dynamic graphs. As shown in

Table 7. Comparison of time complexity for dynamic DFS-Tree algorithms.

Problem	Algorithm	Graph Type	Update Mode	Fully Dynamic	Incremental Dynamic	Decremental Dynamic	Streaming Dynamic
DFS-Tree	Franciosa [95]	DAG	Batch	✗	$O\left(n\right)$	✗	✗
DFS-Tree	Baswana [96]	General	Batch	✗	$O(n^2/m)$	✗	✗
DFS-Tree	Baswana [98]	DAG	Batch	✗	✗	$O(nlogn)$	✗
DFS-Tree	Baswana [94]	General	Batch	$O\left(\sqrt{mn}{log}^{2.5}n\right)$	$O\left(n{log}^{3}n\right)$	✓	✗
DFS-Tree	Chen [91]	General	Batch	$O\left(\sqrt{mn}{log}^{1.5}n\right)$	$O\left(n\right)$	✓	✗
DFS-Tree	Nakamura [92]-A 1	General	Batch	$O\left(\sqrt{mn}{log}^{0.75+ϵ}n\right)$	$O\left(n\sqrt{logn}\right)$	✓	✗
DFS-Tree	Nakamura [92]-B 1	General	Batch	$O\left(\sqrt{mn}{log}^{1.25}n\right)$	$O(nlogn)$	✓	✗
DFS-Tree	Baswana [93]	General	Batch	$O\left(\sqrt{mnlogn}\right)$	✓	✓	✗

¹ Nakamura [92] proposes two algorithms Nakamura-A and Nakamura-B.

, all the algorithms’ worst-time complexity are bounded by a polynomial in n or m, where n is the number of vertices over graph, and m is the number of edges over graph. The DFS-Tree maintenance problem is well studied when the graph is updated in batch. However, the streaming BFS-tree maintenance needs further investigation.

4.4.2. Shortest Distance Queries

Given a graph G, a shortest distance query asks the minimized length of all the paths between two query vertices in G. Without doubt, answering shortest distance queries is one of the most fundamental operations on graphs. It is a primitive as either a main function or a building block of applications including geographic navigation, internet routing, socially tenuous group finding [159], influential community searching [160], and event detection [161]. A straightforward approach to answering shortest distance queries is breadth-first search on unweighted graphs or Dijkstra’s algorithm on positively weighted graphs. However, this approach may traverse the entire graph when two query vertices are far apart, and thus it incurs high computational cost especially when the graph is large. Consequently, indexing methods for efficiently answering shortest distance queries have been intensely studied [162,163]. Considering that real-world networks are highly dynamic, operations of users are bursty in regard to temporal locality [105]; it is tricky to design efficient index maintenance algorithms without reconstructing indices from scratch.

Ref. [107] studies the dynamic shortest path problem, which aims to recompute shortest path trees (SPTs) with a set of edge weight updates on a dynamic graph G. In order to handle multiple edge weight updates, the authors of [107] propose several dynamic SPT algorithms, namely DynDijkstra, MBall-StringInc and MFP, which extend and correct several existing dynamic SPT algorithms [132,164]. To be specific, MBall-StringInc [107] is proposed to amend BallString [164], which cannot update SPTs correctly in the case of multiple edge weight increase. MFP [107] is proposed to tackle the inefficiency problem of DynamicSWSF-FP [132], and it supports fully dynamic edge weight updates (i.e., with both edge weight increases and decreases). DynDijkstra [107] is a simple dynamic version of Dijkstra, which includes the algorithms of DynDijkstraInc and DynDijkstraDec that are designed to handle multiple edge weight increases and decreases, respectively.

Ref. [108] investigates dynamic single-source shortest path (SSSP) computation, and introduces two algorithms: LazyDijkDec for edge weight decreases and LazyDijkInc for increases. LazyDijkDec optimizes DynDijkstraDec [107] by terminating SPT computation upon finding the target path. LazyDijkInc reformulates DynDijkstraInc [107] into a set of edge weight decreases in an altered graph enabling LazyDijkDec to handle subsequent updates without intermediate SPT computation. Experimental results indicate these methods offer only marginal improvements over [107]’s original approaches.

While [107,108]’s Dijkstra-based algorithms can efficiently solve shortest distance queries, high computational cost incurs when the graph is large. Consequently, significant research has focused on developing efficient indexing techniques for shortest-path queries. Ref. [105] introduces two dynamic indexing structures for shortest-path and distance queries on large time-evolving graphs, which represent the first practical exact solutions capable of simultaneously handling both real-time distance queries and graph updates in evolving networks. And then, Ref. [105] proposes a dynamic indexing scheme, namely dynamic pruned landmark labeling, for queries on the last snapshot.

While the indexing framework in [105] lacks support for edge deletions, this operation frequently occurs in practical scenarios such as social network analysis, where user relationships dissolve. To address this limitation, the work in [109] develops specialized algorithms for computing the shortest path distance, particularly under decremental updates. They propose maintenance algorithms based on 2-hop cover, which can handle decremental updates efficiently. Similarly, the work in [100] develops a general approach for answering distance queries in fully dynamic graphs. Specifically, they propose a novel dynamic algorithm to update 2-hop cover labels during edge deletions, ensuring the minimality of the labels—an important feature that influences both storage requirements and query performance.

The aforementioned algorithms for processing shortest-distance queries on dynamic graphs are primarily designed for in-memory computation, limiting their applicability to large-scale graphs. To address this issue, several external-memory algorithms have been developed. For instance, the work in [106] investigates exact shortest-distance queries on disk-resident scale-free dynamic graphs and introduces two I/O-efficient algorithms for updating canonical labeling—a specialized form of 2-hop distance labeling. Meanwhile, the study in [104] concentrates on the incremental maintenance of all-pairs shortest distances. Their algorithms utilize general operators that can be adapted across various database management systems (DBMSs), making them compatible with both in-memory and disk-based DBMS implementations.

Ref. [103] presents a deterministic data structure for incremental SSSP in weighted directed graphs with total update time $\tilde{O}(n^{2}log{\displaystyle \frac{w}{{ϵ}^{O\left(1\right)}}})$ which is near-optimal for very dense graphs. Here, w is the ratio of the largest weight in the graph to the smallest, and n is the number of vertices in the graph. Ref. [101] investigates the k-shortest paths in a dynamic road network and proposes a distributed algorithm for finding k-shortest paths in a dynamic graph. Current studies that employ hub labeling techniques for real-time shortest path counting are limited by their dependence on a pre-computed index, which cannot tackle frequent updates over dynamic graphs. To address this, Ref. [102] proposes a novel approach for maintaining the index in response to change in the graph structure and develops incremental and decremental update algorithms for inserting and deleting vertices/edges, respectively. The main idea of these two algorithms is to update only the affected vertices, significantly reducing the time cost. Both [102,105] study the maintenance of SD-Index, but the pruning conditions of [105] are insufficient. In addition, the method in [105] only records the shortest distance in the BFS process, not the number of shortest paths. Ref. [99] studies the exact fully dynamic shortest paths problem. It gives a Monte Carlo randomized fully dynamic reachability data structure processing single-edge updates in $\tilde{O}\left(n\sqrt{m}\right)$ worst-case time and queries in $O\left(\sqrt{m}\right)$ time.

Algorithm analysis. Many existing dynamic shortest path algorithms rely on index-based structures to efficiently maintain and update shortest path information as the graph changes. These indices are designed to reduce the need for recomputing shortest paths from scratch after each update, which is especially important in large-scale or highly dynamic graphs.

4.4.3. Reachability Queries

The above index maintenance algorithms of shortest distance queries can be easily adapted to answer reachability queries, i.e., if the returned shortest distance is infinity, the reachability query answers false. Otherwise, it answers true. In addition to these algorithms for shortest distance queries, there are also some dedicated index maintenance algorithms for efficiently answering reachability queries.

To efficiently manage large-scale graphs, Ref. [110] introduces a foundational framework on reachability indices for dynamic graphs. Ref. [110] introduces a total order labeling (TOL) framework that summarizes a family of reachability indices with the best performance among the existing techniques for static graphs. The work in [165] investigates reachability-preserving compression, a technique that produces compact graph representations while retaining all the necessary information for answering reachability queries, without requiring decompression. Notably, incRPCO guarantees optimal compression ratios in its output, whereas incRPCF prioritizes speed by only modifying nodes and edges that impact reachability relationships. Recent research by [166] introduces a specialized indexing structure known as the WTB-index, which is specifically optimized for reachability queries in such temporal bipartite graphs.

4.5. Graph Separation

Graph separation is a fundamental problem in graph theory and has significant applications in areas like communication networks, parallel processing, data mining and community discovery in social networks. Partitioning the graph for distributed systems and finding dense clusters are two key directions in this field.

4.5.1. Graph Partitioning

Effective problem decomposition plays a pivotal role in both distributed computing systems and the optimization of sequential processing. Among various decomposition strategies, graph partitioning has emerged as a particularly prominent approach. At its core, this technique involves splitting a graph into multiple subgraphs of approximately equal size while simultaneously reducing the number of connections between these partitions. This is a well-studied challenge that has attracted significant research attention [5].

Definition 15

(Graph Partitioning). Given a graph $G=(V,E)$ and an integer k, graph partitioning is to divide V into k blocks of vertices $V_1,\dots ,V_k$ such that $V_1\cup \dots \cup V_k=V$ and $V_i\cap V_j=\varnothing$ for $i,j\in [1,k]$, $i\ne j$, while simultaneously optimizing an objective function and maintaining balance: $\forall i\in \{1,\dots ,k\}:|V_i|\le (1+ϵ)\lceil |V|/k\rceil$ for some $ϵ\ge 0$. The most common objective is to minimize the total cut ${\Sigma }_{i<j}\left|E_{ij}\right|$, where $E_{ij}=\{\{u,v\}\in e:u\in V_i,v\in V_j\}$.

Recent research has increasingly focused on dynamic graph partitioning, recognizing its crucial role in the preprocessing stage of distributed graph processing systems. While traditional approaches primarily addressed static graphs, the growing need to handle evolving graph structures in distributed analytics has spurred significant interest in dynamic partitioning methods.

In response to this challenge, Ref. [111] introduces an adaptive partitioning algorithm specifically designed for dynamic graphs. This decentralized approach employs an iterative vertex migration strategy that operates from any initial partition configuration. LogGP [117] introduces an innovative partition refinement approach that leverages both historical partitioning data and real-time statistical log information. Hermes [24] presents an efficient local-view approach for dynamic graph repartitioning. The system focuses on progressively enhancing existing partitions by reducing edge-cuts while preserving near-perfect load balance. Building upon existing streaming techniques [116], Leopard [112] presents an innovative approach to dynamic graph partitioning. The algorithm models evolving graphs as transitional states within a single-pass partitioning framework, effectively adapting traditional one-pass heuristics to dynamic scenarios. Ref. [113] proposes an alternative to conventional single-vertex migration approaches.

Different from the above researches that focus on the practical performance of the dynamic graph partitioning algorithms in distributed graph analytic systems, Ref. [115] theoretically proves that the dynamic graph partitioning problem is NP-complete and unbounded. Due to the intractability and unboundedness of the problem, Ref. [115] proposes a notion of heuristic boundedness to characterize the effectiveness of incremental heuristic algorithms and devises corresponding heuristically bounded dynamic graph partitioning algorithms based on the existing batch graph partition algorithms, such as DNE [167], KGGGP [168], FENNEL [116], and HDRF [169].

Recently, starting from the focus and characteristics of different dynamic graph partitioning algorithms, Ref. [170] systematically introduces various algorithms that can be used to solve the dynamic graph partitioning problem.

4.5.2. Graph Clustering

Graph clustering involves grouping vertices into clusters based on their connectivity patterns. The goal is to identify dense subgraphs where vertices within a cluster are more densely connected to each other than to vertices outside the cluster. Graph clustering has numerous applications, including social network analysis, recommendation systems, and biological network analysis.

Definition 16

(Clustering). Given a graph $G=(V,E)$, a cluster C ∈ V is a non-empty subset of V, representing a group of “similar” vertices. These vertices are densely connected within the group but sparsely connected to those outside it.

SCAN, a fundamental structural graph clustering algorithm, serves as a cornerstone for graph data management and analysis. Despite its importance, computational intensity of the method creates significant runtime challenges, restricting its real-world adoption. To overcome this limitation, Ref. [120] developes anySCAN, an innovative interactive solution optimized for multicore processors. The study in [118] enhances the DynStrClu approximate clustering algorithm based on Jaccard similarity, addressing a key limitation of traditional SCAN clustering which requires careful parameter tuning for optimal results. The work presented in [119] introduces DPISCAN, a thread-level parallel processing approach implemented on Apache Spark’s distributed framework.

Algorithm analysis. We analyze different type of graph separation algorithms over dynamic graphs. As shown in

Table 8. Comparison of time complexity for dynamic graph separation algorithms.

Problem	Algorithm	Graph Type	Update Mode	Fully Dynamic	Incremental Dynamic	Decremental Dynamic	Streaming Dynamic
Partitioning	Vaquero [111]	General	Single	✓	✓	✓	✓
Partitioning	LogGP [117]	General	Single	✗	✗	✗	✓
Partitioning	Hermes [24]	General	(distributed)	✗	✓	✗	✗
Partitioning	Leopard [112]	General	Batch	✓	✓	✓	✗
Partitioning	Li [113]	General	Batch	$O\left(\right|C{S}_i|+|C{S}_i|·log|C{S}_i\left|\right)$	✓	✓	✗
Partitioning	IncDNE [115]	General	Batch	✗	✓	✗	✗
Partitioning	IncKGGGP [115]	General	Batch	✗	✓	✗	✗
Clustering	danySCAN [120]	Weighted	Single	✗	✓	✗	✗
Clustering	BOTBIN [118]	General	Single	$O(logn·log{\displaystyle \frac{M+m}{p_f}})$	✓	✓	✗
Clustering	DPISCAN [119]	General	Batch (distributed & parallel)	✗	$O\left({\displaystyle \frac{(loglogn)m+\delta }{T}}\right)$	✗	✗

, most algorithms support incremental dynamic graphs. For the time complexity, Ref. [113] has to check the set of candidate vertices for movement in partition $P_i$. Additionally, for the time complexity of clustering, Ref. [118] returns clustering result satisfying the approximation probability $1-p_f$ after up to M edge updates. In [119], $\delta$ is the communication overhead in the Apache Spark cluster, and T is the number of executor nodes in the Spark cluster.

Discussion of large-update scenarios. In our survey, we categorize dynamic graph algorithms into three paradigms based on how they handle updates: single update algorithms (process updates one-by-one), batch update algorithms (process grouped updates simultaneously), and streaming algorithms (process updates continuously as they arrive). Our analysis reveals that as the number of updates grows, computational costs increase significantly for both single update and batch update approaches. This scalability limitation motivates the need for streaming algorithms, which are specifically designed for dynamic graphs with continuous updates (referred to as “streaming graphs“). While our survey covers the existing single and batch algorithms, we identify a notable research gap in streaming dynamic graph algorithms. Current approaches often struggle to maintain efficiency under sustained high update rates.

5. Systems

Graph processing systems serve as a specialized computational framework for managing and analyzing massive graph-structured data. These platforms are specifically engineered to address the unique demands of processing extremely large graphs, including social networks, web connectivity graphs, and biological interaction networks that typically comprise billions of interconnected nodes and edges. By providing optimized storage and processing capabilities, such systems overcome the significant computational challenges inherent in working with graph data at scale.

The study in [171] introduces a distributed in-memory graph management system specifically designed for handling large-scale dynamically changing graphs while ensuring efficient query processing. STINGER (Spatio-Temporal Interaction Networks and Graph Extensible Representation) [122] represents an open-source, high-performance data structure specifically designed for dynamic graph analysis. Building on a block-linked list architecture, this framework allows for the gradual expansion of both vertices and edges through incremental block additions. Recognizing STINGER’s limitations in distributed environments, DISTINGER [123] is developed as an extension to enable cluster-based graph analytics. This enhanced version implements a master/slave architecture optimized for cluster deployment, incorporating hash-based partitioning and message batching techniques. DISTINGER maintains all native STINGER operations while adding distributed support for vertex and edge modifications across the computing cluster. The EAGr system introduced in [172] provides an efficient solution for processing numerous continuous neighborhood-based aggregate queries on large, rapidly changing graphs.

Effective workload distribution plays a crucial role in determining the overall performance of distributed graph processing systems. The dynamic nature of evolving graphs often creates significant workload imbalances, as certain vertices may experience substantially higher update frequencies than others during specific time intervals. To address this challenge, Ref. [121] introduces iGraph, a specialized system designed for efficient processing of continuously changing graphs while maintaining balanced workloads. The computational power of GPUs has been widely leveraged to speed up graph processing tasks. Addressing this opportunity, Ref. [124] introduces a GPU-optimized dynamic graph storage architecture designed for seamless integration with existing graph algorithms.

6. Future Work

Here, we explore the research opportunities for the future, which will promote the development of dynamic graph processing.

6.1. Optimizations for High Efficiency

While numerous algorithms currently exist for handling dynamic graphs, improving these algorithms’ time and space efficiency remains a critical objective as graph data scales and complexity increases. Future algorithms should aim to minimize resource requirements of update processing. Investigate which types of graph computations can be performed incrementally, allowing for partial updates without recalculating from scratch.

6.2. Dynamic Algorithms for Various Types of Graphs

Most existing works focus on general graphs without any detailed informations such as labels, attributes, and signs. This becomes an urgent issue for dynamic algorithms on various types of graphs.

-

Attributed graphs—extend algorithms to account for attributed graphs, which are critical for applications such as social network analysis where metadata can provide important context.

-

Uncertain graphs—develop methods that can handle uncertainty in graph data, such as probabilistic edges, which are common in real-world networks like communication or transportation systems.

-

Signed graphs—incorporate positive and negative relationships between nodes into the analysis, which is essential for understanding dynamics in social networks, recommendation systems, and more.

-

Temporal graphs—analyze graphs that change over time, capturing the evolution of relationships and identifying patterns or anomalies that occur at different vertices in time.

6.3. Parallel and Distributed Approaches for Large-Scale Graphs

Further optimized algorithms for different update scenarios such as in-memory updates, parallel updates, and distributed updates play a crucial role in various application contexts. For instance, parallel Processing utilizes multi-core processors and GPUs to perform multiple graph operations simultaneously, which can significantly accelerate processing speeds. Besides, distributed computing on graphs leverages frameworks like Pregel to distribute the graph processing task across a cluster of machines, enabling the handling of extremely large datasets.

6.4. Efficient Approaches for Streaming Graphs

Streaming graph algorithms are an emerging and important area of research, especially as real-world graphs (e.g., social networks, communication networks, and sensor networks) increasingly involve dynamic changes such as the arrival of new vertices and edges over time. While there has been significant progress in dynamic graph algorithms, streaming graph algorithms are still relatively underexplored. By focusing on problems like community detection, path planning, and clustering, and leveraging approximate approaches to balance efficiency and accuracy, researchers can develop scalable and practical solutions for dynamic graphs. Future work should also explore theoretical foundations, adaptive algorithms, and integration with real-world systems to further advance this field.

7. Conclusions

As real-world networks continue to grow in size and complexity, dynamic graph algorithms will play an increasingly vital role in real-time analytics such as anomaly detection and risk assessment and recommendation, where responsiveness is critical. In this paper, we conduct an extensive survey on recent advances in efficient dynamic graph processing. We systematically review over 170 research articles, focusing on the latest developments in handling dynamic graphs. We first analyze and compare different computational complexity models designed to evaluate algorithm efficiency in dynamic graphs. Then, we classify studies on dynamic graph processing according to different problems, including centrality, coloring, cohesive subgraph, path traversal, and graph separation. For each class of works, we review the representative studies addressing various types of graph problems under different update types. These approaches commonly leverage localized re-computation, parallel, and distributed processing, and adaptive data structures to improve overall performance.

However, limitations of existing works still persist, particularly in scenarios involving large-scale, high-frequency updates or wholesale graph restructuring, where some algorithms still suffer from high computational complexity. Efficiency is highly dependent on factors such as update patterns, graph size, and structural properties. Future research directions should focus on (1) optimizations for high efficiency, tightening worst-case guarantees for dynamic graph problems; (2) dynamic algorithms for various types of graphs, such as attributed, uncertain, and temporal graphs; (3) parallel and distributed approaches for large-scale graphs, leveraging GPU acceleration and distributed frameworks; (4) efficient approaches for streaming graphs, developing algorithms that efficiently handle continuous, high-velocity updates. Bridging the gap between theoretical advances and practical implementations will be crucial for unlocking their full potential in more realistic applications.