Neural-Network-Based Synchronization Acquisition with Hankelization Preprocessing

Abstract

Conventional synchronization signal detection methods rely on linear correlation function analysis with fixed thresholds, which are insufficient for handling the nonlinear characteristics of practical wireless communication systems. In such environments, the usage of a long synchronization signal is beneficial for ensuring sufficient correlation information and enhancing detection robustness. To address these problems, this paper proposes a novel framework that combines Hankelization-based preprocessing with the operation of a neural network (NN). The proposed method enhances feature extraction through the inverse Fourier transform and Hankel matrix construction, followed by singular value decomposition (SVD) to preserve dominant signal features and suppress noise components. Leveraging the ability of NNs to learn nonlinear patterns, the proposed method eliminates the need for fixed thresholds and achieves robust synchronization signal detection. The simulation results demonstrate superior accuracy in various environments compared to conventional methods, underscoring the potential of Hankelization-based preprocessing in future wireless communication systems.

1. Introduction

In wireless communication systems, the preamble is a fundamental component for achieving synchronization between the transmitter and the receiver. It is a specially designed signal sequence transmitted at the start of communication to ensure precise alignment between the two ends. This process involves synchronizing the time, frequency, and phase of the transmitted and received signals, which is crucial for enabling efficient and reliable data transmission. A representative sequence used in preamble design is the Zadoff–Chu (ZC) sequence [1]. The ZC sequence is a complex-valued sequence with constant amplitude and excellent correlation properties. It exhibits zero autocorrelation for cyclic shifts and maintains low cross-correlation between different root sequences, making it effective for synchronization, channel estimation, and interference mitigation. Due to its ideal correlation characteristics, the ZC sequence has been adopted for use in random access in LTE and 5G NR [2,3]. The transmitter generates a ZC sequence based on a specific length and root index, modulates it, and transmits it. As the signal travels through the wireless channel, it encounters multipath fading, Doppler shifts, thermal noise, and interference. The receiver correlates the received signal with the ZC sequence to determine the transmission time and compensate for frequency offsets. Because the ZC sequence exhibits ideal autocorrelation properties, a distinct correlation peak appears at the correct timing. This feature enables the base station to detect new terminals and coordinate access.

Accurate synchronization minimizes timing and frequency errors, thereby reducing data transmission errors. Conversely, failure in synchronization acquisition can compromise the integrity of the transmitted data, leading to communication failures. As such, preamble-based synchronization acquisition is a critical technique for ensuring stable and robust communication performance in wireless systems.

Preamble detection method-based synchronization acquisition techniques have been extensively studied in various environments. Previous research on preamble detection algorithms includes the peak-to-average ratio after deleting quasi-users (PAR-DQ) preamble detection technique for LTE-satellite communication systems [4] and 5G physical random access channel (PRACH)-based preamble detection methods [5], both of which aim to enhance detection performance in multipath environments. Additionally, energy efficient random access techniques for low-Earth-orbit (LEO) systems have gained attention [6]. Traditional random access methods tend to consume excessive power to ensure high reliability. Moreover, a study on preamble detection performance in long-range (LoRa) systems [7] evaluated cross-correlation-based preamble detection techniques and proposed performance optimization strategies for low-power wide-area networks.

In general, synchronization acquisition typically involves calculating the cross-correlation function between the received signal and the known preamble. However, this method typically relies on a predefined threshold, which may fail to provide optimal performance in dynamic environments. An improperly low threshold increases the risk of false detections due to noise, while an excessively high threshold may result in missed detections. To overcome this issue, the constant false alarm rate (CFAR) technique has been adopted to dynamically adjust the threshold in response to changing noise conditions [8,9]. CFAR optimizes detection performance by analyzing the noise distribution, setting the threshold based on the average noise level, and maintaining a consistent false alarm rate [10,11,12].

Recent advancements in wireless communication have highlighted the potential of machine learning (ML)-based signal processing methods to improve detection performance, particularly in noisy environments. While traditional methods are predominantly based on linear signal models, practical wireless channels often exhibit nonlinear characteristics. However, ML-based approaches are relatively robust against this dependency due to using the correlation function outputs as training data to learn the patterns associated with signal presence and absence [13,14]. One such approach is the threshold-free random access preamble detection method based on a statistical analysis of the timing metric and K-means clustering [15]. Leveraging this approach provides more adaptive synchronization performance than conventional methods and demonstrates the potential to overcome the limitations of fixed-threshold-based approaches. ML techniques, such as neural networks (NNs), excel in learning such nonlinear patterns, enabling more robust signal detection. Through this learning process, the NN detects synchronization signals in an effective way, overcoming the limitations of static threshold settings.

Additionally, [16] explored deep learning methods as an alternative to correlation-based packet detection in satellite-based massive machine-type communication (mMTC) and Internet of Things (IoT) scenarios. This study demonstrates that supervised learning techniques, including random forests, can significantly enhance detection performance even in the presence of interference.

Similarly, another deep learning-based approach proposed in [17] addresses preamble detection in asynchronous grant-free random access. This work demonstrates that ML-based methods can outperform traditional correlator-based methods by adapting to complex channel conditions and extracting more representative signal features. The results suggest that deep learning models can effectively overcome the limitations of static threshold settings in synchronization acquisition and provide more adaptive and reliable detection performance.

To further enhance the effectiveness of NN-based synchronization acquisition, this paper proposes a novel framework leveraging a Hankelization-based preprocessing technique [18,19]. Conventional correlation function-based methods often struggle to distinguish signals from noise, particularly in low signal-to-noise-ratio (SNR) environments where the false detection rate can increase significantly due to threshold sensitivity. To address this issue, the proposed Hankelization-based method can emphasize the structural characteristics of the signal, providing higher detection performance compared to conventional methods. Additionally, by utilizing SVD to extract meaningful information from the signal, this approach maintains accuracy. Furthermore, by using a low-dimensional feature vector as the input for the NN, effective learning can be achieved even with a limited amount of data.

The proposed Hankelization-based method addresses these issues through a three-step process. First, the inverse Fourier transform is applied to the correlation result between the desired and received signals. Second, the transformed signal is converted into a Hankel matrix, followed by singular value decomposition (SVD). Finally, the resulting singular value vector is used as the input for the NN for synchronization signal acquisition [20]. This preprocessing approach emphasizes the structural characteristics of the signal, facilitating more effective NN training. More specifically, the proposed method is based on the hypothesis that treating the cross-correlation results between signals as an approximate sparse vector, followed by inverse Fourier transform and Hankelization, enables the extraction of data that are more conducive to optimizing the NN model. Similar Hankelization-based techniques have demonstrated their utility in prior studies. For instance, such preprocessing was employed to enhance signal classification performance in Rician and Rayleigh fading channels [21]. Another study utilized Hankelization to classify near-field and far-field signals in extremely large-scale massive multiple-input multiple-output (XL-MIMO) systems [22]. By minimizing noise and extracting dominant signal features, the proposed method improves synchronization signal detection accuracy, establishing its potential as an effective tool for modern wireless communication systems.

The remainder of this paper is organized as follows: Section 2 presents the system model and problem formulation. In Section 3, the Hankelization-based preprocessing and NN design are presented, along with an analysis of the effectiveness of the proposed method through the low-rank property of the Hankel matrix. In Section 4, we present the simulation results, covering experimental configurations and performance evaluations against baseline approaches. Finally, Section 5 presents the concluding remarks.

2. System Model and Problem Formulation

Throughout this paper, the synchronization signal is constructed using the ZC sequence [23], which is renowned for its exceptional correlation properties. The ZC sequence exhibits sharp autocorrelation peaks and uniform energy distribution, making it particularly suitable for robust synchronization signal detection in wireless communication systems [24]. The K-th ZC sequence, denoted as ${\mathbf{x}}_K\in {\mathbb{C}}^P$, is expressed as:

$${\mathbf{x}}_K\left[n\right]=e^{-{\displaystyle \frac{j\pi Kn(n+1)}{P}}},$$

(1)

where $n\in \{0,1,\dots ,P-1\}$. Here, P represents the length of the sequence, chosen to be a prime number, and K is the root index that determines the characteristics of the sequence. In general, K is set as a prime number less than or equal to $P-1$ to guarantee the correlation characteristic of ZC sequences.

The objective is to reliably detect the presence of the desired signal embedded in noisy observations. The desired signal, represented by the ZC sequence, is known a priori. The problem is framed as a binary classification task, where the goal is to determine whether the desired synchronization signal is present within the received noisy signal $\mathbf{y}$. The correlation function between $\mathbf{y}$ and the ZC sequence ${\mathbf{x}}_K$ is computed and transformed into a structured Hankel matrix via the inverse Fourier transform. This transformation effectively highlights the dominant features of the desired signal while suppressing noise and residual components. Singular values extracted from the Hankel matrix are then utilized as inputs to a NN, which performs binary classification to determine the presence or absence of the synchronization signal. This approach ensures reliable and accurate synchronization detection across a range of challenging scenarios.

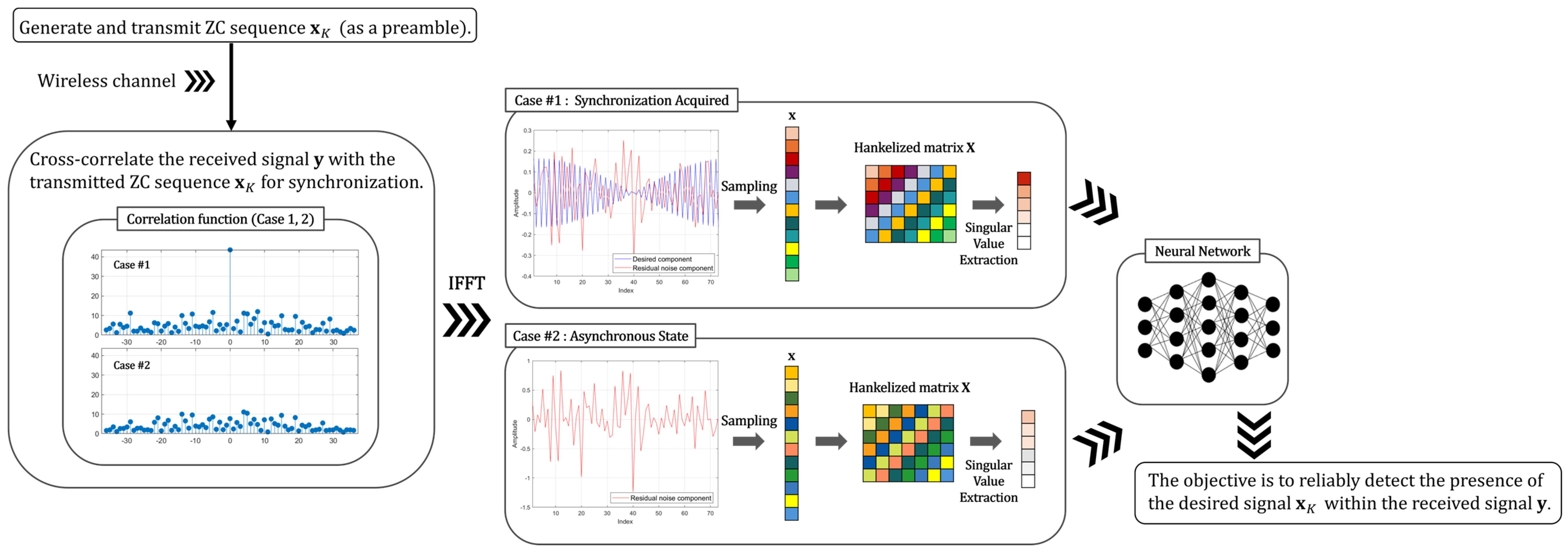
3. Proposed Method

3.1. Brief Introduction of Preprocessor Design Based on Hankelization

This paper introduces a preprocessing approach that constructs a Hankel matrix by applying the inverse Fourier transform to the correlation function, rather than directly using the correlation function as the input for the NN. SVD is applied to the Hankel matrix to extract a vector of singular values, which is used as the input for the NN. This method effectively preserves the primary signal features while reducing noise. By converting the correlation function into a structured matrix representation, the key characteristics of the signal are highlighted and efficiently utilized for further processing. This preprocessing step enhances the overall performance of the synchronization detection framework.

Figure 1 presents the framework of the NN-based synchronization signal detection system incorporating Hankelization preprocessing proposed in this paper. The inverse Fourier transform of the correlation function maps its frequency-domain representation to the time domain, with dominant features corresponding to the peaks of the correlation function, while residual components reflect less significant contributions.

3.2. Effectiveness of the Proposed Method Related to the Low Rank Properties of a Hankelized Matrix

The inverse fast Fourier transform (IFFT) of the correlation function, denoted as $\mathbf{z}\in {\mathbb{C}}^{2P-1}$, is reconstructed into a Hankel matrix $\mathbf{Z}\in {\mathbb{C}}^{P\times P}$, as given below:

$$\mathbf{Z}[i,j]=\mathbf{z}[i+j-1],\forall i,j\in \{1,2,\dots \}.$$

(2)

Here, $\mathbf{z}$ is derived from the cross-correlation between the received noisy signal $\mathbf{y}$ and the ZC sequence ${\mathbf{x}}_K$. The cross-correlation function is expressed as

$${\mathcal{R}}_{\mathbf{y}{\mathbf{x}}_K}\left[m\right]=\sum _{p=0}^{P-1}\mathbf{y}\left[p\right]·{\mathbf{x}}_K[p+m],\forall m\in \{-P+1,\dots ,P-1\}.$$

(3)

and the IFFT is applied to $R_{\mathbf{y}{\mathbf{x}}_K}\left[m\right]$, resulting in $\mathbf{z}$ used to construct the Hankel matix:

$$\mathbf{z}\left[n\right]={\displaystyle \frac{1}{2P-1}}\sum _{m=0}^{2P-2}{R}_{\mathbf{y}{\mathbf{x}}_K}\left[m\right]·e^{j{\displaystyle \frac{2\pi mn}{2P-1}}},\forall n\in \{0,1,\dots ,2P-2\}.$$

(4)

The sequence $\mathbf{z}$ captures the correlation properties between the received signal $\mathbf{y}$ and the ZC sequence ${\mathbf{x}}_K$. When used to construct the Hankel matrix $\mathbf{Z}$, $\mathbf{z}$ generally results in a full-rank matrix. This is caused not only by noise-induced variations in practical scenarios but also by the intrinsic correlation characteristics of the ZC sequence, which can introduce small residual variations even under ideal noise-free conditions. Despite being full-rank, $\mathbf{Z}$ retains significant information about the synchronization signal. Specifically, the dominant periodic patterns of the reference sequence, which are critical for synchronization, remain embedded within the structure of $\mathbf{Z}$.

To validate this, we analyze an idealized scenario where the received signal $\mathbf{y}$ is identical to the ${\mathbf{x}}_K$. In this ideal case, the cross-correlation function ${\mathcal{R}}_{\mathbf{y}{\mathbf{x}}_K}$ simplifies to the autocorrelation of ${\mathbf{x}}_K$, dominated by its periodic structure. The dominant periodic component is characterized by the peak index $f_p$ of the autocorrelation function:

$$f_p=arg\underset{m}{max}\left|R_{\mathbf{y}(={\mathbf{x}}_K){\mathbf{x}}_K}\left[m\right]\right|.$$

(5)

Based on (5), an ideal sequence $\mathbf{s}\in {\mathbb{C}}^{2P-1}$ can be expressed as $\mathbf{s}\left[n\right]=e^{j2\pi n{f}_p/(2P-1)}$ for $n\in \{0,1,\dots ,2P-2\}$. From this sequence, a Hankel matrix $\mathbf{S}\in {\mathbb{C}}^{P\times P}$ is constructed following (2), and in the ideal case, $\mathbf{S}$ exhibits a rank-1 property. To validate this claim, we analyze the row structure of $\mathbf{S}$. From (2), the u-th row of $\mathbf{S}$ can be represented as follows:

$$\mathbf{S}[u,:]=e^{j2\pi u{f}_p/(2P-1)}·\mathbf{v},$$

(6)

where $\mathbf{v}=[1,e^{j2\pi f_p/(2P-1)},e^{j4\pi f_p/(2P-1)},\dots ,e^{j2\pi (P-1)f_p/(2P-1)}]$ serves as the basis vector for all rows of $\mathbf{S}$. This indicates that all rows of $\mathbf{S}$ are constant multiples of the basis vector $\mathbf{v}$. Specifically, any two rows $\mathbf{S}[u,:]$ and $\mathbf{S}[v,:]$ satisfy the following relationship:

$$\mathbf{S}[u,:]=e^{j2\pi f_p(u-v)/(2P-1)}·\mathbf{S}[v,:],\forall u,v\in \{1,2,\dots ,P\}.$$

(7)

Since all rows are scalar multiples of the same basis vector, $\mathbf{S}$ has a rank-1 in the ideal case. In accordance with the symmetry, the same property holds for the columns of $\mathbf{S}$. Thus, $\mathbf{S}$ is confirmed to exhibit a rank-1 structure under ideal conditions. This ideal rank-1 structure of $\mathbf{S}$ ensures that the underlying synchronization signal is well represented in the matrix. As noted, in practical scenarios, the presence of noise and residual components causes the Hankel matrix $\mathbf{Z}$, constructed from the noisy signal, to deviate from the ideal rank-1 property. Nevertheless, $\mathbf{Z}$ preserves the dominant structures associated with the synchronization signal, which can be effectively extracted and analyzed through SVD.

3.3. NN Design via Hankelization-Based Preprocessing

As previously discussed, although the rank-1 property of the Hankel matrix $\mathbf{Z}$ is no longer satisfied due to noise-induced variations and the intrinsic correlation of the ZC sequence, $\mathbf{Z}$ retains useful information related to the synchronization signal. Therefore, we leverage its singular values to construct an efficient latent space.

Now, we propose an integrated framework that combines Hankelization and NN utilization to identify the low-dimensional representation of complex data. To achieve this, we define the required terms as follows:

• $\overline{\sigma }\in {\mathbb{R}}_{+}^P$: The vector of singular values of the Hankel matrix $\mathbf{Z}$, which is sorted in descending order.
• $\mathbf{e}\in \{{[1,0]}^T,{[0,1]}^T\}$: The one-hot encoding vector representing whether the synchronization signal is present or absent, where ${[·]}^T$ denotes the transpose operator. We set the presence and absence of the synchronization signal as ${[1,0]}^T$ and ${[0,1]}^T$, respectively.
• $\mathcal{L}$: The loss function, e.g., the mean squared error (MSE).
• $\Theta$: The model parameter, i.e., weight matrices and bias vectors.
• ${\nabla }_{\Theta }$: The gradient operator with respect to $\Theta$.
• $P_L$: The latent space dimension.
• d: The NN model depth.
• M: The size of the training dataset.
• N: The size of the test dataset.

With these terms, we define the fully-connected (FC) NN model denoted by $\mathcal{N}$. Finally, we can define the optimized NN model, denoted by ${\mathcal{N}}^{\ast }$, as follows:

$${\mathcal{N}}^{\ast }=\underset{\mathcal{N}}{arg\; min}\sum _{i=1}^M\mathcal{L}({\mathbf{e}}^{\left(i\right)},\mathcal{N}\left({\overline{\sigma }}^{\left(i\right)}\right)),$$

(8)

where i is the index of the training dataset. In addition, we use the MSE as the loss function $\mathcal{L}$. We choose the stochastic gradient descent with momentum (SGDM) as the optimizer for the update rule for the model; thus, the parameter ${\Theta }_t$ at iteration t is computed as follows:

$${\Theta }_{t+1}\leftarrow {\Theta }_t-\eta \sum _{i\in {\mathcal{B}}_t}{\nabla }_{\Theta }\mathcal{L}({\mathbf{e}}^{\left(i\right)},\mathcal{N}\left({\overline{\sigma }}^{\left(i\right)}\right))+\gamma ({\Theta }_t-{\Theta }_{t-1}),$$

(9)

where $\eta$ is the learning rate, ${\mathcal{B}}_t$ represents the set containing the indices of the input/output pairs in the current mini-batch, and $\gamma$ is the momentum coefficient that determines the contribution of the previous gradient step to the current update. Through the procedures of (8) and (9), we can optimize the NN model. Now, we can use the optimized NN model for the hypothesis testing of binary classification as follows:

$$\widehat{\mathbf{e}}\left[0\right]\underset{Present}{\overset{Absent}{\lessgtr }}\widehat{\mathbf{e}}\left[1\right],\mathrm{where}\widehat{\mathbf{e}}={\mathcal{N}}^{\ast }\left(\overline{\sigma }\right).$$

(10)

Based on (10), we now evaluate the performance of the optimized NN model ${\mathcal{N}}^{\ast }$ through numerical simulations in the next section.

To analyze the computational efficiency of the proposed method, considering the Hankel matrix dimensions P, the latent space dimension $P_L$, and the NN model depth d, the proposed method requires a floating-point operation (FLOP) complexity $\mathcal{O}\left(dP{P}_L\right)$ in terms of online complexity for an FC model’s operation. This complexity is comparable to, or even lower than, that of conventional NN models. However, the proposed method incurs an additional online complexity of $\mathcal{O}\left(P^3\right)$ FLOP for singular value extraction. Although this additional cost increases computational demand, it improves overall performance.

4. Simulation Results

4.1. Simulation Configurations

The parameters configured for the simulations in this paper are summarized in

Table 1. Default configuration in the experiments.

Parameters	Values
Length of sequence (P)	37, 41
Root index (K)	A randomly selected prime number under P
Size of training dataset	${10}^4$
Size of test dataset	${10}^4$
NN depth d	2
NN width	24
Max. epochs	30
NN connection type	Fully-connected
Learning rate	${10}^{-3}$
Activation function	Leaky ReLU
Loss function	MSE
Optimizer	SGDM
Momentum	$0.8$

. The ZC sequence utilized requires the sequence length and root index as key parameters. For the simulations, we set the sequence lengths to 37 and 41 and observed the resulting performance. The configurations of the NN used in the simulations are also detailed in the table above. Instead of focusing on the complexity of the NN structure, the emphasis of this study is on extracting and utilizing key information from the data to enhance detection performance. Therefore, a relatively simple NN architecture was adopted, ensuring that the model remains efficient while effectively leveraging the preprocessed features from the proposed method.

The metric for the simulations is the detection error rate, which quantifies the ratio of incorrectly classified samples to the total number of samples in the test dataset of size N. For each test sample j, the true label vector ${\mathbf{e}}^{\left(j\right)}$ is represented as a one-hot encoded vector. The predicted label vector for the same sample is denoted by ${\widehat{\mathbf{e}}}^{\left(j\right)}$. The detection error rate is defined as the complement of the classification accuracy:

$$\mathrm{detection}\mathrm{error}\mathrm{rate}=1-{\displaystyle \frac{\mathrm{card}\{j\mid {\widehat{\mathbf{e}}}_H^{\left(j\right)}={\mathbf{e}}^{\left(j\right)}\}}{N}},$$

(11)

where $\mathrm{card}\{·\}$ represents the cardinality of the set. Additionally, ${\widehat{\mathbf{e}}}_H$ is ${\left[H(\widehat{\mathbf{e}}\left[0\right]-\widehat{\mathbf{e}}\left[1\right])H(\widehat{\mathbf{e}}\left[1\right]-\widehat{\mathbf{e}}\left[0\right])\right]}^T$ for hard decisions via the Heaviside function $H(·)$. This metric provides a clear and quantitative measure of detection performance across different configurations.

To evaluate the performance of the proposed method, two baseline schemes were used for comparison:

• Baseline 1 (Deep learning method based on cross-correlation): The NN-based method employing absolute correlation values as in conventional methods.
• Baseline 2 (Deep learning method based on IFFT-processed cross-correlation): The NN-based method employing absolute values of IFFT-applied correlation results as in conventional methods.
• Baseline 3 (Random forest method): The ML-based method that classifies signals using statistical features extracted from the absolute values of IFFT-processed cross-correlation results, following the approach in [16].
• Baseline 4 (Adaptive threshold method): A non-ML-based approach that detects signals by applying an adaptive threshold to the absolute values of IFFT-processed cross-correlation results based on estimated noise levels, following the approach in [25].

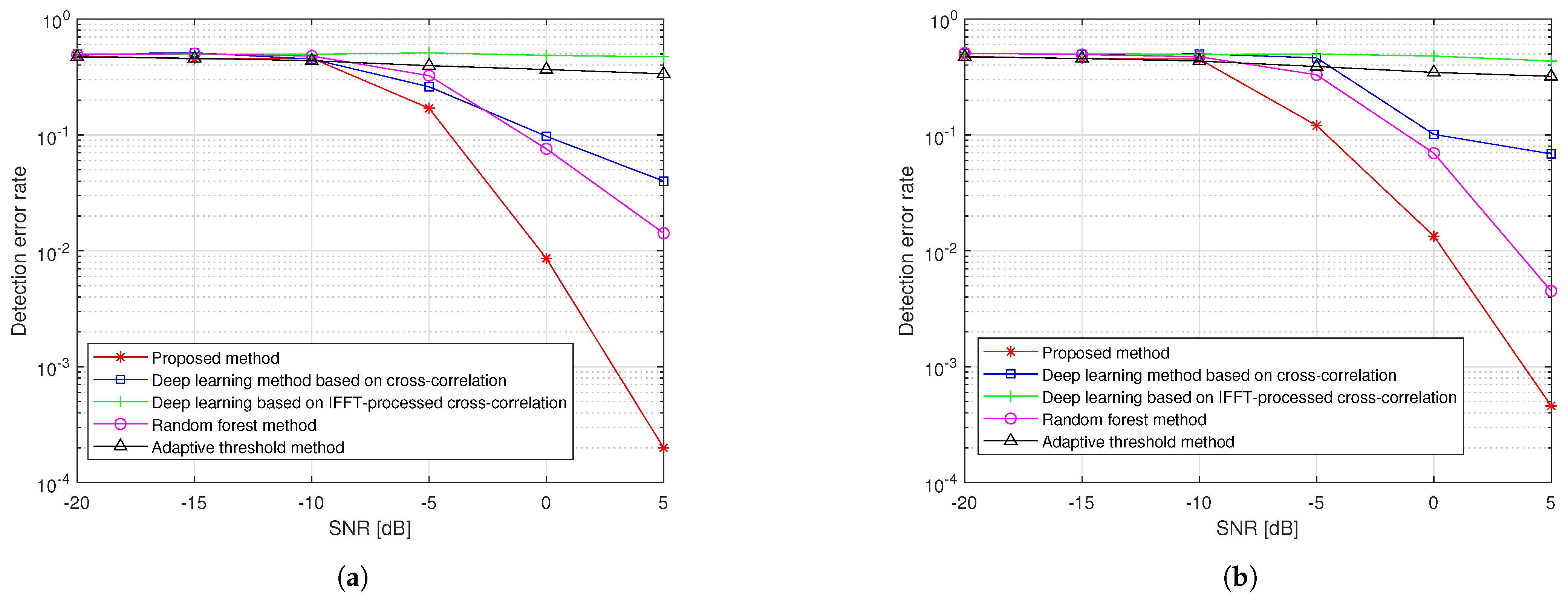
4.2. Performance for Detecting Synchronization Signal

Figure 2 shows the classification accuracy of the proposed method. Specifically, the row-normalized results depict the percentages of correctly and incorrectly classified observations for each true class, while the column-normalized results represent the percentages for each predicted class. For instance, as shown in Figure 2a, the classification accuracy for signals with the presence of synchronization signals is $98.3\%$. Furthermore, among the predicted signals, the percentages of correct and incorrect classifications are $99.8\%$ and $0.2\%$, respectively.

Figure 3 presents the detection error performance of the proposed method compared to conventional approaches for synchronization signal detection. The simulations used ${10}^4$ training data points within an SNR range of $-20$ dB to 5 dB. Figure 3a shows the results for $P=37$, and Figure 3b shows the results for $P=41$. The proposed method employs a Hankelization-based preprocessing technique, while conventional methods use the absolute values of the correlation function or the IFFT results as the input for the NN, the random forest method, and the adaptive threshold method. In Figure 3a, the proposed method achieves significantly lower detection error rates across all SNR levels. For SNR values above 0 dB, the error rate is below ${10}^{-3}$, while conventional methods remain above ${10}^{-2}$, showing minimal improvement even at higher SNR levels. Similarly, in Figure 3b, the proposed method maintains superior performance, achieving error rates below ${10}^{-3}$ for SNR values exceeding 0 dB. Conventional methods, particularly the IFFT-based approach, show persistently high error rates and negligible improvement. These results highlight the effectiveness of the proposed Hankelization-based preprocessing technique in achieving robust detection performance under various SNR conditions.

Figure 4 shows the detection error rate of the proposed method compared to other baseline methods under different training dataset sizes. The proposed method consistently achieves the lowest detection error rate, demonstrating stable performance across different training dataset sizes. These results confirm the robustness of the proposed method in synchronization signal detection, ensuring reliable performance regardless of the dataset size.

Figure 5 shows the detection rate of the proposed method compared to four baseline methods across different sequence lengths P and NN widths. Based on (11), the detection rate is derived from the detection error rate, reflecting its complementary relationship. In Figure 5a, the proposed method consistently achieves superior accuracy, even with a constrained NN width of 24, maintaining over $90\%$ detection accuracy for longer sequence lengths. In contrast, the baseline methods exhibit noticeable performance degradation for longer lengths of sequence. This indicates the ability of the proposed method to handle increased data complexity and dimensionality efficiently. Also, Figure 5b shows the detection rate with an increased NN width of 48. The baseline methods exhibit improved performance for longer sequence lengths compared to the results in Figure 5a, particularly Baseline 1 (Deep learning method based on cross-correlation). However, the proposed method remains largely unaffected by the increase in NN complexity, consistently achieving high detection accuracy regardless of the NN width. This robustness highlights the efficiency of the proposed method in extracting and utilizing critical features without relying on a highly complex NN architecture. These results highlight the effectiveness and adaptability of the proposed method for synchronization signal detection across varying configurations.

Figure 6 shows the detection error rate of the methods when the NN model is optimized at 0 dB and tested under varying SNR levels. For instance, an SNR margin of 10 dB means that the NN model was trained at SNR 0 dB but was tested randomly at SNR within the $[-5,5]$ dB region. The simulation results demonstrate that the proposed method effectively mitigates the degradation of performance compared to baseline methods when the training and test SNR conditions are significantly different. This suggests that the proposed method is a scheme that can adapt robustly to the change in SNR in online execution, and it is obvious that it can be very useful in dynamic environments.

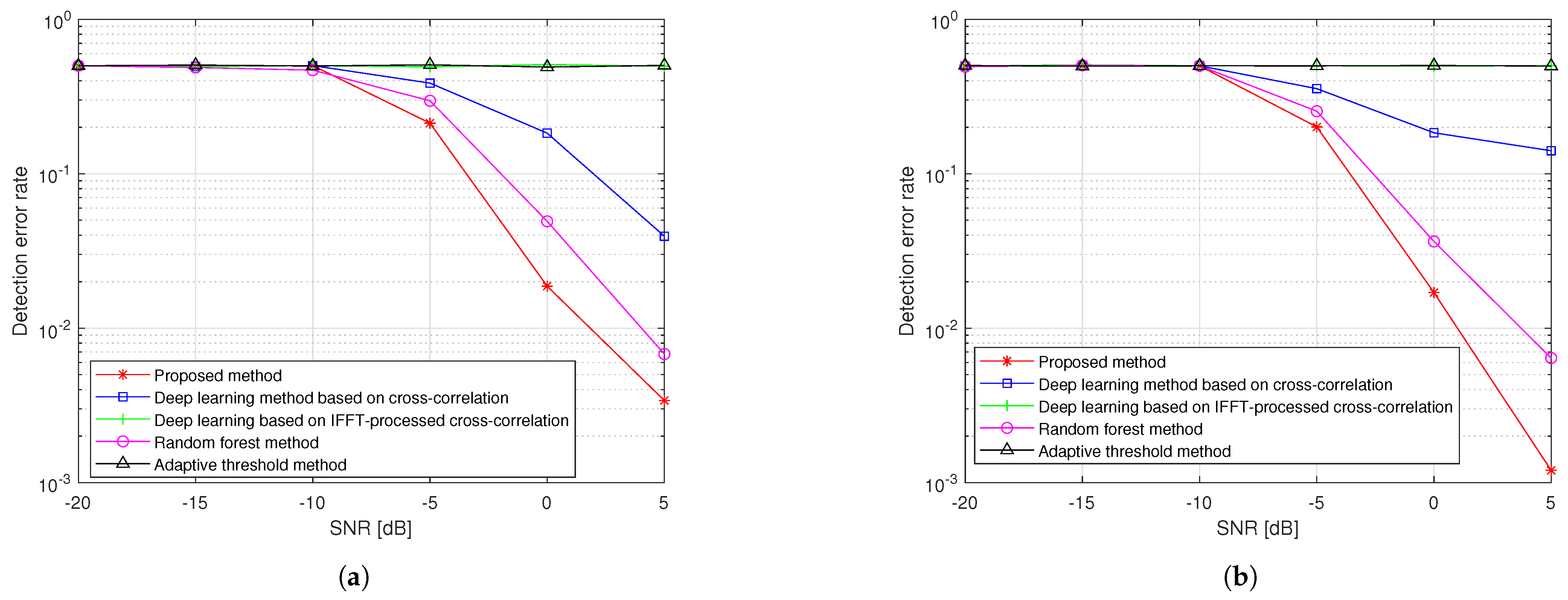
4.3. Performance for Detecting Synchronization Signal with m-Sequences

In this subsection, we evaluate the performance of the proposed method when m-sequences are used as synchronization signals instead of ZC sequences. m-sequences are commonly utilized in random access scenarios [26], making it valuable to examine the applicability of the proposed approach with different sequences. The NN architecture used in this experiment is the same as described in Table 1.

Figure 7 shows the detection error rate of the proposed method compared to the baseline approaches under varying SNR levels when m-sequences are employed. The results show that the proposed method maintains a lower detection error rate than the baseline methods. This suggests that the proposed approach can effectively adapt to different synchronization sequences while preserving reliable detection performance. These results suggest that the proposed method can be applied to different types of synchronization sequences while maintaining consistent detection performance. This flexibility highlights its potential usefulness in various random access scenarios where different preamble designs are employed.

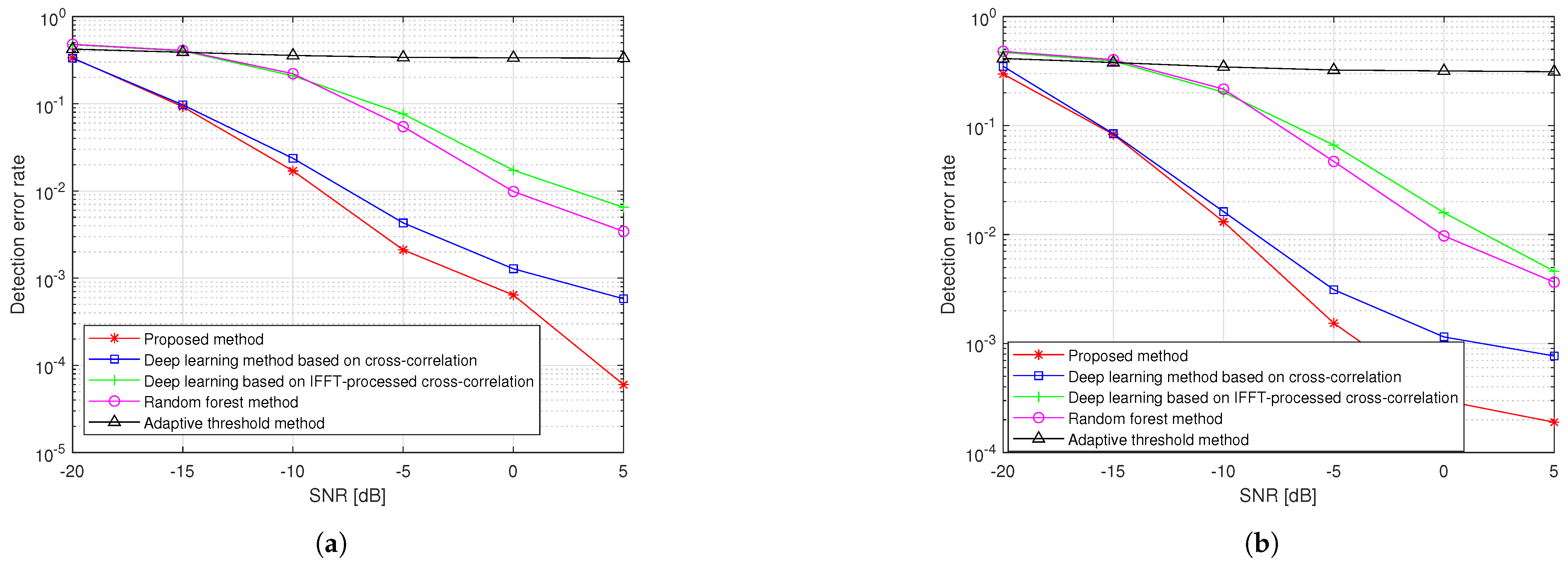
4.4. Performance for Detecting Synchronization Signal Under Practical Channel Condition

In this subsection, we evaluate the performance of the proposed method in a practical channel environment to assess its robustness under realistic conditions. To this end, we incorporate the tap delay line-B (TDL-B) channel model, which effectively captures multipath fading effects encountered in wireless communication systems [27]. The simulation parameters related to the channel configuration are summarized in

Table 2. Default configuration for practical channel experiments.

Parameters	Values
Carrier frequency	3.5 GHz
Sampling frequency	15.36 MHz
Subcarrier spacing	15 kHz
Number of paths	6
Path gain and delay	TDL-B [27]

, while the NN architecture remains consistent with the configuration presented in Table 1.

Figure 8 shows the detection error rate of the proposed method in comparison to various baseline approaches under different SNR conditions within a practical channel setting. The results demonstrate that the proposed method consistently outperforms conventional techniques, maintaining a significantly lower detection error rate. In particular, while the baseline methods experience some performance degradation due to multipath fading, the proposed approach maintains enhanced resilience, achieving reliable synchronization detection even in low-SNR environments. These findings suggest the effectiveness of the Hankelization-based preprocessing technique in ensuring reliable synchronization detection, even in the presence of multipath fading.

5. Conclusions

In this paper, we propose an NN model combined with a Hankelization-based preprocessing technique to enhance synchronization signal detection in wireless communication systems. Unlike traditional methods that directly utilize the correlation function as the input for the NN, the proposed approach applies the inverse Fourier transform and Hankelization to the correlation function, followed by SVD to extract primary signal features. These features are then used as inputs to the NN, effectively addressing the noise sensitivity and processing inefficiencies of conventional synchronization detection methods. By incorporating this preprocessing step, the proposed method achieves optimized detection performance, particularly in low-SNR environments. Simulation results demonstrate that the Hankelization-based preprocessing technique significantly improves synchronization signal detection accuracy compared to conventional methods. This approach exhibits robustness against noise and outperforms existing methods by enhancing detection reliability, particularly in conditions with low signal quality. These observations validate the effectiveness of the proposed NN-based synchronization detection model, showcasing its potential to overcome the limitations of existing approaches.

While the proposed method exhibits strong performance in synchronization acquisition, further refinements can enhance its applicability for practical deployment. In particular, the computational complexity of the SVD may introduce challenges for real-time implementation, and the singular value spectrum can exhibit numerical sensitivity under extreme noise conditions. To mitigate these issues, in future work, we will extend our research by applying approximate SVD algorithms, such as the randomized SVD method, which utilizes random sampling, and the truncated SVD method, which selectively retains only the dominant singular values, to reduce computational complexity. Additionally, we will conduct a broad investigation into various algorithms to improve numerical stability, ultimately working towards enhancing our approach with more advanced algorithms. From the perspective of integration with system performance evaluation, especially in ultra-reliable communications, a comprehensive bit error rate (BER) analysis remains critical to fully assessing the broader impact of the proposed method on overall system performance. Expanding the evaluation framework to include BER analysis would offer deeper insights into the effectiveness of the proposed approach in enhancing the reliability of random access communication systems. Finally, we aim to further explore the adaptability of our method to realistic conditions, where SNR variations may occur, thereby enhancing its practical applicability and robustness.