Abstract
With the rapid development of precision instruments, aerospace, and automotive industries, the demand for compact vibration isolators capable of suppressing low-frequency vibrations has surged. Although prior reviews have established the theoretical framework of quasi-zero stiffness (QZS) isolators, critical gaps persist in addressing their compact design under strong nonlinear dynamics and diverse engineering constraints. This review systematically analyzes the dynamic characteristics of QZS systems under nonlinear effects and evaluates five innovative design methodologies for compact QZS isolators: special spring type, magnetic type, bionic type, metamaterials-based type, and origami-inspired type. Key findings reveal that special spring-type isolators are simple to design and space-efficient but difficult to machine. Magnetic-type isolators achieve ultra-low start-up frequencies but face thermal instability. Metamaterial designs enable multifunctional integration at the cost of manufacturing complexity, while bionic-inspired and origami-inspired isolators are difficult to abstract for practical applications. We find that current research tends to prioritize miniaturization over the synergistic optimization of load capacity, broadband isolation, and adaptability. Future research should focus on multi-degree-of-freedom systems, coupled metamaterials-bionic structures, and active magnetic control. This work provides a key roadmap for advancing compact QZS technology in space-constrained applications.
1. Introduction
With accelerating industrialization, vibration-related challenges have garnered significant attention across engineering applications. In the fields of precision instruments, aerospace, automotive, construction, etc., the impact of vibration is particularly significant. Vibration compromises the functional stability of precision instruments [1,2,3,4], induces instability and deformation in ship mechanical structures [5], degrades vehicle stability and comfort [6,7], impairs aerospace equipment fatigue life and attitude control accuracy [8,9], and causes catastrophic destruction of buildings [10,11,12]. Therefore, effective isolation of vibration has become an important research direction in engineering technology.
Vibration isolation is mainly divided into passive vibration isolation, active vibration isolation, and hybrid vibration isolation. Passive vibration isolation has a simple structure and high reliability, but there are problems such as a narrow frequency band of vibration isolation and poor vibration isolation effect under large amplitude. Active vibration isolation measures the state signals of the vibration isolation system through sensors, feeds the signals back to the control system, and then the actuator controls the vibration of the vibration isolation object, which realizes the results of widening the vibration isolation frequency band and improving the vibration isolation efficiency [13], but the high-precision sensors and actuators lead to the system’s complexity and high cost. In order to combine the advantages of passive and active vibration isolation techniques, hybrid systems have emerged. These systems combine passive damping materials, mechanical elements, and active control mechanisms to achieve better vibration isolation. Hybrid systems are able to provide greater adaptability and versatility, especially when dealing with complex vibration environments [14,15]. However, in the low-frequency range, especially when the vibration is close to zero frequency, i.e., static offset, it is often difficult for the above vibration isolators to effectively reduce the transmission of low-frequency vibration. Based on the classical linear vibration isolation theory, in order to obtain effective vibration isolation, it is necessary to ensure that the ratio of the excitation frequency to the intrinsic frequency of the system is greater than √2 [16], as shown in Figure 1. In order to achieve effective suppression of low-frequency vibration, it is necessary to reduce the intrinsic frequency of the system. In the engineering application of the load mass, it is certain that we need to reduce the stiffness of the system to reduce the intrinsic frequency of the system, and the reduction of stiffness will lead to system stability deterioration. This contradiction has been restricting the practical application of low-frequency vibration isolation technology.
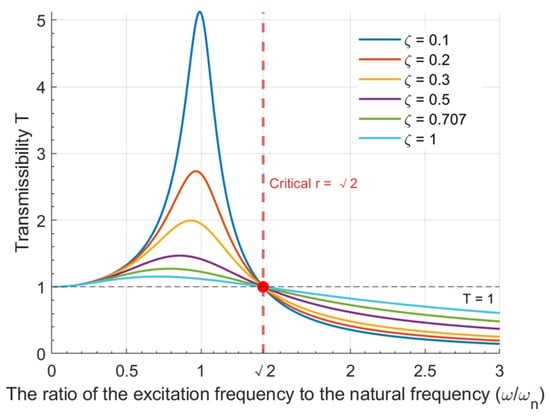
Figure 1.
Amplitude-frequency characteristic curves under different damping.
Researchers have proposed a vibration isolator with high static stiffness and low dynamic stiffness, which can exhibit very low stiffness in the low-frequency range while providing excellent load stability through the parallel connection of positive and negative stiffness. This type of isolation is called quasi-zero stiffness (QZS). QZS isolation has both high static stiffness and low dynamic stiffness characteristics. High static stiffness means that the vibration isolator can provide high stiffness under the self-weight of the mechanical equipment and vibration isolation source. This means that under normal working conditions, the deformation of the vibration isolator is small, and it can effectively support heavy objects and maintain stability; low dynamic stiffness means that under the action of vibration impact, external excitation, etc., the vibration isolation device can provide low stiffness, and it can effectively absorb and reduce vibration transmitted through the equipment. QZS isolation provides an excellent vibration isolation effect in the low-frequency range close to zero frequency, and it can effectively inhibit the propagation of low-frequency vibration.
The key to the design of QZS isolation is how to choose a reasonable negative stiffness structure, and in the actual engineering, there are many components with negative stiffness characteristics. The review [17] systematically summarizes the structure of negative stiffness, mainly including mechanical spring structure, flexural beam structure, geometrically nonlinear structure, magnetic structure, metamaterials, and bionic structure. Each method has its own advantages, disadvantages, and scope of application. In contrast, this review focuses mainly on space-limited engineering applications and provides a systematic summary of existing compact designs of QZS isolators.
In many engineering application scenarios, the available space is often very limited. In the aerospace field, for example, the space left for vibration isolation systems is extremely scarce because of the need to carry all kinds of complex instruments and equipment inside the aircraft. The traditional QZS isolation is not compact enough and occupies a large space, which may limit the layout of other equipment. Therefore, the compact design of QZS isolation is particularly important, which can make the space layout more reasonable and provide the possibility of optimizing the layout of the vibration isolator. Compact design is not simply to reduce the volume but requires comprehensive consideration of space volume, load-carrying capacity, vibration isolation frequency band, dynamic travel, and other multi-objective parameters. Its essence is to solve the engineering contradiction of “small volume, large load, wide frequency vibration isolation” through the innovation of nonlinear mechanics and multidisciplinary integration.
In this paper, we systematically sort out the design mechanism of compact design, comprehensively analyze its research status, and elaborate on the applicable occasions. Section 1 introduces the engineering significance of the compact design of QZS isolators, and Section 2 describes the basic principles, design process, and nonlinear dynamic properties of the QZS system. Section 3 analyzes and discusses the compact design methods, vibration isolation performance, application scenarios, and current research bottlenecks. Section 4 summarizes the whole paper and gives an outlook and further proposes prospective and feasible research directions for the reference of researchers in related fields.
2. Fundamentals of QZS
2.1. Basic Principle of QZS
The QZS system is composed of a positive stiffness structure and a negative stiffness structure through parallel connection. Positive stiffness refers to a material or structure’s ability to resist elastic deformation under external forces, providing the primary load-carrying capacity in a QZS system. The opposite is true for negative stiffness, in which the direction between force and displacement is opposite in this type of structure and does not provide load-carrying capacity [18]. According to the basic principle of vibration isolation, the total stiffness of the parallel elastic element system is the sum of the elastic element stiffnesses, . As shown in Figure 2, in the negative stiffness region of the negative stiffness element, the total stiffness of the system is close to zero, and in the non-negative stiffness interval, the parallel system has a greater load-carrying capacity compared to a single positive stiffness element. Therefore, by reasonably selecting the positive and negative stiffness elements to isolate the system from low-frequency vibration in the neighborhood [x1, x2] of the desired static equilibrium position, it is possible to design a vibration isolation device with both high load-bearing capacity and low stiffness characteristics. Compared with the single elastic element system, it can play a vibration isolation effect in the ultra-low frequency, and through the appropriate structural design, it can enhance its energy dissipation characteristics to further improve the vibration isolation effect, which is the optimal choice for the current low-frequency vibration isolation.
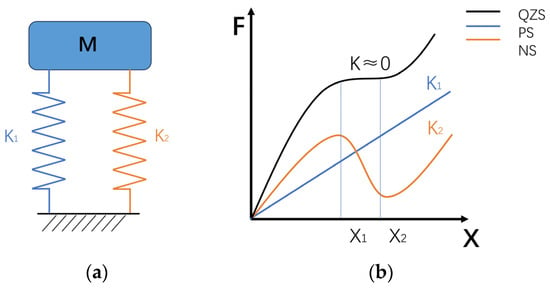
Figure 2.
Realization principle of QZS isolator: (a) Schematic diagram of parallel connection of springs; (b) Schematic diagram of force and displacement principle.
2.2. The Design Flow of QZS Isolation
Figure 3 shows the idea and framework of the overall design of the QZS isolation system. First of all, in the specific application background, select the appropriate positive and negative stiffness structure, analyze the mechanical properties of negative stiffness and zero stiffness realization conditions, and establish the theoretical model of the designed vibration isolator. Under multiple excitations, the nonlinear analysis method is adopted to explore the force and displacement transfer characteristics of the vibration isolation system under different parameter conditions and to obtain the optimal design parameters. Based on the above parameters, the designed prototype is compared with the traditional vibration isolator in terms of vibration isolation performance, and the differences between the experimental results and the theoretical results are analyzed, and conclusions and improvement measures are proposed.
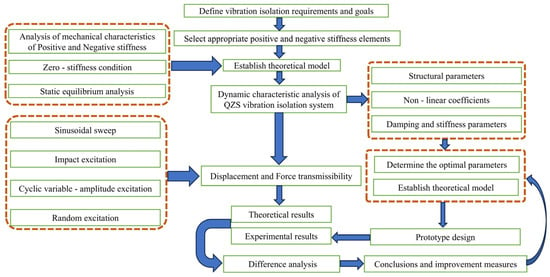
Figure 3.
Flowchart for the design of QZS isolators.
2.3. Dynamic Characteristics of QZS Isolation
QZS isolators exhibit unique advantages for low-frequency vibration isolation; however, their strong nonlinearity may lead to oversensitivity and reduced stability. They may also produce complex behaviors such as chaos, oscillations, and bifurcations, which are highly time-varying and spatially complex phenomena. Therefore, studying the nonlinear dynamics of QZS isolation helps us to design, control, and optimize the isolation system more accurately. Scholars have done much research in this area.
Carrella et al. [19,20,21,22] carried out a deep theoretical analysis of the system structure and mechanical properties of a three-spring quasi-zero-stiffness vibration isolation device, investigated the optimal relationship between the geometry, inclination, and relative stiffness of the springs, deduced the expressions of the system’s force transmittance and displacement transmittance, and provided an explanation for the phenomenon of the damping threshold that exists for the displacement transmittance. Tian et al. [23,24] have investigated the SD oscillator under nonlinear damping perturbations and explored the residual dimensional bifurcation, periodic solution, and Hopf bifurcation phenomena of the SD oscillator. Kovacic et al. [25], based on the classical triple-spring structure, introduced the softened springs with pre-compression and found that the system may exhibit the doubled-periodic bifurcation under asymmetric excitation. In a subsequent study [26], the harmonic equilibrium method was used to solve the principal resonance response of the asymmetric Duff oscillator to quantize the nonlinear error and to solve for the frequency of bifurcation of the system as well as the possibility of developing chaotic phenomena. Santhosh et al. [27] investigated the periodic motions of SD oscillators under simple harmonic excitation and revealed the bifurcation properties of the system, the symmetry breaking around the saddle point, and the doubly periodic bifurcation leading to the chaotic. Gianluca et al. [28] studied a two-degree-of-freedom forced nonlinear system, simulated a QZS single-degree-of-freedom system excited by a linear oscillator, applied the averaging method to derive the amplitude-frequency equations for the relative motion of a small mass at the excitation frequency, and determined the stability conditions for both the steady-state solution and the unsteady-state solution. Sharma et al. [29] found that the nonlinear damping can reduce the critical value of the system for the first time entering the critical value of the chaotic state and expand the parameter space in which chaos occurs. Ho et al. [30] analyzed the role of nonlinear stiffness and nonlinear damping on the dynamic behavior of the Duffing system based on the output frequency response function method, and the conclusions show that nonlinear damping is beneficial in suppressing the resonance peaks of the vibration isolation system and in improving the stability of the system. Shahraeeni et al. [31] based on the harmonic equilibrium method and numerical extension method to analyze the displacement, force transfer rate, and system stability of the QZS isolator under large amplitude excitation and derived the corresponding analytical expressions, and it was found that nonlinear damping helps to remove or reduce the unwanted isolated subharmonic branches. It cannot be ignored that all numerical models usually have some degree of uncertainty [32,33], especially in the analysis of nonlinear dynamical systems, where complex dynamic behaviors can further amplify model errors. In this context, machine learning [34,35] provides a new path to solve this problem through data-driven multi-parameter optimization and accurate modeling capabilities.
In summary, it can be seen that for the vibration isolation system to appear chaotic, oscillatory, and bifurcated, and other unstable phenomena, it can be avoided by parameter design. However, problems such as parameter misalignment and polarization are inevitable in engineering applications. Although the introduction of nonlinear damping helps to reduce the resonance phenomenon of the system and improve the high-frequency transmission characteristics, its effect depends on a variety of factors such as the excitation amplitude of the system, the operating frequency, and so on. Different types of nonlinear damping also have different effects on the system, and more theoretical support is still needed.
3. Compact Design of QZS Isolation
Although the QZS isolator has become an important means of solving low-frequency vibration isolation problems, the low-frequency vibration isolation performance of the traditional QZS isolator is seriously limited in practical engineering applications due to the limited installation space of the vibration isolator. Therefore, the design of a compact structure and superior performance of the QZS isolator will be the main direction of future development!
3.1. Special Spring Type
3.1.1. Disc Springs
Disc springs have many advantages, such as high allowable load, small spring deflection, compact structure, and relatively simple design and assembly [36], and have become an important research object for scholars. Figure 4 illustrates two typical models of disc spring quasi-zero stiffness isolators, where the disc springs are both negative stiffness elements.
Zhou et al. [37] carried out quasi-static and dynamic compression experiments on individual disc springs under symmetric and asymmetric friction conditions for different series of disc springs and further investigated the mechanical properties of multiple disc springs stacked in parallel to obtain the full range of load-displacement curves under quasi-static and dynamic compression. Niu et al. [38] designed a QZS isolator with slotted conical disc springs and vertical wire springs connected in parallel and established the corresponding mathematical model to optimize the structural parameters, and the results show that the structure has better vibration isolation performance at low frequency isolation. Similarly, Meng et al. [39] compared the static characteristics of variable thickness disc springs and constant thickness disc springs, optimized the configuration parameters to achieve a wider QZS region, and investigated the effects of different offset displacements and excitation amplitudes on the vibration isolation performance under overload and bias load conditions. Yu et al. [40] used disc springs to provide asymmetric negative stiffness and the positive stiffness provided by worm springs to share the load-carrying capacity in the QZS region, which provides a new idea and solution for the design of a heavy-duty vibration isolation system, while Liu et al. [41] combined the disc springs and helical springs to design the compression bar QZS element, built a 6-DOF vibration isolator platform, and analyzed in detail the force transfer rate under the harmonic excitation and the dynamic characteristics. Yu et al. [42] focus on the multi-directional isolation performance, adopting shape memory alloy U-shaped dampers to provide self-resetting performance in the horizontal direction and parallel disc springs to achieve quasi-zero stiffness in the vertical direction. Based on this, the friction slip isolator is introduced to optimize the response in both horizontal and vertical directions. This study provides an important reference in the field of three-dimensional isolation.
Figure 4.
Disc spring QZS Isolator Models: (a) Disc spring QZS isolator model proposed by Niu et al. [38]; (b) Disc spring-worm spring QZS model proposed by Yu et al. [40].
3.1.2. Wave Springs
Multi-coil wave springs [43] can provide the same force and deflection characteristics using only half of the space of a coil spring, a property that makes them highly advantageous in space-constrained application scenarios. Wang et al. [44] connected a wave spring in parallel with a pair of permanent magnet negative stiffness elements, called WQZS isolator, as depicted in Figure 5, and derived an empirical formula for the restoring force of the wave spring based on experimental data using the least squares method. The experimental results showed that the isolation frequency of the isolator was reduced by 48.89%, and the peak transfer rate was reduced by 59.33% compared with the linear isolator.
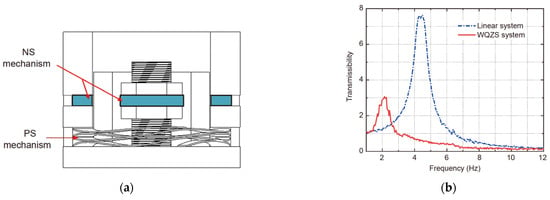
Figure 5.
WQZS isolator proposed by Wang et al. [44]: (a) Front section view of the isolator; (b) Displacement transmissibility.
3.1.3. Planar Springs
Lan et al. [45] proposed a special planar spring structure, as Figure 6 demonstrates, which can be designed for stiffness by adjusting the thickness of the face wall of the planar spring, and proposed a lateral adjustment mechanism to adjust the amount of preload to accommodate different load variations. It was shown to be effective in attenuating external excitation as low as 2.3 Hz under load conditions of 0–6 kg.
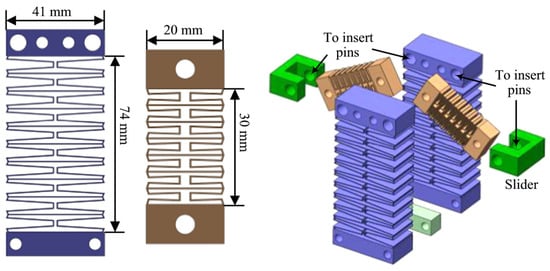
Figure 6.
The planar spring structure proposed by Lan et al. [45].
3.1.4. Transverse Notch Springs
Liu et al. [46] constructed and investigated a prototype QZS isolator with negative stiffness provided by two pairs of transverse notch springs. Figure 7a illustrates the model diagram. Compared with coil springs, the transverse notch springs have the advantages of compact structure and designability. They analyzed the stiffness characteristics, dynamic response, vibration isolation performance, and the influence of parameters of the structure theoretically and designed the prototype and tested the force-displacement curves. The experimental data for Figure 7b show that the structure has a good vibration isolation effect under the excitation of the 3–15 Hz frequency band, which further confirms the feasibility and effectiveness of transverse notch springs in the design of QZS isolators.
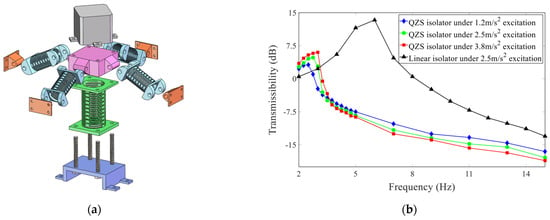
Figure 7.
QZS isolator with transverse notch special spring structure proposed by Liu et al. [46]: (a) Prototype model; (b) Experimental transmissibility curves (dB) under different excitation amplitudes.
In summary, the special spring has a compact structure, which has a significant advantage in space utilization efficiency compared to the QZS isolation constructed with conventional coil springs. A large stiffness coefficient is the key to the compact design. The high stiffness coefficient effectively suppresses the displacement of the vibration isolation object, which significantly expands the working area of the vibration isolator and enhances the stability and reliability of the vibration isolation effect. However, special springs face many difficulties in the design and processing process. Due to their special structure and performance requirements, accurate mechanical calculations and simulation analysis are indispensable, and in-depth investigation of the non-linear factors introduced by the special structure is needed to investigate the mechanism of the overall performance; in the processing and manufacturing process, the complexity of special springs requires very high processing accuracy, and the slightest deviation may result in a significant reduction in the performance of the springs, which in turn affects the isolation performance of the vibration isolator.
3.2. Magnetic Type
Magnetic QZS isolation has many unique advantages. In terms of structural design, it can reach a wider range of zero stiffness areas through reasonable construction of space layout and can also be used to design a multi-directional vibration isolation platform. The magnetic negative stiffness element has the advantages of non-contact characteristics, a compact structure, and a higher degree of design freedom. These advantages make the magnetic QZS isolation in the vibration isolation application have greater potential and value, whether in response to a complex vibration environment or to meet the diverse needs of vibration isolation, and can play a positive and effective role. The more common is the magnetic spring based on permanent magnets and electromagnetic coils.
3.2.1. Permanent Iron Type Magnetic Springs
Shi et al. [47,48] proposed a novel magnetic negative stiffness damper consisting of multiple coaxially arranged permanent magnets, which is a compact and simple design that effectively integrates negative stiffness and eddy current damping. Wang et al. [49] proposed a compact energy-harvesting vibration isolator consisting of a negative-stiffness magnetic spring, a helical bending spring, and a coil, as illustrated in Figure 8a, which can suppress low-frequency vibrations in the range of 3.7–6.1 Hz and can achieve a maximum output power of 1.51 mW under 4.5 Hz. A maximum output power of 1.51 mW can be achieved under external excitation with a load resistance of 300 ohms. Sun [50,51] et al. proposed a novel electromagnetic negative stiffness element consisting of a coaxial permanent magnet toroidal magnet and a coil with a rectangular cross-section and adjustable negative stiffness characteristics. The element is quite compact due to the nested layout and the use of mechanical springs, and its stiffness can also be varied by changing the excitation current, which has the unique advantages of generating a wide range of adjustable negative stiffness characteristics and easy integration with semi-active control algorithms.
Using different magnetic coupling arrays to increase the magnetic density can also achieve the goal of a compact design. Figure 8b illustrates the schematic of a compact magnetic spring array with rectangular arrays proposed by Wu et al. [52], which can provide the same negative stiffness with less space consumption compared to non-arrayed magnetic springs. Similarly, as Figure 8c illustrates, Zhang et al. [53] proposed a magnetic Halbach high-negative-stiffness vibration isolator and verified that, when the size and weight are the same, the magnetic negative stiffness of the Halbach array is higher than other magnetic arrays, which is important in some practical situations with space and weight constraints. Subsequently, Zhang et al. [54] proposed a toroidal Halbach torsional negative stiffness isolator, and the starting isolation frequency of the toroidal Halbach isolator can be reduced by 32.57% compared with that of a linear isolator. Wu et al. [55] proposed a compact magnetic spring consisting of two sets of alternating permanent magnets with high linear negative stiffness. Figure 8d shows a schematic of the magnetic negative stiffness mechanism proposed by Wu et al., and the resonance frequency of the experimental prototype was reduced from 6.93 Hz to 1.10 Hz.
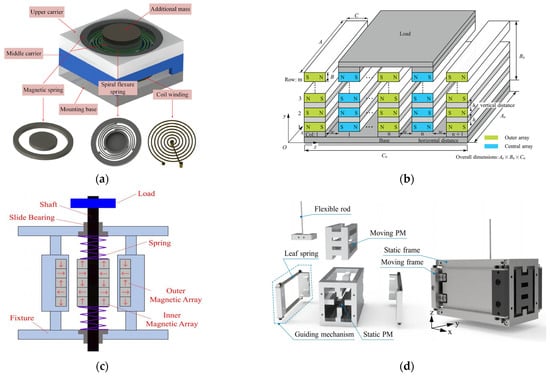
Figure 8.
QZS isolator with Permanent Magnet Magnetic Spring: (a) Energy harvesting dynamic damper [49]; (b) Schematic diagram of a compact array of magnetic springs [52]; (c) Structure of a Halbach high negative stiffness vibration isolator [53]; (d) a magnetic negative stiffness mechanism with a high linear negative stiffness [55].
3.2.2. Electromagnetic Coil-Based Magnetic Springs
Figure 9 illustrates four types of QZS isolators with solenoid coil magnetic springs. Zhao et al. [56] made the structure more compact by nesting a toroidal permanent magnet in the electromagnetic coil winding. Also using a permanent magnet nested in the solenoid winding structure, Zhang et al. [57] developed a magnetic negative stiffness isolator based on Maxwell’s normal stresses, which can produce a higher magnetic negative stiffness compared to a magnetic negative stiffness isolator with the same size and weight. Similarly, Yuan et al. [58] design a new magnetic circuit to greatly improve the adjustable range and capacity utilization of negative stiffness springs. However, the difference is that Yuan discarded the permanent magnet element to avoid the disadvantage that permanent magnets would demagnetize and be fragile at high temperatures. Pu et al. [59] proposed a new compact, non-contact, and negative stiffness adjustable multi-layer electromagnetic spring, which can adjust the negative stiffness by controlling the current, and the 6-layer electromagnetic spring can generate variable stiffness from −9800 N/m to 9800 N/m with only 1 × 10−4 m3 of compact volume.
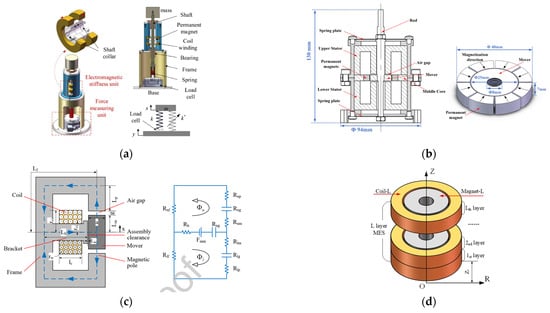
Figure 9.
QZS isolator with solenoid Coil Magnetic Spring: (a) Electromagnetic QZS model [56]; (b) Magnetic negative stiffness configuration based on Maxwell’s magnetic normal stress [57]; (c) Adjustable negative stiffness spring consisting of a stator, a mover, and coils using Maxwell’s normal stresses [58]; (d) Multilayer electromagnetic spring model [59].
To sum up, the fundamental compact design of the magnetic structure lies in how to improve the magnetic intensity density, and the current research mostly focuses on exploring the two directions of the new permanent magnet array arrangement and magnetic circuit optimization. However, the magnetic structure is prone to unstable magnetic field strength, which leads to the failure of positive and negative stiffness matching and the decrease in vibration isolation performance and even may play a negative role. Therefore, the introduction of active control strategies to realize precise regulation is a key research direction for the follow-up.
3.3. Bionic Type
Structural geometry by mimicking biological systems is likewise a popular research direction for optimizing vibration isolation models [60]. They are mainly categorized as leg-mimicking structures, bird-neck-mimicking structures, and insect-mimicking structures.
3.3.1. Bionic Leg Structure
As shown in Figure 10a, Dai et al. [61,62,63] proposed a bionic quadrilateral X structure based on the running of a kangaroo, aiming at suppressing periodic or impulsive force vibrations suffered by a free-floating spacecraft during an orbital maintenance mission.
Bian et al. [64] investigated a new type of passive vibration isolation support with a compact X-shape structure with ideal weak nonlinear characteristics to achieve QZS characteristics at large amplitudes, combined with a special tilting and adjustable spring mechanism, which is capable of adjusting the stiffness according to the different payloads. Chai et al. [65] proposed a passive compact X-shape vibration isolation mechanism possessing three-directional QZS characteristics, and through the rational arrangement of the X-shaped mechanism, one can obtain multi-directional vibration isolation capacity and adjustable nonlinear characteristics, with a large stroke, a large load-carrying capacity, and wider QZS characteristics, and also be able to optimize the vibration isolation capacity according to the demand of three-directional vibration isolation by using the key parameters. Jing et al. [66] proposed a variety of adjustable nonlinear stiffness systems. On the basis of the basic X-mechanism, X-aSpr with a spring with a controlled delayed tensioning mechanism is installed; X-aSpr-aS with additional fixed support and installation of a horizontal spring is introduced; X-vSpr consisting of a vertical linear spring is introduced; and on the basis of the X-aSpr mechanism, the structure X-aSpr-aC is further designed as an adjustable contact. All of these systems can be easily fabricated with reliable and simple mathematical models for analyzing and designing nonlinear phenomena with a compact, in-situ adjustable resonance frequency of about 1 Hz, vibration transmission rate attenuation of 20 dB, etc. Zeng et al. [67] found that the M-shaped leg structure of frogs possesses excellent vibration suppression during jumping, and inspired by the M-shaped-like leg structure, a new type of biomimetic vibration isolator was designed by using torsion springs; the isolator model is shown in Figure 10b. And in Figure 10c, Yan et al. [68] developed a polygonal skeleton by simulating spinal control and leg structure of cat structure that can effectively suppress vibration under multiple excitations. Experimental results show that this polygonal bone structure can effectively isolate vibrations with frequencies above 3 Hz.
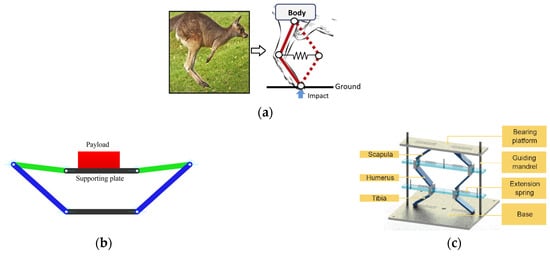
Figure 10.
Bionic leg structure: (a) Bionic kangaroo leg isolator model [61]; (b) Bionic frog leg isolator model [67]; (c) Bionic cat leg isolator model [68].
3.3.2. Bionic Neck Structure
Birds have very flexible necks, which are able to bend and twist significantly in different directions and exhibit QZS-like behaviors in certain postures, due to the fact that the necks of birds are usually composed of multiple vertebrae, which are connected by soft tissues and can be flexibly controlled by adjusting the elasticity of the soft tissues. Deng et al. [69] were inspired by the stability of fixed gaze in bird head space by simulating the multi-vertebrae structure of the bird neck and utilizing a three-spring vibration isolator with dampers and preloaded springs instead of the single-layer structure of the neck and proposed a multilayered bionic vibration isolator consisting of multiple sets of three springs connected in series, as shown in Figure 11, and the multilayered QZS system effectively enlarges the effective range of the working stroke and provides more efficient vibration isolation performance. Sun et al. [70,71] Based on the cavity structure and muscle action mechanism of the bird, a multilayer QZS isolator is proposed to achieve vibration suppression for ultra-low frequency excitation in the range of 0.1~1 Hz.
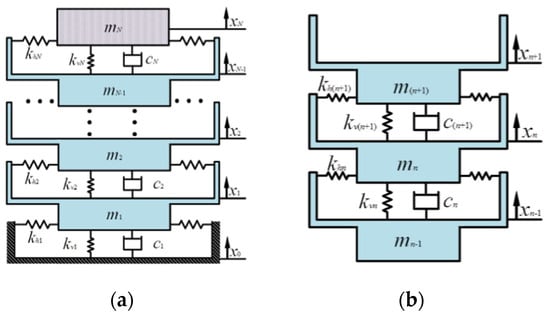
Figure 11.
Diagram of multi-layer QZS isolation system model [69]: (a) Overall model diagram; (b) Nth layer structure diagram.
3.3.3. Bionic Beetle Structure
There are a large number of insects in nature that can carry loads far beyond their own weight, providing much inspiration for the design of vibration isolators. Ling et al. [72] designed a cockroach-like structure, where the exoskeleton is mimicked by a diamond-shaped cavity, the restoring force is provided by a spring, and the mimicry of the front legs relies on rods and sliders. The resonance frequency of this structure is as low as 1.4 Hz, and its nonlinear characteristics can significantly reduce the resonance frequency and peak transfer rate, and an anti-resonance phenomenon occurs at large inertia. And later, as shown in Figure 12, Ling et al. [73], inspired by the three postures of the beetle, namely the unyielding, downward bending, and upward bending postures, proposed a vibration isolation structure consisting of three rods and two springs, which can change the stiffness by adjusting the initial assembly angle, length ratio, and linear stiffness, and its transmission rate can be reduced to 7 dB and the resonance frequency can be less than 2 Hz.
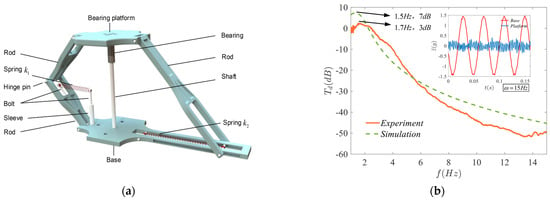
Figure 12.
Bionic beetle vibration isolator proposed by ling et al. [73]: (a) Model of vibration isolator; (b) Experimental and simulation transmissibility comparison, where the corresponding time histories of the load platform and the base plate at 15 Hz.
Although bionic design has great potential in theory, how to effectively apply it to practical engineering is still a relatively less studied topic. Current research has focused on extracting nonlinear properties from nature and using them to improve the efficiency and stability of vibration isolation performance. Future research should further explore how to optimize the design of bionic QZS isolators, select appropriate materials, and better construct abstract models to promote their application in more complex engineering environments.
3.4. Metamaterials-Based Type
Metamaterials are artificially engineered materials that attain unique physical properties through microstructural design. The uniqueness of such materials lies in the fact that their properties originate from the layout of the internal crystal structure. In recent years, the development of metamaterials theory has opened up new research directions in many engineering fields. By precisely designing the microstructure of metamaterials, it is possible to integrate multiple functional properties in the same material. Hamzehei et al. [74] focused on metamaterial lattice structures possessing high-static and low-motion properties and summarized the design strategies for lattice metamaterials with this feature. This chapter provides an overview of compactly designed metamaterial structures. Figure 13 illustrates several typical approaches to the design of metamaterials.
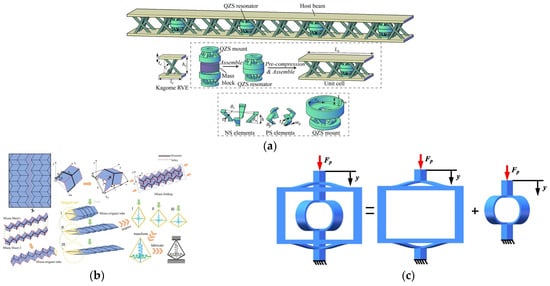
Figure 13.
Metamaterial cell: (a) Lattice core sandwich beam design proposed by Xiao et al. [75]; (b) Miur tube and QZS structure proposed by Wan et al. [76]; (c) Multi-stage QZS metamaterial cell design proposed by Guo et al. [77].
Xiao et al. [75] proposed an arrayed lattice core sandwich beam design embedded in a 3D printed quasi-zero stiffness resonator, which exhibits broadband vibration isolation far beyond the corresponding linear object bandgap. Zhao et al. [76] proposed the lightweight design of 3D QZS meta structures with beam-like monoclinic cells, which used an optimized design approach to enable vibration isolation meta structures to achieve customizable QZS properties in complex operating environments. Guo et al. [77] proposed a structural unit consisting of an elastic ring with two cross-bent beams, which can be realized by structural design to achieve metamaterials with multilevel QZS regions. Wan et al. [78] fabricated a metamaterial with quasi-zero stiffness properties inspired by Miura origami by laser powder bed fusion printing technique, which shows great potential in longitudinal vibration. Meng et al. [79] Inspired by the honeycomb morphology structure with negative Poisson’s ratio characteristics, a symmetric concave thin-walled structure is used to provide the main load-carrying capacity, and the staggered arrangement of the load-carrying units is used to design a lightweight, compact mechanical metamaterial configuration with a low initial load and a large densification strain. Zhang et al. [80] proposed a class of customized mechanical metamaterials containing specific geometrically shaped bending beams to provide the QZS characteristics. In the compression test, the bending beam reaches the preset operating range sequentially, forming a customized stepped force-displacement curve with multiple working ranges.
Xu et al. [81] proposed a topology optimization scheme for the reverse design of QZS meta-structures with smooth boundaries, which resulted in a compact superstructure with smooth boundaries and no post-processing, integrating lightweighting, load-carrying capacity, and vibration isolation. Hu et al. [82] implemented the optimization of trajectories at the center of the cross-section of bent beams with the help of a genetic algorithm. Through this operation, customizable stiffness and load-carrying capacity were successfully achieved, and multiple QZS regions were constructed. The optimized design was proven to be effective in isolating vibrations with frequencies above 4.67 Hz, and its mass was only 3.2% of the load-carrying capacity. Liu et al. [83] proposed a one-dimensional bandgap-tunable QZS metamaterial consisting of a single unit centered on a truncated conical shell. Compared with conventional vibration isolation structures, the material significantly reduces the weight and decreases the size, and the onset frequency is reduced to 15.01 Hz, which is 46.6%.
Despite the great potential of metamaterials in realizing vibration and noise reduction, they still face problems such as high manufacturing costs, limited scope of application, and poor performance stability. Future research needs to make more progress in reducing cost, improving performance stability, broadening application areas, and optimizing design methods.
3.5. Origami-Inspired Type
Origami-inspired structural design represents a geometrically driven methodology founded upon principles derived from traditional paper folding art. This approach employs systematic folding methodologies to generate sophisticated geometric configurations and spatial architectures. Such origami-derived structures exhibit inherent mechanical characteristics of significant scientific interest, including bistable behavior, pronounced nonlinear responses, and adjustable stiffness properties. These distinctive attributes establish novel application prospects for developing QZS isolators. As demonstrated in Figure 14, exemplary configurations of origami-based isolators showcase the practical implementation of these structural principles.
Ye et al. [84] introduced a truss spring-based design to replace the deformable creases in the traditional origami structure to improve the realizability in engineering applications and also to achieve the bistable and QZS properties by adjusting the system parameters and selecting different springs. Based on the above model, Ye et al. [85] investigated the effects of self-weight and damping nonlinearity of the origami structure on the dynamic performance of origami vibration isolators and concluded that the faceted mass of the origami structure and the lighter bottom faceted plate would provide better isolation performance. Liu et al. [86] proposed an origami-based vibration isolation system integrated with elastic joints, and vibration experiments showed that the effective isolation frequency of this vibration isolator was below 2 Hz. Han et al. [87] proposed a lightweight vibration isolator based on the Kresling origami module with expandable and QZS characteristics, which can achieve the full frequency range of vibration isolation with small excitation amplitude and high damping and can increase the suppression effect of large-value vibration by series connection arrangement. Inspired by the symmetric conical Kresling origami unit and an axial spring, Zhou et al. [88] proposed a vibration isolation system consisting of two symmetric conical Kresling origami units and an axial spring, which has a lower starting vibration isolation frequency compared with the existing QZS damper system. Yu et al. [89] proposed a new combined truss spring structure based on a triangular cylindrical origami model with an additional inertia mechanism, which uses elastic connecting rods to simulate all the folds to realize the adjustable stiffness and inertia.
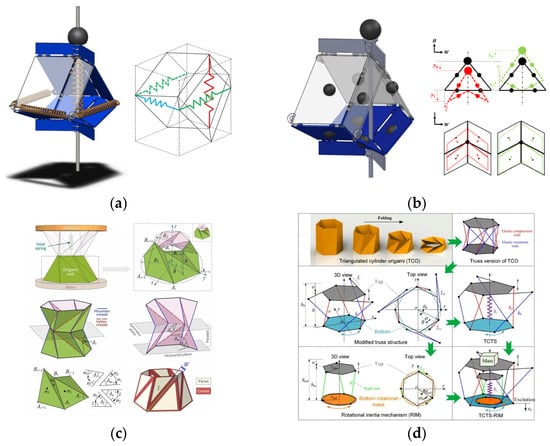
Figure 14.
Origami structure: (a) Truss spring instead of deformable crease [84]; (b) Schematic of origami structure with self-weighting blocks [85]; (c) Two symmetrical conical Kresling origami units and an axial spring form the vibration isolation system [88]; (d) Truss-spring structure with additional inertia mechanism combination [89].
The foldability, lightweight, and specific mechanical properties of origami structures make them ideal for QZS isolation design. However, there are many challenges in the practical application, the most critical one being how to smoothly transition from abstract theoretical modeling to practical engineering applications.
3.6. Other Type
In the compact design of QZS isolation, many scholars have put forward various distinctive design solutions.
3.6.1. Geometric Nonlinear Structure
Wang [90] et al. proposed a negative stiffness element consisting of an inner and outer roller-spring to counteract the positive stiffness of the coil spring and established an ADAMS simulation model to evaluate the vibration isolation effect of the system. Jiao et al. [91] used a spring-rod mechanism to provide the main negative stiffness, as shown in the basic schematic in Figure 15, and combined it with a compensating force provided by a cam-roller mechanism to avoid complex nonlinear behavior.
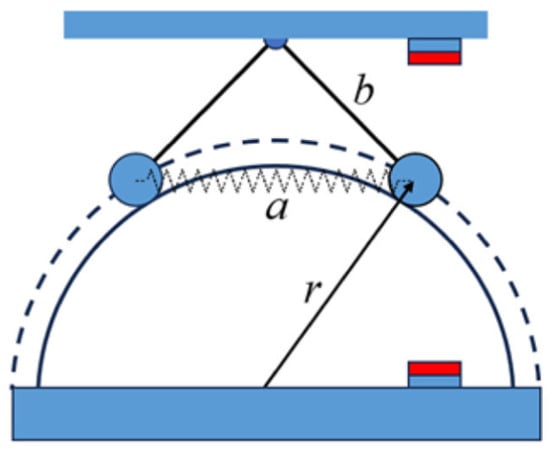
Figure 15.
Schematic diagram of the vibration isolator model proposed by Jiao et al. [91].
3.6.2. Leveraged Magnification Principle
Deng et al. [92] based on the lever structure amplification effect to amplify the negative stiffness by one order of magnitude to effectively reduce the volume or weight of the negative stiffness mechanism, and the negative stiffness can be controlled by adjusting the leverage ratio to meet the different positive stiffness requirements in engineering applications. As depicted in Figure 16, the operational principles of this isolator are formalized through a simplified lumped-parameter analytical model.
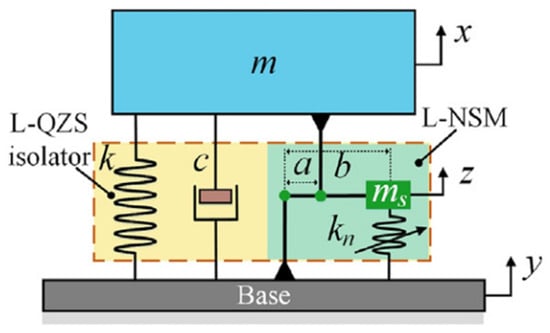
Figure 16.
The simplified lumped parameter models of L-QZS isolator proposed by Deng et al. [92].
3.6.3. Single Structure
Anvar Valeev et al. [93] successfully realized the QZS characteristics by using a single element, a dome diaphragm. This structure has the advantages of simplicity, high reliability, and low space occupation. In addition, the design avoids the problem of performance degradation due to the high friction between multiple elements and effectively improves the vibration isolation performance of the prototype. Xu et al. [94] proposed a compact W-shaped flexure mechanism with QZS characteristics, as shown in Figure 17, which is friendly to manufacture, requires no assembly, is easy to miniaturize, and has a great potential for low-frequency energy harvesting and vibration isolation applications.
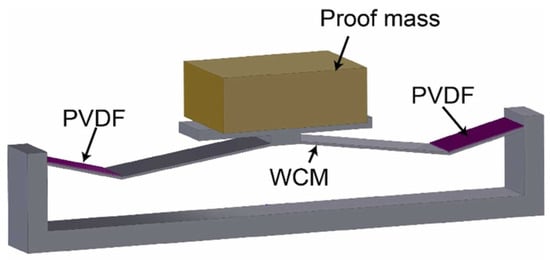
Figure 17.
Schematic diagram of the energy harvester [94].
3.6.4. Compliant Structure
Zhang et al. [95] introduced a stiffness combination-compatible constant force mechanism consisting of flexible components to design an isolator, assembled in the form of Figure 18, in which a folded beam provides positive stiffness while an articulated bent beam provides negative stiffness, which is more compact, lighter, and easier to fabricate compared to a QZS isolator consisting of mechanical components. Similarly, Li et al. [96] proposed a compact tripod-type QZS isolation based on a flexible constant-force mechanism with a form factor of only 240 × 240 × 130 cubic millimeters, which is capable of effectively suppressing vibrations above 9 Hz when carrying a load of 6 kg. Lu et al. [97] proposed a near-zero-frequency flexible curved beam support, which utilizes the nonlinear negative stiffness provided by the curved beam support to neutralize the nonlinear positive stiffness of the helical beam support. The stiffness can be adjusted by translational transformation of negative stiffness structures. Experiments show that the structure achieves near-zero vibration isolation from 0.8 Hz onwards.

Figure 18.
Compliant quasi-zero-stiffness [95]: 1—a folded beam, 2—a curved beam, 3—the outer connecting ring, 4—the inner connecting disc, 5—a bolt hole, 6—a through hole for mounting the limit shaft, and 7—a groove.
3.6.5. Air Spring Structure
Air springs can realize strong output force in a small space and can adjust the air pressure inside the airbag to change the stiffness. Shuai et al. [98] developed an unrestrained air spring configuration by eliminating conventional guide rods and constraints, proposing a hybrid vibration isolation system comprising orthogonally arranged vertical and transverse air spring assemblies. Through parametric optimization of the system geometry and pressure distribution, the transverse air springs were engineered to generate precisely tuned negative stiffness, thereby synergistically counterbalancing the positive stiffness of the vertical components to achieve quasi-zero stiffness (QZS) operational characteristics. The analytical framework for this coupled stiffness interaction is illustrated in Figure 19. Abuabiah Mohammad et al. [99] used sleeve air springs to improve the load-carrying capacity based on the triple-spring structure, and the overall system was simple and compact, which could effectively isolate the unpredictable roadway low-frequency interference.
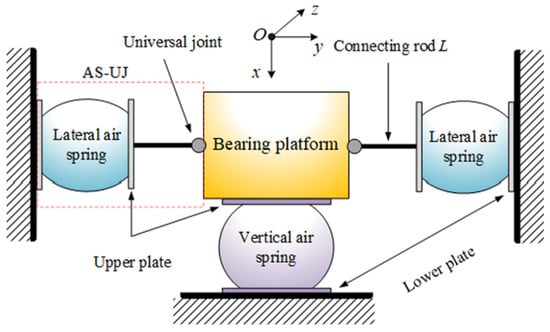
Figure 19.
HSLDS structure with no restrainers and guidance bars [98].
In conclusion, existing research has explored a wide range of engineering applications under space-constrained conditions, mainly involving the introduction of elastic elements with high positive and negative stiffness, embedded structural design, and the development of new compact materials. However, most of the studies tend to focus on compactness, while other important characteristics such as load-carrying capacity, large amplitude vibration isolation, broadband vibration isolation, and adaptive capability are often not taken into account. Future research should more systematically consider the synergistic optimization of multiple characteristics to achieve comprehensive performance improvement and design optimization.
4. Summary and Outlook
4.1. Summary
As one of the innovations in low-frequency vibration isolation technology, QZS isolation has made significant progress in recent years, and its design mechanism mainly relies on the use of negative stiffness elements, which can realize the effect of QZS through specific geometric configurations or material properties. In this paper, we systematically summarize the design mechanism, research status, and applications of compact QZS, such as special springs, magnetic, bionic, metamaterials, and origami structures for vibration isolation in space-constrained application scenarios. Special spring-type isolators have a compact structure, high space utilization, and adjustable preload, but the machining precision requirements are extremely high, and slight deviations can easily lead to performance degradation. Magnetic-type isolators demonstrate the advantages of non-contact and control, but the challenges of thermal demagnetization and electromagnetic saturation of permanent magnets remain to be solved. Metamaterial-based type isolators can realize multifunctional integrated designs but are limited by expensive manufacturing costs. Biomechanically inspired QZS isolators can realize multidimensional vibration isolation, but complex intrinsic models are difficult for engineering applications. Similarly, origami-inspired types break through the bottleneck of compact design; however, the configuration is still far away from engineering realization.
In terms of the current compact QZS research dynamics, most of them utilize large stiffness components to replace the original QZS structure, and there are fewer studies on the nesting and coupling design of positive and negative stiffness components.
However, this paper only summarizes the compact design, with less consideration of other key design factors such as stroke, load-bearing mass, and vibration amplitude. The subsequent study will focus on the multi-featured optimal design method.
4.2. Outlook
- (i).
- Currently, most of the vibration isolation devices focus on the suppression in the vertical direction, but in practical engineering, such as the suppression of seismic loads in high-risk buildings, the vibration and noise reduction design of ships coupled with waves and engine vibration, and the vibration design of airplanes under airflow disturbances and landing impacts, the multidirectional and complex excitations cannot be avoided. Therefore, the multi-degree-of-freedom QZS system has a broader application potential. However, there is a lack of systematic modeling methods for key issues such as nonlinear stiffness matching and decoupling of energy transfer paths under multidirectional excitation. Future research is urgently needed to establish a multidirectional collaborative design theory that integrates the negative stiffness regulation mechanism and, at the same time, develops optimization algorithms that can take into account the coordination of axial load-carrying capacity and multidirectional stiffness to cope with the complex effects of multidimensional excitations in practical engineering.
- (ii).
- The combination of metamaterials and biomimetic design provides more freedom in the design of QZS isolation, especially in improving structural durability and saving space. In the future, the performance and adaptability of vibration isolators can be further enhanced through the development of new tunable composite materials and bionic structures, especially for applications in extreme operating environments.
- (iii).
- Magnetic compact design mainly focuses on the optimization of space structure and the improvement of magnetic density. In general, permanent magnets can provide greater magnetic field strength than electromagnetic coils, but permanent magnets are fragile and demagnetized at high temperatures, which limits the application of permanent magnet coils in strong shock and high-temperature environments. Electromagnetic coils are difficult to develop a large enough magnetic stiffness, which requires optimization in the magnetic circuit design.
- (iv).
- Due to the significant differences in different application scenarios, the design requirements of QZS isolation show diverse characteristics. Compact structural design, strong load-bearing capacity, flexible adjustability, sufficient travel, and effective isolation of vibrations of different amplitudes are all key factors to be considered in the design process. Therefore, the development of QZS isolation with multiple characteristics has become a core direction for future research. By integrating the above characteristics, it is expected to break through the limitations of the existing vibration isolation technology, better meet the increasingly complex and demanding vibration isolation needs in various fields, and promote the wide application and in-depth development of vibration isolation technology in engineering practice.
Author Contributions
Conceptualization, Y.Z. and Q.Y.; methodology, Q.Y.; validation, Q.Y.; formal analysis, Q.Y.; investigation, S.L.; writing—original draft preparation, Y.Z.; writing review and editing, S.L.; supervision, K.C.; funding acquisition, K.C. All authors have read and agreed to the published version of the manuscript.
Funding
Research on these results was supported by the National Natural Science Foundation of China (NSFC) under grant number 52471354.
Data Availability Statement
Not applicable.
Acknowledgments
There is no other support that is not covered.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QZS | quasi-zero stiffness |
References
- Wang, X.; Liu, X.; Shan, Y.; He, T. Design, Simulation and Experiment of Particle Dampers Attached to a Precision Instrument in Spacecraft. J. Vibroeng. 2015, 17, 1605–1614. [Google Scholar]
- Hermsdorf, G.L.; Szilagyi, S.A.; Rösch, S.; Schäffer, E. High Performance Passive Vibration Isolation System for Optical Tables Using Six-Degree-of-Freedom Viscous Damping Combined with Steel Springs. Rev. Sci. Instrum. 2019, 90, 015113. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Li, X.; Zhang, X.; Xu, G.; Wu, A. Measurements and Evaluation of Road Traffic-Induced Micro-Vibration in a Workshop Equipped with Precision Instruments. Buildings 2024, 14, 1142. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Sun, Z.; Wang, C.; Shi, Y. A Compound Regulative Pneumatic Vibration Isolator with Quasi-Zero Stiffness Mechanism for Load Variable Instruments. IEEE Trans. Instrum. Meas. 2024, 73, 7505610. [Google Scholar] [CrossRef]
- Tian, Z.; Yan, X.P.; Zhang, C.; Xiong, Y.P.; Yang, P. Vibration Characteristics Analysis on Ship Propulsion System Taking Hull Deformations into Account. Teh. Vjesn.-Tech. Gaz. 2016, 23, 783–790. [Google Scholar]
- Li, S.; Feng, G.; Zhao, Q. Design and Research of Semiactive Quasi-Zero Stiffness Vibration Isolation System for Vehicles. Shock Vib. 2021, 2021, 5529509. [Google Scholar] [CrossRef]
- Shen, Y.; Hua, J.; Fan, W.; Liu, Y.; Yang, X.; Chen, L. Optimal Design and Dynamic Performance Analysis of a Fractional-Order Electrical Network-Based Vehicle Mechatronic ISD Suspension. Mech. Syst. Signal Process. 2023, 184, 109718. [Google Scholar] [CrossRef]
- Gao, P.; Yu, T.; Zhang, Y.; Wang, J.; Zhai, J. Vibration Analysis and Control Technologies of Hydraulic Pipeline System in Aircraft: A Review. Chin. J. Aeronaut. 2021, 34, 83–114. [Google Scholar] [CrossRef]
- He, Z.; Feng, X.; Zhu, Y.; Yu, Z.; Li, Z.; Zhang, Y.; Wang, Y.; Wang, P.; Zhao, L. Progress of Stewart Vibration Platform in Aerospace Micro–Vibration Control. Aerospace 2022, 9, 324. [Google Scholar] [CrossRef]
- Habib, A.; Yildirim, U. Influence of isolator properties and earthquake characteristics on the seismic behavior of RC structure equipped with quintuple friction pendulum bearings. Int. J. Struct. Stab. Dyn. 2023, 23, 2350060. [Google Scholar] [CrossRef]
- Habib, A.; Yildirim, U. Proposing unsupervised clustering-based earthquake records selection framework for computationally efficient nonlinear response history analysis of structures equipped with multi-stage friction pendulum bearings. Soil Dyn. Earthq. Eng. 2024, 182, 108732. [Google Scholar]
- Habib, A.; Junaid, M.T.; Dirar, S.; Barakat, S.; Al-Sadoon, Z.A. Machine learning-based estimation of reinforced concrete columns stiffness modifiers for improved accuracy in linear response history analysis. J. Earthq. Eng. 2025, 29, 130–155. [Google Scholar]
- Yang, T.; Zhou, S.; Fang, S.; Qin, W.; Inman, D.J. Nonlinear Vibration Energy Harvesting and Vibration Suppression Technologies: Designs, Analysis, and Applications. Appl. Phys. Rev. 2021, 8, 031317. [Google Scholar]
- Zhu, Z.; Tang, H.; Huang, Y.; Lin, Z.; Tian, Y.; Yu, P.; Su, C. A Compliant Self-Stabilization Nanopositioning Device with Modified Active–Passive Hybrid Vibration Isolation Strategy. IEEE ASME Trans. Mechatron. 2023, 28, 3305–3316. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, L.; Dong, Q.; Sui, J.; Sun, M.; Wang, J.; Yu, X. Experimental Study on the Active Control and Dynamic Characteristics of Electromagnetic Active–Passive Hybrid Vibration Isolation System. Appl. Sci. 2023, 13, 10565. [Google Scholar] [CrossRef]
- De Silva, C.W. (Ed.) Vibration and Shock Handbook, 1st ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Ma, Z.; Zhou, R.; Yang, Q. Recent Advances in Quasi-Zero Stiffness Vibration Isolation Systems: An Overview and Future Possibilities. Machines 2022, 10, 813. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lakes, R.S. Extreme Stiffness Systems Due to Negative Stiffness Elements. Am. J. Phys. 2004, 72, 40–50. [Google Scholar]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static Analysis of a Passive Vibration Isolator with Quasi-Zero-Stiffness Characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Optimization of a Quasi-Zero-Stiffness Isolator. J. Mech. Sci. Technol. 2007, 21, 946–949. [Google Scholar]
- Carrella, A.; Brennan, M.J.; Kovacic, I.; Waters, T.P. On the Force Transmissibility of a Vibration Isolator with Quasi-Zero-Stiffness. J. Sound Vib. 2009, 322, 707–717. [Google Scholar]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V. Force and Displacement Transmissibility of a Nonlinear Isolator with High-Static-Low-Dynamic-Stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Tian, R.; Cao, Q.; Yang, S. The Codimension-Two Bifurcation for the Recent Proposed SD Oscillator. Nonlinear Dyn. 2010, 59, 19–27. [Google Scholar] [CrossRef]
- Rui-Lan, T.; Qing-Jie, C.; Zhi-Xin, L. Hopf Bifurcations for the Recently Proposed Smooth-and-Discontinuous Oscillator. Chin. Phys. Lett. 2010, 27, 074701. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J.; Waters, T.P. A Study of a Nonlinear Vibration Isolator with a Quasi-Zero Stiffness Characteristic. J. Sound Vib. 2008, 315, 700–711. [Google Scholar]
- Kovacic, I.; Brennan, M.J.; Lineton, B. Effect of a Static Force on the Dynamic Behaviour of a Harmonically Excited Quasi-Zero Stiffness System. J. Sound Vib. 2009, 325, 870–883. [Google Scholar]
- Santhosh, B.; Padmanabhan, C.; Narayanan, S. Numeric-Analytic Solutions of the Smooth and Discontinuous Oscillator. Int. J. Mech. Sci. 2014, 84, 102–119. [Google Scholar] [CrossRef]
- Gatti, G.; Kovacic, I.; Brennan, M.J. On the Response of a Harmonically Excited Two Degree-of-Freedom System Consisting of a Linear and a Nonlinear Quasi-Zero Stiffness Oscillator. J. Sound Vib. 2010, 329, 1823–1835. [Google Scholar] [CrossRef]
- Sharma, A.; Patidar, V.; Purohit, G.; Sud, K.K. Effects on the Bifurcation and Chaos in Forced Duffing Oscillator Due to Nonlinear Damping. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2254–2269. [Google Scholar] [CrossRef]
- Ho, C.; Lang, Z.-Q.; Billings, S.A. A Frequency Domain Analysis of the Effects of Nonlinear Damping on the Duffing Equation. Mech. Syst. Signal Process. 2014, 45, 49–67. [Google Scholar] [CrossRef]
- Shahraeeni, M.; Sorokin, V.; Mace, B.; Ilanko, S. Effect of Damping Nonlinearity on the Dynamics and Performance of a Quasi-Zero-Stiffness Vibration Isolator. J. Sound Vib. 2022, 526, 116822. [Google Scholar]
- Habib, A.; Al Houri, A.; Habib, M.; Elzokra, A.; Yildirim, U. Structural performance and finite element modeling of roller compacted concrete dams: A review. Lat. Am. J. Solids Struct. 2021, 18. [Google Scholar] [CrossRef]
- al Houri, A.; Habib, A.; Al-Sadoon, Z. Artificial intelligence-based design and analysis of passive control structures: An overview: An overview. J. Soft Comput. Civ. Eng. 2024, 145–182. [Google Scholar]
- Jin, L.; Liu, Z.; Li, L. Prediction and identification of nonlinear dynamical systems using machine learning approaches. J. Ind. Inf. Integr. 2023, 35, 100503. [Google Scholar] [CrossRef]
- Wang, X.S.; Turner, J.D.; Mann, B.P. Constrained attractor selection using deep reinforcement learning. J. Vib. Control 2021, 27, 502–514. [Google Scholar] [CrossRef]
- Valeev, A.R.; Zotov, A.N.; Kharisov, S.A. Application of Disk Springs for Manufacturing Vibration Isolators with Quasi-Zero Stiffness. Chem. Pet. Eng. 2015, 51, 194–200. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, D.; He, J.; Chen, W.; Zhu, R. Investigation on Quasi-Static and Dynamic Mechanical Properties of Disc Springs Considering Asymmetric Frictional Boundary. J. Mech. Sci. Technol. 2023, 37, 5943–5955. [Google Scholar] [CrossRef]
- Niu, F.; Meng, L.; Wu, W.; Sun, J.; Zhang, W.; Meng, G.; Rao, Z. Design and Analysis of a Quasi-Zero Stiffness Isolator Using a Slotted Conical Disk Spring as Negative Stiffness Structure. J. Vibroeng. 2014, 16, 1769–1785. [Google Scholar]
- Meng, L.; Sun, J.; Wu, W. Theoretical Design and Characteristics Analysis of a Quasi-Zero Stiffness Isolator Using a Disk Spring as Negative Stiffness Element. Shock Vib. 2015, 2015, 813763. [Google Scholar] [CrossRef]
- Yu, K.; Chen, Y.; Yu, C.; Zhang, J.; Lu, X. A Compact Nonlinear Stiffness-Modulated Structure for Low-Frequency Vibration Isolation under Heavy Loads. Nonlinear Dyn. 2024, 112, 5863–5893. [Google Scholar] [CrossRef]
- Liu, Y.; Ji, W.; Gu, H.; Deng, E.; Wang, X.; Song, C. Force Transmissibility of a 6-DOF Passive Quasi-Zero Stiffness Vibration Isolation Platform. J. Mech. Sci. Technol. 2021, 35, 2313–2324. [Google Scholar] [CrossRef]
- Yu, T.; Huang, Z.; Zhang, C.; Huang, W.; Bao, W.; Liu, Y. Numerical investigation of three-dimensional isolator and mitigation for single-layer lattice shell structure. Structures 2024, 62, 106235. [Google Scholar] [CrossRef]
- Erfanian-Naziftoosi, H.R.; Shams, S.S.; Elhajjar, R. Composite Wave Springs: Theory and Design. Mater. Des. 2016, 95, 48–53. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Wang, K.; Xu, D.; Wen, G. Design and Experimental Study of a Compact Quasi-Zero-Stiffness Isolator Using Wave Springs. Sci. China Technol. Sci. 2021, 64, 2255–2271. [Google Scholar] [CrossRef]
- Lan, C.-C.; Yang, S.-A.; Wu, Y.-S. Design and Experiment of a Compact Quasi-Zero-Stiffness Isolator Capable of a Wide Range of Loads. J. Sound Vib. 2014, 333, 4843–4858. [Google Scholar]
- Liu, C.; Yu, K. Design and Experimental Study of a Quasi-Zero-Stiffness Vibration Isolator Incorporating Transverse Groove Springs. Archiv. Civ. Mech. Eng. 2020, 20, 67. [Google Scholar]
- Shi, X.; Zhu, S. Magnetic Negative Stiffness Dampers. Smart Mater. Struct. 2015, 24, 072002. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S. Simulation and Optimization of Magnetic Negative Stiffness Dampers. Sens. Actuators A Phys. 2017, 259, 14–33. [Google Scholar]
- Wang, Q.; Zhou, J.; Wang, K.; Lin, Q.; Xu, D.; Wen, G. A Compact Quasi-Zero-Stiffness Device for Vibration Suppression and Energy Harvesting. Int. J. Mech. Sci. 2023, 250, 108284. [Google Scholar]
- Sun, Y.; Zhao, J.; Wang, M.; Sun, Y.; Pu, H.; Luo, J.; Peng, Y.; Xie, S.; Yang, Y. High-Static–Low-Dynamic Stiffness Isolator with Tunable Electromagnetic Mechanism. IEEE ASME Trans. Mechatron. 2020, 25, 316–326. [Google Scholar] [CrossRef]
- Sun, Y.; Meng, K.; Yuan, S.; Zhao, J.; Xie, R.; Yang, Y.; Luo, J.; Peng, Y.; Xie, S.; Pu, H. Modeling Electromagnetic Force and Axial-Stiffness for an Electromagnetic Negative-Stiffness Spring Toward Vibration Isolation. IEEE Trans. Magn. 2019, 55, 8000410. [Google Scholar]
- Wu, J.; Zeng, L.; Han, B.; Zhou, Y.; Luo, X.; Li, X.; Chen, X.; Jiang, W. Analysis and Design of a Novel Arrayed Magnetic Spring with High Negative Stiffness for Low-Frequency Vibration Isolation. Int. J. Mech. Sci. 2022, 216, 106980. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Q.; Lei, Y.; Cao, J.; Liao, W.-H. Halbach High Negative Stiffness Isolator: Modeling and Experiments. Mech. Syst. Signal Process. 2023, 188, 110014. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Q.; Lei, Y.; Cao, J.; Liao, W.-H. Circular Halbach Negative Stiffness Isolating from Torsional Vibration: Design, Modeling and Experiments. Mech. Syst. Signal Process. 2023, 202, 110711. [Google Scholar] [CrossRef]
- Wu, M.; Wu, J.; Che, J.; Gao, R.; Chen, X.; Li, X.; Zeng, L.; Jiang, W. Analysis and Experiment of a Novel Compact Magnetic Spring with High Linear Negative Stiffness. Mech. Syst. Signal Process. 2023, 198, 110387. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, Y.; Li, J.; Yuan, S.; Wang, M.; Ding, J.; Pu, H.; Luo, J.; Peng, Y.; Xie, S. A Novel Electromagnet-Based Absolute Displacement Sensor with Approximately Linear Quasi-Zero-Stiffness. Int. J. Mech. Sci. 2020, 181, 105695. [Google Scholar] [CrossRef]
- Zhang, F.; Shao, S.; Tian, Z.; Xu, M.; Xie, S. Active-Passive Hybrid Vibration Isolation with Magnetic Negative Stiffness Isolator Based on Maxwell Normal Stress. Mech. Syst. Signal Process. 2019, 123, 244–263. [Google Scholar] [CrossRef]
- Yuan, S.; Sun, Y.; Wang, M.; Ding, J.; Zhao, J.; Huang, Y.; Peng, Y.; Xie, S.; Luo, J.; Pu, H.; et al. Tunable Negative Stiffness Spring Using Maxwell Normal Stress. Int. J. Mech. Sci. 2021, 193, 106127. [Google Scholar] [CrossRef]
- Pu, H.; Yuan, S.; Peng, Y.; Meng, K.; Zhao, J.; Xie, R.; Huang, Y.; Sun, Y.; Yang, Y.; Xie, S.; et al. Multi-Layer Electromagnetic Spring with Tunable Negative Stiffness for Semi-Active Vibration Isolation. Mech. Syst. Signal Process. 2019, 121, 942–960. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.-X.; Wang, S.; Zhao, L.-C.; Wu, Z.-Y.; Zhang, W.-M. Bio-Inspired Vibration Isolation: Methodology and Design. Appl. Mech. Rev. 2021, 73, 020801. [Google Scholar] [CrossRef]
- Dai, H.; Jing, X.; Wang, Y.; Yue, X.; Yuan, J. Post-Capture Vibration Suppression of Spacecraft via a Bio-Inspired Isolation System. Mech. Syst. Signal Process. 2018, 105, 214–240. [Google Scholar] [CrossRef]
- Dai, H.; Jing, X.; Sun, C.; Wang, Y.; Yue, X. Accurate Modeling and Analysis of a Bio-Inspired Isolation System: With Application to on-Orbit Capture. Mech. Syst. Signal Process. 2018, 109, 111–133. [Google Scholar] [CrossRef]
- Dai, H.; Cao, X.; Jing, X.; Wang, X.; Yue, X. Bio-Inspired Anti-Impact Manipulator for Capturing Non-Cooperative Spacecraft: Theory and Experiment. Mech. Syst. Signal Process. 2020, 142, 106785. [Google Scholar]
- Bian, J.; Jing, X. Analysis and Design of a Novel and Compact X-Structured Vibration Isolation Mount (X-Mount) with Wider Quasi-Zero-Stiffness Range. Nonlinear Dyn. 2020, 101, 2195–2222. [Google Scholar]
- Chai, Y.; Jing, X.; Guo, Y. A Compact X-Shaped Mechanism Based 3-DOF Anti-Vibration Unit with Enhanced Tunable QZS Property. Mech. Syst. Signal Process. 2022, 168, 108651. [Google Scholar]
- Jing, X.; Chai, Y.; Chao, X.; Bian, J. In-Situ Adjustable Nonlinear Passive Stiffness Using X-Shaped Mechanisms. Mech. Syst. Signal Process. 2022, 170, 108267. [Google Scholar]
- Zeng, R.; Wen, G.; Zhou, J.; Zhao, G. Limb-Inspired Bionic Quasi-Zero Stiffness Vibration Isolator. Acta Mech. Sin. 2021, 37, 1152–1167. [Google Scholar] [CrossRef]
- Yan, G.; Wang, S.; Zou, H.; Zhao, L.; Gao, Q.; Zhang, W. Bio-Inspired Polygonal Skeleton Structure for Vibration Isolation: Design, Modelling, and Experiment. Sci. China Technol. Sci. 2020, 63, 2617–2630. [Google Scholar] [CrossRef]
- Deng, T.; Wen, G.; Ding, H.; Lu, Z.-Q.; Chen, L.-Q. A Bio-Inspired Isolator Based on Characteristics of Quasi-Zero Stiffness and Bird Multi-Layer Neck. Mech. Syst. Signal Process. 2020, 145, 106967. [Google Scholar] [CrossRef]
- Sun, X.; Wang, F.; Xu, J. A Novel Dynamic Stabilization and Vibration Isolation Structure Inspired by the Role of Avian Neck. Int. J. Mech. Sci. 2021, 193, 106166. [Google Scholar]
- Sun, X.; Qi, Z.; Xu, J. A Novel Multi-Layer Isolation Structure for Transverse Stabilization Inspired by Neck Structure. Acta Mech. Sin. 2022, 38, 521543. [Google Scholar]
- Ling, P.; Miao, L.; Zhang, W.; Wu, C.; Yan, B. Cockroach-Inspired Structure for Low-Frequency Vibration Isolation. Mech. Syst. Signal Process. 2022, 171, 108955. [Google Scholar]
- Ling, P.; Miao, L.; Ye, B.; You, J.; Zhang, W.; Yan, B. Ultra-Low Frequency Vibration Isolation of a Novel Click-Beetle-Inspired Structure with Large Quasi-Zero Stiffness Region. J. Sound Vib.. 2023, 558, 117756. [Google Scholar] [CrossRef]
- Hamzehei, R.; Bodaghi, M.; Wu, N. Mastering the Art of Designing Mechanical Metamaterials with Quasi-Zero Stiffness for Passive Vibration Isolation: A Review. Smart Mater. Struct. 2024, 33, 083001. [Google Scholar]
- Xiao, L.; Sun, X.; Cheng, L.; Yu, X. Broadband and Robust Vibration Reduction in Lattice-Core Sandwich Beam with 3D-Printed QZS Resonators. Compos. Struct. 2025, 352, 118626. [Google Scholar]
- Wan, H.; Chen, H.; Wang, Y.; Fang, X.; Liu, Y.; Kosiba, K. Laser Additive Manufacturing of Miura-Origami Tube Inspired Quasi-Zero Stiffness Metamaterial with Prominent Longitudinal Wave Propagation. Virtual Phys. Prototyp. 2024, 19, e2299691. [Google Scholar]
- Guo, S.; Gao, R.; Tian, X.; Liu, S. A Quasi-Zero-Stiffness Elastic Metamaterial for Energy Absorption and Shock Attenuation. Eng. Struct. 2023, 280, 115687. [Google Scholar]
- Zhao, J.; Zhou, G.; Zhang, D.; Kovacic, I.; Zhu, R.; Hu, H. Integrated Design of a Lightweight Metastructure for Broadband Vibration Isolation. Int. J. Mech. Sci. 2023, 244, 108069. [Google Scholar] [CrossRef]
- Jia, M.; Dai, N.; Wang, T.; Cao, Q.; Yan, L.; Dai, H. A Compact Quasi-Zero Stiffness Metamaterial for Energy Absorption and Impact Protection. Thin-Walled Struct. 2024, 205, 112360. [Google Scholar]
- Zhang, Q.; Guo, D.; Hu, G. Tailored Mechanical Metamaterials with Programmable Quasi-Zero-Stiffness Features for Full-Band Vibration Isolation. Adv. Funct. Mater. 2021, 31, 2101428. [Google Scholar]
- Xu, Y.; Dong, H.-W.; Wang, Y.-S. Topology Optimization of Programable Quasi-Zero-Stiffness Metastructures for Low-Frequency Vibration Isolation. Int. J. Mech. Sci. 2024, 280, 109557. [Google Scholar]
- Hu, C.; Wan, Z.; Li, Z.; Tan, X.; Wang, L.; Chen, M. Inverse-Designed Metastructures with Customizable Low Dynamic Stiffness Characteristics for Low-Frequency Vibration Isolation. Eur. J. Mech. A Solids 2025, 110, 105515. [Google Scholar] [CrossRef]
- Liu, X.; Chen, S.; Wang, B.; Tan, X.; Yu, L. A Compact Quasi-Zero-Stiffness Mechanical Metamaterial Based on Truncated Conical Shells. Int. J. Mech. Sci. 2024, 277, 109390. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C. An Origami Inspired Quasi-Zero Stiffness Vibration Isolator Using a Novel Truss-Spring Based Stack Miura-Ori Structure. Mech. Syst. Signal Process. 2022, 165, 108383. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C. Dynamic Analysis of the Effects of Self-Weight Induced Structural and Damping Nonlinearity on the Performance of an Origami-Inspired Vibration Isolator. J. Sound Vib.. 2023, 547, 117538. [Google Scholar] [CrossRef]
- Liu, S.; Peng, G.; Li, Z.; Li, W.; Sun, L. Low-Frequency Vibration Isolation via an Elastic Origami-Inspired Structure. Int. J. Mech. Sci. 2023, 260, 108622. [Google Scholar] [CrossRef]
- Han, H.; Sorokin, V.; Tang, L.; Cao, D. Lightweight Origami Isolators with Deployable Mechanism and Quasi-Zero-Stiffness Property. Aerosp. Sci. Technol. 2022, 121, 107319. [Google Scholar] [CrossRef]
- Zhou, H.; Gao, J.; Chen, Y.; Shen, Z.; Lv, H.; Sareh, P. A Quasi-Zero-Stiffness Vibration Isolator Inspired by Kresling Origami. Structures 2024, 69, 107315. [Google Scholar] [CrossRef]
- Yu, K.; Chen, Y.; Yu, C.; Li, P.; Ren, Z.; Zhang, J.; Lu, X. Origami-Inspire Quasi-Zero Stiffness Structure for Flexible Low-Frequency Vibration Isolation. Int. J. Mech. Sci. 2024, 276, 109377. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, D.; Zhou, J.X. Characteristic analysis of a ball-type vibration isolator with quasi-zero-stiffness. J. Vib. Shock 2015, 34, 142–147. (In Chinese) [Google Scholar]
- Jiao, G.; Zeng, J.; Wang, S. A Compact Magnetic-Curved-Spring QZS Isolator for Supporting Uncertain Loads. Nonlinear Dyn. 2024, 113, 9217–9238. [Google Scholar] [CrossRef]
- Deng, J.; Yang, J.; Zhao, J.; Long, X. An Approach for Realizing Lightweight Quasi-Zero Stiffness Isolators via Lever Amplification. J. Sound Vib. 2025, 596, 118740. [Google Scholar] [CrossRef]
- Anvar Valeev, R.T.; Boris, M. Designing and Experimental Study of Compact Vibration Isolator with Quasi-Zero Stiffness. Struct. Eng. Mech. 2021, 79, 415–428. [Google Scholar]
- Xu, L.; Xiang, Z. Compliant Quasi-Zero Stiffness Device for Vibration Energy Harvesting and Isolation. Sens. Actuator A-Phys. 2022, 347, 113964. [Google Scholar] [CrossRef]
- Zhang, C.; He, J.; Zhou, G.; Wang, K.; Xu, D.; Zhou, J. Compliant Quasi-Zero-Stiffness Isolator for Low-Frequency Torsional Vibration Isolation. Mech. Mach. Theory 2023, 181, 105213. [Google Scholar]
- Li, X.; Ding, B.; Ran, J.; Li, C.; Dong, X.; Chen, S.-C. Design and Characterization of a Compact Tripod Quasi-Zero-Stiffness Device for Isolating Low-Frequency Vibrations. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2024, 91, 632–643. [Google Scholar] [CrossRef]
- Lu, J.-J.; Qi, W.-H.; Liu, F.-R.; Cao, Y.-B.; Zhao, T.-Y.; Cai, L.-Q.; Li, Y.; Yan, G.; Zhang, W.-M. Compliant Curved Beam Support with Flexible Stiffness Modulation for Near-Zero Frequency Vibration Isolation. J. Sound Vib. 2025, 595, 118702. [Google Scholar] [CrossRef]
- Shuai, C.; Li, B.; Ma, J.; Yang, Z. A Novel Low Stiffness Air Spring Vibration-Isolation Mounting System. Shock Vib. 2022, 2022, 5598689. [Google Scholar]
- Abuabiah, M.; Dabbas, Y.; Herzallah, L.; Alsurakji, I.H.; Assad, M.; Plapper, P. Analytical Study on the Low-Frequency Vibrations Isolation System for Vehicle’s Seats Using Quasi-Zero-Stiffness Isolator. Appl. Sci. 2022, 12, 2418. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).