Methodology and Experimental Investigation of Linear Creep Behavior in Two-Layer Reinforced Concrete Beams
Abstract
1. Introduction
2. Research Aims, Scope, and Novelty
- -
- Experimental investigation of the linear creep effect in TLBs;
- -
- Applicability of the previously proposed algorithm [15] to obtained experimental results;
- -
- Analyzing the linear creep effect on the interaction between the TLB layers;
- -
- Studying the influence of cracks on TLB specimens under long-term loading (90 days).
3. Experimental Program
3.1. Materials’ Properties’ Subsection
- -
- Portland cement CEM I 52.5 with a density of 3.1 kg/dm3;
- -
- Fly ash with a density of 2.3 kg/dm3;
- -
- Poly-carboxylic ether-based superplasticizer with a density of about 1.07 kg/dm3;
- -
- Natural sand with a fraction size of 0 to 2 mm;
- -
- Two different types of gravel with fraction sizes of 2 to 8 mm and 8 to 16 mm.
3.2. Cubic Specimens
3.3. Testing Procedure
- -
- Case 1. Two TLB specimens were tested under long-term loading, corresponding to 70% of the ultimate load;
- -
- Case 2. Two TLB specimens were previously loaded up to cracking and unloaded. After that, the specimens were tested under long-term loading, corresponding to 70% of the ultimate load;
- -
- Case 3. Two other TLB specimens were tested under long-term loading, corresponding to about 85% of the ultimate load.
4. Experimental Results and Discussion
4.1. Beams’ Cracking
4.2. Analysis of Linear Creep
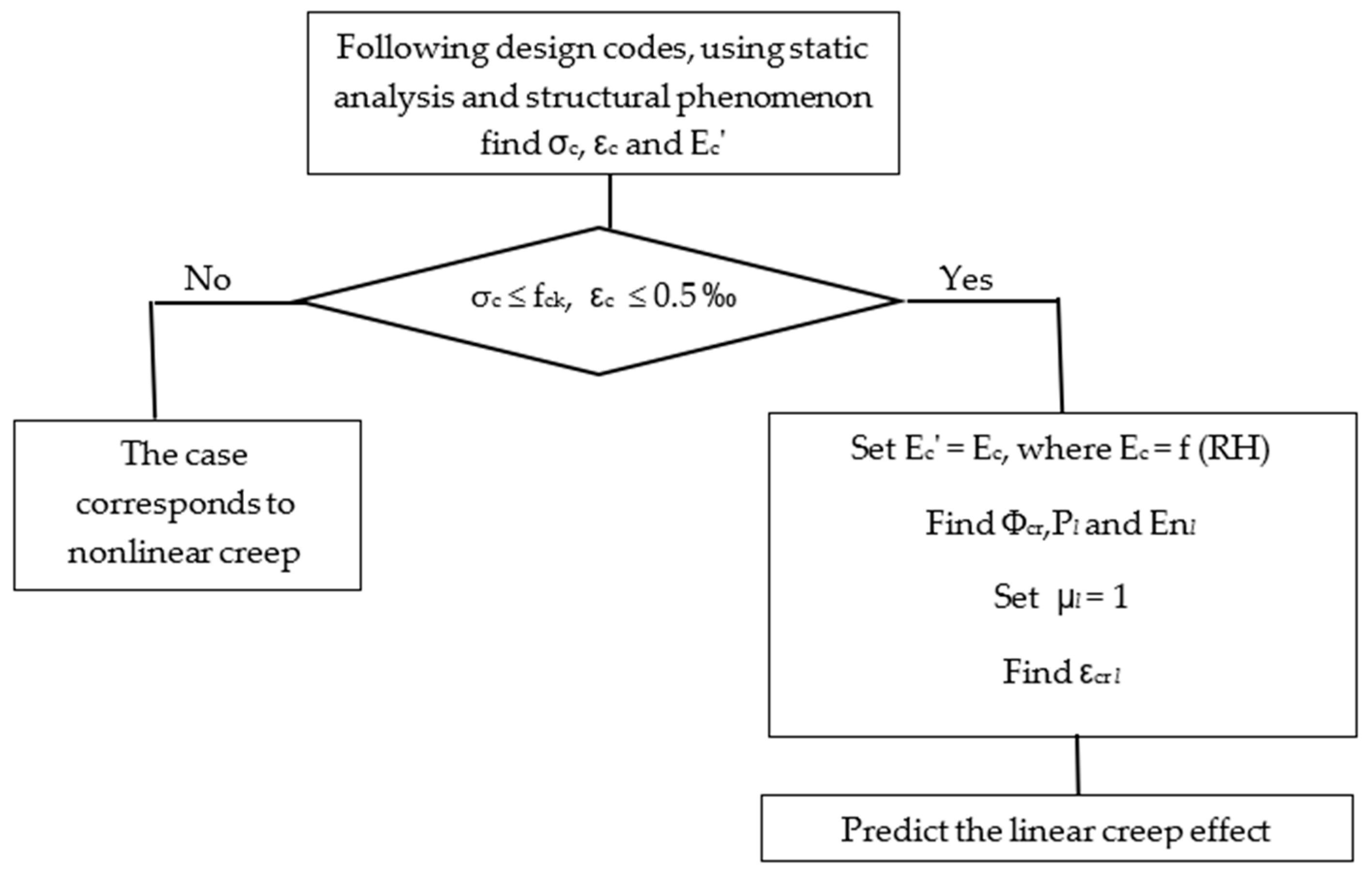
5. Concrete Linear Creep Algorithm
- -
- According to modern codes, concrete creep increases up to 4–5 years, and after that it asymptotically approaches a constant value, but the main effect is achieved during the first year;
- -
- Uniaxial concrete compression at constant stress was assumed;
- -
- The concrete creep increases as an exponential curve that becomes practically parallel to the time axis.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, X.; Park, P.; Rew, Y.; Huang, K.; Sim, C. Constitutive behaviors of steel fiber reinforced concrete under uniaxial compression and tension. Constr. Build. Mater. 2020, 233, 117316. [Google Scholar]
- Xu, H.; Wang, Z.; Shao, Z.; Cai, L.; Jin, H.; Zhang, Z.; Qiu, Z.; Rui, X.; Chen, T. Experimental study on durability of fiber reinforced concrete: Effect of cellulose fiber, polyvinyl alcohol fiber and polyolefin fiber. Constr. Build. Mater. 2021, 306, 124867. [Google Scholar]
- De Azevedo, A.R.; Marvila, M.T.; Tayeh, B.A.; Cecchin, D.; Pereira, A.C.; Monteiro, S.N. Technological performance of açaí natural fibre reinforced cement-based mortars. J. Build. Eng. 2021, 33, 101675. [Google Scholar]
- Song, P.; Hwang, S. Mechanical properties of high-strength steel fiber-reinforced concrete. Constr. Build. Mater. 2004, 18, 669–673. [Google Scholar]
- Jindra, D.; Hradil1, P.; Kala, J. Stress relaxation of concrete beams caused by creep and shrinkage effects. MATEC Web Conf. 2024, 396, 05018. [Google Scholar] [CrossRef]
- Ghali, A.; Favre, R.; Eldbadry, M. Concrete Structures. Stresses and Deformation; Taylor & Francis: New York, NY, USA, 2002. [Google Scholar]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. 2004. Available online: https://archive.org/details/bs_en_1992-1-1-2004_eurocode_2 (accessed on 10 December 2024).
- SI 466 part 1; The Standards Institution of Israel. Concrete Code: General Principles. Amendment 3. 2012. Available online: https://docplayer.gr/106673223-Si-466-part-1-june-amendment-no-4-the-standards-institution-of-israel-concrete-code-general-principles-november-2016.html#google_vignette (accessed on 10 December 2024). (in Hebrew)
- ACI Committee 318-05; Building Code Requirements for Structural Concrete. 2005. Available online: https://www.concrete.org/Portals/0/Files/PDF/Previews/318-05_preview.pdf (accessed on 10 December 2024).
- BR 52-101-2003; Non-Pre-Stressed Concrete and Reinforced Concrete Structures. NIIZhB: Moscow, Russia, 2004. (In Russian)
- Model Code 2010, final draft, vol. 1; Bulletin 65; Federation Internationale du Beton (fib): Lausanne, Switzerland, 2012; Volume 2.
- Marzouk, H. Creep of high–strength concrete and normal–strength concrete. Mag. Concr. Res. 1991, 43, 121–126. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, W.; Yan, P. Measurement and modeling of creep property of high-strength concrete considering stress relaxation effect. J. Build. Eng. 2022, 56, 104726. [Google Scholar] [CrossRef]
- Dias-da-Costa, D.; Júlio, E.N.B.S. Modelling creep of high strength concrete. Comput. Concr. 2010, 7, 533–547. [Google Scholar]
- Iskhakov, I.; Ribakov, Y. New Model of Linear and Non- linear Concrete Creep. Rom. J. Mater. 2021, 51, 528–535. [Google Scholar]
- Xue, W.; Liu, T.; Zeng, M. Prediction of long-term deflections for high-speed railway prestressed concrete beams. ACI Struct. J. 2016, 113, 769–778. [Google Scholar] [CrossRef]
- Pan, Z.; Lü, Z.; Fu, C.C. Experimental study on creep and shrinkage of high-strength plain concrete and reinforced concrete. Adv. Struct. Eng. 2011, 14, 235–247. [Google Scholar]
- Yang, M.; Jin, S.; Gong, J. Concrete creep analysis method based on a long-term test of prestressed concrete beam. Adv. Civ. Eng. 2020, 2020, 3825403. [Google Scholar] [CrossRef]
- Tho, P.D.; Tien, T.M.; Thanh, D.T.; Ngan, V.M.; Ngoc, V.M.; Sorelli, L. Experimental investigation of the secondary creep of fiber reinforced concrete at high stress: Macroscopic measurement and digital image correlation. J. Sci. Technol. Civ. Eng. 2022, 16, 19–28. [Google Scholar] [CrossRef]
- Abrishambaf, A.; Barros, J.A.O.; Cunha, V.M.C.F. Time-dependent flexural behaviour of cracked steel fibre reinforced self-compacting concrete panels. Cem. Concr. Res. 2015, 72, 21–36. [Google Scholar]
- García-Taengua, E.; Arango, S.; Martí-Vargas, J.R.; Serna, P. Flexural creep of steel fiber reinforced concrete in the cracked state. Constr. Build. Mater. 2014, 65, 321–329. [Google Scholar]
- Cao, X.Y.; Feng, D.C.; Wu, G.; Wang, Z. Experimental and Theoretical Investigations of the Existing Reinforced Concrete Frames Retrofitted with the Novel External SC-PBSPC BRBF Sub-Structures. Eng. Struct. 2022, 256, 113982. [Google Scholar] [CrossRef]
- Wang, H.T.; Tang, C.; Chen, M.S.; Shi, J.; Cao, X.Y. Experimental Study on the Flexural Performance of Prestressed RC Beams with Post-Tensioned CFRP Strands. Eng. Struct. 2024, 309, 118118. [Google Scholar] [CrossRef]
- Iskhakov, I.; Ribakov, Y.; Holschemacher, K.; Mueller, T. Experimental Investigation of Full Scale Two-Layer Reinforced Concrete Beams. Mech. Adv. Mater. Struct. 2014, 21, 273–283. [Google Scholar]
- Iskhakov, I.; Ribakov, Y.; Holschemacher, K. Experimental Investigation of Continuous Two-Layer Reinforced Concrete Beam. Struct. Concr. 2016, 18, 205–215. [Google Scholar]
- Iskhakov, I.; Ribakov, Y.; Holschemacher, K.; Kaesberg, S. Experimental Case study and Recommendations for Practical Implementation of Real Pre-Stressed Two Layer Reinforced Concrete Beams. Structures 2023, 47, 1284–1294. [Google Scholar]
- STRAP—Structural Analysis Programs. ATIR Engineering Software Development, Users’ Manual. 2021. Available online: https://atirsoft.com/wp-content/uploads/2020/09/STRAP_Manual.pdf (accessed on 29 January 2025).
- Iskhakov, I.; Ribakov, Y. Structural Phenomenon of Cement-Based Composite Elements in Ultimate Limit State. Adv. Build. Technol. Constr. Mater. 2016, 2016, 4710752. [Google Scholar]
- Deutscher Beton- und Bautechnik-Verein e.V. (Hrsg.). DBV-Merkblatt Stahlfaserbeton; Deutscher Beton- und Bautechnik-Verein e.V.: Wiesbaden, Germany, 2001. (In German) [Google Scholar]
- Deutscher Ausschuss für Stahlbeton (DAfStb). Richtlinie Stahlfaserbeton; 23. Entwurf; Beuth Verlag GmbH: Berlin/Köln, Germany, 2007. (In German) [Google Scholar]
- DIN 1045-1; Tragwerke aus Beton, Stahlbeton und Spannbeton—Teil 1 Bemessung und Konstruktion. DIN Deutsches Institut für Normung e.V: Berlin, Germany, 2008. Available online: https://regbar.com/ar/wp-content/uploads/2019/09/DIN-1045-1-2008.pdf (accessed on 10 December 2024). (In German)
- Junker, F.; Holschemacher, K. Creep Behavior of Steel Fiber Reinforced Lightweight Concrete Beams Under Flexural Loading. Proc. Int. Struct. Eng. Constr. 2022, 9, 1–6. [Google Scholar] [CrossRef]
- HBM (Hottinger Baldwin Messtechnik GmbH) Software: Catman Professional Rel. 4.5. 2004. Available online: https://www.hbkworld.com/en/services-support/support/support-hbm/downloads/downloads-software/support-downloads-catman (accessed on 10 March 2025).

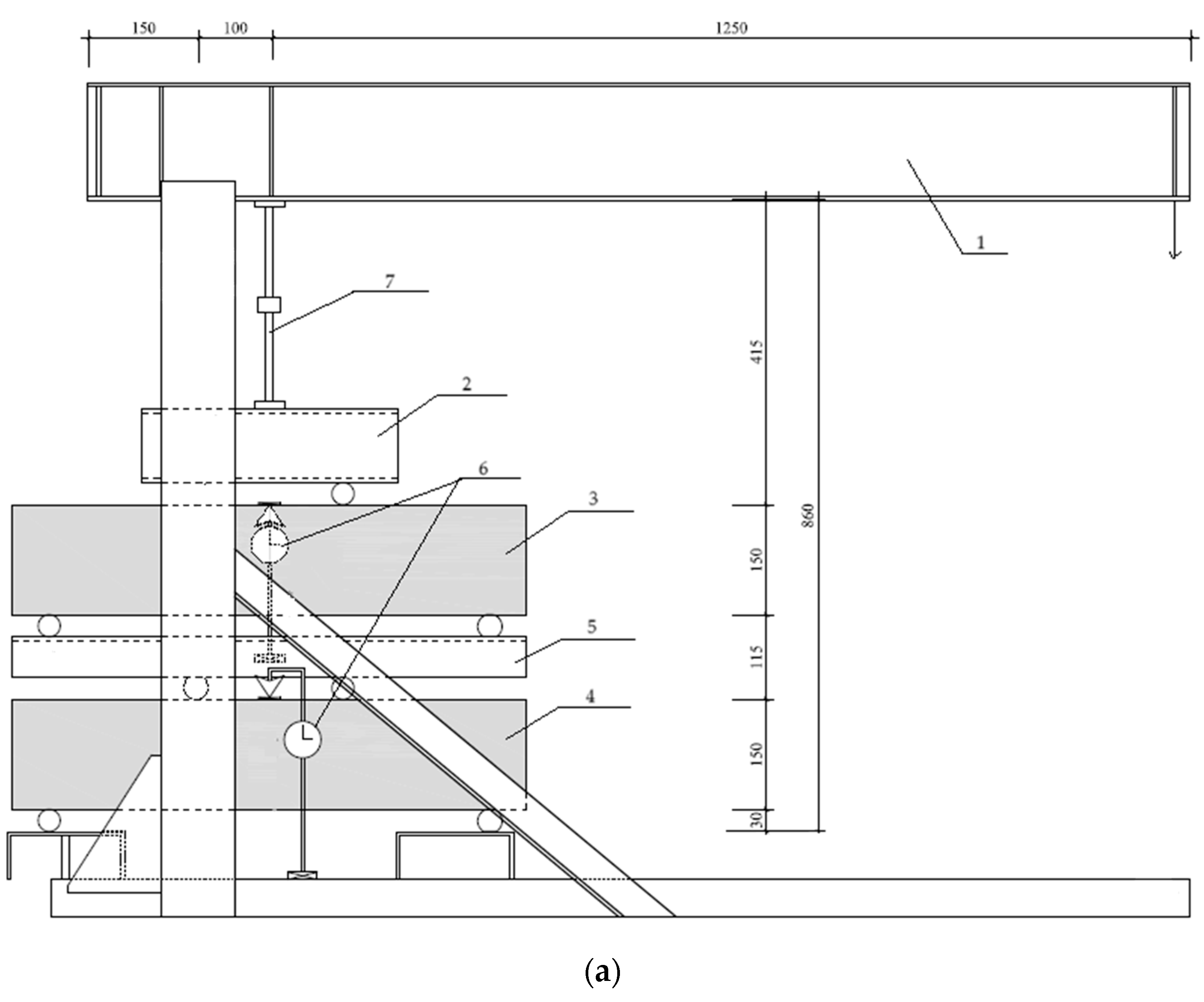



| Components | Quantity, kg/m3 | |
|---|---|---|
| SFHSC | NSC | |
| Cement (C) | 400 | 300 |
| Water (W) | 152 | 180 |
| Fly ash (FA) | 100 | 0 |
| Superplasticizer | 15.4 | 0 |
| 0/2 sand | 675.43 | 659.36 |
| 2/8 gravel | 429.71 | 560.91 |
| 8/16 gravel | 618.78 | 654.40 |
| Compressive | Splitting Tensile |
|---|---|
| 96.52 | 6.14 |
| 95.51 | 6.27 |
| 94.81 | 5.93 |
| Load Case | Specimen | Cracks’ Opening, mm | |||||
|---|---|---|---|---|---|---|---|
| Crack 1 | Crack 2 | Crack 3 | |||||
| Depth | Width | Depth | Width | Depth | Width | ||
| 1 | Top | - | - | - | - | - | - |
| Bottom | 80 | 0.1 | - | - | - | - | |
| 2 | Top | 70 | 0.1 | 70 | 0.1 | 70 | 0.1 |
| Bottom | 100 | 0.1 | 70 | 0.1 | - | - | |
| 3 | Top | 80 | 0.1 | 80 | 0.1 | 60 | 0.1 |
| Bottom | 100 | 0.1 | 100 | 0.1 | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iskhakov, I.; Holschemacher, K.; Kaeseberg, S.; Ribakov, Y. Methodology and Experimental Investigation of Linear Creep Behavior in Two-Layer Reinforced Concrete Beams. Appl. Sci. 2025, 15, 3456. https://doi.org/10.3390/app15073456
Iskhakov I, Holschemacher K, Kaeseberg S, Ribakov Y. Methodology and Experimental Investigation of Linear Creep Behavior in Two-Layer Reinforced Concrete Beams. Applied Sciences. 2025; 15(7):3456. https://doi.org/10.3390/app15073456
Chicago/Turabian StyleIskhakov, Iakov, Klaus Holschemacher, Stefan Kaeseberg, and Yuri Ribakov. 2025. "Methodology and Experimental Investigation of Linear Creep Behavior in Two-Layer Reinforced Concrete Beams" Applied Sciences 15, no. 7: 3456. https://doi.org/10.3390/app15073456
APA StyleIskhakov, I., Holschemacher, K., Kaeseberg, S., & Ribakov, Y. (2025). Methodology and Experimental Investigation of Linear Creep Behavior in Two-Layer Reinforced Concrete Beams. Applied Sciences, 15(7), 3456. https://doi.org/10.3390/app15073456







