Abstract
Accurate long-term cloud demand forecasting is critical for optimizing resource procurement and cost management in cloud computing, yet it remains challenging due to dynamic demand trends, limited historical data, and the poor generalization of existing models in few-shot scenarios. This paper proposes DimAug-TimesFM, a dimension-augmented framework for long-term cloud demand forecasting, which addresses these challenges through two key innovations. First, Delivery Period Extracting identifies critical resource delivery phases by analyzing smoothed utilization trends and differencing thresholds, enabling focused modeling on periods reflecting actual demand. Second, Dimension-Augmented TimesFM enhances the pretrained TimesFM model by integrating cross-pool data via Dynamic Time Warping based similarity matching, enriching training data while mitigating distribution discrepancies. Experiments on real-world cloud resource utilization data demonstrate that DimAug-TimesFM significantly outperforms SOTA baselines (e.g., TimesFM, DLinear, PatchTST) in both short-term (16-day) and long-term (64-day and 128-day) forecasting tasks, achieving average reductions 72.9–81.7% in RMSE. DimAug-TimesFM also exhibits better robustness in scenarios where TimesFM fails, attributed to its synergistic integration of temporal feature enhancement and cross-pool data augmentation. This work provides a practical solution for few-shot cloud demand forecasting, enabling enterprises to align resource allocation with dynamic usage patterns and reduce operational costs.
1. Introduction
As enterprises continue to advance their digital transformation initiatives, cloud computing has emerged as an indispensable component of modern business operations. However, managing costs in a cloud environment remains a critical challenge, which is a central focus of FinOps (Financial Operations) [1]. Moreover, the inherent uncertainty of resource demands often hinders enterprises’ ability to align their allocations with actual usage, resulting in both over-provisioning and under-utilization.
In the context of cloud resource acquisition, organizations frequently face several notable challenges. These include inaccurate demand forecasting and inflexible resource allocation mechanisms. Many organizations tend to enter into long-term contracts or acquire on-demand resources without a thorough understanding of their usage patterns, which often leads to cost overruns or resource under-utilization [2]. Addressing these challenges requires a more strategic approach to cloud resource management and financial planning.
Cloud demand forecasting (CDF) uses historical data and usage patterns to enable enterprises to accurately predict future resource demands and forecast the time when resource pool utilization reaches procurement thresholds, thus optimizing procurement and allocation strategies and enabling rational procurement before resource depletion [3]. As shown in Figure 1, this process helps to ensure timely procurement before resource depletion. Furthermore, CDF provides data-driven decision-making support, empowering enterprises to make more informed decisions when navigating complex vendor pricing models and resource options. Studies [4] suggest that the implementation of precise cloud demand forecasting strategies can significantly improve resource utilization and simultaneously ensure business performance and reliability.
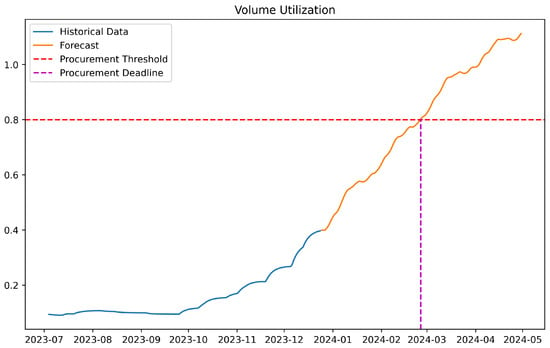
Figure 1.
An example of CDF that enables users to predict the time when the resource pool utilization rate will reach the procurement threshold, so as to complete reasonable procurement before resource depletion.
However, accurately predicting long-term resource utilization remains challenging due to (1) highly dynamic demand trends influenced by business operations, (2) limited historical data in few-shot scenarios (e.g., 30–60 days of observations for newly deployed resource pools), and (3) the poor generalization in existing models, such as TimesFM, when confronted with distribution discrepancies across pools or extended prediction horizons. Traditional statistical models, such as ARIMA, rely on sufficient historical data for parameter estimation, and struggle when faced with short observation windows. Transformer-based deep learning models, while effective in large-scale data settings, often overfit in low-data regimes, limiting their generalization. TimesFM, a state-of-the-art time series foundation model, improves performance through pretraining and fine-tuning but still encounters significant failures when applied to cloud resource forecasting with highly heterogeneous and distributionally mismatched data across resource pools.
To bridge these gaps, we propose DimAug-TimesFM, a dimension-augmented framework tailored to long-term cloud demand forecasting in few-shot settings. Our work is motivated by two critical observations.
- Resource utilization patterns exhibit distinct phases (e.g., rapid growth during delivery vs. stabilized usage during maintenance), yet existing models lack mechanisms to prioritize phases reflecting actual demand;
- Cross-pool data augmentation, if improperly implemented, introduces artificial temporal features that degrade model performance.
Our core contributions are threefold:
- Delivery Period Extracting: A novel method to identify resource delivery phases by analyzing smoothed utilization trends and differencing thresholds, enabling targeted modeling of periods critical for accurate forecasting;
- Dimension-Augmented TimesFM: A pretrained time series model enhanced with cross-pool data augmentation, leveraging DTW-based similarity matching to align and integrate related time series while mitigating distribution shifts;
- Comprehensive Validation: Extensive experiments on real-world cloud resource data from a Chinese telecom operator demonstrate that our framework reduces prediction errors by 73.7–82.1% (MAE), 73.8–79.1% (MAPE), and 72.9–81.7% (RMSE) compared to state-of-the-art baselines, while exhibiting superior robustness in challenging scenarios.
This work provides enterprises with a practical solution to align resource allocation with dynamic demand patterns, ultimately reducing operational costs and improving sustainability in cloud ecosystems.
2. Background and Motivation
CDF is a critical task in achieving efficient operation and resource optimization in cloud data centers. Accurate prediction of resource demand can ensure service quality, improve resource utilization, and reduce operational costs. However, due to the operational characteristics of cloud resource pools and the limitations of historical data, capacity forecasting still faces several challenges. As shown in Figure 2, these challenges significantly impact the accuracy and reliability of cloud demand forecasting.
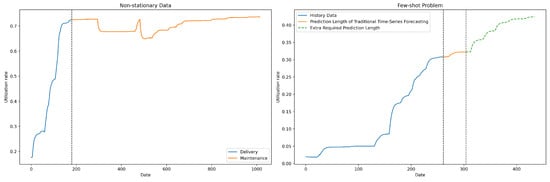
Figure 2.
Few-shot problem.
2.1. Non-Stationary Data
Non-stationary data [5,6] refers to time series data in which the statistical properties, such as the mean, variance, and covariance, change over time. In the context of time series forecasting, non-stationary data pose significant challenges because models trained on stationary assumptions may fail to capture the evolving nature of the underlying patterns, especially when real-world events cause sudden bursts or shifts in trends.
In cloud demand forecasting, the changing trends in cloud resource demand are highly dynamic, and data characteristics evolve over time, making direct prediction challenging for model convergence. After analyzing trend variations in the data, the capacity variation of resource pools can be divided into two phases: the resource delivery phase and the resource maintenance phase. The resource delivery phase is characterized by a rapid increase in resource utilization, and its usage curve accurately reflects the user demand for resources, making it the main focus of capacity forecasting. In contrast, during the resource maintenance phase, administrators intervene to control resource allocation and release, causing resource usage during this phase to deviate from actual demand. As a result, capacity forecasting must focus on predicting demand within the resource pools that are in the resource delivery phase. This imposes higher requirements on the model’s ability to extract time series features and distinguish between phases.
2.2. The Few-Shot Problem
The few-shot problem [7,8] in time series prediction refers to the challenge of making accurate forecasts when only limited training data are available, necessitating models that can generalize effectively from just a few examples. Several critical issues stem from this scarcity of data, including the limitation of prediction length and model overfitting [9], as accurately modeling long-term dependencies with insufficient historical information becomes challenging.
In CDF, the few-shot problem could be more acute. CDF requires forecasting future trend changes over periods of 2 to 4 months to allow sufficient time for resource procurement. However, traditional time series forecasting algorithms require extensive historical data, of more than 300 days, to achieve a reliable generalization to achieve a prediction length of 60 days. In practice, resource pools during the resource delivery phase often contain merely 30 to 60 days of data. This significant shortfall exacerbates the challenge of limited prediction length and overfitting. Consequently, enhancing prediction accuracy under these constraints through few-shot models or by integrating data augmentation becomes essential in CDF.
2.3. Motivation for Dimension Augmentation
Given the scarcity of historical data within individual resource pools and the presence of multiple correlated resource pools, an opportunity arises to enhance the dataset of a target resource pool through cross-pool data augmentation. This approach, which we refer to as dimension augmentation (DimAug), aims to improve the generalizability of the forecasting model.
However, directly concatenating time series data from disparate pools may introduce artificial temporal features, potentially degrading model performance due to inconsistencies or misleading information. To address this issue, DimAug incorporates techniques to ensure that the augmented data remain consistent with the underlying patterns of the target resource pool. Specifically, DimAug employs a method that aligns the temporal features of the source and target data, thereby minimizing the risk of introducing artificial trends.
By leveraging cross-pool data augmentation, DimAug seeks to overcome the limitations imposed by the few-shot problem and improve the accuracy and reliability of capacity forecasting in cloud data centers.
3. Related Work
Time series data, characterized by their temporal dependencies and dynamic patterns, play a crucial role in various domains, such as finance, healthcare, and climate science. However, the limited availability of labeled data often poses significant challenges for model training and generalization. To address this issue, data augmentation techniques have been extensively explored to generate synthetic data that can enhance model performance. Additionally, the development of time series prediction algorithms has also seen substantial progress, ranging from traditional statistical models to advanced deep learning frameworks. In this section, we provide a brief discussion of the related work in these two areas.
3.1. Time Series Data Augmentation
The remarkable success of deep learning in fields such as computer vision (CV), natural language processing (NLP), and speech processing heavily relies on the availability of large-scale training data to avoid overfitting. However, many time series tasks, such as classification, prediction, and anomaly detection, face the challenge of limited labeled data. Data augmentation, which generates synthetic data covering unexplored regions of the input space while maintaining label consistency, has emerged as a crucial tool for improving model generalization. Although data augmentation techniques in the domains of images and speech have matured, time series data, with their unique temporal dependencies, multivariate dynamic associations, and task-specific nature (such as the differences between classification and anomaly detection goals), require the design of specialized augmentation methods.
Early research primarily borrowed simple transformations from the image domain, such as cropping, flipping, and jittering, and applied them to time series data [10]. Subsequently, researchers began exploring the transformation of time series into the frequency domain (e.g., Fourier Transform) or time–frequency domain (e.g., wavelet transform), where modifications to spectral components generated new samples [11]. Another approach involved the use of signal decomposition techniques, such as STL and EMD, to separate the trend, seasonality, and residual components, with independent enhancement of these sub-components followed by reconstruction [12].
With the rise of deep learning, generative models such as GANs and VAEs have been extended to time series generation, notably with models like TimeGAN and AnoGAN. Another line of work focused on embedding-space augmentation, where perturbations were applied to intermediate representations in models, such as LSTM hidden states, to enhance feature robustness [13]. Additionally, automatic augmentation techniques leveraging reinforcement learning or optimization algorithms have been explored to dynamically search for optimal augmentation strategies [14,15].
3.2. Time Series Prediction Algorithm
3.2.1. Traditional Time Series Model
Temporal variation modeling has been a central focus in time series analysis, evolving from classical statistical methods to advanced deep learning approaches. Traditional models like ARIMA, Holt-Winter, and Prophet rely on pre-defined temporal patterns, which often fail to capture the complexity of real-world data. Recent advances in deep learning have introduced diverse frameworks, such as MLP, TCN, and RNN-based models, and Transformers, each leveraging unique mechanisms to encode temporal dependencies [16].
MLP-based methods process temporal information through fixed-layer parameters, while TCNs use convolutional kernels to identify variations across time [17]. RNN-based approaches utilize recurrent structures to implicitly capture temporal relationships through state transitions [18]. Transformers, with their attention mechanisms, excel at discovering temporal dependencies and handling intricate patterns by leveraging innovations like AutoCorrelation (Autoformer) and seasonal-trend decomposition (FEDformer) [19,20,21].
Building on these developments, recent research explores multi-periodicity and temporal 2D variations, introducing task-general models that transcend specific analysis tasks. These approaches leverage computer vision techniques to enhance temporal modeling, marking a significant step toward unified solutions for complex time series challenges [22].
3.2.2. Large-Scale Time Series Model
Large-scale Time Series Models (LTSMs) represent a significant leap in the application of advanced neural architectures, originally designed for natural language processing, to the realm of numerical time series forecasting. By leveraging the capabilities of pretrained large language models (LLMs), LTSMs aim to bridge the gap between text generation and time series forecasting. The foundational concept behind LTSMs involves utilizing the inherent pattern recognition abilities of LLMs, initially trained on vast amounts of temporal data, and applying these skills to forecast time series with minimal or no additional training.
Several groundbreaking works have propelled the field forward, showcasing diverse approaches to integrating LLMs with time series forecasting. Among these, LLMTime [23] exemplifies the zero-shot forecasting capability of pretrained LLMs through a novel tokenization scheme that transforms real-valued data into string representations, enabling forecasts from models like GPT-3 without further tuning. Following this, GPT4TS [24] was created by adapting a pretrained GPT-2 model specifically for time series tasks, focusing on fine-tuning positional embeddings and layer normalization parameters while employing patch embeddings for efficient processing. In contrast, TimesFM [25] introduces a decoder-only foundation model tailored for time series forecasting, featuring an increased output patch size for faster decoding. This approach emphasizes scalability and efficiency by pretraining the model on extensive Google Trends and Wiki pageview data, alongside open-source datasets. Meanwhile, Time-LLM [26] pushes the boundaries by aligning time series patches with textual prototypes and prompting frozen LLMs, though it requires domain-specific fine-tuning for optimal performance. Lastly, Chronos [27] represents a unique strategy, training language models from scratch on large-scale time series datasets using scaling and quantization techniques, thus avoiding reliance on pretrained LLMs altogether.
In summary, LTSMs highlight the transformative potential of adapting LLMs for time series forecasting, offering innovative solutions ranging from zero-shot prediction to specialized fine-tuning methods. Despite notable advancements, challenges such as computational costs and the necessity for domain-specific adjustments persist, motivating continuous research towards developing more efficient and versatile models capable of handling diverse datasets with enhanced accuracy and scalability.
4. Proposed Method
4.1. Delivery Period Extracting
The resource delivery period is a period when the resource pool has abundant resources and resource applications are not artificially controlled by administrators, characterized by a rapid increase in resource utilization, significant fluctuations, and minimal human intervention. We utilize the weighted moving average as a smoothing technique to process historical time series data, with the aim of extracting the long-term trend. Subsequently, we perform differencing on the data that have been smoothed. Based on the distribution of the differenced data, we establish the thresholds and . When the difference value exceeds , it is marked as an upward trend, when it is less than , it is marked as a downward trend, and other periods are marked as stable. Finally, as illustrated in Figure 3, we marked the longest upward trend as the delivery period.
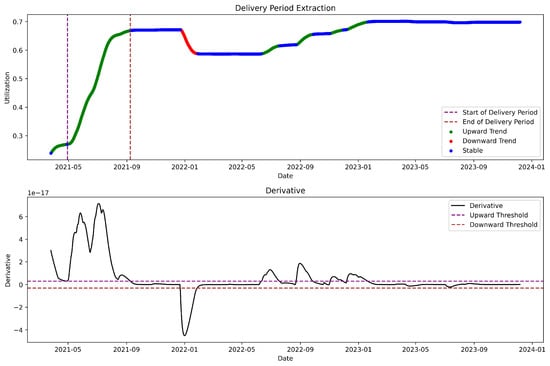
Figure 3.
An example of delivery period extracting.
4.2. Dimension-Augmented TimesFM
4.2.1. TimesFM
Pretrained Large Time-Series Models (LTSMs) are able to obtain universal temporal feature representations by pretraining on massive amounts of time series data [28]. The pretraining paradigm enables the model to effectively migrate prior knowledge to improve prediction performance when facing downstream few-shot tasks. Among the existing pretrained transformer-based temporal models, TimesFM has attracted much attention due to its excellent few-shot learning capability, wide range of applications, and ease of use.
However, there are significant challenges in applying TimesFM directly to the cloud demand prediction task, which stems mainly from the inherent feature distribution characteristics of the cloud resource demand data. During the performance evaluation of the TimesFM prediction model, when the prediction window length was set to 128, approximately 38% of the test resource pools experienced prediction failure. In contrast, when the prediction window length was adjusted to 64, the proportion of test resource pools with prediction failure was approximately 23%. TimesFM exhibits severe performance degradation on the CDF task, which may be attributed to the significant distributional discrepancy between the forecasting data and the training data, resulting in a weak pool adaptation capability of the model. Additionally, it was observed that the severity of this issue escalates as the prediction length (pred_len) increases.Although we try to optimize the model performance through fine-tuning strategies, it is difficult to find an optimization solution that can effectively balance these distributional differences due to the high distributional heterogeneity of cloud resource demand time series data. This issue arises primarily from two factors: distribution discrepancy and error accumulation. TimesFM’s pretrained model is optimized on a dataset with ample historical data, but in few-shot scenarios, the target resource pool’s data distribution often differs significantly, making it difficult for the model to capture local demand patterns. Additionally, as the forecasting horizon increases, small errors compound over time, further exacerbating prediction failures. To address these limitations, DimAug-TimesFM incorporates two key innovations: Delivery Period Extracting and dimension augmentation.
4.2.2. Implementation of DimAug-TimesFM
To mitigate the performance degradation of TimesFM caused by distributional discrepancies in cloud resource demand forecasting, we propose DimAug. This method enhances the training set by incorporating relevant cross-pool information while preserving the integrity of the time series pattern, which encompasses two key steps, as illustrated in Figure 4:
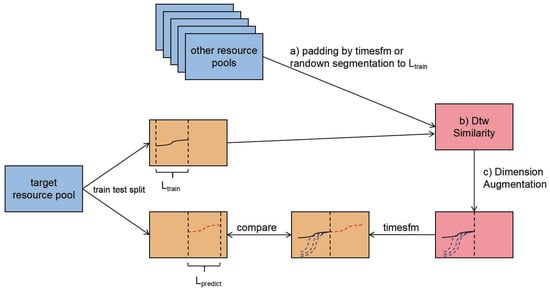
Figure 4.
The workflow of DimAug-Timesfm. The method processes target and auxiliary resource pools through (a) time series padding or segmentation, to standardize sequences to length (Equation (1)); (b) DTW similarity calculation between pools (Equation (2)); and (c) dimension augmentation by integrating the K most similar pools with the target pool (Equation (3)).
- Alignment and Adjustment of Resource Pool Data: Let denote the univariate time series of the target resource pool, where T represents the total observation length. We first define a critical parameter (training window length) based on the target resource pool’s delivery period characteristics. For auxiliary resource pools , their delivery period sequences are processed as follows:where generates synthetic values to extend short sequences, and extracts contiguous subsequences of length . This ensures uniformity in temporal resolution across heterogeneous pools.
- Differential Processing and Similarity Matching: For each aligned series , we compute its differenced representation to emphasize trend dynamics. The similarity between the target resource pool and auxiliary resource pool is quantified using Dynamic Time Warping (DTW):where is a warping path adhering to boundary, continuity, and monotonicity constraints. The top-K most similar resource pools (minimizing DTW) are selected and concatenated as exogenous variables:This multi-dimensional input enables the model to capture cross-pool temporal dependencies while retaining univariate forecasting capability.
5. Experiment and Evaluation
5.1. Dataset Description
We use data from a well-known telecommunications operator in China to evaluate the performance of our model. Specifically, the dataset covers monitoring data from March 2021 to December 2023, spanning 138 resource pools, 31,924 servers, and 392 PB of storage. The data have been aggregated by resource pools and include daily records of storage resource usage. Due to variations in business operations and geographical factors, the demand patterns for cloud resources exhibit significant differences across different resource pools.
5.2. Data Preprocess
Differencing Method: To better capture the trend of storage resource utilization, we applied the differencing method to transform the original storage utilization data into growth rates. The differencing method eliminates trends and seasonality in time series data by calculating the difference between consecutive time points, thereby reflecting the rate of change more effectively. This reduces non-stationarity in the data and enhances the predictive performance of the model.
Let denote the original storage utilization time series, where t represents the time point. The growth rate after differencing can be calculated using the following formula:
where
- represents the storage utilization at the current time point;
- represents the storage utilization at the previous time point;
- represents the growth rate of storage utilization, expressed as a percentage.
5.3. Experiment Setup
Experimental Environment
Hardware Environment: The experiments were conducted on a Linux server equipped with two NVIDIA GeForce RTX 3090Ti GPU.
Software Environment: The software environment includes Python 3.8 and PyTorch 1.10, along with libraries such as NumPy, Pandas, and Scikit-learn for data processing and machine learning.
Parameter Settings: In our experimental investigation, the TimesFM model was implemented with the following parameter configurations: a context length of 64 units was established to facilitate temporal pattern recognition, while the forecast horizon was set equivalent to the training data duration to maximize predictive capacity. The model architecture incorporated an input patch length of 32, a dimensional parameter of 1280, and 20 transformer layers to ensure comprehensive feature extraction and pattern analysis. Computational efficiency was optimized through a per-core batch size of 4, with the processing backend specifically configured for CPU operation. Additionally, the model was designed with positional embeddings disabled to evaluate performance under pure sequential learning conditions.
5.4. Evaluation
This section evaluates the effectiveness of DimAug-TimesFM in addressing the challenges of long-term cloud demand forecasting, particularly in few-shot scenarios. Through extensive experiments, we compare its performance with state-of-the-art baselines, analyze its advantages in both short-term and long-term forecasting, and assess its robustness in scenarios where TimesFM fails. The results demonstrate that DimAug-TimesFM significantly enhances prediction accuracy and generalization by leveraging Delivery Period Extraction and cross-pool data augmentation, validating its effectiveness in mitigating data scarcity and distribution shift issues.
5.4.1. Short-Term Forecasting
First, we set up a short-term prediction experiment with a forecast length of 16 days. Due to the sufficient number of samples, we were able to compare our model with traditional time series methods that lack few-shot learning capabilities. The experimental results demonstrate that our model achieved the best performance across three key metrics—MAE, MAPE, and RMSE—with average values of 0.0056, 1.1144, and 0.0067, respectively, significantly outperforming all benchmark models. Figure 5 presents a comparative analysis of the average performance of different models on the short-term forecasting task. Specifically, compared to TimesFM, our model reduces MAE, MAPE, and RMSE by approximately 77.6%, 83.7%, and 76.0%, respectively; compared to Informer, Dlinear, and PatchTST, our model achieves reductions of over 99% on all metrics.
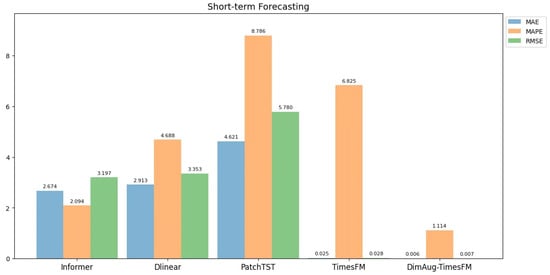
Figure 5.
Comparison of short-term forecasting performance (16-day prediction) across five models. DimAug-TimesFM achieves lower values in all three key metrics (MAE, MAPE, and RMSE) than the four benchmark models, demonstrating superior short-term forecasting performance.
Additionally, Table 1 provides detailed prediction results for two representative resource pools, further validating the superior performance of our model across different resource environments.

Table 1.
Short-term forecasting performance (16-day prediction) on two representative resource pools.
5.4.2. Long-Term Forecasting
To compare the long-term forecasting capabilities before and after data augmentation, we selected five representative resource pools with extended delivery periods and conducted experiments with prediction lengths (pred_len) of 64 and 128 days. Table 2 presents a detailed performance comparison of the two models in the long-term forecasting task. The experimental results indicate that our model continues to excel in long-term forecasting tasks, significantly outperforming TimesFM. In the 64-day prediction task, our model achieved average MAE, MAPE, and RMSE values of 0.0249, 7.5091, and 0.0289, respectively, representing reductions of approximately 73.7%, 73.8%, and 72.9% compared to TimesFM’s 0.0945, 28.6700, and 0.1066. In the 128-day prediction task, our model further optimized these metrics to 0.0222, 7.6792, and 0.0271, respectively, reflecting reductions of about 82.1%, 79.1%, and 81.7% compared to TimesFM’s 0.1241, 36.8240, and 0.1484. As depicted in Figure 6, the performance comparison using data from resource pool 357 further illustrates our model’s superiority in long-term forecasting tasks. These results demonstrate that our model possesses stronger generalization capabilities and stability in long-term forecasting tasks, effectively capturing trends in cloud resource demand. This superior performance is primarily attributed to the synergistic effect of the model’s feature enhancement module and cross-pool learning module, which extract more representative features from cross-pool data and, through data augmentation techniques, further enhance the model’s predictive ability for long-sequence data.

Table 2.
Performance comparison of two models in long-term forecasting (64-day and 128-day prediction) across five resource pools.
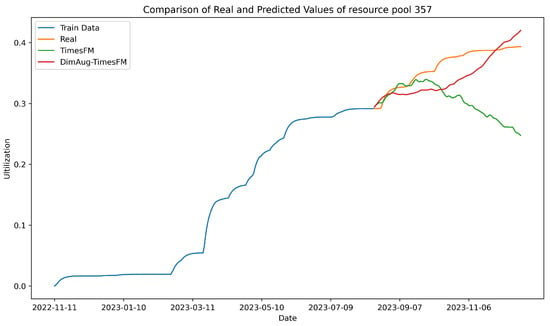
Figure 6.
Long-term predication comparison between TimesFM and DimAug-TimesFM using data from resource pool 357. The result indicates that DimAug-TimesFM outperforms TimesFM in long-term forecasting tasks.
5.4.3. Robustness of Prediction
To evaluate the robustness of DimAug-TimesFM, we conducted comparative experiments in resource pools where TimesFM exhibited significant performance degradation. The experimental results demonstrate that DimAug-TimesFM effectively mitigates 78% of the performance decline observed in TimesFM, significantly enhancing the model’s prediction stability in complex scenarios.
Taking two representative resource pools as examples, Table 3 presents the detailed performance of TimesFM and our model on 64-day and 128-day forecasting tasks. In the 64-day forecasting task for resource pool 190, TimesFM’s MAE, MAPE, and RMSE reached 69.2020, 20030.6820, and 83.1930, respectively. In contrast, our model optimized these metrics to 0.1347, 39.0636, and 0.1514, achieving reductions of over 99% in MAE and RMSE, and a 99.8% reduction in MAPE. Similarly, in the 128-day forecasting task for resource pool 229, TimesFM’s MAE, MAPE, and RMSE were 121.0135, 24054.3601, and 149.4365, respectively, whereas our model improved them to 0.6453, 128.2051, and 0.7477, reducing MAE and RMSE by over 99% and MAPE by 99.5%.

Table 3.
Robustness evaluation of DimAug-TimesFM on typical resource pools with TimesFM performance anomalies.
These results indicate that DimAug-TimesFM maintains outstanding predictive performance even in complex scenarios. Our data augmentation technique further enhances the model’s adaptability to anomalous data, significantly improving its overall robustness.
6. Conclusions and Future Work
This study addresses the critical challenge of long-term cloud demand forecasting in few-shot scenarios through the proposed DimAug-TimesFM framework. By integrating Delivery Period Extracting and Dimension-Augmented TimesFM, the framework effectively mitigates dynamic demand trends, limited historical data, and distribution discrepancies inherent in cloud resource utilization. The dimension augmentation strategy enriches training data by aligning cross-pool time series via DTW-based similarity matching, thereby enhancing the generalization of the pretrained TimesFM model. Extensive experiments on real-world cloud resource data from a Chinese telecom operator demonstrate the framework’s superiority over state-of-the-art baselines (e.g., TimesFM, DLinear, PatchTST), achieving average reductions of 73.7–82.1% in MAE, 73.8–79.1% in MAPE, and 72.9–81.7% in RMSE across short-term (16-day) and long-term (64- to 128-day) forecasting tasks. Furthermore, the framework exhibits exceptional robustness in scenarios where traditional models fail, underscoring the synergy between temporal feature enhancement and cross-pool data augmentation.
Although DimAug-TimesFM demonstrates significant improvements, several research directions are worth further exploration.
- Integration of External Factors: Future efforts will incorporate quantifiable external drivers, such as business growth metrics (e.g., quarterly revenue, user acquisition rates), and seasonal indices (e.g., holiday-induced workload fluctuations) into the framework. This will extend DimAug-TimesFM to multivariate forecasting, enhancing its ability to model demand dynamics under real-world constraints.
- Multi-Resource Forecasting: Although the framework is theoretically extensible to the concurrent prediction of heterogeneous resources (e.g., CPU, memory, storage), empirical validation is required to assess its capability in capturing cross-resource interdependencies. Planned work includes constructing multi-resource time series datasets and introducing composite metrics like Joint RMSE (J-RMSE) to evaluate prediction coherence.
- Generalizability Enhancement: Applying dimension augmentation to state-of-the-art large time series models (e.g., Chronos, Timer) and validation on diverse few-shot datasets will further validate the robustness of the framework.
These extensions aim to strengthen the framework’s adaptability to more real-world application scenarios and advance scalable and sustainable FinOps practices.
Author Contributions
Methodology, X.Y., Q.Z. and X.Z.; validation, X.Y., Q.Z. and M.L.; formal analysis, X.Y.; investigation, Z.H.; data curation, J.Z.; writing—original draft preparation, X.Y. and X.Z.; writing—review and editing, X.Y.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Storment, J.R.; Fuller, M. Cloud FinOps; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2023. [Google Scholar]
- Ambati, P.; Bashir, N.; Irwin, D.; Hajiesmaili, M.; Shenoy, P. Hedge Your Bets: Optimizing Long-Term Cloud Costs by Mixing VM Purchasing Options. In Proceedings of the 2020 IEEE International Conference on Cloud Engineering (IC2E), Sydney, NSW, Australia, 21–24 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 105–115. [Google Scholar]
- Tay, C.K.L.; Shim, K.J. A Cloud-Based Data Gathering and Processing System for Intelligent Demand Forecasting. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 5451–5453. [Google Scholar]
- Gao, J.; Wang, H.; Shen, H. Machine Learning-Based Workload Prediction in Cloud Computing. In Proceedings of the 2020 29th International Conference on Computer Communications and Networks (ICCCN), Honolulu, HI, USA, 3–6 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–9. [Google Scholar]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-Stationary Transformers: Exploring the Stationarity in Time Series Forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 9881–9893. [Google Scholar]
- Dai, T.; Wu, B.; Liu, P.; Li, N.; Yuerong, X.; Xia, S.; Zhu, Z. DDN: Dual-Domain Dynamic Normalization for Non-Stationary Time Series Forecasting. Adv. Neural Inf. Process. Syst. 2024, 37, 108490–108517. [Google Scholar]
- Iwata, T.; Kumagai, A. Few-Shot Learning for Time-Series Forecasting. arXiv 2020, arXiv:2009.14379. [Google Scholar]
- Ekambaram, V.; Jati, A.; Nguyen, N.H.; Dayama, P.; Reddy, C.; Gifford, W.M.; Kalagnanam, J. Tiny Time Mixers (TTMs): Fast Pre-Trained Models for Enhanced Zero/Few-Shot Forecasting of Multivariate Time Series. Adv. Neural Inf. Process. Syst. 2024, 37, 74147–74181. [Google Scholar]
- Tsoumplekas, G.; Athanasiadis, C.; Doukas, D.I.; Chrysopoulos, A.; Mitkas, P. Few-Shot Load Forecasting Under Data Scarcity in Smart Grids: A Meta-Learning Approach. Energies 2025, 18, 742. [Google Scholar] [CrossRef]
- Chen, M.; Xu, Z.; Zeng, A.; Xu, Q. Fraug: Frequency Domain Augmentation for Time Series Forecasting. arXiv 2023, arXiv:2302.09292. [Google Scholar]
- Wirsing, K. Time Frequency Analysis of Wavelet and Fourier Transform. In Wavelet Theory; BoD—Books on Demand: Norderstedt, Germany, 2020; pp. 3–20. [Google Scholar]
- Deshcherevskii, A.V.; Sidorin, A.Y. Iterative Algorithm for Time Series Decomposition into Trend and Seasonality. Izv. Atmos. Ocean. Phys. 2021, 57, 813–836. [Google Scholar] [CrossRef]
- Niu, Z.; Yu, K.; Wu, X. LSTM-Based VAE-GAN for Time-Series Anomaly Detection. Sensors 2020, 20, 3738. [Google Scholar] [CrossRef] [PubMed]
- Mumuni, A.; Mumuni, F. Data Augmentation with Automated Machine Learning. arXiv 2024, arXiv:2403.08352. [Google Scholar]
- Zhang, C.; Cui, J.; Yang, B. Learning Optimal Data Augmentation Policies via Bayesian Optimization. arXiv 2019, arXiv:1905.02610. [Google Scholar]
- Zhu, Q.; Han, J.; Chai, K.; Zhao, C. Time Series Analysis Based on Informer Algorithms. Symmetry 2023, 15, 951. [Google Scholar] [CrossRef]
- Taud, H.; Mas, J.F. Multilayer Perceptron (MLP). In Geomatic Approaches for Modeling Land Change Scenarios; Springer: Berlin/Heidelberg, Germany, 2018; pp. 451–455. [Google Scholar]
- Sherstinsky, A. Fundamentals of Recurrent Neural Networks (RNN) and LSTM. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Y.; Liu, X.; Qiu, X. A Survey of Transformers. AI Open 2022, 3, 111–132. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. Fedformer: Frequency Enhanced Decomposed Transformer. In Proceedings of the International Conference on Machine Learning, PMLR. Baltimore, MD, USA, 17–23 July 2022; pp. 27268–27286. [Google Scholar]
- Wu, S.; Fei, H.; Qu, L.; Ji, W.; Chua, T. Next-GPT: Any-to-Any Multimodal LLM. arXiv 2023, arXiv:2309.05519. [Google Scholar]
- Gruver, N.; Finzi, M.; Qiu, S.; Wilson, A.G. Large Language Models Are Zero-Shot Time Series Forecasters. Adv. Neural Inf. Process. Syst. 2023, 36, 19622–19635. [Google Scholar]
- Zhou, T.; Niu, P.; Wang, X.; Sun, L.; Jin, R. One Fits All: Power General Time Series Analysis by Pretrained LM. Adv. Neural Inf. Process. Syst. 2023, 36, 43322–43355. [Google Scholar]
- Das, A.; Kong, W.; Sen, R.; Zhou, Y. A Decoder-Only Foundation Model for Time-Series Forecasting. arXiv 2023, arXiv:2310.10688. [Google Scholar]
- Jin, M.; Wang, S.; Ma, L.; Chu, Z.; Zhang, J.Y.; Shi, X.; Chen, P.; Liang, Y.; Li, Y.; Pan, S.; et al. Time-LLM: Time Series Forecasting by Reprogramming Large Language Models. arXiv 2023, arXiv:2310.01728. [Google Scholar]
- Ansari, A.F.; Stella, L.; Turkmen, A.C.; Zhang, X.; Mercado, P.; Shen, H.; Wang, B. Chronos: Learning the Language of Time Series. Trans. Mach. Learn. Res. 2023. [Google Scholar]
- Liang, Y.; Wen, H.; Nie, Y.; Jiang, Y.; Jin, M.; Song, D.; Pan, S.; Wen, Q. Foundation Models for Time Series Analysis: A Tutorial and Survey. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 6555–6565. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).