Fault Diagnosis of Wind Turbine Blades Based on One-Dimensional Convolutional Neural Network-Bidirectional Long Short-Term Memory-Adaptive Boosting and Multi-Source Data Fusion
Abstract
1. Introduction
2. Designed 1D CNN-BiLSTM-AdaBoost Model
2.1. Model Overview
2.2. Detailed Model Description
2.2.1. Design of the 1D CNN
2.2.2. Data Fusion
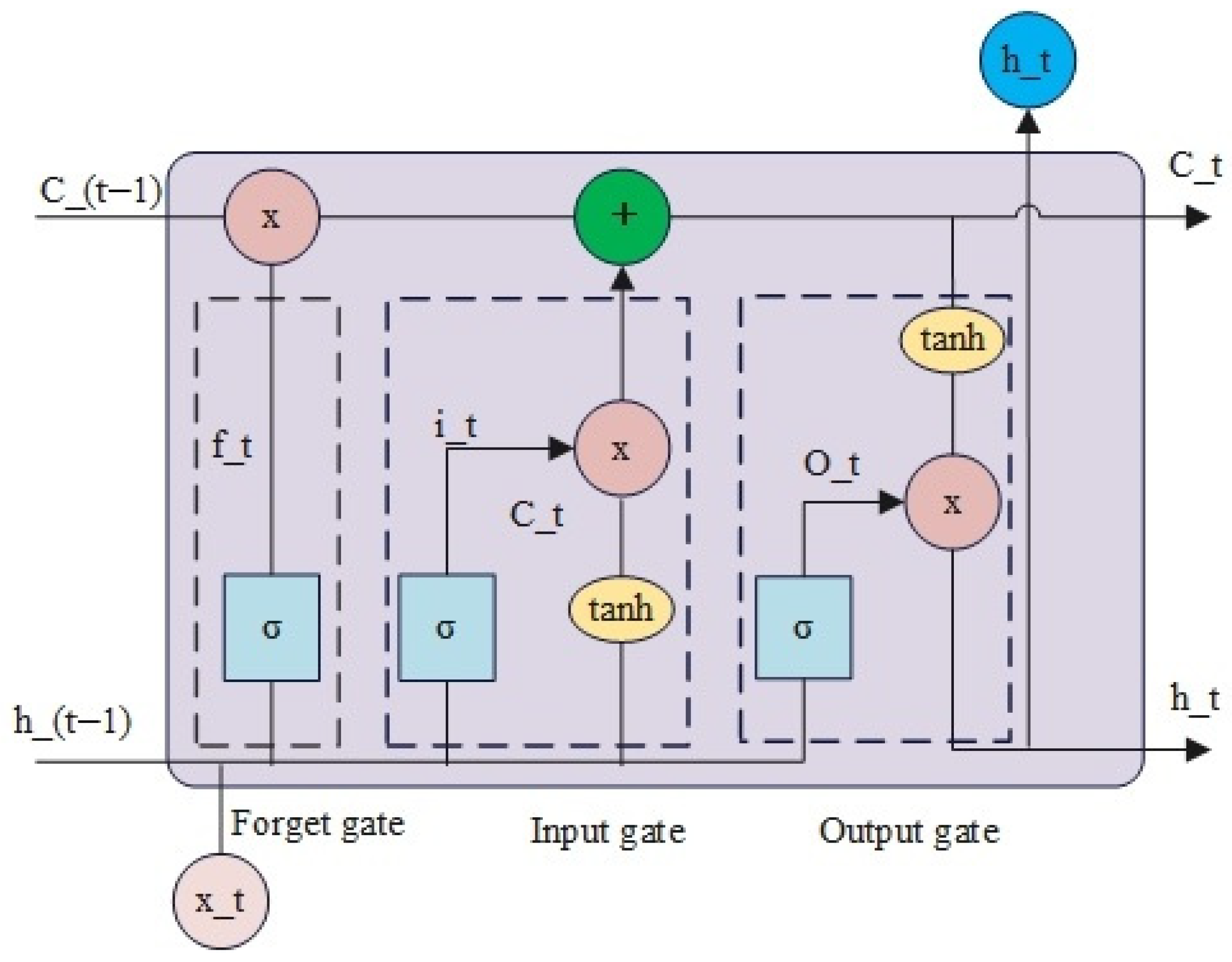
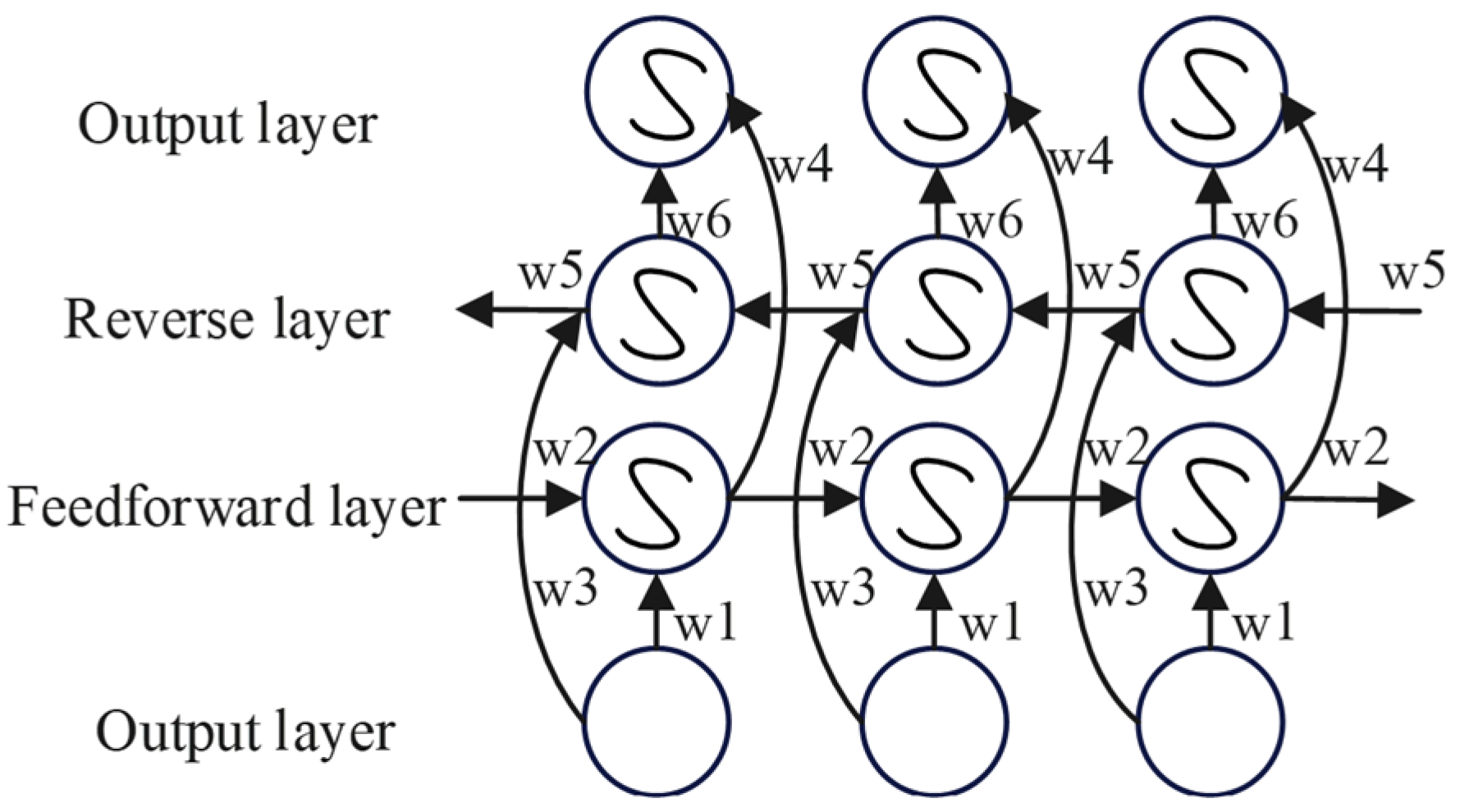
2.2.3. BiLSTM Architecture
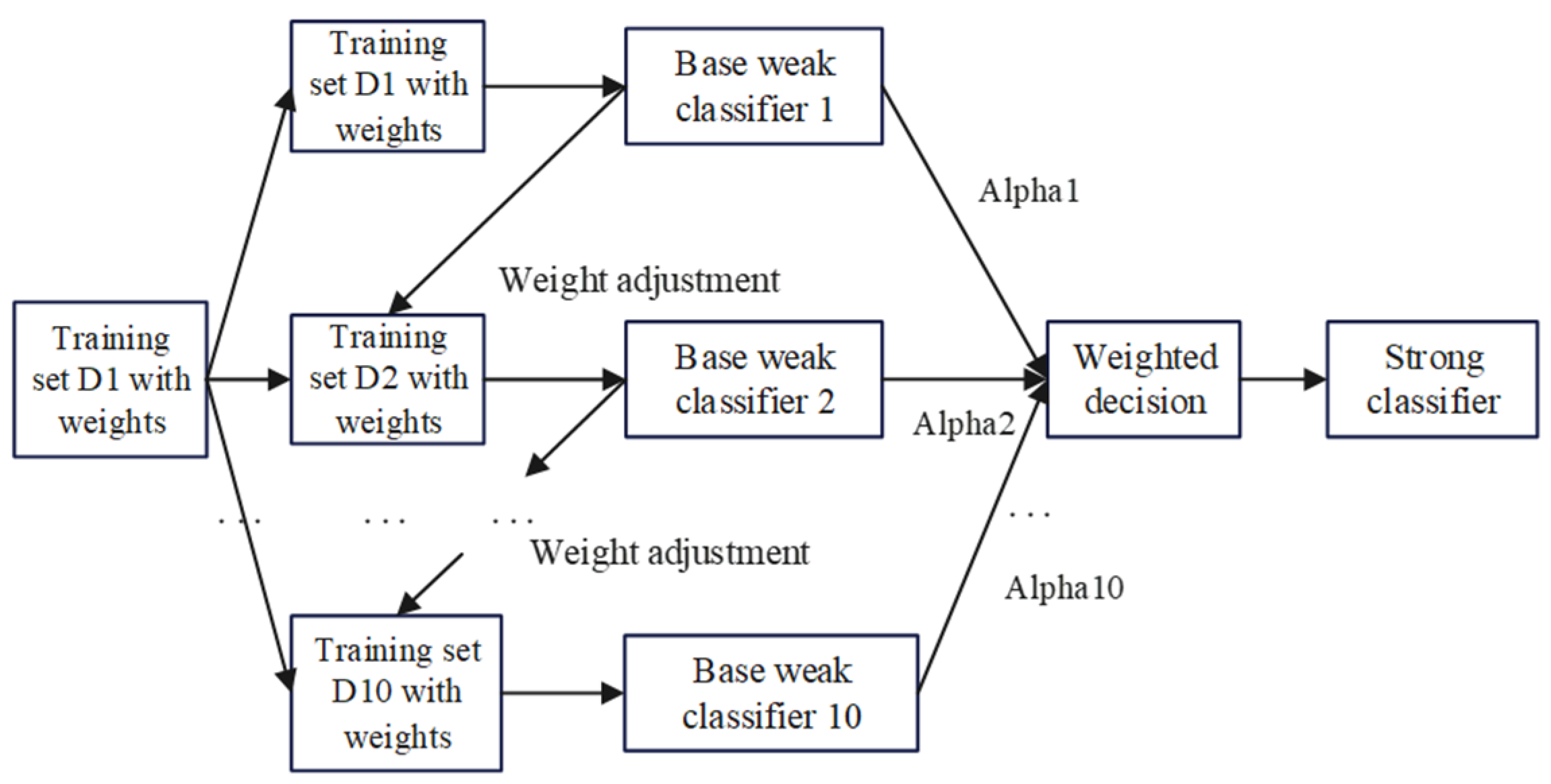
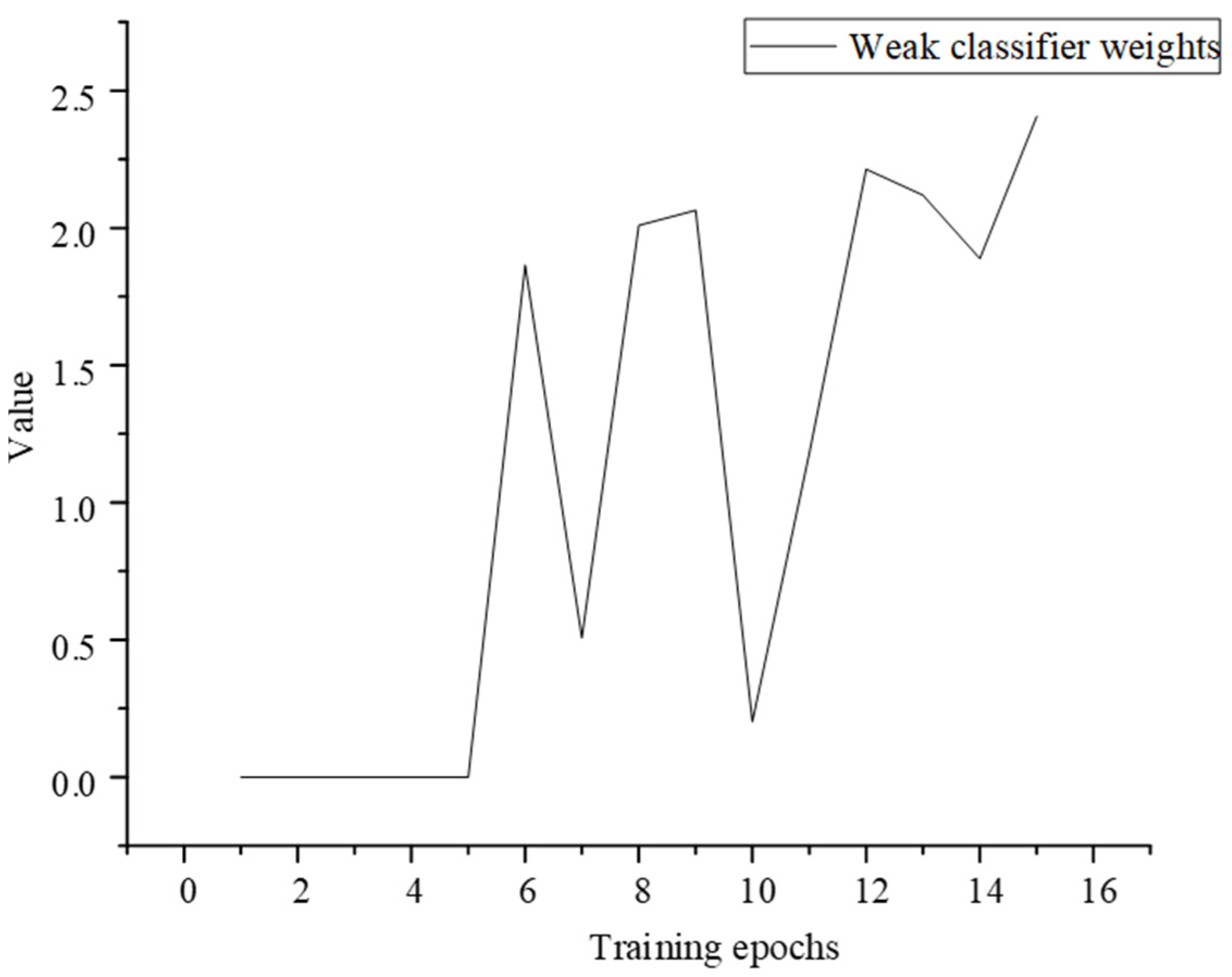
2.2.4. AdaBoost Network Architecture
| Algorithm 1: AdaBoost-1DCNN-BiLSTM | |
| Input: Training dataset , weak classifier 1DCNN-BiLSTM, number of iterations T | |
| Output: Final strong classifier f(x) | |
| 1. Initialize the weight distribution | |
| Assign an initial weight to each training sample according to Equation (6). | |
| 2. Iterative training of weak classifiers | |
| For t = 1, 2, …, T, perform the following steps: | |
① Train the weak classifier and compute the error rate
| |
| ② Compute the weight of the weak classifier | |
| Determine the weight coefficient of in the final ensemble model using Equation (10). | |
| ③ Update the weight distribution of training samples | |
| Update the weight of each sample according to Equation (11) to guide the next iteration. | |
| 3. Construct the strong classifier | |
| ① Combine all weak classifiers and their corresponding weights using Equation (12); | |
| ② Obtain the final strong classifier f(x) through Equation (13). | |
3. Wind Turbine Blade Fault Dataset and Fault Diagnosis Model Training
3.1. Data Collection
3.2. Model Fault Training
3.3. Model Hyperparameter Setting
4. Model Verification and Comparison Based on 1DCNN-BiLSTM-AdaBoost
4.1. Evaluation Indicators
4.1.1. Confusion Matrix
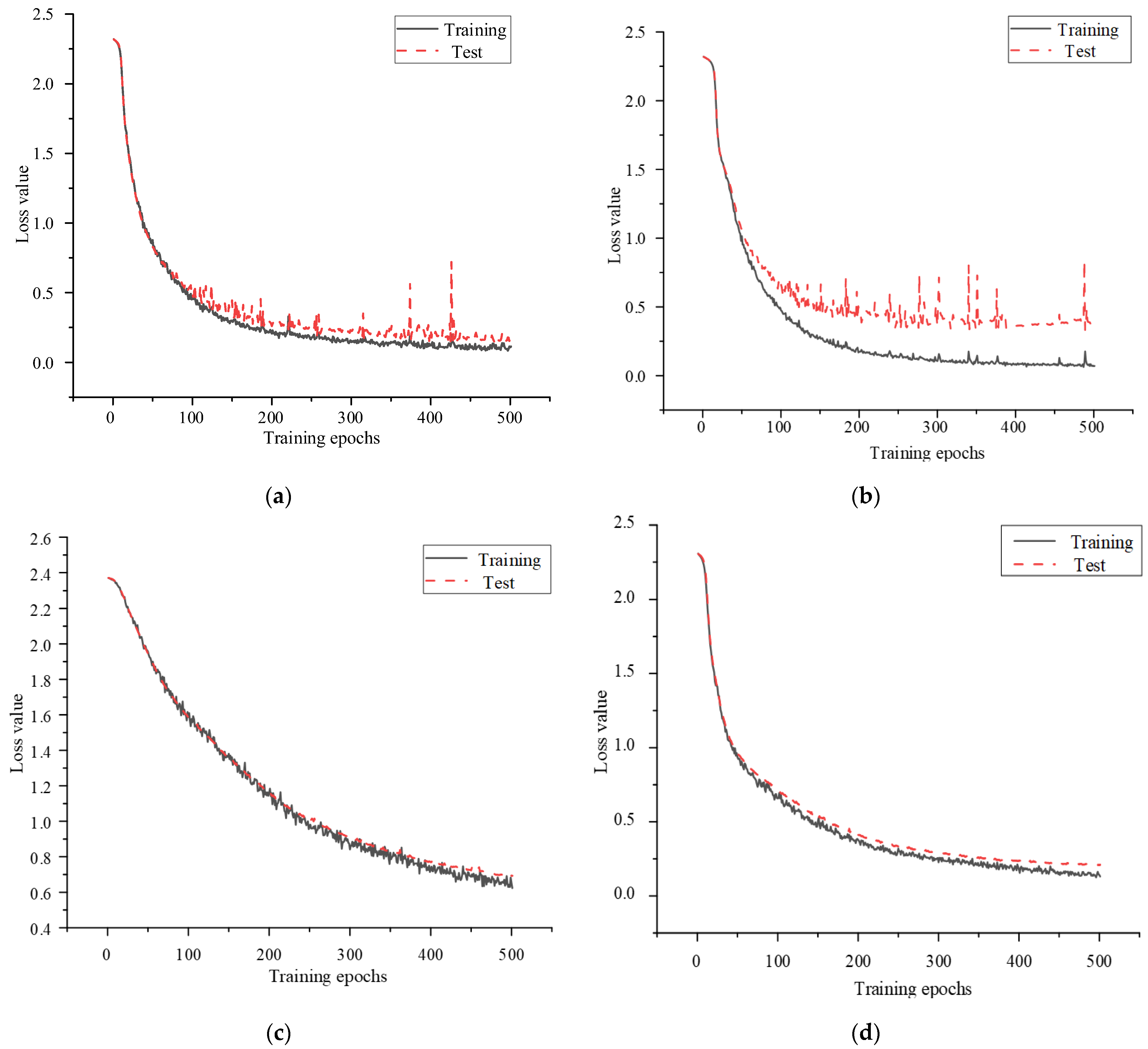
4.1.2. Loss Function
4.1.3. Indicators
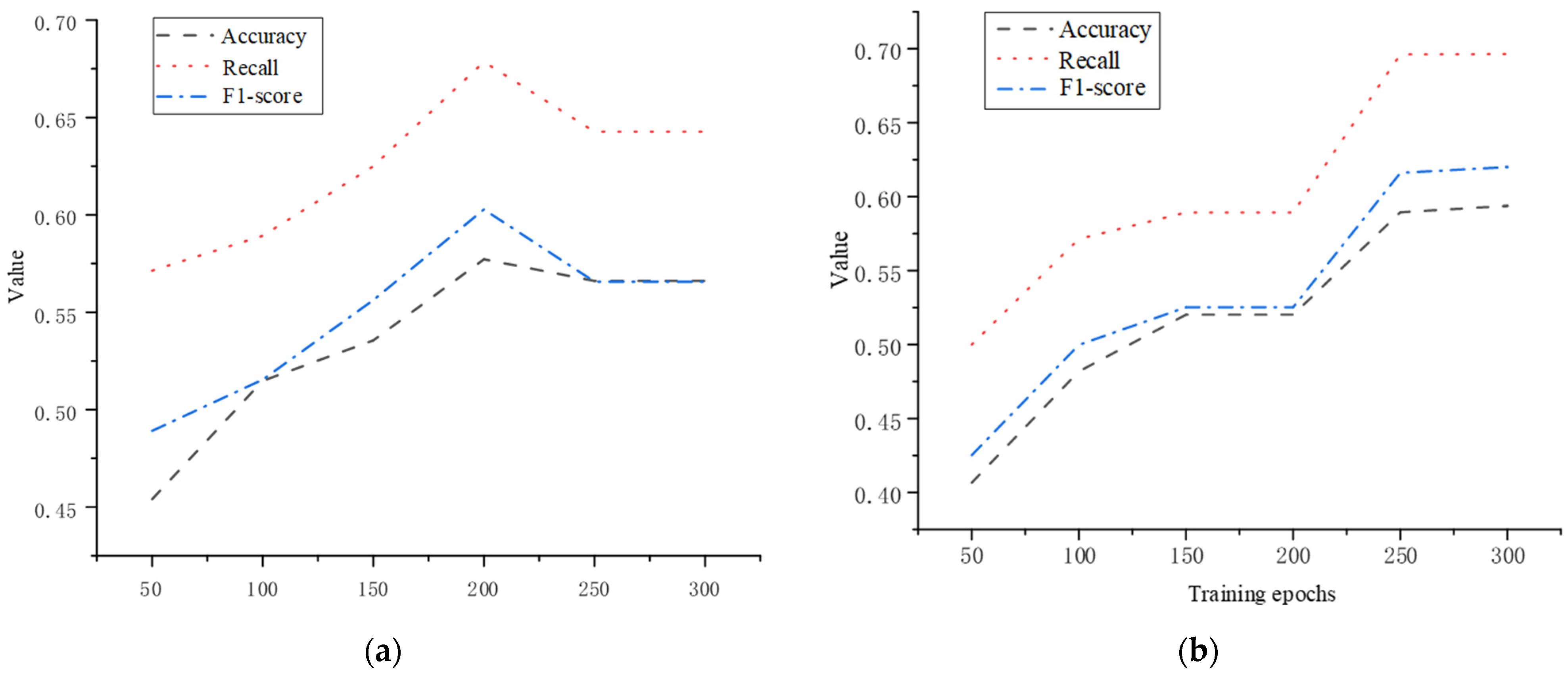
4.2. Model Verification Based on 1DCNN-BiLSTM-AdaBoost
4.3. Algorithm Comparison and Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, D.; Shao, D.; Cui, L. CTNet: A data-driven time-frequency technique for wind turbines fault diagnosis under time-varying speeds. ISA Trans. 2024, 154, 335–351. [Google Scholar]
- Jian, T.; Cao, J.; Liu, W.; Xu, G.; Zhong, J. A novel wind turbine fault diagnosis method based on compressive sensing and lightweight squeezenet model. Expert Syst. Appl. 2025, 260, 125440. [Google Scholar]
- Shi, P.; Jia, L.; Yi, S.; Han, D. Wind turbines fault diagnosis method under variable working conditions based on AMVMD and deep discrimination transfer learning network. Meas. Sci. Technol. 2024, 35, 046120. [Google Scholar]
- Zhao, K.; Liu, Z.; Li, J.; Zhao, B.; Jia, Z.; Shao, H. Self-paced decentralized federated transfer framework for rotating machinery fault diagnosis with multiple domains. Mech. Syst. Signal Process. 2024, 211, 111258. [Google Scholar]
- Ren, X.; Wang, S.; Zhao, W.; Kong, X.; Fan, M.; Shao, H.; Zhao, K. Universal federated domain adaptation for gearbox fault diagnosis: A robust framework for credible pseudo-label generation. Adv. Eng. Inform. 2025, 65, 103233. [Google Scholar]
- Liu, Y.; Jiang, H.; Yao, R.; Zeng, T. Counterfactual-augmented few-shot contrastive learning for machinery intelligent fault diagnosis with limited samples. Mech. Syst. Signal Process. 2024, 216, 111507. [Google Scholar]
- Chao, Q.; Gao, H.; Tao, J.; Liu, C.; Wang, Y.; Zhou, J. Fault diagnosis of axial piston pumps with multi-sensor data and convolutional neural network. Front. Mech. Eng. 2022, 17, 36. [Google Scholar] [CrossRef]
- Guo, Y.; Mao, J.; Zhao, M. Rolling bearing fault diagnosis method based on attention CNN and BiLSTM network. Neural Process. Lett. 2023, 55, 3377–3410. [Google Scholar]
- Fu, G.; Wei, Q.; Yang, Y.; Li, C. Bearing fault diagnosis based on CNN-BiLSTM and residual module. Meas. Sci. Technol. 2023, 34, 125050. [Google Scholar]
- Hong, D.; Kim, B. 1D convolutional neural network-based adaptive algorithm structure with system fault diagnosis and signal feature extraction for noise and vibration enhancement in mechanical systems. Mech. Syst. Signal Process. 2023, 197, 110395. [Google Scholar]
- Wang, Q.; Cao, D.; Zhang, S.; Zhou, Y.; Yao, L. The Cable Fault Diagnosis for XLPE Cable Based on 1DCNNs-BiLSTM Network. J. Control Sci. Eng. 2023, 2023, 1068078. [Google Scholar]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar]
- Eren, L.; Ince, T.; Kiranyaz, S. A generic intelligent bearing fault diagnosis system using compact adaptive 1D CNN classifier. J. Signal Process. Syst. 2019, 91, 179–189. [Google Scholar]
- Chen, C.C.; Liu, Z.; Yang, G.; Wu, C.C.; Ye, Q. An improved fault diagnosis using 1d-convolutional neural network model. Electronics 2020, 10, 59. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, Q.; Tang, X.; Zhao, S.; Lu, X. A novel fault diagnosis method based on CNN and LSTM and its application in fault diagnosis for complex systems. Artif. Intell. Rev. 2022, 55, 1289–1315. [Google Scholar]
- Shi, J.; Peng, D.; Peng, Z.; Zhang, Z.; Goebel, K.; Wu, D. Planetary gearbox fault diagnosis using bidirectional-convolutional LSTM networks. Mech. Syst. Signal Process. 2022, 162, 107996. [Google Scholar]
- Zhao, K.; Jia, F.; Shao, H. Unbalanced fault diagnosis of rolling bearings using transfer adaptive boosting with squeeze-and-excitation attention convolutional neural network. Meas. Sci. Technol. 2023, 34, 044006. [Google Scholar]
- Guo, J.; Song, X.; Liu, C.; Zhang, Y.; Guo, S.; Wu, J.; Cai, C.; Li, Q. Research on the Icing Diagnosis of Wind Turbine Blades Based on FS-XGBoost-EWMA. Energy Eng. 2024, 121, 1739–1758. [Google Scholar]
- An, G.; Jiang, Z.; Cao, X.; Liang, Y.; Zhao, Y.; Li, Z.; Dong, W.; Sun, H. Short-term wind power prediction based on particle swarm optimization-extreme learning machine model combined with AdaBoost algorithm. IEEE Access 2021, 9, 94040–94052. [Google Scholar]
- Singh, S.K.; Khawale, R.P.; Hazarika, S.; Bhatt, A.; Gainey, B.; Lawler, B.; Rai, R. Hybrid physics-infused 1D-CNN based deep learning framework for diesel engine fault diagnostics. Neural Comput. Appl. 2024, 36, 17511–17539. [Google Scholar]
- He, D.; Lao, Z.; Jin, Z.; He, C.; Shan, S.; Miao, J. Train bearing fault diagnosis based on multi-sensor data fusion and dual-scale residual network. Nonlinear Dyn. 2023, 111, 14901–14924. [Google Scholar]
- Zhang, Z.; Jiao, Z.; Li, Y.; Shao, M.; Dai, X. Intelligent fault diagnosis of bearings driven by double-level data fusion based on multichannel sample fusion and feature fusion under time-varying speed conditions. Reliab. Eng. Syst. Saf. 2024, 251, 110362. [Google Scholar]
- Wang, D.; Li, Y.; Song, Y.; Zhuang, Y. Bearing Fault Diagnosis Method based on Multiple-level Feature Tensor Fusion. IEEE Sens. J. 2024, 24, 23108–23116. [Google Scholar] [CrossRef]
- Xu, X.; Song, D.; Wang, Z.; Zheng, Z. A Novel Collaborative Bearing Fault Diagnosis Method Based on Multisignal Decision-level Dynamically Enhanced Fusion. IEEE Sens. J. 2024, 24, 34766–34776. [Google Scholar] [CrossRef]





| Fusion Type | Advantages | Disadvantages |
|---|---|---|
| Data-level fusion | Provides rich information with high accuracy | Requires handling different data formats and precision |
| Feature-level fusion | Combines features from different sensors, enhancing robustness and efficiency | Effective feature extraction and selection can be complex |
| Decision-level fusion | Allows independent decision-making by each sensor, offering flexibility | More complex; decision-making at the sensor level is challenging |
| Label | Description |
|---|---|
| R | Healthy state |
| C | Mass block added (3 × 44 g) to simulate icing fault |
| H | Crack = 10 cm, Crack = 10 cm, Crack = 5 cm |
| L | Crack = 15 cm, Crack = 15 cm, Crack = 15 cm |
| Hyperparameter | Value |
|---|---|
| Learning rate | 0.00002 |
| Batch_size | 8 |
| Number of training rounds | 500 |
| Number of convolution kernels | 1408 |
| Number of convolution kernels | 32, 3, 5, 7 |
| Number of BiLSTM neurons | 64 |
| Number of BiLSTM layers | 2 |
| Activation function | ReLU |
| Optimizer | AdamW |
| Drop_out | 0.5 |
| Loss function | Cross entropy |
| Number of weak classifiers | 10 |
| Real Situation | Prediction Result | |
|---|---|---|
| Prediction Value = True Class | Prediction Value = False Class | |
| True value = true class | TP (true class) | FN (false negative class) |
| True value = false class | FP (false positive class) | TN (true negative class) |
| Model | Metric 1 | Metric 2 | Metric 3 | Metric 4 |
|---|---|---|---|---|
| LSTM | 0.6427 | 0.5661 | 0.6429 | 0.5673 |
| BiLSTM | 0.6964 | 0.5938 | 0.6967 | 0.6130 |
| 1D CNN | 0.7400 | 0.6250 | 0.7400 | 0.6667 |
| 1D CNN-BiLSTM (Single-Channel) | 0.7800 | 0.6450 | 0.7791 | 0.6863 |
| 1D CNN-BiLSTM (Dual-Channel) | 0.9375 | 0.9500 | 0.9377 | 0.9395 |
| Proposed Method (This Paper) | 0.9688 | 0.9722 | 0.9692 | 0.9686 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, K.; Wang, Y.; Yang, Y. Fault Diagnosis of Wind Turbine Blades Based on One-Dimensional Convolutional Neural Network-Bidirectional Long Short-Term Memory-Adaptive Boosting and Multi-Source Data Fusion. Appl. Sci. 2025, 15, 3440. https://doi.org/10.3390/app15073440
Ma K, Wang Y, Yang Y. Fault Diagnosis of Wind Turbine Blades Based on One-Dimensional Convolutional Neural Network-Bidirectional Long Short-Term Memory-Adaptive Boosting and Multi-Source Data Fusion. Applied Sciences. 2025; 15(7):3440. https://doi.org/10.3390/app15073440
Chicago/Turabian StyleMa, Kangqiao, Yongqian Wang, and Yu Yang. 2025. "Fault Diagnosis of Wind Turbine Blades Based on One-Dimensional Convolutional Neural Network-Bidirectional Long Short-Term Memory-Adaptive Boosting and Multi-Source Data Fusion" Applied Sciences 15, no. 7: 3440. https://doi.org/10.3390/app15073440
APA StyleMa, K., Wang, Y., & Yang, Y. (2025). Fault Diagnosis of Wind Turbine Blades Based on One-Dimensional Convolutional Neural Network-Bidirectional Long Short-Term Memory-Adaptive Boosting and Multi-Source Data Fusion. Applied Sciences, 15(7), 3440. https://doi.org/10.3390/app15073440





