An Over-Deterministic Method for Mode III SIF Calculation Using Full-Field Experimental Displacement Fields
Abstract
1. Introduction
2. Literature Review
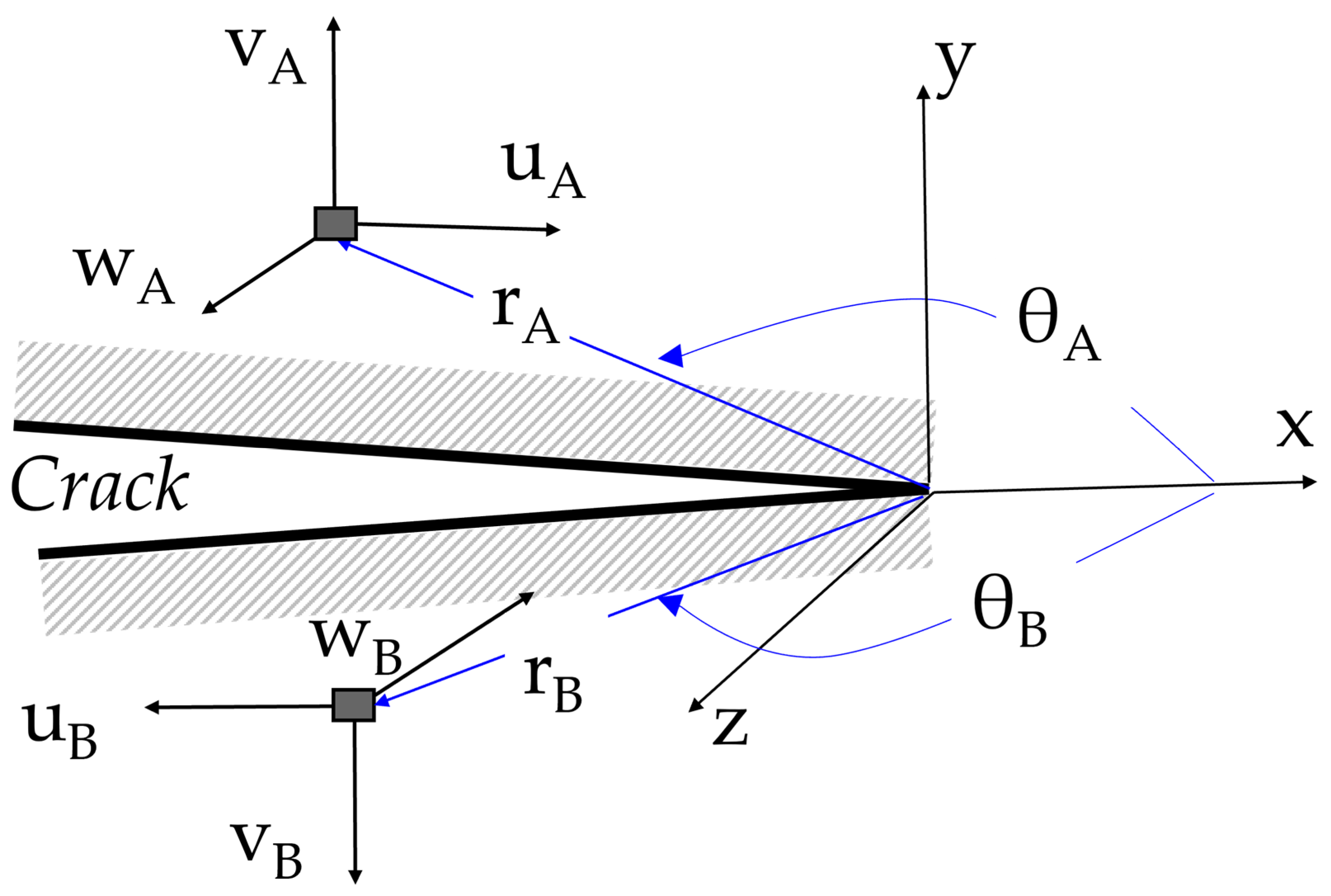
2.1. Theoretical Background
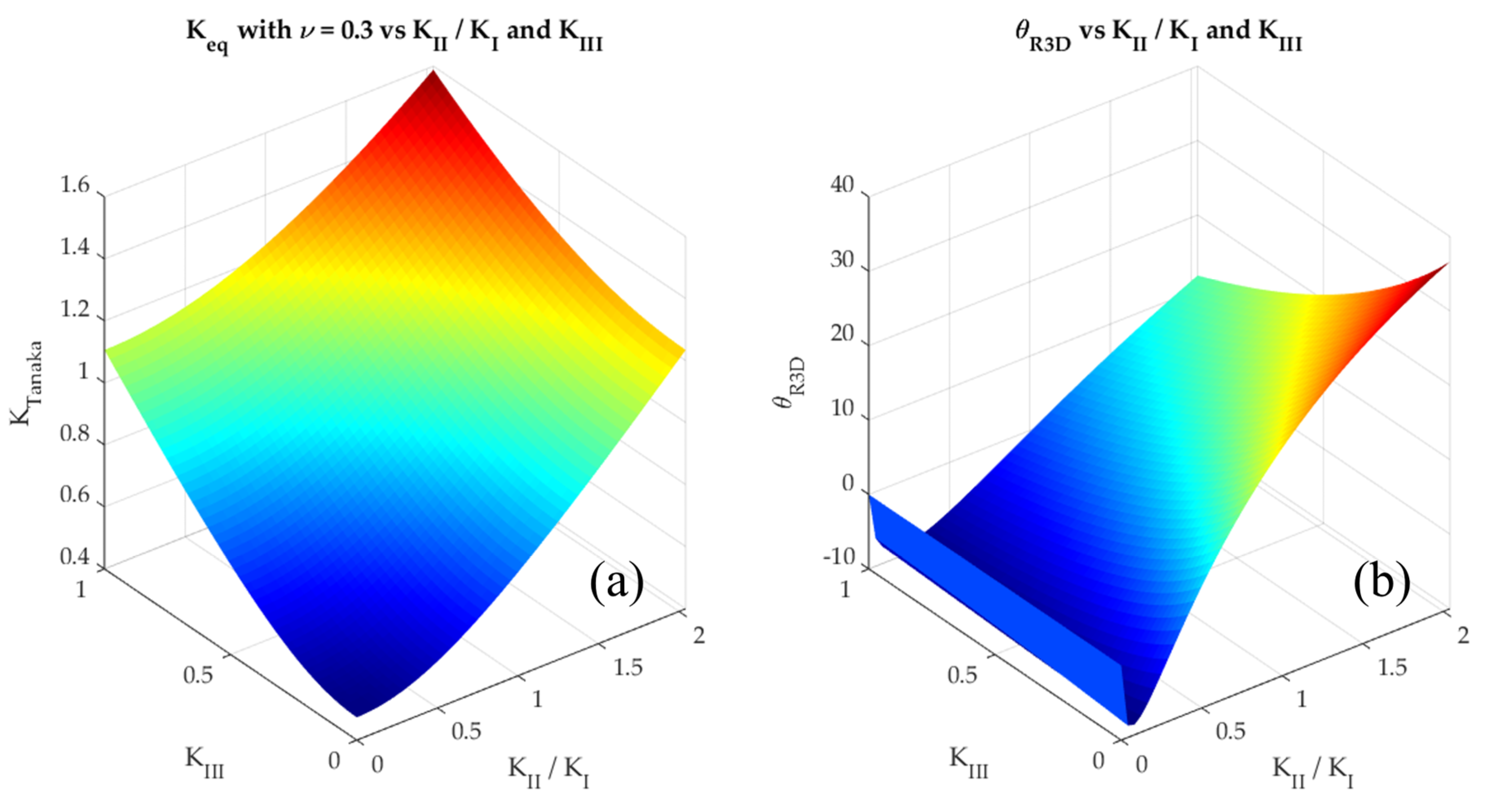
2.2. Plausible Effects of Ignoring KIII on CP and Keq
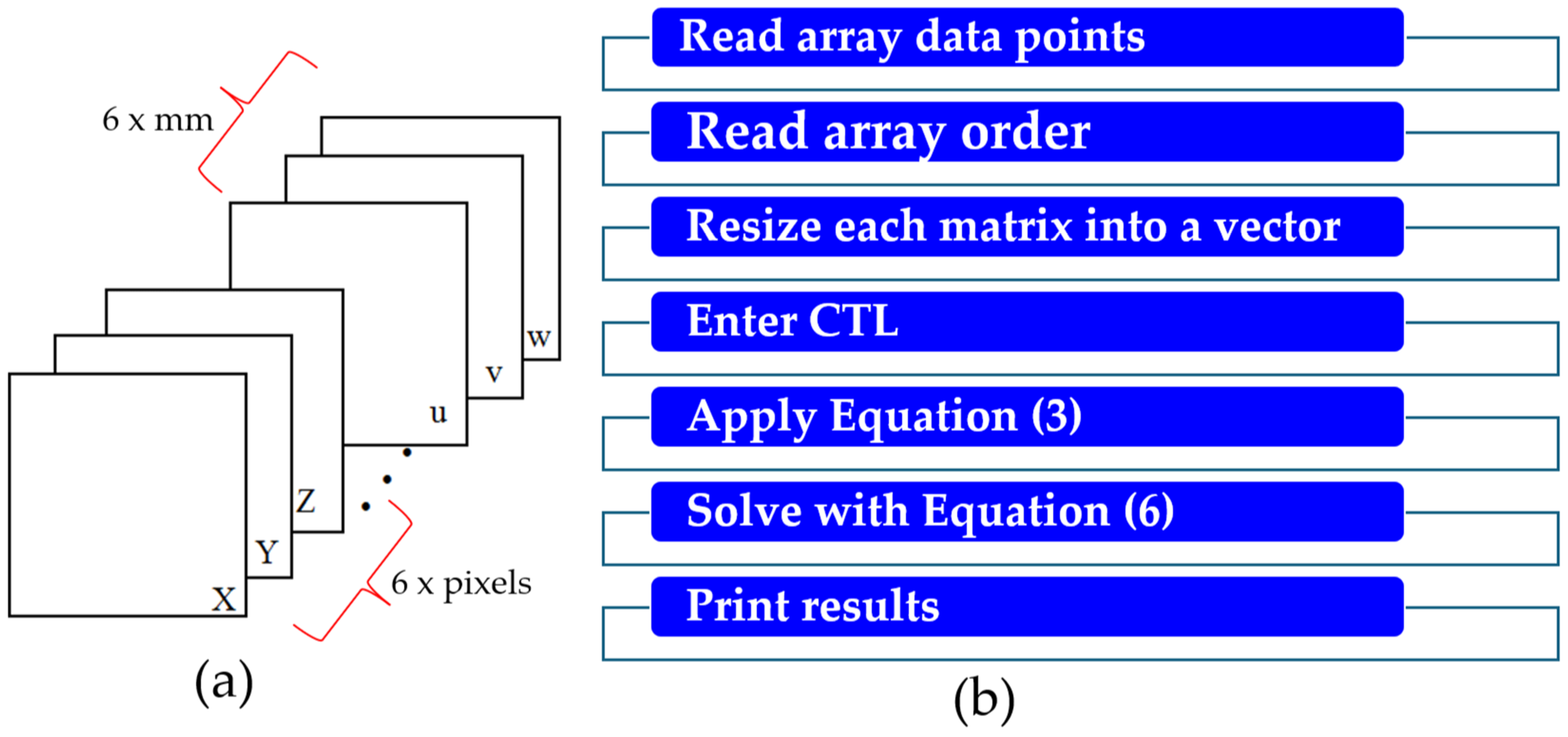
3. Proposed Scheme for Mode III Estimation
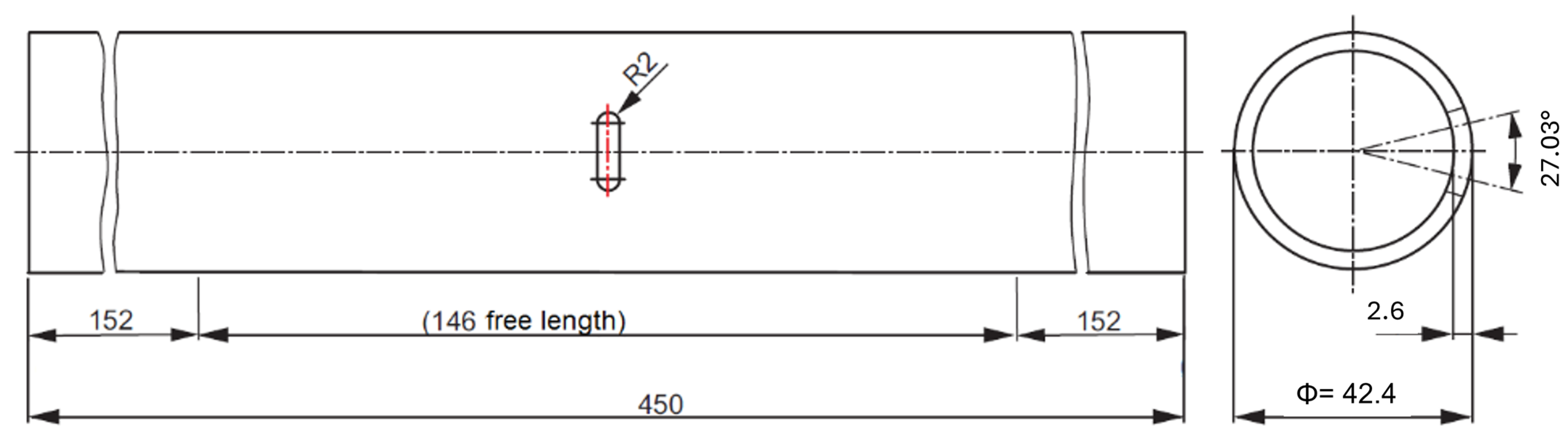
4. Materials and Methods
5. Results and Discussion
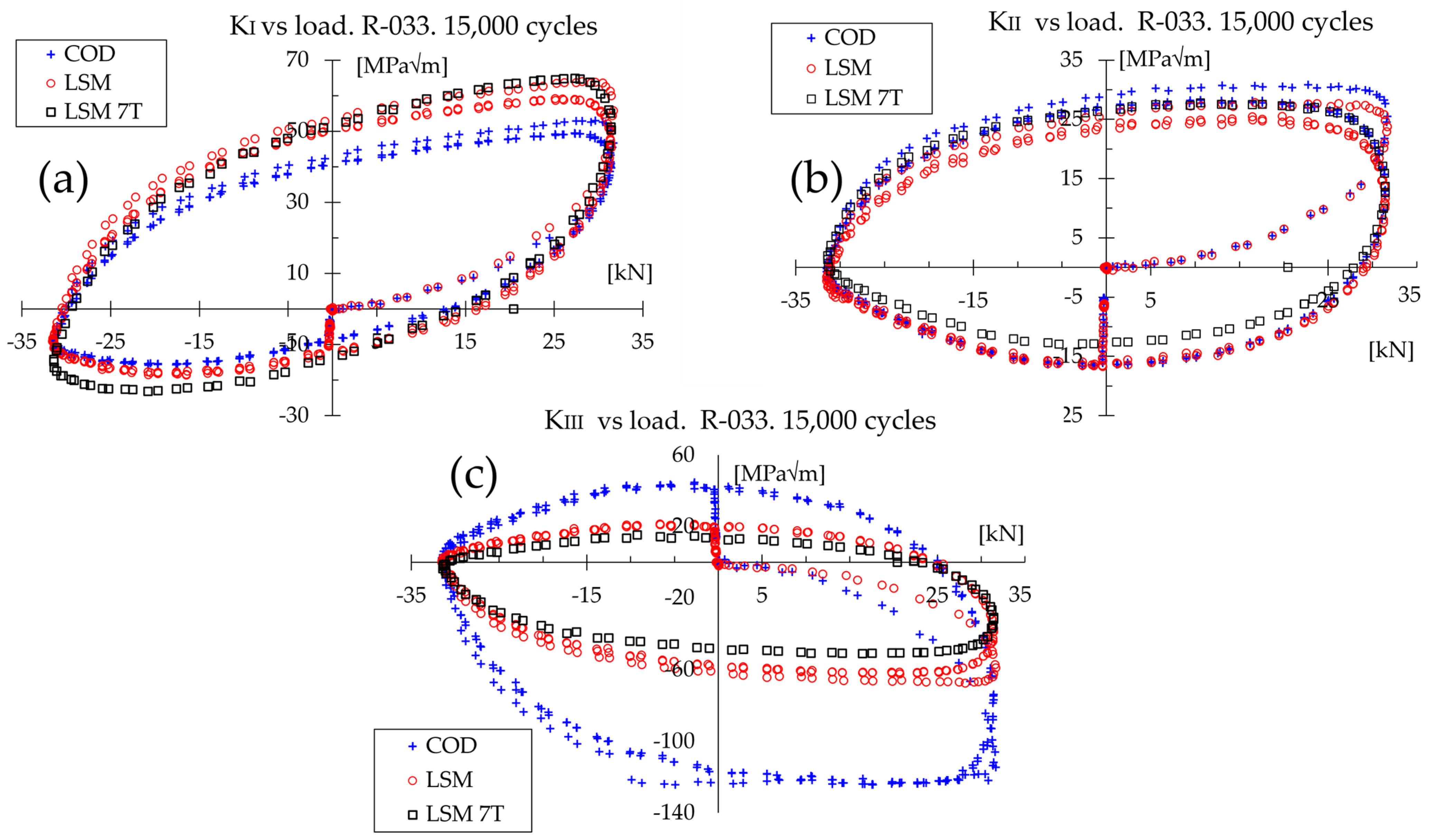
5.1. Results for Non-Proportional (45° Out-of-Phase Tension and Torsion) Loading
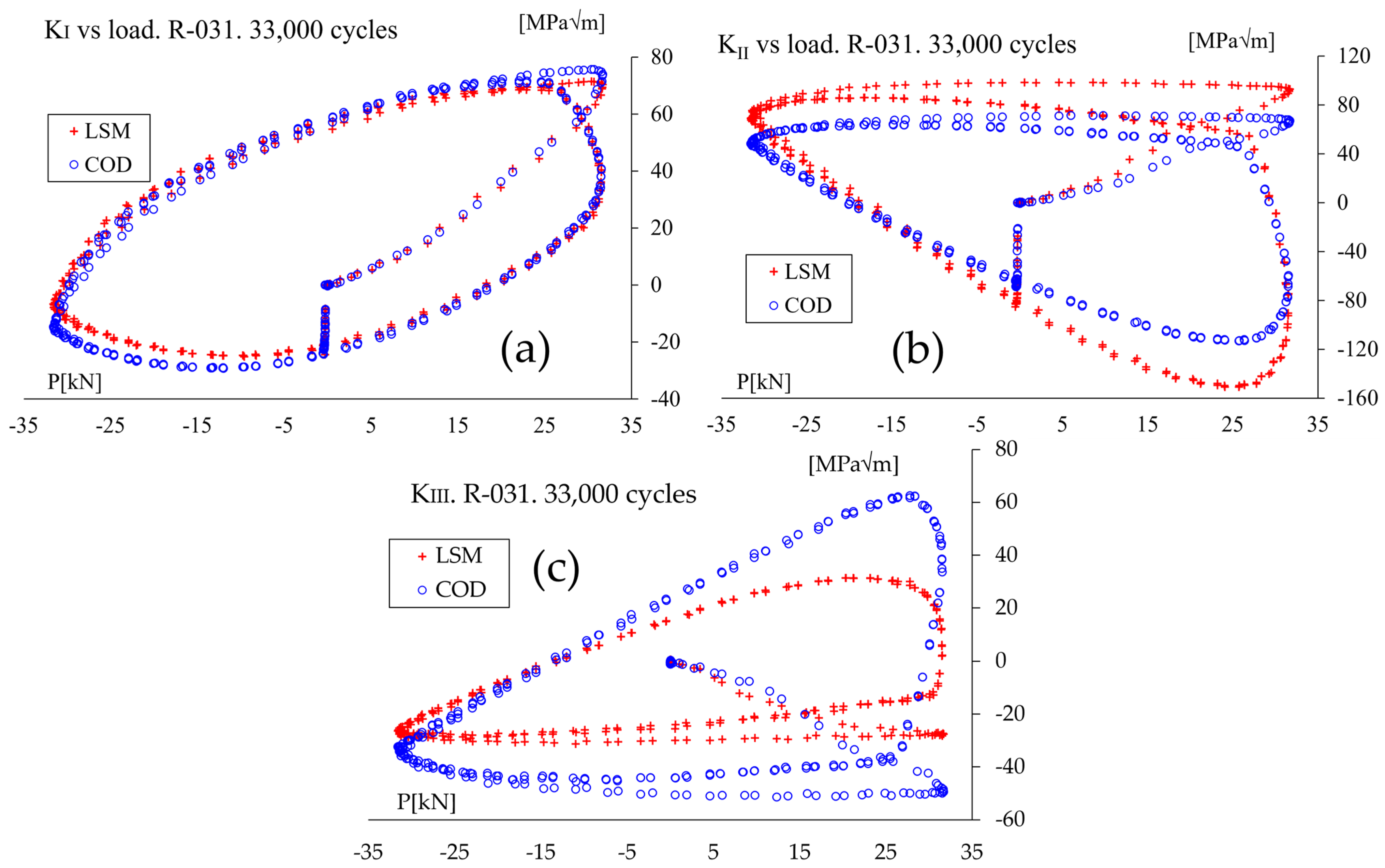
5.2. Results for Non-Proportional (90° Out-of-Phase Tension and Torsion) Loading
5.3. Results for Proportional (In-Phase Tension and Torsion) Loading
5.4. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| COD | Crack Opening Displacement |
| DIC | Digital Image Correlation |
| E | Young’s modulus |
| G | Shear modulus |
| K, SIF | Stress Intensity Factor |
| RL | Axial load reversal ratio |
| RT | Torsional load reversal ratio |
| u | Displacement in the X direction |
| v | Displacement in the Y direction |
| w | Displacement in the Z direction |
| X | X direction, parallel to the crack |
| Y | Y direction, perpendicular to the crack |
| Z | Z direction, out of plane displacement |
| ν | Poisson modulus |
| θ | Crack growth angular direction |
| θR3D | Crack propagation angle according to Richard model |
| r | radius |
| k | Kolosov’s constant |
| Ti | rigid body displacement in the i direction |
| Ri | rigid body rotation around the i axis |
| [h] | concatenated vector of measured displacements |
| [Δ] | vector of unknown coefficients in Williams’ series |
| [b] | form function in Williams’ series |
References
- Kotousov, A.; Lazzarin, P.; Berto, F.; Pook, L.P. Three-Dimensional Stress States at Crack Tip Induced by Shear and Anti-Plane Loading. Eng. Fract. Mech. 2013, 108, 65–74. [Google Scholar] [CrossRef]
- Fremy, F.; Pommier, S.; Poncelet, M.; Raka, B.; Galenne, E.; Courtin, S.; Roux, J.C. Le Load Path Effect on Fatigue Crack Propagation in I + II + III Mixed Mode Conditions—Part 1: Experimental Investigations. Int. J. Fatigue 2014, 62, 104–112. [Google Scholar] [CrossRef]
- Schöllmann, M.; Richard, H.A.; Kullmer, G.; Fulland, M. A New Criterion for the Prediction of Crack Development in Multiaxially Loaded Structures. Int. J. Fract. 2002, 117, 129–141. [Google Scholar] [CrossRef]
- Bonniot, T.; Doquet, V.; Mai, S.H. Mixed Mode II and III Fatigue Crack Growth in a Rail Steel. Int. J. Fatigue 2018, 115, 42–52. [Google Scholar] [CrossRef]
- Ju, Y.; Zhang, Y.; Wang, K.; Zhou, H. 3D-Generalized Maximum Tangential Strain Criterion for Predicting Mixed-Mode I/II/III Fracture Initiation of Brittle Materials Considering T-Stress Effects. Theor. Appl. Fract. Mech. 2024, 131, 104382. [Google Scholar] [CrossRef]
- Miao, X.; Zhang, J.; Hong, H.; Peng, J.; Zhou, B.; Li, Q. Study on Elastic Mixed Mode Fracture Behavior and II-III Coupling Effect. Materials 2023, 16, 4879. [Google Scholar] [CrossRef] [PubMed]
- Vormwald, M.; Hos, Y.; Freire, J.L.F.; Gonzáles, G.L.G.; Díaz, J.G. Crack Tip Displacement Fields Measured by Digital Image Correlation for Evaluating Variable Mode-Mixity during Fatigue Crack Growth. Int. J. Fatigue 2018, 115, 53–66. [Google Scholar] [CrossRef]
- Sipos, A.A.; Cao, S. About Measuring the Stress Intensity Factor of Cracks in Curved, Brittle Shells. Frat. Ed. Integrità Strutt. 2024, 18, 1–17. [Google Scholar] [CrossRef]
- Petureau, L.; Doquet, V.; Dieu, B. Influence of a Static Torque on Plasticity and Asperity-Induced Closure Effects during Fatigue Crack Growth in Bainitic Steel Cylinders Loaded in Push-Pull. Int. J. Fatigue 2022, 155, 106628. [Google Scholar] [CrossRef]
- Diaz, J.G.; Marques, L.F.N.; Guzmán, R.E. Mixed-Mode Stress Intensity Factors for Tubes under Pure Torsion Loading. Key Eng. Mater. 2018, 774, 373–378. [Google Scholar] [CrossRef]
- Mirzaei, A.M.; Sapora, A.; Cornetti, P. Asymptotic Stress Field for the Blunt and Sharp Notches in Bi-Material Media Under Mode III Loading. J. Appl. Mech. 2024, 91, 051008. [Google Scholar] [CrossRef]
- Ju, Y.; Zhang, Y.; Yu, H. Numerical Prediction and Experiments for 3D Crack Propagation in Brittle Materials Based on 3D-Generalized Maximum Tangential Strain Criterion. Theor. Appl. Fract. Mech. 2025, 135, 104747. [Google Scholar] [CrossRef]
- Molteno, M.R.; Becker, T.H. Mode I–III Decomposition of the J-Integral from DIC Displacement Data. Strain 2015, 51, 492–503. [Google Scholar] [CrossRef]
- Yu, X.; Li, L.; Proust, G. Fatigue Crack Growth of Aluminium Alloy 7075-T651 under Proportional and Non-Proportional Mixed Mode I and II Loads. Eng. Fract. Mech. 2017, 174, 155–167. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhang, B.; Li, C.-Q. A Review on Mixed Mode Fracture of Metals. Eng. Fract. Mech. 2020, 235, 107126. [Google Scholar] [CrossRef]
- Pook, L. The Fatigue Crack Direction and Threshold Behaviour of Mild Steel under Mixed Mode I and III Loading. Int. J. Fatigue 1985, 7, 21–30. [Google Scholar] [CrossRef]
- Saboori, B.; Ayatollahi, M.R. A Novel Test Configuration Designed for Investigating Mixed Mode II/III Fracture. Eng. Fract. Mech. 2018, 197, 248–258. [Google Scholar] [CrossRef]
- Aliha, M.R.M.; Bahmani, A.; Akhondi, S. Determination of Mode III Fracture Toughness for Different Materials Using a New Designed Test Configuration. Mater. Des. 2015, 86, 863–871. [Google Scholar] [CrossRef]
- Jalayer, R.; Saboori, B.; Ayatollahi, M.R. A Novel Test Specimen for Mixed Mode I/II/III Fracture Study in Brittle Materials. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1908–1920. [Google Scholar] [CrossRef]
- Pham, K.H.; Ravi-Chandar, K. On the Growth of Cracks under Mixed-Mode I + III Loading. Int. J. Fract. 2016, 199, 105–134. [Google Scholar] [CrossRef]
- Bahrami, B.; Nejati, M.; Ayatollahi, M.R.; Driesner, T. True Mode II Fracturing of Rocks: An Axially Double-Edge Notched Brazilian Disk Test. Rock. Mech. Rock. Eng. 2022, 55, 3353–3365. [Google Scholar] [CrossRef]
- Qin, X.; Su, H.; Yu, L.; Wang, H.; Jiang, Y.; Pham, T.N. Differential Response of Fracture Characterization of Mode III Fracture in Sandstone Under Dynamic Versus Static Loading. Fatigue Fract. Eng. Mater. Struct. 2024, 48, 1315–1329. [Google Scholar] [CrossRef]
- Moradi, E.; Zeinedini, A. On the Mixed Mode I/II/III Inter-Laminar Fracture Toughness of Cotton/Epoxy Laminated Composites. Theor. Appl. Fract. Mech. 2020, 105, 102400. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, K.; Wang, C. Review of Fracture Test Methods. In Rock Fracture Mechanics and Fracture Criteria; Springer: Singapore, 2024; pp. 29–45. [Google Scholar]
- Maneschy, J.E.; Miranda, C.A.d.J. Application of Fracture Mechanics in the Nuclear Industry, 1st ed.; Eletrobras, Ed.; Eletrobras: Rio de Janeiro, Brazil, 2023; ISBN 9788599092026. [Google Scholar]
- Zhang, R.; He, L. Measurement of Mixed-Mode Stress Intensity Factors Using Digital Image Correlation Method. Opt. Lasers Eng. 2012, 50, 1001–1007. [Google Scholar] [CrossRef]
- Ramaswamy, G.; Ramesh, K.; Saravanan, U. Influence of Contact Stresses on Crack-Tip Stress Field: A Multiparameter Approach Using Digital Photoelasticity. Exp. Mech. 2024, 64, 785–804. [Google Scholar] [CrossRef]
- Ju, S.H.; Chung, H.Y. Accuracy and Limit of a Least-Squares Method to Calculate 3D Notch SIFs. Int. J. Fract. 2007, 148, 169–183. [Google Scholar] [CrossRef]
- Strohmann, T.; Melching, D.; Paysan, F.; Dietrich, E.; Requena, G.; Breitbarth, E. Next Generation Fatigue Crack Growth Experiments of Aerospace Materials. Sci. Rep. 2024, 14, 14075. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, M.; Teixeira, P.; Wrobel, L.C.; Martinez, M. A New Displacement-Based Approach to Calculate Stress Intensity Factors with the Boundary Element Method. Lat. Am. J. Solids Struct. 2015, 12, 1677–1697. [Google Scholar] [CrossRef]
- Gómez-Gamboa, E.; Díaz-Rodríguez, J.G.; Mantilla-Villalobos, J.A.; Bohórquez-Becerra, O.R.; Martínez, M.d.J. Experimental and Numerical Evaluation of Equivalent Stress Intensity Factor Models under Mixed-Mode (I+II) Loading. Infrastructures 2024, 9, 45. [Google Scholar] [CrossRef]
- Díaz, J.G.; Freire, J.L.d.F. LEFM Crack Path Models Evaluation under Proportional and Non-Proportional Load in Low Carbon Steels Using Digital Image Correlation Data. Int. J. Fatigue 2022, 156, 106687. [Google Scholar] [CrossRef]
- Langlois, C.R.; Gravouil, A.; Baietto, M.-C.; Réthoré, J. Three-dimensional Simulation of Crack with Curved Front with Direct Estimation of Stress Intensity Factors. Int. J. Numer. Methods Eng. 2015, 101, 635–652. [Google Scholar] [CrossRef]
- Kujawski, D. Discussion and Comments on KOP and ∆Keff. Materials 2020, 13, 4959. [Google Scholar] [CrossRef] [PubMed]
- Tavares, S.M.O.; de Castro, P.M.S.T. Equivalent Stress Intensity Factor: The Consequences of the Lack of a Unique Definition. Appl. Sci. 2023, 13, 4820. [Google Scholar] [CrossRef]
- Yoneyama, S.; Arikawa, S.; Kusayanagi, S.; Hazumi, K. Evaluating J-Integral from Displacement Fields Measured by Digital Image Correlation. Strain 2014, 50, 147–160. [Google Scholar] [CrossRef]
- Richard, H.A.; Fulland, M.; Sander, M. Theoretical Crack Path Prediction. Fatigue Fract. Eng. Mater. Struct. 2004, 28, 3–12. [Google Scholar] [CrossRef]
- Harilal, R.; Vyasarayani, C.P.; Ramji, M. A Linear Least Squares Approach for Evaluation of Crack Tip Stress Field Parameters Using DIC. Opt. Lasers Eng. 2015, 75, 95–102. [Google Scholar] [CrossRef]
- Vormwald, M.; Hos, Y.; Freire, J.L.F.; Gonzáles, G.L.G.; Díaz, J.G. Variable Mode-Mixity during Fatigue Cycles—Crack Tip Parameters Determined from Displacement Fields Measured by Digital Image Correlation. Frat. Ed. Integrità Strutt. 2017, 11, 314–322. [Google Scholar] [CrossRef]
- Camacho-Reyes, A.; Gómez-Gonzales, G.; Vasco-Olmo, J.; Díaz, F.A. Cálculo de Los Parámetros Gobernantes de La Singularidad En El Vértice de Grieta En Superficies Cilíndricas Empleando Geometría Diferencial y Correlación Digital de Imágenes 3D. Rev. Mecánica La. Fract. 2023, 5, 63–67. [Google Scholar]
- Kolditz, L.M.; Dray, S.; Kosin, V.; Fau, A.; Hild, F.; Wick, T. Employing Williams’ Series for the Identification of Fracture Mechanics Parameters from Phase-Field Simulations. Eng. Fract. Mech. 2024, 307, 110298. [Google Scholar] [CrossRef]
- Tschegg, E.K. Sliding Mode Crack Closure and Mode III Fatigue Crack Growth in Mild Steel. Acta Metall. 1983, 31, 1323–1330. [Google Scholar] [CrossRef]
- Ritchie, R.; McClintock, F.; Tschegg, E.; Nayeb-Hashemi, H. Mode III Fatigue Crack Growth Under Combined Torsional and Axial Loading. In Multiaxial Fatigue; ASTM: West Conshohocken, PA, USA, 1985; pp. 203–227. [Google Scholar]
- Kujawski, D.; Vasudevan, A.K.; Ricker, R.E.; Sadananda, K. On 50 Years of Fatigue Crack Closure Dispute. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 2816–2829. [Google Scholar] [CrossRef]



| Specimen | R-030 | R-031 | R-033 |
|---|---|---|---|
| Type of load | In-phase tension and torsion | 90° out-of-phase tension and torsion | 45° out-of-phase tension and torsion |
| Load ratio | RL = RT = −1 | RL = RT = −1 | RL = RT = −1 |
| Measured SIF range | ΔKI, ΔKII, ΔKIII | ΔKI, ΔKII, ΔKIII | ΔKI, ΔKII, ΔKIII |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Rodríguez, J.G.; Valencia-Niño, C.H.; Rodríguez-Torres, A. An Over-Deterministic Method for Mode III SIF Calculation Using Full-Field Experimental Displacement Fields. Appl. Sci. 2025, 15, 3404. https://doi.org/10.3390/app15063404
Díaz-Rodríguez JG, Valencia-Niño CH, Rodríguez-Torres A. An Over-Deterministic Method for Mode III SIF Calculation Using Full-Field Experimental Displacement Fields. Applied Sciences. 2025; 15(6):3404. https://doi.org/10.3390/app15063404
Chicago/Turabian StyleDíaz-Rodríguez, Jorge Guillermo, Cesar Hernando Valencia-Niño, and Andrés Rodríguez-Torres. 2025. "An Over-Deterministic Method for Mode III SIF Calculation Using Full-Field Experimental Displacement Fields" Applied Sciences 15, no. 6: 3404. https://doi.org/10.3390/app15063404
APA StyleDíaz-Rodríguez, J. G., Valencia-Niño, C. H., & Rodríguez-Torres, A. (2025). An Over-Deterministic Method for Mode III SIF Calculation Using Full-Field Experimental Displacement Fields. Applied Sciences, 15(6), 3404. https://doi.org/10.3390/app15063404







