Concentrated Couple in a Plane and in a Half-Plane in the Framework of Fractional Nonlocal Elasticity
Abstract
1. Introduction
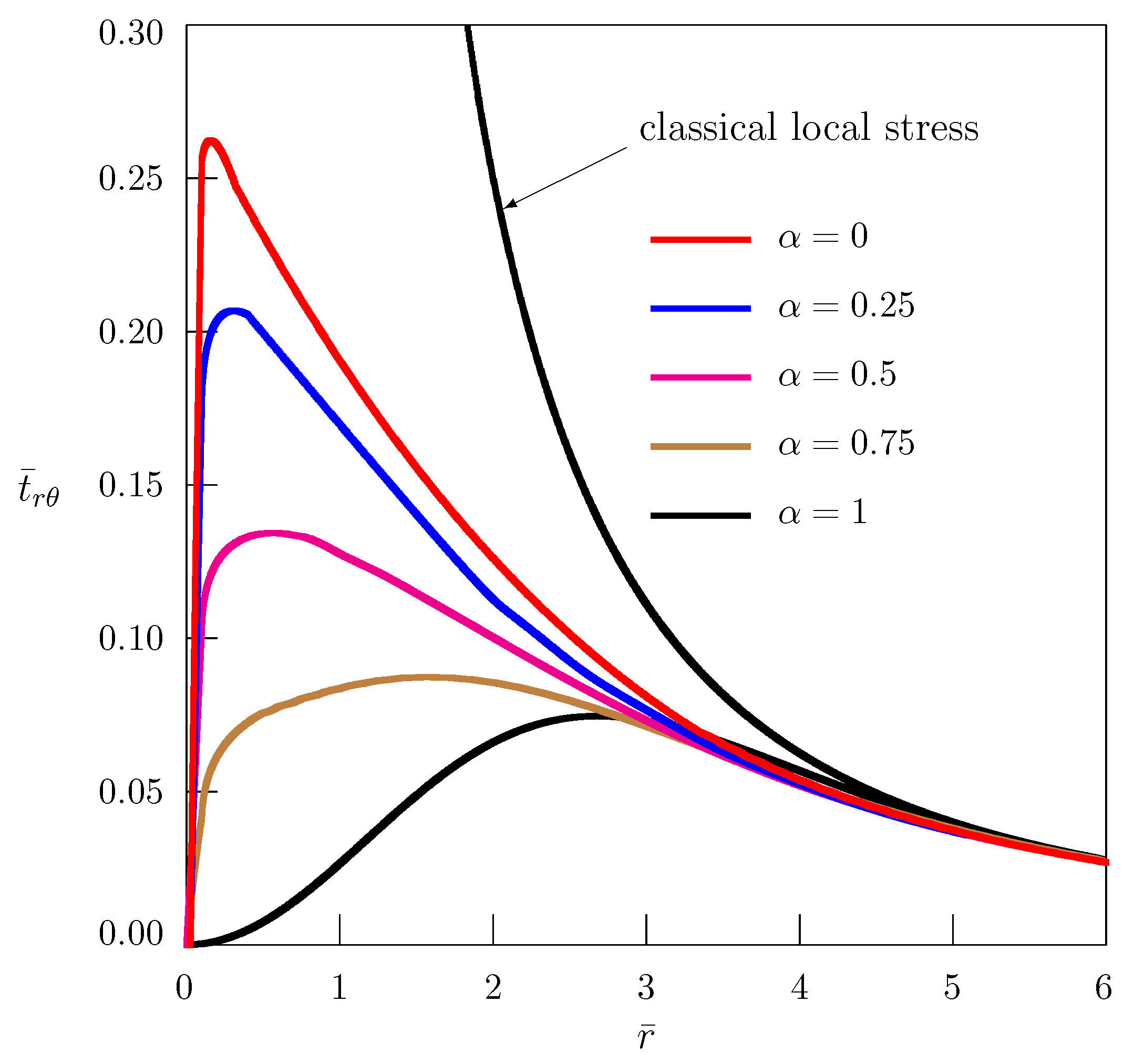
2. Concentrated Couple in a Plane
3. Concentrated Couple on the Boundary of a Half-Plane
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Kröner, E. Elasticity theory of materials with long range cohesive forces. Int. J. Solids Struct. 1967, 3, 731–742. [Google Scholar] [CrossRef]
- Podstrigach, Y.S. On a nonlocal theory of solid body deformation. Sov. Appl. Mech. 1967, 3, 44–46. [Google Scholar] [CrossRef]
- Krumhansl, J.A. Some considerations of the relation between solid state physics and generalized continuum mechanics. In Mechanics of Generalized Continua; Springer: Berlin/Heidelberg, Germany, 1968; pp. 298–311. [Google Scholar]
- Eringen, A.C. Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 1972, 10, 425–435. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar field theories. In Continuum Physics, vol. 4, Polar and Nonlocal Field Theories; Academic Press: New York, NY, USA, 1976; pp. 205–267. [Google Scholar]
- Kunin, I.A. Elastic Media with Microstructure I. One-Dimensional Models; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Kunin, I.A. Elastic Media with Microstructure II. Three-Dimensional Models; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Vistas on nonlocal continuum physics. Int. J. Eng. Sci. 1992, 30, 1551–1565. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Lazar, M.; Maugin, G.A.; Aifantis, E.C. On a theory of nonlocal elasticity of bi-Helmholtz type and some applications. Int. J. Solids Struct. 2006, 43, 1404–1421. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; Marotti de Sciarra, F. Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: Redding, CA, USA, 2006. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Lnear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Atanacković, T.M.; Pilipovć, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity; Springer: New York, NY, USA, 2015. [Google Scholar]
- Chu, J.; Liu, Y. Coupling model of a generalized second grade fluid flow and fractional Cattaneo heat transfer with magnetic field and radiation. Results Phys. 2024, 57, 107409. [Google Scholar] [CrossRef]
- Seadway, A.R.; Ali, A.; Bekir, A.; Cevikel, A.C. Analysis of the(3+1)-dimensional fractional Kadomtsev– Petviashvili–Boussinesq equation: Solitary, bright, singular, and dark solitons. Fractal Fract. 2024, 8, 515. [Google Scholar] [CrossRef]
- Singh, D.; Srivastava, H.M.; Nieto, J.J. (Eds.) Handbook of Fractional Calculus for Engineering and Science; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Zhou, Y. Fractional Diffusion and Wave Equations; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Kevrekidis, P.G.; Cuevas-Maraver, J. (Eds.) Fractional Dispersive Models and Applications: Recent Developments and Future Perspectives; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Sun, H.G.; Li, Z.; Nie, S. Fractional and Fractal Derivative Models for Anomalous Sediment Transport; De Gruyter: Berlin/Heidelberg, Germany, 2025. [Google Scholar]
- Di Paola, M.; Zingales, M. Long-range cohesive interactions of non-local continuum faced by fractional calculus. Int. J. Solids Struct. 2008, 45, 5642–5659. [Google Scholar] [CrossRef]
- Challamel, N.; Zorica, D.; Atanacković, T.M.; Spasić, D.T. On the fractional generalization of Eringen’s nonlocal elasticity for wave propagation. C. R. Mec. 2013, 341, 298–303. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Sapora, A. Nonlocal elasticity: An approach based on fractional calculus. Meccanica 2014, 49, 2551–2569. [Google Scholar] [CrossRef]
- Povstenko, Y. Generalized theory of diffusive stresses associated with the time-fractional diffusion equation and nonlocal constitutive equations for the stress tensor. Comput. Math. Appl. 2019, 78, 1819–1825. [Google Scholar] [CrossRef]
- Autuori, G.; Cluni, F.; Gusella, V.; Pucci, P. Effects of the fractional Laplacian order on the nonlocal elastic rod response. ASME J. Risk Uncertain. Part B 2017, 3, 030902. [Google Scholar] [CrossRef]
- Evgrafov, A.; Bellido, J.C. From non-local Eringen’s model to fractional elasticity. Math. Mech. Solids 2019, 24, 1935–1953. [Google Scholar] [CrossRef]
- Alotta, G.; Di Paola, M.; Pinnola, F.P. An unified formulation of strong non-local elasticity with fractional order calculus. Meccanica 2022, 57, 793–805. [Google Scholar] [CrossRef]
- Challamel, N.; Atanacković, T.; Zhang, Y.P.; Wang, C.M. A fractional nonlocal elastic model for lattice wave analysis. Mech. Res. Commun. 2022, 126, 103999. [Google Scholar] [CrossRef]
- Challamel, N.; Atanacković, T.; Zhang, Y.P.; Wang, C.M. Fractional nonlocal elastic rod, beam, and plate models applied to lattice structural mechanics. In Nanomechanics of Structures and Materials; Żur, K.K., Faghidian, S.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 335–360. [Google Scholar]
- Povstenko, Y. Fractional nonlocal elasticity and solutions for straight screw and edge dislocations. Phys. Mesomech. 2020, 23, 547–555. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Fundamental solutions for isotropic size-dependent couple stress elasticity. Int. J. Solids Struct. 2013, 50, 1253–1265. [Google Scholar] [CrossRef]
- Hattoria, G.; Trevelyana, J.; Gourgiotis, P.A. An isogeometric boundary element formulation for stress concentration problems in couple stress elasticity. Comput. Meth. Appl. Mech. Eng. 2023, 407, 115932. [Google Scholar] [CrossRef]
- Gourgiotis, P.; Rizzi, G.; Lewintan, P.; Bernardini, D.; Sky, A.; Madeo, A.; Neff, P. Green’s functions for the isotropic planar relaxed micromorphic model – Concentrated force and concentrated couple. Int. J. Solids Struct. 2024, 292, 112700. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Povstenko, Y. Some applications of the Wright function in continuum physics: A survey. Mathematics 2021, 9, 198. [Google Scholar] [CrossRef]
- Erdéelyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1955; Volume 3. [Google Scholar]
- Kachanov, M.; Shafiro, B.; Tsukrov, I. Handbook of Elasticity Solutions; Springer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Ghavanloo, E.; Fazelzadeh, S.A.; Marotti de Sciarra, F. (Eds.) Size-Dependent Continuum Mechanics Approaches: Theory and Applications; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Panin, V.E.; Egorushkin, V.E.; Panin, A.V. Physical mesomechanics of a deformed solid as a multilevel system. I. Physical fundamentals of the multilevel approach. Phys. Mesomech. 2006, 9, 9–20. (In Russian) [Google Scholar]
- Povstenko, Y. Straight disclinations in nonlocal elasticity. Int. J. Eng. Sci. 1995, 33, 575–582. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Povstenko, Y.; Kyrylych, T.; Woźna-Szcześniak, B.; Szcześniak, I.; Yatsko, A. Concentrated Couple in a Plane and in a Half-Plane in the Framework of Fractional Nonlocal Elasticity. Appl. Sci. 2025, 15, 2048. https://doi.org/10.3390/app15042048
Povstenko Y, Kyrylych T, Woźna-Szcześniak B, Szcześniak I, Yatsko A. Concentrated Couple in a Plane and in a Half-Plane in the Framework of Fractional Nonlocal Elasticity. Applied Sciences. 2025; 15(4):2048. https://doi.org/10.3390/app15042048
Chicago/Turabian StylePovstenko, Yuriy, Tamara Kyrylych, Bożena Woźna-Szcześniak, Ireneusz Szcześniak, and Andrzej Yatsko. 2025. "Concentrated Couple in a Plane and in a Half-Plane in the Framework of Fractional Nonlocal Elasticity" Applied Sciences 15, no. 4: 2048. https://doi.org/10.3390/app15042048
APA StylePovstenko, Y., Kyrylych, T., Woźna-Szcześniak, B., Szcześniak, I., & Yatsko, A. (2025). Concentrated Couple in a Plane and in a Half-Plane in the Framework of Fractional Nonlocal Elasticity. Applied Sciences, 15(4), 2048. https://doi.org/10.3390/app15042048





