A Symmetric Projection Space and Adversarial Training Framework for Privacy-Preserving Machine Learning with Improved Computational Efficiency
Abstract
1. Introduction
- Low-dimensional data abstraction based on symmetric projection: This method uses symmetry design and nonlinear transformations to project high-dimensional sensitive data into a lower-dimensional abstract space, achieving obfuscated data representation while effectively retaining key features required for training and inference.
- Privacy-preserving module combining adversarial training and autoencoders: Within the adversarial training framework, the generator is responsible for generating obfuscated data, while the discriminator optimizes its discriminative ability, forming a dynamic adversarial mechanism. Meanwhile, the introduction of the autoencoder enables the efficient separation and reconstruction of sensitive and nonsensitive information, ensuring both data privacy and enhanced model utility.
- Wide adaptability and performance validation for multi-task data: The proposed framework has been validated on multiple datasets, including time-series and image data, demonstrating its generality and performance advantages. The method shows outstanding results in terms of privacy protection and computational efficiency.
2. Related Work
2.1. Latent Space
2.2. Adversarial Learning
2.3. Autoencoders
3. Materials and Methods
3.1. Dataset Collection
3.2. Data Augmentation
3.2.1. Time-Series Data Cleaning and Imputation
3.2.2. Image Data Augmentation
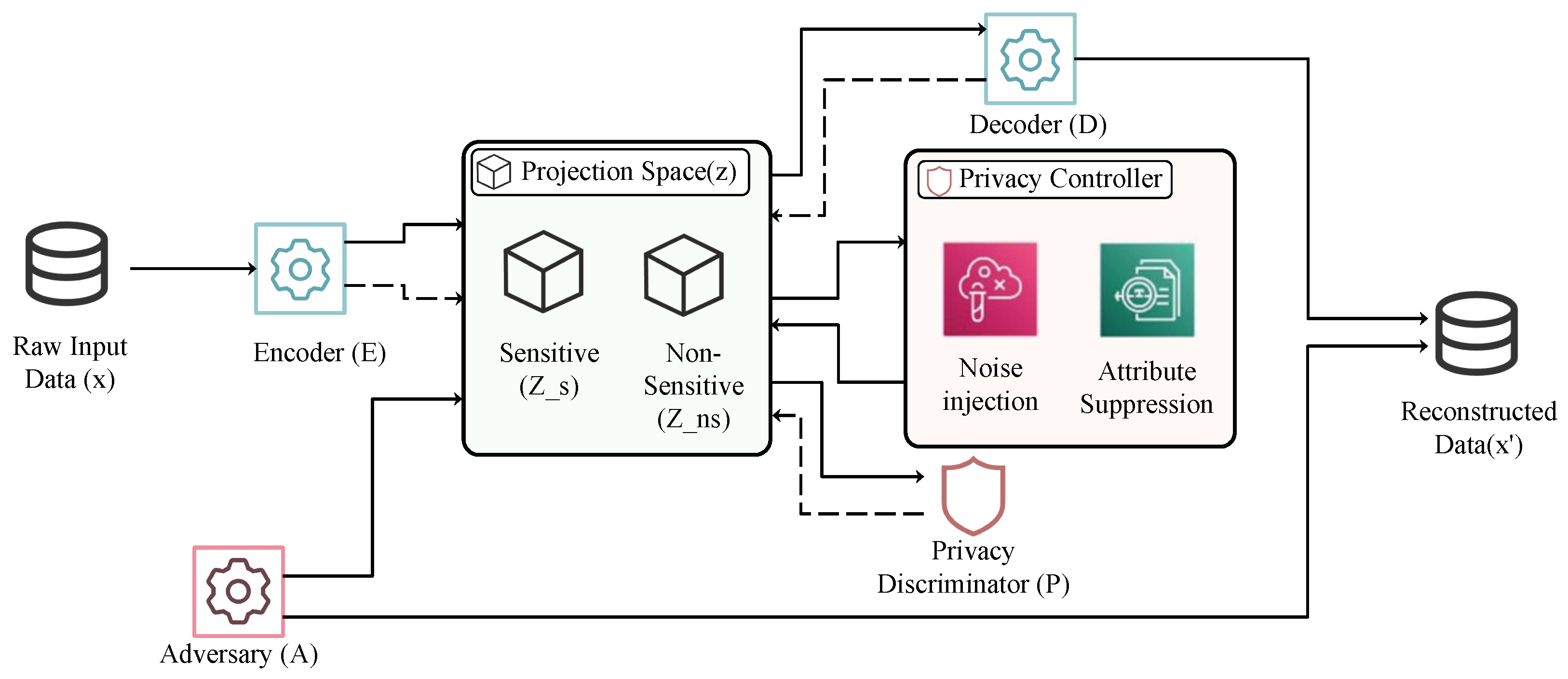
3.3. Proposed Method
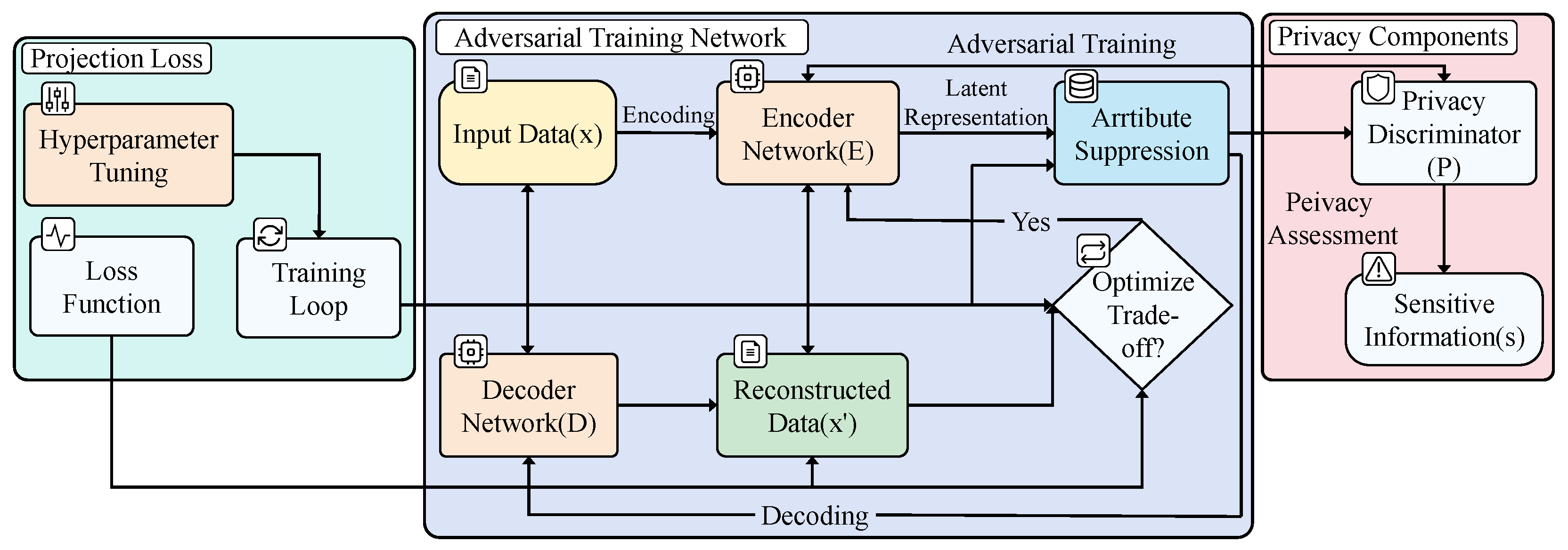
3.3.1. Adversarial Training Network Framework
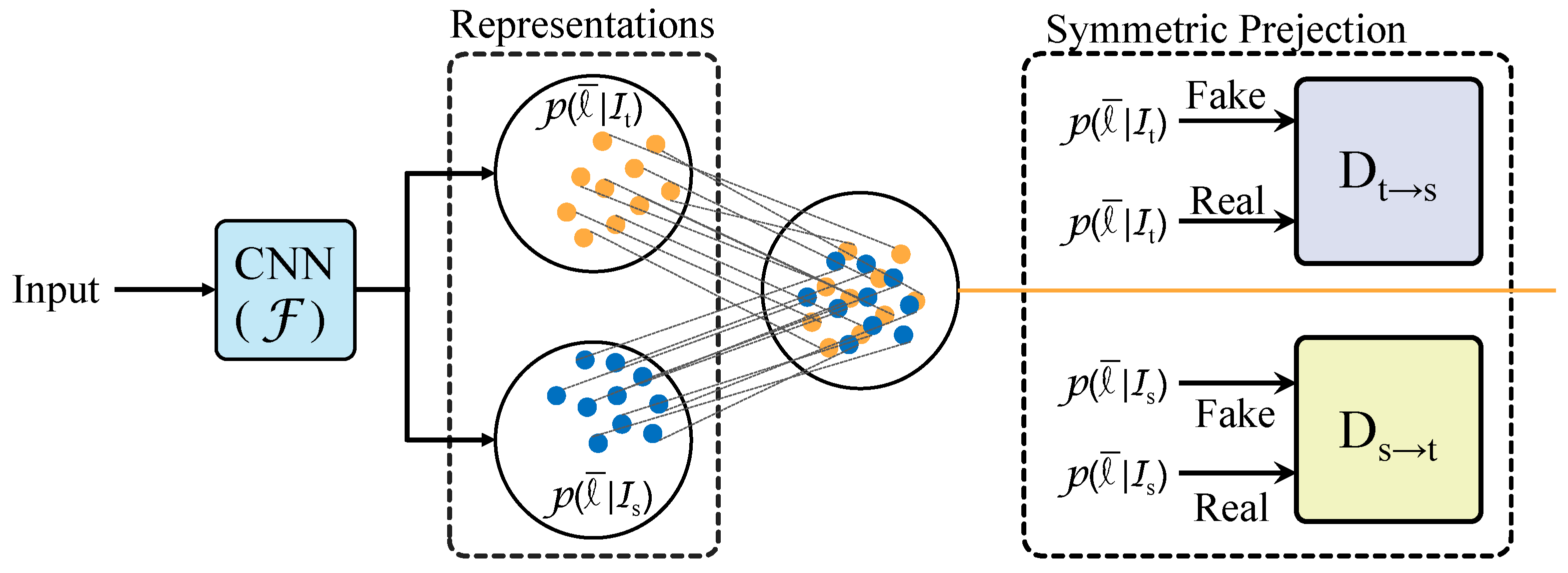
3.3.2. Symmetric Projection Space Extractor
- 1.
- Input layer: The input data are mapped through a fully connected layer with output dimension . Assuming the input feature dimension is d, the parameters of the first layer are and the bias is , with the activation function being ReLU:where .
- 2.
- Hidden layers: Data are transformed through multiple hidden layers, with the output dimension gradually decreasing. The parameters of the i-th layer are , the bias is , and the activation function remains ReLU:where .
- 3.
- Output layer: The final layer maps the data to the low-dimensional latent space , where k is the latent space dimension. The output layer’s parameters are , the bias is , and the activation function is a linear function to ensure continuous output:where is the low-dimensional latent representation.
3.3.3. Autoencoder-Based Data Generation Module

- 1.
- Encoder design: The encoder consists of several fully connected layers designed to map the input data to a low-dimensional latent space . Assume the input data have dimension d, and the encoder’s output has dimension k (typically, ). The first layer of the encoder maps the input data to an intermediate layer using a fully connected layer, with parameters , and bias , using the ReLU activation function. This process continues, progressively compressing the data features down to the latent space .
- 2.
- Decoder design: The decoder’s task is to reconstruct the original data from the latent representation . The structure of the decoder is similar to the encoder and consists of several fully connected layers. Assume that the final output of the decoder is the reconstructed data . The first layer of the decoder maps the latent representation back to the high-dimensional space:where is the weight matrix of the decoder, is the bias, and the activation function is Sigmoid (or ReLU, depending on the task requirements), ensuring that the reconstructed data maintain the structure of the original data.
- 3.
- Network parameter design: For each layer of the network, careful consideration is given to the matching of input and output dimensions and the network’s expressiveness. The encoder typically uses intermediate layers , where is the output of the first layer, progressively increasing the feature abstraction capacity until the data are compressed into the latent space . The decoder then reconstructs the original data dimensions based on the latent space data through reverse mapping.
3.3.4. Projection Loss Function

3.4. Experimental Setup
3.4.1. Hardware and Software Platforms
3.4.2. Hyperparameters and Training Configuration
3.4.3. Baseline Methods
3.5. Evaluation Metrics
4. Results and Discussion
4.1. Financial Fraud Detection Results
4.2. Image and Semantic Classification Detection Results
4.3. Computational Efficiency Analysis
4.4. Ablation Experiment on Different Loss Functions Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, P.; Xiong, N.; Ren, J. Data security and privacy protection for cloud storage: A survey. IEEE Access 2020, 8, 131723–131740. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y. Confidential Federated Learning for Heterogeneous Platforms against Client-Side Privacy Leakages. In Proceedings of the ACM Turing Award Celebration Conference 2024, Changsha, China, 5–7 July 2024; pp. 239–241. [Google Scholar]
- Kaissis, G.A.; Makowski, M.R.; Rückert, D.; Braren, R.F. Secure, privacy-preserving and federated machine learning in medical imaging. Nat. Mach. Intell. 2020, 2, 305–311. [Google Scholar] [CrossRef]
- Oyewole, A.T.; Oguejiofor, B.B.; Eneh, N.E.; Akpuokwe, C.U.; Bakare, S.S. Data privacy laws and their impact on financial technology companies: A review. Comput. Sci. Res. J. 2024, 5, 628–650. [Google Scholar]
- Huang, L. Ethics of artificial intelligence in education: Student privacy and data protection. Sci. Insights Educ. Front. 2023, 16, 2577–2587. [Google Scholar] [CrossRef]
- Ponomareva, N.; Hazimeh, H.; Kurakin, A.; Xu, Z.; Denison, C.; McMahan, H.B.; Vassilvitskii, S.; Chien, S.; Thakurta, A.G. How to dp-fy ml: A practical guide to machine learning with differential privacy. J. Artif. Intell. Res. 2023, 77, 1113–1201. [Google Scholar] [CrossRef]
- Jin, W.; Yao, Y.; Han, S.; Gu, J.; Joe-Wong, C.; Ravi, S.; Avestimehr, S.; He, C. FedML-HE: An efficient homomorphic-encryption-based privacy-preserving federated learning system. arXiv 2023, arXiv:2303.10837. [Google Scholar]
- Chen, J.; Yan, H.; Liu, Z.; Zhang, M.; Xiong, H.; Yu, S. When federated learning meets privacy-preserving computation. ACM Comput. Surv. 2024, 56, 1–36. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Y.; Jiang, H.; Zhao, Z. Ppefl: Privacy-preserving edge federated learning with local differential privacy. IEEE Internet Things J. 2023, 10, 15488–15500. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y.; Ren, J.; Li, Q.; Zhang, Y. You Can Use But Cannot Recognize: Preserving Visual Privacy in Deep Neural Networks. arXiv 2024, arXiv:2404.04098. [Google Scholar]
- Li, Q.; Ren, J.; Zhang, Y.; Song, C.; Liao, Y.; Zhang, Y. Privacy-Preserving DNN Training with Prefetched Meta-Keys on Heterogeneous Neural Network Accelerators. In Proceedings of the 2023 60th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 9–13 July 2023; pp. 1–6. [Google Scholar]
- Yan, Y.; Wang, X.; Ligeti, P.; Jin, Y. DP-FSAEA: Differential Privacy for Federated Surrogate-Assisted Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2024. [CrossRef]
- Wang, G.; Li, C.; Dai, B.; Zhang, S. Privacy-Protection Method for Blockchain Transactions Based on Lightweight Homomorphic Encryption. Information 2024, 15, 438. [Google Scholar] [CrossRef]
- Pan, Y.; Chao, Z.; He, W.; Jing, Y.; Hongjia, L.; Liming, W. FedSHE: Privacy preserving and efficient federated learning with adaptive segmented CKKS homomorphic encryption. Cybersecurity 2024, 7, 40. [Google Scholar] [CrossRef]
- Xie, Q.; Jiang, S.; Jiang, L.; Huang, Y.; Zhao, Z.; Khan, S.; Dai, W.; Liu, Z.; Wu, K. Efficiency optimization techniques in privacy-preserving federated learning with homomorphic encryption: A brief survey. IEEE Internet Things J. 2024, 11, 24569–24580. [Google Scholar] [CrossRef]
- Vahdat, A.; Kreis, K.; Kautz, J. Score-based generative modeling in latent space. Adv. Neural Inf. Process. Syst. 2021, 34, 11287–11302. [Google Scholar]
- Zhang, Y.; Wa, S.; Zhang, L.; Lv, C. Automatic plant disease detection based on tranvolution detection network with GAN modules using leaf images. Front. Plant Sci. 2022, 13, 875693. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, D.; Bremond, F.; Dantcheva, A. Latent image animator: Learning to animate images via latent space navigation. arXiv 2022, arXiv:2203.09043. [Google Scholar]
- Kwon, M.; Jeong, J.; Uh, Y. Diffusion models already have a semantic latent space. arXiv 2022, arXiv:2210.10960. [Google Scholar]
- Chen, X.; Jiang, B.; Liu, W.; Huang, Z.; Fu, B.; Chen, T.; Yu, G. Executing your commands via motion diffusion in latent space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 18000–18010. [Google Scholar]
- Pang, B.; Han, T.; Nijkamp, E.; Zhu, S.C.; Wu, Y.N. Learning latent space energy-based prior model. Adv. Neural Inf. Process. Syst. 2020, 33, 21994–22008. [Google Scholar]
- Maus, N.; Jones, H.; Moore, J.; Kusner, M.J.; Bradshaw, J.; Gardner, J. Local latent space bayesian optimization over structured inputs. Adv. Neural Inf. Process. Syst. 2022, 35, 34505–34518. [Google Scholar]
- Zhang, Y.; Wa, S.; Liu, Y.; Zhou, X.; Sun, P.; Ma, Q. High-accuracy detection of maize leaf diseases CNN based on multi-pathway activation function module. Remote Sens. 2021, 13, 4218. [Google Scholar] [CrossRef]
- Wu, C.H.; De la Torre, F. A latent space of stochastic diffusion models for zero-shot image editing and guidance. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 7378–7387. [Google Scholar]
- Tzelepis, C.; Tzimiropoulos, G.; Patras, I. Warpedganspace: Finding non-linear rbf paths in gan latent space. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 6393–6402. [Google Scholar]
- Ramaswamy, V.V.; Kim, S.S.; Russakovsky, O. Fair attribute classification through latent space de-biasing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9301–9310. [Google Scholar]
- Pang, B.; Wu, Y.N. Latent space energy-based model of symbol-vector coupling for text generation and classification. In Proceedings of the International Conference on Machine Learning, PMLR, Online; 2021; pp. 8359–8370. [Google Scholar]
- Chen, L.; Li, J.; Peng, J.; Xie, T.; Cao, Z.; Xu, K.; He, X.; Zheng, Z.; Wu, B. A survey of adversarial learning on graphs. arXiv 2020, arXiv:2003.05730. [Google Scholar]
- Zhang, W.; Li, X. Federated transfer learning for intelligent fault diagnostics using deep adversarial networks with data privacy. IEEE/Asme Trans. Mechatron. 2021, 27, 430–439. [Google Scholar] [CrossRef]
- Zhao, K.; Hu, J.; Shao, H.; Hu, J. Federated multi-source domain adversarial adaptation framework for machinery fault diagnosis with data privacy. Reliab. Eng. Syst. Saf. 2023, 236, 109246. [Google Scholar] [CrossRef]
- Croce, D.; Castellucci, G.; Basili, R. GAN-BERT: Generative adversarial learning for robust text classification with a bunch of labeled examples. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 2114–2119. [Google Scholar]
- Wu, Z.; Wang, H.; Wang, Z.; Jin, H.; Wang, Z. Privacy-preserving deep action recognition: An adversarial learning framework and a new dataset. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2126–2139. [Google Scholar] [CrossRef] [PubMed]
- Xiao, T.; Tsai, Y.H.; Sohn, K.; Chandraker, M.; Yang, M.H. Adversarial learning of privacy-preserving and task-oriented representations. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA; 2020; Volume 34, pp. 12434–12441. [Google Scholar]
- Liu, X.; Xie, L.; Wang, Y.; Zou, J.; Xiong, J.; Ying, Z.; Vasilakos, A.V. Privacy and security issues in deep learning: A survey. IEEE Access 2020, 9, 4566–4593. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, B.; Luo, W.; Chen, F. Autoencoder-based representation learning and its application in intelligent fault diagnosis: A review. Measurement 2022, 189, 110460. [Google Scholar] [CrossRef]
- Qian, J.; Song, Z.; Yao, Y.; Zhu, Z.; Zhang, X. A review on autoencoder based representation learning for fault detection and diagnosis in industrial processes. Chemom. Intell. Lab. Syst. 2022, 231, 104711. [Google Scholar] [CrossRef]
- Vahdat, A.; Kautz, J. NVAE: A deep hierarchical variational autoencoder. Adv. Neural Inf. Process. Syst. 2020, 33, 19667–19679. [Google Scholar]
- Zhang, Y.; Lv, C. TinySegformer: A lightweight visual segmentation model for real-time agricultural pest detection. Comput. Electron. Agric. 2024, 218, 108740. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, X.; Liu, Y.; Zhou, J.; Huang, Y.; Li, J.; Zhang, L.; Ma, Q. A time-series neural network for pig feeding behavior recognition and dangerous detection from videos. Comput. Electron. Agric. 2024, 218, 108710. [Google Scholar] [CrossRef]
- Chen, X.; Ding, M.; Wang, X.; Xin, Y.; Mo, S.; Wang, Y.; Han, S.; Luo, P.; Zeng, G.; Wang, J. Context autoencoder for self-supervised representation learning. Int. J. Comput. Vis. 2024, 132, 208–223. [Google Scholar] [CrossRef]
- Ge, T.; Hu, J.; Wang, L.; Wang, X.; Chen, S.Q.; Wei, F. In-context autoencoder for context compression in a large language model. arXiv 2023, arXiv:2307.06945. [Google Scholar]
- Liang, Y.; Liang, W. ResWCAE: Biometric Pattern Image Denoising Using Residual Wavelet-Conditioned Autoencoder. arXiv 2023, arXiv:2307.12255. [Google Scholar]
- He, Y.; Carass, A.; Zuo, L.; Dewey, B.E.; Prince, J.L. Autoencoder based self-supervised test-time adaptation for medical image analysis. Med. Image Anal. 2021, 72, 102136. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, P.; Lin, N.; Zhang, Z.; Wang, Z. A novel battery abnormality detection method using interpretable Autoencoder. Appl. Energy 2023, 330, 120312. [Google Scholar] [CrossRef]
- Mao, Y.; Xue, F.F.; Wang, R.; Zhang, J.; Zheng, W.S.; Liu, H. Abnormality detection in chest x-ray images using uncertainty prediction autoencoders. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2020: 23rd International Conference, Lima, Peru, 4–8 October 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 529–538. [Google Scholar]
- Saad, O.M.; Chen, Y. Deep denoising autoencoder for seismic random noise attenuation. Geophysics 2020, 85, V367–V376. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy. In Proceedings of the International Colloquium on Automata, Languages, and Programming, Venice, Italy, 10–14 July 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–12. [Google Scholar]
- Li, L.; Fan, Y.; Tse, M.; Lin, K.Y. A review of applications in federated learning. Comput. Ind. Eng. 2020, 149, 106854. [Google Scholar] [CrossRef]
- Knott, B.; Venkataraman, S.; Hannun, A.; Sengupta, S.; Ibrahim, M.; van der Maaten, L. Crypten: Secure multi-party computation meets machine learning. Adv. Neural Inf. Process. Syst. 2021, 34, 4961–4973. [Google Scholar]
- Munjal, K.; Bhatia, R. A systematic review of homomorphic encryption and its contributions in healthcare industry. Complex Intell. Syst. 2023, 9, 3759–3786. [Google Scholar] [CrossRef]
| Method | Privacy Protection | Model Utility | Computational Efficiency | Complexity |
|---|---|---|---|---|
| Differential Privacy | High | Moderate | Low | High |
| Homomorphic Encryption | Very High | Low | Very Low | Very High |
| Federated Learning | Moderate | High | Moderate | Moderate |
| Proposed Method | High | Very High | High | Low |
| Dataset Name | Quantity | Task Type |
|---|---|---|
| MNIST | 70,009 | Image Classification |
| USPS | 9298 | Image Classification |
| CelebA | 200,703 | Facial Attribute Prediction and Classification |
| Credit Card Fraud Detection | 284,807 | Financial Fraud Detection |
| IMDb Reviews | 50,379 | Sentiment Classification |
| BreakHis | 7909 | Image Classification (Benign/Malignant) |
| Model | Precision | Recall | F1 Score | Accuracy | Computation Complexity |
|---|---|---|---|---|---|
| Multi-party Secure Computation | 0.83 | 0.78 | 0.80 | 0.80 | 12.83 |
| Homomorphic Encryption | 0.86 | 0.82 | 0.84 | 0.84 | 83.14 |
| Differential Privacy | 0.89 | 0.86 | 0.87 | 0.88 | 4.71 |
| Federated Learning | 0.92 | 0.89 | 0.90 | 0.91 | 31.65 |
| Proposed Method | 0.95 | 0.91 | 0.93 | 0.93 | 3.28 |
| Model | Precision | Recall | F1 Score | Accuracy | mAP@50 | mAP@75 | Computation Complexity |
|---|---|---|---|---|---|---|---|
| Multi-party Secure Computation | 0.84 | 0.80 | 0.82 | 0.82 | 0.81 | 0.80 | 27.03 |
| Homomorphic Encryption | 0.86 | 0.82 | 0.84 | 0.84 | 0.84 | 0.83 | 215.81 |
| Differential Privacy | 0.89 | 0.86 | 0.87 | 0.87 | 0.88 | 0.87 | 11.54 |
| Federated Learning | 0.91 | 0.88 | 0.89 | 0.89 | 0.90 | 0.89 | 63.96 |
| Proposed Method | 0.93 | 0.90 | 0.91 | 0.91 | 0.91 | 0.90 | 7.27 |
| Model | Raspberry Pi | Jetson | NVIDIA 3080 GPU |
|---|---|---|---|
| Multi-party Secure Computation | 24.64 | 37.73 | 43.91 |
| Homomorphic Encryption | 28.25 | 39.67 | 42.94 |
| Differential Privacy | 15.03 | 41.27 | 51.48 |
| Federated Learning | 26.79 | 43.02 | 48.39 |
| Proposed Method | 29.93 | 46.64 | 57.89 |
| Model | Precision | Recall | F1 Score | Accuracy |
|---|---|---|---|---|
| Cross-Entropy Loss | 0.77 | 0.72 | 0.74 | 0.75 |
| Focal Loss | 0.86 | 0.81 | 0.83 | 0.84 |
| Projection Loss | 0.95 | 0.91 | 0.93 | 0.93 |
| Model | Precision | Recall | F1 Score | Accuracy | mAP@50 | mAP@75 |
|---|---|---|---|---|---|---|
| Cross-Entropy Loss | 0.71 | 0.67 | 0.69 | 0.69 | 0.68 | 0.67 |
| Focal Loss | 0.82 | 0.78 | 0.80 | 0.80 | 0.79 | 0.78 |
| Projection Loss | 0.93 | 0.90 | 0.91 | 0.91 | 0.91 | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Zhou, S.; Zeng, X.; Shi, J.; Lin, Q.; Huang, C.; Yue, Y.; Jiang, Y.; Lv, C. A Symmetric Projection Space and Adversarial Training Framework for Privacy-Preserving Machine Learning with Improved Computational Efficiency. Appl. Sci. 2025, 15, 3275. https://doi.org/10.3390/app15063275
Li Q, Zhou S, Zeng X, Shi J, Lin Q, Huang C, Yue Y, Jiang Y, Lv C. A Symmetric Projection Space and Adversarial Training Framework for Privacy-Preserving Machine Learning with Improved Computational Efficiency. Applied Sciences. 2025; 15(6):3275. https://doi.org/10.3390/app15063275
Chicago/Turabian StyleLi, Qianqian, Shutian Zhou, Xiangrong Zeng, Jiaqi Shi, Qianye Lin, Chenjia Huang, Yuchen Yue, Yuyao Jiang, and Chunli Lv. 2025. "A Symmetric Projection Space and Adversarial Training Framework for Privacy-Preserving Machine Learning with Improved Computational Efficiency" Applied Sciences 15, no. 6: 3275. https://doi.org/10.3390/app15063275
APA StyleLi, Q., Zhou, S., Zeng, X., Shi, J., Lin, Q., Huang, C., Yue, Y., Jiang, Y., & Lv, C. (2025). A Symmetric Projection Space and Adversarial Training Framework for Privacy-Preserving Machine Learning with Improved Computational Efficiency. Applied Sciences, 15(6), 3275. https://doi.org/10.3390/app15063275





