A Secure and Efficient Framework for Multimodal Prediction Tasks in Cloud Computing with Sliding-Window Attention Mechanisms
Abstract
1. Introduction
2. Related Work
2.1. Federated Learning
2.2. Secure Multi-Party Computation
2.3. Homomorphic Encryption
2.4. Multimodal Fusion Techniques: Transformers and Cross-Modal GANs
3. Materials and Methods
3.1. Dataset Collection
3.2. Dataset Preprocessing
3.3. Proposed Method
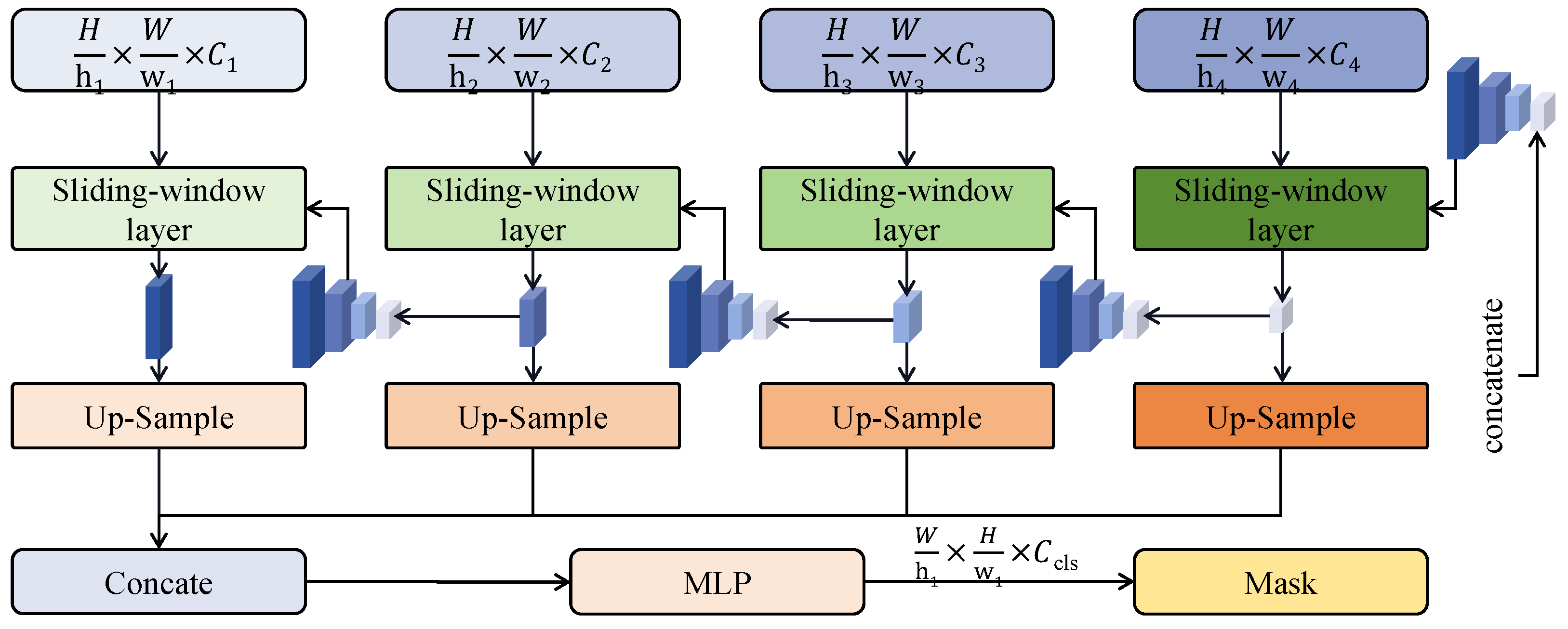
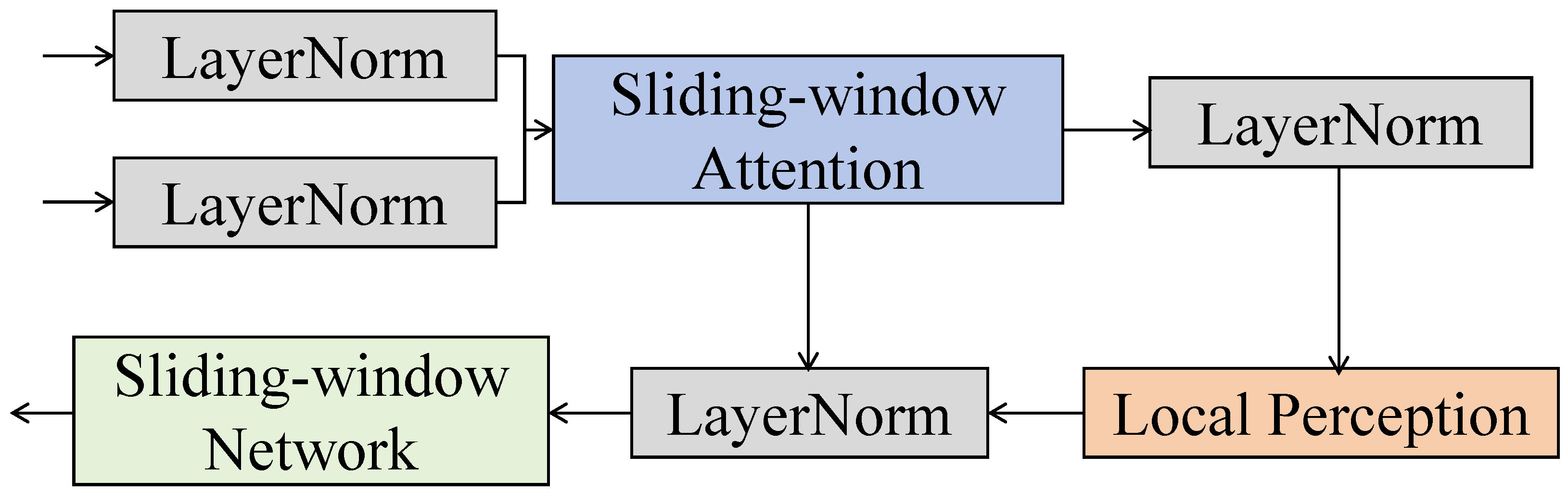
3.3.1. Sliding-Window Computation Network
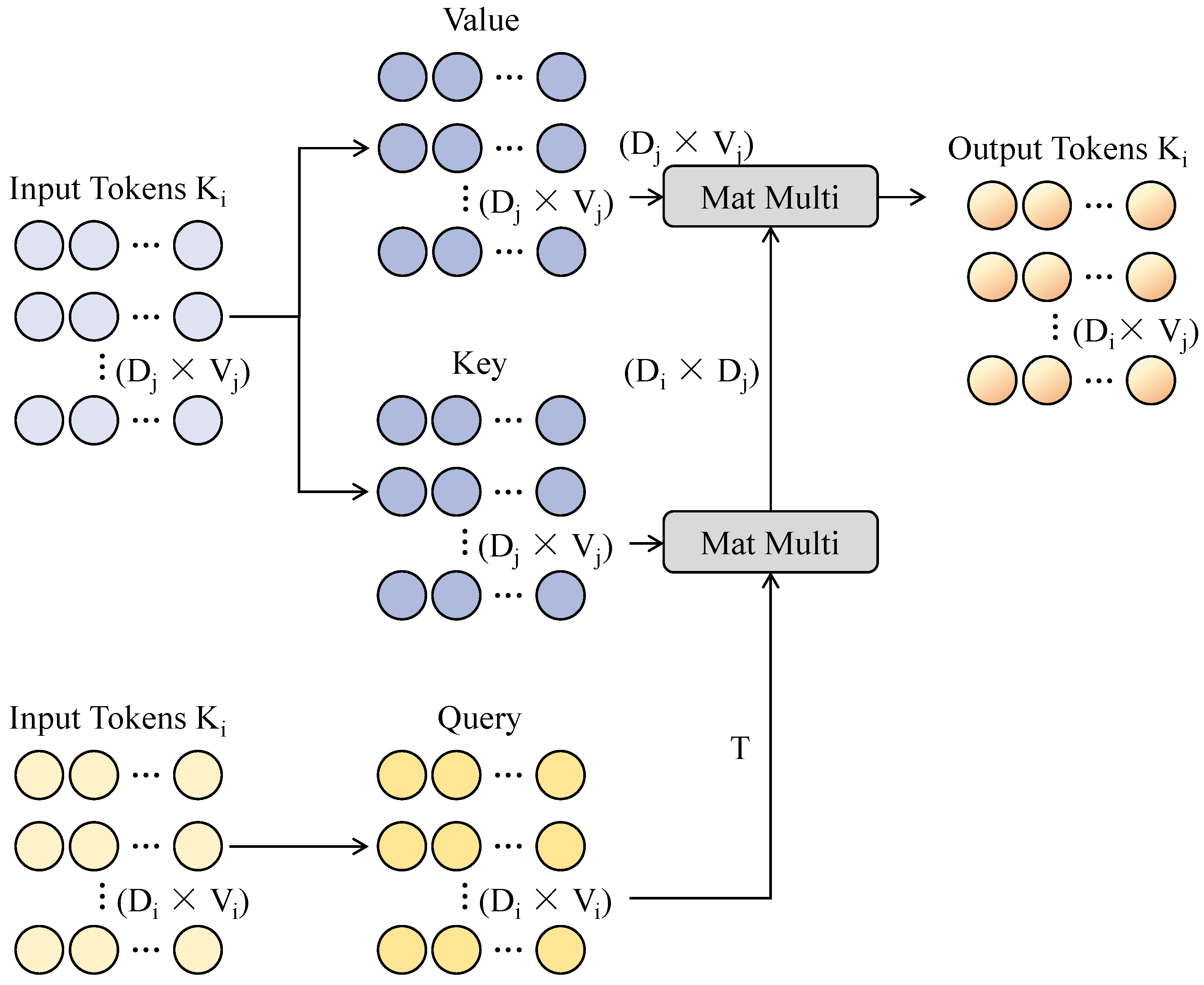
3.3.2. Sliding-Window Attention Mechanism
3.3.3. Time-Series and Space Fusion Module
3.3.4. Sliding Loss Function
3.4. Security Analysis
3.5. Experimental Design
3.5.1. Evaluation Metrics
3.5.2. Hardware and Software Platforms
3.5.3. Dataset Partitioning and Hyperparameter Configuration
3.5.4. Baselines
4. Results and Discussion
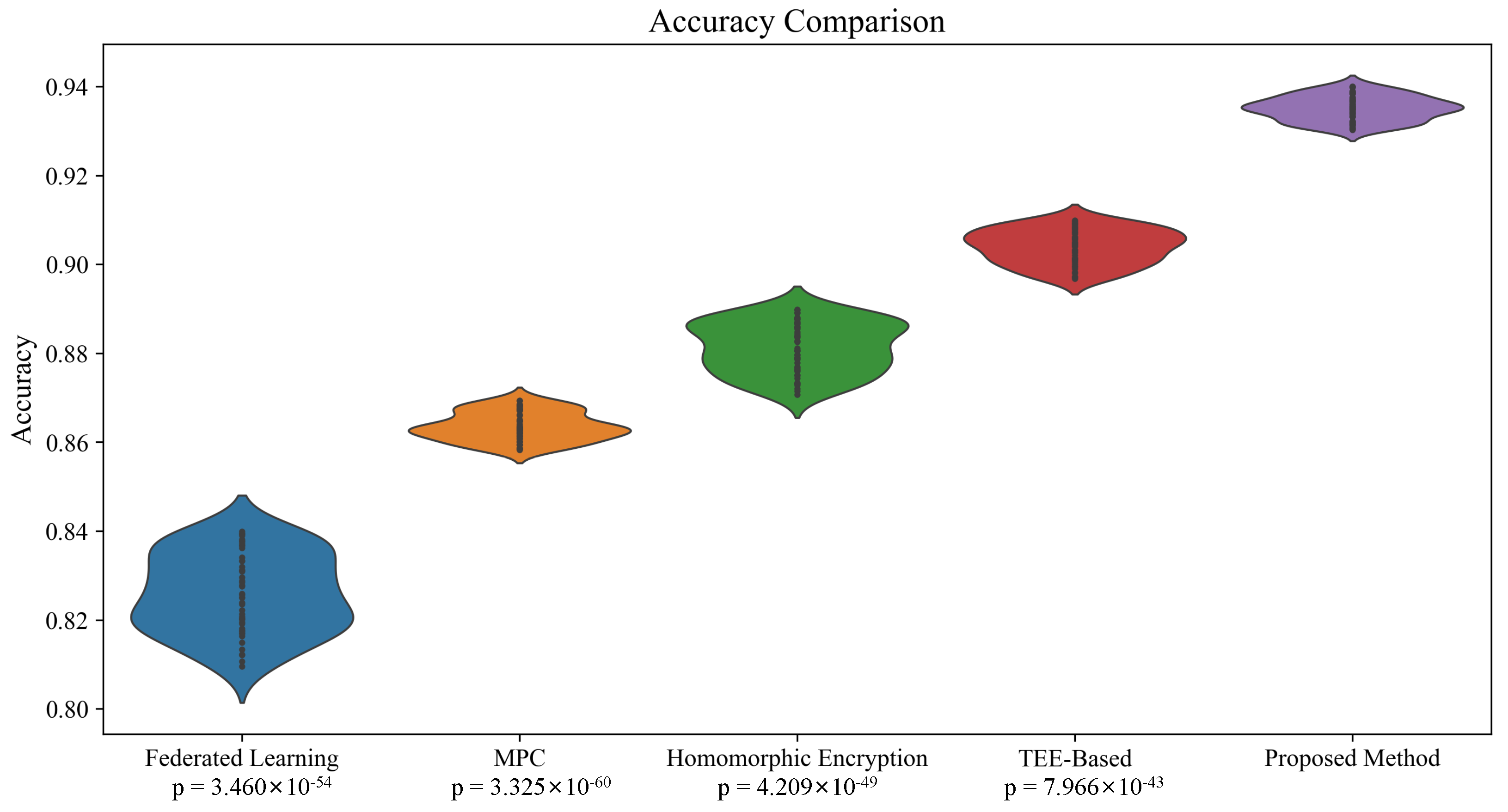
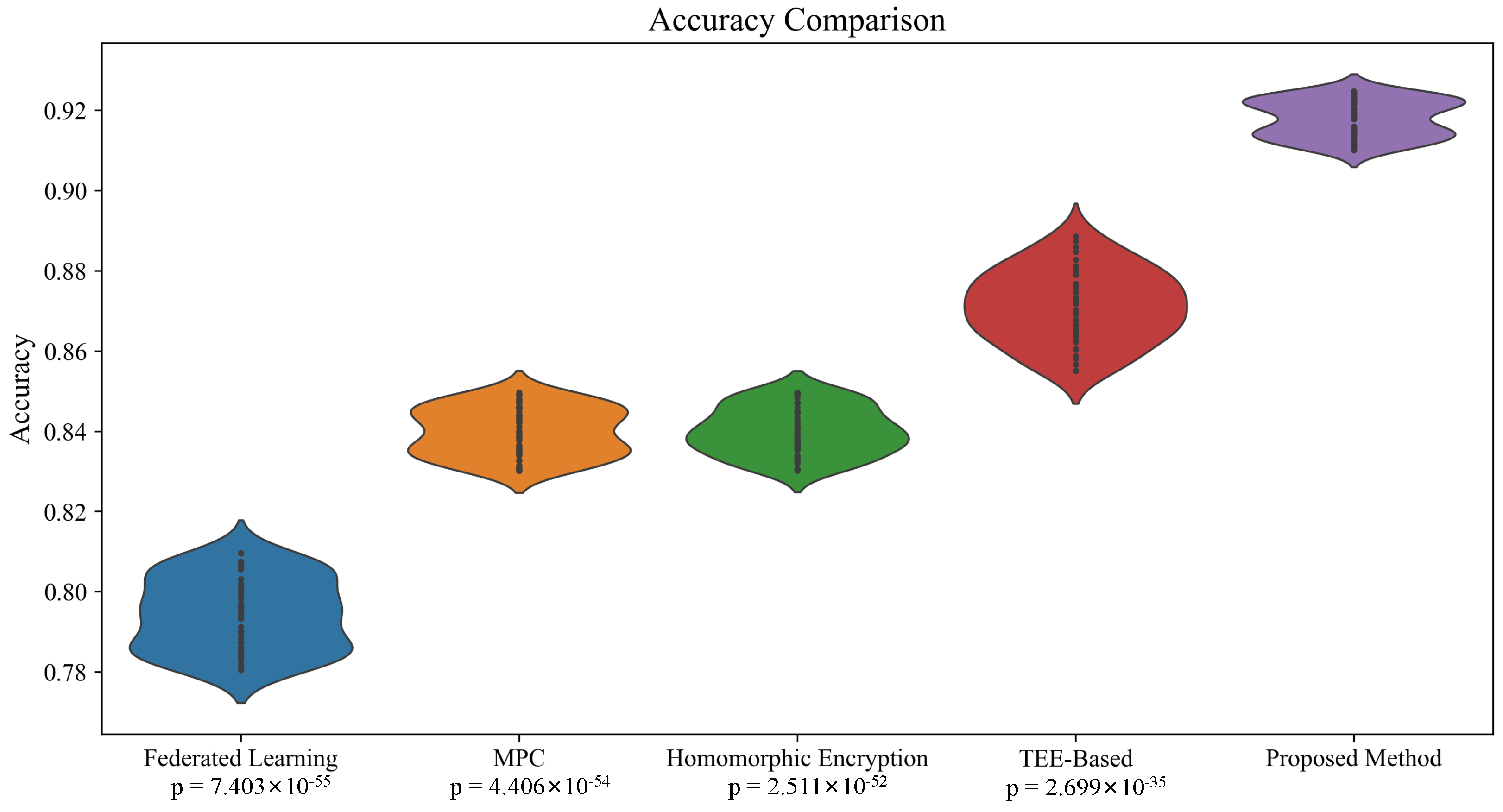
4.1. Time-Series Data Testing Results
4.2. Spatial Data Testing Results
4.3. Ablation Study on Different Attention Mechanisms
4.4. Ablation Study on Different Loss Functions
4.5. Evaluation of Model Robustness Under Synthetic Data and Adversarial Samples
4.6. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, S.; Zhou, Z.; Wang, C.; Liang, Y.; Wang, L.; Zhang, J.; Zhang, J.; Lv, C. A User-Centered Framework for Data Privacy Protection Using Large Language Models and Attention Mechanisms. Appl. Sci. 2024, 14, 6824. [Google Scholar] [CrossRef]
- An, H.; Ma, R.; Yan, Y.; Chen, T.; Zhao, Y.; Li, P.; Li, J.; Wang, X.; Fan, D.; Lv, C. Finsformer: A Novel Approach to Detecting Financial Attacks Using Transformer and Cluster-Attention. Appl. Sci. 2024, 14, 460. [Google Scholar] [CrossRef]
- Al-Ansi, A.; Al-Ansi, A.M.; Muthanna, A.; Elgendy, I.A.; Koucheryavy, A. Survey on intelligence edge computing in 6G: Characteristics, challenges, potential use cases, and market drivers. Future Internet 2021, 13, 118. [Google Scholar] [CrossRef]
- Arciniegas-Ayala, C.; Marcillo, P.; Valdivieso Caraguay, A.L.; Hernandez-Alvarez, M. Prediction of Accident Risk Levels in Traffic Accidents Using Deep Learning and Radial Basis Function Neural Networks Applied to a Dataset with Information on Driving Events. Appl. Sci. 2024, 14, 6248. [Google Scholar] [CrossRef]
- Shen, J.; Wang, N.; Wan, Z.; Luo, Y.; Sato, T.; Hu, Z.; Zhang, X.; Guo, S.; Zhong, Z.; Li, K.; et al. Sok: On the semantic ai security in autonomous driving. arXiv 2022, arXiv:2203.05314. [Google Scholar]
- Zhang, Y.; Wang, H.; Xu, R.; Yang, X.; Wang, Y.; Liu, Y. High-Precision Seedling Detection Model Based on Multi-Activation Layer and Depth-Separable Convolution Using Images Acquired by Drones. Drones 2022, 6, 152. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Wa, S.; Liu, Y.; Kang, J.; Lv, C. GenU-Net++: An Automatic Intracranial Brain Tumors Segmentation Algorithm on 3D Image Series with High Performance. Symmetry 2021, 13, 2395. [Google Scholar] [CrossRef]
- Kumar, R.; Wang, W.; Kumar, J.; Yang, T.; Khan, A.; Ali, W.; Ali, I. An integration of blockchain and AI for secure data sharing and detection of CT images for the hospitals. Comput. Med. Imaging Graph. 2021, 87, 101812. [Google Scholar] [CrossRef]
- Zhang, Y.; He, S.; Wa, S.; Zong, Z.; Lin, J.; Fan, D.; Fu, J.; Lv, C. Symmetry GAN detection network: An automatic one-stage high-accuracy detection network for various types of lesions on CT images. Symmetry 2022, 14, 234. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y.; Ren, J.; Li, Q.; Zhang, Y. You Can Use But Cannot Recognize: Preserving Visual Privacy in Deep Neural Networks. arXiv 2024, arXiv:2404.04098. [Google Scholar]
- Li, Q.; Zhang, Y. Confidential Federated Learning for Heterogeneous Platforms against Client-Side Privacy Leakages. In Proceedings of the ACM-TURC ’24: ACM Turing Award Celebration Conference-China 2024, Changsha, China, 5–7 July 2024; pp. 239–241. [Google Scholar]
- Song, L.; Wang, J.; Wang, Z.; Tu, X.; Lin, G.; Ruan, W.; Wu, H.; Han, W. Pmpl: A robust multi-party learning framework with a privileged party. In Proceedings of the CCS ’22: 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, CA, USA, 7–11 November 2022; pp. 2689–2703. [Google Scholar]
- Mammen, P.M. Federated learning: Opportunities and challenges. arXiv 2021, arXiv:2101.05428. [Google Scholar]
- Arora, S.; Beams, A.; Chatzigiannis, P.; Meiser, S.; Patel, K.; Raghuraman, S.; Rindal, P.; Shah, H.; Wang, Y.; Wu, Y.; et al. Privacy-preserving financial anomaly detection via federated learning & multi-party computation. arXiv 2023, arXiv:2310.04546. [Google Scholar]
- Odeh, A.; Abdelfattah, E.; Salameh, W. Privacy-Preserving Data Sharing in Telehealth Services. Appl. Sci. 2024, 14, 10808. [Google Scholar] [CrossRef]
- Pulido-Gaytan, B.; Tchernykh, A.; Cortés-Mendoza, J.M.; Babenko, M.; Radchenko, G.; Avetisyan, A.; Drozdov, A.Y. Privacy-preserving neural networks with homomorphic encryption: C hallenges and opportunities. Peer-Netw. Appl. 2021, 14, 1666–1691. [Google Scholar]
- Imteaj, A.; Amini, M.H. Leveraging asynchronous federated learning to predict customers financial distress. Intell. Syst. Appl. 2022, 14, 200064. [Google Scholar] [CrossRef]
- Ali, A.; Pasha, M.F.; Ali, J.; Fang, O.H.; Masud, M.; Jurcut, A.D.; Alzain, M.A. Deep learning based homomorphic secure search-able encryption for keyword search in blockchain healthcare system: A novel approach to cryptography. Sensors 2022, 22, 528. [Google Scholar] [CrossRef]
- El Ouadrhiri, A.; Abdelhadi, A. Differential privacy for deep and federated learning: A survey. IEEE Access 2022, 10, 22359–22380. [Google Scholar]
- Sander, T.; Stock, P.; Sablayrolles, A. Tan without a burn: Scaling laws of dp-sgd. In Proceedings of the 40th International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 29937–29949. [Google Scholar]
- Wu, P.; Ning, J.; Shen, J.; Wang, H.; Chang, E.C. Hybrid Trust Multi-party Computation with Trusted Execution Environment. In Proceedings of the Network and Distributed Systems Security (NDSS) Symposium, San Diego, CA, USA, 24–28 April 2022. [Google Scholar]
- Zhou, L.; Diro, A.; Saini, A.; Kaisar, S.; Hiep, P.C. Leveraging zero knowledge proofs for blockchain-based identity sharing: A survey of advancements, challenges and opportunities. J. Inf. Secur. Appl. 2024, 80, 103678. [Google Scholar]
- Liu, Q.; Yang, L.; Liu, Y.; Deng, J.; Wu, G. Privacy-Preserving Recommendation Based on a Shuffled Federated Graph Neural Network. IEEE Internet Comput. 2024, 28, 17–24. [Google Scholar] [CrossRef]
- Li, L.; Gou, J.; Yu, B.; Du, L.; Tao, Z.Y.D. Federated distillation: A survey. arXiv 2024, arXiv:2404.08564. [Google Scholar]
- Wen, J.; Zhang, Z.; Lan, Y.; Cui, Z.; Cai, J.; Zhang, W. A survey on federated learning: Challenges and applications. Int. J. Mach. Learn. Cybern. 2023, 14, 513–535. [Google Scholar]
- Kanchan, S.; Jang, J.W.; Yoon, J.Y.; Choi, B.J. GSFedSec: Group Signature-Based Secure Aggregation for Privacy Preservation in Federated Learning. Appl. Sci. 2024, 14, 7993. [Google Scholar] [CrossRef]
- Li, Q.; Ren, J.; Zhang, Y.; Song, C.; Liao, Y.; Zhang, Y. Privacy-Preserving DNN Training with Prefetched Meta-Keys on Heterogeneous Neural Network Accelerators. In Proceedings of the 2023 60th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 9–13 July 2023; pp. 1–6. [Google Scholar]
- Byrd, D.; Polychroniadou, A. Differentially private secure multi-party computation for federated learning in financial applications. In Proceedings of the First ACM International Conference on AI in Finance, New York, NY, USA, 15–16 October 2020; pp. 1–9. [Google Scholar]
- Liu, X.; Liu, X.; Zhang, R.; Luo, D.; Xu, G.; Chen, X. Securely Computing the Manhattan Distance under the Malicious Model and Its Applications. Appl. Sci. 2022, 12, 11705. [Google Scholar] [CrossRef]
- Zhou, I.; Tofigh, F.; Piccardi, M.; Abolhasan, M.; Franklin, D.; Lipman, J. Secure Multi-Party Computation for Machine Learning: A Survey. IEEE Access 2024, 12, 53881–53899. [Google Scholar] [CrossRef]
- Dhiman, S.; Nayak, S.; Mahato, G.K.; Ram, A.; Chakraborty, S.K. Homomorphic encryption based federated learning for financial data security. In Proceedings of the 2023 4th International Conference on Computing and Communication Systems (I3CS), Shillong, India, 16–18 March 2023; pp. 1–6. [Google Scholar]
- Acar, A.; Aksu, H.; Uluagac, A.S.; Conti, M. A survey on homomorphic encryption schemes: Theory and implementation. ACM Comput. Surv. 2018, 51, 79. [Google Scholar]
- Fan, J.; Vercauteren, F. Somewhat Practical Fully Homomorphic Encryption. Cryptology ePrint Archive. 2012; p. 144. Available online: https://eprint.iacr.org/2012/144 (accessed on 27 March 2025).
- Damgård, I.; Pastro, V.; Smart, N.; Zakarias, S. Multiparty computation from somewhat homomorphic encryption. In Advances in Cryptology—CRYPTO 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 643–662. [Google Scholar]
- Lee, E.; Lee, J.W.; Kim, Y.S.; No, J.S. Optimization of homomorphic comparison algorithm on rns-ckks scheme. IEEE Access 2022, 10, 26163–26176. [Google Scholar]
- Zhang, Y.; Yin, Z.; Li, Y.; Yin, G.; Yan, J.; Shao, J.; Liu, Z. Celeba-spoof: Large-scale face anti-spoofing dataset with rich annotations. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Part XII 16. pp. 70–85. [Google Scholar]
- Contreras, J.; Espinola, R.; Nogales, F.J.; Conejo, A.J. ARIMA models to predict next-day electricity prices. IEEE Trans. Power Syst. 2003, 18, 1014–1020. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Networks Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The long-document transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Zaheer, M.; Guruganesh, G.; Dubey, K.A.; Ainslie, J.; Alberti, C.; Ontanon, S.; Pham, P.; Ravula, A.; Wang, Q.; Yang, L.; et al. Big bird: Transformers for longer sequences. Adv. Neural Inf. Process. Syst. 2020, 33, 17283–17297. [Google Scholar]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and open problems in federated learning. Found. Trends® Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Evans, D.; Kolesnikov, V.; Rosulek, M. A pragmatic introduction to secure multi-party computation. Found. Trends® Priv. Secur. 2018, 2, 70–246. [Google Scholar] [CrossRef]
- Naehrig, M.; Lauter, K.; Vaikuntanathan, V. Can homomorphic encryption be practical? In Proceedings of the 3rd ACM Workshop on Cloud Computing Security Workshop, Chicago, IL, USA, 21 October 2011; pp. 113–124. [Google Scholar]
- Sabt, M.; Achemlal, M.; Bouabdallah, A. Trusted execution environment: What it is, and what it is not. In Proceedings of the 2015 IEEE Trustcom/BigDataSE/ISPA, Helsinki, Finland, 20–22 August 2015; Volume 1, pp. 57–64. [Google Scholar]
- Yang, Z.; Li, P.; Bao, Y.; Huang, X. Speeding Up Multivariate Time Series Segmentation Using Feature Extraction. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; Volume 1, pp. 954–957. [Google Scholar] [CrossRef]
- Zhou, N.; Zheng, Z.; Zhou, J. Prediction of the RUL of PEMFC based on multivariate time series forecasting model. In Proceedings of the 2023 3rd International Symposium on Computer Technology and Information Science (ISCTIS), Chengdu, China, 7–9 July 2023; pp. 87–92. [Google Scholar]
- Di Mauro, M.; Galatro, G.; Postiglione, F.; Song, W.; Liotta, A. Hybrid learning strategies for multivariate time series forecasting of network quality metrics. Comput. Netw. 2024, 243, 110286. [Google Scholar] [CrossRef]
- Du, W.; Côté, D.; Liu, Y. Saits: Self-attention-based imputation for time series. Expert Syst. Appl. 2023, 219, 119619. [Google Scholar] [CrossRef]
- Liang, Y.; Lin, Y.; Lu, Q. Forecasting gold price using a novel hybrid model with ICEEMDAN and LSTM-CNN-CBAM. Expert Syst. Appl. 2022, 206, 117847. [Google Scholar] [CrossRef]
- Ramachandran, P.; Parmar, N.; Vaswani, A.; Bello, I.; Levskaya, A.; Shlens, J. Stand-alone self-attention in vision models. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Du, R.; Chen, H.; Yu, M.; Li, W.; Niu, D.; Wang, K.; Zhang, Z. 3DTCN-CBAM-LSTM short-term power multi-step prediction model for offshore wind power based on data space and multi-field cluster spatio-temporal correlation. Appl. Energy 2024, 376, 124169. [Google Scholar] [CrossRef]
| Data Type | Number of Entries |
|---|---|
| Stock Prices | 50,923 |
| Stock Volatility | 37,010 |
| Market Sentiment Index | 29,741 |
| Trading Volume | 40,532 |
| Turnover Rate | 25,994 |
| Category | Number of Entries |
|---|---|
| Smiling | 9760 |
| Not Smiling | 8341 |
| Wearing Glasses | 9957 |
| Not Wearing Glasses | 7803 |
| Other | 8675 |
| Model | Precision | Recall | Accuracy | F1-Score | FPS |
|---|---|---|---|---|---|
| Federated Learning [42] | 0.86 | 0.81 | 0.84 | 0.83 | 29 |
| MPC [43] | 0.88 | 0.85 | 0.87 | 0.86 | 34 |
| Homomorphic Encryption [44] | 0.90 | 0.87 | 0.89 | 0.88 | 37 |
| TEE-Based [44] | 0.92 | 0.89 | 0.91 | 0.90 | 40 |
| Proposed Method | 0.95 | 0.91 | 0.93 | 0.93 | 46 |
| Model | Precision | Recall | Accuracy | F1-Score | FPS |
|---|---|---|---|---|---|
| Federated Learning | 0.84 | 0.79 | 0.81 | 0.81 | 26 |
| MPC | 0.87 | 0.83 | 0.85 | 0.85 | 32 |
| Homomorphic Encryption | 0.88 | 0.84 | 0.86 | 0.85 | 38 |
| TEE-Based | 0.91 | 0.87 | 0.89 | 0.89 | 42 |
| Proposed Method | 0.93 | 0.90 | 0.92 | 0.91 | 49 |
| Model | Precision | Recall | Accuracy | F1-Score | FPS |
|---|---|---|---|---|---|
| Time-Series—Standard Self-Attention [49] | 0.73 | 0.70 | 0.72 | 0.71 | 31 |
| Time-Series—CBAM [50] | 0.85 | 0.81 | 0.83 | 0.83 | 35 |
| Time-Series—Proposed Method | 0.95 | 0.91 | 0.93 | 0.93 | 46 |
| Spatial Data—Standard Self-Attention [51] | 0.71 | 0.68 | 0.70 | 0.69 | 33 |
| Spatial Data—CBAM [52] | 0.83 | 0.80 | 0.82 | 0.81 | 40 |
| Spatial Data—Proposed Method | 0.93 | 0.90 | 0.92 | 0.91 | 49 |
| Model | Precision | Recall | Accuracy | F1-Score | FPS |
|---|---|---|---|---|---|
| Time-Series—Cross-Entropy Loss | 0.69 | 0.65 | 0.67 | 0.67 | 27 |
| Time-Series—Focal Loss | 0.87 | 0.82 | 0.84 | 0.83 | 34 |
| Time-Series—Proposed Method | 0.95 | 0.91 | 0.93 | 0.93 | 46 |
| Spatial Data—Cross-Entropy Loss | 0.66 | 0.63 | 0.65 | 0.64 | 30 |
| Spatial Data—Focal Loss | 0.84 | 0.80 | 0.82 | 0.82 | 37 |
| Spatial Data—Proposed Method | 0.93 | 0.90 | 0.92 | 0.91 | 49 |
| Model | Precision | Recall | Accuracy | F1-Score | FPS |
|---|---|---|---|---|---|
| Time-Series—None | 0.63 | 0.60 | 0.62 | 0.61 | 28 |
| Time-Series—Synthetic Data | 0.74 | 0.71 | 0.73 | 0.73 | 34 |
| Time-Series—Adversarial Samples | 0.88 | 0.83 | 0.85 | 0.84 | 37 |
| Time-Series—Proposed Method | 0.95 | 0.91 | 0.93 | 0.93 | 46 |
| Spatial Data—None | 0.65 | 0.68 | 0.66 | 0.67 | 31 |
| Spatial Data—Synthetic Data | 0.73 | 0.70 | 0.72 | 0.71 | 38 |
| Spatial Data—Adversarial Samples | 0.85 | 0.81 | 0.83 | 0.82 | 42 |
| Spatial Data—Proposed Method | 0.93 | 0.90 | 0.92 | 0.91 | 49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, W.; Lin, Q.; Shi, J.; Zhou, X.; Li, Z.; Zhan, H.; Qin, Y.; Lv, C. A Secure and Efficient Framework for Multimodal Prediction Tasks in Cloud Computing with Sliding-Window Attention Mechanisms. Appl. Sci. 2025, 15, 3827. https://doi.org/10.3390/app15073827
Cui W, Lin Q, Shi J, Zhou X, Li Z, Zhan H, Qin Y, Lv C. A Secure and Efficient Framework for Multimodal Prediction Tasks in Cloud Computing with Sliding-Window Attention Mechanisms. Applied Sciences. 2025; 15(7):3827. https://doi.org/10.3390/app15073827
Chicago/Turabian StyleCui, Weiyuan, Qianye Lin, Jiaqi Shi, Xingyu Zhou, Zeyue Li, Haoyuan Zhan, Yihan Qin, and Chunli Lv. 2025. "A Secure and Efficient Framework for Multimodal Prediction Tasks in Cloud Computing with Sliding-Window Attention Mechanisms" Applied Sciences 15, no. 7: 3827. https://doi.org/10.3390/app15073827
APA StyleCui, W., Lin, Q., Shi, J., Zhou, X., Li, Z., Zhan, H., Qin, Y., & Lv, C. (2025). A Secure and Efficient Framework for Multimodal Prediction Tasks in Cloud Computing with Sliding-Window Attention Mechanisms. Applied Sciences, 15(7), 3827. https://doi.org/10.3390/app15073827





