MSSP: A Blockchain Sharding Protocol Based on Multi-Shard Storage

Abstract

Sharding is currently one of the mainstream technologies for solving the scalability problem in blockchain systems. However, with the increase in shard numbers, the coordination and management of cross-shard transactions become more complex, limiting the scalability of the system. Existing methods usually split cross-shard transactions into multiple sub-transactions for processing, which not only reduces throughput but also increases transaction latency. This paper proposes a blockchain sharding protocol based on multi-shard storage to address this issue. In this protocol, nodes can store data from multiple shards, and nodes that store the same shard set form a consensus zone, which can directly handle cross-shard transactions and improve transaction processing efficiency. We propose a priority sorting mechanism to defend against double-spending attacks effectively. In addition, we introduce a P-probability return update completion proof mechanism to ensure node data consistency while enhancing blockchain security. Finally, we conduct a security analysis and performance testing of this protocol. The results show that the multi-shard storage protocol has significant advantages in terms of throughput, latency, and security compared to traditional sharding protocols.

1. Introduction

The rise of cryptocurrencies such as Bitcoin [1] and Ethereum [2] has brought widespread attention to blockchain technology. It is composed of interconnected blocks, forming an immutable transaction ledger, with each block containing verified transactions and the hash value of the previous block [3]. Currently, blockchain technology has been significantly applied in various fields including supply chain management [4], digital identity authentication [5], digitization of healthcare information [6], and the Internet of Things (IoT) [7,8].

With the development of blockchain technology, scalability has become a key attribute affecting the widespread application of blockchain technology [9,10]. Sharding is currently one of the most promising technologies to improve the scalability of blockchain systems [11,12]. Its basic principle is to divide nodes into multiple shards, with each shard responsible for maintaining an independent blockchain and only processing transactions related to its own stored state [13]. Sharding technology has been widely applied in multiple blockchain projects, such as ELASTICO [14] and Zilliqa [15]. In recent years, this technology has continued to evolve, with optimizations in throughput, latency, consensus protocols, and other aspects [16,17,18].

Although sharding technology has significantly improved the performance and scalability of blockchain systems, it still faces numerous challenges in handling cross-shard transactions [19]. Cross-shard transactions involve data synchronization and communication between multiple shards, leading to additional overhead, which reduces system efficiency and increases latency. To address this issue, existing research has proposed various sharding system solutions. For instance, RapidChain [20] and RepChain [21] divide cross-shard transactions into multiple sub-transactions, which are processed separately by the relevant shards. However, this approach may result in a surge in the number of sub-transactions, thereby undermining the advantages of sharding. BrokerChain [22] proposes a broker mechanism that utilizes Broker accounts to handle cross-shard transactions, achieving load balancing. Additionally, Estuary [23] has designed a multi-level state model that introduces state splitting and aggregation mechanisms, making state management more flexible and dynamically adjustable according to demand. This mechanism significantly reduces the number of cross-shard transactions and lowers communication overhead and complexity. Although the aforementioned methods have improved system performance to some extent, they have not completely eliminated the additional communication overhead caused by cross-shard transactions. Therefore, further optimizing the processing mechanisms for cross-shard transactions remains an important direction for future research.

This paper proposes a new blockchain sharding protocol based on multi-shard storage. The core idea is to allow some nodes in the blockchain to store multiple shard data, and these nodes can directly process cross-shard transactions, thus improving the efficiency of cross-shard transaction processing. In MSSP, the consensus zone consists of nodes storing the same multiple shards, making shards no longer equivalent to consensus zones. Therefore, the content stored by consensus nodes in the same shard may be inconsistent. This change transforms the data structure of the blockchain in a shard from a chain to a tree, eliminating the ability of traditional blockchains to defend against double-spending attacks [24]. To address this issue, we propose a priority sorting mechanism. It is crucial for all nodes storing relevant account data to be promptly updated after cross-shard transaction processing is completed. To ensure this, we propose a P-probability return update completion proof mechanism to guarantee that relevant nodes are promptly updated and enhance the security of the blockchain. Finally, experimental verification demonstrates that MSSP has significant advantages over traditional sharding protocols in terms of throughput, latency and security.

The contributions of this paper are as follows:

• Proposed a sharding protocol MSSP based on multi-shard storage for blockchain. Multi-shard storage is a novel storage mechanism in which nodes in the blockchain network store data from multiple shards. The collection of nodes storing the same multiple shards forms a consensus zone. These consensus zones enable direct processing of cross-shard transactions related to the stored shards, eliminating the need for complex coordination between separate shards. Compared to traditional single-shard storage, multi-shard storage significantly reduces the communication overhead and latency associated with cross-shard transactions, thereby improving transaction throughput and overall system performance.
• Designed a priority sorting mechanism to ensure the security of the blockchain system. This mechanism sets priorities for consensus zones, automatically adjusts them based on specified conditions, and sorts blocks according to the priorities of consensus zones. This mechanism provides the ability to resist double-spending attacks for the tree-like blockchain structure under the protocol while ensuring fairness.
• Introduced a P-probability return update completion proof mechanism, allowing nodes to probabilistically return a proof indicating that an update has been completed. This mechanism ensures that after cross-shard transactions are completed, all nodes storing relevant account data can be updated promptly and enhances the security of the blockchain.
• Conducted a theoretical analysis of the security of MSSP, implementation of a prototype of the scheme, and evaluation of its performance. The results indicate that compared to traditional sharding, this protocol exhibits significant performance and security advantages.

2. Related Work

Kokoris-Kogias et al. [16] proposed the first complete sharded blockchain system OmniLedger in 2018. However, while sharding improves efficiency it also brings challenges in the form of cross-shard transactions. OmniLedger adopts a client-driven mechanism for cross-shard transactions. Clients generate cross-shard transaction requests and send them to shard nodes in the network, which then forward the requests to target shard nodes. The target shard nodes verify and execute the transactions, and return the results to the clients for final confirmation and state update. This mechanism heavily relies on clients, adding extra burden to user nodes.

Rapidchain [20] proposed a sharding-driven mechanism based on the UTXO model to handle cross-shard transactions. When a cross-shard transaction occurs, the system generates a new transaction to transfer the corresponding UTXOs to the same shard. As a result, cross-shard transactions become intra-shard transactions and can be processed within a single shard. Monoxide [25] introduced a relay mechanism in account/balance-based systems to handle cross-shard transactions through inter-shard message passing. It decomposes cross-shard transactions into multiple sub-transactions. When transitioning from one sub-transaction to another, i.e., from one shard to another, an additional relay transaction is used to pass inter-shard messages. Ultimately, this transforms cross-shard transactions into multiple intra-shard transactions for processing.

The basic idea of the cross-shard mechanism in the above-mentioned sharding system is to divide each cross-shard transaction into multiple sub-transactions, which are then sent to their respective shards for validation and execution. The cross-shard transaction can only be considered completed when the sub-transactions on each shard are confirmed. This greatly impacts the performance of sharded blockchains in terms of throughput and latency.

The excessively high cross-shard transaction rate not only adds extra transaction load to the system but also results in a significant amount of cross-shard communication overhead [26,27]. Therefore, much research has focused on reducing the number of cross-shard transactions. BrokerChain [22] proposed a new mechanism for handling cross-shard transactions. This mechanism partitions the state of selected accounts designated as Brokers so that they exist in each shard. When there are cross-shard transactions between shards, Brokers can be used for processing. By introducing Broker accounts to reduce the number of cross-shard transactions and accelerate their on-chain processing.

In recent years, researchers have proposed numerous cross-shard transaction processing schemes to optimize the performance of blockchain systems. Below is a summary of some representative processing schemes. Liu et al. [28] designed a cross-shard Byzantine fault-tolerant protocol to reduce the confirmation latency when processing cross-shard transactions. Han et al. [29] proposed a graph-based sharding blockchain transaction optimization scheme, addressing the issue of uneven shard load caused by excessive cross-shard transactions. Recently, Zhang et al. [30] introduced an off-chain execution model called ShardCon, which decouples contract execution from cross-shard consensus to achieve efficient execution of complex cross-shard contracts. Jia et al. [23] put forward a novel low-cross-shard blockchain sharding protocol Estuary. Starting from the state model, Estuary designed a multi-level state model and state splitting aggregation mechanism that decouples the identity and quantity of state units, enabling transactions between users to be completed within one shard. Xu et al. [31] designed a blockchain system for optimizing cross-shard transaction processing by allocating transactions to shards based on historical transaction patterns to minimize cross-shard transactions as much as possible. However, although these methods can improve system performance, the additional communication overhead required for cross-shard transactions still exists.

3. System Model and Threat Model

3.1. System Model

MSSP uses an account/balance model to represent the status of the ledger. The nodes in the blockchain are network entities that run this protocol and are interconnected through P2P networks. The system uses PBFT (Practical Byzantine Fault Tolerance) [32], which is a consensus algorithm designed to tolerate Byzantine faults to achieve consensus between nodes. In traditional sharding protocols, each node is assigned to a shard, where the nodes in the shard only participate in maintaining and preserving the blockchain data of that shard. MSSP enables nodes to store data from multiple shards. Therefore, compared with traditional sharding protocols, MSSP divides nodes into two types:

• s-node: each s-node is responsible for storing the data of a single shard and handling internal transactions of the stored shard, similar to nodes in traditional sharded blockchains.
• m-node: each m-node stores the data of multiple shards and can process cross-shard transactions among the shards that it stores.

The classification of nodes in MSSP is shown in Figure 1. In shard A, nodes that only store the blockchain data of shard A are s-nodes, while nodes that store both shard A and shard B, as well as nodes that store both shard A and shard C, are m-nodes. Nodes that only store data from shard A are responsible for processing internal transactions within shard A, while nodes that store data from both shard A and shard B are responsible for processing cross-shard transactions between shard A and shard B.

3.2. Threat Model

In MSSP, nodes are categorized into honest nodes and malicious nodes. Honest nodes strictly adhere to the blockchain protocols, actively participate in consensus, and ensure the normal operation of the network. In contrast, malicious nodes do not follow the prescribed rules and may engage in various destructive behaviors, such as broadcasting false information, attempting double-spending attacks, or colluding with other malicious nodes to disrupt consensus. These behaviors pose significant threats to the security and credibility of the blockchain. In our study, we assume a slow-adaptive attack model [16], where the set of malicious nodes remains fixed during each epoch and can only change between epochs.

4. System Design

MSSP allows nodes to store data from multiple shards, enabling them to directly handle cross-shard transactions without the need for additional inter-shard communication. This protocol adopts a space-for-time strategy, effectively reducing the complexity of cross-shard transaction communication and improving the performance of sharded systems. The relevant terms are shown in

Table 1. Terminology explanation.

Terminology	Explanation
N	Number of blockchain nodes
S	Number of shards
n	Number of nodes in each shard
M	Number of m-nodes in each shard
$Ni$	Blockchain node numbering
f	The number of malicious nodes
k	Number of shards stored in m-node
$\lambda$	Security parameter
$Si$	Blockchain shard numbering
$ss$	The collection of selected storage shards
R	A public random number
A	The address of the blockchain node
$Ci$	Consensus zone numbering
$cp$	Consensus zone priority

.

Next, we will provide a detailed introduction to MSSP in terms of four elements: multi-shard selection, consensus zone division, block sorting, and data update.

4.1. Multi-Shard Selection

At the initial stage, the blockchain is divided into S shards, with the i-th shard denoted as $Si$. After the shard division is completed, a portion of nodes are designated as m-nodes. The task of these m-nodes is to store multiple shards, with the number of stored shards represented by k. The value of k cannot exceed the number of shards S.

For ease of description, we illustrate the process with the example of $k=2$. When k is set to 2, m-nodes within ${\mathrm{shard}}_i$ will store data from both ${\mathrm{shard}}_i$ and ${\mathrm{shard}}_j$, where $i\ne j$. The ${\mathrm{shard}}_j$ is calculated by concatenating the address A of the blockchain node with the public random number R:

$$j=\mathrm{TRUNCATE}\left(\mathrm{SHA}-256\right(A \Vert R),5)$$

(1)

SHA-256 is an encryption hash function that takes $A \Vert R$ as input and produces a 256-bit hash value. TRUNCATE(∗, 5) truncates the first 5 bits of the string to form the identifier for ${\mathrm{shard}}_j$. This multi-shard selection scheme allows consensus nodes to easily verify whether other nodes have correctly selected and stored shards. Nodes that do not meet this standard will be rejected by the consensus nodes.

The multi-shard selection algorithm is illustrated in Algorithm 1. After selecting the m-node from the shard, k shards are chosen for storage based on Equation (1). R is a randomly generated value that changes each time the hash is computed, ensuring that the hash function produces random outputs each time. As a result, the final outcome of j will be uniformly distributed, guaranteeing that the multi-shard storage selection for m-nodes is both random and balanced.

Algorithm 1 Select-shard algorithm

Input: S: Number of shards, $S_i$: Blockchain shard numbering, k: Number of shards stored in m-node, R: A random number, A: The address of the blockchain node, m: Number of m-node in each shard, $N_i$: Blockchain node numbering Output: $SS$: The collection of selected storage shards   1: procedure SelectShard($S,k,m$)   2:    for shardNumber from 1 to S do   3:          $N_i=\mathtt{SelectNodes}(S_i,m)$   4:          for nodeNumber from 1 to m do   5:             $SS.n_i\leftarrow S_i\cup SS.n_i$   6:             while length($SS.n_i$) < k do   7:                   $S_i=\mathtt{TRUNCATE}(\mathtt{HASH}(A\parallel R),5)$   8:                   if $S_i\notin SS.n_i$ then   9:                      $SS.n_i\leftarrow S_i\cup SS.n_i$ 10:                      $R=\mathtt{updateR}\left(R\right)$ 11:                   end if 12:             end while 13:             $SS\leftarrow SS\cup SS.n_i$ 14:         end for 15:   end for 16: end procedure

4.2. Consensus Zone Division

In MSSP, a node is allowed to store data from multiple shards. The selection of multiple-shard storage on a node is random, and this randomness can lead to inconsistent storage content among different consensus nodes in the same shard. Therefore, the relationship between the consensus zone and shards is no longer one-to-one.The consensus zone consists of nodes that store multiple identical shards.

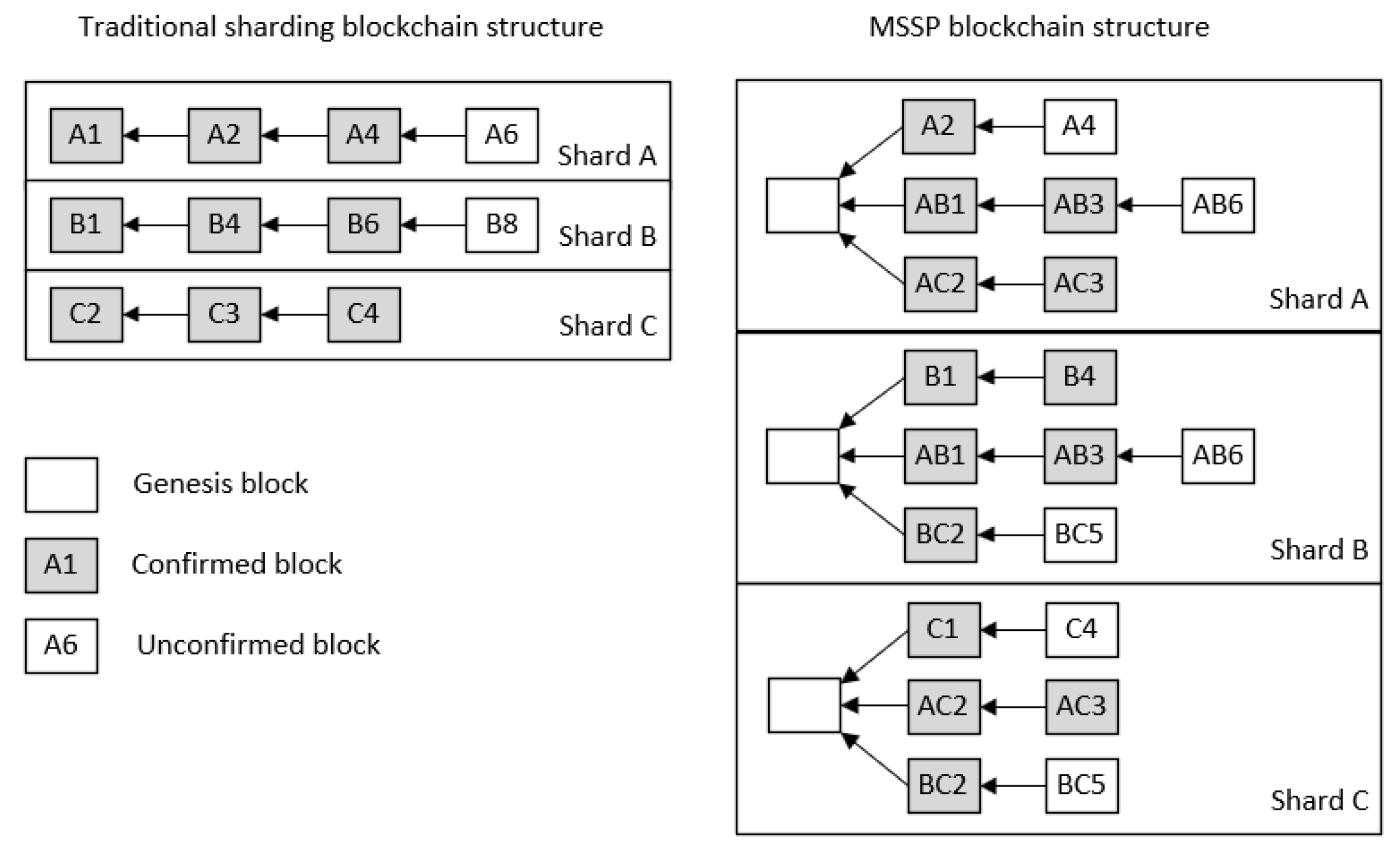
Figure 2 illustrates the relationship between sharding and consensus zones in MSSP. It can be observed from the figure that nodes storing AB in shard A and nodes storing AB in shard B form a consensus zone, which can directly verify and execute cross-shard transactions involving shard A and shard B without the traditional two-stage commit (2PC) process. The set of nodes that store both shard A and shard B is referred to as the consensus zone AB. It is important to note that when it comes to state updates, ensuring consistency of cross-shard transactions by synchronously updating all relevant shards is crucial.

In MSSP, the processing of cross-shard transactions is carried out by a specific set of consensus nodes. This designated consensus cluster is responsible for validating cross-shard transactions and packaging them into the corresponding data blocks. For example, the cross-shard transactions between ${\mathrm{shard}}_i$ and ${\mathrm{shard}}_j$ are handled by the nodes that store these two shards. These transactions are recorded in their respective data blocks, with each such data block containing only the transactions involving these two shards.This method of handling cross-shard transactions can be flexibly extended to scenarios involving three or more shards.

4.3. Block Sorting

4.3.1. Blockchain Structure

In the blockchain system using MSSP, m-nodes in the consensus zone will randomly store data from multiple shards. Therefore, nodes in different consensus zones may store data of the same shard, and a block generated by a certain consensus zone may need to be stored by nodes that do not belong to this consensus zone. For example, nodes in shard A and shard B must both store the blocks generated by consensus zone AB, even if some nodes in the shard do not belong to consensus zone AB. This design leads to a blockchain data structure in the shard that is similar to a tree rather than a linear chain with each fork in the tree corresponding to a consensus zone. As shown in Figure 3, the multi-shard stored blockchain structure is a tree, with shard A containing three chains where blocks on these three chains are generated, respectively, by consensus zone A, AB, and AC.

4.3.2. Priority Sorting Mechanism

The tree like structure of blockchain eliminates the network’s ability to resist double-spending attacks. To better understand this issue, we consider a specific scenario as shown in Figure 4. In shard A, a node ${\mathrm{n}}_1$ attempts to execute two transactions simultaneously, intending to send the same token to node ${\mathrm{n}}_2$ in shard B and node ${\mathrm{n}}_3$ in shard C. At this point, the balance in the account of ${\mathrm{n}}_1$ is only 1, which is insufficient to complete both transactions. However, due to the independent operation of nodes in consensus zones AB and AC, they may not be able to verify the transaction information of the other party promptly and mistakenly assume that both transactions are valid. As a result, these two consensus zones independently add the transactions to their respective created blocks. Given the tree-like structure of the blockchain at this point, each consensus zone generates mutually independent chains, thus, the traditional mechanism for resolving transaction conflicts through rollback becomes ineffective.

To address this issue, we propose a priority sorting mechanism.This mechanism consists of two parts: block sorting and priority auto-tuning. The consensus zone priority is set based on the total number of valid blocks generated in a cycle in the consensus zone. The block sorting process is shown in Figure 5. During the traversal process, a confirmed block is selected from each branch and sorted based on the consensus zone priority. This iteration process transforms the tree-shaped blockchain into a linear chain structure. When encountering conflicting blocks, their priorities are first checked. If a block has a higher priority, it is sorted while other conflicting blocks are discarded. Under this sorting mechanism, only blocks that have successfully passed through the sorting process without conflicts and have been confirmed are considered as valid components of the blockchain.

After the sorting process, the blockchain is restored to a traditional linear structure, thereby regaining the ability to resist double-spending attacks. However, this sorting mechanism is inherently unfair because blocks generated by consensus zones with higher priority are given precedence in the ordering. Since the priority of consensus zones cannot dynamically change, they become predictable, and malicious attackers can purposefully elevate the priority of their controlled consensus zones. This predictability allows them to gain an advantage more easily within the network.

To address the fairness and security issues caused by static priorities, we propose a priority auto-tuning method. The priority auto-tuning method is shown in Algorithm 2. In this method, each consensus zone is assigned an initial priority, which decreases gradually with each block submission until it reaches the lowest priority level (Line 1–3). Once the lowest priority is reached, the priority is reset to the highest level based on predefined conditions (Line 4–6). This dynamic adjustment mechanism reduces the predictability of consensus zone priorities, making it more difficult for attackers to exploit the system and enhancing overall fairness and security.

Algorithm 2 Adjust consensus zone priority algorithm

Input: $C_i$: Consensus zone numbering Output: $cp$: Consensus zone priority 1: if  Block confirmation then 2:    $cp=\mathtt{decreaseCP}\left(C_i\right)$ 3:    if $cp==\mathtt{MIN}\_\mathtt{CP}$ then 4:         $confirmations=\mathtt{getConfirmations}\left(C_i\right)$ 5:         if $confirmations\ge \mathtt{REQUIRED}\_\mathtt{CONFIRMATIONS}$ then 6:              $cp=\mathtt{increaseCP}\left(C_i\right)$ 7:         end if 8:    end if 9: end if

4.4. Data Update

After the completion of cross-shard transaction processing, all nodes storing relevant account data must be updated to ensure data consistency. Due to the nature of MSSP, synchronization may be required across multiple shards after a cross-shard transaction is completed. For example, a cross-shard transaction processed by consensus zone AC should be simultaneously updated in shard A and shard C.

The MSSP requires leaders of the consensus zone to be responsible for sending notifications to relevant shards to update their status. These update notifications include transaction details, proofs, and the account data required for updates. Subsequently, the nodes receiving the update notifications return proofs to indicate the completion of the update process. In addition, the P-probability return update completion proof mechanism is adopted to probabilistically return proofs of completion, with the size of the probability p determined by the update status of previous rounds of nodes.

The system has a buffer maintained collectively by all nodes, specifically for storing information on whether each node has completed updates promptly in the most recent four rounds. When a node needs to return proof of completion of updates, it will check the buffer. If the node has failed to complete an update on time once within these four rounds, it will return the proof with a probability of 1/4. If there are two missed updates, the probability of returning the proof will increase to 1/2. If there are three missed updates, the node must provide proof of completion for the update. If there are four missed updates, it is determined that this node has an issue. In this case, the manager is notified to detect and prevent its participation in subsequent consensus processes, thereby reducing errors caused by faulty nodes.

5. System Analysis

5.1. Security Analysis

5.1.1. Shard Selection Security

MSSP allows nodes to select multiple shards for storage, ensuring the verifiability of multi-shard selection by introducing a common random number R and an encrypted hash function SHA-256. The node address A of each shard is concatenated with the common random number R, and then processed through the SHA-256 hash function to generate a 256-bit hash value. Subsequently, the TRUNCATE function is used to truncate the first 5 bits of the hashed value, forming a unique identifier for the shard. This identifier is based on the encrypted result of the node address and common random number, making it unique and unforgeable for each node.

Due to the irreversibility and collision resistance of the hash function, even a slight change in input will result in a huge change in output. Therefore, nodes cannot predict or control the generated shard identifier by arbitrarily selecting addresses and random numbers. This approach ensures that nodes cannot select specific shards for storage by manipulating addresses and random numbers, thus preventing computing power aggregation attacks. Any malicious node attempting to violate the rules of shard selection will be rejected by other consensus nodes, as its stored shards will not pass identifier verification.

5.1.2. Protocol Security

After the blocks in MSSP are added to the chain, they will be sorted according to the priority of the consensus zone. During the sorting process, the system will discard conflicting blocks submitted by malicious nodes by comparing priorities, to defend against double-spending attacks. To prevent malicious nodes from predicting the priority of the consensus zone in advance, MSSP dynamically adjusts the priority of the consensus zone after each block submission. This flexible adjustment of priorities ensures fairness within the system.

Upon completion of cross-shard transactions, relevant nodes are required to update their data. The leader initiates a request to update the data for the nodes. Once the node has completed its data update, it will probabilistically return a proof of completion based on its own recent four rounds of updates. This probabilistic approach to returning proofs helps prevent malicious nodes from evading system monitoring. Nodes that consistently fail to complete updates promptly will be deemed as faulty and will no longer be able to participate in the consensus process. This method of restricting nodes to actively maintain data consistency enhances the overall security and reliability of the blockchain network.

The security and liveness of the MSSP system depend not only on the design of the protocol but also on the underlying PBFT consensus algorithm. In PBFT, if the total number of nodes is $3f+1$, there can be at most f malicious nodes, and there must be at least $2f+1$ honest nodes in the system to achieve consensus. Therefore, if the number of malicious nodes in each shard does not exceed ${\displaystyle \frac{1}{3}}$ of the total number of nodes, protocol security can be guaranteed.

5.2. Scalability Analysis

By analyzing the distribution of consensus zones, the bandwidth, storage, and communication complexity of nodes, we can assess the scalability of MSSP. Unlike traditional sharding that divides consensus regions based on shards, in MSSP, consensus regions are composed of nodes that store multiple identical shards. The distribution of consensus zones is defined as $m=\{m_1,m_2,\dots ,m_{S-1}\}$, where $m_1$ represents the number of consensus zones composed of nodes storing a single shard, and $m_i$ ($2\le i\le S-1$) represents the number of consensus zones composed of nodes storing i shards. We define the scalability parameter $\omega$ as the average complexity of bandwidth, storage, and communication for a single node in the system. From Section 4.2, it can be inferred that a consensus zone consisting of m-nodes storing i shards needs to process and validate cross-shard transactions between i shards. Therefore, its bandwidth, storage, and communication complexity is $i/S$. Similarly, the scalability parameter for multi-shard storage systems can be expressed as:

$${\omega }^{MSSP}={\displaystyle \frac{1}{S}}·{\displaystyle \frac{m_1}{S}}+{\displaystyle \frac{2}{S}}·{\displaystyle \frac{m_2}{S}}+\cdots +{\displaystyle \frac{S-1}{S}}·{\displaystyle \frac{m_{S-1}}{S}}={\displaystyle \frac{m_1+{\sum }_{2\le i\le S-1}i{m}_i}{S^2}}$$

(2)

The scalability parameter for traditional sharding is ${\omega }^{traditional}={\displaystyle \frac{1}{S}}$, while the non-sharding scalability parameter is ${\omega }^{non}=1$.

The scalability parameter of multi-shard storage falls between traditional sharding and non-sharding blockchains, which means it strikes a balance in terms of resource utilization and processing efficiency. The main advantage of the multi-shard storage protocol over traditional sharding lies in the handling of cross-shard transactions. In traditional sharding systems, cross-shard transactions require multiple rounds of submission and processing because each sub-transaction must be confirmed on the corresponding shard. In contrast, MSSP utilizes nodes that store the same multiple shards to form a consensus zone, enabling it to process cross-shard transactions within one round without the need for cross-shard communication, thus reducing additional communication and coordination overheads.

5.3. Performance Analysis

A performance evaluation of MSSP is conducted by analyzing transaction throughput and latency. For blockchain systems employing sharding techniques, the performance will be affected by cross-shard transactions.

To comprehensively analyze the performance of sharded systems, it is essential to consider the distribution of cross-shard transactions across the entire system. Define the transaction distribution $\alpha =\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_S\}$, where ${\alpha }_1$ represents the percentage of internal transactions and ${\alpha }_j$ represents the percentage of cross-shard transactions involving j shards.

The nodes within the shard need to communicate and coordinate with each other in order to reach consensus. As the number of nodes within a shard increases, so does the complexity of communication among them, leading to increased delays in the consensus process. Define a function $f\left(n\right)$ [33] to represent the time delay for one round of consensus in a shard with n nodes, where parameter C denotes the number of transactions processed in one round of consensus within a shard.

In a traditional sharding system, if a relay mechanism is used to process cross-shard transactions, the cross-shard transactions between j shards need to be divided into j sub-transactions for processing. Therefore, the maximum transaction throughput of a traditional sharding system with S shards is

$${\mathrm{TPS}}^{\mathrm{traditional}}={\displaystyle \frac{SC}{f(N/S)}}\left({\alpha }_1+{\displaystyle \frac{{\alpha }_2}{2}}+\cdots +{\displaystyle \frac{{\alpha }_S}{S}}\right)$$

(3)

In a non-sharding system, there are no cross-shard transactions, so the transaction throughput of a non-sharding system is ${\mathrm{TPS}}^{\mathrm{non}}={\displaystyle \frac{C}{f\left(N\right)}}$. Ideally, in a multi-shard storage system, cross-shard transactions can be processed directly without affecting the throughput. The throughput of a multi-shard storage system with S shards is ${\mathrm{TPS}}^{\mathrm{MSSP}}={\displaystyle \frac{SC}{f(N/S)}}$. It can be seen that compared to traditional sharding systems and non-sharding systems, MSSP has significant advantages in terms of throughput.

In traditional sharding systems, the submission of each sub-transaction in a cross-shard transaction may need to wait for the completion of other sub-transactions on different shards. This leads to the necessity of submitting sub-transactions round by round, resulting in a confirmation latency of traditional sharding systems as

$${\mathrm{CONF}}^{\mathrm{traditional}}=f\left({\displaystyle \frac{N}{S}}\right)\sum _{1\le i\le S}i{\alpha }_i$$

(4)

The confirmation latency in non-sharding systems is ${\mathrm{CONF}}^{\mathrm{non}}=f\left(N\right)$. In a multi-shard storage system, if the cross-shard transaction is handled by the m-node that stores the related shards, it can be submitted within one round, significantly reducing the overall confirmation latency. Therefore, the confirmation latency in MSSP is ${\mathrm{CONF}}^{\mathrm{MSSP}}=f(N/S)$. MSSP exhibits lower confirmation latency compared to traditional sharding and non-sharding systems.

6. Experiment

6.1. Experimental Implementation

We implemented a prototype of MSSP using the Go language (v1.13) to evaluate its performance. Additionally, we developed four complete sharding prototypes for comparative analysis. The main difference among these four prototypes lies in their approaches to handling cross-shard transactions. The first one employs the relay mechanism of Monoxide [25], the second utilizes the Broker account mechanism of BrokerChain [22], the third method uses the hierarchical design of Pyramid [34], and the fourth leverages the state splitting mechanism of Estuary [23].

For our experiments, we deployed a private cloud environment consisting of eight physical machines, each equipped with a 64-core Intel(R) Xeon(R) Gold 5218R CPU @ 2.10 GHz processor, 128 GB of RAM, and 1 TB of SSD storage. Each block was configured to contain up to 2000 transactions with an 8-s generation interval per shard, and the bandwidth for each node was capped at 20 Mbps to simulate realistic network conditions. We varied the number of shards from 4 to 14 to evaluate scalability and performance, using a real-world Ethereum transaction dataset from XBlock [35] and injecting transactions at rates ranging from 1000 to 10,000 transactions per second.

To assess robustness, we simulated common attack vectors, including Sybil attacks (up to 18% malicious nodes), and double-spending attempts.We assume that Sybil attacks are limited by the cost of identity creation, and double-spending attempts can be detected through priority sorting. Our protocol assumes a majority of honest nodes, reliable message delivery, and reasonable network latency (<100 ms). A potential limitation is the lack of handling for dynamic network topology changes, which may impact performance in highly dynamic environments. We measured system throughput and average transaction latency across different shard configurations to evaluate performance.

In terms of security, a shard is considered insecure when the number of malicious nodes f in a shard exceeds $n/3$. To set the security level of the system and provide an adjustable method to adjust the security, a security parameter $\lambda$ is introduced to set the probability threshold. The system can be considered sufficiently secure if it meets the following conditions:

$$\mathrm{SP}[f\ge \lceil n/3\rceil ]<2^{-\lambda }$$

Increasing the value of $\lambda$ will enhance the security level of the system. We set the security parameter $\lambda$ to 15, which means that the probability of failure needs to be less than $2^{-15}$.

6.2. Transaction Throughput

Figure 6 compares the transaction throughput of traditional sharding and multi-shard storage schemes under different shard quantities. The experimental results show that compared with the other four shard designs, the multi-shard storage scheme increases transaction throughput by 1.4 to 3.1 times. When there are 14 shards, the maximum throughput is 2654 TPS. As the number of shards increases, the throughput of MSSP shows a nearly linear growth trend, demonstrating good scalability. In summary, multi-shard storage solutions have significant advantages over traditional shard technologies.

Section 3.1 discusses the system model of MSSP, in which the types of blockchain nodes are divided into s-nodes and m-nodes. S-nodes are only responsible for processing internal transactions within their respective shards, while m-nodes can directly handle cross-shard transactions involving related shards. Figure 7 shows the transaction throughput at different m-node proportions. It can be seen from the figure that when the proportion of m-nodes is between 20% and 25%, the throughput reaches its maximum value. If the proportion of m-nodes is too large or too small, it will lead to a decrease in throughput.

When the proportion of m-nodes is too low, it may cause an imbalance in the load of cross-shard transactions, with some nodes bearing too large a transaction processing burden while others are relatively idle, thereby reducing overall throughput. When there are too many m-nodes, cross-shard transactions require more inter-node communication and synchronization, leading to a decrease in throughput due to increased communication overhead.

6.3. Confirmation Latency

The confirmation latency is a key indicator for evaluating the performance of the blockchain. Figure 8 provides comparative data on confirmation latency between traditional sharding techniques and multi-shard storage solutions. It is evident from the data that, compared to traditional sharding systems, the latency in multi-shard storage has been reduced by 40% to 84%. This significant improvement can be attributed to the mechanism for handling cross-shard transactions in multi-shard storage structures, which reduces transaction confirmation latency by eliminating the need for additional communication with nodes in other shards.

6.4. Storage Overhead

We evaluated the storage overhead per node after processing 500,000 transactions under different scalability parameters $\omega$ in a system consisting of 14 shards and 2000 nodes, and the results are presented in Figure 9. The experiments show that as the value of $\omega$ increases, both the transaction throughput and the average storage overhead of the system exhibit an upward trend. Specifically, when $\omega$ is set to 0.5, multi-shard storage can increase transaction throughput by 2.75 times compared to Monoxide, while also increasing storage overhead by 8.5 times. It is important to note that the primary bottleneck in current sharded blockchain systems typically lies in transaction throughput rather than storage overhead, as the latter can be effectively mitigated through techniques such as state compaction. Furthermore, the design of multi-shard storage not only enhances performance but also maintains controllability over storage overhead, providing greater potential for the long-term scalability of the system.

6.5. Security

Figure 10 illustrates a comparison of transaction throughput between MSSP and traditional sharding in the presence of different proportions of malicious nodes. The data in the figure indicate that even with the existence of malicious nodes, the transaction throughput of MSSP is still significantly higher than the other four sharding schemes. This result demonstrates that MSSP is effective in resisting the impact of malicious nodes and maintaining high performance and stability in the system.

To meet the security requirements mentioned in Section 6.1, the failure probability must be below the threshold of $2^{-15}$, as shown by the green dashed line in Figure 11. Analysis of the figure reveals that to satisfy a failure probability below $2^{-15}$, the percentage of malicious nodes must be less than 14% for a multi-shard storage system to be considered secure. Additionally, as shown in the graph, with an increase in the proportion of malicious nodes, the failure rate of the system also increases, and the transaction throughput of MSSP decreases approximately proportionally. This situation occurs because within the safe threshold range, although malicious nodes cannot tamper with data, they may waste consensus time when acting as leaders. In conclusion, MSSP can ensure timely identification and prevention of blocks submitted by malicious nodes, thereby maintaining the overall security and efficiency of the system.

6.6. Reliability

MSSP adopts a mechanism of sending update proofs to achieve data updates, thereby ensuring the consistency of cross-shard transactions. The mechanism updates the data by sending a proof of update to the nodes. After the node completes a data update, it can take three different actions: (1) return a proof to confirm the completion of the update; (2) not return any confirmation; or (3) return a proof of completion with a random probability p, as discussed in Section 4.4. The following will explore the advantages and disadvantages of the probability P returning to update completion proof mechanism from the perspectives of latency and security, compared to the other two methods.

Figure 12 illustrates the latency situation corresponding to three different update proof return strategies. It can be seen from the figure that the strategy of always returning proof results in the longest latency, while the strategy of not returning proof at all corresponds to the shortest latency. The latency for returning proof with a probability P falls between these two extremes. However, in a well-networked environment, the difference in latency among these three strategies is not significant, usually on a millisecond level or shorter. This is mainly because the completed update proof file has a small volume, and its transmission time is mainly affected by one-way network delay. Therefore, although there are differences in latency among these three strategies, overall, this difference is mainly influenced by network conditions.

The advantage of the P-probability returning update completion proof mechanism over the other two mechanisms is as follows:

1.

Faulty node exclusion: by detecting whether nodes complete updates on time within a certain time range, faulty nodes can be effectively excluded, thereby improving the fault tolerance of the system.

2.

Reducing the impact of malicious nodes: By introducing the mechanism of random return proof, nodes are allowed to decide whether to return proofs and the probability of returning proofs based on their performance within a certain time window. This flexibility and randomness can prevent malicious nodes from evading system monitoring through simple pattern recognition.

3.

Saving communication overhead: Compared to requiring all nodes to return proofs, this approach can save communication overhead. Not all nodes need to return proofs after each update. Nodes can decide whether to return proofs based on a certain probability, thus reducing communication load.

4.

Enhancing auditability: The buffer records whether nodes have completed updates on time in recent rounds, providing a basis for system auditing. By analyzing the information provided by the buffer, potential abnormal behavior can be detected and addressed.

In summary, compared with the other two mechanisms, the P-probability returning update completion proof mechanism has significant advantages that effectively address threats from faulty nodes and malicious behavior while enhancing system stability and reliability.

7. Conclusions

This paper proposes a multi-shard storage blockchain sharding protocol that achieves efficient processing of cross-shard transactions and improves system security. By allowing a single node to store data from multiple shards, this protocol introduces a new consensus partition method, where nodes storing the same multiple shards of data form a consensus partition. This strategy enables the consensus zone to directly handle cross-shard transactions without the need for cross-shard communication. Based on the tree structure of a multi-shard storage blockchain, this protocol introduces a priority sorting mechanism to enhance the blockchain’s ability to resist double-spending attacks while ensuring fairness. We have designed a P-probability return update completion proof mechanism to ensure the consistency of node data after cross-shard-transactions. Finally, the experimental results showed that compared with existing sharding techniques, MSSP increased transaction throughput by 1.4 to 3.1 times, while reducing confirmation latency by 40% to 84%. In terms of storage overhead, when the scalability parameter $\omega$ is set to 0.5, compared to Monoxide, multi-shard storage increases transaction throughput by 2.75 times and storage overhead by 8.5 times. Considering the significant performance improvement, this trade-off is completely acceptable. In addition, in terms of security, even in the presence of malicious nodes, MSSP’s throughput is 30% to 70% higher than other sharding techniques, effectively reducing the impact of faulty nodes and malicious behavior on the system.