From Battlefield to Building Site: Probabilistic Analysis of UXO Penetration Depth for Infrastructure Resilience
Abstract
1. Introduction
2. Problem Definition
Penetration Model
- If , the projectile collapses on the surface of the target, and no penetration occurs.
- If , penetration occurs. The projectile decelerates and fails gradually during penetration.
- If , penetration occurs. The projectile decelerates but does not deform during penetration. This is the case of rigid UXOs penetrating soils, as considered for this study.
3. Random Variables
3.1. Uncertainties of Soil Parameters
3.1.1. Sandy Soil Parameters
3.1.2. Clayey Sand Soil Parameters
3.1.3. Clayey Soil Parameters
3.2. Distribution of Random Variables
3.2.1. Restrict Normal Distribution to COV Values Lower than 30%
3.2.2. Restrict Lognormal Distribution to COV Values Lower than 30%
3.2.3. Unrestricted Lognormal Distribution
3.2.4. Use of Mixed Normal and Lognormal Distributions
4. Monte Carlo Simulations
4.1. Pseudorandom Sampling (PRS)
4.2. Latin Hypercube Sampling (LHS)
4.3. Gaussian Process Response Surface Method (GP_RSM)
5. Results and Discussion
6. Limitations
7. Summary and Conclusions
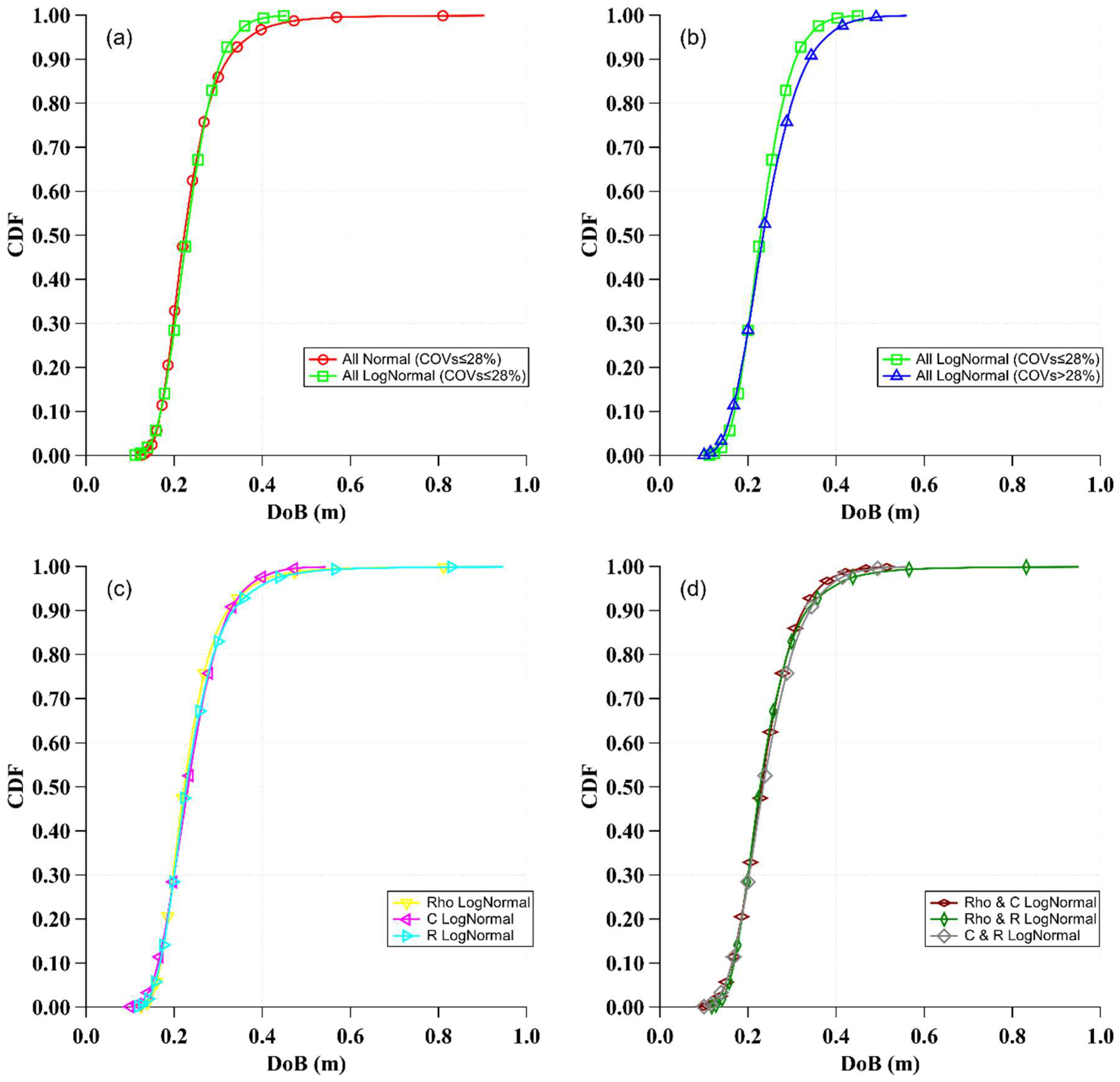
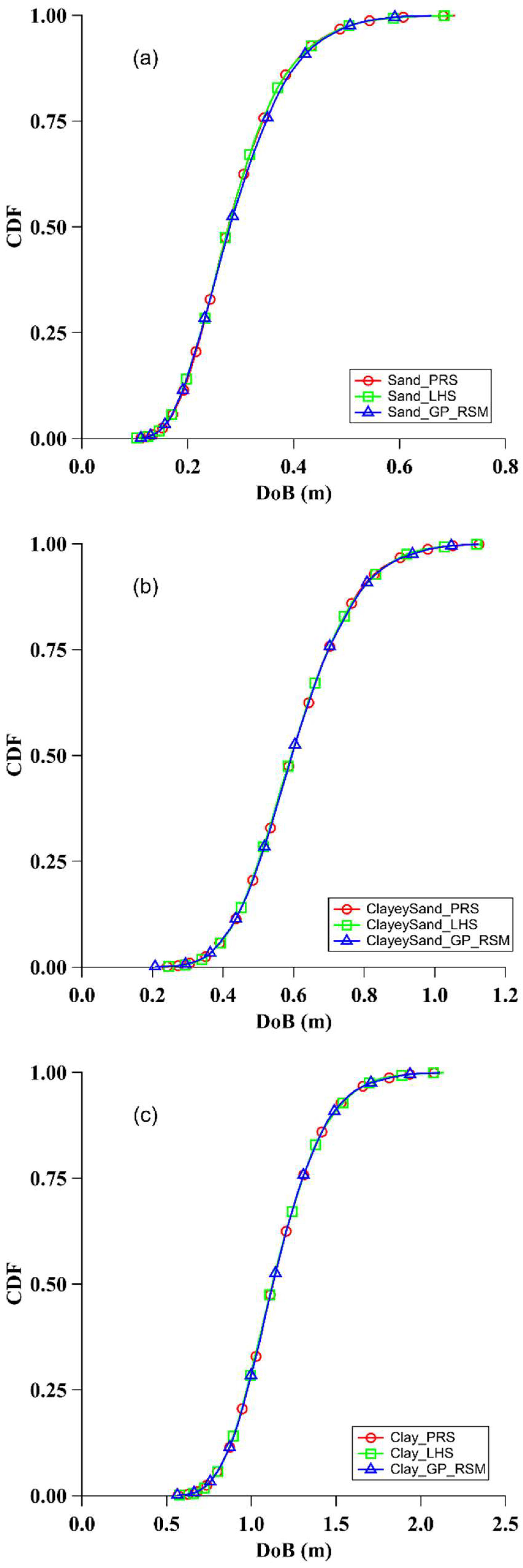
- Various sampling techniques provide comparable predictions of the DoB, suggesting that all investigated methods are effective in capturing the uncertainties associated with the munitions’ burial depth. It has been noticed in all simulations that PRS and LHS consumed approximately similar run time, while the GP_RSM was the fastest sampling technique.
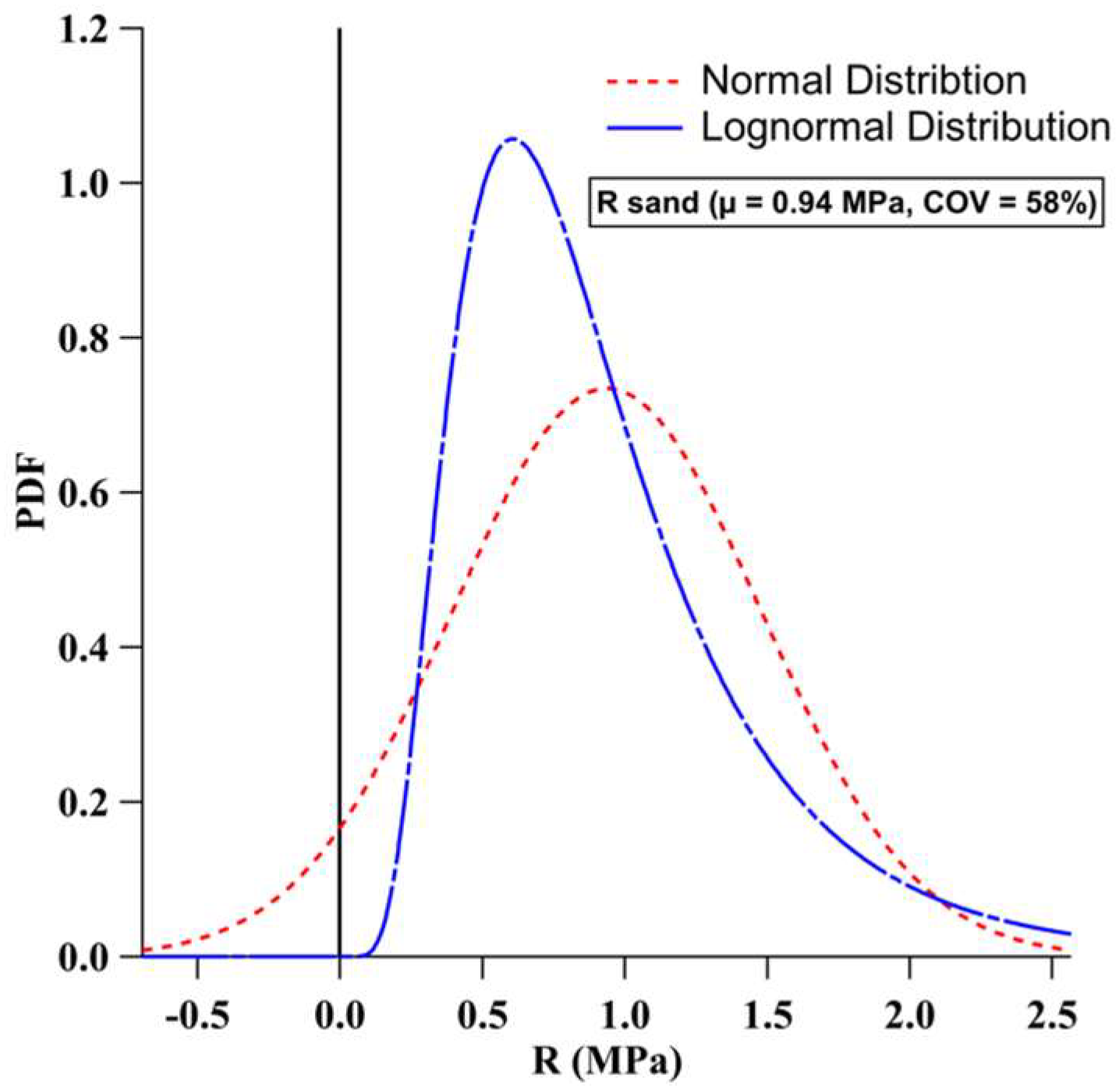
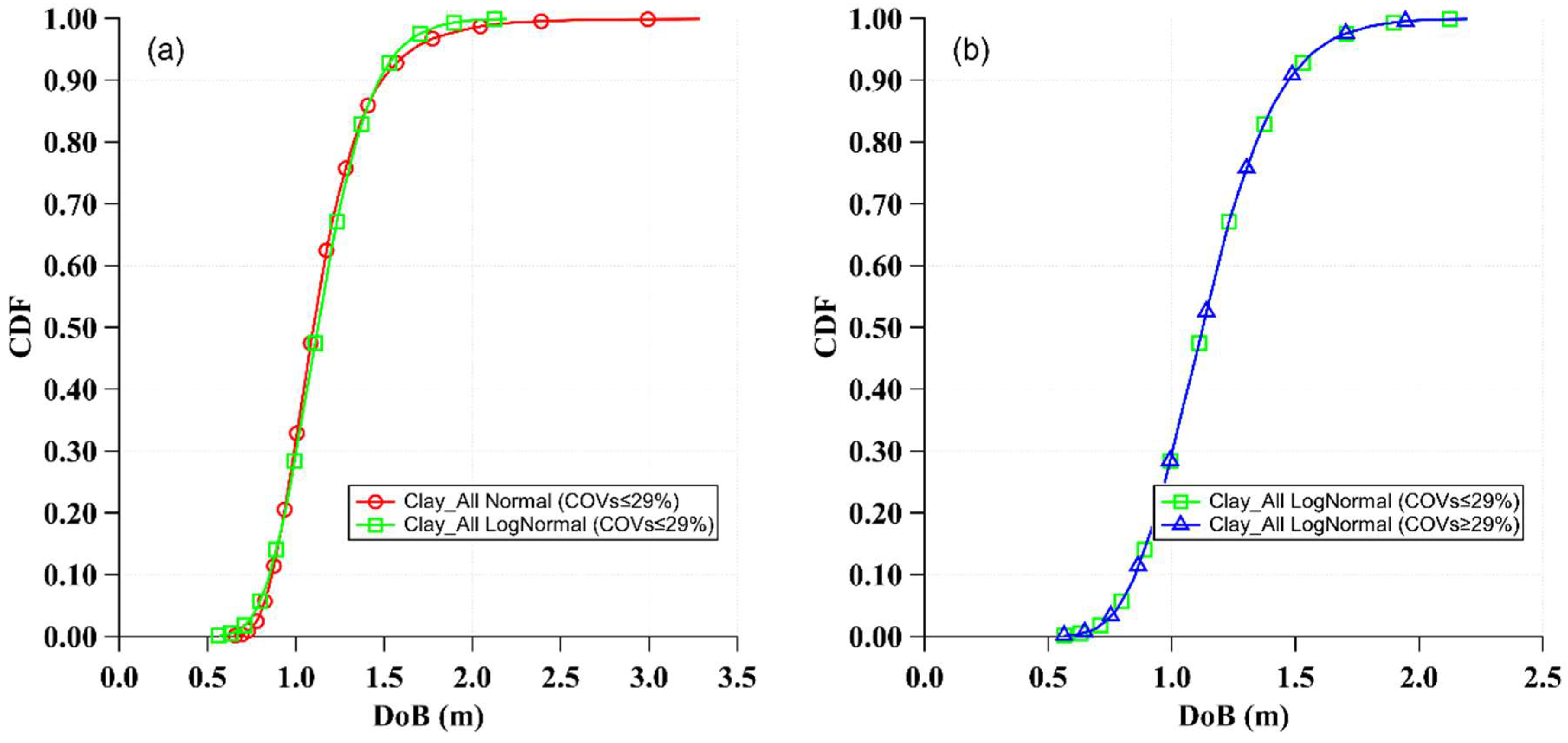
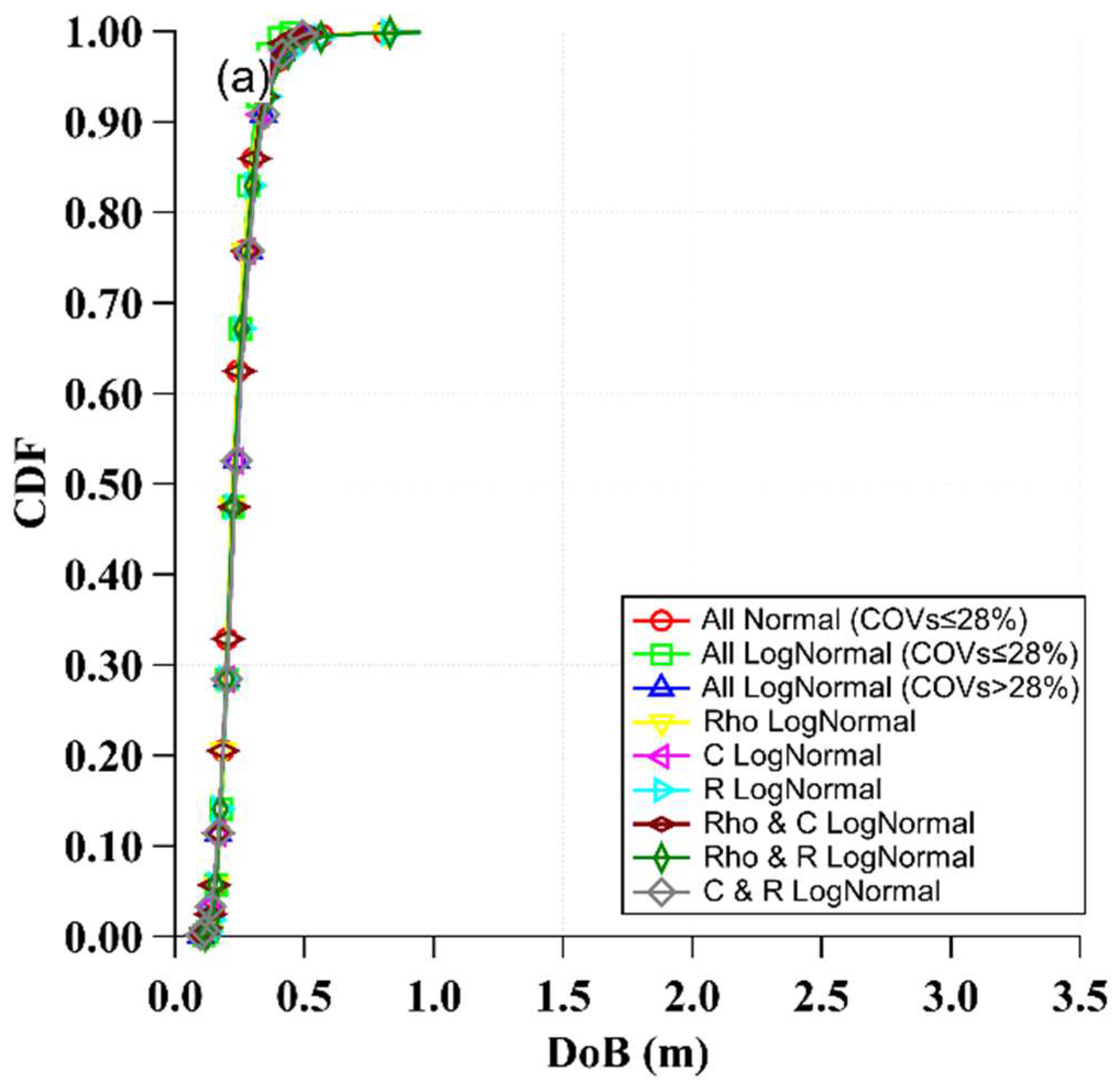
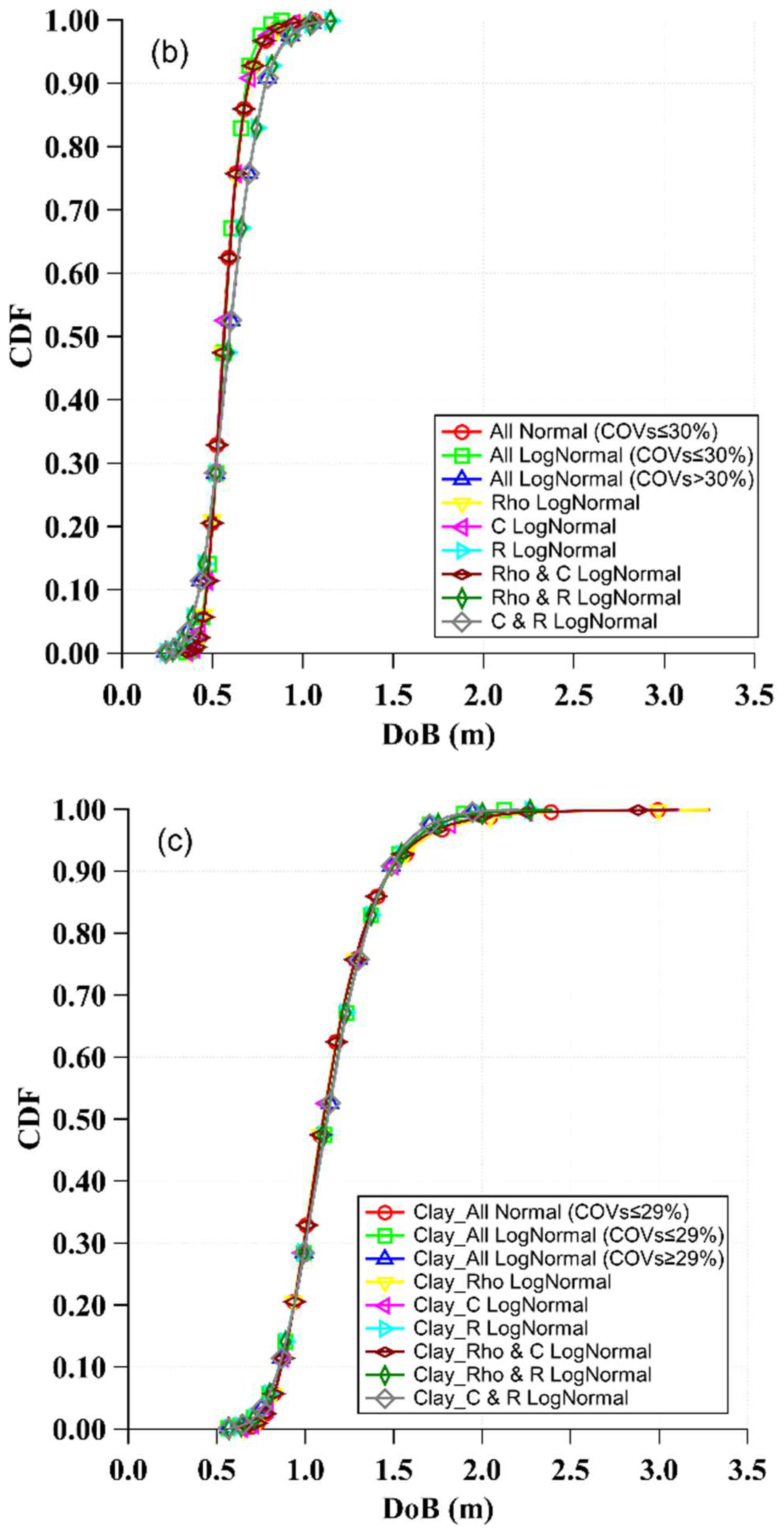
- Sampling uncertainties from a normal or a lognormal distribution did not significantly impact the DoB predictions. However, the high uncertainties of the studied random variables resulted in normal distribution sampling physically inadmissible values for COVs above 28%. Thus, a lognormal distribution is preferred for use in sampling Poncelet drag and bearing coefficients when conducting probabilistic predictions of the DoB of unexploded UXOs.
- Taking into account the inherent uncertainties associated with soil properties can have important impacts on the predicted DoB. The typical coefficient of variation in the DoB is approximately 32% in sand, 25% in clayey sand, and 22% in clay. These uncertainties can significantly influence the required cleanup depth for the redevelopment of sites afflicted by the presence of UXOs, with associated financial impacts on restoring former defense and battlefield sites.
- The uncertainty of the density, drag coefficient, and bearing coefficient primarily influenced the depth of burial (DoB) in sandy soil, whereas in clayey sand soils, the uncertainty in the bearing coefficient was the dominant factor. In clayey soil, all variables under various distribution conditions resulted in approximately identical predictions, with no single variable appearing to be dominant.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- OSCE. The Impact of Mines, Unexploded Ordnance and Other Explosive Objects on Civilians in the Donetsk and Luhansk Regions of Eastern Ukraine, Report, Special Monitoring Mission to Ukraine, Organization for Security and Cooperation in Europe (OSCE). 2019. Available online: https://www.osce.org/ukraine-smm (accessed on 12 February 2025).
- Beran, L.; Zelt, B. Risk assessment for unexploded ordnance remediation. Stoch. Environ. Res. Risk Assess. 2015, 29, 1051–1061. [Google Scholar] [CrossRef]
- McKenna, S.A.; Pulsipher, B. Quantifying and reducing uncertainty in UXO site characterization. Stoch. Environ. Res. Risk Assess. 2009, 23, 153–154. [Google Scholar] [CrossRef]
- Ostrouchov, G.; Doll, W.E.; Beard, L.P.; Morris, M.D.; Wolf, D.A. Multiscale structure of UXO site characterization: Spatial estimation and uncertainty quantification. Stoch. Environ. Res. Risk Assess. 2009, 23, 215–225. [Google Scholar] [CrossRef]
- Roberts, B.L.; McKenna, S.A. The use of secondary information in geostatistical target area identification. Stoch. Environ. Res. Risk Assess. 2009, 23, 227–236. [Google Scholar] [CrossRef]
- Matzke, B.D.; Wilson, J.E.; Hathaway, J.E.; Pulsipher, B.A. Statistical algorithms accounting for background density in the detection of UXO target areas at DoD munitions sites. Stoch. Environ. Res. Risk Assess. 2009, 23, 181–191. [Google Scholar] [CrossRef]
- McKenna, S.A. UXO target area identification with hidden Markov models. Stoch. Environ. Res. Risk Assess. 2009, 23, 193–202. [Google Scholar] [CrossRef]
- Tantum, S.L.; Zhu, Q.; Torrione, P.A.; Collins, L.M. Modeling position error probability density functions for statistical inversions using a Goff–Jordan rough surface model. Stoch. Environ. Res. Risk Assess. 2009, 23, 155–167. [Google Scholar] [CrossRef]
- Walsh, S.; Anderson, K.; Hathaway, J.; Pulsipher, B. A Bayesian approach to monitoring and assessing unexploded ordnance remediation progress from munitions testing ranges. Stoch. Environ. Res. Risk Assess. 2011, 25, 805–814. [Google Scholar] [CrossRef]
- Robins, B. New Principles of Gunnery (Originially published in 1742). In Mathematical tracts of the Late Benjamin Ribins; Wilson, J., Ed.; Kessinger Publishing: London, UK, 1761; Volume 1, p. 341. [Google Scholar]
- Wang, W.; Wang, X.; Yu, G. Penetration depth of torpedo anchor in cohesive soil by free fall. Ocean Eng. 2016, 116, 286–294. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Liang, R.Y.; Zhu, H.; Di, H. A hidden Markov random field model based approach for probabilistic site characterization using multiple cone penetration test data. Struct. Saf. 2018, 70, 128–138. [Google Scholar] [CrossRef]
- Ads, A.; Bless, S.; Iskander, M. Shape effects on penetration of dynamically installed anchors in a transparent marine clay surrogate. Acta Geotech. 2023, 18, 3043–3059. [Google Scholar] [CrossRef]
- Raaj, S.K.; Saha, N.; Sundaravadivelu, R. Exploration of deep-water torpedo anchors-A review. Ocean Eng. 2023, 270, 113607. [Google Scholar] [CrossRef]
- Omidvar, M.; Iskander, M.; Bless, S. Response of granular media to rapid penetration. Int. J. Impact Eng. 2014, 66, 60–82. [Google Scholar] [CrossRef]
- Iskander, M.; Bless, S.; Omidvar, S. Rapid Penetration Into Granular Media: Visualizing the Fundamental Physics of Rapid Earth Penetration; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Kim, Y.H.; Hossain, M.S.; Wang, D. Effect of strain rate and strain softening on embedment depth of a torpedo anchor in clay. Ocean Eng. 2015, 108, 704–715. [Google Scholar] [CrossRef]
- Liu, H.; Xu, K.; Zhao, Y. Numerical investigation on the penetration of gravity installed anchors by a coupled Eulerian–Lagrangian approach. Appl. Ocean Res. 2016, 60, 94–108. [Google Scholar] [CrossRef]
- White, R. Large Deformation Explicit Finite Element Simulations of High Strain Rate Loading and rapid Penetration of Clay; Manhattan College: Bronx, NY, USA, 2021. [Google Scholar]
- Phoon, K.-K. Role of reliability calculations in geotechnical design. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2017, 11, 4–21. [Google Scholar] [CrossRef]
- Phoon, K.-K. What Geotechnical Engineers Want to Know about Reliability. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2023, 9, 03123001. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Zhu, D.; Huang, J.; Fenton, G.A. Observations on probabilistic slope stability analysis. In Proceedings of the 6th Asian-Pacific Symposium on Structural Reliability and Its Applications (APSSRA 2016), Shanghai, China, 28–30 May 2016. [Google Scholar]
- Zhang, J.; Zhang, L.M.; Tang, W.H. Bayesian Framework for Characterizing Geotechnical Model Uncertainty. J. Geotech. Geoenviron. Eng. 2009, 135, 932–940. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, W.H.; Zhang, L.M.; Huang, H.W. Characterising geotechnical model uncertainty by hybrid Markov Chain Monte Carlo simulation. Comput. Geotech. 2012, 43, 26–36. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.X.; Yu, G.L. Penetration depth of torpedo anchor in two-layered cohesive soil bed by free fall. China Ocean Eng. 2018, 32, 706–717. [Google Scholar] [CrossRef]
- Poncelet, J.V. Introduction Il la Mechanique Industrielle, 2nd ed.; Meline, Cans et Compagnie: Brussels, Belgium, 1839; p. 271. [Google Scholar]
- Kenneally, B.; Omidvar, M.; Bless, S.; Iskander, M. Observations of velocity-dependent drag and bearing stress in sand penetration. In Dynamic Behavior of Materials, Volume 1: Proceedings of the 2020 Annual Conference on Experimental and Applied Mechanics; Springer International Publishing: Cham, Switzerland, 2021; pp. 29–35. [Google Scholar]
- Thacker, B.H.; Riha, D.S.; Fitch, S.H.K.; Huyse, L.J.; Pleming, J.B. Probabilistic engineering analysis using the NESSUS software. Struct. Saf. 2006, 28, 83–107. [Google Scholar] [CrossRef]
- Bless, S.; Peden, B.; Guzman, I.; Omidvar, M.; Iskander, M. Poncelet Coefficients of Granular Media; Springer International Publishing: Cham, Switzerland, 2014; pp. 373–380. [Google Scholar] [CrossRef]
- Omidvar, M.; Bless, S.; Iskander, M. Recent Insights into Penetration of Sand and Similar Granular Materials. Shock. Phenom. Granul. Porous Mater. 2019, 2019, 137–163. [Google Scholar] [CrossRef]
- Tate, A. Further results in the theory of long rod penetration∗. J. Mech. Phys. Solids 1969, 17, 141–150. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Das, B.M. (Ed.) . Geotechnical Engineering Handbook; J. Ross Publishing: New York, NY, USA, 2011. [Google Scholar]
- Lumb, P. Application of statistics in soil mechanics. In Soil Mechanics: New Horizons; Lee, I.K., Ed.; Newnes-Butterworth: London, UK, 1974; pp. 44–112. [Google Scholar]
- Mercurio, S.R.; Bless, S.; Ads, A.; Omidvar, M.; Iskander, M. Rate Dependence of Penetration Resistance in a Cohesive Soil. Society for Experimental Mechanics Annual Conference and Exposition; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Mercurio, S.R.; Iskander, M.; Omidvar, M.; Bless, S. Calibration of the Geoponcelet Penetration Model in Cohesive Soil. ASCE J. Geotech. Geoenviron. Eng. 2024; In Preparation. [Google Scholar]
- Omidvar, M.; Dinotte, J.; Giacomo, L.; Bless, S.; Iskander, M. Photon Doppler velocimetry for resolving vertical penetration into sand targets. Int. J. Impact Eng. 2024, 185, 104827. [Google Scholar] [CrossRef]
- Omidvar, M.; Dinotte, J.; Giacomo, L.; Bless, S.; Iskander, M. Dynamics of sand response to rapid penetration by rigid projectiles. Granul. Matter 2024, 26, 73. [Google Scholar] [CrossRef]
- He, R.; Wu, C.; Xing, X.; Li, J. Dependence Structures of Soil Parameters in Sandy Clay. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 05021005. [Google Scholar] [CrossRef]
- Mercurio, S.; Grace, D.; Bless, S.; Iskander, M.; Omidvar, M. Frequency-shifted photonic doppler velocimetry (PDV) for measuring deceleration of projectiles in soils. In Acta Geotechnica; Springer Nature: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Morkos, B.N.; White, R.; Omidvar, M.; Iskander, M.; Bless, S. Numerical Simulation of High-Speed Penetration of Munitions in Clay. In GSP 352: Geo-Congress 2024, Geotechnical Data Analysis and Computation; ASCE: New York, NY, USA, 2024; pp. 82–91. [Google Scholar] [CrossRef]
- Duncan, J.M. Factors of Safety and Reliability in Geotechnical Engineering. J. Geotech. Geoenviron. Eng. 2000, 126, 307–316. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D.V. Risk Assessment in Geotechnical Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Nadim, F. Tools and Strategies for Dealing with Uncertainty in Geotechnics. In Probabilistic Methods in Geotechnical Engineering; Springer: Vienna, Austria, 2007; pp. 71–95. [Google Scholar] [CrossRef]
- Nadarajah, S. A generalized normal distribution. J. Appl. Stat. 2005, 32, 685–694. [Google Scholar] [CrossRef]
- Forbes, C.; Evans, M.; Hastings, N.; Peacock, B. Statistical Distributions; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ang, A.H.-S.; Tang, W.H. Probability Concepts in Engineering: Emphasis on Applications In Civil and Environmental Engineering; Wiley: Hoboken, NJ, USA, 1975; Volume 1. [Google Scholar]
- Griffiths, D.V.; Fenton, G.A. Probabilistic Methods in Geotechnical Engineering; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Schmidt, A.F.; Finan, C. Linear regression and the normality assumption. J. Clin. Epidemiol. 2018, 98, 146–151. [Google Scholar] [CrossRef]
- Xiao, T.; Zhang, L.-M.; Li, X.-Y.; Li, D.-Q. Probabilistic Stratification Modeling in Geotechnical Site Characterization. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, 04017019. [Google Scholar] [CrossRef]
- Fan, H.; Liang, R. Application of Monte Carlo Simulation to Laterally Loaded Piles. GeoCongress 2012, 2012, 376–384. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D.V. The Random Finite Element Method (RFEM) in Bearing Capacity Analyses. In Probabilistic Methods in Geotechnical Engineering; Springer: Vienna, Austria, 2007; pp. 295–315. [Google Scholar] [CrossRef]
- Ji, J.; Wang, L.P. Efficient geotechnical reliability analysis using weighted uniform simulation method involving correlated nonnormal random variables. J. Eng. Mech. 2022, 148, 06022001. [Google Scholar] [CrossRef]
- Li, X.; Chi, S.W.; Foster, C.D. Sensitivity analysis of a three-invariant plasticity model with different sampling algorithms. Int. J. Geotech. Eng. 2023, 17, 221–233. [Google Scholar] [CrossRef]
- Mckay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computer Code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Loh, W.-L. On Latin hypercube sampling. Ann. Stat. 1996, 24, 62310. [Google Scholar] [CrossRef]
- Kang, F.; Han, S.; Salgado, R.; Li, J. System probabilistic stability analysis of soil slopes using Gaussian process regression with Latin hypercube sampling. Comput. Geotech. 2015, 63, 13–25. [Google Scholar] [CrossRef]
- Toufigh, V.; Pahlavani, H. Probabilistic-Based Analysis of MSE Walls Using the Latin Hypercube Sampling Method. Int. J. Geomech. 2018, 18, 04018109. [Google Scholar] [CrossRef]
- Olsson, A.M.J.; Sandberg, G.E. Latin Hypercube Sampling for Stochastic Finite Element Analysis. J. Eng. Mech. 2002, 128, 121–125. [Google Scholar] [CrossRef]
- Riha, D.; Bichon, B.; Mcfarland, J.; Fitch, S. NESSUS Users’ Manual; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Wang, D.; Ye, X.; Zheng, X. The scaling and dynamics of a projectile obliquely impacting a granular medium. Eur. Phys. J. E 2012, 35, 7. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, H.; Cheng, H.; Wang, X.; Zhang, D. The force and dynamic response of low-velocity projectile impact into 3D dense wet granular media. Powder Technol. 2024, 434, 119309. [Google Scholar] [CrossRef]
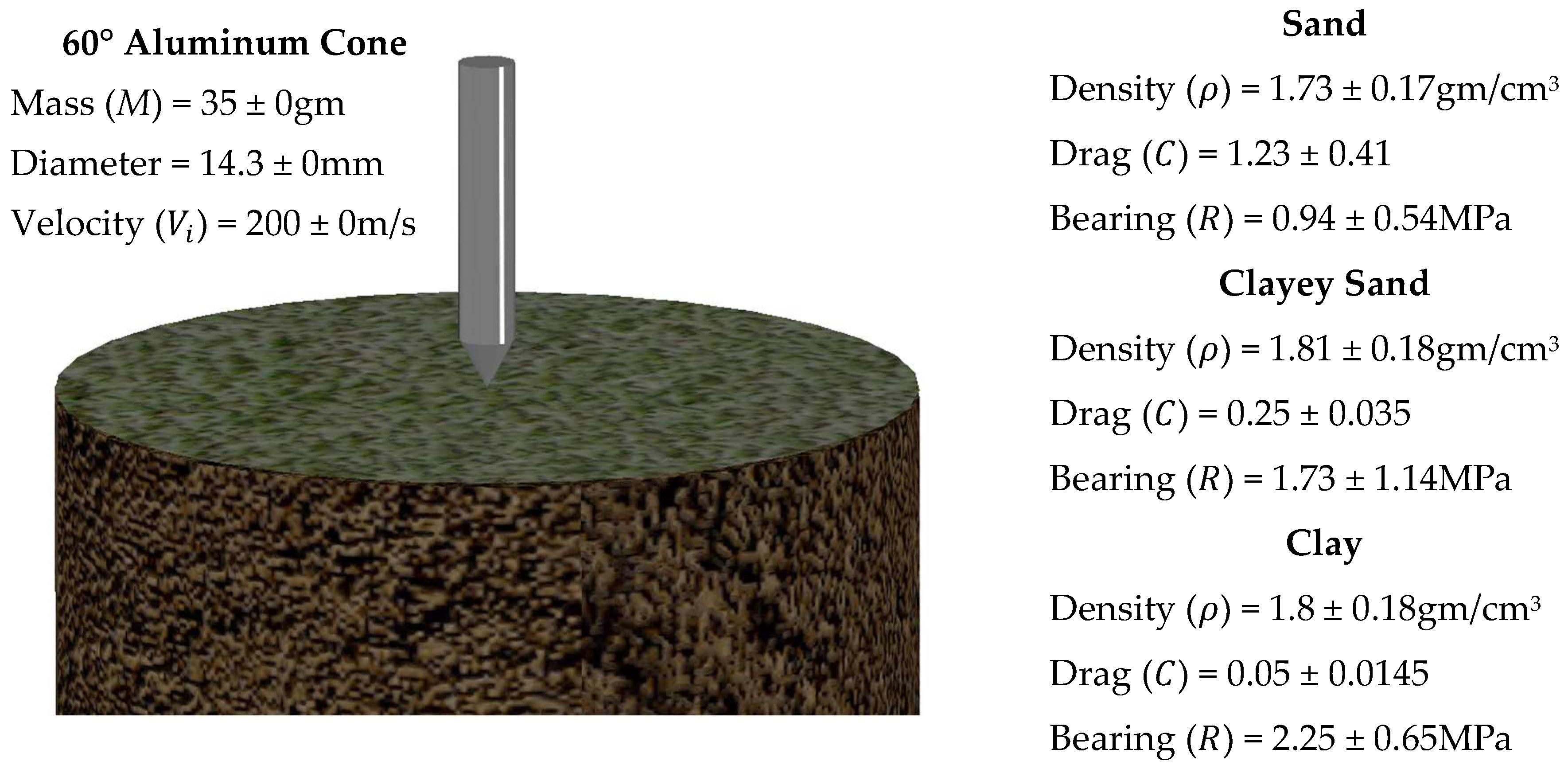


| Soil Type | Random Variable | Range | Mean () | COV (%) |
|---|---|---|---|---|
| Dry Sand [37,38] | Density () (gm/cm3) | 1.57–1.82 | 1.73 | 6 |
| Poncelet Drag () | 0.84–1.68 | 1.23 | 33 | |
| Poncelet Bearing Resistance () (MPa) | 0.40–1.78 | 0.94 | 58 | |
| Clayey Sand [35,36,40] | Density () (gm/cm3) | 1.78–1.85 | 1.81 | 1 |
| Poncelet Drag () | 0.21–0.32 | 0.25 | 14 | |
| Poncelet Bearing Resistance () (MPa) | 0.62–3.38 | 1.73 | 66 | |
| Clay [19,41] | Density () (gm/cm3) | … | 1.8 | 10 |
| Poncelet Drag () | … | 0.05 | 29 | |
| Poncelet Bearing Resistance () (MPa) | … | 2.25 | 29 | |
| Projectile | Mass () (gm) | … | 35 | (Deterministic) |
| Diameter () (mm) | … | 14.3 | (Deterministic) | |
| Impact Velocity () (m/s) | … | 200 | (Deterministic) |
| Condition | Variables | Distribution | Sand COV (%) | Clayey Sand COV (%) | Clay COV (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ | C | R | ρ | C | R | ρ | C | R | |||
| 1 | ρ, C, R | Normal | 10 | 28 | 28 | 10 | 14 | 30 | 10 | 29 | 27 |
| 2 | ρ, C, R | Lognormal | 10 | 28 | 28 | 10 | 14 | 30 | 10 | 29 | 27 |
| 3 | ρ, C, R | Lognormal | 10 | 33 | 58 | 10 | 14 | 66 | 10 | 29 | 29 |
| 4 | C, R | Normal | … | 28 | 28 | … | 14 | 30 | … | 29 | 27 |
| ρ | Lognormal | 10 | … | … | 10 | … | … | 10 | … | … | |
| 5 | ρ, R | Normal | 10 | … | 28 | 10 | … | 30 | 10 | … | 27 |
| C | Lognormal | … | 33 | … | … | 14 | … | … | 29 | … | |
| 6 | ρ, C | Normal | 10 | 28 | … | 10 | 14 | … | 10 | 29 | … |
| R | Lognormal | … | … | 58 | … | … | 66 | … | … | 29 | |
| 7 | R | Normal | … | … | 28 | … | … | 30 | … | … | 27 |
| ρ, C | Lognormal | 10 | 33 | … | 10 | 14 | … | 10 | 29 | … | |
| 8 | C | Normal | … | 28 | … | … | 14 | … | … | 29 | … |
| ρ, R | Lognormal | 10 | … | 58 | 10 | … | 66 | 10 | … | 29 | |
| 9 | ρ | Normal | 10 | … | … | 10 | … | … | 10 | … | … |
| C, R | Lognormal | … | 33 | 58 | … | 14 | 66 | … | 29 | 29 | |
| F-Statistic | Fc | ||
|---|---|---|---|
| Sand | 0.73 | 1.96 | 0.67 |
| Clayey Sand | 0.19 | 1.96 | 0.99 |
| Clay | 0.42 | 1.96 | 0.9 |
| Sampling Method | Mean DoB m | % | % | Computational Effort | |
|---|---|---|---|---|---|
| Sand | PRS | 0.28 | 27–34 | 31 | 100% |
| LHS | 0.28 | 27–36 | 31 | 105% | |
| GP_RSM | 0.28 | 28–37 | 32 | 35% | |
| Clayey Sand | PRS | 0.60 | 22–26 | 24 | 100% |
| LHS | 0.60 | 22–27 | 24 | 102% | |
| GP_RSM | 0.60 | 22–27 | 25 | 36% | |
| Clay | PRS | 1.13 | 19–24 | 22 | 100% |
| LHS | 1.12 | 19–24 | 21 | 103% | |
| GP_RSM | 1.13 | 19–24 | 22 | 37% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morkos, B.N.; Iskander, M.; Omidvar, M.; Bless, S. From Battlefield to Building Site: Probabilistic Analysis of UXO Penetration Depth for Infrastructure Resilience. Appl. Sci. 2025, 15, 3259. https://doi.org/10.3390/app15063259
Morkos BN, Iskander M, Omidvar M, Bless S. From Battlefield to Building Site: Probabilistic Analysis of UXO Penetration Depth for Infrastructure Resilience. Applied Sciences. 2025; 15(6):3259. https://doi.org/10.3390/app15063259
Chicago/Turabian StyleMorkos, Boules N., Magued Iskander, Mehdi Omidvar, and Stephan Bless. 2025. "From Battlefield to Building Site: Probabilistic Analysis of UXO Penetration Depth for Infrastructure Resilience" Applied Sciences 15, no. 6: 3259. https://doi.org/10.3390/app15063259
APA StyleMorkos, B. N., Iskander, M., Omidvar, M., & Bless, S. (2025). From Battlefield to Building Site: Probabilistic Analysis of UXO Penetration Depth for Infrastructure Resilience. Applied Sciences, 15(6), 3259. https://doi.org/10.3390/app15063259







