Abstract
This study presents a comprehensive framework for evaluating community-level flood resilience by integrating the fragility of individual buildings, the functionality of critical infrastructure sectors, and their interdependencies. Using performance-based engineering principles, the framework quantifies resilience through isolated building fragility curves, sector-specific functionality fragility curves, and a synthesized community-level functionality model. Applied to a virtual community of 1000 archetypal buildings, the analysis reveals that community functionality decreases with increasing flood depth, reaching a critical threshold of 0.87 at 1.57 m. The sensitivity analysis underscores the importance of accounting for intersectoral dependencies, as they significantly influence community-wide functionality. The results highlight the residential sector’s dominant role in shaping resilience and its cascading effects on other sectors. This framework provides actionable insights for planners and stakeholders, emphasizing the need to prioritize interventions in sectors with the highest vulnerability and dependency to enhance disaster preparedness and response strategies. This framework, novel in its integration of building-level fragility curves with community-wide intersectoral dependencies, provides actionable insights for planners and stakeholders, emphasizing targeted interventions in vulnerable sectors to enhance flood resilience.
1. Introduction
Flooding represents a pervasive and economically detrimental hazard, impacting global communities with increasing frequency and severity. As one of the most widespread natural disasters, floods affect nearly every aspect of societal function, from physical infrastructure to socio-economic stability. In the United States alone, 98% of counties have been subjected to floods, leading to infrastructural and functional losses with associated costs frequently escalating into billions of dollars annually [1]. Beyond the immediate physical destruction, flooding disrupts the operational continuity of critical systems, including transportation networks, healthcare facilities, and power grids, compounding recovery challenges. Additionally, communities suffer long-term economic turmoil, disrupting the lives of residents, displacing populations, and hindering the operations of businesses [1].
Exacerbating these challenges, the escalation of climate change-related impacts is predicted to augment flood occurrences significantly. This is especially evident in regions such as North-Western Europe and the British Isles, where projections suggest up to a 50% increase in decadal high flow events by the end of the 21st century [2,3]. Similarly, in many parts of the world, rising sea levels and extreme weather patterns are expected to contribute to more frequent and severe flooding events, threatening the resilience of coastal and inland communities alike.
Urbanization and land-use changes further amplify flood risks by altering natural hydrological systems. The conversion of permeable surfaces into impermeable ones, coupled with inadequate drainage infrastructure, increases surface runoff and exacerbates flooding intensity in urban areas. As cities expand, the exposure of critical infrastructure and densely populated regions to flood hazards magnifies the potential for catastrophic losses, underscoring the need for adaptive flood management strategies [4]. Advanced modeling approaches, such as the Smoothed Particle Hydrodynamics model used by [5] to simulate large floating bodies in urban flash-floods, illustrate the potential for detailed flood dynamics analysis to inform resilience strategies.
Table 1 summarizes key measures and policies proven effective in mitigating flood impacts, providing a practical reference for resilience enhancement.

Table 1.
The key measures and policies proven effective in mitigating flood impacts.
This impending escalation highlights the critical need for comprehensive flood risk assessments that account for not only physical damage but also the cascading impacts on interconnected socio-economic and infrastructural systems. Innovative methodologies for quantifying these risks and developing robust mitigation strategies are essential to reduce vulnerabilities, enhance adaptive capacities, and ensure the long-term sustainability of flood-prone communities [4].
Increasing attention has been directed toward the quantification of community-level resilience, a multifaceted endeavor encompassing hazard analysis, the responsiveness of the built environment, the loss of functionality, and the financial implications of these events. This focus aims to anticipate potential damages and evaluate their impact on overall community resilience, enabling a more nuanced understanding of socio-economic fortitude in the face of such calamities [10,11]. By systematically assessing these factors, researchers and practitioners can better identify vulnerabilities and implement targeted strategies to mitigate risks and enhance recovery efforts. Alternative approaches, such as machine learning for predictive damage modeling or agent-based modeling to simulate community responses, also offer promising avenues, though they often require extensive data or computational resources compared to our fragility-based method.
At the community level, resilience is defined as the capacity to minimize damages and recover swiftly, resuming everyday life soon after a hazard strikes. Achieving this requires comprehensive preparedness measures, robust infrastructure, and adaptive socio-economic systems [12]. When resilience is insufficient, the consequences can be catastrophic, as demonstrated by the aftermath of Hurricane Katrina in New Orleans. In this case, inadequate preparedness and systemic vulnerabilities resulted in widespread and prolonged inundation, tragic loss of life, significant population displacement, and severe environmental degradation [13]. This tragic example underscores the importance of proactive planning and resilient design to reduce the long-term impacts of flood events.
The concept of community resilience is often expressed and quantified in terms of performance, quality, or functionality over time, as illustrated conceptually in Figure 1. This temporal perspective highlights the dynamic nature of resilience, reflecting not only the immediate impacts of a hazard but also the trajectory of recovery and adaptation. By capturing this evolving process, resilience assessments can provide critical insights into the effectiveness of preparedness strategies and inform the development of policies and interventions to strengthen community systems against future hazards.

Figure 1.
Schematic description of community-level resilience.
As shown in Figure 1, community-level resilience is fundamentally associated with two main parameters: reliability and recovery [14]. Reliability refers to the capacity of a community to maintain a baseline level of functionality during and after a disruptive event, while recovery denotes the ability to restore functionality within a reasonable timeframe. These parameters are influenced by four critical attributes. Robustness represents the ability to withstand an extreme event and deliver a certain level of service even as the event unfolds. Rapidity reflects the speed at which a system can recover and restore its desired functionality. Redundancy describes the extent to which critical components of a system can be substituted by others to sustain essential functions. Resourcefulness, on the other hand, pertains to the capacity to identify problems, establish priorities, and mobilize resources effectively in response to extreme events. In this paper, the focus is placed on assessing the impact of flooding on a community by evaluating both the immediate damage and the resulting loss of functionality.
To appropriately measure community resilience, it is crucial to define the concept of “community”. Traditionally, a community is understood as an assemblage of individuals living within a shared geographical area, supported by interconnected infrastructure that includes essential systems such as residential, commercial, and industrial structures [15]. These physical systems are typically governed by existing building codes and construction practices, which prioritize life safety as the primary objective. However, such infrastructure often remains vulnerable to significant disruptions and losses in the aftermath of disasters, revealing the limitations of conventional design approaches. This underscores the urgent need to transition toward the construction of resilient infrastructure, a paradigm that extends beyond ensuring life safety to focus on the sustained viability and functionality of the community fabric [16].
Resilience in this context demands infrastructure systems that can absorb shocks, adapt to evolving conditions, and support rapid recovery. However, capturing the complexity of community resilience, particularly in the context of flooding, remains a formidable challenge. The intricate, non-linear interactions among variables, the integration of diverse data sources, and the lack of standardized mathematical models add layers of complexity to resilience assessments. Additionally, critical data gaps and the absence of universally applicable frameworks further hinder the accurate quantification and evaluation of resilience [17]. These challenges highlight the necessity for innovative approaches that address the multifaceted nature of community resilience while accommodating the unique characteristics of flooding events.
Various models and frameworks have been proposed to evaluate and quantify resilience, addressing many of the challenges inherent in community-level resilience assessment. Among these are simulation-based approaches, which model system behaviors under different scenarios [9,18], probabilistic methods that quantify uncertainties and predict outcomes [19,20], and fuzzy logic methods, which handle imprecision and ambiguity in resilience evaluations [21]. In addition to these approaches, fragility analysis has emerged as a reliable and valuable tool for resilience-based decision-making, offering planners and stakeholders actionable insights.
For instance, ref. [16] introduced the concept of the building portfolio fragility function, defined as the probability that a building portfolio fails to achieve specified performance objectives under a given earthquake scenario. They demonstrated its application using the Centerville community to illustrate how this approach characterizes building vulnerability. Similarly, ref. [22] underscored the importance of developing appropriate fragility models to advance performance-based engineering. They proposed a methodology to assess the probable response of light-frame residential infrastructure exposed to natural and human-made hazard levels. In another example, the hurricane and earthquake models in HAZUS incorporate fragility functions to describe the vulnerability of buildings, further validating the utility of this approach in resilience assessments [23]. Building on this foundation, the proposed method in this study employs flooding-specific fragilities and integrates functional interdependence to establish a connection between community-level resilience, the functionality of key building sectors, and individual building archetypes.
The primary objective of this investigation is to rigorously evaluate and quantify community resilience in the context of flood-related events. To achieve this, the proposed methodological framework is constructed upon three core components. First, discrete building fragility curves are formulated using principles from performance-based engineering, drawing parallels with established methodologies for seismic assessment. Second, fragility curves for essential building sectors are developed at the sub-assembly level to capture their contribution to the overall functionality of the community fabric. Third, these efforts are synthesized into community-wide functionality fragility curves, providing a holistic measure of resilience at the macroscopic level.
Fragility curves for supporting building sectors are integrated with an interaction matrix within a community-level model to evaluate residual functionality, enabling more effective risk-informed decision-making and response strategies. This proposed method represents a significant advancement in quantitative community-level resilience analysis by addressing the unique challenges posed by flood events. While innovative in its application to flooding resilience, this approach can also be adapted to incorporate additional community sectors, ensuring flexibility and broader applicability. By bridging the gap between traditional fragility analyses and community-wide functionality assessments, this framework aims to enhance resilience planning and facilitate the development of better-informed strategies for mitigating flood-related risks. The paper is structured as follows: Section 2 details the methodology, Section 3 presents the results and analysis applied to a virtual community, and Section 4 concludes with key findings and implications.
2. Methodology
2.1. Overall Procedure
The overall procedure of this study is outlined in Figure 2, which provides a step-by-step framework for evaluating community-level flood resilience. The process begins by identifying flooding hazard features that effectively represent the level of damage caused by flooding. These features are critical for characterizing the severity and scope of flood events and serve as the foundation for subsequent analyses. The next step involves analyzing the vulnerability of various infrastructure types to flooding. This is depicted in the second panel of Figure 2, which presents fragility curves for different infrastructure categories, including residential, commercial, and industrial buildings. Each curve illustrates how the probability of reaching specific damage states increases with flood depth. This analysis is essential for identifying which structures are most at risk and determining the thresholds of flood intensity that pose the greatest concern. Following the fragility curve analysis, the survivability of individual buildings is evaluated across a range of increasing flood depths. The third panel in Figure 2 displays a cumulative distribution function that quantifies the likelihood of buildings maintaining functionality as flood intensity escalates. This step provides valuable insights into structural vulnerabilities and supports the development of targeted strategies, such as structural reinforcements and other mitigation measures, to enhance building resilience. In the fourth step, the focus shifts to assessing the interdependencies among critical community sectors, including water, power, and transportation systems. The interdependency matrix shown in the fourth panel quantifies how failures in one sector can propagate and impact others. This analysis highlights key areas where joint resilience strategies could effectively reduce the cascading effects of sectoral failures, ensuring a more robust response to flooding events. Finally, the data from all preceding steps are synthesized to evaluate the overall functionality of the community in the face of floods. The fifth panel in Figure 2 presents a cumulative distribution function that illustrates the probability of maintaining community-wide functionality as flood depths increase. This comprehensive assessment provides a macroscopic perspective on the broader impacts of floods, enabling strategic planning for disaster preparedness, response, and recovery. By integrating hazard characterization, infrastructure vulnerability analysis, interdependency assessment, and community-wide functionality evaluation, this methodology offers a systematic approach to understanding and enhancing flood resilience at the community level.
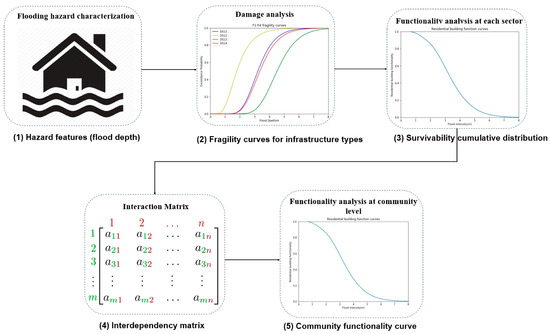
Figure 2.
Community level resilience quantification process.
2.2. Quantification of Community-Level Resilience
The quantification of community-level resilience currently depends on F(t), which represents the priority given to maintaining vital functionality () of infrastructure systems over time (t). F(t) can be calculated through an equation, as shown below:
where F(t) is the community-level functionality at time t, is the proportion of the ith sector’s contribution to community functionality, and is the damage function of the ith sector over time due to flooding.
This measure ensures access to critical resources for all citizens and is represented on the vertical axis in Figure 2. A prototypical community is a synergy of social and physical infrastructures, with the former being influenced by factors such as demographic dynamics, economic stability, educational breadth, and healthcare provision, and the latter by the integrity of housing, water, electrical, and transportation networks [24]. Therefore, community-level F(t) is a multi-dimensional function that is classified into four dimensions. The four considerable dimensions are as follows: 1. technical—denoting the resilience of physical systems to maintain operability under hazard stress; 2. organizational—reflecting the preparedness and adaptive decision-making process of entities managing critical services; 3. social—concerned with strategies aimed at curtailing the proliferation of adverse outcomes post-disaster; and 4. financial—encompassing the capability to mitigate direct and ancillary economic repercussions resultant from flood events [14].
The quantification of these four dimensions of community-level performance requires multi-dimensional measurements. As the basis for evaluating the possible impacts on the social, organizational, and economic performance of a community, it is urgent to assess technical functionality loss evaluation for individual buildings and infrastructure sectors [25,26]. This paper focuses on the technical resilience of infrastructure portfolios and four main sectors in a community [27,28].
2.3. Flood Intensity Level and Fragility Curve
To quantify community-level resilience, the measurement of community-level functionality should be defined first. Conceptually, the community-level resilience should be measured by the probability of its “undesired outcome”, which refers to the occurrence of an adverse impact on a community’s ability to keep its original-level function [29]. It is also important to consider that community-level resilience is always influenced by many factors related to human activities, and the risk occurs when people, communities, or infrastructures can be negatively impacted by a natural hazard. Among these human activities, population dislocation has often been used as a metric for overall community resilience [30,31,32]. Considerable population dislocation is an undesired outcome resulting from a flooding event and will be used herein as the community resilience metric, as this is a good index reflecting the potential occupation of a community.
It should be noted that for all building archetypes, flood depth is measured from First-Floor Elevation (FFE). However, for these with crawl space foundations, it is measured from ground elevation, and the FFE is assumed to be at 1.0 m from the ground elevation; this also means that DS0 only exists in these buildings with crawl space foundations.
The level of damage caused by a flooding hazard is influenced by several parameters, including the flooding depth, duration, velocity, the rate of rise in water levels, impulse (a product of water level and velocity), warning time, and frequency of occurrence. Among these factors, flooding depth is considered the most critical parameter, as it effectively determines the flood hazard’s risk indices [33]. Consequently, flooding depth is used as the primary measure of flood hazard intensity in this study. Damage states (DSs) probabilities are used to describe the conditions of buildings under flooding hazards, categorized into five levels: insignificant damage (DS0), slight damage (DS1), moderate damage (DS2), extensive damage (DS3), and complete damage (DS4). This is outlined in Table 2 and based on prior studies [6]. Within the same community, buildings may experience different damage states due to variations in structural characteristics and environmental factors. Following the assumptions in [16], buildings in DS3 or DS4 are deemed unsafe for occupation unless they undergo repairs or replacement. These damage states and their corresponding probabilities provide a critical foundation for assessing building vulnerability and resilience, enabling a comprehensive analysis of flood impacts [6,17,34].

Table 2.
The description and functionality of each DS.
As for the flooding intensity measure, a single-variable approach based on the flooding depth is used to measure the flooding hazard damage. Reference [6] articulated a component-based numerical fragility and loss approach. Then, a Monte Carlo Simulation (MCS) is applied to propagate uncertainties in the resistance statistics of each component (e.g., cabinets or drywall) and for the whole-building fragility to flooding depth. The MCS was implemented using MATLAB R2024a, a computational platform chosen for its robust statistical and probabilistic modeling capabilities. Specifically, the analysis involved generating 10,000 random samples of flood depth and component resistance parameters, based on lognormal distributions with median (λ) and standard deviation (ξ) values derived from [6]. These samples were used to compute the exceedance probabilities of the damage states (DS0–DS4) for each building archetype, producing the fragility curves.
The exceedance probability (fitted) of each DS conditioned on the flooding hazard intensity measure (IM) is uncertain and assumed to be fitted by a lognormal cumulative distribution function (CDF) in Equation (2):
where Fr is the lognormal fitted fragility function when IM is x, and and are the logarithmic median and standard deviation of each damage state, respectively. For individual buildings, the fragility function indicates the fitted probability that the individual building fails to provide safe occupancy; and for building sectors consisting of various buildings, the fragility function describes the ratio of buildings failing to provide safe occupancy for people living in the community. The fragility information on individual buildings, like the logarithmic median and standard deviation, can be obtained from Nofal’s work [6]. This foundational study provides a robust portfolio of minimal building flood fragility and loss functions, directly supporting our community-level resilience analysis.
The fragility curves utilized in this study were derived from a curated dataset based on specific inclusion and exclusion criteria to ensure applicability to flood resilience assessment. The inclusion criteria for the flood damage data included the following: (1) empirical or simulated flood depth–damage relationships from peer-reviewed sources, primarily [6], covering a range of building archetypes relevant to the virtual community; (2) data reflecting damage states (DS0 to DS4) aligned with population dislocation as the resilience metric; and (3) availability of probabilistic parameters suitable for lognormal cumulative distribution functions. The exclusion criteria comprised the following: (1) datasets lacking flood depth as a primary intensity measure, as this study focuses on depth-dependent damage; (2) data from non-representative building types not applicable to the wood-frame dominated virtual community; and (3) studies with insufficient sample sizes or unvalidated simulation outputs, which could compromise the reliability of fragility estimates. This rigorous selection ensured that the fragility curves accurately represented the vulnerability of the selected archetypes under varying flood intensities.
2.4. Uncertainty Propagation
Significant uncertainties are associated with community-level resilience assessment and quantification, propagating from hazard intensity to damage estimation. The distribution of community-level functionality (), conditioned on a predefined flooding scenario (Sf) characterized by the specific intensity flood depth, can be formulated according to Lin’s work [16] as shown in Equation (3).
where , , and are the probability density functions (PDFs) of flood depth conditioned for the flood scenario event, DS conditioned on flooding intensity, and damage value (DV) conditioned on DS, respectively. Additionally, is the cumulative distribution function (CDF) of community-level functionality conditioned on DV. This formulation directly relates the community-level functionality to the flooding hazard scenario. In this convolution, an MCS is used to capture the uncertainties propagating from hazard intensity to damage estimation. This analysis was conducted in MATLAB, where the MCS framework simulated 10,000 iterations to convolve the probability density functions (PDFs) of flood depth, damage states, and damage values, as defined in Equation (3). The tool’s matrix computation capabilities facilitated the integration of these distributions, yielding the cumulative distribution function (CDF) of community-level functionality. This process ensured a robust quantification of uncertainties across the virtual community’s building sectors.
To prevent the possible occurrence of significant population dislocation, the vital community functions must be in regular service even when flooding hazards occur. Population dislocation is the result of several factors. For example, if we consider four building sectors and the functional interdependencies among them, then we respectively use Pd,i, Pd,ij, Pd,ijk, and Pd,ijkl to denote the population dislocation based on the loss of a single sector i, two sectors (i and j), three sectors (i, j, and k), and all four sectors (i, j, k, and l) simultaneously. Here, j, k, and l represent the remaining three sectors. Letting Pi represent the probability of functionality loss in sector i, the expected population dislocation ratio, Ppd, is calculated according to the total probability theorem and can be simplified by neglecting the last two higher order terms in the whole probability equation as follows:
It can also be expressed in matrix form, as shown in Equation (5):
It should be noted that Equation (4) has been simplified to this format based on the assumption that the probability of functionality loss for three or four essential building sectors’ functions is typically small [8]. In Equation (5), [A] is a damage augmented adjacency matrix, which is explained in detail in the following section.
2.5. The Functional Interdependencies Among Different Building Sectors
Rinaldi et al. classified interdependencies among infrastructure systems into four types: physical, cyber, geographic, and logical [35]. These interdependencies are inherent in each system and are highly complex. In this work, the proposed damage augmented adjacency matrix was applied with a likelihood/weight Matrix A, as shown in Equation (5), to simplify and address these challenges in simulating and understanding the functional interdependencies among four essential sectors in a community suffering from flooding hazard, e.g., a sector of residential buildings (R.S.), a sector of business facilities (B.S.), a sector of education (E.S.), and a sector of public service (P.S.). Note that the likelihood/weight Matrix A is a key parameter set that quantifies intersector dependency correlations. While it reflects the characteristics of an interdependent system of multiple sectors, it is hard to define theoretical calculation methods to determine specific numbers in [A]. Thus, researchers established an empirical parameter set to approximate the true values and the results have been validated successfully [8]. These four sectors were chosen based on previous studies focusing on other hazards’ damage evaluation, e.g., earthquakes [8,29].
where (for i ∈ {1,2,3,4}) denotes the population dislocation conditional on the fraction loss of only sector i (Pi), and (i ∈ {1,2,3,4}, j∈ {1,2,3,4}, I ≠ j) denotes the additional loss to the sector i due to the fraction loss of sector j. All these coefficients in matrix A account for the functional interdependencies among the four sectors.
Intersectoral dependencies were parameterized using empirical weights from [8], adjusted for flood impacts based on sector criticality. The adjacency matrix simplifies complex interactions into a weighted grid, validated in earthquake studies and here adapted for flood scenarios, as seen in post-Hurricane Katrina infrastructure analyses.
For the case study presented later in this paper, the matrix used was calibrated according to the analysis presented in [29], which links community-level resilience goals to specific functionality targets for different supporting building sectors in the built environment. According to this framework, four functional states (F.S.s)—green, yellow, orange, and red—are defined for each community sector. The fractional losses () of each sector correspond to each of the F.S.s listed in Figure 3, reflecting the relative importance of the four sectors to preserve the overall community function (i.e., preventing significant population dislocation in this case).
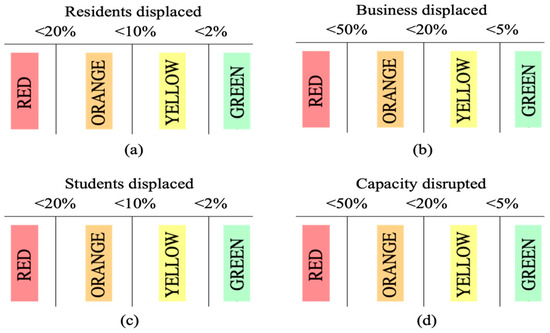
Figure 3.
The functional states and corresponding damage percentages for four sectors. (a) Residential and business sectors at 1.57 m flood depth; (b) Educational and public service sectors at 1.57 m flood depth; (c) Residential and business sectors at 3 m flood depth; (d) Educational and public service sectors at 3 m flood depth.
While there are 44 (total 256) possible community function levels resulting from the specific combinations of the four F.S.s of the four sectors, significant dislocation was assumed to occur only when two or more community sectors were “in red” or three or more were “in orange or red”, which represent 104 combinations out of the 256 cases [29]. Therefore, the total probability of the 104 undesired sequences in Figure 3 must be less than the target objective. Note that the total probability of all 256 outcomes is 100% because the outcomes are collectively exhaustive.
2.6. Flood Performance of Community Supporting Building Sectors
The above illustration provides a suitable community-level resilience quantification system for the damage augmentation matrix. The determination of specific values in matrix A is challenging due to the complex nature of physical community-level interactions among individual sectors. Common practices that have been successfully conducted by other researchers are based on sensitivity analysis [36]. For a real community in a flooding hazard, the matrix can only be determined through analysis of the previous hazard-related history data or empirical judgment from the engineering team, stakeholders, and other related experts in the absence of useful data. In the case study section, to demonstrate the feasibility, we refer to a study conducted by [29]. to approach one of the most realistic values of matrix A using sensitivity analyses [29]. Furthermore, upon applying matrix A, the 104 combinations mentioned in Section 2.4 remained in an undesired condition. A community functionality loss of 13% and a damage augmentation matrix, as shown in Equation (7), were obtained by optimizing the damage matrix and the value of community functionality loss against the scenario presented in the study conducted by [29]. The final damage augmentation matrix A is given as follows:
It should be noted that the interdependency matrix for the four sectors represents just one potential outcome among many possible outcomes of the proposed framework. Based on empirical data, both diagonal and off-diagonal elements were adapted from reference [8], where empirical parameters for earthquakes were established. We conducted a series of numerical tests with all possible values in the range of [0,1] for the off-diagonal elements. Ultimately, we found that matrix A is not sensitive to different hazard modes, meaning that the off-diagonal elements could be applied to various hazard modes without causing significant discrepancies. Thus, we reused the empirical-based off-diagonal elements for our flooding matrix, and the results were acceptable.
Each community will need to adapt different aspects of the framework to suit their specific circumstances, resulting in modifications to the matrix values in Equation (7). Furthermore, we conducted a sensitivity analysis to examine the impact of matrix application on calculating the loss of functionality at the community level. In this example, we primarily focused on four different models based on the level of interdependency from 0 to 1. Note that a value of 0 indicates that the loss of essential function in one sector does not result in any additional loss to the essential function of other sectors. A value of 1 signifies that the loss of essential function in one sector will cause the total function loss of another sector. Model 1 represents the scenario where functionality interdependencies among the four sectors are fully realized, reaching 100%. Model 2 represents the functional interdependencies matrix in reference paper [8]. Model 3 incorporates the matrix described in Equation (6). Model 4 utilizes a matrix with all values set to 0.5.
2.7. Calculation of Community Resilience
In this case, the four sectors in the same community are further divided into 11 building categories, and the flood sensitivity of different building categories is different; thus, the functionality loss index (L) and survived functionality (F) of the building sector i is estimated as follows:
The probability that building sector i is lost () can also be interpreted as the percentage of lost buildings in sector i. With this interpretation, we further define community functionality loss (L.C.) and the residual post-disaster functionality level (F.C.), measured herein by the population dislocation percentage for a scenario event.
3. Results and Analysis
3.1. The Basic Description of the Virtual Community Case
As discussed in previous studies [8,29,36], the use of virtual community resilience testbeds is increasingly prevalent in natural hazard engineering research. These testbeds allow researchers to evaluate and validate resilience algorithms at various scales and spatial resolutions, departing from traditional component- and building-level simulations. This section introduces a simplified virtual community used to demonstrate the application of fragility curves and an interaction matrix for quantifying flood resilience at the community level.
To ensure the virtual community represents a realistic yet manageable testbed for flood resilience analysis, the data selection process involved specific inclusion and exclusion criteria. The inclusion criteria encompassed the following: (1) building archetypes commonly found in flood-prone U.S. communities; (2) availability of fragility curve parameters (lognormal median λ and standard deviation ξ) from the established literature to ensure consistency with performance-based engineering principles; and (3) relevance to the four critical sectors (residential, business, educational, and public service) that collectively support community functionality. The exclusion criteria included the following: (1) building types with insufficient flood vulnerability data, such as specialized industrial facilities or high-rise structures not typically represented in small-scale communities; (2) archetypes lacking empirical or simulated flood damage records, which would preclude reliable fragility curve development; and (3) structures irrelevant to the study’s focus on population dislocation as a resilience metric. This selection process resulted in a consolidated set of 11 building archetypes (as detailed in Table 3), balancing representativeness and analytical feasibility.

Table 3.
Lognormal parameters of the developed fragility for the selected building archetypes.
The hypothetical community comprises approximately 1000 buildings distributed across four zones—residential, business, educational, and public service—as depicted in Figure 4. Building types in the residential zone include one-story and two-story single-family and multi-family residential buildings, while the business zone features multi-unit retail buildings, small commercial facilities, and large retail centers located along major roads. The public service zone consists of essential facilities such as hospitals, clinics, and gas stations, while the education sector includes one-story and two-story school buildings. To simplify the analysis, the building types within each zone are consolidated into archetypal categories that represent the minimum components necessary for a resilient built environment. This approach aligns with methodologies employed in previous resilience studies [8,36], ensuring that the results remain generalizable. The virtual community serves as a case study to demonstrate the integration of fragility curves and interaction matrices in assessing flood resilience, providing insights into how these tools can guide planning and decision-making processes.
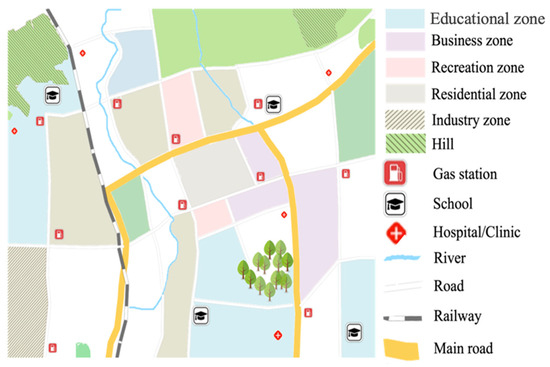
Figure 4.
Zoning map of the virtual community.
3.2. The Fragility Curves of Community Components
The fragility curves of community components play a critical role in quantifying flood resilience. For this analysis, a simplified hypothetical community is considered, encompassing four key sectors: residential (R.S.), business (B.S.), educational (E.S.), and public service (P.S.). Each sector comprises multiple building archetypes, each designed with distinct service objectives and structural characteristics. For instance, the residential sector includes one-story single-family homes, one-story multi-family homes, two-story single-family homes, and two-story multi-family homes. The fragility curves for these archetypes, as derived from [6], are shown in Figure 5a.
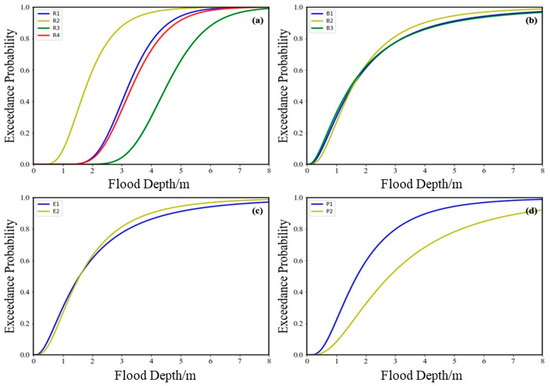
Figure 5.
Fragility curves in four sectors: (a) R.S.; (b) B.S.; (c) E.S.; and (d) P.S.
Similarly, the fragility curves for business facilities (Figure 5b), educational buildings (Figure 5c), and public service structures (Figure 5d) illustrate the probability of damage states at varying flood depths. These curves depict the exceedance probability, which quantifies the likelihood of reaching or exceeding specific damage states given a certain flood intensity. Such probabilities are critical for understanding how individual components within each sector contribute to sector-wide functionality loss during flood events.
Table 3 provides the lognormal parameters—logarithmic medians (λ) and standard deviations (ξ)—for the developed fragility curves of each building archetype. For example, one-story single-family residential buildings (R1) exhibit a λ of 1.173 and a ξ of 0.278, indicating their relative vulnerability compared to other archetypes. These parameters enable a probabilistic understanding of structural performance under varying flood intensities. It can be observed that these fragility curves underscore the heterogeneity in resilience across building types. They reveal that while some archetypes are more robust against flood hazards, others face significant vulnerabilities, requiring targeted mitigation strategies. By integrating these fragility curves with interaction matrices, this study provides a comprehensive framework for evaluating the resilience of individual sectors and the community as a whole.
3.3. Functionality at Sector Scale and Community Scale
For a flood intensity ranging from 0 m to 8 m with an increment of 1 m, the sustainable functionality of each sector immediately following the hazard is estimated based on individual building fragilities, as shown in Figure 6.
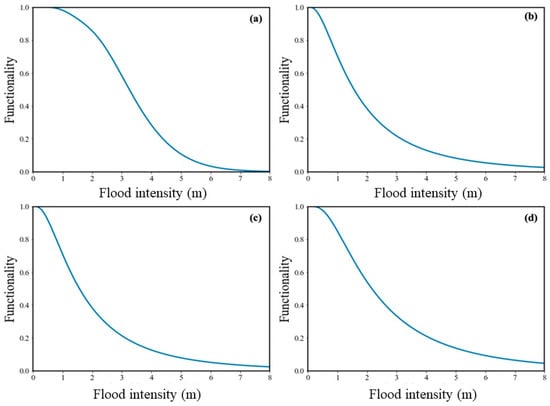
Figure 6.
Exceedance probability results for each sector: (a) R.S.; (b) B.S.; (c) E.S.; and (d) P.S.
Our findings align with the depth–damage curve delineated by [7], which correlates the flood depth experienced by structures with the percentage loss in structural value due to flood damages. The analysis reveals a pronounced decline in functionality across all four sectors, approaching zero when flood levels hit the 8 m mark. Notably, the business sector exhibits the steepest reduction in operational capacity, while the residential sector demonstrates a relatively gradual descent post-flooding. This observed homogeneity in resilience among the various supporting building sectors may be attributed to a shared vulnerability profile among individual structures. Figure 6 illustrates this phenomenon, where a 50% probability of retained functionality corresponds to flood depths of 3 m, 1.5 m, 1.5 m, and 2 m for the R.S., B.S., E.S., and P.S. building sectors, respectively.
With the optimized community-level resilience model, the overall community functionality defined in Equation (4) is assessed using matrix A. The result is plotted in Figure 7.
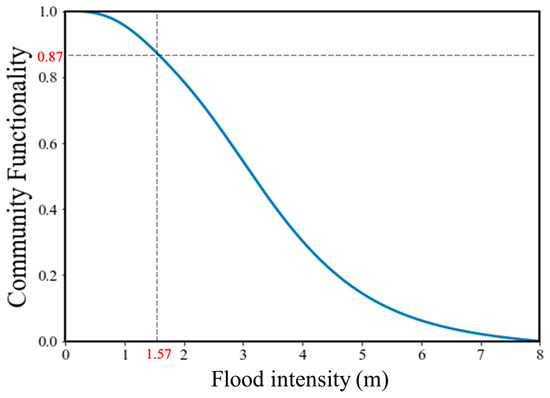
Figure 7.
Community-level functionality as a function of flood intensity (m).
The community functionality decreases with an increase in the measured intensity of flood depth (m), reaching 0.87, which is the threshold of proper functionality, as discussed in Section 2. When the flood intensity is at this threshold, the flood depth reaches 1.57 m, as listed in Table 4.

Table 4.
The loss and residual functionality at the threshold (15% population dislocation) derived from Monte Carlo Simulations.
At this intensity of threshold, the residual functionalities for R.S., B.S., E.S., and P.S. drop to 0.80, 0.50, 0.55, and 0.67, respectively. The main purpose of this study is to provide a methodology for assessing flood resilience at the community level. The hypothetical community consisting of wood frame buildings is case-specific. Further study should be performed to estimate flood resilience more accurately based on more comprehensive data, providing more reliable results.
Figure 8 shows the relative contribution of each community supporting the building sector to community-level residual functionality immediately after a flood disaster. It can be observed that residential buildings have the most important impact on community-level functionality, while the other three sectors seem relatively less impacted during flood scenarios, and the variation in the functionality of residential buildings is bigger than in the other three sectors. Also, it is found that the community-level functionality loss is attributed mostly to the loss of the residential building sector, specifically when the community-level functionality decreases below 90% of the original level. However, when community-level functionality is lower than 90% of the normal level, the functionality of the education sector is the highest among these four sectors. Figure 9 illustrates the sensitivity analysis findings.
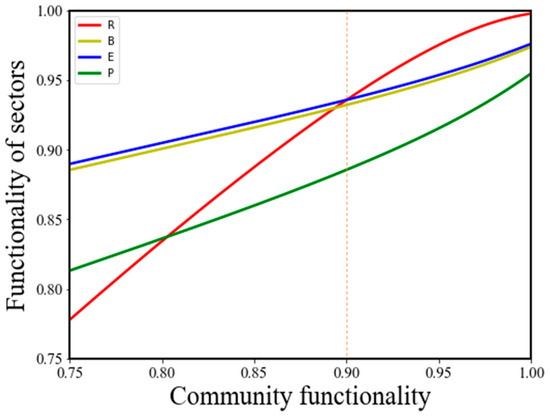
Figure 8.
The overall variation of each Sector in a community.
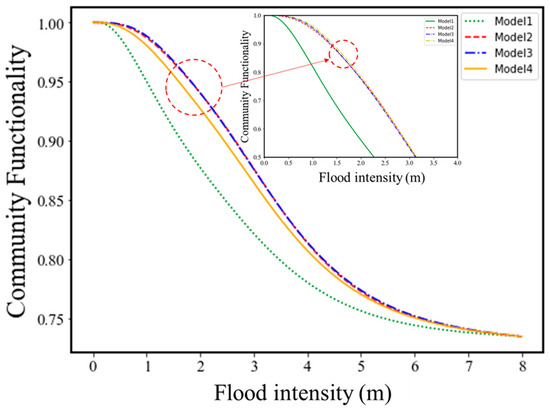
Figure 9.
Sensitivity analysis of community-level functionality in the four different models.
It is important to note that the disparity between the scenarios where the functional loss of one sector leads to the complete functional loss of other sectors and the scenarios that do consider these interdependencies is more significant. However, the variation among scenarios that accounts for functional interdependencies with different matrices is comparatively smaller. This emphasizes the need to consider the functional interdependencies among various building sectors when assessing community functionality.
The evaluation of immediately post-disaster functionality in this paper can directly reflect the community’s ability to resist flood hazards. In addition, according to the results presented, the residential sector has the greatest impact on community resilience. This may be due to the larger number of buildings in the residential sector than in other sectors, which contributes more to the community-level resilience. On the other hand, some residential buildings have no significant damage to their frameworks. However, due to the loss function of the infrastructure they are dependent on, their occupancy cannot be successfully provided, which can lead to additional population dislocation. These all suggest that generally, attention should be given to the residential buildings when incorporating mitigation during a hazard and reducing their dependence on other sectors should be more effective.
Comparing these findings with prior studies provides further context. The community functionality threshold of 0.87 at 1.57 m flood depth aligns with [6], who noted significant functionality loss in wood-frame residential buildings at similar depths, confirming the validity of our fragility parameters. Extending the analysis to flood depths beyond 1.57 m (e.g., 3 m) shows functionality dropping below 0.50, underscoring the need for robust mitigation at higher intensities. However, our focus on intersectoral dependencies—evidenced by residential impacts cascading to business (0.50) and education (0.55)—extends their building-centric analysis, echoing [8]’s earthquake resilience work where residential dominance also emerged, though with different hazard metrics.
This study further diverges from qualitative approaches like [29], who broadly categorized functionality states, by offering precise, quantitative residual functionality estimates. This precision highlights a novel contribution: a flood-specific framework integrating building fragility with community-wide interdependencies. These comparisons not only validate our results against the existing literature but also underscore the added value of a systems-based approach for flood resilience assessment.
4. Conclusions
This study presents a comprehensive framework for quantifying flood resilience at the community level, incorporating the fragility of individual buildings, the functionality of critical infrastructure sectors, and the interdependencies among these sectors. The methodology includes three key components: (1) the development of isolated building fragility curves through a performance-based engineering approach consistent with seismic resilience methods; (2) the formulation of fragility curves for community-level infrastructure sectors at the subassembly level; and (3) the synthesis of community-level functionality fragility curves to evaluate overall resilience. These elements are integrated into a community-level model via an interaction matrix to quantify residual functionality and support risk-informed decision-making.
The application of this framework to a virtual community case study, consisting of 1000 archetypal buildings across the residential, business, educational, and public service sectors, demonstrates its efficacy. The findings reveal that community functionality decreases with increasing flood depth, with the critical threshold of proper functionality (0.87) occurring at a flood depth of 1.57 m. At this threshold, the residual functionalities for the residential, business, educational, and public service sectors are 0.80, 0.50, 0.55, and 0.67, respectively. The results highlight the dominant role of the residential sector in influencing overall community resilience, particularly when functionality drops below 90%. In extreme flood scenarios, the education sector demonstrates relatively higher resilience, providing critical support during recovery efforts.
This study emphasizes the importance of incorporating functional interdependencies into resilience assessments. The sensitivity analysis results underscore that accounting for intersectoral dependencies significantly enhances the accuracy of community functionality evaluations. These insights provide actionable guidance for prioritizing interventions, such as strengthening the resilience of residential buildings and mitigating the cascading impacts of interdependent sector failures.
While this study advances the field of flood resilience quantification, it acknowledges several limitations. The reliance on flood depth as the sole hazard intensity parameter simplifies the analysis but may not capture the full complexity of flood scenarios, such as flood duration or velocity. Additionally, the lack of post-disaster empirical data for validating the model highlights the need for future studies to incorporate finer-resolution inputs, such as data on power stations, wastewater treatment plants, or other critical infrastructure. Expanding the framework to include additional infrastructure systems, such as telecommunication networks or transportation systems, would further enhance its applicability.
In conclusion, this framework represents a significant step forward in quantifying community-level flood resilience, integrating functional interdependencies to provide a holistic and actionable understanding of vulnerability and functionality. Future research should aim to refine and validate the model using real-world data, expand its scope to encompass additional hazard parameters and infrastructure systems, and incorporate human impacts to offer a more comprehensive perspective on community resilience. Incorporating social vulnerability metrics or applying the framework to real-world cases like the Houston flooding could further enhance its robustness and relevance.
This study’s results highlight critical insights for urban planning and flood risk management, revealing a community functionality threshold of 0.87 at a 1.57 m flood depth, driven largely by the residential sector’s influence (0.80 residual functionality). This suggests prioritizing mitigation in residential zones—such as elevating buildings or using flood-resistant materials—while integrating redundant systems like decentralized power to address intersectoral dependencies, as losses cascade to the business (0.50) and education (0.55) sectors. The framework’s ability to quantify sectoral functionality loss supports targeted investments in green infrastructure, like permeable pavements, to keep flood depths below this threshold, though future efforts should also consider flood velocity and duration for a holistic approach, advocating a proactive, systems-based strategy.
This study’s findings carry practical implications for urban planners and risk management officials. The critical functionality threshold of 0.87 at 1.57 m flood depth highlights the need to elevate residential buildings or retrofit them with flood-resistant materials, especially in dense urban areas where the residential sector dominates resilience (0.80 residual functionality). Strategies like installing permeable pavements or retention basins can reduce flood depths below this threshold, while decentralized utilities—such as local power or water systems—can mitigate cascading failures across sectors like business (0.50) and education (0.55), offering urban realities a proactive, cost-effective path to bolster flood resilience.
Author Contributions
Conceptualization, Y.L. and D.W.; Methodology, Y.L., G.Z. and D.W.; Validation, G.Z.; Formal analysis, D.W.; Investigation, Y.L., G.Z. and D.W.; Data curation, G.Z.; Writing—original draft, Y.L.; Writing—review & editing, D.W.; Visualization, G.Z.; Project administration, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
These data pertain to an ongoing doctoral research project. For access, please contact the corresponding author directly.
Acknowledgments
Special appreciation goes to the editors and reviewers who contributed to improving the quality of this article by providing constructive comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Joyner, M.D.; Sasani, M. Multihazard Risk-Based Resilience Analysis of East and West Coast Buildings Designed to Current Codes. J. Struct. Eng. 2018, 144, 04018102. [Google Scholar] [CrossRef]
- Morita, M. Quantification of Increased Flood Risk Due to Global Climate Change for Urban River Management Planning. Water Sci. Technol. 2011, 63, 2967–2974. [Google Scholar] [CrossRef] [PubMed]
- Ghazali, D.A.; Guericolas, M.; Thys, F.; Sarasin, F.; Arcos Gonzalez, P.; Casalino, E. Climate Change Impacts on Disaster and Emergency Medicine Focusing on Mitigation Disruptive Effects: An International Perspective. Int. J. Environ. Res. Public Health 2018, 15, 1379. [Google Scholar] [CrossRef] [PubMed]
- Morrison, A.; Westbrook, C.J.; Noble, B.F. A Review of the Flood Risk Management Governance and Resilience Literature. J. Flood Risk Manag. 2018, 11, 291–304. [Google Scholar] [CrossRef]
- Albano, R.; Sole, A.; Mirauda, D.; Adamowski, J. Modelling Large Floating Bodies in Urban Area Flash-Floods via a Smoothed Particle Hydrodynamics Model. J. Hydrol. 2016, 541, 344–358. [Google Scholar] [CrossRef]
- Nofal, O.M.; van de Lindt, J.W. Minimal Building Flood Fragility and Loss Function Portfolio for Resilience Analysis at the Community Level. Water 2020, 12, 2277. [Google Scholar] [CrossRef]
- FEMA. Flood-Resistant Design and Construction; FEMA: Washington, DC, USA, 2003. [Google Scholar]
- Feng, K.; Wang, N.; Li, Q.; Lin, P. Measuring and Enhancing Resilience of Building Portfolios Considering the Functional Interdependence among Community Sectors. Struct. Saf. 2017, 66, 118–126. [Google Scholar] [CrossRef]
- Mugume, S.N.; Gomez, D.E.; Fu, G.; Farmani, R.; Butler, D. A Global Analysis Approach for Investigating Structural Resilience in Urban Drainage Systems. Water Res. 2015, 81, 15–26. [Google Scholar] [CrossRef]
- Wright, D.B. Methods in Flood Hazard and Risk Assessment; International Bank for Reconstruction and Development, The World Bank: Washington, DC, USA, 2015. [Google Scholar]
- Poland, C.D.; SPUR Resilient City Goals; McAllister, T.; McAllister, T. Developing Guidelines and Standards for Disaster Resilience of the Built Environment: A Research Needs Assessment; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Patel, S.S.; Rogers, M.B.; Amlôt, R.; Rubin, G.J. What Do We Mean by ‘Community Resilience’? A Systematic Literature Review of How It Is Defined in the Literature. PLoS Curr. 2017, 9. [Google Scholar]
- Rogers, J.D.; Kemp, G.P.; Bosworth, H., Jr.; Seed, R.B. Interaction between the US Army Corps of Engineers and the Orleans Levee Board Preceding the Drainage Canal Wall Failures and Catastrophic Flooding of New Orleans in 2005. Water Policy 2015, 17, 707–723. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Von Winterfeldt, D. A Framework to Quantitatively Assess and Enhance the Seismic Resilience of Communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Mayunga, J.S. Understanding and Applying the Concept of Community Disaster Resilience: A Capital-Based Approach. In Proceedings of the Summer Academy for Social Vulnerability and Resilience Building, Munich, Germany, 22–28 July 2007; Volume 1, pp. 1–16. [Google Scholar]
- Lin, P.; Wang, N. Building Portfolio Fragility Functions to Support Scalable Community Resilience Assessment. Sustain. Resilient Infrastruct. 2016, 1, 108–122. [Google Scholar] [CrossRef]
- Sen, M.K.; Dutta, S.; Kabir, G. Flood Resilience of Housing Infrastructure Modeling and Quantification Using a Bayesian Belief Network. Sustainability 2021, 13, 1026. [Google Scholar] [CrossRef]
- Borba, M.; Warner, J.; Porto, M. Urban Stormwater Flood Management in the Cordeiro Watershed, São Paulo, Brazil: Does the Interaction between Socio-Political and Technical Aspects Create an Opportunity to Attain Community Resilience? J. Flood Risk Manag. 2016, 9, 234–242. [Google Scholar] [CrossRef]
- Hossain, N.U.I.; El Amrani, S.; Jaradat, R.; Marufuzzaman, M.; Buchanan, R.; Rinaudo, C.; Hamilton, M. Modeling and Assessing Interdependencies between Critical Infrastructures Using Bayesian Network: A Case Study of Inland Waterway Port and Surrounding Supply Chain Network. Reliab. Eng. Syst. Saf. 2020, 198, 106898. [Google Scholar] [CrossRef]
- Queiroz, C.; Garg, S.K.; Tari, Z. A Probabilistic Model for Quantifying the Resilience of Networked Systems. IBM J. Res. Dev. 2013, 57, 3:1–3:9. [Google Scholar] [CrossRef]
- Heaslip, K.; Louisell, W.; Collura, J.; Urena Serulle, N. A Sketch Level Method for Assessing Transportation Network Resiliency to Natural Disasters and Man-Made Events. In Proceedings of the Transportation Research Board 89th Annual Meeting, Washington, DC, USA, 10–14 January 2010; Transportation Research Board: Washington, DC, USA, 2010. [Google Scholar]
- Rosowsky, D.V.; Ellingwood, B.R. Performance-Based Engineering of Wood Frame Housing: Fragility Analysis Methodology. J. Struct. Eng. 2002, 128, 32–38. [Google Scholar] [CrossRef]
- Gidaris, I.; Padgett, J.E.; Barbosa, A.R.; Chen, S.; Cox, D.; Webb, B.; Cerato, A. Multiple-Hazard Fragility and Restoration Models of Highway Bridges for Regional Risk and Resilience Assessment in the United States: State-of-the-Art Review. J. Struct. Eng. 2017, 143, 04016188. [Google Scholar] [CrossRef]
- Ellingwood, B.R.; Cutler, H.; Gardoni, P.; Peacock, W.G.; van de Lindt, J.W.; Wang, N. The Centerville Virtual Community: A Fully Integrated Decision Model of Interacting Physical and Social Infrastructure Systems. Sustain. Resilient Infrastruct. 2016, 1, 95–107. [Google Scholar] [CrossRef]
- Enderami, S.A.; Sutley, E.J. Social Vulnerability Score: A Scalable Index for Representing Social Vulnerability in Virtual Community Resilience Testbeds. Nat. Hazards 2024, 120, 6457–6480. [Google Scholar] [CrossRef]
- Nofal, O.M.; van de Lindt, J.W. Probabilistic Flood Loss Assessment at the Community Scale: Case Study of 2016 Flooding in Lumberton, North Carolina. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2020, 6, 05020001. [Google Scholar] [CrossRef]
- House, W. Presidential Policy Directive/PPD 21—Critical Infrastructure Security and Resilience; The White House: Washington, DC, USA, 2013. [Google Scholar]
- McGrath, H.; Abo El Ezz, A.; Nastev, M. Probabilistic Depth–Damage Curves for Assessment of Flood-Induced Building Losses. Nat. Hazards 2019, 97, 1–14. [Google Scholar] [CrossRef]
- Mieler, M.; Stojadinovic, B.; Budnitz, R.; Comerio, M.; Mahin, S. A Framework for Linking Community-Resilience Goals to Specific Performance Targets for the Built Environment. Earthq. Spectra 2015, 31, 1267–1283. [Google Scholar] [CrossRef]
- Guidotti, R.; Gardoni, P.; Rosenheim, N. Integration of Physical Infrastructure and Social Systems in Communities’ Reliability and Resilience Analysis. Reliab. Eng. Syst. Saf. 2019, 185, 476–492. [Google Scholar] [CrossRef]
- Van de Lindt, J.W.; Peacock, W.G.; Mitrani-Reiser, J.; Rosenheim, N.; Deniz, D.; Dillard, M.; Crawford, P.S. Community Resilience-Focused Technical Investigation of the 2016 Lumberton, North Carolina, Flood: An Interdisciplinary Approach. Nat. Hazards Rev. 2020, 21, 04020029. [Google Scholar] [CrossRef]
- Wang, W.; van de Lindt, J.W.; Cutler, H.; Rosenheim, N.; Koliou, M.; Lee, J.S.; Calderon, D. Community Resilience Assessment of an EF-5 Tornado Using the IN-CORE Modeling Environment. In Life-Cycle Civil Engineering: Innovation, Theory and Practice; CRC Press: Boca Raton, FL, USA, 2021; pp. 394–398. [Google Scholar]
- Dang, N.M.; Babel, M.S.; Luong, H.T. Evaluation of Food Risk Parameters in the Day River Flood Diversion Area, Red River Delta, Vietnam. Nat. Hazards 2011, 56, 169–194. [Google Scholar] [CrossRef]
- Nofal, O.M.; van de Lindt, J.W.; Do, T.Q. Multi-Variate and Single-Variable Flood Fragility and Loss Approaches for Buildings. Reliab. Eng. Syst. Saf. 2020, 202, 106971. [Google Scholar] [CrossRef]
- Rinaldi, S.M.; Peerenboom, J.P.; Kelly, T.K. Identifying, Understanding, and Analyzing Critical Infrastructure Interdependencies. IEEE Control. Syst. Mag. 2001, 21, 11–25. [Google Scholar]
- Fu, Z.; Gao, R.; Li, Y. Measuring Seismic Resilience of Building Portfolios Based on Innovative Damage Ratio Assessment Model. Structures 2021, 30, 1109–1126. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).