Research on Order Allocation Strategies for Ride-Hailing Platforms Considering Passenger Order Cancellations During Order Overflow

Abstract

The rise of ride-hailing services has brought new riding experiences for passengers and exerted a profound impact on the traditional taxi market. To enhance patrol efficiency, increase revenue, and promote sustainable development in the taxi industry, traditional taxis have actively undergone transformation and adopted an integrated “online-offline” operating model, combining online order acceptance with offline order-taking. Meanwhile, a considerable number of orders are canceled by passengers after being accepted, leading to a waste of platform capacity, reduced order dispatch efficiency, and additional empty-running costs for drivers. This issue is particularly prominent during peak hours with order overflow. Based on the changes in taxi order acceptance during order overflow, this paper constructs a model for passenger order cancellation probability during peak hours, examines the relationship between regional order density and the proportion of offline taxi order acceptance, discusses the impact of regional order density changes on the passenger order cancellation probability and stakeholder returns, and proposes optimal order dispatch strategies for ride-hailing platforms with different order densities. Additionally, it analyzes more optimal taxi operating models under varying arrival states. The research findings provide more scientific and efficient operational recommendations for ride-hailing platforms and taxis, promoting sustainable development in the entire travel market and thereby contributing to a greener and more efficient travel environment.

1. Introduction

With the advancement of informatization and the prosperity of the digital economy, the shared economy model has flourished globally. Ride-hailing platforms such as Gaode, Didi, and Uber have rapidly expanded, bringing convenience to passengers and swiftly securing a significant position in the ride market. These platforms provide ride services on demand, plan routes for vehicles, effectively reduce the cost of driver–passenger matching, and significantly enhance operational efficiency in the taxi market [1]. The scale of ride-hailing users and the market in China have continued to expand. As of 2023, the number of ride-hailing users in China reached 528 million, with 337 ride-hailing platform companies nationwide obtaining operational licenses. The ride-hailing regulatory information interaction system indicates that a total of 9.114 billion orders were received throughout 2023.

Due to factors such as convenience, price advantages, and better hygiene conditions, ride-hailing platforms have attracted the favor of a large number of passengers, leading to a gradual decline in the business volume of traditional taxis [2]. The traditional taxi industry faces new challenges. The traditional cruising mode, which solely relies on taxi drivers randomly seeking passengers on the street, has become unsustainable. The new operational model, combining online order-taking through ride-hailing platforms with offline cruising, known as the “online-offline” model, has emerged as an inevitable choice for the transformation and upgrading of the taxi industry. In response, the General Office of the State Council of China actively advocates for the transformation and upgrading of cruising taxis and promotes the integrated development of cruising taxis and ride-hailing. In 2024, the China Smart Cruising and Ride-Hailing Integration Alliance was established, and the compilation of the “White Paper on the Integrated Development of Cruising and Ride-hailing Taxis” was initiated, marking the continuous development of the taxi industry on the path of digitization. Through the integration of cruising and ride-hailing, traditional cruising taxis can leverage internet technology to achieve online order-taking and intelligent dispatch, improving operational efficiency and service quality. On the other hand, ride-hailing platforms can also utilize the offline operational experience and professional capabilities of cruising taxis to further standardize and improve their services. Shantou City leverages CaoCao Inc., a Chinese ride-hailing platform, to provide “online-offline” ride services, which has not only enhanced the quality of taxi services but also significantly increased drivers’ incomes and passenger satisfaction. Data indicate that, under this model, the driver turnover rate is only 5%, while passenger satisfaction reaches as high as 93.8%.

After taxis join ride-hailing platforms to accept orders, the service offerings of these platforms are enriched. Given their retained ability to accept street hails, this has a significant impact on passengers’ travel choices. Research shows that, when passengers encounter cruising taxis while waiting for a response to their online order or during the ride to pick them up, they may cancel their online order and switch to a cruising taxi. Therefore, it is particularly important for ride-hailing platforms to balance order allocation between taxis and ride-hailing vehicles. If platforms allocate too few orders to taxis, it will lead a large number of taxis to continue using the traditional cruising mode, increasing the probability of passengers canceling orders and resulting in a waste of vehicles and drivers’ resources. Conversely, if platforms allocate more orders to taxis, it will cause dissatisfaction among ride-hailing drivers, which is detrimental to the platform’s long-term stable development. This challenge is even more critical during peak hours when orders overflow. During peak travel times, passenger orders are concentrated, greatly reducing the cost for taxis to cruise for passengers. Many taxis will choose to accept street hails to avoid the commission fees charged by ride-hailing platforms, which directly leads to a decrease in the number of vehicles accepting online orders, thereby increasing passengers’ waiting times for online orders, influencing their decisions to cancel orders, and ultimately causing a backlog of orders on the platform, which increases the pressure on order dispatch. Therefore, it is worth further studying how ride-hailing platforms allocate orders during order overflow and what impact changes in order density have on ride-hailing platforms’ order allocation strategies.

This paper focuses on the unique attribute of taxis accepting both online and street hail orders, fully considers passengers’ order cancellation behavior, and examines the order dispatch strategy of ride-hailing platforms in scenarios of order overflow. At the same time, combining with changes in regional order density, this paper provides suggestions for ride-hailing platforms’ order dispatch strategies, aiming to achieve a more beneficial order allocation for all parties involved.

2. Literature Review

The ride-hailing industry, as an emerging sector that has rapidly developed in recent years, has attracted extensive attention from scholars. Numerous discussions have been conducted surrounding issues such as order dispatch, pricing [3], and route optimization within ride-hailing platforms. Effective order allocation strategies contribute to enhancing the operational efficiency of ride-hailing platforms, reducing user waiting times, and minimizing vehicle empty-running times. In the existing literature, research on order dispatch strategies for ride-hailing platforms primarily considers factors such as waiting time, travel distance, and expected earnings, studying these from the perspectives of multiple participants in the ride-hailing system, including passengers, drivers, and ride-hailing platforms [4].

Feng et al. [5] focused on passenger waiting time, comparing ride-hailing and traditional street-hailing taxi services. They proposed and validated that incorporating a maximum distance limit for responding to passenger requests in ride-hailing order allocation can improve matching efficiency. Shi et al. [6] considered driver heterogeneity by categorizing drivers into part-time and full-time drivers, and they proposed a prioritized order allocation strategy to increase the number of order matches and platform revenue. Gao et al. [7] moved beyond the traditional model of competition between taxis and ride-hailing services, considering allocating orders to idle taxis. They proposed optimal dispatch strategies from the perspectives of passenger waiting time, vehicle deadheading distance, and taxi revenue. Yang et al. [8] argued that the matching radius and matching time interval are key to optimizing order dispatch in ride-hailing platforms, and they discussed the platform’s optimal order-matching strategies under different supply and demand conditions. Yan et al. [9] focused on the emerging carpooling matching mechanism, combining a dynamic waiting matching mechanism with dynamic pricing to study the impact of different pricing and matching mechanisms. They found that this can reduce price fluctuations and lead to more efficient resource utilization. Ramezani and Valadkhani [10] considered road network congestion and proposed an algorithm to dynamically determine the optimal matching time interval and maximum matching distance, optimizing passenger waiting time. Özkan [11] analyzed the interaction between pricing decisions and matching decisions in ride-hailing platforms, finding that optimizing one in isolation does not yield good results.

Research on customer order cancellation behavior spans various fields, such as flight order cancellations [12,13], outpatient appointment cancellations [14,15], and hotel reservation cancellations [16]. Currently, research on passenger cancellations of ride-hailing orders is still in its developmental stage. Wang et al. were the first scholars in China to focus on order cancellation issues on ride-hailing platforms. Based on real data from the Didi Chuxing platform, they proposed the idea that passengers may cancel online orders due to the availability of cruising taxis and constructed a market equilibrium model based on passenger order cancellations [17]. He et al. [18], focusing on the parallel ride market of ride-hailing and traditional taxis, emphasized the study of optimal pricing and penalty/compensation strategies for platforms, proposing pricing models from two different management objectives: platform revenue and social welfare. Sun et al. [19] extracted features potentially related to passenger order cancellations, such as passenger waiting time and vehicle arrival speed, through data cleaning, and they established a deep learning model based on a deep residual network to predict the probability of order cancellation. As ride-hailing platforms continue to develop and improve, they have introduced various penalty rules for passenger order cancellations, such as deducting credit points and imposing fines, to constrain passenger behavior. Li et al. [20], based on scenarios where passengers are fined for canceling orders, studied two strategies, time-based fines and fixed fines, and they proposed an optimal solution from the perspective of minimizing social costs.

Rush hour represents the peak moment of urban traffic pressure, and it is an inevitable issue accompanying urban development. During this time, vehicles are densely packed on roads, passenger travel demand spikes, and it is accompanied by certain spatiotemporal characteristics. For ride-hailing platforms, peak hours present both opportunities and challenges. On the one hand, high demand brings opportunities for increased revenue; on the other hand, imbalances between supply and demand may lead to a decline in service quality. Xu et al. [21] studied the supply curve of the ride-hailing system and posited that the concentration of demand during peak hours can lead to order-matching failures and exacerbate supply shortages. Pan et al. [22] analyzed travel market data from New York City and found that, compared to markets with only traditional taxis, the entry of ride-hailing into the travel market results in higher service equity during peak hours. Through analyzing ride-hailing data from Xiamen, China, Xiong et al. revealed the spatiotemporal characteristics of ride-hailing operations, finding that full-time ride-hailing services are most active during morning and evening peak hours [23]. In contrast, Guda and Subramanian drew opposite conclusions in their discussion on the effect of surge pricing on ride-hailing driver mobility, pointing out that increased prices during peak hours suppress demand, potentially leading drivers to leave high-demand areas [24]. Some scholars have focused on the earnings of participants in the ride-hailing market during peak hours, providing suggestions for ride-hailing platforms’ strategies during this special period. Wong and Szeto [25] studied the impact of surcharges during rush hour on passengers’ travel decisions and found that, in peak hours and congested areas, surcharges can effectively control the proportion of empty taxis searching for customers in central business districts, achieving a more even distribution of taxi supply. Chen et al. [26] comprehensively considered factors such as peak pricing, passenger and driver incentives, and proposed strategies for maximizing revenue from the platform’s perspective and optimizing social welfare from the government’s perspective. Cachon et al. [27] found that, when platforms have the option to choose contracts, implementing peak pricing is beneficial to all stakeholders.

The existing research on ride-hailing platform dispatch problems, passenger order cancellation issues, and peak-hour ride-hailing market problems have yielded a series of valuable results, providing theoretical support and practical guidance for optimizing passenger waiting times, reducing drivers’ empty-running times and increasing their earnings, ensuring platform economic benefits, and maintaining an overall supply–demand balance. However, with the rapid development of the travel market, the role of taxis has gradually shifted from the traditional cruising mode to a combination of online and cruising operations, and the rules of ride-hailing platforms are constantly being updated and improved. These changes have made passenger order cancellation behavior more complex and posed new challenges to ride-hailing platforms’ dispatch strategies. We compared the similarities and differences with related studies, as shown in

Table 1. Comparative Research.

Study	Relevance	Differences from Our Study
He et al. (2018) [18]	Both studies consider taxis accepting orders online and offline and the impact of cancellation penalties.	We focus on peak-hour offline order acceptance strategies by taxis, while He et al. focus on platform pricing strategies.
Wang et al. (2019) [17]	Both studies consider the impact of traditional taxis on passenger cancellation behavior.	We extend the analysis to peak-hour scenarios and discuss taxi strategies under such conditions.
Ramezani and Valadkhani (2023) [11]	Both studies address order allocation under road network congestion.	They propose an algorithm for optimal matching intervals and distances, while we develop a vehicle arrival probability model to study order allocation between taxis and ride-hailing vehicles.
Wong and Szeto (2022) [25]	Both studies examine the impact of taxi search behavior on the ride-hailing market during peak hours.	They focus on the effects of peak-hour and congestion surcharges on passenger and taxi decisions, while we focus on order allocation strategies during peak hours.
Guda and Subramanian (2019) [24]	Both studies investigate taxi order acceptance behavior during peak hours and the impact of peak pricing.	They analyze whether taxis remain in high-demand areas during peak hours, while we focus on changes in taxi order acceptance modes.

. Most of the current studies focus on issues in purely ride-hailing operating environments or environments where taxis only accept cruising orders, neglecting the impact of traditional taxis integrating online order acceptance. The reasons and patterns for passenger order cancellations are also diversifying, especially during peak-hour travel times. This not only increases the complexity of platform management but also adversely affects the income stability of drivers. Therefore, the dispatch strategies of ride-hailing platforms in the context of taxis adopting a combination of online and cruising operations are topics worthy of further in-depth exploration.

3. Model

3.1. Distribution Model for Taxi Arrival Time Intervals

The symbols used in this article and their meanings are shown in

Table 2. Definition of Symbols.

Symbol	Meaning
N	Total number of taxis
$t_i$	Any given moment
$N_i$	Number of taxis operating offline at any given moment
D	Total number of orders received by the ride-hailing platform at any given moment
$\alpha$	Proportion of orders allocated to taxis by the ride-hailing platform
$\theta$	Proportion of taxis accepting offline orders at any given moment
E	Number of taxis operating vacant due to canceled orders at any given moment
S	Total mileage of urban roads (km)
v	Average operating speed of taxis (km/h)
$\eta$	Taxi vacancy rate
$T_P$	Critical time for imposing penalties on order cancellations by the platform
$F_P$	Penalty amount for order cancellation by the customer on the platform
L	Passenger-carrying distance of the order
R	Passenger time cost
${\delta }_i$	Time preference coefficient of Passenger i
$M_C$	Ride-hailing platform unit cost
$M_T$	Taxi unit cost
$M_E$	Passenger’s expected unit cost for the travel
$\beta$	Revenue sharing ratio of the ride-hailing platform
$G_T$	Distrust towards the platform caused by passenger order cancellations
$G_M$	Disutility experienced by passengers when need to pay cancellation penalties
f	Coefficient of driver disutility from pick-up time
H	Emotional loss experienced by drivers due to passenger order cancellations
$\mu$	Additional offline customer-seeking costs of taxis
$\epsilon$	Proportion of taxi drivers in the travel market

.

At any given time, $t_i$, the number of offline cruising taxis, $N_i$, is influenced by several factors, including the total number of taxis in the city, N, the number of taxis assigned to online orders, $\alpha D$, and the number of taxis whose status changes due to passenger order cancellations at a particular time, E. This is represented as $N_i=N-\alpha D+E$. Here, D denotes the total number of travel orders received by the ride-hailing platform at time $t_i$, and $\alpha D$ represents the number of orders assigned to taxis by the platform.

In the passenger order cancellation model considered in this paper, we account for situations where passengers cancel online orders upon encountering empty cruising taxis while waiting for pick-up. In such cases, the number of occupied empty cruising taxis is the same as the number of taxis with canceled online orders. Therefore, from an overall perspective, the number of taxis changing status is effectively zero. Hence, in this model, the number of offline operating taxis, $N_i$, at any given time, $t_i$, is calculated as $N_i=N-\alpha D$.

When order overflow occurs, some drivers choose to no longer cooperate with the ride-hailing platform and instead opt to only accept orders through cruising due to the reduced cost of finding passengers offline. Let $\theta$ represent the proportion of taxis accepting offline orders at time $t_i$. Then, the number of offline operating taxis at any given time, $t_i$, can be expressed as Equation (1).

$$N_i=N\theta +(1-\theta )(N-\alpha D)=N-(1-\theta )\alpha D$$

(1)

When taxis are distributed in a single lane on the road, the average spacing distance between offline cruising taxis can be expressed as $S/N_i$, where S represents the total mileage of urban roads (km). Considering that taxis travel on two-way lanes, the time, $t_d$, that it takes for a cruising taxi to traverse the urban roads unilaterally at any given time, $t_i$, can be represented by Equation (2), where v is the average travel speed of taxis (km/h).

The model in this paper, based on the assumption of taxi single-file distribution, aims to provide a theoretical analysis framework for general scenarios. Given the complexity of urban roads and buildings, which leads to variations in vehicle density across different areas, a regional division approach can be considered to classify the city into multiple grid areas with differing levels of congestion. By calculating the time taken for taxis to traverse roads in each area, the overall traversal time can be obtained, thereby enhancing the accuracy of the model.

$$t_d=\frac{2S/N_i}{v}=\frac{2S}{[N-(1-\theta \left)\alpha D\right]v}$$

(2)

Taking into account the vacant rate of cruising taxis, $\eta$ (i.e., the proportion of time or distance traveled without passengers to the total operating time or total distance traveled during the taxi’s operation), some of the offline operating taxis, $N_i$, are already occupied with passengers. Therefore, the average time that a passenger needs to wait for the first available cruising taxi, $T_F$, can be expressed as Equation (3).

$$T_F=\frac{t_d}{\eta }=\frac{2S/N_i}{v}=\frac{2S}{[N-(1-\theta \left)\alpha D\right]v\eta }$$

(3)

The arrival of taxis is a random event occurring independently at an average rate. Therefore, the arrival time of cruising taxis follows an exponential distribution with a parameter, $\lambda$. Let $T_X$ represent the arrival time of a cruising taxi. Then, the probability distribution function for the taxi arrival time intervals is given by $f\left(T_X\right)=\lambda e^{-\lambda T_X}$. Meanwhile, from Equation (3), we can derive the expression for $\lambda$, as shown in Equation (4). Consequently, the probability distribution function for taxi arrival-time intervals during order overflow can be expressed as Equation (5).

$$\lambda =\frac{1}{T_F}=\frac{[N-(1-\theta \left)\alpha D\right]v\eta }{2S}$$

(4)

$$f\left(T_X\right)=\frac{[N-(1-\theta \left)\alpha D\right]v\eta }{2S}{e}^{-\frac{[N-(1-\theta \left)\alpha D\right]v\eta }{2S}TX}$$

(5)

3.2. Passenger Order Cancellation Model

With the continuous development of ride-hailing platforms, order cancellation rules have gradually improved. Currently, mainstream platforms primarily implement penalty mechanisms for order cancellations based on time nodes. For instance, Didi stipulates no additional fee for cancellations within 2 min after order acceptance, whereas cancellations thereafter will incur a cancellation fee. Uber specifies that passengers will be charged if they cancel after the driver accepts the ride or if the driver cancels after waiting at the designated pickup location for a certain period. Bolt charges for cancellations after the free cancellation period (within 2 min after order acceptance), but it exempts drivers from the fee if they unilaterally cancel without waiting for the passenger at the pickup location for 3–8 min.

Given the widespread adoption of time-node-based cancellation penalty rules by ride-hailing platforms globally, this paper introduces a time node, $T_P$, for penalty imposition in model construction. When passengers cancel before $T_P$, the platform imposes no additional fee; otherwise, a fixed penalty fee, $F_P$, is charged as compensation for the platform and driver if the cancellation occurs after $T_P$.

When a passenger encounters an empty cruising taxi while waiting for a pick-up and, after considering factors such as waiting time costs and order cancellation penalties, deems it more beneficial to cancel the online order and take the cruising taxi instead, the passenger will cancel the online order.

3.2.1. Passengers Incur No Penalty for Order Cancellation

For ride-hailing platforms dispatching orders to taxis, the cost, $C_Q$, for a passenger to cancel an order and take a cruising taxi and the cost, $C_{KT}$, for a passenger to keep an online taxi order are shown in Equations (6) and (7), respectively. These costs consist of the fare paid by the passenger and the waiting time cost, where ${\delta }_i$ represents the time preference coefficient of passenger i. Different passengers have varying degrees of travel urgency, which affects their waiting time cost accordingly. Passengers with lower travel urgency have lower time preference coefficients and thus lower actual waiting time costs. Conversely, for passengers with higher travel urgency, their time preference coefficient ${\delta }_i>1$, leading to a significant increase in waiting time costs. According to loss aversion theory, the psychological pain of a loss is 2 to 2.5 times that of a gain of the same amount. With passengers’ waiting time costs considered a “loss”, ${\delta }_i$ is set within the range of ${\delta }_i\in (0,2.5)$.

$$C_Q=M_{T}L+{\delta }_{i}R{T}_X$$

(6)

$$C_{KT}=M_{T}L+{\delta }_{i}RT$$

(7)

The issue of passenger order cancellation considered in this paper arises when a passenger encounters a cruising taxi before the arrival of an online-hailed taxi, i.e., $T_X<T$. Within this timeframe, $C_{KT}>C_Q$, passengers who have placed online orders assigned to taxis by the platform will cancel their platform orders upon encountering an empty cruising taxi while waiting. Therefore, when no penalty is incurred for order cancellation, the probability that a passenger will cancel a taxi order assigned by the platform, $P_T$, can be expressed as Equation (8).

$$P_T={\int }_0^{T_P}f\left(T_X\right)d{T}_X=1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}{T}_P}$$

(8)

For cases where ride-hailing platforms assign orders to private vehicles, the cost for passengers to retain the platform’s order consists of two parts: the fare paid and the cost of passenger waiting time, as shown in Equation (9).

$$C_{KC}=M_{C}L+{\delta }_{i}RT$$

(9)

The equilibrium point for order cancellation before the penalty time $T_P$ is $T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}$. When $0\le T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}<T_P$, passengers will cancel their online order allocated to ride-hailing cars and switch to a cruising taxi, when the arrival time of the cruising taxi is within $0\le T_X<T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}$. Therefore, when no penalty is incurred for order cancellation, and the cost advantage of ride-hailing cars is significant, the probability of passengers canceling their orders allocated to ride-hailing cars is given by Equation (10).

$$P_C={\int }_0^{T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}}f\left(T_X\right)d{T}_X=1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}\left[T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}\right]}$$

(10)

When $0\le T_X<T_P\le T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}$, passengers will cancel their orders and switch to a cruising taxi if ${0\le T}_X<T_P$. In this scenario, where no penalty is incurred for order cancellation and ride-hailing cars do not have a significant cost advantage, the probability of passengers canceling their ride-hailing orders is given by Equation (11).

$$P_C={\int }_0^{T_P}f\left(T_X\right)d{T}_X=1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}{T}_P}$$

(11)

3.2.2. Passenger Order Cancellation with Penalty

For cases where ride-hailing platforms assign orders to taxis, passengers need to consider the penalty fee, $F_P$, when canceling orders. In such situations, the cost for passengers to cancel the order and take a cruising taxi, $C_Q$, and the cost for passengers to retain the online taxi order, $C_{KT}$, are given by Equations (12) and (13), respectively:

$$C_Q=M_{T}L+{\delta }_{i}R{T}_X+F_P$$

(12)

$$C_{KT}=M_{T}L+{\delta }_{i}R$$

(13)

In this case, the equilibrium point is $T-\frac{F_P}{{\delta }_{i}R}.\mathrm{When}T-\frac{F_P}{{\delta }_{i}R}$ falls within the range of $\left(T_P,T\right)$, passengers will cancel their online taxi order and switch to a cruising taxi if the taxi’s arrival time, $T_X$, is within $[T_P,T-\frac{F_P}{{\delta }_{i}R})$. When a penalty is incurred for passenger order cancellation, the probability, $P_T$, of passengers canceling their online taxi orders is given by Equation (14).

$$P_T={\int }_0^{T-\frac{Fp}{{\delta }_{i}R}}f\left(T_X\right)d{T}_X=1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}\left(T-\frac{Fp}{{\delta }_{i}R}\right)}$$

(14)

In other intervals, the conditions for imposing a penalty for order cancellation are not met, meaning passengers will not cancel their orders, and thus, $P_T=0$.

For cases where ride-hailing platforms assign orders to ride-hailing cars, the equilibrium point for order cancellation after the penalty time, $T_P$, is $T-\frac{\left(M_T-M_C\right)L+F_P}{{\delta }_{i}R}$. In scenarios where passengers need to pay a penalty for canceling their orders, when $T-\frac{\left(M_T-M_C\right)L+F_P}{{\delta }_{i}R}$ falls within the range of $\left(T_P,T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}\right)$, passengers will cancel their ride-hailing orders and switch to a cruising taxi if the arrival time of the cruising taxi is within ${0\le T}_X<T-\frac{\left(M_T-M_C\right)L+F_P}{{\delta }_{i}R}$. Therefore, when a penalty is incurred for order cancellation, the probability of passengers canceling their ride-hailing orders is given by Equation (15).

$$P_C={\int }_0^{T-\frac{\left(M_T-M_C\right)L+Fp}{{\delta }_{i}R}}f\left(T_X\right)d{T}_X=1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}\left[T-\frac{\left(M_T-M_C\right)L+Fp}{{\delta }_{i}R}\right]}$$

(15)

In other cases, the conditions for imposing a penalty for order cancellation are not met, meaning passengers will not cancel their orders. At this point, $P_C=0$.

In summary, for cases where ride-hailing platforms assign orders to taxis, the probability, $P_T$, of passengers canceling their orders can be expressed as Equation (16).

$$P_T=\left\{\begin{array}{cc}1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}{T}_P}& {0\le T}_X<T_{P}and{T}_X<T\\ 1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}\left(T-\frac{Fp}{{\delta }_{i}R}\right)}& {T_P\le T}_X<T-\frac{F_P}{{\delta }_{i}R}\\ 0& other\end{array}\right.$$

(16)

For cases where ride-hailing platforms assign orders to their own ride-hailing vehicles, the probability, $P_C$, of passengers canceling their orders can be expressed as Equation (17).

$$P_C=\left\{\begin{array}{cc}1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}\left[T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}\right]}& 0\le T_X<T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}<T_P\\ 1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}{T}_P}& 0\le T_X{<T}_P<T-\frac{\left(M_T-M_C\right)L}{{\delta }_{i}R}\\ 1-e^{-\frac{\left[N-\left(1-\theta \right)\alpha D\right]v\eta }{2S}\left[T-\frac{\left(M_T-M_C\right)L+F_P}{{\delta }_{i}R}\right]}& T_P\le T_X<T-\frac{\left(M_T-M_C\right)L+F_P}{{\delta }_{i}R}\\ 0& other\end{array}\right.$$

(17)

3.3. Revenue Models for All Parties

The revenue of ride-hailing platforms comes from the commission on passenger fares and the commission on penalty fees paid by passengers for canceling orders. With a revenue-sharing ratio of $\beta$, the single-order revenue for orders assigned to taxis, $U_T$, and the single-order revenue for orders assigned to ride-sharing vehicles, $U_C$, can be expressed as Equations (18) and (19), respectively.

$$U_T=\left(1-P_T\right)M_{T}L\beta +P_T{F}_P\beta \omega$$

(18)

$$U_C=\left(1-P_C\right)M_{C}L\beta +P_C{F}_P\beta \omega$$

(19)

where $\omega$ is a 0–1 variable:

$$\omega =\left\{\begin{array}{cc}0& T_X<T_P\\ 1& T_X\ge T_P\end{array}\right.$$

(20)

The revenue for a single order on the ride-hailing platform U can be expressed as Equation (21).

$$U=\alpha U_T+{\left(1-\alpha \right)U}_C$$

(21)

For passengers, their travel utility is influenced by the expected travel cost per unit, $M_E$, the penalty for canceling an order, $F_P$, the disutility associated with canceling an order, $G_T$, and the emotional cost incurred by paying the penalty, $G_M$. Specifically, $G_T$ refers to passengers’ dissatisfaction with the inconvenience caused by cancellation, which arises when passengers cancel their orders. $G_M$ represents passengers’ impatience and low willingness to pay the penalty, which occurs when passengers pay the cancellation penalty.

By denoting both the taxi fare, $M_T$, and the ride-hailing fare, $M_C$, collectively as M, the utilities for passengers who do not cancel their orders, passengers who cancel their orders without incurring a penalty, and passengers who cancel their orders and incur a penalty can be expressed as shown in Equations (21) to (23), respectively.

$$W_1=\left(M_E-M\right)L-RT$$

(22)

$$W_2={(M}_E-M_T)L-R{T}_X-G_T$$

(23)

$$W_3={(M}_E-M_T)L-R{T}_X-G_T-G_M-F_P$$

(24)

In summary, when the probability of a passenger canceling a taxi order, $P_T$, is denoted, and the probability of canceling a ride-hailing order, $P_C$, collectively as P, the passenger utility W for a single order can be expressed as Equation (25).

$$W=\left(1-P\right)W_1+P\left[\omega W_2+\left(1-\omega \right)W_3\right]$$

(25)

For drivers on the ride-hailing platform, their earnings consist of the commission from the passenger’s order payment and the commission from any penalty fees paid by passengers for canceling orders. Simultaneously, the driver’s patience decreases with an increase in the pick-up time, T, resulting in a negative utility with a coefficient of f. Additionally, drivers experience an emotional loss, H, due to passengers’ order cancellation behavior, characterized by feelings of disappointment and frustration. The driver’s earnings for a single order received through the platform can be expressed as Equation (26). Drivers experience emotional loss H due to passengers’ order cancellation behavior, characterized by feelings of disappointment and frustration.

$$K_1=(1-P)(M-fT)L\left(1-\beta \right)+P{[F}_P\left(1-\beta \right)\omega -H]$$

(26)

For taxi drivers who operate both on the street and through ride-hailing platforms, the earnings for a single order are given by Equation (27), where $\mu$ represents the additional offline customer-seeking costs.

$$K_2=\theta {(M}_T-\mu )L+\left(1-\theta \right)K_1$$

(27)

Denote $\epsilon$ as the proportion of taxi drivers in the travel market relative to the total number of taxi drivers and ride-hailing drivers. Then, the average earnings, K, per order for drivers can be expressed as Equation (28).

$$K=\left(1-\epsilon \right)K_1+\epsilon K_2$$

(28)

This paper studies the scenario of excessive order demand in the general travel market, where taxis can accept rides through both cruising and ride-hailing platforms, and it discusses passenger order cancellation behavior and ride-hailing platforms’ order dispatch strategies. The uniqueness of our model lies primarily in taxis’ ability to accept orders through both online and offline channels. However, not all regions currently support taxis accepting orders on ride-hailing platforms. For regions where only taxi cruising is supported, the model can be simplified by excluding the probability of taxis accepting offline orders, with corresponding adjustments needed for the passenger order cancellation model. Furthermore, in some regions with more diversified taxi-hailing methods, such as supporting taxi-hailing via phone calls or designated taxi zones, our model needs to be adjusted in accordance with local taxi operation characteristics.

4. Simulation Analysis

Ride-hailing platforms have accumulated extensive regional order information and real-time traffic data. By studying the relationship between changes in regional order density and the probability of taxi drivers accepting offline orders, especially the tendency of taxis to choose offline orders when orders overflow, we can provide references for ride-hailing platforms to make dispatching decisions in overflow scenarios. This section simulates the scenario of taxi drivers accepting offline orders during order overflow and analyzes the relationship between order density and the probability of taxi drivers accepting offline orders.

The decision-making of taxi drivers to accept rides online or offline is influenced by a combination of factors, such as expected income, road conditions, and personal preferences. This paper introduces a weighted function to calculate the driver’s decision value, as shown in Equation (29). In this equation, $L_C$ represents road conditions, reflecting driving elements such as traffic congestion that affect the driver’s efficiency and pickup time. $K_I$ denotes the driver’s visual range, i.e., the distance within which the driver can observe potential passengers on the road, influencing offline ride acceptance opportunities. $P_J$ indicates platform incentives, affecting the expected income from online ride acceptance. $K_E$ signifies past experience, influencing the driver’s comprehensive judgment of different ride acceptance methods, and ${\xi }_1$, ${\xi }_2$, ${\xi }_3$… are the weights of each factor, with ${\sum }_{i=1}^4{\xi }_i=1$. When the decision value $D_{ec}$ is above a threshold, the driver chooses to accept rides offline; otherwise, they choose to accept rides online.

$$D_{ec}={\xi }_1{L}_C+{\xi }_2{K}_I+{\xi }_3{P}_J+{\xi }_4{K}_E$$

(29)

Based on relevant data released by the Wuxi Transportation Bureau, an experiment was conducted with 750 taxis and 4250 ride-hailing vehicles operating within a unit area of 100 square kilometers. The vehicle speed was set to 28 km/h, based on the average speed during peak hours in Wuxi’s road network. Given limited vehicle resources, new orders will begin to queue when all vehicles are in service. Therefore, the simulation experiment started with a consistent order density of 5000 orders in the unit area (100 square kilometers). The results, as shown in

Table 3. Example of changes in order density and proportion of taxis’ offline order acceptance.

Order Volume	5000	10,000	15,000	20,000	25,000	30,000	35,000	40,000	45,000	50,000
Number of orders completed by taxis	3680	3717	3716	3746	3759	3720	3770	3768	3730	3761
Number of orders completed offline	847	1260	1611	1810	2045	2194	2360	2568	2749	2845
Proportion of offline orders accepted by taxis	23.02%	33.90%	43.35%	48.32%	54.40%	58.98%	62.60%	68.15%	73.70%	75.64%

, illustrate the number of offline taxi orders, the total number of completed orders within the area, and the proportion of offline taxi orders under different order densities.

This section describes eight independent experiments that were conducted, and the mean proportion of offline taxi orders was calculated after each experiment, as shown in

Table 4. Probability of taxis accepting offline orders and order fulfillment probability under different order densities.

Order Volume	The Probability of Taxi Hailing During Cruising
	Mean Value 1	Mean Value 2	Mean Value 3	Mean Value 4	Mean Value 5	Mean Value 6	Mean Value 7	Mean Value 8
5000	23.02%	23.34%	23.25%	23.41%	23.56%	23.58%	23.66%	23.72%
10,000	33.90%	33.94%	34.53%	34.85%	34.23%	34.10%	34.22%	34.12%
15,000	43.35%	42.83%	42.07%	42.48%	42.87%	42.74%	42.73%	42.80%
20,000	48.32%	48.86%	48.62%	48.66%	49.13%	49.34%	49.25%	49.19%
25,000	54.40%	54.14%	53.59%	54.14%	54.42%	54.49%	54.54%	54.63%
30,000	58.98%	58.63%	58.60%	59.26%	59.25%	59.29%	59.28%	59.40%
35,000	62.60%	63.84%	63.48%	63.47%	63.57%	63.83%	63.74%	63.66%
40,000	68.15%	69.07%	69.11%	69.01%	69.02%	69.06%	69.03%	69.29%
45,000	73.70%	74.37%	73.15%	73.47%	73.36%	73.08%	73.07%	73.00%
50,000	75.64%	75.76%	76.53%	76.38%	76.16%	76.34%	76.37%	76.46%

. Notably, the mean values of the proportion of offline orders accepted by taxis, $\theta$, corresponding to different order densities, exhibited a stable trend, as illustrated in Figure 1. Therefore, when the Lagrange interpolation method is used, the correlation between order density, $\rho$, and the proportion of offline orders accepted by taxis, $\theta$, can be visualized more intuitively, as shown in Figure 2. This smooth curve illustrates the corresponding relationship between order density and the probability of offline taxi orders.

The experimental data revealed that, as the number of regional orders increased, i.e., as order density, $\rho$, continued to rise, the proportion of taxis choosing to accept offline orders gradually increased. This change will have an impact on the order processing speed of ride-hailing platforms. Simultaneously, the growth rate of the proportion of offline taxi orders showed a gradually slowing trend. The reason is that, despite high order density, the starting and ending points of orders are random, which means taxi drivers may not always find waiting passengers within their visual range when searching for customers. Furthermore, taxis face competitive pressure when accepting offline rides. When the number of empty taxis near passengers in a certain area exceeds passenger demand, some taxis may fail to secure rides at that location. Additionally, the order allocation mechanism of ride-hailing platforms and dynamic fluctuations in the supply–demand relationship in the ride-hailing market further complicate the process of offline ride acceptance for taxis. These factors limit the unlimited growth of the proportion of offline ride acceptance for taxis.

5. Numerical Analysis

This section conducts a numerical analysis using Wuxi City, China, as an example. Based on data from the Wuxi Transportation Bureau, the “Wuxi Statistical Yearbook”, and other materials, Wuxi currently has 4040 taxis and a total urban road mileage of 4049 km. With reference to Wuxi’s per capita disposable income, the passenger’s waiting time cost is set to 33 CNY per hour. According to government pricing standards, the unit price for taxi rides is 2.76 CNY per kilometer. When urban road speed limits are considered, the average driving speed of vehicles is set to 40 km per hour. Statistics show that the average commuting distance for Wuxi residents is 6.6 km, and the average daily number of ride-hailing orders in Wuxi reached 240,200 in the first half of 2023.

The data related to ride-hailing platforms in this section refer to the Didi platform. The unit price for ride-hailing rides is 2.49 CNY per kilometer. For passenger order cancellations, the platform stipulates that, if a passenger cancels an order more than 2 min after it is assigned, the platform will charge the passenger a cancellation fee of 3 CNY per order.

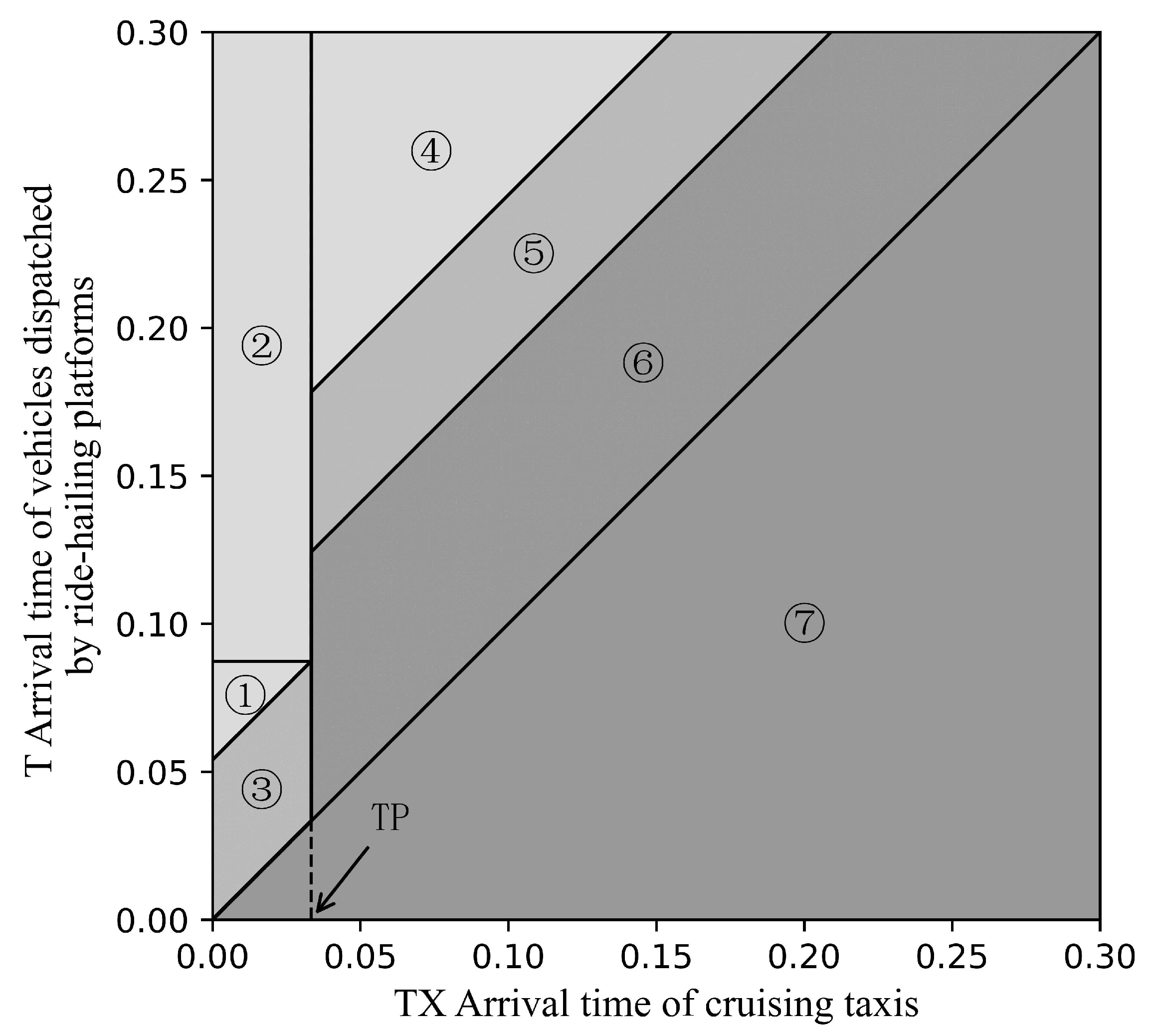
Passengers’ decisions to cancel orders are influenced by the arrival time of cruise taxis, $T_X$, and the pickup time of online-responding vehicles, T. Based on the model established earlier, passengers’ order cancellation decisions can be categorized into seven different scenarios for different vehicle arrival situations and types of vehicles assigned to orders, as shown in Figure 3.

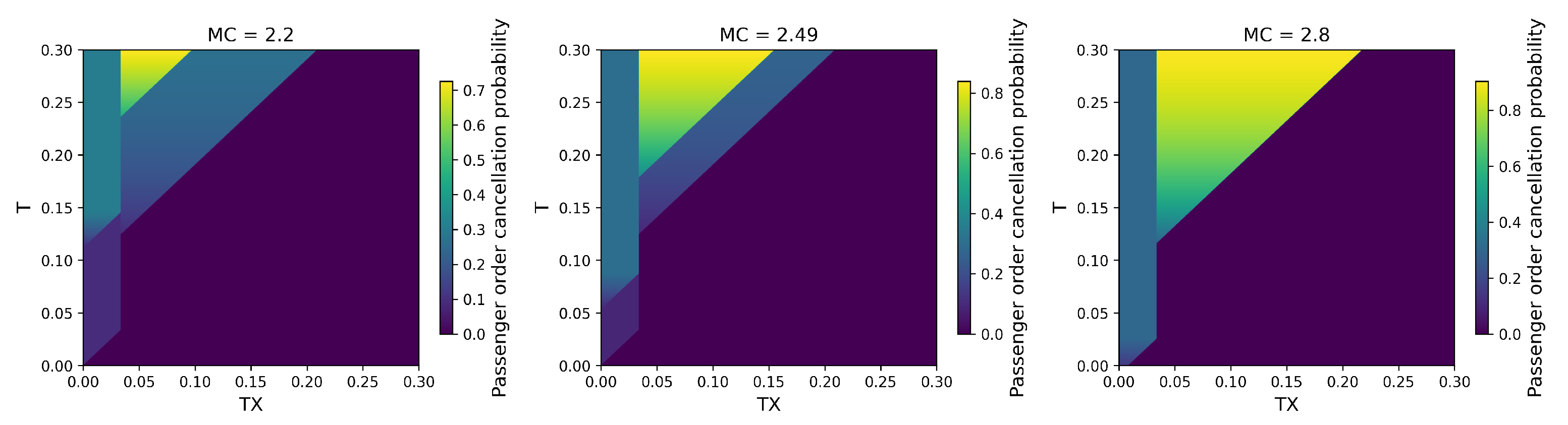
Intervals 1–3 belong to the range where passengers do not need to pay a penalty for canceling their orders. Passengers who cancel orders within intervals 4–6 will incur penalties. In intervals 1, 2, and 4, when passengers encounter cruise taxis, they will cancel their orders, regardless of whether the platform assigns a taxi or a ride-hailing vehicle. In intervals 3 and 5, passengers will only cancel orders assigned to taxis through the platform. Passengers in interval 6 will not cancel any orders. Interval 7 represents the situation where vehicles assigned through the platform arrive earlier than cruise taxis, and passengers in this range will directly take the vehicles assigned through the platform.

5.1. Passenger Order Cancellation Probability Under Different Order Densities

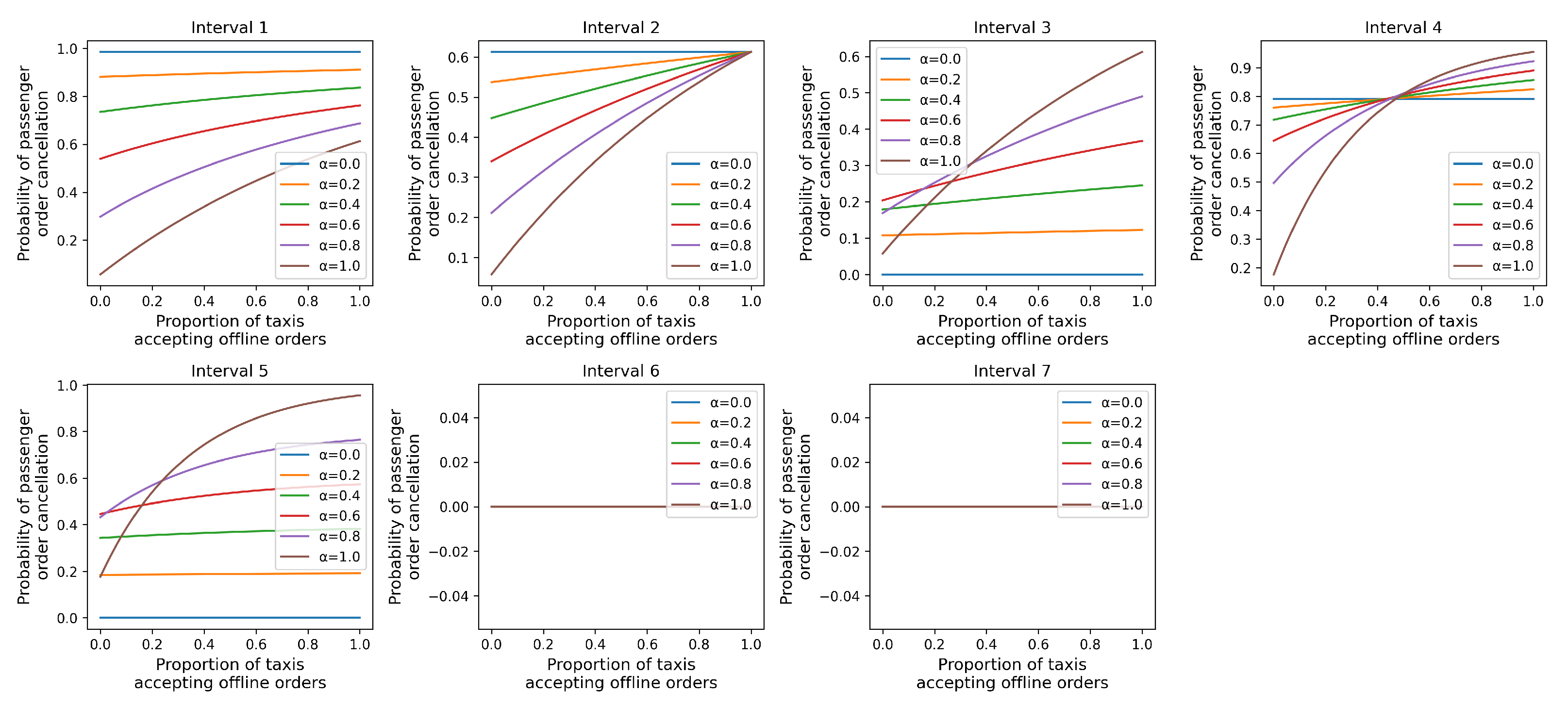
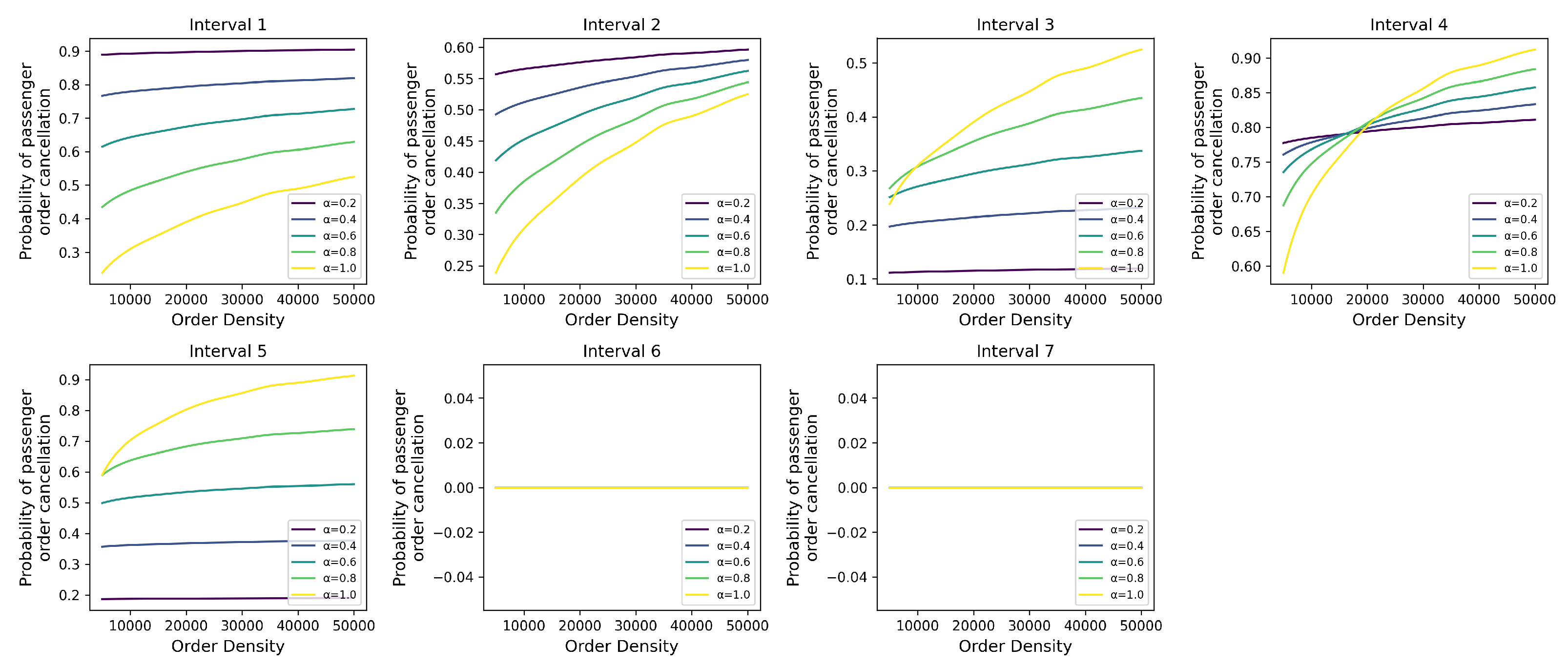
When the proportion of taxi offline orders, denoted as $\theta$, fluctuates within the interval $\left[0,1\right]$, we can plot the changes in passenger order cancellation probability across different ride intervals for varying proportions, $\alpha$, of orders allocated to taxis through ride-hailing platforms, as shown in Figure 4. Based on the previous simulation analysis of regional order density and offline taxi order proportions during order overflow, we further depict the distribution of passenger order cancellation probability under different order densities, as illustrated in Figure 5.

In intervals 1 and 2, as the proportion of orders allocated to taxis through ride-hailing platforms increases, the impact of changes in taxis’ offline order proportions on passenger order cancellation probability becomes more pronounced. This is significantly influenced by changes in regional order density. An increase in regional order density leads more taxis to opt for cruising to pick up passengers, thereby enhancing the likelihood of passengers encountering empty cruising taxis. However, due to the high order density, the overall passenger order cancellation probability is notably affected by the proportion of offline cruising orders.

In intervals 3 and 5, since passengers only cancel orders assigned to taxis via the platform, the overall passenger order cancellation probability increases correspondingly with an increase in the proportion of platform-assigned orders. To control the passenger order cancellation probability and reduce the workload of order assignment, platforms may consider allocating a small proportion of orders to taxis. Specifically, in interval 3, where taxis can arrive before passengers incur a penalty for canceling orders, platforms may also consider assigning orders to all taxis when the regional order density does not exceed twice the number of vehicles to reduce the likelihood of passengers canceling orders.

Passengers in interval 4 need to pay a penalty to cancel orders. When the regional order density does not exceed four times the number of vehicles, platforms should maximize the proportion of orders allocated to taxis in order to keep the passenger order cancellation probability at a low level. However, when the regional order density exceeds four times the number of vehicles, ride-hailing platforms should immediately adopt a low order allocation proportion. By comparing Figure 3 and Figure 4, it can be observed that there is a slight lag in taxi offline order choices relative to regional order density, reflecting the time required for taxi drivers to adjust their order-taking strategies based on road conditions and order status, and for these adjustments to impact ride-hailing platforms.

In intervals 6 and 7, passengers do not cancel orders assigned through the platform, and adjustments to the ride-hailing platform’s order assignment strategy do not affect the passenger order cancellation probability.

5.2. Platform Order Dispatch Strategies Under Different Order Densities

To investigate the optimal order allocation ratio, $\alpha$, in various scenarios, this paper designs the following algorithmic procedure tailored to different travel market conditions. (1) Initialization: Input the order scale to generate the initial order set, D. Input the ride-hailing vehicle set, $V_C$, and the taxi set, $V_T$, and initialize vehicle locations and statuses. (2) Order allocation: Calculate the offline order acceptance decision value for taxis to determine their order acceptance mode. Allocate orders to vehicles in the system based on the order allocation mechanism. (3) Parameter space traversal: Traverse the parameter combinations, $\left(T_X,T,\alpha \right)$, and compute the objective function value for each combination. (4) Optimal $\alpha$ selection: For each parameter pair ${(T}_X,T)$, retain the $\alpha$ value that maximizes the objective function and output it. Based on this algorithmic procedure, the optimal $\alpha$ values for platform revenue, passenger utility, driver earnings, and their combined total under different regional order densities were plotted, as shown in Figure 6.

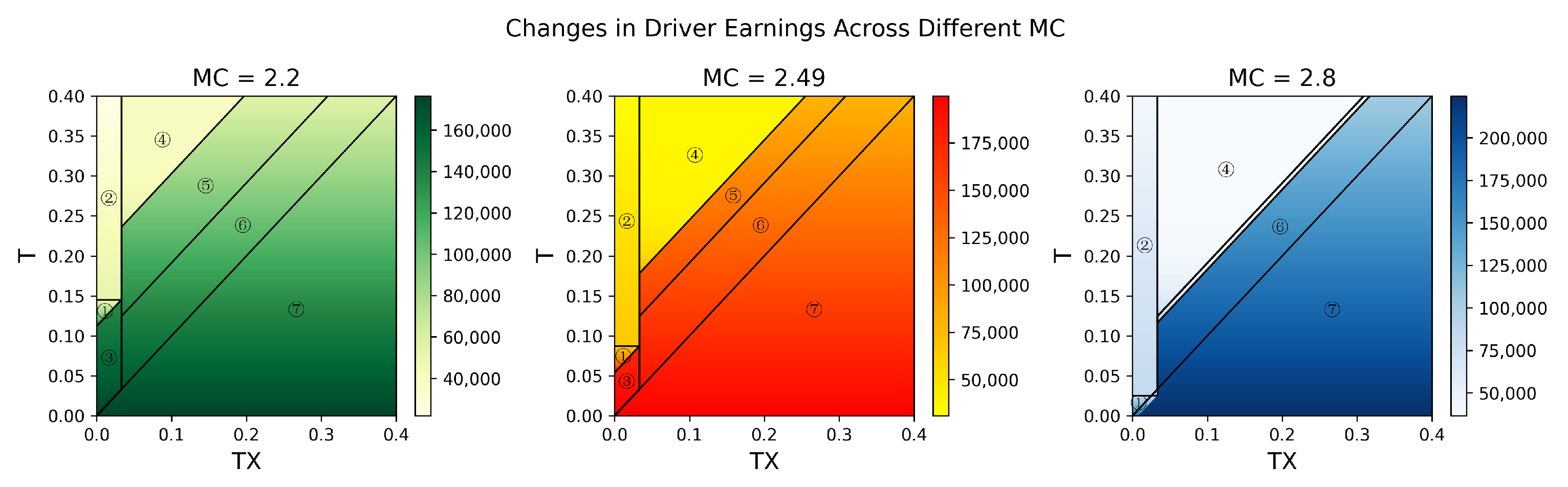
From the perspective of overall social welfare, an increase in order density significantly affects situations where taxi arrival times exceed the penalty threshold for passenger order cancellation, while ride-hailing vehicles from the platform take longer to arrive. When order density is low, ride-hailing platforms can adjust the number of cruising taxis in the road network by increasing the proportion of orders allocated to taxis, thereby regulating the probability of passenger order cancellations. However, as regional order density increases, both taxi and platform ride-hailing vehicle pick-up times increase significantly. In this case, increasing the proportion of orders allocated to platform ride-hailing vehicles instead helps maintain social welfare at a higher level.

For ride-hailing platforms, allocating orders to taxis generates additional commissions. Therefore, in scenarios where passengers are unlikely to cancel orders, allocating more orders to taxis is always beneficial to the platform. However, as order density increases and the probability of taxi offline order acceptance rises, platforms should also consider allocating more orders to their own ride-hailing vehicles for situations where online vehicles require longer pick-up times to reduce revenue losses due to passenger order cancellations. Nevertheless, passengers prefer that platforms allocate orders to their own ride-hailing vehicles, as this increases their chances of encountering empty cruising taxis. This preference becomes more apparent as order density increases, which is also related to the decrease in the number of taxis participating in online order dispatch during high order overflow. When order overflow is relatively mild, passengers are willing to wait longer for orders that are responded to online.

5.3. Impact of Dynamic Pricing Mechanism on Ride-Hailing Platform’s Order Allocation Strategy

5.3.1. Impact of Ride-Hailing Unit Cost Changes on Platform Order Allocation Strategy

In ride-hailing operations, differential pricing mechanisms are widely adopted, especially during periods of order overflow. When the ride-hailing fare, $M_C$, is subject to differential pricing, the changes in passenger order cancellation probabilities are illustrated in Figure 7, while the changes in driver earnings are depicted in Figure 8.

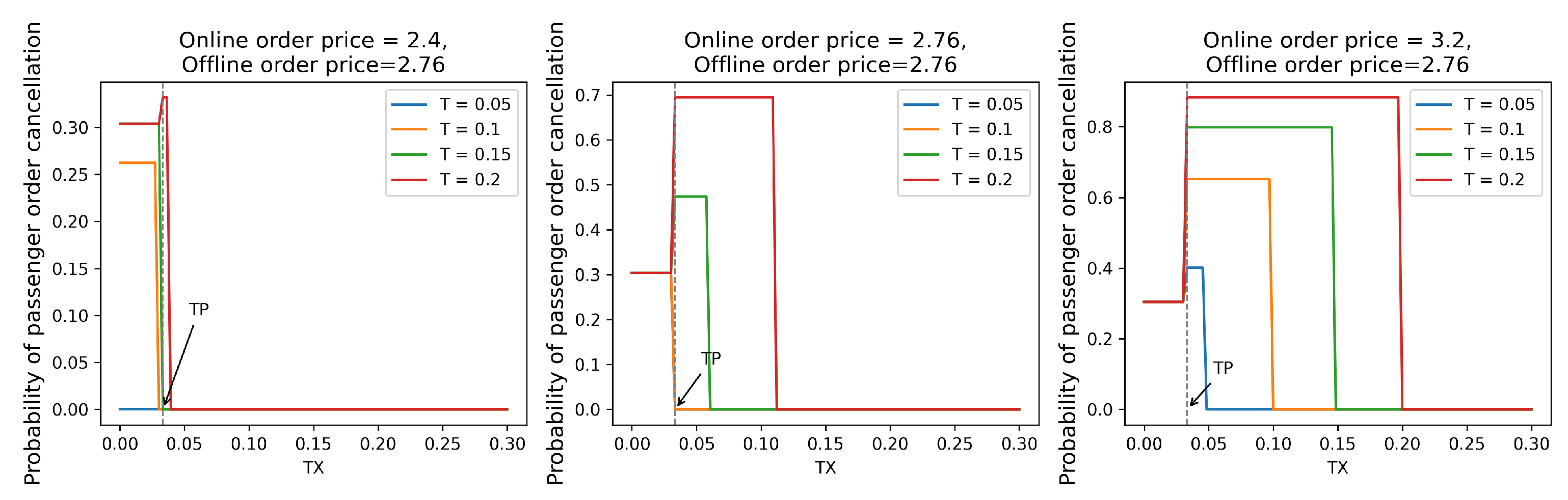
An increase in the ride-hailing unit cost, $M_C$, narrows the price gap between ride-hailing vehicles and taxis, reducing the price advantage when orders are assigned to ride-hailing vehicles. Consequently, passengers are more likely to cancel their orders and switch to taxis. This is visually represented in Figure 7 by the expansion of zones 2 and 4 and the contraction of zones 3 and 5, accompanied by a slight increase in the upper limit of order cancellation probabilities.

For drivers, a higher ride-hailing fare increases their overall earnings range. However, the rise in order cancellation probabilities also expands the area of lower earnings. Therefore, when drivers can quickly reach the passenger locations assigned by the platform, the earnings increase from a higher fare is more significant. Conversely, if the pick-up time is longer, due to factors such as deadhead costs, the earnings gain from a higher fare becomes less pronounced.

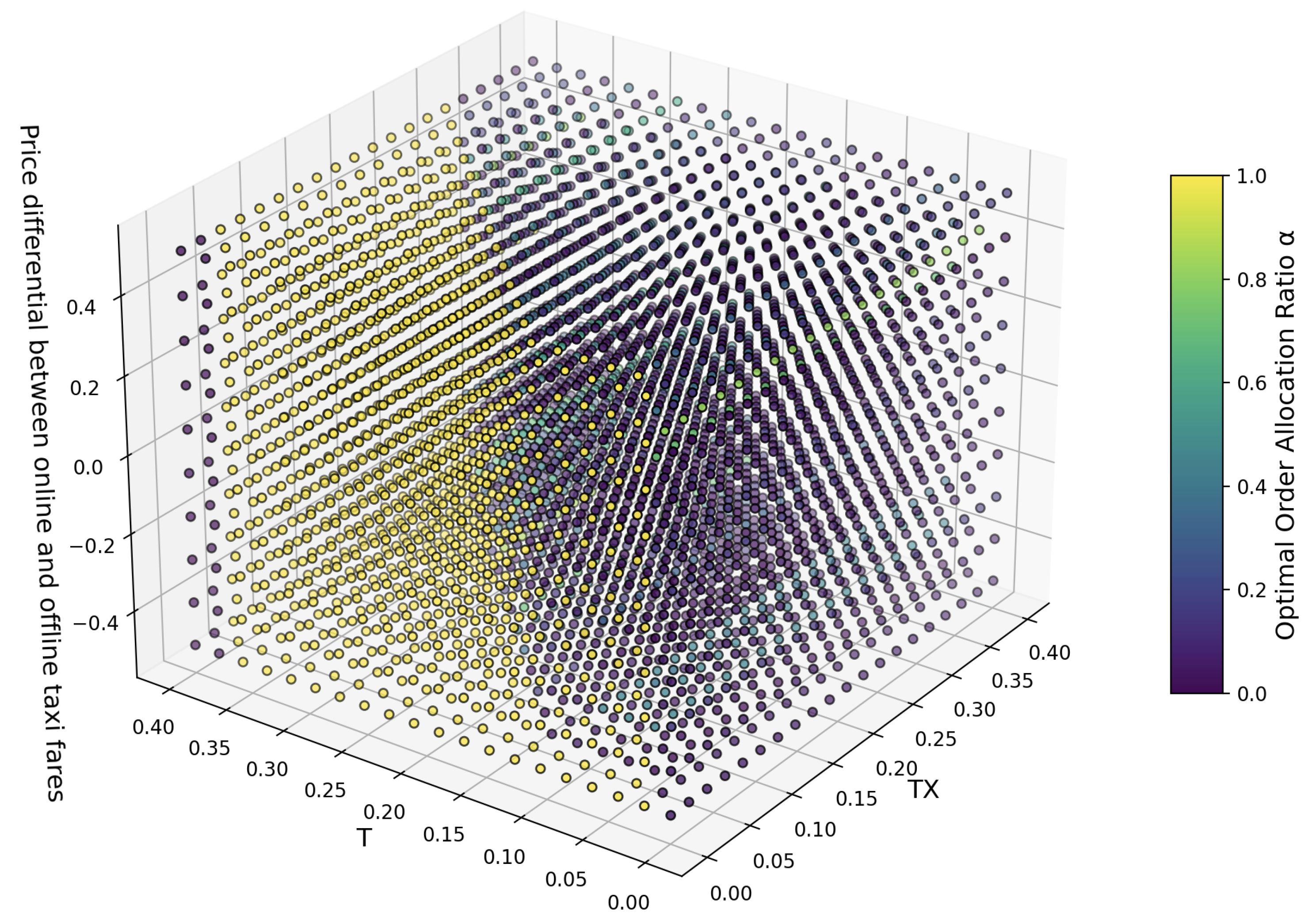
With fluctuations occurring in the ride-hailing unit price, $M_C$, the optimal order allocation ratio, $\alpha$, for maximizing social welfare is illustrated in Figure 9. For cases where the arrival time of cruising taxis, $T_X$, precedes the penalty time, $T_P$, for passenger order cancellation, it is generally observed that utility is maximized when $\alpha$ is set to 1, and this range expands as the fare increases. This implies that, as the ride-hailing fare, $M_C$, rises, the platform needs to allocate more orders to taxis in order to mitigate the negative utility associated with passenger cancellations. Consequently, the platform will continuously adjust the order allocation ratio, $\alpha$, towards 1 earlier, considering the arrival times of ride-hailing vehicles in the system. For situations where cruising taxis arrive after the penalty time for cancellation, as the ride-hailing fare, $M_C$, increases, changes in taxi arrival times more frequently influence variations in the order allocation ratio, $\alpha$, at the same ride-hailing vehicle arrival time level. Moreover, when the ride-hailing fare, $M_C$, is either low or high, achieving optimal social welfare requires larger adjustments in the order allocation ratio, $\alpha$, compared to when $M_C$ is at realistic average prices. This underscores the rationality of ride-hailing platform pricing in practice.

5.3.2. Impact of Taxi Unit Cost Changes on Ride-Hailing Platform’s Order Allocation Strategy

Although taxi fares are uniformly regulated by the government, ride-hailing platforms flexibly reduce the actual cost of taxi rides on their platforms through subsidies and other means or moderately increase taxi prices during periods of tight vehicle supply to ensure order responsiveness and attractiveness to passengers. Therefore, when taxis implement differentiated pricing strategies between online and offline services, their impact on the probability of passenger order cancellation is illustrated in Figure 10.

When online taxi fares are advantageous, the probability of passenger order cancellation quickly approaches zero, with only a slight increase in cancellation probability at the penalty point for cancellations if the online taxi pick-up time exceeds 0.2 h. When online and offline prices are the same, the probability of passenger order cancellation remains unchanged for online taxi pick-up times within 0.1 h, but wait times exceeding 0.1 h make passengers more willing to take cruising taxis. When online taxi prices are higher than offline prices, the impact of cancellation penalties on passengers’ decision to cancel orders decreases significantly. Beyond the penalty point, the probability of passenger order cancellation increases with the length of online taxi pick-up time, showing marginal diminishing increases, with the function value remaining high.

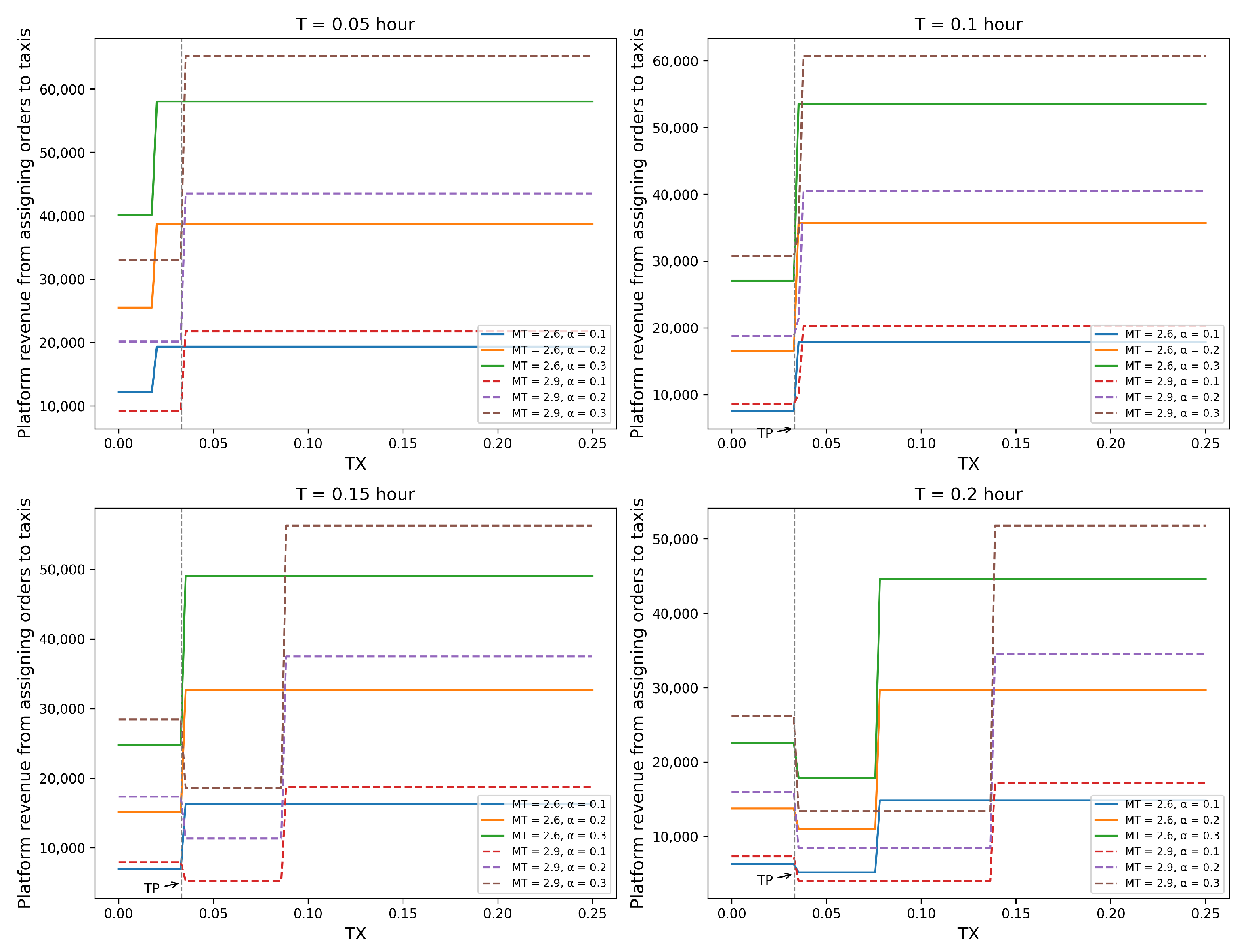
In cases of differentiated pricing between online and offline taxis, when online prices are lower or higher than offline prices, ride-hailing platforms allocate different proportions of orders to taxis, and changes in driver earnings are shown in Figure 11. In general, an increase in online vehicle arrival times leads to a decline in driver income. Specifically, when online taxis can pick up passengers within 0.05 h, higher online prices than offline can actually reduce driver income in the period before the cancellation penalty point. However, when online taxi pick-up times increase to 0.1 h, raising online taxi prices always prompts drivers to earn higher incomes. In view of this, when online vehicle pick-up times are relatively short, increasing online taxi prices is generally beneficial for improving driver income.

If pick-up times extend to 0.15 h, the high-pricing model for online taxis will experience a significant decline in income after the cancellation penalty point, with the decline becoming more pronounced as the dispatch ratio increases. Meanwhile, driver income in the low-pricing model shows an upward trend. When pick-up times exceed 0.2 h, driver income will decline for both high and low online pricing models, with the high-pricing model lasting longer and showing a more significant decline. Therefore, to reduce the driver income risk, the low-pricing model can be selected at this point.

When the taxi unit price, $M_T$, fluctuates, changes in the optimal order allocation ratio, $\alpha$, for maximizing social welfare are shown in Figure 12. For cases where the arrival time of cruising taxis, $T_X$, precedes the penalty time, $T_P$, for passenger order cancellation, an increase in taxi fares, $M_T$, significantly affects the order allocation ratio, $\alpha$, when ride-hailing vehicles arrive later. An increase in taxi fares, $M_T$, raises the cost of switching to another mode for passengers, reducing the probability of order cancellation. Therefore, when taxi fares are higher, ride-hailing platforms need to allocate as many orders as possible to taxis. For cases where cruising taxis arrive after the penalty time for cancellations, an increase in taxi fares, $M_T$, leads to more frequent changes in the optimal order allocation ratio, $\alpha$.

With differentiated pricing implemented between online and offline taxis, the impact of changes in the price difference between the two on the optimal order allocation ratio, $\alpha$, for maximizing social welfare is shown in Figure 13. In general, to maintain the stable operation of the ride-hailing market, the price difference between online and offline taxi services is limited to a relatively narrow range, so fluctuations in the difference have a limited impact on order allocation strategies. For scenarios where online-dispatched vehicles can quickly arrive at the passenger’s designated location, when online taxi fares are set higher than offline fares, the optimal order allocation ratio, $\alpha$, tends to be relatively higher. Conversely, in scenarios where online-dispatched vehicles take longer to arrive, the opposite trend is observed.

5.4. Taxi Decision-Making Between Online and Offline Order Acceptance

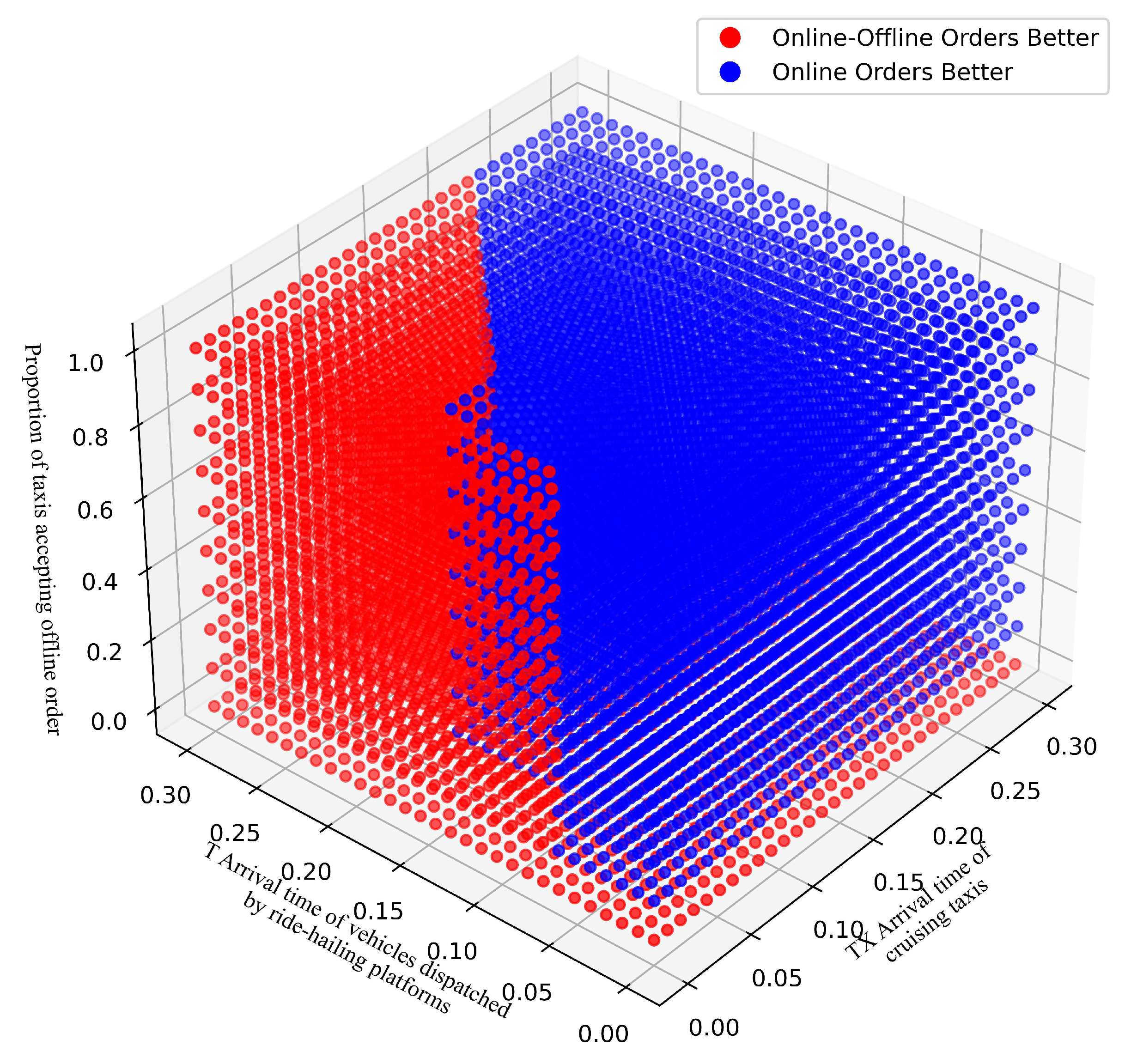
For taxi drivers, by comparing the earnings from adopting two strategies—accepting orders solely through ride-hailing platforms versus a combination of online and offline (street-hailing) methods—for individual orders, as illustrated in Figure 14—higher earnings can be achieved through the combined method in intervals 1, 2, and 4 and parts of interval 5. However, in the scenarios corresponding to the remaining intervals, opting for the strategy of accepting orders solely through ride-hailing platforms yields more substantial earnings. Specifically, for empty-running taxis, when order density is high enough for them to find passengers with travel needs within a short period, coupled with ride-hailing vehicles having potentially later arrival times, offline order acceptance results in higher earnings. Meanwhile, due to the convenience offered via services such as route planning and order allocation provided through ride-hailing platforms, taxis tend to continue accepting orders through these platforms at most intervals, even when passenger travel orders overflow.

6. Conclusions

With the rapid development of the ride-hailing industry, people’s travel habits have undergone significant changes. This paper has delved into the behavior of passenger order cancellations in a system where taxis participate in order dispatch through ride-hailing platforms, focusing on the specific scenario of order overflow. We constructed models for passenger order cancellations and earnings for all parties involved. Through simulations, we analyzed the relationship between order density and the proportion of offline order acceptance by taxis, and we conducted numerical analyses to discuss the impact of changes in dispatch ratios on passenger order cancellation probabilities, optimal dispatch ratios under different order densities, and taxi order acceptance strategies under various vehicle arrival scenarios. Our findings reveal the following:

-

From the perspective of passenger order cancellation probabilities, as the proportion of orders allocated to taxis via the platform increases, the sensitivity of passenger order cancellation probabilities to order density rises markedly. Ride-hailing platforms possess the ability to effectively regulate passenger order cancellation behavior by controlling dispatch ratios. In intervals 1 and 2, adopting higher order allocation ratios can reduce passenger order cancellation probabilities. However, in other intervals, to achieve lower cancellation probabilities, the ideal strategy is to prioritize allocating all orders to ride-hailing vehicles. Additionally, there is a slight lag in the changes in taxis’ choices regarding offline order acceptance relative to changes in regional order density.

-

From the perspective of earnings for all parties involved, changes in order density significantly impact intervals 4 and 5, where taxi arrival times exceed the penalty threshold for passenger order cancellations, while ride-hailing vehicles from the platform take longer to arrive. For scenarios where taxis can arrive before the penalty for order cancellation is imposed, from the perspectives of enhancing social welfare, platform earnings, and driver earnings, ride-hailing platforms tend to allocate as many orders as possible to taxis. However, this strategy results in a relative decrease in passenger utility. The impact of passenger utility is evident in scenarios where taxis arrive after the penalty for order cancellation is imposed. At this point, to optimize social welfare, the proportion of orders allocated to taxis should be reduced.

-

From the perspective of taxi order acceptance strategies, we find that a large-scale shift to offline order acceptance by taxis does not occur solely during order overflow. Although taxi customers’ acquisition costs decrease when order density is high, this cost remains a significant factor influencing taxi choices. Corresponding to passenger order cancellation behavior, taxis are more inclined to adopt offline order acceptance strategies, primarily in situations where passengers may cancel orders dispatched through any platform.

When exploring the issue of order dispatch by ride-hailing platforms and considering passenger order cancellations in the context of order overflow, the model in this paper does not consider passenger heterogeneity. In the actual ride-hailing market, passengers may prefer certain types of rides due to factors such as personal preferences, demographics, and past riding experiences. Similarly, drivers may also be inclined to accept orders through different channels influenced by their personal characteristics, work experience, and other factors. In light of this, future research can further expand by incorporating the personalized needs and preferences of drivers and passengers into consideration, thereby more comprehensively revealing the complexity and diversity of order dispatch mechanisms in ride-hailing platforms.