All-Integer Quantization for Low-Complexity Min-Sum Successive Cancellation Polar Decoder
Abstract
1. Introduction
- Proposal of an All-Integer-Quantized MS-SC Decoder: We introduce an integer-based quantized min-sum SC (QMS-SC) decoder that eliminates floating-point computations, making it more suitable for hardware implementations.
- Performance–Complexity Trade-off Analysis: We investigate the impact of integer-based quantization and demonstrate that 5-bit integer quantization approaches a performance comparable with high-precision MS-SC decoding. We also analyze the decoding performance over fading channels, showing that quantization beyond 5 bits leads to performance saturation.
- Computational Complexity Reduction: The all-integer QMS-SC decoder reduces computational complexity by approximately 75% compared to the conventional SC decoder, significantly improving efficiency.
2. Background and System Model
2.1. Polar Codes
2.2. Successive Cancellation Decoding Algorithm
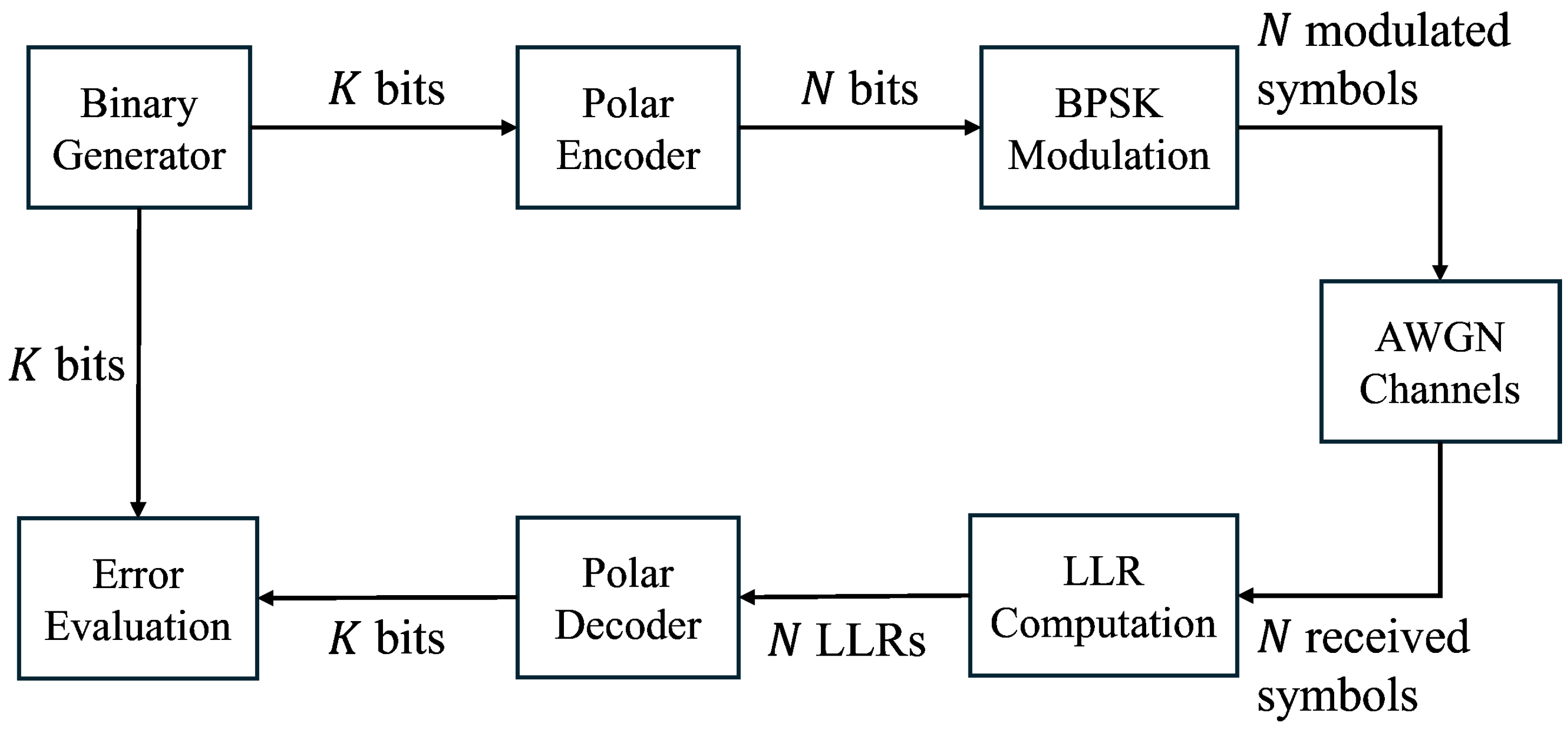
2.3. System Model
3. Related Work
4. All-Integer Quantization for Successive Cancellation Decoding Algorithm
| Algorithm 1: Successive Cancellation Decoding Algorithm |
 |
| Algorithm 2: RecursivelyUpdateLLR() |
 |
5. Experimental Results
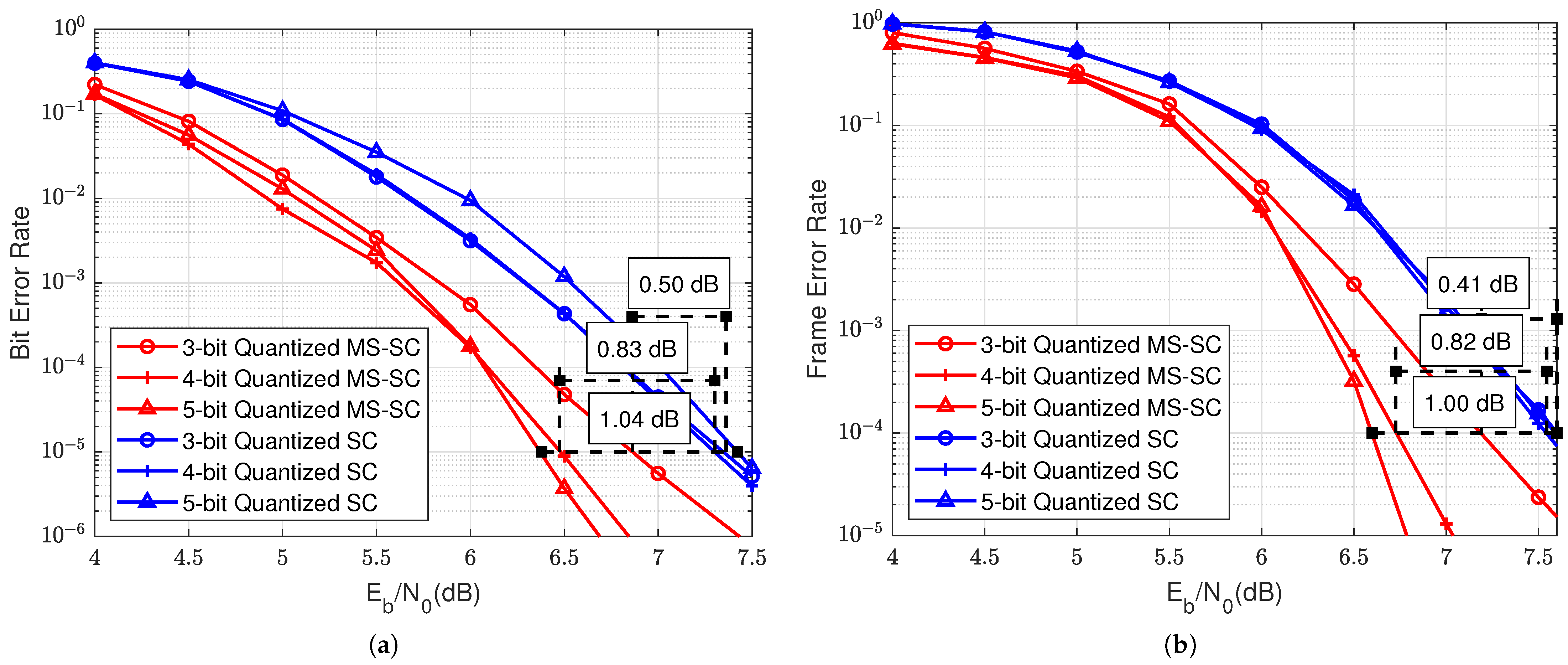
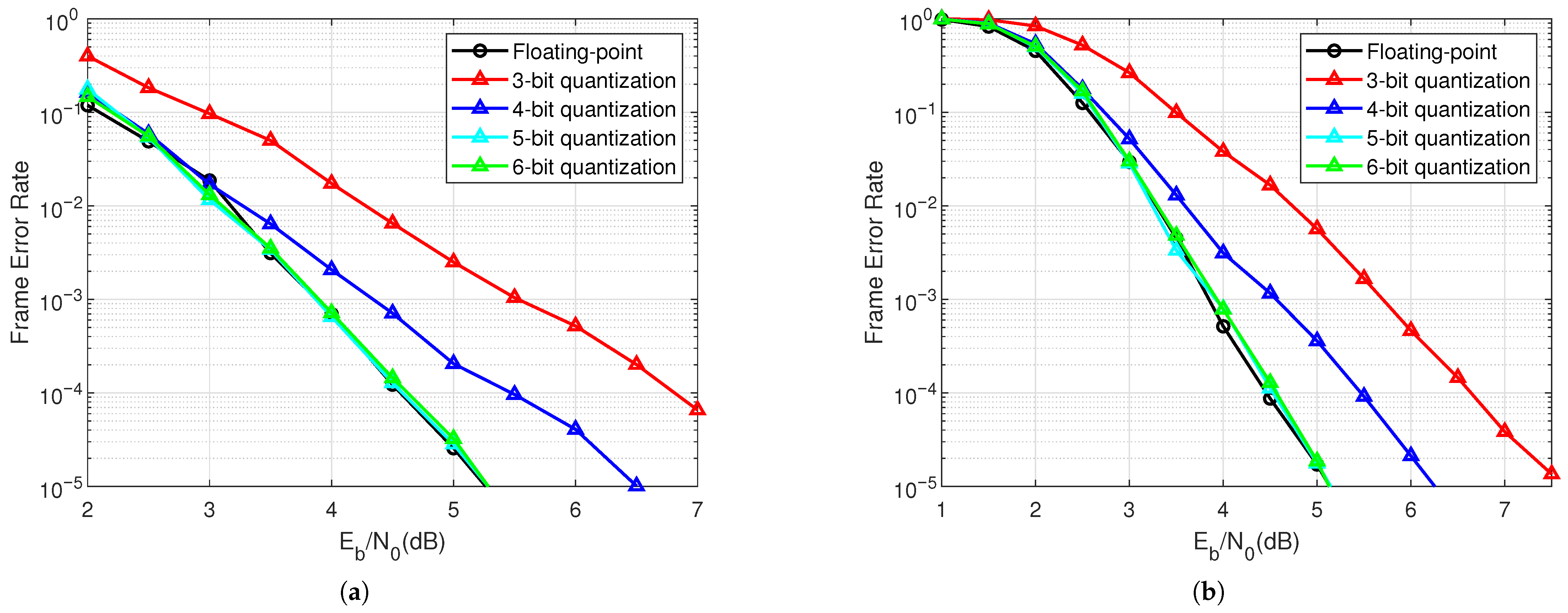
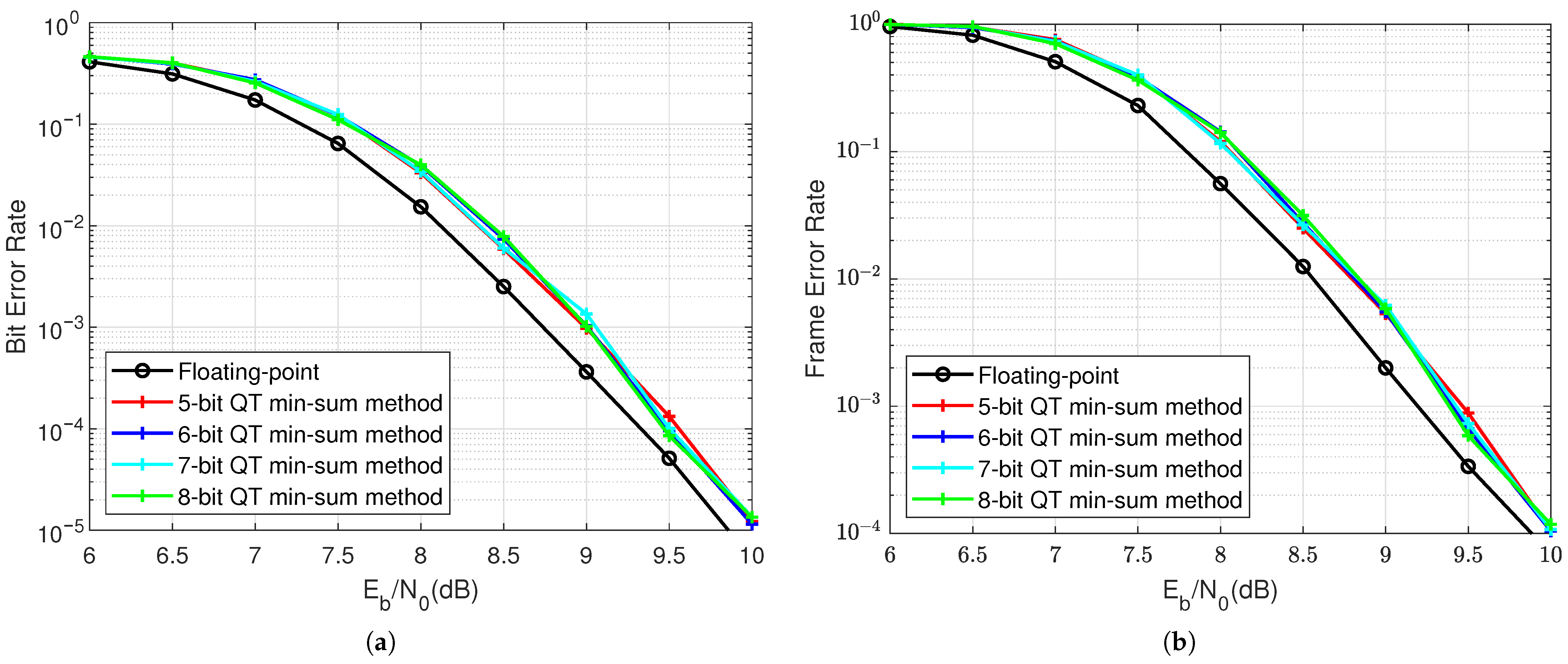
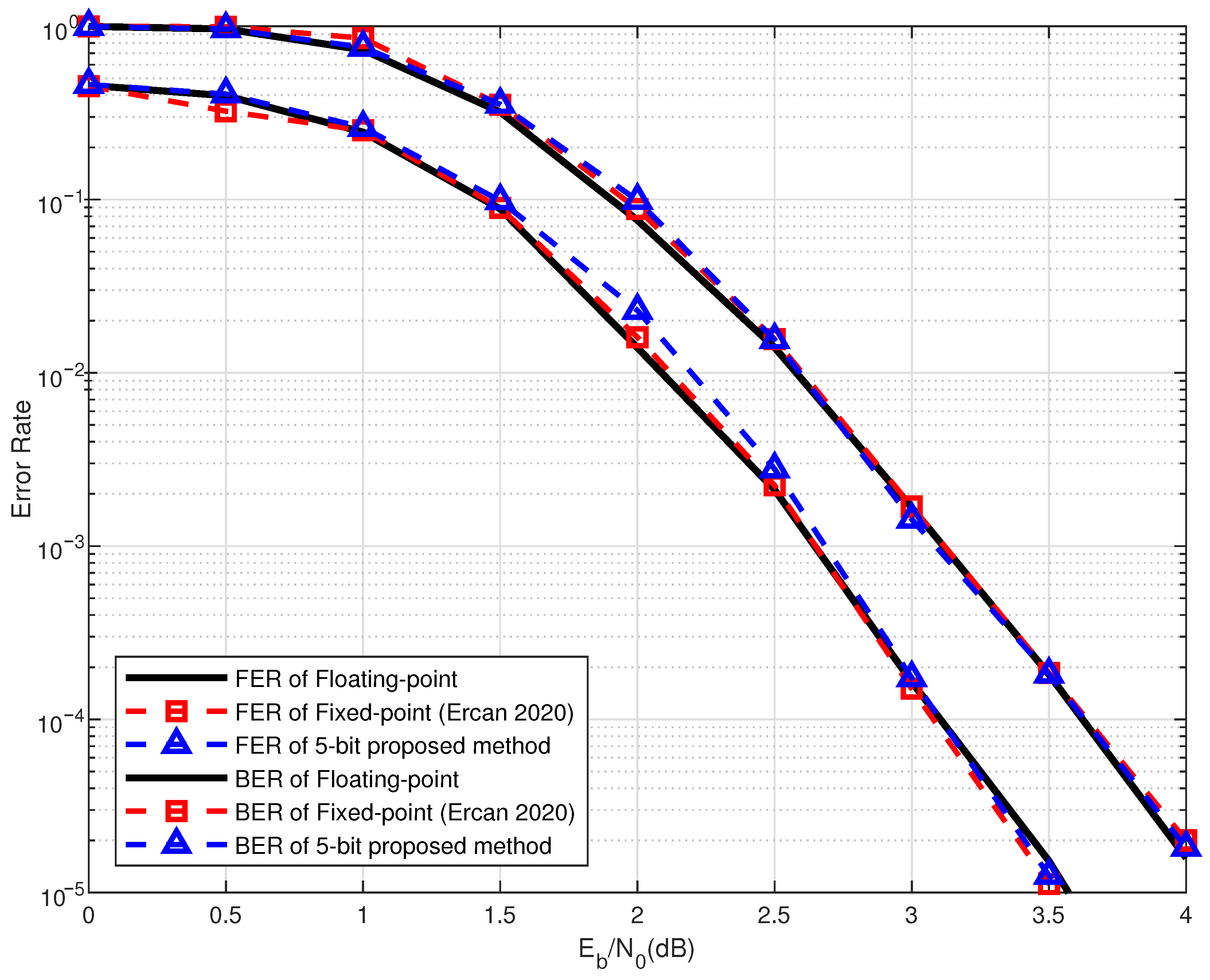
5.1. Decoding Performance Under Integer Quantization
5.2. Optimal Integer Quantization Level
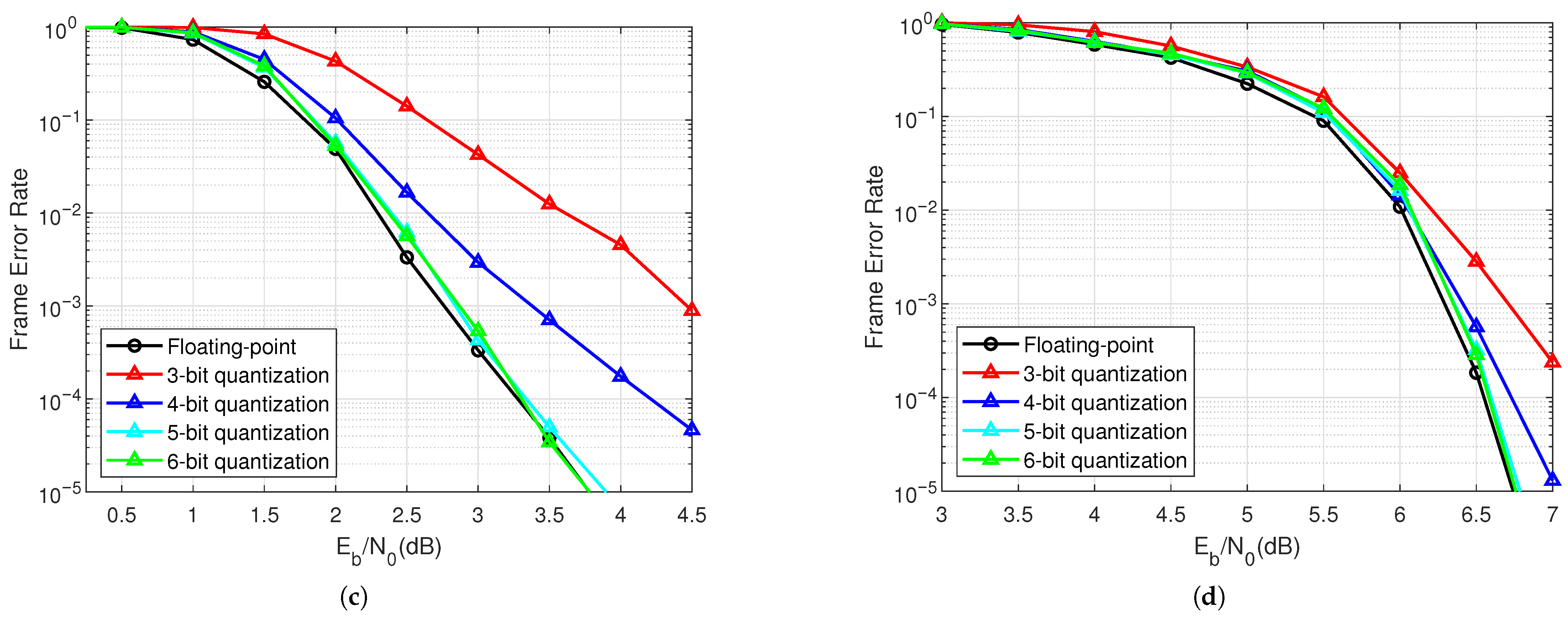
5.3. Performance over Fading Channels
5.4. Complexity Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arikan, E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Leroux, C.; Raymond, A.J.; Sarkis, G.; Tal, I.; Vardy, A.; Gross, W.J. Hardware implementation of successive-cancellation decoders for polar codes. J. Signal Process. Syst. 2012, 69, 305–315. [Google Scholar] [CrossRef]
- Tal, I.; Vardy, A. List Decoding of Polar Codes. IEEE T. Inf. Theory 2015, 61, 2213–2226. [Google Scholar] [CrossRef]
- 3GPP TSG RAN1; R1-1611109: Evaluation on Channel Coding Candidates for eMBB Control Channel. 3GPP TSG RAN WG1 Meeting #86: Gothenburg, Sweden, 2016.
- Zhao, S.; Shi, P.; Wang, B. Polar codes and its application in speech communication. In Proceedings of the 2011 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 9–11 November 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Shamer, Z.M.; Abdulkadhim Hamad, A. FPGA-Based Implementation of Polar Code Using Successive Cancelation Decoding. In Proceedings of the 2022 2nd International Conference on Advances in Engineering Science and Technology (AEST), Babil, Iraq, 14–15 December 2022; pp. 351–356. [Google Scholar] [CrossRef]
- Niu, K.; Zhang, P.; Dai, J.; Si, Z.; Dong, C. A golden decade of polar codes: From basic principle to 5G applications. China Commun. 2023, 20, 94–121. [Google Scholar] [CrossRef]
- Monsees, T.; Griebel, O.; Herrmann, M.; Wübben, D.; Dekorsy, A.; Wehn, N. Minimum-Integer Computation Finite Alphabet Message Passing Decoder: From Theory to Decoder Implementations towards 1 Tb/s. Entropy 2022, 24, 1452. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Shin, D.J. A Nonuniform-Quantized Successive Cancellation Decoding of Polar Codes Over AWGN Channels. IEEE Access 2021, 9, 80221–80235. [Google Scholar] [CrossRef]
- Cao, Z.; Zhu, H.; Zhao, Y.; Li, D. Nonuniform Quantized Decoder for Polar Codes With Minimum Distortion Quantizer. IEEE Commun. Lett. 2021, 25, 835–839. [Google Scholar] [CrossRef]
- Gao, J.; Niu, K.; Dong, C. Learning to Decode Polar Codes With One-Bit Quantizer. IEEE Access 2020, 8, 27210–27217. [Google Scholar] [CrossRef]
- Lewandowsky, J.; Bauch, G. Trellis based node operations for LDPC decoders from the Information Bottleneck method. In Proceedings of the 2015 9th International Conference on Signal Processing and Communication Systems (ICSPCS), Cairns, QLD, Australia, 14–16 December 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Stark, M.; Bauch, G. Design of Quantized Decoders for Polar Codes using the Information Bottleneck Method. In Proceedings of the SCC 2019; 12th International ITG Conference on Systems, Communications and Coding, Rostock, Germany, 11–14 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Muangkammuen, P.; Vongjampa, W.; Suthisopapan, P. On the Performance of Rate-Compatible LDPC Codes under All-Integer Quantization Decoding. J. Electr. Comput. Eng. 2022, 2022, 3076517:1–3076517:8. [Google Scholar] [CrossRef]
- Zakariyya, R.S.; Jewel, K.H.; Fadamiro, A.O.; Famoriji, O.J.; Lin, F. An Efficient Polar Coding Scheme for Uplink Data Transmission in Narrowband Internet of Things Systems. IEEE Access 2020, 8, 191472–191481. [Google Scholar] [CrossRef]
- Ali, M.M.; Hashim, S.J.; Chaudhary, M.A.; Ferré, G.; Rokhani, F.Z.; Ahmad, Z. A Reviewing Approach to Analyze the Advancements of Error Detection and Correction Codes in Channel Coding With Emphasis on LPWAN and IoT Systems. IEEE Access 2023, 11, 127077–127097. [Google Scholar] [CrossRef]
- Yu, X.; He, J.; Li, Q.; Zhang, B.; Wang, X.; Wang, Q.; Huo, Z. DMMC: A Polar Code Construction Method for Improving Performance in TLC NAND Flash. IEEE Embed. Syst. Lett. 2024, 16, 146–149. [Google Scholar] [CrossRef]
- Trifonov, P. Efficient Design and Decoding of Polar Codes. IEEE Commun. 2012, 60, 3221–3227. [Google Scholar] [CrossRef]
- Vangala, H.; Viterbo, E.; Hong, Y. A comparative study of polar code constructions for the AWGN channel. arXiv 2015, arXiv:1501.02473. [Google Scholar]
- Fossorier, M.; Mihaljevic, M.; Imai, H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation. IEEE Trans. Commun. 1999, 47, 673–680. [Google Scholar] [CrossRef]
- Leroux, C.; Raymond, A.J.; Sarkis, G.; Gross, W.J. A Semi-Parallel Successive-Cancellation Decoder for Polar Codes. IEEE Trans. Signal Process. 2013, 61, 289–299. [Google Scholar] [CrossRef]
- Giard, P.; Thibeault, C.; Gross, W.J. Fast Low-Complexity Hardware Decoders for Low-Rate Polar Codes. In High-Speed Decoders for Polar Codes; Springer: Berlin/Heidelberg, Germany, 2017; pp. 21–47. [Google Scholar] [CrossRef]
- Rezaei, H.; Rajatheva, N.; Latva-Aho, M. Low-Latency Multi-Kernel Polar Decoders. IEEE Access 2022, 10, 119460–119474. [Google Scholar] [CrossRef]
- Yan, C.; Cui, Y.; Chen, K.; Wu, B.; Liu, W. Hardware Efficient Successive-Cancellation Polar Decoders Using Approximate Computing. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 189–200. [Google Scholar] [CrossRef]
- Ali, Y.; Xia, Y.; Manzoor, T.; Ali, S.; Abouhawwash, M.; Askar, S.S.; Kumar, A.K.; Ma, R. Efficient Hardware Realization of SC Polar Decoders Using Compound Pipelined Processing Units and Auxiliary Registers. IEEE Access 2024, 12, 23808–23826. [Google Scholar] [CrossRef]
- Ercan, F.; Tonnellier, T.; Gross, W.J. Energy-Efficient Hardware Architectures for Fast Polar Decoders. IEEE TCAS-I 2020, 67, 322–335. [Google Scholar] [CrossRef]
- Arikan, E. Systematic Polar Coding. IEEE Commun. Lett. 2011, 15, 860–862. [Google Scholar] [CrossRef]
- IEEE Std 754-2019 (Revision of IEEE 754-2008); IEEE Standard for Floating-Point Arithmetic. IEEE: New York, NY, USA, 2019; pp. 1–84. [CrossRef]


| Decoding | Rate | Length | Average | ||
|---|---|---|---|---|---|
| 3-Bit | 4-Bit | 5-Bit | |||
| Quantized MS-SC | 0.5 | 256 | ≈0.84 | ≈0.75 | ≈0.72 |
| 0.83 | 4096 | ≈2.02 | ≈1.29 | ≈1.28 | |
| Quantized SC | 0.5 | 256 | ≈1.26 | ≈3.77 | ≈15.7 |
| 0.83 | 4096 | ≈2.06 | ≈1.54 | ≈3.53 | |
| Decoding | Reduction Gain per Block Length (Bits) | |||
|---|---|---|---|---|
| 256 | 1024 | 4096 | 16,384 | |
| Integer-quantized MS-SC | ||||
| Fixed-point MS-SC | ||||
| Feature | CPU (Floating-Point) | FPGA (Fixed-Point/Integer) |
|---|---|---|
| Precision | High (32-bit/64-bit) | Limited (fixed-point) |
| Computation Type | Floating-point and integer | Mostly fixed-point or integer |
| Multiplication, Division | Fast and direct | Uses *DSPs or shift-add approximations |
| Nonlinear Functions (atanh, tanh, sqrt, exp) | Direct computation | Approximated using *LUTs, or Taylor series |
| Hardware Flexibility | No constraints on arithmetic complexity | Needs optimization for area, power, and latency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pimsri, W.; Muangkammuen, P.; Suthisopapan, P.; Imtawil, V. All-Integer Quantization for Low-Complexity Min-Sum Successive Cancellation Polar Decoder. Appl. Sci. 2025, 15, 3241. https://doi.org/10.3390/app15063241
Pimsri W, Muangkammuen P, Suthisopapan P, Imtawil V. All-Integer Quantization for Low-Complexity Min-Sum Successive Cancellation Polar Decoder. Applied Sciences. 2025; 15(6):3241. https://doi.org/10.3390/app15063241
Chicago/Turabian StylePimsri, Wittawad, Patinya Muangkammuen, Puripong Suthisopapan, and Virasit Imtawil. 2025. "All-Integer Quantization for Low-Complexity Min-Sum Successive Cancellation Polar Decoder" Applied Sciences 15, no. 6: 3241. https://doi.org/10.3390/app15063241
APA StylePimsri, W., Muangkammuen, P., Suthisopapan, P., & Imtawil, V. (2025). All-Integer Quantization for Low-Complexity Min-Sum Successive Cancellation Polar Decoder. Applied Sciences, 15(6), 3241. https://doi.org/10.3390/app15063241







