Motion Tactics Model Combining Multiple Tactics to Represent Individual Differences in Human Running Motion

Abstract

Human running is a simple, periodic motion; however, the underlying mechanisms that generate this motion are complex, resulting in individual variations even when the same locomotion goal is pursued. Current generalized locomotion studies have not adequately explained these variations. To address this gap, we focus on the concept of motion strategy, which involves selecting different approaches to accomplish a task. Our objective is to develop a simulation that integrates these motion strategies. Achieving this requires both a deep understanding of the mechanisms behind human motion generation and the development of a system that can reproduce these mechanisms within a simulation. In this study, we propose a motion tactics model and develop a simulation system to replicate motions guided by these strategies. The simulation results were compared with experimental data to assess the effectiveness of the proposed model in replicating individual differences in motion. The model generated multiple motion states and showed it could select unique outcomes by combining different tactics, confirming its validity and feasibility. This approach demonstrated the potential for representing the characteristics in individual motion.

1. Introduction

Running motion is a simple, periodic movement characterized by up and down oscillations; however, the mechanisms involved in generating and controlling the motion are highly complex. This complexity arises from dynamic redundancy, as there are multiple ways to achieve a movement goal despite humans demonstrating skillful and efficient motion. Using multiple evaluation criteria, dynamic optimization has been employed to select a single motion from this redundancy [1,2,3]. This approach has facilitated the recalculation of muscle exertion and joint angles during exercise [4,5], the generation of movements based on evaluation criteria [6], and has provided valuable insights into the underlying mechanisms of motion generation. Although previous research explains the general mechanisms of human motion, it has not yet succeeded in replicating the unique characteristics of individual movement.

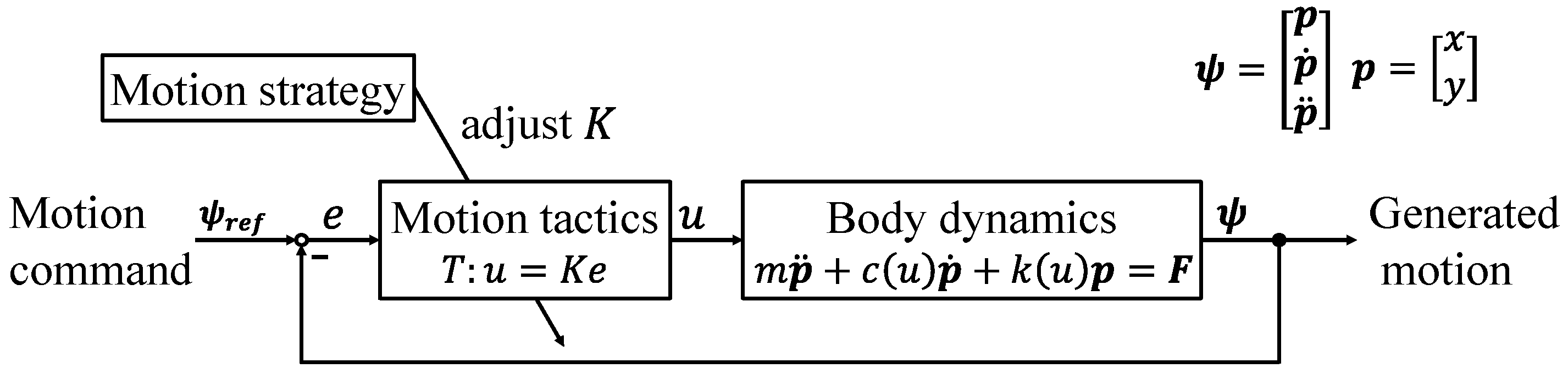
Therefore, our research aims to elucidate human motion mechanisms and develop a simulation that represents individual differences. We focus on motion strategy to capture the unique characteristics of individual movement. Motion strategy prioritizes evaluation criteria, optimizing them within the constraints of limited resources. Movements aimed at achieving specific goals are generated based on an objective function that incorporates these prioritized criteria. The body’s movements for this optimization process are referred to as motion tactics. Due to the dynamic redundancy of the human body, individuals can employ multiple tactics, resulting in purposeful and varied movements. By modeling motion tactics, describing motion strategies, and replicating individual motion characteristics in simulations become feasible. This paper proposes a motion tactics model that enables the use of multiple tactics to represent individual differences in running motion under identical conditions.

Initially, the paper mentioned the background and purpose of our research. Next, we review previous studies related to our research and describe the positioning and novelty of the study in Section 2. In the following, Section 3 details an explanation of our motion generation mechanism. In Section 4, the paper shows the results of the simulation with the proposed model. Lastly, the paper discusses whether the proposed model can successfully replicate individual motion characteristics based on the results of running simulations.

2. Related Research

2.1. Review of Related Research

Research on human motion generation has focused on improving performance, preventing injury, and designing robot control systems that replicate human motion. Two primary methods for motion generation have emerged: data-driven approaches, which leverage machine learning and AI, and model-based approaches, such as dynamic optimization.

Data-driven motion generation can accurately replicate movements from actual data. Deep reinforcement learning and neural network models have been successfully employed to generate motion for new tasks [7,8]. However, a significant limitation of these methods is that the generation process is often black-boxed [9,10], rendering it difficult to understand the underlying mechanisms or to represent them mathematically.

Model-based motion generation provides more accurate simulations, as the models are grounded in physical laws and physiological knowledge. This approach enables the quantitative interpretation of motion based on simulation results. However, it requires expert knowledge and careful validation of the model design, tuning, and understanding of its representation limits. Whole-body musculoskeletal models have been utilized to understand human motion by quantifying movements through joint angle and torque calculations [4,5]. These models enable the analysis of athletic performance and the estimation of internal loads on the musculoskeletal system. However, they may be unsuitable for real-time processing owing to their long computation times. To address this limitation, simplified models that exclude less impactful elements have been proposed. The inverted pendulum model is widely used to reproduce human locomotion as a simple model to represent human locomotion. The realistic simulation of human motion has been applied to animation generation [11,12] and robot hopping and movement [13,14,15]. Among them, many valuable insights regarding the control of biped robots have been obtained, including a new approach to the dynamic control of robot running and hopping [16], and a control method based on dynamic optimization aimed at enhancing robot stability and efficiency [17].

Many studies on motion generation have employed dynamic optimization. Davy et al. [18] demonstrated the generation of typical muscle activity during walking through dynamic optimization, which accounted for energy consumption, to predict muscle activity during the flight phase. Similarly, Anderson et al. [19] focused on movement economy by minimizing metabolic energy expenditure per unit distance traveled, resulting in simulation outcomes that closely resembled actual motion characteristics motion.

In optimization, multiple evaluation criteria, rather than a single criterion, have been explored to generate more human-like motion [6,20,21,22,23]. Schultz et al. [24] utilized energy consumption and motion smoothness as weighted evaluation functions for motion generation, which resulted in sprinter-like running patterns. Mombaur et al. [25] proposed an inverse optimization control method that derives the weights of basis functions in the motion generation optimization problem from actual motion data, enabling the generation of motion paths that closely mimic actual human behavior.

2.2. Novelty and Contribution of This Study

The novelty of this study lies in the development of a motion control model capable of representing individual motion generation. Previous studies have designed optimization problems for motion generation and provided valuable insights into movement mechanisms. However, they primarily focused on applying human motion to bipedal robot control and trajectory generation without fully explaining individual differences or the complete process of motion generation. Additionally, while machine learning-based motion generation achieves high accuracy, its generative mechanism remains a black box, making the process from input to output unclear.

In this study, we aim to construct motion control by adopting a bottom-up approach, systematically integrating the fundamental elements of motion generation. Specifically, we emphasize a white-box design to ensure transparency in control mechanisms, thereby establishing a framework that allows an intuitive and mathematical understanding of motion generation principles. Moreover, human body control exhibits redundancy, leading to an overwhelming amount of information that must be accounted for. To address this issue, we employ a simple dynamical model to capture motion holistically and regulate its parameters to abstractly represent the complex human system, thereby simplifying the problem.

Based on this approach, we design controllers that incorporate factors such as energy and stability, which are presumed to be considered in human movement optimization. This allows us to describe movement’s abstract and linguistically challenging aspects as “motion strategy”. Furthermore, we introduce a new concept, “motion tactics”, which serve as a bridge between strategies and dynamics, enabling the implementation of strategy-based movement generation. Additionally, by adjusting the weighting of multiple tactics, we aim to represent individual differences in movement. Through this, we construct a model that quantitatively describes individual movement generation, contributing to a more systematic understanding of movement.

3. Method of Generating Running Motion

This section outlines the generation of running motions through simulation using the spring-loaded inverted pendulum (SLIP) model [26]. In Section 3.1, we introduce the concepts of motion strategy and tactics to characterize human motion. In Section 3.2, we detail the simulation method used in this study to generate running movements. This section is further divided into specific parts. Section 3.2.1 explains the fundamental structure of the SLIP model and the extensions incorporated in this. Section 3.2.2 presents the three tactics introduced to optimize the running behavior. Finally, Section 3.2.3 describes the approach used to optimize the weighting and control gains of each tactic to produce individual running motions.

3.1. Concept of Motion Generation Mechanism

In this section, we present our hypothesis on the mechanism of motion generation. We assume that human motion is guided by multiple evaluation criteria, which are combined to form an objective function for motion generation. The objective of motion is expressed as a weighted sum of these evaluation criteria ${\varphi }_i$, as shown in Equation (1).

$$O=\sum _{i=1}^n{s}_i{\varphi }_i$$

(1)

Here, $S=s_1,s_2,\dots ,s_n$ represents the motion strategy that formulates the objective function by weighting each basis.

Motion tactics regulate body control to optimize each evaluation criterion. The movement of the body is adjusted by modifying its dynamics. Given the existence of multiple motion tactics, this concept can be generalized in Equation (2).

$$T:u=\sum _j\left\{{}^P{K}_j{e}_j+{}^I{K}_j\int e_{j}dt+{}^D{K}_j{\displaystyle \frac{d{e}_j}{dt}}\right\}$$

(2)

In this equation, u, ${}^{\ast }{K}_j$, and $e_j$ represent the control input, control gain, and deviation from the reference motion state, respectively. The parameter u represents the controllable body dynamics, such as human stiffness and viscous terms that can be varied in body control. This parameter is further regulated by the control gain ${}^{\ast }{K}_j$ and the deviation $e_j$ between the feedback motion state—such as velocity and acceleration—and the desired motion state. In this framework, motion tactics function as compensators in the motion generation process (Figure 1).

The control gains ${}^{\ast }{K}_j$ determine the influence of each motion tactic on the overall motion. The gain of a tactic is expressed as a function of the strategy, as following equation.

$$\begin{array}{c}\hfill {}^{\ast }{K}_j=H(s_1,s_2,\cdots ,s_n)\end{array}$$

(3)

From the above, the influence of tactics on motion varies according to the gain determined by the motion strategy (Equation (3)). Consequently, the control method for the motion is established (Equation (2)), and the motion is generated in alignment with the strategy to achieve the objective (Equation (1)).

3.2. Method of Simulation to Generate Human Running Motion

3.2.1. SLIP-Based Simulation

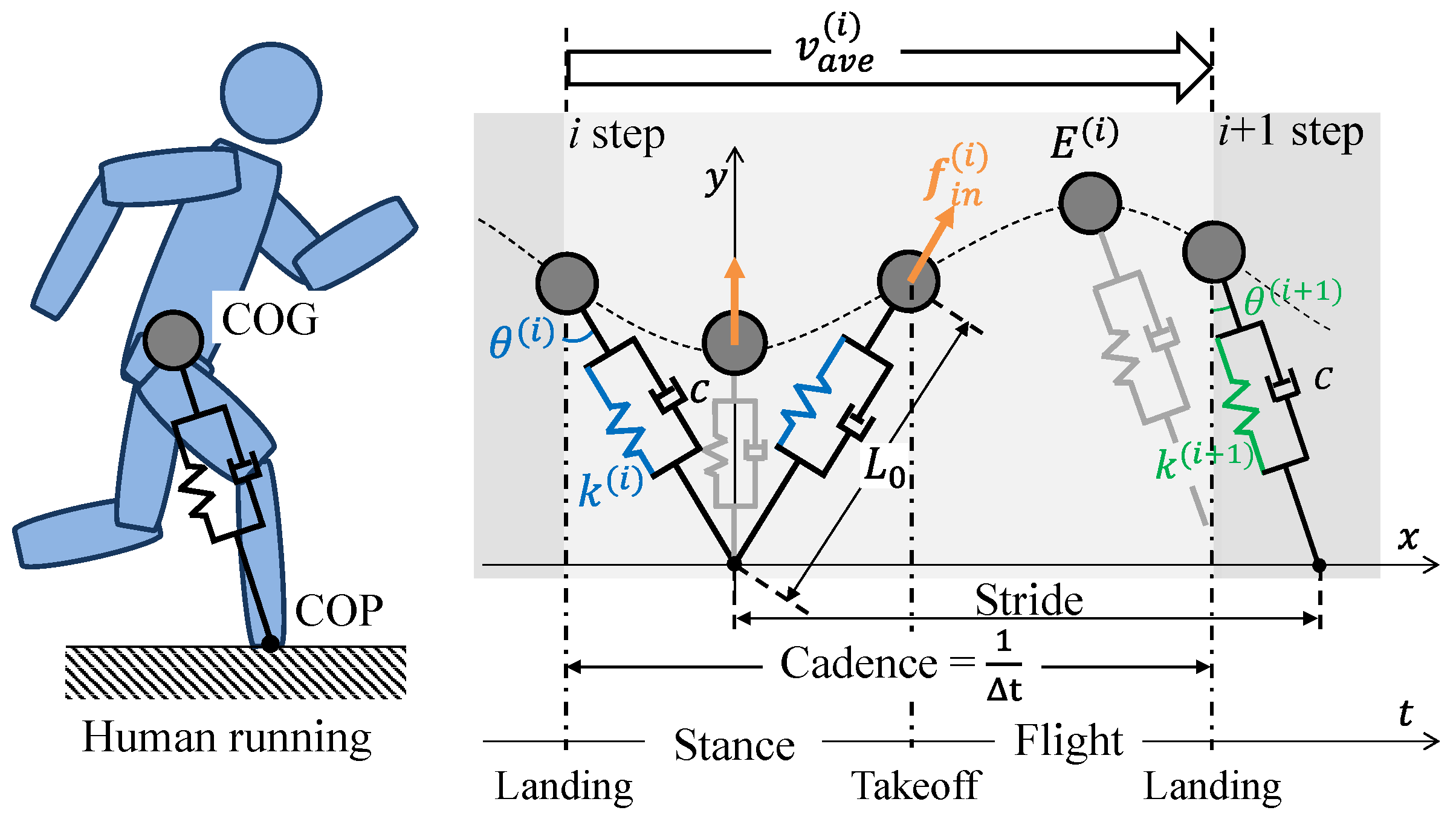
The SLIP model was employed as the foundational framework for motion generation simulation based on the proposed mechanism. The SLIP model, a simplified and less redundant representation of locomotion dynamics, captures essential motion characteristics using only mass and springs and has been widely recognized as an effective approximation of locomotion dynamics. This study introduced an energy-tunable structure by adding a parallel damper and force application (Figure 2). The force application $f_{in}$ is explained in Section 3.2.2 as part of the tactics model. The model parameters included the damper’s viscosity c, mass m, stiffness k, and spring’s natural length $L_0$, which were identified based on experimental data.

The simulation was conducted using the SLIP model and the motion tactics model, considering only horizontal and vertical motion for simplicity. In running, the gait cycle consists of two main phases: the swing phase and the stance phase. The flight phase is the period when the foot is off the ground. The stance phase is the period when the foot is in contact with the ground, providing support and propulsion. The equation of motion was derived for both the flight phase and stance phase in the mass coordinate system $\mathit{p}={\left[\begin{array}{c}xy\end{array}\right]}^{\top }$ with the landing point as the origin given by Equation (4).

$$\left\{\begin{array}{cc}m\ddot{\mathit{p}}+m\mathit{g}=0\hfill & \mathrm{Flight}\hfill \\ m\ddot{\mathit{p}}+c{\displaystyle \frac{dl}{dt}}{\displaystyle \frac{\mathit{p}}{\left|\mathit{p}\right|}}+kl{\displaystyle \frac{\mathit{p}}{\left|\mathit{p}\right|}}+m\mathit{g}={\mathit{f}}_{\mathrm{in}}\hfill & \mathrm{Stance}\hfill \end{array}\right.$$

(4)

Here, l represents the SLIP model’s leg length. Two boundary conditions were defined: landing and takeoff. Landing occurred when the y-coordinate of the mass point was $y=L_{0}cos\theta$. The leg left the ground and entered the flight phase when the leg length reached its natural length. The simulation was initiated when the SLIP model was at its apex during the flight phase. The initial conditions, including the vertical position $y_0$, horizontal velocity $x_0$, and leg angle ${\theta }_0$ were set to values that ensured stable running of the SLIP model, as the range of stable running for this model is inherently limited. These conditions were carefully chosen based on prior experimental data to ensure the model remained within the stable operational range throughout the simulation. The total simulation time was set to 60 s to observe running dynamics over multiple cycles.

3.2.2. Motion Tactics Model Applied to the SLIP Model

A motion tactics model was introduced to the SLIP model to generate motion based on the motion strategy. This model enables dynamic optimization of running by adjusting parameters and applied forces using feedback from the current motion state. In this study, three tactics ($T_k,T_{\theta },T_f$) are empirically designed using the SLIP model parameters. Each tactic adjusts the parameters for the next step based on the feedback from the previous step’s motion state. Notably, the tactics are designed with stability, speed, and energy as the primary evaluation criterion without considering time-series motion changes.

 T_k 

Speed tactic with stiffness control

This tactic $T_k$ was designed to run at reference speed as a strategy. The stiffness was adjusted so that the running speed approached the reference speed. The deviation $e_v^{\left(i\right)}(=v_{\mathrm{ref}}-v_{\mathrm{ave}}^{\left(i\right)})$ between the reference speed $v_{\mathrm{ref}}$ and the running speed at i step $v_{\mathrm{ave}}^{\left(i\right)}$ was fed back. The stiffness at $i+1$ step, $k^{(i+1)}$, was adjusted as in Equation (5).

$$u_k:k^{(i+1)}=k^{\left(i\right)}+K_k{e}_v^{\left(i\right)}$$

(5)

 T_θ 

Stabilizing tactic by landing posture control

This tactic ensured stable running without falling or backward motion. If the landing posture deviated significantly from the desired range, the SLIP model failed to maintain stability. To counteract this, landing posture was adjusted at each step to eliminate acceleration changes. The angle between the legs of the SLIP model and the vertical direction at the landing of the i step was denoted as ${\theta }^{\left(i\right)}$.

$$u_{\theta }:{\theta }^{(i+1)}={\theta }^{\left(i\right)}+K_{\theta }(e_v^{\left(i\right)}-e_v^{(i-1)})$$

(6)

 T_f 

Energy tactic by force control

The tactic $T_f$ was designed as a strategy to maintain system energy at the reference state during running. The total mechanical energy was regulated by controlling a jumping force applied along the axial direction of the SLIP model from the point of maximum compression to takeoff. The force magnitude remained constant during each step. The applied force at $i+1$ step, $f_{\mathrm{in}}^{(i+1)}$, was updated based on the difference between the current energy $E^{\left(i\right)}$ and the reference energy $E_{\mathrm{ref}}$, as described in Equation (7). The $E^{\left(i\right)}$ was calculated as the energy at the flight phase of the i step.

$$u_{f_{in}}:f_{\mathrm{in}}^{(i+1)}=f_{\mathrm{in}}^{\left(i\right)}+K_f(E_{\mathrm{ref}}-E^{\left(i\right)})$$

(7)

3.2.3. Method of Generating Motion by Combining Tactics

As the motion strategy has not yet been explicitly modeled, in this study, weights w and a base gain $K_{\mathrm{base}}$ were assigned to each tactic as Equations (8)–(10).

$$\begin{array}{ccc}\hfill K_k& =& w_k{K}_{k\_\mathrm{base}}\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill K_{\theta }& =& w_{\theta }{K}_{\theta \_\mathrm{base}}\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill K_f& =& w_f{K}_{f\_\mathrm{base}}\hfill \end{array}$$

(10)

In this study, gain optimization was performed to explore appropriate parameters for achieving stable running motion. First, the base gain $K_{{\ast }_{\mathrm{base}}}$ was determined through an exhaustive search to minimize the time required to reach a steady state, identifying the value that stabilized the motion most rapidly. The corresponding weight was set to 1.0. Next, to examine the potential for representing individual movement, the weight $0.0\le w\le 2.0$ was varied in increments of 0.1. The stride and cadence were used as matching criteria since their balance can be freely adjusted even at a constant speed. Given that running speed is defined as the product of stride and cadence, individual differences in motion were assumed to be reflected in their ratio. Additionally, the minimum energy value $E_{\mathrm{ref}}$ was calculated based on the landing condition $L_{0}cos\theta$ and the reference speed of 2.22 m/s. Simulations were conducted every 1 Nm within a range of +300 Nm from the minimum value. Since the gain values required to achieve a stable running motion without falling were unknown, and their characteristics were uncertain, a comprehensive search was conducted to identify feasible parameter ranges.

4. Simulation of Running Motion Generation

4.1. Running Experiment

The running experiment was conducted to identify the parameters of the SLIP model and to validate the simulation result with the proposed model. Four healthy participants took part in the running experiment. Their height and weight are presented in

Table 1. Participants details(left) and SLIP parameters(right).

Participant	Height (m)	Weight (kg)	m (kg)	k (kN/m)	c (Ns/m)	${\mathit{L}}_0$ (m)
P.1	1.76	72.4	72.4	28.5	205	1.03
P.2	1.72	71.6	71.6	27.3	121	1.02
P.3	1.64	64.7	64.7	31.8	264	0.97
P.4	1.71	55.0	55.0	20.0	67	1.00

. All participants provided informed consent. Our study protocol was approved by the local institutional review board and conformed to the guidelines outlined in the Declaration of Helsinki (1983). A split-belt treadmill equipped with force plates (ITR5018-11C, Bertec, Columbus, OH, USA) was used to measure the ground reaction force at a sampling rate of 1 kHz. The running motion was captured using a commercial marker-based optical motion-capture system (Raptor-4S, Motion Analysis Co., Santa Rosa, CA, USA) operating at a frame rate of 200 Hz. The participants wore 57 markers, and their positions were determined based on an improved version of the Helen Hayes Hospital marker set. Participants ran at the speed of 2.22 m/s, and the running was measured for 2 min. The collected data were low-pass filtered using a fourth-order zero-lag Butterworth filter with a 20 Hz cutoff frequency [27]. The stance phase, during which the foot is in contact with the ground, was defined as the period when the ground reaction force equaled or exceeded 50 N. Conversely, the flight phase was defined as the period when neither foot was in contact with the ground, indicated by a ground reaction force below 50 N for both feet.

From the processed data, the parameters of the SLIP model (mass m, stiffness k, the damper’s viscosity c, and spring’s natural length $L_0$) were identified. The model’s mass was set to the participant’s body weight. The remaining parameters were identified using Equation (11) to develop a running model tailored for each participant.

$$J_{k,c,L_0}=\sum {\left\{f_{\mathrm{grf}}\left(t\right)-c{\displaystyle \frac{dl\left(t\right)}{dt}}-k\left\{L_0-l\left(t\right)\right\}\right\}}^2$$

(11)

Here, $f_{\mathrm{grf}}\left(t\right)$ represents the ground reaction force, and $l\left(t\right)$ donates the distance from the center of pressure (COP) to the COG. Each parameter was derived as an average value of the entire running.

Table 2. Simulation initial values.

Participant	${\mathit{\theta }}_0$ (deg)	${\mathit{v}}_{\mathit{x}0}$ (m/s)	${\mathit{y}}_0$ (m)
P.1	10.7	2.25	1.10
P.2	11.8	2.29	1.05
P.3	10.6	2.29	1.01
P.4	11.7	2.28	1.05

also presents the model parameters identified from the experimental data for each participant.

4.2. Simulation Results

Table 2 summarizes the initial values used in the simulation.

Table 3. Base gain.

Participant	${\mathit{K}}_{\mathit{k}\_\mathbf{base}}$	${\mathit{K}}_{\mathit{\theta }\_\mathbf{base}}$	${\mathit{K}}_{\mathit{f}\_\mathbf{base}}$	${\mathit{E}}_{\mathbf{min}}$
P.1	−1000	0.15	11	900
P.2	−1200	0.16	10	890
P.3	−2000	0.16	14	770
P.4	−600	0.15	8	660

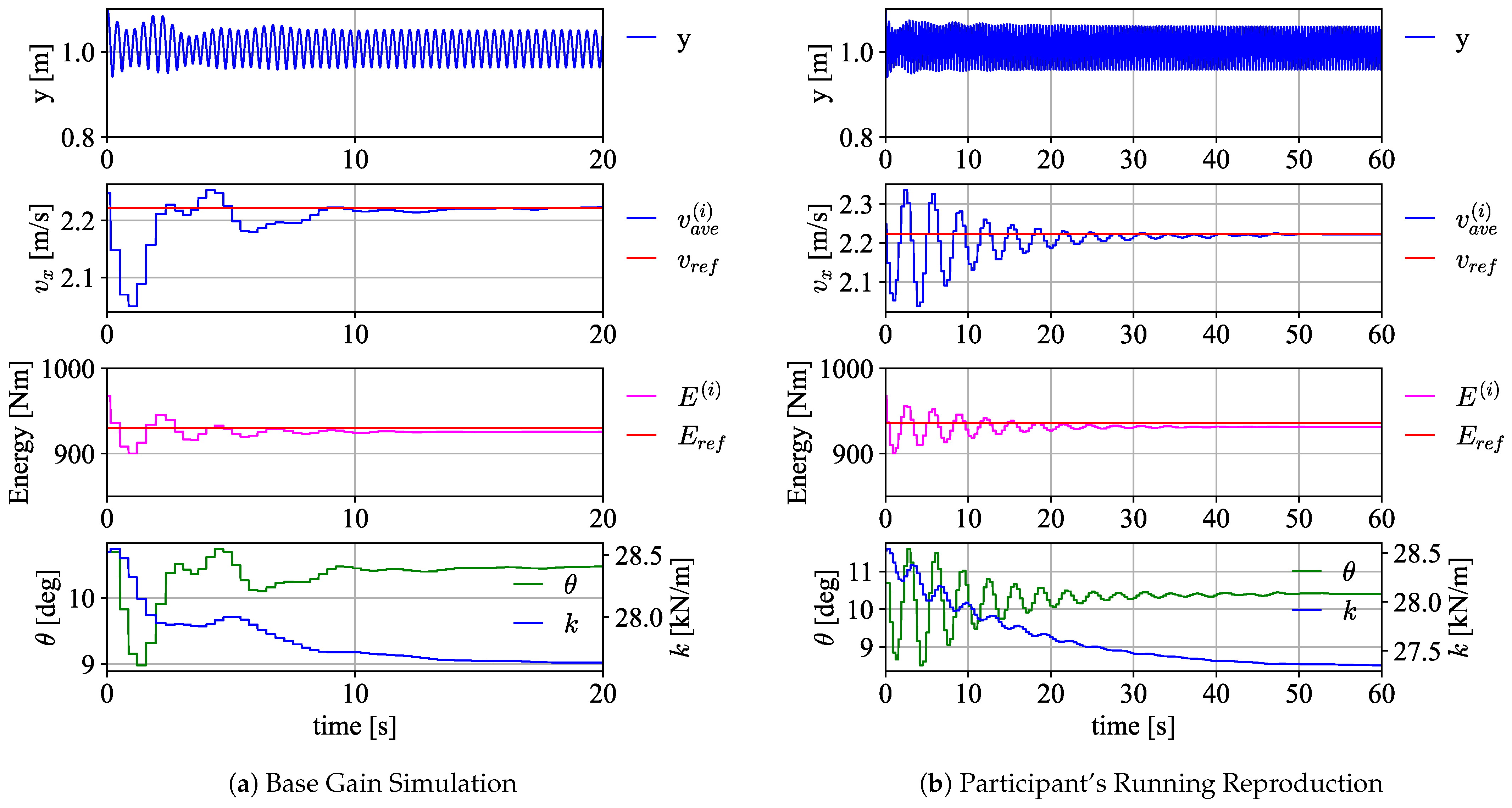
displays the value of the base gain $K_{\ast \_\mathrm{base}}$ and the minimum values of $E_{\mathrm{ref}}$ for each tactic. Figure 3a presents the results of Participant 1’s running simulation with the base gain, serving as a representative example. This simulation achieved a stable running state after approximately 10 s. Figure 3b presents the results that most closely matched Participant 1’s experimental data by adjusting the combination of tactics through varying weight assignments. 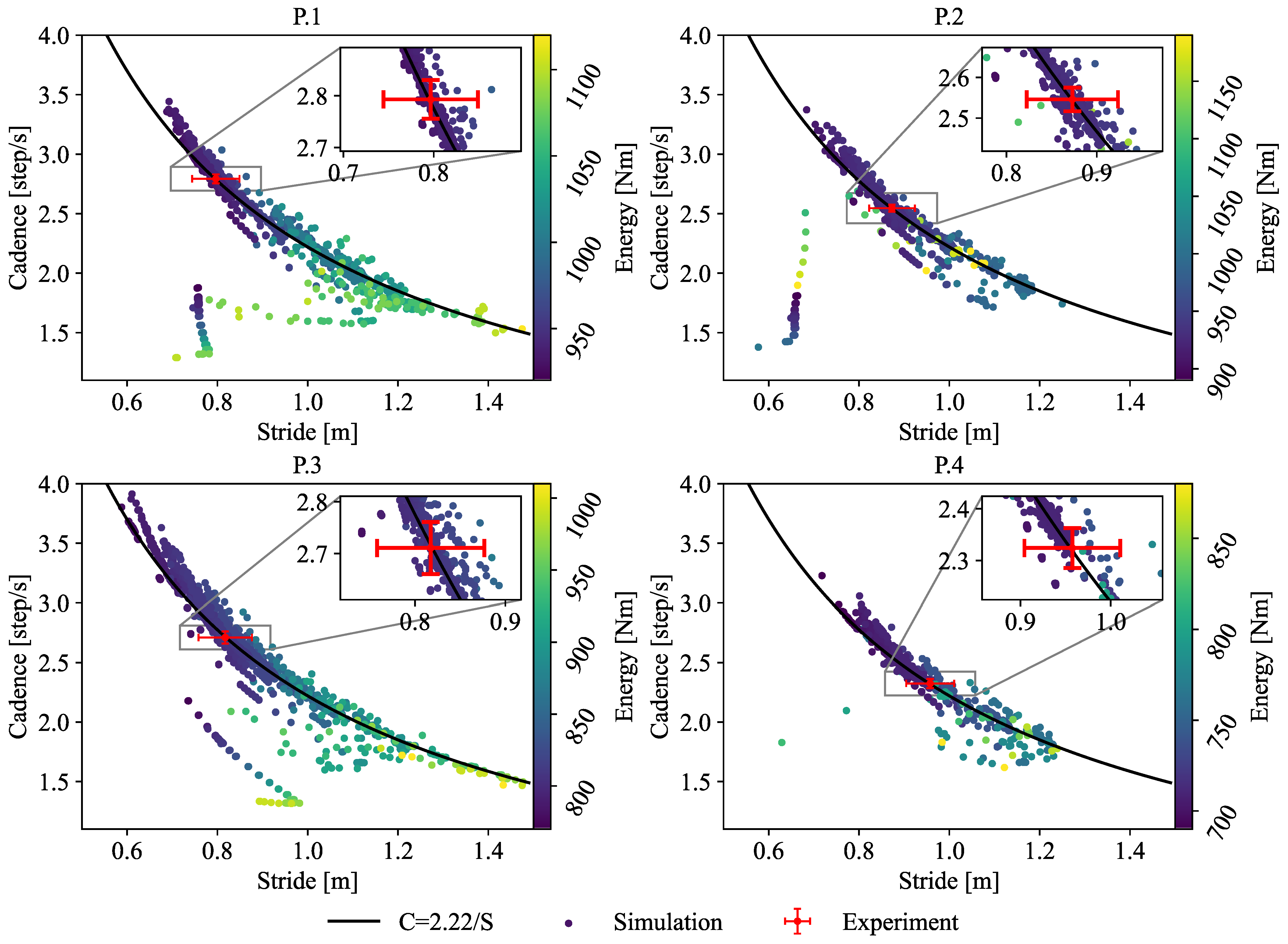Figure 4 plots all the results obtained for stride and cadence across various gain weights and applied energy levels. Stride was calculated as the distance between consecutive landing points, while cadence was determined as the inverse of the time taken for one complete cycle of running. The amplitude was calculated using the difference between the highest and lowest COG points in one step.

Table 4. Explored weights.

Participant	${\mathit{w}}_{\mathit{k}}$	${\mathit{w}}_{\mathit{\theta }}$	${\mathit{w}}_{\mathit{f}}$	${\mathit{E}}_{\mathbf{ref}}$
P.1	0.6	1.2	0.6	936
P.2	0.6	1.0	2.0	926
P.3	0.4	1.0	0.4	804
P.4	1.0	0.8	1.8	710

provides corresponding weight values w and energy $E_{\mathrm{ref}}$ applied to the model, whereas

Table 5. Comparison of Simulation and Experiment Results. The table presents the mean and standard deviation (SD) of stride length, cadence, and amplitude for simulation (Sim) and experimental (Exp) conditions. The 95% confidence interval (CI) represents the range of mean differences between the two conditions.

		Mean		SD
Participant	Metric	Sim	Exp	Sim	Exp	95% CI
P.1	Stride (m)	0.796	0.797	1.40 $\times {10}^{-4}$	2.22 $\times {10}^{-2}$	[−7.15 $\times {10}^{-3}$, 5.15 $\times {10}^{-3}$]
	Cadence (steps/s)	2.79	2.79	5.40 $\times {10}^{-4}$	2.05 $\times {10}^{-2}$	[−8.59 $\times {10}^{-3}$, 2.79 $\times {10}^{-3}$]
	Amplitude (mm)	50.1	41.4	2.85 $\times {10}^{-2}$	1.05	[8.43, 9.01]
P.2	Stride (m)	0.871	0.873	7.00 $\times {10}^{-4}$	2.31 $\times {10}^{-2}$	[−4.81 $\times {10}^{-3}$, 1.93 $\times {10}^{-3}$]
	Cadence (steps/s)	2.55	2.55	3.79 $\times {10}^{-3}$	1.47 $\times {10}^{-2}$	[ 7.42 $\times {10}^{-4}$, 6.26 $\times {10}^{-3}$]
	Amplitude (mm)	61.8	43.4	2.45 $\times {10}^{-1}$	1.26	[1.82 $\times {10}^1$, 1.87 $\times {10}^1$]
P.3	Stride (m)	0.819	0.817	8.90 $\times {10}^{-4}$	2.48 $\times {10}^{-2}$	[−1.86 $\times {10}^{-3}$, 4.88 $\times {10}^{-3}$]
	Cadence (steps/s)	2.71	2.71	3.37 $\times {10}^{-3}$	2.12 $\times {10}^{-2}$	[−4.25 $\times {10}^{-3}$, 2.25 $\times {10}^{-3}$]
	Amplitude (mm)	56.5	46.8	1.76 $\times {10}^{-1}$	1.01	[9.54, 9.86]
P.4	Stride (m)	0.954	0.958	3.70 $\times {10}^{-4}$	3.05 $\times {10}^{-2}$	[−8.05 $\times {10}^{-3}$, 1.03 $\times {10}^{-3}$]
	Cadence (steps/s)	2.33	2.32	2.00 $\times {10}^{-3}$	2.14 $\times {10}^{-2}$	[ 2.58 $\times {10}^{-3}$, 9.22 $\times {10}^{-3}$]
	Amplitude (mm)	77.9	60.2	1.69 $\times {10}^{-1}$	1.93	[1.74 $\times {10}^1$, 1.80 $\times {10}^1$]

summarizes the running parameters from both the experiment and the simulation results for comparison. We calculated the 95% confidence intervals for stride, cadence, and amplitude and conducted statistical tests to determine whether the mean values of the simulation data and experimental data were consistent. The results are summarized in Table 5.

5. Discussion

This study examines the effectiveness of the proposed simulation of motion generation by focusing on running speed, which utilizes objectives, strategies, and tactics to represent motion generation. Based on the results obtained, the expressive potential of the proposed model is evaluated and discussed.

5.1. The Capability to Represent the Individual Motion of the Proposed Method

In the motion tactics model proposed in Section 3, we explored the parameter space where the system remains stable and determined the gain $K_{base}$ that allows the system to reach steady-state running in the shortest time. Figure 3a shows that the model with base gain achieves stable running in approximately 10 s, during which the stiffness and attitude angle are dynamically optimized. Beyond optimizing for stability and convergence speed, we also examined how individual movements can be represented within the constructed solution space. By adjusting the gain weights to align stride and cadence with experimental values, we investigated whether the model could account for variations in human running patterns. As shown in Table 4, we confirmed the existence of parameter sets that can represent individual motion. Figure 3b presents the simulation results when gain weights were adjusted to reproduce the motion. Although the convergence time is slower than that of the simulation using $K_{base}$, stable running results are obtained. Table 5 further evaluates the accuracy of this personalized modeling, comparing simulated results to experimental data. Notably, for cadence in P.2 and P.4, the confidence intervals do not include zero; however, the values remain sufficiently close to zero, suggesting that the differences between simulation and experimental data are minimal.

These findings showed that adjusting the gain weights enables the model to better approximate participant-specific variations in stride and cadence. This indicates that the proposed model, which generates running by combining motion tactics, can represent the performance to be evaluated.

Although gain adjustments were performed through an exhaustive search in this study, we believe that this process can be automated using optimization frameworks, such as machine learning algorithms.

5.2. Discussion on Redundant Motion Representation

This study’s explicit objective for running was set at a reference speed of 2.22 m/s. As speed is expressed as the product of stride and cadence, the balance between these two parameters can be freely adjusted, even at a constant speed. Figure 4 plots the stride and cadence for each of the simulations, which were run for 60 s. This figure illustrates that many of the plots are distributed near the curve where cadence = 2.22/stride; only some plots deviate from this curve. The plots that deviate from the curve correspond to simulations where the gain $K_k$ is small, indicating that these simulations did not employ tactics to adjust the speed to the reference, failing to achieve the running objective. In contrast, the plots near the curve demonstrate that multiple combinations of stride and cadence can be achieved by adjusting the tactics within the proposed model. This suggests that the simulation can reproduce various motion states, offering the flexibility to freely select the balance between stride and cadence.

Therefore, the results indicate that the proposed model can generate redundant human motions, including cases where the objective is not achieved. The model’s ability to reproduce experimental data within the representable range of motion supports its validity. Furthermore, the combination of tactics was able to generate unique motions from redundant tasks, suggesting that the proposed model has the potential to capture the individual characteristics of human motions.

In this paper, we designed a motion tactics model that incorporates stability, speed, and energy as a key strategy and successfully achieved multiple stable runs at 2.22 m/s, extending beyond the stability range established in previous studies [28,29]. From Figure 4 and Table 4, it was confirmed that changes in control gain can represent individual differences in motion, even when performed under the same conditions and for the same purpose. Therefore, the proposed model can be considered viable for representing the motion characteristics necessary for motion evaluation.

5.3. Limitation and Future Works

5.3.1. Discrepancies on the Running Parameter

The tactics incorporated in this paper achieved running stability and reference speed by adjusting k and $\theta$, while force control enabled the regulation of the energy state. We adjusted the weighting parameters to reproduce motion, focusing on matching stride and cadence. As a result, discrepancies increased in another motion parameter, amplitude. These discrepancies can be attributed to errors in both the dynamical model and the control model, suggesting that certain aspects of motion cannot be fully represented by the SLIP model. For instance, while the SLIP model assumes a single spring, the human body has multiple joints. Furthermore, this study experimentally incorporates only three strategies, meaning that not all tactics used by humans are included. As a result, achieving a perfect match across all motion parameters proved challenging. In the current simulation, the swing phase maintains a constant velocity in the direction of progression, meaning that the stride can be adjusted by modifying the vertical jump. Additionally, the implemented force control applies forces only in the axial direction without adjusting their orientation. In the model, stride is increased by applying greater propulsion forces, which in turn leads to excessive vertical jumping and, consequently, errors in amplitude.

A possible future improvement is to introduce mechanisms that allow for differential energy distribution. The current force control system provides feedback on the overall energy state, where kinetic energy is modulated by stiffness control. However, potential energy is not explicitly controlled. Incorporating a strategy to regulate potential energy may improve the accuracy of motion reproduction.

5.3.2. Consideration of Tactics Interaction

In this study, we incorporated three tactical components: Stiffness Tactic $T_k$: Controls stiffness based on velocity feedback to minimize the difference between actual and target speed. Landing Posture Tactic $T_{\theta }$: Adjusts landing posture by feeding back the velocity difference between steps to minimize acceleration between strides. Force Tactic $T_f$: Regulates force control based on the energy state to achieve a target energy condition. Among these, $T_k$ and $T_{\theta }$ both utilize velocity feedback $e_v$, indicating a potential interdependency. Additionally, since $T_f$ operates based on the abstract physical quantity of energy, it may interact indirectly with the other tactics.

While each tactic’s gain could be optimized independently, in this study, we optimized them collectively to adapt stride and cadence to each individual while ensuring stable running motion. If too many tactical parameters are introduced, redundancy may compromise stability, whereas an insufficient number of tactics may fail to capture individual characteristics effectively. Based on our findings, we estimate that the proposed tactics provide a necessary and sufficient basis for adaptive individual motion generation.

Although we did not conduct an explicit analysis of the interdependence between tactics, their interactions were inherently considered in the optimization objective function. A more detailed investigation into these interactions will be addressed in future research.

5.3.3. Expandability of Tactics Model

The current tactics model relies on a short-term dynamic optimization approach, where each state is determined solely based on the previous state. As a result, optimizations that consider the long-term motion state or more refined tactics capable of controlling the system within a single step were not addressed. Additional tactics could be incorporated to enhance further the model’s expressiveness, such as time-varying tactics to account for fatigue or an energy-focused strategy to optimize the running economy.

The movements of professional runners are optimized through training, making their motion tactics distinct. By constructing a motion tactics model based on such representative motion data, it becomes possible to investigate the tactics required to maximize a given objective. Based on the findings, we can analyze how tactics change over time and identify the necessary strategies for energy optimization, enabling the rational addition of new tactics. Furthermore, in the automation of gain tuning, we propose constructing a feasible parameter space based on typical movements. By subsequently applying optimization algorithms or machine learning techniques, the tuning process can be automated effectively.

It is, however, impractical to include all aspects of human body control in the model; rather, it is essential to design the model appropriately based on the specific kinematic elements that are to be reproduced. Designing a tactics model tailored to the specific motion to be reproduced enables simulating motion generation according to the desired objectives.

5.3.4. Integration of Biomechanical Considerations

This study employed a simplified model that enables a parametric representation of essential movement characteristics. High-dimensional models require biomechanically consistent control for each joint and segment; however, their computational cost is substantial, making practical simulations challenging. The SLIP model allows for the expression of ground reaction force transmission and changes in the center-of-mass motion through stiffness parameters. Furthermore, the force control, introduced as a motion tactic, captures dynamic interactions beyond passive elements, such as the influence of upper body movement and arm swings on the center of mass. This approach enables a systematic examination of the biomechanical factors affecting running performance through abstract yet interpretable parameters. For example, in biomechanics, running economy is often evaluated based on factors such as reduced vertical oscillation and increased leg stiffness [30,31,32]. The proposed model parametrically represents these aspects while also allowing for the mathematical description of individual stiffness characteristics. Integrating a motion tactics model enables the quantification of key movement factors through comparisons with professional runners. Additionally, we acknowledge the importance of discussing the limitations and broader applications of this study. The concepts of “motion strategy” and “motion tactics” introduced here provide a structured framework for evaluating overall movement patterns while maintaining biomechanical coherence. This approach is valuable not only for research but also for practical applications in areas such as sports coaching. Clarifying the strategic aspects of movement supports systematic performance enhancement. Furthermore, a mathematical description of motor control characteristics provides a foundation for skill transmission, which has traditionally relied on empirical knowledge, fostering a more structured approach to movement optimization.

6. Conclusions

Our objective was to propose a motion tactics model that enables the use of multiple motion tactics and simulates individual differences in motion under the same conditions. The simulation results confirmed that the model could reproduce various motion states, including experimental values. Additionally, the model demonstrated the ability to select unique motion outcomes by combining tactics. Therefore, it can be concluded that the proposed model represents multiple motion states and captures individual differences.

In motion generation, humans employ various strategies and tactics, rendering full reproduction of all physical controls challenging. Rather than attempting to replicate every aspect of human motion control, future efforts should focus on designing models tailored to specific evaluation criteria to optimize and better understand movement. It is crucial to explore which types of motion can be effectively reproduced and evaluated through the design of strategies and tactics.