Abstract
The orthogonal frequency-division multiplexing (OFDM) transmission technique is well known to be efficient for data transmission but is susceptible to performance degradation due to factors such as high-order modulation schemes, multipath fading, and noise. In this paper, an approach for reconstructing images received by the OFDM transmission technique is proposed based on generative AI. The approach exploits a conditional diffusion model (CDM) that incorporates conditional factors reflecting the degree of distortion in the received images by the OFDM technique. Additionally, it employs a method to learn the variance in the reverse process during training, considering the level of distortion associated with various modulation schemes. Through this adaptability, the proposed model is experimentally demonstrated to optimize image reconstruction performance under various modulation schemes in low-SNR environments. The proposed conditional diffusion model can enhance the PSNR of OFDM-based received images by up to 8 dB in low-SNR conditions with various modulation schemes.
1. Introduction
In wireless communication systems, orthogonal frequency-division multiplexing (OFDM) plays a crucial role in enabling efficient data transmission over multipath channels [1]. OFDM is a multicarrier modulation scheme that divides a single data stream into several parallel sub-streams, each transmitted over its subcarrier. This approach utilizes bandwidth through multiple subcarriers, thereby significantly enhancing data transmission rates.
Despite the aforementioned advantages, OFDM signals can be vulnerable to channel impairments during transmission and signal degradation when high-order modulation schemes are utilized under low-signal-to-noise-ratio (SNR) conditions [2,3]. Key challenges include distortion from high-order modulation schemes, which increases the computational complexity of signal detection and recovery, as well as channel noise and multipath fading, which can severely affect the quality of the received signal [3]. As a result of these factors, degradation in signal fidelity can lead to substantial distortion of the received images, negatively affecting image quality and interpretability. In order to address these issues that degrade signal fidelity, the development of effective reconstruction techniques may be required to reconstruct the distorted image at the receiver side.
The advent of generative artificial intelligence (AI) models has led to significant innovations across various industries, particularly in natural language processing (NLP) [4], computer vision [5], and data synthesis [6]. These advancements have transformed the way that data are generated, processed, and utilized, paving the way for more efficient and sophisticated applications [7]. Generative AI models focus on creating new data instances that resemble the training data, often from unstructured or partially structured inputs. They enable a more comprehensive exploration of data distribution, ultimately enabling the generation of high-fidelity data samples [6,7].
The existing generative AI models employ various methods to generate data, with two prominent methods being generative adversarial networks (GANs) [8] and variational autoencoders (VAEs) [9]. A GAN consists of two neural networks, namely, a generator and a discriminator. The generator aims to create data that closely resemble real data, while the discriminator tries to distinguish between actual and generated data. Through this competitive framework, GANs can produce highly realistic images. However, training GANs can be unstable and may suffer from issues like mode collapse, where the generator fails to produce diverse outputs [10,11]. In contrast, VAEs operate by learning a latent space to generate new data. They compress the input data into latent variables and then reconstruct them to create new samples. While VAEs can effectively capture complex distributions, the quality of the generated data can be limited, sometimes lacking fine detail [12].
Recently, an alternative approach known as the diffusion model, introduced by Ho et al. [13], has garnered significant attention. Unlike GANs and VAEs, the diffusion model operates through a systematic process of progressively adding noise to the data. During the training phase, this noise addition process is learned in reverse to reconstruct the original data. One of the primary strengths of the diffusion model is its enhanced robustness in generating high-dimensional data, effectively mitigating the common mode collapse issue faced by GANs. Moreover, it is known to generate more realistic and higher quality samples than VAEs.
The processes and characteristics of diffusion models can be particularly advantageous in applications such as data reconstruction in communication systems, where maintaining a high-quality data representation is crucial. Thanks to their strengths in restoring data, there have been various studies on applying diffusion models to improve signal fidelity and data recovery processes in wireless communications [14,15,16,17]. In [14], it was demonstrated that a generative diffusion model can rapidly synthesize reliable wireless channel samples from limited data. The channel noise reduction diffusion model (CDDM) [15] has been used to effectively remove channel noise and improve the clarity and fidelity of the transmitted signal. The authors of [16] utilized a diffusion model for end-to-end channel coding. This model was integrated into the channel coding process to enhance data transmission and signal fidelity, thereby improving the robustness of communication systems against noise.
In this paper, a conditional diffusion model (CDM) is proposed for the reconstruction of OFDM-based images by leveraging the ability of diffusion models to denoise and restore images. To mitigate the complexity of OFDM-based image reconstruction, the proposed CDM incorporates a conditional factor that reflects the degree of distortion in the received signal. In contrast to existing methods in which a fixed variance (FV) is used to simplify the loss function during learning, the proposed model utilizes a learnable variance (LV). Through this process, an optimal variance can be selected based on the modulation scheme of OFDM signals, even under low-SNR conditions. The main contributions of this paper can be summarized as follows:
- A CDM that addresses distorted OFDM-based images in wireless communication is introduced. While the existing diffusion models have only considered Gaussian noise in the diffusion process, the proposed model is designed to handle the image distortion that occurs in OFDM-based wireless communication. This adaptation allows the model to effectively account for varying levels of signal degradation, leading to improved reconstruction performance.
- The proposed CDM dynamically learns the variance during the training process, in contrast to diffusion models that learn through a fixed variance. This flexibility enables the model to optimally adjust to different modulation schemes and diverse SNR conditions, enhancing the overall training effectiveness and the rapidity of image reconstruction.
- A performance analysis is conducted on the proposed CDM under diverse modulation schemes and SNR conditions. From the simulation results, it is confirmed that the proposed CDM with learnable variance (CDM-LV) is effective in reconstructing OFDM-based images from received signals in highly deteriorated environments.
The remainder of this paper is organized as follows. Section 2 provides an overview of the OFDM technique and diffusion model. Section 3 details the proposed CDM, focusing on the integration of diffusion models in the context of OFDM-based image reconstruction. Section 4 presents the findings of the experiments conducted to evaluate the proposed approach. Finally, Section 5 summarizes the main findings and outlines potential directions for future research.
2. Problem Formulation
In wireless communication systems, the efficient transmission of high-quality images is one of the key applications. By utilizing subcarriers, OFDM is adopted to optimize the bandwidth and increase the data transmission rates. However, as the modulation order increases, it becomes more susceptible to inter-symbol interference and channel distortion, which can result in high error rates under challenging channel conditions. The proposed CDM is applied to reduce the error rate at high modulation orders, and its block diagram for OFDM-based image reconstruction is presented in Figure 1. Through the application of the proposed CDM, the distortion in the received image can be mitigated, producing high-quality image samples. This section provides an overview of the OFDM system and discusses the diffusion model.
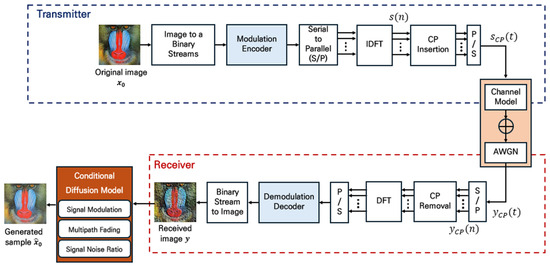
Figure 1.
Scheme for OFDM-based image reconstruction in wireless communication utilizing the CDM.
2.1. OFDM-Based Communication Systems
The proposed system for OFDM-based image reconstruction is designed to operate within the conventional OFDM communication framework, where image data are transmitted as symbols modulated over multiple orthogonal subcarriers. This subsection provides an overview of the OFDM-based transmission process and the distortion of the received signal.
2.1.1. OFDM Systems for Image Transmission and Signal Processing
In the OFDM system for image transmission, initially, the pixel values of the image data are converted into a binary sequence, and then the binary stream is mapped into a complex-valued in-phase and quadrature (IQ) constellation plan according to modulation schemes such as -PSK ( and -QAM (. The frequency domain OFDM symbol is transformed into the time domain OFDM symbol s using an -point inverse discrete Fourier transform (IDFT) through parallel-to-serial (P/S) transmission. The IDFT equation is as follows:
where is an imaginary unit, and is the discrete Fourier transform (DFT) length. The addition of a cyclic prefix (CP) is crucial, as it helps maintain the orthogonality of the subcarriers by preventing interference between them during transmission. The length of the CP is chosen to be larger than the expected delay spread. The OFDM symbol with a CP length of is represented as follows:
The signal is transmitted to the receiver through a wireless channel. During transmission, the signal is affected by multipath fading, which results in the distortion of the received signal. The multipath channel in the wireless channel is represented as , and the received signal at the receiver is expressed as follows:
where , ,, , and represent the number of multipath components, the attenuation coefficient, the time delay, the convolution operator, and additive white Gaussian noise (AWGN), respectively. At the receiver end, the received signal is processed through CP removal, DFT, parallel-to-serial conversion, and demodulation to obtain the received image .
2.1.2. Distortion of the Received Signal
Despite the inherent advantages of OFDM, the received signal can be vulnerable to various forms of signal degradation caused by the channel conditions. Signal distortions resulting from additive noise, multipath fading, higher-order modulation schemes, etc., can significantly compromise transmission integrity [3]. High-order modulation schemes require higher levels of received signal-to-noise and interference ratio (SNIR) to correctly demodulate the transmission signals due to their sensitivity to noise, non-linearities, distortion, and interference. If not adequately addressed, these factors can lead to significant performance degradation, especially in OFDM-based image communication systems.
Common sources of distortion include environmental factors such as changes in the physical landscape, the presence of obstacles that obstruct the signal paths, and variations in the channel conditions over time. Multipath propagation, where signals arrive at the receiver through multiple paths with different delays, can cause inter-symbol interference (ISI), further complicating the recovery of the transmitted data. As a result, effective strategies to mitigate these distortions are crucial for maintaining the integrity and reliability of OFDM signals.
A comparative analysis of processed images across various modulation schemes and SNR levels for the CIFAR-10 image dataset is presented in Figure 2. The rows correspond to different modulation schemes, i.e., -PSK and -QAM. The columns display the original image alongside images with distorted received signals at SNR levels of 0 dB, 5 dB, 10 dB, and 15 dB. Notably, it was determined that in the same SNR condition, the distortion of the images increases as the complexity of the modulation scheme increases. Higher-order modulation techniques, such as 32QAM and 64QAM, respond more sensitively to noise, leading to a more pronounced degradation in image quality compared to lower modulations such as BPSK and QPSK. These results indicate the trade-off between modulation complexity and the ensuing distortion.

Figure 2.
Comparison of received signal under the modulation schemes -PSK and -QAM at different SNR levels (0 dB to 15 dB) for CIFAR-10 images.
2.1.3. Diffusion Model for Image Reconstruction in OFDM
As illustrated in Figure 3, generative AI models have attracted considerable attention in the field of communication owing to their capacity to model nonlinear functions and adapt to challenging channel conditions [18,19]. The increased demand for high-dimensional data transmission necessitates the implementation of high-order modulation schemes. Nevertheless, in the context of image transmission utilizing OFDM, the presence of noise and channel impairments degrades the fidelity of the transmitted images. As the modulation order increases, distortions become more apparent, thereby impairing the quality of the transmitted images.
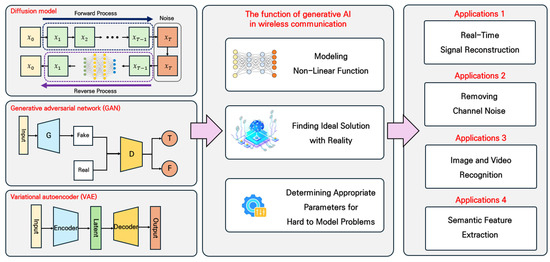
Figure 3.
Overview of wireless communication based on generative AI.
Generative models, including GANs and VAEs, were employed for image restoration. Nevertheless, these models often face difficulties when dealing with the complex distortions introduced by wireless channels. In order to tackle these issues, the CDM has emerged as a viable option for reconstructing distorted images in OFDM-based image communication. In the context of the CDM, the distortions resulting from multipath fading and interference within OFDM channels are addressed as a forward process. The diffusion model is designed to learn the reverse process by systematically eliminating noise [13].
During CDM training [13], noise is steadily inserted into the data until the signal itself is entirely distorted. Then, the model is trained to systematically eliminate the noise, thereby reconstructing a signal that closely approximates the original data. In contrast to VAEs, which operate under the assumption of solely Gaussian noise, CDMs adeptly manage intricate distortions, including multipath fading. Furthermore, by calibrating the model based on parameters such as SNR and modulation order, CDMs can more reliably adjust to diverse channel distortions, leading to enhanced image reconstruction.
2.2. Diffusion Probabilistic Model
The diffusion model comprises a diffusion process that perturbs the data with noise and a reverse process that transforms the noisy data generated by the diffusion process back into the original data. This framework is modeled by the Markov chain. The former is typically designed to transform the data distribution into a standard Gaussian, while the latter learns a transition kernel parameterized by a deep neural network to invert the former process. Given the distribution of ground-truth data , the diffusion process generates a sequence of random variables with a transition kernel . By utilizing the chain rule of probabilities along with the Markov property, the joint distribution of conditioned on can be represented as , which can be expressed as follows:
In diffusion models, the transition kernel is explicitly designed to gradually transform the data distribution into a tractable prior distribution. The typical design of the transition kernel involves Gaussian perturbation, which is given below:
where is a variance schedule that controls the step size of the diffusion process. Due to the diffusion process, the data sample gradually loses its characteristics as increases, and ultimately, as goes to infinity, converges to an isotropic Gaussian distribution.
As mentioned in [13], by iteratively applying the reparameterization trick, it is possible to sample any step of noise conditioned directly on the input through the diffusion process defined in Equation (6), which is defined as follows:
where , and According to Equation (7), given , the sample can be easily obtained by sampling a Gaussian vector :
In order to generate true samples from Gaussian noise , the diffusion model first generates an unstructured noise vector from a prior distribution that is generally challenging to handle and then executes a learned reverse process to gradually remove the noise. Specifically, the reverse process is parameterized by the prior distribution and a learnable transition kernel . This learnable transition kernel takes the following form:
where represents the model parameter, the mean being parameterized by a deep neural network such as U-Net, is the variance of the reverse process, and denotes the estimated Gaussian noise in . This reverse process allows us to generate the data sample by first sampling the noise vector . Subsequently, the learnable transition kernel is repeatedly sampled until to generate the data sample .
The loss function for neural network training is derived through the variational lower bound of and as follows [20]:
where and are computed in closed form, while is learned to minize the diffenrence between the means ( of and of . According to [13], is simplified as follows:
3. Conditional Diffusion Model for OFDM-Based Image Reconstruction
In this section, the proposed CDM for the reconstruction of distorted images in OFDM-based wireless communications is introduced. As the modulation schemes increase in complexity, the received signals become more sensitive to channel conditions and noise. The proposed CDM was designed to integrate factors that contribute to the distortion of the received signals, based on the ideas presented with regard to the conditional diffusion model [21]. These factors include the modulation schemes, the SNR conditions, and multipath fading. Furthermore, both the diffusion process and the reverse process were designed to find the optimal variance for each transmission environment. OFDM-based image reconstruction using the proposed CDM is depicted in Figure 4. The CDM utilizes an interpolation parameter, , to design a diffusion process to learn the distortions that occur in wireless communications.
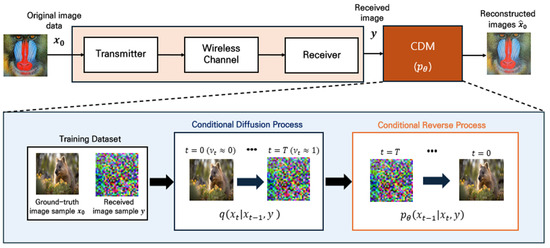
Figure 4.
Conditional diffusion and reverse processes for OFDM-based image reconstruction.
The CDM is trained using pairs of and from a training dataset. This training step enables the CDM to learn the relationship between the original and the distorted images. After training, the CDM is used for reconstruction. A distorted image , which could be any arbitrarily distorted image received through OFDM transmission, is input into the trained CDM.
3.1. Conditional Diffusion and Reverse Processes
In order to reconstruct OFDM-based images, the proposed CDM modifies the mean of the Gaussian noise addition step from the existing diffusion process defined in Equation (7) by introducing the interpolation parameter . It was assumed that starts with 0 at and increases by gradual steps to reach at , so that the average of changes from the original image data to the distorted OFDM-based image , as shown in Figure 4. This parameter integrates both the original image data and the distorted received signal into the conditional diffusion process as follows:
where denotes the variance of the conditional diffusion process, which is set in such a manner as to generalize the variance of the conventional diffusion process as follows:
The probability distribution of can be derived from the relationship between and , after defining and based on Equation (17) as follows:
In the reverse process of the CDM, the conditional denoising process is carried out based on the distorted images resulting from the conditional diffusion process. Based on Equations (17) and (19), can be derived through Bayes’ theorem and the Markov chain property as follows [21]:
In order to predict from and in the conditional reverse process, it is necessary to employ a probability distribution such as , which can be defined as:
where represents the mean of the probability distribution used to predict during the reverse process, and denotes the estimated noise vector at time step t, conditioned on the current noisy data and the distorted image . The coefficients , , and of can be derived by combining Equations (17) and (21) as follows:
3.2. Learnable Variance in the Conditional Diffusion Model
According to the authors of [13], when designing the loss function in diffusion models, it is preferable to fix as or to derive , rather than treating it as a learnable variance (LV), as this approach demonstrates better sampling performance. However, the sampling performance seems to be affected by depending on the adjustment of when the diffusion time step is small [22].
In wireless communications, it is important to accurately reconstruct distorted signals, but fast data processing is also critical. Therefore, the proposed CDM with LV (CDM-LV) optimizes the selection of variance based on the modulation scheme and SNR conditions, while also adjusting through learning to achieve high-quality sampling with small diffusion time steps. In the proposed CDM, the learnable was considered in the design of the loss function , which is given by the following equations:
where denotes the weight of . A summary of the training and sampling processes is presented in Algorithm 1 and Algorithm 2, respectively.
| Algorithm 1: Training algorithm in CDM-LV | ||
| 1 | for do | |
| 2 | Sample ( | |
| 3 | ||
| 4 | ||
| 5 | Compute | |
| 6 | Compute | |
| 7 | end for | |
| Algorithm 2: Sampling algorithm in the CDM-LV | ||
| 1 | Sample | |
| 2 | for do | |
| 3 | Compute , , using Equations (25)–(27) | |
| 4 | Sample | |
| 5 | end for | |
| 6 | return | |
3.3. Performance Metrics
In this paper, a peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) were used to evaluate the performance of the OFDM-based image reconstruction. The PSNR is a widely used metric for quantifying the quality of reconstructed images compared to their original versions. It measures the ratio between the maximum possible power of a signal and the power of corrupting noise that affects its representation. The PSNR is expressed in dB and can be calculated using the following formula:
where is the maximum possible pixel value, and is the mean squared error between the original and the reconstructed images. A higher PSNR value indicates a better quality of reconstruction. The SSIM is a more sophisticated metric that assesses the visual quality of images based on structural information. Unlike the PSNR, the SSIM considers changes in texture, contrast, and structural patterns. The SSIM index ranges from 0 to 1, where 1 indicates perfect structural similarity. It is defined as:
where , , and denote the average pixel value, the variance, and the covariance, respectively. The constants and are small values added to stabilize the division.
4. Simulation Results
4.1. Simulation Setup
To simulate the modulation of image data into OFDM signals, MATLAB R2024b was employed. In the simulation, various modulation schemes of OFDM communication, including -PSK ( and -QAM (, were utilized to validate the proposed CDM. The simulations were conducted in an SNR range from 0 dB to 15 dB. A detailed configuration of the dataset is presented in Table 1.

Table 1.
Experimental setup for generating an OFDM-based received dataset.
In the training of the CDM, a U-Net with an input size of was utilized for the learning process of the reverse process. The hyperparameter of the variance schedule was set from to 0.035. The interpolation parameter was set to . The training was conducted with 50 diffusion steps, a learning rate of , and a dropout rate of 0.1. In Equation (28), the weight for in the learning of was set to to prevent from overshadowing . A summary of the simulation parameters is shown in Table 2. The simulation was run on a desktop with AMD PRO 5975WX, with memory of 32 GB DDR4, and NVIDIA GeForce RTX 4090 GPU.

Table 2.
Hyperparameters with model architecture for training the proposed CDM-LV.
4.2. Performance Evaluation
As presented in Figure 5, the performance of the proposed conditional diffusion model for OFDM-based image reconstruction was demonstrated across a range of modulation schemes.
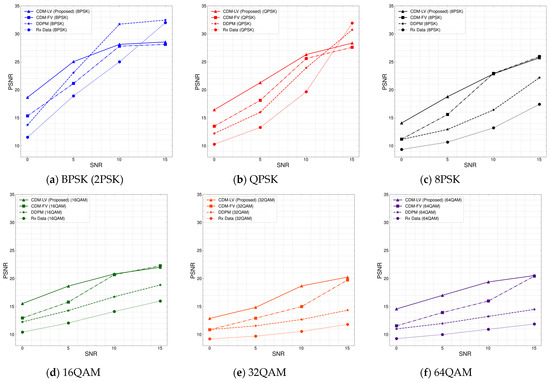
Figure 5.
PSNR performance of the conditional diffusion model across different modulation schemes. CDM-LV: conditional diffusion model with learnable variance, CDM-FV: conditional diffusion with fixed variance, DDPM: denoising diffusion probabilistic model, Rx Data: distorted image data at the receiver.
In Figure 5a–c, the PSNR for the -PSK schemes is presented for the varying SNR conditions. In low-SNR conditions, specifically ranging from 0 dB to 5 dB, the poor quality of the received images led to lower PSNR values. In this low-SNR condition, it was observed that the CDM model improved the PSNR with all -PSK schemes, demonstrating its effectiveness in reconstructing the quality of distorted OFDM-based images through increasing the PSNR by up to 5 dB at an SNR of 0 dB and to 8 dB at an SNR of 5 dB. However, in relatively higher SNR conditions of more than 15 dB, the received images in the BPSK and QPSK scenarios exhibited higher PSNR values compared to the images reconstructed by the proposed CDM. This observation can be due to the fact that the images received with BPSK and QPSK at SNR 15 dB were almost distortion-free, and the denoising process of the CDM unintentionally degraded the image quality of the received distortion-free images. Furthermore, it was observed that the conventional diffusion model resulted in lower PSNR values than the CDM under low-SNR conditions in BPSK and QPSK, and in higher PSNR values than the CDM under high-SNR conditions. This confirmed that the conditional diffusion model, which reflects the distorted signal, is effective in recovering distorted data in low-SNR environments where signal modulation is highly distorted. On the other hand, under high-SNR conditions, the conventional diffusion model performs better because it is less distorted by modulation. For learnable and fixed variances in the conditional diffusion model, it can be noted that the CDM-LV resulted in an improvement of approximately 3 dB to 4 dB in the PSNR. This result highlights the effectiveness of learnable variance in the context of OFDM-based image reconstruction.
In Figure 5d–f, the PSNR for the -QAM schemes is presented for a varying SNR. The proposed diffusion model demonstrated consistent improvements in PSNR performance through the overall SNR range, indicating its effectiveness in reconstructing the distorted OFDM-based image under -QAM schemes. Furthermore, it was observed that the CDM-LV approach improved the PSNR by around 4 dB at an SNR of 0 dB and 5 dB compared to the CDM-FV approach.
In Figure 6, the results of the SSIM are presented for a varying SNR. It was observed that the CDM particularly enhanced the SSIM in the received data, especially in low-SNR conditions. It can also be noted that the case with the CDM-LV approach achieved an improvement higher than 0.1 at an SNR of 0 dB and 5 dB compared to that with the CDM-FV approach. This improvement implies that the proposed model can effectively preserve the structural quality of images affected by distortion, resulting in a closer alignment with the original data under low-SNR conditions.
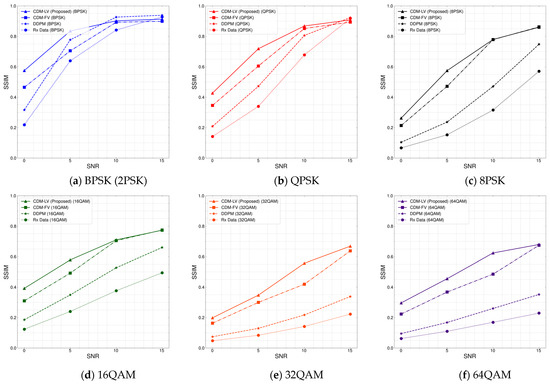
Figure 6.
SSIM performance of the conditional diffusion model across different modulation schemes. CDM-LV: conditional diffusion model with learnable variance, CDM-FV: conditional diffusion with fixed variance, DDPM: denoising diffusion probabilistic model, Rx Data: distorted image data at the receiver.
In Figure 7, the variances corresponding to the time steps are presented for the conventional diffusion process (), reverse process (.), and LV (). In the CDM for OFDM-based image restoration, the initial phase of the diffusion process adheres to a fixed variance of . However, with an increasing number of diffusion steps, the LV tends to adopt . It was confirmed that a flexible variance achieved through LV can give robustness to OFDM-based image reconstruction compared to a fixed variance.
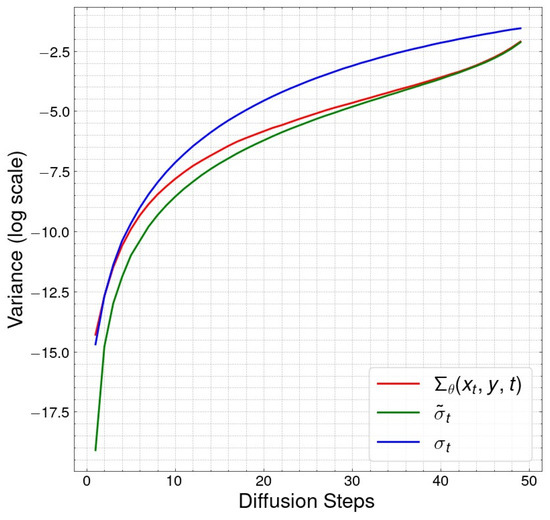
Figure 7.
Change in learnable variance with respect to the number of diffusion time steps. LV (): learnable variance, : variance of the conditional reverse process, : variance of the conventional diffusion process.
Furthermore, the proposed CDM model demonstrated a processing speed of 50 images reconstructed per second, regardless of the modulation schemes, when using the CIFAR-10 dataset. This reconstructed rate indicates the model’s practical applicability in real-time scenarios with present-day computational capability, making it suitable for dynamic environments where timely image restoration is essential.
In Figure 8, the visual representations of the reconstructed images are illustrated over different modulation schemes. In the case of an SNR of 0 dB across all modulation schemes, significant distortion was confirmed. It can be visually confirmed that the images were greatly reconstructed through the proposed CDM compared to the received OFDM-based images. Overall, these results demonstrate that CDM is highly effective in ensuring image fidelity, particularly in environments characterized by varying levels of distortion.

Figure 8.
Comparison of reconstructed images for various modulation schemes under different SNR levels (0 dB to 15 dB). Each subfigure corresponds to a specific modulation scheme: (a) BPSK, (b) QPSK, (c) 8PSK, (d) 16QAM, (e) 32QAM, and (f) 64QAM. The first row of images represents the original images , the second row depicts the received images at the receiver, and the third row illustrates the reconstructed images resulting from the proposed scheme.
5. Conclusions
In this paper, a CDM was designed to improve OFDM-based image reconstruction in wireless communication systems. The proposed scheme addressed the limitations of traditional OFDM-based image reconstruction by leveraging the robustness of diffusion models and incorporating conditional factors that adapt to varying levels of OFDM-based image distortion. A variance learning mechanism can further enhance the reconstruction performance across various modulation schemes, with the simulation results demonstrating significant improvements, particularly in low-SNR scenarios.
The efficiency of the proposed CDM is expected to be particularly useful under the low-SNR conditions of LEO satellite communications, suggesting that it can be widely applied to autonomous systems for estimating communication parameters and reconstructing distorted images. However, challenges remain in addressing real-world LEO complexities such as the variable Doppler shift, atmospheric interference, and dynamic link conditions. Future research will focus on mitigating these issues and further optimizing the CDM for different communication scenarios.
Author Contributions
Conceptualization, S.K., J.K. (Jinwook Kim), and Y.S.; methodology, S.K., and J.K. (Jinwook Kim); simulation, S.K. and J.K. (Jinwook Kim); formal analysis, S.K., S.L., and J.S.; resources, S.K., B.H., and Y.S.; writing—original draft preparation, S.K., J.K. (Jinwook Kim), J.K. (Jeongho Kim); writing—review and editing, J.S., K.K., and Y.S.; visualization, S.K., J.K. (Jinwook Kim) and S.L.; supervision, Y.S. and J.K. (Jinyoung Kim); project administration, S.K. and Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in [CIFAR-10] at https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 12 December 2024).
Acknowledgments
This work was partly supported by an Institute of Information and Communications Technology Planning and Evaluation (IITP) grant funded by the Ministry of Science and ICT (MSIT) (No. 2021-0-00892-005, “Research on Advanced Physical-Layer Technologies of Low-Earth Orbit (LEO) Satellite Communication Systems for Ubiquitous Intelligence in Space”) and supported by the MSIT, Korea, under the ITRC (Information Technology Research Center) support program (IITP-2025-RS-2023-00258639) supervised by the IITP.
Conflicts of Interest
Author Youngghyu Sun was employed by the company SMARTEVER, Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial of financial relationships that could be construed as a potential conflict of interest.
References
- Li, Y.; Cimini, L.J.; Sollenberger, N.R. Robust channel estimation for OFDM systems with rapid dispersive fading channels. IEEE Trans. Commun. 1998, 46, 902–915. [Google Scholar] [CrossRef]
- Wulich, D. Definition of efficient PAPR in OFDM. IEEE Commun. Lett. 2005, 9, 832–834. [Google Scholar] [CrossRef]
- Otsuka, H.; Tian, R.; Senda, K. Transmission performance of an OFDM-based higher-order modulation scheme in multipath fading channels. J. Sens. Actuator Netw. 2019, 8, 19. [Google Scholar] [CrossRef]
- Hagos, D.H.; Battle, R.; Rawat, D.B. Recent advances in generative AI and large language models: Current status, challenges, and perspectives. IEEE Trans. Artif. Intell. 2024, 5, 5873–5893. [Google Scholar] [CrossRef]
- Simion, A.-M.; Radu, Ș.; Florea, A.M. A review of generative adversarial networks for computer vision tasks. Electronics 2024, 13, 713. [Google Scholar] [CrossRef]
- Goyal, M.; Mahmoud, Q.H. A systematic review of synthetic data generation techniques using generative AI. Electronics 2024, 13, 3509. [Google Scholar] [CrossRef]
- Bengesi, S.; El-Sayed, H.; Sarker, M.K.; Houkpati, Y.; Irungu, J.; Oladunni, T. Advancements in generative AI: A comprehensive review of GANs, GPT, autoencoders, diffusion model, and transformers. IEEE Access 2024, 12, 69812–69837. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Kingma, D.P.; Welling, M. An introduction to variational autoencoders. FNT Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Kossale, Y.; Airaj, M.; Darouichi, A. Mode collapse in generative adversarial networks: An overview. In Proceedings of the 2022 8th International Conference on Optimization and Applications (ICOA), Genoa, Italy, 6–7 October 2022; pp. 1–6. [Google Scholar]
- Thanh-Tung, H.; Tran, T. Catastrophic forgetting and mode collapse in GANs. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–10. [Google Scholar]
- Daunhawer, I.; Sutter, T.M.; Chin-Cheong, K.; Palumbo, E.; Vogt, J.E. On the limitations of multimodal VAEs 2022. arXiv 2022, arXiv:2110.04121. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Proceedings of the Advances in Neural Information Processing Systems 33 (NeurIPS 2020), Virtual, 6–12 December 2020; Volume 33, pp. 6840–6851. [Google Scholar]
- Sengupta, U.; Jao, C.; Bernacchia, A.; Vakili, S.; Shiu, D. Generative diffusion models for radio wireless channel modelling and sampling. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 February 2023; pp. 4779–4784. [Google Scholar]
- Wu, T.; Chen, Z.; He, D.; Qian, L.; Xu, Y.; Tao, M.; Zhang, W. CDDM: Channel denoising diffusion models for wireless semantic communications. IEEE Trans. Wirel. Commum. 2024, 23, 11168–11183. [Google Scholar] [CrossRef]
- Kim, M.; Fritschek, R.; Schaefer, R.F. Learning end-to-end channel coding with diffusion models. In Proceedings of the WSA & SCC 2023; 26th International ITG Workshop on Smart Antennas and 13th Conference on Systems, Communications, and Coding, Braunschweig, Germany, 27 February 2023; pp. 1–6. [Google Scholar]
- Letafati, M.; Ali, S.; Latva-Aho, M. Conditional denoising diffusion probabilistic models for data reconstruction enhancement in wireless communications. IEEE Trans. Mach. Learn. Commun. Netw. 2025, 3, 133–146. [Google Scholar] [CrossRef]
- Merluzzi, M.; Borsos, T.; Rajatheva, N.; Benczúr, A.A.; Farhadi, H.; Yassine, T.; Müeck, M.D.; Barmpounakis, S.; Strinati, E.C.; Dampahalage, D.; et al. The hexa-X project vision on artificial intelligence and machine learning-driven communication and computation co-design for 6G. IEEE Access 2023, 11, 65620–65648. [Google Scholar] [CrossRef]
- Van Huynh, N.; Wang, J.; Du, H.; Hoang, D.T.; Niyato, D.; Nguyen, D.N.; Kim, D.I.; Letaief, K.B. Generative AI for physical layer communications: A survey. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 706–728. [Google Scholar] [CrossRef]
- Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In Proceedings of the 32nd International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 2256–2265. [Google Scholar]
- Lu, Y.-J.; Wang, Z.-Q.; Watanabe, S.; Richard, A.; Yu, C.; Tsao, Y. Conditional diffusion probabilistic model for speech enhancement. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 7402–7406. [Google Scholar]
- Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. In Proceedings of the 38th International Conference on Machine Learning (ICML), Virtual, 18–24 July 2021; pp. 8162–8171. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).