Spatiotemporal Modeling of Connected Vehicle Data: An Application to Non-Congregate Shelter Planning During Hurricane-Pandemics
Abstract
1. Introduction
- The Generalized Additive Model (GAM) based framework enables to capture complex, non-linear spatial and temporal evacuation patterns, addressing gaps in traditional static forecasting models and providing real-time insights into evacuation trends and shelter utilization hotspots for emergency planners.
- Improved Shelter Demand Prediction Accuracy: The proposed model significantly outperforms the baseline Generalized Linear Model (GLM), reducing prediction errors (RMSE) and improving correlation with observed shelter demand for both shelters and lodging facilities.
- Consideration of Non-Congregate Shelters During Hurricane-Pandemics: Unlike most existing studies that focus on congregate shelters (e.g., schools, community centers), we examine hotels and lodging facilities as alternative non-congregate shelters, crucial for mitigating pandemic-related risks.
- Impact Analysis of School Closures on Evacuation Patterns: We quantify the influence of school closures on evacuation behaviors and shelter demand, providing key insights for policymakers in adaptive disaster planning.
2. Materials and Methods
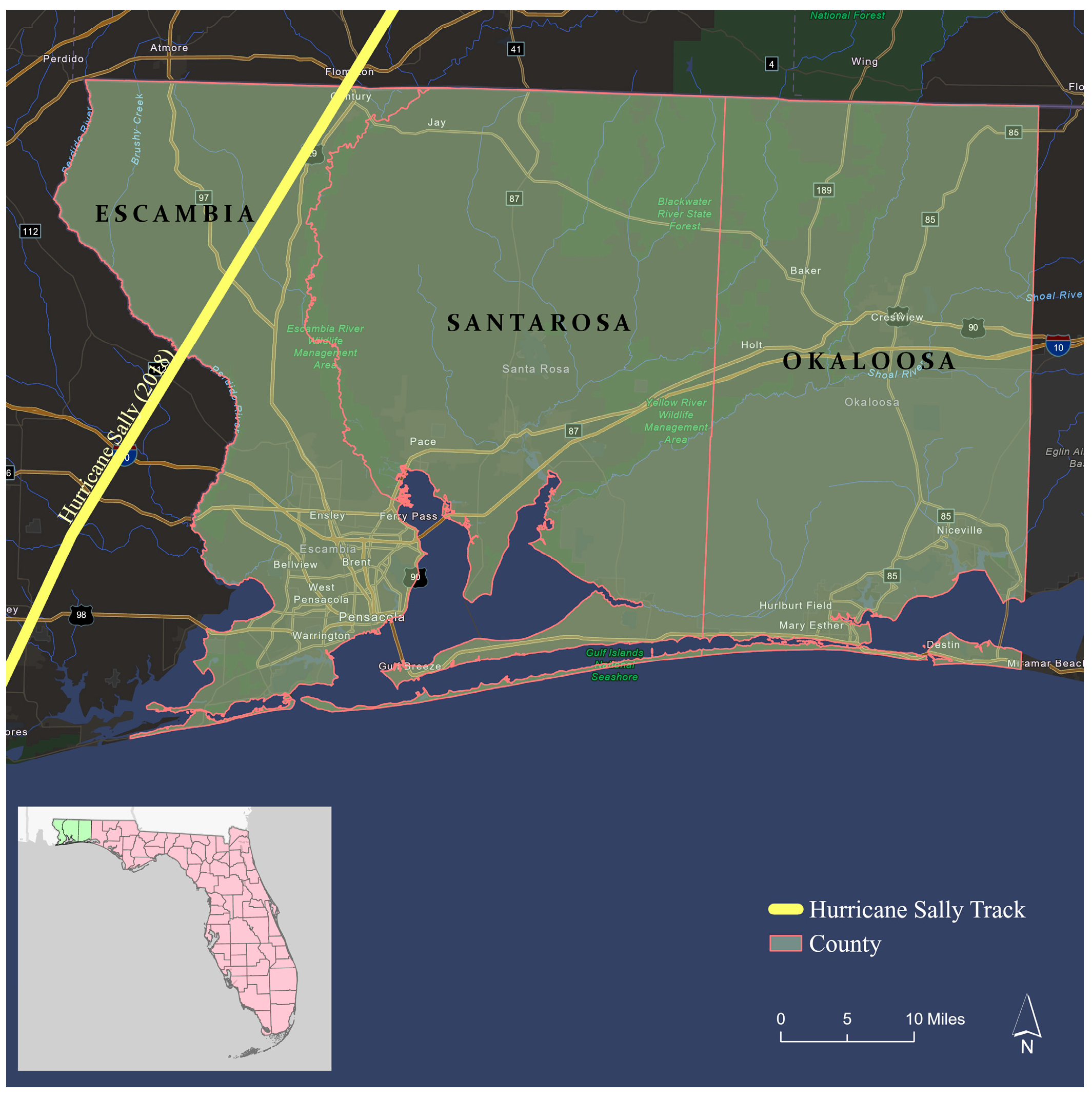
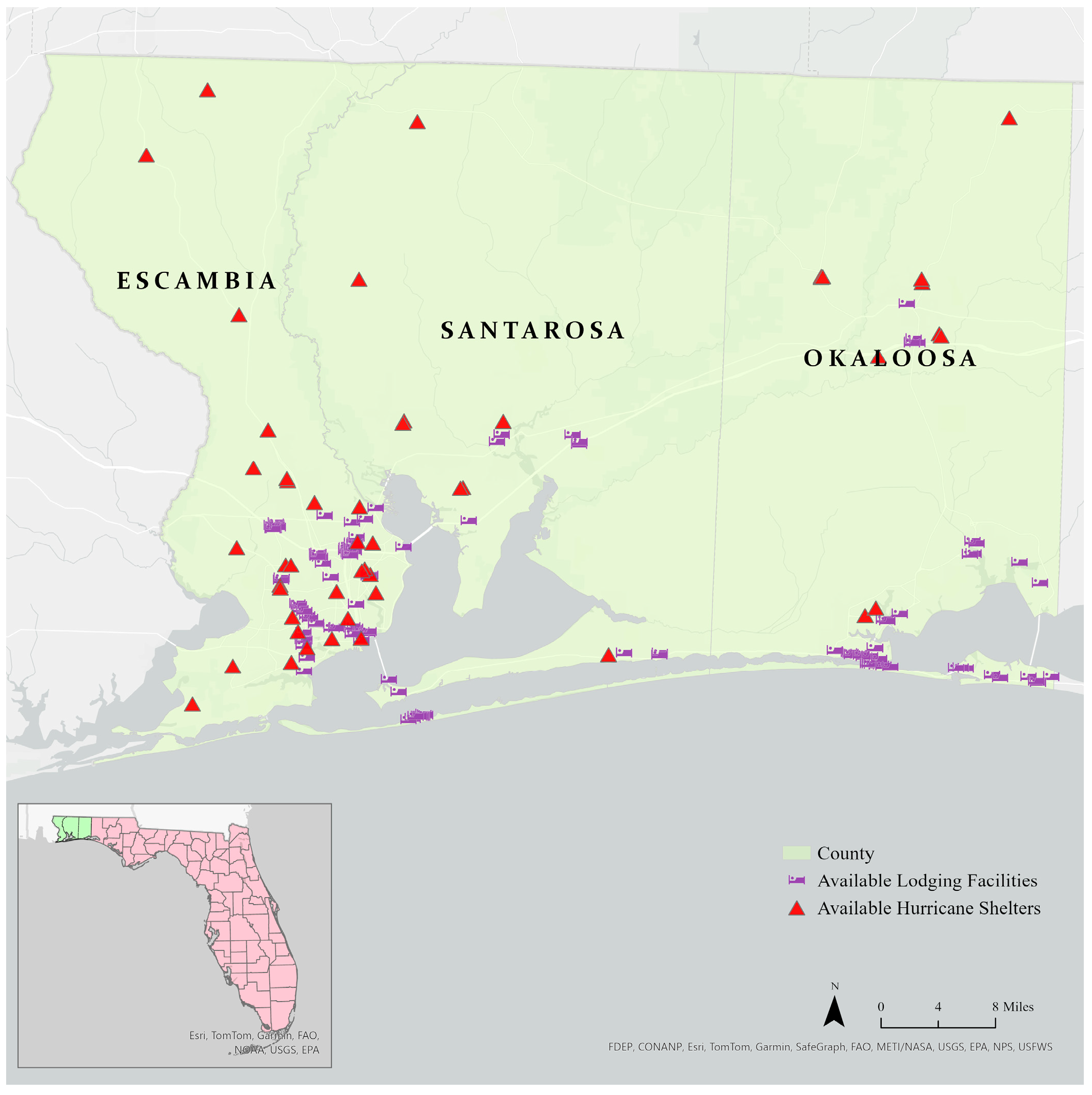
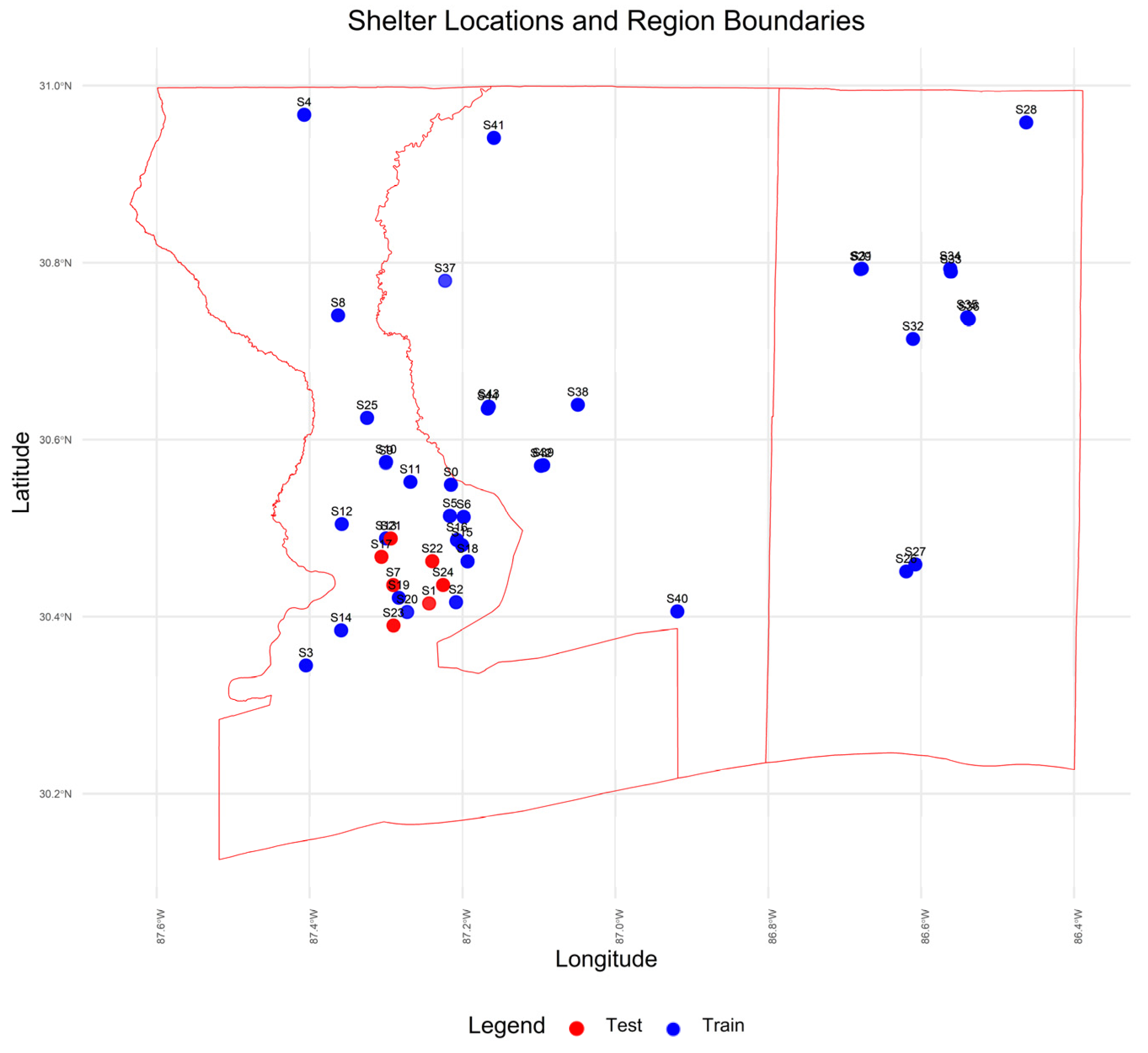
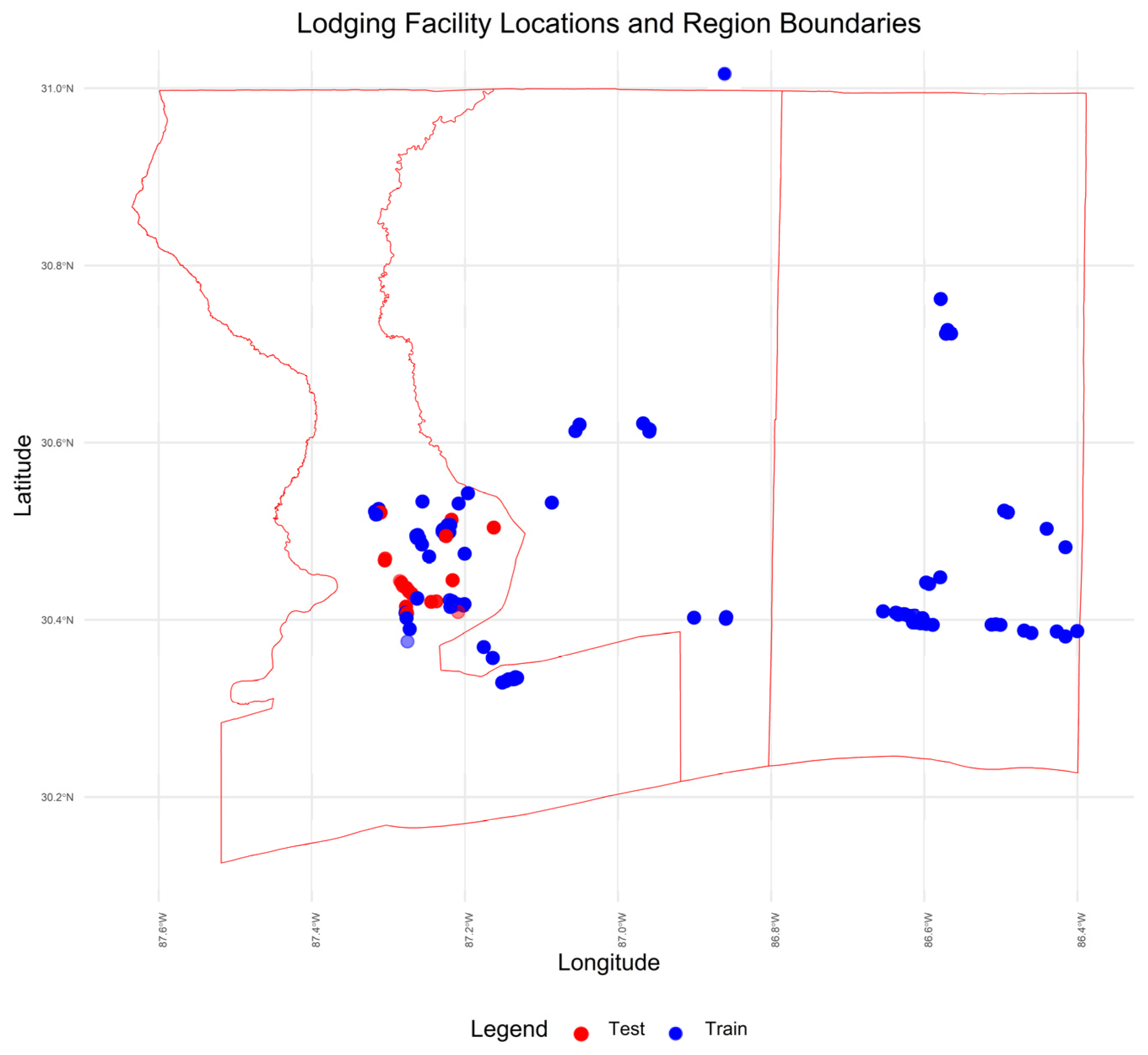
2.1. Study Region and Dataset
2.2. Data Processing
- Spatial Matching Condition: The end location (, ) of one trip must spatially match the start location (, ) of the next trip.
- Temporal Precedence Condition: The start time () of the second trip must be chronologically after the end time () of the first trip.
- Ignition Status Verification: The first journey must end with = “key-off”, and the second trip must start with = “key-on”, ensuring a logical vehicle stop before the subsequent trip.
2.3. Generalized Additive Model (GAM) Implementation
2.4. Justification of the Model Choice
2.5. Benchmark GLM for Comparative Study
3. Results
3.1. Effects of Data Normalization on Model Performance
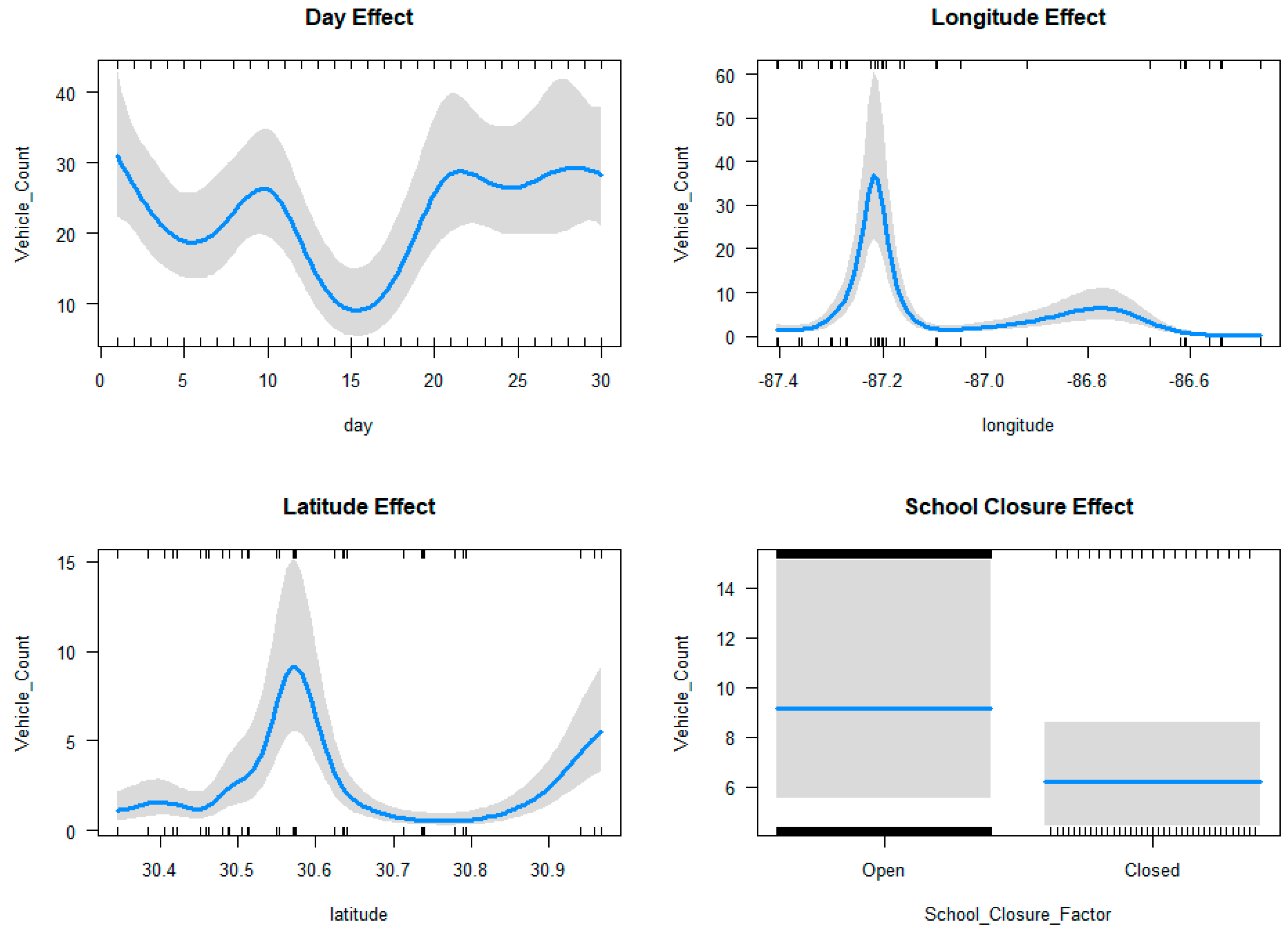
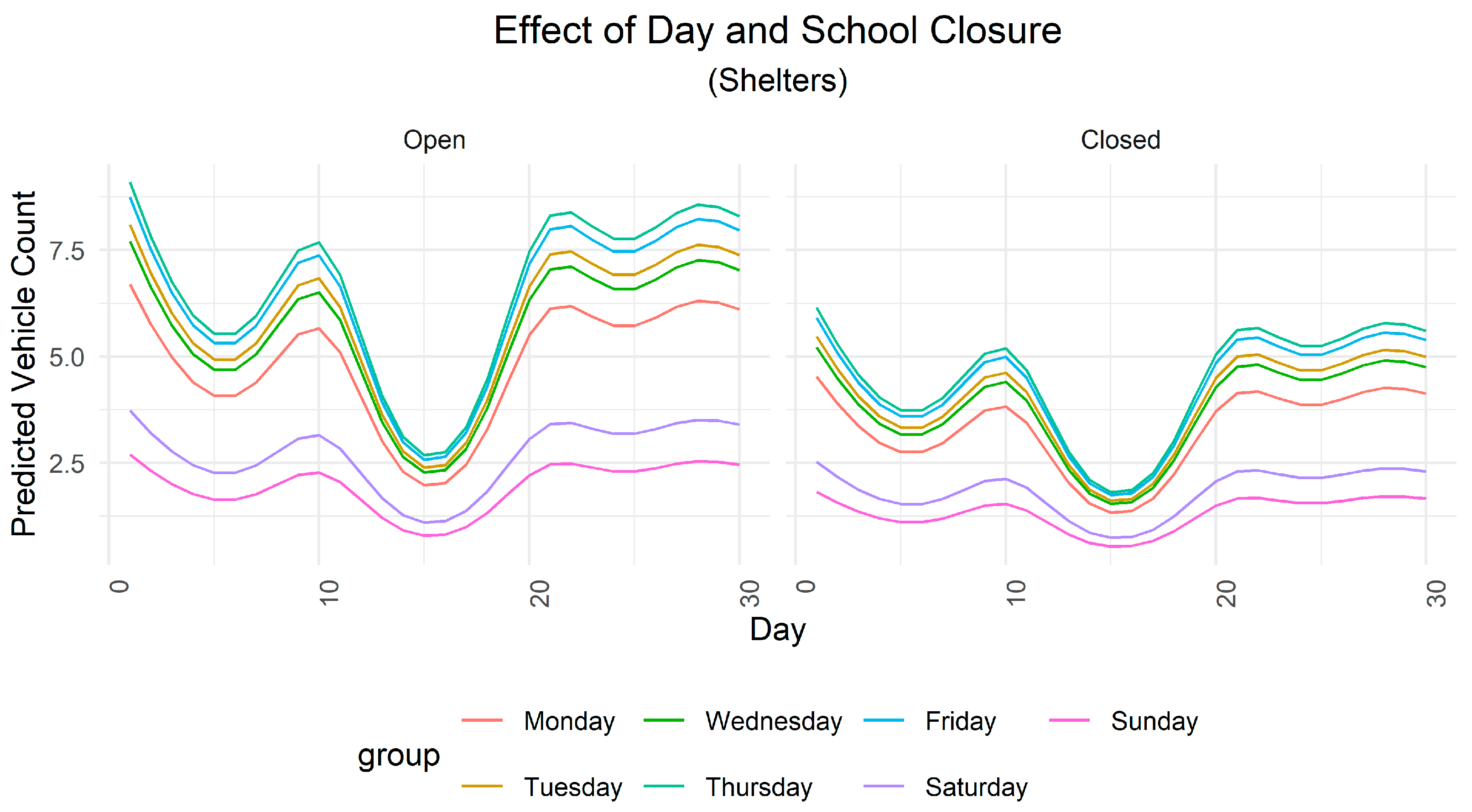
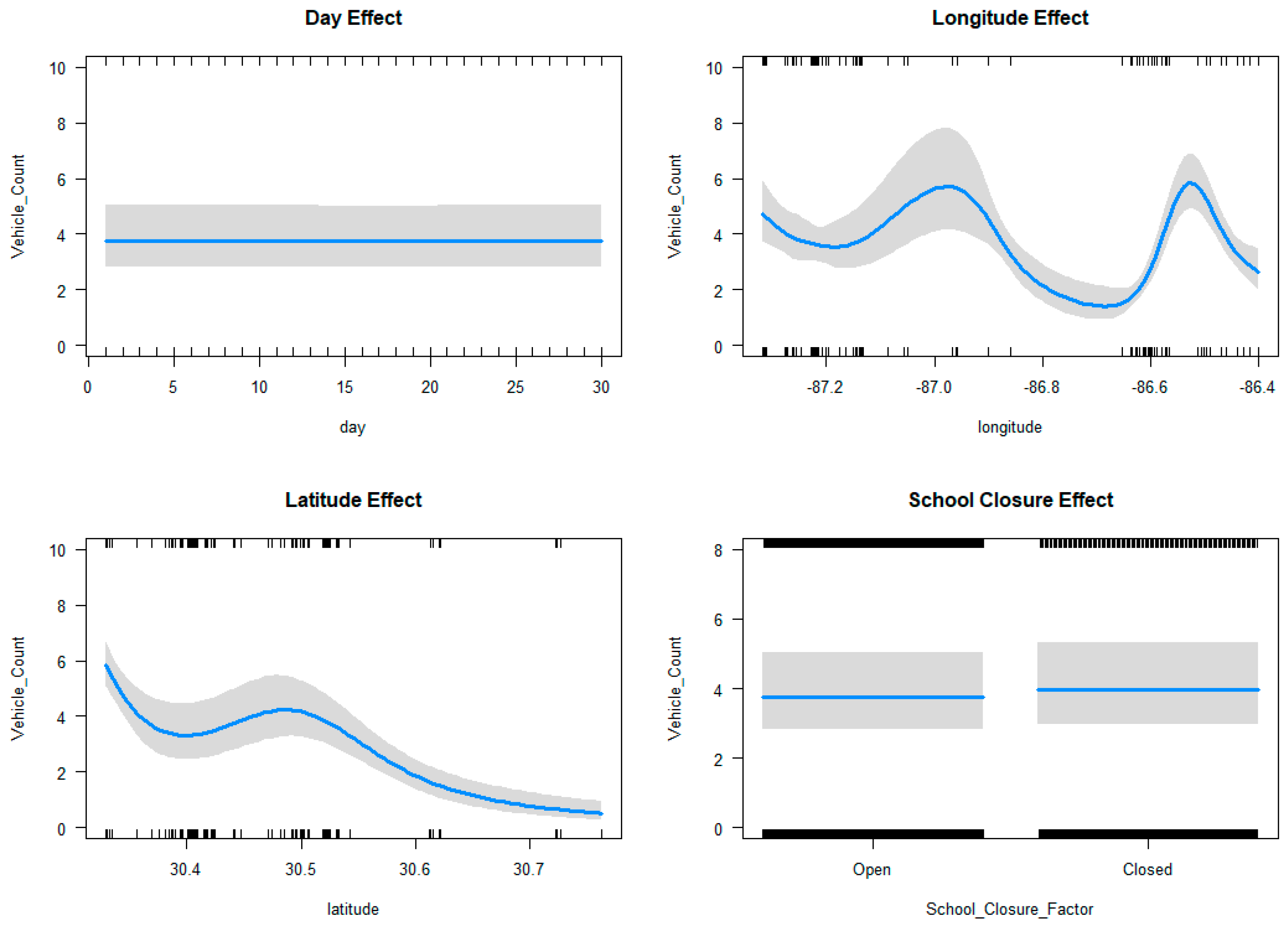
3.2. Effects of School Closure and Geographic Location on Shelter Demand
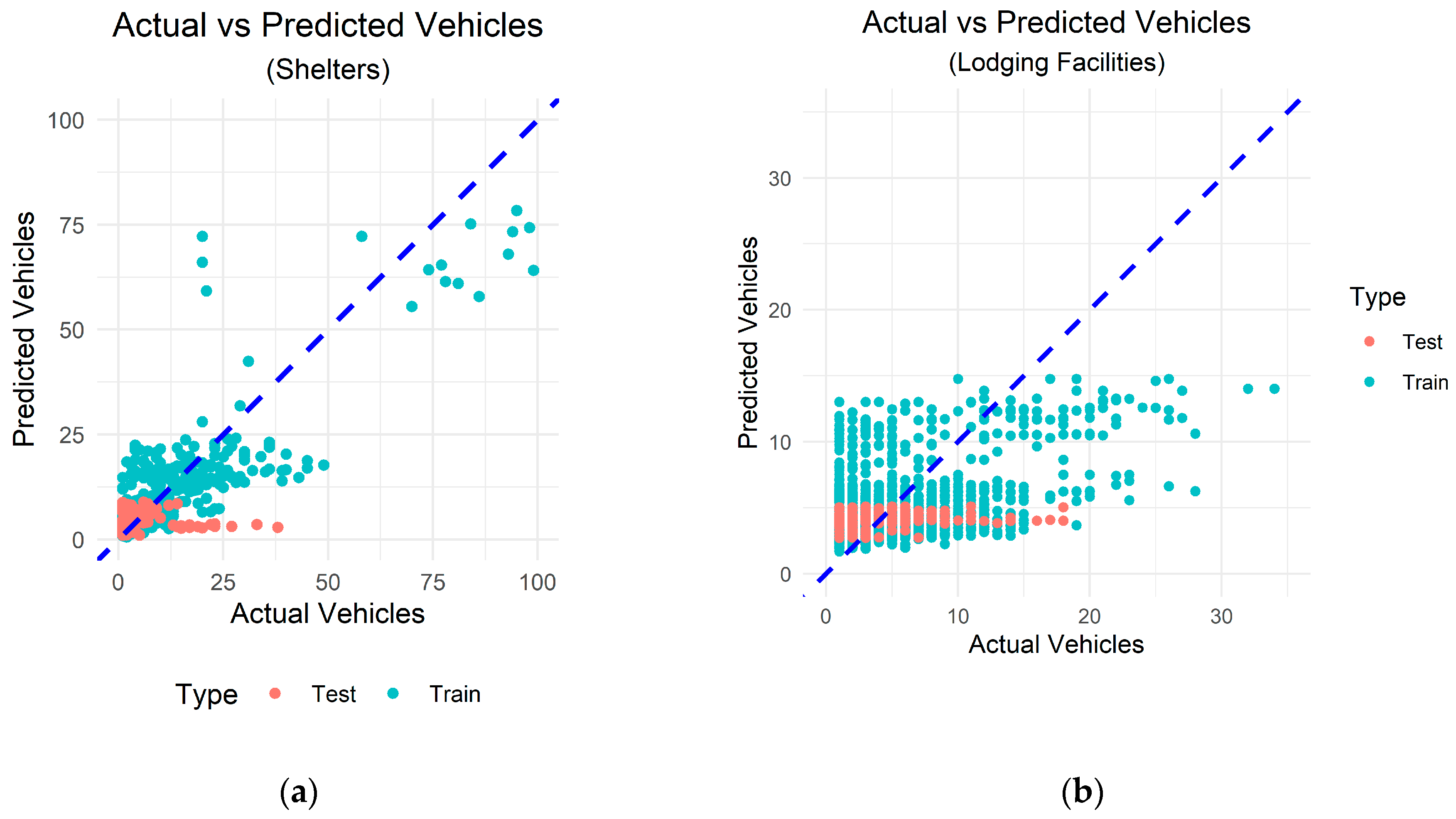
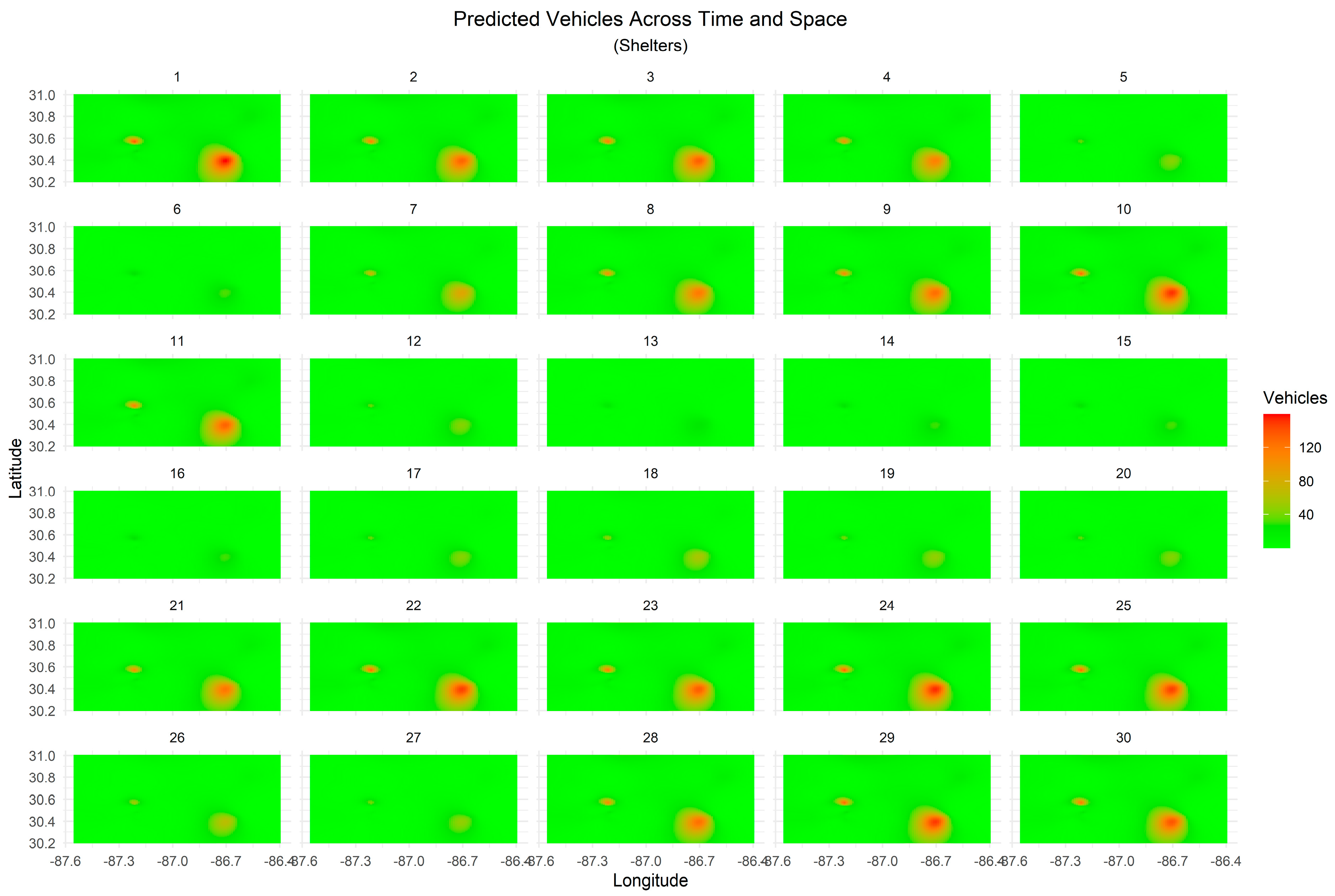
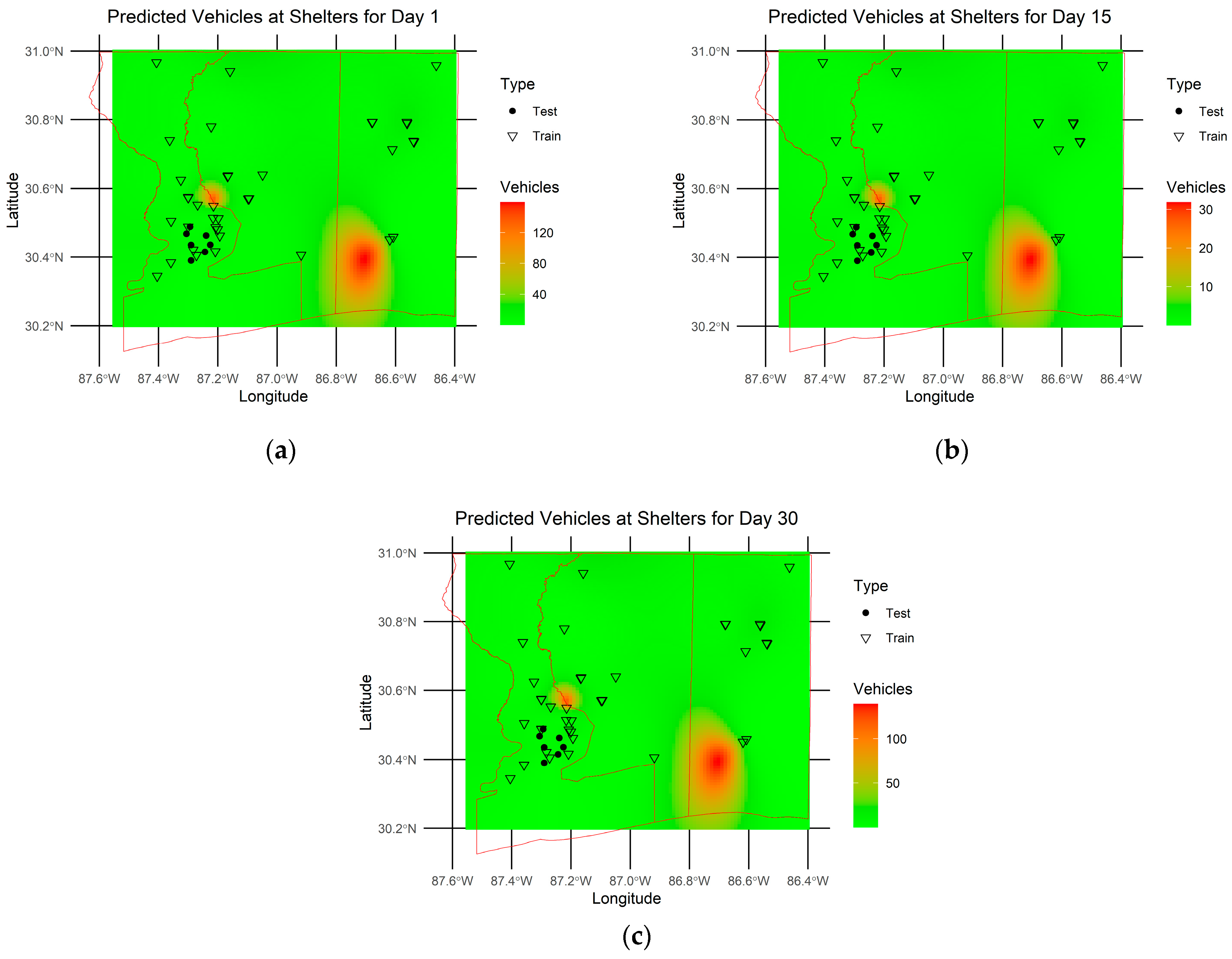
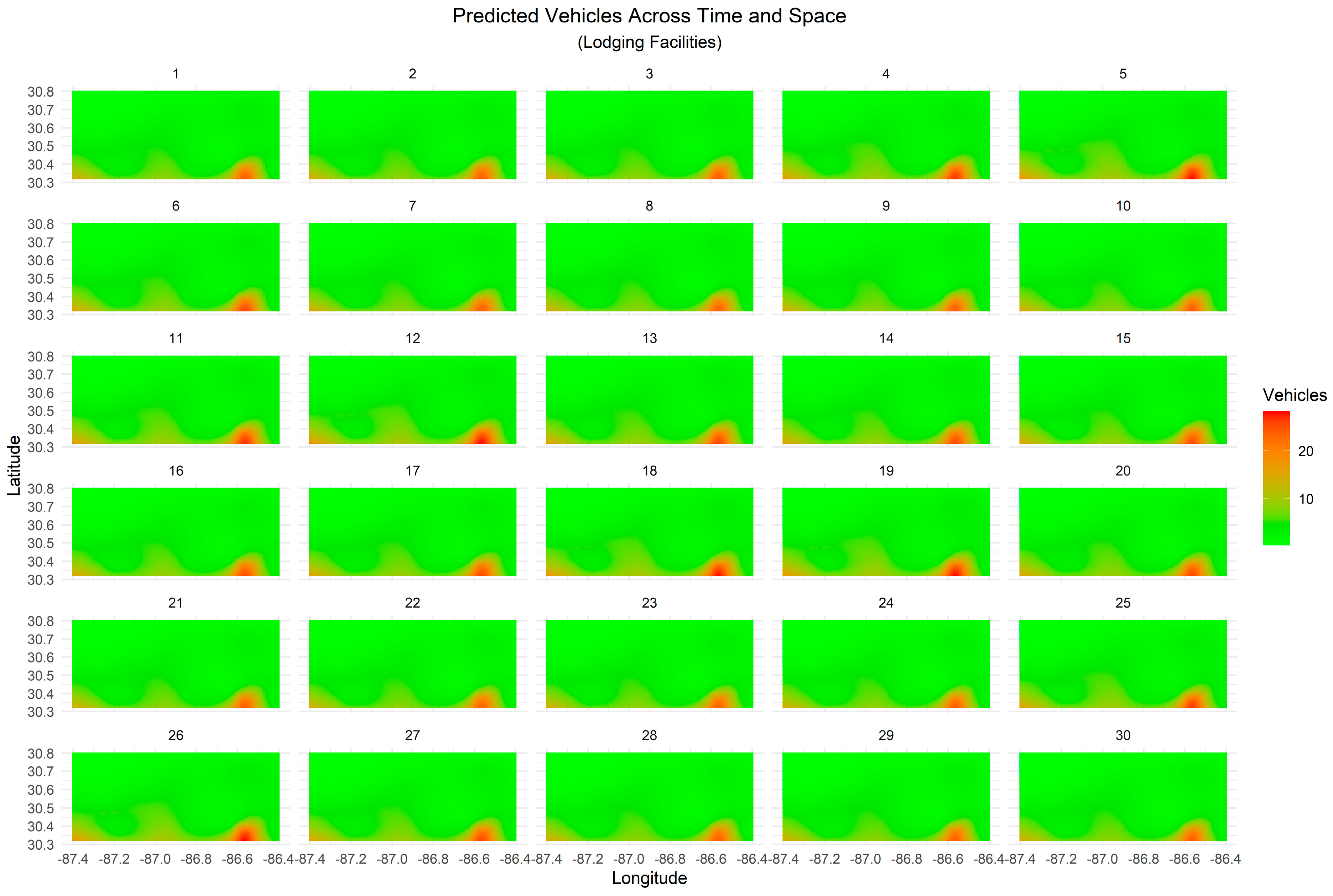
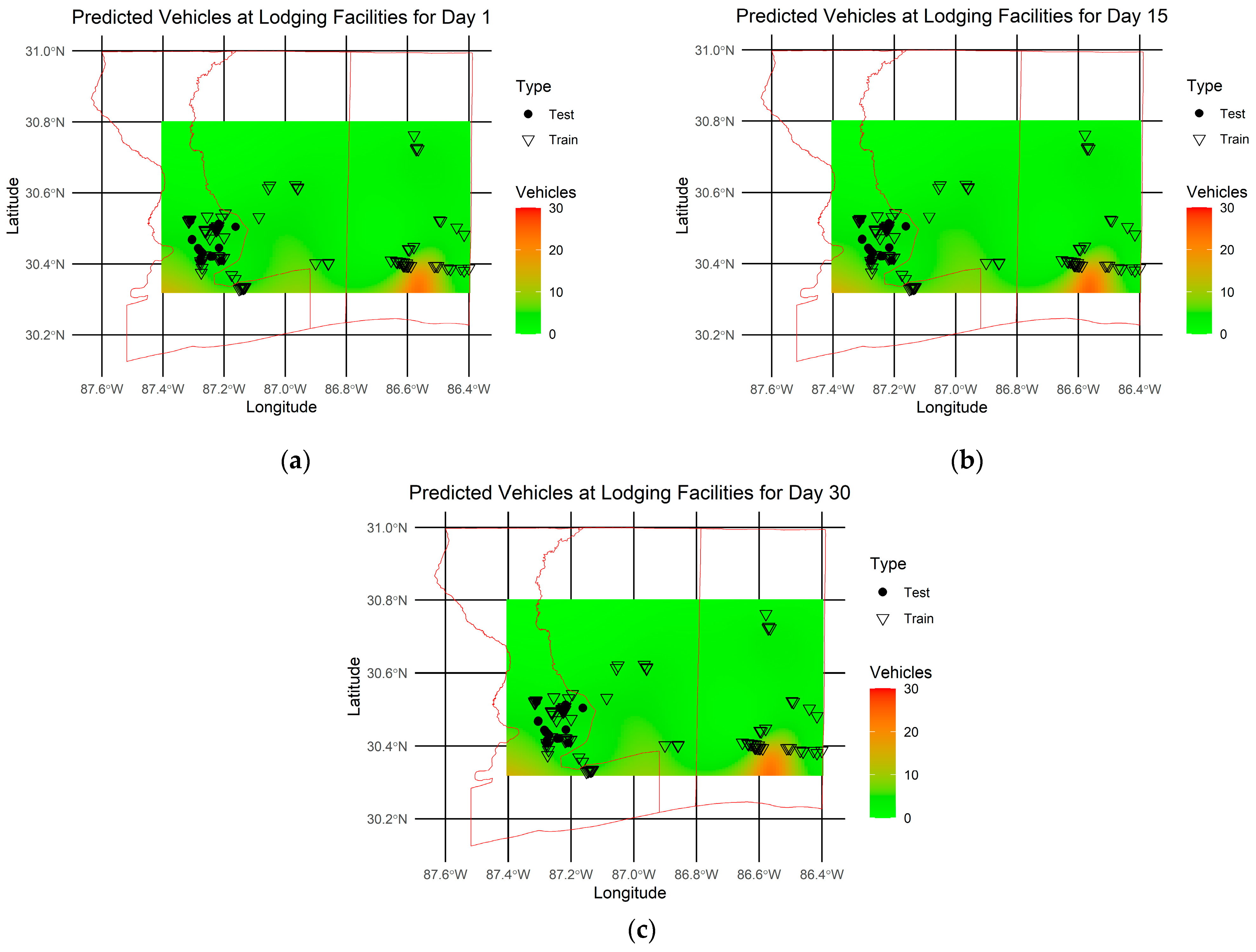
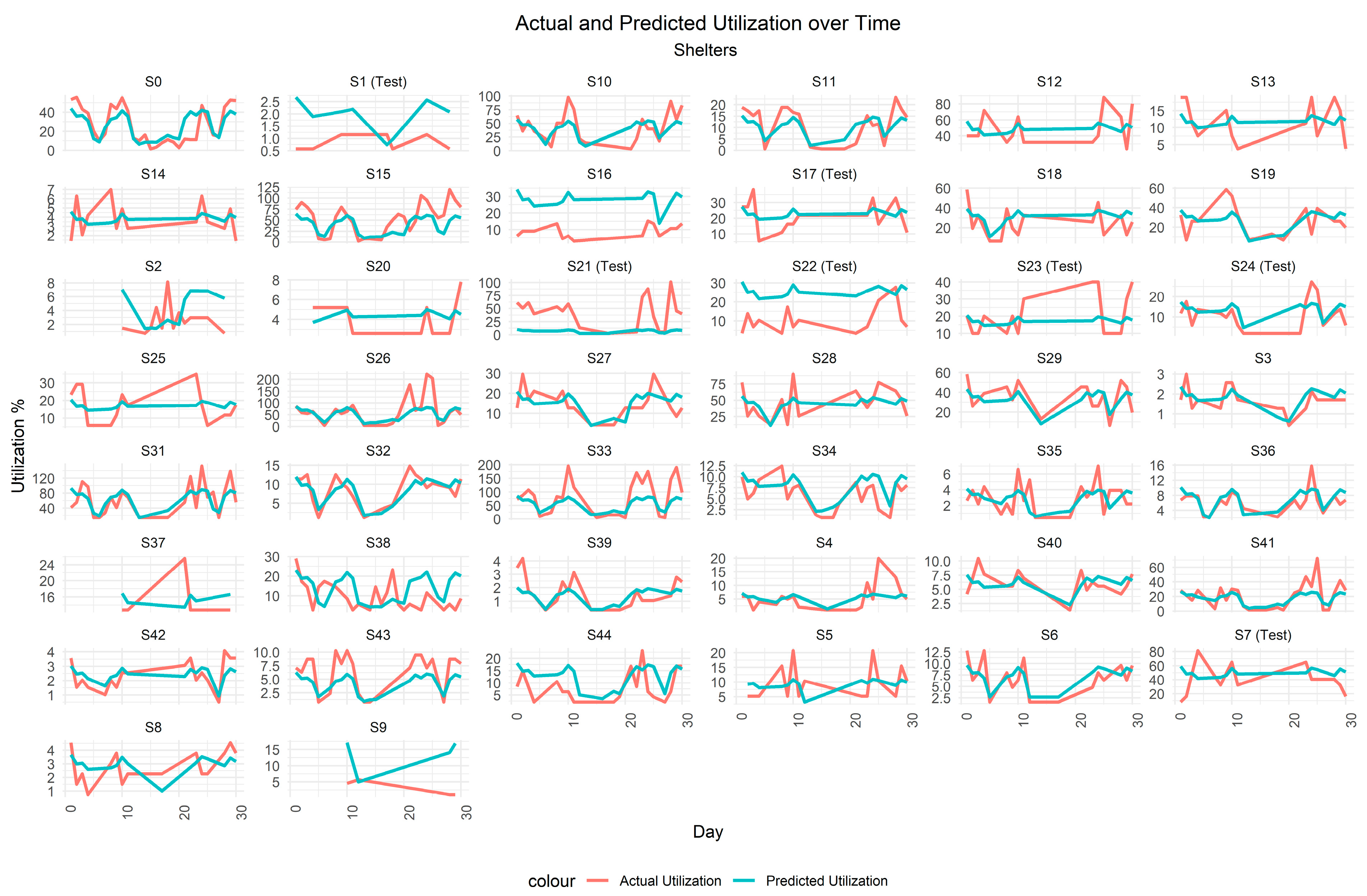
3.3. Spatiotemporal Demand Prediction
3.4. Comparison of Predicted Demand and Available Capacity
3.5. Model Performance on 15-Day Subset of the Training Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jadaan, K.; Zeater, S.; Abukhalil, Y. Connected Vehicles: An Innovative Transport Technology. Procedia Eng. 2017, 187, 641–648. [Google Scholar] [CrossRef]
- Lim, J.; Pyun, D.; Choi, D.; Bok, K.; Yoo, J. Efficient Dissemination of Safety Messages in Vehicle Ad Hoc Network Environments. Appl. Sci. 2023, 13, 6391. [Google Scholar] [CrossRef]
- Barth, M. Co-Benefits and Tradeoffs Between Safety, Mobility, and Environmental Impacts for Connected and Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 184–213. [Google Scholar] [CrossRef]
- Du, J.; Ahn, K.; Farag, M.; Rakha, H. Environmental and Safety Impacts of Vehicle-to-Everything Enabled Applications: A Review of State-of-the-Art Studies. arXiv 2021, arXiv:2202.01675. [Google Scholar]
- Raja, G.; Saravanan, G. Eco-Friendly Disaster Evacuation Framework for 6G Connected and Autonomous Vehicular Networks. IEEE Trans. Green Commun. Netw. 2022, 6, 1368–1376. [Google Scholar] [CrossRef]
- Meehl, G.A.; Washington, W.M.; Ammann, C.M.; Arblaster, J.M.; Wigley, T.M.L.; Tebaldi, C. Combinations of Natural and Anthropogenic Forcings in Twentieth-Century Climate. 2004. Available online: https://journals.ametsoc.org/view/journals/clim/17/19/1520-0442_2004_017_3721_conaaf_2.0.co_2.xml (accessed on 14 August 2024).
- Meehl, G.A.; Arblaster, J.M.; Tebaldi, C. Contributions of natural and anthropogenic forcing to changes in temperature extremes over the United States. Geophys. Res. Lett. 2007, 34, L19709. [Google Scholar] [CrossRef]
- Holland, G.; Bruyère, C.L. Recent intense hurricane response to global climate change. Clim. Dyn. 2014, 42, 617–627. [Google Scholar] [CrossRef]
- Mudd, L.; Wang, Y.; Letchford, C.; Rosowsky, D. Assessing Climate Change Impact on the U.S. East Coast Hurricane Hazard: Temperature, Frequency, and Track. Nat. Hazards Rev. 2014, 15, 04014001. [Google Scholar] [CrossRef]
- Conzatti, A.; Kershaw, T.; Copping, A.; Coley, D. A review of the impact of shelter design on the health of displaced populations. J. Int. Humanit. Action 2022, 7, 18. [Google Scholar] [CrossRef]
- Samad, M.H.A.; Ismail, M.; Nordin, J.; Tharim, A.H.A. Post-Disaster Shelters: A Review of Strategies and Design Framework. In Carving The Future Built Environment: Environmental, Economic and Social Resilience; Wahid, P.A.J., Aziz Abdul Samad, P.I.D.A., Sheikh Ahmad, P.D.S., Pujinda, A.P.D.P., Eds.; European Proceedings of Multidisciplinary Sciences; Future Academy: Frinton-on-Sea, UK, 2017; Volume 2, pp. 337–350. [Google Scholar] [CrossRef]
- Cruz, M.A.; Garcia, S.; Chowdhury, M.A.B.; Malilay, J.; Perea, N.; Williams, O.D. Assessing the Congregate Disaster Shelter: Using Shelter Facility Assessment Data for Evaluating Potential Hazards to Occupants During Disasters. J. Public Health Manag. Pract. 2017, 23, 54. [Google Scholar] [CrossRef]
- Sanusi, F.; Choi, J.; Ulak, M.B.; Ozguven, E.E.; Abichou, T. Metadata-Based Analysis of Physical–Social–Civic Systems to Develop the Knowledge Base for Hurricane Shelter Planning. J. Manag. Eng. 2020, 36, 04020041. [Google Scholar] [CrossRef]
- Karb, R.; Samuels, E.; Vanjani, R.; Trimbur, C.; Napoli, A. Homeless Shelter Characteristics and Prevalence of SARS-CoV-2. West. J. Emerg. Med. 2020, 21, 1048–1053. [Google Scholar] [CrossRef] [PubMed]
- Executive Orders|Executive Office of the Governor. Available online: https://www.flgov.com/eog/sites/default/files/executive-orders/2024/EO_20-208.pdf (accessed on 23 January 2025).
- Colburn, G.; Fyall, R.; McHugh, C.; Moraras, P.; Ewing, V.; Thompson, S.; Dean, T.; Argodale, S. Hotels as Noncongregate Emergency Shelters: An Analysis of Investments in Hotels as Emergency Shelter in King County, Washington During the COVID-19 Pandemic. Hous. Policy Debate 2022, 32, 853–875. [Google Scholar] [CrossRef]
- Pei, S.; Dahl, K.A.; Yamana, T.K.; Licker, R.; Shaman, J. Compound Risks of Hurricane Evacuation Amid the COVID-19 Pandemic in the United States. GeoHealth 2020, 4, e2020GH000319. [Google Scholar] [CrossRef]
- Meyer, M.A.; Mitchell, B.; Purdum, J.C.; Breen, K.; Iles, R.L. Previous hurricane evacuation decisions and future evacuation intentions among residents of southeast Louisiana. Int. J. Disaster Risk Reduct. 2018, 31, 1231–1244. [Google Scholar] [CrossRef]
- Sadri, A.M.; Ukkusuri, S.V.; Murray-Tuite, P.; Gladwin, H. How to Evacuate: Model for Understanding the Routing Strategies During Hurricane Evacuation. J. Transp. Eng. 2014, 140, 61–69. [Google Scholar] [CrossRef]
- Yang, H.; Morgul, E.F.; Ozbay, K.; Xie, K. Modeling Evacuation Behavior Under Hurricane Conditions. Transp. Res. Rec. 2016, 2599, 63–69. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, K.; Ozbay, K.; Yang, H. Hurricane Evacuation Modeling Using Behavior Models and Scenario-Driven Agent-based Simulations. Procedia Comput. Sci. 2018, 130, 836–843. [Google Scholar] [CrossRef]
- Ma, J.; Dou, J. Machine Learning Modeling for Spatial-Temporal Prediction of Geohazard. Sensors 2023, 23, 9262. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, S.; Liu, Z.; Ren, Z.; Lei, D.; Tan, C.; Guo, H. Machine Learning Models for Slope Stability Classification of Circular Mode Failure: An Updated Database and Automated Machine Learning (AutoML) Approach. Sensors 2022, 22, 9166. [Google Scholar] [CrossRef]
- Wu, T.; Yu, H.; Jiang, N.; Zhou, C.; Luo, X. Slope with Predetermined Shear Plane Stability Predictions Under Cyclic Loading with Innovative Time Series Analysis by Mechanical Learning Approach. Sensors 2022, 22, 2647. [Google Scholar] [CrossRef] [PubMed]
- Miao, F.; Xie, X.; Wu, Y.; Zhao, F. Data Mining and Deep Learning for Predicting the Displacement of “Step-like” Landslides. Sensors 2022, 22, 481. [Google Scholar] [CrossRef] [PubMed]
- Hussain, M.A.; Chen, Z.; Zheng, Y.; Shoaib, M.; Shah, S.U.; Ali, N.; Afzal, Z. Landslide Susceptibility Mapping Using Machine Learning Algorithm Validated by Persistent Scatterer In-SAR Technique. Sensors 2022, 22, 3119. [Google Scholar] [CrossRef]
- Abdalla, R. Evaluation of spatial analysis application for urban emergency management. SpringerPlus 2016, 5, 2081. [Google Scholar] [CrossRef]
- Matias, L.M.; Gama, J.; Ferreira, M.; Moreira, J.M.; Damas, L. Time-Evolving O-D Matrix Estimation Using High-Speed GPS Data Streams. 2016. Available online: http://repositorio.inesctec.pt/handle/123456789/5315 (accessed on 5 November 2023).
- Schlosser, F.; Maier, B.F.; Jack, O.; Hinrichs, D.; Zachariae, A.; Brockmann, D. COVID-19 lockdown induces disease-mitigating structural changes in mobility networks. Proc. Natl. Acad. Sci. USA 2020, 117, 32883–32890. [Google Scholar] [CrossRef]
- Shaw, R.; Kim, Y.; Hua, J. Governance, technology and citizen behavior in pandemic: Lessons from COVID-19 in East Asia. Prog. Disaster Sci. 2020, 6, 100090. [Google Scholar] [CrossRef]
- FEMA. 4564|FEMA.gov. Available online: https://www.fema.gov/disaster/4564 (accessed on 15 August 2024).
- Averhart, S. “Escambia Schools to Open Wednesday”, WUWF. Available online: https://www.wuwf.org/local-news/2020-09-21/escambia-schools-to-open-wednesday (accessed on 25 August 2024).
- Tomecek, N. Northwest Florida School Closures Due to Hurricane Sally (Closed Tues. Sept. 15). The Northwest Florida Daily News. Available online: https://www.nwfdailynews.com/story/news/2020/09/14/northwest-florida-school-closures-due-hurricane-sally-tues-sept-15/5794682002/ (accessed on 25 August 2024).
- FloridaDisaster. 20200916 The State of Florida Issues Hurricane Sally Updates. Available online: https://www.floridadisaster.org/news-media/news/20200916-the-state-of-florida-issues-hurricane-sally-updates/ (accessed on 15 August 2024).
- Florida Geographic Data Library. Available online: https://fgdl.org/ (accessed on 2 March 2025).
- Dimitrijevic, B.; Zhong, Z.; Zhao, L.; Besenski, D.; Lee, J. Assessing Connected Vehicle Data Coverage on New Jersey Roadways. arXiv 2022, arXiv:2208.04703. [Google Scholar]
- Hunter, M.; Mathew, J.K.; Li, H.; Bullock, D.M. Estimation of Connected Vehicle Penetration on US Roads in Indiana, Ohio, and Pennsylvania. J. Transp. Technol. 2021, 11, 597–610. [Google Scholar] [CrossRef]
- Mathew, J.K.; Li, H.; Landvater, H.; Bullock, D.M. Using Connected Vehicle Trajectory Data to Evaluate the Impact of Automated Work Zone Speed Enforcement. Sensors 2022, 22, 2885. [Google Scholar] [CrossRef]
- Wikle, C.K.; Zammit-Mangion, A.; Cressie, N. Spatio-Temporal Statistics with R.; Chapman and Hall/CRC: New York, NY, USA, 2019; ISBN 978-1-351-76972-3. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. An Introduction to Statistical Learning: With Applications in Python; Springer Nature: Berlin/Heidelberg, Germany, 2023; ISBN 978-3-031-38747-0. [Google Scholar]
- Wood, S. mgcv: Mixed GAM Computation Vehicle with Automatic Smoothness Estimation. p. 1.9-1. 2000. Available online: https://cran.r-project.org/web/packages/mgcv/index.html (accessed on 10 February 2025).
- Rudin, C.; Chen, C.; Chen, Z.; Huang, H.; Semenova, L.; Zhong, C. Interpretable machine learning: Fundamental prin-ciples and 10 grand challenges. Stat. Surv. 2022, 16, 1–85. [Google Scholar] [CrossRef]
- Reyes, M.; Meier, R.; Pereira, S.; Silva, C.A.; Dahlweid, F.-M.; von Tengg-Kobligk, H.; Summers, R.M.; Wiest, R. On the Interpretability of Artificial Intelligence in Radiology: Challenges and Op-portunities. Radiol. Artif. Intell. 2020, 2, e190043. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Xiao, T.; Wang, L.; Huang, W. Using Complementary Ensemble Empirical Mode Decomposition and Gated Recurrent Unit to Predict Landslide Displacements in Dam Reservoir. Sensors 2022, 22, 1320. [Google Scholar] [CrossRef] [PubMed]
- Geyer, J.A.; Ragland, D.R. Vehicle Occupancy and Crash Risk. Transp. Res. Rec. 2005, 1908, 187–194. [Google Scholar] [CrossRef]
- Lokmic-Tomkins, Z.; Bhandari, D.; Bain, C.; Borda, A.; Kariotis, T.C.; Reser, D. Lessons Learned from Natural Disasters around Digital Health Technologies and Delivering Quality Healthcare. Int. J. Environ. Res. Public Health 2023, 20, 4542. [Google Scholar] [CrossRef]
- Waugh, W.L., Jr.; Streib, G. Collaboration and Leadership for Effective Emergency Management. Public Adm. Rev. 2006, 66, 131–140. [Google Scholar] [CrossRef]
- Yapar, O. Real-Time Big Data Analytics for National Emergency Response: Challenges and Solutions. Social Science Research Network, Rochester, NY: 4982768. 2022. Available online: https://papers.ssrn.com/abstract=4982768 (accessed on 14 February 2025).
- Haseley, A.; Karnik, C.; Kamoie, B.; Sinha, I.; Mariani, J.; Egizi, A. “Leveraging AI for Effective Emergency Management and Crisis Response”, Deloitte Insights. Available online: https://www2.deloitte.com/us/en/insights/industry/public-sector/automation-and-generative-ai-in-government/leveraging-ai-in-emergency-management-and-crisis-response.html (accessed on 14 February 2025).
- Zhang, J.; Tang, H.; Tannant, D.D.; Lin, C.; Xia, D.; Wang, Y.; Wang, Q. A Novel Model for Landslide Displacement Prediction Based on EDR Selection and Multi-Swarm Intelligence Optimization Algorithm. Sensors 2021, 21, 8352. [Google Scholar] [CrossRef]
- Flachaire, E.; Hacheme, G.; Hué, S.; Laurent, S. GAM (L) A: An econometric model for interpretable Machine Learning. arXiv 2022, arXiv:2203.11691. [Google Scholar]




| Destination County | School Closure | Mean (Hours) | Std. Deviation (Hours) | Total (Hours) | Trip Counts |
|---|---|---|---|---|---|
| Escambia | Open | 0.327 | 0.654 | 321,038.4 | 982,476 |
| Escambia | Closed | 0.374 | 0.970 | 60,938.6 | 163,088 |
| Okaloosa | Open | 0.286 | 0.510 | 234,899.2 | 820,439 |
| Okaloosa | Closed | 0.281 | 0.412 | 37,239.6 | 132,302 |
| Santa Rosa | Open | 0.319 | 0.949 | 175,409.3 | 549,458 |
| Santa Rosa | Closed | 0.333 | 1.370 | 32,752.1 | 98,267 |
| Outside region of interest | Open | 0.455 | 0.689 | 72,793.8 | 159,900 |
| Outside region of interest | Closed | 0.453 | 0.620 | 11,220.1 | 24,794 |
| Model | Strengths | Limitations |
|---|---|---|
| GAM (our approach) | High interpretability, allowing policymakers to assess individual predictor contributions. Handles nonlinear relationships effectively. Supports spatial smoothing (e.g., longitude-latitude effects). [42] | It assumes smooth effects, and may underperform for highly complex spatial dependencies. [42] |
| ML-GAM (Machine Learning-GAM Hybrid) | Retains interpretability of GAMs while leveraging machine learning for feature selection and optimization. [42] | Requires careful model tuning to balance interpretability and complexity. [42] |
| Convolutional Neural Networks (CNNs) | Strong in detecting spatial patterns in image-like data. [43] Useful for remote sensing and satellite-based disaster modeling. | Requires large training datasets and lacks interpretability for decision-makers. [43] Less suited for tabular movement data like vehicle tracking. |
| Recurrent Neural Networks (RNNs)/ LSTMs | Captures time-series dependencies well. Effective for sequential mobility forecasting. [44] | Computationally expensive, it suffers from vanishing gradient issues. Requires extensive hyperparameter tuning. |
| Agent-Based Models (ABMs) | Simulates individual decision-making in evacuations. Can incorporate social-behavioral dynamics. [42] | Computationally intensive for large populations. Requires fine-tuned assumptions on agent behavior. [42] |
| XGBoost | High predictive accuracy and efficiency due to gradient boosting. [26] | Requires extensive hyperparameter tuning for optimal performance. [26] |
| Random Forest (RF) | Robust to noise and handles high-dimensional data well. [44] | Lacks interpretability; feature importance is difficult to translate into actionable policy insights. [44] |
| Feature | Description | Unit of Measurement |
|---|---|---|
| LABEL | Shelter or lodging facility identifier | Categorical (e.g., S0, L1) |
| Vehicle Count (per day) | Number of vehicles recorded at the facility per day | Count |
| Date | Date of the observation | YYYY-MM-DD |
| Total Spaces | Total available spaces at the facility | Count |
| ZIP Code | ZIP code of the facility location | Numeric (5-digit ZIP code) |
| County | The county where the facility is located | Categorical (e.g., Escambia, Okaloosa, Santa Rosa) |
| Longitude | Longitude coordinate of the facility | Decimal degrees |
| Latitude | Latitude coordinate of the facility | Decimal degrees |
| School Closure Factor | Indicates if schools were open or closed on the observation day | Categorical (Open/Closed) |
| Day | Day number relative to the study period | Integer (e.g., 1–30) |
| Day of the week | Day of the week for the observation | Categorical (e.g., Monday) |
| RMSE | MAE | MAPE | CORR | |
|---|---|---|---|---|
| Train Data | 12.9735 | 7.4704 | 182.33% | 0.1760 (<0.001) |
| Test Data | 8.6798 | 7.7795 | 333.87% | 0.1419 (0.1590) |
| RMSE | MAE | MAPE | CORR | |
|---|---|---|---|---|
| Train Data | 4.6103 | 3.1109 | 127.02% | 0.2897 (<0.001) |
| Test Data | 3.5807 | 2.6938 | 115.62% | −0.0989 (0.1354) |
| RMSE | MAE | MAPE | CORR | |
|---|---|---|---|---|
| Train Data | 6.7791 | 3.8745 | 79.41% | 0.8593 (<0.001) |
| Test Data | 7.7213 | 4.4823 | 107.01% | −0.0835 (0.4087) |
| RMSE | MAE | MAPE | CORR | |
|---|---|---|---|---|
| Train Data | 4.0368 | 2.7591 | 108.76% | 0.5485 (<0.001) |
| Test Data | 3.4211 | 2.57656 | 113.80% | 0.2096 (0.0014) |
| County | Population | Available Spaces | Vehicle Counts | Veh Ct/Av Sp | ||
|---|---|---|---|---|---|---|
| Escambia | 0.592 | 0.480 | 330,000 | 21,997 | 4097 | 0.19 |
| Okaloosa | 0.599 | 0.682 | 220,000 | 9819 | 1727 | 0.18 |
| Santa Rosa | 0.705 | 0.671 | 200,000 | 13,351 | 1003 | 0.08 |
| County | Population | Available Spaces | Vehicle Counts | Veh Ct/Av Sp | ||
|---|---|---|---|---|---|---|
| Escambia | 0.951 | 0.950 | 330,000 | 5417 | 5535 | 1.02 |
| Okaloosa | 1.182 | 0.798 | 220,000 | 3404 | 4320 | 1.27 |
| Santa Rosa | 1.010 | 0.906 | 200,000 | 668 | 951 | 1.42 |
| Shelters | Lodging Facilities | |
|---|---|---|
| Closure Effect–Open (C.I.) | 9.17 (15.11, 5.57) | 3.77 (5.02, 2.83) |
| Closure Effect–Closed (C.I.) | 6.20 (8.59, 4.47) | 3.97 (5.33, 2.96) |
| 0.0032 | 0.0632 | |
| 0.0076 | 55,945 |
| RMSE | MAE | MAPE | CORR | |
|---|---|---|---|---|
| Training | 6.7778 | 3.7317 | 84.0176% | 0.8126 (<0.001) |
| Test | 5.9453 | 3.6453 | 115.855% | −0.0532 (0.7647) |
| RMSE | MAE | MAPE | CORR | |
|---|---|---|---|---|
| Training | 4.0464 | 2.8338 | 113.0784% | 0.5326 (<0.001) |
| Test | 3.6256 | 2.6322 | 104.0038% | 0.1511 (0.1169) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsekeni, D.E.; Alisan, O.; Yang, J.; Vanli, O.A.; Ozguven, E.E. Spatiotemporal Modeling of Connected Vehicle Data: An Application to Non-Congregate Shelter Planning During Hurricane-Pandemics. Appl. Sci. 2025, 15, 3185. https://doi.org/10.3390/app15063185
Tsekeni DE, Alisan O, Yang J, Vanli OA, Ozguven EE. Spatiotemporal Modeling of Connected Vehicle Data: An Application to Non-Congregate Shelter Planning During Hurricane-Pandemics. Applied Sciences. 2025; 15(6):3185. https://doi.org/10.3390/app15063185
Chicago/Turabian StyleTsekeni, Davison Elijah, Onur Alisan, Jieya Yang, O. Arda Vanli, and Eren Erman Ozguven. 2025. "Spatiotemporal Modeling of Connected Vehicle Data: An Application to Non-Congregate Shelter Planning During Hurricane-Pandemics" Applied Sciences 15, no. 6: 3185. https://doi.org/10.3390/app15063185
APA StyleTsekeni, D. E., Alisan, O., Yang, J., Vanli, O. A., & Ozguven, E. E. (2025). Spatiotemporal Modeling of Connected Vehicle Data: An Application to Non-Congregate Shelter Planning During Hurricane-Pandemics. Applied Sciences, 15(6), 3185. https://doi.org/10.3390/app15063185










