Abstract
Aeromagnetic compensation is the main method for eliminating magnetic interference on flight platforms. With the improved sensitivity of aeromagnetic sensors, the generalization and compensation accuracy of existing aeromagnetic compensation methods have become insufficient to meet the needs of current aeromagnetic survey applications. In this article, we propose an aeromagnetic compensation method based on temporal convolutional networks to improve both generalization and compensation accuracy. In the proposed method, a neural network based on separable convolution with a residual connection is employed to improve the compensation accuracy and convergence stability, and a gradient correction loss function based on the Tolles–Lawson model is used to improve the generalization ability. We conducted experiments based on both simulated and real datasets and compared typical neural network compensation methods proposed by previous researchers. The results indicate that the method proposed in this article can achieve a lower standard deviation of residual magnetic interference than other neural network methods, demonstrating a better compensation performance and generalization ability.
1. Introduction
Aeromagnetic surveys are widely used to aid in the production of geological maps and are also commonly used during mineral exploration and petroleum exploration. The signals collected during aeromagnetic surveys include various interferences, which affect the survey’s accuracy. Therefore, it is necessary to study aeromagnetic compensation to eliminate aeromagnetic interference.
In the early 1950s, Tolles and Lawson first analyzed the main sources of magnetic interference on flight platforms [1,2,3,4], including those from intrinsic magnetic fields, induced magnetic fields, and eddy-current magnetic fields. In 1961, Leliak further proposed a mathematical model for describing aeromagnetic interference: the Tolles–Lawson model (T–L model) [5]. In 1980, Leach described the solution of the T–L model as a linear regression problem and proposed a ridge regression method, which reduces the multicollinearity of the solving process [6]. In 2022, Feng proposed a compensation method to resist the interference of geomagnetic gradients in aeromagnetic surveys [7]. In 2023, Chen proposed a joint compensation method based on an inertial navigation system and a three-axis fluxgate magnetometer to improve the compensation accuracy [8] and then proposed a compensation method for airborne electronic equipment interference [9].
Considering the insufficient accuracy of traditional linear regression methods, more researchers have started studying neural-network-based aeromagnetic compensation methods. In 1993, Williams first used neural networks for aeromagnetic compensation and tested the effects of fully connected neural networks at different layers. The results showed that the neural network compensation method had a similar accuracy to the T–L model compensation method and could be used as an alternative [10].
In the study on maneuvering interference and low-frequency interference compensation methods (usually within 0.1–0.6 Hz frequency [11]), Ma proposed a dual estimation method based on an unscented Kalman filter in 2017, which combines the T–L model with a neural network to improve the compensation accuracy, and noise was added manually to solve the overfitting problem of neural networks [12]. In 2020, Xu proposed an end-to-end neural network model for magnetic anomaly detection and aeromagnetic compensation. The model consisted of two parts: a binary classification network for magnetic anomaly detection and a regression network for geomagnetic noise suppression [13]. In 2021, Yu proposed a neural network compensation method based on a generalized regression neural network to solve the overfitting problem of neural networks [14]. In the same year, Li designed a neural network compensation method based on physical features with the Levenberg–Marquardt backpropagation algorithm, which displayed an improved compensation accuracy [15]. In 2022, Yu proposed a neural network compensation method that combines a backpropagation neural network and a residual connection to address the vanishing-gradient problem during neural network training [16]. In the same year, Zhou proposed a compensation method based on a radial basis function artificial neural network, which uses the radial basis function as the activation function to improve the neural network’s generalization [17]. Jiao proposed a model compression method to optimize the backpropagation neural network to solve the problem of insufficient computing resources during the training process on unmanned aerial vehicles [18]. In 2024, Wang proposed an incremental learning neural network compensation method that reduces the time required for neural network retraining [19].
In the study of high-frequency interference compensation algorithms, Albert used open flight data from the Massachusetts Institute of Technology and the Department of the Air Force Artificial Intelligence Accelerator Program (hereafter DAF-MIT AIA Open Flight Data) [20] and a simple, fully connected neural network to analyze the impact of different inputs on compensation accuracy in 2022 [21]. The results show that the current and voltage data input of some airborne electronic equipment can significantly improve compensation accuracy. In the same year, Wang proposed a compensation method combining wavelet decomposition and a long short-term memory neural network to reduce interference with airborne electronic equipment [22].
In recent years, time convolutional networks have been widely applied in various temporal tasks [23,24,25]. In order to establish connections between features and aeromagnetic interference in time series, improve both generalization and compensation accuracy, prevent exploding gradients, and achieve fast convergence, in this article, we propose an aeromagnetic compensation method based on temporal convolutional networks (hereafter MagTCN). In the proposed method, a neural network based on separable convolution with a residual connection is employed to improve the compensation accuracy and convergence stability, and a gradient correction loss function based on the T–L model is used to improve the generalization ability. MagTCN was applied to simulation datasets and DAF-MIT AIA Open Flight Data to verify its effectiveness.
2. Materials and Methods
2.1. Tolles–Lawson Model
The Tolles–Lawson model (T–L model) is widely used in aeromagnetic compensation of fixed-wing aircraft. The basic idea is to use the magnetic measurements of the vector magnetometer to calibrate the scalar magnetometer.
The main components of aeromagnetic survey data can be expressed as follows:
where represents the total magnetic field acquired by the magnetic sensor; represents the geomagnetic field; represents the magnetic anomaly of the target; represents the magnetic interference caused by the flight platform; and represents the diurnal variation in the geomagnetic field.
During short-term navigation, the diurnal variation in the geomagnetic field can be removed through monitoring stations. When there is no target, it can be assumed that the total magnetic field only includes the geomagnetic field and the magnetic interference of the flight platform , which can be expressed as follows:
The above equation can be further derived as follows:
The magnetic interference of a flight platform, with a capacity of about 100 nT, is much smaller than that of the geomagnetic field, with a capacity of about 50,000 nT, so the term can be ignored. Therefore, the above equation can be simplified as follows:
Using the first-order form of the series expansion formula, can be expressed as follows:
By using a three-axis fluxgate magnetometer, the direction of the total magnetic field can be measured:
Substituting Equation (9) into Equation (8) yields the following:
represents the projection of the magnetic interference of the flight platform onto the total magnetic field, as shown in Figure 1.
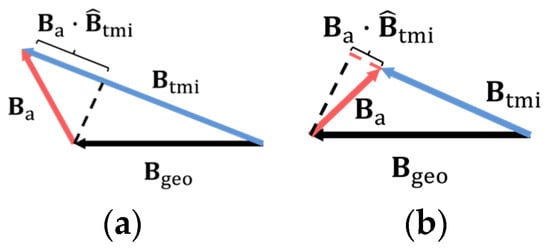
Figure 1.
Modulus variation in the total magnetic field. (a) The situation where magnetic interference is in the same direction as the background geomagnetic field; (b) the situation where the magnetic interference is opposite to the background geomagnetic field.
If we can restore the geomagnetic field strength , we can further obtain and establish the relationship between the flight platform attitude angle and . Then, in the aeromagnetic survey, we can obtain the magnetic interference through the attitude angle and restore the magnetic anomaly of the target .
From the quasi-static electrodynamics model developed by Darwin [26], magnetic induction can be expressed as follows:
where represents the current density; represents the permittivity of free space; and represents the electric field generated by Coulomb charges.
According to Ohm’s law, Equation (11) can be further expressed as follows:
where represents any unchanging currents; represents the eddy currents.
Assume that is permanent magnetization. Therefore, the time-varying field can be expressed as
A magnetization density can be expressed as a bound current . Then, Equation (13) can be further expressed as
Further assuming that is proportional to the external field , the relationship between the -field and the -field can be expressed as
where represents the vacuum magnetic permeability.
In general, the magnetization model can be expressed as
where represents a constant magnetic permeability.
Permanent magnetization and induced magnetization are both related to . Considering the contribution of eddy currents, the total magnetic field can be expressed as
The second part on the right side of the above equation is the magnetic interference , which can be expressed as
The above equation can be simplified as follows:
where , , and represent the unknown coefficient vector; represents a time-derivative.
Based on the above equation, the T–L model identifies the magnetic interference of the flight platform in three parts: the constant magnetic interference field , the induced magnetic interference field , and the eddy-current magnetic interference field . It can be expressed as follows:
The inherent magnetic field of the flight platform is generated by permanent magnets, such as engines and motor cores, and its direction remains unchanged relative to the axial direction of the flight platform. The contribution of multiple intrinsic magnetic field sources to the load of the optical pump magnetic sensor is formed by vector superposition to form a fixed magnetic field bias, which can be expressed as follows:
where represents the intrinsic magnetic field coefficient composed of .
The induced magnetic field of the flight platform is the result of the ferromagnetic components of the aircraft being excited by the background magnetic field, and its magnitude and direction are influenced by the strength, direction, and material magnetization of the components. The contribution of the induced magnetic field of the flight platform can be expressed as follows:
where represents the induced magnetic field coefficient composed of .
The eddy-current magnetic field of the flight platform is generated by the change in magnetic flux caused by the cutting of magnetic induction lines on the fuselage metal. Eddy currents generate eddy magnetic fields through electromagnetic induction, and their magnitude and direction are influenced by the properties of conductive materials and the relative rate of change in external magnetic fields. They can be expressed as follows:
where represents the eddy-current magnetic field coefficient composed of ; represents the rate of change in direction of .
Based on the above Equations (20)–(23), can be expressed as follows:
Let , , and represent the direction cosine of the angle between the airborne coordinate system and the geomagnetic field vector, and let , , and . The relationship between , , and is as follows:
can be simplified as follows:
where ~ represent the 16 coefficients to be calculated in the T–L model; represents the background magnetic field strength.
The background magnetic field term can be considered a constant and calculated together with the coefficient, so the value of can be further simplified as follows:
where represents the coefficient matrix to be calculated in the T–L model; represents the direction cosine matrix of the angle between the airborne coordinate system and the geomagnetic field vector.
During the calibration flight phase, we first collect and and then calculate the coefficient matrix . During the survey phase, we calculate through and the collected .
2.2. MagTCN
2.2.1. Separable Convolution Module
In MagTCN, we introduce separable convolutions, including depth-wise convolutions (DWConv) and point-wise convolutions (PWConv) [27]. Compared with the traditional convolution that mixes multi-dimensional information, the decoupled design makes it easier for MagTCN to model magnetic interference and reduces computational complexity.
As shown in Figure 2, for an input with a sequence length of and channels, DWConv simultaneously uses a filter for each channel, resulting in an output dimension of .
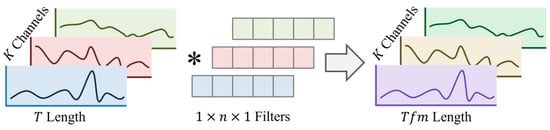
Figure 2.
The convolution process of depth-wise convolutions. (*) indicates the operation of convolution on the input.
As shown in Figure 3, for an input with a sequence length of and channels, PWConv uses a filter with a dimension of to cover all of the channels. This performs stationary convolution on multiple variables at each time point, resulting in an output dimension of .
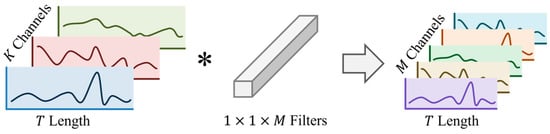
Figure 3.
The convolution process of point-wise convolutions. (*) indicates the operation of convolution on the input.
2.2.2. Gaussian Error Linear Unit
The Gaussian Error Linear Unit (GELU) is a nonlinear activation function that provides random regularity to the activation function by inputting its own probability statistics to improve the generalization of neural networks [28]. The specific form can be expressed as follows:
where represents the cumulative function of the Gaussian normal distribution of , which can be expressed as follows:
where and represent the mean and standard deviation of a normal distribution, respectively.
For input , the GELU has approximately linear output; for input , the output of the GELU is 0; when input x approaches 0, the GELU has nonlinear output, maintaining the continuity of the entire activation function.
2.2.3. Reversible Instance Normalization Module
In time-domain aeromagnetic compensation tasks, the difference in the mean or variance between the training and testing datasets leads to a decrease in compensation accuracy. To address the issue of distribution differences between different survey data, we introduced a reversible instance normalization module (RevIN) [29], on both sides of MagTCN, consisting of a normalization module and a denormalization module.
The input of the MagTCN backbone is represented as , and the corresponding output is represented as . If is the number of channels, is the length of the input sequence, and is the length of the output sequence, then there exists an input and an output .
For the normalization part of the MagTCN backbone input, the mean and variance are used for normalization. The mean can be expressed as follows:
The variance can be expressed as follows:
The normalization process can be expressed as follows:
where represent learnable affine transformation parameters.
The denormalization process can be expressed as follows:
2.2.4. The Structure of MagTCN
The structure of MagTCN is shown in Figure 4, where represents the variable dimension, represents the time dimension, and represents the feature dimension. In MagTCN, we refer to the design of the Transformer [30]. DWConv is used to learn the time information between tokens for each feature, and a large kernel is used in DWConv to increase the receptive field and improve the temporal modeling ability, which has the same function as the self-attention module of the Transformer. Each point-wise convolutional block (PWBlock) consists of two PWConvs and one GELU. The first PWConv in PWBlock increases the dimension of the input vector, and the second one reduces the dimension of the vector again, which has the same function as the feedforward layer of the Transformer. The GELU in PWBlock is used to improve the generalization of MagTCN. Reshape and permute are used between the two PWBlocks to allow MagTCN to learn the temporal dependency and cross-variable dependency of features at the same time. The input of MagTCN is first normalized by RevIN’s normalization module and then fed into the MagTCN backbone. After backbone processing, the data are fed into RevIN’s denormalization module and residual connection. Finally, the output is formed by a linear layer and a flat layer.
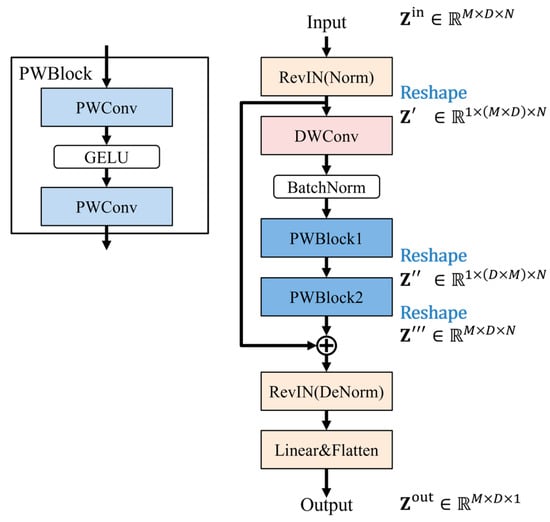
Figure 4.
The neural network structure of the proposed method.
The residual connection in MagTCN can be expressed as follows:
where represents the output of the residual connection; represents the input of MagTCN; and represents the backbone of MagTCN.
2.3. Loss Function
In order to ensure the steady improvement in the compensation accuracy and the generalization of MagTCN during neural network training, two types of losses are introduced: loss , based on the T–L model, and truth loss . These two types of losses are based on the mean square error (MSE), which can be expressed as follows:
where is the true label of the -th sample, and is the predicted value of the neural network model. When calculating , is the signal after aeromagnetic compensation via the T–L model; when calculating , is the signal without interference.
In addition, the above two types of losses are combined and applied to neural network training through weights: at the th iteration, the weight decay rate is , the initial value of the weight decay coefficient is , and the total weight value is . The loss function can be expressed as follows:
To prevent vanishing gradients, the gradient correction algorithm is introduced for the above two losses.
The cosine similarity between the gradients and of the loss terms and is calculated as follows:
The gradient is updated to the following:
The final loss function can be expressed as follows:
3. Experimental Details
3.1. Data Preparation
3.1.1. Simulation Dataset
Based on the ArduPilot simulation flight control software, we simulated the aeromagnetic compensation calibration flight process for the fixed-wing aircraft Cessna-208B. The simulated flight path and maneuvering angle changes are shown in Figure 5, where the start recording position is 112.729° E, 16.720° N, the stop recording position is 112.734° E, 16.779° N (excluding takeoff and landing), and the average flight altitude is 3000 m. The simulated flight consists of two maneuvering circles, each consisting of four orthogonal flight segments with a length of 10 km on one side. The aircraft performs pitch, yaw, and roll movements of 5° to 15° in each of the four orthogonal directions.
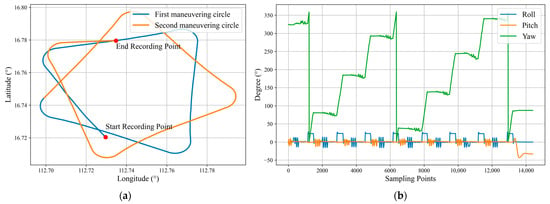
Figure 5.
The flight maneuver simulation results: (a) the longitude and latitude of the flight path; (b) flight attitude changes during the route.
We simulated the main magnetic interference components of the flight platform based on the magnetic inclination, magnetic declination, and geomagnetic field strength at an altitude of 3000 m in the South China Sea (112.7° E, 17.6° N). The intrinsic magnetic field was simulated through the magnetic dipoles of motors and engines located on the aircraft’s flaps, elevators, and rudders as field sources, as shown in Figure 6a. The induced magnetic field was simulated through finite element models of the aircraft’s aluminum fuselage, steel fuel tank, and engine compartment, as shown in Figure 6b. In order to simulate the eddy-current magnetic field, the aircraft skin was regarded as equivalent to multiple coils located on the wings, nose, and tail, as shown in Figure 6c. Changes in the background magnetic field will cause changes in the magnetic flux passing through the coils, thereby generating eddy currents. The current will continue to change to form the corresponding eddy-current magnetic field. An optical pump magnetic sensor and a three-axis fluxgate sensor are installed in the center of the cabin to calculate the three types of magnetic interference at the sensor location.
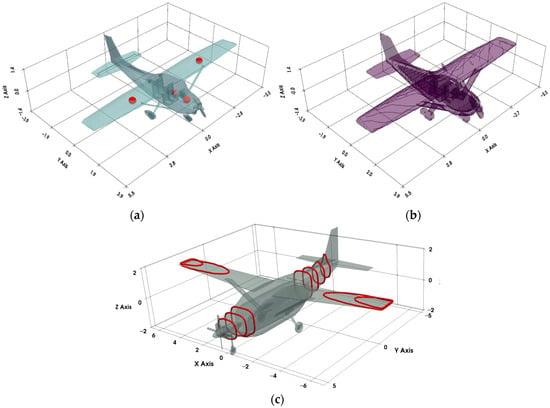
Figure 6.
Illustration of flight platform interference simulation, where the gray part represents the aircraft model: (a) position of magnetic dipoles in intrinsic magnetic field simulation (indicated by red dots); (b) finite element division in induced magnetic field simulation (indicated by the purple square); (c) position of equivalent coils in eddy-current magnetic field simulation (indicated by red lines).
The magnetic signal on the route was collected at a frequency of 10 Hz based on the above simulation strategy, as shown in Figure 7.
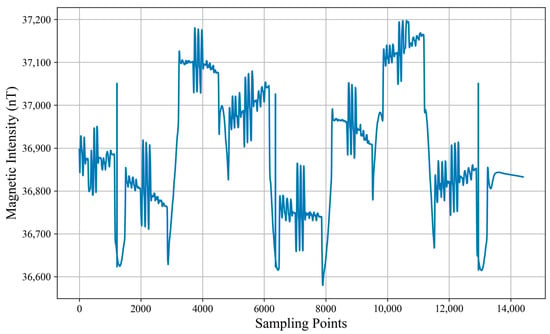
Figure 7.
Total magnetic signal collected on the simulated route.
3.1.2. Real Dataset
The real dataset is based on flights 1002.02, 1002.20, and 1006.06 of the DAF-MIT AIA Open Flight Data [20], with 1002.02 used for training and the rest used for testing. The data collected include the aircraft attitude angle, magnetic sensors, accelerometers, longitude, latitude, altitude, current, and voltage. Among the five optical pump magnetic sensors, sensor 1 is located on the tail of the aircraft; sensors 2 and 5 are located at the front and rear of the cabin, respectively; and sensors 3 and 4 are located in the middle of the cabin. Fluxgate sensor B is located in the rear of the cabin, while sensors A, C, and D are located in the middle of the cabin. In this article, we will use data from optical pump sensor 5 and fluxgate sensor B.
3.2. Model Parameters
In terms of the input dimension of the neural network, based on a 10 Hz sampling rate, the input sequence length was set to 320 sampling points (32 s). The different datasets have different input features. In the simulation dataset experiment, 16 direction cosine coefficients (mentioned in Section 2.1) and three attitude angles (roll, pitch, and yaw) were selected as input features. In the real dataset experiment, nine additional current and voltage terms were added.
In terms of the convolutional layer parameters, the convolution kernel size of DWConv is set to 51, and the stride is set to 1; the convolution kernel size of PWConv is set to 1, and the stride is set to 1. For model training, the batch size is set to 256, the neural network optimizer is Adam, the learning rate is set to 0.001, and the number of training epochs is set to 200. In terms of the hardware environment, we used a computer with an Intel 12th Core Gen i5-13600KF CPU and a GeForce RTX 4060Ti GPU.
3.3. Evaluation Metrics
The standard deviation (STD) of the residual magnetic interference after aeromagnetic compensation and the improvement ratio (IR) are usually used to evaluate compensation accuracy. The standard deviation can be expressed as follows:
where represents the residual magnetic interference of the signal after aeromagnetic compensation, which is obtained by bandpass filtering (usually within 0.1–0.6 Hz frequency [11]); represents the -th sampling point; represents the arithmetic mean within the bandpass; and represents the number of sampling points, which is consistent with the length of the original signal before aeromagnetic compensation.
The improvement rate is used to evaluate the degree of reduction in magnetic interference. It is calculated as the ratio of the standard deviation of magnetic interference in the bandpass before and after compensation and can be expressed as follows:
where represents the standard deviation of the magnetic interference in the bandpass of the original signal; represents the standard deviation of the magnetic interference in the bandpass after aeromagnetic compensation. The higher the improvement ratio, the higher the compensation accuracy.
4. Results and Discussion
4.1. Simulation Dataset Test Results
In this section, we compare MagTCN with several typical aeromagnetic compensation methods, including the three-branch neural network method proposed by Williams (hereafter WilliamsNN) [10], the simple backpropagation neural network method without a convolution structure (hereafter BPNN) [19], the convolutional residual neural network method using normal convolution (hereafter ResNet) [16], and the traditional linear regression T–L model method (hereafter T–L model) [6].
During the neural network training phase, we compared the convergence capabilities of several methods based on the data from the first maneuvering circle, as shown in Figure 8 and Table 1. The x-axis (Epochs) represents the number of times the entire training dataset is propagated forward and backward in the neural network. The y-axis (Loss) represents the error between the model’s predicted values and the actual target values, as described in Section 2.3. Curves of different colors represent the loss between the predicted and label values of the corresponding neural network during the training process as the number of epochs increases. The faster the loss drops to a flat state, the faster the convergence. In Figure 8, WilliamsNN and BPNN do not fully converge at the 200th epoch. WilliamsNN has the slowest convergence speed and maintains a stable decline rate throughout the training phase. BPNN has a slightly better convergence speed, maintaining a faster decline rate before the sixth epoch and then maintaining a stable decline rate. ResNet and MagTCN both have faster convergence speeds and can achieve lower losses in the first few epochs, reaching full convergence in the 150th and 110th epochs, respectively. However, ResNet’s loss fluctuates throughout the training phase and is relatively unstable. In contrast, MagTCN’s loss is the fastest to reach a stable state with the same hyperparameters, demonstrating its fast and stable convergence ability.
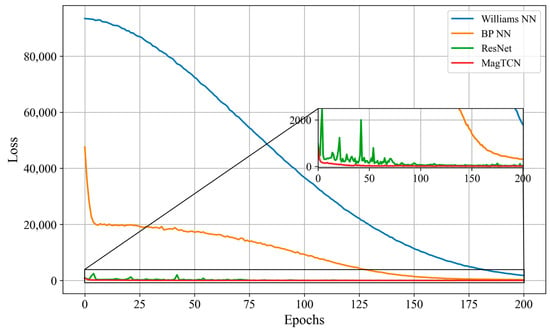
Figure 8.
The losses of neural networks using simulation datasets.

Table 1.
Statistics of neural network losses using simulation datasets.
Next, we compared the compensation accuracy and generalization of several compensation methods based on the data from the second maneuvering circle. Figure 9 shows the residual interference in the bandpass (0.1–0.6 Hz) of the magnetic signal on the route, where the curve named “origin” represents the interference before compensation, and the other curves represent the residual interference after compensation by the corresponding method. Large maneuvers during flight can cause large interferences (such as in the interval around the 1000th sampling point). The purpose of the compensation method is to eliminate these interferences as much as possible. The less residual interference there is after compensation, the better the compensation method. WilliamsNN has the worst compensation effect, and there is still more than 10 nT residual interference in some intervals (such as in the intervals from 4000 to 5000 sampling points and from 1500 to 2000 sampling points). BPNN has a slightly better compensation effect and can keep the residual interference within 1 nT in most intervals. However, in some intervals, residual interference is greater with BPNN than with WilliamsNN (as shown in the local enlarged figure of Figure 9). The T–L model, ResNet, and MagTCN all maintain low residual interference in the entire interval, making them much better than BPNN and WilliamsNN. In order to further compare the performance of several compensation methods, we calculated their STDs and IRs after compensation (as defined in Section 3.3, the lower the STD and the higher the IR, the better the compensation performance). As shown in Table 2, WilliamsNN has the worst STD and IR, which are 1.320 nT and 12.276, respectively. Those of BPNN are slightly better: 0.551 nT and 29.401, respectively. The compensation performance of the T–L model is better than that of BPNN and WilliamsNN, with an STD and IR of 0.037 nT and 427.641, respectively, which shows that the neural network compensation method that has not fully converged performs worse than the traditional T–L model compensation method. ResNet and MagTCN achieve full convergence in the training phase due to the convolutional structure and residual connection. Therefore, they are better than the T–L model in compensation performance. Among them, the STD and IR of ResNet are 0.033 nT and 480.082, respectively, and those of MagTCN are 0.024 nT and 651.61, respectively. The above results show that, based on the separable convolutional neural network structure and loss function proposed in this article, MagTCN is better than ResNet in compensation performance and has achieved the best compensation performance and generalization ability among the above compensation methods.
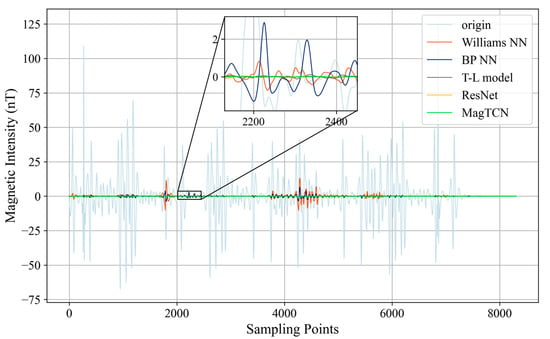
Figure 9.
Compensation results within the bandpass from simulation datasets.

Table 2.
The statistics of compensation results within the bandpass from simulation datasets.
4.2. DAF-MIT AIA Open Flight Data Test Results for Flight 1002.20
In this section, we compare MagTCN with several typical aeromagnetic compensation methods, including WilliamsNN, BPNN, and ResNet.
During the neural network training phase, we compared the convergence capabilities of several methods based on flight 1002.02 of the DAF-MIT AIA Open Flight Data mentioned in Section 3.1.2, as shown in Figure 10 and Table 3. The x-axis (Epochs) represents the number of times the entire training dataset is propagated forward and backward in the neural network. The y-axis (Loss) represents the error between the model’s predicted values and the actual target values, as described in Section 2.3. Curves of different colors represent the loss between the predicted and label values of the corresponding neural network during the training process as the number of epochs increases. The faster the loss drops to a flat state, the faster the convergence. In Figure 10, WilliamsNN and BPNN do not fully converge at the 200th epoch. WilliamsNN has the slowest convergence speed and maintains a stable decline rate throughout the training phase. BPNN has a slightly better convergence speed, maintaining a faster decline rate before the sixth epoch and then maintaining a stable decline rate. ResNet and MagTCN both have faster convergence speeds and can achieve lower losses in the first few epochs, reaching full convergence in the 150th and 100th epochs, respectively. However, ResNet’s loss fluctuates throughout the training phase and is relatively unstable. In contrast, MagTCN’s loss is the fastest to reach a stable state with the same hyperparameters, demonstrating its fast and stable convergence ability.
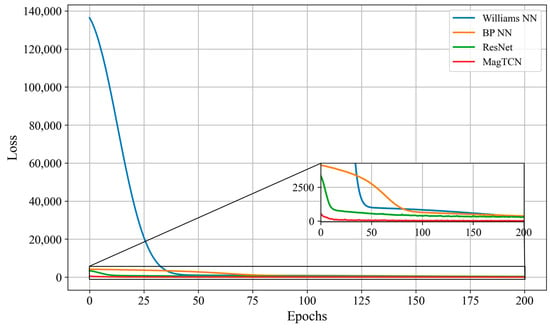
Figure 10.
The losses of neural networks using real datasets.

Table 3.
The statistics of neural network losses using real datasets.
Next, we compared the compensation accuracy and generalization of several compensation methods based on flight 1002.20 of the DAF-MIT AIA Open Flight Data. Figure 11 shows the residual interference in the bandpass (0.1–0.6 Hz) of the magnetic signal on the route, where the curve named “origin” represents the interference before compensation, and the other curves represent the residual interference after compensation by the corresponding method. Large maneuvers during flight can cause large interference (such as around the 1000th sampling point). The purpose of the compensation method is to eliminate these interferences as much as possible. The less residual interference there is after compensation, the better the compensation method. WilliamsNN has the worst compensation effect, and there is still more than 5 nT residual interference in some intervals (such as in the intervals from 5000 to 5500 sampling points, from 7500 to 8000 sampling points, and from 12000 to 12500 sampling points). BPNN has a slightly better compensation effect and can keep the residual interference within 5 nT in most intervals. However, in some intervals, residual interference is greater with BPNN than with WilliamsNN (as shown in the local enlarged figure in Figure 11). ResNet and MagTCN all maintain low residual interference in the entire interval, making them much better than BPNN and WilliamsNN. In order to further compare the performance of several compensation methods, we calculated their STDs and IRs after compensation (as defined in Section 3.3, the lower the STD and the higher the IR, the better the compensation performance). As shown in Table 4, WilliamsNN has the worst STD and IR, which are 1.399 nT and 8.342, respectively. Those of BPNN are slightly better: 1.098 nT and 10.629, respectively. ResNet and MagTCN are better than WilliamsNN and BPNN in compensation performance due to their convolutional structures and residual connections. The STD and IR of ResNet are 0.028 nT and 402.786, respectively, and those of MagTCN are 0.025 nT and 455.920, respectively. The above results show that MagTCN has achieved the best compensation performance and generalization ability among the above compensation methods.
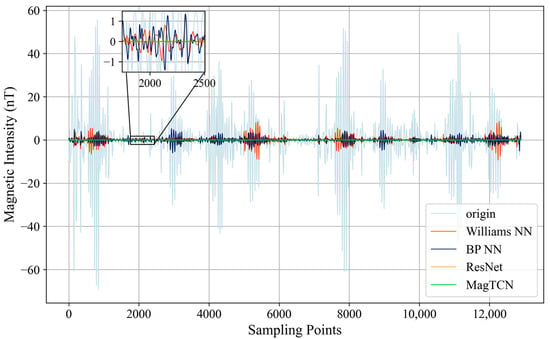
Figure 11.
Compensation results within the bandpass of the flight 1002.20 signal.

Table 4.
The statistics of compensation results within the bandpass of the flight 1002.20 signal.
4.3. DAF-MIT AIA Open Flight Data Test Results for Flight 1006.06
In this section, we compare the compensation accuracy and generalization of several compensation methods based on flight 1006.06 of the DAF-MIT AIA Open Flight Data. Figure 12 shows the residual interference in the bandpass (0.1–0.6 Hz) of the magnetic signal on the route, where the curve named “origin” represents the interference before compensation, and the other curves represent the residual interference after compensation by the corresponding method. Large maneuvers during flight can cause large interference (such as around the 5000th sampling point). The purpose of the compensation method is to eliminate these interferences as much as possible. The less residual interference there is after compensation, the better the compensation method. BPNN has the worst compensation effect due to its poor generalization ability, and the residual interference is close to that before compensation in most intervals. Only some intervals (such as in the interval from 4000 to 6000 sampling points) have compensation effects. WilliamsNN has a better compensation effect and can keep the residual interference within 10 nT in most intervals. However, in some intervals (such as around the 500th and 6000th sampling points), there are still obvious residual interferences. ResNet and MagTCN all maintain low residual interference in the entire interval, which is much better than BPNN and WilliamsNN. In order to further compare the performance of several compensation methods, we calculated their STDs and IRs after compensation (as defined in Section 3.3, the lower the STD and the higher the IR, the better the compensation performance). As shown in Table 5, BPNN has the worst STD and IR, which are 10.664 nT and 1.436, respectively. Those of WilliamsNN are better: 2.099 nT and 7.298, respectively. ResNet and MagTCN are better than WilliamsNN and BPNN in compensation performance due to their convolutional structures and residual connections. The STD and IR of ResNet are 0.049 nT and 308.679, respectively, and those of MagTCN are 0.037 nT and 414.090, respectively. The above results show that MagTCN has achieved the best compensation performance and generalization ability among the above compensation methods.
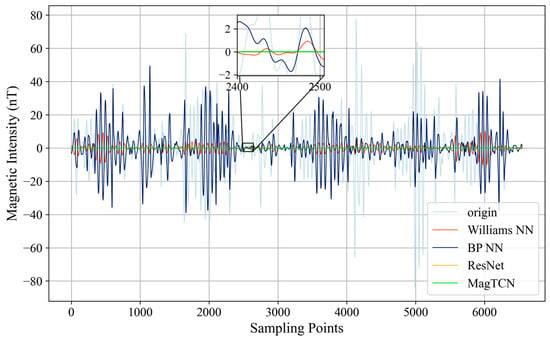
Figure 12.
Compensation results within the bandpass of the flight 1006.06 signal.

Table 5.
The statistics of compensation results within the bandpass of the flight 1006.06 signal.
4.4. Compensation Algorithm Resource Consumption Test Results
In this section, we compare the time cost and floating-point operations (FLOPs) of MagTCN and the other compensation algorithms mentioned above to ensure that the proposed method can meet the requirements of real-time aeromagnetic compensation. The hardware and hyperparameters used in the experiment are basically the same as those in Section 3.2. In addition, we set the batch size to 1 to simulate the real-time environment and selected 30,000 inputs to test the average time cost.
As shown in Table 6, BPNN and WilliamsNN have lower average time costs and FLOPs due to their simple structures. The average time cost and FLOPs of BPNN are 0.428 ms and 0.238 MB, respectively, and those of WilliamsNN are 0.428 ms and 0.238 MB, respectively. ResNet and MagTCN take more time, 1.240 ms and 1.837 ms, respectively, but still meet the real-time requirements at a sampling frequency of 10 Hz (<100 ms). Their FLOPs can also be achieved by most graphics processing units [31].

Table 6.
Resource consumption of several compensation algorithms.
5. Conclusions
Past research into neural-network-based aeromagnetic compensation methods usually employed normal convolution structures, resulting in low generalization of the algorithm. In this article, we propose an aeromagnetic compensation method, MagTCN, based on temporal convolutional networks, to improve both generalization and compensation accuracy. In the proposed method, a neural network based on separable convolution with a residual connection is employed to improve the compensation accuracy and convergence stability, and a gradient correction loss function based on the Tolles–Lawson model is used to improve the generalization ability. We conducted experiments based on both simulated and real datasets and compared typical neural network compensation methods proposed by previous researchers. The results indicate that the method proposed in this article can achieve a lower standard deviation of residual magnetic interference than other neural network methods, demonstrating a better compensation performance and generalization ability. In future work, we will further study the relationship between the input sequence length, convolution kernel receptive field, and compensation accuracy in temporal convolutional networks to achieve higher compensation performance.
Author Contributions
Conceptualization, B.Z.; methodology, B.Z. and H.W.; software, H.W.; validation, B.Z. and H.W.; formal analysis, B.Z.; investigation, B.Z. and H.W.; resources, B.Z.; data curation, B.Z.; writing—original draft preparation, H.W.; writing—review and editing, B.Z. and H.W.; visualization, H.W.; supervision, B.Z.; project administration, B.Z.; funding acquisition, B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the School of Computer Science, China University of Geosciences (Wuhan), for providing the deep learning servers.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tolles, W.E.; Lawson, J.D. Magnetic Compensation of MAD Equipped Aircraft; Airborne Instruments Lab. Inc.: Mineola, NY, USA, 1950; p. 201. [Google Scholar]
- Tolles, W.E. Compensation of Aircraft Magnetic Fields. U.S. Patent 2,692,970, 26 October 1954. [Google Scholar]
- Tolles, W.E. Magnetic Field Compensation System. U.S. Patent 2,706,801, 19 April 1955. [Google Scholar]
- Tolles, W.E. Eddy-Current Compensation. U.S. Patent 2,802,983, 13 August 1957. [Google Scholar]
- Leliak, P. Identification and evaluation of magnetic-field sources of magnetic airborne detector equipped aircraft. IRE Trans. Aerosp. Navig. Electron. 1961, ANE-8, 95–105. [Google Scholar] [CrossRef]
- Leach, B.W. Aeromagnetic compensation as a linear regression problem. In Information Linkage Between Applied Mathematics and Industry; Elsevier: Amsterdam, The Netherlands, 1980; pp. 139–161. [Google Scholar]
- Feng, Y.; Zhang, Q.; Zheng, Y.; Qu, X.; Wu, F.; Fang, G. An improved aeromagnetic compensation method robust to geomagnetic gradient. Appl. Sci. 2022, 12, 1490. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, K.; Yan, B.; Zhu, W. The Conjunctive Compensation Method Based on Inertial Navigation System and Fluxgate Magnetometer. Appl. Sci. 2023, 13, 5138. [Google Scholar] [CrossRef]
- Chen, B.; Huang, L.; Zhang, K.; Hu, J.; Zhu, W. Magnetic interference analysis and compensation method of airborne electronic equipment in an unmanned aerial vehicle. Appl. Sci. 2023, 13, 7455. [Google Scholar] [CrossRef]
- Williams, P.M. Aeromagnetic compensation using neural networks. Neural Comput. Appl. 1993, 1, 207–214. [Google Scholar] [CrossRef]
- Bickel, S.H. Small signal compensation of magnetic fields resulting from aircraft maneuvers. IEEE Trans. Aerosp. Electron. Syst. 2007, AES-15, 518–525. [Google Scholar] [CrossRef]
- Ma, M.; Zhou, Z.; Cheng, D. A dual estimate method for aeromagnetic compensation. Meas. Sci. Technol. 2017, 28, 115904. [Google Scholar] [CrossRef]
- Xu, X.; Huang, L.; Liu, X.; Fang, G. Deepmad: Deep learning for magnetic anomaly detection and denoising. IEEE Access 2020, 8, 121257–121266. [Google Scholar] [CrossRef]
- Yu, P.; Zhao, X.; Jia, J.; Zhou, S. An improved neural network method for aeromagnetic compensation. Meas. Sci. Technol. 2021, 32, 045106. [Google Scholar] [CrossRef]
- Li, L.; Xu, Q.; Gu, H.; Zhou, L.; Liu, Z.; Cao, L. Aeromagnetic compensation algorithm based on levenberg-marquard neural network. J. Geod. Geoinf. Sci. 2021, 4, 74–83. [Google Scholar]
- Yu, P.; Bi, F.; Jiao, J.; Zhao, X.; Zhou, S.; Su, Z. An Aeromagnetic Compensation Algorithm Based on a Residual Neural Network. Appl. Sci. 2022, 12, 10759. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, C.; Su, Z.; Yu, P.; Jiao, J. An aeromagnetic compensation algorithm based on radial basis function artificial neural network. Appl. Sci. 2022, 13, 136. [Google Scholar] [CrossRef]
- Jiao, J.; Yu, P.; Zhao, X.; Bi, F. Real-time aeromagnetic compensation with compressed and accelerated neural networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, Q.; Song, J.; Zuo, C.; Dong, K.; Jin, F. An Aeromagnetic Compensation Algorithm Based on Broad Learning System. In Proceedings of the 2024 3rd International Conference on Robotics, Artificial Intelligence and Intelligent Control (RAIIC), Mianyang, China, 5–7 July 2024; pp. 373–377. [Google Scholar]
- Gnadt, A.R.; Belarge, J.; Canciani, A.J.; Conger, L.; Curro II, J.A.; Edelman, A.; Morales, P.; O’Keeffe, M.F.; Taylor, J.; Jacobs, D. DAF-MIT AIA Open Flight Data for Magnetic Navigation Research. Available online: https://zenodo.org/records/12723700 (accessed on 7 February 2025).
- Gnadt, A. Machine learning-enhanced magnetic calibration for airborne magnetic anomaly navigation. In Proceedings of the AIAA SciTech 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1760. [Google Scholar]
- Wang, Y.; Han, Q.; Zhan, D.; Li, Q. A data-driven OBE magnetic interference compensation method. Sensors 2022, 22, 7732. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Zhang, L.; Liu, S. A-TCN: Attention-Based TCN for OSS Reliability Prediction on High-Dimensional Fault Dataset. In Proceedings of the 2024 IEEE 24th International Conference on Software Quality, Reliability, and Security Companion (QRS-C), Cambridge, UK,, 1–5 July 2024; pp. 187–195. [Google Scholar]
- Xiang, X.; Li, X.; Zhang, Y.; Hu, J. A short-term forecasting method for photovoltaic power generation based on the TCN-ECANet-GRU hybrid model. Sci. Rep. 2024, 14, 6744. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Wang, Z. TCN-attention-HAR: Human activity recognition based on attention mechanism time convolutional network. Sci. Rep. 2024, 14, 7414. [Google Scholar] [CrossRef] [PubMed]
- Larsson, J. Electromagnetics from a quasistatic perspective. Am. J. Phys. 2007, 75, 230–239. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Kim, T.; Kim, J.; Tae, Y.; Park, C.; Choi, J.-H.; Choo, J. Reversible instance normalization for accurate time-series forecasting against distribution shift. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Vassilieva, N. Characterization and Benchmarking of Deep Learning. 2017. Available online: https://www.hpcuserforum.com/presentations/Wisconsin2017/HPDLCookbook4HPCUserForum.pdf (accessed on 7 February 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).