Tuning Optical Performance of Silicon Solar Cells with Micro-Structured Multilayer Antireflection Coatings
Abstract
1. Introduction
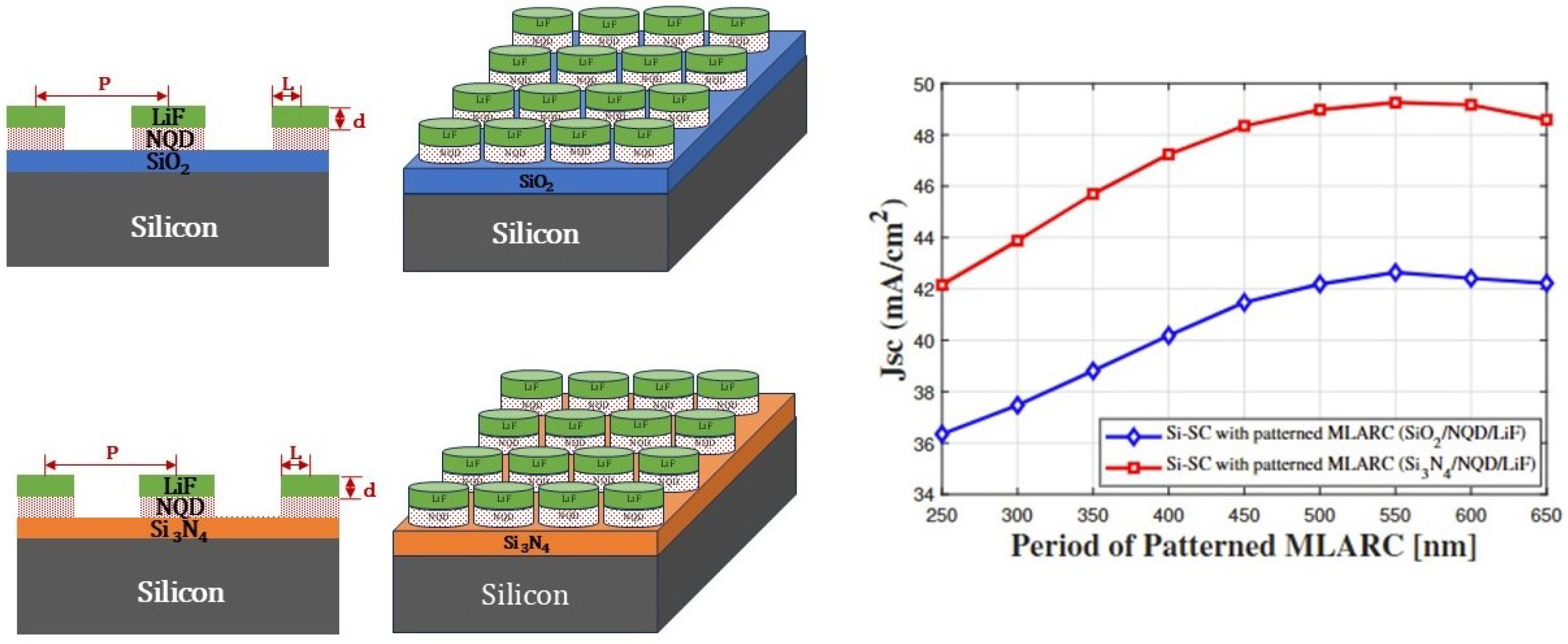
2. Proposed Device Structures
3. Experimental Procedure
4. Experimental Characterization of Si-SC Structures with SLARC
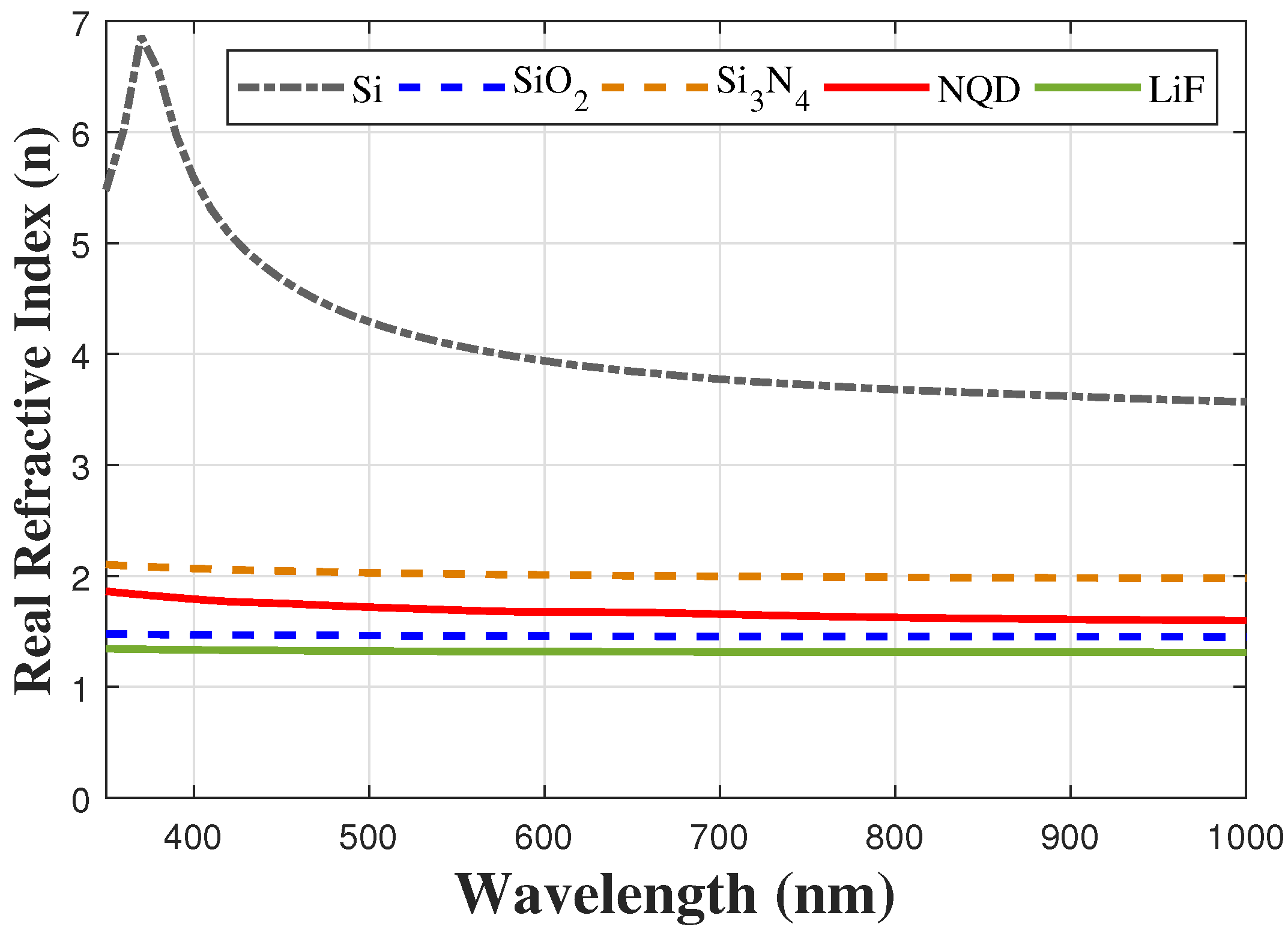
4.1. Refractive Index Characteristics
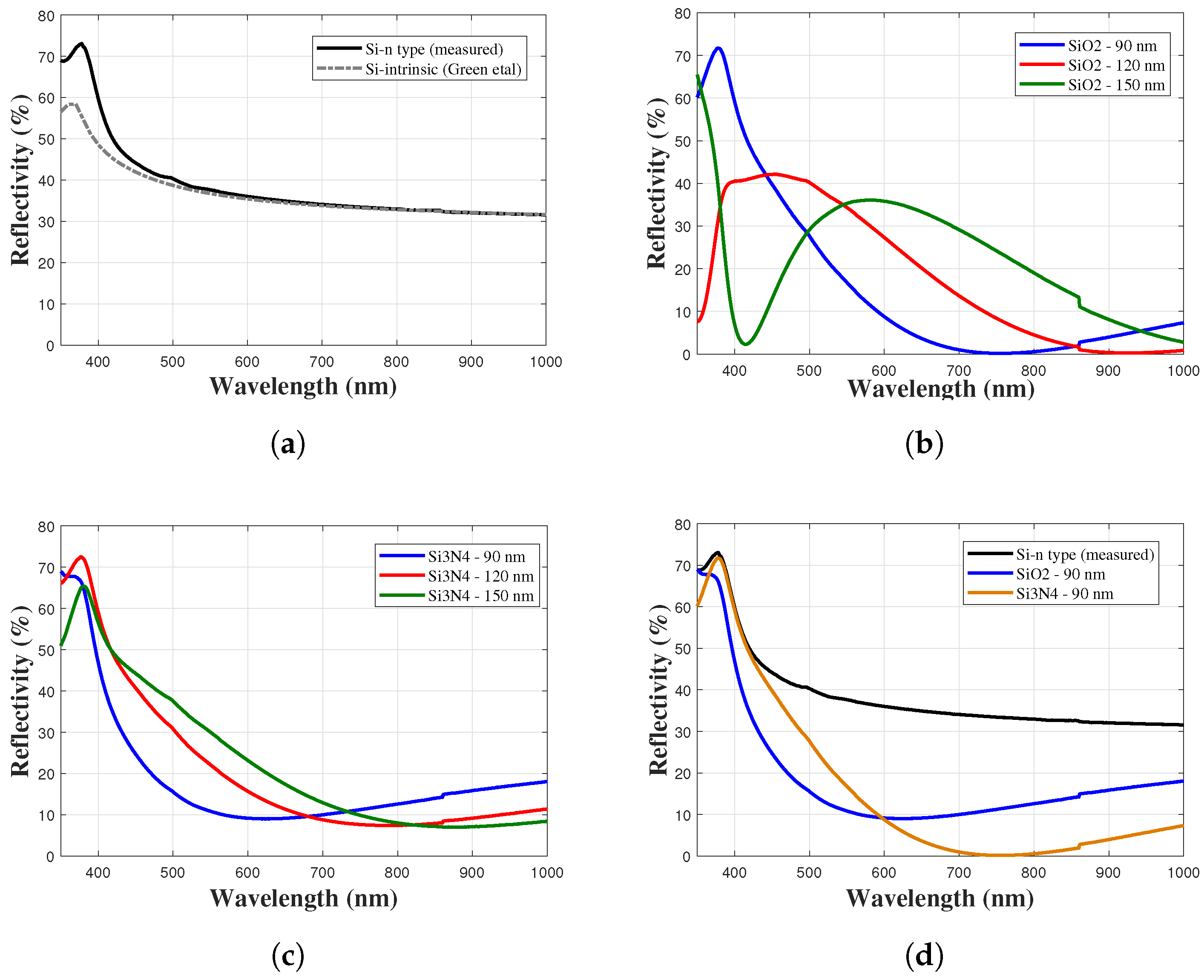
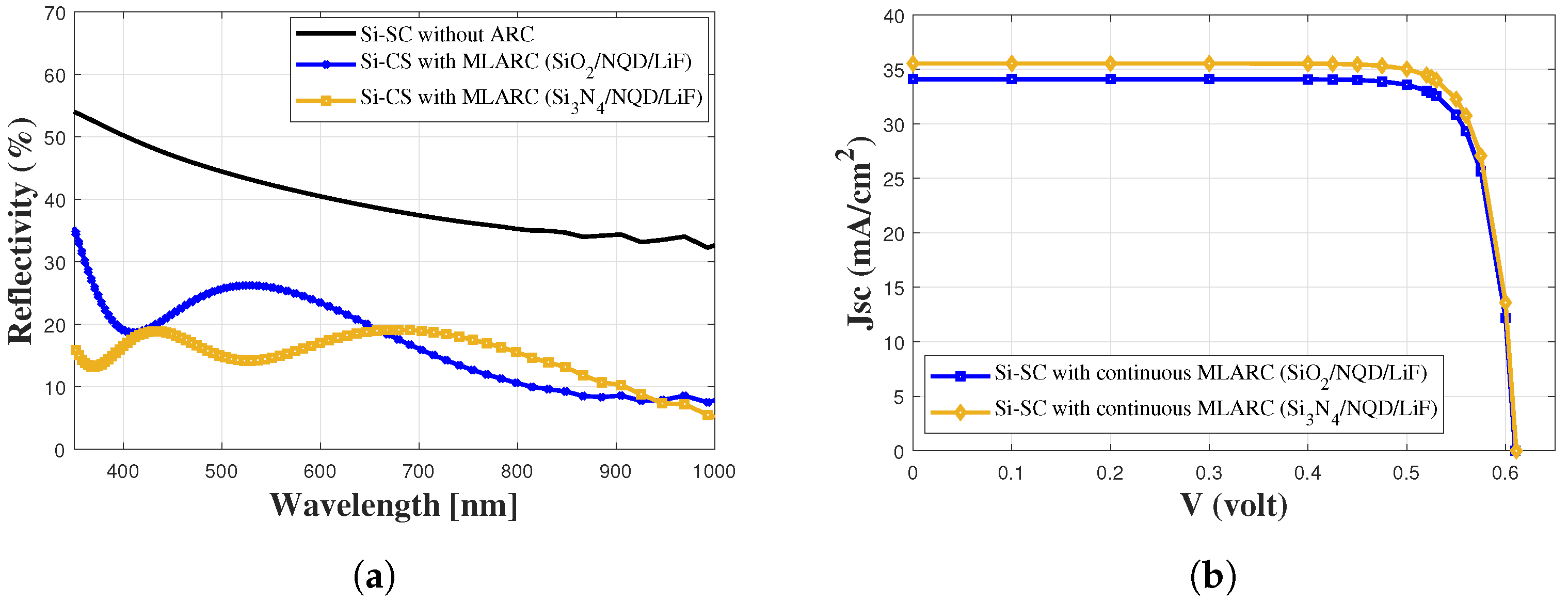
4.2. Optical Reflectivity Characteristics
5. Modeling and Simulating Si-SC Structures
5.1. Optical Modeling and Simulation
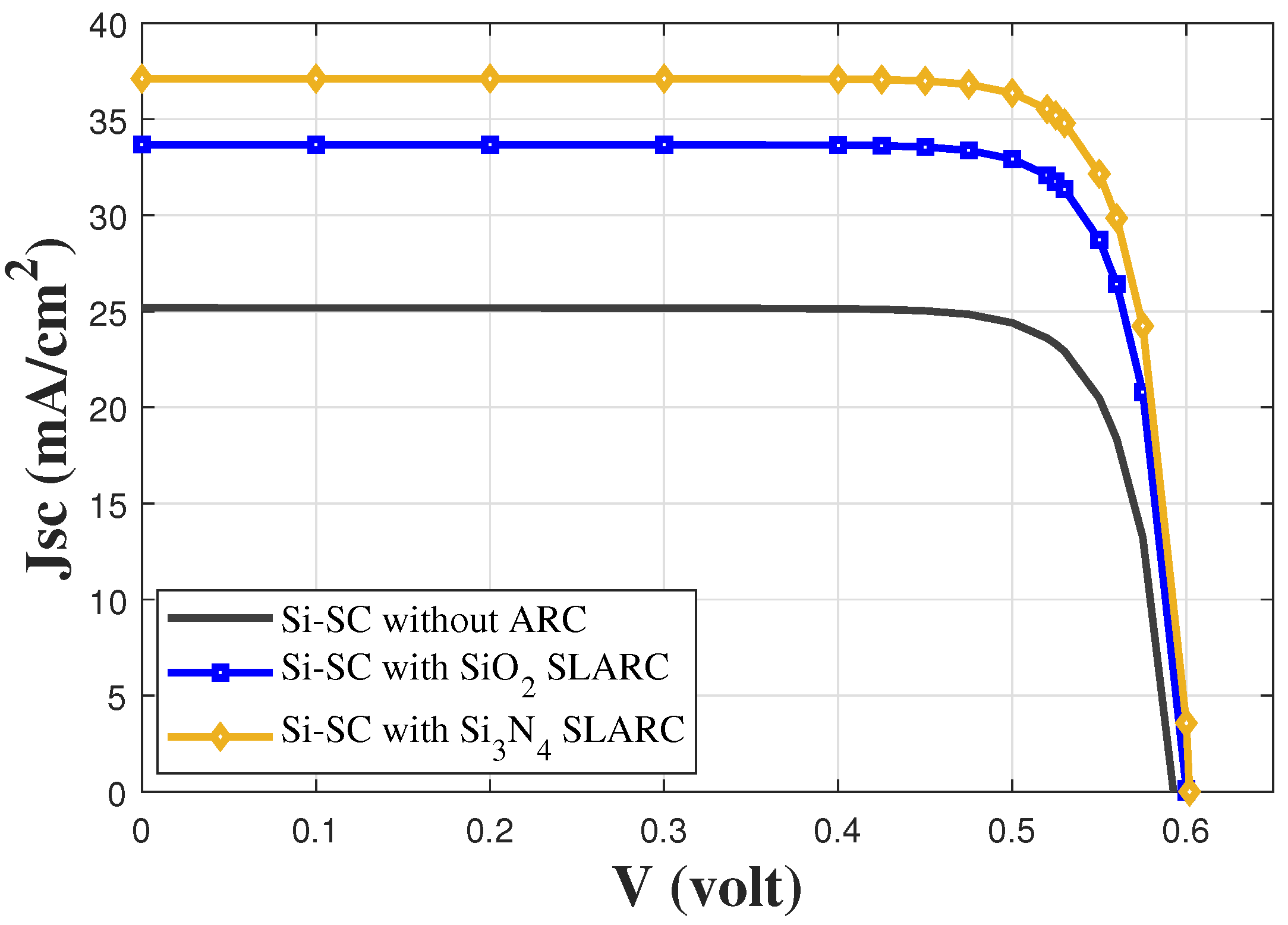
5.2. Electrical Modeling and Simulation
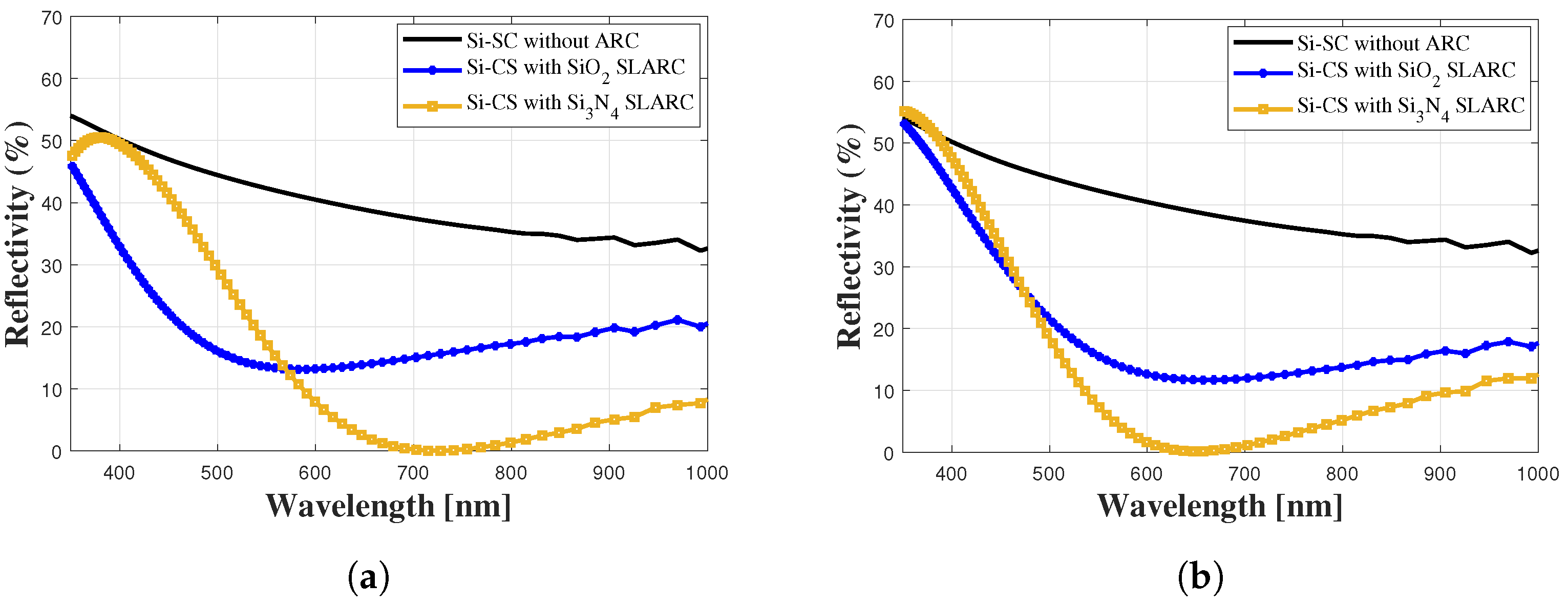
5.3. Modeling and Simulation of Si-SC with SLARC
5.4. Modeling and Simulation of Si-SC with Continuous MLARC
5.5. Modeling and Simulation of Si-SC with Patterned MLARC
- Improved light trapping: The periodic patterns scatter incident light, increasing the optical path length within the active region and promoting multiple reflections, leading to enhanced light absorption.
- Enhanced carrier generation: The NQD layer absorbs photons at shorter wavelengths and re-emits them at longer wavelengths through a downshifting process. These downshifted photons are more effectively absorbed by the semiconductor layer, resulting in increased carrier generation.
- Reduced reflection losses: The optimized pattern design minimizes reflection at the top surface of the solar cell, allowing a higher proportion of incident light to be coupled into the device.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Machín, A.; Márquez, F. Advancements in Photovoltaic Cell Materials: Silicon, Organic, and Perovskite Solar Cells. Materials 2024, 17, 1165. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.J.; Sun, M.; Davis, K.O. Photon management in silicon photovoltaic cells: A critical review. Sol. Energy Mater. Sol. Cells 2024, 267, 112715. [Google Scholar] [CrossRef]
- Dhawan, P.; Gaudig, M.; Sprafke, A.; Piechulla, P.; Wehrspohn, R.B.; Rockstuhl, C. Anti-Reflective Graded-Index Metasurface with Correlated Disorder for Light Management in Planar Silicon Solar Cells. Adv. Opt. Mater. 2024, 12, 2302964. [Google Scholar] [CrossRef]
- Valiei, M.; Shaibani, P.M.; Abdizadeh, H.; Kolahdouz, M.; Asl Soleimani, E.; Poursafar, J. Design and optimization of single, double and multilayer anti-reflection coatings on planar and textured surface of silicon solar cells. Mater. Today Commun. 2022, 32, 104144. [Google Scholar] [CrossRef]
- Ovcharenko, O.; Dyakonenko, N.; Tavrina, T.; Lyubchenko, O. Computation of the parameters of single- and double-layer anti-reflective coatings for their effective use. In Proceedings of the 2022 IEEE 3rd KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 3–7 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Addie, A.J.; Ismail, R.A.; Mohammed, M.A. Amorphous carbon nitride dual-function anti-reflection coating for crystalline silicon solar cells. Sci. Rep. 2022, 12, 9902. [Google Scholar] [CrossRef] [PubMed]
- Dumont, L.; Benzo, P.; Cardin, J.; Yu, I.S.; Labbe, C.; Marie, P.; Dufour, C.; Zatryb, G.; Podhorodecki, A.; Gourbilleau, F. Down-shifting Si-based layer for Si solar applications. Sol. Energy Mater. Sol. Cells 2017, 169, 132–144. [Google Scholar] [CrossRef]
- Lv, T.; Tang, Y.; Fan, H.; Liu, S.; Zeng, S.; Liu, W. Carbon quantum dots anchored on the anti-reflection silica layer as solid luminescence down-shifting materials in solar panel encapsulation. Sol. Energy Mater. Sol. Cells 2022, 235, 111450. [Google Scholar] [CrossRef]
- Feng, B.; Chen, W.; Xing, G.; Chen, X.; Li, H.; Sun, Z.; Zhang, Y.; Liu, Y.; Du, X. Influence of inverted pyramid texturization on front metallization and performance of crystalline silicon solar cells. Sol. Energy Mater. Sol. Cells 2024, 272, 112919. [Google Scholar] [CrossRef]
- Lopez-Delgado, R.; Higuera-Valenzuela, H.; Zazueta-Raynaud, A.; Ramos-Carrazco, A.; Pelayo, J.; Berman-Mendoza, D.; Álvarez-Ramos, M.; Ayon, A. Solar cell efficiency improvement employing down-shifting silicon quantum dots. Microsyst. Technol. 2018, 24, 495–502. [Google Scholar] [CrossRef]
- Flores-Pacheco, A.; Álvarez-Ramos, M.E.; Ayón, A. Down-shifting by quantum dots for silicon solar cell applications. In Solar Cells and Light Management; Elsevier: Amsterdam, The Netherlands, 2020; pp. 443–477. [Google Scholar]
- Masaadeh, Q.; Kaplani, E.; Chao, Y. Luminescent downshifting silicon quantum dots for performance enhancement of polycrystalline silicon solar cells. Electronics 2022, 11, 2433. [Google Scholar] [CrossRef]
- Sabeeh, A.H.; Price, J.S.; Ruzyllo, J. Effect of lift-off conditions on micropatterning of nanocrystalline quantum dot films. J. Vac. Sci. Technol. B 2017, 35, 061802. [Google Scholar] [CrossRef]
- Sabeeh, A.H.; Brigeman, A.N.; Ruzyllo, J. Performance of single-crystal silicon solar cells with mist-deposited nanocrystalline quantum dot downshifting films. IEEE J. Photovolt. 2019, 9, 1006–1011. [Google Scholar] [CrossRef]
- Green, M.A.; Keevers, M.J. Optical properties of intrinsic silicon at 300 K. Prog. Photovolt. Res. Appl. 1995, 3, 189–192. [Google Scholar] [CrossRef]
- Green, M.A. Improved silicon optical parameters at 25 C, 295 K and 300 K including temperature coefficients. Prog. Photovolt. Res. Appl. 2022, 30, 164–179. [Google Scholar] [CrossRef]
- Arkhipov, V.; Poortmans, J. Thin Film Polycrystalline Silicon Solar Cells. In Thin Film Solar Cells: Fabrication, Characterization and Applications; Wiley: Hoboken, NJ, USA, 2006; pp. 97–131. [Google Scholar]
- Dement, D.B.; Puri, M.; Ferry, V.E. Determining the Complex Refractive Index of Neat CdSeCdS Quantum Dot Films. J. Phys. Chem. C 2018, 122, 21557–21568. [Google Scholar] [CrossRef]
- Dauer, V. Optical constants of lithium fluoride thin films in the far ultraviolet. J. Opt. Soc. Am. B 2000, 17, 300–303. [Google Scholar] [CrossRef]
- Hussain, S.; Mehmood, H.; Khizar, M.; Turan, R. Design and analysis of an ultra-thin crystalline silicon heterostructure solar cell featuring SiGe absorber layer. IET Circuits Devices Syst. 2018, 12, 309–314. [Google Scholar] [CrossRef]



| Structure | Thickness (nm) | Wavelength (nm) | ||||
|---|---|---|---|---|---|---|
| 350 | 450 | 550 | 650 | 750 | ||
| Si (no ARC) | intrinsic | 56.45 | 41.96 | 36.73 | 34.73 | 33.24 |
| Si (no ARC) | n-type | 68.98 | 44.18 | 37.63 | 34.93 | 33.43 |
| Si with SiO2 SLARC | 90 | 68.95 | 24.67 | 10.85 | 9.15 | 11.24 |
| 120 | 66.15 | 40.70 | 22.10 | 11.34 | 7.64 | |
| 150 | 50.97 | 44.23 | 30.02 | 17.37 | 9.88 | |
| Si with Si3N4 SLARC | 90 | 60.20 | 39.76 | 16.77 | 3.64 | 0.16 |
| 120 | 7.62 | 42.11 | 34.35 | 20.15 | 8.36 | |
| 150 | 65.46 | 12.92 | 35.30 | 33.31 | 24.17 | |
| Structure | Type | Wavelength (nm) | ||||
|---|---|---|---|---|---|---|
| 350 | 450 | 550 | 650 | 750 | ||
| Si-SC (no ARC) | measured | 68.98 | 44.18 | 37.63 | 34.93 | 33.43 |
| simulated | 51.98 | 45.77 | 41.50 | 38.45 | 35.86 | |
| Si-SC with SiO2 SLARC | measured | 68.95 | 24.67 | 10.85 | 9.15 | 11.24 |
| simulated | 46.62 | 22.52 | 13.52 | 13.85 | 16.27 | |
| Si-SC with Si3N4 SLARC | measured | 60.20 | 39.76 | 16.77 | 3.64 | 0.16 |
| simulated | 47.54 | 41.61 | 16.98 | 2.58 | 0.23 | |
| IQE | EQE | |||||
|---|---|---|---|---|---|---|
| Structure | 350 | 550 | 750 | 350 | 550 | 750 |
| Si-SC (no ARC) | 90.54 | 96.71 | 99.36 | 43.46 | 56.57 | 63.49 |
| Si-SC with SiO2 SLARC | 95.93 | 96.69 | 99.47 | 46.65 | 82.19 | 87.13 |
| Si-SC with Si3N4 SLARC | 90.55 | 96.60 | 99.25 | 41.81 | 93.14 | 94.05 |
| Structure | () | (mA/cm2) | FF | PCE (%) |
|---|---|---|---|---|
| Si-SC (no ARC) | ||||
| Si-SC with SiO2 SLARC | ||||
| Si-SC with Si3N4 SLARC |
| IQE | EQE | |||||
|---|---|---|---|---|---|---|
| Structure | 350 | 550 | 750 | 350 | 550 | 750 |
| Si-SC (no ARC) | 90.54 | 96.71 | 99.36 | 43.46 | 56.57 | 63.49 |
| Si-SC with SiO2/NQD/LiF C-MLARC | 96.49 | 98.12 | 99.59 | 63.09 | 72.73 | 86.96 |
| Si-SC with Si3N4/NQD/LiF C-MLARC | 96.48 | 98.34 | 99.51 | 81.16 | 83.93 | 82.07 |
| Structure | ( ) | (mA/cm2) | FF | PCE (%) |
|---|---|---|---|---|
| Si-SC (no ARC) | ||||
| Si-SC with SiO2/NQD/LiF C-MLARC | ||||
| Si-SC with Si3N4/NQD/LiF C-MLARC |
| IQE (%) | EQE (%) | |||||
|---|---|---|---|---|---|---|
| Structure | 350 | 550 | 750 | 350 | 550 | 750 |
| Si-SC (no ARC) | 90.54 | 96.71 | 99.36 | 43.46 | 56.57 | 63.49 |
| Si-SC with SiO2/NQD/LiF P-MLARC | 96.47 | 98.12 | 99.50 | 58.39 | 86.35 | 87.27 |
| Si-SC with Si3N4/NQD/LiF P-MLARC | 95.95 | 97.80 | 99.41 | 64.62 | 94.96 | 95.08 |
| Structure | () | (mA/cm2) | FF | PCE (%) |
|---|---|---|---|---|
| Si-SC (no ARC) | ||||
| Si-SC with SiO2/NQD/LiF P-MLARC | ||||
| Si-SC with Si3N4/NQD/LiF P-MLARC |
| Structure | Optical Parameters | Electrical Parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| 350 (nm) | 550 (nm) | 750 (nm) | - | |||||
| R (%) | EQE (%) | R (%) | EQE (%) | R (%) | EQE (%) | J (mA/cm2) | PCE (%) | |
| Si-SC (no ARC) | 51.98 | 43.46 | 41.50 | 56.57 | 35.86 | 63.49 | 25.18 | 12.27 |
| Si-SC (SiO2 SLARC) | 51.85 | 46.65 | 14.99 | 82.19 | 12.39 | 87.13 | 33.67 | 16.68 |
| Si-SC (SiO2 C-MLARC) | 34.62 | 63.09 | 25.68 | 72.73 | 12.68 | 86.96 | 34.10 | 17.26 |
| Si-SC (SiO2 P-MLARC) | 39.47 | 58.39 | 11.99 | 86.35 | 12.16 | 87.27 | 39.52 | 20.13 |
| Si-SC (Si3N4 SLARC) | 53.83 | 41.81 | 3.58 | 93.14 | 5.01 | 94.05 | 37.11 | 18.47 |
| Si-SC (Si3N4 C-MLARC) | 15.89 | 81.16 | 14.65 | 83.94 | 17.52 | 82.07 | 35.54 | 18.02 |
| Si-SC (Si3N4 P-MLARC) | 32.64 | 64.62 | 2.91 | 94.96 | 4.35 | 95.08 | 48.04 | 24.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khawaji, I.H.; Sabeeh, A.H.; Ismail, T.; Abu-Elmaaty, B.E. Tuning Optical Performance of Silicon Solar Cells with Micro-Structured Multilayer Antireflection Coatings. Appl. Sci. 2025, 15, 3053. https://doi.org/10.3390/app15063053
Khawaji IH, Sabeeh AH, Ismail T, Abu-Elmaaty BE. Tuning Optical Performance of Silicon Solar Cells with Micro-Structured Multilayer Antireflection Coatings. Applied Sciences. 2025; 15(6):3053. https://doi.org/10.3390/app15063053
Chicago/Turabian StyleKhawaji, Ibrahim H., Ala H. Sabeeh, Tawfik Ismail, and Basma E. Abu-Elmaaty. 2025. "Tuning Optical Performance of Silicon Solar Cells with Micro-Structured Multilayer Antireflection Coatings" Applied Sciences 15, no. 6: 3053. https://doi.org/10.3390/app15063053
APA StyleKhawaji, I. H., Sabeeh, A. H., Ismail, T., & Abu-Elmaaty, B. E. (2025). Tuning Optical Performance of Silicon Solar Cells with Micro-Structured Multilayer Antireflection Coatings. Applied Sciences, 15(6), 3053. https://doi.org/10.3390/app15063053






