Characterization of the Sedimentary Cover in the City of Aïn Témouchent, Northwest Algeria, Using Ambient Noise Measurements
Abstract
1. Introduction
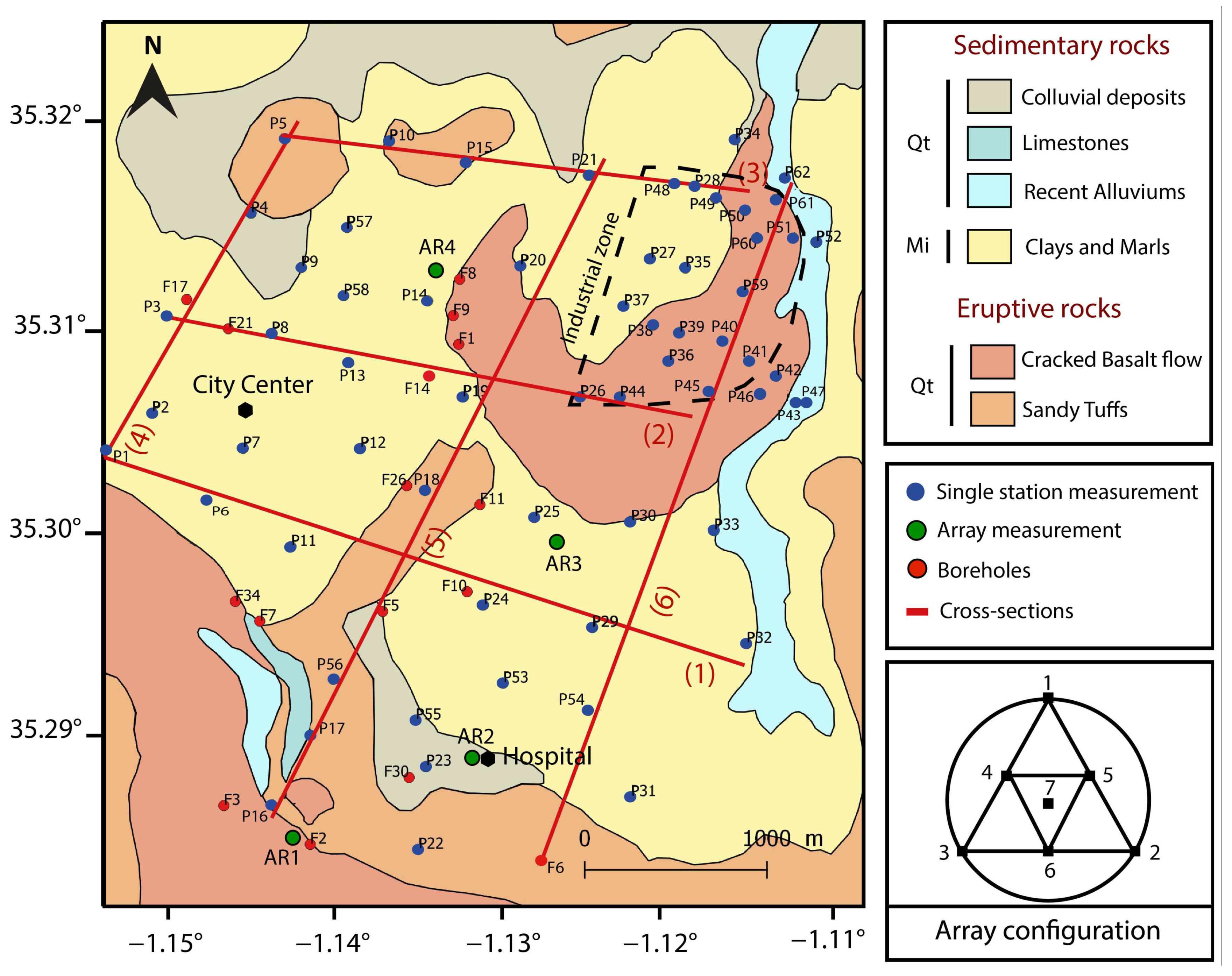
2. Geological Framework
3. Data and Methodology
3.1. Applied Techniques
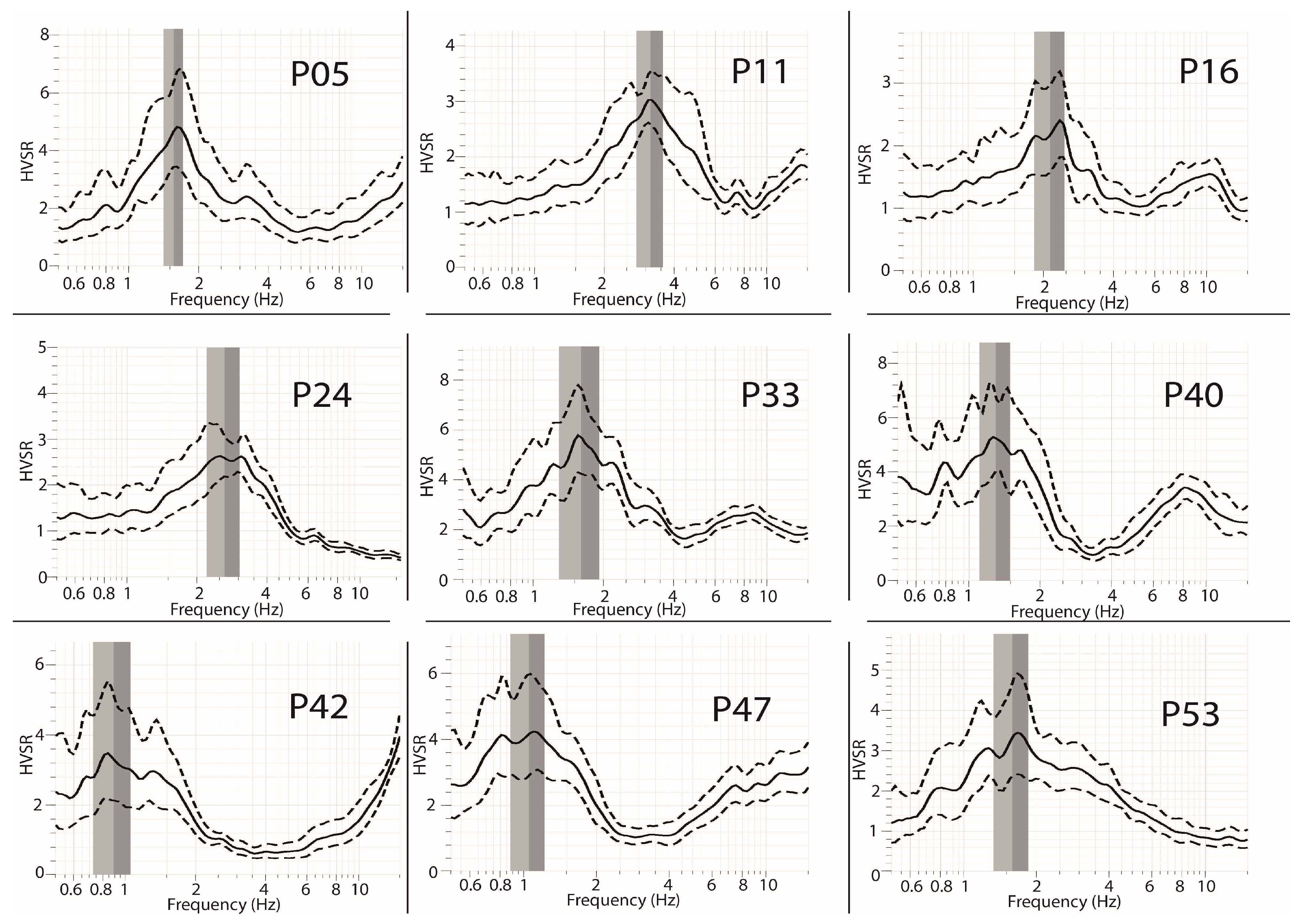
3.1.1. Horizontal-to-Vertical Spectral Ratio Technique
3.1.2. Spatial Autocorrelation (SPAC) Technique
3.1.3. Vulnerability Index
3.1.4. Vs30 Values and Soil Classification
3.2. Data Acquisition and Processing
3.2.1. Single-Station Measurements
3.2.2. Array Measurements
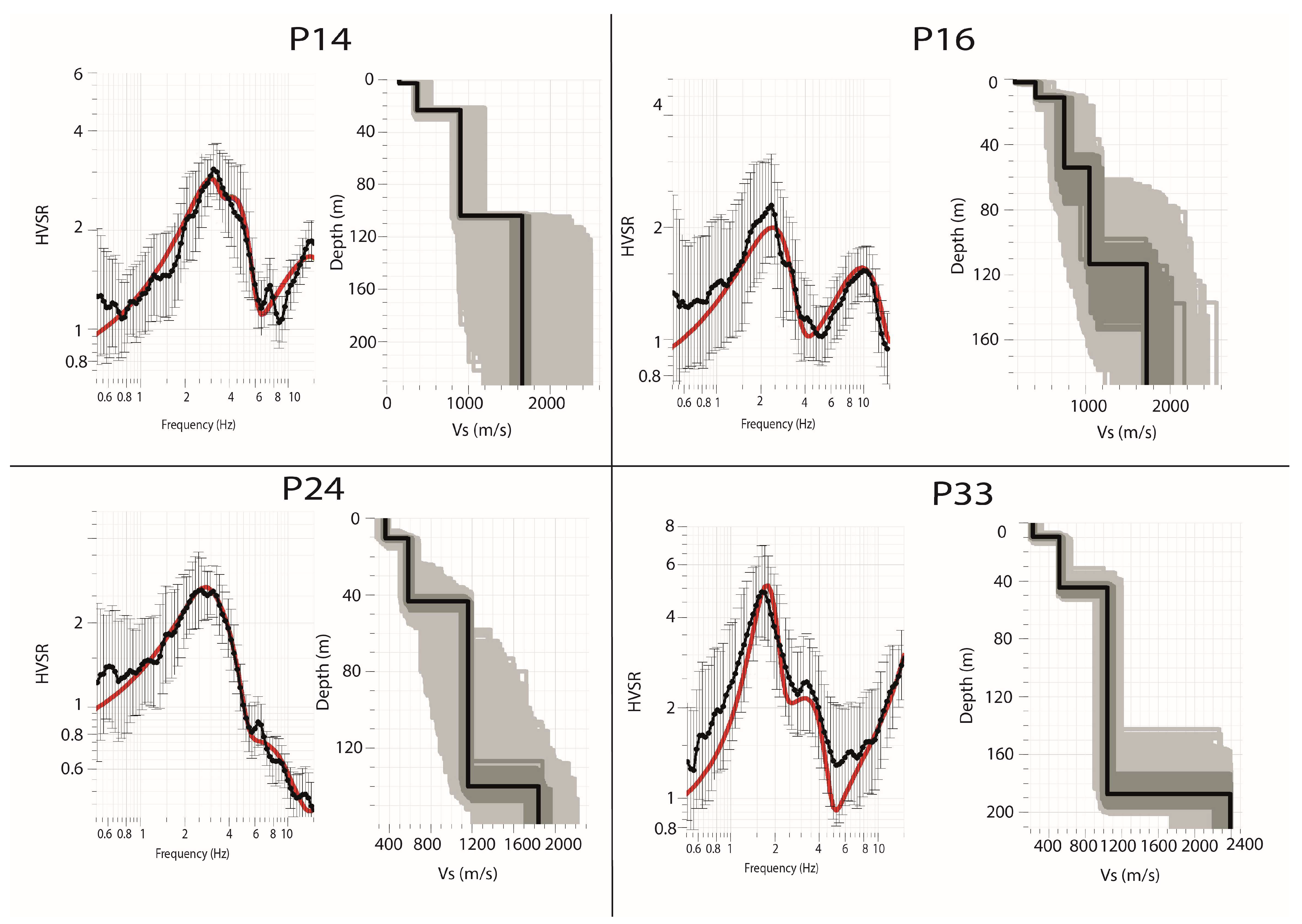
3.2.3. Inversion of HVSR and Dispersion Curves
4. Results and Discussion
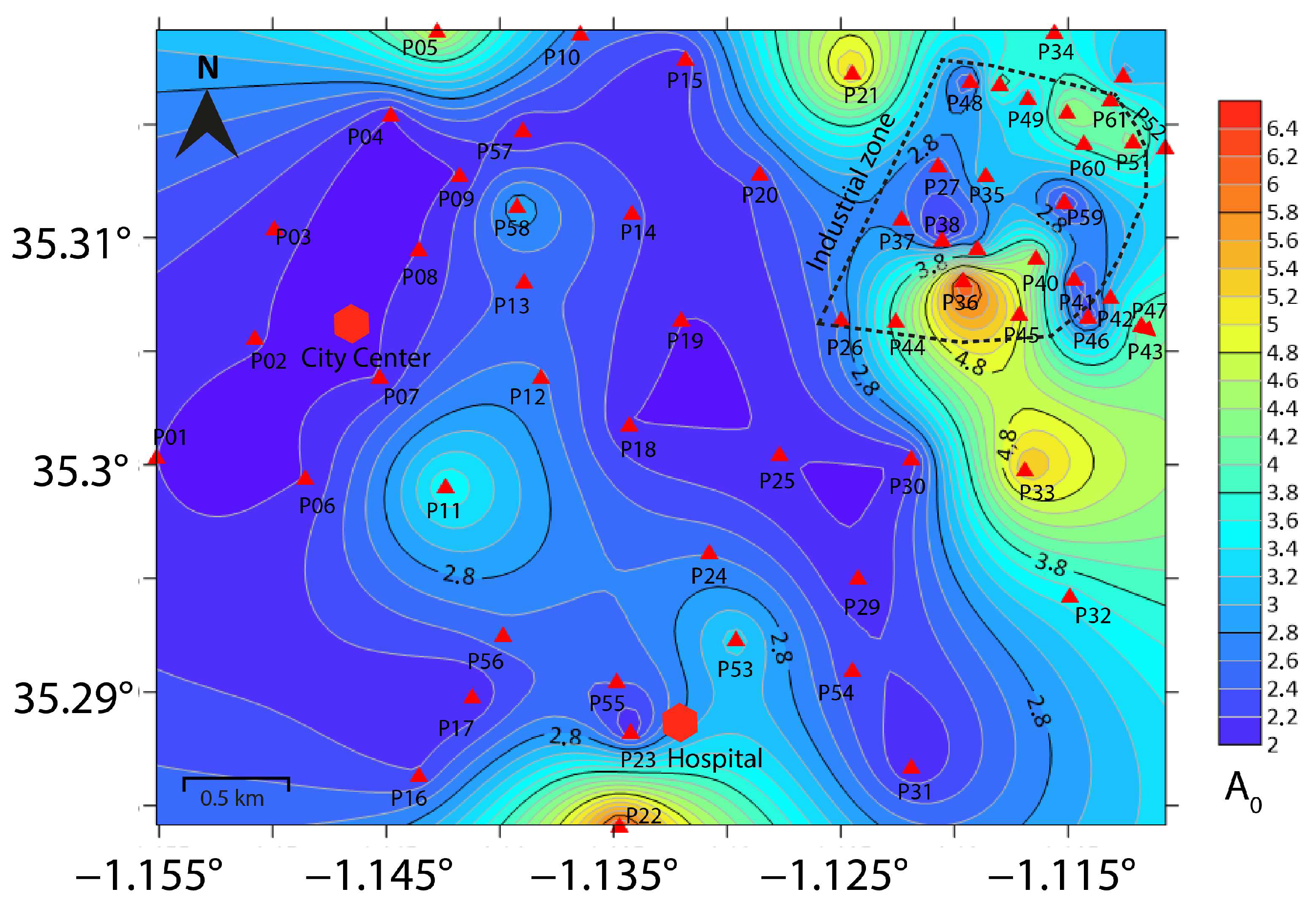
4.1. Fundamental Frequency Peaks and Corresponding Amplitudes
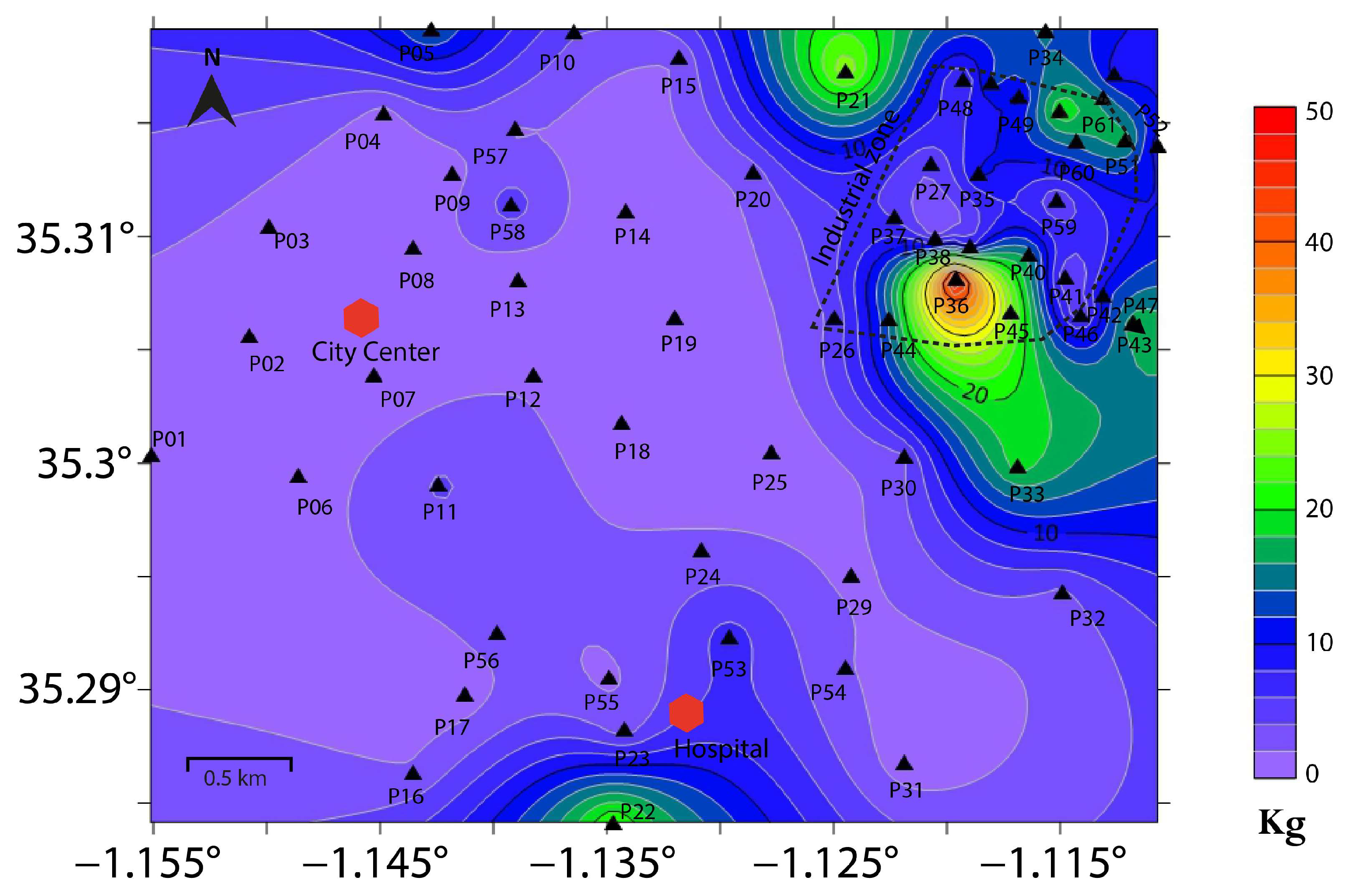
4.2. The Vulnerability Index ()
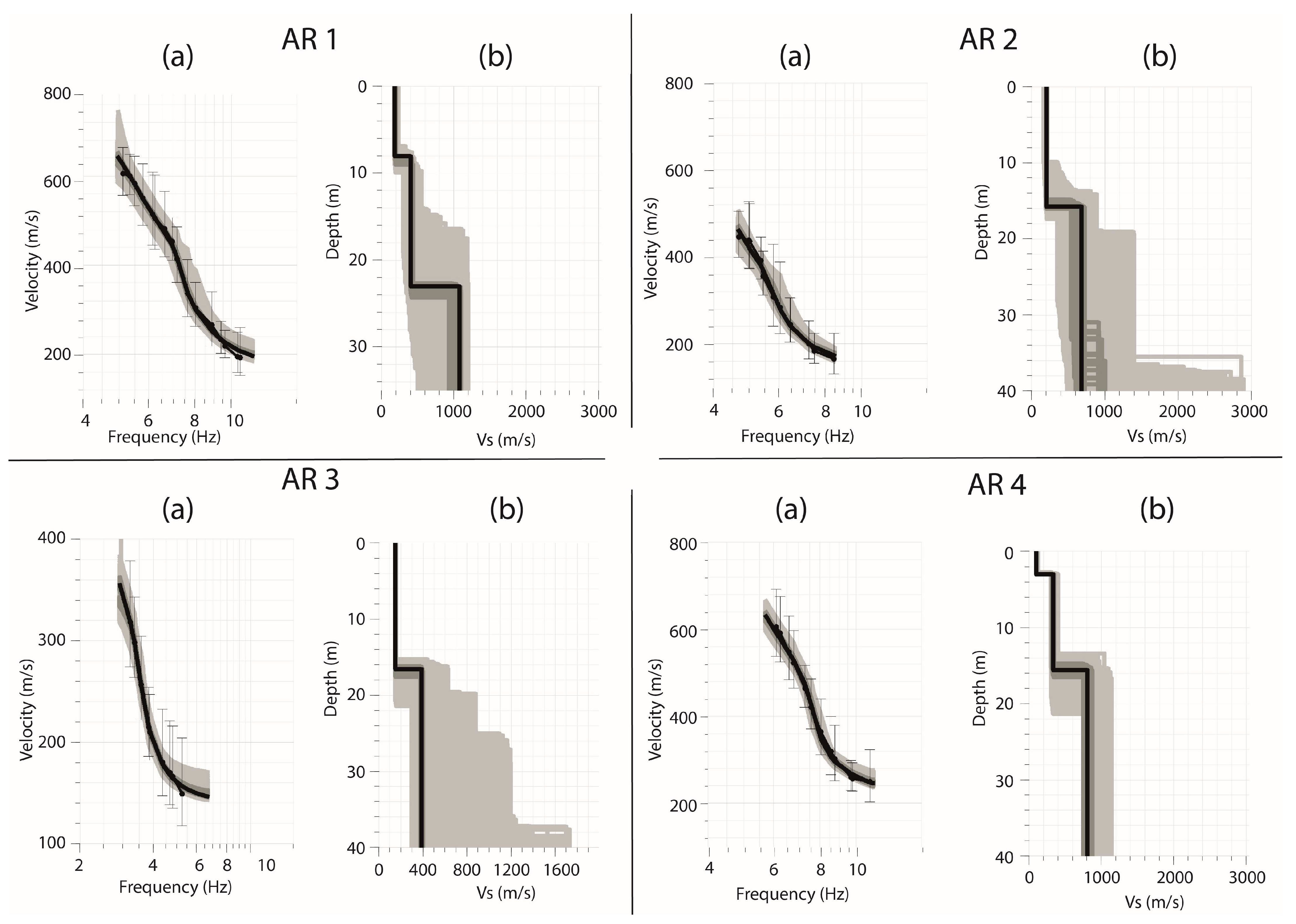
4.3. Rayleigh Wave Dispersion Curves
4.4. Shear Wave Velocity Models
4.5. Vs30 and Soil Classification
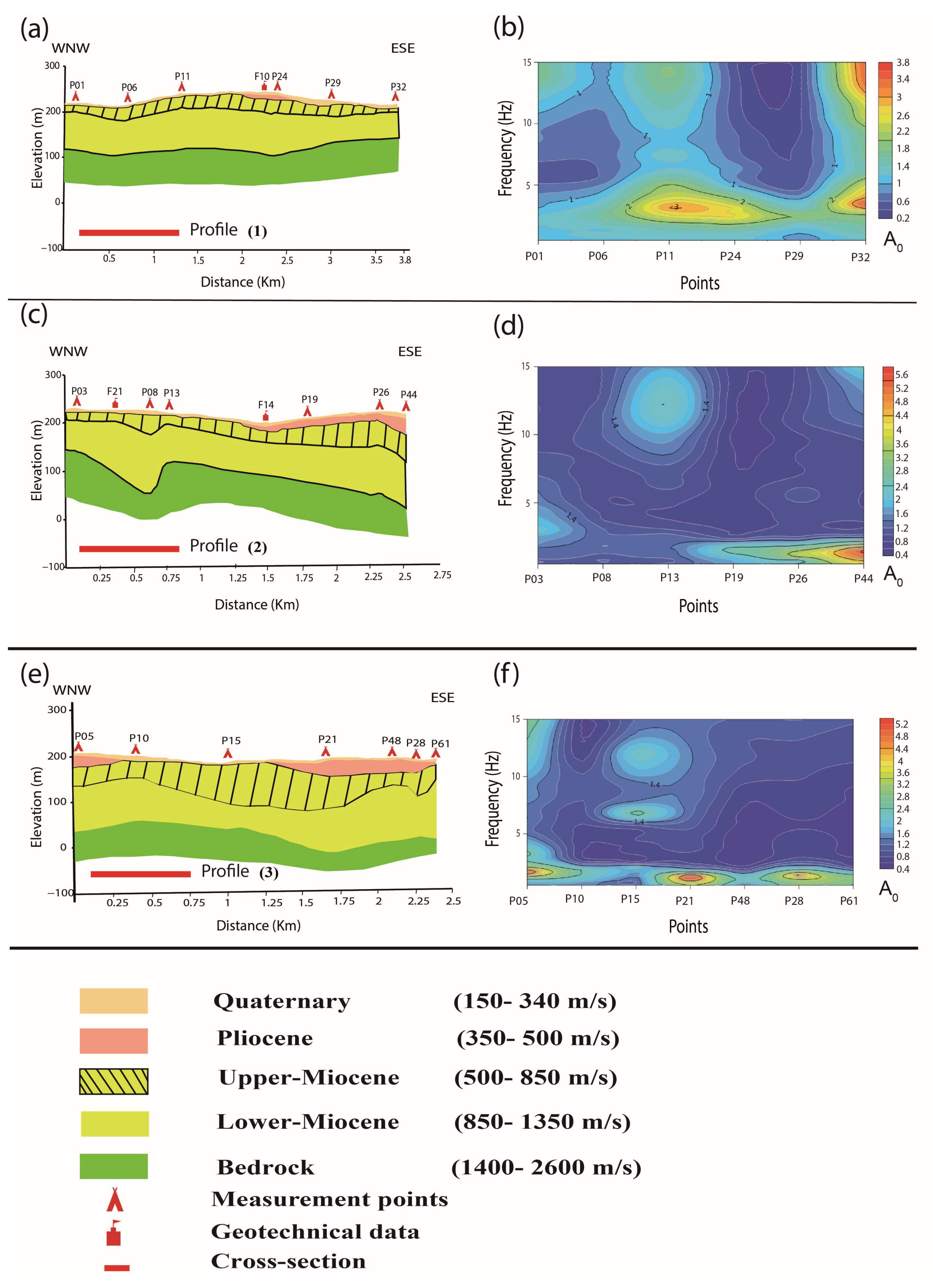
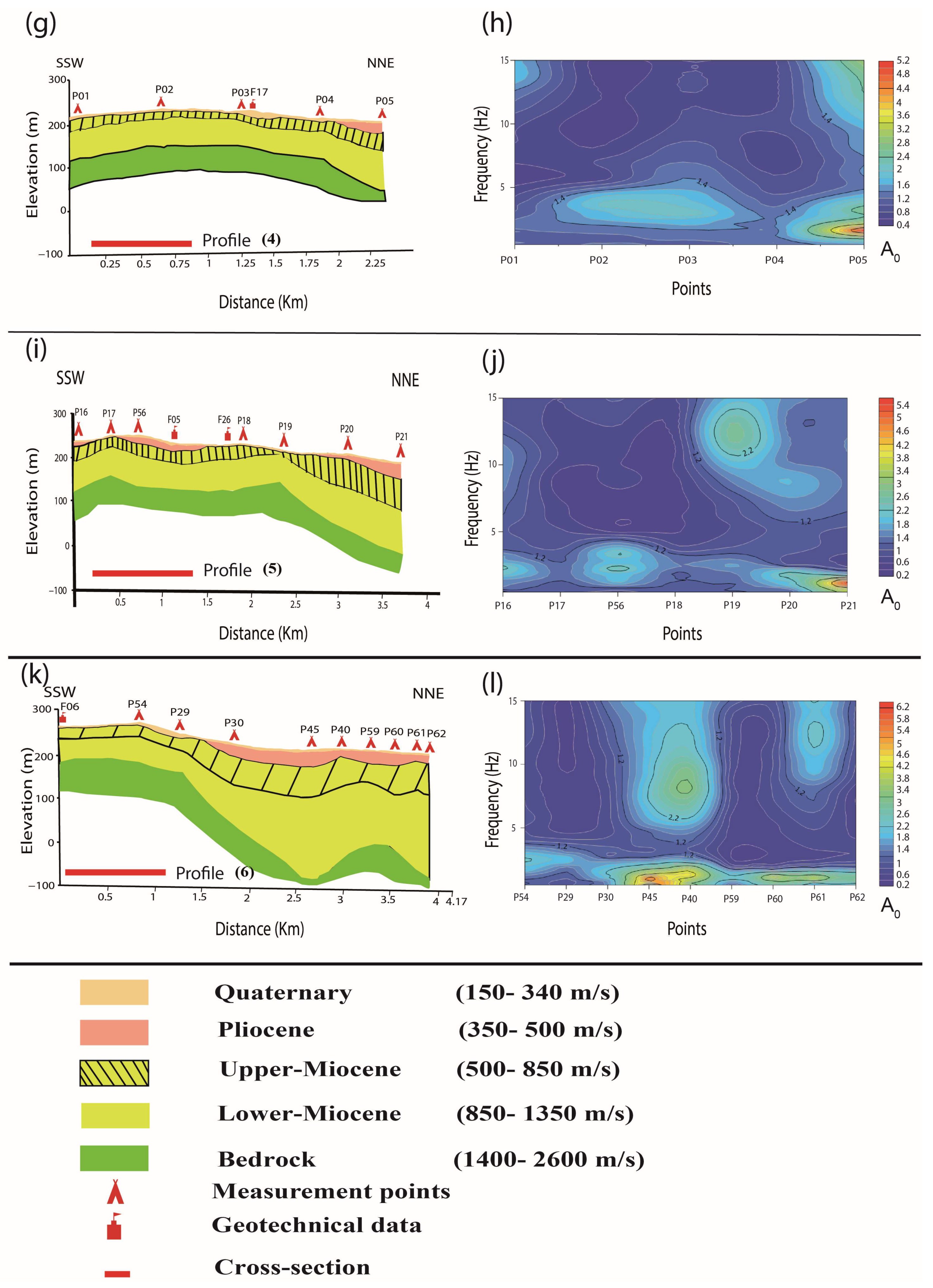
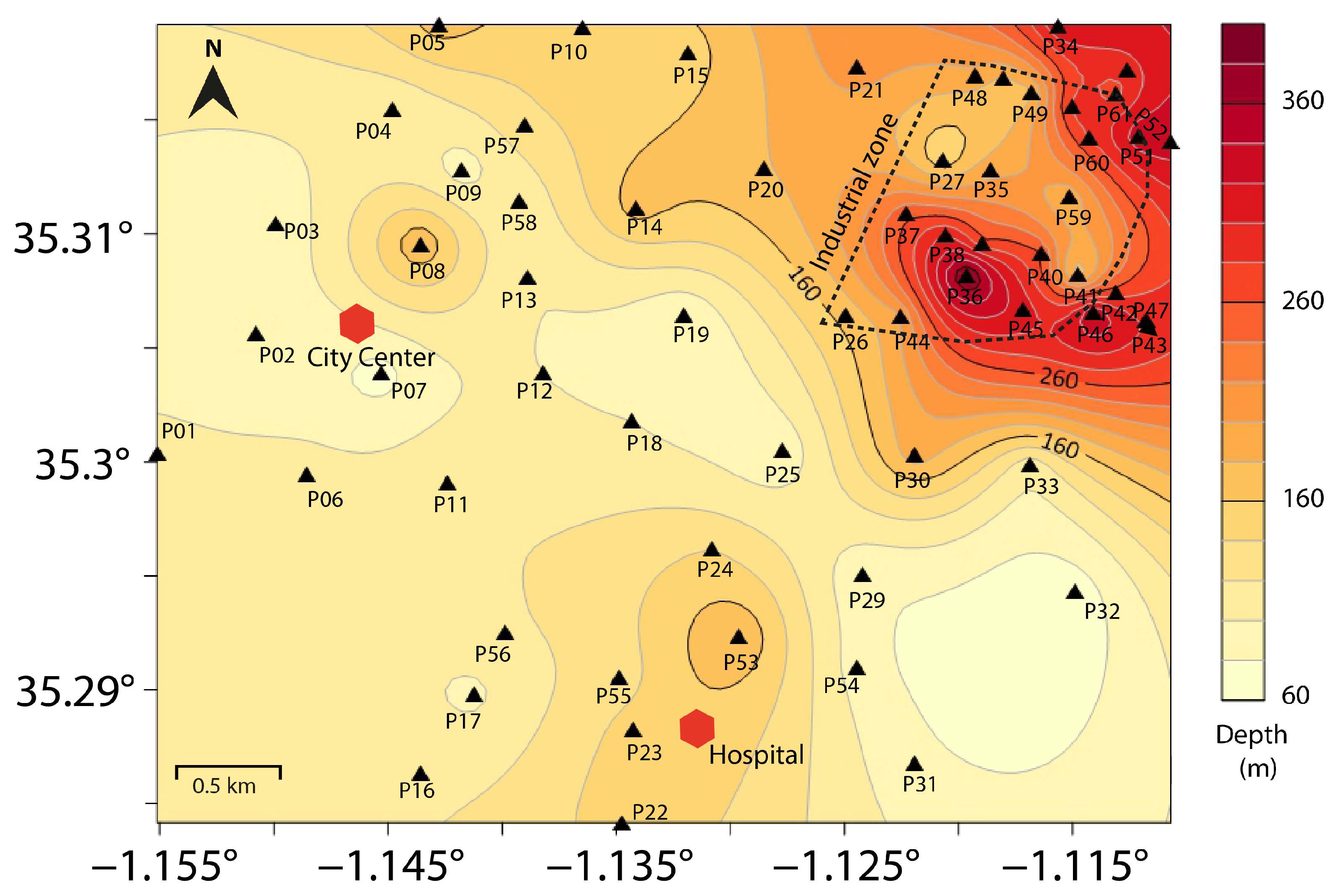
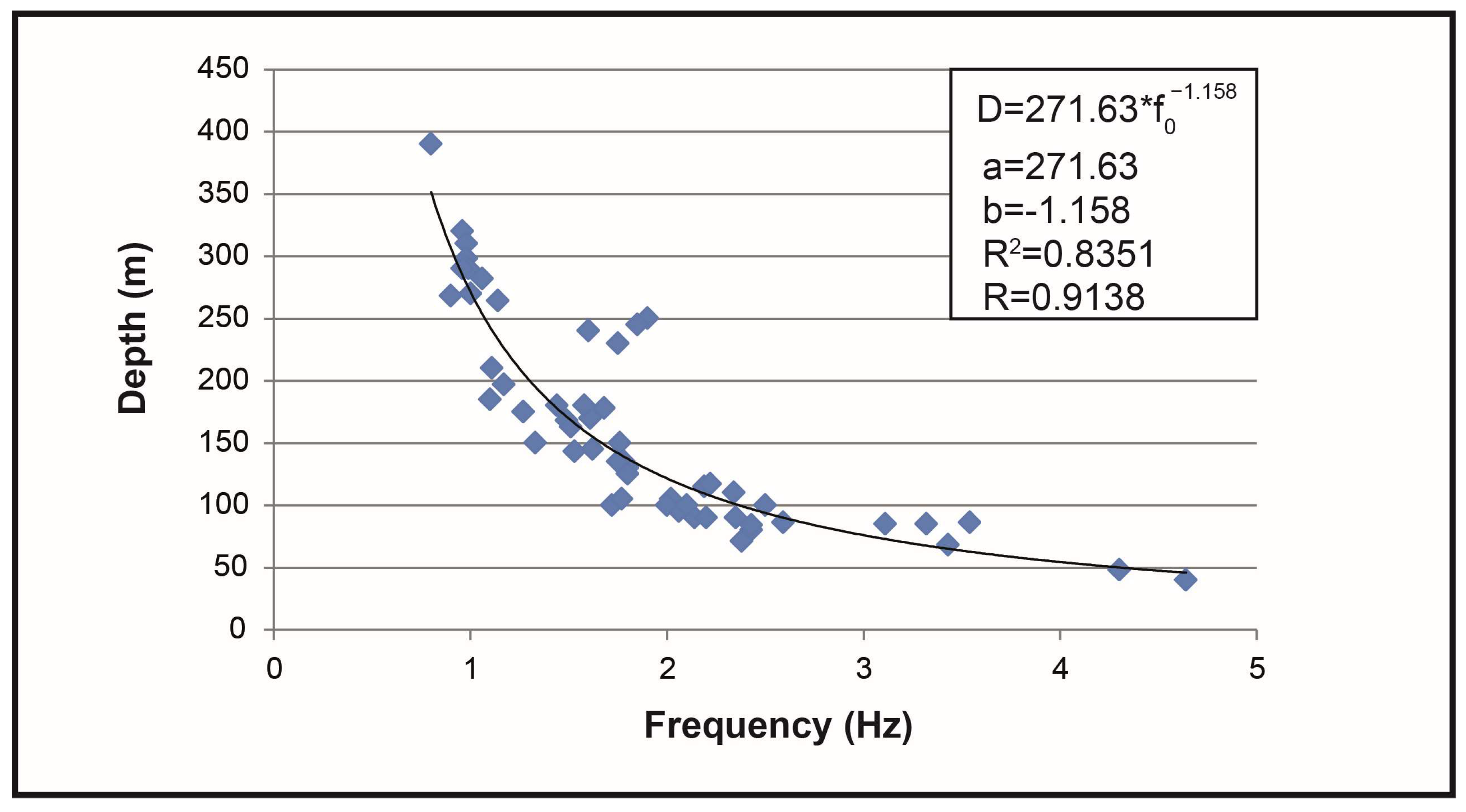
4.6. Correlation Between Bedrock and Frequency
4.7. Technical Limitations
5. Conclusions
- -
- Environmental noise analysis: Using the HVSR method to analyze ambient environmental noise, the study identifies predominant single-peak curves across the study area, with the fundamental frequency () ranging between 0.8 and 4.8 Hz. In areas with Quaternary deposits, two frequency peaks are observed. The secondary frequency peak (6–15 Hz) corresponds to impedance contrasts at shallow depths between Quaternary and Mio-Pliocene deposits.
- -
- Stratigraphic model: The HVSR and dispersion curve inversion reveals a five-layer stratigraphic structure for the city. The Quaternary layer, at the surface, exhibits shear wave velocities of 150–350 m/s and thicknesses ranging from 1 to 14 m. Beneath this is the Pliocene layer, with shear wave velocities of 350–500 m/s and thicknesses of 1 to 43 m. Below the Pliocene, the Miocene layer is identified, characterized by shear wave velocities of 500–850 m/s and thicknesses of 10 to 124 m. Deeper still, the Lower Miocene sediments show velocities of 850–1350 m/s and thicknesses of 47 to 284 m. At the base of the sequence lies the Mesozoic basement, composed of Cretaceous and/or Jurassic materials, with shear wave velocities ranging from 1400 to 2600 m/s.
- -
- Lateral variations: The inversion of HVSR curves highlights significant lateral variations in both shear wave velocity and sediment thickness across Aïn Témouchent. The resulting shear wave velocity models offer valuable insights for simulating ground motions in the far western region of the Lower Cheliff Basin.
- -
- Soil and liquefaction potential: The area is predominantly composed of very dense soils and soft rocks, with stiff soils concentrated in and south of the industrial zone. The vulnerability index () shows a marked increase in the industrial zone, indicating a higher potential for liquefaction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ouyed, M. Le Tremblement de Terre d’El Asnam du 10 Octobre 1980: Étude des Répliques. Ph.D. Thesis, Universite Scientifique et Medicale de Grenoble, Grenoble, France, 1981. [Google Scholar]
- Beldjoudi, H.; Delouis, B. Reassessing the rupture process of the 2003 Boumerdes-Zemmouri earthquake (Mw 6.8, northern Algeria) using teleseismic, strong motion, InSAR, GPS, and coastal uplift data. Mediterr. Geosci. Rev. 2022, 4, 471–494. [Google Scholar] [CrossRef]
- Nakamura, Y. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Railw. Tech. Res. Inst. Q. Rep. 1989, 30, 25–33. [Google Scholar]
- Parolai, S.; Bindi, D.; Trojani, L. Site response for the RSM seismic network and source parameters in the Central Apennines (Italy). Pure Appl. Geophys. 2001, 158, 695–715. [Google Scholar] [CrossRef]
- Layadi, K.; Semmane, F.; Yelles-Chaouche, A. Site-Effects Investigation in the City of Chlef (Formerly El-Asnam), Algeria, Using Earthquake and Ambient Vibration Data. Bull. Seismol. Soc. Am. 2016, 106, 2185–2196. [Google Scholar] [CrossRef]
- Issaadi, A.; Semmane, F.; Yelles-Chaouche, A.; Galiana-Merino, J.J.; Mazari, A. Shallow S-wave velocity structure in the Middle-Chelif Basin, Algeria, using ambient vibration single-station and array measurements. Appl. Sci. 2021, 11, 11058. [Google Scholar] [CrossRef]
- Perrodon, A. Etude géologique des bassins sublittoraux de l’Algérie occidentale. Publ. Serv. Carte Géol. L’algérie NS Bull 1957, 12, 328. [Google Scholar]
- Meghraoui, M. Géologie des Zones Sismiques du Nord de L’ALGERIE: Paleosismologie, Tectonique Active et Synthèse Sismotectonique. Ph.D. Thesis, Université Paris-Saclay, Paris, France, 1988. [Google Scholar]
- Chimouni, R.; Harbi, A.; Boughacha, M.S.; Hamidatou, M.; Kherchouche, R.; Sebaï, A. The 1790 Oran earthquake, a seismic event in times of conflict along the Algerian coast: A critical review from western and local source materials. Seismol. Res. Lett. 2018, 89, 2392–2403. [Google Scholar] [CrossRef]
- Yelles-Chaouche, A.; Djellit, H.; Beldjoudi, H.; Bezzeghoud, M.; Buforn, E. The Ain Temouchent (Algeria) Earthquake of December 22 nd, 1999. Pure Appl. Geophys. 2004, 161, 607–621. [Google Scholar] [CrossRef]
- Belabbès, S.; Meghraoui, M.; Çakir, Z.; Bouhadad, Y. InSAR analysis of a blind thrust rupture and related active folding: The 1999 Ain Temouchent earthquake (M w 5.7, Algeria) case study. J. Seismol. 2009, 13, 421–432. [Google Scholar] [CrossRef]
- Benfedda, A.; Bouhadad, Y.; Boughacha, M.; Guessoum, N.; Abbes, K.; Bezzeghoud, M. The Oran January 9th (Mw 4.7) and June 6th, 2008 (Mw 5.4) earthquakes: Seismological study and seismotectonic implication. J. Afr. Earth Sci. 2020, 169, 103896. [Google Scholar] [CrossRef]
- Guardia, P. Géodynamique de la Marge Alpine du Continent Africain D’après L’étude de L’oranie Nord-Occidentale. Ph.D. Thesis, Université de Nice-Sophia Antipolis, Toulouse, France, 1975. [Google Scholar]
- Thomas, G. Géodynamique d’un Bassin Intramontagneux: Le Bassin du bas Chéliff Occidental (Algérie) Durant le Mio-Plio-Quaternaire. Ph.D. Thesis, Université de Pau, Pau, France, 1985. [Google Scholar]
- Bénamar, A. Elaboration de la Carte Géotechnique de la ville d’Ain témouchent. Ph.D. Thesis, Université Bel hadj Bouchaib Ain Témouchent, Ain Temouchent, Algeria, 2023. [Google Scholar]
- Boudiaf, A.; Swan, F.; Youngs, R. Evaluation de L’aléa Sismique et Etude de Microzonage Sismique de la Wilaya de Ain Temouchent-Algérie; Direction de l’Urbanisme et de la Construction, Wilaya de Ain Temouchent: Ain Temouchent, Algeria, 2003. [Google Scholar]
- Esmaeilabadi, R.; Abasszadeh Shahri, A.; Behzadafshar, K.; Gheirati, A.; Nosrati Nasrabadi, J. Frequency content analysis of the probable earthquake in Kopet Dagh region—Northeast of Iran. Arab. J. Geosci. 2015, 8, 3833–3844. [Google Scholar] [CrossRef]
- Farsijani, D.; Gholam, S.; Karampour, H.; Talebian, N. The impact of the frequency content of far-field earthquakes on the optimum parameters and performance of tuned mass damper inerter. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; p. 105925. [Google Scholar]
- Hassannejad, A.; Moghaddam, A.B.; Beydokhti, E.Z. Influence of ground motion frequency content on the nonlinear response and seismic performance of RC moment frame structures. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 476–486. [Google Scholar]
- Bonnefoy-Claudet, S.; Cornou, C.; Bard, P.Y.; Cotton, F.; Moczo, P.; Kristek, J.; Fäh, D. H/V ratio: A tool for site effects evaluation: Results from 1D noise simulations. J. Appl. Geophys. 2006, 167, 827–837. [Google Scholar] [CrossRef]
- Albarello, D.; Lunedei, E. Alternative interpretations of horizontal to vertical spectral ratios of ambient vibrations: New insights from theoretical modeling. Bull. Earthq. Eng. 2010, 8, 519–534. [Google Scholar] [CrossRef]
- Zhu, C.; Pilz, M.; Cotton, F. Evaluation of a novel application of earthquake HVSR in site-specific amplification estimation. Soil Dyn. Earthq. Eng. 2020, 139, 106301. [Google Scholar] [CrossRef]
- Neukirch, M.; García-Jerez, A.; Villaseñor, A.; Luzón, F.; Ruiz, M.; Molina, L. Horizontal-to-Vertical Spectral Ratio of Ambient Vibration Obtained with Hilbert–Huang Transform. Sensors 2021, 21, 3292. [Google Scholar] [CrossRef]
- Xu, R.; Wang, L. The horizontal-to-vertical spectral ratio and its applications. EURASIP J. Adv. Signal Process. 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Molnar, S.; Sirohey, A.; Assaf, J.; Bard, P.-Y.; Castellaro, S.; Cornou, C.; Cox, B.; Guillier, B.; Hassani, B.; Kawase, H. A review of the microtremor horizontal-to-vertical spectral ratio (MHVSR) method. J. Seismol. 2022, 26, 653–685. [Google Scholar] [CrossRef]
- Kula, D.; Olszewska, D.; Dobiński, W.; Glazer, M. Horizontal-to-vertical spectral ratio variability in the presence of permafrost. Geophys. J. Int. 2018, 214, 219–231. [Google Scholar] [CrossRef]
- Fat-Helbary, R.E.-S.; El-Faragawy, K.O.; Hamed, A. Application of HVSR technique in the site effects estimation at the south of Marsa Alam city, Egypt. J. Afr. Earth Sci. 2019, 154, 89–100. [Google Scholar] [CrossRef]
- Khedr, F.; Marzouk, I.; Elrayess, M. Site effect estimation using Horizontal to Vertical (H/V) spectral ratio technique in Nile Delta, Egypt. NRIAG J. Astron. Geophys. 2019, 8, 84–96. [Google Scholar] [CrossRef][Green Version]
- Zavala, N.; Clemente-Chávez, A.; Figueroa-Soto, Á.; González-Martínez, M.; Sawires, R. Application of horizontal to Vertical Spectral Ratio microtremor technique in the analysis of site effects and structural response of buildings in Querétaro city, Mexico. J. South Am. Earth Sci. 2021, 108, 103211. [Google Scholar] [CrossRef]
- Thornley, J.D.; Dutta, U.; Douglas, J.; Yang, Z.J. Evaluation of horizontal to vertical spectral ratio and standard spectral ratio methods for mapping shear wave velocity across Anchorage, Alaska. Soil Dyn. Earthq. Eng. 2021, 150, 106918. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, Y. Characteristics of horizontal to vertical spectral ratio of InSight seismic data from Mars. J. Geophys. Res. Planets 2022, 127, e2020JE006813. [Google Scholar] [CrossRef]
- Layadi, K.; Semmane, F.; Yelles-Chaouche, A. S-wave velocity structure of Chlef City, Algeria, by inversion of Rayleigh wave ellipticity. Near Surf. Geophys. 2018, 16, 328–339. [Google Scholar] [CrossRef]
- Issaadi, A.; Saadi, A.; Semmane, F.; Yelles-Chaouche, A.; Galiana-Merino, J.J. Liquefaction potential and Vs30 structure in the Middle-Chelif Basin, Northwestern Algeria, by ambient vibration data inversion. Appl. Sci. 2022, 12, 8069. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Capon, J.; Greenfield, R.J.; Kolker, R.J. Multidimensional maximum-likelihood processing of a large aperture seismic array. Proc. IEEE 1967, 55, 192–211. [Google Scholar] [CrossRef]
- Kelly, E.J.; Levin, M.J. Signal Parameter Estimation for Seismometer Arrays; MIT Lincoln Laboratory: Lexington, MA, USA, 1964. [Google Scholar]
- Lacoss, R.T.; Kelly, E.J.; Toksöz, M.N. Estimation of seismic noise structure using arrays. Geophysics 1969, 34, 21–38. [Google Scholar] [CrossRef]
- Aki, K. Space and time spectra of stationary stochastic waves, with special reference to microtremors. Bull. Earthq. Res. Inst. 1957, 35, 415–456. [Google Scholar]
- Bettig, B.; Bard, P.; Scherbaum, F.; Riepl, J.; Cotton, F.; Cornou, C.; Hatzfeld, D. Analysis of dense array noise measurements using the modified spatial auto-correlation method (SPAC): Application to the Grenoble area. Boll. Geofis. Teor. Appl. 2001, 42, 281–304. [Google Scholar]
- Ling, S. An extended use of the spatial autocorrelation method for the estimation of geological structure using microtremors. Proc. 89th SEGJ Conf. 1993, 1993, 44–48. [Google Scholar]
- Okada, H. The Microtremor Survey Method, Geophysical Monograph Series 12; Asten, M.W., Ed.; Society of Exploration Geophysicists: Tulsa, OK, USA, 2003. [Google Scholar]
- Louie, J.; Faster, B. Shear Wave Velocity to 100 Meters Depth from Refraction Micro tremor Array. Bull. Seism. Soc. Am. 2001, 91, 347–364. [Google Scholar] [CrossRef]
- Pancha, A.; Pullammanappallil, S.; Louie, J.N.; Cashman, P.H.; Trexler, J.H. Determination of 3D basin shear-wave velocity structure using ambient noise in an urban environment: A case study from Reno, Nevada. Bull. Seismol. Soc. Am. 2017, 107, 3004–3022. [Google Scholar] [CrossRef]
- Ulysse, S.; Boisson, D.; Dorival, V.; Guerrier, K.; Préptit, C.; Cauchie, L.; Mreyen, A.-S.; Havenith, H.-B. Site effect potential in Fond Parisien, in the East of Port-au-Prince, Haiti. Geosciences 2021, 11, 175. [Google Scholar] [CrossRef]
- Saadi, A.; Issaadi, A.; Semmane, F.; Yelles-Chaouche, A.; Galiana-Merino, J.J.; Layadi, K.; Chimouni, R. 3D shear-wave velocity structure for Oran city, northwestern Algeria, from inversion of ambient vibration single-station and array measurements. Soil Dyn. Earthq. Eng. 2023, 164, 107570. [Google Scholar] [CrossRef]
- Nogoshi, M. On the amplitude characteristics of microtremor, Part II. J. Seismol. Soc. Jpn. 1971, 24, 26–40. [Google Scholar]
- La Rocca, M.; Chiappetta, G.; Gervasi, A.; Festa, R.L. Non-Stability of the noise HVSR at sites near or on topographic heights. Geophys. J. Int. 2020, 222, 2162–2171. [Google Scholar] [CrossRef]
- Ishihara, K.; Koga, Y. Case studies of liquefaction in the 1964 Niigata earthquake. Soils Found. 1981, 21, 35–52. [Google Scholar] [CrossRef]
- Nakamura, Y. Seismic vulnerability indices for ground and structures using microtremor. In Proceedings of the World Congress on Railway Research, Florence, Italy, 16–19 November 1997. [Google Scholar]
- Nakamura, Y. Real-time information systems for seismic hazards mitigation UrEDAS, HERAS and PIC. Q. Rep.-Rtri 1996, 37, 112–127. [Google Scholar]
- Code, P. Eurocode 8: Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Council, B.S.S. NEHRP Recommended Provisions for Seismic Regulations for New Buildings and Other Structures (FEMA 450); NEHRP: Washington, DC, USA, 2003. [Google Scholar]
- Abbaszadeh Shahri, A.; Chunling, S.; Larsson, S. A hybrid ensemble-based automated deep learning approach to generate 3D geo-models and uncertainty analysis. Eng. Comput. 2024, 40, 1501–1516. [Google Scholar] [CrossRef]
- Vanem, E.; Gramstad, O.; Bitner-Gregersen, E.M. A simulation study on the uncertainty of environmental contours due to sampling variability for different estimation methods. Appl. Ocean. Res. 2019, 91, 101870. [Google Scholar] [CrossRef]
- Wu, S.; Heitzler, M.; Hurni, L. Leveraging uncertainty estimation and spatial pyramid pooling for extracting hydrological features from scanned historical topographic maps. GISci. Remote Sens. 2022, 59, 200–214. [Google Scholar] [CrossRef]
- Delfgou, C.; Bakogiannis, N.; Laube, P. Uncertainty analysis of geodata derived from digital map processing. Int. J. Geogr. Inf. Sci. 2023, 37, 1667–1691. [Google Scholar] [CrossRef]
- Acerra, C.; Aguacil, G.; Anastasiadis, A.; Atakan, K.; Azzara, R.; Bard, P.-Y.; Basili, R.; Bertrand, E.; Bettig, B.; Blarel, F. Guidelines for the Implementation of the H/V Spectral Ratio Technique on Ambient Vibrations Measurements, Processing and Interpretation; European Commission–EVG1-CT-2000-00026 SESAME; European Commission: Brussels, Belgium, 2004. [Google Scholar]
- Wathelet, M.; Chatelain, J.L.; Cornou, C.; Giulio, G.D.; Guillier, B.; Ohrnberger, M.; Savvaidis, A. Geopsy: A user-friendly open-source tool set for ambient vibration processing. Seismol. Res. Lett. 2020, 91, 1878–1889. [Google Scholar] [CrossRef]
- Konno, K.; Ohmachi, T. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor. Bull. Seismol. Soc. Am. 1998, 88, 228–241. [Google Scholar] [CrossRef]
- Sánchez-Sesma, F.J.; Rodríguez, M.; Iturrarán-Viveros, U.; Luzón, F.; Campillo, M.; Margerin, L.; García-Jerez, A.; Suarez, M.; Santoyo, M.A.; Rodriguez-Castellanos, A. A theory for microtremor H/V spectral ratio: Application for a layered medium. Geophys. J. Int. 2011, 186, 221–225. [Google Scholar] [CrossRef]
- Poggi, V.; Fäh, D.; Burjanek, J.; Giardini, D. The use of Rayleigh-wave ellipticity for site-specific hazard assessment and microzonation: Application to the city of Lucerne, Switzerland. Geophys. J. Int. 2012, 188, 1154–1172. [Google Scholar] [CrossRef]
- Wathelet, M. An improved neighborhood algorithm: Parameter conditions and dynamic scaling. Geophys. Res. Lett. 2008, 35, NIL_26–NIL_30. [Google Scholar] [CrossRef]
- Sharma, H.D.; Dukes, M.T.; Olsen, D.M. Field measurements of dynamic moduli and Poisson’s ratios of refuse and underlying soils at a landfill site. Geotech. Waste Fill.–Theory Pract. ASTM STP 1990, 1070, 57–70. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Shahri, A.; Esfandiyari, B.; Rajablou, R. A proposed geotechnical-based method for evaluation of liquefaction potential analysis subjected to earthquake provocations (case study: Korzan earth dam, Hamedan province, Iran). Arab. J. Geosci. 2012, 5, 555–564. [Google Scholar] [CrossRef]
- Saadi, A.; Galiana-Merino, J.J.; Semmane, F.; Yelles-Chaouche, A.; Issaadi, A. Characterization of Shallow Sedimentary Layers in the Oran Region Using Ambient Vibration Data. Appl. Sci. 2024, 14, 7364. [Google Scholar] [CrossRef]
- Mazanec, M.; Valenta, J.; Málek, J. Does VS30 reflect seismic amplification? Observations from the West Bohemia Seismic Network. Nat. Hazards 2024, 120, 12181–12202. [Google Scholar] [CrossRef]
- Parolai, S.; Bormann, P.; Milkereit, C. New relationships between Vs, thickness of sediments, and resonance frequency calculated by the H/V ratio of seismic noise for the Cologne area (Germany). Bull. Seismol. Soc. Am. 2002, 92, 2521–2527. [Google Scholar] [CrossRef]
- Francesco, P.; Salvatore, M.; Roberto, I.; Antonella, P.; Giuseppe, L.; Pauline, G.; Daniela, F. Ambient noise techniques to study near-surface in particular geological conditions: A brief review. In Innovation in near-surface Geophysics; Elsevier: Amsterdam, The Netherlands, 2019; pp. 419–460. [Google Scholar]
- Benjumea, B.; Gaite, B.; Schimmel, M.; Bohoyo, F.; Spica, Z.; Mancilla, F.; Li, Y.; Almendros, J.; Morales, J. Subsurface imaging in urban areas with ambient noise using DAS and seismometer data sets: Granada, Spain. J. Geophys. Res. Solid Earth 2024, 129, e2024JB029820. [Google Scholar] [CrossRef]
- Dal Moro, G.; Panza, G. Multiple-peak HVSR curves: Management and statistical assessment. Eng. Geol. 2022, 297, 106500. [Google Scholar] [CrossRef]



| Borehole | Quaternary [m] | Pliocene [m] | Miocene [m] | ||
|---|---|---|---|---|---|
| F1 | 14.0 | >13 | 0.0 | – | |
| F2 | 14.0 | 7 | 0.0 | 78 | 0.0 |
| F3 | 14.0 | 7 | 0.0 | 78 | 0.0 |
| F5 | 7.5 | >10 | 0.0 | – | |
| F6 | 1.0 | – | >35 | 0.0 | |
| F7 | 1.0 | – | >19 | 0.0 | |
| F8 | 2.0 | >9 | 0.5 | – | |
| F9 | 2.0 | 17 | 0.0 | >2 | 0.0 |
| F10 | 4.0 | >5 | 0.5 | – | |
| F11 | 4.0 | >5 | 0.5 | – | |
| F14 | 1.0 | 4 | 0.0 | >11.0 | |
| F17 | 8.0 | >10 | 0.0 | – | |
| F21 | 2.0 | – | >20 | 0.0 | |
| F26 | 1.0 | – | >7 | 0.0 | |
| F30 | 7.5 | >10 | 0.0 | – | |
| F34 | >12.0 | – | – | ||
| Sedimentary Layers | Vp Range [m/s] | Vs Range [m/s] | Density Range [kg/m3] |
|---|---|---|---|
| Quaternary | 150–1200 | 100–400 | 1600–2000 |
| Pliocene | 450–1650 | 300–550 | 1800–2100 |
| Upper Miocene | 600–2700 | 400–900 | 1900–2200 |
| Lower Miocene | 1200–4200 | 800–1400 | 2000–2400 |
| Bedrock | 2000–7000 | 1300–2750 | 2200–2800 |
| Vs (m/s) | Soil Type | Classification of Soil |
|---|---|---|
| Vs > 1500 | Hard rock | A |
| 760 < Vs ≤ 1500 | Rock | B |
| 360 < Vs ≤ 760 | Very dense soil and soft rock | C |
| 180 < Vs ≤ 360 | Stiff soil | D |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saadi, A.; Semmane, F.; Galiana-Merino, J.J.; Yelles-Chaouche, A.; Issaadi, A.; Melouk, B. Characterization of the Sedimentary Cover in the City of Aïn Témouchent, Northwest Algeria, Using Ambient Noise Measurements. Appl. Sci. 2025, 15, 2967. https://doi.org/10.3390/app15062967
Saadi A, Semmane F, Galiana-Merino JJ, Yelles-Chaouche A, Issaadi A, Melouk B. Characterization of the Sedimentary Cover in the City of Aïn Témouchent, Northwest Algeria, Using Ambient Noise Measurements. Applied Sciences. 2025; 15(6):2967. https://doi.org/10.3390/app15062967
Chicago/Turabian StyleSaadi, Ahmed, Fethi Semmane, Juan José Galiana-Merino, Abdelkrim Yelles-Chaouche, Abdelouahab Issaadi, and Billel Melouk. 2025. "Characterization of the Sedimentary Cover in the City of Aïn Témouchent, Northwest Algeria, Using Ambient Noise Measurements" Applied Sciences 15, no. 6: 2967. https://doi.org/10.3390/app15062967
APA StyleSaadi, A., Semmane, F., Galiana-Merino, J. J., Yelles-Chaouche, A., Issaadi, A., & Melouk, B. (2025). Characterization of the Sedimentary Cover in the City of Aïn Témouchent, Northwest Algeria, Using Ambient Noise Measurements. Applied Sciences, 15(6), 2967. https://doi.org/10.3390/app15062967








