Abstract
This work involves the development of a hydrodynamic fertilizer injector (HFI), which uses an integrated axial-flow turbine (AFT) and a diaphragm pump to absorb liquid fertilizer. Three structural parameters—the number of impellers (M1), average number of blades per impeller (M2), and arrangement pattern (M3)—are considered, and 12 AFT designs are developed. Using a combination of CFD numerical simulations and hydraulic performance testing, the response of the AFT output power (P), blade negative pressure (NP), and fertilizer injection flow rate (Qinj) to structural parameters and inlet pressure (H) is investigated. The results show that the normalized root mean square error between the simulated outlet flow rate (Qs) and the measured flow rate (Qm) is 5.1%, indicating high accuracy in the grid motion simulation method. P increases first and then decreases with the increase in impeller speed (n). The maximum P (Pmax) ranges from 150.1 to 201.4 W. Pmax increases with H, decreases with increasing M1 and M2, and shows little change with M3. At H = 0.14 MPa, M1 and M2 have a significant influence, and at H ≥ 0.14 MPa, M1 becomes the most significant factor (p < 0.05). Low-speed flow and negative pressure cavitation zones at the leading edge of the blade suction surface cause flow blockage and affect the lifespan of the AFT. These regions decrease in size as H increases but increase with M1. The negative pressure (NP) decreases as M2 increases. When M1, M2, and M3 are 2, 3, and identical (D33), the Pmax of the AFT is maximized, increasing by 6.7% to 33.5% compared with those of the other combinations. The Qinj of D33, D34, D43, and D44 at H = 0.12~0.18 MPa range from 288.6 to 847.3 L/h, which is 38.7% to 461.0% higher than that of domestic and international venturi injectors. When considering cavitation issues and the manufacturing cost of the AFT mold, D44 may be chosen. Although its Qinj is 7.0% lower than that of D33, NP is reduced by 37.9%. These findings provide a basis for the development of the HFI with AFT as the driving unit.
1. Introduction
Integrated water and fertilizer technology uses irrigation systems to dissolve fertilizer in water, enabling simultaneous irrigation and fertilization to meet the water and nutrient needs of crops in a timely and appropriate manner [1]. By 2020, the area of integrated water and fertilizer technology in China reached 10 million ha, accounting for 17.1% of the total irrigated area [2], which is used primarily in sprinkler and drip irrigation systems. Compared with traditional fertilizer broadcasting or burial methods, integrated water and fertilizer technology in drip irrigation systems has increased crop yield by 5% to 12% and fertilizer utilization efficiency by 30% to 50% [3]. The fertilizing devices for integrated water and fertilizer can be divided into the hydraulic type and the electric-driven type. Hydraulic-driven fertilizer injectors include venturi injectors, proportionate fertilizer pumps, and pressure-differential fertilizer tanks [4]. The first two are proportional fertilization systems where the fertilizer concentration does not change significantly over time, but the inlet pressure (H) required is relatively high, generally above 0.14 MPa (with the outlet pressure (Hout) calculated at 0.1 MPa) [5]. The pressure-differential fertilizer tank is a fixed-rate fertilization system that requires a lower H (H ≥ 0.11 MPa, Hout = 0.1 MPa) [6], but it faces the issue of rapid concentration decay over time, resulting in reduced fertilization uniformity and crop yield [7]. To increase the irrigation area for each wheel irrigation system and prevent damage to driplines from excessive pressure, many farmers operate drip irrigation systems at low pressures (H< 0.12 MPa). Therefore, most drip irrigation systems in China for food crops use pressure-differential fertilizer tanks [8]. For traditional surface irrigation (furrow irrigation and border irrigation), the use of integrated water and fertilizer technology has been shown to significantly improve nitrogen fertilizer distribution uniformity, the nitrogen storage rate, and crop yield by 4.0% to 14.5%, 2.2% to 14.3%, and 1.7% to 19.9%, respectively [9,10]. However, owing to the lack of pipeline water supply infrastructure and fertilizer injection equipment [4], integrated water and fertilizer technology for traditional surface irrigation has not been widely applied. To reduce water transport losses and improve transport efficiency, some irrigation areas in China have shifted to low-pressure pipeline systems recently for water delivery to field distribution points (H = 0.05 to 0.15 MPa) [11]. This shift provides a platform for implementing integrated water and fertilizer technology in surface irrigation systems, which account for 85% of China’s total irrigated area [2]. Therefore, for sprinklers, drip irrigation, or surface irrigation systems, the need for low-pressure hydrodynamic fertilizer injectors to inject fertilizer solution proportionally into the pipeline system is urgent.
To reduce the minimum inlet pressure (Hmin) required for the operation of venturi injectors and proportional fertilizer pumps, as well as to increase the fertilizer injection flow rate (Qinj) under the same pressure conditions, researchers have conducted extensive studies using hydraulic performance testing and CFD simulations. Structural parameters such as the angle of the suction port, the throat diameter and length, and the length-to-diameter ratio are key factors influencing the fertilizer injection performance of venturi injectors. Studies on the response of Qinj to these parameters through hydraulic performance testing have shown that optimized venturi injectors achieve 70.8% to 90.2% increases in Qinj [12,13]. Traditional venturi injectors have symmetrical structures in which negative pressure is annularly distributed around the throat. When they are upgraded to an asymmetrical structure, the streamlined transitions in the contraction and diffusion sections become smoother along the upper part of the throat, resulting in a semi-ring distribution of negative pressure, a smaller cavitation region, and a 16.5% to 49.2% increase in Qinj under the same inlet pressure [14,15]. Further optimization of the center axis offset distance in the diffusion section of asymmetrical venturi injectors reduced Hmin by 8.2% and increased Qinj by 13.7% [16]. Proportional fertilizer pumps have much more complex structures than venturi injectors do. Factors such as the diameter of the suction chamber and the stiffness of the reversing spring significantly impact performance. For example, increasing the suction chamber diameter from 15 mm to 21 mm resulted in a 21.9% average increase in Qinj but a 10.3% decrease in the fertilizer chamber utilization efficiency [17]. Additionally, optimizing the piston rod diameter and the stroke of the sealing ring can improve the fit between moving components, thereby increasing Qinj [18]. While these studies have reduced Hmin and improved Qinj for venturi injectors and proportional fertilizer pumps to some extent, the improvement in performance is inherently limited by their operating principles. Venturi injectors, as jet pumps, rely on high-pressure and high-velocity driving water to create negative pressure in the throat for suction. The mixing and collision of driving water with low-pressure, low-velocity fertilizer solution in the throat results in significant energy loss. Proportional fertilizer pumps, on the other hand, generate negative pressure through the reciprocating motion of a piston driven by water flow, but only half of the work performed by the piston is used for suction. Moreover, the use of multiple check valves, directional valves, and moving seals results in low efficiency when water energy is converted to pressure energy. Under an outlet pressure (Hout) of 0.1 MPa, the optimized venturi injectors and proportional fertilizer pumps require Hmin values ranging from 0.12 to 0.15 MPa. At an inlet pressure of 0.14 MPa, Qinj ranges from 25.2 to 78.3 L/h. However, current hydraulic fertilizer injectors still require high operating pressures, and their efficiency remains to be improved [10].
Many researchers have proposed using impact-type [19], axial-flow [20], or mixed-flow water turbines [21] recently as the power source for hydrodynamic fertilizer injectors, converting hydraulic energy to mechanical energy to drive diaphragm pumps and inject fertilizer into the pipeline system. These authors generally believe that hydraulic fertilization devices based on water turbines have a higher energy conversion efficiency than venturi fertilization devices do and proportional fertilization pumps do and that under the same energy input conditions, they can increase the Qinj. However, most of the research has remained at the conceptual stage, primarily in patents, with no physical devices yet presented. Water turbines are typically used in hydraulic engineering projects, especially ultralow-head hydropower stations and tidal power stations. For these stations, the flow rate is ≥30 m3/h, with a head (H) < 0.1 MPa, which is similar to the operating conditions of an irrigation unit. Therefore, it is highly feasible to apply the turbine to the irrigation pipeline system, and there have been examples of applying the turbine to the agricultural irrigation system at home and abroad [22]. Under these conditions, axial-flow turbines (AFTs) are better suited than mixed-flow and impact turbines because of their higher specific speed [23]. The impeller is the core component of the turbine, and optimizing the impeller structure can significantly improve the output power of the turbine [24]. The main simulation optimization methods include the 6-DOF dynamic mesh simulation method (where the impeller speed (n) is not an input parameter) [25,26] and the fixed n-value mesh motion simulation method (where n is an input parameter) [27,28]. The latter method has lower simulation difficulty and higher simulation accuracy. For low-head hydropower stations, Janjua et al. [29] used the mesh motion simulation method to analyze the output power and pressure variation on the blade surface of an AFT for five different blade angles (10.1°–18.1°). The results show that the optimal flow guiding effect occurred at a 10.12° blade angle, increasing the AFT output power by 4.4%. Researchers have used CFD simulations combined with RBF neural networks to establish a mapping relationship between turbine efficiency and structural parameters and then applied the NSGA-II genetic algorithm for multi-objective optimization. After optimization, the pressure, flow velocity, and turbulent kinetic energy flow fields inside the turbine significantly improved, and the energy conversion efficiency increased by 5.7% [30,31]. Moreover, AFTs also serve as the main components of hydraulic turbines in petrochemical industries and urban high-rise water supply systems [28]. By optimizing the geometry of the blades, the energy conversion efficiency of the AFT can be improved by 1.2% [32].
In this study, we develop a hydrodynamic fertilizer injector (HFI) based on an axial-flow turbine (AFT), which uses an AFT to convert the kinetic energy of water to mechanical energy and then generates negative pressure through a diaphragm pump to achieve fertilizer injection. Drawing from optimization methods for AFTs used in hydraulic engineering and hydraulic turbine devices, we combine hydraulic performance testing with CFD numerical simulations. The focus is on structural parameters such as the number of impellers, the number of blades on each impeller, and the arrangement of impellers. We explore the response patterns of the output power and cavitation resistance to these impeller structural parameters. Additionally, the internal flow field distribution characteristics of the AFT were analyzed, and the structure of the AFT was further optimized from the perspective of negative pressure cavitation. The optimized design will undergo prototype fabrication and fertilization performance testing. These results provide a basis for the development of hydraulic fertilization injectors.
2. Materials and Methods
2.1. HFI Design and Working Principle
The HFI consists mainly of an AFT and diaphragm pumps and is capable of transferring energy by “water flow kinetic energy → rotational mechanical energy → negative pressure absorption energy”, allowing for the injection of fertilizer liquid into the irrigation system without the need for electrical power [33]. The AFT includes the impeller assembly, shaft, mechanical seals, and K-shaped pipelines. The water flow enters the AFT through the inlet of the K-shaped pipeline and returns to the main pipeline through the outlet of the K-shaped pipeline. The rotation of the impeller assembly and shaft drives the diaphragm pump, creating negative pressure to absorb energy. The fertilizer mixture is drawn into the diaphragm pump through the suction port and then injected into the main pipeline through the injection port (Figure 1).
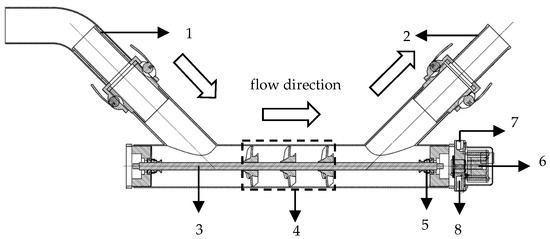
Figure 1.
Schematic of the main components of the hydrodynamic fertilizer injector. 1—Inlet of K-shaped pipeline; 2—outlet of K-shaped pipeline; 3—shaft; 4—impeller group; 5—mechanical seal; 6—diaphragm plunger pump; 7—fertilizer suction port; 8—fertilizer injection port.
2.2. Analysis of Parameters Affecting the Hydraulic Performance of the HFI
In practical engineering, the fertilizer injection flow rate (Qinj), inlet pressure (H), and minimum pressure required for fertilizer injection (Hmin) are key hydraulic performance indicators of the HFI. A larger Qinj indicates higher fertilizer injection efficiency, a smaller H indicates lower energy consumption for the same Qinj, and a smaller Hmin indicates broader applicability of the HFI. When the diaphragm plunger pump in Figure 2 remains unchanged, the power–flow curve of the pump shows that Qinj increases with increasing P [34]. Therefore, P can be used to characterize Qinj, and P is influenced mainly by the structural parameters of the AFT [35,36]. In addition, as the water flows over the blade surfaces, negative pressure can be generated, resulting in cavitation, which, if severe, may cause blade cavitation and affect the service life of the AFT [37,38,39]. To improve the fertilizer injection performance of the HFI, this study aims to determine suitable structural design parameters for AFT impeller assembly by increasing P and reducing the negative pressure.
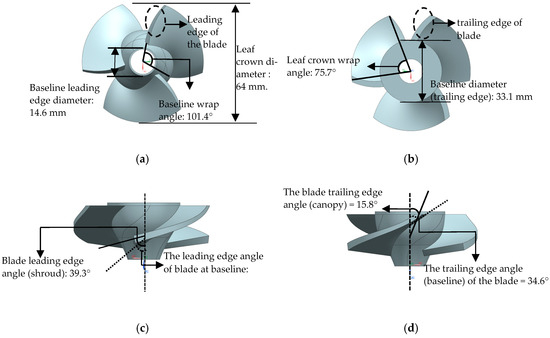
Figure 2.
Axial-flow turbine impeller structure top view (a), top view (b), front view (c), and right view (d).
2.2.1. Experimental Design
The structural design parameters of the AFT impeller assembly include the number of impellers (M1), the average number of blades per impeller (M2), and the arrangement sequence (M3). M1 represents the number of impellers on the AFT, which is three gradients: 2, 3, and 4. M2 is the ratio of the total number of blades (N) to M1 and is three gradients: few (N/M1 = 3), medium (N/M1 = 3.3–3.7), and many (N/M1 = 4.0). M3 includes three arrangement patterns: “same”, “few-to-many”, and “many-to-few”. “Same” indicates that each impeller has the same number of blades (e.g., D33); “few-to-many” indicates that the arrangement follows a pattern such as “few blades–many blades” (e.g., D34), “few blades–many blades–few blades” (e.g., T343), or “few blades–many blades–few blades–many blades” (e.g., F3434); “many-to-few” follows a similar pattern, corresponding to D43, T434, and F4343. The experiment includes 12 impeller assembly structural designs (Table 1). Abbas et al. [27] optimized the blade design parameters of similar size turbines and significantly improved P. Therefore, the blade design parameters such as the leading edge angle at the blade baseline and the leading edge angle at the blade crown in this paper are based on the data of this paper (Figure 2).

Table 1.
Structural design of the axial-flow turbine impeller group for the hydrodynamic fertilizer injector.
2.2.2. Test Methods and Monitoring Indices
In this study, Fluent (Ansys Fluent 2022R2, Kingston, NY, USA) is used to perform numerical simulations of the 12 AFT impeller assemblies. The hydraulic performance test results of the HFI consisting of two of these AFT impeller assemblies are used to validate the simulation accuracy.
Hydraulic Performance Test
The hydraulic performance test of the HFI was carried out in accordance with the national water-saving irrigation engineering technology research center (Beijing Daxing). the water source was 23 ± 2 °C tap water and the temperature was 25 °C. Water was used instead of liquid fertilizer [40]. After the HFI composed of T333 and F3434 AFTs, as shown in Table 1, was connected to the test platform, the centrifugal pump was started and the control valve and outlet valve were adjusted such that the inlet pressure (H) ranged from 0.12 to 0.18 MPa, with a pressure change gradient (ΔH) of 0.01 MPa, and the outlet pressure (Hout) was 0.1 MPa. After the system had been running stably for 5 min, the actual outlet flow rate (Qm) of the HFI was measured via an ultrasonic flowmeter (Figure 3). Qm was used to verify the accuracy of the numerical simulation.
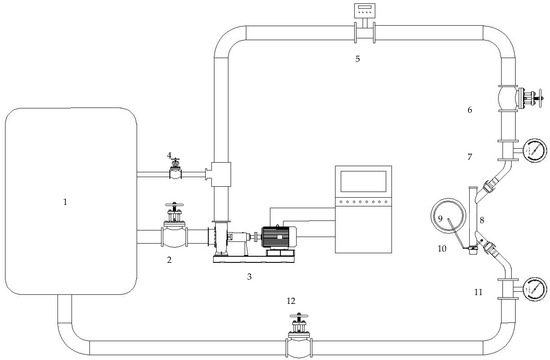
Figure 3.
Schematic of the HFI hydraulic performance test platform. 1—Water storage barrel; 2—inlet valve; 3—centrifugal pump; 4—pressure relief valve; 5—ultrasonic flowmeter; 6—control valve; 7—inlet pressure gauge; 8—HFI device; 9—fertilization barrel; 10—suction tube; 11—outlet pressure gauge; 12—return valve.
For the optimized HFI, the optimized AFT was fabricated using a photopolymerization 3D printer. After the AFT was assembled with a diaphragm pump to form the HFI, it was installed on the test platform. By adjusting the control and outlet valves, Hout was set to 0.1 MPa and H was gradually increased from 0 MPa to 0.12 MPa. The pressure at which the HFI began to inject fertilizer was recorded as Hmin. H was then set to 0.12~0.18 MPa, with ΔH = 0.01 MPa. After the system operated stably for 5 min, a mass of water (M, in kg) was added to the injection bucket and the suction pipe was placed in the bucket. A stopwatch was started to measure the time (t, in s) required to completely empty the bucket. Qinj (L/h) was calculated as Qinj = 3600 M/t. At each H, Qm was measured using an ultrasonic flowmeter.
The precision of the photopolymerization 3D printer is 0.02 mm; the centrifugal pump head and flow rate are 0.5 MPa and 75 m3/h, respectively; the pressure gauge range is 0~0.6 MPa with a precision of 0.4; and the ultrasonic flow meter range is 1.25~170 m3/h with a precision of ±2%.
CFD Numerical Simulation of Hydraulic Turbines
(1) 3D model construction
The AFT blades are parametrically modeled via CFturbo 2022 (CFturbo GMBH, Dresden, Germany), whereas the AFT shaft, K-shaped pipeline, and other components are drawn using UG 12.0 (Unigraphics NX 12.0, Plano, TX, USA). To obtain stable outlet flow simulation results, the inlet and outlet of the K-shaped pipeline are extended to four times the pipe diameter.
(2) Grid division and independence verification
Using the Mesh module in ANSYS Workbench 22R2 (Ansys Inc., Canonsburg, WA, USA), the fluid domain was meshed, with the fluid domain controlled by the impeller group set as a rotating domain and the other regions set as stationary domains (Figure 4). The entire fluid domain was meshed with a structured tetrahedral grid configuration. For the mesh independence verification, H was 0.16 MPa, the outlet was set to a free outflow, with Hout = 0 MPa, and n was 1500 rpm. The variation in the AFT outlet flow rate (Qs) was calculated via Equation (1), and the corresponding change rate (E) was obtained. The variation in E with the number of mesh elements (N) showed that when N reached 1 million, corresponding to a grid size of 5~10 mm, with the impeller surface mesh refined to 1.5 mm and a growth rate of 1.1, E was less than 0.5% (Figure 5), which meets the requirements for turbine numerical simulation [41].
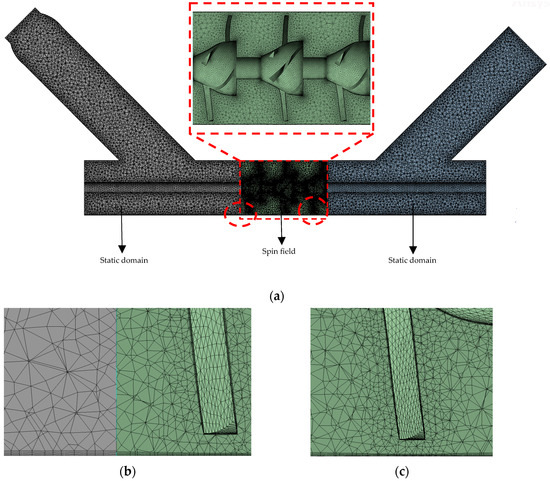
Figure 4.
Fluid domain division and mesh generation of axial-flow turbine (a), boundary layer expansion (b), and impeller edge mesh refinement (c).
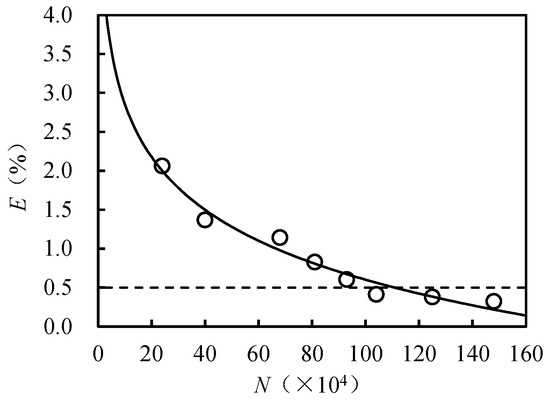
Figure 5.
Grid independence verification of the change rate of outlet flow (E) with the number of grids (N).
In the equation, Qs(i+1) and Qs(i) represent the AFT outlet flow simulation results when the number of meshes is Ni+1 and Ni, respectively, with units of kg/s, where Ni+1 > Ni.
(3) Simulation settings
For hydraulic performance numerical simulations of the AFT and other rotating machinery, the SST k-ω turbulence model is generally used [41]. The wall boundary establishes a no-slip condition, and the interface between the stationary domain and the rotating domain is treated as a coupled wall. The solver uses the SIMPLE algorithm, and momentum is solved using a second-order upwind scheme. The calculation time step is determined on the basis of the Courant number criterion, which is 0.0008 s, with a maximum of 20 iterations and 2000 time steps.
During the numerical simulation, H was 0.14~0.18 MPa, with ΔH = 0.01 MPa and Hout = 0.1 MPa. For five different H conditions, n was in the range of 500~3000 rpm, with a step size (Δn) of 500 rpm, resulting in six values for n. Each AFT included 30 operating condition combinations, and with 12 AFTs, a total of 360 simulation scenarios were generated.
(4) Monitoring and calculation indicators
The AFT output torque (T), AFT outlet flow rate (Qs), internal flow field of the AFT, and blade surface pressure (BP) curves can be obtained using the CFD postprocessing module in ANSYS Workbench (Figure 6). P can be calculated using Equation (2). In the equation, the angle θ is the angle between the flow direction and the blade pressure surface. Along the flow direction, θ gradually decreases.

Figure 6.
Internal flow field of axial flow turbine (a) and blade surface pressure; (b) observation surface and data point diagram. Note: In the figure, the gray area is the observation surface of the internal flow field of the axial flow turbine; the red arrow on the blade surface is the force of water flow on the pressure surface of the blade; the blue arrow on the blade surface is the force of the fluid on the suction surface of the blade; the blue arrow in the gray area is the direction of water flow; the green line is the sampling line of the leaf BP curve; A1 is the leading edge of the suction surface; A2 is the leading edge of the pressure surface; B1 is the trailing edge of the pressure surface; and B2 is the suction surface inlet trailing edge. x is the horizontal distance between the data point on the A1B1 or A2B2 line and the leading edge of the blade; x/L is the relative position of the data point; x/L = 0 represents the position of A1 and A2; and x/L = 1 represents the position of B1 and B2.
In the equation, P represents the AFT output power (W), n represents the rotational speed (rpm), and T represents the AFT torque (N·m).
2.3. Data Processing
2.3.1. Verification of the CFD Simulation Results
To verify the reliability of the AFT simulation results, this study calculates the normalized root mean square error (nRMSE) between Qs and Qm via Equation (3) [42]:
where represents the average of the measured outlet flow rates and m is the number of measured values. The interpretation of the nRMSE is as follows: nRMSE ≤ 10%: high simulation accuracy; 10% < nRMSE ≤ 20%: moderate simulation accuracy; 20% < nRMSE ≤ 30%: Average simulation accuracy; and nRMSE > 30%: poor simulation accuracy.
2.3.2. Optimization of the Impeller Structure Parameter Combination
On the basis of the simulation results from the 360 scenarios, the P–n curve can be used to determine the AFT structural design parameters that maximize P. When the impact of cavitation on the AFT service life is considered, the blade BP curve can be used to identify the optimal impeller structure for cavitation resistance. The P–n curve and the blade BP curve are plotted via Excel 2019 (Microsoft Office Excel, Redmond, WA, USA), whereas the significance analysis of the effects on P is performed via R-Project (R Foundation for Statistical Computing, Vienna, Austria). The overall technical roadmap is shown in Figure 7.
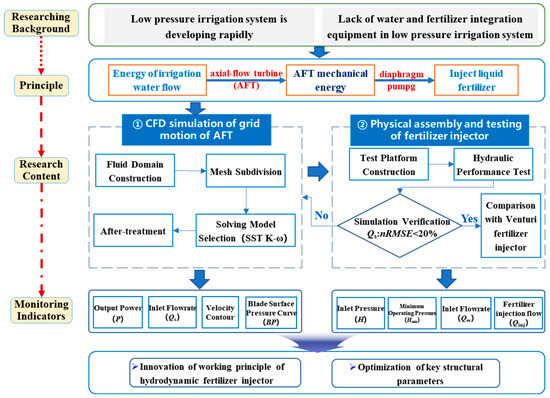
Figure 7.
Design flow chart of hydrodynamic fertilizer injector based on CFD numerical simulation and hydraulic performance measurement.
3. Results and Analysis
3.1. Response Law of Outlet Flow and Output Power of AFT to Rotational Speed
3.1.1. Simulation Verification
The Qs and Qm of both T333 and F3434 AFT increase as H increases. The average nRMSE for the two methods is 5.1%, indicating high simulation accuracy (Figure 8).
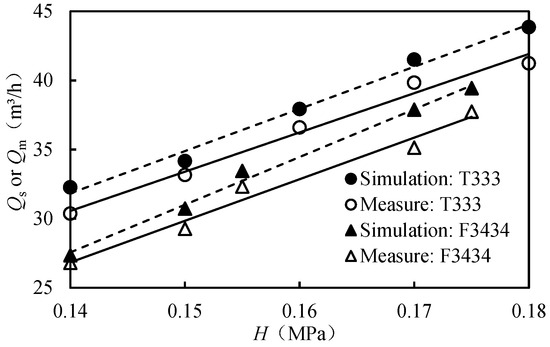
Figure 8.
Comparison of the simulated value (Qs) and measured value (Qm) of AFT outlet flow.
3.1.2. Variation Law of the Output Power of the Axial-Flow Turbine with Rotational Speed
When H = 0.14~0.18 MPa and n = 500~3000 rpm, the P of the 12 AFTs ranges from 35 to 310 W. P increases with n, then decreases, increases with H, and decreases as M1 and M2 increase (Figure 9).
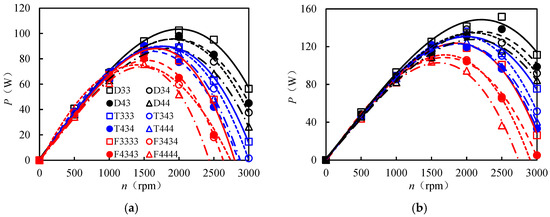
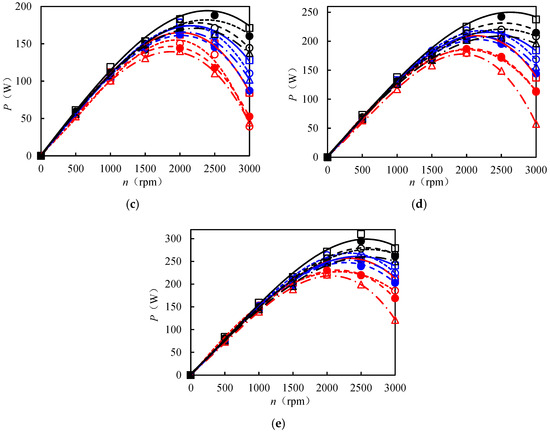
Figure 9.
The output power (P) versus rotational speed (n) curves of different AFTs at H = 0.14 (a), 0.15 (b), 0.16 (c), 0.17 (d), and 0.18 MPa (e).
The maximum value of P (Pmax) in Figure 9 was extracted for analysis (Table 2). Since Pmax exhibited minimal variation with M3, a significance analysis was conducted solely on the effects of M1 and M2 on Pmax. When H = 0.14~0.18 MPa, Pmax for D33 was the highest, 5.3~55.6% greater than that of the other AFTs. Additionally, Pmax at M1 = 2 was 9.1% and 27.7% higher than that at M1 = 3 and M1 = 4, respectively. The influence of M1 on Pmax reached a statistically significant level (p < 0.05). The average Pmax of D33 across the five H values was 6.7~33.5% greater than that of the other AFTs, and the average Pmax at M1 = 2 was 8.7% and 22.7% greater than that at M1 = 3 and M1 = 4, respectively. The influence of M1 on the mean Pmax also reached a statistically significant level (p < 0.05). Compared with D33, the average Pmax for D34, D43, and D44 decreased by 10.7%, 6.3%, and 15.1%, respectively.

Table 2.
Significance analysis of the effects of M1 and M2 on the maximum output power (Pmax) under different inlet pressures (H).
3.2. Internal Flow Field of AFT
3.2.1. Velocity Cloud Diagram
For all 12 AFT blades, a low-speed fluid region (reg-lv) exists within a certain range at the leading edge of the suction surface (A1 position), where the flow velocity (v) is less than 2 m/s. A thin reg-lv region also exists along the inner wall of the pipe and on the blade surface. Downstream of position A1 and upstream of the trailing edge of the pressure surface (position B2), a high-speed fluid region (reg-hv) exists where v > 12 m/s (Figure 10).
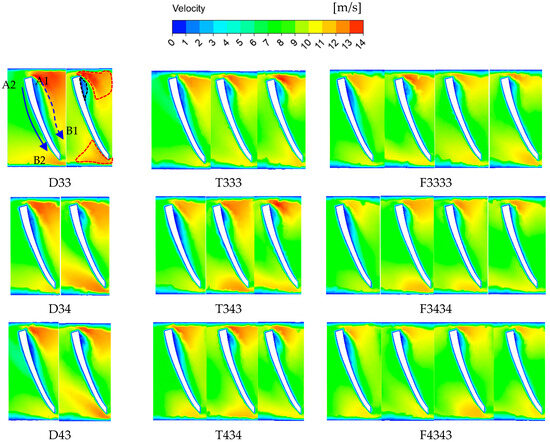
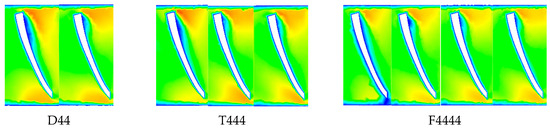
Figure 10.
The internal flow velocity contours of 12 AFTs under the inlet pressure (H) of 0.18 MPa and the rotational speed (n) of 2500 rpm. Note: A1 is the leading edge of the suction surface, A2 is the leading edge of the pressure surface, B1 is the trailing edge of the pressure surface, and B2 is the trailing edge of the suction surface. The area surrounded by the red dotted line represents reg-hv, and the area surrounded by the black dotted line represents reg-lv.
For the blade pressure surface, the flow v gradually increases from upstream of A2 to upstream of B2 (blue solid arrow). For the blade suction surface, the velocity decreases gradually from downstream of A1 to downstream of B1 (blue dashed arrow). When H = 0.18 MPa and n = 2500 rpm, along the flow direction, the areas of the reg-lv and reg-hv regions gradually decrease. The velocity in the reg-lv region gradually increases, whereas the velocity in the reg-hv region gradually decreases. As M1 increases from 2 to 4, the area of the reg-lv region on the first blade gradually decreases, but the reg-lv region area on the other blades does not significantly change with M1. The area of the reg-hv region and its velocity decrease gradually as M1 increases. Both the area and velocity of reg-lv and reg-hv decrease as M2 increases, but the changes are relatively small. When M2 is at a “medium” level, M3 with “low-high” (D34, T343, and F3434) and “high-low” (D43, T434, and F4343) arrangements has little effect on the flow field. When H and n are the same, the reg-hv area and v of D33 are greater than those of the other AFTs.
Using D33 as an example, when n increases from 2000 rpm to 3000 rpm, the area of the reg-lv region gradually decreases, whereas the area and v of the reg-hv region gradually increase. When H increases from 0.14 MPa to 0.18 MPa, the area and v of the reg-hv region gradually increase, whereas the area of the reg-lv region remains almost unchanged (Figure 11).
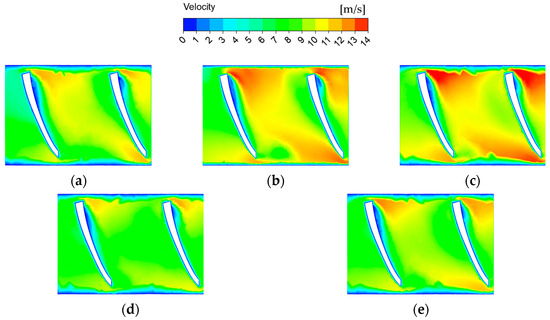
Figure 11.
Internal flow velocity contours of D33 at H = 0.18 MPa with n = 2000 rpm (a), 2500 rpm (b), and 3000 rpm (c) and at H = 0.14 (d), at H = 0.16 MPa (e), and at H = 0.18 MPa (b) with n = 2500 rpm.
3.2.2. Blade Surface Pressure Curve
For the AFT with Pmax (M1 = 2), the BP curves show a similar trend across the four AFTs when H = 0.18 MPa and n = 2500 rpm. The BP curve on the pressure surface, when x/L is 0~0.1, increases sharply and then decreases sharply, whereas the BP curve on the suction surface, with the exception of D44, decreases sharply and then increases sharply. When x/L is 0.1~0.8, the BP curve on the pressure surface decreases slowly, whereas the BP curve on the suction surface increases slowly. When x/L is 0.8~1.0, both the pressure and suction surface BP curves decrease sharply and then increase sharply, reaching a minimum value at x/L = 0.93 (Figure 12).
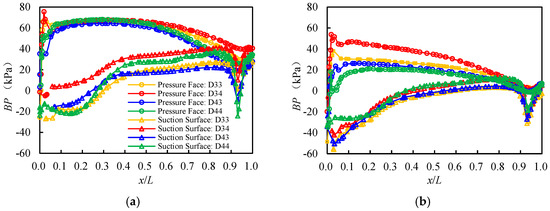
Figure 12.
The blade surface pressure curves of the first impeller (a) and the second impeller (b) along the inlet direction of four kinds of axial-flow turbines with M1 = 2 at an inlet pressure (H) of 0.18 MPa and a rotational speed (n) of 2500 rpm are plotted.
The difference in BP (ΔBP) was calculated on the basis of the pressure and suction surfaces at different positions on each blade. The average values () for impellers D33, D34, D43, and D44 were 36.2 kPa, 27.6 kPa, 31.7 kPa, and 26.1 kPa, respectively. decreased with increasing M2. Compared with those of D33, the values of D34, D43, and D44 were 23.7%, 12.4%, and 27.9% lower, respectively. When M2 = 3.5, the of the “more-less” AFT (based on M3) was 14.8% greater than that of the “fewer” AFT. Additionally, exhibited a positive correlation with Pmax.
When x/L is in the range of 0~0.1 or 0.8~1.0, the BP values on the suction surface of the AFT are less than zero (BP < 0). In these regions, |BP| is defined as the NP, where a larger NP value indicates a greater likelihood of cavitation at that position, potentially resulting in erosion. The NP values at x/L = 0~0.1 are, on average, 23.6% higher than those at x/L = 0.8~1.0. For the first impeller along the water flow direction, the NP values for D33, D34, D43, and D44 are 26.9, 4.2, 15.8, and 18.5 kPa, respectively. D33 has the highest NP value, which is 84.3%, 41.2%, and 80.8% higher than those of D34, D43, and D44, respectively. For the second impeller along the water flow direction, the NP values for D33, D34, D43, and D44 are 55.9 kPa, 42.1 kPa, 50.5 kPa, and 34.7 kPa, respectively. Compared with D34, D43, and D44, D33 still has the highest NP value but is 24.7%, 9.6%, and 37.9% lower, respectively.
For D33, when n increases from 2000 rpm to 3000 rpm, the BP curves of the two blades exhibit minimal changes (Figure 13). When the pressure (H) is between 0.14 MPa and 0.18 MPa, as H increases, the BP values on the pressure surface and of the AFT gradually increase, whereas the change in BP values on the suction surface is relatively small (Figure 14).
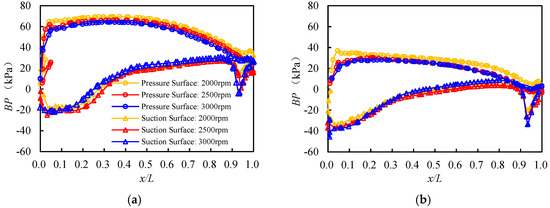
Figure 13.
The blade surface pressure curves of the first impeller (a) and the second impeller (b) at an inlet pressure (H) of 0.18 MPa and a rotational speed (n) of 2000, 2500, and 3000 rpm are plotted.
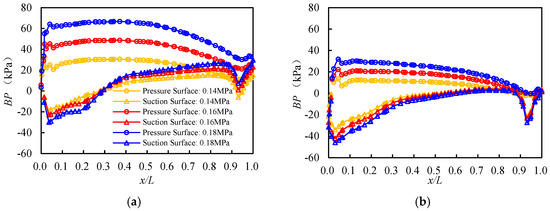
Figure 14.
The blade surface pressure curves of the first impeller (a) and the second impeller (b) at an inlet pressure (H) of 0.14~0.18 MPa and a rotational speed (n) of 2500 rpm are plotted.
3.3. Fertilization Performance of the Optimized HFI
On the basis of the P–n curve, internal flow field characteristics, and BP curve, this study selected the impeller structure with M1 = 2 for processing. The structure was assembled with a diaphragm pump to form an HFI, and its fertilizer injection performance was tested (Figure 15). The Hmin values for D33, D34, D43, and D44 were less than 0.12 MPa. When H = 0.12~0.18 MPa, the Qinj of the four HFIs gradually increased (R2 = 0.986), with D33 exhibiting the highest Qinj (366.4~847.3 L/h), representing average increases of 1.3%, 5.6%, and 7.0% compared with D34, D43, and D44, respectively.
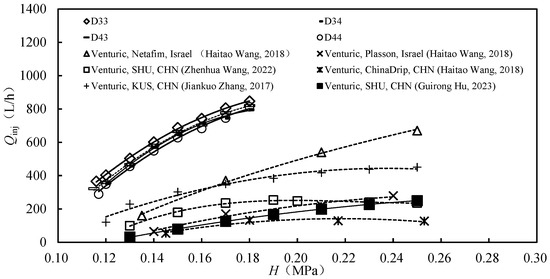
Figure 15.
Variation curves of the optimized axial-flow hydrodynamic fertilizer injectors (D33, D44) and the fertilizer injection flow (Qinj) of the domestic and foreign venturi fertilizer injectors with the inlet pressure (H) [12,15,16,43].
For the three optimized venturi fertilizer injectors reported in the literature [12,15,16] and the three commercial venturi fertilizer injectors [43], when Hout was 0.1 MPa, Hmin ranged from 0.12 to 0.145 MPa and Qinj ranged from 30.7 to 670.0 L/h. Compared with the fertilization performance of these six venturi injectors, the Hmin of the four HFIs with M1 = 2 decreased by 0.005~0.03 MPa, whereas the Qinj increased by an average of 38.7~461.0%.
4. Discussion
4.1. Response Law of AFT Hydraulic Performance to Structural Parameters
In order to study the variation law of P within the range of n = 0~3000 rpm, this paper conducts simulation research by using Fluent 2022 R1 and adopts the grid motion simulation method with a fixed n value. Due to certain limitations of CFD simulation, factors such as friction loss and the mass of the shaft are not considered. The nRMSE between the simulated values and the measured values is 5.1%. The simulation precision is relatively high, but there are still certain deviations.
AFTs can be utilized in hydroelectric power generation to convert water energy to electrical energy. At small- and medium-sized river power stations, for AFTs with M1 = 1 and an impeller diameter of 76 mm, P increases and then decreases with increasing n (0~3000 rpm), following a quadratic relationship [27,44]. This trend is consistent with the relationship observed in this study for AFTs with M1 = 2 to 4 and an impeller diameter of 63 mm. When the impeller diameter or operating conditions of AFTs change, Pmax varies with the impeller structure. For example, in hydraulic turbines for residual pressure recovery during oil drilling, where H is 10 MPa (53.3 times greater than that in this study), Pmax increases with M2 when n = 735 rpm, M1 = 1, and M2 = 3 to 5 [45]. However, in this study, Pmax decreases as M2 increases. Similarly, tidal energy generators, which use AFTs with diameters of 3500 to 4500 mm (63.5 times the size of AFTs in this study) to convert flow kinetic energy to mechanical and electrical energy, operate with a flow rate (Qs) of 25,000 to 40,000 m3/h (101.6 times that in this study). For these systems, Pmax increases with M1; when M1 increases from 1 to 3, Pmax increases by an average of 14.0% [46,47]. However, in this study, when M1 increases from 2 to 4, Pmax decreases by an average of 10.2%. A significance analysis of Pmax in the P–n curve shows that AFTs with M1 = 2 achieve average increases of 8.7% and 22.7% in Pmax compared with those with M1 = 3 and M1 = 4, respectively. Among the impellers analyzed, the Pmax of D33 is the highest, with an average increase of 6.7% to 33.5% compared with those of the other AFTs across all H conditions.
4.2. Internal Flow Field and Selection of AFTs
For the AFT in this study, there was a viscous boundary layer on the blade surface and the internal pipe wall, which resulted in the presence of a thin reg-lv 46. The relatively large area of reg-lv at the leading edge of the blade suction surface is caused mainly by the direct impact of the flow on the blade (θ > 0° in Figure 6a), resulting in flow separation and vortex formation. Along the flow direction, θ gradually decreases because of the straightening effect of the impeller, which weakens the flow separation and vortex phenomena at the leading edge of the blade suction surface. As a result, the area of reg-lv in successive stages of the impeller gradually decreases in the direction of the flow (Figure 10).
When H and n are constant, as M1 and M2 increase, the areas of reg-lv and reg-hv increase and then decrease, whereas v in the reg-hv area gradually decreases. For the same AFT, the areas of reg-lv and reg-hv, as well as the velocity in the reg-hv region, follow an increasing trend as H increases. These trends in the internal flow field of the AFT with respect to the structural parameters and operating conditions are consistent with the variation in Pmax. For D33, when H and n are constant, both the area and v of reg-hv are maximized.
BP is a quantitative indicator that characterizes the impact of water flow on the AFT. The variation in BP with x/L in existing studies is consistent with the results presented in this paper [48]. From the perspective of energy transfer, reflects the work performed by the turbine and is positively correlated with Pmax [49]. In this study, the response of to structural parameters and operating conditions is consistent with that of Pmax. for D33 is 26.5% greater than that for D34, D43, and D44.
According to Figure 12, Figure 13 and Figure 14, at the x/L position of 0~0.1 on the suction side, the BP of the blade is less than 0. The negative pressure at this location is caused by the presence of the reg-lv region, which generates many vortices and low-energy fluid pockets. At the x/L = 0.93 position, a sharp pressure change occurs due to flow separation at the trailing edge [49,50]. Numerous studies have shown that when negative pressure zones occur on a blade, cavitation can occur, with the water flow in these regions being prone to cavitation and bubble formation. When the bubble clusters collapse after they leave the negative pressure region, they produce high-intensity shock waves traveling at speeds of 10~100 m/s, which can erode the blade and shorten its lifespan [51]. The larger the NP value is, the greater the likelihood that cavitation will occur on the blade [52]. Since the NP of D33 is on average 32.6% greater than those of D34, D43, and D44 are, it is more susceptible to cavitation, whereas D44 has the smallest NP value.
When the maximum Pmax is reached, the optimal distribution characteristics of the internal flow field (the maximum area and v of reg-hv) and the maximum are the optimal targets, and D33 is optimal. When the cavitation phenomenon is considered, compared with D33, for D34 and D44, Pmax is reduced by 10.7% and 15.1%, respectively; is reduced by 23.7% and 27.9%, respectively; but NP is reduced by 30.5% and 37.9%, respectively.
4.3. Response Law of HFI Fertilizer Injection Performance to AFT Structure Design
Since an HFI is a combination of an AFT and diaphragm pumps, Qinj is influenced primarily by the AFT output power, the energy conversion efficiency of the diaphragm pump, and the mechanical transfer between the two. Therefore, when H is 0.12~0.18 MPa, the Qinj of the HFI composed of D33 is, on average, 1.3%, 5.6%, and 7.0% higher than those of D34, D43, and D44, respectively, which is smaller than the differences in Pmax and among the four participants in the numerical simulation. The venturi fertilizer injector is widely used in the integration of drip irrigation with water and fertilizer because of its advantages, such as its simple structure and low cost [53]. Both domestic and international researchers, as well as microirrigation equipment manufacturers, have conducted extensive research aimed at reducing Hmin and improving Qinj under the same H [15,16,42,54,55]. During the operation of the venturi fertilizer injector, the collision and mixing of high-pressure, high-speed water flow with low-pressure, low-speed fertilizer liquid easily results in the formation of whirlpools and low-energy fluid clusters. This disrupts the normal flow of internal water, resulting in significant pressure loss and turbulent kinetic energy loss at the fertilizer suction port [15,56]. Therefore, the Hmin of optimized or mass-produced venturi fertilizer injectors is typically ≥0.12 MPa, which is higher than the Hmin in this study. Under an H of 0.12~0.18 MPa, the Qinj of the venturi injector ranges from 30.7 to 119.9 L/h, which is lower than the Qinj in this paper. The main reason for this phenomenon is that the flow driven by the AFT in the HFI does not interfere with the flow path through which the diaphragm pump draws the fertilizer. Therefore, the applicability of the HFI proposed in this paper—specifically, its Hmin and fertilizer injection efficiency (i.e., Qinj under the same H)—can meet engineering requirements and enable the integration of water and fertilizer for surface irrigation or sprinkler/drip irrigation systems. This holds true for both low-pressure pipeline irrigation systems (water supply pressure < 0.15 MPa) and high-pressure sprinkler irrigation systems. Considering both the fertilizer injection efficiency and service life, the Qinj for the HFI corresponding to D34 and D44 is 1.3% and 7.0% lower, respectively, than that of D33, and the NP of the second impeller is 24.7% and 37.9% lower, respectively, than that of D33. Considering the additional production and installation costs associated with two sets of molds for the HFI based on D34, D44 was ultimately chosen as the finalized impeller structure for the HFI. Compared with a venturi injector, an HFI has smaller pressure loss and higher Qinj. However, an HFI has many overall components, high manufacturing costs, and requires more thorough cleaning after each irrigation. So, it is more suitable for low-pressure conditions where a venturi injector cannot work normally. When the irrigation system pressure is high, the use of a venturi fertilizer injector will have higher economic benefits.
5. Conclusions
In this work, we developed an HFI based on an AFT as a component for water energy conversion. To target M1, M2, and M3 of the AFT, hydraulic performance testing and CFD numerical simulation were integrated to optimize the AFT structure. The conclusions are as follows: the nRMSE between the simulated and measured AFT outlet flow values is 5.1%, revealing the high accuracy of the mesh rotation simulation method with a fixed n. The P of the AFT increases and then decreases with increasing n, whereas it increases with increasing H. Regarding the distribution characteristics of the AFT output power and internal flow field, the Pmax of D33 is the highest, increasing by 6.7~33.5% compared with those of the other treatments. In the flow field of D33, the reg-lv area is small, whereas the reg-hv and v areas are large, resulting in high energy conversion efficiency. The measured Qinj values of D33, D34, and D44 were 288.6~847.3 L/h, and their Hmin values were less than 0.12 MPa, which was 0.005~0.030 MPa lower than that of the venturi fertilizer injector, whereas Qinj increased by 38.7%~461.0% on average. Considering the effect of cavitation on the impeller life, D34 and D44 are more suitable as impeller structure combinations for the HFI. Pmax decreased by an average of 10.7% and 15.1% under each H, and Qinj decreased by 1.3% and 7.0%, respectively, compared with D33, but NP decreased by 30.5% and 37.9% for D34 and D44, respectively. Considering the fertilizer injection efficiency, impeller service life, and additional costs of multiple mold openings in actual production, D44 was ultimately selected as the impeller structure combination for the HFI. In addition, the HFI will be further improved in the future, the replacement of impeller materials will be explored to improve the wear resistance of the AFT, the long-term use reliability of the HFI will be tested for different irrigation environments, and the overall structure design will be changed to improve the long-term use reliability of HFI.
Author Contributions
Conceptualization, Y.M. and C.Z.; methodology, C.Z. and Y.M.; software, C.Z.; validation, Y.M., S.L. and B.Z.; formal analysis, C.Z., Q.Z., S.L., B.Z. and Y.G.; investigation, C.Z.; resources, S.L.; data curation, C.Z.; writing—original draft preparation, C.Z.; writing—review and editing, Y.M. and S.L.; visualization, B.Z. and Y.G.; supervision, J.X. and Y.M.; project administration, Y.M.; funding acquisition, Y.M. and J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Science and Technology Project for Revitalization of Inner Mongolia, China (2022EEDSKJXM004) and the Research and Development Support Program of China Institute of Water Resources and Hydropower Research (ID0145B042021).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| HFI | Hydrodynamic fertilizer injector |
| AFT | Axial-flow water turbine |
| M1 | Number of impellers |
| M2 | Average number of blades of a single impeller |
| M3 | Layout mode |
| P | Output power |
| NP | Leaf negative pressure |
| Qinj | Fertilizer injection flow |
| H | Inlet pressure |
| Qs | Simulated value of outlet flow |
| Qm | The measured value of outlet flow |
| nRMSE | Root mean square error |
| Pmax | Maximum output power |
| NP | Negative pressure value |
| Hout | Outlet pressure |
| Hmin | Minimum inlet pressure |
| N | Number of all leaves on AFT |
| M | Quality of clear water |
| ΔH | Pressure gradient. |
| t | The time required for the water in the fertilizer barrel to be sucked cleanly |
| E | Rate of change |
| n | Revolution speed |
| N | Grid number |
| Δn | Gradient of speed change |
| BP | Blade surface pressure |
| θ | The angle between water flow direction and blade pressure surface |
| x | It is the horizontal distance between the data points on the straight line a1b1 or a2b2 and the leading edge of the blade. |
| L | For the total length of a1b1 |
| T | AFT torque |
| reg-lv | Low-velocity fluid region |
| reg-hv | High-speed fluid region |
| v | Flow velocity |
| ΔBP | BP difference between pressure surface and suction surface |
| Average value of ΔBP | |
| R2 | Correlation coefficient |
References
- Kabirigi, M.; Prakash, S.O.; Prescella, B.V.; Niamwiza, C.; Quintin, S.P.; Mwamjengwa, I.A.; Zhang, C. Fertigation for environmentally friendly fertilizers application: Constraints and opportunities for its application in developing countries. Agric. Sci. 2017, 8, 292. [Google Scholar] [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. China Water Resources Statistical Yearbook in 2021. 2022. Available online: https://data.cnki.net/yearBook/single?id=N2023110278&pinyinCode=YSLTJ (accessed on 24 December 2024).
- Fan, J.; Lu, X.; Gu, S.; Guo, X. Improving nutrient and water use efficiencies using water-drip irrigation and fertilization technology in Northeast China. Agric. Water Manag. 2020, 241, 106352. [Google Scholar] [CrossRef]
- Li, H.; Tang, P.; Chen, C.; Zhang, Z.; Xia, H. Research status and development trend of fertilization equipment used in fertigation in China. J. Drain. Irrig. Mach. Eng. 2021, 39, 200–209. [Google Scholar] [CrossRef]
- Mazzei Injector Company. Performance Data Drawings: Venturi Injectors. 2023. Available online: https://mazzei.net/support/performance-data-drawings/performance-data-drawings-venturi-injectors/ (accessed on 13 March 2023).
- Fan, J.; Wu, L.; Zhang, F.; Yan, S.; Xiang, Y. Evaluation of drip fertigation uniformity affected by injector type, pressure difference and lateral layout. Irrig. Drain. 2017, 66, 520–529. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, F.; Wu, L.; Yan, S.; Xiang, Y. Field evaluation of fertigation uniformity in a drip irrigation system with a pressure differential tank. Trans. Chin. Soc. Agric. Eng. 2016, 32, 96–101. [Google Scholar] [CrossRef]
- Hu, X.; Yan, H.; Chen, X. Calculation method of fertilizer concentration at outlet based on differential pressure tank considering fertilizer dissolution. Trans. Chin. Soc. Agric. Eng. 2020, 36, 99–106. [Google Scholar] [CrossRef]
- Gu, S.; Gao, J.; Deng, Z.; Lü, M.; Liu, J.; Zong, J.; Fan, X. Effects of border irrigation and fertilization timing on soil nitrate nitrogen distribution and winter wheat yield. Trans. Chin. Soc. Agric. Eng. 2020, 36, 134–142. [Google Scholar] [CrossRef]
- Qi, Z.; Gao, Y.; Sun, C.; Ramos, T.B.; Mu, D.; Xun, Y.; Huang, G.; Xu, X. Assessing water-nitrogen use, crop growth and economic benefits for maize in upper Yellow River basin: Feasibility analysis for border and drip irrigation. Agric. Water Manag. 2024, 295, 108771. [Google Scholar] [CrossRef]
- Song, J.; He, W. Optimization design of large-scale irrigation pipe network under the conditions of pump pressure. Yellow River 2016, 38, 145–148. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J. Optimization analysis of the key working parameters of a potato cleaning machine. J. Agric. Mech. Res. 2018, 40, 28–32. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J. Experiment and analysis of Venturi injector fertilizer performance in a low-pressure irrigation system. J. Agric. Mech. Res. 2019, 41, 183–186. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Yang, B.; Mo, Y. Numerical simulation of Venturi injector with non-axis-symmetric structure. J. Drain. Irrig. Mach. Eng. 2018, 36, 1098–1103. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, G.; Liu, N.; Liu, P.; Cao, Y.; Zhang, D. Effects of diffusion section structure on vortex characteristics and fertilizer absorption performance of non-axisymmetric Venturi injector. Trans. Chin. Soc. Agric. Eng. 2022, 38, 61–69. [Google Scholar] [CrossRef]
- Hu, G.; Guan, X.; Li, S.; Liu, N.; Zhang, J.; Yam, P.D.; Zhang, J.; Wang, Z. Structure optimization and fertilizer injection performance analysis of a non-axisymmetric Venturi injector. Irrig. Drain. 2024, 73, 400–414. [Google Scholar] [CrossRef]
- Luo, Z.; Li, H.; Yang, D. Analysis on volumetric efficiency of proportional dosing pumps. China Rural. Water Hydropower 2016, 9, 91–94. [Google Scholar]
- Zhang, Q.; Li, H.; Tang, P.; Sun, C. Improved design and experimental research of the fertilizer suction structure of a valve-regulated proportional fertilization pump. J. Water Resour. Water Eng. 2020, 31, 186–192. [Google Scholar] [CrossRef]
- Ma, L. Hydraulic Fertilizer Applicator. Patent No. CN201020190348.9, 5 January 2011. [Google Scholar]
- Wang, Z.; Wang, Q.; Li, W.; Zhang, J.; Xie, D. A Hydraulic Drive Fertilizer Pump. Patent No. CN201810671578.8, 12 September 2023. [Google Scholar]
- Yu, L.; Qu, M. A Hydrodynamic Pump Drive Device, Hydrodynamic Pump, and Fertilizer Machine. Patent No. CN202320210091.6, 26 September 2023. [Google Scholar]
- Rodríguez-Pérez, A.M.; Rodríguez-González, C.A.; López, R.; Hernández-Torres, J.A.; Caparrós-Mancera, J.J. Water microturbines for sustainable applications: Optimization analysis and experimental validation. Water Resour. Manag. 2024, 38, 1011–1025. [Google Scholar] [CrossRef]
- Chattha, J.A.; Khan, M.S. Experimental study to test an axial flow pump as a turbine and development of performance characteristics for micro-hydro power plant. ASME Power Conf. 2007, 42738, 615–621. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Z.H.; Wang, G. Shuǐlì Jīxiè [Hydraulic Machinery]; China Water & Power Press: Beijing, China, 2015. [Google Scholar]
- Zhang, R.; Wang, J.; Qian, W.; Geng, L. Optimization of magnetic pump impeller based on blade load curve and internal flow study. Mathematics 2024, 12, 607. [Google Scholar] [CrossRef]
- Betancour, J.; Velásquez, L.; Rubio Clemente, A.; Chica, E. Performance simulation of water turbines by using 6-DoF UDF and sliding mesh methods. J. Appl. Res. Technol. 2023, 21, 181–195. [Google Scholar] [CrossRef]
- Abbas, A.I.; Qandil, M.D.; Al-Haddad, M.; Amano, R.S. Investigation of horizontal micro Kaplan hydro turbine performance using multi-disciplinary design optimization. J. Energy Resour. Technol. 2020, 142, 5. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Miao, S.; Bai, X. Hydraulic performance experiment and numerical simulation of a hydraulic turbine at different speeds. Water Resour. Power 2024, 42, 186–190. [Google Scholar] [CrossRef]
- Janjua, A.B.; Khalil, M.S.; Saeed, M. Blade profile optimization of Kaplan turbine using CFD analysis. Mehran Univ. Res. J. Eng. Technol. 2013, 32, 559–574. Available online: https://www.researchgate.net/publication/352708109_Blade_Profile_Optimization_of_Kaplan_Turbine_Using_CFD_Analysis (accessed on 24 December 2024).
- Yang, S.S.; Kong, F.Y.; Qu, X.Y.; Jiang, W.M. Influence of blade number on the performance and pressure pulsations in a pump used as a turbine. J. Fluids Eng. 2012, 134, 124503. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, Z.; Ran, J.; Li, H. Multi-objective parameter optimization of turbine impeller based on RBF neural network and NSGA-II genetic algorithm. Energy Rep. 2021, 7, 584–593. [Google Scholar] [CrossRef]
- Derakhshan, S.; Kasaeian, N. Optimization, numerical, and experimental study of a propeller pump as turbine. J. Energy Resour. Technol. 2014, 136, 012005. [Google Scholar] [CrossRef]
- Mo, Y.; Zhao, C.; Zhang, B.; Zhang, Y.; Gong, S.; Jiao, X.; Gong, Y.; Lin, J.; Zhang, X. Low-Pressure Pipeline Water Conveyance Irrigation Hydrodynamic Fertilization. Device. Patent No. CN202410441384.4, 9 August 2024. [Google Scholar]
- Liu, C. (Ed.) Pumps and Pump Stations; China Water & Power Press: Beijing, China, 2009. [Google Scholar]
- Ohiemi, I.E.; Sunsheng, Y.; Singh, P.; Li, Y.; Osman, F. Evaluation of energy loss in a low-head axial flow turbine under different blade numbers using entropy production method. Energy 2023, 274, 127262. [Google Scholar] [CrossRef]
- Wang, S.; Ma, C.; Zhang, C. Optimization of residual pressure turbine impeller in oilfield water injection pipeline based on Fluent. Manuf. Autom. 2023, 45, 144–148. [Google Scholar] [CrossRef]
- Wu, H.; Feng, J.; Wu, G.; Guo, P.; Luo, X. The blade geometry modification and performance research for bulb turbine based on CFD. J. Xi’an Univ. Technol. 2013, 29, 290–294. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, N.J.; Wata, J.V.; Hwang, Y.C.; Kim, Y.T.; Lee, Y.H. Analysis of a pico tubular-type hydro turbine performance by runner blade shape using CFD. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 042031. [Google Scholar] [CrossRef]
- Yang, S.; Fang, T.; Zhou, C.; Zhao, E.; Wang, T. Influence of axial spacing on hydraulic performance of tubular turbine. J. Drainage Irrig. Mach. Eng. 2023, 41, 338–345. [Google Scholar] [CrossRef]
- GB/T 19792-2012; Agricultural Irrigation Equipment Hydraulic Chemical Fertilizer-Pesticide Injection Pumps. National Agricultural Machinery Standardization Technical Committee: Beijing, China, 2013.
- Muis, A.; Sutikno, P.; Soewono, A.; Hartono, F. Design optimization of axial hydraulic turbine for very low head application. Energy Procedia 2015, 68, 263–273. [Google Scholar] [CrossRef]
- Hoghooghi, H.; Durali, M.; Kashef, A. A new low-cost swirler for axial micro hydro turbines of low head potential. Renew. Energy 2018, 128, 375–390. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Wang, J.; Yang, B.; Mo, Y. Experimental study on comprehensive working performance of Venturi injector. J. Drainage Irrig. Mach. Eng. 2018, 36, 340–346. [Google Scholar] [CrossRef]
- Nishi, Y.; Kobori, T.; Mori, N.; Inagaki, T.; Kikuchi, N. Study of the internal flow structure of an ultra-small axial flow hydraulic turbine. Renew. Energy 2019, 139, 1000–1011. [Google Scholar] [CrossRef]
- Wang, S.; Gong, F.; Li, Z. Optimization design and experimental study of hydraulic turbine based on residual pressure power generation system. J. Mach. Des. 2022, 39, 77–83. [Google Scholar] [CrossRef]
- Wang, S.; Li, M.; Li, Z. Influence of impeller stage on hydrodynamic performance of a tidal turbine. Ship Eng. 2020, 42, 23–28. [Google Scholar] [CrossRef]
- Zhao, Z.; He, J.; Wang, C. Hydraulics, 3rd ed.; Tsinghua University Press: Beijing, China, 2021. [Google Scholar]
- Fang, T. Numerical Calculation and Experimental Study of Micro Shaft-Extension Axial Turbine. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2022. [Google Scholar] [CrossRef]
- Miao, S.; Wu, H.; Wang, X.; Shi, F.; Yang, J. Research on internal energy loss mechanism of axial pump as turbine based on entropy production theory. J. Xihua Univ. Nat. Sci. Ed. 2023, 42, 1–9. Available online: http://kns.cnki.net/kcms/detail/51.1686.N.20240528.0924.002.html (accessed on 24 December 2024).
- Guo, Y.; Yang, C.; Mo, Y.; Wang, Y.; Lv, T.; Zhao, S. Numerical study on the mechanism of fluid energy transfer in an axial flow pump impeller under the rotating coordinate system. Front. Energy Res. 2023, 10, 1106789. [Google Scholar] [CrossRef]
- Kan, K.; Binama, M.; Chen, H.; Zheng, Y.; Zhou, D.; Su, W.; Muhirwa, A. Pump as turbine cavitation performance for both conventional and reverse operating modes: A review. Renew. Sustain. Energy Rev. 2022, 168, 112786. [Google Scholar] [CrossRef]
- Wu, R.; Liu, H.; Chen, W.; Ji, S.; Cao, L.; Wu, D. Experimental investigation of propeller blade back cavitation induced pressure pulses by synchronous observation. Ocean Eng. 2024, 298, 116971. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, H.; Zhang, S.; Fan, G.; Li, Y.; Song, Y. Experimental research on efficient irrigation system with mixed fertilizer in integration of water and fertilizer. J. Phys. Conf. Ser. 2020, 1550, 042004. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Yang, B.; Mo, Y.; Zhang, Y.; Ma, X. Simulation and optimization of Venturi injector by machine learning algorithms. J. Irrig. Drain. Eng. 2020, 146, 04020021. [Google Scholar] [CrossRef]
- García-Saldaña, M.D.; Castañeda-Chávez, A.; Pérez-Vázquez, J.P.; Martínez-Dávila, E.; Carrillo-Ávila, E. Design of venturi-type fertilizer injectors to low-pressure irrigation systems. J. Agric. Sci. 2023, 15, 25. [Google Scholar] [CrossRef]
- Shi, Y.; Hu, Z.; Wang, X.; Odhiambo, M.O.; Sun, G. Fertilization strategy and application model using a centrifugal variable-rate fertilizer spreader. Int. J. Agric. Biol. Eng. 2018, 11, 41–48. Available online: https://www.ijabe.org/index.php/ijabe/article/view/3789 (accessed on 24 December 2024). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).