Susceptibility and Remanent Magnetization Estimates from Orientation Tools in Borehole Imaging Logs
Abstract
1. Introduction
2. Materials and Methods
3. Results
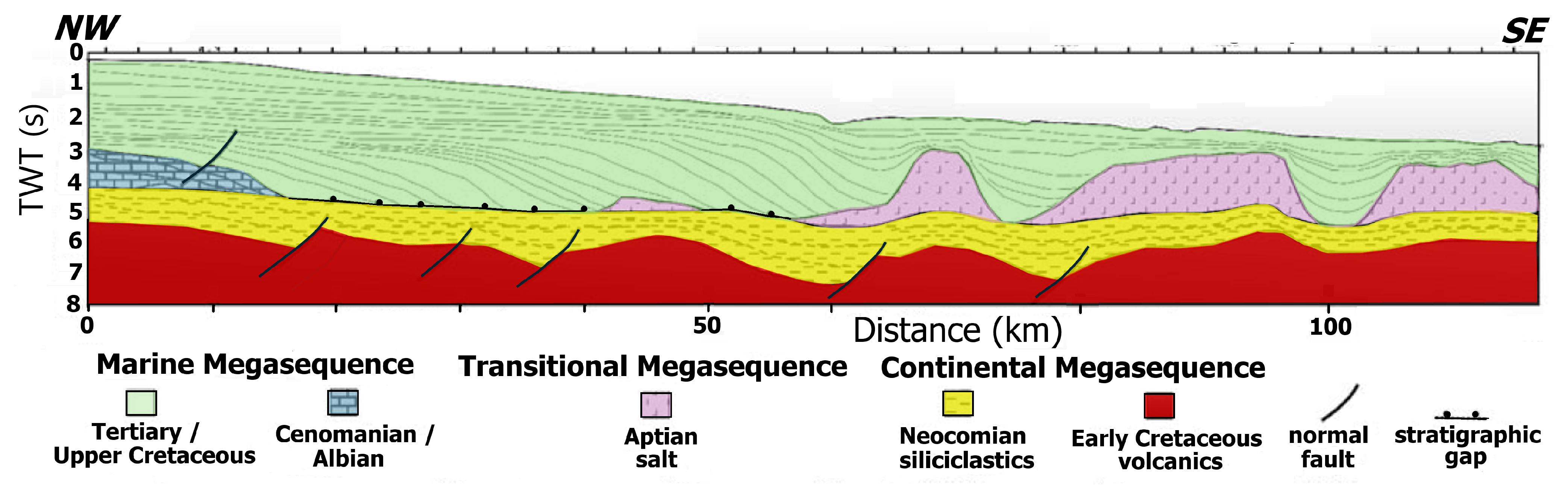
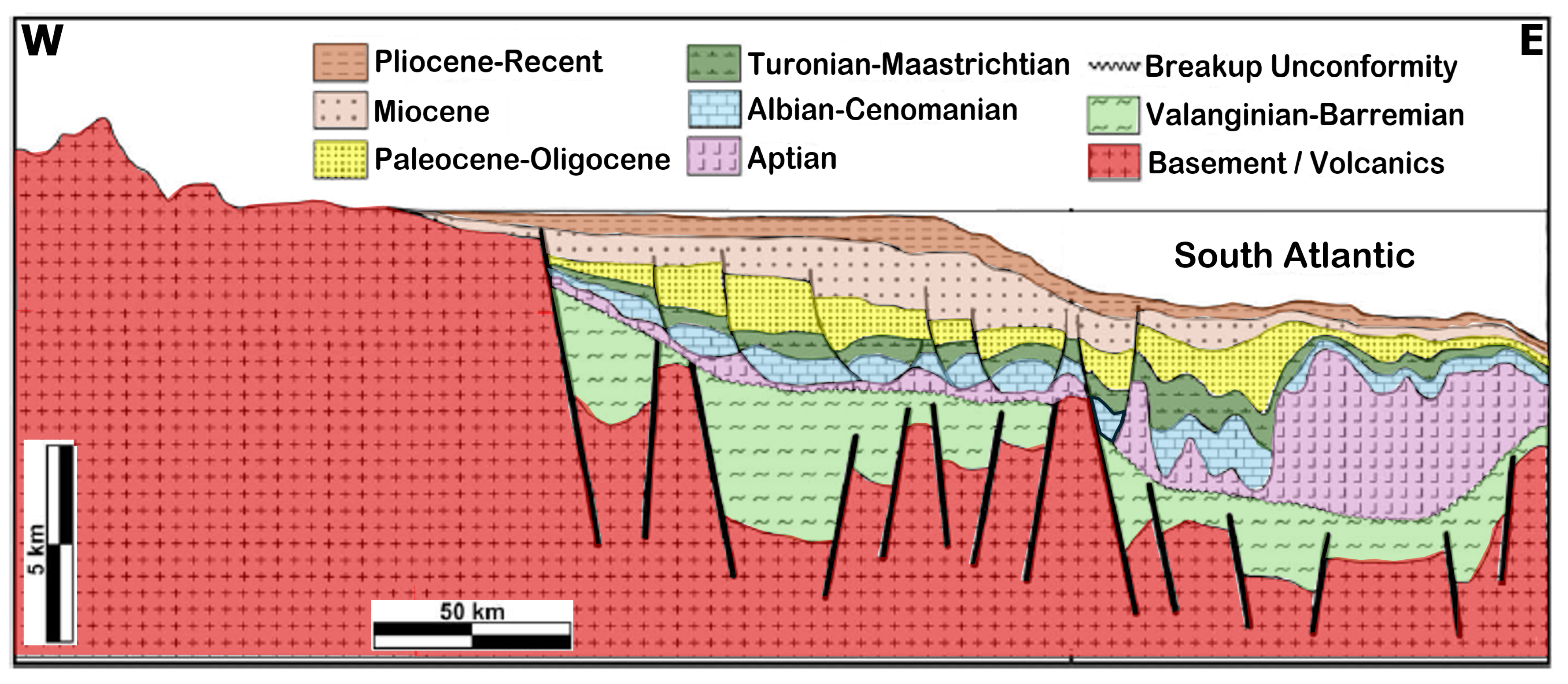
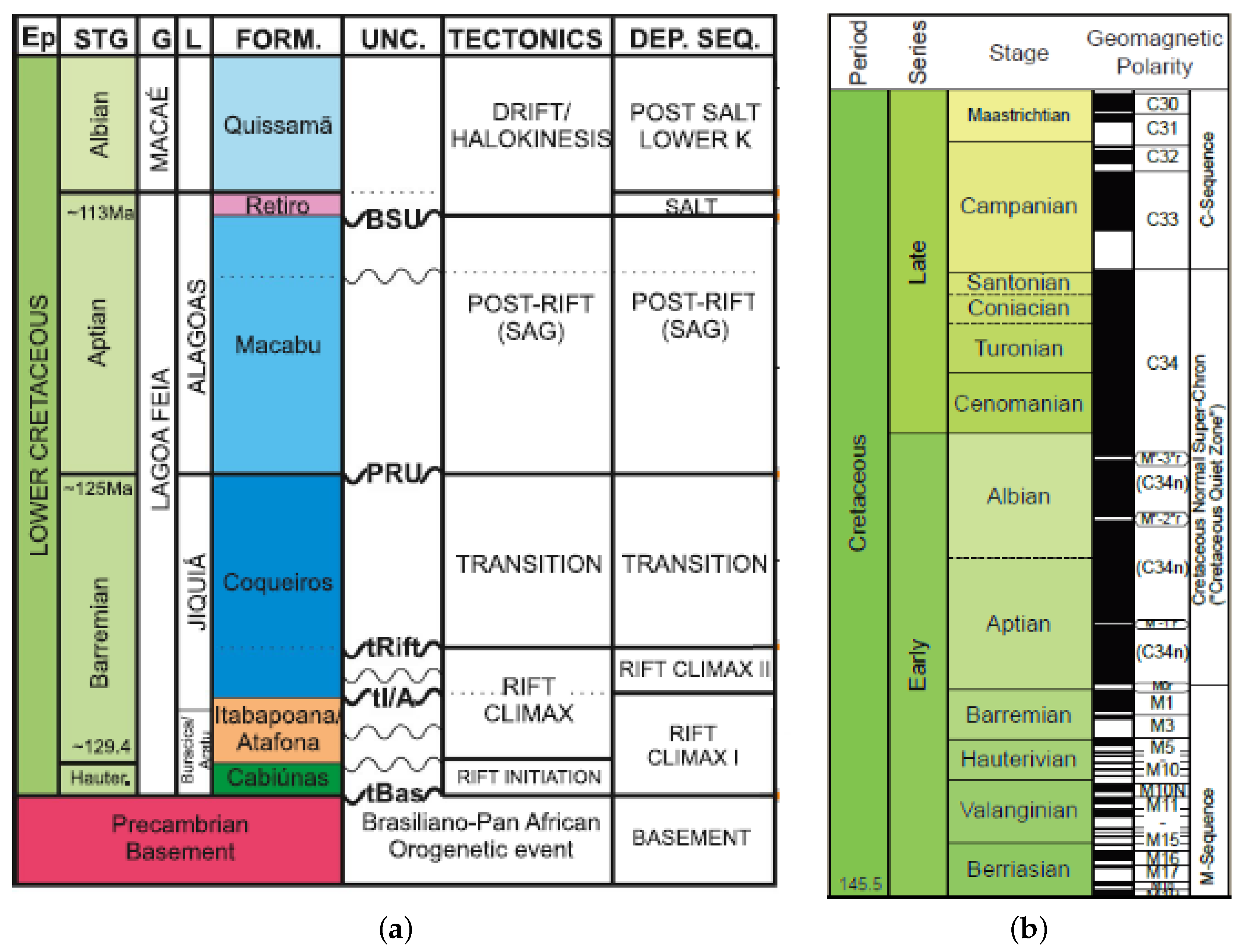
3.1. Campos Basin Geologic Settings
3.2. Magnetic Dataset
3.2.1. Magnetic Sample Analysis
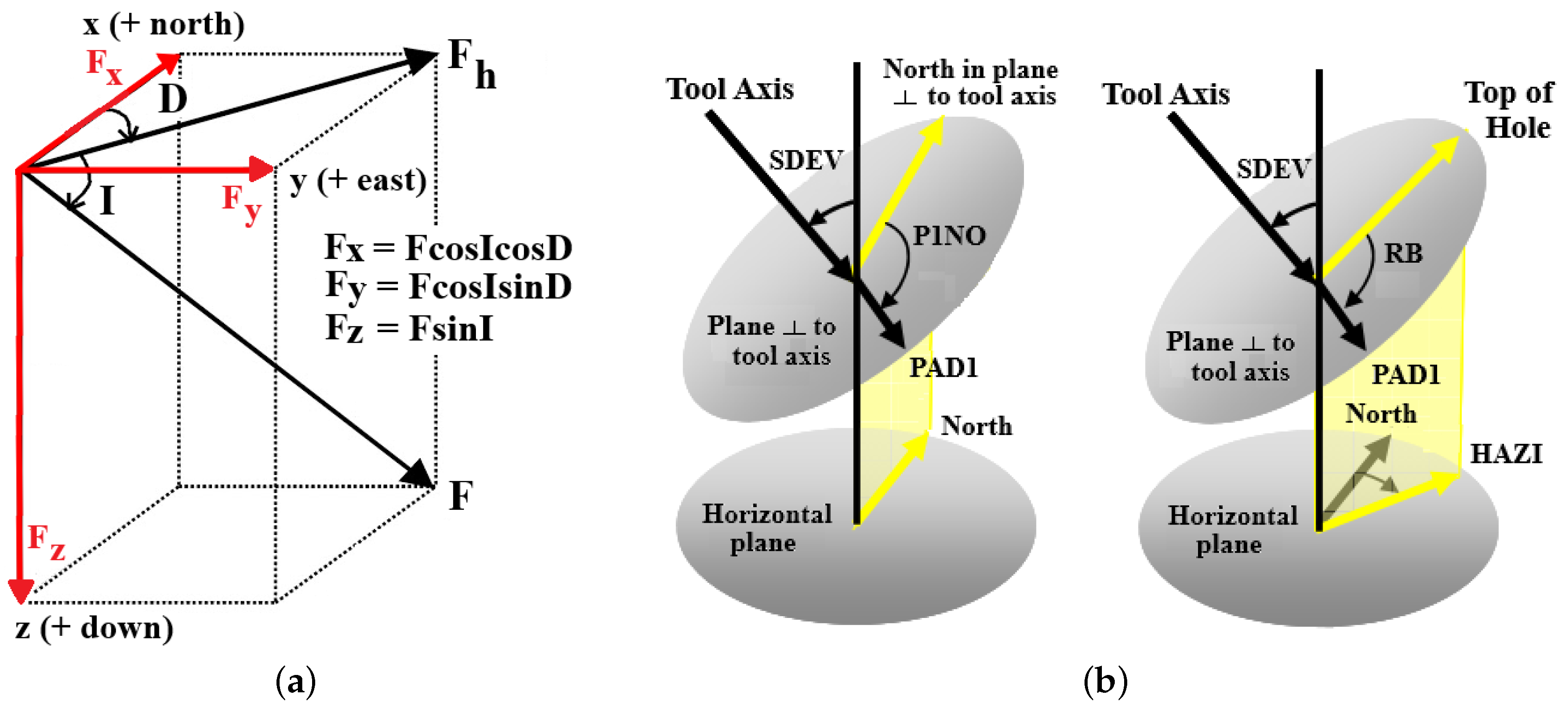
3.2.2. Magnetic Field Data
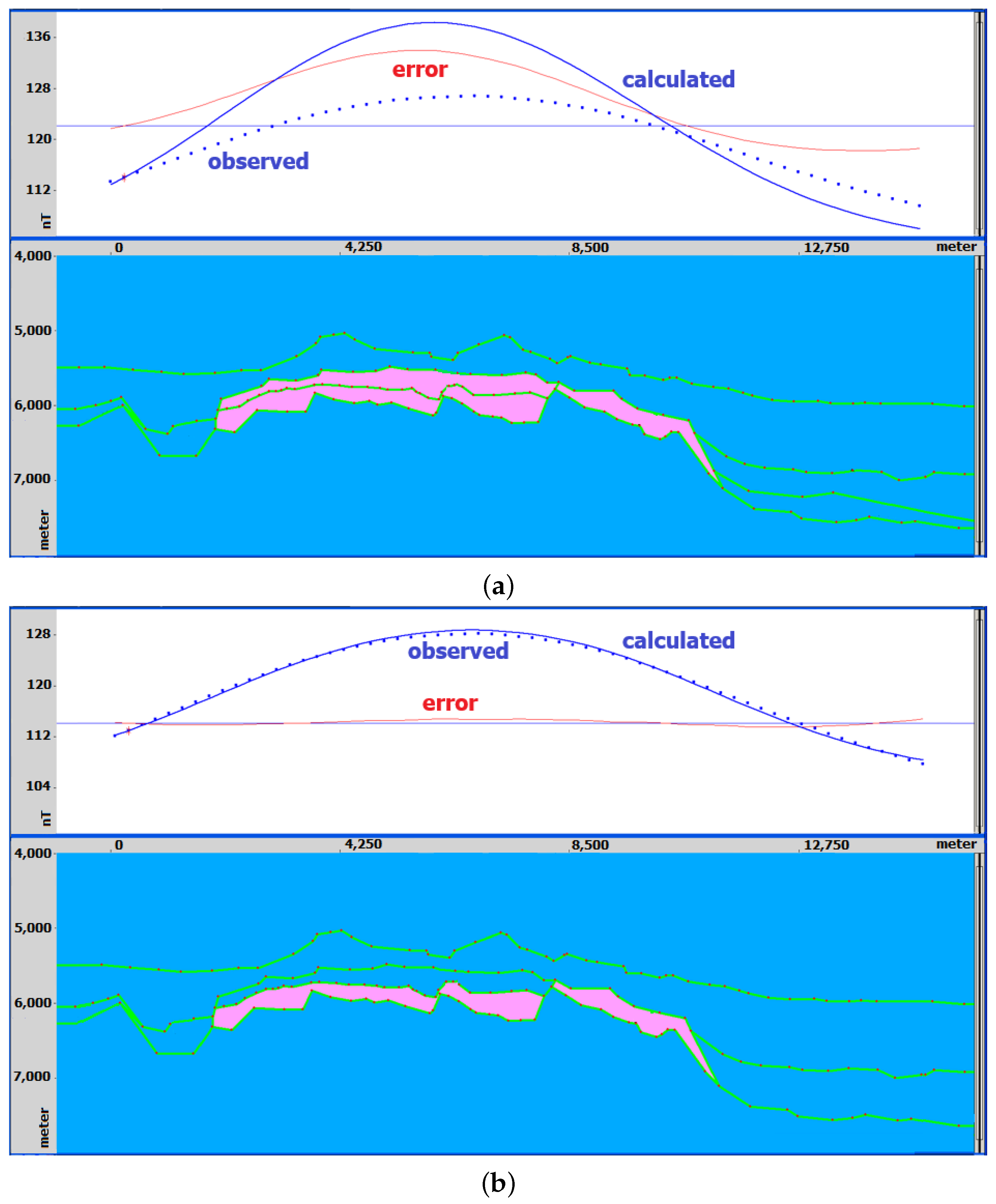
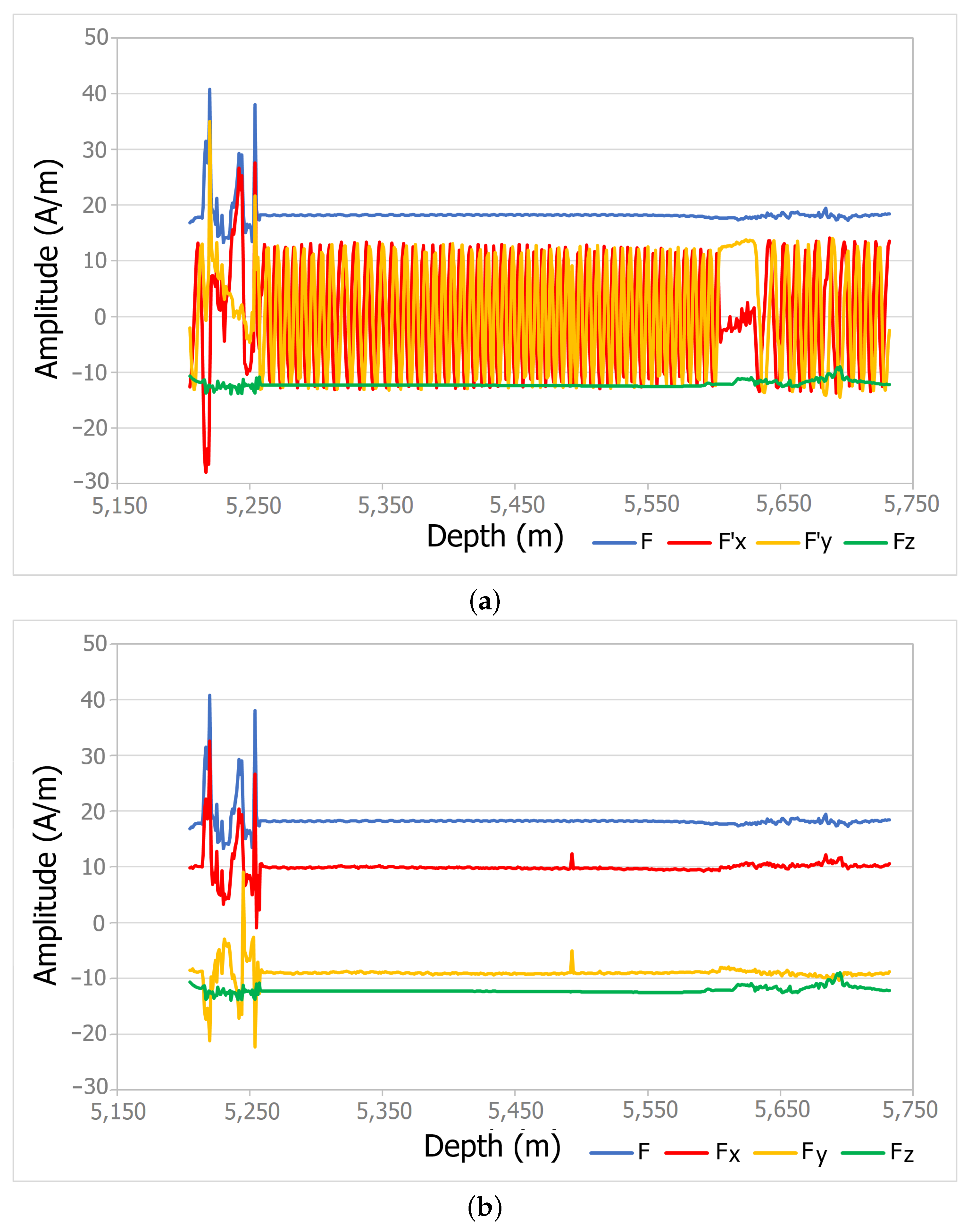
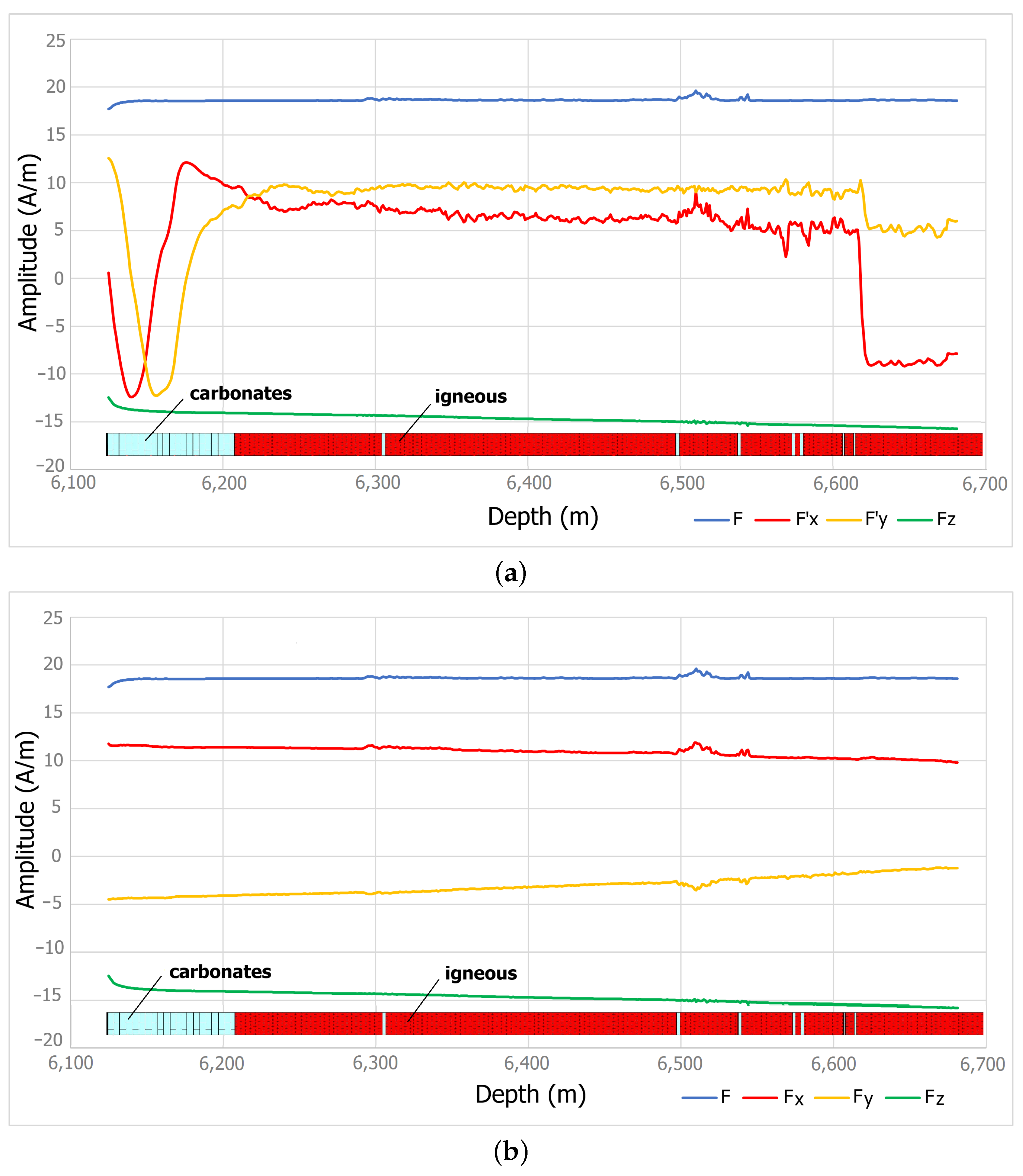
3.3. Magnetic Corrections
3.3.1. Magnetic Amplitude Correction
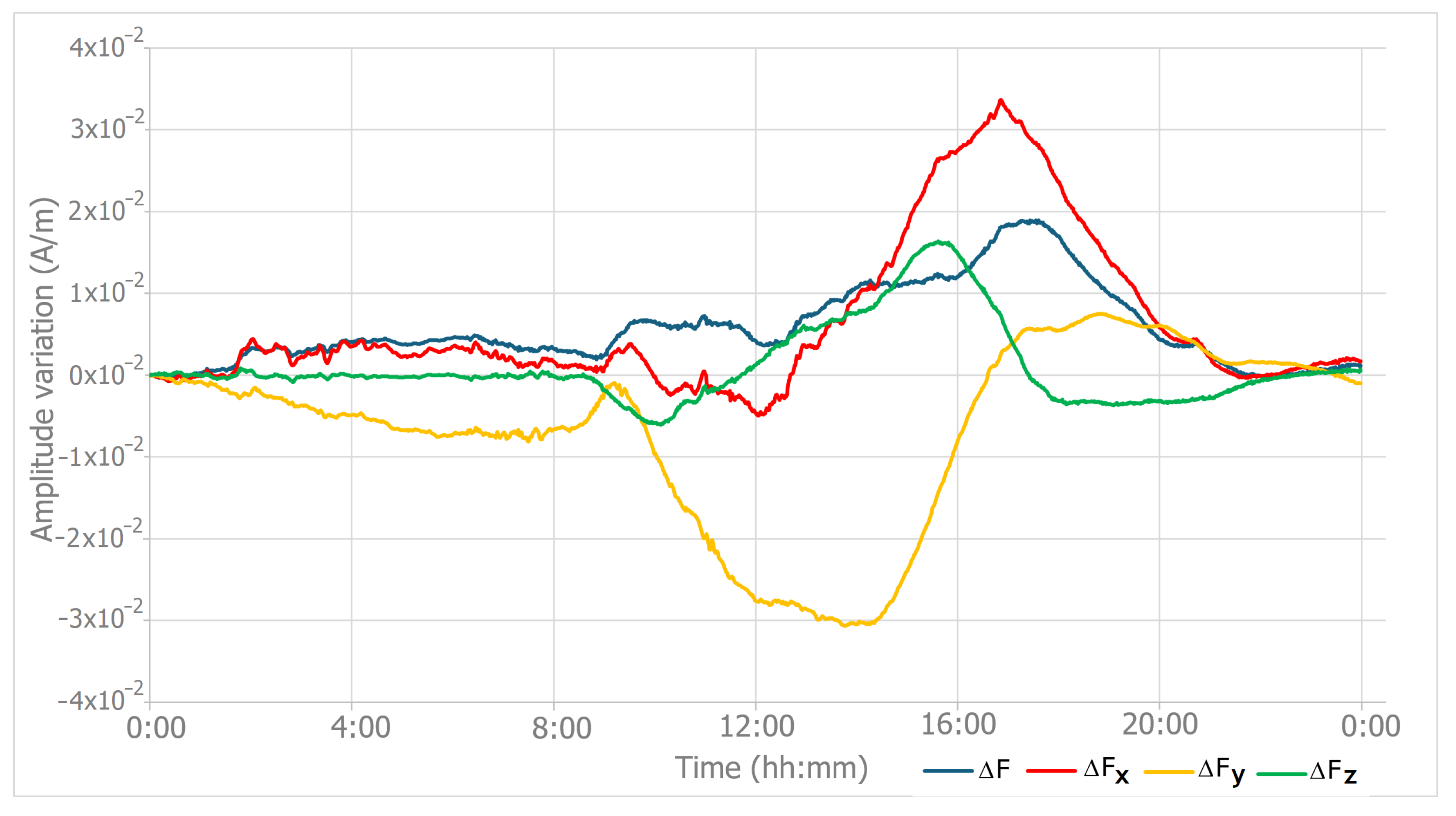
3.3.2. Magnetic Diurnal Variation Correction
3.4. Magnetic Susceptibility Estimates
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laier, A.P.; Jesus, C.M.; Ferraz, E.K.P.; Caires, A.C.B.; Júnior, J.C. Implicações Exploratórias da Orientação de Perfis de Imagem. In Proceedings of the XI Seminário de Interpretação Exploratória, Petrobras, Rio de Janeiro, Brazil, 12 March 2018. [Google Scholar]
- Oliveira, J.A.B. Modelagens Magnéticas Como Suporte ao Mapeamento de Rochas Ígneas; Nota técnica; Petrobras: Rio de Janeiro, Brazil, 2017. [Google Scholar]
- Pozzi, J.P.; Martin, J.P.; Pocachard, J.; Feinberg, H.; Galdeano, A. In-situ magnetostratigraphy: Interpretation of magnetic logging in sediments. Earth Planet. Sci. Lett. 1988, 88, 357–373. [Google Scholar] [CrossRef]
- Nelson, P.H. Magnetic susceptibility logs from sedimentary and volcanic environments. In Proceedings of the SPWLA 34th Annual Logging Symposium, Calgary, AB, Canada, 13–16 June 1993. [Google Scholar]
- Broding, R.; Zimmerman, C.; Somers, E.; Wilhelm, E.; Stripling, A. Magnetic well logging. Geophysics 1952, 17, 1–26. [Google Scholar] [CrossRef]
- Lalanne, B.; Bouisset, P.; Pages, G.; Pocachard, J. Magnetic Logging: Borehole Magnetostratigraphy and Absolute Datation in Sedimentary Rocks. In Proceedings of the Middle East Oil Show, Manama, Bahrain, 16–19 November 1991; SPE-21437-MS. pp. 841–850. [Google Scholar]
- Pages, G.; Boutemy, Y.; Barthies, V.; Pocachard, J. Wireline Magnetostratigraphy Principles And Field Results. In Proceedings of the SPWLA 35th Annual Logging Symposium, Tulsa, OK, USA, 19–22 June 1994. [Google Scholar]
- Emilia, D.A.; Allen, J.W.; Chessmore, R.B.; Wilson, R.B. The DOE/Simplec magnetic susceptibility logging system. In Proceedings of the SPWLA 22nd Annual Logging Symposium, Mexico City, Mexico, 23–26 June 1981. [Google Scholar]
- Scott, J.H.; Seeley, R.L.; Barth, J.J. A magnetic susceptibility well-logging system for mineral exploration. In Proceedings of the SPWLA 22nd Annual Logging Symposium, Mexico City, Mexico, 23–26 June 1981. [Google Scholar]
- McNeill, J.D.; Hunter, J.A.; Bosnar, M. Application of a borehole induction magnetic susceptibility logger to shallow lithological mapping. J. Environ. Eng. Geophys. 1996, 1, 77–90. [Google Scholar] [CrossRef]
- Leslie, K.; Foss, C.A.; Hillan, D.; Blay, K. A downhole magnetic tensor gradiometer for developing robust magnetisation models from magnetic anomalies. In Proceedings of the Iron Ore, Perth, WA, Australia, 13–15 July 2015; pp. 1–11. [Google Scholar]
- Barber, T.; Anderson, B.; Mowat, G. Using induction tools to identify magnetic formations and to determine relative magnetic susceptibility and dielectric constant. Log Anal. 1995, 36, 16–26. [Google Scholar]
- Mitchell, J. Monitoring Lithology Variations in Drilled Rock Formations Using NMR Apparent Magnetic Susceptibility Contrast. Appl. Magn. Reson. 2020, 51, 205–219. [Google Scholar] [CrossRef]
- Huret, E.; Thiesson, J.; Tabbagh, A.; Galbrun, B.; Collin, P. Improvement of cyclostratigraphic studies by processing of high-resolution magnetic susceptibility logging: Example of PEP1002 borehole (Bure, Meuse, France). Comptes Rendus Geosci. 2011, 343, 379–386. [Google Scholar] [CrossRef]
- Crow, H.L.; Hunter, J.A.; Olson, L.C.; Pugin, A.J.M.; Russell, H.A.J. Borehole geophysical log signatures and stratigraphic assessment in a glacial basin, southern Ontario. Can. J. Earth Sci. 2018, 55, 829–845. [Google Scholar] [CrossRef]
- Nowaczyk, N.R. Logging of Magnetic Susceptibility. In Tracking Environmental Change Using Lake Sediments: Basin Analysis, Coring, and Chronological Techniques; Last, W.M., Smol, J.P., Eds.; Springer: Dordrecht, The Netherlands, 2001; pp. 155–170. [Google Scholar] [CrossRef]
- Bloemendal, J.; Tauxe, L.; Valet, J.P. High-resolution, whole-core magnetic susceptibility logs from LEG 1081. In Ocean Drilling Program: Initial Report; Ocean Drilling Program; Texas A&M University: College Station, TX, USA, 1986; Volume 108, p. 1005. [Google Scholar]
- Dalan, R.A. A review of the role of magnetic susceptibility in archaeogeophysical studies in the USA: Recent developments and prospects. Archaeol. Prospect. 2008, 15, 1–31. [Google Scholar] [CrossRef]
- To, T.H.; Nguyen, T.V.; Nguyen, L.K.; Dinh, H.D. A review of the applications of magnetic susceptibility measurements for improved reservoir characterization. J. Min. Earth Sci. 2022, 63, 25–34. [Google Scholar] [CrossRef] [PubMed]
- Cheung, P.; Hayman, A.; Vessereau, P.; Verges, P.; Laval, L.; Yerbes, M.; Rylander, E. In Situ Correction of Wireline Triaxial Accelerometer and Magnetometer Measurements. In Proceedings of the SPWLA 48th Annual Logging Symposium, Austin, TX, USA, 3–6 June 2007. [Google Scholar]
- ANP—Agência Nacional de Petróleo, Gás Natural e Biocombustíveis. Boletim da Produção de Petróleo e Gás Natural—06/2024. 2024. Available online: https://www.gov.br/anp/pt-br/centrais-de-conteudo/publicacoes/boletins-anp/boletins/arquivos-bmppgn/2024/junho.pdf (accessed on 6 August 2024).
- Rodrigues, A.N.G. Propriedades Magnéticas do poço 1-RJS-755-RJ (Urissanê), Intervalo 6137.70–6683.00 m, Bacia de Campos (Brasil); Relatório Interno; Petrobras: Rio de Janeiro, Brazil, 2021. [Google Scholar]
- Cainelli, C.; Mohriak, W.U. Some remarks on the evolution of sedimentary basins along the Eastern Brazilian continental margin. Episodes J. Int. Geosci. 1999, 22, 206–216. [Google Scholar] [CrossRef] [PubMed]
- Fetter, M. The role of basement tectonic reactivation on the structural evolution of Campos Basin, offshore Brazil: Evidence from 3D seismic analysis and section restoration. Mar. Pet. Geol. 2009, 26, 873–886. [Google Scholar] [CrossRef]
- Cobbold, P.R.; Szatmari, P. Radial gravitational gliding on passive margins. Tectonophysics 1991, 188, 249–289. [Google Scholar] [CrossRef]
- Demercian, S.; Szatmari, P.; Cobbold, P.R. Style and pattern of salt diapirs due to thin-skinned gravitational gliding, Campos and Santos basins, offshore Brazil. Tectonophysics 1993, 228, 393–433. [Google Scholar] [CrossRef]
- Chang, H.K.; Kowsmann, R.O.; Figueiredo, A.M.F.; Bender, A.A. Tectonics and stratigraphy of the East Brazil Rift system: An overview. Tectonophysics 1992, 213, 97–138. [Google Scholar] [CrossRef]
- Strugale, M.; Schmitt, R.S.; Cartwright, J. Basement geology and its controls on the nucleation and growth of rift faults in the northern Campos Basin, offshore Brazil. Basin Res. 2021, 33, 1906–1933. [Google Scholar] [CrossRef]
- Ogg, J.G.; Ogg, G.M.; Gradstein, F.M. The Concise Geologic Time Scale; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- NOAA/NCEI—National Center for Environmental Information. Enhanced Magnetic Model (EMM). 2022. Available online: https://www.ngdc.noaa.gov/geomag/EMM (accessed on 6 August 2024).
- Lowrie, W. Fundamentals of Geophysics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Glatzmaiers, G.A.; Roberts, P.H. A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 1995, 377, 203–209. [Google Scholar] [CrossRef]


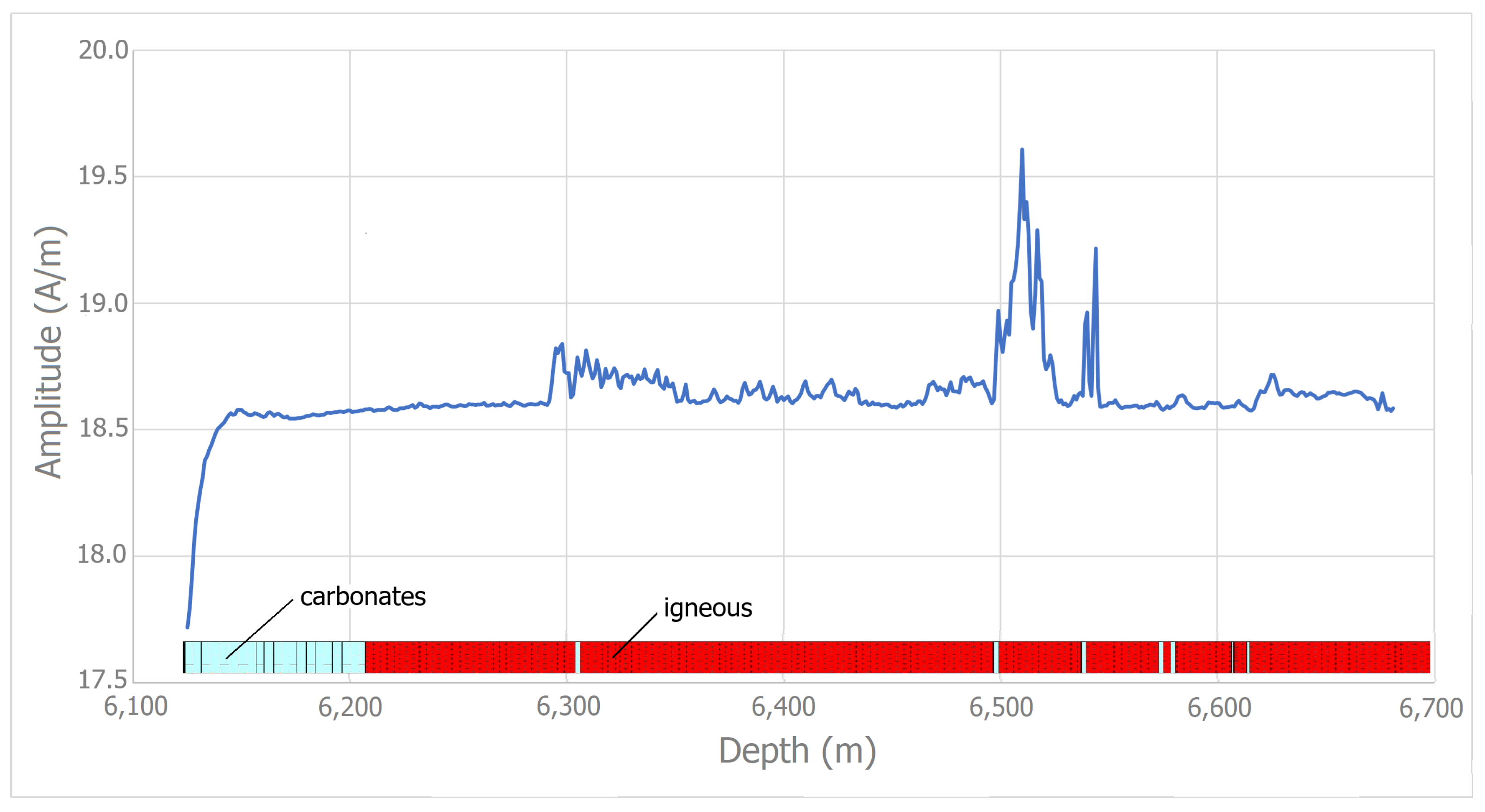


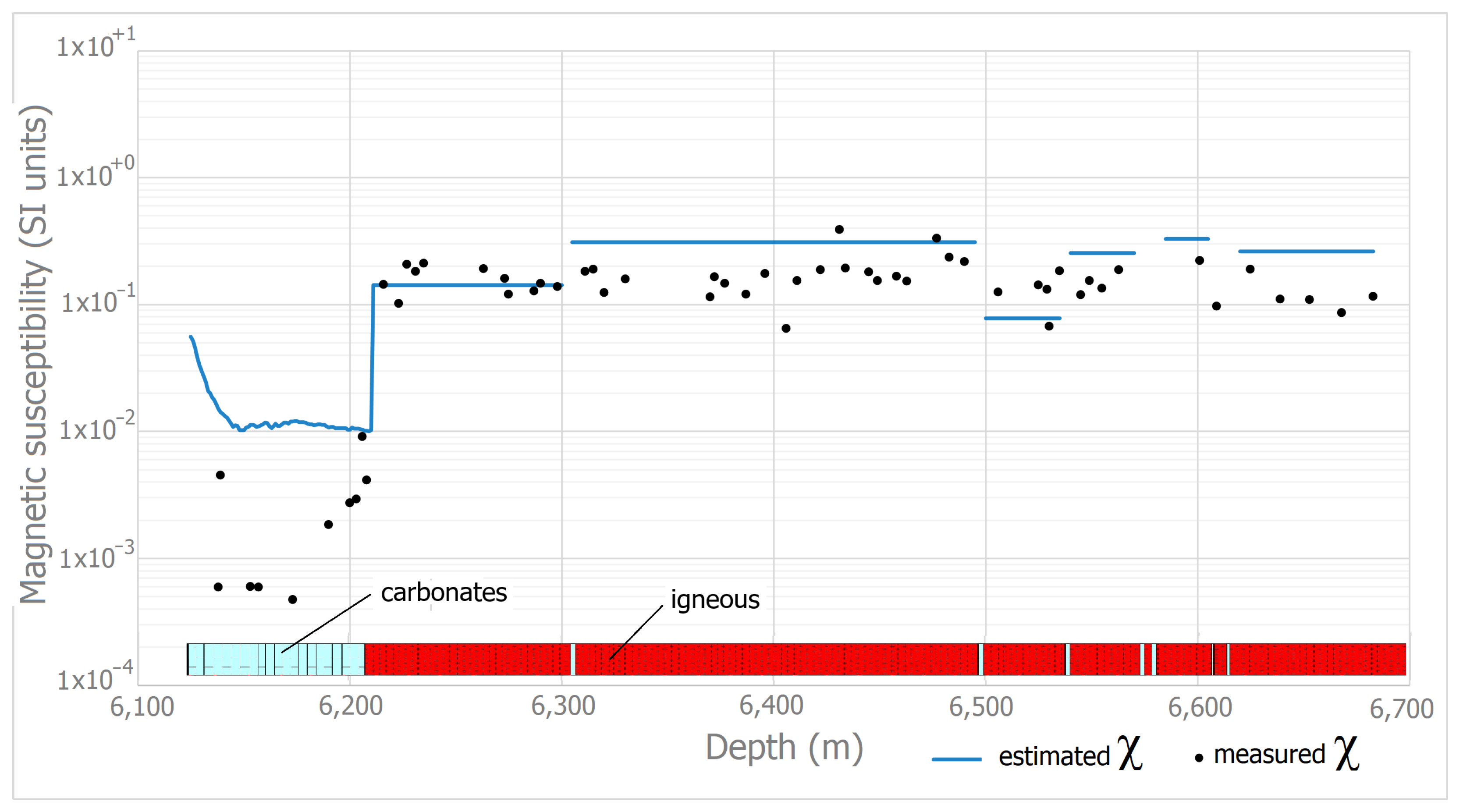
| Minimum | ||||
| Maximum | ||||
| Mean | ||||
| Standard deviation |
| Interval (m) | ||||||
|---|---|---|---|---|---|---|
| Estimates | 6211–6300 | 6305–6495 | 6500–6535 | 6540–6570 | 6585–6605 | 6620–6681 |
| (A/m) | ||||||
| (A/m) | ||||||
| (A/m) | ||||||
| (A/m) | ||||||
| Interval (m) | ||
|---|---|---|
| 6211–6300 | ||
| 6305–6495 | ||
| 6500–6535 | ||
| 6540–6570 | ||
| 6585–6605 | ||
| 6620–6681 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyrio, J.C.S.O.; Laier, A.P.C.C.; Junior, J.C.; Rodrigues, A.N.G.; Martins, L.d.S. Susceptibility and Remanent Magnetization Estimates from Orientation Tools in Borehole Imaging Logs. Appl. Sci. 2025, 15, 2873. https://doi.org/10.3390/app15052873
Lyrio JCSO, Laier APCC, Junior JC, Rodrigues ANG, Martins LdS. Susceptibility and Remanent Magnetization Estimates from Orientation Tools in Borehole Imaging Logs. Applied Sciences. 2025; 15(5):2873. https://doi.org/10.3390/app15052873
Chicago/Turabian StyleLyrio, Julio Cesar S. O., Ana Patrícia C. C. Laier, Jorge Campos Junior, Ana Natalia G. Rodrigues, and Luciano dos Santos Martins. 2025. "Susceptibility and Remanent Magnetization Estimates from Orientation Tools in Borehole Imaging Logs" Applied Sciences 15, no. 5: 2873. https://doi.org/10.3390/app15052873
APA StyleLyrio, J. C. S. O., Laier, A. P. C. C., Junior, J. C., Rodrigues, A. N. G., & Martins, L. d. S. (2025). Susceptibility and Remanent Magnetization Estimates from Orientation Tools in Borehole Imaging Logs. Applied Sciences, 15(5), 2873. https://doi.org/10.3390/app15052873






