Novel Real-Time Acoustic Power Estimation for Dynamic Thermoacoustic Control
Abstract
1. Introduction
2. Materials and Methods
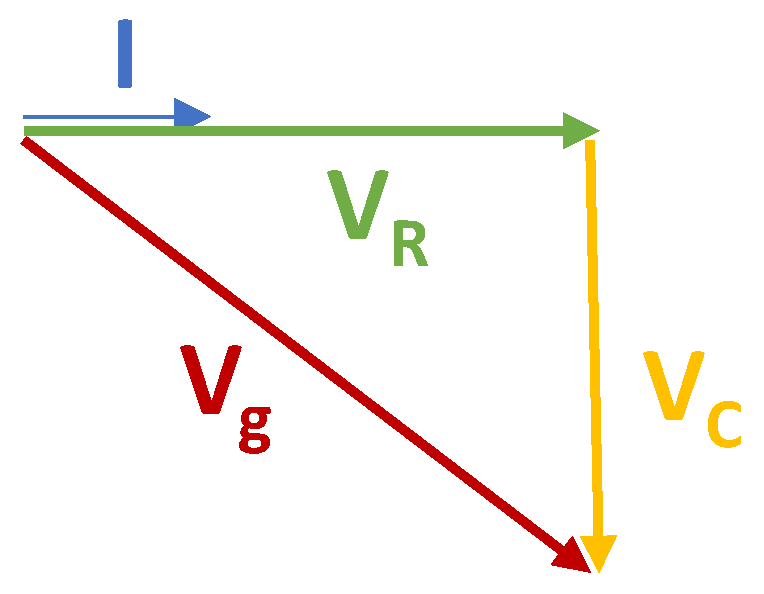
2.1. RC Equivalent Model in Electrical Analogy
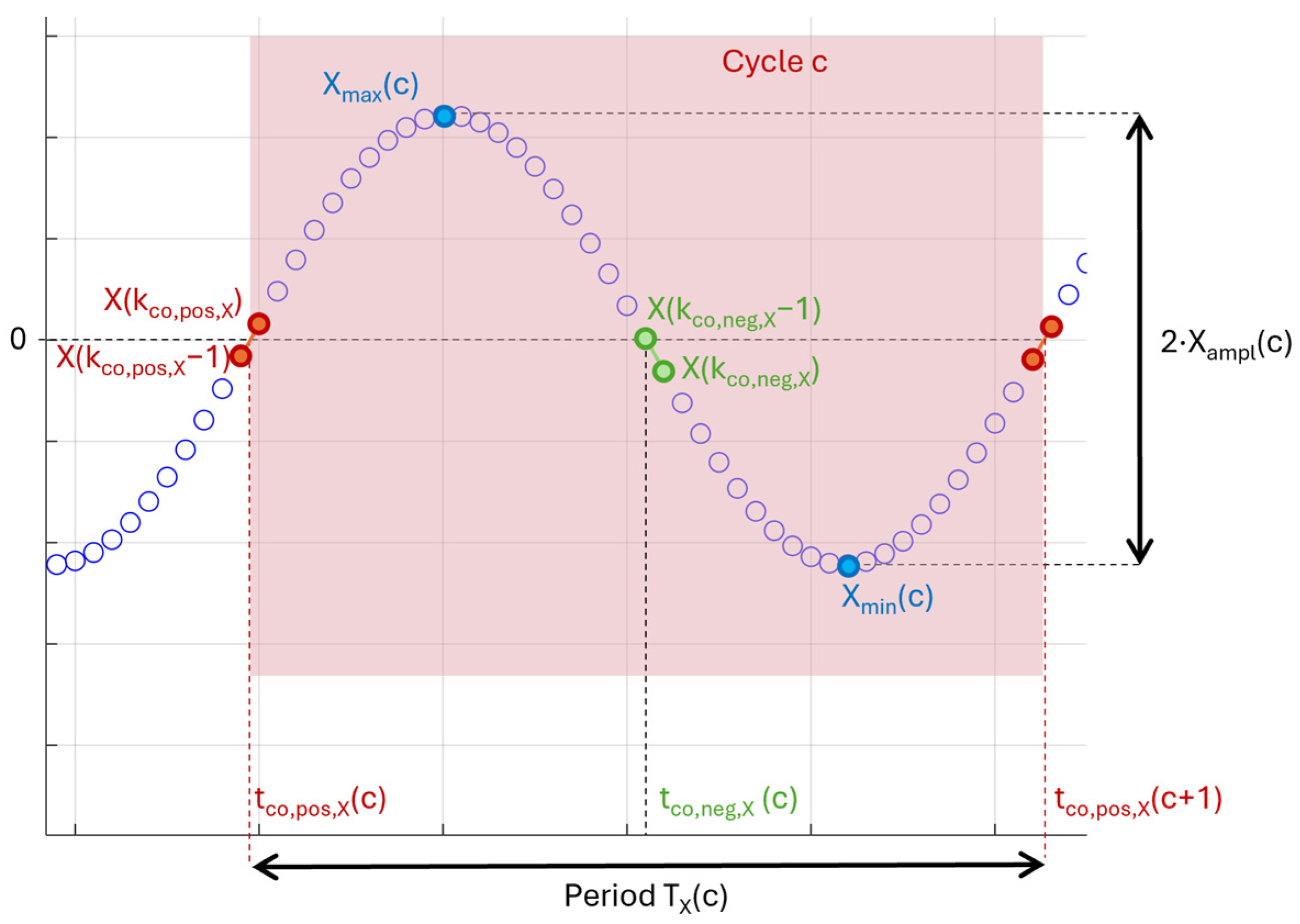
2.2. Average Power Estimation
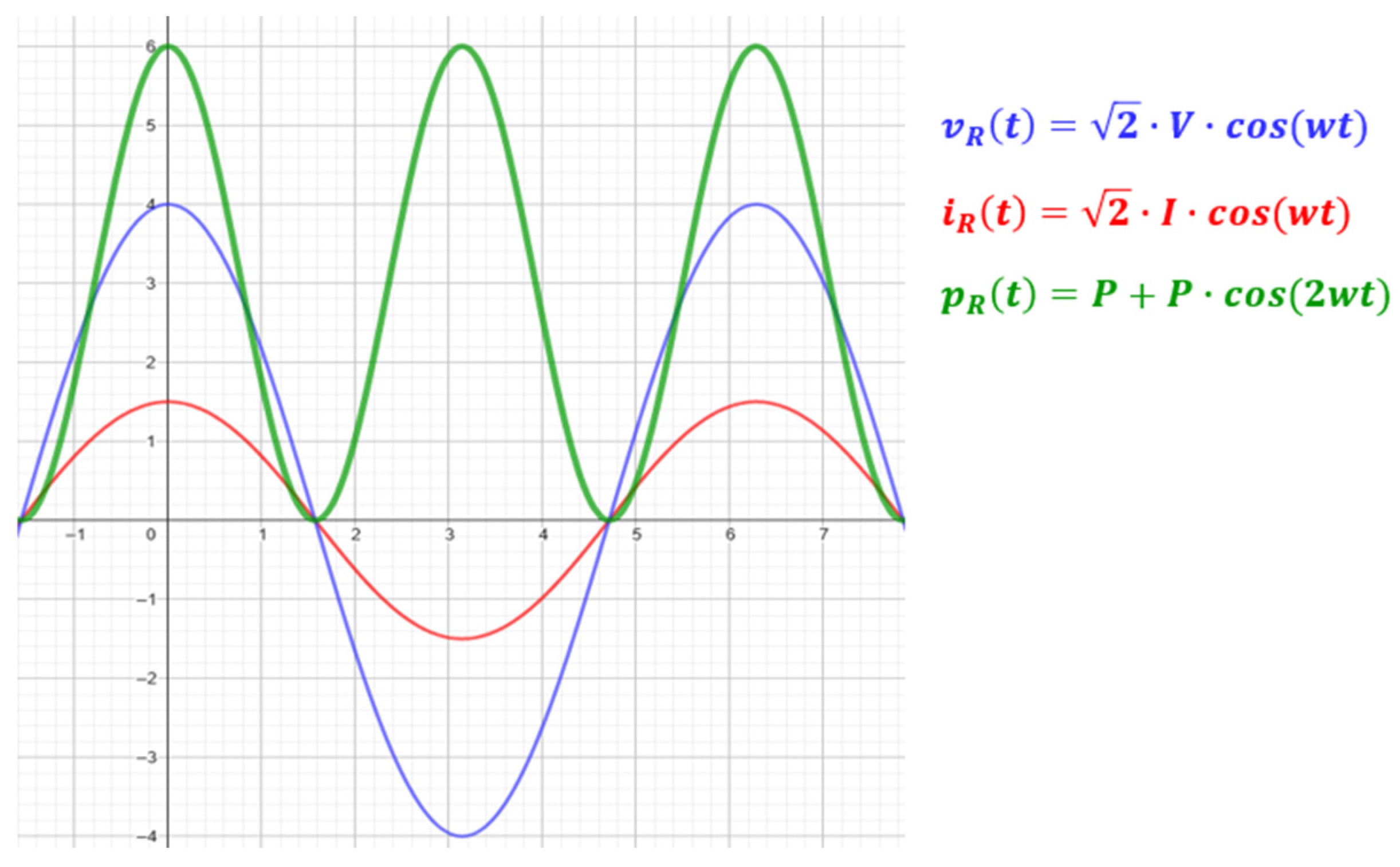
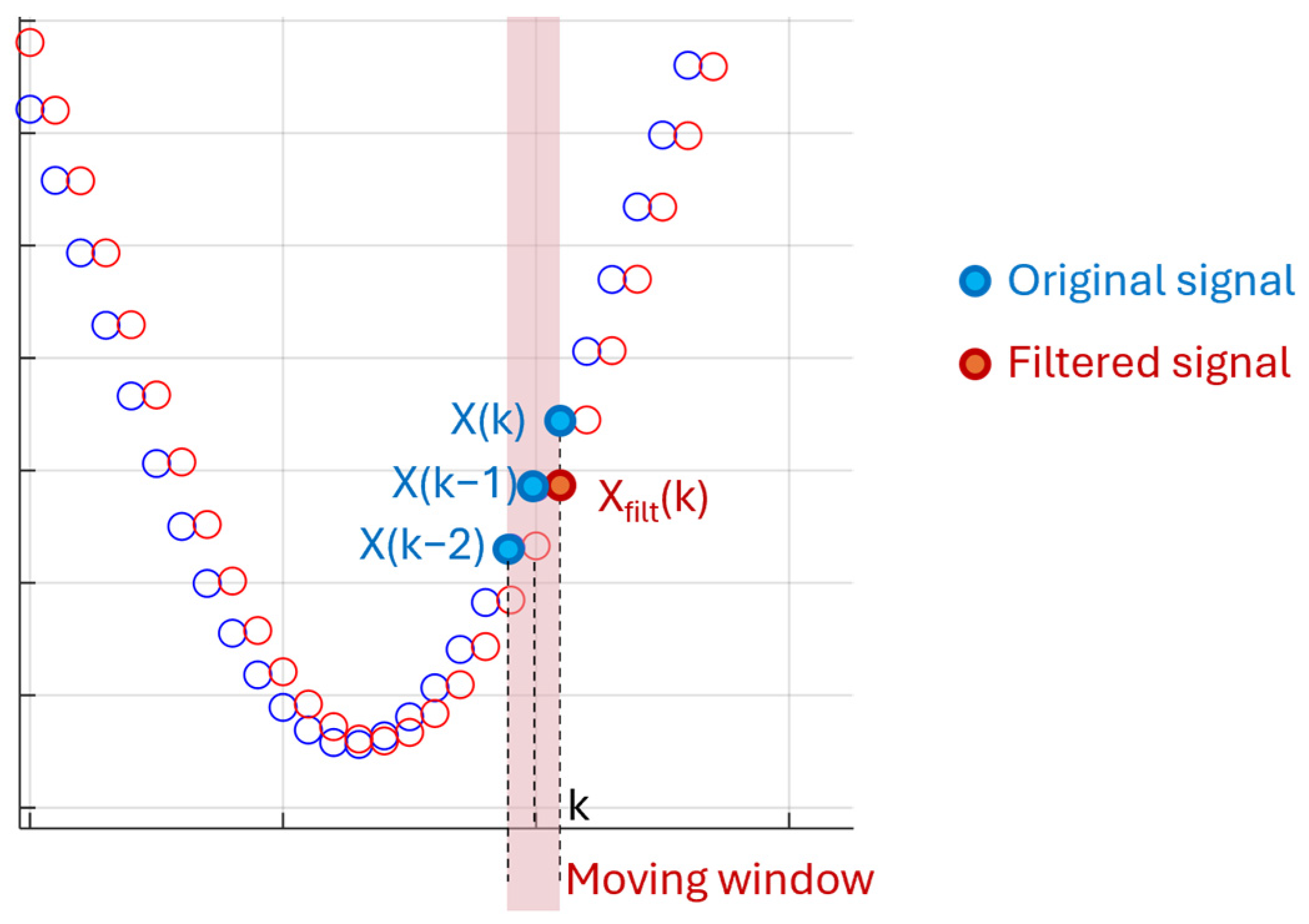
2.3. Instantaneous Power Estimation
3. Results
- Instantaneous power evaluation (method 1), which consists of using the instantaneous power consumed in the resistance of the equivalent RC model of the load;
- One-period average power calculation (method 2), in which the procedure established by Fusco et al. [17] is adapted to be used each single period for each single period of the signal.
3.1. Measurements Conditioning
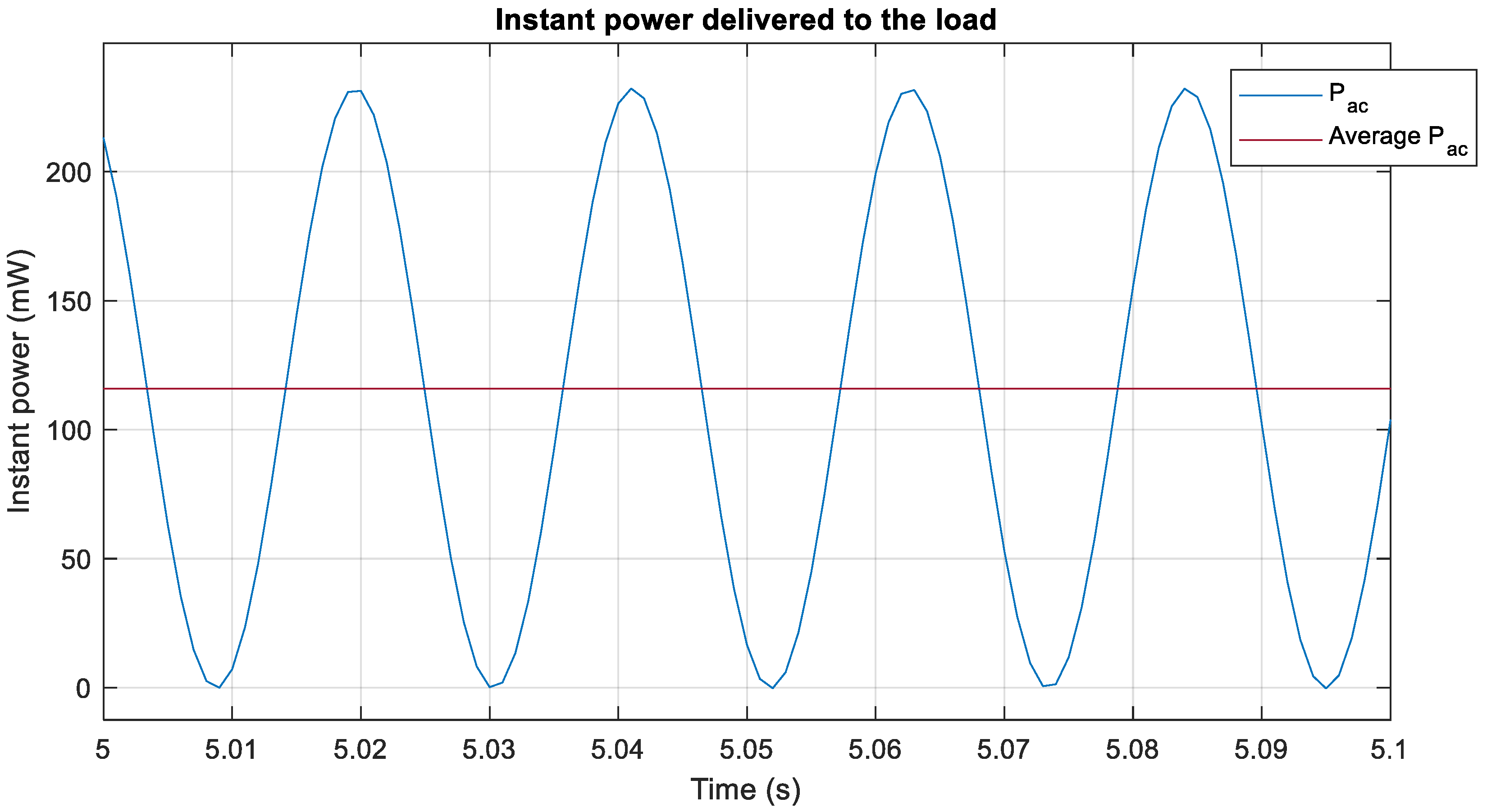
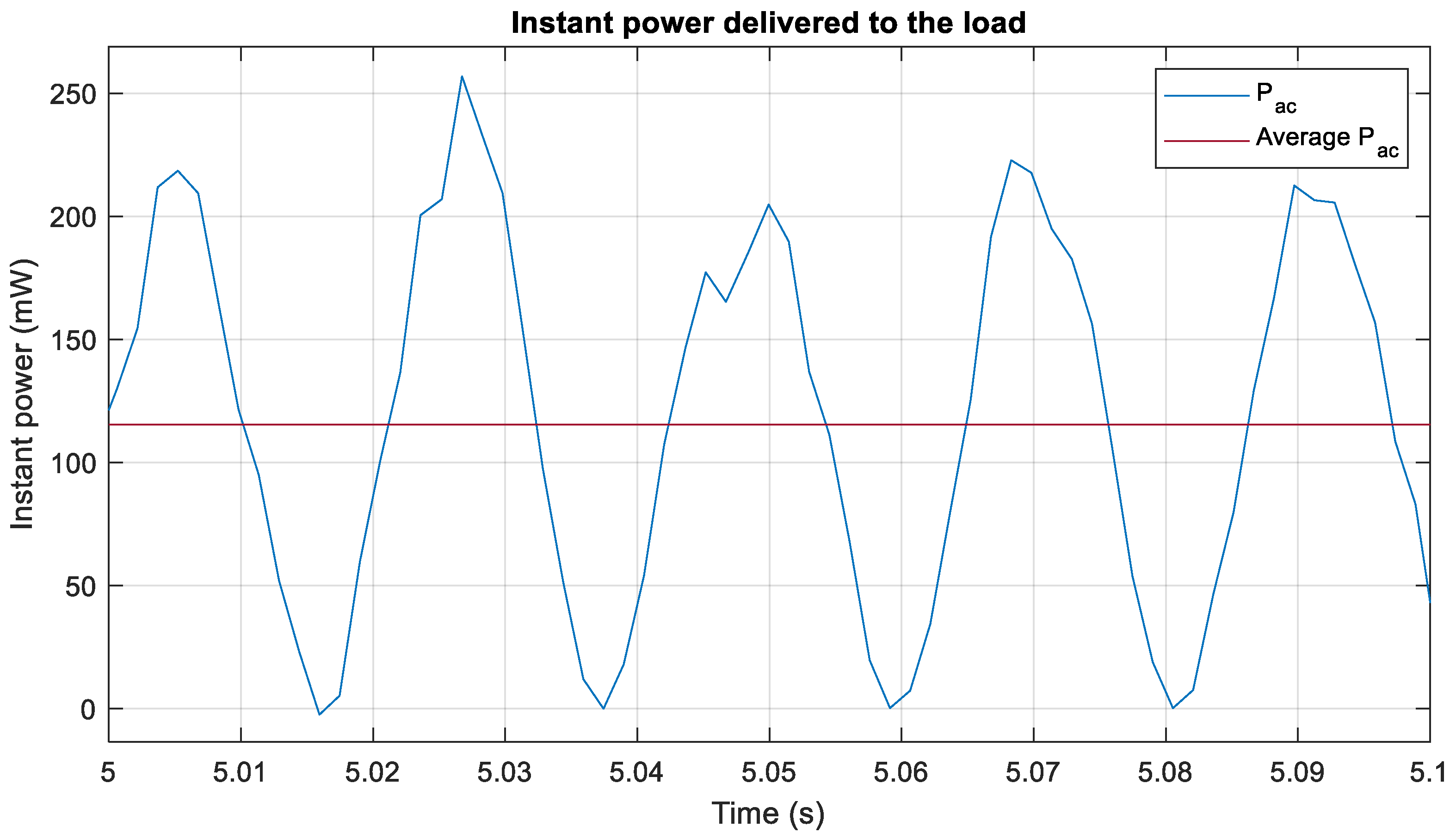
3.2. Instantaneous Power Calculation by Method 1
3.3. One-Period Average Power Calculation by Method 2
4. Discussion
- First, simulated values of and with no noise and a good sampling frequency are considered. The average power delivered to the load is calculated using the proposed methods and compared to the results obtained with the reference procedure [17].
- Then, the sensitivity to the noise is analysed, for which a random noise is added to the simulated of and ;
- Afterwards, the sensitivity to the measurement frequency is analysed, for which the sampling frequency of and is reduced;
- Finally, real measurements of and are used to conduct the analysis.
4.1. Results Using Ideal Signals
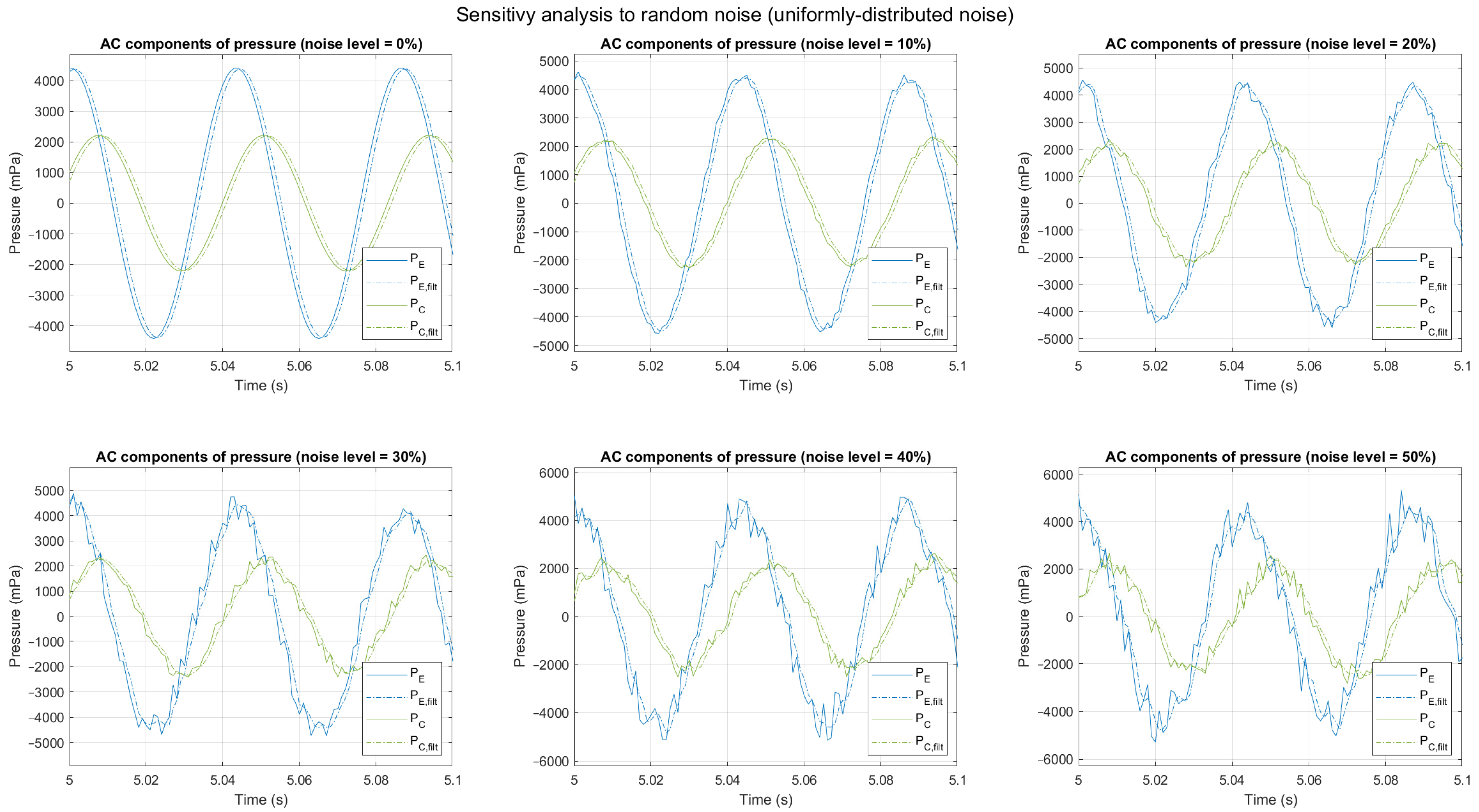
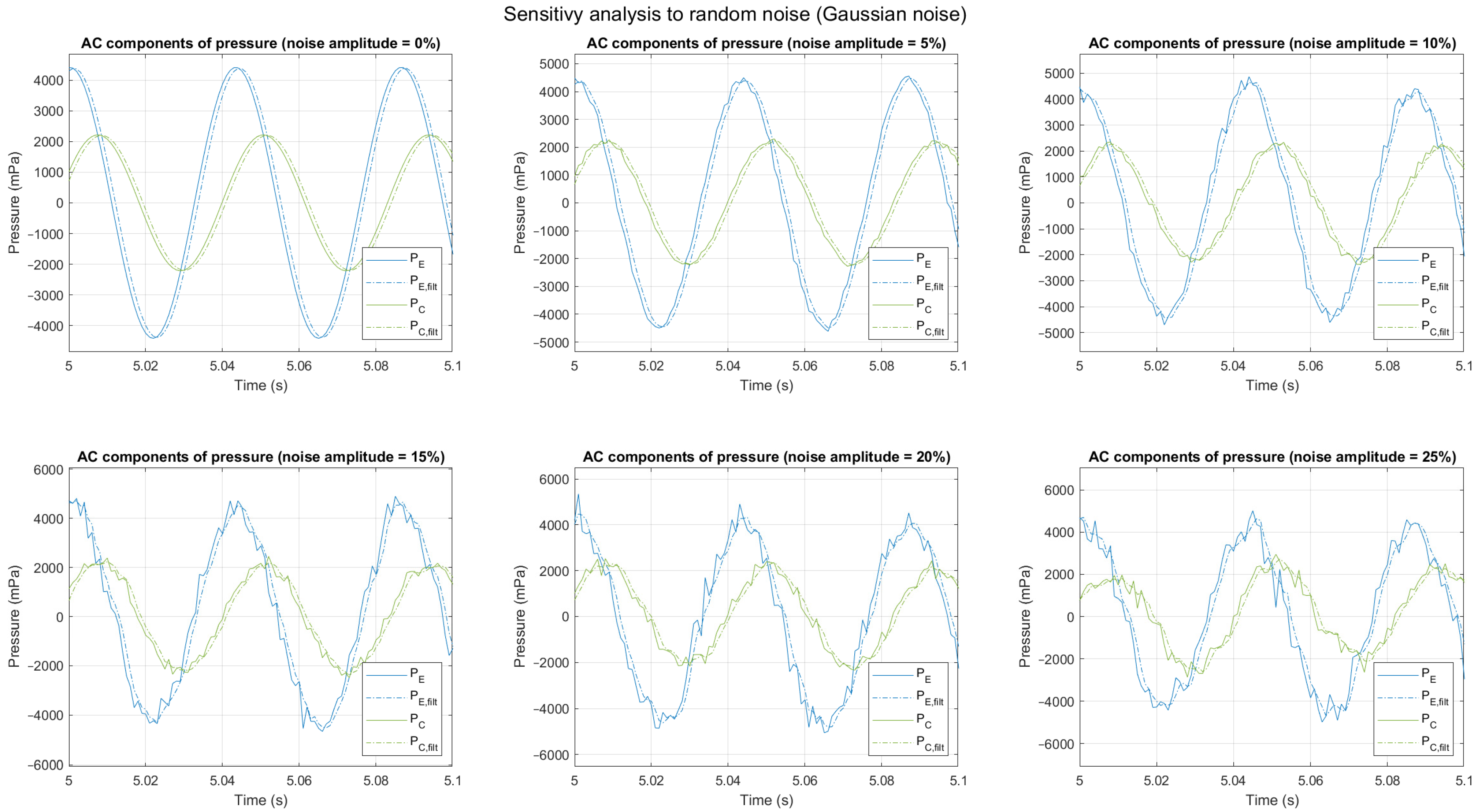
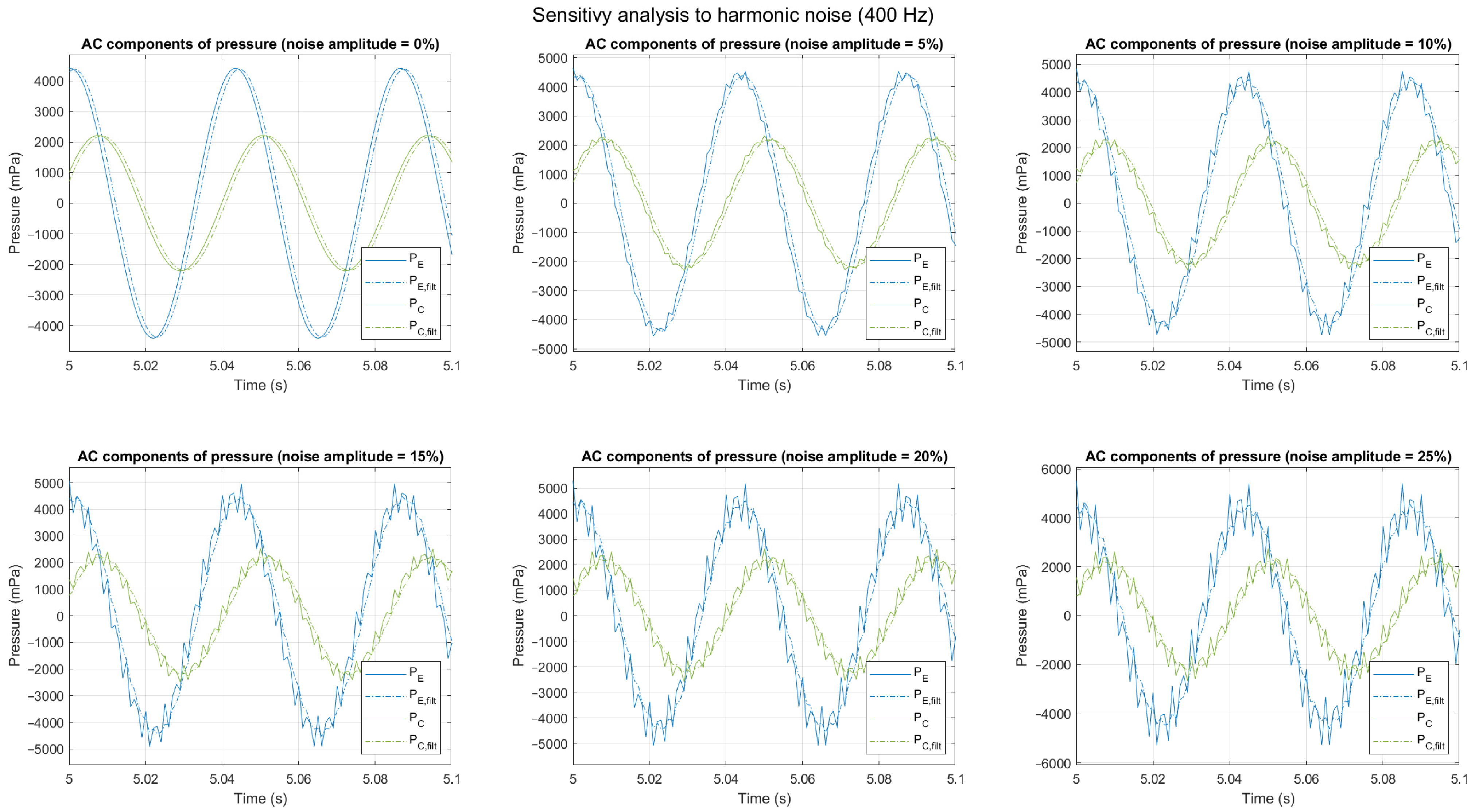
4.2. Sensitivity to Noise
4.2.1. Uniformly-Distributed Random Noise
4.2.2. Gaussian Random Noise
4.2.3. Harmonic Noise
4.3. Sensitivity to the Sampling Frequency
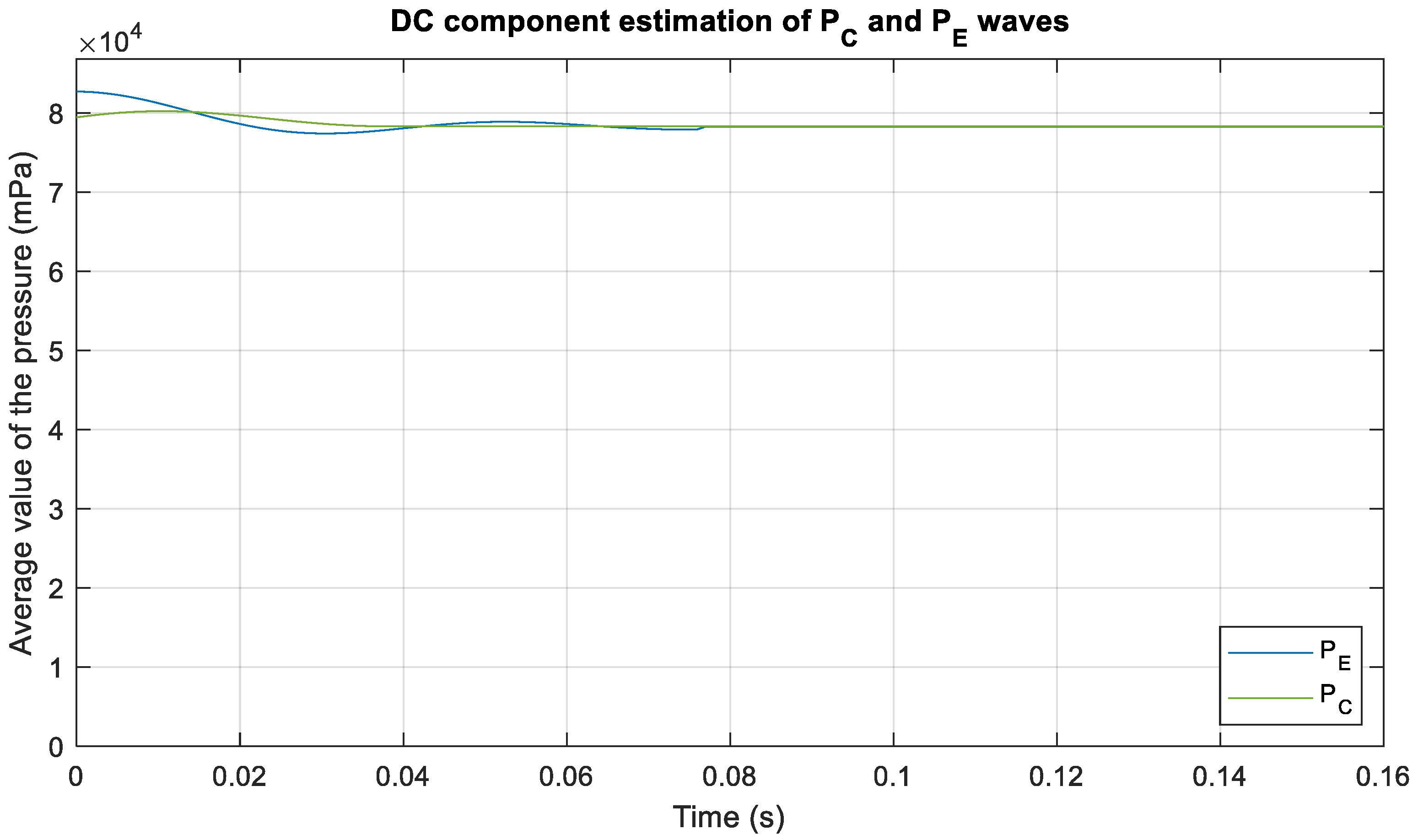
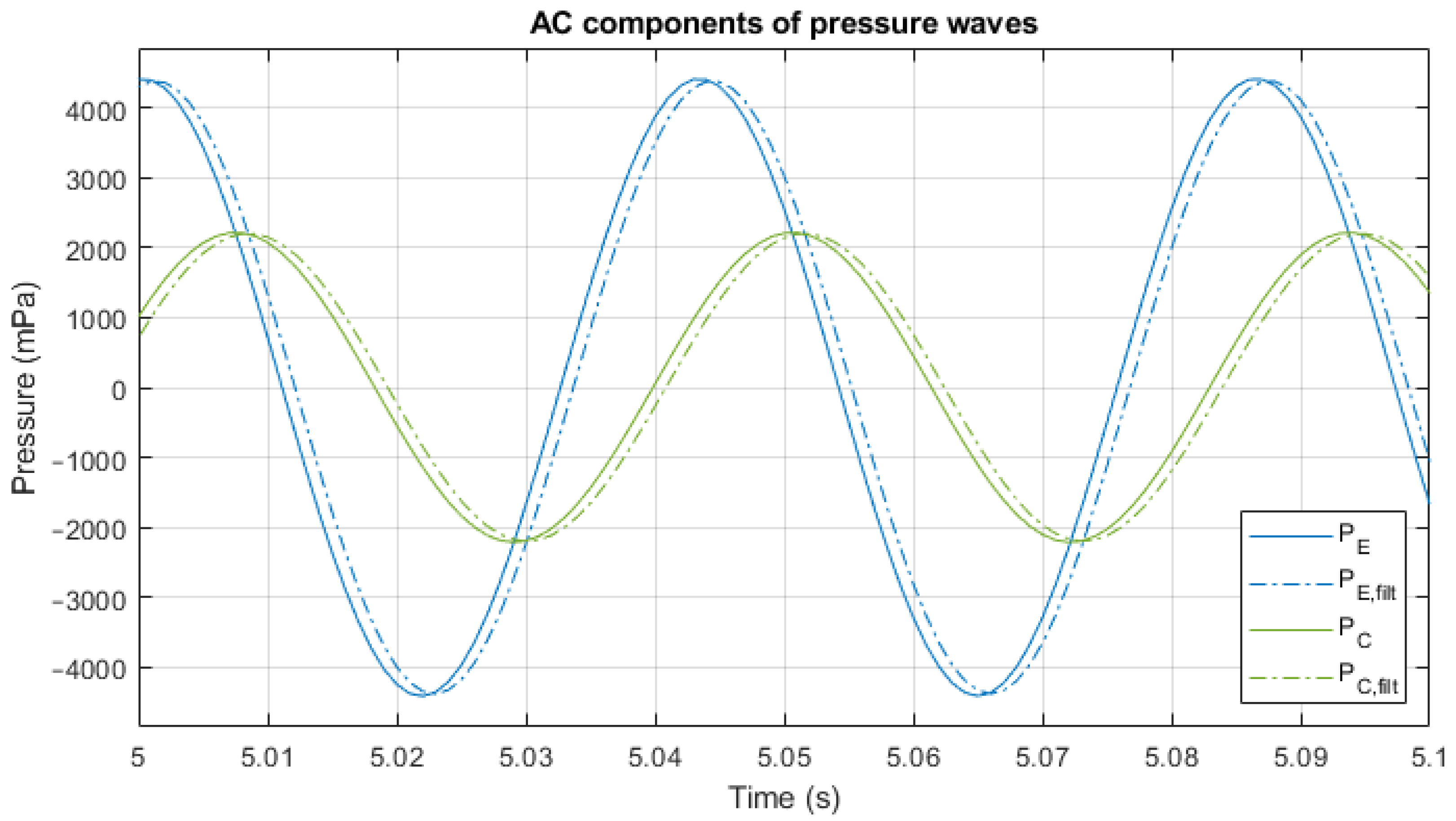
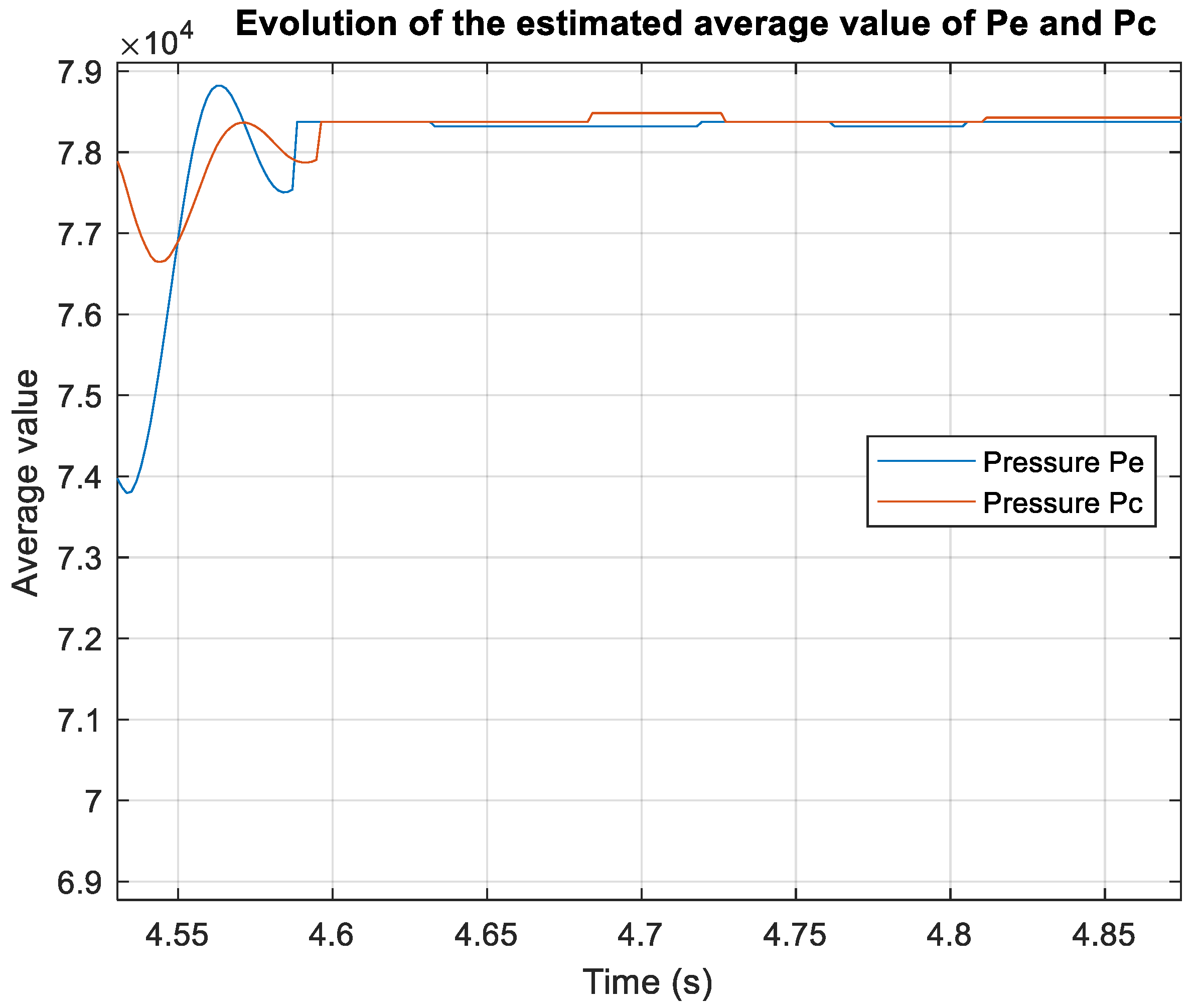
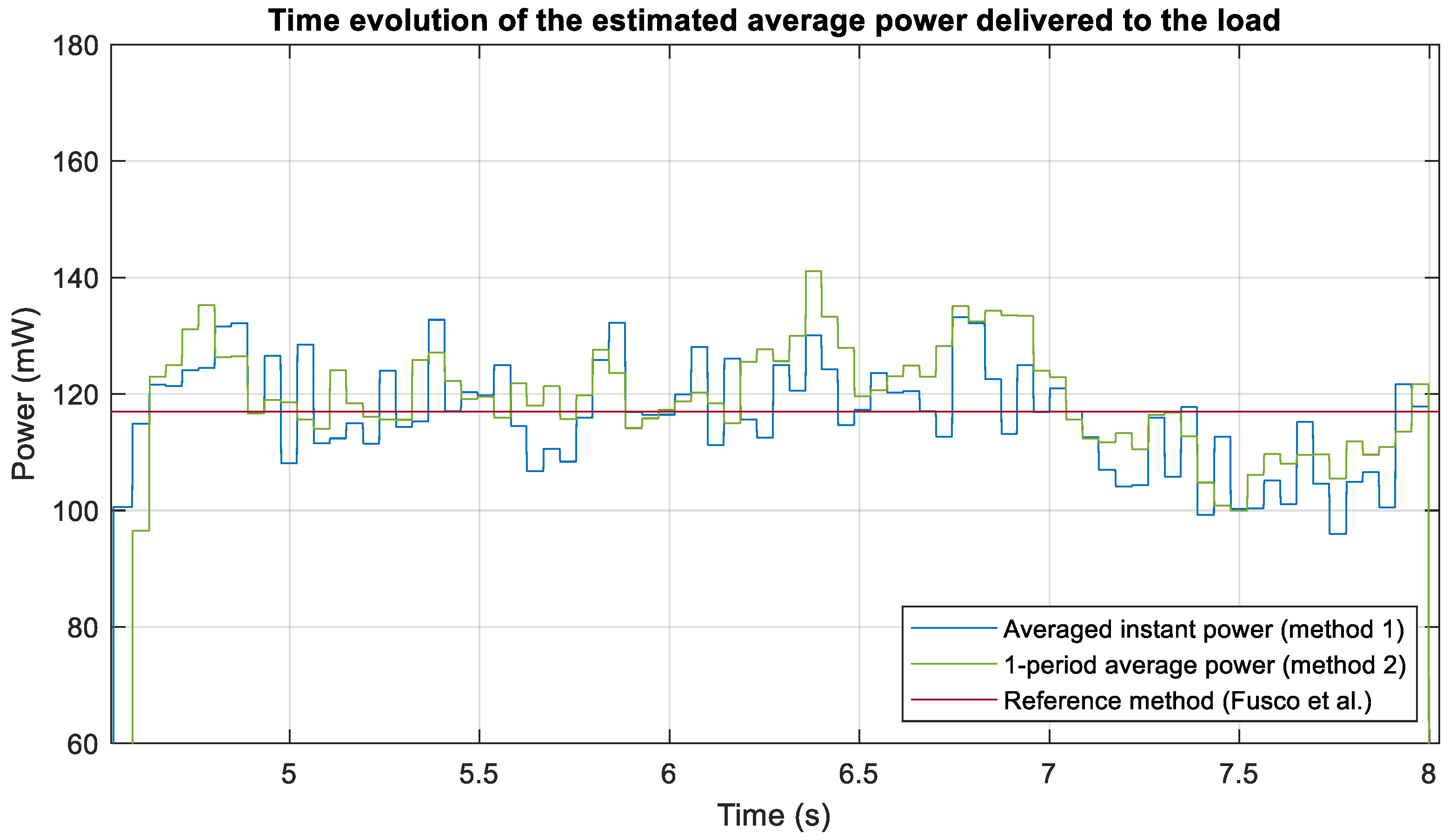
4.4. Analysis Using Experimental Measurements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TA-SLiCE | thermoacoustic Stirling-like cycle engine |
| RC | resistance–capacitance |
| DC | direct current |
| RMS | root mean square |
| FFT | Fast Fourier Transform |
| AC | alternating current |
References
- Swift, G.W. Thermoacoustics: A Unifying Perspective for Some Engines and Refrigerators, 2nd ed.; ASA Press/Springer: Cham, Switzerland, 2017; ISBN 978-3-319-66932-8. [Google Scholar]
- Backhaus, S.; Swift, G.W. A Thermoacoustic-Stirling Heat Engine: Detailed Study. J. Acoust. Soc. Am. 2000, 107, 3148–3166. [Google Scholar] [CrossRef] [PubMed]
- Farikhah, I.; Ueda, Y. Numerical Calculation of the Performance of a Thermoacoustic System with Engine and Cooler Stacks in a Looped Tube. Appl. Sci. 2017, 7, 672. [Google Scholar] [CrossRef]
- Rott, N. Damped and Thermally Driven Acoustic Oscillations in Wide and Narrow Tubes. J. Appl. Math. Phys. 1969, 20, 230–243. [Google Scholar] [CrossRef]
- Ceperley, P.H. A Pistonless Stirling Engine—The Traveling Wave Heat Engine. J. Acoust. Soc. Am. 1979, 66, 1508–1513. [Google Scholar] [CrossRef]
- Ceperley, P.H. Resonant Travelling Wave Heat Engine. U.S. Patent 4355517, 26 October 1982. [Google Scholar]
- Swift, G.W. Thermoacoustic Engines. J. Acoust. Soc. Am. 1988, 84, 1145–1180. [Google Scholar] [CrossRef]
- Ward, W.C.; Swift, G.W. Design Environment for Low-Amplitude Thermoacoustic Engines. J. Acoust. Soc. Am. 1994, 95, 3671–3672. [Google Scholar] [CrossRef]
- Zare, S.; Tavakolpour-Saleh, A.R.; Aghahosseini, A.; Mirshekari, R. Thermoacoustic Stirling Engines: A Review. Int. J. Green Energy 2023, 20, 89–111. [Google Scholar] [CrossRef]
- Iniesta, C.; Olazagoitia, J.L.; Vinolas, J.; Aranceta, J. Review of Travelling-Wave Thermoacoustic Electric-Generator Technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 232, 940–957. [Google Scholar] [CrossRef]
- Chen, G.; Tang, L.; Mace, B.; Yu, Z. Multi-Physics Coupling in Thermoacoustic Devices: A Review. Renew. Sustain. Energy Rev. 2021, 146, 111170. [Google Scholar] [CrossRef]
- Backhaus, S.; Swift, G. A Thermoacoustic Stirling Heat Engine. Nature 1999, 399, 335–338. [Google Scholar] [CrossRef]
- Iniesta, C.; Olazagoitia, J.; Vinolas, J.; Gros, J. Assessing the Performance of Design Variations of a Thermoacoustic Stirling Engine Combining Laboratory Tests and Model Results. Machines 2022, 10, 958. [Google Scholar] [CrossRef]
- Nabavi, M.; Siddiqui, K. A Critical Review on Advanced Velocity Measurement Techniques in Pulsating Flows. Meas. Sci. Technol. 2010, 21, 042002. [Google Scholar] [CrossRef]
- Clapp, C.W.; Firestone, F.A. The Acoustic Wattmeter, an Instrument for Measuring Sound Energy Flow. J. Acoust. Soc. Am. 1941, 13, 124–136. [Google Scholar] [CrossRef]
- Seybert, A.F. Two-Sensor Methods for the Measurement of Sound Intensity and Acoustic Properties in Ducts. J. Acoust. Soc. Am. 1988, 83, 2233–2239. [Google Scholar] [CrossRef]
- Fusco, A.M.; Ward, W.C.; Swift, G.W. Two-Sensor Power Measurements in Lossy Ducts. J. Acoust. Soc. Am. 1992, 91, 2229–2235. [Google Scholar] [CrossRef] [PubMed]
- Luo, E.C.; Ling, H.; Dai, W.; Yu, G.Y. Experimental Study of the Influence of Different Resonators on Thermoacoustic Conversion Performance of a Thermoacoustic-Stirling Heat Engine. Ultrasonics 2006, 44, 1507–1509. [Google Scholar] [CrossRef]
- Hamood, A.; Jaworski, A.J.; Mao, X. Development and Assessment of Two-Stage Thermoacoustic Electricity Generator. Energies 2019, 12, 1790. [Google Scholar] [CrossRef]
- Backhaus, S. Initial Tests of a Thermoacoustic Space Power Engine; AIP Publishing: Melville, NY, USA, 2003; pp. 641–647. [Google Scholar]
- Tijani, M.E.H.; Spoelstra, S. A Hot Air Driven Thermoacoustic-Stirling Engine. Appl. Therm. Eng. 2013, 61, 866–870. [Google Scholar] [CrossRef]
- Yang, P.; Liu, Y.-W. Computation of the Influence of a Phase Adjuster on Thermo-Acoustic Stirling Heat Engine. J. Power Energy 2015, 229, 73–87. [Google Scholar] [CrossRef]
- Olivier, C.; Penelet, G.; Poignand, G.; Lotton, P. Active Control of Thermoacoustic Amplification in a Thermo-Acousto-Electric Engine. J. Appl. Phys. 2014, 115, 174905. [Google Scholar] [CrossRef]
- Chen, G.; Tang, L.; Yang, Z.; Tao, K.; Yu, Z. An Electret-Based Thermoacoustic-Electrostatic Power Generator. Int. J. Energy Res. 2020, 44, 2298–2305. [Google Scholar] [CrossRef]
- Iniesta, C.; Olazagoitia, J.L.; Vinolas, J.; Gros, J. New Method to Analyse and Optimise Thermoacoustic Power Generators for the Recovery of Residual Energy. Alex. Eng. J. 2020, 59, 3907–3917. [Google Scholar] [CrossRef]
- Chakradeo, A.P.; Anagolkar, S.P.; Shendge, A.B.; Pawar, P.M.; Ganeshkar, J.D. Design, Development and Manufacturing of Thermoacoustic Cooler. Int. J. Eng. Res. Technol. 2019, 8, 576–582. [Google Scholar]
- Tijani, M.E.H.; Lycklama à Nijeholt, J.A.; Spoelstra, S. Amplifying the Power Density in Thermoacoustic Systems Using a Spring Component. J. Acoust. Soc. Am. 2024, 156, 202–213. [Google Scholar] [CrossRef] [PubMed]
- Moreno, C.; González, A.; Olazagoitia, J.L.; Vinolas, J. The Acquisition Rate and Soundness of a Low-Cost Data Acquisition System (LC-DAQ) for High Frequency Applications. Sensors 2020, 20, 524. [Google Scholar] [CrossRef]
- Moreno-Ramírez, C.; Iniesta, C.; González, A.; Olazagoitia, J.L. Development and Characterization of a Low-Cost Sensors System for an Acoustic Test Bench. Sensors 2020, 20, 6663. [Google Scholar] [CrossRef]
- Iniesta, C.; Vinolas, J.; Prieto, F.; Olazagoitia, J.L.; Soliverdi, L. Experimental Performance Evaluation of a Thermoacoustic Stirling Engine with a Low-Cost Arduino-Based Acquisition System. Appl. Sci. 2024, 14, 6049. [Google Scholar] [CrossRef]
- Callanan, J.; Nouh, M. Optimal Thermoacoustic Energy Extraction via Temporal Phase Control and Traveling Wave Generation. Appl. Energy 2019, 241, 599–612. [Google Scholar] [CrossRef]
- Bertuccio, G. On the Physical Origin of the Electro-Mechano-Acoustical Analogy. J. Acoust. Soc. Am. 2022, 151, 2066–2076. [Google Scholar] [CrossRef]
- Al-Kayiem, A.; Yu, Z. Using a Side-Branched Volume to Tune the Acoustic Field in a Looped-Tube Travelling-Wave Thermoacoustic Engine with a RC Load. Energy Convers. Manag. 2017, 150, 814–821. [Google Scholar] [CrossRef]

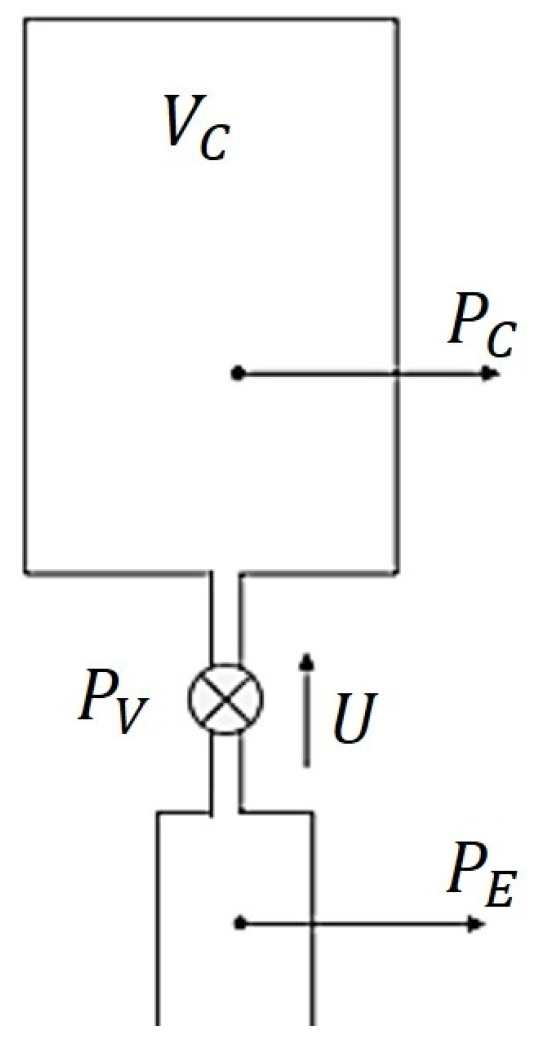
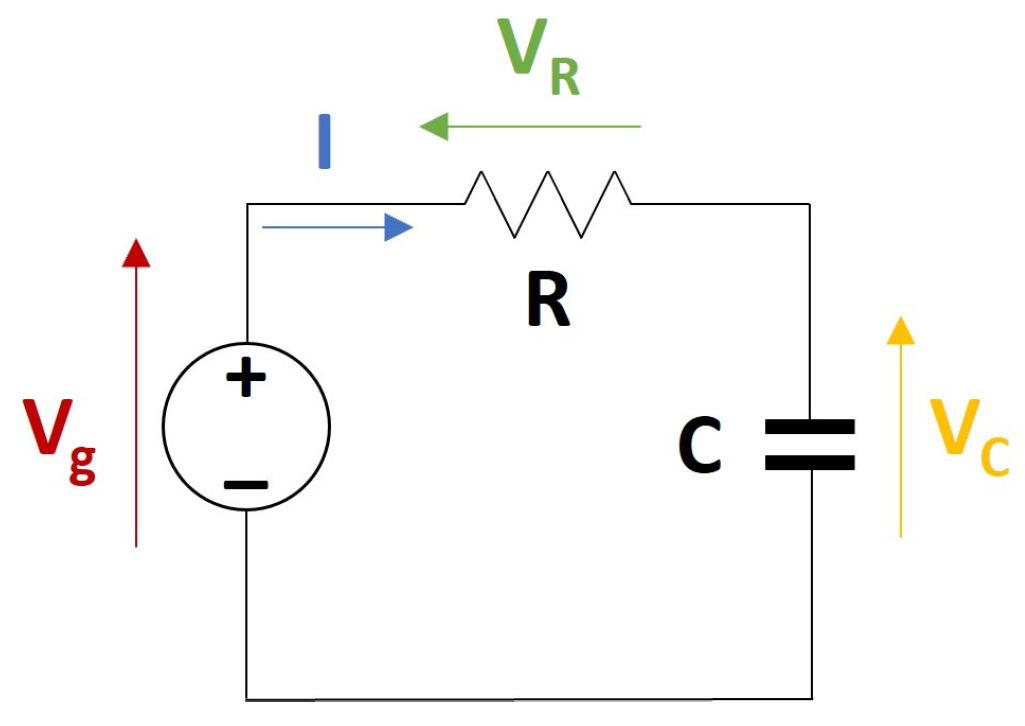





| Physical Variable | Electrical Analogy |
|---|---|
| Acoustic pressure (P) | Electrical voltage (V) |
| Volume flow rate (U) | Current (I) |
| Resistance (R) | Resistance (R) |
| Compliance (C) | Capacitance (C) |
| Electric power (Pelec) |
| Method | Average Power (mW) | Error (%) |
|---|---|---|
| Reference method | 118.05 | -- |
| Instantaneous power (method 1) | 115.97 | 1.75 |
| One-period average (method 2) | 116.69 | 1.15 |
| Method | Average Power (mW) for Different Levels of Noise (Uniformly Distributed Noise) | |||||
|---|---|---|---|---|---|---|
| 0% | 5% | 10% | 15% | 20% | 25% | |
| Reference method | 118.05 | 117.969 | 118.377 | 117.987 | 118.310 | 117.931 |
| Instantaneous power (method 1) | 115.983 | 115.814 | 115.788 | 115.216 | 114.332 | 113.789 |
| One-period average (method 2) | 116.691 | 117.355 | 119.879 | 122.161 | 126.007 | 128.734 |
| Method | Average Power (mW) for Different Levels of Noise (Gaussian Noise) | |||||
|---|---|---|---|---|---|---|
| 0% | 5% | 10% | 15% | 20% | 25% | |
| Reference method | 118.05 | 117.924 | 118.086 | 117.418 | 118.265 | 117.952 |
| Instantaneous power (method 1) | 115.983 | 115.817 | 115.665 | 115.065 | 115.022 | 114.140 |
| One-period average (method 2) | 116.691 | 117.288 | 119.136 | 121.281 | 124.101 | 126.584 |
| Method | Average Power (mW) for Different Levels of Noise (Harmonic Noise, 400 Hz) | |||||
|---|---|---|---|---|---|---|
| 0% | 5% | 10% | 15% | 20% | 25% | |
| Reference method | 118.05 | 118.052 | 118.053 | 118.054 | 118.055 | 118.056 |
| Instantaneous power (method 1) | 115.983 | 116.015 | 116.281 | 116.727 | 117.351 | 118.155 |
| One-period average (method 2) | 116.691 | 117.751 | 119.426 | 121.266 | 123.170 | 125.137 |
| Method | Average Power (mW) for Different Sampling Periods Ts | ||||||
|---|---|---|---|---|---|---|---|
| 0.1 ms | 0.5 ms | 1 ms | 2 ms | 3 ms | 4 ms | 5 ms | |
| Reference method | 118.050 | 118.050 | 118.050 | 118.050 | 118.050 | 118.050 | 118.050 |
| Instantaneous power (method 1) | 118.025 | 117.530 | 115.983 | 109.957 | 100.417 | 88.3360 | 74.2730 |
| One-period average (method 2) | 118.551 | 118.097 | 116.691 | 111.200 | 102.506 | 91.3430 | 77.9310 |
| Method | Average Power (mW) | Error (%) |
|---|---|---|
| Reference method | 116.962 | -- |
| Instantaneous power (method 1) | 115.735 | 1.295 |
| One-period average (method 2) | 121.236 | −3.654 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilo de la Fuente, E.; Gros, J.; Simón Rodríguez, M.A.; Velasco, A.-I.; Iniesta, C. Novel Real-Time Acoustic Power Estimation for Dynamic Thermoacoustic Control. Appl. Sci. 2025, 15, 2838. https://doi.org/10.3390/app15052838
Pilo de la Fuente E, Gros J, Simón Rodríguez MA, Velasco A-I, Iniesta C. Novel Real-Time Acoustic Power Estimation for Dynamic Thermoacoustic Control. Applied Sciences. 2025; 15(5):2838. https://doi.org/10.3390/app15052838
Chicago/Turabian StylePilo de la Fuente, Eduardo, Jaime Gros, María Antonia Simón Rodríguez, Ana-Isabel Velasco, and Carmen Iniesta. 2025. "Novel Real-Time Acoustic Power Estimation for Dynamic Thermoacoustic Control" Applied Sciences 15, no. 5: 2838. https://doi.org/10.3390/app15052838
APA StylePilo de la Fuente, E., Gros, J., Simón Rodríguez, M. A., Velasco, A.-I., & Iniesta, C. (2025). Novel Real-Time Acoustic Power Estimation for Dynamic Thermoacoustic Control. Applied Sciences, 15(5), 2838. https://doi.org/10.3390/app15052838









