Space–Time Stress Variations near the East Anatolian Fault Zone and the Triggering Relationship of Earthquakes
Abstract
1. Introduction
2. Background
3. Materials and Methods
3.1. Coulomb Failure Stress Changes
3.2. Stress Tensor Inversion
3.3. Data
4. Results
4.1. Results of Stress Tensor Inversion
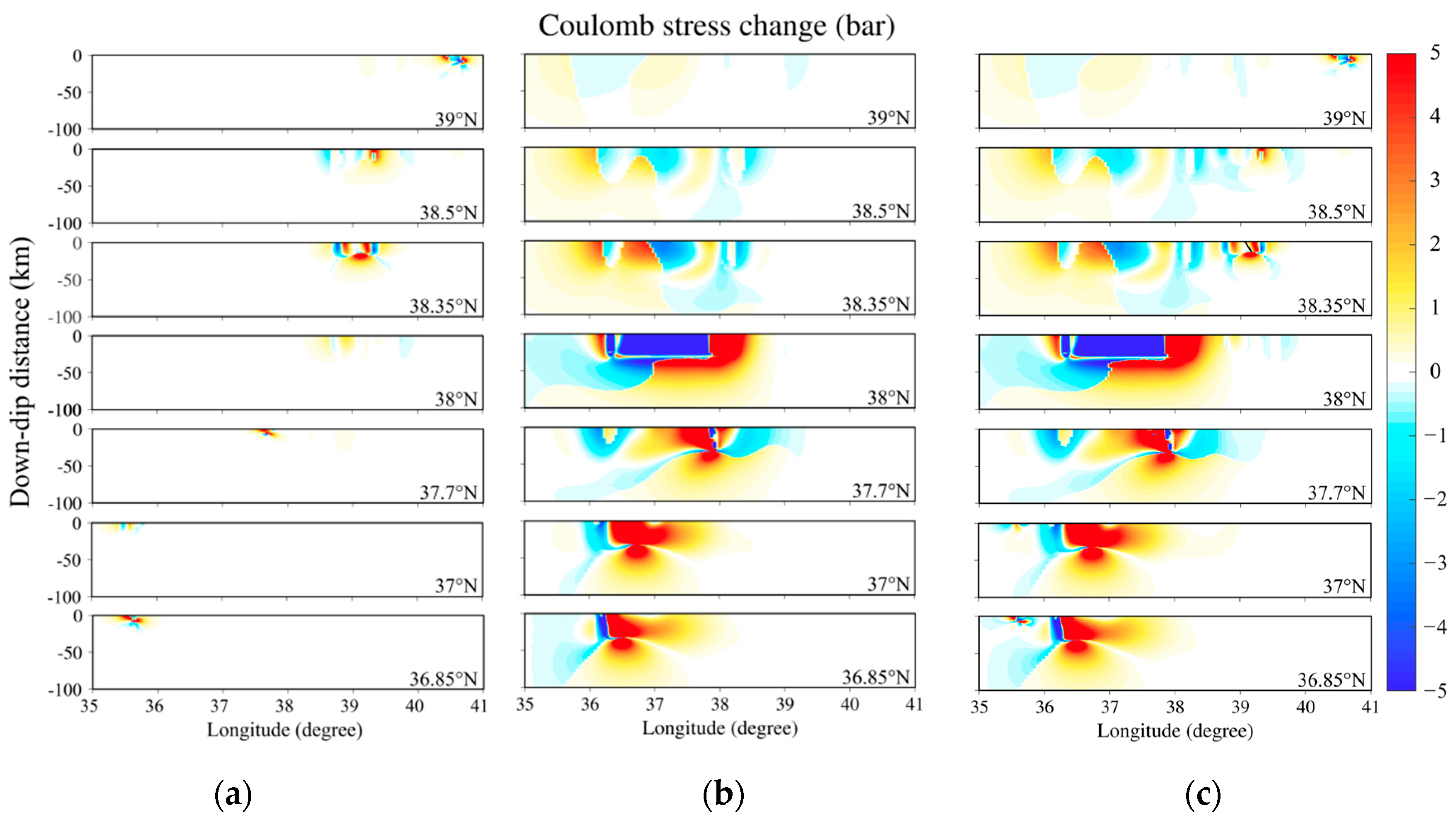
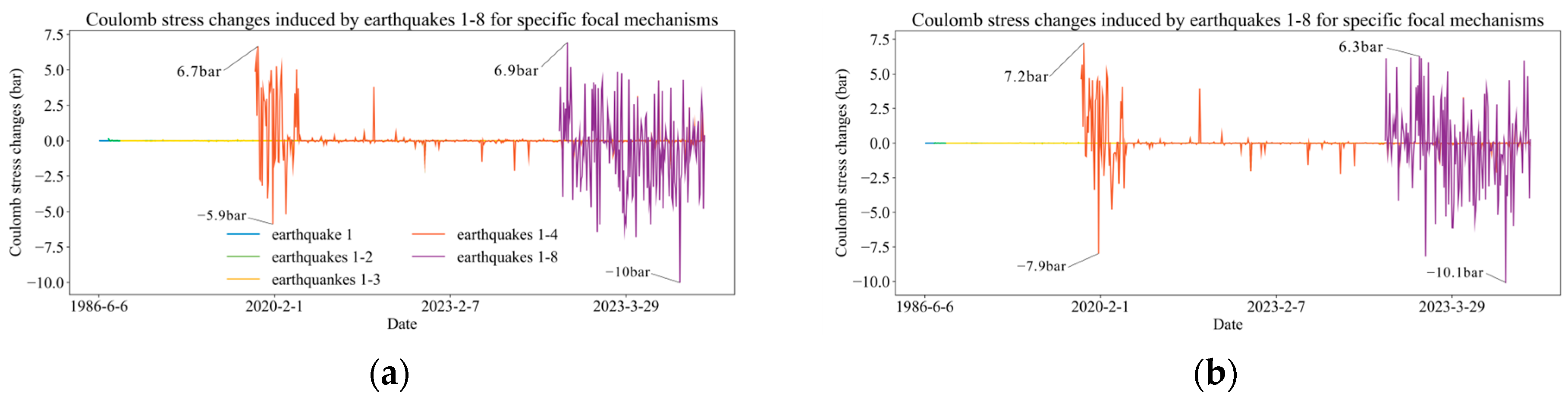
4.2. Results of Coulomb Failure Stress Changes
5. Discussion
6. Conclusions
- (1)
- The resulting from the 7.7 Mw and 7.6 Mw earthquakes in 2023 near the East Anatolian fault zone exhibited significantly larger values and broader effects compared to several other seismic events. While the induced by three earthquakes between 1986 and 2003 only influenced the subsurface up to 10 km, the 6.8 Mw earthquake in 2020 impacted the subsurface up to 50 km. The major earthquakes in 2023 affected the subsurface up to 100 km.
- (2)
- Near 36.7 E, the value of is very high in the range of 37 N–36.85 N. Especially near the depth of 10–20 km, the average value reaches about 1.74–2.41 bar, which is very likely to trigger new earthquakes. In the Çardak fault zone, there is a Coulomb stress drop zone, and the drop mean value is about −2.9 bar, which significantly inhibits the continuation of earthquakes in this area.
- (3)
- The northeastern and southwestern segments of the EAFZ have experienced Coulomb stress increases with 1.5–2.5 bar, identifying these areas as high-risk zones for future seismic activity, particularly at shallow depths (10–20 km). These areas may be accumulating strain energy, increasing the possibility of future ruptures. On the contrary, there is a 0.25–1 bar Coulomb stress drop zone in the northwest of the Çardak fault zone, where stress shadows temporarily suppress seismic activity and significantly reduce seismic risk in this region.
- (4)
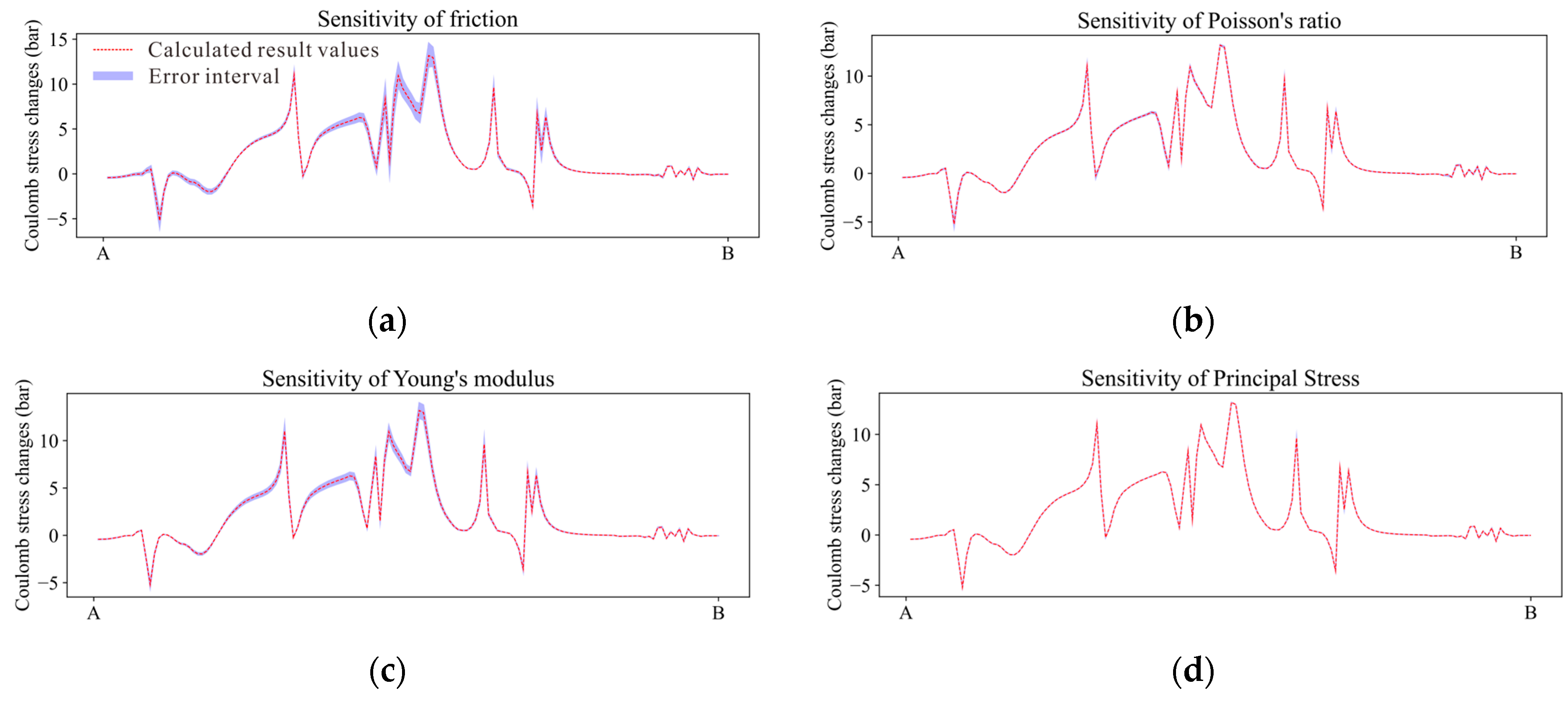
- The sensitivity analysis of to various parameters revealed that the calculations were most influenced by the strike angle in the focal mechanism model, with averaging differences in results reaching up to 1.33 bar. Conversely, the direction of the principal stress axes in the study area had the least impact on Coulomb stress changes. This underscores the importance of utilizing a highly accurate focal mechanism model when conducting Coulomb stress change calculations to ensure reliable outcomes.
- (5)
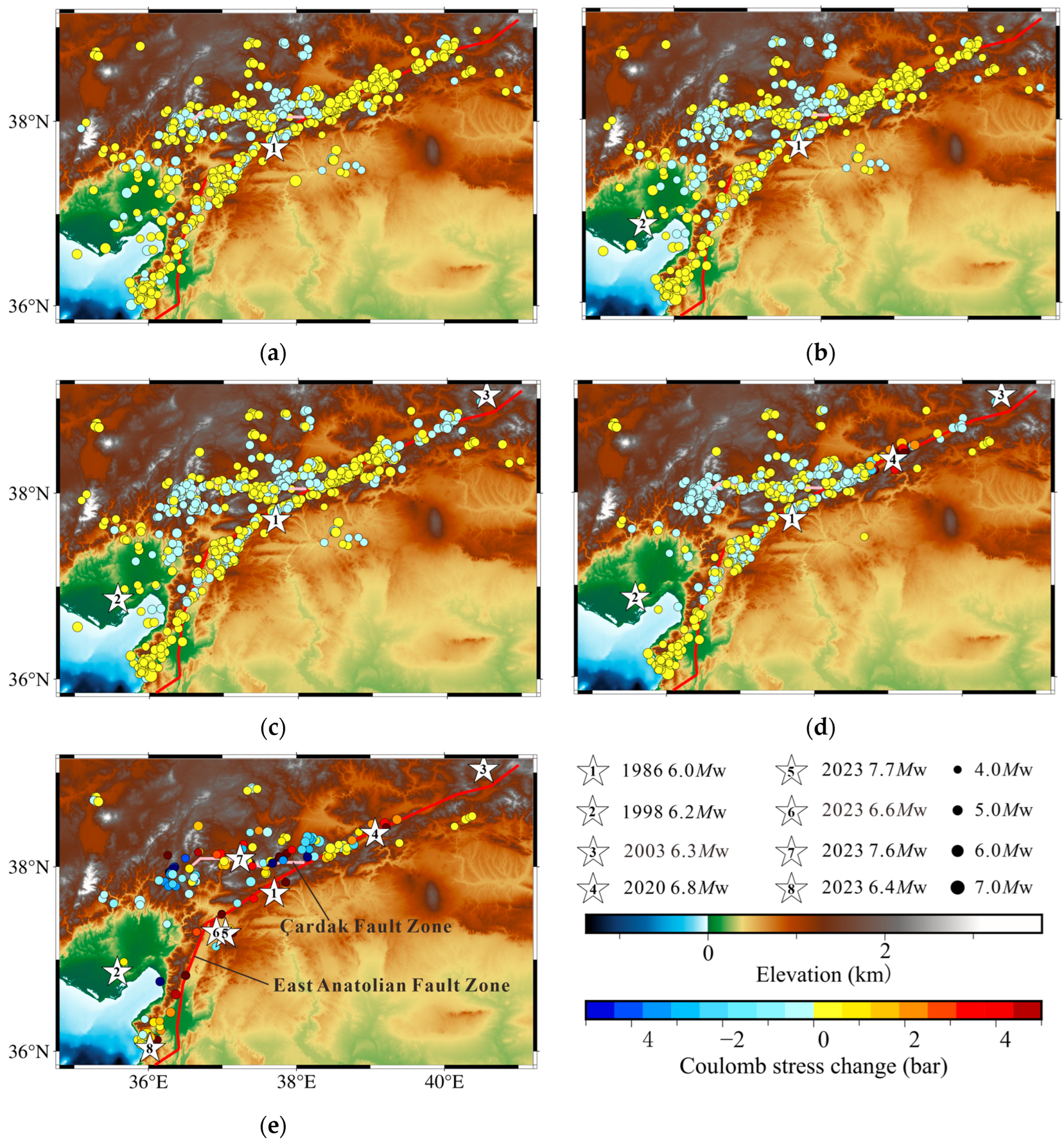
- The three major earthquakes during 1986–2003 did not produce high for subsequent nearby earthquakes. In contrast, the five major earthquakes between 2020 and 2023 resulted in a higher for certain subsequent earthquakes in proximity. The 6.8 Mw earthquake in 2020 produced a 2-year greater than 0.1 bar on the subsequent surrounding earthquakes, which indicates that this earthquake has a promoting effect on the large earthquakes in 2023.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Wang, X.; Tao, T.; Zhu, Y.; Qu, X.; Li, Z.; Huang, J.; Song, S. Source Model of the 2023 Turkey Earthquake Sequence Imaged by Sentinel-1 and GPS Measurements: Implications for Heterogeneous Fault Behavior along the East Anatolian Fault Zone. Remote Sens. 2023, 15, 2618. [Google Scholar] [CrossRef]
- Mahmoud, Y.; Masson, F.; Meghraoui, M.; Cakir, Z.; Alchalbi, A.; Yavasoglu, H.; Yönlü, O.; Daoud, M.; Ergintav, S.; Inan, S. Kinematic Study at the Junction of the East Anatolian Fault and the Dead Sea Fault from GPS Measurements. J. Geodyn. 2013, 67, 30–39. [Google Scholar] [CrossRef]
- Reilinger, R.; McClusky, S.; Vernant, P.; Lawrence, S.; Ergintav, S.; Cakmak, R.; Ozener, H.; Kadirov, F.; Guliev, I.; Stepanyan, R.; et al. GPS Constraints on Continental Deformation in the Africa-Arabia-Eurasia Continental Collision Zone and Implications for the Dynamics of Plate Interactions. J. Geophys. Res. Solid Earth 2006, 111, B05411. [Google Scholar] [CrossRef]
- Yilmaz, H.; Over, S.; Ozden, S. Kinematics of the East Anatolian Fault Zone between Turkoglu (Kahramanmaras) and Celikhan (Adiyaman), Eastern Turkey. Earth Planets Space 2006, 58, 1463–1473. [Google Scholar] [CrossRef]
- Disaster and Emergency Management Authorit. 06 Şubat 2023 Pazarcık (Kahramanmaraş) Mw 7.7 ve Elbistan (Kahramanmaraş) Mw 7.6 Depremlerine Iliskin Ön Degerlendirme Raporu; Disaster and Emergency Management Authorit: Ankara, Turkey, 2023. [Google Scholar]
- Barbot, S.; Luo, H.; Wang, T.; Hamiel, Y.; Piatibratova, O.; Javed, M.T.; Braitenberg, C.; Gurbuz, G. Slip Distribution of the February 6, 2023 Mw 7.8 and Mw 7.6, Kahramanmaraş, Turkey Earthquake Sequence in the East Anatolian Fault Zone. Seismica 2023, 2. [Google Scholar] [CrossRef]
- Liu, C.; Shi, Y. Space-Time Stress Variations on the Palu-Koro Fault Impacting the 2018 Mw 7.5 Palu Earthquake and Its Seismic Hazards. Geochem. Geophys. Geosyst. 2021, 22, e2020GC009552. [Google Scholar] [CrossRef]
- Harris, R.A. Introduction to Special Section: Stress Triggers, Stress Shadows, and Implications for Seismic Hazard. J. Geophys. Res. 1998, 103, 24347–24358. [Google Scholar] [CrossRef]
- Hardebeck, J.L.; Nazareth, J.J.; Hauksson, E. The Static Stress Change Triggering Model: Constraints from Two Southern California Aftershock Sequences. J. Geophys. Res. Solid Earth 1998, 103, 24427–24437. [Google Scholar] [CrossRef]
- Gomberg, J.; Beeler, N.M.; Blanpied, M.L.; Bodin, P. Earthquake Triggering by Transient and Static Deformations. J. Geophys. Res. Solid Earth 1998, 103, 24411–24426. [Google Scholar] [CrossRef]
- Scholz, C.H. Earthquakes and Friction Laws. Nature 1998, 391, 37–42. [Google Scholar] [CrossRef]
- Rybicki, K. Analysis of Aftershocks on the Basis of Dislocation Theory. Phys. Earth Planet. Inter. 1973, 7, 409–422. [Google Scholar] [CrossRef]
- Das, S.; Scholz, C.H. Off-Fault Aftershock Clusters Caused by Shear Stress Increase? Bull. Seismol. Soc. Am. 1981, 71, 1669–1675. [Google Scholar] [CrossRef]
- Stein, R.S.; Lisowski, M. The 1979 Homestead Valley Earthquake Sequence, California: Control of Aftershocks and Postseismic Deformation. J. Geophys. Res. Solid Earth 1983, 88, 6477–6490. [Google Scholar] [CrossRef]
- Wang, M.; Liu, Z.; Luo, R. Stress Triggering Effect on the 2022 Honghe MS5.0 Earthquake with Historical Strong Earthquakes. Geod. Geodyn. 2024, 15, 107–113. [Google Scholar] [CrossRef]
- Stein, R.S.; King, G.C.P.; Lin, J. Change in Failure Stress on the Southern San Andreas Fault System Caused by the 1992 Magnitude = 7.4 Landers Earthquake. Science 1992, 258, 1328–1332. [Google Scholar] [CrossRef]
- Anderson, G.; Aagaard, B.; Hudnut, K. Fault Interactions and Large Complex Earthquakes in the Los Angeles Area. Science 2003, 302, 1946–1949. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Banerjee, P.; Bürgmann, R.; Hashimoto, M.; Choosakul, N. Stress Changes along the Sunda Trench Following the 26 December 2004 Sumatra-Andaman and 28 March 2005 Nias Earthquakes. Geophys. Res. Lett. 2006, 33, L06309. [Google Scholar] [CrossRef]
- Shan, B.; Xiong, X.; Wang, R.; Zheng, Y.; Yang, S. Coulomb Stress Evolution along Xianshuihe–Xiaojiang Fault System since 1713 and Its Interaction with Wenchuan Earthquake, May 12, 2008. Earth Planet. Sci. Lett. 2013, 377–378, 199–210. [Google Scholar] [CrossRef]
- Herman, M.W.; Furlong, K.P.; Hayes, G.P.; Benz, H.M. Foreshock Triggering of the 1 April 2014 Mw 8.2 Iquique, Chile, Earthquake. Earth Planet. Sci. Lett. 2016, 447, 119–129. [Google Scholar] [CrossRef]
- Jia, Z.; Jin, Z.; Marchandon, M.; Ulrich, T.; Gabriel, A.-A.; Fan, W.; Shearer, P.; Zou, X.; Rekoske, J.; Bulut, F.; et al. The Complex Dynamics of the 2023 Kahramanmaraş, Turkey, Mw 7.8–7.7 Earthquake Doublet. Science 2023, 381, 985–990. [Google Scholar] [CrossRef]
- Liu, C.; Dong, P.; Zhu, B.; Shi, Y. Stress Shadow on the Southwest Portion of the Longmen Shan Fault Impacted the 2008 Wenchuan Earthquake Rupture. JGR Solid Earth 2018, 123, 9963–9981. [Google Scholar] [CrossRef]
- Meade, B.J.; DeVries, P.M.R.; Faller, J.; Viegas, F.; Wattenberg, M. What Is Better Than Coulomb Failure Stress? A Ranking of Scalar Static Stress Triggering Mechanisms from 105 Mainshock-Aftershock Pairs. Geophys. Res. Lett. 2017, 44, 11409–11416. [Google Scholar] [CrossRef]
- Pang, Y. Stress Evolution on Major Faults in Tien Shan and Implications for Seismic Hazard. J. Geodyn. 2022, 153–154, 101939. [Google Scholar] [CrossRef]
- Alkan, H.; Büyüksaraç, A.; BEKTAŞ, Ö. Investigation of Earthquake Sequence and Stress Transfer in the Eastern Anatolia Fault Zone by Coulomb Stress Analysis. Turk. J. Earth Sci. 2024, 33, 56–68. [Google Scholar] [CrossRef]
- Bayrak, E.; Coban, K.H. Evaluation of 08 August 2019 Bozkurt (Denizli-Turkey, Mw 6.0) Earthquake in Terms of Strong Ground-Motion Parameters and Coulomb Stress Changes. Environ. Earth Sci. 2023, 82, 470. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Jankowski, R. Machine Learning-Based Seismic Fragility and Seismic Vulnerability Assessment of Reinforced Concrete Structures. Soil Dyn. Earthq. Eng. 2023, 166, 107761. [Google Scholar] [CrossRef]
- Xu, J.; Liu, C.; Xiong, X. Source Process of the 24 January 2020 Mw 6.7 East Anatolian Fault Zone, Turkey, Earthquake. Seismol. Res. Lett. 2020, 91, 3120–3128. [Google Scholar] [CrossRef]
- Dogan, U.; Demir, D.Ö.; Çakir, Z.; Ergintav, S.; Ozener, H.; Akoğlu, A.M.; Nalbant, S.S.; Reilinger, R. Postseismic Deformation Following the Mw 7.2, 23 October 2011 Van Earthquake (Turkey): Evidence for Aseismic Fault Reactivation: October 23, 2011 Van Earthquake (Turkey). Geophys. Res. Lett. 2014, 41, 2334–2341. [Google Scholar] [CrossRef]
- Duman, T.Y.; Emre, Ö. The East Anatolian Fault: Geometry, Segmentation and Jog Characteristics. Geol. Soc. Lond. Spec. Publ. 2013, 372, 495–529. [Google Scholar] [CrossRef]
- Wollin, C.; Bohnhoff, M.; Vavryčuk, V.; Martínez-Garzón, P. Stress Inversion of Regional Seismicity in the Sea of Marmara Region, Turkey. Pure Appl. Geophys. 2019, 176, 1269–1291. [Google Scholar] [CrossRef]
- Ma, J.; Wang, P.; Vavryčuk, V.; Wu, S.; Hou, J.; Qi, Z. Tectonic Stress Field Related to the Eastern Turkey from 1976 to 2024. J. Seismol. 2025. [Google Scholar] [CrossRef]
- Ren, C.; Wang, Z.; Taymaz, T.; Hu, N.; Luo, H.; Zhao, Z.; Yue, H.; Song, X.; Shen, Z.; Xu, H.; et al. Supershear Triggering and Cascading Fault Ruptures of the 2023 Kahramanmaraş, Türkiye, Earthquake Doublet. Science 2024, 383, 305–311. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S. The Role of Stress Transfer in Rupture Nucleation and Inhibition in the 2023 Kahramanmaraş, Türkiye, Sequence, and a One-Year Earthquake Forecast. Seismol. Res. Lett. 2024, 95, 596–606. [Google Scholar] [CrossRef]
- Tung, S.; Sippl, C.; Shirzaei, M.; Taymaz, T.; Masterlark, T.; Medved, I. Structural Controls on Fault Slip Models of the 6 February 2023 Kahramanmaraş, Türkiye Earthquake Doublet with Finite Element Analyses. Geophys. Res. Lett. 2024, 51, e2023GL107472. [Google Scholar] [CrossRef]
- Kobayashi, T.; Munekane, H.; Kuwahara, M.; Furui, H. Insights on the 2023 Kahramanmaraş Earthquake, Turkey, from InSAR: Fault Locations, Rupture Styles and Induced Deformation. Geophys. J. Int. 2024, 236, 1068–1088. [Google Scholar] [CrossRef]
- Liu, C.; Lay, T.; Wang, R.; Taymaz, T.; Xie, Z.; Xiong, X.; Irmak, T.S.; Kahraman, M.; Erman, C. Complex Multi-Fault Rupture and Triggering during the 2023 Earthquake Doublet in Southeastern Türkiye. Nat. Commun. 2023, 14, 5564. [Google Scholar] [CrossRef]
- Gallovič, F.; Zahradník, J.; Plicka, V.; Sokos, E.; Evangelidis, C.; Fountoulakis, I.; Turhan, F. Complex Rupture Dynamics on an Immature Fault during the 2020 Mw 6.8 Elazığ Earthquake, Turkey. Commun. Earth Environ. 2020, 1, 40. [Google Scholar] [CrossRef]
- Cakir, Z.; Doğan, U.; Akoğlu, A.M.; Ergintav, S.; Özarpacı, S.; Özdemir, A.; Nozadkhalil, T.; Çakir, N.; Zabcı, C.; Erkoç, M.H.; et al. Arrest of the Mw 6.8 January 24, 2020 Elaziğ (Turkey) Earthquake by Shallow Fault Creep. Earth Planet. Sci. Lett. 2023, 608, 118085. [Google Scholar] [CrossRef]
- Ding, H.; Zhou, Y.; Ge, Z.; Taymaz, T.; Ghosh, A.; Xu, H.; Irmak, T.S.; Song, X. High-Resolution Seismicity Imaging and Early Aftershock Migration of the 2023 Kahramanmaraş (SE Türkiye) MW7.9 & 7.8 Earthquake Doublet. Earthq. Sci. 2023, 36, 417–432. [Google Scholar] [CrossRef]
- Wu, F.; Xie, J.; An, Z.; Lyu, C.; Taymaz, T.; Irmak, T.S.; Li, X.; Wen, Z.; Zhou, B. Pulse-like Ground Motion Observed during the 6 February 2023 MW7.8 Pazarcık Earthquake (Kahramanmaraş, SE Türkiye). Earthq. Sci. 2023, 36, 328–339. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, X.; Liu, D.; Taymaz, T.; Eken, T.; Guo, R.; Zheng, Y.; Wang, J.; Sun, H. Geometric Controls on Cascading Rupture of the 2023 Kahramanmaraş Earthquake Doublet. Nat. Geosci. 2023, 16, 1054–1060. [Google Scholar] [CrossRef]
- Hasterok, D.; Halpin, J.A.; Collins, A.S.; Hand, M.; Kreemer, C.; Gard, M.G.; Glorie, S. New Maps of Global Geological Provinces and Tectonic Plates. Earth-Sci. Rev. 2022, 231, 104069. [Google Scholar] [CrossRef]
- Bird, P. An Updated Digital Model of Plate Boundaries. Geochem. Geophys. Grosyst. 2003, 4, 1027. [Google Scholar] [CrossRef]
- King, G.C.P.; Stein, R.S.; Lin, J. Static Stress Changes and the Triggering of Earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar] [CrossRef]
- Freed, A.M. Earthquake Triggering by Static, Dynamic, and Postseismic Stress Transfer. Annu. Rev. Earth Planet. Sci. 2005, 33, 335–367. [Google Scholar] [CrossRef]
- Stein, R.S. The Role of Stress Transfer in Earthquake Occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
- Harris, R.A.; Simpson, R.W.; Reasenberg, P.A. Influence of Static Stress Changes on Earthquake Locations in Southern California. Nature 1995, 375, 221–224. [Google Scholar] [CrossRef]
- Harris, R.A.; Simpson, R.W. Suppression of Large Earthquakes by Stress Shadows: A Comparison of Coulomb and Rate-and-State Failure. J. Geophys. Res. Solid Earth 1998, 103, 24439–24451. [Google Scholar] [CrossRef]
- Okada, Y. Internal Deformation Due to Shear and Tensile Faults in a Half-Space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
- Lin, J.; Stein, R.S. Stress Triggering in Thrust and Subduction Earthquakes and Stress Interaction between the Southern San Andreas and Nearby Thrust and Strike-Slip Faults: Stress Triggering and Fault Interaction. J. Geophys. Res. 2004, 109, B02303. [Google Scholar] [CrossRef]
- Toda, S. Forecasting the Evolution of Seismicity in Southern California: Animations Built on Earthquake Stress Transfer. J. Geophys. Res. 2005, 110, B05S16. [Google Scholar] [CrossRef]
- Gephart, J.W.; Forsyth, D.W. An Improved Method for Determining the Regional Stress Tensor Using Earthquake Focal Mechanism Data: Application to the San Fernando Earthquake Sequence. J. Geophys. Res. 1984, 89, 9305–9320. [Google Scholar] [CrossRef]
- Hardebeck, J.L.; Michael, A.J. Damped Regional-Scale Stress Inversions: Methodology and Examples for Southern California and the Coalinga Aftershock Sequence. J. Geophys. Res. Solid Earth 2006, 111, B11310. [Google Scholar] [CrossRef]
- Lund, B.; Slunga, R. Stress Tensor Inversion Using Detailed Microearthquake Information and Stability Constraints: Application to Ölfus in Southwest Iceland. J. Geophys. Res. 1999, 104, 14947–14964. [Google Scholar] [CrossRef]
- Michael, A.J. Use of Focal Mechanisms to Determine Stress: A Control Study. J. Geophys. Res. 1987, 92, 357–368. [Google Scholar] [CrossRef]
- Vavryčuk, V. Iterative Joint Inversion for Stress and Fault Orientations from Focal Mechanisms|Geophysical Journal International|Oxford Academic. Available online: https://academic.oup.com/gji/article/199/1/69/723251 (accessed on 14 October 2022).
- Bott, M.H.P. The Mechanics of Oblique Slip Faulting. Geol. Mag. 1959, 96, 109–117. [Google Scholar] [CrossRef]
- Wallace, R.E. Geometry of Shearing Stress and Relation to Faulting. J. Geol. 1951, 59, 118–130. [Google Scholar] [CrossRef]
- Michael, A.J. Determination of Stress from Slip Data: Faults and Folds. J. Geophys. Res. 1984, 89, 11517–11526. [Google Scholar] [CrossRef]
- Lentas, K. Towards Routine Determination of Focal Mechanisms Obtained from First Motion P-Wave Arrivals. Geophys. J. Int. 2018, 212, 1665–1686. [Google Scholar] [CrossRef]
- Lentas, K.; Di Giacomo, D.; Harris, J.; Storchak, D.A. The ISC Bulletin as a Comprehensive Source of Earthquake Source Mechanisms. Earth Syst. Sci. Data 2019, 11, 565–578. [Google Scholar] [CrossRef]
- Xiong, X.; Shan, B.; Zhou, Y.M.; Wei, S.J.; Li, Y.D.; Wang, R.J.; Zheng, Y. Coulomb Stress Transfer and Accumulation on the Sagaing Fault, Myanmar, over the Past 110 Years and Its Implications for Seismic Hazard. Geophys. Res. Lett. 2017, 44, 4781–4789. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New Empirical Relationships among Magnitude, Rupture Length, Rupture Width, Rupture Area, and Surface Displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar] [CrossRef]
- Stein, R.S.; Toda, S.; Özbakir, A.D.; Sevilgen, V.; Gonzalez-Huizar, H.; Lotto, G.; Sevilgen, S. Interactions, Stress Changes, Mysteries, and Partial Forecasts of the 2023 Kahramanmaraş, Türkiye, Earthquakes. 2023. Available online: https://temblor.net/ (accessed on 12 May 2024).
- Zaccagnino, D.; Telesca, L.; Tan, O.; Doglioni, C. Clustering Analysis of Seismicity in the Anatolian Region with Implications for Seismic Hazard. Entropy 2023, 25, 835. [Google Scholar] [CrossRef] [PubMed]
- Alkan, H.; Büyüksaraç, A.; Bektaş, Ö.; Işık, E. Coulomb Stress Change before and after 24.01.2020 Sivrice (Elazığ) Earthquake (Mw = 6.8) on the East Anatolian Fault Zone. Arab. J. Geosci. 2021, 14, 2648. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef]

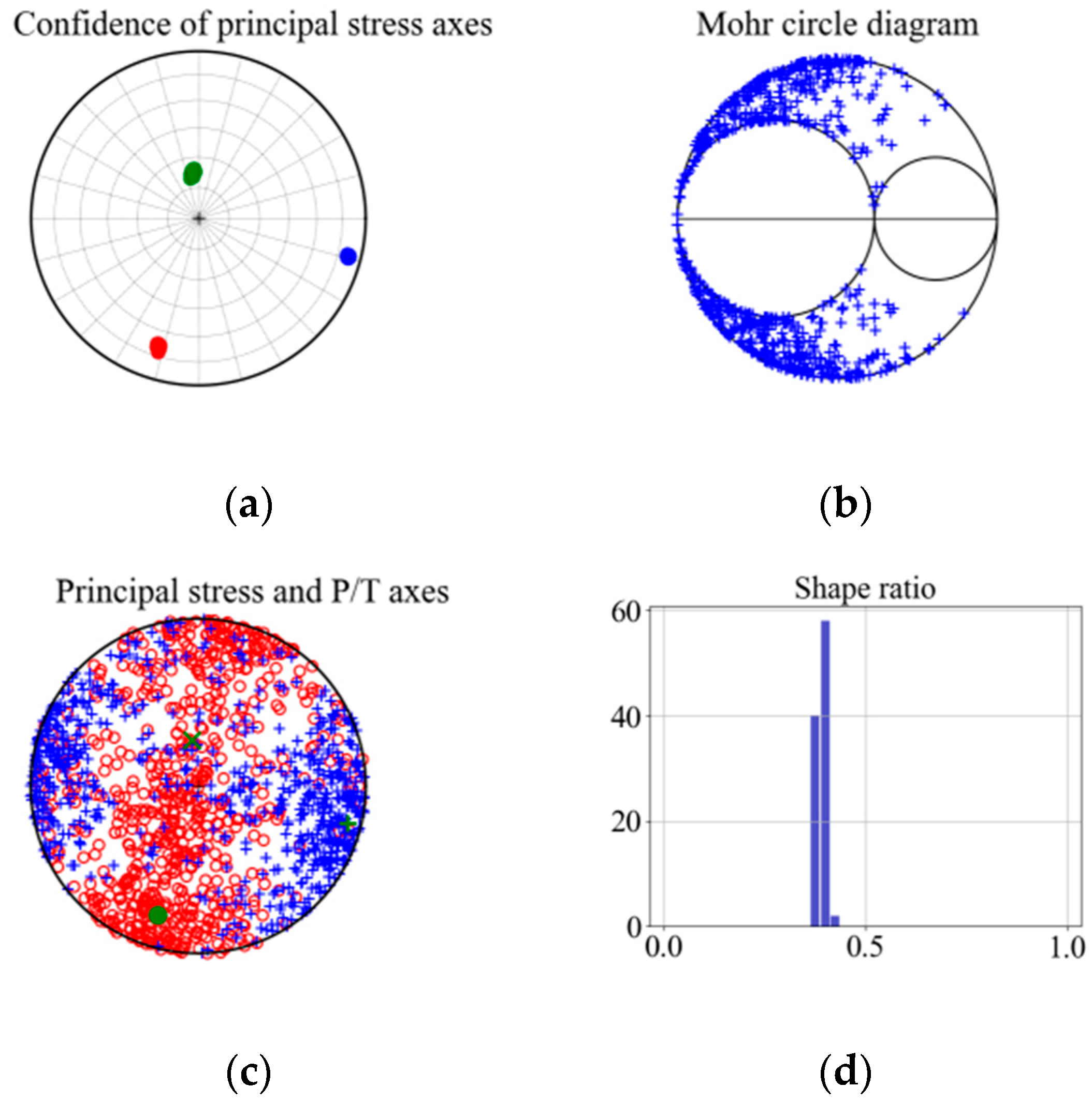


| Azimuth1 | Plung1 | Azimuth2 | Plung2 | Azimuth3 | Plung3 |
| 197.3915 | 20.51909 | 352.331 | 67.5516 | 104.1035 | 8.712759 |
| See | Sen | Seu | Snn | Snu | Suu |
| −0.646715 | −0.442439 | 0.181673 | 0.851544 | 0.236023 | −0.204829 |
| Strike1 (°) | Dip1 (°) | Rake1 (°) | Strike2 (°) | Dip2 (°) | Rake2 (°) |
| 347.600 | 88.049 | −157.630 | 221.980 | 72.523 | −14.314 |
| Date | Latitude (°N) | Longitude (°E) | Depth (km) | Magnitude (Mw) | Strike (°) | Dip (°) | Rake (°) |
|---|---|---|---|---|---|---|---|
| 05-05-1986 | 37.72 | 37.70 | 15.0 | 6.0 | 215.9670 | 81.8935 | 105.2100 |
| 27-06-1998 | 36.87 | 35.58 | 29.5 | 6.2 | 168.6750 | 53.4500 | 68.4607 |
| 01-05-2003 | 39.04 | 40.53 | 15.0 | 6.3 | 43.6277 | 35.1118 | 119.0660 |
| 24-01-2020 | 38.36 | 39.06 | 8.1 | 6.8 | 248.0000 | 76.0000 | 1.0000 |
| 06-02-2023 | 37.29 | 37.04 | 8.6 | 7.7 | 233.0000 | 74.0000 | 18.0000 |
| 06-02-2023 | 37.30 | 36.92 | 6.2 | 6.6 | 186.3580 | 42.2270 | −30.5910 |
| 06-02-2023 | 38.09 | 37.24 | 7.0 | 7.6 | 89.7601 | 84.2631 | 17.0882 |
| 20-02-2023 | 36.04 | 36.02 | 21.7 | 6.4 | 214.0000 | 57.0000 | −44.0000 |
| Year | Longitude (°E) | Latitude (°N) | Depth (km) | Magnitude (Mw) | Coulomb1 (bar) | Coulomb2 (bar) |
|---|---|---|---|---|---|---|
| Induced by earthquake 1 | ||||||
| 06-02-2023 | 37.67 | 37.83 | 0.43 | 4.6 | 0.53 | 0.33 |
| 07-02-2023 | 37.65 | 37.81 | 8.44 | 5.4 | −0.23 | 0.29 |
| Induced by earthquakes 1–2 | ||||||
| 28-06-1998 | 35.54 | 36.89 | 10.00 | 4.9 | 0.13 | −0.02 |
| 06-02-2023 | 37.67 | 37.83 | 0.43 | 4.6 | 0.53 | 0.33 |
| 06-02-2023 | 35.89 | 36.73 | 7.27 | 4.1 | 0.19 | 0.02 |
| 07-02-2023 | 37.65 | 37.81 | 8.44 | 5.4 | −0.23 | 0.29 |
| 11-03-2023 | 35.67 | 36.98 | 7.00 | 4.0 | 0.06 | 0.57 |
| Induced by earthquakes 1–3 | ||||||
| 06-02-2023 | 37.67 | 37.83 | 0.43 | 4.6 | 0.53 | 0.33 |
| 06-02-2023 | 35.89 | 36.73 | 7.27 | 4.1 | 0.19 | 0.02 |
| 07-02-2023 | 37.65 | 37.81 | 8.44 | 5.4 | −0.23 | 0.29 |
| 11-03-2023 | 35.67 | 36.98 | 7.00 | 4.0 | 0.06 | 0.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Wang, P.; Liang, W. Space–Time Stress Variations near the East Anatolian Fault Zone and the Triggering Relationship of Earthquakes. Appl. Sci. 2025, 15, 2759. https://doi.org/10.3390/app15052759
Ma J, Wang P, Liang W. Space–Time Stress Variations near the East Anatolian Fault Zone and the Triggering Relationship of Earthquakes. Applied Sciences. 2025; 15(5):2759. https://doi.org/10.3390/app15052759
Chicago/Turabian StyleMa, Ju, Peicong Wang, and Weizhang Liang. 2025. "Space–Time Stress Variations near the East Anatolian Fault Zone and the Triggering Relationship of Earthquakes" Applied Sciences 15, no. 5: 2759. https://doi.org/10.3390/app15052759
APA StyleMa, J., Wang, P., & Liang, W. (2025). Space–Time Stress Variations near the East Anatolian Fault Zone and the Triggering Relationship of Earthquakes. Applied Sciences, 15(5), 2759. https://doi.org/10.3390/app15052759








