A Status Evaluation of Rock Instability in Metal Mines Based on the SPA–IAHP–PCN Model
Abstract
Featured Application
Abstract
1. Introduction
2. Methodology
2.1. Calculation of Index Weight Value
2.2. Establishment of Five-Element Identical-Discrepancy-Contrary Model
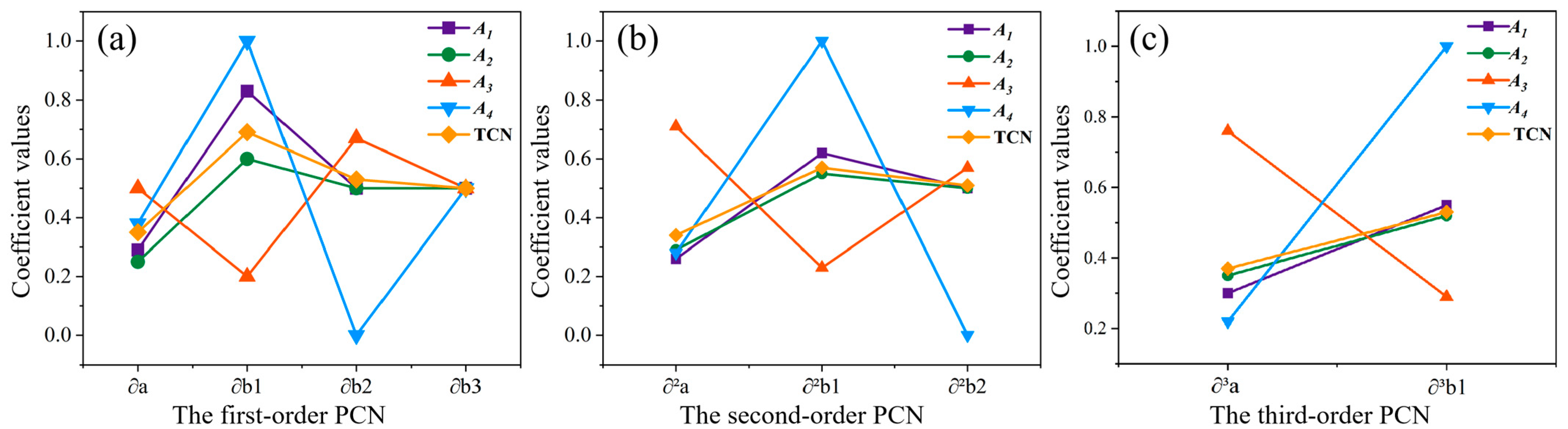
2.3. Conformation of PCN
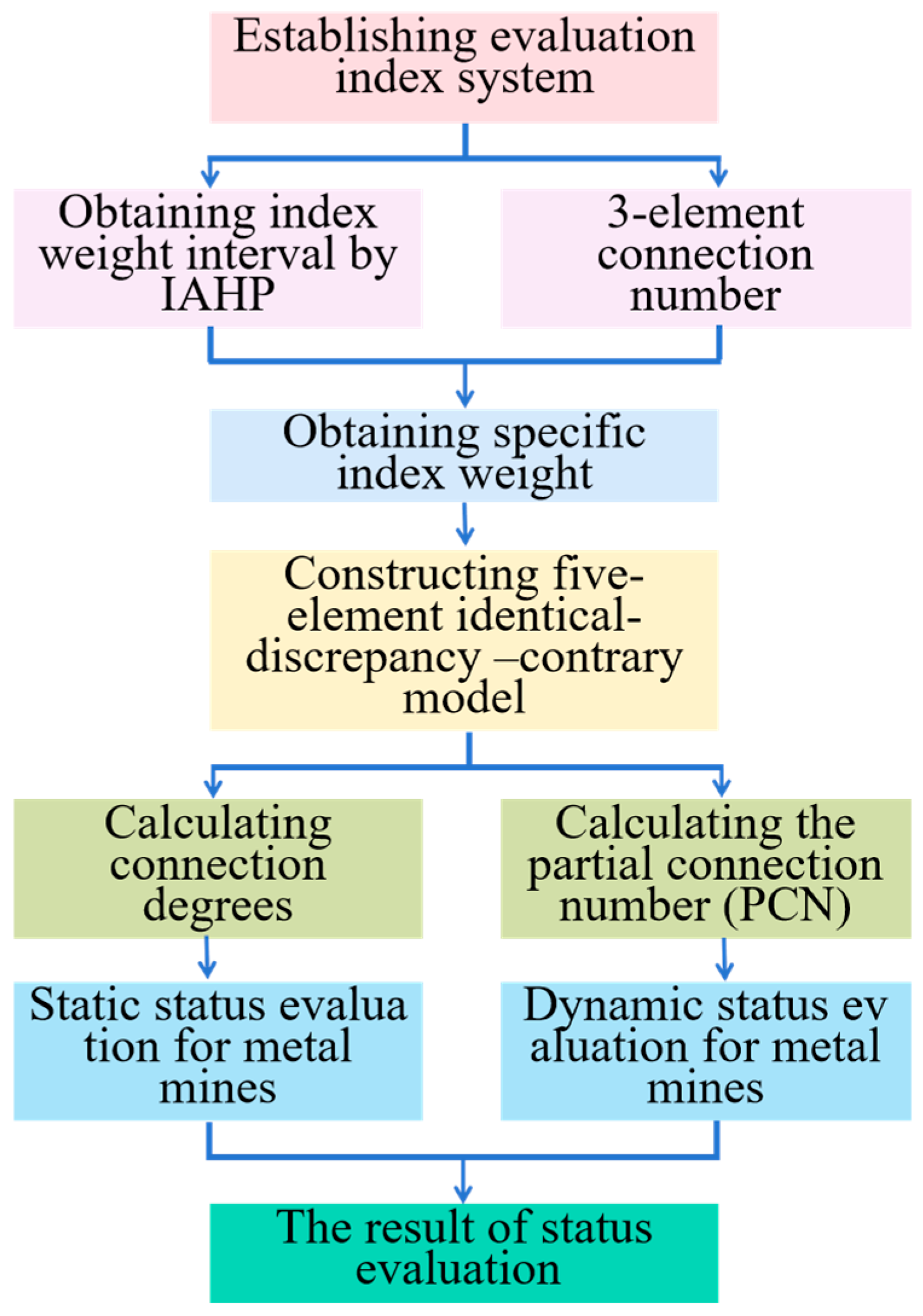
2.4. SPA–IAHP–PCN Model
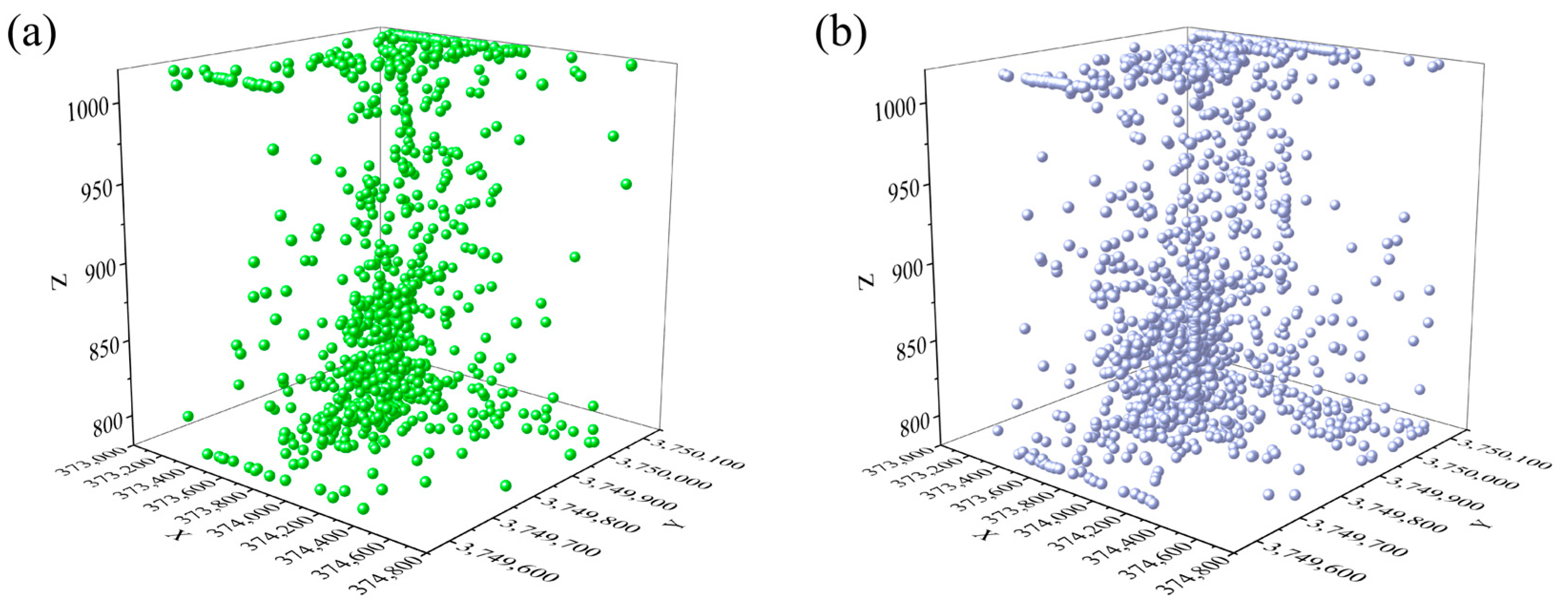
3. Case Study
4. Results and Discussion
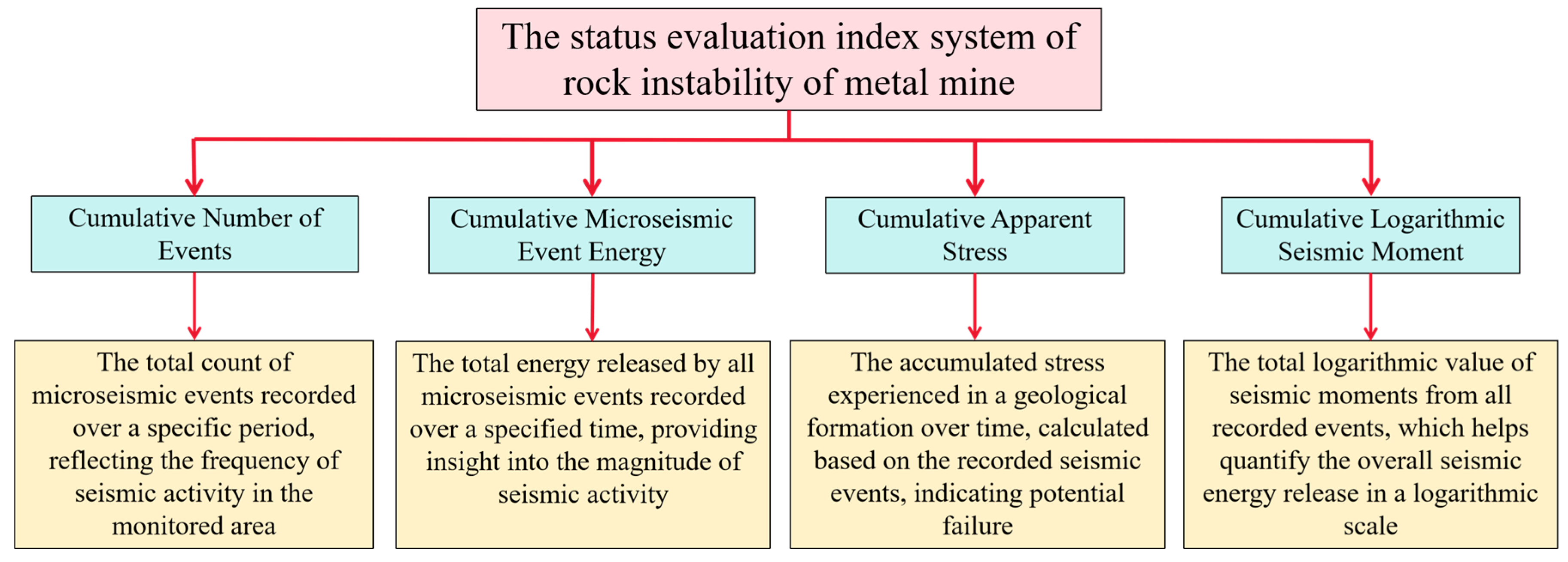
4.1. Establishment of the Status Evaluation Index
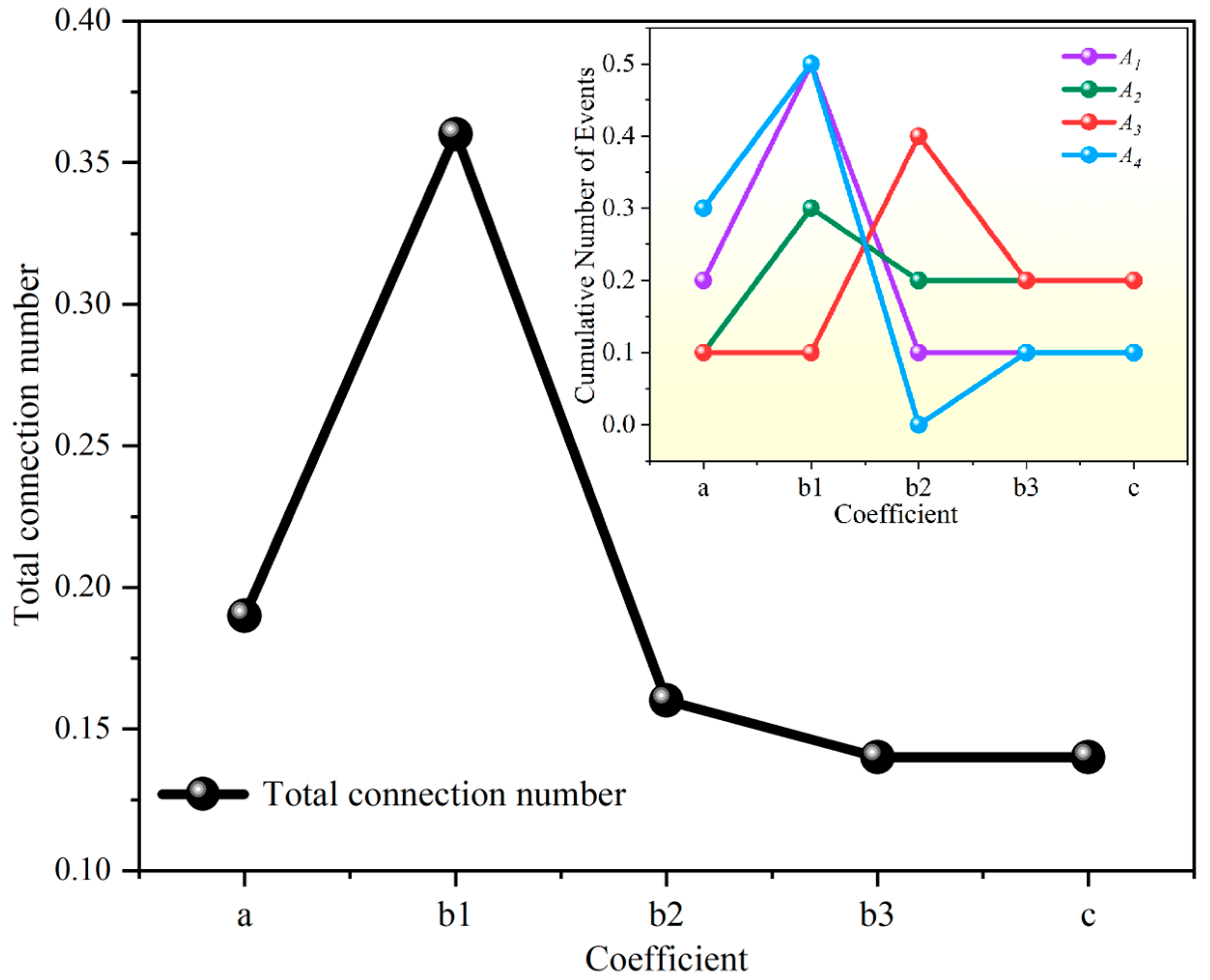
4.2. Calculation of the Weight
4.3. Construction Five-Element Connection Number Evaluation Model
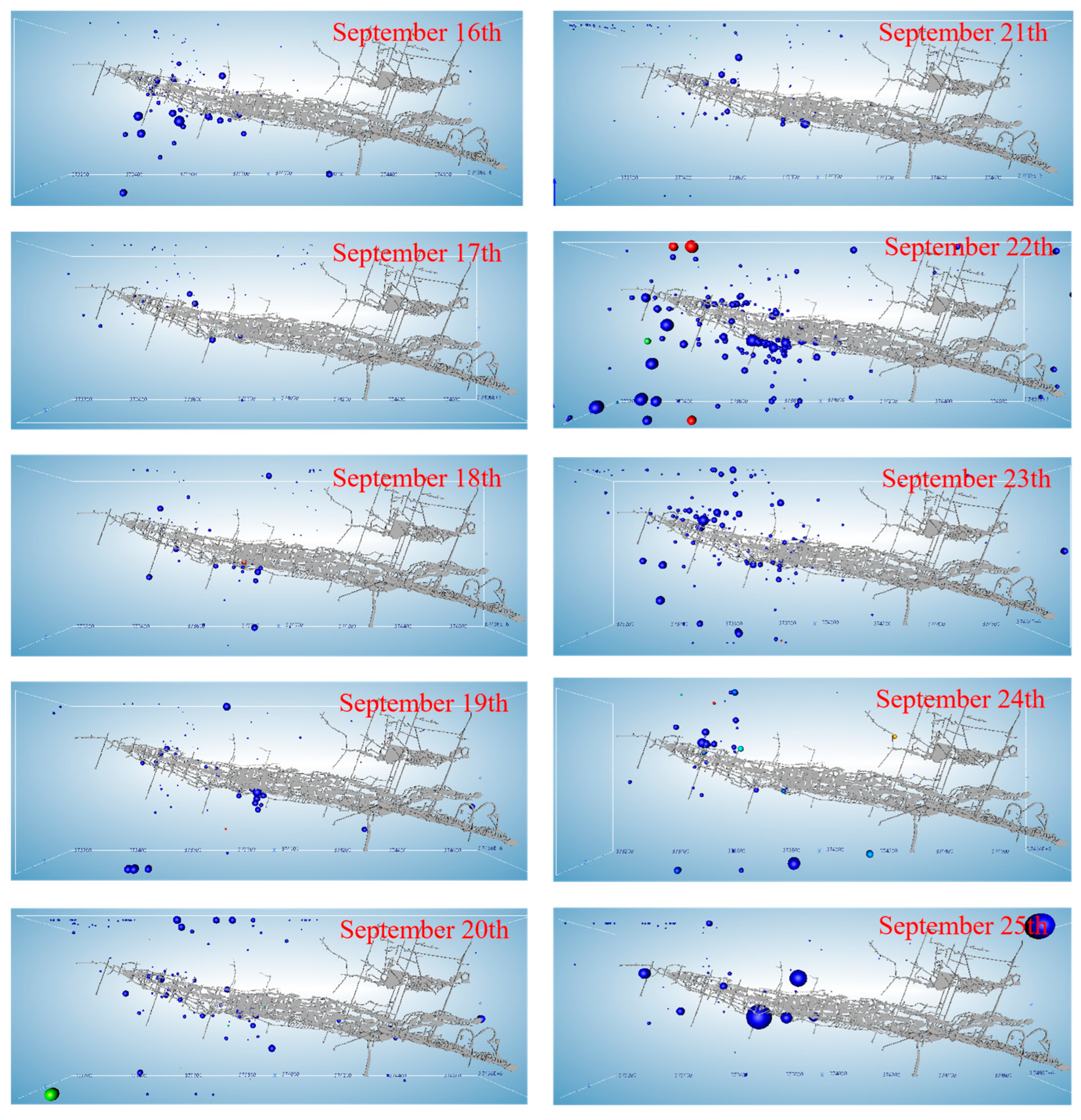
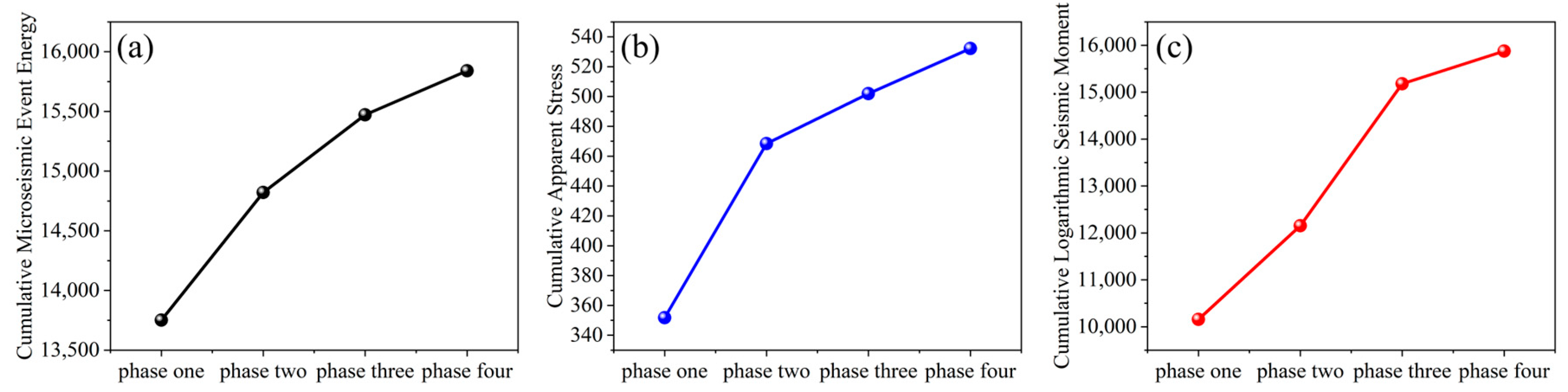
4.4. Risk Variation of Rock Instability
4.5. Verification of Risk Assessment Result
4.6. Comparison of the Evaluation Result Utilizing FCEM
4.7. Prospects and Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Prior, T.; Giurco, D.; Mudd, G.; Mason, L.; Behrisch, J. Resource depletion, peak minerals and the implications for sustainable resource management. Glob. Environ. Chang. 2012, 22, 577–587. [Google Scholar] [CrossRef]
- Biao, Y. Key design consideration for the mine engineering in the alpine and high-altitude regions. China Molybdenum Ind. 2018, 42, 11–16. [Google Scholar]
- Dong, L.J.; Yan, X.H.; Wang, J.; Tang, Z. Case study of microseismic tomography and multi-parameter characteristics under mining disturbances. J. Cent. South Univ. 2023, 30, 2252–2265. [Google Scholar] [CrossRef]
- Zuo, S.; Dai, Z.; Zhao, L.; Hu, S.; Huang, D.; Lv, G. Reliability Back Analysis of the Parameters of Rock Landslides with the Nonlinear Hoek-Brown Failure Criterion. Int. J. Geomech. 2024, 24, 06024005. [Google Scholar] [CrossRef]
- Yang, F.; Li, S.; Wu, X.; Ge, F. Accident causation analysis of metal processing plants based on questionnaire and Bayesian network. J. Saf. Sustain. 2024, 1, 247–256. [Google Scholar] [CrossRef]
- AN, S.; LONG, J. Model of Satellite System State Evaluation Based on Bayers Network. Trans. Beijing Inst. Technol. 2010, 5, 548–551. [Google Scholar]
- Sun, L.; Liu, Y.; Zhang, B.; Shang, Y.; Yuan, H.; Ma, Z. An integrated decision-making model for transformer condition assessment using game theory and modified evidence combination extended by D numbers. Energies 2016, 9, 697. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, H.; Zhang, Y.; Wei, H.; Liao, R. Grey relational analysis for insulation condition assessment of power transformers based upon conventional dielectric response measurement. Energies 2017, 10, 1526. [Google Scholar] [CrossRef]
- Guo, L.; Li, K.; Liang, Y.; Sun, L. HV circuit breaker state assessment based on gray-fuzzy comprehensive evaluation. Electr. Power Autom. Equip. 2014, 34, 161–167. [Google Scholar]
- Yang, Y.; Zhang, M.; Dai, Y. A Fuzzy Comprehensive CS-SVR Model-based health status evaluation of radar. PLoS ONE 2019, 14, e0213833. [Google Scholar] [CrossRef] [PubMed]
- Gan, L.; Zuo, J.; Wang, Y.; Low, T.S.; Wang, K. Comprehensive health condition assessment on partial sewers in a southern Chinese city based on fuzzy mathematic methods. Front. Environ. Sci. Eng. 2014, 8, 144–150. [Google Scholar] [CrossRef]
- Tian, F.; Jing, Z.; Zhao, H.; Zhang, E.; Liu, J. A synthetic condition assessment model for power transformers using the fuzzy evidence fusion method. Energies 2019, 12, 857. [Google Scholar] [CrossRef]
- Liao, R.; Meng, F.; Zhou, N. Assessment Strategy for Inner Insulation Condition of Power Transformer Based on Set-pair Analysis and Evidential Reasoning Decision-making. High Volt. Eng. 2014, 40, 474–481. [Google Scholar]
- Zhao, K.Q. Set pair and set pair analysis-a new concept and systematic analysis method. In Proceedings of the State Forum on System Theory and Regional Planning in China, Baotou, China, 4 June 1989; p. 5. [Google Scholar]
- Hu, P.; Tanchak, R.; Wang, Q. Developing risk assessment framework for wildfire in the United States–A deep learning approach to safety and sustainability. J. Saf. Sustain. 2024, 1, 26–41. [Google Scholar] [CrossRef]
- Yu, Q.; Li, W. Application of fuzzy set pair analysis model to power transformer condition assessment. J. Cent. South Univ. (Sci. Technol.) 2013, 44, 598–603. [Google Scholar]
- Zhou, Q.; Xu, Q.; Jian, L. Wind turbine operating state assessment based on fusion set pair analysis and evidence theory. Electr. Power Autom. Equip. 2017, 37, 38–45. [Google Scholar]
- Zuo, S.; Zhao, L.; Deng, D.; Wang, Z.; Zhao, Z. Reliability back analysis of landslide shear strength parameters based on a general nonlinear failure criterion. Int. J. Rock Mech. Min. Sci. 2020, 126, 104189. [Google Scholar] [CrossRef]
- Su, M.; Yang, Z.; Chen, B. Relative urban ecosystem health assessment: A method integrating comprehensive evaluation and detailed analysis. Ecohealth 2010, 7, 459–472. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, S.; Liu, Y.; Wang, X. River ecosystem assessment and application in ecological restorations: A mathematical approach based on evaluating its structure and function. Ecol. Eng. 2015, 76, 151–157. [Google Scholar] [CrossRef]
- Du, C.; Yu, J.; Zhong, H.; Wang, D. Operating mechanism and set pair analysis model of a sustainable water resources system. Front. Environ. Sci. Eng. 2015, 9, 288–297. [Google Scholar] [CrossRef]
- Su, S.; Chen, X.; DeGloria, S.D.; Wu, J. Integrative fuzzy set pair model for land ecological security assessment: A case study of Xiaolangdi Reservoir Region, China. Stoch. Environ. Res. Risk Assess. 2010, 24, 639–647. [Google Scholar] [CrossRef]
- Yan, F.; Xu, K.; Li, D.; Zhang, X. Hazard assessment for biomass gasification station using general set pair analysis. BioResources 2016, 11, 8307–8324. [Google Scholar] [CrossRef]
- Wang, M.; Xu, X.; Li, J.; Jin, J.; Shen, F. A novel model of set pair analysis coupled with extenics for evaluation of surrounding rock stability. Math. Probl. Eng. 2015, 2015, 892549. [Google Scholar] [CrossRef]
- Zou, Q.; Zhou, J.; Zhou, C.; Song, L.; Guo, J. Comprehensive flood risk assessment based on set pair analysis-variable fuzzy sets model and fuzzy AHP. Stoch. Environ. Res. Risk Assess. 2013, 27, 525–546. [Google Scholar] [CrossRef]
- Li, C.; Sun, L.; Jia, J.; Cai, Y.; Wang, X. Risk assessment of water pollution sources based on an integrated k-means clustering and set pair analysis method in the region of Shiyan, China. Sci. Total Environ. 2016, 557, 307–316. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Jing, H.; Yu, L.; Su, H.; Luo, N. Set pair analysis for risk assessment of water inrush in karst tunnels. Bull. Eng. Geol. Environ. 2017, 76, 1199–1207. [Google Scholar] [CrossRef]
- Chong, T.; Yi, S.; Heng, C. Application of set pair analysis method on occupational hazard of coal mining. Saf. Sci. 2017, 92, 10–16. [Google Scholar] [CrossRef]
- Zhao, K. Partial connection number. In Progress of Artificial Intelligence 2005; Beijing University of Posts and Telecommunications (BUPT) Publishing House: Beijing, China, 2005; pp. 882–885. [Google Scholar]
- Xie, X.; Guo, D. Human factors risk assessment and management: Process safety in engineering. Process Saf. Environ. Prot. 2018, 113, 467–482. [Google Scholar] [CrossRef]
- Su, H.; Wen, Z.; Sun, X.; Yan, X. Multisource information fusion-based approach diagnosing structural behavior of dam engineering. Struct. Control Health Monit. 2018, 25, e2073. [Google Scholar] [CrossRef]
- Xie, H.T.; Li, B.; Zhao, Y.S. Study on risk trend assessment of metro tunnel crossing underground pipeline based on partial connection number. Appl. Mech. Mater. 2014, 580, 1283–1287. [Google Scholar] [CrossRef]
- Shi, Z.J.; Wang, H.W.; Wang, X. Risk state evaluation of aviation maintenance based on multiple connection number set pair analysis. Syst. Eng. Electron. 2016, 38, 588–594. [Google Scholar]
- Li, C.; Chen, J.; Yang, S.; Zhou, H. Application of Five-element Connection Number to Comprehensive Evaluation of risks Involved with Subway Construction. China Saf. Sci. J. 2013, 23, 21–26. [Google Scholar]
- Zhao, J.; Gao, H.; Cheng, J. Research on Evolution of Participation Willingness in Network Public Opinion: Based on Three-element Connection Number. Inf. Sci. 2017, 35, 118–120. [Google Scholar]
- Wu, T. Application on the Analysis of Developmental Trend of the Student Mark with Five-Element Partial Connection Number. Math. Pract. Theory 2009, 39, 53–59. [Google Scholar]
- Ren, J. Sustainability prioritization of energy storage technologies for promoting the development of renewable energy: A novel intuitionistic fuzzy combinative distance-based assessment approach. Renew. Energy 2018, 121, 666–676. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, C. Comprehensive benefit evaluation of the power distribution network planning project based on improved IAHP and multi-level extension assessment method. Sustainability 2016, 8, 796. [Google Scholar] [CrossRef]
- Shah, S.M.T.; Ullah, A. A System Dynamics Approach to plan Strategy for managing factors influencing safety hazards on construction sites in developing countries. J. Saf. Sustain. 2024, 1, 141–150. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H. Evaluation on Cost Overrun Risks of Long-distance Water Diversion Project Based on SPA-IAHP Method. In Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 113, p. 012012. [Google Scholar]
- Su, M.R.; Yang, Z.F.; Chen, B.; Ulgiati, S. Urban ecosystem health assessment based on emergy and set pair analysis—A comparative study of typical Chinese cities. Ecol. Model. 2009, 220, 2341–2348. [Google Scholar] [CrossRef]
- Wang, W.; Jin, J.; Ding, J.; Li, Y. A new approach to water resources system assessment—Set pair analysis method. Sci. China Ser. E Technol. Sci. 2009, 52, 3017–3023. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Zhou, H.; Yuan, Y.; Liu, C.; Wu, C.; Zhang, M. Extension model for safety appraisal of existing concrete members based on an improved comprehensive weighting method. Adv. Civ. Eng. 2018, 2018, 1217543. [Google Scholar] [CrossRef]
- Yan, F.; Xu, K.; Li, D.; Cui, Z. A novel hazard assessment method for biomass gasification stations based on extended set pair analysis. PLoS ONE 2017, 12, e0185006. [Google Scholar] [CrossRef]
- Zhu, S.; Feng, Y.; Jiang, F.; Liu, J. Mechanism and risk assessment of overall-instability-induced rockbursts in deep island longwall panels. Int. J. Rock Mech. Min. Sci. 2018, 106, 342–349. [Google Scholar] [CrossRef]



| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|
| ζ | 0.9376 | 0.8266 | 0.7658 | 0.6660 | 0.6285 | 0.6381 | 0.6215 | 0.5876 |
| Index | Normalized Result | ||||
|---|---|---|---|---|---|
| 0–0.2 | 0.2–0.4 | 0.4–0.6 | 0.6–0.8 | 0.8–1 | |
| Cumulative Number of Events | I | II | III | IV | V |
| Cumulative Microseismic Event Energy | I | II | III | IV | V |
| Cumulative Apparent Stress | I | II | III | IV | V |
| Cumulative Logarithmic Seismic Moment | I | II | III | IV | V |
| Status evaluation of rock instability of metal mine | Cumulative Number of Events A1 |
| Cumulative Microseismic Event Energy A2 | |
| Cumulative Apparent Stress A3 | |
| Cumulative Logarithmic Seismic Moment A4 |
| Expert | Professional Position | Education Background | Work Experience (Year) |
|---|---|---|---|
| Expert 1 | Student | Master | 7 |
| Expert 2 | Worker | Bachelor | 16 |
| Expert 3 | Worker | Master | 14 |
| Expert 4 | Engineer | Master | 26 |
| Expert 5 | Engineer | PhD | 31 |
| Expert 6 | Engineer | Master | 37 |
| Expert 7 | Professor | PhD | 15 |
| Expert 8 | Professor | PhD | 20 |
| Expert 9 | Professor | PhD | 32 |
| Expert 10 | Professor | PhD | 44 |
| Index | Weight |
| Cumulative Number of Events (A1) | 0.1918 |
| Cumulative Microseismic Event Energy (A2) | 0.2028 |
| Cumulative Apparent Stress (A3) | 0.2467 |
| Cumulative Logarithmic Seismic Moment (A4) | 0.3587 |
| Index | Date | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| Cumulative Number of Events | II | I | II | II | III | II | V | IV | I | II |
| Cumulative Microseismic Event Energy | II | III | IV | V | V | II | IV | II | I | III |
| Cumulative Apparent Stress | IV | V | V | V | IV | IV | I | II | V | V |
| Cumulative Logarithmic Seismic Moment | III | V | IV | III | V | IV | III | III | I | II |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, F.; Li, X.; Dong, L.; Du, S.; Wang, H.; Sun, D. A Status Evaluation of Rock Instability in Metal Mines Based on the SPA–IAHP–PCN Model. Appl. Sci. 2025, 15, 2614. https://doi.org/10.3390/app15052614
Yan F, Li X, Dong L, Du S, Wang H, Sun D. A Status Evaluation of Rock Instability in Metal Mines Based on the SPA–IAHP–PCN Model. Applied Sciences. 2025; 15(5):2614. https://doi.org/10.3390/app15052614
Chicago/Turabian StyleYan, Fang, Xuan Li, Longjun Dong, Shengnan Du, Hongwei Wang, and Daoyuan Sun. 2025. "A Status Evaluation of Rock Instability in Metal Mines Based on the SPA–IAHP–PCN Model" Applied Sciences 15, no. 5: 2614. https://doi.org/10.3390/app15052614
APA StyleYan, F., Li, X., Dong, L., Du, S., Wang, H., & Sun, D. (2025). A Status Evaluation of Rock Instability in Metal Mines Based on the SPA–IAHP–PCN Model. Applied Sciences, 15(5), 2614. https://doi.org/10.3390/app15052614










