Abstract
Asphalt mastic serves as a critical binding material in hot mix asphalt mixtures, significantly influencing the performance and durability of asphalt pavements. The interaction between asphalt and mineral fillers directly affects the binding properties of the mastic. In this study, the adsorbed asphalt film thickness was used as an indicator to evaluate the interaction between asphalt and mineral fillers. A micromechanical approach was proposed to calculate this thickness, and the results were compared using the Hashin model, the Mori–Tanaka model, and the generalized self-consistent model. The results demonstrate that the adsorbed asphalt film thickness, as determined using the micromechanical approach, ranged from 0.01 to 0.37 µm. The Hashin model was found to provide the most accurate characterization of the interaction between the asphalt and the mineral fillers. The order of adsorbed asphalt film thickness was as follows: coal gangue asphalt mastic > limestone asphalt mastic > fly ash asphalt mastic. Higher concentrations of acidic SiO2 in the mineral fillers resulted in a weaker interaction between the asphalt and the fillers. When the temperature was below the softening point of the asphalt, the interaction strength decreased as frequency increased. Conversely, when the temperature exceeded the softening point, the interaction strength increased with frequency. The effect of temperature on the interaction capability was further influenced by the characteristics of the mineral fillers. The micromechanical-based method proposed in this study eliminates the dependency of the evaluation indicator on the volume fraction of mineral fillers, thereby providing a more accurate characterization of the interaction between asphalt and fillers. This approach provides a theoretical foundation to guide the design of asphalt mixtures.
1. Introduction
Asphalt pavements offer several advantages, such as enhanced driving comfort, reduced noise levels, minimal dust, and ease of maintenance. Consequently, asphalt mixtures are widely used as the primary material for highway pavement construction [1,2]. However, asphalt pavements are susceptible to various forms of distress, including cracking, loosening, and particle loss. These issues not only shorten the service life, but also pose significant challenges in achieving the designed lifespan of pavements [3,4]. Therefore, improving the performance and extending the service life of asphalt pavements has become a central focus of research.
The service life of asphalt pavements is closely related to the performance of asphalt mixtures. Asphalt mixtures are multiphase composites composed of asphalt, aggregates, and mineral fillers blended in specific proportions. The asphalt mastic, consisting of asphalt and mineral fillers, serves as a binder in asphalt mixtures. Previous studies have identified asphalt mastic as the most vulnerable component in asphalt mixtures [5]. The properties of asphalt mastic significantly influence the high-temperature stability, low-temperature crack resistance, and water resistance of asphalt mixtures [6,7]. The performance of asphalt mastic is primarily determined by the interaction between asphalt and mineral filler. Therefore, the characterization of the interactions between asphalt and mineral fillers, along with the exploration of their influencing factors, is critical for enhancing the performance of asphalt mastic.
The rheological properties of asphalt mastic are significantly influenced by the addition of mineral fillers. Early studies assessed the effects of mineral fillers on asphalt properties using indicators such as softening point, penetration, ductility, and viscosity. While these methods provide a clear understanding of how mineral fillers affect asphalt properties, they do not adequately characterize or evaluate the interaction between asphalt and mineral filler [8,9]. In recent years, the assessment of this interaction has increasingly relied on a series of interaction indices based on rheological properties, which are primarily categorized into three types.
Phase-Angle-Based Indices: The Luis Ibrarra-A index evaluates the interaction between asphalt and mineral fillers by measuring energy dissipation at the interface through the loss factor (tanδ) [10]. Ziegel et al. proposed that mineral filler adsorbs free asphalt, forming an interfacial layer that enhances its effective volume fraction. The Ziegel-B index quantifies this interaction by adjusting the filler volume fraction based on the phase angle [11].
Viscosity-Based Indices: Einstein’s model describes a linear relationship between spherical particle volume fraction and solution viscosity, applicable only for fractions below 0.1 and neglecting particle–solution interactions [12]. Chong et al. developed a semi-empirical viscosity equation that incorporates interaction effects [13]. Tan et al. introduced the composite viscosity coefficient Δη*, which reflects asphalt–filler interactions but is also influenced by filler particle size and shape [14].
Complex Shear-Modulus-Based Indices: Tan et al. proposed the complex shear modulus coefficient ΔG* to characterize asphalt–filler interactions [15]. Ziegel and Romanov further developed a coefficient, denoted as C, to assess the interaction between asphalt and mineral fillers. This coefficient is referred to as the Palierne-C index [11].
Tan et al. concluded that the Ziegel-B index is more sensitive and physically significant than the Luis Ibrarra-A, ΔG*, and Δη* indices [14]. Liu et al. found that ΔG* and the Palierne-C index better reflect interaction capability than the Einstein coefficient but show lower sensitivity to changes in asphalt properties [16]. Guo’s analysis indicated that all three indices are influenced by filler volume fraction, with the Palierne-C index exhibiting the least dependence [17].
From the above analysis, it is clear that the applicability of interaction evaluation methods based on rheological properties varies under different conditions. Moreover, these methods also exhibit dependence on the volume fraction of the mineral filler. Guo analyzed the variations in three indicators—Luis Ibrarra-A, Ziegel-B, and Palierne-C—relative to the volume fraction of mineral filler. The results indicated that all three indicators are influenced by the volume fraction of mineral filler, with the Palierne-C index showing the least dependence [17]. Since these interaction indicators are calculated at a single volume fraction of mineral filler, this dependency affects the accuracy of the interaction evaluation.
In addition to rheology-based evaluation indices, relevant standards have also established parameters for assessing the interaction between bitumen and mineral fillers, such as the Bitumen Capacity Index (BCI). The BCI is a key parameter for quantifying the interaction between bitumen and mineral fillers, as defined in the European Standard EN 13179-2 [18]. The calculation of BCI typically involves determining the bitumen adsorption, viscosity, and specific surface area of the filler, as well as its chemical reactivity. However, these standard methods have certain limitations. They require multiple steps and sophisticated equipment, which can be time-consuming and resource-intensive [19]. Moreover, these methods primarily focus on adsorption and chemical reactivity but may not completely capture the full range of physical and mechanical interactions between bitumen and fillers under operational conditions.
According to the research of L.A. Repin on the interaction between asphalt and mineral filler, physicochemical interactions occur between asphalt and mineral filler during high-temperature mixing. Asphalt undergoes a rearrangement of its chemical components on the surface of the mineral filler, forming a structural asphalt layer [20]. The thickness of this layer is referred to as the adsorbed asphalt film thickness. The thickness of the adsorbed asphalt film is directly proportional to the intensity of the physicochemical interaction between the asphalt and the mineral filler. Therefore, compared to rheological property-based evaluation indicators, the adsorbed asphalt film thickness provides a more accurate representation of the interaction capability between asphalt and mineral fillers.
To measure the thickness of the adsorbed asphalt film on mineral filler, Tan et al. employed Differential Scanning Calorimetry (DSC) to determine the glass transition temperature of asphalt mastic. The thickness of the adsorbed asphalt film was calculated based on changes in specific heat capacity during the glass transition process. Using this method, the calculated thickness ranged from 0.02 to 5.28 nm [20]. However, DSC is typically applicable to homogeneous materials, where thermal properties such as specific heat capacity and thermal conductivity are uniform throughout the sample. For asphalt mastic, which is a heterogeneous material, the results obtained from DSC may not accurately reflect the true thermal behavior of the material. Wide-Angle X-ray Diffraction (WAXD) offers several advantages over DSC for analyzing the crystalline structure of asphalt mastic. WAXD can directly observe the presence and arrangement of crystalline domains, providing detailed information on the crystalline phases and molecular orientation within the material. This technique is particularly suitable for heterogeneous materials like asphalt mastic, as it can provide spatially resolved information on the crystalline structure. Recent studies, such as the work by Pipintakos et al. [21], have demonstrated the feasibility of using WAXD to characterize the crystalline structure and its changes under different conditions, suggesting that WAXD could be a valuable tool for measuring the adsorbed asphalt film thickness.
Guo et al. utilized toluene to sequentially elute and separate free asphalt from structural asphalt, subsequently calculating the adsorbed asphalt film thickness, which was approximately 1 μm. However, the accuracy of these results may be influenced by the complexity of the elution experiments and measurement errors [22,23]. Therefore, precise determination of the adsorbed asphalt film thickness necessitates further in-depth research.
The road performance of asphalt mixtures is primarily influenced by the properties of the asphalt mastic, which result from the interactions between the asphalt and the mineral filler. However, the interactions between asphalt and mineral filler within the mastic, as well as the reinforcement mechanisms of the mineral filler, remain subjects that require further investigation. The micromechanics of composite materials provides an effective approach for studying the interaction mechanisms among the various components of asphalt mastic [24,25].
Numerous scholars have extensively studied micromechanics models, including the Hashin model [26], the Mori–Tanaka (MT) model [27], the Generalized Self-Consistent (GSC) model [28], the Differential Scheme (DS) model [29], and the Periodic Structure (PS) model [30]. Among these, the Hashin model, the Mori–Tanaka (MT) model, and the generalized self-consistent (GSC) model are the most widely applied and foundational. The Hashin model is primarily designed for two-phase and multiphase heterogeneous materials [31], assuming that spherical inclusions are uniformly distributed in an isotropic homogeneous matrix, with no interaction between inclusion particles. It uses linear elastic variational principles to derive expressions for the elastic modulus, offering a concise formula with clear physical significance. The Mori–Tanaka model assumes that ellipsoidal inclusions of varying sizes are randomly distributed in the matrix and calculates the average stress within the matrix. This model effectively addresses the key theoretical challenges associated with applying Eshelby’s equivalent inclusion principle under finite volume fraction conditions [32]. The generalized self-consistent model assumes spherical inclusions surrounded by a matrix shell embedded in an effectively infinite medium. In this model, the volume fraction of inclusions in the composite material is defined as the ratio of the inclusion to the matrix shell. Christensen and Lo proposed a three-phase generalized self-consistent inclusion model [28], and Shashidhar and Shenoy simplified the complex equations of the generalized self-consistent model through data analysis, providing a theoretical foundation for the use of micromechanics models in predicting the properties of asphalt mastic [31].
The reinforcement mechanisms of mineral filler in asphalt mastic mainly include volumetric filling reinforcement, physicochemical interaction reinforcement, and interparticle interaction reinforcement. Buttlar et al. proposed that micromechanics models can be employed to distinguish these three reinforcement mechanisms in asphalt mastic [33]. Shashidhar and Shenoy investigated the capability of the generalized self-consistent (GSC) model in predicting the dynamic mechanical behavior of asphalt mastic with mineral filler volume fractions of up to 31% [31]. The study found that the GSC model underestimates the effective shear modulus, primarily due to its incomplete representation of the volumetric reinforcement effect of mineral filler. Aigner et al. used BBR (Bending Beam Rheometer) and DSR (Dynamic Shear Rheometer) tests to determine the viscoelastic properties of asphalt. They proposed a multiscale model based on the Mori–Tanaka model to predict the viscoelastic behavior of asphalt mastic and examined the effects of voids and aggregates [33]. Kim conducted experiments on four different materials at mineral filler volume fractions of 5%, 10%, and 25%. The experimental results were compared with predictions from the Hashin model and the generalized self-consistent model. The study found that the predictions aligned more closely with the experimental results at lower mineral filler volume fractions, suggesting that interparticle and physicochemical interactions enhance the performance of asphalt–aggregate mixtures [34]. Underwood evaluated and compared 12 existing micromechanics models. Based on the limitations of these models, a new micromechanics model was proposed, incorporating physicochemical interactions. The results showed that this new model provides accurate predictions for asphalt mastic with mineral filler volume fractions of up to 40% [35].
In recent years, micromechanics models have been increasingly applied to calculate the thickness of adsorbed asphalt films. Buttlar et al. proposed a micromechanics-based method for determining the thickness of adsorbed asphalt films while investigating the generalized self-consistent (GSC) model’s ability to predict the mechanical properties of asphalt mastic. Using this method, the calculated thickness ranged from 0.02 to 0.1 μm [33]. Li et al. employed the Hashin model to calculate the thickness of the adsorbed asphalt films and evaluated the physicochemical interactions between asphalt and mineral filler based on the derived film thickness [36,37]. Utilizing micromechanics methods to calculate the thickness of adsorbed asphalt films effectively mitigates the influence of experimental and measurement errors, thereby improving the accuracy of the results. However, existing studies have predominantly relied on a single micromechanics model for these calculations. Further research is needed to assess the applicability of various micromechanics models for calculating the thickness of adsorbed asphalt films and to analyze the factors that influence this thickness in greater detail.
The research objectives of this paper are as follows:
- (1)
- To calculate the thickness of the adsorbed asphalt film using the Hashin, Mori–Tanaka (MT), and generalized self-consistent (GSC) models, and to perform a comparative analysis of the values obtained from these models to identify the most appropriate one.
- (2)
- To determine the critical volume fraction of mineral fillers using nonlinear fitting, and to refine the interaction evaluation indices based on micromechanical models, removing their dependence on the volume fraction of mineral fillers.
- (3)
- To analyze the influence of the chemical composition, testing frequency, and temperature of mineral fillers on the interaction between asphalt and mineral fillers through a micromechanical approach.
2. Calculation of Adsorbed Asphalt Film Thickness Based on Micromechanical Model
2.1. Hashin Model
The Hashin model, based on the variational principle of linear elasticity, utilizes an approximate approach to derive the elastic modulus expression for two-phase or multiphase heterogeneous materials. This model assumes that inclusions are spherical and uniformly distributed within an isotropic, homogeneous matrix, with no interaction between the inclusion particles. This configuration is illustrated schematically in Figure 1.
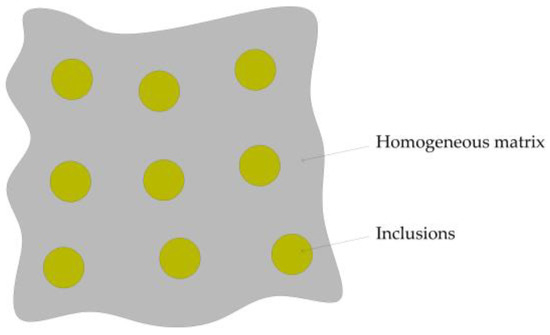
Figure 1.
Schematic diagram of the Hashin model.
The effective shear modulus of the model is calculated using Equation (1):
where Gc represents the complex shear modulus of the asphalt mastic, Gm is the complex shear modulus of the asphalt, Gf is the complex shear modulus of the mineral filler, and νm denotes the Poisson’s ratio of the asphalt. When rigid mineral filler particles are dispersed in a viscoelastic medium, it is reasonable to assume that Gf ≫ Gm, implying that Gm/Gf ≫ 1 [31]. Under this assumption, Equation (1) can be simplified to Equation (2):
By substituting the experimental value of Gc/Gm into Equation (2), the effective volume fraction of the mineral filler (ϕeff) can be determined, as expressed in Equation (3):
Buttlar et al. [33] proposed a micromechanical approach to calculate the thickness of the adsorbed asphalt film, as shown in Equation (4):
where d represents the adsorbed asphalt film thickness, ϕeff is the effective volume fraction of the mineral filler, ϕf is the volume fraction of the mineral filler, Gs is the apparent density of the mineral filler, and S is the specific surface area of the mineral filler. By incorporating ϕeff into Equation (4), the thickness of the adsorbed asphalt film based on the Hashin model can be accurately determined.
2.2. Mori–Tanaka Model
In 1973, Mori and Tanaka resolved the fundamental theoretical issues associated with the application of Eshelby’s equivalent inclusion principle in finite volume fractions by calculating the average stress within the matrix. Since then, the Mori–Tanaka model has been extensively employed to predict the effective properties of various composite materials [32]. This model assumes that the inclusions are ellipsoidal particles with random orientations and varying sizes, as illustrated in Figure 2.
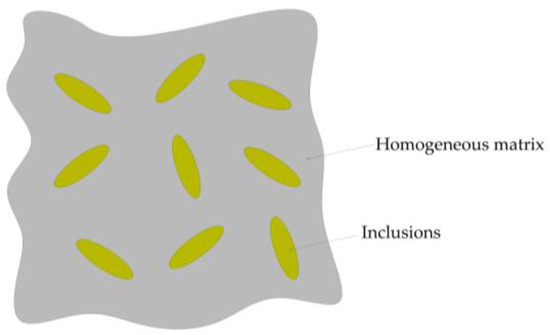
Figure 2.
Schematic diagram of the Mori–Tanaka model.
When applying the Mori–Tanaka model to predict the effective shear modulus of asphalt mastic, Underwood et al. derived the following formula [35]:
Considering the mineral filler particles as rigid inclusions, i.e., Gf/Gm ≫ 1 [33], Equation (5) can be simplified to
By substituting the experimental value of Gc/Gm into Equation (6), the effective volume fraction of the mineral filler (ϕeff) can be determined as follows:
The thickness of the adsorbed asphalt film based on the Mori–Tanaka model can be calculated by incorporating ϕeff into Equation (4).
2.3. The Generalized Self-Consistent Model
Christensen et al. proposed the generalized self-consistent (GSC) model, which is a three-phase model comprising inclusions, a matrix shell, and an effective medium. In this model, the proportion of inclusions and the matrix shell correspond precisely to the volume fraction of inclusions in the composite material [28], as illustrated in Figure 3.
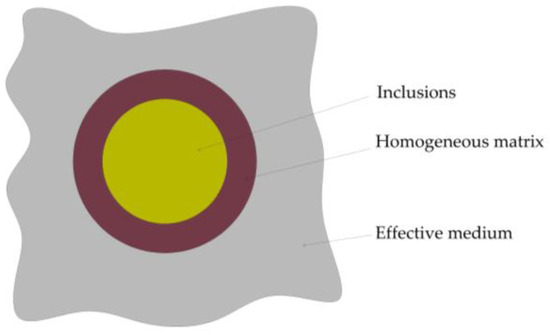
Figure 3.
Schematic diagram of the generalized self-consistent model.
The effective shear modulus of the composite material is given by
where A, B, and C are complex functions related to the ratio of the shear moduli of the mineral filler and asphalt (Gm/Gf).
Shashidhar et al. simplified the generalized self-consistent model for application in asphalt mastic by considering the condition Gf ≫ Gm [33]. This simplification resulted in a micromechanical prediction model for the shear modulus of asphalt mastic, expressed as
with the following parameters:
where νm denotes the Poisson’s ratio of the asphalt.
The effective volume fraction of the mineral filler (ϕeff) can be determined by substituting the measured value of Gc/Gm into Equations (9) and (10). Using the obtained ϕeff, the thickness of the adsorbed asphalt film based on the generalized self-consistent model can then be accurately calculated through Equation (4).
3. Experimental Methods and Model Parameters
3.1. Experimental Methods
The asphalt used in this study is Liaohe 90# base asphalt, sourced from Panjin, Liaoning Province, China. The basic properties of the asphalt are summarized in Table 1.

Table 1.
Basic properties of asphalt.
Three types of mineral fillers were selected for this study: limestone filler, fly ash, and coal gangue filler. Natural limestone was sourced from Zhengzhou, Henan, China, while fly ash was obtained from the Zhengzhou Power Plant, and coal gangue filler was derived from crushed unburned coal gangue from the Zhengzhou Coal Mine. The appearance of these fillers is shown in Figure 4. The specific surface area of the three fillers was measured using the Brunauer–Emmett–Teller Surface Area Analyzer (Autosorb-iQ, Quantachrome Instruments, Boynton Beach, FL, USA). The basic properties of the fillers are presented in Table 2.

Figure 4.
Pile appearance of different fillers: (a) limestone filler; (b) fly ash; (c) coal gangue filler.

Table 2.
Basic properties of fillers.
A laser particle size analyzer was employed to sequentially test the three types of mineral powders. The average of three measurements was taken to plot the particle size distribution curves, as shown in Figure 5. The results indicate that among the three types of mineral powders, the fly ash powder exhibits the finest particle size, with 90% of the particles having a diameter below 26.942 μm. The particle sizes of the three mineral powders, in ascending order, are as follows: fly ash < limestone filler < coal gangue filler.
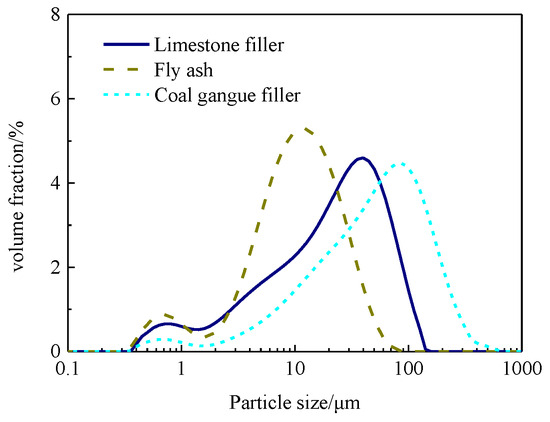
Figure 5.
Particle size distribution of different types of mineral fillers.
Three types of fillers were selected and mixed with 90# base asphalt to prepare the asphalt mastics. The filler-to-binder (F/B) ratios were set at 0.4, 0.8, 1.2, 1.6, and 2.0. The resulting mastics were designated as limestone asphalt mastic (LAM), fly ash asphalt mastic (FAM), and coal gangue asphalt mastic (CAM). The preparation process of the asphalt mastic was as follows: The fillers were first dried in an oven at 165 °C for 2 h to remove any residual moisture. Subsequently, the dried fillers were cooled to room temperature in a desiccator to ensure thermal stability prior to mixing. Meanwhile, the base asphalt was heated to 140 °C to achieve optimal fluidity for uniform mixing. After weighing the fillers and asphalt according to the predetermined filler-to-binder ratios, the components were mixed in a preheated iron pan to ensure thorough dispersion and adhesion between the fillers and asphalt binder. The mixture was then stirred with an electric stirrer at a speed of 300 RPM and a temperature of 150 °C for 15 min, until homogeneity was achieved and no air bubbles were present on the surface of the asphalt mastic.
A Bohlin Gemini rheometer was utilized to conduct temperature–frequency scanning tests on the asphalt and asphalt mastic samples to measure their complex shear modulus values. An 8 mm diameter parallel plate was used, with a sample thickness of 2 mm. The loading rate ranged from 0.628 to 125.7 rad/s, corresponding to frequencies from 0.1 to 20 Hz. The tests were performed at temperatures of 28 °C, 40 °C, and 52 °C, with a loading strain of 0.1%.
3.2. Model Parameters
In the micromechanical model, the complex shear modulus of both the asphalt and asphalt mastic was determined through Dynamic Shear Rheometer (DSR) tests. The volume fraction of filler in the asphalt mastic was calculated based on the filler-to-binder (F/B) ratio, with the results presented in Table 3.

Table 3.
Volume fraction of different fillers in asphalt mastic.
Di Benedetto et al. observed that the Poisson’s ratio of asphalt varies slightly with frequency. The range is reported as 0.48–0.5 [38]. For the purpose of simplification, this study assumes a constant Poisson’s ratio of 0.49, disregarding minor frequency-dependent variations.
3.3. Critical Volume Fraction of Mineral Filler in Asphalt Mastic
To investigate the interaction mechanism between asphalt and mineral filler, Faheem and Bahia classified the variation in the complex shear modulus (G*) of asphalt mastic with the volume fraction of mineral filler into two distinct regions: the “dilution zone” and the “aggregation zone” [39]. In the dilution zone, where the volume fraction of mineral filler is relatively low, asphalt can completely encapsulate the mineral filler particles, preventing any contact between them. The reinforcement effect of the mineral filler in this region primarily results from the volumetric filling effect and the physicochemical interactions between the mineral filler and asphalt. As the volume fraction of mineral filler increases to a specific threshold, the particles, although still largely encapsulated by asphalt, begin to make contact with each other. At this point, a network structure starts to form among the particles, and the corresponding volume fraction is defined as the critical volume fraction. In the aggregation zone, when the mineral filler volume fraction exceeds the critical value, clustering of the mineral filler particles occurs. Asphalt can no longer fully encapsulate the particles, and significant interactions between the particles take place. Therefore, accurately determining the critical volume fraction of mineral filler is crucial. Additionally, when studying the interaction between asphalt and mineral filler, the mineral filler volume fraction should be maintained within the critical volume fraction range.
To accurately calculate the critical volume fraction of mineral filler and establish the research range for the interaction between asphalt and mineral filler, this study employed the asphalt mastic model proposed by Faheem and Bahia [39]. This model predicts the hardening effect of mineral filler on asphalt based on the intrinsic properties of asphalt and filler. The governing equations of the model are expressed as follows:
where Gr is the shear modulus ratio of asphalt mastic to asphalt (dimensionless); Gc is the complex shear modulus of asphalt mastic (kPa); Gm is the complex shear modulus of asphalt (kPa); ϕ is the volume fraction of mineral filler (%); ϕc is the critical volume fraction of mineral filler (%); and G1, G2, a1, and a2 are fitting parameters (dimensionless).
Equations (11) and (12) served as the fitting functions for determining the critical volume fraction of mineral filler. Nonlinear fitting was performed on the experimental data of the shear modulus ratio of the asphalt mastic at various mineral filler volume fractions. The fitting results, along with the goodness of fit, are presented in Table 4.

Table 4.
Fitting results and goodness of fit for critical volume fraction of filler.
As shown in Table 4, the critical volume fraction (ϕc) of mineral filler in different types of asphalt mastic ranges from 30% to 45%, aligning well with findings from previous studies [40]. This consistency validates the reliability of the results obtained through the fitting process using Equations (11) and (12).
Specifically, the critical volume fractions for limestone asphalt mastic, fly ash asphalt mastic, and coal gangue asphalt mastic are 30.65%, 44.96%, and 41.15%, respectively. To minimize the influence of interactions between mineral filler particles on the analysis, subsequent investigations into the interaction mechanisms between asphalt and mineral filler should be restricted to the critical volume fraction ranges identified above.
4. Results and Discussion
4.1. Dynamic Shear Rheometer (DSR) Test Results
The variation in the complex shear modulus (|G∗|) with frequency is illustrated in Figure 6. The incorporation of mineral fillers significantly enhances the complex shear modulus of the matrix asphalt, thereby improving the high-temperature performance of the asphalt mastic. Moreover, as the filler-to-binder (F/B) ratio increases, the complex shear modulus exhibits a corresponding rise, consistent with the fundamental principles governing the reinforcing effect of mineral fillers on asphalt.
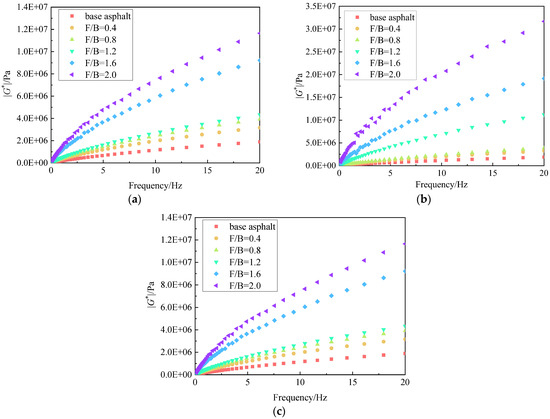
Figure 6.
Complex shear modulus of asphalt mastic and base asphalt: (a) LAM; (b) FAM; (c) CAM.
4.2. Comparative Analysis of Adsorbed Asphalt Film Thickness Based on Different Micromechanical Models
The adsorbed asphalt film thickness was calculated using three micromechanical models to enable a comparative evaluation. The calculations were derived from Dynamic Shear Rheometer (DSR) test data. For consistency in the analysis, the film thickness was determined under controlled conditions at a temperature of 28 °C and a frequency of 5 Hz, while the effects of temperature and frequency variations were excluded. The results are presented in Figure 7.
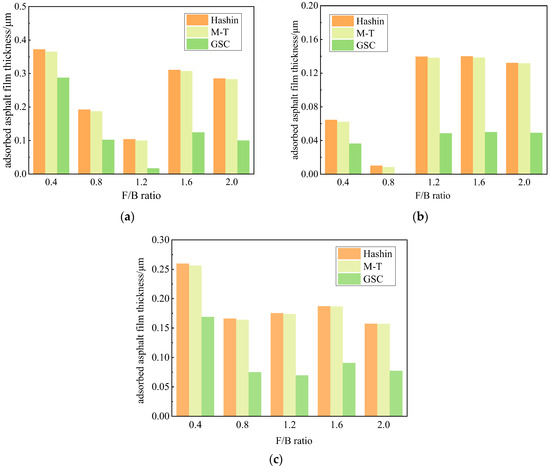
Figure 7.
Adsorbed asphalt film thickness based on different micromechanical models: (a) LAM; (b) FAM; (c) CAM.
As illustrated in Figure 7, the thickness of the adsorbed asphalt film between the asphalt and mineral filler ranges from 0.01 to 0.45 μm. The film thickness, calculated using the three micromechanical models, exhibits a similar trend with the filler-to-binder (F/B) ratio: initially decreasing and then increasing as the F/B ratio increases. This behavior is attributed to the reduction in asphalt content as the volume fraction of mineral filler rises, resulting in a thinner adsorbed film. When the mineral filler volume fraction exceeds the critical value, particle interactions become significant, resulting in a rapid increase in the shear modulus of the asphalt mastic and, consequently, an increase in the calculated film thickness.
As shown in Figure 7b, the GSC model predicts a negative film thickness for FAM when the F/B ratio is 0.8. To investigate the cause of this discrepancy, the experimental Gc/Gm values for various asphalt mastics were compared with the predictions of micromechanical models, as illustrated in Figure 8.
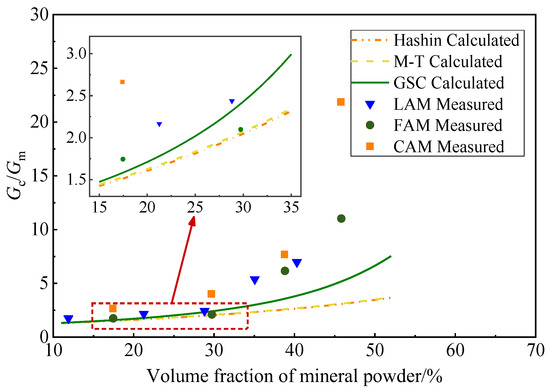
Figure 8.
Comparison between measured value and calculated value of Gc/Gm for different mastics.
Figure 8 indicates that for FAM with a mineral filler volume fraction of 29.73%, the experimental Gc/Gm value is lower than the GSC model’s prediction. At this stage, the effective volume fraction (ϕeff) calculated using the GSC model is lower than the filler volume fraction (ϕf), resulting in the negative value observed in Figure 7b. Therefore, within a certain range of mineral filler content, the accuracy of the adsorbed asphalt film thickness predicted by the GSC model requires further validation.
The micromechanical models employed in this study—namely, the Hashin model, Mori–Tanaka model, and generalized self-consistent (GSC) model—provide valuable insights into the interaction between asphalt and mineral fillers. However, these models are based on certain assumptions that may not fully account for the complexities of the actual internal structure of asphalt mastic. For instance, asphalt mastic may contain internal voids, and the interface between the mineral filler and asphalt may not always be perfectly bonded [24,25]. These factors are not explicitly considered in the models, leading to potential discrepancies between the model predictions and the actual internal structure of asphalt mastic. It should be noted that this limitation is not unique to these models; experimental methods for measuring the adsorbed asphalt film thickness also have inherent sources of error [15,17]. Achieving a completely accurate measurement of the adsorbed asphalt film thickness remains a challenge at the current stage of technology and requires further in-depth research. The trends in the adsorbed asphalt film thickness are analyzed through the application of these micromechanical models, rather than focusing on the absolute accuracy of the predictions. This approach enables meaningful conclusions to be drawn regarding relative interaction strengths, which are crucial for understanding the performance of asphalt mastics.
Figure 9 presents a comparison of film thickness predictions from three micromechanical models. It illustrates the relationship between the effective volume fraction of the mineral filler and the experimental Gc/Gm value. To eliminate the influence of factors such as mineral filler type, volume fraction, and temperature, the experimental Gc/Gm value for LAM with a mineral filler volume fraction of 11.89% at 28 °C was selected. In Figure 9, ϕ1, ϕ2, and ϕ3 denote the differences between the effective volume fraction (ϕeff) and the filler volume fraction (ϕf) as predicted by the Hashin model, Mori–Tanaka model, and GSC model, respectively, for arbitrary experimental Gc/Gm values. According to Equation (4), for asphalt mastics with the same filler volume fraction, film thickness is determined by the difference between ϕeff and ϕf. Thus, ϕ1, ϕ2, and ϕ3 serve as indicators of film thickness trends predicted by the three micromechanical models.
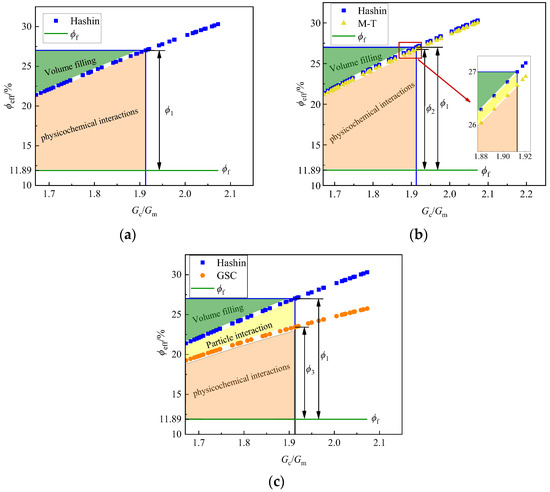
Figure 9.
Relationship between the effective volume fraction of mineral filler and the experimental Gc/Gm value for three micromechanical models: (a) Hashin model only; (b) Hashin and Mori–Tanaka (M-T) models; (c) Hashin and GSC models.
Within the critical volume fraction range of mineral filler defined in Section 3.3, before particles establish a contact network, their reinforcement effect on asphalt primarily results from volumetric filling and physicochemical interactions, without direct particle contact. The Hashin model captures the volumetric filling effect, whereas the Mori–Tanaka and GSC models incorporate inter-particle interactions to varying extents. The Mori–Tanaka model accounts for inter-particle interactions less comprehensively.
In Figure 9, shaded areas of varying intensity represent the magnitudes of volumetric filling enhancement and inter-particle interaction enhancement. The physicochemical interaction capability between mineral filler and asphalt is reflected in the thickness of the adsorbed asphalt film, which depends on the difference between ϕeff and ϕf. The lower shaded area (marked in the figure) represents the enhancement due to physicochemical interactions. The enlarged view of the Hashin and Mori–Tanaka model curves in Figure 9b shows that, compared to the Hashin model, the Mori–Tanaka model’s consideration of inter-particle interactions results in a slight underestimation of physicochemical interactions between the asphalt and mineral filler. Consequently, the Mori–Tanaka model predicts a slightly smaller film thickness than the Hashin model.
A comparison of Figure 9a,c reveals that the GSC model significantly underestimates the physicochemical interactions between the asphalt and mineral filler due to its consideration of inter-particle interactions. As a result, the GSC model predicts a significantly smaller film thickness than the other two methods and may even yield negative values. Based on this analysis, the Hashin model is chosen to determine the adsorbed asphalt film thickness for evaluating asphalt–mineral filler interaction capability.
4.3. Improvement in Evaluation Indicators for the Interaction Between Asphalt and Mineral Filler Based on Hashin Model
As discussed in Section 4.2, while the Hashin model provides a more accurate representation of the physicochemical interactions between asphalt and mineral filler, the adsorbed asphalt film thickness remains influenced by the mineral filler volume fraction. Eliminating this dependency is essential to ensure a more reliable evaluation. To achieve this, further refinement of the calculation method for adsorbed asphalt film thickness is required to establish a more accurate and representative interaction evaluation indicator. This section introduces a nonlinear fitting method for calculating adsorbed asphalt film thickness, transforming it into an independent interaction evaluation indicator while removing its dependency on the mineral filler volume fraction. This refinement enables a clearer distinction between the influence of material properties and external environmental factors on the interaction capability between asphalt and mineral fillers.
Based on the derivation results of the adsorbed asphalt film thickness presented in Section 2.1, the fitting formula for the interaction evaluation indicator based on the micromechanical model can be derived from Equations (3) and (4) as follows:
where Gc/Gm is the experimental value of the shear modulus ratio of asphalt mastic. ϕf is taken as the independent variable, the measured value of Gc/Gm as the dependent variable, and d as the fitting parameter for nonlinear fitting. To ensure that the physicochemical interactions between the asphalt and mineral filler dominate without being affected by inter-particle interactions, the volume fraction of mineral filler should be restricted within the critical volume fraction range during fitting. The fitting process is shown in Figure 10.
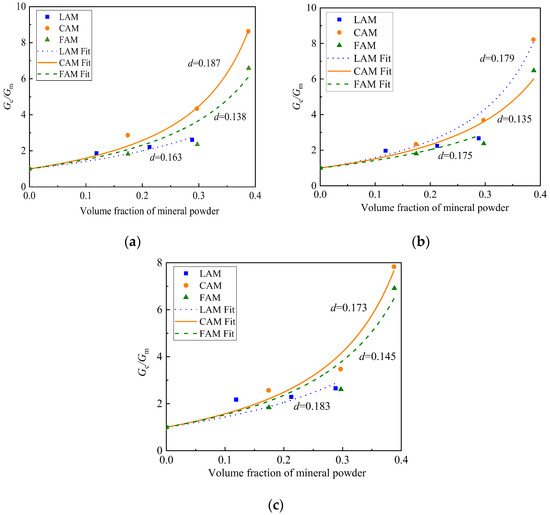
Figure 10.
Fitting of adsorbed bitumen film thickness at different temperatures: (a) 28 °C; (b) 40 °C; (c) 52 °C.
The fitting results of the adsorbed asphalt film thickness for different asphalt mastics and their corresponding goodness of fit are presented in Table 5.

Table 5.
Fitting results and goodness of fit for adsorbed film thickness for different types of asphalt mastic.
As presented in Table 5, the fitted values of film thickness d remain consistent across all temperatures and demonstrate a high goodness of fit. The adsorbed asphalt film thickness follows a clear trend: CAM exhibits the thickest film, followed by LAM, while FAM has the thinnest. This consistency indicates that the nonlinear fitting method effectively eliminates the influence of the original filler volume fraction. Consequently, this study employs the fitted values of the adsorbed asphalt film thickness to assess the interaction capability between asphalt and mineral filler.
4.4. Analysis of Factors Affecting the Interaction Capability Between Asphalt and Mineral Filler
4.4.1. Influence of Mineral Filler Chemical Composition on the Interaction Capacity Between Asphalt and Mineral Filler
To examine the effect of mineral filler chemical composition on the interaction capacity between asphalt and mineral filler, asphalt mastics prepared with three different types of mineral fillers, each exhibiting distinct chemical compositions, were evaluated using 90# base asphalt under identical experimental conditions of temperature and loading frequency. For analytical consistency, the chemical composition of the mineral fillers was characterized by their SiO2 content.
Mineral filler acidity/alkalinity is a chemical property, whereas the thickness of the adsorbed asphalt film in asphalt mastic is also affected by the specific surface area of the mineral filler. Therefore, to exclusively analyze the relationship between the interaction capability of asphalt and mineral filler and the acidity/alkalinity of the mineral filler, this study introduced a coefficient dS, defined as the adsorbed asphalt film thickness per unit of specific surface area. Based on the specific surface area and the fitted adsorbed asphalt film thickness of the three mineral fillers, the dS values of the three types of asphalt mastics were determined. A higher dS value indicates a stronger interaction capability between asphalt and mineral filler.
The relative content of chemical components in the three mineral fillers was determined via XRD analysis. The diffraction peak patterns of the XRD results were integrated, and the relative content of each compound was calculated by dividing the sum of the peak areas corresponding to each compound by the total peak area. The relative content of each compound is shown in Table 6. Figure 11 illustrates the relationship between the dS value of asphalt mastic and the SiO2 content of mineral filler.

Table 6.
Relative content of chemical components in fillers.
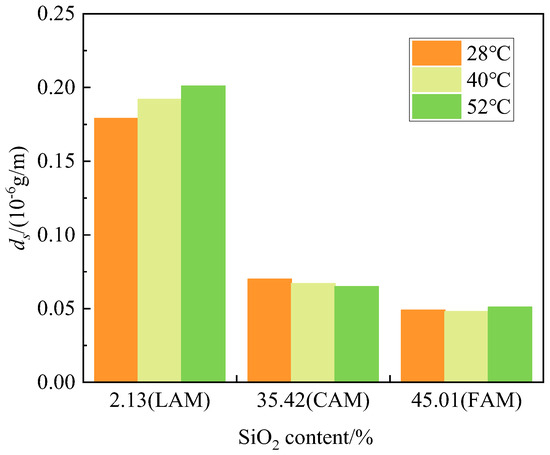
Figure 11.
Effect of SiO2 content on the thickness of the adsorbed asphalt film.
Table 6 presents the relative chemical composition of the three mineral fillers. Among them, limestone filler has the lowest SiO2 content and the highest CaO content (51.48%), being an alkaline compound. Coal gangue filler contains 19.01% CaO and a relatively high amount of Al2O3 (25.93%)—another alkaline component. In contrast, fly ash has a lower content of alkaline compounds and primarily consists of acidic SiO2.
As shown in Figure 11, within the critical volume fraction range of mineral filler, the interaction capability between asphalt and mineral filler decreases with increasing SiO2 content. This is because asphalt contains a significant amount of asphaltenes and anhydrides, while SiO2, an acidic component in mineral filler, negatively impacts the adhesion between asphalt and mineral filler [41]. A higher SiO2 content makes it more difficult for asphalt to interact physically and chemically with the mineral filler, resulting in a thinner adsorbed asphalt film and weaker interaction capability. According to chemical reaction theory, when the content of alkaline components (e.g., CaO) in mineral filler increases, the physical and chemical interactions with asphalt are enhanced, leading to a thicker adsorbed asphalt film and stronger interaction capability.
4.4.2. Influence of Temperature on the Interaction Capability Between Asphalt and Mineral Fillers
The effect of temperature on the interaction capability between asphalt and mineral fillers was examined by analyzing the variation in adsorbed asphalt film thickness for three types of asphalt mastics, as illustrated in Figure 12.
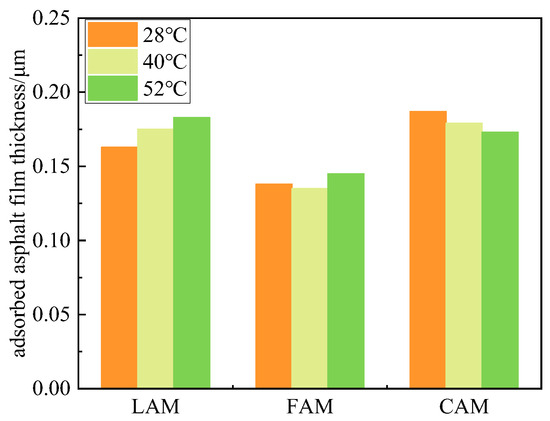
Figure 12.
Variation in adsorbed asphalt film thickness with temperature for different asphalt mastics.
Figure 12 demonstrates that, within the investigated range of mineral filler volume fractions, the adsorbed asphalt film thickness of limestone asphalt mastic increases with rising temperature. This trend can be attributed to two factors. The primary reason is that when the temperature surpasses the softening point of asphalt (48 °C), asphalt transitions from a semi-solid to a viscous flow state, improving its contact and wetting ability with the mineral filler [42]. Additionally, elevated temperatures enhance the adhesion between asphalt and the alkaline mineral components of the filler. Since limestone contains 51.48% CaO, the adhesion between asphalt and CaO strengthens with increasing temperature, thereby improving the interaction between asphalt and the limestone mineral filler.
For fly ash asphalt mastic, the adsorbed asphalt film thickness exhibits minimal variation with temperature. This is primarily due to the low CaO content in fly ash, which is only 2.8%. As a result, the adhesion between asphalt and CaO remains nearly unchanged with rising temperature. Fly ash particles possess a dense CaO-SiO2-Al2O3 system, and their glassy phase forms a smooth, compact, and robust Si-O-Si and Si-O-Al network structure [43]. Therefore, even when the temperature exceeds the asphalt softening point and transitions it into a viscous flow state, the effective wetting of fly ash particles remains limited. Consequently, temperature variations exert little influence on the interaction between asphalt and fly ash.
In coal gangue asphalt mastic, the adsorbed asphalt film thickness decreases as temperature rises. This reduction is primarily due to the high SiO2 content and large specific surface area of coal gangue. With increasing temperature, asphalt more effectively contacts coal gangue; however, the acidic SiO2 inhibits its interaction with the mineral filler. Even beyond the asphalt softening point, the inhibitory effect of SiO2 in coal gangue surpasses the enhancement from asphalt wetting. As a result, the interaction capability continues to weaken at 52 °C.
4.4.3. Influence of Frequency on the Interaction Capability Between Asphalt and Mineral Filler
Figure 13 illustrates the variation in adsorbed asphalt film thickness with experimental frequency for three types of asphalt mastics at different temperatures. As the influence of the filler-to-binder ratio is not considered in this analysis, the film thickness results at a constant filler-to-binder ratio were selected for investigation. Given that the mineral filler volume fraction of FAM, CAM, and LAM falls within the critical range at a filler-to-binder ratio of 0.4, this value was chosen to minimize the influence of inter-particle interactions on the analysis results.
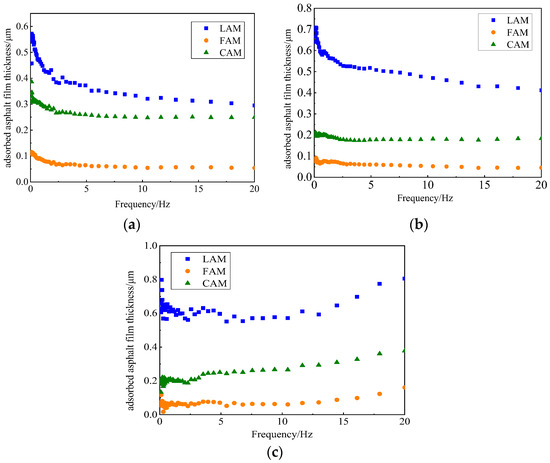
Figure 13.
Variation in adsorbed asphalt film thickness with experimental frequency at different temperatures: (a) 28 °C; (b) 40 °C; (c) 52 °C.
Figure 13 demonstrates that adsorbed asphalt film thickness varies with experimental frequency, reflecting changes in interaction capability. Thus, the interaction capability between asphalt and mineral filler is frequency-dependent. Figure 13a,b indicate that at 28 °C and 40 °C, adsorbed asphalt film thickness decreases as frequency increases. This suggests that at lower temperatures, increasing frequency weakens the interaction capability between asphalt and mineral filler. As frequency increases, the shear modulus of asphalt and asphalt mastic rises, causing asphalt to gradually transition from viscoelastic to elastic behavior [44]. This transition reduces the wetting ability of asphalt, thereby weakening its interaction with the mineral filler. Figure 13c reveals that at 52 °C, adsorbed asphalt film thickness increases with frequency. Since this temperature surpasses the asphalt softening point (48 °C), the material transitions from a semi-solid to a viscous flow state. At this stage, the wetting effect of asphalt outweighs the influence of frequency, enhancing its interaction with the mineral filler.
5. Conclusions
This study employed the Hashin model, Mori–Tanaka model, and generalized self-consistent (GSC) model to calculate the adsorbed asphalt film thickness, compare and optimize these calculations, and establish this factor as an indicator for evaluating interaction capability. Additionally, the effects of temperature, frequency, and the chemical composition of mineral fillers on the rheological properties of asphalt mastics and their interaction capability were examined. The primary conclusions are as follows:
- (1)
- The adsorbed asphalt film thickness was calculated using the Hashin model, the Mori–Tanaka model, and the GSC model. The resulting thickness ranged from 0.01 to 0.37 µm, determined by calculating the difference between the effective and initial volume fractions of the mineral filler.
- (2)
- A comparison was made of the adsorbed asphalt film thicknesses, calculated using the three micromechanical models. The film thickness based on the Hashin model was slightly greater than that derived from the Mori–Tanaka model, while the GSC model produced a significantly thinner film. In comparison to the film thicknesses obtained from the GSC and Mori–Tanaka models, the Hashin model provided a clearer physical interpretation, with no negative values and a simpler formula. It offered a more effective evaluation of the interaction capability between asphalt and mineral filler.
- (3)
- The shear modulus ratios of asphalt mastic under different filler volume fractions were subjected to nonlinear fitting, which allowed for a more accurate calculation of the critical filler volume fractions. The critical filler volume fractions for LAM, FAM, and CAM were determined to be 30.65%, 44.96%, and 41.15%, respectively. These values provide a basis for the scope of research on the interaction between asphalt and fillers. The results of the fitting provided a single film thickness for each type of asphalt mastic, demonstrating good fitting quality. At all temperatures, the film thickness followed a consistent trend: CAM > LAM > FAM. This method eliminated the dependence of the interaction evaluation indicator on the mineral filler volume fraction.
- (4)
- The interaction capacity between asphalt and mineral fillers was systematically investigated. It was found that the incorporation of mineral fillers significantly enhances the complex shear modulus of base asphalt, thereby increasing its elasticity while reducing its viscosity. Within the critical filler volume fraction range, rutting resistance is predominantly influenced by the material properties of the fillers. The interaction capability between asphalt and mineral filler is influenced by multiple factors. A higher SiO2 content in mineral filler weakens the interaction with asphalt. The effect of frequency varies with temperature: below the softening point, a higher frequency reduces the interaction capability, whereas above this threshold, the interaction capability increases. The interaction between limestone filler and asphalt strengthens as temperature rises. The compact CaO-SiO2-Al2O3 structure of fly ash minimizes sensitivity to temperature changes, while the high SiO2 content in coal gangue inhibits its interaction with asphalt.
Author Contributions
Conceptualization, S.W. and Z.W.; methodology, S.W. and Z.W.; validation, S.W., Z.W. and H.Y.; formal analysis, S.W. and A.Y.; investigation, S.W. and Z.W.; resources, Z.W., F.Z. and Z.H.; data curation, S.W., A.Y. and X.M.; writing—original draft preparation, S.W. and A.Y.; writing—review and editing, S.W. and Z.W.; visualization, S.W. and A.Y.; supervision, Z.W. and Z.G.; project administration, Z.W. and D.G.; funding acquisition, Z.W. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Heilongjiang Provincial Natural Science Foundation of China [grant no YQ2022E038], the Key Project of Scientific Research Project of Hunan Provincial Department of Education (Grant No. 24A0752), the Excellent Youth Project of Scientific Research Project of Hunan Provincial Department of Education (Grant No. 24B1069), the National Natural Science Foundation of China (Grant No. 52278454).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All relevant data are contained in the present manuscript.
Acknowledgments
The authors would like to thank Jianming Liu from Shiyanjia Lab (www.shiyanjia.com (accessed on 1 March 2025)) for the BET analysis.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sousa, M.; Dinis Almeida, M.; Fael, C.; Bentes, I. Permeable Asphalt Pavements (PAP): Benefits, Clogging Factors and Methods for Evaluation and Maintenance—A Review. Materials 2024, 17, 6063. [Google Scholar] [CrossRef] [PubMed]
- Habbouche, J.; Hajj, E.Y.; Piratheepan, M.; Sebaaly, P.E. Impact of high polymer modification on reflective cracking performance life of asphalt concrete overlays. Int. J. Pavement Res. Technol. 2020, 13, 510–523. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, Q.; Gu, X. Classification of Asphalt Pavement Defects for Sustainable Road Development Using a Novel Hybrid Technology Based on Clustering Deep Features. Sustainability 2024, 16, 10145. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, N.; Wang, S.; Xu, Y. Prediction of highway asphalt pavement performance based on Markov chain and artificial neural network approach. J. Supercomput. 2021, 77, 1354–1376. [Google Scholar] [CrossRef]
- Veytskin, Y.; Bobko, C.; Castorena, C.; Kim, Y. Nanoindentation investigation of asphalt binder and mastic cohesion. Constr. Build. Mater. 2015, 100, 163–171. [Google Scholar] [CrossRef]
- Das, A.K.; Singh, D. Investigation of rutting, fracture and thermal cracking behavior of asphalt mastic containing basalt and hydrated lime fillers. Constr. Build. Mater. 2017, 141, 442–452. [Google Scholar] [CrossRef]
- Zeng, M.; Wu, C. Effects of Type and Content of Mineral Filler on Viscosity of Asphalt Mastic and Mixing and Compaction Temperatures of Asphalt Mixture. Transp. Res. Rec. 2008, 2051, 31–40. [Google Scholar] [CrossRef]
- Mansor, N.; Sevil, K. Effect of filler types and asphalt penetration grade on properties of asphalt mastic. Petrol. Sci. Technol. 2018, 36, 1503–1509. [Google Scholar] [CrossRef]
- Pereira, L.; Freire, A.C.; da Costa, M.S.; Antunes, V.; Quaresma, L.; Micaelo, R. Experimental study of the effect of filler on the ductility of filler-bitumen mastics. Constr. Build. Mater. 2018, 189, 1045–1053. [Google Scholar] [CrossRef]
- Ibarra, L.; Paños, D. Dynamic properties of thermoplastic butadiene–styrene (SBS) and oxidized short carbon fiber composite materials. J. Appl. Polym. Sci. 1998, 67, 1819–1826. [Google Scholar] [CrossRef]
- Ziegel, K.D.; Romanov, A. Modulus reinforcement in elastomer composites. I. Inorganic fillers. Appl. Polym. Sci. 2010, 17, 1041–1050. [Google Scholar] [CrossRef]
- Einstein, A. Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 1906, 324, 289–306. [Google Scholar] [CrossRef]
- Chong, J.S.; Christiansen, E.B.; Baer, A.D. Rheology of Concentrated Suspensions. J. Appl. Polym. Sci. 1971, 15, 2007–2021. [Google Scholar] [CrossRef]
- Tan, Y.; Li, X.; Wu, J. Evaluation Indices of Interaction Ability of Asphalt and Aggregate Based on Rheological Characteristics. J. Wuhan Univ. Technol. 2012, 27, 979–985. [Google Scholar] [CrossRef]
- Tan, Y.Q.; Wu, J.T.; Li, X.M.; Ji, L. Evaluation indices of interaction ability of asphalt and aggregate. J. Harbin Inst. Technol. 2009, 41, 81–84. [Google Scholar] [CrossRef]
- Liu, G.; Jia, Y.; Pan, Y.; Yang, T.; Zhao, Y.; Zhang, J. Quantitative comparison of evaluation indices for asphalt–filler interaction ability within filler critical volume fraction. Road Mater. Pavement Des. 2018, 21, 906–926. [Google Scholar] [CrossRef]
- Guo, M. Mechanism of Asphalt-Mineral Interaction and Multi-Scale Evaluation Methods. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar] [CrossRef]
- EN 13179-2:2002; Bituminous Binders—Test Methods—Part 2: Determination of the Interaction Between Bitumen and Mineral Fillers. European Committee for Standardization (CEN): Brussels, Belgium, 2002.
- Teixeira, A.; Lesueur, D. Impact of Different Fillers on the Properties of Asphalt Mixtures. In RILEM International Symposium on Bituminous Materials; ISBM 2020, RILEM Bookseries; Springer: Cham, Switzerland, 2022; Volume 27, pp. 1007–1013. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, M. Interfacial thickness and interaction between asphalt and mineral fillers. Mater. Struct. 2014, 47, 605–614. [Google Scholar] [CrossRef]
- Pipintakos, G.; Soenen, H.; Goderis, B.; Blom, J.; Lu, X. Crystallinity of Bitumen via WAXD and DSC and Its Effect on the Surface Microstructure. Crystals. 2022, 12, 755. [Google Scholar] [CrossRef]
- Guo, M.; Bhasin, A.; Tan, Y.Q. Effect of mineral fillers adsorption on rheological and chemical properties of asphalt binder. Constr. Build. Mater. 2017, 141, 152–159. [Google Scholar] [CrossRef]
- Guo, M.; Tan, Y.; Yu, J.; Hou, Y.; Wang, L. A direct characterization of interfacial interaction between asphalt binder and mineral fillers by atomic force microscopy. Mater. Struct. 2017, 50, 141. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, N.; Xu, Y.; Wang, S. Micromechanical prediction model of viscoelastic properties for asphalt mastic based on morphologically representative pattern approach. Adv. Mater. Sci. Eng. 2020, 5, 7915140. [Google Scholar] [CrossRef]
- Wang, Z.; Jin, X.; Sun, Y.; Wang, S. Micromechanics approach to calculate the adsorbed asphalt film thickness on mineral fillers and evaluate physiochemical interactions. Int. J. Pavement Eng. 2024, 25, 2303670. [Google Scholar] [CrossRef]
- Hashin, Z. The Elastic Moduli of Heterogeneous Materials. J. Appl. Mech. 1962, 29, 2938–2945. [Google Scholar] [CrossRef]
- Benveniste, Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Christensen, R.M.; Lo, K.H. Solutions for effective shear properties in three phase sphere and cylinder models. J. Mech. Phys. Solids 1979, 27, 315–330. [Google Scholar] [CrossRef]
- Kim, M. Development of differential scheme micromechanics modeling framework for predictions of hot-mix asphalt (HMA) complex modulus and experimental validations. Diss. Theses-Gradworks 2009, 7, 64–105. [Google Scholar] [CrossRef]
- Yin, H.M.; Sun, L.Z.; Paulino, G.H. Micromechanics-based elastic model for functionally graded materials with particle interactions. Acta Mater. 2004, 52, 3535–3543. [Google Scholar] [CrossRef]
- Shashidhar, N.; Shenoy, A. On using micromechanical models to describe dynamic mechanical behavior of asphalt mastics. Mech. Mater. 2002, 34, 657–669. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Buttlar, W.; Bozkurt, D.; Al-Khateeb, G.; Waldhoff, A. Understanding Asphalt Mastic Behavior Through Micromechanics. Transp. Res. Rec. 1999, 1681, 157–169. [Google Scholar] [CrossRef]
- Kim, Y.R.; Little, D.N. Linear Viscoelastic Analysis of Asphalt Mastics. J. Mater. Civ. Eng. 2004, 16, 122–132. [Google Scholar] [CrossRef]
- Underwood, B.S.; Kim, Y.R. A four phase micro-mechanical model for asphalt mastic modulus. Mech. Mater. 2014, 75, 13–33. [Google Scholar] [CrossRef]
- Li, F.; Yang, Y. Understanding the temperature and loading frequency effects on physicochemical interaction ability between mineral filler and asphalt binder using molecular dynamic simulation and rheological experiments. Constr. Build. Mater. 2020, 244, 118311. [Google Scholar] [CrossRef]
- Li, F.; Yang, Y.; Wang, L. Evaluation of physicochemical interaction between asphalt binder and mineral filler through interfacial adsorbed film thickness. Constr. Build. Mater. 2020, 252, 119135. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Olard, F.; Sauzéat, C.; Delaporte, B. Linear viscoelastic behavior of bituminous materials: From binders to mixes. Road Mater. Pavement Des. 2004, 5, 163–202. [Google Scholar] [CrossRef]
- Faheem, A.F.; Bahia, H.U. Modelling of Asphalt Mastic in Terms of Filler-Bitumen Interaction. Road Mater. Pavement Des. 2010, 11 (Suppl. S1), 281–303. [Google Scholar] [CrossRef]
- Fan, L.; Lin, J.T.; Li, Y.Z. Characterization of mineral filler particles related to asphalt mastic properties. J. Wuhan Univ. Technol. (Transp. Sci. Eng.) 2021, 45, 82–87. [Google Scholar]
- Cheng, Y.; Tao, J.; Jiao, Y.; Tan, G.; Guo, Q.; Wang, S.; Ni, P. Influence of the properties of filler on high and medium temperature performances of asphalt mastic. Constr. Build. Mater. 2016, 118, 268–287. [Google Scholar] [CrossRef]
- Tan, Y.Q.; Li, X.L.; Wu, J.T.; Luo, D.S.; Cao, L.P. Effect of temperature and loading frequency on asphalt-aggregate interaction ability. China J. Highw. Transp. 2012, 25, 65–72. [Google Scholar] [CrossRef]
- Ke, G.J.; Yang, X.F.; Peng, H.; Jia, F.; Yue, H.T. Research progress on the mechanism of chemical activation of fly ash. J. China Coal Soc. 2005, 30, 366–370. [Google Scholar] [CrossRef]
- Zhou, Z.X. Study on the Influence of Filler on the High and Low Temperature Performance of Asphalt Mastic and Prediction of Asphalt Mastic Properties. Master’s Thesis, Hunan University, Changsha, China, 2013. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).