Improving Freight Traffic Efficiency at Urban Intersections Using Heavy Vehicle Platooning

Abstract

The increasing presence of heavy connected vehicles (HCVs) in urban traffic necessitates optimized signal-control strategies to improve efficiency. This study develops a platoon-based signal-optimization algorithm to reduce delays, minimize stops, and enhance traffic flow at intersections. The algorithm collects real-time CV data (speed, position, and inter-vehicle distances) to identify platoons, then dynamically adjusts signal timings using platoon-prioritized signal control and advisory speed coordination to synchronize HCV arrivals with green intervals. The algorithm was tested using a VISSIM microscopic traffic-simulation model, calibrated with real-world traffic data from Tallahassee, Florida, under varying traffic-demand scenarios and connected vehicle penetration levels. Performance was evaluated based on average HCV delay and the total number of stops, comparing the platoon-based approach to actuated and vehicle-based signal-control methods. Results show a significant reduction in both delay and stops, with the greatest improvements observed under higher CV penetration and over-saturated conditions. These findings confirm the effectiveness of platoon-based optimization in improving intersection performance and overall traffic progression. Future research will focus on multi-intersection applications and V2I integration to further optimize signal-control strategies.

1. Introduction

Efficient urban traffic management is critical to sustaining economic productivity and maintaining the functionality of modern cities [1]. Among the most pressing challenges is the delay experienced by logistics vehicles at signalized intersections, which increases operational costs, disrupts supply chain efficiency, and contributes to excessive fuel consumption and emissions [2]. Heavy vehicles (HVs), particularly freight trucks, are disproportionately affected by congestion due to their slower acceleration, larger spatial footprint, and frequent stop-and-go cycles, leading to extended idling times at intersections and increased economic and environmental impacts [3]. As urban freight transportation-demand grows, there is an increasing need for traffic-management strategies that prioritize HV mobility while ensuring overall intersection efficiency [4].

Platoon-based traffic signal optimization has emerged as a promising solution to mitigating delays for heavy vehicles by leveraging advancements in connected vehicle (CV) technology [5,6]. Recent studies have demonstrated that HCV platooning, where groups of heavy connected vehicles (HCVs) travel in close formation under coordinated control, can significantly improve traffic flow, reduce stops, and enhance fuel efficiency [7,8]. The concept of HCV platooning is enabled by Cooperative Adaptive Cruise Control (CACC), which allows vehicles within a platoon to communicate and synchronize speed, acceleration, and braking [9]. 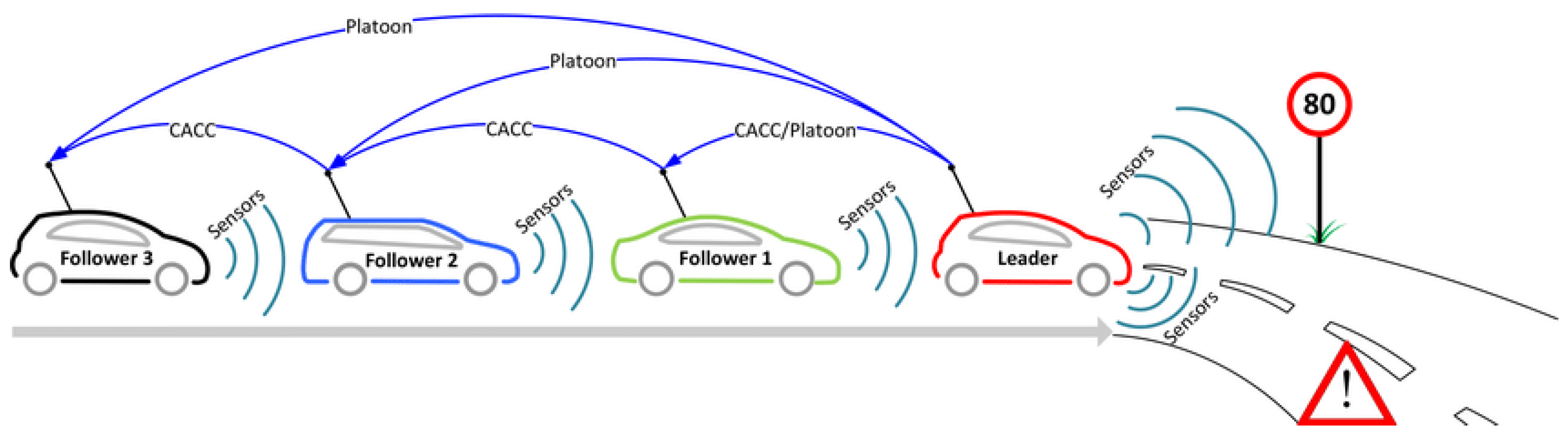Figure 1 illustrates the structure of an HCV platoon, where a leader vehicle determines movement dynamics while following vehicles respond accordingly. However, while platoon-based optimization has been explored for passenger vehicles, existing traffic signal-control frameworks rarely consider the unique operational constraints of heavy vehicles, such as increased braking distances, cargo priority, and intersection clearance requirements [10].

This study proposes a novel platoon-based signal-optimization algorithm tailored specifically for HCVs operating in a CV-enabled environment. The algorithm integrates two synergistic control mechanisms:

• Platoon-prioritized signal control: This dynamically adjusts green phase durations based on real-time HCV platoon data, including size, approach speed, and location.
• Advisory speed coordination: This guides platoon leaders to synchronize arrival times with green intervals, reducing stop frequency and smoothing acceleration and deceleration profiles.

By leveraging these mechanisms, the algorithm aims to minimize HCV delays, reduce the number of stops, and enhance overall intersection efficiency while maintaining coordination with surrounding traffic.

To validate the proposed approach, a case study was conducted at a major high-traffic intersection in Tallahassee, Florida (Orange Ave and Adams Street), a key corridor for logistics operations. Figure 2 presents an overview of the study site, highlighting its relevance for evaluating platoon-based signal optimization in real-world freight-movement scenarios. The VISSIM microscopic traffic-simulation model, calibrated to Florida Department of Transportation (FDOT) guidelines, was used to replicate real-world traffic conditions, incorporating distinct behavioral models for non-CVs, platoon leaders, and platoon followers [12]. The performance of the developed algorithm was compared against actuated signal control and individual vehicle-based optimization strategies across varying CV penetration levels.

The key contributions of this study include:

• A platoon-centric signal-optimization model specifically designed for HCVs, addressing a critical gap in passenger vehicle-dominated traffic-management approaches.
• The incorporation of HCV-specific parameters, such as acceleration constraints, spatial requirements, and cargo priority, into adaptive traffic signal logic.
• Empirical validation Demonstrating a significant reduction in HCV delay and stop frequency, with up to a 50% decrease in idling time and improved traffic flow efficiency for platooned vehicles.

This paper is structured as follows: Section 2 presents a review of existing literature on traffic signal optimization and heavy vehicle management, highlighting the need for HCV-focused strategies. Section 3 details the methodology, including the development of the adaptive signal-control algorithm, data-collection protocols, simulation modeling, and calibration processes. Section 4 presents the results, demonstrating the algorithm’s effectiveness in reducing HCV delays and stops under varying traffic scenarios. Finally, Section 5 discusses real-world applicability, challenges, and future research directions, including the integration of AI-based optimizations and vehicle-to-infrastructure (V2I) advancements.

By addressing the unique challenges of HCVs at signalized intersections, this study advances a platoon-centric paradigm for urban logistics management, offering practical insights for optimizing freight mobility within connected transportation systems.

2. Related Work

Connected Vehicle (CV) technology, coupled with traffic signal-control algorithms, has garnered increasing attention as researchers seek to optimize traffic flow and reduce logistic delays at intersections [13,14]. Many recent studies leverage real-time vehicle data—such as speed, location, and acceleration/deceleration—to inform signal timing decisions, leading to reduced queue lengths and delays [15,16,17,18,19]. While these CV-based methods often outperform traditional control strategies, they frequently assume high or even full CV penetration rates [20], an assumption that is unlikely to be realized in the near term [21].

Simultaneously, research on intersection logistics highlights the unique challenges faced by heavy vehicles (e.g., large freight carriers), which account for a substantial share of urban goods movement yet experience disproportionately longer idling times due to slower acceleration, larger spatial footprints, and more frequent stop-and-go cycles [22]. These delays inflate operational costs and increase environmental impacts, underscoring a clear need for tailored traffic signal strategies that accommodate the specific demands of freight vehicles [23]. An emerging area that promises to address both CV-based control and heavy vehicle management is platooning, wherein connected heavy vehicles follow a designated leader at coordinated speeds [24]. Studies indicate that platooning can streamline traffic flow, reduce fuel consumption, and cut emissions [25]. However, many existing approaches to CV platooning and adaptive signal control either assume homogeneous traffic (mostly passenger vehicles) or 100% CV penetration [14,26], limiting their applicability in mixed-fleet conditions where both connected and non-connected vehicles coexist. Moreover, few of these studies consider heavy vehicle-specific factors such as platoon size, inter-vehicle spacing, cargo priority, or their impact on signal timing optimization in oversaturated intersections [27].

Other research strands—such as reservation-based strategies for intersections—show potential in reducing vehicle delays by allowing vehicles to reserve time blocks at a signal [28,29]. While these approaches may theoretically improve intersection performance, concerns about safety, compatibility with existing infrastructure, and partial penetration of CV technology persist [30]. Furthermore, a number of studies propose CV-based algorithms that optimize individual vehicle trajectories for reducing delay or fuel consumption [31,32], but these algorithms can become computationally intensive, hindering their real-world deployment [33].

Adjusting signal timings in a connected vehicle (CV) environment can unintentionally disrupt traffic dynamics and vehicle performance, despite the goal of improving flow and reducing delays [34,35]. Sudden changes in signal phases may force connected vehicles to perform more acceleration and deceleration maneuvers, creating shock waves in traffic flow that increase idling, fuel consumption, and emissions, ultimately reducing the expected efficiency of coordinated vehicle movements [36]. Simulation-based approaches and spatiotemporal models for delay analysis have proven valuable in modeling intersection performance [37], yet they frequently overlook how CV technology and platooning specifically transform traffic dynamics [38].

Overall, existing literature underscores the promise of CV-enabled traffic control for mitigating intersection delay but reveals several critical gaps. Namely, heavy connected vehicles require specialized strategies that account for their distinct operational profiles and that function effectively under partial CV environments. Addressing these issues is key to unlocking substantial improvements in freight efficiency and environmental performance. The present study aims to fill this gap by introducing a platoon-centric traffic signal-optimization framework tailored for heavy connected vehicles, which seeks to reduce delay and stops at congested intersections through realistic assumptions of mixed vehicle penetration, multi-vehicle coordination, and integration of logistics-specific parameters.

3. Methodology

The methodology employed in this study aims to assess the performance of the HCV platoon-based adaptive signal-control algorithm in a real-world setting using actual logistics traffic data collected from a complex intersection in Tallahassee City. The algorithm’s primary objective is to provide dual levels of signal-optimization control by integrating departure sequence optimization and advisory speed coordination specifically for HCV platoons. Unlike conventional signal-control strategies that manage individual vehicles separately, this approach leverages real-time connectivity and vehicle-to-infrastructure (V2I) communication among heavy connected vehicles to minimize intersection delays and stops.

The HCV platoon-based adaptive signal-control algorithm presents several advantages over traditional vehicle-based optimization methods. First, the algorithm uses HCV-specific connectivity data to identify platoons of arriving or stopped heavy vehicles and optimizes the signal timing plan based on platoon size, location, and approach speed. This allows for efficient green phase allocation, reducing computational complexity and enabling deployment in realistic, high-volume intersections with complex logistics traffic flows. Second, the algorithm incorporates an advisory speed-coordination strategy, minimizing the number of stops for HCV platoons while considering upstream traffic flow. By synchronizing platoon arrivals with green intervals, fuel consumption, idling time, and emissions are significantly reduced.

Third, the developed algorithm provides advisory speed guidance exclusively to the lead HCV in each platoon, which then communicates with following vehicles using Cooperative Adaptive Cruise Control (CACC). This reduces computational overhead, as only the platoon leader processes speed guidance while ensuring that all platoon members follow a coordinated trajectory through the intersection. Lastly, the algorithm integrates a modified Intelligent Driving Model (IDM), specifically adapted to HCV dynamics, considering slower acceleration rates, longer braking distances, and increased intersection clearance times. These adjustments ensure a realistic representation of HCV movement and enhance the accuracy of advisory speed recommendations.

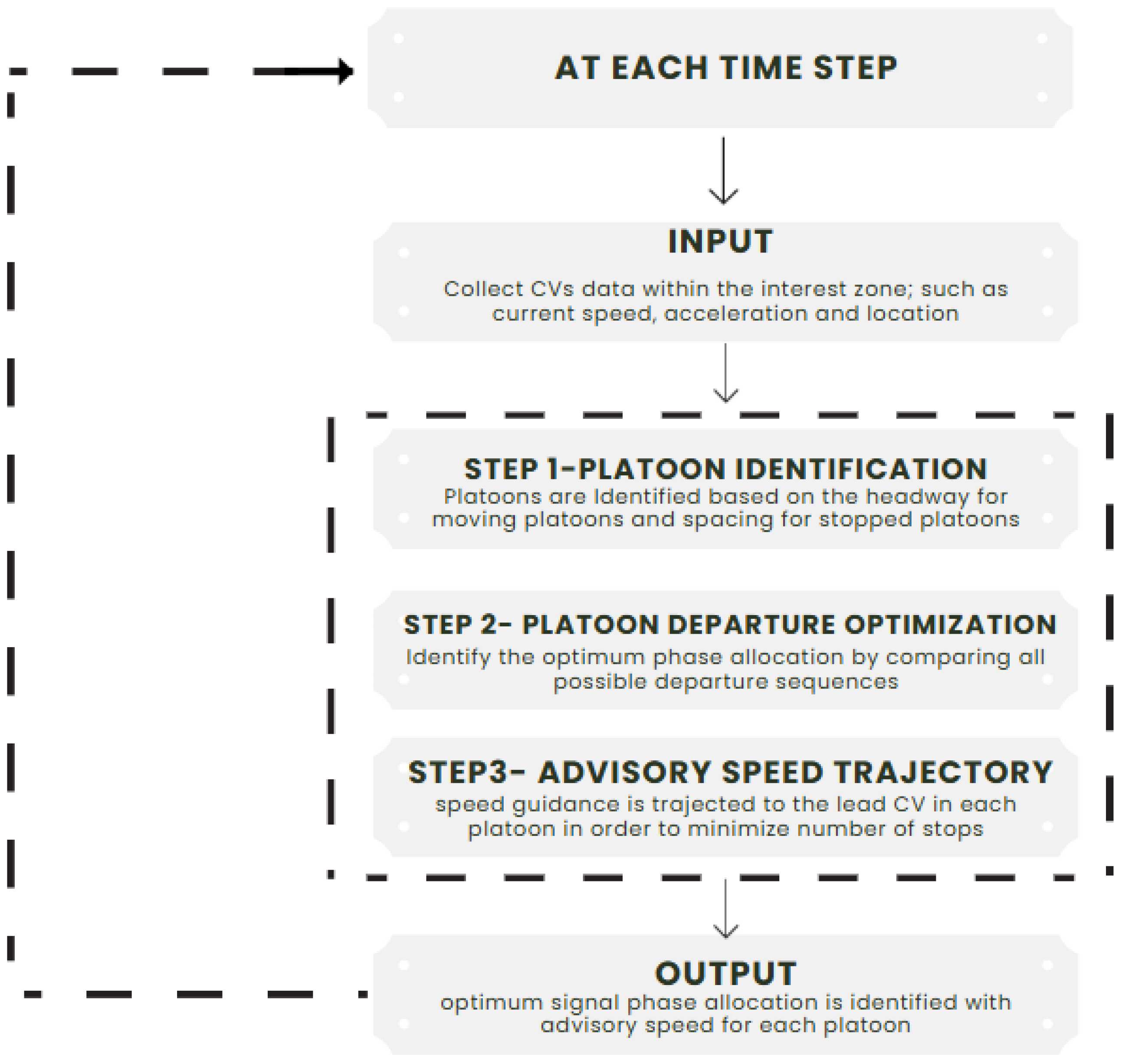
Figure 3 illustrates the logic of the HCV platoon-based adaptive signal-control algorithm, highlighting the various components involved in optimizing signal timings for mixed traffic environments, where HCVs interact with non-CVs and smaller vehicles. The control algorithm operates as a discrete loop, continuously updating itself at each time step based on real-time traffic conditions.

The first step in the algorithm involves HCV platoon identification, where both stopped and moving platoons are detected. Stopped platoons are identified based on queue lengths and headway analysis, ensuring accurate detection of waiting HCV groups. Moving platoons are recognized using real-time vehicle trajectory data, analyzing speed differentials and inter-vehicle distances. Additionally, the algorithm estimates the presence of non-CVs (unequipped heavy vehicles) and incorporates them into signal-control decisions to maintain operational realism.

The second step selects the optimal signal phase based on HCV platoon characteristics, including location, speed, number of vehicles, and lane assignments. Given that the intersection features shared through-right lanes and exclusive left-turn lanes, the algorithm dynamically adjusts green times to prioritize HCV platoon movements while maintaining balanced intersection operations for all users. The objective of this step is to minimize the overall average delay for HCVs and improve their throughput at the intersection.

The third step determines the advisory speed for each departure sequence, minimizing the number of stops and ensuring smoother traffic flow through the intersection. The algorithm employs the modified Intelligent Driving Model (IDM) to adjust advisory speeds, considering HCV acceleration limitations and intersection clearance constraints. The advisory speed $V_a$ for the platoon leader is calculated as:

$$V_a={\displaystyle \frac{d_a}{T_g}}$$

(1)

where:

• $V_a$ is the advisory speed of the lead HCV in the platoon;
• $d_a$ is the distance to the stop line;
• $T_g$ is the remaining green time.

If the computed speed exceeds a safe acceleration threshold for HCVs, the algorithm adjusts it to prevent excessive fuel consumption, engine strain, or unstable braking patterns.

The signal phase selection and advisory speed-coordination steps operate in parallel, ensuring that both signal allocation and speed recommendations are synchronized. This proactive approach allows for real-time adjustments, unlike traditional actuated control methods that reactively change signals based on vehicle detection. By optimizing both signal timings and advisory speeds simultaneously, the HCV platoon-based adaptive signal-control algorithm effectively reduces delays, idling time, and fuel consumption, while enhancing the efficiency of logistics operations.

3.1. Step 1—Platoon Identification

To identify HCV platoons at intersections, headway and spacing thresholds are used to evaluate the distance between moving and stationary vehicles. Both connected and conventional heavy vehicles are considered in the platooning process, but conventional heavy vehicles are only assessed based on their spacing. The process of identifying HCV platoons is divided into two main steps: identifying stationary platoons by estimating queue length and identifying moving platoons based on data input from connected HCVs.

3.1.1. Queue Length Estimation

HCV platoons are identified by analyzing data from individual connected HCVs, using headway and spacing thresholds to determine if vehicles are part of a platoon. The process involves identifying stationary and moving platoons, with data from connected HCVs used to anticipate queues. The developed algorithm assumes the availability of real-time location and speed of connected HCVs and a penetration ratio. To construct a comprehensive picture of traffic conditions at the intersection, four assumptions are made:

• At each time step, it is possible to gather data on the location and velocity of every individual CV.
• When a CV is not in a queue, it is always moving at a speed higher than the speed at which it would come to a stop.
• Stopped CVs near the intersection will leave a reasonable spacing headway with the preceding vehicle.
• The last reported stopped connected CV on an approach is the last vehicle in the queue.

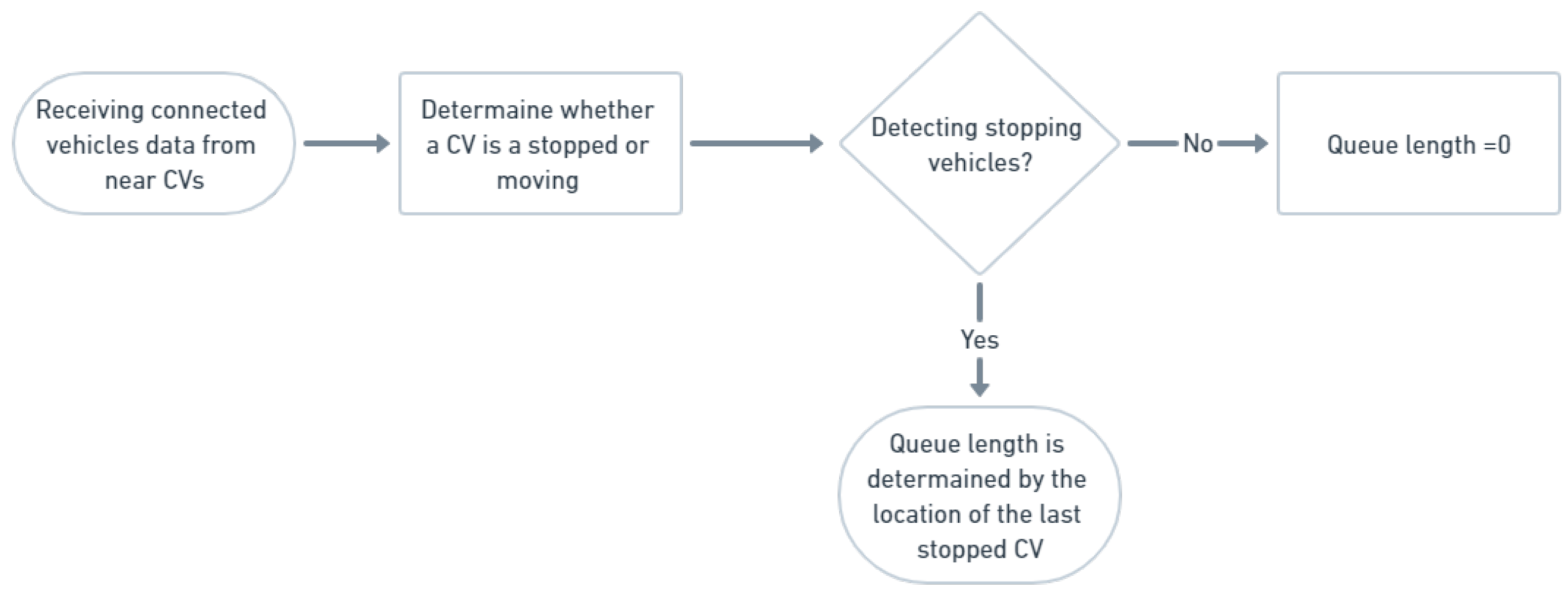
The estimation of queue length involves acquiring data of all connected HCVs, categorizing them based on their speed, and estimating the length of the queue when no stopped connected HCVs are observed or when at least one is observed.

Figure 4 illustrates a visual representation of the queue-estimation algorithm. The algorithm receives as input a collection of projected arrival times at the intersection stop line for all detected connected HCVs within a designated zone surrounding the intersection. This list of vehicles and their anticipated arrival times is updated at every time step.

Data from stopped connected HCVs is utilized to identify the existence of conventional heavy vehicles positioned downstream of a stopped connected HCV. The presence of such traditional vehicles is inferred when the distance between a stationary connected HCV and the intersection stop bar or the closest downstream connected HCV in the same lane exceeds a vehicle length, indicating the potential presence of a non-connected heavy vehicle. Conventional heavy vehicles identified in this manner are then incorporated into the vehicle set considered by the algorithm.

To estimate the conventional heavy vehicles located between connected HCVs or between a connected HCV and the stop line, Equations (2) and (3) can be employed, respectively. These equations provide a mathematical framework for estimating the number and position of conventional heavy vehicles, further enhancing the algorithm’s ability to optimize traffic flow in mixed-traffic environments.

$$\begin{array}{cc}\hfill {\mathit{n}}_{\mathrm{con}}& =⌊{\displaystyle \frac{{\mathbf{x}}_c-\left({\mathit{x}}_{c^{\prime }}+{\mathit{l}}_c\right)}{{\mathit{l}}_c}}⌉\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\mathit{n}}_{\mathrm{con}}& =⌊{\displaystyle \frac{{\mathbf{x}}_c}{{\mathit{l}}_c}}⌉\hfill \end{array}$$

(3)

where ${\mathit{x}}_{\mathit{c}}$ is the distance of the connected HCV labeled as ($\mathit{c}$) to the downstream end of the intersection, and ${\mathit{x}}_{c^{\prime }}$ is the distance of the preceding connected HCV labeled as (${\mathit{c}}^{\prime }$) to the downstream end of the intersection. ${\mathit{l}}_{\mathit{c}}$ represents the average spacing between vehicles.

3.1.2. Moving Platoon

The moving platoon detection algorithm is critical to adaptive traffic signal systems as it allows real-time adjustment of signal timings to optimize traffic flow and reduce delays. The algorithm detects moving HCV platoons by grouping heavy vehicles based on the assigned headway threshold, which is the distance between one vehicle’s leading edge and the following vehicle’s leading edge. The algorithm considers factors such as lane changes, turns, and heavy vehicles leaving or joining a platoon to accurately detect and track moving HCV platoons on the road. The algorithm is applicable to all approaches of the intersection and is designed to operate effectively even in scenarios where a stopped queue of heavy vehicles exists at the intersection or where no vehicles are currently waiting.

The moving platoon detection algorithm has been shown to be particularly effective in improving traffic conditions when connected HCVs on the road have a high penetration rate. However, the presence of conventional heavy vehicles within a platoon can present challenges for accurate platoon detection, as their behavior may not be as predictable as that of connected HCVs. A more comprehensive approach that considers the behavior of both connected and conventional heavy vehicles within platoons is required to accurately detect and track moving HCV platoons for adaptive traffic signal control.

3.2. Platoon Departure Sequence Optimization

Optimizing traffic signal timings and reducing congestion greatly depend on the departure sequence of HCV platoons, as it plays a crucial role. The platoon-based algorithm takes into account all heavy vehicles within each platoon, enabling them to depart as a cohesive group. This approach reduces the number of vehicle departure sequences, streamlining traffic flow through the intersection.

To determine the most efficient departure sequence, the algorithm calculates the average vehicle delay for each platoon departure sequence and selects the one with the minimum delay. Traffic signal timings are then adapted to accommodate the prioritized platoon. Equations (4)–(7) consider various factors such as distance traveled, acceleration, deceleration, and time spent waiting at intersections to find the minimum average vehicle delay.

$$\begin{array}{c}\hfill minA{D}_s=\Sigma \left(D_{p,s}-V_p\right)\end{array}$$

(4)

The symbol ${\mathit{AD}}_{\mathit{s}}$ represents the average delay of all vehicles for departure sequence $\mathit{s}$, while ${\mathit{D}}_{\mathit{p},\mathit{s}}$ indicates the estimated time for platoon $\mathit{p}$ to leave the downstream end of the intersection in sequence $\mathit{s}$. This estimated time is equivalent to the expected time for the final vehicle in the platoon to depart (${\mathit{D}}_{{\mathit{c}}_{\mathit{s}}}$), which can be computed using Equation (5).

$$D_{c,s}=\left\{\begin{array}{cc}{D}_{c^{\prime },s}+P_{c,s}\hfill & \hfill \mathrm{for}\mathrm{the}\mathrm{first}\mathrm{vehicle}\mathrm{in}\mathrm{the}\mathrm{stopped}\mathrm{queue}\\ D_{c^{\prime },s}+{\displaystyle \frac{1}{s_m}}\hfill & \hfill \mathrm{for}\mathrm{vehicles}\mathrm{in}\sec \mathrm{ond}\mathrm{position}\mathrm{or}\mathrm{greater}\end{array}\right.$$

(5)

An HCV $\mathit{c}$ takes time to accelerate and pass through the intersection. This time is called the delay penalty ${\mathit{P}}_{\mathit{c}}$, and Equation (6) is used to calculate it. Saturation headway is referred to as ${\mathit{S}}_{\mathit{m}}$ for approach $\mathit{m}$.

$$P_{c,s}={\displaystyle \frac{\sqrt{2\times a\times l}}{a}}$$

(6)

$$D_{c,p}=\left\{\begin{array}{c}{P}_{c,s}+{\displaystyle \frac{1}{s_m}}\times (n-1)\mathrm{If}\mathrm{there}\mathrm{is}\mathrm{a}\mathrm{queue}\hfill \\ {\displaystyle \frac{S_p}{R_p}}+{\displaystyle \frac{1}{s_m}}\times (n-1)\mathrm{If}\mathrm{the}\mathrm{platoon}\mathrm{does}\mathrm{not}\mathrm{stop}\hfill \end{array}\right.$$

(7)

Equations (5)–(7) were employed to derive Equation (8), which plays a crucial role in the algorithm’s process of optimizing traffic signal timings. Equation (8) is specifically designed to calculate the delay time of a platoon at sequence $\mathit{j}$. Using this equation, the algorithm can accurately estimate the delays associated with different departure sequences, enabling it to identify and prioritize the sequence with the minimum delay.

$$D_{p,s}=n\times P_{c_s}+\left({\displaystyle \frac{n^2-n}{2}}\times {\displaystyle \frac{1}{S_m}}\right)-\left(n\times l+\left({\displaystyle \frac{n^2-n}{2}}\right)\times S\right)/U_f$$

(8)

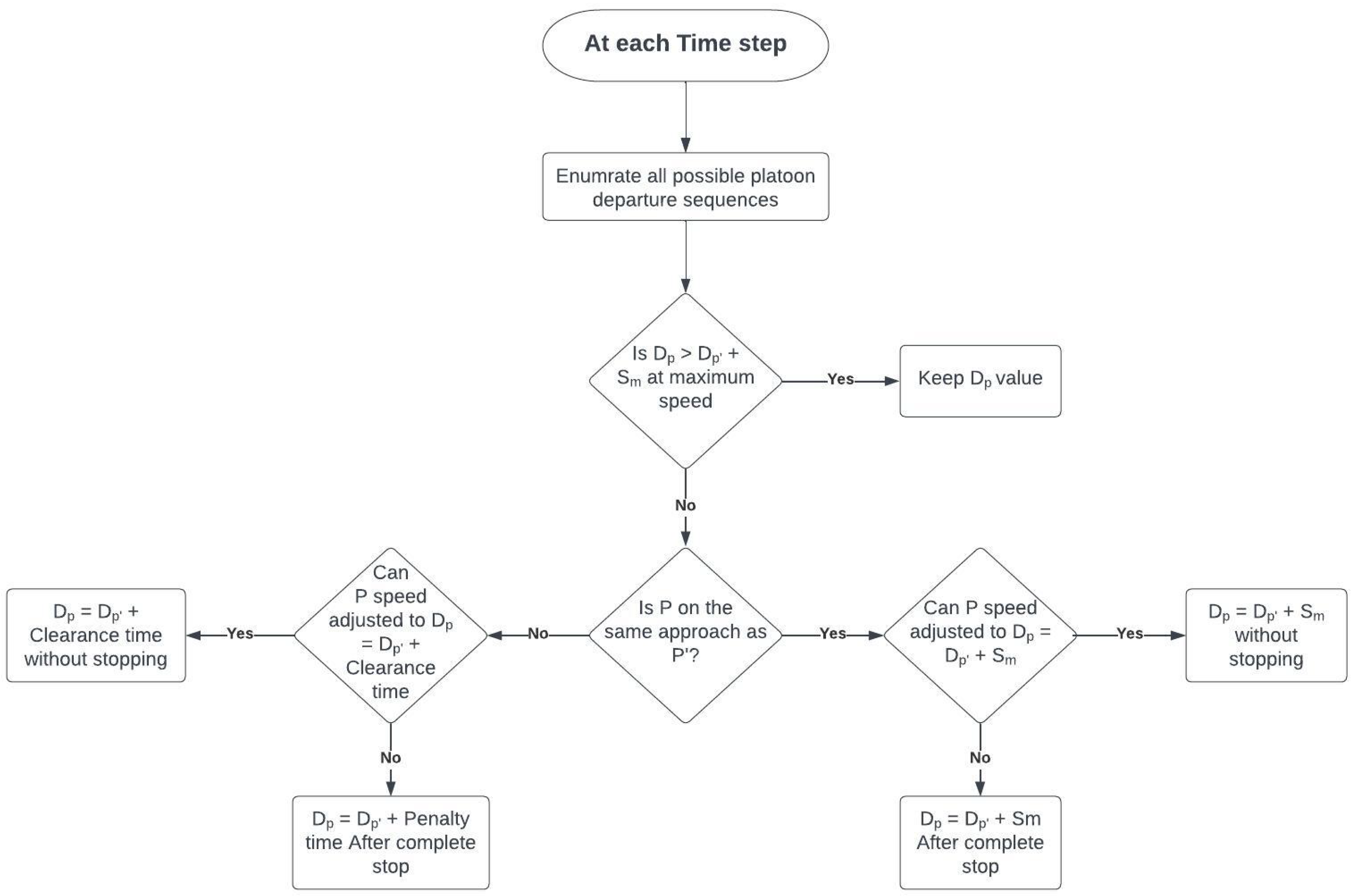
Figure 5 visually represents the departure sequence algorithm’s flowchart, illustrating how the algorithm operates at each time step. The traffic signal enumerates all possible platoon departure sequences for every time step. The algorithm then evaluates each departure sequence to determine the associated average vehicle delay. Ultimately, the departure sequence with the smallest average vehicle delay is selected, ensuring the most efficient progression of platoons through the intersection. The algorithm optimizes signal timings and improves overall traffic flow by continuously adapting to the evolving traffic conditions.

In summary, the algorithm collects data from connected HCVs to estimate and identify platoons, calculates the average vehicle delay for each departure sequence, and selects the one with the minimum delay. Subsequently, traffic signal timings are adapted to accommodate the optimized platoon departure sequence, enhancing intersection efficiency and reducing congestion.

3.3. Advisory Speed Trajectory Algorithm

The advisory speed trajectory algorithm employs different strategies to optimize traffic flow and safety, aiming to minimize the number of stops and reduce travel time by allowing some heavy vehicles (HCVs) to accelerate and pass through intersections before the traffic light turns red. This approach ensures smoother traffic flow by enabling some HCVs to clear the intersection without stopping. To achieve this, the algorithm modifies the Intelligent Driver Model (IDM) to better accommodate the unique operational constraints of heavy vehicle drivers approaching the intersection. The algorithm continuously searches for the optimal platoon departure order using Equation (4) at each time step, prioritizing the departure sequence that minimizes the average vehicle delay. An advisory speed is assigned to the lead HCV of each platoon based on three distinct scenarios:

• Maximum Speed Strategy: If the platoon can reach the intersection within the current green phase while maintaining the flow speed, it follows the maximum speed strategy. The advisory speed is set to the predefined maximum allowable speed ($V_{max}$), which aligns with legal speed limits for heavy vehicles.
• Deceleration Speed Strategy: If the platoon cannot reach the intersection within the current green even at $V_{max}$, but can reach the next green phase while traveling within the allowable speed range ($V_{min}\le V\le V_{max}$), it follows a deceleration speed strategy. The advisory speed is adjusted dynamically to ensure smooth progression without stopping.
• Deceleration Stop Strategy: If the platoon cannot reach the current green at $V_{max}$ and would arrive too early at the next green phase even at $V_{min}$, the deceleration stop strategy is applied. In this case, the platoon follows a gradual deceleration while maintaining a safe driving speed until it reaches the intersection. The deceleration rate follows the standard behavior modeled in VISSIM’s internal engine for heavy vehicles.

To ensure the algorithm’s effectiveness, the advisory speed updates are synchronized with the simulation time step, allowing real-time adjustments based on traffic conditions. The threshold for selecting the maximum speed strategy is determined by a predefined time-to-intersection value relative to the green light duration. This ensures that platoons are dynamically assigned speeds that optimize their progression while avoiding unnecessary stops. Additionally, if a platoon cannot pass within the available green time due to signal constraints, the algorithm dynamically shifts its strategy by either adjusting speed or transitioning it to the next green cycle.

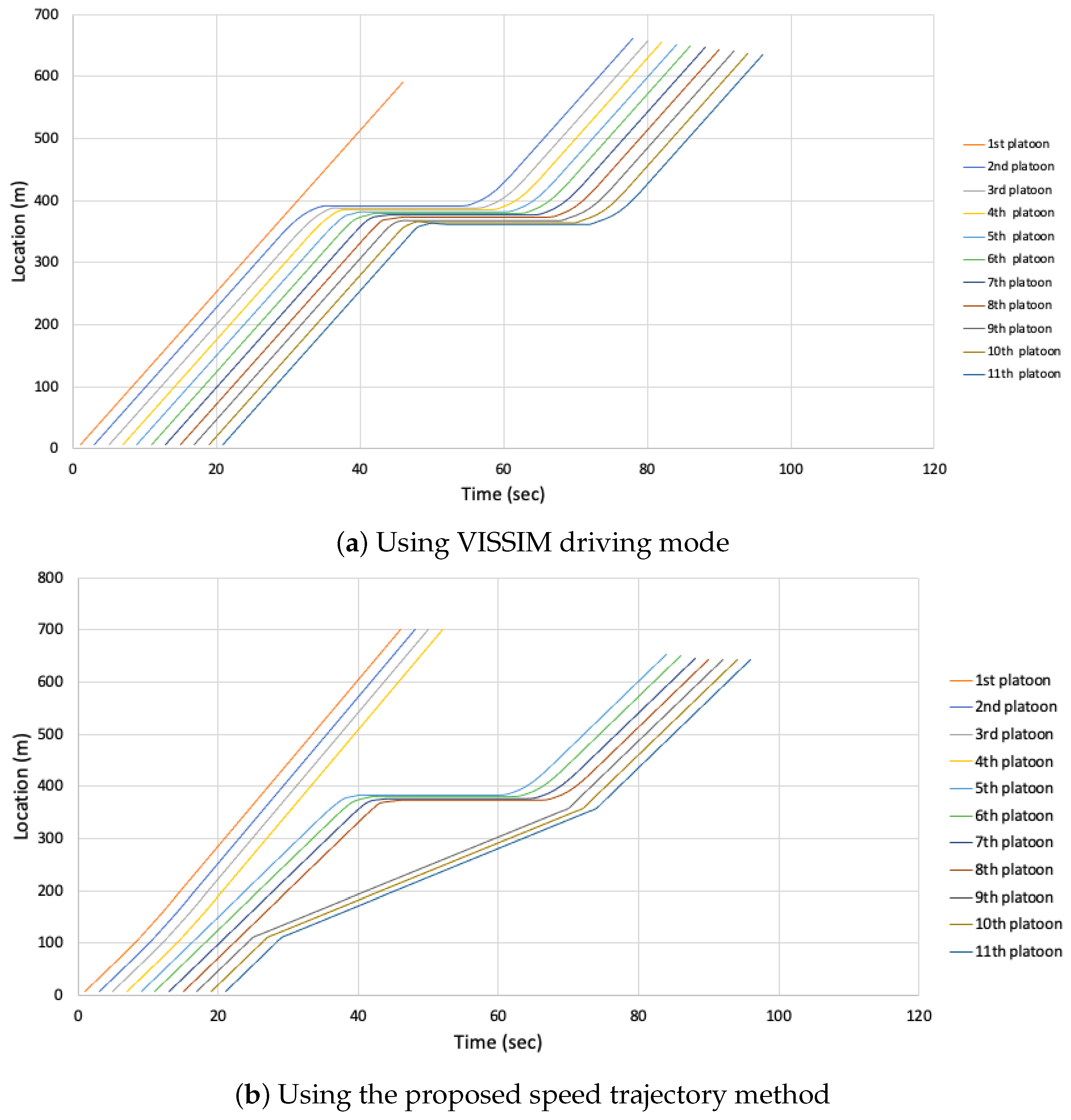
By integrating the Intelligent Driver Model (IDM) with the three adaptive speed scenarios, the proposed advisory speed trajectory algorithm effectively reduces the number of stops, minimizes delays, and enhances intersection efficiency for heavy vehicle platoons. Figure 6 visually demonstrates the impact of this approach on HCV progression through intersections.

3.4. Study Area

This research leverages the simulation of a real-world intersection—Orange Avenue intersecting Adams Street in Tallahassee, Florida—to assess the performance of the developed algorithm for optimized signal control. This intersection, chosen due to its unique geometric design and high traffic volume, including a substantial proportion of heavy connected vehicles (HCVs), offers an ideal environment to test the algorithm’s effectiveness in managing HCV platoon departure sequences and reducing intersection delays. The simulation accurately mimics the intersection’s actual traffic conditions and traffic signal system, providing a cost-effective, efficient, and safe platform to fine-tune and optimize the algorithm’s parameters before potential real-world deployment. This precise representation of real-world traffic flow yields critical insights into the algorithm’s likely performance under genuine traffic conditions and its potential in enhancing traffic flow and freight logistics operations at intersections, ultimately contributing to more efficient urban traffic management.

Field Data Collection

Field data collection is an essential component of traffic studies as it provides real-world information to improve the accuracy and reliability of simulation models [39]. This study collected data on the number of heavy vehicles on each approach, Traffic-Movement Counts (TMC), queue lengths, and average speeds for each approach. The collected data, including speed, queue length, and TMC information, were used for calibration and as inputs for the simulation model, providing a more realistic representation of traffic conditions and enabling a more robust analysis of the study area.

3.5. Base Model Development

The simulation experiments were conducted using VISSIM. The study site was a major intersection in Tallahassee, Florida (Orange Ave and Adams Street), selected due to its high volume of freight traffic. The simulation was configured to replicate real-world conditions, incorporating distinct behavior models for non-CVs, platoon leaders, and platoon followers.

The development of a VISSIM base model is a critical step in traffic-simulation modeling, as it provides the foundation for subsequent evaluations and analyses. The base model was constructed to replicate real-world traffic conditions accurately while adhering to the Florida Department of Transportation (FDOT) Traffic Engineering Manual guidelines. The base model-development process involved the following components:

• Network Design: The intersection layout, lane configurations, and approach geometries were modeled based on actual roadway characteristics.
• Signal Timing: The signal phasing and timing plans were obtained directly from traffic signal engineers, ensuring that the simulation accurately reflects real-world operations.
• Speed Profile: Speed limits and acceleration/deceleration profiles were assigned based on observed vehicle behavior to maintain realistic vehicle movements.
• Vehicle Input: Traffic input was derived from field-collected data, including traffic-movement counts, queue lengths, and average speeds, to represent real-world demand.
• Vehicle Routing: Origin–destination flows were modeled based on observed movement patterns to ensure that vehicle distributions were realistic.

Once the base models were developed, a calibration procedure was conducted to ensure accuracy in simulating field operations, after which they were executed under the PM peak hour scenario.

3.5.1. Simulation Configuration

Each simulation scenario was run for a total duration of 3600 s, with a simulation step of 1 s to ensure accurate vehicle-movement representation. The total intersection demand was 5200 veh/hr, distributed across all approaches based on observed turning movement counts, with a heavy vehicle composition of 28%. The Wiedemann 99 car-following model was used, with parameter adjustments to reflect platoon behavior and heavy vehicle acceleration constraints. A total of 20 replications were conducted to ensure statistical significance and account for variability in stochastic traffic conditions. For each scenario, results were averaged across 20 replications, and 95% confidence intervals were calculated to validate statistical significance. To ensure reproducibility, the key simulation parameters are summarized in

Table 1. Simulation configuration in VISSIM.

Parameter	Value	Source
Simulation Duration	3600 s	Scenario Definition
Simulation Resolution	1 s	VISSIM Default
Number of Replications	20	Recommended for statistical significance
Traffic Flow	5200 veh/h	Manual Counts
Heavy Vehicle Percentage	28%	Manual Counts
Car-Following Model	Wiedemann 99	VISSIM Default
Minimum Time Headway	1 s	Calibrated value

.

3.5.2. Driving Model

In order to accurately simulate the different types of vehicles and their driving behavior within the VISSIM model, three distinct scenarios were considered based on the vehicle type and its position within an HCV platoon.

In the first scenario, if the vehicle is a traditional heavy vehicle, the standard VISSIM internal driving model is adopted. This model accounts for the typical driving behavior and characteristics of traditional heavy vehicles, such as acceleration, deceleration, and car-following patterns.

In the second scenario, if the vehicle is a connected heavy vehicle (HCV) and it is a follower vehicle within a platoon, the cooperative adaptive cruise control (CACC) model is adopted. Lastly, if the vehicle is a connected HCV and it is the leader of a platoon, the Intelligent Driver Model (IDM) with trajectory advisory speed is adopted. This approach allows the lead vehicle to receive guidance on optimal speeds to minimize the number of stops at intersections, ultimately improving the overall traffic flow and reducing congestion for the entire platoon.

By considering these three scenarios in the VISSIM model, the simulation can accurately represent the diverse driving behaviors and interactions between traditional and connected HCVs in real-world traffic conditions, ultimately providing a more reliable and valid evaluation of the proposed HCV platoon-based algorithm’s performance.

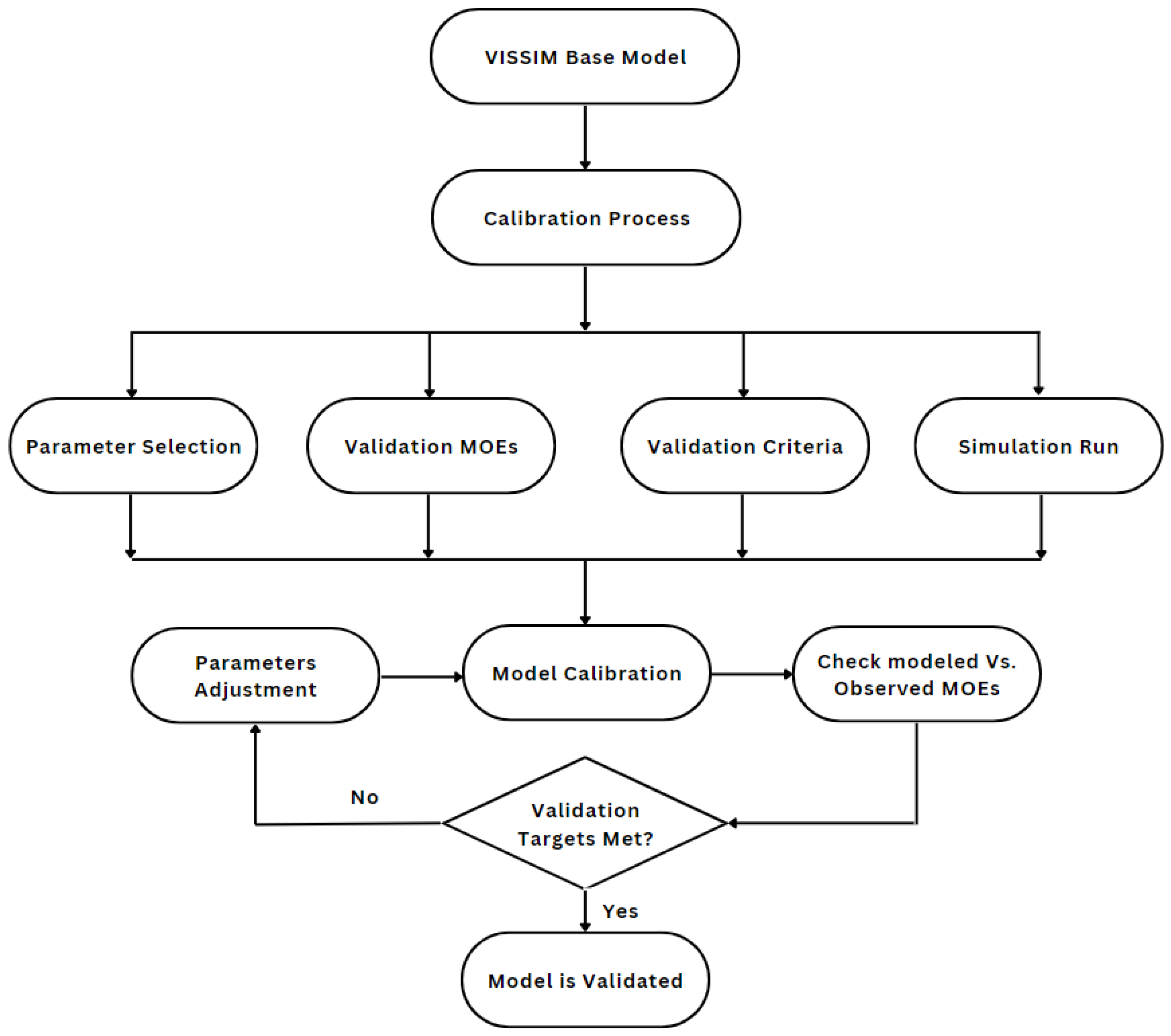
3.5.3. Model Calibration

The calibration of traffic-simulation models such as VISSIM is essential to ensure accurate predictions of traffic flow and safety [39]. This process involves adjusting the model’s parameters to match observed traffic data. Before calibration, model verification strategies should be conducted to increase the effectiveness of the verification process in micro-simulation analysis. These strategies include observing vehicle behavior at low demand levels, reviewing MOEs, following a single vehicle through the network, and performing visual inspections to ensure the model replicates field observations. The latest software version should be used, and simple test problems should be coded for manual comparison. Color codes should also be used to identify links, and intersection attributes should be reviewed. The verification process was conducted for the VISSIM model. These strategies were instrumental in ensuring the model’s accuracy and served as a crucial first step in the calibration process.

The model calibration process involves determining which parameters require calibration, selecting suitable measures of effectiveness (MOEs) and data for model validation, calculating the number of simulation runs needed to achieve a 95% confidence level with a 5% margin of error for all MOEs, identifying validation criteria and targets, and adjusting the selected parameters iteratively until the model outputs accurately reflect the observed field traffic conditions or meet the validation targets. Figure 7 shows a general model calibration procedure that transportation professionals can use to calibrate simulation models accurately.

For the VISSIM model used in this study, the main calibration focus was parameters related to driver behavior and heavy vehicle characteristics. The calibration process involved adjusting commonly used driver behavior parameters, such as Wiedemann’s 1974 car-following model, waiting time before diffusion, and minimum headway in the lane-changing algorithm.

Vehicle parameters, including traffic composition, vehicle length, desired speed, desired acceleration/deceleration, maximum acceleration/deceleration, and other attributes associated with each modeled heavy vehicle type, were also examined. Additionally, signal-control parameters and the impact of simulation resolution on the response to traffic controls were considered.

The validation stage involved comparing simulated MOEs to their corresponding observed values, and three MOEs were selected for validation purposes: traffic movements, queue length, and link speed. These MOEs were used to ensure that the calibrated model accurately reflected real-world traffic conditions and produced reliable results.

4. Results

To evaluate the effectiveness of the developed platoon-based signal-optimization algorithm, two key performance metrics were considered:

• Average HCV delay: The delay experienced by heavy connected vehicles (HCVs), calculated in VISSIM as the difference between actual travel time and the time required to traverse the intersection under free-flow conditions.
• Total number of stops: The average number of times HCVs come to a complete stop before crossing the intersection.

To assess the effectiveness of the developed algorithm, a non-dimensional Performance Index (PI) was applied, integrating both delay and stop frequency into a single measure. The transformation strategy follows Equation (9):

$$\mathit{PI}=\mathit{Average} \mathit{HCVD} \mathit{Delay} \mathit{Ratio}+\mathit{Average} \mathit{Number} \mathit{of} \mathit{Stops} \mathit{Ratio}$$

(9)

Each metric is normalized based on the maximum observed value across all scenarios, ensuring comparability across different control methods. The performance measure ratio is computed using Equation (10):

$$\mathit{Performance} \mathit{Measure} \mathit{Ratio}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{x_i}{X_{max{x}_i}}}$$

(10)

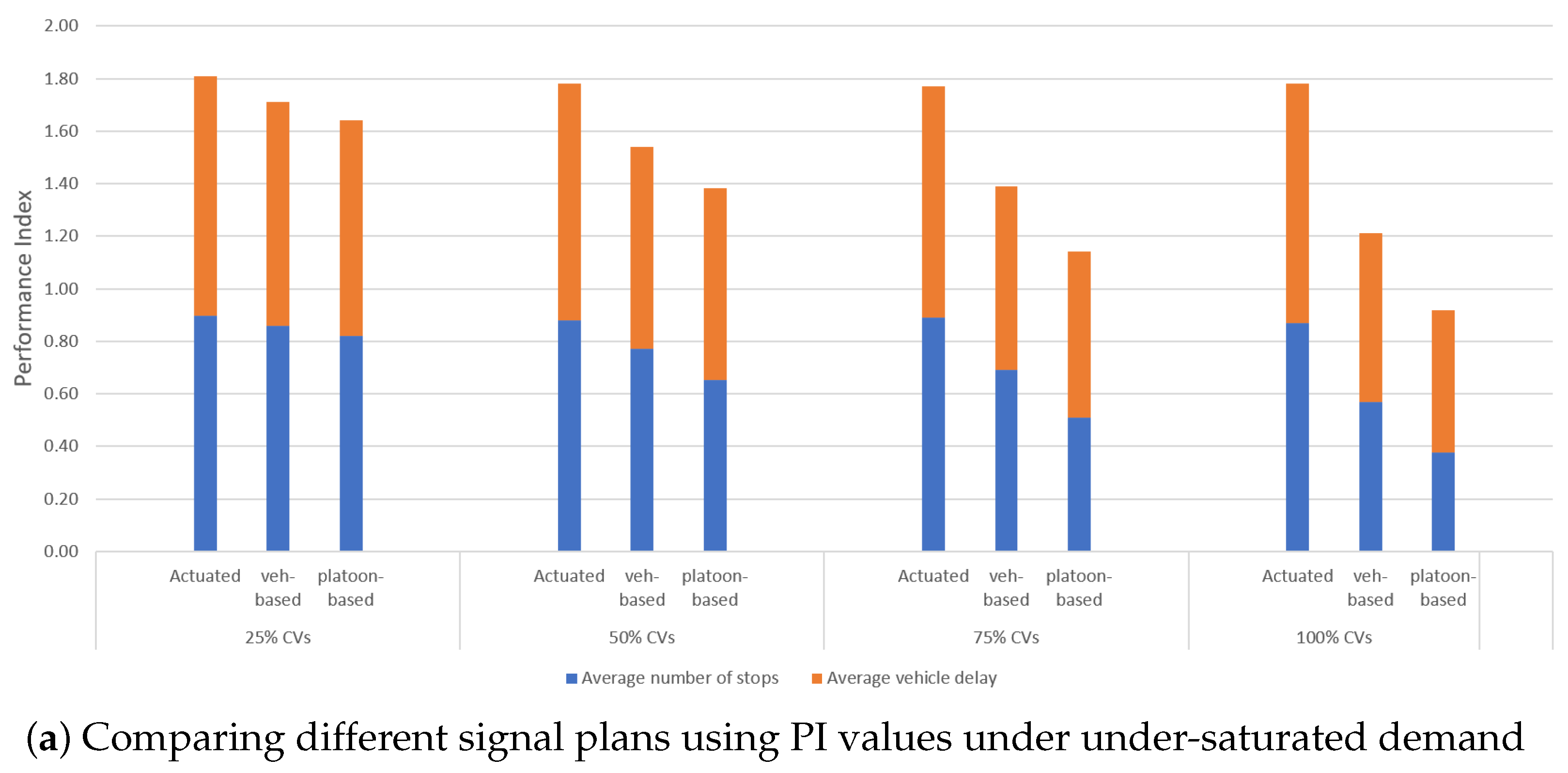
where n represents the total number of simulation runs, $x_i$ is the average performance measure for each run, and $X_{max{x}_i}$ is the highest observed performance measure across all runs. The PI values were calculated for all 24 scenarios tested in VISSIM, with results presented in Figure 8.

4.1. Statistical Validation

Given that all results were obtained through simulation-based experiments, statistical validation was performed to confirm the significance of the observed improvements:

A t-test was conducted to compare the platoon-based approach against the actuated signal-control method, analyzing differences in both delay and number of stops. Confidence intervals (95%) were calculated to account for variability across multiple simulation runs. Results showed statistically significant improvements (p < 0.05) for all penetration levels of connected vehicles (CVs), confirming that the observed reductions in delay and stops were not due to random variations.

The following sections present a detailed analysis of HCV delay and total number of stops, highlighting the advantages of the platoon-based approach over conventional signal-control strategies.

4.1.1. Average HCV Delay

Reducing delay is a primary objective of the platoon-based signal-optimization algorithm. The analysis examined how the algorithm improves HCV delay compared to both actuated signal control and the individual vehicle-based approach across different connected vehicle (CV) penetration levels.

The results as shown in

Table 2. Reduction in HCV delay across CV penetration levels.

Condition	Platoon-Based vs. Actuated (%)	p-Value	Platoon-Based vs. Vehicle-Based (%)
Under-Saturated	50%	<0.001	30%
Over-Saturated	30%	<0.05	18%

indicate that the platoon-based algorithm significantly reduces HCV delay under both under-saturated and over-saturated conditions. In under-saturated demand conditions, the algorithm achieved a 50% reduction in delay compared to actuated signal control, with statistical significance (p < 0.001). When compared to the vehicle-based approach, the reduction was 30% (p < 0.01). Under over-saturated demand conditions, the delay reduction was 30% relative to actuated signal control (p < 0.05), while the improvement over the vehicle-based method was 18% (p < 0.05). These reductions highlight the efficiency of the platoon-based approach in minimizing delay across varying traffic scenarios.

4.1.2. Total Number of Stops

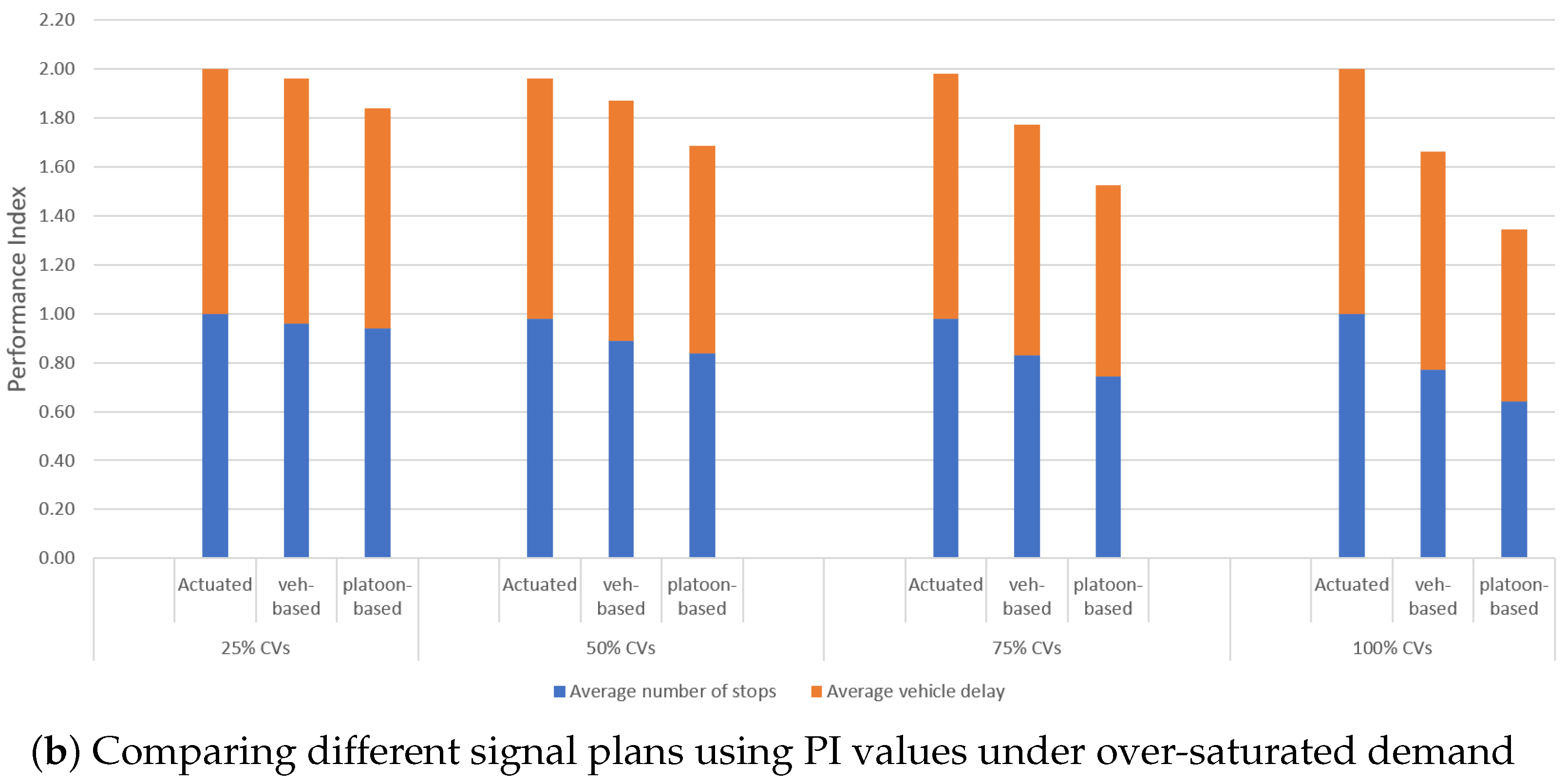
Minimizing the number of stops is a key objective of the platoon-based signal-optimization algorithm, as reducing unnecessary stopping improves traffic flow and overall intersection efficiency. The analysis compared the performance of the platoon-based approach against both actuated signal control and the individual vehicle-based algorithm across different penetration levels of connected vehicles (CVs).

The findings demonstrate that the platoon-based algorithm effectively decreases the frequency of stops in both under-saturated and over-saturated traffic scenarios, as shown in

Table 3. Reduction in the number of stops across CV penetration levels.

Condition	Platoon-Based vs. Actuated (%)	p-Value	Platoon-Based vs. Vehicle-Based (%)
Under-Saturated	55%	<0.001	40%
Over-Saturated	35%	<0.01	17%

. Under under-saturated demand conditions, the number of stops decreased by 55% compared to actuated signal control (p < 0.001) and by 40% when compared to the vehicle-based algorithm (p < 0.01). Under over-saturated demand conditions, the reduction in the number of stops was 35% relative to actuated signal control (p < 0.01), while the improvement over the vehicle-based method was 17% (p < 0.05). These reductions highlight the ability of the platoon-based approach to optimize vehicle movements and minimize unnecessary stopping.

The reduction in the number of stops is most pronounced under under-saturated conditions, where smoother platoon coordination allows vehicles to pass through intersections with minimal disruption. By prioritizing platoon movements and synchronizing their arrivals with green signal phases, the algorithm significantly reduces stop occurrences, leading to improved traffic progression.

In over-saturated conditions, although the reduction in stops is lower compared to under-saturated scenarios, the platoon-based approach still provides statistically significant improvements. The efficiency of the algorithm under these conditions suggests its robustness in handling high traffic volumes while minimizing disruptions caused by frequent stopping.

Overall, these findings reinforce the effectiveness of the platoon-based optimization strategy in reducing stop occurrences, particularly at high CV penetration levels. The ability to limit stop frequency contributes to smoother traffic flow and enhances intersection efficiency, making this approach a viable alternative to conventional signal-control methods.

4.2. Computational Efficiency

Computational efficiency is a critical factor in determining the feasibility of implementing real-time traffic signal-optimization algorithms. The computational performance of the developed platoon-based algorithm was compared against the vehicle-based approach to assess its scalability and processing time under varying traffic conditions. Two Python-based implementations were developed to compute the optimal signal plans and advisory speed trajectories: one following a vehicle-based optimization and the other utilizing the platoon-based strategy. Both algorithms were executed on the same computing environment to ensure a fair comparison. The total computational time required for each algorithm was measured as a function of the total number of vehicles within the interest zone.

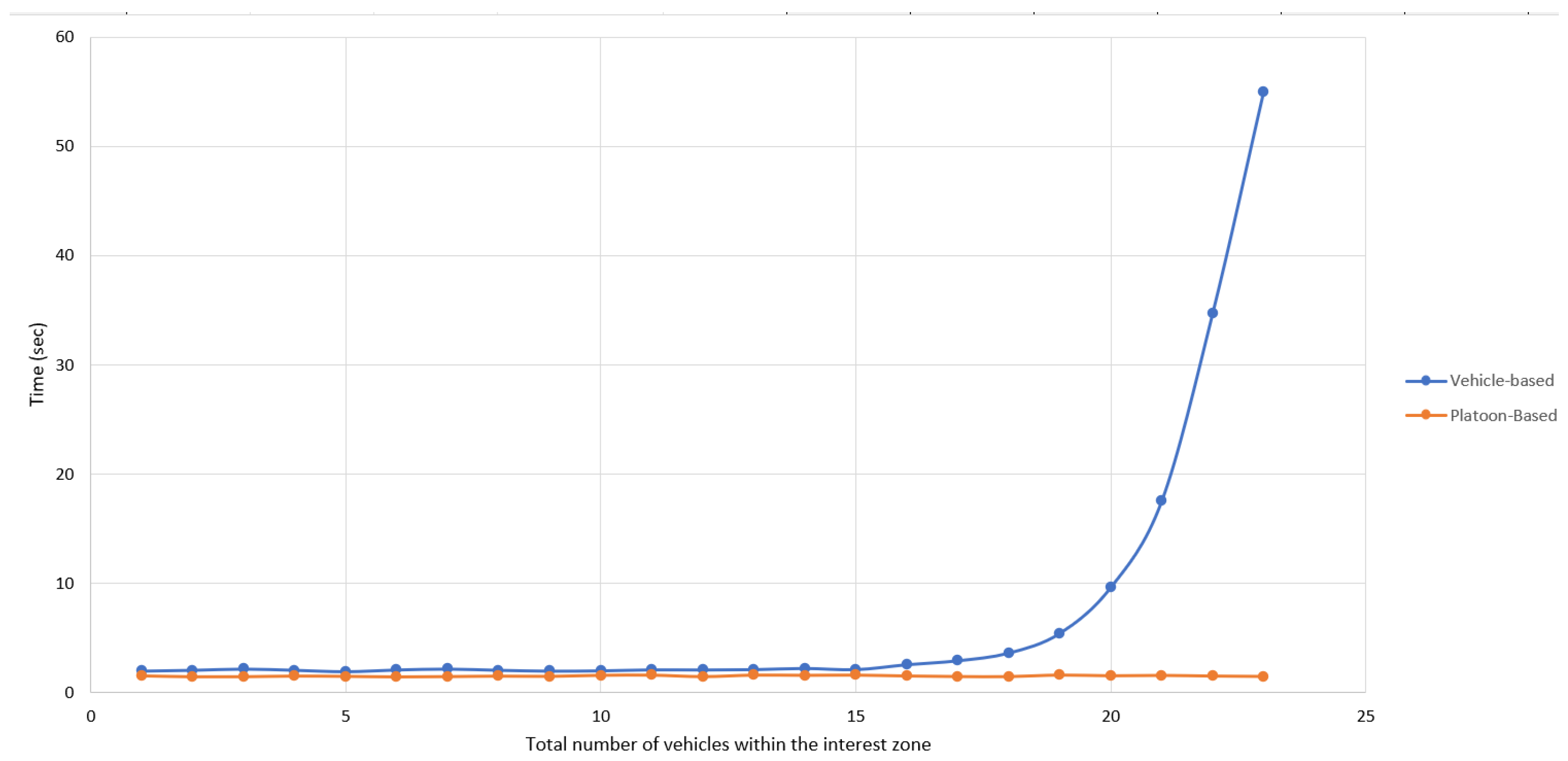
Figure 9 illustrates the computational time required by both approaches as the number of vehicles increases. The results demonstrate that the vehicle-based algorithm experiences an exponential increase in computational time as the number of vehicles grows. This is attributed to the significant increase in possible departure sequences that need to be evaluated. For example, with just ten vehicles on each approach, the number of possible sequences exceeds 180,000, while increasing this to eleven vehicles results in more than 700,000 possible departure sequences. Consequently, the vehicle-based approach becomes computationally impractical for large-scale applications.

In contrast, the platoon-based algorithm maintains a stable and low computational time, even as the number of vehicles within the interest zone increases. Since the platoon-based approach treats a group of vehicles as a single unit rather than individually optimizing each vehicle’s movement, the total number of computations remains significantly lower. This characteristic makes the platoon-based algorithm highly scalable and suitable for real-time traffic-management applications.

These findings confirm that the platoon-based algorithm not only enhances traffic efficiency but also ensures computational feasibility, making it a practical solution for real-time traffic signal control in connected vehicle environments.

4.3. Real-World Applicability, Challenges, and Future Research Directions

The effectiveness of the platoon-based signal-optimization algorithm in simulation suggests its potential for real-world implementation. However, several challenges must be addressed to ensure its practical deployment, while further research is needed to enhance its adaptability to various traffic and logistical conditions.

One of the key challenges in real-world implementation is the dependency on a well-established CV infrastructure, including vehicle-to-infrastructure (V2I) communication and reliable data-collection systems. The effectiveness of the platoon-based approach relies on a sufficient number of CHVs forming and maintaining platoons. In scenarios with low CV penetration rates, the benefits of the algorithm may be diminished, necessitating strategies to handle mixed traffic conditions. Additionally, variations in driver compliance and platoon stability due to unexpected traffic disruptions must be considered.

Integrating the algorithm with existing traffic-management systems presents another challenge. While the proposed approach optimizes signal timings dynamically, real-world constraints such as emergency vehicle prioritization, pedestrian crossings, and mixed traffic conditions introduce complexities that must be accounted for in future research. Moreover, computational efficiency, which has been demonstrated in simulation, must be validated under real-time traffic conditions to ensure the algorithm can function effectively within urban signal-control frameworks.

To improve the robustness and adaptability of the platoon-based approach, future research should explore the impact of different logistics and HV parameters on algorithm performance. Factors such as vehicle load, acceleration and deceleration characteristics, and route scheduling could influence platoon behavior and signal timing efficiency. Incorporating these parameters into the optimization process could lead to further refinements and increased applicability across diverse freight corridors.

Sensitivity analysis should also be conducted to assess how variations in key parameters, such as CV penetration rate, traffic volume, platoon size, and intersection configurations, influence the algorithm’s performance. Understanding these sensitivities will help refine the model to ensure it remains effective under a wide range of operating conditions.

Additionally, integrating artificial intelligence (AI) and machine learning techniques could enhance the adaptability of the algorithm by predicting traffic-demand fluctuations and adjusting signal timings dynamically. AI-driven models could also help refine platoon formation strategies, optimize gap acceptance, and improve decision-making in mixed traffic conditions. Further research could explore how AI-based approaches compare to rule-based optimization methods in different urban settings.

Extending the optimization to multi-intersection networks, rather than a single isolated intersection, would also provide a more comprehensive traffic-management strategy for urban environments. Additionally, evaluating the algorithm’s performance under adverse weather conditions, such as heavy rain or fog, would be essential to ensure its reliability in real-world deployments.

Finally, integrating the developed algorithm with existing traffic-management platforms and conducting real-world pilot studies will be crucial steps in validating its effectiveness beyond simulations. Collaboration with transportation agencies and logistics companies could facilitate testing in operational environments, helping bridge the gap between simulation-based research and large-scale implementation.

These research directions will contribute to refining the platoon-based signal-optimization approach, making it a more adaptable and scalable solution for improving intersection performance in connected vehicle environments.

5. Conclusions

This study introduced a platoon-based signal-optimization algorithm designed for heavy connected vehicles (HCVs) in connected vehicle (CV) environments. The algorithm prioritizes platoon movements by dynamically adjusting signal timings and providing advisory speed guidance, aiming to minimize HCV delays and the number of stops. A comprehensive evaluation was conducted using a microscopic traffic-simulation model, comparing the performance of the proposed approach against conventional actuated signal control and vehicle-based optimization strategies.

The results demonstrated that the platoon-based algorithm significantly enhances intersection performance. Under under-saturated demand conditions, HCV delay was reduced by 50% compared to actuated signal control and by 30% compared to the vehicle-based method. Similarly, the reduction in the number of stops reached 55% relative to actuated signal control and 40% compared to the vehicle-based method. Under over-saturated demand conditions, delay reductions of 30% and 18% were observed compared to actuated and vehicle-based control, respectively, while the number of stops was reduced by 35% and 17%. These improvements indicate that the platoon-based approach effectively reduces traffic disruptions, smoothens vehicle flow, and enhances intersection efficiency. Additionally, the algorithm demonstrated superior computational efficiency, as it maintained stable processing times even with increasing traffic volumes, making it a scalable solution for real-time traffic management.

Beyond traffic efficiency, the proposed algorithm also presents potential environmental and economic benefits. By minimizing stop-and-go movements and optimizing signal timings, the algorithm reduces fuel consumption, leading to lower greenhouse gas (GHG) emissions. Over time, widespread adoption of such an approach in freight corridors could contribute to significant reductions in transportation-related carbon footprints. From an economic standpoint, logistics companies could benefit from reduced fuel costs, improved delivery reliability, and lower vehicle maintenance expenses due to decreased braking and acceleration cycles. Future research should focus on quantifying these benefits using empirical fuel-consumption and emissions data to further validate the long-term sustainability of platoon-based signal control.

The implementation of the proposed algorithm in urban traffic systems requires a robust CV infrastructure, including vehicle-to-infrastructure (V2I) communication and widespread HCV adoption. While the algorithm has shown promising results in simulation, real-world deployment would need to address several challenges. One major challenge is the mixed traffic environment, where not all vehicles are equipped with CV technology. The effectiveness of the platoon-based approach may be limited when CV penetration rates are low, requiring adaptive strategies to handle conventional vehicles. Additionally, integration with existing traffic-management systems must consider factors such as pedestrian crossings, emergency vehicle prioritization, and multi-modal transportation networks. Despite these challenges, the potential benefits include reduced congestion, improved freight mobility, and enhanced traffic flow efficiency, making the algorithm a valuable component in future smart city transportation systems.

Although the study provides strong evidence supporting the effectiveness of the proposed algorithm, certain limitations should be acknowledged. First, the results are based on simulation data, which inherently involves assumptions about traffic conditions, vehicle behavior, and infrastructure capabilities. Real-world traffic dynamics, including unpredictable driving behavior and external disruptions, could influence the performance of the algorithm. Additionally, the study assumes relatively high CV penetration rates, which may not yet be feasible in all regions. The algorithm’s effectiveness under mixed traffic conditions, where only a fraction of HCVs are connected, needs further investigation. Furthermore, while computational efficiency was validated within the simulation framework, real-time implementation in large-scale networks may present additional processing constraints. Future studies should assess these challenges to ensure the practical feasibility of the proposed approach.

To further enhance the applicability of the platoon-based signal-optimization approach, several future research directions are proposed. First, integrating artificial intelligence (AI) and machine learning techniques could improve the adaptability of the algorithm by enabling real-time predictive adjustments based on evolving traffic patterns. AI-driven models could also help refine platoon formation strategies, optimize gap acceptance, and improve decision-making in mixed traffic conditions. Second, real-world pilot studies should be conducted to validate the algorithm’s effectiveness beyond simulation, assessing its performance in mixed traffic environments and varying infrastructure conditions. Third, expanding the optimization framework to multi-intersection networks would provide a more comprehensive traffic-management strategy, allowing coordinated platoon movements across multiple traffic signals. Additionally, sensitivity analysis should be conducted to examine the impact of different traffic and logistics parameters, such as varying vehicle loads, acceleration characteristics, and route scheduling, on the algorithm’s performance. Lastly, the integration of the platoon-based approach with smart city infrastructures, including connected traffic-control centers and autonomous freight systems, could further enhance the efficiency and sustainability of urban transportation networks.

This study presents a platoon-based signal-optimization algorithm that significantly reduces HCV delay and stops while improving computational efficiency. While real-world implementation faces challenges related to CV infrastructure, traffic heterogeneity, and system integration, the potential benefits for freight transportation and overall intersection performance are substantial. Future research should focus on AI-based optimizations, real-world pilot implementations, and multi-intersection scalability to ensure the broader applicability of the proposed approach. With continued advancements in connected vehicle technology, the integration of platoon-based signal control into urban traffic systems could play an important role in improving mobility and efficiency in the freight sector.