Influence of Crank Angle Offset on the Mechanical Performance of Different Hydrogen-Fueled Opposed-Piston Engine Architectures
Abstract
1. Introduction
2. Problem Description
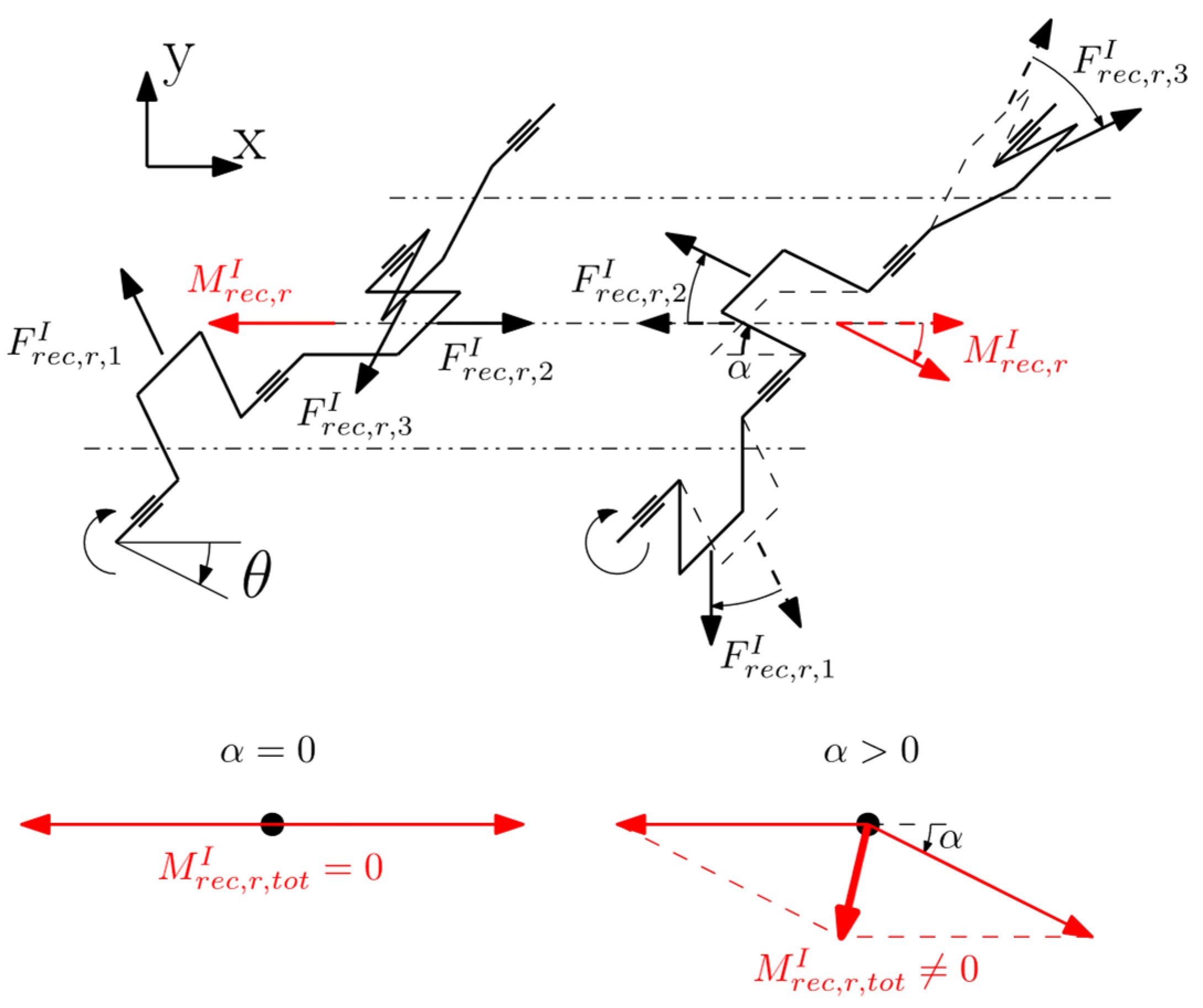
2.1. Engine Balancing Criteria
- the center of mass of the system lies on the crankshaft axis of rotation which for multi-cylinder architectures, with a generic number of cylinders , means that the vector sum of the centrifugal forces, , generated by each crank mechanism is zero:
- the vector sum of the moments generated by the centrifugal forces of each crank mechanism composing the multicylinder architecture, , is zero. Specifically, given any point along the crankshaft axis, each moment is obtained multiplying the centrifugal force by its respective lever arm with respect to the considered point, :
2.2. Design Parameters
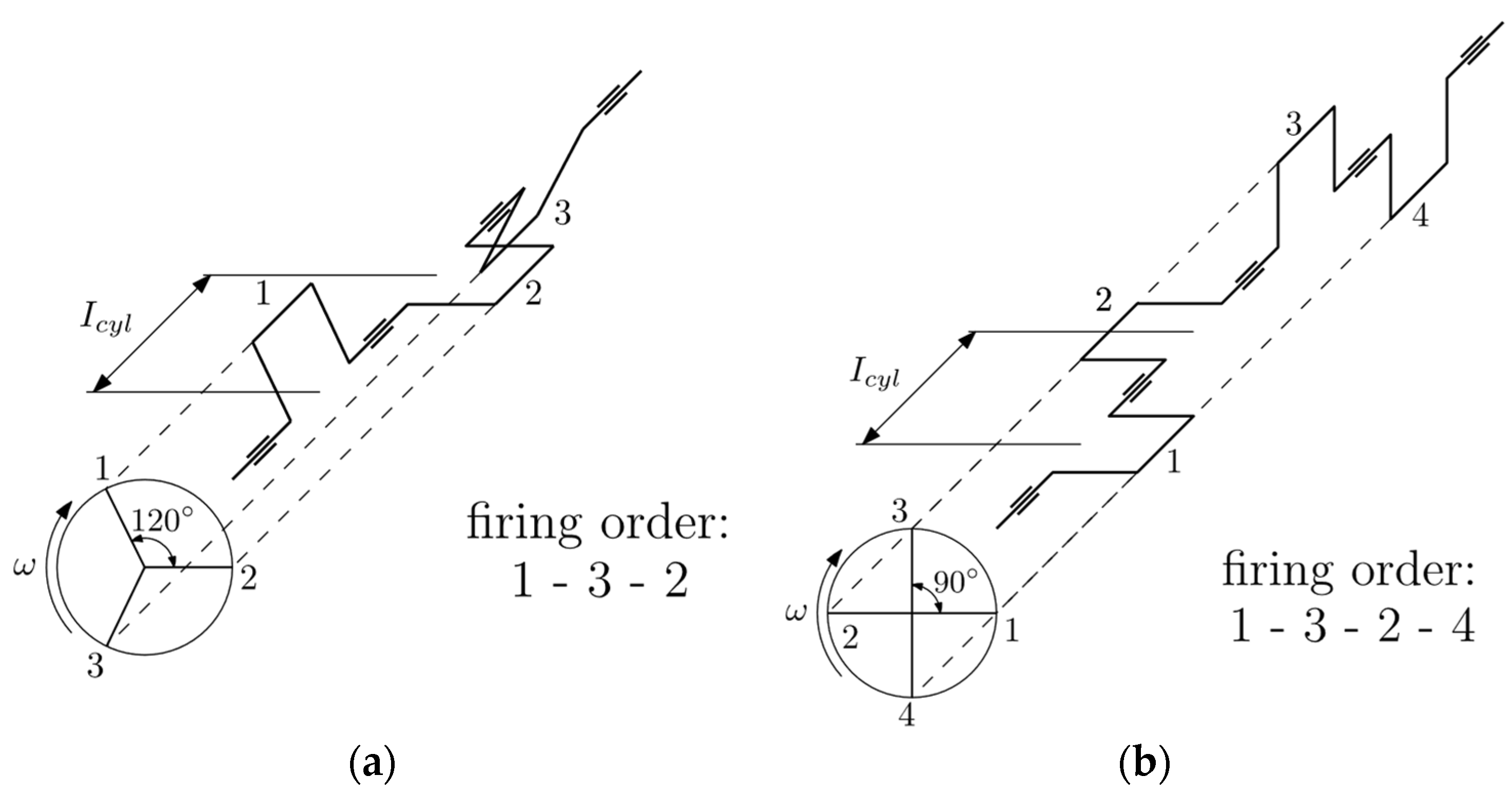
2.2.1. Number of Cylinders
- 3-cylinder;
- 4-cylinder.
2.2.2. Angle Between Crank Throws
- for the 3-cylinder crankshaft,
- for the 4-cylinder crankshaft.
2.2.3. Direction of Rotation of the Crankshafts
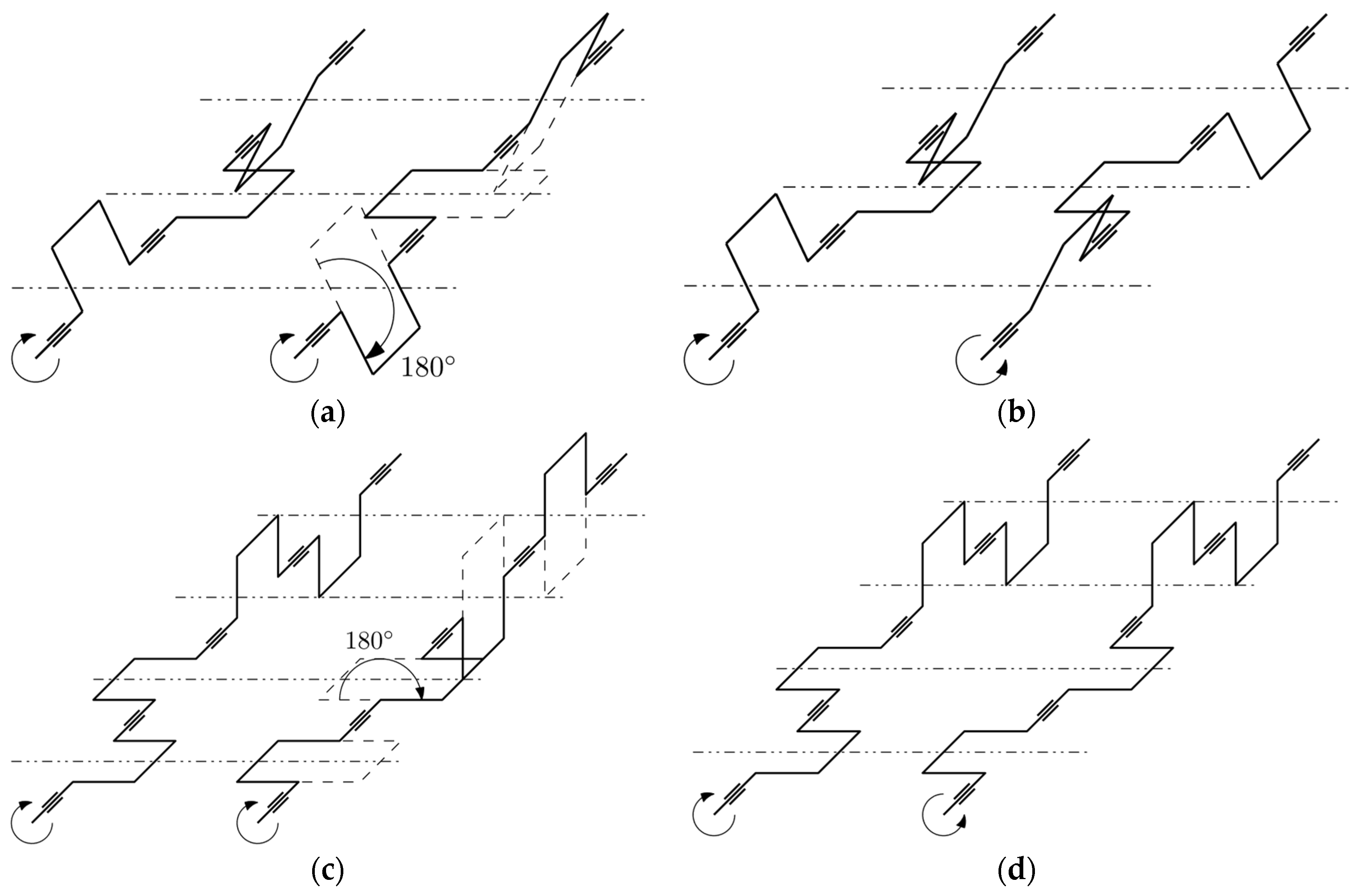
2.2.4. Offset Angle Between the Two Crankshafts
3. Model Description
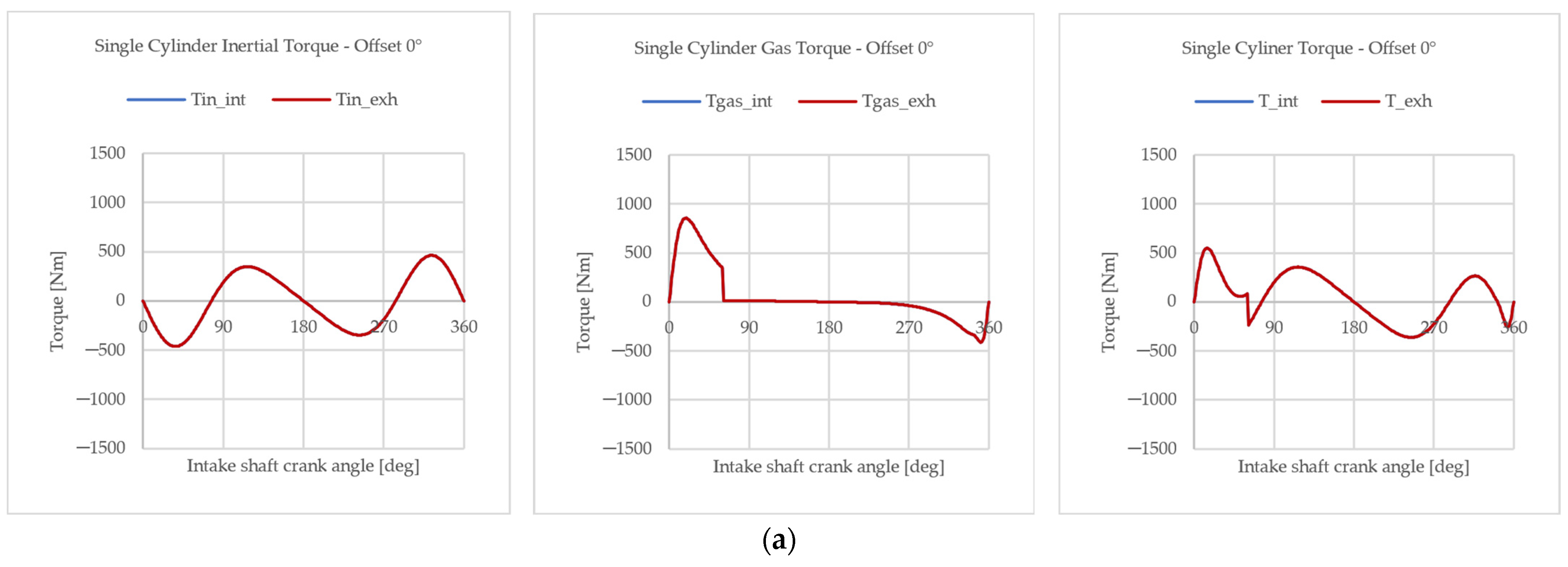
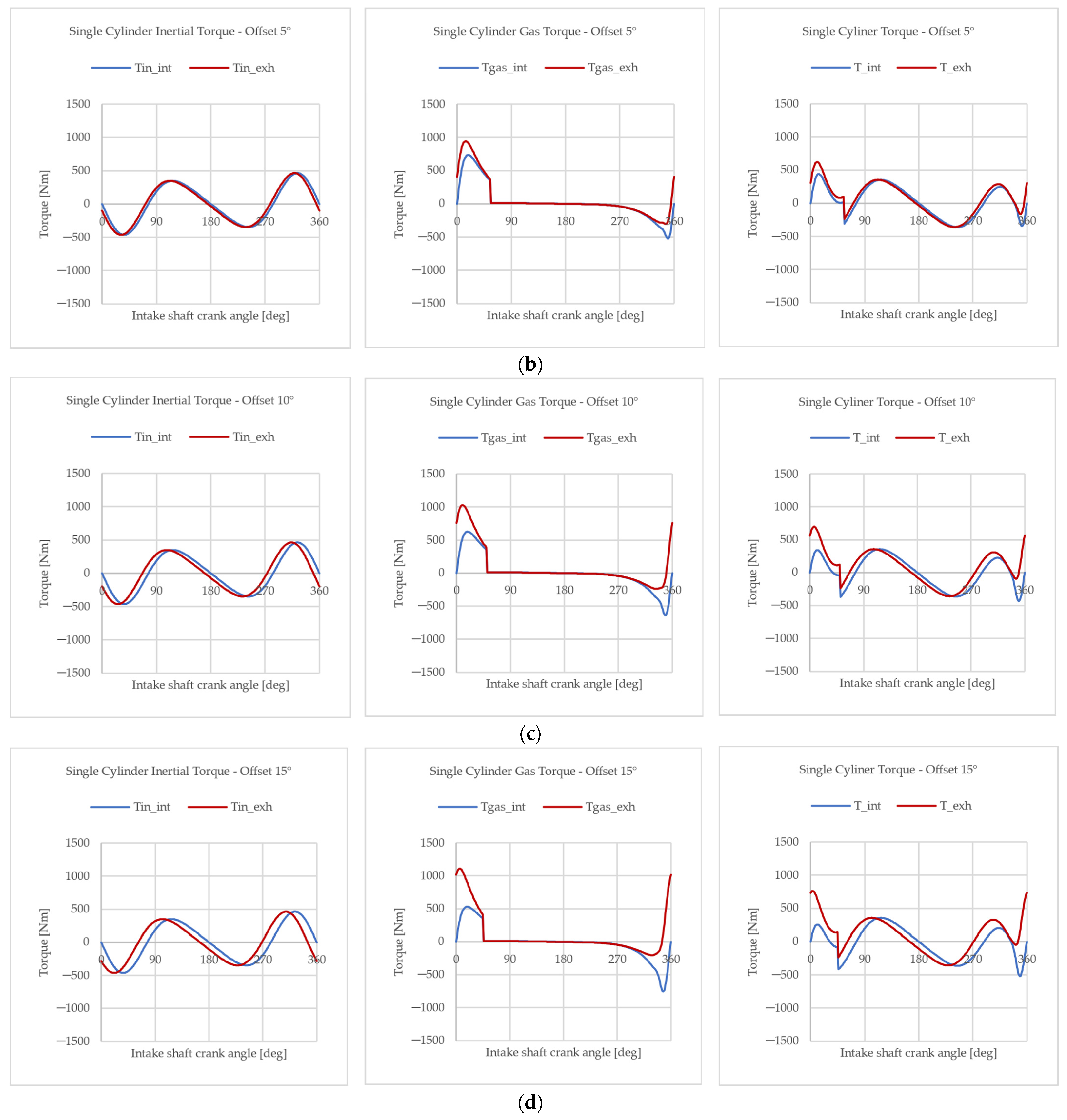
3.1. Offset Modeling
3.2. Engine Parameters
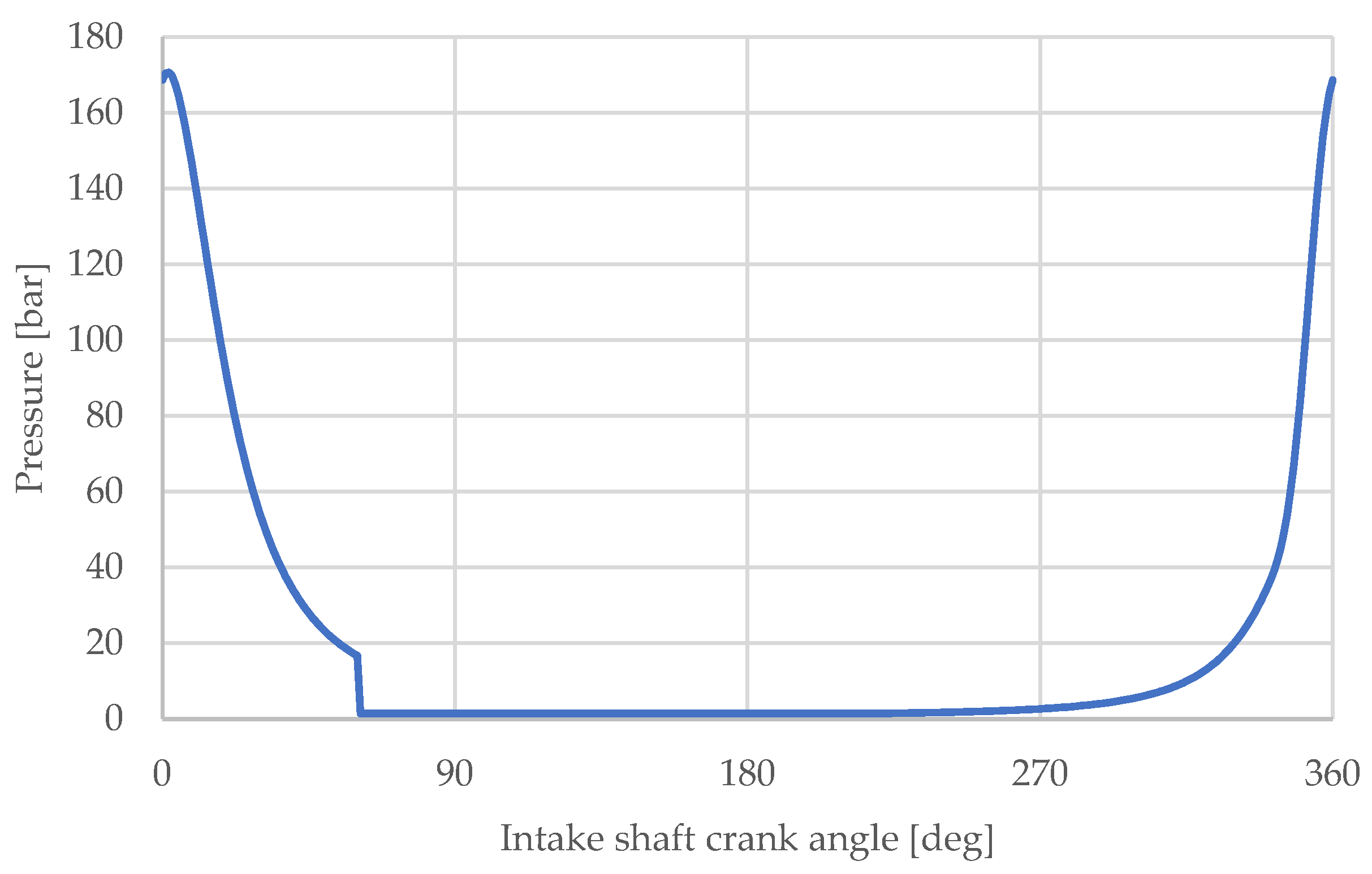
4. Results
4.1. Engine Balancing
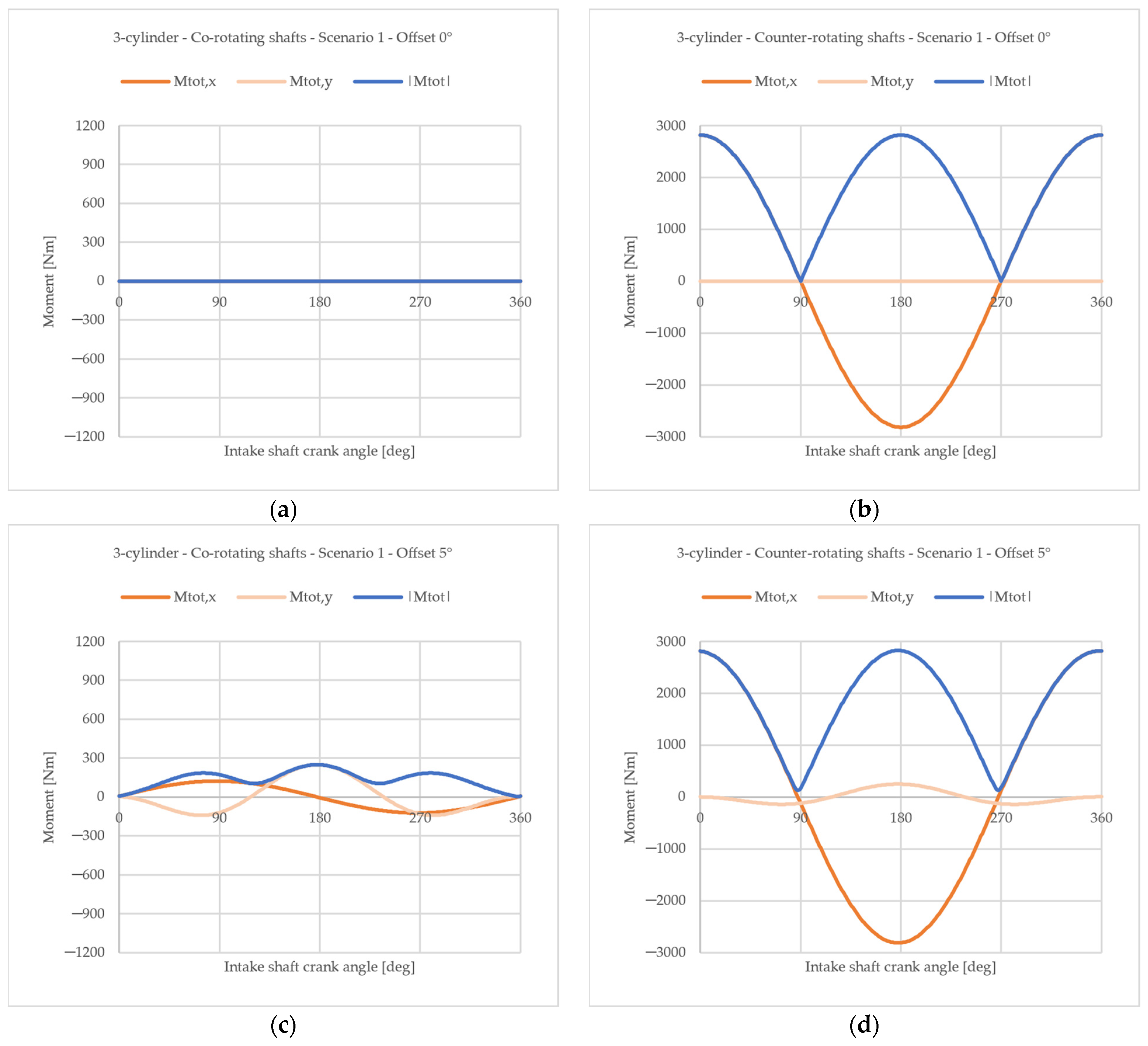
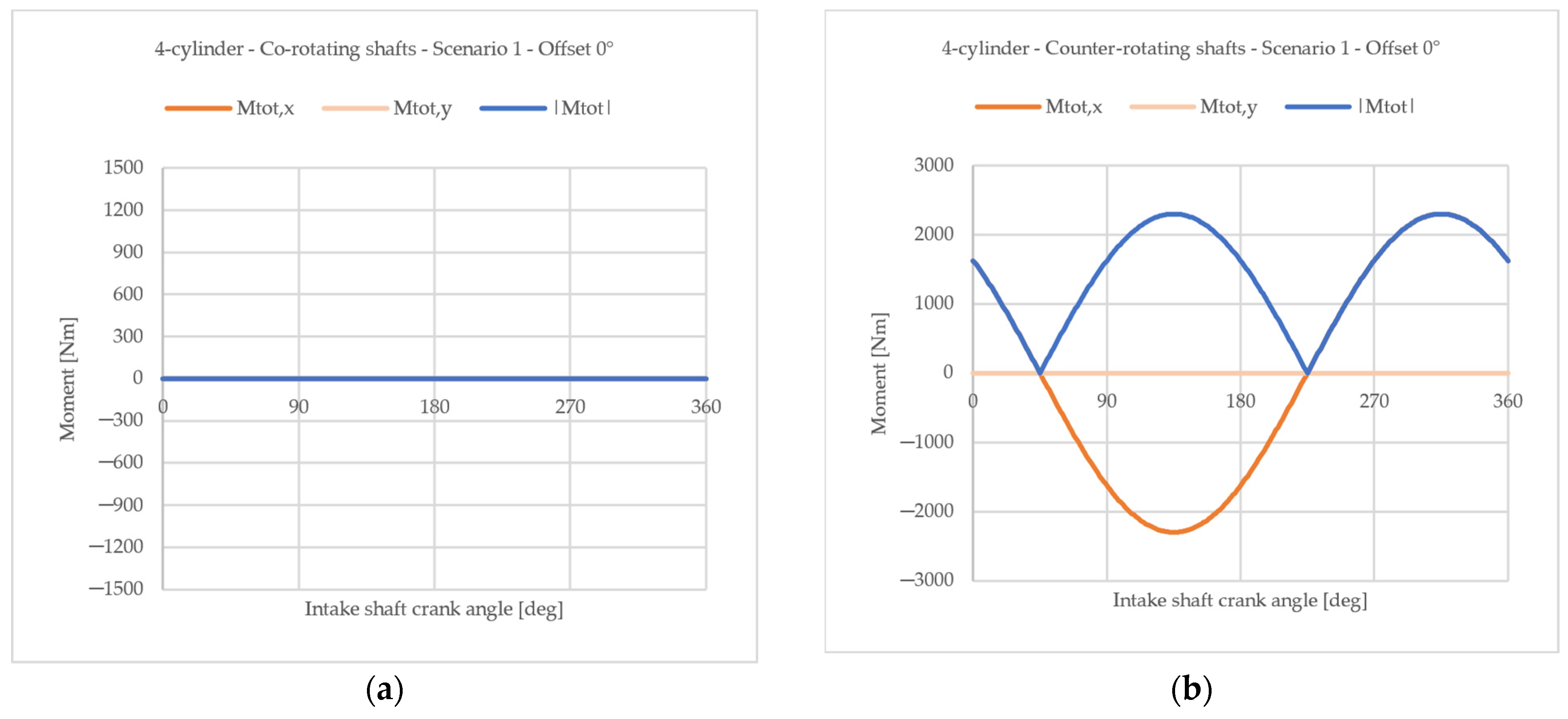
- Maximum achievable local balance with counterweights (each crank throw is balanced with respect to the centrifugal forces and the rotating portion of the first-order reciprocating forces with the consequent balancing with respect to the corresponding moments). This choice is the one that minimize the load on main journal bearings, therefore is the best in term of bearing reliability.
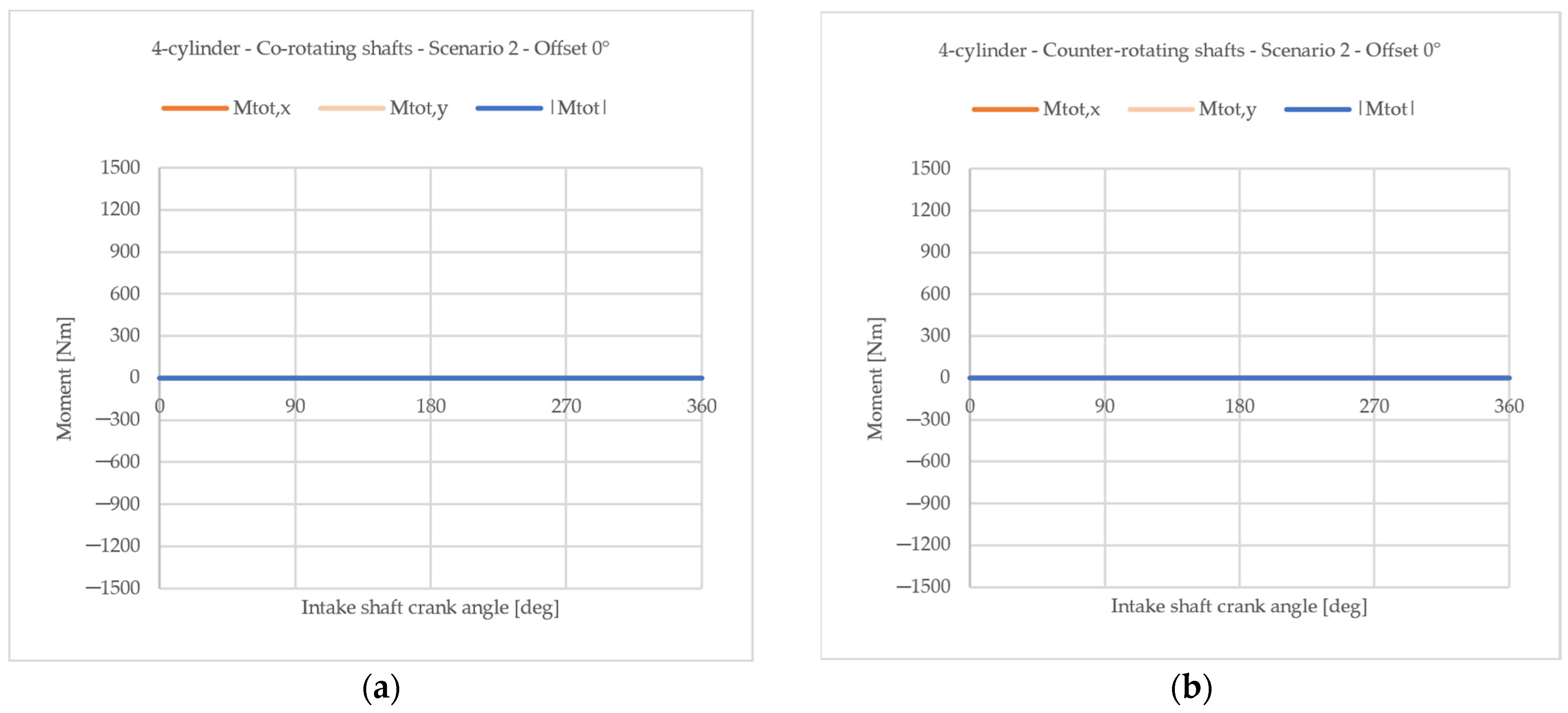
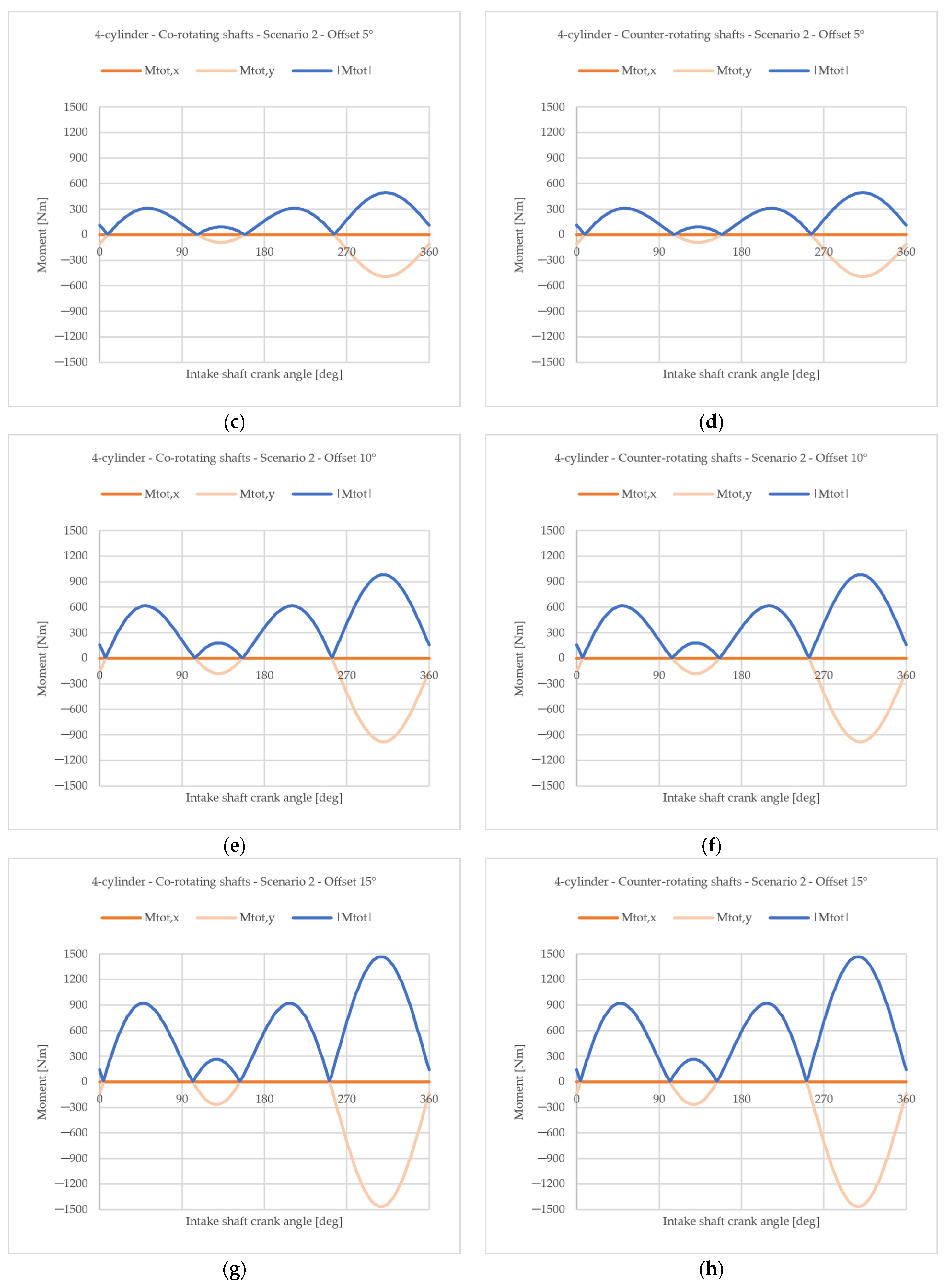
- Crank throws are balanced solely with respect to the centrifugal forces with the consequent balancing with respect to the corresponding moments (the rotating portion of the first-order reciprocating forces of each crank mechanism and the corresponding moments intentionally remain unbalanced). This choice is the one that maximize the possible interaction between the moments generated by the two crankshafts.
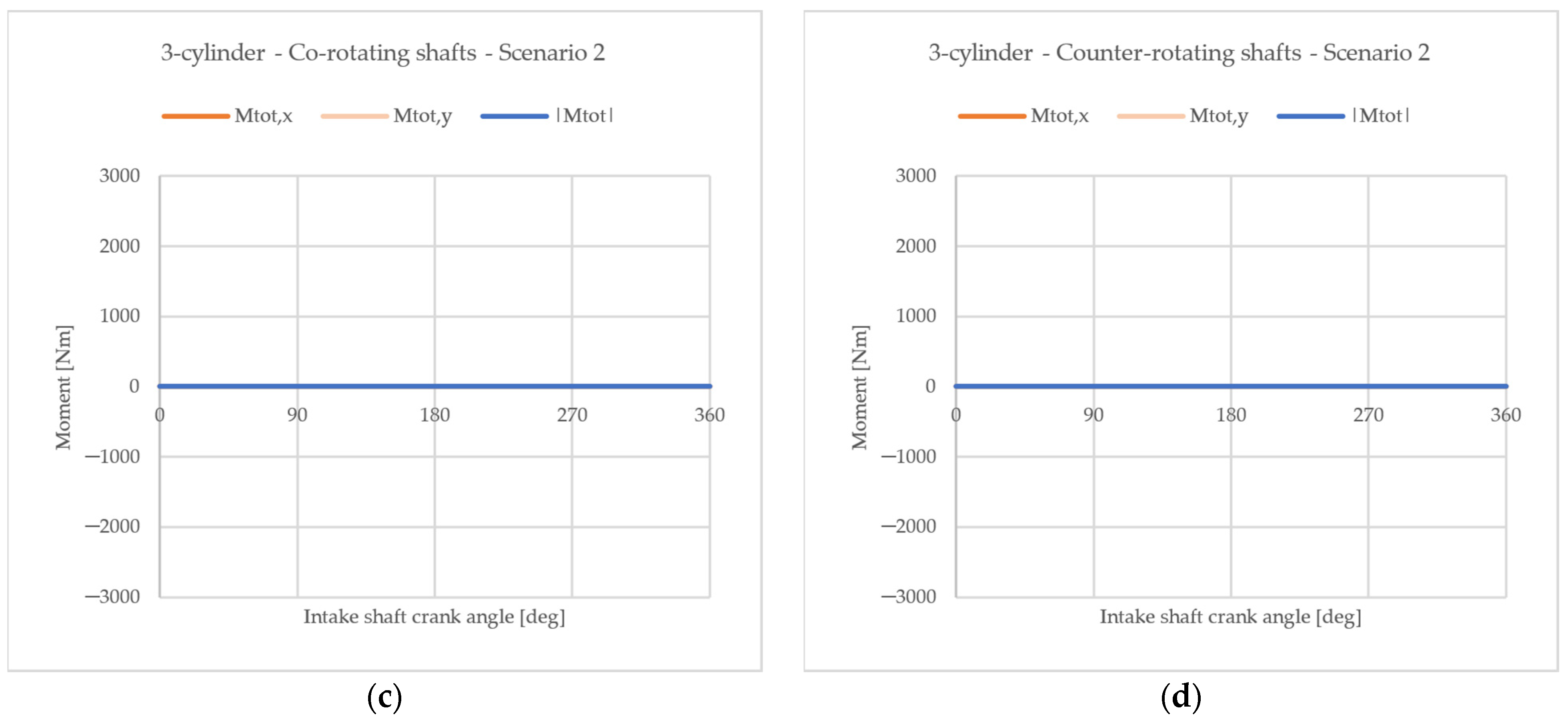
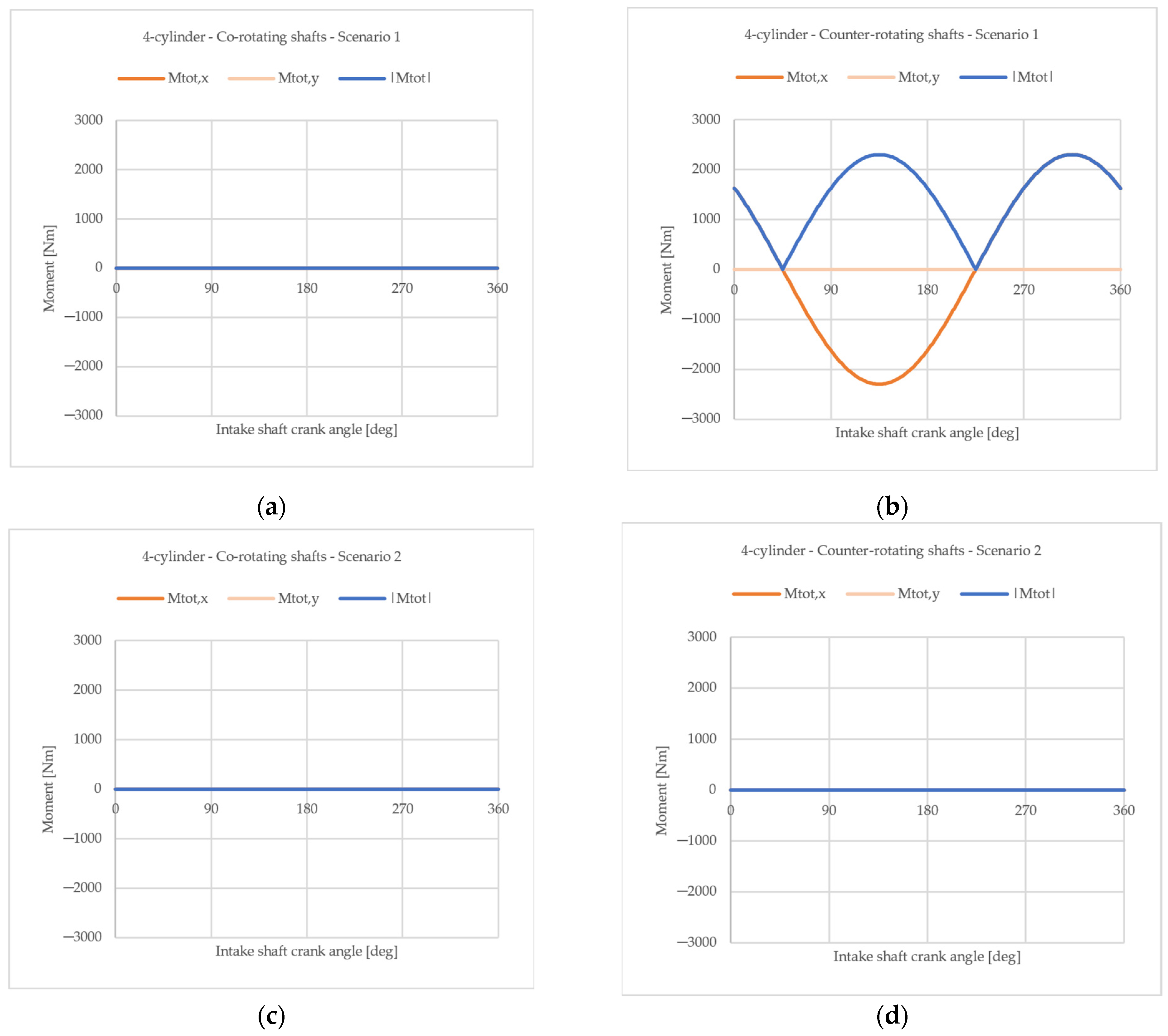
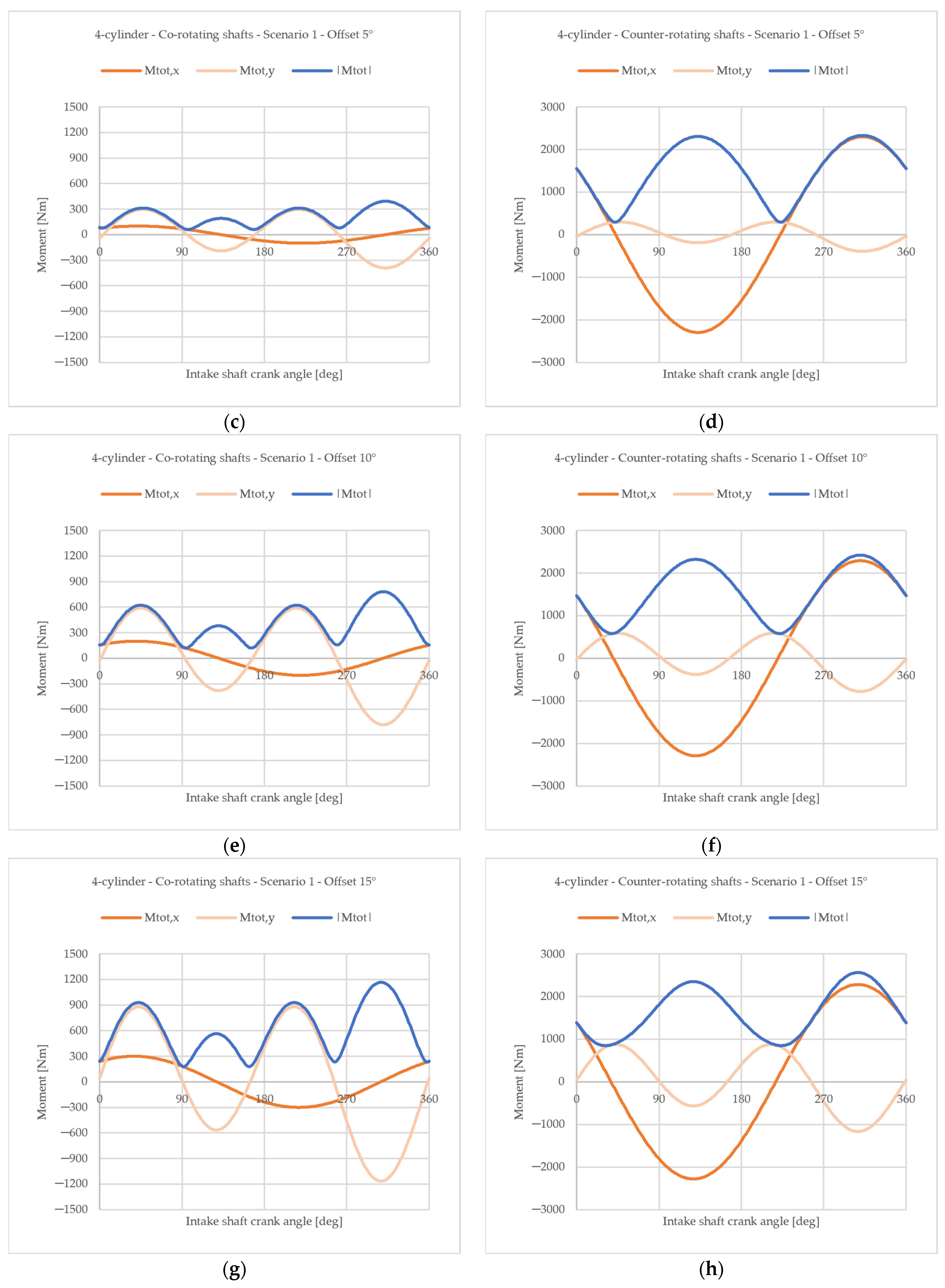
4.1.1. Difference Between Co-Rotating and Counter-Rotating Configurations
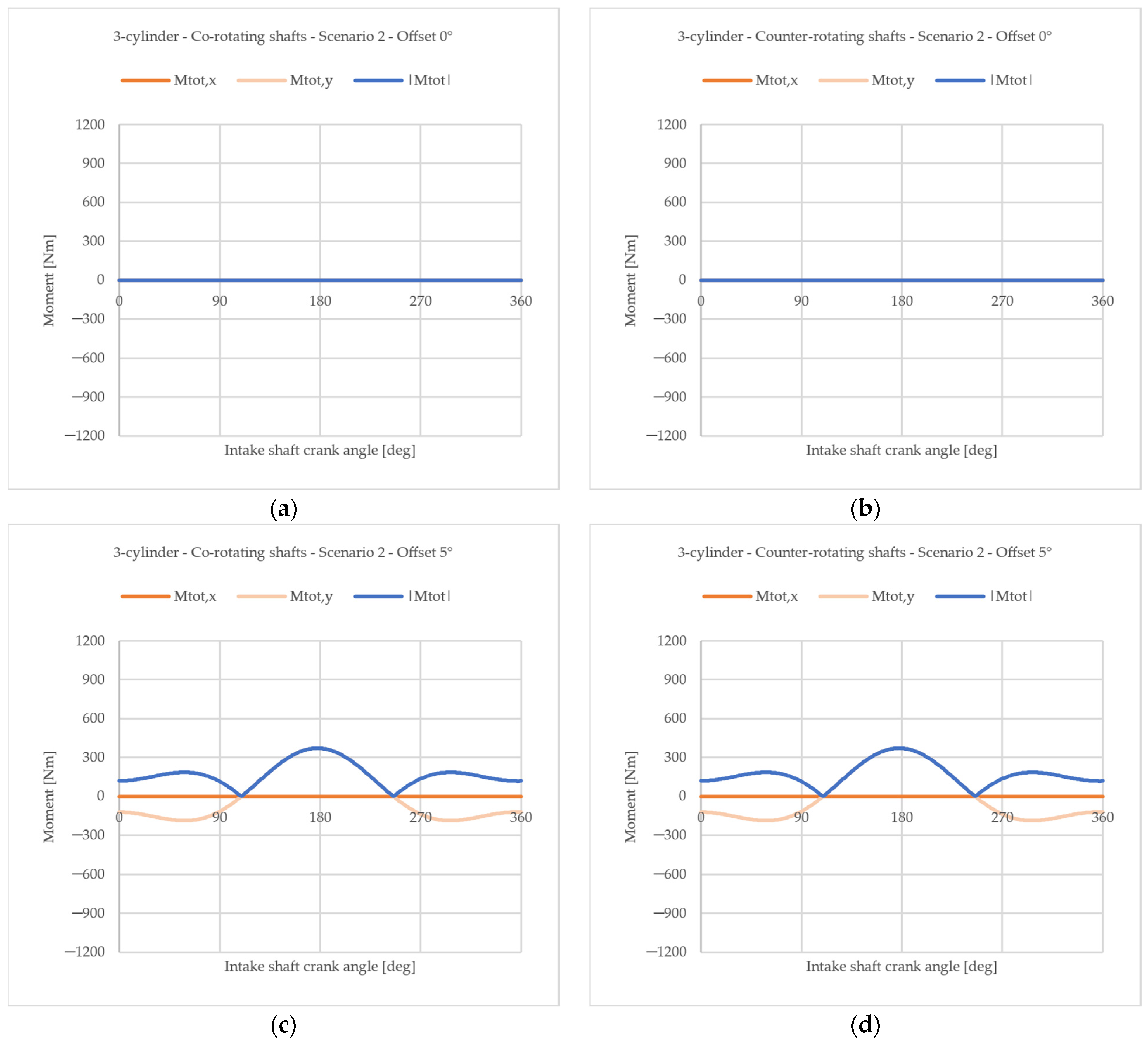
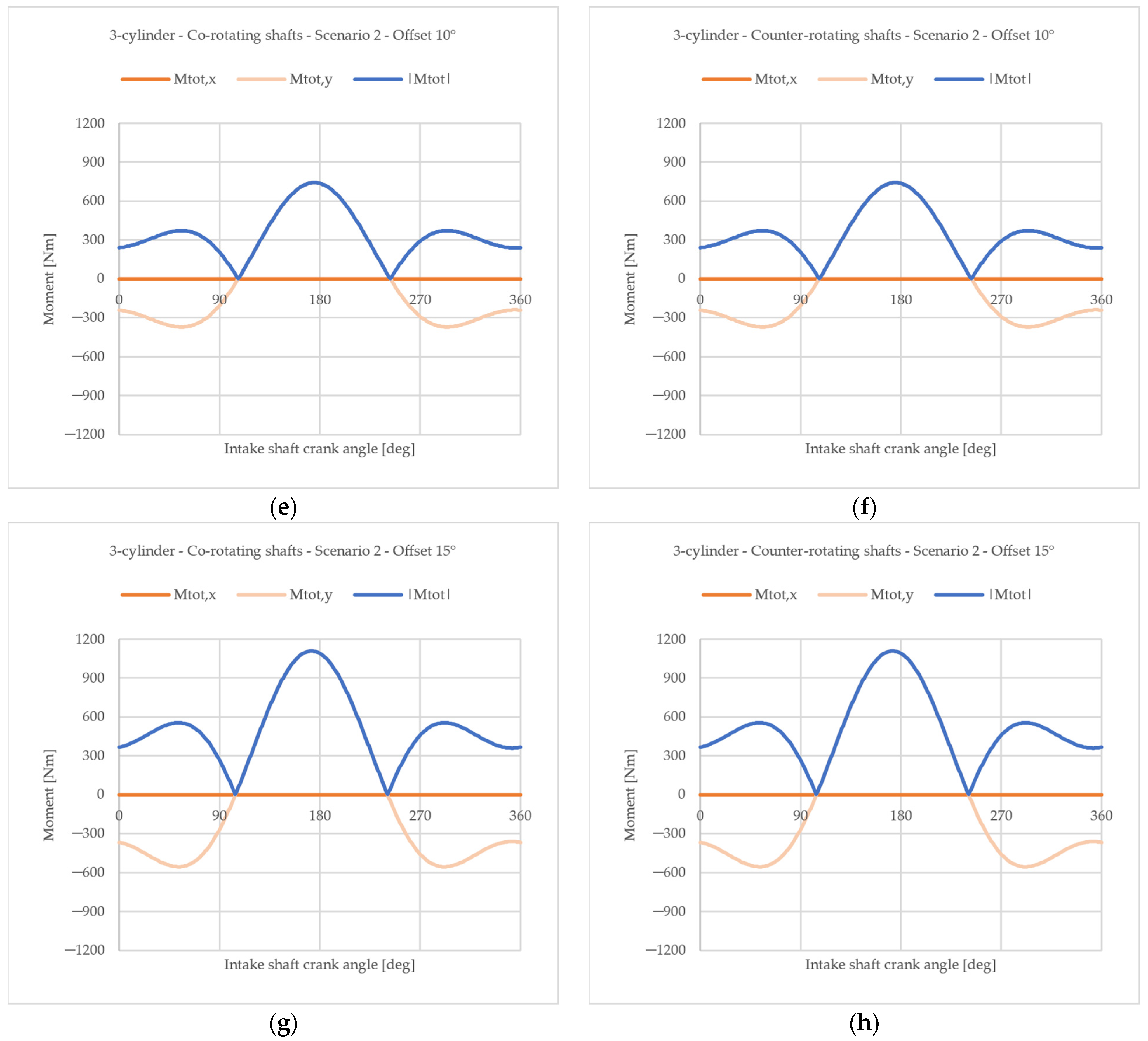
4.1.2. Influence of an Offset Angle Between the Two Crankshafts
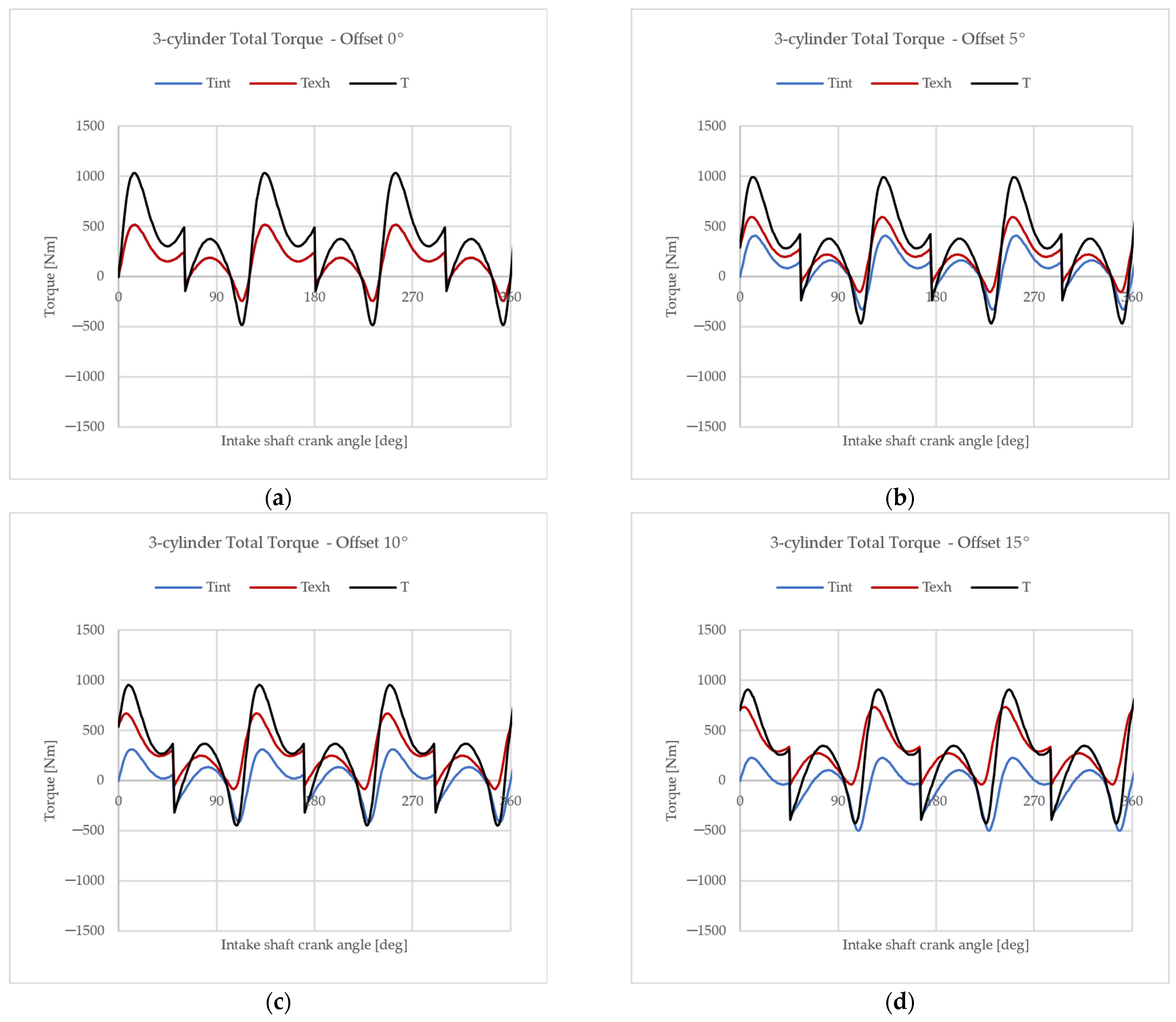
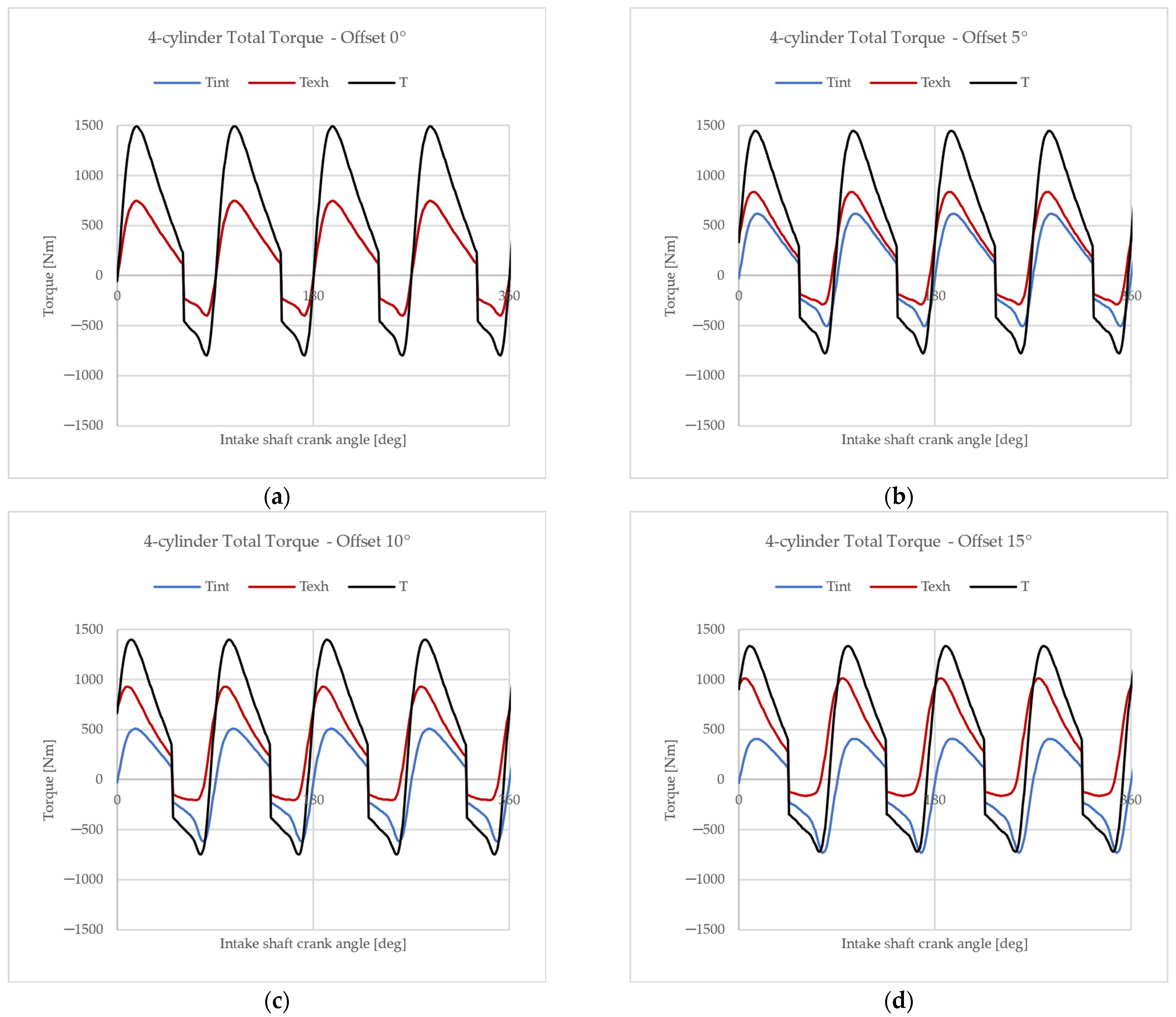
4.2. Output Torque
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Definition |
| Offset angle | |
| Angle between crank throws | |
| Crank angle | |
| Engine cycle duration | |
| Conrod ratio | |
| Engine speed | |
| Force | |
| Centrifugal forces | |
| Reciprocating forces | |
| Rotating component of first-order reciprocating forces | |
| Counter-rotating component of first-order reciprocating forces | |
| Rotating component of second-order reciprocating forces | |
| Counter-rotating component of second-order reciprocating forces | |
| Conrod length | |
| Conrod rotating mass | |
| Crank pin mass | |
| Crank web mass | |
| Total reciprocating masses | |
| Moment | |
| Moment generated by rotating component of first-order reciprocating forces | |
| Moment generated by counter-rotating component of first-order reciprocating forces | |
| Moment generated by rotating component of second-order reciprocating forces | |
| Moment generated by counter-rotating component of second-order reciprocating forces | |
| Number of cylinders | |
| Number of crank mechanisms | |
| Gas pressure | |
| Gas pressure at start of compression stroke | |
| Gas pressure at start of expansion stroke | |
| Crank radius | |
| Counterweights radius | |
| Volume | |
| Volume at start of compression stroke | |
| Volume at start of expansion stroke |
References
- Estevez, R.; Aguado-Deblas, L.; López-Tenllado, F.J.; Bautista, F.M.; Romero, A.A.; Luna, D. Internal Combustion Engines and Carbon-Neutral Fuels: A Perspective on Emission Neutrality in the European Union. Energies 2024, 17, 1172. [Google Scholar] [CrossRef]
- Bao, J.; Wang, H.; Wang, R.; Wang, Q.; Di, L.; Shi, C. Comparative Experimental Study on Macroscopic Spray Characteristics of Various Oxygenated Diesel Fuels. Energy Sci. Eng. 2023, 11, 1579–1588. [Google Scholar] [CrossRef]
- Shi, C.; Cheng, T.; Yang, X.; Zhang, Z.; Duan, R.; Li, X. Implementation of Various Injection Rate Shapes in an Ammonia/Diesel Dual-Fuel Engine with Special Emphasis on Combustion and Emissions Characteristics. Energy 2024, 304, 132035. [Google Scholar] [CrossRef]
- Piergiacomi, A.; Barbieri, S.G.; Renso, F.; Mangeruga, V.; Giacopini, M. Investigation via Finite Element Analysis of the Influence of Boiling on the Thermo-Structural Behavior of the Engine. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Serrano, J.R.; Novella, R.; Piqueras, P. Why the Development of Internal Combustion Engines Is Still Necessary to Fight against Global Climate Change from the Perspective of Transportation. Appl. Sci. 2019, 9, 4597. [Google Scholar] [CrossRef]
- Martins, J.; Brito, F.P. Alternative Fuels for Internal Combustion Engines. Energies 2020, 13, 4086. [Google Scholar] [CrossRef]
- Volza, A.; Scrignoli, F.; Caprioli, S.; Mattarelli, E.; Rinaldini, C.A. Exploring the Potential of Hydrogen Opposed Piston Engines for Single-Cylinder Electric Generators: A Computational Study. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Verhelst, S.; Wallner, T. Hydrogen-Fueled Internal Combustion Engines. Prog. Energy Combust. Sci. 2009, 35, 490–527. [Google Scholar] [CrossRef]
- Shi, C.; Lei, J.; Tian, G.; Ma, Z.; Yang, X.; Zhu, J. Numerical Investigation on Recess Geometry Amelioration of an Ammonia-Hydrogen Zero-Carbon Wankel Engine. Renew. Energy 2025, 242, 122497. [Google Scholar] [CrossRef]
- Pirault, J.-P.; Flint, M. Opposed Piston Engines: Evolution, Use, and Future Applications; SAE International: Warrendale, PA, USA, 2010; ISBN 978-0-7680-1800-4. [Google Scholar]
- Mattarelli, E.; Cantore, G.; Alberto, C. Advances in The Design of Two-Stroke, High Speed, Compression Ignition Engines. In Advances in Internal Combustion Engines and Fuel Technologies; InTech: London, UK, 2013. [Google Scholar] [CrossRef]
- Herold, R.E.; Wahl, M.H.; Regner, G.; Lemke, J.U.; Foster, D.E. Thermodynamic Benefits of Opposed-Piston Two-Stroke Engines. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Mattarelli, E.; Caprioli, S.; Savioli, T.; Volza, A.; Di Gaetano Iftene, C.M.; Rinaldini, C.A. Virtual Development of a Single-Cylinder Hydrogen Opposed Piston Engine. Energies 2024, 17, 5262. [Google Scholar] [CrossRef]
- Lee, H.; Lee, M.-J. Recent Advances in Ammonia Combustion Technology in Thermal Power Generation System for Carbon Emission Reduction. Energies 2021, 14, 5604. [Google Scholar] [CrossRef]
- Ma, F.; Guo, L.; Li, Z.; Zeng, X.; Zheng, Z.; Li, W.; Zhao, F.; Yu, W. A Review of Current Advances in Ammonia Combustion from the Fundamentals to Applications in Internal Combustion Engines. Energies 2023, 16, 6304. [Google Scholar] [CrossRef]
- Sharma, V.; Panesar, A.; de Sercey, G.; Begg, S. A Review of Ammonia Combustion and Emissions Characteristics in Spark-Ignition Engines and Future Road Map. Energies 2024, 18, 41. [Google Scholar] [CrossRef]
- Heifetz, M.; Marsh, M. Engine Dynamics and Balancing. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 1984. [Google Scholar] [CrossRef]
- Dagna, A.; Delprete, C.; Gastaldi, C. A General Framework for Crankshaft Balancing and Counterweight Design. Appl. Sci. 2021, 11, 8997. [Google Scholar] [CrossRef]
- Changming, H.; Sichuan, X. The Investigation of Self-Balanced Property and Vibration on the Particular Crankshaft System for an Opposed Piston Engine. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Ferrari, G. Internal Combustion Engines; Societa Editrice Esculapio: Bologna, Italy, 2014; ISBN 9788874887651. [Google Scholar]
- Hoag, K.; Dondlinger, B. Vehicular Engine Design; Powertrain; Springer: Vienna, Austria, 2016; ISBN 978-3-7091-1858-0. [Google Scholar]
- Basshuysen, V. Fred Schäfer Internal Combustion Engine Handbook: Basics, Components, Systems, and Perspectives; SAE International: Warrendale, PA, USA, 2016; ISBN 978-0-7680-8024-7. [Google Scholar]
- Mattarelli, E.; Rinaldini, C.; Savioli, T.; Cantore, G.; Warey, A.; Potter, M.; Gopalakrishnan, V.; Balestrino, S. Scavenge Ports Optimization of a 2-Stroke Opposed Piston Diesel Engine. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2017; Volume 2017. [Google Scholar] [CrossRef]
- Taylor, C.F. Internal Combustion Engine in Theory and Practice; The MIT Press: Cambridge, MA, USA, 1985; ISBN 9780262311021. [Google Scholar]
- Morton, R.; Riviere, R.; Geyer, S. Understanding Limits to the Mechanical Efficiency of Opposed Piston Engines. In SAE Technical Papers; SAE International: Warrendale, PA, USA, 2017; Volume 2017. [Google Scholar]




| 3-cylinder | 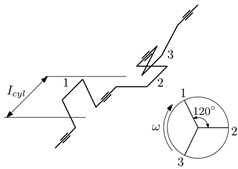 | 0 | |||
| 0 | |||||
| 0 | |||||
| 0 | |||||
| 4-cylinder |  | 0 | |||
| 0 | |||||
| 0 | |||||
| 0 |
| Engine Main Parameters | ||
|---|---|---|
| Engine maximum speed | 6000 rpm | |
| Bore | 80 mm | |
| Stroke | 90 mm | |
| Single cylinder displacement | 900 cm3 | |
| Total displacement | 3-cylinder 4-cylinder | 2700 cm3 3600 cm3 |
| Conrod length | 175 mm | |
| Conrod ratio | 0.257 | |
| Cylinder center distance | 100 mm | |
| Masses | ||
| Assembled conrod | 665 g | |
| Sliding bearing | 13.5 g | |
| Conrod rotating mass | 469 g | |
| Conrod reciprocating mass | 209.5 g | |
| Piston | 550 g | |
| Piston pin | 137.50 g | |
| Total piston rings | 18.50 g | |
| Total reciprocating masses | 915.5 g | |
| Crankpin | 330 g | |
| Co-Rotating Shafts | Counter-Rotating Shafts | |
|---|---|---|
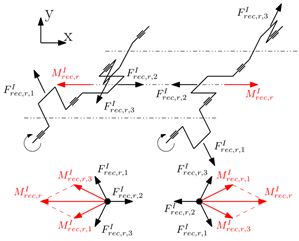 | 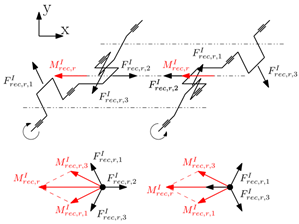 | |
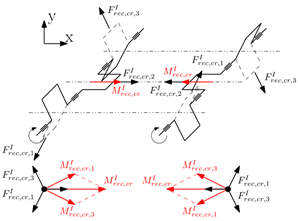 | 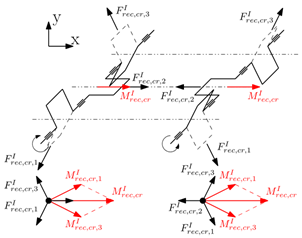 | |
 | 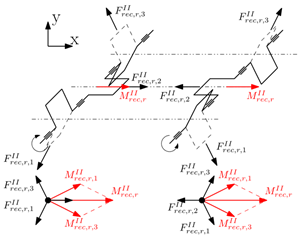 | |
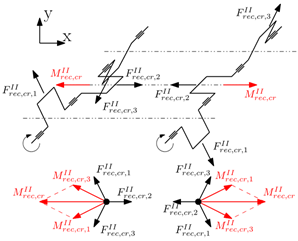 | 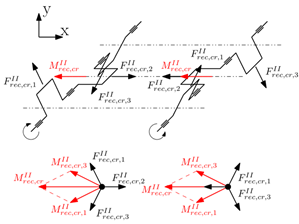 |
| Architecture | Offset Angle | Averaged Output Torque |
|---|---|---|
| 3-cylinder | 0° | 318 Nm |
| 5° | 294 Nm | |
| 10° | 269 Nm | |
| 15° | 240 Nm | |
| 4-cylinder | 0° | 424 Nm |
| 5° | 392 Nm | |
| 10° | 359 Nm | |
| 15° | 320 Nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piergiacomi, A.; Barbieri, S.G.; Mangeruga, V.; Giacopini, M. Influence of Crank Angle Offset on the Mechanical Performance of Different Hydrogen-Fueled Opposed-Piston Engine Architectures. Appl. Sci. 2025, 15, 2537. https://doi.org/10.3390/app15052537
Piergiacomi A, Barbieri SG, Mangeruga V, Giacopini M. Influence of Crank Angle Offset on the Mechanical Performance of Different Hydrogen-Fueled Opposed-Piston Engine Architectures. Applied Sciences. 2025; 15(5):2537. https://doi.org/10.3390/app15052537
Chicago/Turabian StylePiergiacomi, Andrea, Saverio Giulio Barbieri, Valerio Mangeruga, and Matteo Giacopini. 2025. "Influence of Crank Angle Offset on the Mechanical Performance of Different Hydrogen-Fueled Opposed-Piston Engine Architectures" Applied Sciences 15, no. 5: 2537. https://doi.org/10.3390/app15052537
APA StylePiergiacomi, A., Barbieri, S. G., Mangeruga, V., & Giacopini, M. (2025). Influence of Crank Angle Offset on the Mechanical Performance of Different Hydrogen-Fueled Opposed-Piston Engine Architectures. Applied Sciences, 15(5), 2537. https://doi.org/10.3390/app15052537







