Meta-Data-Guided Robust Deep Neural Network Classification with Noisy Label

Abstract

Deep neural network (DNN)-based classifiers have witnessed great applications in various fields. Unfortunately, the labels of real-world training data are commonly noisy, i.e., the labels of a large percentage of training samples are wrong, which negatively affects the performance of a trained DNN classifier during inference. Therefore, it is challenging to practically formulate a robust DNN classifier using noisy labels in training. To address the above issue, our work designs an effective architecture for training the robust DNN classifier with noisy labels, named a cross dual-branch network guided by meta-data on a single side (CoNet-MS), in which a small amount of clean data, i.e., meta-data, are used to guide the training of the DNN classifier. Specifically, the contributions of our work are threefold. First, based on the principle of small loss, each branch using the base classifier as a neural network module infers partial samples with pseudo-clean labels, which are then used for training another branch through a cross structure that can alleviate the cumulative impact of mis-inference. Second, a meta-guided module is designed and inserted into the single branch, e.g., the upper branch, which dynamically adjusts the ratio between the observed label and the pseudo-label output by the classifier in the loss function for each training sample. The asymmetric dual-branch design makes two classifiers diverge, which facilitates them to filter different types of noisy labels and avoid confirmation bias in self-training. Finally, thorough experiments demonstrate that the trained classifier with our proposal is more robust: the accuracy of the classifier trained with our proposed CoNet-MS on multiple datasets under various ratios of noisy labels and noise types outperforms other classifiers of learning with noisy labels (LNLs), including the state-of-the-art meta-data-based LNL classifier.

1. Introduction

Deep neural networks (DNNs) have witnessed great applications in various fields, enabling remarkable advancements in supervision-based classification tasks, due to the existence of a huge volume of training data with correct labels. However, practically, real-world datasets often face the problem of the high cost of manual labeling and even disagreement among experts in specialized fields [1], which always make the labels of training samples noisy, i.e., not sufficiently correct. The ubiquitous presence of noisy labels in real-world training data poses a significant challenge: DNNs are capable of memorizing the entire data, which easily overfits noisy labels and leads to poor performance during inference [2]. Therefore, it is particularly important to improve the accuracy and robustness of deep learning models, when facing noisy labels in training data [3,4].

Existing methods for learning with noisy labels (LNLs), such as the noise transition matrix [5], mainly focus on modeling noisy data. However, in practical applications, the noise types are usually dependent on the features of the samples. Thus, it is difficult to estimate the noise transition matrix, especially when the number of classes is large [6]. Therefore, instead of modeling noisy labels, based on the observation that DNNs often tend to fit samples with clean labels, i.e., learning simple patterns before fitting noisy labels, recent research such as MentorNet [7] aims to select clean samples out of the noisy ones and then uses them to update the DNN classifier through treating low-loss samples as clean [8]. To alleviate the accumulated error caused by the biased selection of training samples, co-teaching [9] maintains two neural networks simultaneously, in which each network feeds its filtered small-loss samples to teach its peer network for updating the parameters. However, the drawback of the above sample-selection-based methods lies in that they only use filtered clean samples for training and overlook training subsets which may affect performance in high-noise scenarios.

Unlike approaches that discard samples with noisy labels, meta-learning methods assign adaptive weights to each sample, with noisier ones receiving lower weights. Specifically, MetaLabelNet [10] uses a portion of existing clean samples in each training batch to train a classifier, which is then used to generate soft labels for other samples to train the base classifier. However, directly training the model on clean data may cause it to overfit, resulting in poor performance on the test dataset. Different from MetaLabelNet, with the help of a partially clean dataset, Learning to Bootstrap (L2B) [11] relabels training samples and further reweights different loss terms. However, the potentially biased relabeling of samples in L2B may lead to accumulative errors and consequently limit the performance of the model.

In brief, unlike previous approaches that directly utilize clean data to generate pseudo-labels or rely only on single models to reweight samples [10,11,12], we propose a novel classifier framework robust to a high noise ratio, called a cross dual-branch network guided by meta-data on a single side (CoNet-MS), which fully exploits the DNN training characteristics and prevents the accumulation of errors under a meta-learning framework. Specifically, our contribution can be summarized as follows:

• We propose a cross dual-branch classifier framework enhanced with meta-learning to guide each other and achieve adaptive sample relabeling, CoNet-MS. CoNet-MS can improve the accuracy of classifiers by cross-guiding dual-branch and reweighting labels with the meta-guided module on the upper branch. Two classifier networks with divergent initialization can facilitate learning complementary features to filter distinct errors from noisy labels. Following the small-loss principle [13] where DNNs prioritize clean samples, each branch treats low-loss samples as high-confidence pseudo-clean ones. Cross-filtering high-confidence samples can alleviate error accumulation and mitigate overfitting to noisy labels. The meta-guided module in the upper branch further diversifies the dual branches, enhancing framework robustness.
• Furthermore, the innovative meta-net module in the upper branch dynamically adjusts the weights of the output of the observed and pseudo-label by the upper classifier in the loss function, using part of the clean dataset. In brief, the clean data information is implicitly utilized to guide the pseudo-labeling correction of the samples instead of participating directly in training.
• We experimentally demonstrate that the proposed meta-learning enhanced cross-dual network framework, CoNet-MS can improve the robustness of the model to label noise. Specifically, CoNet-MS achieves significant performance improvements compared to L2B. In addition, we also provide a comprehensive comparison with state-of-the-art (SOTA) techniques [9,10,11], and the result shows that our method has superior performance, highlighting the advantages of CoNet-MS in the field of meta-learning and LNLs.

This paper is organized as follows. Section 2 summarizes the research work related to LNLs. Section 3 describes our proposed framework CoNet-MS and its main modules and functionalities in detail. Section 4 thoroughly presents the experimental setting and results, and an ablation study is also provided. Finally, Section 5 briefly concludes this paper.

2. Related Works

This section introduces the related works of LNLs in the field of deep learning, which is categorized as schemes directly learning with noisy labels and meta-learning-assisted learning with noisy labels.

Directly learning with noisy labels. The field of noisy label learning has proposed several approaches to address the challenges of training models using noisy labeled data [2]. A noise transition matrix is used to capture the transition probability between the noisy labels and true labels [13,14]. However, the size of the noise transition matrix grows exponentially as the number of dataset categories increases, making it intractable to calculate. To avoid modeling noise, some methods commonly rely on the internal noise tolerance of the classifier and aim to boost performance by regularizing undesired memorization of noisy data [15,16,17,18]. Although these methods enhance the scalability of the LNL algorithm, they are highly dependent on the internal noise tolerance of the classifier and do not fully exploit the valid information in the noisy sample data [19]. Noise detection methods, on the other hand, focus on utilizing semi-supervised learning to identify and generate target probabilities. By guiding the model to the target probabilities, these methods avoid memorizing noisy labels and mitigate the effects of bad sample data [3,20]. In addition, label correction techniques aim to generate pseudo-labels that are more consistent with real labels [21]. Some methods strengthen sample selection through unsupervised contrastive learning, thus emphasizing robust representation learning [21,22,23,24]. Several studies have focused on selecting high-confidence samples and reweighting them. Ref. [25] proposed a co-optimization framework that can correct labels during training by alternating updates of network parameters and labels. Similarly, Ref. [9] proposed a co-teaching framework that aims to train two deep neural networks simultaneously. This framework is based on the property that deep neural networks tend to preferentially learn simple and correct samples [13]. The framework utilizes the small loss principle [4,7,26,27] to filter out reliable clean samples to guide the training of the other networks. Due to the differences in the initial parameters of the two networks, they can filter out the noisy labels when guiding each other’s training, thus mitigating the effect of noise on the model. Another sample-selecting method is Curriculum Learning (CL), which starts with simple samples and adds difficult samples for training as the model gradually improves [28]. Based on the CL theory, clean-labeled data are considered simple samples, while noise-labeled data are considered difficult tasks. Therefore, researchers start with confident clean samples and learn complex samples after the model is improved. Filtering clean samples can be performed by using a specific filtering loss function to rank the instances based on their characteristics [29].

Meta-learning with noisy labels. Meta-learning aims to learn a meta-task, which is a higher-level learning objective than classical supervised learning. The goal of meta-learning is to train a model on a variety of learning tasks, such that it can solve label noise tasks using only a small number of training samples. For the field of LNLs, technically, meta-learning methods use part of clean datasets to guide model optimization [10,12,14,30,31,32]. Based on meta-learning, Model-Agnostic Meta-Learning (MAML) is compatible with any model trained with gradient descent and applicable to a variety of different learning problems, such as label noise learning [33]. A similar approach consists of finding model parameters that minimize the effect of noisy labels in meta-learning-based noise-tolerant (MLNT) training [30]. In this framework, MLNT formulates a meta-objective as training the model such that after it learns from various synthetic noisy labels using gradient update, the updated models give consistent predictions. In addition, another study called MetaLabelNet aims to train the base classifier on soft labels produced according to a meta-objective [10]. Although MetaLabelNet claims to fully utilize the information from the noisy data, the model’s accuracy on the meta-data is often significantly higher than that on the test dataset because the meta-labels are directly derived from meta-data. Unlike MetaLabelNet, L2B enables models to bootstrap themselves using their own predictions without being adversely affected by erroneous pseudo-labels, and since the clean data are not directly involved in the network update, this avoids overfitting the model to a small number of correct datasets [11].

Different from the above schemes of directly using clean data for sample relabeling or reweighting, we propose a generic learning framework that simultaneously trains dual-branch classifiers with different initializations and cross guidance. Furthermore, the meta-guided module is designed to reweight training samples and diversify the dual classifier branches.

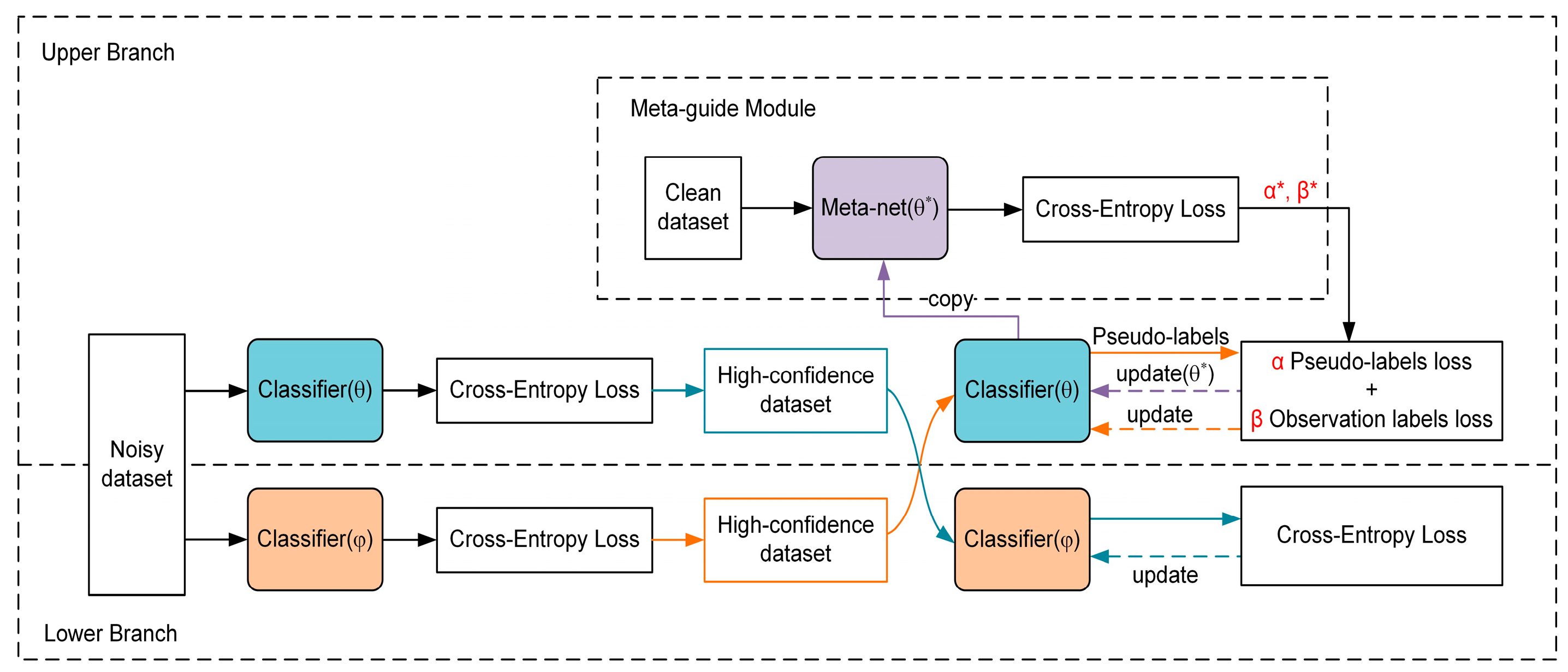
3. The Proposed CoNet-MS Framework and Its Main Modules

The main notations and their meanings used in this paper are given in

Table 1. Main notations and their meanings throughout this paper.

Notation	Description
$N$	The number of samples in the training set
$M$	The number of samples in the clean validation set
$n$	The batch size of training set
$m$	The batch size of clean validation set
$D_{tra}$	$\mathrm{The}\mathrm{set}\mathrm{of}\mathrm{all}\mathrm{training}\mathrm{samples}\left\{\left.\left(x_i,y_i\right)\right|i=1,\cdots ,N\right\}$
$D_{val}$	$\mathrm{The}\mathrm{set}\mathrm{of}\mathrm{all}\mathrm{validation}\mathrm{samples}\left\{\left.\left(x_i^v,y_i^v\right)\right|i=1,\cdots ,M\right\}$
$D_{test}$	$\mathrm{The}\mathrm{set}\mathrm{of}\mathrm{all}\mathrm{test}\mathrm{samples}\left\{\left(x_i^t,y_i^t\right)\right|i=1,\dots ,S\}$
$f_{\theta }$	$\mathrm{The}\mathrm{classifier}\mathrm{parameterized}\mathrm{by}\theta$
$f_{\phi }$	$\mathrm{The}\mathrm{classifier}\mathrm{parameterized}\mathrm{by}\phi$
$L$	Cross-entropy loss function
$y_i^{pseudo}$	Pseudo-label of the sample $x_i$
$C$	The number of classes in dataset
$f_{\theta }\left(x_i\right)$	$\mathrm{The}\mathrm{class}\mathrm{probability}\left\{p_1,p_2,\dots ,p_C\right\}$$\mathrm{of}{x}_i$$\mathrm{output}\mathrm{by}\mathrm{classifier}(\theta$)
$P\left(t\right)$	The high-confidence proportion of samples in the $t$-th epoch
${\alpha }_i$	The weight loss of the pseudo-label for $x_i$
${\beta }_i$	$\mathrm{The}\mathrm{weight}\mathrm{loss}\mathrm{of}\mathrm{the}\mathrm{observed}\mathrm{label}\mathrm{for}{x}_i$
${\alpha }_i^{*},{\beta }_i^{*}$	$\mathrm{The}\mathrm{normalized}\mathrm{weights}\mathrm{of}{\alpha }_i$  $\mathrm{and}{\beta }_i$
$\{x_{\theta },y_{\theta }\}$	The high-confidence dataset selected by $f_{\theta }$
$\{x_{\phi },y_{\phi }\}$	The high-confidence dataset selected by $f_{\phi }$
${\theta }^{*}$	Parameters of the meta-net
${\theta }^{\left(t\right)}$	Parameters of the upper-branch classifier in the $t$-th epoch
$\eta$	$\mathrm{The}\mathrm{step}\mathrm{size}\mathrm{for}\mathrm{updating}\alpha ,\beta$
$\lambda$	$\mathrm{The}\mathrm{step}\mathrm{size}\mathrm{for}\mathrm{updating}\theta ,\phi$

for clarity of presentation.

3.1. Problem Statement

In supervised learning, assume that there are $N$ training samples consisting of the dataset $D_{tra}=\left\{\left.\left(x_i,y_i\right)\right|i=1,\cdots ,N\right\}$, where $x_i\in X$ denotes the i-th sample, e.g., image, $y_i\in Y$ denotes the label of the i-th sample, $X$ is the feature space, and $Y$ is the label space. The observed label of each training sample is encoded as a one-hot vector with the length C. In addition, we introduce a clean dataset $D_{val}=\left\{\left.\left(x_i^v,y_i^v\right)\right|i=1,\cdots ,M\right\}$ without noise, where $M\ll N$ and the superscript $v$ denotes that the dataset is the validation set. Our goal is to find a model mapping function $f:X\to Y$ parameterized by $\theta$, where $X$ denotes the model input and $Y$ denotes the model prediction. Typically, the empirical risk $R\left(f\right)$ is computed on the training samples, shown as Equation (1).

$$R\left(f_{\theta }\right)=E_{\left(x,y\right)\in D_{tra}}\left[L\right(f_{\theta }\left(x_i\right),y_i\left)\right]$$

(1)

In Equation (1), the expectation $E\left(L\right)$ denotes the math expectation of the loss function, and $L(f_{\theta }\left(x_i\right),y_i)$ is the cross entropy, shown as Equation (2).

$$L\left(f_{\theta }\left(x_i\right),y_i\right)=-y_{i}log{f}_{\theta }\left(x_i\right)$$

(2)

The optimal classifier $f$ parameterized by ${\theta }^{*}$ aims to minimize the risk, given as Equation (3).

$${\theta }^{*}=\arg \underset{\theta }{\min }R\left(f_{\theta }\right)$$

(3)

If the labels of the dataset are exactly correct, the classifier parameter $\theta$ can be learned by optimizing Equation (3) via the gradient descent method. However, in this study, there exist unknown noise types and distributions in the training dataset $D_{tra}$, and the classifier can only observe the set of noisy training labels $y_i$. The task involves training a DNN to reduce the negative impact of the noisy labels and predict the true labels. In the following subsections, we describe the training process of the proposed method on noisy datasets.

3.2. The Overall Framework of CoNet-MS

As shown in Figure 1, CoNet-MS contains an asymmetric dual-branch classifier network structure: upper branch and low branch. Specifically, besides the same modules in the lower branch, the upper branch additionally includes a meta-guided module. The purpose of the meta-guided module is to learn to reweight loss values between the pseudo-label and the observed label of each training sample $x_i$, i.e., ${\alpha }_i$ and ${\beta }_i$. Note that the diverse dual classifier branches can be cross-guided between each other and, due to the different learning abilities, can filter out some erroneous tendencies thus realizing self-correction.

The main modules of the proposed CoNet-MS framework are respectively presented in the following subsections.

3.3. Cross Dual-Branch Classifier Network Architecture

In this paper, we aim to reduce the accumulation of errors in the classifier by filtering the noisy labeled samples by exchanging the high-confidence samples between two networks. To achieve this, we designed the crossed dual-branch network architecture. During training, in each batch of data, samples with high confidence are filtered out based on the small-loss principle, and the high-confidence samples are fed into another branch of its classifier. Note that both classifiers in dual branches have the same neural network structure, but the upper-branch classifier is parameterized by $\theta$, and the lower-branch classifier is parameterized by $\phi$. Specifically, we first create two neural networks with different initial parameters. During each batch, classifiers make predictions for all samples ${\{x}_i,y_i\}$, and the loss values are computed. Subsequently, we select $P\left(t\right)$, the percentage of small-loss instances, out of the batch as high-confidence data, where $t$ denotes the $t$-th training epoch. $\left\{x_{\theta ,i},y_{\theta ,i}\right\}$ denotes the high-confidence dataset from the upper-branch classifier, $\{x_{\phi },y_{\phi }\}$ is the high-confidence dataset of the lower-branch classifier. These samples are fed into another classifier; that is, $\{x_{\theta },y_{\theta }\}$ are input into the lower-branch classifier, and $\{x_{\phi },y_{\phi }\}$ are input into the upper-branch classifier.

The above operation requires the classifier to be robust enough to accurately filter out clean data. To ensure that the high-confidence samples selected in each batch are less noisy, we use the method of dynamically adjusting the memory rate $P\left(t\right)$. Since the network tends to fit simple clean data at the beginning of training, as the loss values can more accurately distinguish between clean and noisy samples, $P\left(t\right)$ is designed to be a larger rate at the beginning of training. As the number of training times increases, $P\left(t\right)$ should correspondingly decrease to avoid model overfitting to noisy labels. The empirical selection $P\left(t\right)$ is given in Section 4.4.

The inferred pseudo-clean dataset by upper and lower branches $\left\{x_{\theta },y_{\theta }\right\}$ and $\{x_{\phi },y_{\phi }\}$ are formulated as Equations (4) and (5), where $\left|\left\{x_i,y_i\right\}\right|$ means the number of samples in the obtained dataset.

$$\left\{x_{\theta },y_{\theta }\right\}={\arg min}_{\left\{x_i,y_i\right\}:\left|\left\{x_i,y_i\right\}\right|\ge P\left(t\right)\cdot n}L(f_{\theta }\left(x_i\right),y_i)$$

(4)

$$\left\{x_{\phi },y_{\phi }\right\}={\arg min}_{\left\{x_i,y_i\right\}:\left|\left\{x_i,y_i\right\}\right|\ge P\left(t\right)\cdot n}L(f_{\phi }\left(x_i\right),y_i)$$

(5)

Next, we input these samples into another branch; that is, $\{x_{\theta },y_{\theta }\}$ are input into the lower-branch classifier, and $\{x_{\phi },y_{\phi }\}$ are input into the upper-branch classifier. Then, the classifiers’ parameters are updated.

3.4. Meta-Guided Module: Reweighting Losses Between the Pseudo-Label and the Observed Label in Upper Branch

Due to the presence of noise in the dataset, Reed et al. proposed a method to generate training targets by using a convex combination of model predictions and training labels to generate pseudo-labels, thus avoiding the need to directly model the noise distribution [34]. Based on this idea, Ref. [11] implicitly filtered samples and corrected the mislabeling by predicting from a model trained on a clean dataset, assigning pseudo-labels to the training data and dynamically adjusting the weights of the samples and pseudo-labels. In our study, shown as Equation (6), pseudo-labels are defined as the maximum probability class predicted by the model, where $C$ is the number of dataset classes.

$$y_i^{pseudo}=\arg \underset{c=1,\dots ,C}{\mathit{min}}{f}_{\theta }\left(x_i\right)$$

(6)

The loss function of the optimization parameter $\theta$ is designed as Equation (7).

$${\theta }^{*}\left(\alpha ,\beta \right)=\arg \underset{\theta }{\mathit{min}}\sum _{i=1}^{N}L(f_{\theta }\left(x_i\right),{\alpha }_i{y}_i+{\beta }_i{y}_i^{pseudo})$$

(7)

where $\alpha$ and $\beta$ are used to balance the weights between the observed sample labels and pseudo-labels output by the upper branch. When $\alpha$ is small and $\beta$ is large, $\theta$ is designed to narrow the gap between the model prediction and the pseudo-label for label correction. When both $\alpha$ and $\beta$ are small, the weight of the samples in the loss accounts for a relatively small amount of weight, whose effect on the parameter update can be ignored, thus implicitly realizing the sample selection.

Therefore, the assignment of $\alpha$ and $\beta$ needs to be very accurate to achieve the above goal. To this end, a method for generating meta-learning weights is introduced, which utilizes a small portion of the clean validation set $D_{val}=\left\{\left.\left(x_i^v,y_i^v\right)\right|i=1,\cdots ,M\right\}$ as the meta-data and generates the optimal loss weights via a meta-net, given as Equation (8).

$$\alpha ,\beta =\arg \underset{\alpha ,\beta \ge 0}{\mathit{min}}{\displaystyle \frac{1}{M}}\sum _{i=1}^{M}L\left(f_{{\theta }^{*}\left(\alpha ,\beta \right)}\right(x_i^v,y_i^v\left)\right)$$

(8)

where ${\theta }^{*}\left(\alpha ,\beta \right)$ is the result of updating the parameter $\theta$ in round t after Equation (7). The solution of Equation (8) can be approximated by the gradient descent on each batch validation set, shown as Equation (9).

$$\left({\alpha }_i,{\beta }_i\right)={\left.-\eta \nabla \left(\sum _{i=1}^m{f}_{{\theta }^{*}\left(\alpha ,\beta \right)}\left(x_i^v,y_i^v\right)\right)\right|}_{{\alpha }_i=0,{\beta }_i=0}$$

(9)

where $\eta$ is the step size for updating.

Then, the following Equations (10) and (11) are simply used to ensure that $\alpha$ and $\beta$ are non-negative and normalized.

$${\alpha }_i=\mathit{max}({\alpha }_i,0),{\beta }_i=max({\beta }_i,0)$$

(10)

$${\alpha }_i^{*}={\displaystyle \frac{{\alpha }_i}{\sum _{i=1}^n{\alpha }_i+{\beta }_i}},{\beta }_i^{*}={\displaystyle \frac{{\beta }_i}{\sum _{i=1}^n{\alpha }_i+{\beta }_i}}$$

(11)

Finally, as shown in Equations (12) and (13), the parameters of dual-branch classifier networks are updated based on the optimal weights obtained, where $\left\{x_{\theta },y_{\theta }\right\}$ and $\left\{x_{\phi },y_{\phi }\right\}$ are the high-confidence samples computed by Equations (4) and (5).

$${\phi }^{(t+1)}={\phi }^{\left(t\right)}-\lambda \nabla \left(\sum _{i=1}^{P\left(t\right)\cdot n}L\left(f_{\phi }\left(x_{\theta ,i}\right),y_{\theta ,i}\right)\right)$$

(12)

$${\theta }^{(t+1)}={\theta }^{\left(t\right)}-\lambda \nabla \left(\sum _{i=1}^{P\left(t\right)\cdot n}{\alpha }_i^{*}L\left(f_{\theta }\left(x_{\phi ,i}\right),y_{\phi ,i}\right)+{\beta }_i^{*}L\left(f_{\theta }\left(x_{\phi ,i}\right),y_{\phi ,i}^{pseudo}\right)\right)$$

(13)

where $\lambda$ is the step size for updating classifier parameters $\theta$ and $\phi$.

3.5. Training Pseudo-Codes

The training pseudo-codes of CoNet-MS are given in the following Algorithm 1.

Algorithm 1 CoNet-MS

1: Input: ${\theta }_0,{\phi }_0,D_{tra},D_{val},n,m,L$

2: Output: ${\theta }_T$

3: for  $t=0$  to  $T-1$  do

4:   $\{x_i, y_i\} \to$ SampleMiniBatch$(D_{tra},n)$

5:   $\{x_v,y_v\}\to$ SampleMiniBatch$(D_{val},m)$

6:   for each sample in $D_{tra}$ do 7:    $y_i^{pseudo}\to \mathrm{a}\mathrm{r}\mathrm{g}ma{x}_{c=1,\dots ,C}f\theta \left(xi\right)$ 8:    Initialize learnable weights $\alpha ,\beta$ 9:    Compute Meta-net parameters ${\theta }^{*}$ by Equation (7) 10:    Update Hyperparameters ${\alpha }^{*},{\beta }^{*}$ by Equation (9)–(11) 11:    Obtain $\{x_{\theta },y_{\theta }\}$ by Equation (4) 12:    Obtain $\{x_{\phi },y_{\phi }\}$ by Equation (5) 13:   end for 14:   Update ${\phi }^{(t+1)}$ by Equation (12) 15:   Update ${\theta }^{(t+1)}$ by Equation (13) 16: end for

The computational complexity of each module in our proposed CoNet-MS framework is given in

Table 2. Computational complexity of each module in the CoNet-MS framework.

Component	Computational Complexity
Cross dual-branch classifier network architecture	$O\left(Tnlogn\right)$
Meta-guided module	$O\left(T\right(n+m\left)\right)$

, where $T$ is the number of training epochs, $n$ is the batch size of the training set, and $m$ is the batch size of the clean validation set.

Specifically, the computational complexity of CoNet-MS is dominated by the cross dual-branch classifier network architecture and meta-guided module. To further elaborate, since the batch size of the clean validation set $m$ is significantly smaller than the training batch size $n$ (i.e., $m\ll n$), the computational complexity of the meta-guided module $O\left(T\right(n+m\left)\right)$ can be simplified to $O\left(Tn\right)$. When combined with the cross dual-branch classifier’s complexity $O\left(Tnlogn\right)$, the overall complexity remains dominated by the higher-order term $O\left(Tnlogn\right)$.

4. Experiments

4.1. Experimental Datasets

To validate the performance of CoNet-MS, this paper conducted experiments on multiple datasets, including the CIFAR10 and ISIC2019 datasets.

For CIFAR10, the dataset contains 60,000 images across 10 balanced categories (6000 per class). We followed a standard split with 50,000 images for training, 5000 for testing and 5000 as metadata.

For the medical image analysis, we adopted the imbalanced ISIC2019 dataset for skin lesion classification. The training set consists of 6120 images with the following class distribution: Melanoma (MEL, 1124), Melanocytic nevus (NV, 3191), Basal cell carcinoma (BCC, 798), Benign keratosis (BKL, 606), Squamous cell carcinoma (SCC, 129), Actinic keratosis (AK, 192), Vascular lesion (VASC, 36) and Dermatofibroma (DF, 44). This reflects a significant class imbalance, where the majority class (NV) has over 70× more samples than the smallest classes (DF and VASC). Additionally, we used 640 images for validation and 4291 images for testing. The imbalance in training data extremely challenges model generalizability, which aligns with our focus on robust performance under real-world clinical scenarios.

In our experiments, the training data labels are corrupted by two kinds of noise types: uniform noise and pair-flipping noise. For uniform noise, labels are flipped uniformly into all the other classes with a given error rate. For pair-flipping noise, labels are flipped into similar classes with a given error rate. Specifically, the training datasets are manually corrupted by the noise transition matrix $Q$, where $Q_{ij}=P\left(\tilde{y}=j\right|y=i)$, given that noisy $\tilde{y}$ is flipped from clean $y$. The precise definitions of uniform noise and pair-flipping noise transfer matrices are given as Equations (14) and (15).

$$\mathrm{U}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m} \mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}:Q=\left[\begin{array}{ccccc}1-ϵ& {\displaystyle \frac{ϵ}{n-1}}& \dots & {\displaystyle \frac{ϵ}{n-1}}& {\displaystyle \frac{ϵ}{n-1}}\\ {\displaystyle \frac{ϵ}{n-1}}& 1-ϵ& {\displaystyle \frac{ϵ}{n-1}}& \dots & {\displaystyle \frac{ϵ}{n-1}}\\ ⋮& & \ddots & & ⋮\\ {\displaystyle \frac{ϵ}{n-1}}& \dots & {\displaystyle \frac{ϵ}{n-1}}& 1-ϵ& {\displaystyle \frac{ϵ}{n-1}}\\ {\displaystyle \frac{ϵ}{n-1}}& {\displaystyle \frac{ϵ}{n-1}}& \dots & {\displaystyle \frac{ϵ}{n-1}}& 1-ϵ\end{array}\right]$$

(14)

$$\mathrm{P}\mathrm{a}\mathrm{i}\mathrm{r} \mathrm{f}\mathrm{l}\mathrm{i}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}:Q=\left[\begin{array}{ccccc}1-ϵ& ϵ& 0& \dots & 0\\ 0& 1-ϵ& ϵ& & 0\\ ⋮& & \ddots & \ddots & ⋮\\ 0& & & 1-ϵ& ϵ\\ ϵ& 0& \dots & 0& 1-ϵ\end{array}\right]$$

(15)

where $n$ is the number of the total classes, and $ϵ$ is the noise rate. Note that the above uniform noise and pair-flipping noise transfer matrices are totally the same as those in co-teaching [9].

4.2. Baselines

In the comparison experiments, this paper presents a comprehensive comparison between CoNet-MS and a variety of state-of-the-art schemes that train classification neural networks using datasets of samples with noisy labels, the comparative schemes are described as follows:

• Conventional cross entropy: Training a classifier neural network directly with noisy data as the most basic and lowest-bound comparison to visualize the effect of noisy labels on classification performance.
• Co-teaching [9]: Simultaneously training two classifier networks. Based on the small-loss principle, each network guides the other network to filter out the noisy data during training to reduce the influence of noisy samples.
• MetaLabelNet [10]: Alternatively training a meta-network using meta-data and letting the meta-network generate pseudo-labels for training samples to guide the updating of a classifier.
• L2B [11]: Using meta-data to reweight loss function weights, adjust sample influence and implicitly correct labels.

4.3. Evaluation Metrics

In this paper, the proposed scheme and all baselines are evaluated in terms of classification accuracy on the test dataset, i.e., test accuracy (TA), which is defined as Equation (16).

$$\mathrm{T}\mathrm{A}={\displaystyle \frac{\left|\left(x_i^t,y_i^t\right){\in D}_{test}:f\left(x_i^t\right)=y_i^t\right|}{D_{test}}}$$

(16)

where $D_{test}$ represents the test set, $x_i^t$ represents the features of the test instance, $y_i^t$ represents the ground-truth label of each sample, and $f\left(x_i^t\right)$ represents the output of the classifier trained by each scheme. If two classifiers are trained in some scheme, e.g., co-teaching and our proposed, $f\left(x_i^t\right)$ is simply set as the average of both classifiers’ output. Note that, intuitively, under the same percentage of noise, the larger the TA is, the more robust the classifier is.

Another evaluation indicator is Macro F1, which is defined as Equation (17).

$$\mathrm{F}1={\displaystyle \frac{2\cdot \mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\cdot \mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}{\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}+\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}}}$$

(17)

$$\mathrm{M}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o} \mathrm{F}1={\displaystyle \frac{\sum \mathrm{F}1scoreforeachclass}{Thenumberofclasses}}$$

(18)

The definitions of precision (P) and recall (R) are given in Equations (19) and (20).

$$\mathrm{P}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}}$$

(19)

$$\mathrm{R}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}$$

(20)

The meanings of TP, FP, FN and TN are illustrated as follows:

• TP (true positive): the number of samples that are actually positive and predicted to be positive;
• FP (false positive): the number of samples that are actually negative but predicted to be positive;
• FN (false negative): the number of samples that are actually positive but predicted to be negative;
• TN (true negative): the number of samples that are actually negative and predicted to be negative.

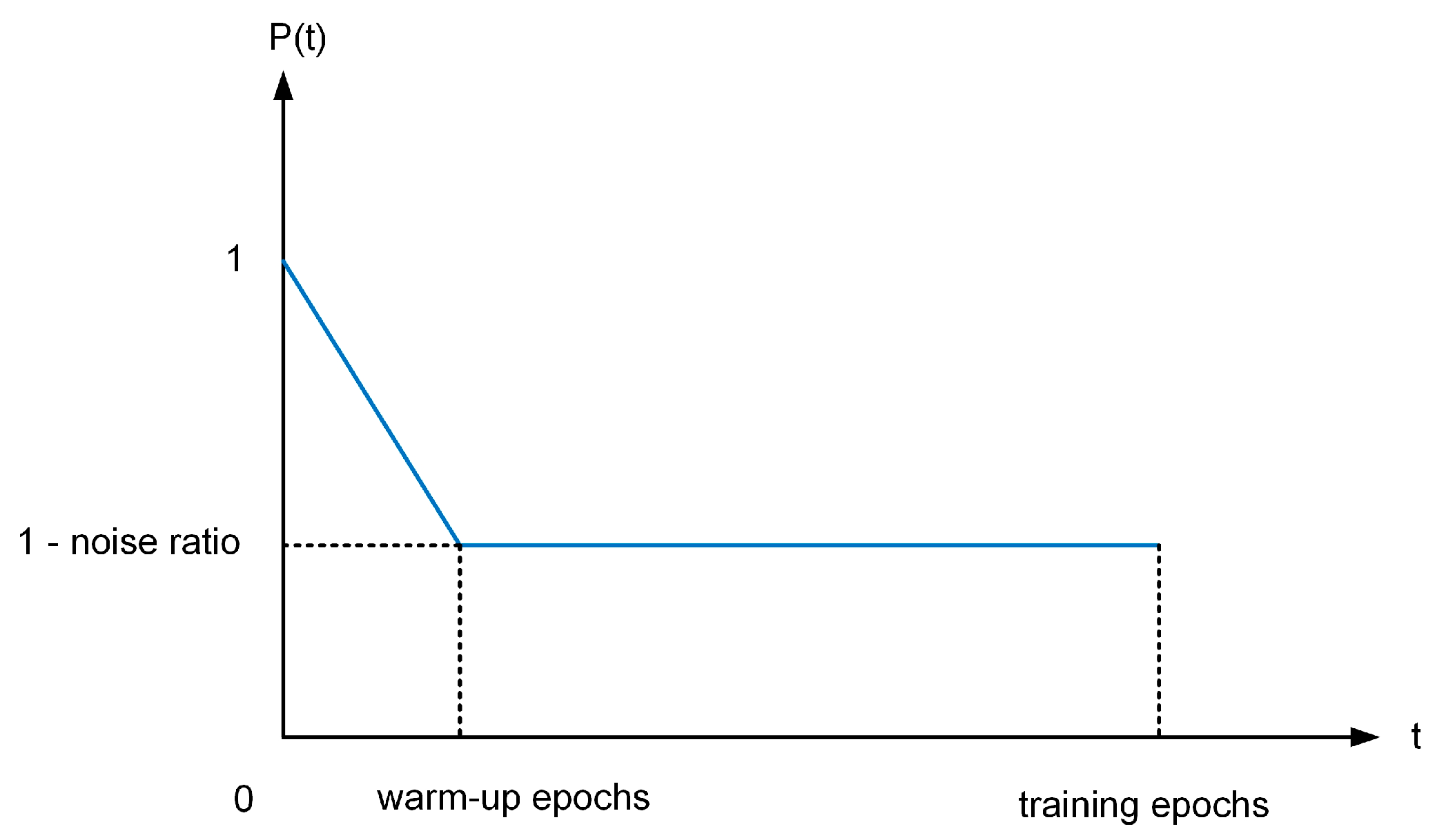
4.4. Experimental Settings

Without the loss of generality, we used a convolutional neural network containing eight layers, including six convolutional layers and two fully connected layers. The batch size was set to 64. The model was trained using stochastic gradient descent (SGD) with a momentum of 0.9 and weight decay of 0.0005. A total of 120 epochs of model training were conducted, with the first 10 epochs set as warm-up training. The initial learning rate was set to 0.15 with a cosine annealing decay. The optimizer and learning rate of the main network and meta-network were kept constant, while the training process was stabilized by gradient clipping. An RTX 4060 GPU was used for the experiments.

In our experiments, as shown in Figure 2, the function of high-confidence sample proportion $P\left(t\right)$ is linearly reduced from 1 to $(1-noiserate)$ in the first 10 warm-up epochs. The rationale lies in that, when the number of epochs gets large, classifiers will eventually overfit on noisy labels, and thus, $P\left(t\right)$ should be set to keep clean instances and drop those noisy ones before classifiers memorize them.

4.5. Performance Evaluation

Comparison with the State-of-the-Art Methods

Table 3. Test accuracy (%) of all schemes under different levels of uniform noise on the CIFAR-10 dataset.

Noise Ratio (%)	20	40	50	60	80
Conventional Cross Entropy	82.86	77.84	72.06	67.62	40.02
Co-teaching [9]	85.88	81.02	75.84	70.28	43.88
MetaLabelNet [10]	83.42	77.74	75.32	71.2	49.98
L2B [11]	89.44	87.86	85.99	77.99	66.09
Ours (CoNet-MS)	91.3	89.61	88.80	80.78	69.11

Bolded and underlined content in the table indicates that it is data from our paper.

shows a comparison of the classification accuracy of each scheme under different uniform noise rates on the dataset CIFAR-10. Our algorithm shows the best performance under all noise rate conditions.

According to the experimental results in Table 3, the following conclusions can be drawn:

• Firstly, CoNet-MS shows the best classification performance under many different noise rates among all schemes, which fully demonstrates the superiority and robustness of our proposed scheme.
• L2B achieves the second-best test accuracy under all noise scenarios by adjusting the loss weights by meta-learning to counteract noisy labels. However, it is not sufficient to reduce the influence of noisy samples in the loss function, and there is a gap between the pseudo-label assigned to the samples and the ground-truth label. Our scheme makes the following improvement: introducing a dual-network sample filtering mechanism to discard samples with lower confidence and retain more valuable samples at each update. Empirically, compared to L2B, our scheme CoNet-MS achieves better classification accuracy at different noise rates, with a $3\%$ improvement in test accuracy under the scenario of high noise rate ($80\%$), demonstrating the high robustness of our scheme to high-ratio noise.
• Although MetaLabelNet uses part of clean data, i.e., meta-data for the relabeling of training samples, the meta-network is only trained on clean datasets and may overfit to these data and lead to the biased soft label for other training samples, which may affect the classifier performance. To solve this problem, CoNet-MS utilizes the meta-net to reweight the loss value between the pseudo-label and the observed label of the training sample while filtering samples through the cross dual-branch structure. As a result, the classification accuracy of the final model is improved by nearly $20\%$ compared to the former in the case of an 80% noise rate.
• The co-teaching method utilizes the “small loss” principle to filter out samples with high confidence and achieves good noise immunity by filtering potentially noisy samples from two networks with different parameters. However, simply using small loss to select training samples may result in leftover noise labels, and even worse, we cannot use the abundant samples with noisy labels, which may negatively affect the model. To address this issue, CoNet-MS proposed implicitly realizes the discarding of noisy samples by dynamically weighting the loss function to reduce the impact of lower confidence samples when updating the network. In addition, CoNet-MS also performs label estimation, which further improves the accuracy of the model by correcting the sample labels.

Figure 3 shows the confusion matrix of our work under the uniform noise rate of 50%. The results demonstrate that our work effectively learns the correct distribution of samples. The diagonal cells in Figure 3 indicate the percentage of samples that are correctly classified by our scheme, while the non-diagonal cells mean the percentage of misclassified samples. Obviously, under a high noise ratio, e.g., 50%, our scheme can achieve outstanding classification performance.

Table 4. Comparison of test accuracy (%) with 40% pair-flipping noise on CIFAR-10 dataset.

Noise Ratio (%)	40
Conventional Cross Entropy	73.24
Co-teaching [9]	73.85
MetaLabelNet [10]	84.66
L2B [11]	87.96
Ours (CoNet-MS)	88.43

Bolded and underlined content in the table indicates that it is data from our paper.

shows a comparison of the classification accuracy of each method under the pair-flipping noise rate of 40% on the dataset Cifar-10. Note that we chose this rate to simulate a moderate to large level of noise that is likely to occur in real-world scenarios. Actually, a similar trend can be obtained for a higher pair-flipping noise rate.

As shown in Table 4, our CoNet-MS achieves the highest test accuracy of 88.43% under 40% pair-flipping noise on CIFAR-10, outperforming L2B (87.96%) and co-teaching (73.85%). Moreover, the following conclusions can be drawn:

• Unlike L2B, which relies solely on meta-weights, CoNet-MS further reduces confirmation bias by cross-validating pseudo-labels between two networks, leading to a 0.47% accuracy gain over L2B.
• Compared to co-teaching (73.85%), our method shows stronger resilience to high noise ratios, indicating that meta-learning enhances the precision of the sample selection of co-teaching.

In terms of the performance metrics accuracy and Macro F1,

Table 5. Performance of all schemes under the uniform noise with a rate of 40% on the dataset ISIC2019 (imbalanced dataset).

Method	Accuracy (%)	Macro F1
Conventional Cross Entropy	70.47	0.6852
Co-teaching [9]	73.43	0.7123
L2B [11]	72.41	0.7098
Ours (CoNet-MS)	74.23	0.7234

Bolded and underlined content in the table indicates that it is data from our paper.

and

Table 6. Performance of all schemes under the pair-flipping noise with a rate of 40% on the dataset ISIC2019 (imbalanced dataset).

Method	Accuracy (%)	Macro F1
Conventional Cross Entropy	62.90	0.5918
Co-teaching [9]	67.49	0.6375
L2B [11]	69.24	0.6658
Ours (CoNet-MS)	69.75	0.6734

Bolded and underlined content in the table indicates that it is data from our paper.

give a comparison of the classification performance of each method under the uniform noise and pair-flipping noise at the rate of 40% on the dataset ISIC2019. Our algorithm shows the best performance.

In detail, the following conclusions can be drawn:

• First of all, under the imbalanced dataset, CoNet-MS outperforms all baseline methods in both noise types. Specifically, under uniform noise, CoNet-MS achieves the highest accuracy of 74.23%, which is a 1.82% improvement compared to L2B. Meanwhile, with a pair-flipping noise rate of 40%, our scheme still achieves the best performance, i.e., 69.75% accuracy, but improves by only 0.51% relative to L2B, reflecting the particular challenges caused by the noise between similar classes in an imbalanced dataset, which should be thoroughly investigated in future work.
• Secondly, compared with results in Table 3 and Table 4, that is, the test accuracy of uniform and pair-flipping noises on the balanced dataset, i.e., CIFAR-10, the results in Table 5 and Table 6 are generally smaller than those in Table 3 and Table 4. It is well known that an imbalanced training dataset will have a negative effect on classification accuracy, even in a training dataset with fully clean labels.
• As shown in Table 5, under uniform noise, our method achieves the Macro F1 of 0.7234, surpassing co-teaching and L2B. This indicates that CoNet-MS not only improves overall accuracy but also better balances precision and recall across imbalanced classes. For pair-flipping noise (Table 6), CoNet-MS attains the Macro F1 of 0.6734, marginally exceeding L2B. The smaller Macro F1 gap (0.0076) compared to the uniform noise scenario (0.0136) aligns with the observed accuracy trend. Specifically, the noise-induced confusion between semantically close classes likely degrades both precision (false positives) and recall (false negatives), thereby limiting Macro F1 gains.

4.6. Ablation Study

To evaluate the effect of different components in our proposed CoNet-MS framework, we conducted ablation experiments.

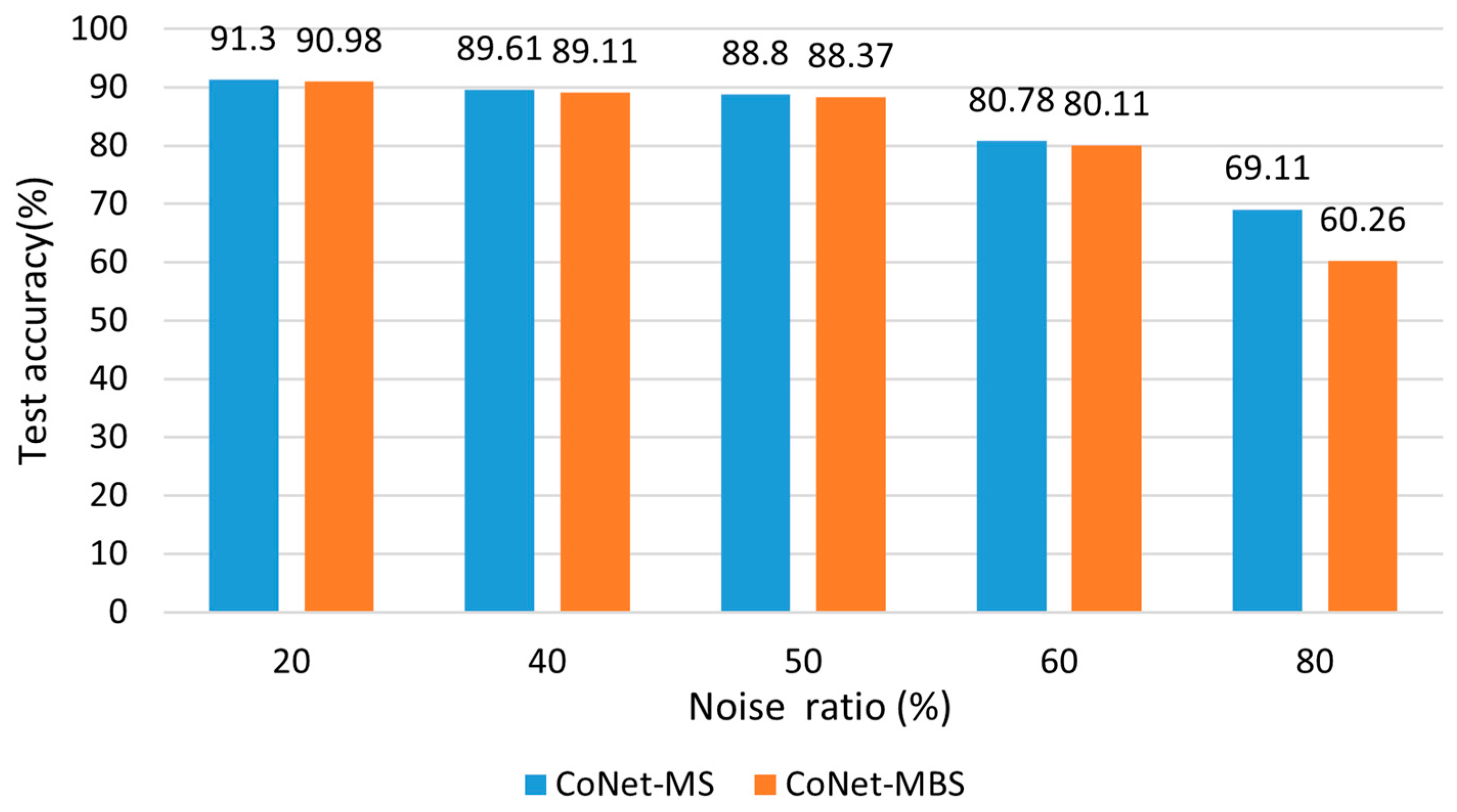
4.6.1. Comparison with Asymmetric CoNet-MS and Symmetric Variant CoNet-MBS

We created a control framework named a cross dual-branch network guided by meta-data on both sides (CoNet-MBS). Specifically, CoNet-MBS adds the meta-guide module to the lower branch of CoNet-MS and modifies its loss function to Equation (7), which is a weighted loss dynamically adjusted by meta-learning. In other words, the framework consists of two symmetric classifiers, but the initial parameters of the two classifiers still differ.

Figure 4 demonstrates the accuracy of the CoNet-MBS model under different uniform noise rates. The following results can be observed:

• The test accuracy of CoNet-MS outperforms CoNet-MBS at all noise rates. A key idea of a dual-branch classifier network to filter out samples is to utilize the difference in learning capabilities between the two networks for mutual supervision to reduce labeling noise. If two networks simultaneously use the same strategy to adjust the weights, they may interfere with the sample selection process and produce redundant and erroneous sample judgments, thus reducing the selection of valid samples, which in turn affects the model performance. In contrast, if only one network performs meta-learning weight adjustment, that network is better able to utilize its features without being disturbed by another network’s adjustment.
• At low noise rates (e.g.,$20\%$ to $60\%$), the performance of the two models is very close, while at a high noise rate of $80\%$, the performance of the CoNet-MS model improves by almost $10\%$ over CoNet-MBS. This is because two networks with simultaneous weight adjustments may lead to overly complex fitting of the model to the training data, especially at high noise rates, which is more likely to result in overfitting, thus reducing the model’s ability to generalize to unseen data.

4.6.2. Comparison of the Outputs of the Upper- and Lower-Branch Classifiers

To comprehend the role of meta-learning, we also compare the performance of different classifiers in CoNet-MS only using the upper-branch classifier, only using the lower-branch classifier, and using both classifiers in dual branches. The final output of CoNet-MS averages the outputs of the upper- and lower-branch classifiers at the Softmax layer. Figure 5 shows the accuracy of the three classifiers at different uniform noise levels. The following results can be observed:

• The test accuracy of CoNet-MS is the highest at all noise rates. This illustrates that the upper and lower-branch classifiers learn different features and patterns from the data, and when their predictions are averaged, they can combine this complementary information to provide more comprehensive and accurate predictions.
• In addition, Figure 5 shows that the lower classifier has higher test accuracy than the upper classifier at all noise rates. This may be due to the fact that the upper branch is embedded with a meta-guided module, which makes the high-confidence samples of its classifier more reliable. By exchanging high-confidence samples through the dual network, the lower branch receives reliable samples from the upper branch, which improves the accuracy of the lower classifier.

5. Conclusions

In this paper, we propose CoNet-MS, a general deep neural network classification framework based on meta-learning with cross dual-branch classifier networks to combat noisy labels in training datasets for classification tasks. Each branch in CoNet-MS firstly filters out the clean data by utilizing the principle of “small loss” of DNN learning characteristics and then is crossed to train each other. In addition, in one branch, we adopt a meta-learning approach, where a small portion of the clean dataset is used as metadata to guide the network in assigning loss weights, implicitly adjusting the sample weights and pseudo-labeling and thus improving the robustness of the model. On multiple datasets including balanced and imbalanced datasets, we compare the proposed CoNet-MS with other baseline schemes under multiple noise types including uniform and pair-flipping noise and various noise rates, and the experimental results show the robustness of the proposed CoNet-MS: achieve the best test accuracy and Macro F1.

Our work can be further improved in the following areas. First, following the convention in meta-learning, in our work, part of the clean validation dataset is assumed to exist, future work could relax this assumption: infer the pseudo-clean validation dataset from the training dataset and investigate its effect on our framework. Second, the small-loss principle is simply used as a sample selection strategy, other more effective principles should be explored for sample selection and would further improve our framework’s performance. In addition, the dual-branch framework has a limited effect on imbalanced datasets, and the design of pseudo-labels needs to be further optimized. Finally, in this paper, we just utilize the maximum probability class predicted by the model on the samples as a pseudo-label. However, under high-noise-rate conditions, model predictions become less reliable, and the maximum probability class pseudo-labeling approach may be misleading to the model. Therefore, some semi-supervised-learning-based label estimation can be used to infer more reliable pseudo-labels through data augmentation and consistency regularization to improve the model performance. These enhancements could further bridge performance gaps in challenging scenarios like pair-flipping noise on imbalanced datasets, advancing real-world applicability in domains where expert annotations are costly and error-prone.