Software Fault Localization Based on SALSA Algorithm
Abstract
1. Introduction
- (1)
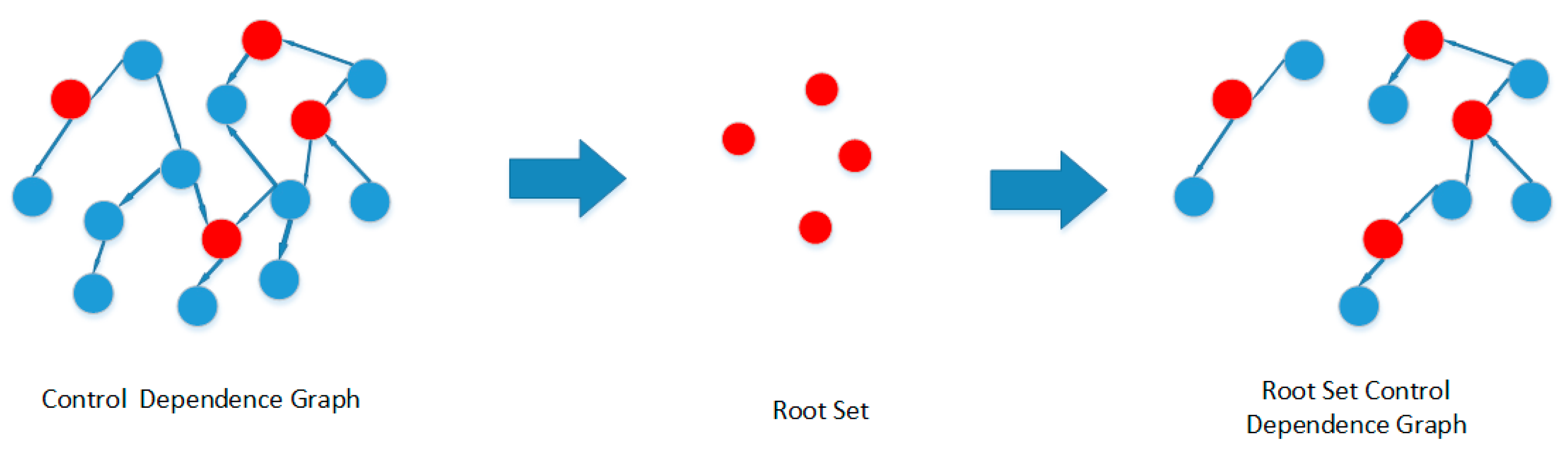
- In response to the situation where previous researchers directly abstracted source code into graph structures, which often included a lot of unimportant information, this paper proposes the Root Set Control Dependency Graph (RSCDG). The RSCDG is a part of the control dependency graph, which not only reduces the computational burden on the computer but also contains key information related to the propagation of software faults.
- (2)
- This paper proposes SA-SBFL, a method based on the principles of the SALSA algorithm, which analyzes the statement link relationships in software fault propagation to achieve accurate fault localization. Additionally, SA-SBFL can effectively address the tie problem present in traditional SBFL techniques.
- (3)
- This paper conducted experiments on SA-SBFL using five benchmark projects from Defects4J and evaluated the experimental results with two metrics: Top-N (N = 1, 3, 5) and Expected Additional Mistakes. The experimental results demonstrate that, compared to traditional SBFL techniques, SA-SBFL has better performance.
2. Related Work
2.1. Spectrum-Based Software Fault Localization
2.2. Software Fault Localization Based on Network Analysis Algorithm
2.3. Program Dependency Graph
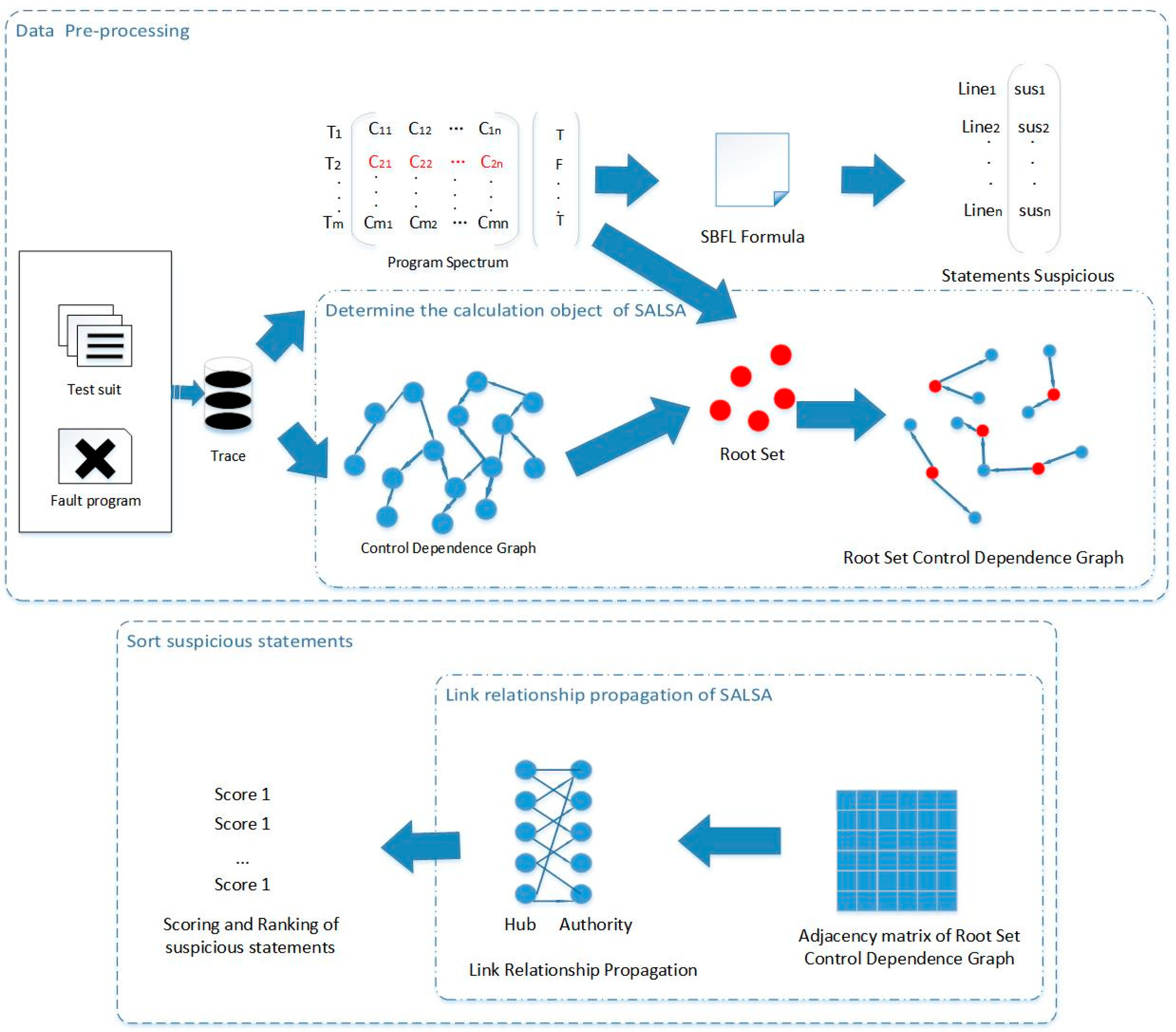
3. Proposed Approach
3.1. Data Pre-Processing
3.1.1. Program Spectrum
3.1.2. Obtain Statement Suspicion Values Based on Statistical Formulas
3.1.3. Obtain the Root Set
3.1.4. Obtain the Root Set Control Dependency Graph
3.2. Sort Suspicious Statements
| Algorithm 1 Link Analysis Algorithm |
| Input: Adjacency matrix: W Initial Hub weights: w_hubs Initial Authority weights: w_authorities Maximum number of iterations: max_iter Output: The final weight of Hub: hubs_scores The final weight of Authority: authorities_score 1: Wr <- normal_row(W) 2: Wc <- normal_col(W) 3: H <- WrWTc 4: A <- WTcWr 5: for i = 1 to max_iter do 6: hubs_new <- w_hubs.A 7: authorities_new <- w_authorities.H 8: if hubs_new-w_hubs<tol and authorities_new-w_authorities<tol then 9: break; 10: end if 11: w_hubs <- hubs_new 12: w_authorities <- authorities_new 13: end for 14: hubs_scores <- hubs_new 15: authorities_score <- authorities_new 16: return hubs_scores, authorities_score |
4. Experimental Settings
4.1. Experimental Subjects
4.2. Evaluation Metrics
- Top-N
- EXAM (Expected Additional Mistakes)
5. Results and Analyses
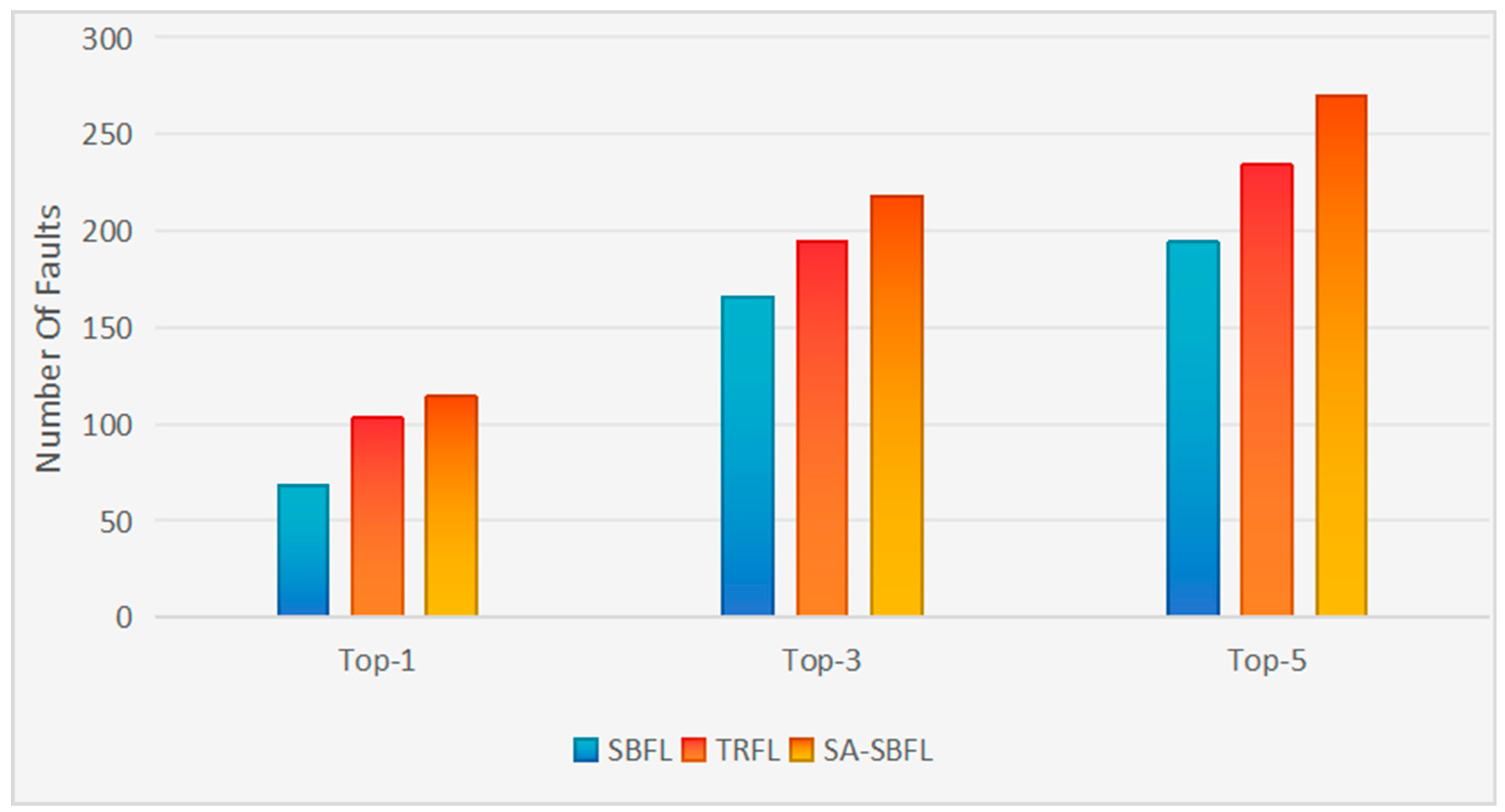
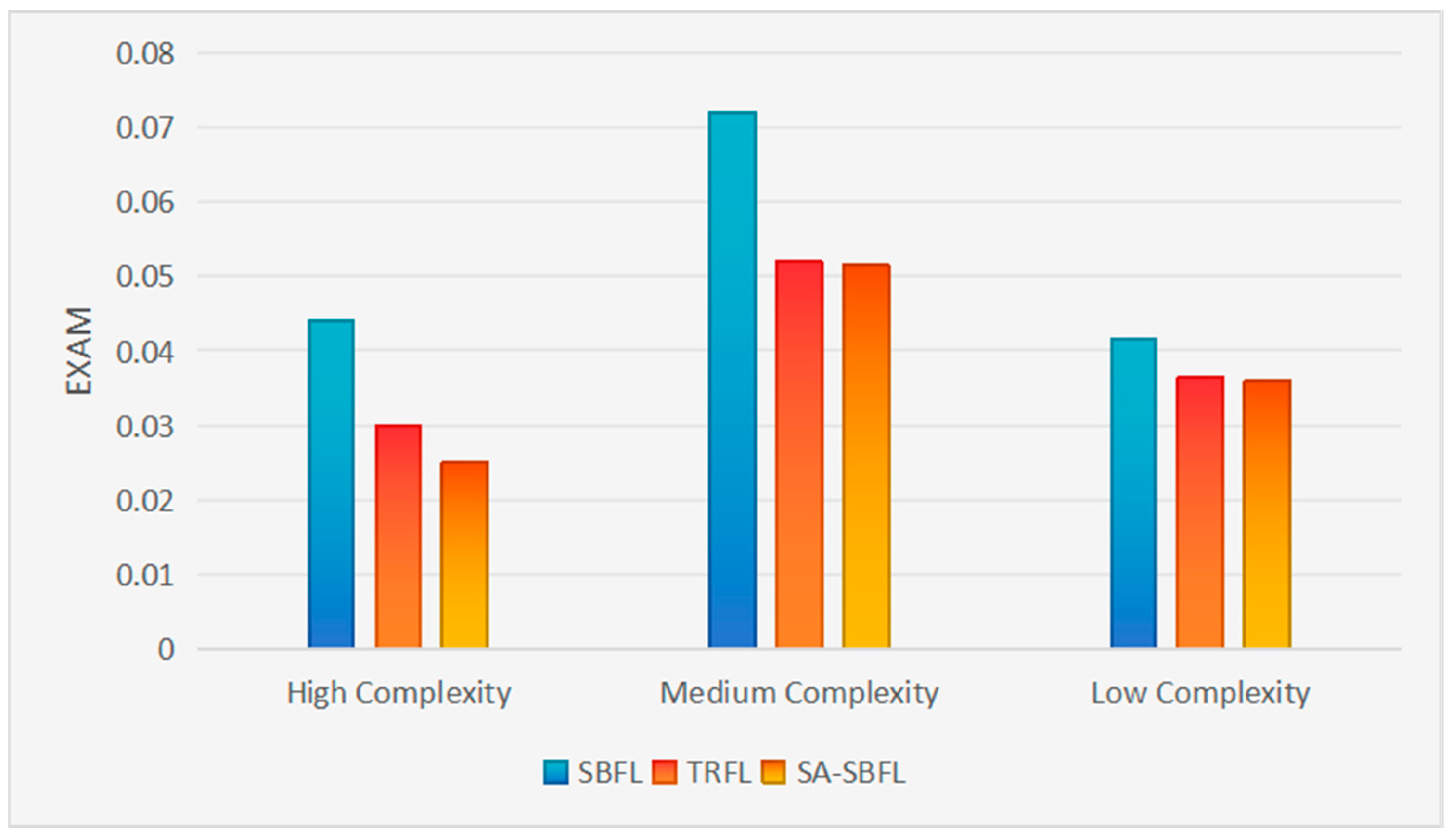
5.1. RQ1: How Accurate Is SA-SBFL in Fault Localization?
5.2. RQ2: Which Score Is More Advantageous in Fault Localization, the Final Hub Score or the Authority Score of the Node?
5.3. RQ3: What Are the Differences in Fault Location Accuracy When Using Suspicious Values Obtained from Different Statistical Formulas as Node Weights?
6. Limitation and Future Work
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Perscheid, M.; Siegmund, B.; Taeumel, M.; Hirschfeld, R. Studying the advancement in debugging practice of professional software developers. Softw. Qual. J. 2017, 25, 83–110. [Google Scholar] [CrossRef]
- Hailpern, B.; Santhanam, P. Software debugging, testing, and verification. IBM Syst. J. 2002, 41, 4–12. [Google Scholar] [CrossRef]
- Wong, W.E.; Gao, R.; Li, Y.; Abreu, R.; Wotawa, F.; Li, D. Software fault localization: An overview of research, techniques, and tools. In Handbook of Software Fault Localization: Foundations and Advances; Wiley-IEEE Press: Hoboken, NJ, USA, 2023; pp. 1–117. [Google Scholar]
- Abreu, R.; Zoeteweij, P.; Van Gemund, A.J.C. On the accuracy of spectrum-based fault localization. In Proceedings of the Testing: Academic and Industrial Conference Practice and Research Techniques-MUTATION (TAICPART-MUTATION 2007), Windsor, UK, 10–14 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 89–98. [Google Scholar]
- Ajibode, A.; Shu, T.; Said, K.; Ding, Z. A fault localization method based on metrics combination. Mathematics 2022, 10, 2425. [Google Scholar] [CrossRef]
- Godboley, S.; Dutta, A.; Mohapatra, D.P.; Mall, R. GECOJAP: A novel source-code preprocessing technique to improve code coverage. Comput. Stand. Interfaces 2018, 55, 27–46. [Google Scholar] [CrossRef]
- Yan, Y.; Jiang, S.; Zhang, Y.; Zhang, S.; Zhang, C. A fault localization approach based on fault propagation context. Inf. Softw. Technol. 2023, 160, 107245. [Google Scholar] [CrossRef]
- Zhao, G.; He, H.; Huang, Y. Fault centrality: Boosting spectrum-based fault localization via local influence calculation. Appl. Intell. 2022, 52, 7113–7135. [Google Scholar] [CrossRef]
- Zhang, Y.; Santelices, R. Prioritized static slicing and its application to fault localization. J. Syst. Softw. 2016, 114, 38–53. [Google Scholar] [CrossRef]
- Hofer, B.; Wotawa, F. Spectrum enhanced dynamic slicing for better fault localization. In ECAI; IOS Press: Amsterdam, The Netherlands, 2012; pp. 420–425. [Google Scholar]
- Qian, J.; Ju, X.; Chen, X. GNet4FL: Effective fault localization via graph convolutional neural network. Autom. Softw. Eng. 2023, 30, 16. [Google Scholar] [CrossRef]
- Ma, Y.F.; Li, M. The flowing nature matters: Feature learning from the control flow graph of source code for bug localization. Mach. Learn. 2022, 111, 853–870. [Google Scholar] [CrossRef]
- Zhang, Z.; Lei, Y.; Mao, X.; Yan, M.; Xia, X.; Lo, D. Context-aware neural fault localization. IEEE Trans. Softw. Eng. 2023, 49, 3939–3954. [Google Scholar] [CrossRef]
- Jones, J.A.; Harrold, M.J. Empirical evaluation of the tarantula automatic fault-localization technique. In Proceedings of the 20th IEEE/ACM international Conference on Automated Software Engineering, Long Beach, CA, USA, 7–11 November 2005; pp. 273–282. [Google Scholar]
- Chen, M.Y.; Kiciman, E.; Fratkin, E.; Fox, A.; Brewer, E. Pinpoint: Problem determination in large, dynamic internet services. In Proceedings of the International Conference on Dependable Systems and Networks, Washington, DC, USA, 23–26 June 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 595–604. [Google Scholar]
- Abreu, R.; Zoeteweij, P.; Golsteijn, R.; Van Gemund, A.J. A practical evaluation of spectrum-based fault localization. J. Syst. Softw. 2009, 82, 1780–1792. [Google Scholar] [CrossRef]
- Naish, L.; Lee, H.J.; Ramamohanarao, K. A model for spectra-based software diagnosis. ACM Trans. Softw. Eng. Methodol. 2011, 20, 1–32. [Google Scholar] [CrossRef]
- Wong, W.E.; Debroy, V.; Gao, R.; Li, Y. The DStar method for effective software fault localization. IEEE Trans. Reliab. 2013, 63, 290–308. [Google Scholar] [CrossRef]
- Yoo, S.; Xie, X.; Kuo, F.C.; Chen, T.Y.; Harman, M. No pot of gold at the end of program spectrum rainbow: Greatest risk evaluation formula does not exist. RN 2014, 14, 14. [Google Scholar]
- de Souza, H.A.; Mutti, D.; Chaim, M.L.; Kon, F. Contextualizing spectrum-based fault localization. Inf. Softw. Technol. 2018, 94, 245–261. [Google Scholar] [CrossRef]
- He, H.; Ren, J.; Zhao, G.; He, H. Enhancing spectrum-based fault localization using fault influence propagation. IEEE Access 2020, 8, 18497–18513. [Google Scholar] [CrossRef]
- Fan, X.; Wu, K.; Zhang, S.; Yu, L.; Zheng, W.; Ge, Y. Fault Localization Using TrustRank Algorithm. Appl. Sci. 2023, 13, 12344. [Google Scholar] [CrossRef]
- Yan, Y.; Jiang, S.; Zhang, Y.; Zhang, C. An effective fault localization approach based on PageRank and mutation analysis. J. Syst. Softw. 2023, 204, 111799. [Google Scholar] [CrossRef]
- Zhang, M.; Li, X.; Zhang, L.; Khurshid, S. Boosting spectrum-based fault localization using pagerank. In Proceedings of the 26th ACM SIGSOFT International Symposium on Software Testing and Analysis, Santa Barbara, CA, USA, 10–14 July 2017; pp. 261–272. [Google Scholar]
- Podgurski, A.; Clarke, L. The implications of program dependencies for software testing, debugging, and maintenance. In Proceedings of the ACM SIGSOFT’89 Third Symposium on Software Testing, Analysis, and Verification, Key West, FL, USA, 13–15 December 1989; pp. 168–178. [Google Scholar]
- Harrold, M.J.; Offutt, A.J.; Tewary, K. An approach to fault modeling and fault seeding using the program dependence graph. J. Syst. Softw. 1997, 36, 273–295. [Google Scholar] [CrossRef]
| e1 | e2 | e3 | e4 | e5 | e6 | e7 | Result | |
|---|---|---|---|---|---|---|---|---|
| T1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| T2 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| T3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| T4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| T5 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| T6 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| Name | Formula |
|---|---|
| Dstar | |
| Jaccard | |
| Tarantula | |
| Ochiai | |
| Ochiai2 | |
| OP2 |
| Element | Description |
|---|---|
| Nef | Number of failed tests to execute the program element |
| Nep | Number of passed tests for executed program elements |
| Nnf | Number of failed tests for non-executed program elements |
| Nnp | Number of passed tests for non-executed program elements |
| ID | Program | #Faults | LoC | #Tests |
|---|---|---|---|---|
| Chart | JFreefigure | 25 | 96 k | 2205 |
| Closure | Closure Compile | 133 | 90 k | 7927 |
| Lang | Apache commons-lang | 65 | 22 k | 2245 |
| Math | Apache commons-math | 98 | 81 k | 3546 |
| Time | Joda-Time | 27 | 28 k | 4130 |
| Project | Technique | Top-1 | Top-3 | Top-5 | EXAM |
|---|---|---|---|---|---|
| Chart | SBFL | 5 | 16 | 19 | 0.041 |
| TRFL | 12 | 23 | 25 | 0.030 | |
| SA-SBFL | 13 | 21 | 25 | 0.031 | |
| Closure | SBFL | 14 | 38 | 39 | 0.044 |
| TRFL | 22 | 44 | 59 | 0.030 | |
| SA-SBFL | 32 | 65 | 87 | 0.025 | |
| Lang | SBFL | 23 | 45 | 55 | 0.044 |
| TRFL | 31 | 52 | 59 | 0.040 | |
| SA-SBFL | 30 | 54 | 59 | 0.040 | |
| Math | SBFL | 20 | 56 | 69 | 0.102 |
| TRFL | 31 | 63 | 79 | 0.074 | |
| SA-SBFL | 32 | 65 | 85 | 0.072 | |
| Time | SBFL | 6 | 11 | 12 | 0.039 |
| TRFL | 7 | 12 | 12 | 0.033 | |
| SA-SBFL | 7 | 13 | 14 | 0.032 |
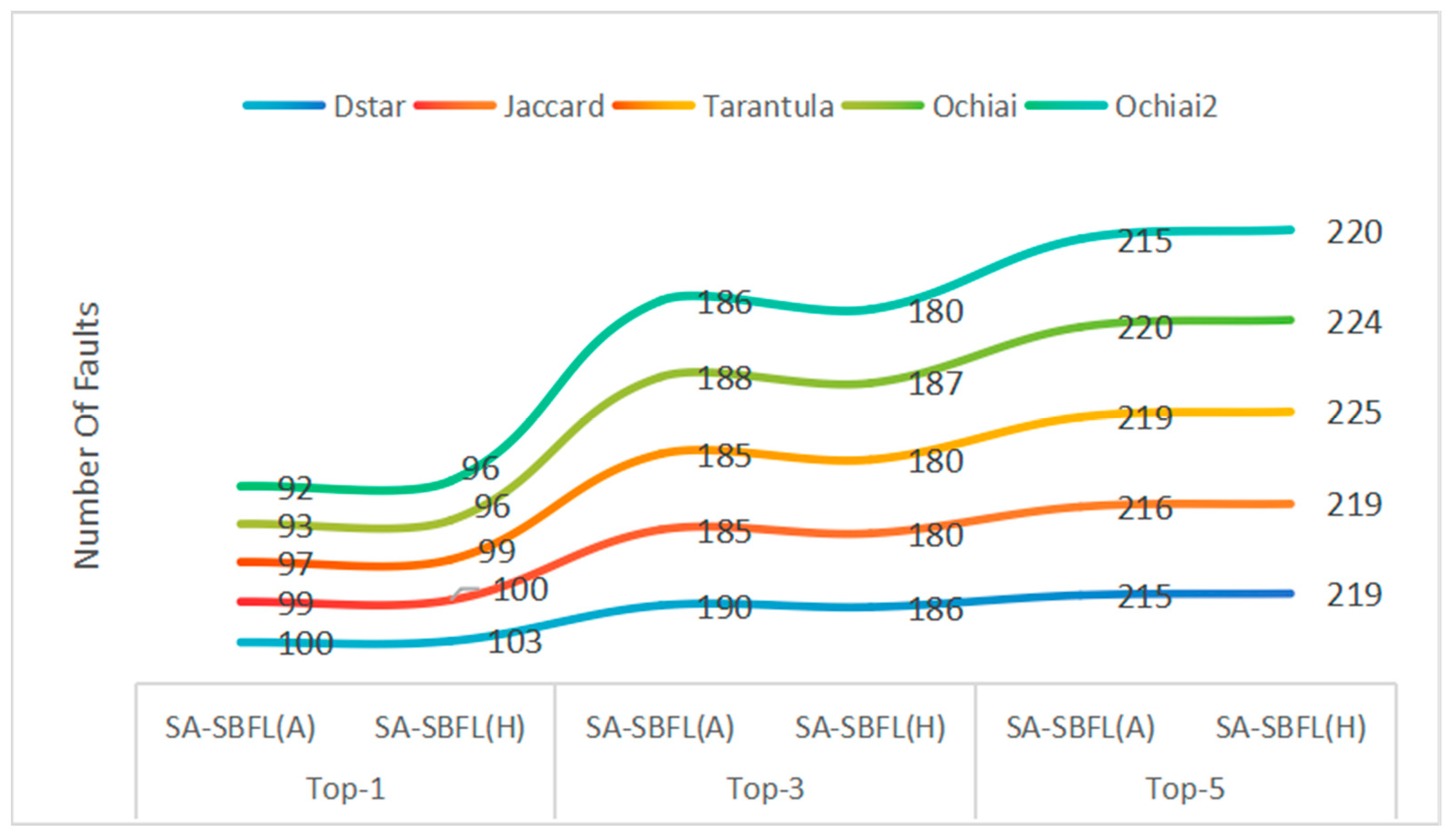
| Project | Formula | Top-1 | Top-3 | Top-5 | EXAM | ||||
|---|---|---|---|---|---|---|---|---|---|
| SA-SBF (A) | SA-SBF (H) | SA-SBF (A) | SA-SBF (H) | SA-SBF (A) | SA-SBF (H) | SA-SBF (A) | SA-SBF (H) | ||
| Defects4j | Dstar | 100 | 103 | 190 | 186 | 215 | 219 | 0.040 | 0.041 |
| Jaccard | 99 | 100 | 185 | 180 | 216 | 219 | 0.041 | 0.043 | |
| Tarantula | 97 | 99 | 185 | 180 | 219 | 225 | 0.040 | 0.041 | |
| Ochiai | 93 | 96 | 188 | 187 | 220 | 224 | 0.041 | 0.043 | |
| Ochiai2 | 92 | 96 | 186 | 180 | 215 | 220 | 0.039 | 0.041 | |
| Op2 | 90 | 92 | 180 | 171 | 207 | 211 | 0.049 | 0.051 | |
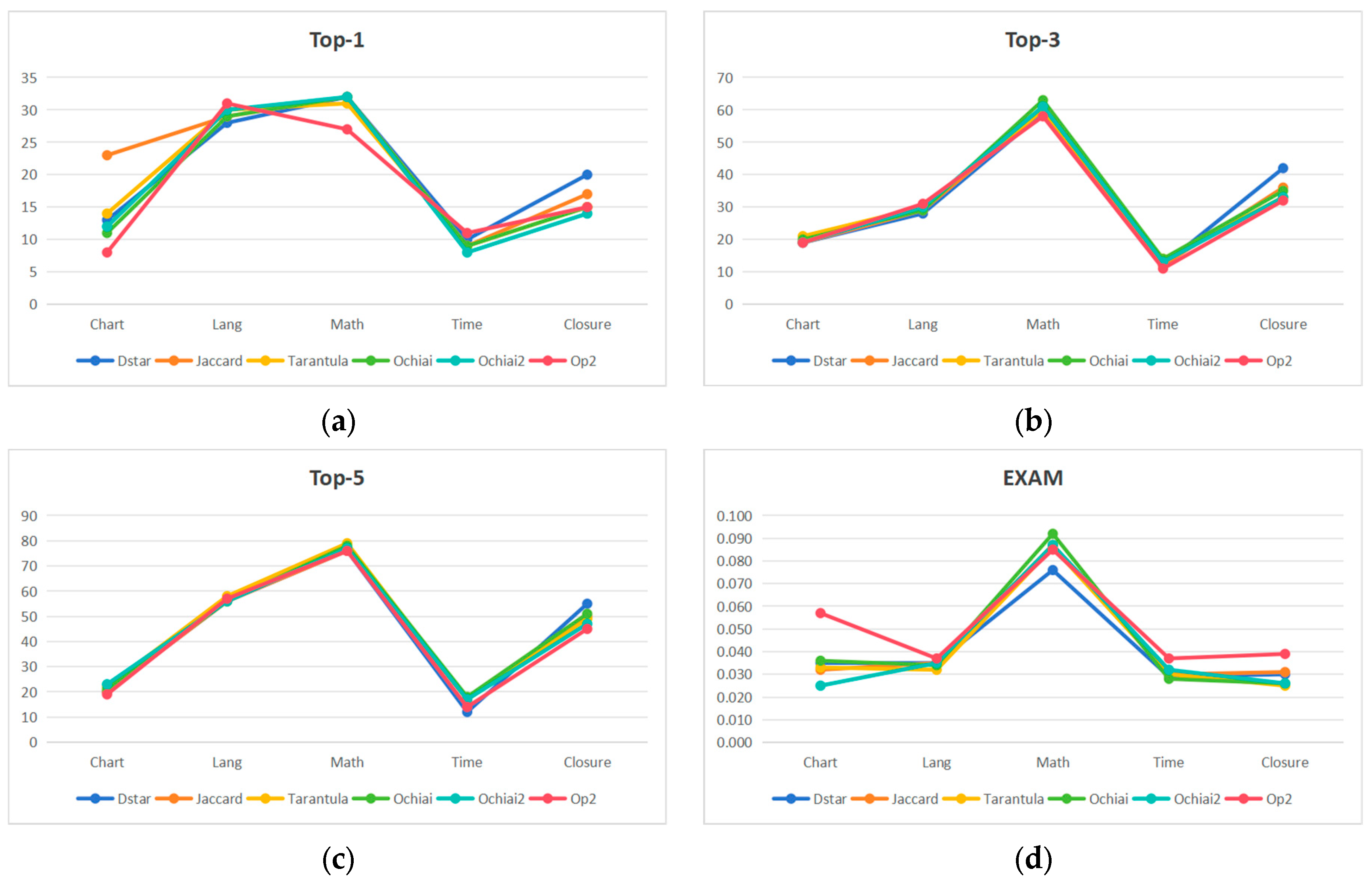
| Project | Technique | Top-1 | Top-3 | Top-5 | EXAM | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| SBFL | SA-SBFL | SBFL | SA-SBFL | SBFL | SA-SBFL | SBFL | SA-SBFL | Improvement | ||
| Chart | Dstar | 5 | 13 | 16 | 19 | 19 | 25 | 0.042 | 0.035 | 26.19% |
| Jaccard | 6 | 13 | 17 | 19 | 20 | 24 | 0.038 | 0.032 | 15.79% | |
| Tarantula | 7 | 14 | 20 | 21 | 22 | 25 | 0.037 | 0.033 | 10.81% | |
| Ochiai | 6 | 11 | 17 | 20 | 19 | 25 | 0.039 | 0.036 | 7.69% | |
| Ochiai2 | 6 | 12 | 17 | 19 | 21 | 23 | 0.028 | 0.025 | 10.71% | |
| Op2 | 5 | 8 | 14 | 19 | 16 | 22 | 0.061 | 0.057 | 6.56% | |
| Lang | Dstar | 23 | 28 | 45 | 54 | 55 | 56 | 0.044 | 0.035 | 20.45% |
| Jaccard | 22 | 29 | 45 | 53 | 56 | 56 | 0.043 | 0.035 | 18.60% | |
| Tarantula | 21 | 30 | 45 | 52 | 57 | 58 | 0.042 | 0.032 | 23.81% | |
| Ochiai | 22 | 29 | 44 | 55 | 56 | 56 | 0.043 | 0.034 | 20.93% | |
| Ochiai2 | 21 | 30 | 45 | 54 | 55 | 56 | 0.042 | 0.035 | 16.67% | |
| Op2 | 23 | 31 | 45 | 51 | 56 | 57 | 0.046 | 0.037 | 19.57% | |
| Math | Dstar | 22 | 32 | 56 | 59 | 69 | 81 | 0.102 | 0.076 | 25.49% |
| Jaccard | 22 | 32 | 57 | 60 | 69 | 79 | 0.109 | 0.087 | 20.18% | |
| Tarantula | 22 | 31 | 57 | 60 | 69 | 79 | 0.102 | 0.086 | 15.69% | |
| Math | Ochiai | 22 | 32 | 58 | 63 | 70 | 81 | 0.102 | 0.092 | 9.80% |
| Ochiai2 | 22 | 32 | 56 | 61 | 69 | 79 | 0.104 | 0.087 | 16.35% | |
| Op2 | 21 | 27 | 52 | 58 | 61 | 78 | 0.110 | 0.085 | 22.73% | |
| Time | Dstar | 6 | 10 | 11 | 12 | 12 | 14 | 0.039 | 0.029 | 25.64% |
| Jaccard | 5 | 9 | 9 | 12 | 18 | 17 | 0.033 | 0.030 | 9.09% | |
| Tarantula | 5 | 9 | 11 | 14 | 16 | 17 | 0.032 | 0.030 | 6.25% | |
| Ochiai | 6 | 9 | 11 | 14 | 18 | 18 | 0.031 | 0.028 | 9.68% | |
| Ochiai2 | 5 | 8 | 11 | 13 | 16 | 17 | 0.037 | 0.032 | 13.51% | |
| Op2 | 8 | 11 | 12 | 11 | 14 | 14 | 0.041 | 0.037 | 9.76% | |
| Closure | Dstar | 14 | 20 | 38 | 42 | 39 | 87 | 0.044 | 0.030 | 31.82% |
| Jaccard | 13 | 17 | 27 | 36 | 37 | 80 | 0.046 | 0.031 | 32.61% | |
| Tarantula | 12 | 15 | 26 | 33 | 36 | 79 | 0.031 | 0.025 | 19.35% | |
| Ochiai | 14 | 15 | 29 | 35 | 39 | 81 | 0.037 | 0.026 | 29.73% | |
| Ochiai2 | 13 | 14 | 27 | 33 | 37 | 77 | 0.036 | 0.026 | 27.78% | |
| Op2 | 17 | 15 | 33 | 32 | 42 | 85 | 0.053 | 0.039 | 26.42% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Shen, Z.; Fu, Z.; Ge, Y. Software Fault Localization Based on SALSA Algorithm. Appl. Sci. 2025, 15, 2079. https://doi.org/10.3390/app15042079
Fan X, Shen Z, Fu Z, Ge Y. Software Fault Localization Based on SALSA Algorithm. Applied Sciences. 2025; 15(4):2079. https://doi.org/10.3390/app15042079
Chicago/Turabian StyleFan, Xin, Zuxiong Shen, Zhenlei Fu, and Yun Ge. 2025. "Software Fault Localization Based on SALSA Algorithm" Applied Sciences 15, no. 4: 2079. https://doi.org/10.3390/app15042079
APA StyleFan, X., Shen, Z., Fu, Z., & Ge, Y. (2025). Software Fault Localization Based on SALSA Algorithm. Applied Sciences, 15(4), 2079. https://doi.org/10.3390/app15042079





