Optimizing Lattice Basis Reduction Algorithm on ARM V8 Processors
Abstract
1. Introduction
2. Technical Background
2.1. Foundation of Lattice
2.2. The Gram0-Schmidt Process
2.3. Lll Algorithm
2.4. Lll _FP Algorithm
| Algorithm 1 Calculation of Gram–Schmitt coefficient. |
|
| Algorithm 2 LLL_FP Algorithm |
|
3. Algorithm Analysis and Optimization
3.1. Algorithm Analysis
3.2. Simd Vectorization
| Algorithm 3 Optimization of Gram–Schmidt coefficient calculation. |
|
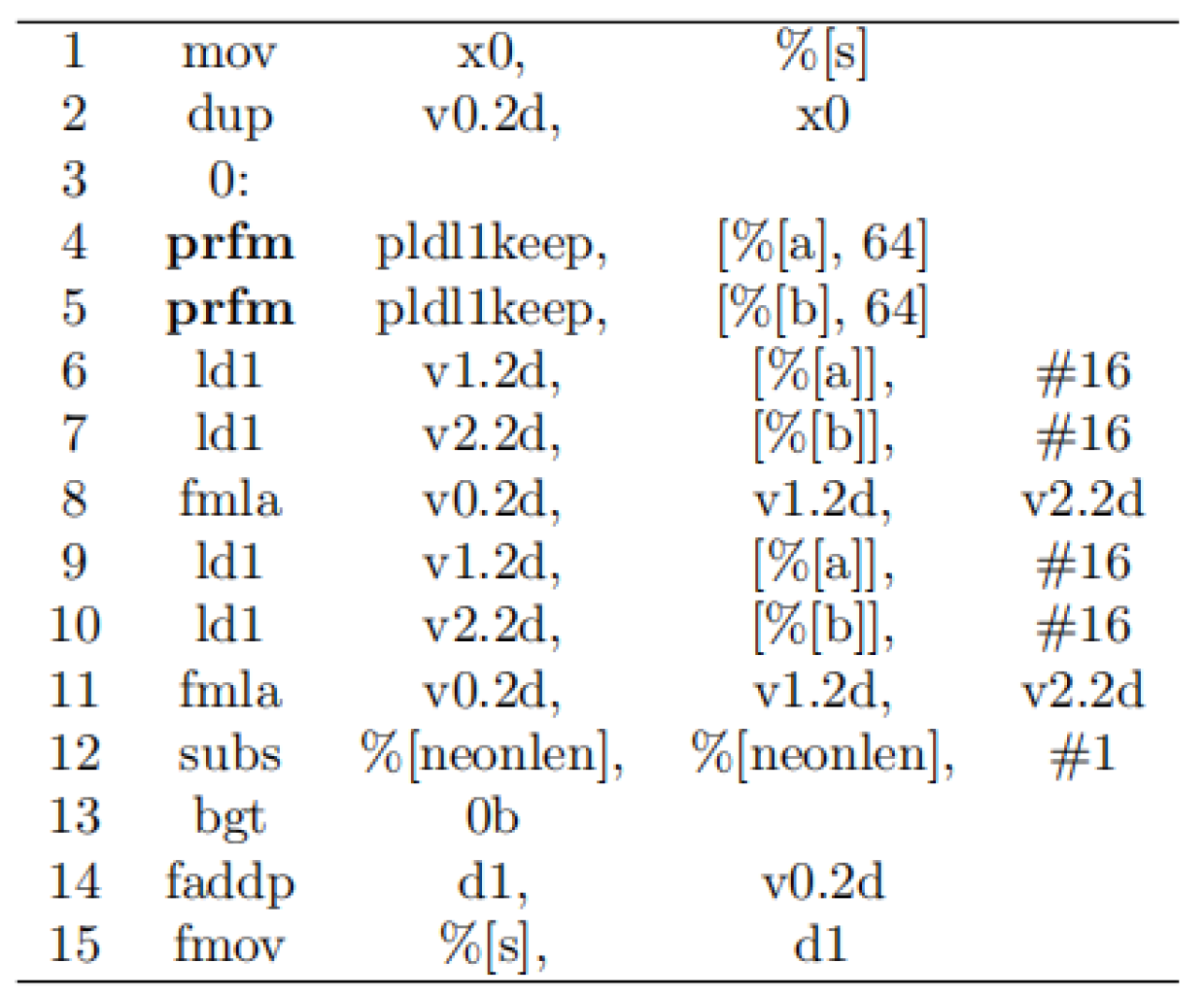
3.3. Assembly Optimization
3.4. Data Prefetch and Loop Unrolling
4. Experimental Results and Performance Analysis
4.1. Experimental Environment
4.2. Correctness Verification
4.2.1. Check the Lattice Vector Correctness
4.2.2. Residual Check
4.2.3. Data Validation
4.2.4. Hadamard Ratio
4.3. Performance Analysis
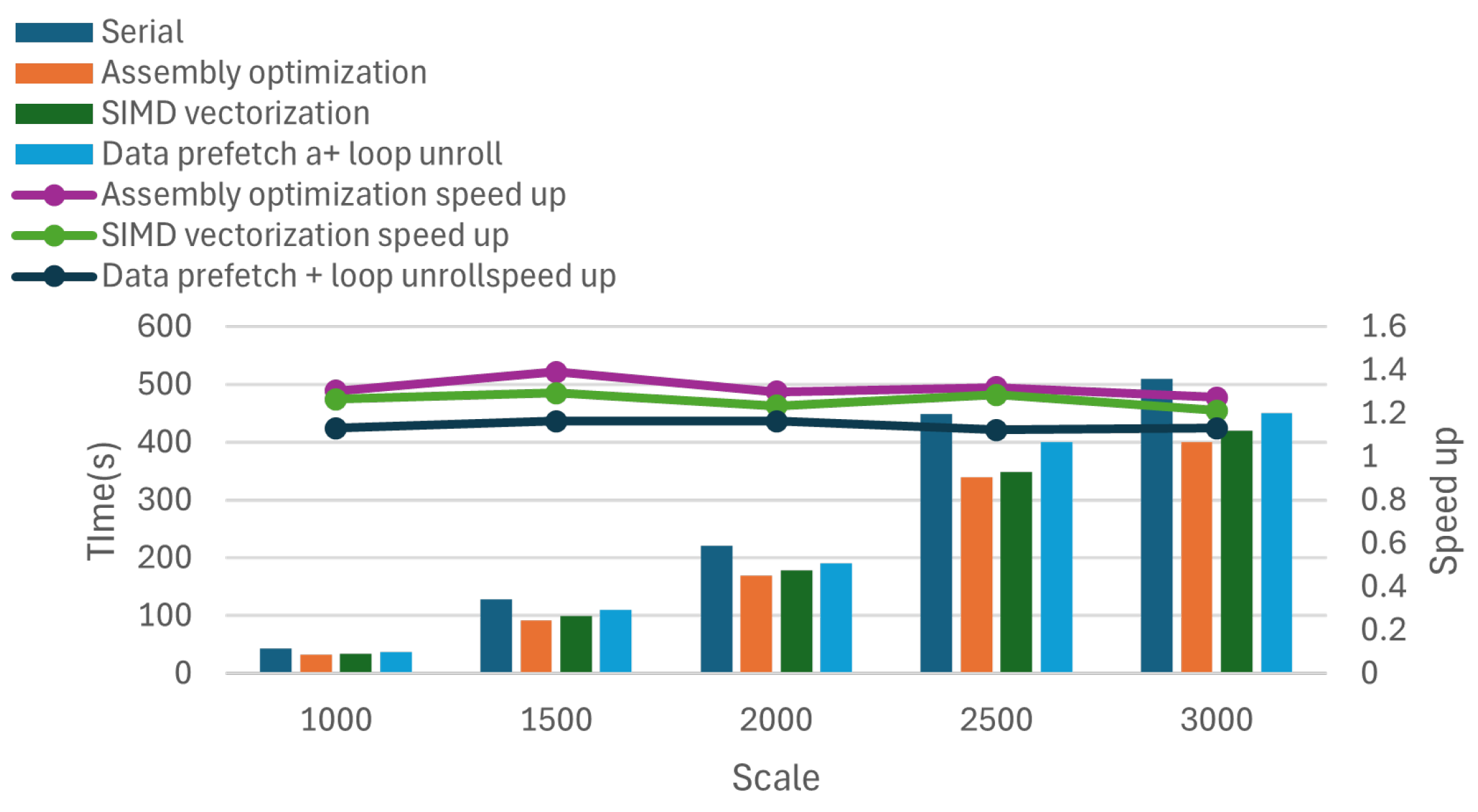
4.3.1. Different Methods to Optimize the Effect
4.3.2. Optimization Effect of Inner Product Calculation
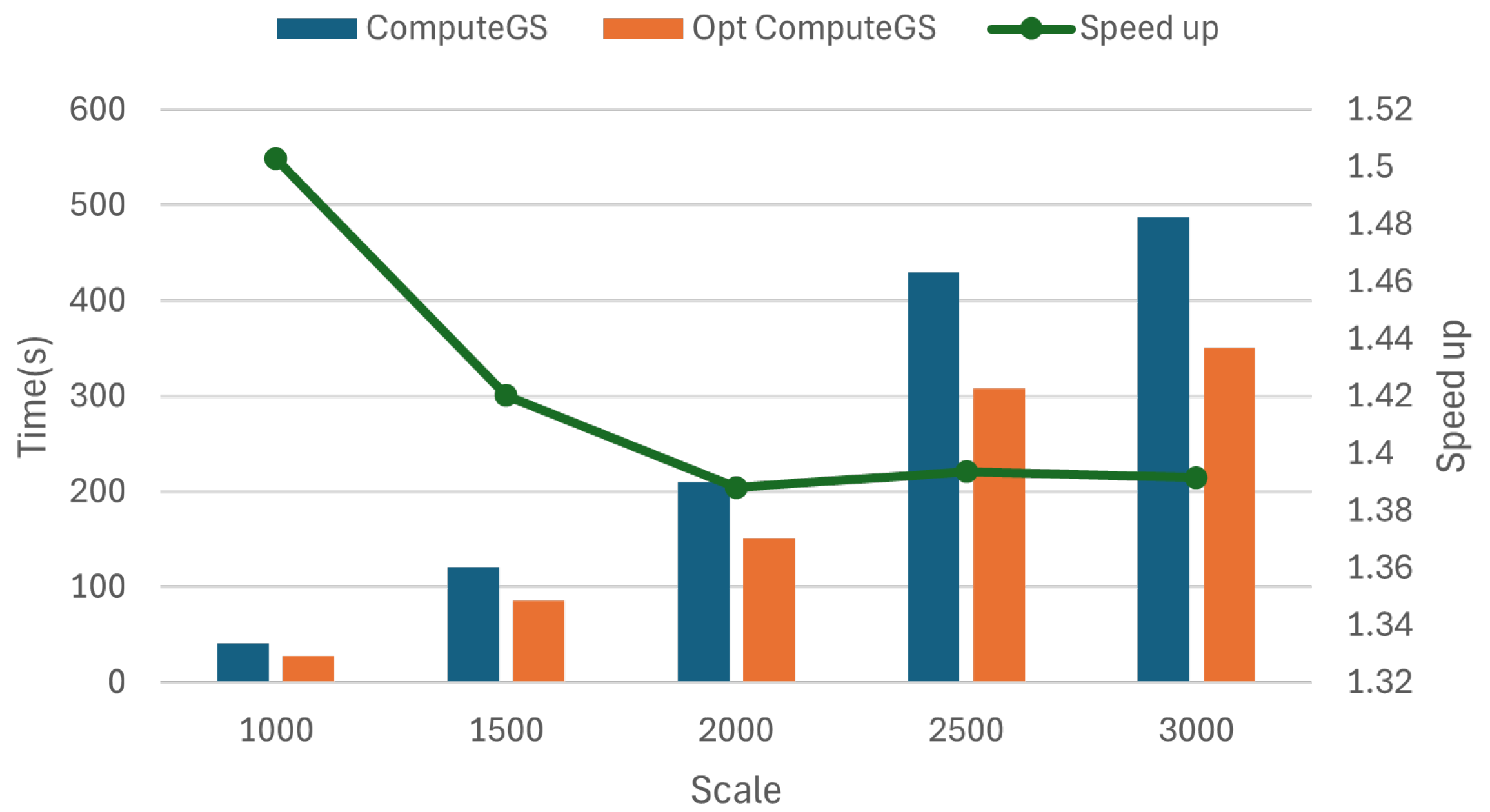
4.3.3. Optimization Effect in Computing Gram–Schmidt Coefficient
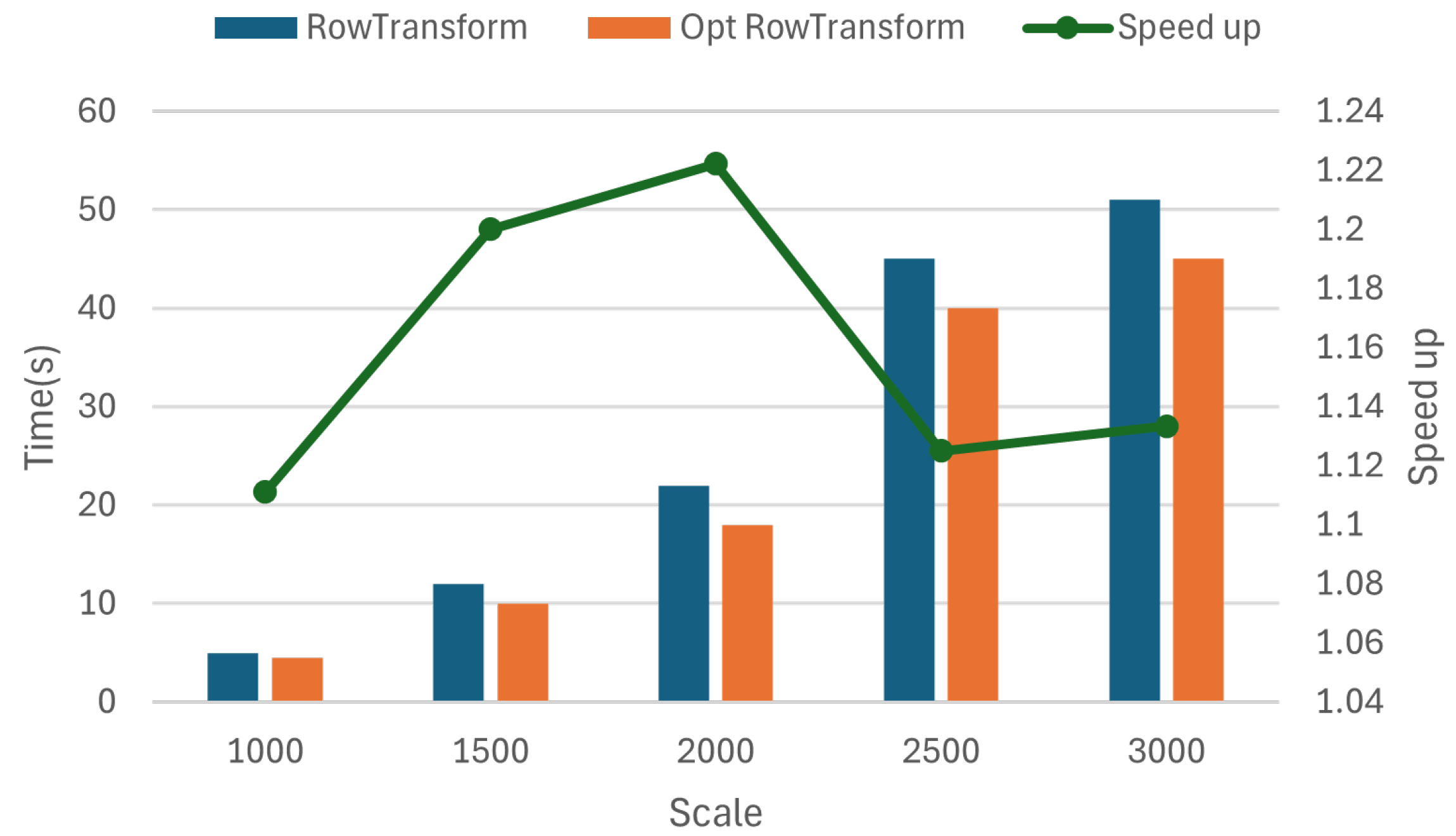
4.3.4. Optimization Effect of Row Transform
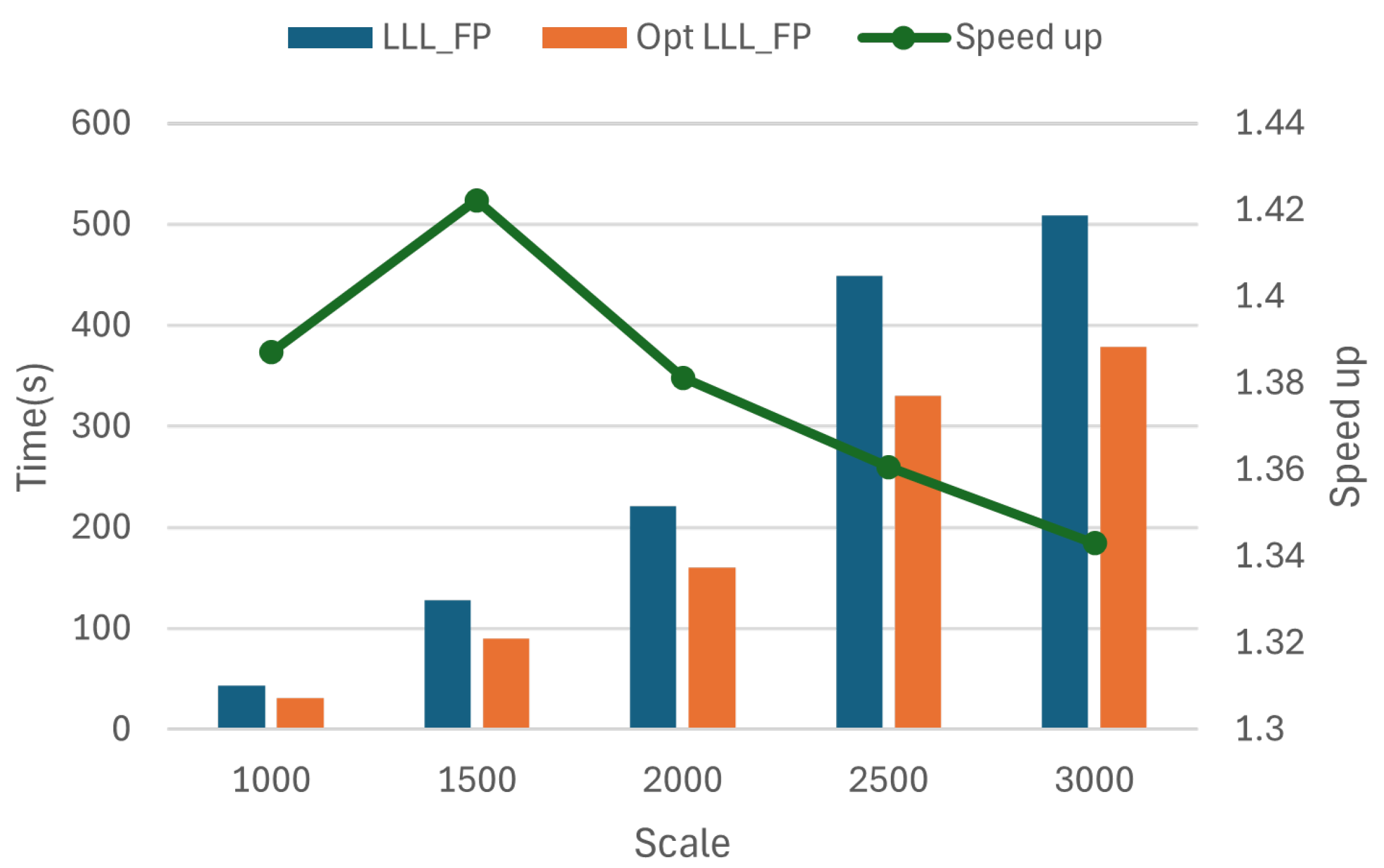
4.3.5. Overall Optimization Effect of LLL _FP Algorithm
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lenstra, A.K.; Lenstra, H.W.; Lovász, L. Factoring polynomials with rational coefficients. Math. Comput. 1982, 39, 607–620. [Google Scholar] [CrossRef]
- Ajtai, M. Generating hard instances of lattice problems. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 99–108. [Google Scholar]
- Albrecht, M.R.; Ducas, L.; Herold, G.; Kirshanova, E.; Postlethwaite, E.W.; Stevens, M. The general sieve kernel and new records in lattice reduction. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer International Publishing: Cham, Switzerland, 2019; pp. 717–746. [Google Scholar]
- Coppersmith, D. Small solutions to polynomial equations, and low exponent RSA vulnerabilities. J. Cryptol. 1997, 10, 233–260. [Google Scholar] [CrossRef]
- Cheng, Y.; Diakonikolas, I.; Ge, R.; Woodruff, D.P. Faster algorithms for high-dimensional robust covariance estimation. In Proceedings of the Conference on Learning Theory, PMLR, Phoenix, AZ, USA, 25–28 June 2019; pp. 727–757. [Google Scholar]
- Eisenträger, K.; Hallgren, S.; Kitaev, A.; Song, F. A quantum algorithm for computing the unit group of an arbitrary degree number field. In Proceedings of the Forty-Sixth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 1–3 June 2014; pp. 293–302. [Google Scholar]
- Hassibi, B.; Vikalo, H. On the sphere-decoding algorithm I. Expected complexity. IEEE Trans. Signal Process. 2005, 53, 2806–2818. [Google Scholar] [CrossRef]
- Chockalingam, A.; Rajan, B.S. Large MIMO Systems; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Lovász, L.; Scarf, H.E. The generalized basis reduction algorithm. Math. Oper. Res. 1992, 17, 751–764. [Google Scholar] [CrossRef]
- Dadush, D.; Végh, L.A.; Zambelli, G. Geometric rescaling algorithms for submodular function minimization. Math. Oper. Res. 2021, 46, 1081–1108. [Google Scholar] [CrossRef]
- Schnorr, C.P.; Euchner, M. Lattice basis reduction: Improved practical algorithms and solving subset sum problems. Math. Program. 1994, 66, 181–199. [Google Scholar] [CrossRef]
- Lyu, S.; Ling, C. Boosted KZ and LLL algorithms. IEEE Trans. Signal Process. 2017, 65, 4784–4796. [Google Scholar] [CrossRef]
- Aono, Y.; Wang, Y.; Hayashi, T.; Takagi, T. Improved progressive BKZ algorithms and their precise cost estimation by sharp simulator. In Proceedings of the Advances in Cryptology-EUROCRYPT 2016: 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Proceedings, Part I 35. Vienna, Austria, 8–12 May 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 789–819. [Google Scholar]
- Neumaier, A.; Stehlé, D. Faster LLL-type reduction of lattice bases. In Proceedings of the ACM on International Symposium on Symbolic and Algebraic Computation, Waterloo, ON, Canada, 19–22 July 2016; pp. 373–380. [Google Scholar]
- Luo, Y.; Qiao, S. A parallel LLL algorithm. In Proceedings of the Fourth International C* Conference on Computer Science and Software Engineering, Montreal, QC, Canada, 16–18 May 2011; pp. 93–101. [Google Scholar]
- Jeremic, F.; Qiao, S. A Parallel Jacobi-Type Lattice Basis Reduction Algorithm. Int. J. Numer. Anal. Model. Ser. B 2014, 5, 1–12. [Google Scholar]
- Tian, Z.; Qiao, S. An enhanced Jacobi method for lattice-reduction-aided MIMO detection. In Proceedings of the 2013 IEEE China Summit and International Conference on Signal and Information Processing, Beijing, China, 6–10 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 39–43. [Google Scholar]
- Wen, Q.; Ma, X. Efficient greedy LLL algorithms for lattice decoding. IEEE Trans. Wirel. Commun. 2016, 15, 3560–3572. [Google Scholar] [CrossRef]
- Gu, B.; Qiu, J.; Chi, X. Performance evaluation analysis and empirical research of parallel computing software for heterogeneous systems. Front. Data Comput. 2024, 6, 116–126. [Google Scholar]
- Park, T.; Seo, H.; Kim, J.; Park, H.; Kim, H. Efficient Parallel Implementation of Matrix Multiplication for Lattice-Based Cryptography on Modern ARM Processor. Secur. Commun. Netw. 2018, 2018, 7012056. [Google Scholar] [CrossRef]
- Hassan, S.A.; Mahmoud, M.M.; Hemeida, A.M.; Saber, M.A. Effective implementation of matrix-vector multiplication on Intel’s AVX multicore processor. Computer Languages. Syst. Struct. 2018, 51, 158–175. [Google Scholar]
- Lee, W.K.; Seo, H.; Zhang, Z.; Hwang, S.O. TensorCrypto: High throughput acceleration of lattice-based cryptography using tensor core on GPU. IEEE Access 2022, 10, 20616–20632. [Google Scholar] [CrossRef]
- Gao, W.; Xu, J.; Sun, H.; Li, M. Research on cycle optimization technology for SIMD vectorization. J. Inf. Eng. Univ. 2016, 17, 496–503. [Google Scholar]
- Higham; Nicholas, J. The accuracy of floating point summation. SIAM J. Sci. Comput. 1993, 14, 783–799. [Google Scholar] [CrossRef]
- Gong, C.; Chen, X.; Lv, S.; Liu, J.; Yang, B.; Wang, Q.; Bao, W.; Pang, Y.; Sun, Y. An efficient image to column algorithm for convolutional neural networks. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar] [CrossRef]

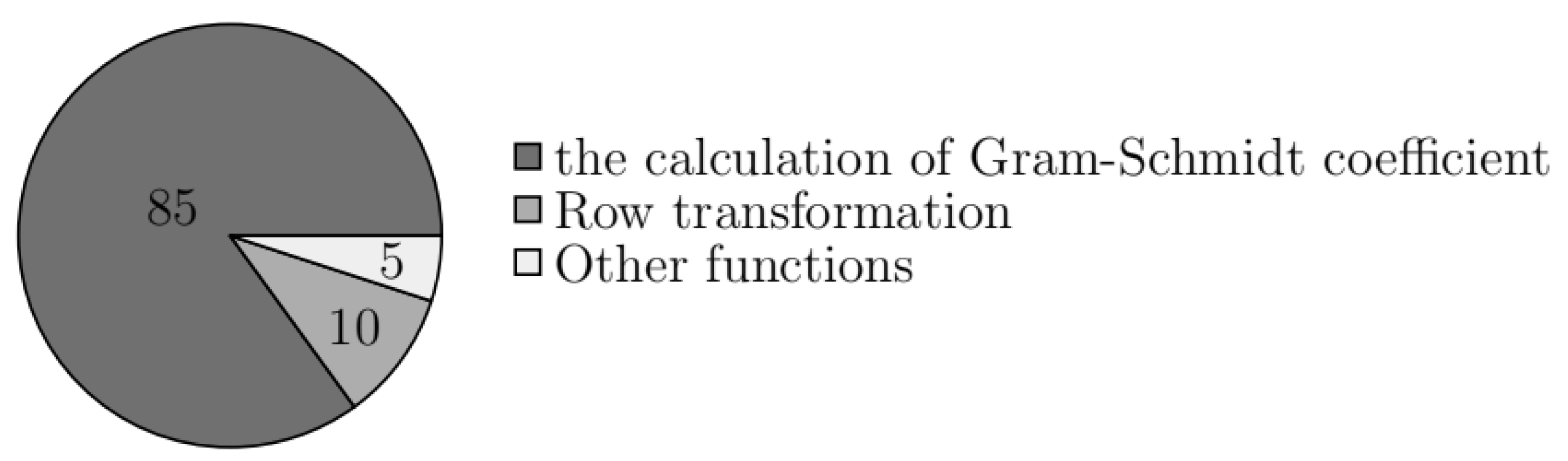




| Combination | Data Prefetch | Loop Unrolling |
|---|---|---|
| 1 | 64 | 2 |
| 2 | 128 | 4 |
| 3 | 256 | 8 |
| CPU | Phytium FT-2000+ | |
| Arch | Aarch64 | |
| Hardware environment | SIMD | 128 bits |
| L1 cache | 2 MiB | |
| L2 cache | 256 MiB | |
| Software environment | Compiler | GCC9.3.0 |
| NTL | 11.5.1 |
| Implementation Method | Descriptor |
|---|---|
| Inner product calculation | InnerProduct |
| Optimize inner product calculation | Opt InnerProduct |
| Calculation of Gram–Schmidt coefficient | ComputeGS |
| Optimize calculation of Gram–Schmidt coefficient | Opt ComputeGS |
| Row transformation | RowTransform |
| Optimize row transformation | Opt RowTransform |
| Floating-point lattice reduction algorithm | LLL_FP |
| Optimized floating point lattice reduction algorithm | Opt LLL_FP |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, R.; Wang, J.; Zheng, L.; Zhou, J.; Wang, H.; Xiao, T.; Gong, C. Optimizing Lattice Basis Reduction Algorithm on ARM V8 Processors. Appl. Sci. 2025, 15, 2021. https://doi.org/10.3390/app15042021
Cao R, Wang J, Zheng L, Zhou J, Wang H, Xiao T, Gong C. Optimizing Lattice Basis Reduction Algorithm on ARM V8 Processors. Applied Sciences. 2025; 15(4):2021. https://doi.org/10.3390/app15042021
Chicago/Turabian StyleCao, Ronghui, Julong Wang, Liming Zheng, Jincheng Zhou, Haodong Wang, Tiaojie Xiao, and Chunye Gong. 2025. "Optimizing Lattice Basis Reduction Algorithm on ARM V8 Processors" Applied Sciences 15, no. 4: 2021. https://doi.org/10.3390/app15042021
APA StyleCao, R., Wang, J., Zheng, L., Zhou, J., Wang, H., Xiao, T., & Gong, C. (2025). Optimizing Lattice Basis Reduction Algorithm on ARM V8 Processors. Applied Sciences, 15(4), 2021. https://doi.org/10.3390/app15042021






