Using Neutrosophic Cognitive Maps to Support Group Decisions About Modeling and Analyzing Smart Port Performance
Abstract
1. Introduction
1.1. Contributions of Article
- In this paper, we propose a novel framework that utilizes NCMs to understand how business strategies and objectives interact with each other and determine which nodes are most impactful. To the best of our knowledge, it is the first time in related literature that a soft computing method such as NCMs has been used to evaluate smart port performance.
- The combination of static and dynamic analysis allows decision-makers to predict possible obstacles and facilitates what-if scenarios, thus prioritizing development areas with more confidence. In this way, stakeholders gain insights into the immediate impacts (static analysis) and evolving outcomes (dynamic analysis) of strategies (e.g., operational, financial, environmental). This dual approach not only solves current gaps in performance evaluation approaches but also delivers actionable insights for long-term competitiveness and innovation in the marine sector.
- In contrast to relying exclusively on FCMs, our model utilizes NCMs due to the increased capabilities of neutrosophic theory in efficiently handling the inherent uncertainty associated with expert judgments. By using neutrosophic logic, our suggested model offers a comprehensive approach for navigating the intricacies of smart port management, ensuring that the analysis accurately represents the various and sometimes contradictory viewpoints of stakeholders.
- To validate the usefulness, reliability, and objectivity of the proposed method, an illustrative example of smart port performance evaluation under group decision support environment is introduced. This example serves as a proof-of-concept to demonstrate the practicality of the suggested method. The findings show that NCMs may successfully model complex interrelationships between performance factors, giving useful insights for decision-making in real-world smart port management. This enhanced framework, which can increase the reliability of an NCM by incorporating the opinions of more than one domain experts, has the potential to reform decision-making processes in the smart port management field, offering stakeholders a stronger and more informed basis for strategic planning and operational optimization.
- Unlike traditional MCDM models, which often overlook the numerous linkages between strategies, our work introduces a new method that delves deeper into understanding these interrelationships. Traditional MCDM models typically evaluate factors affecting port performance using set criteria, but our proposed technique conducts a more in-depth analysis by considering the dynamic interactions between strategies. By adopting this innovative approach, we aim to illuminate the subtle interactions and dependencies between the various techniques, offering valuable insights into their overall impact on port performance.
1.2. Structure of Article
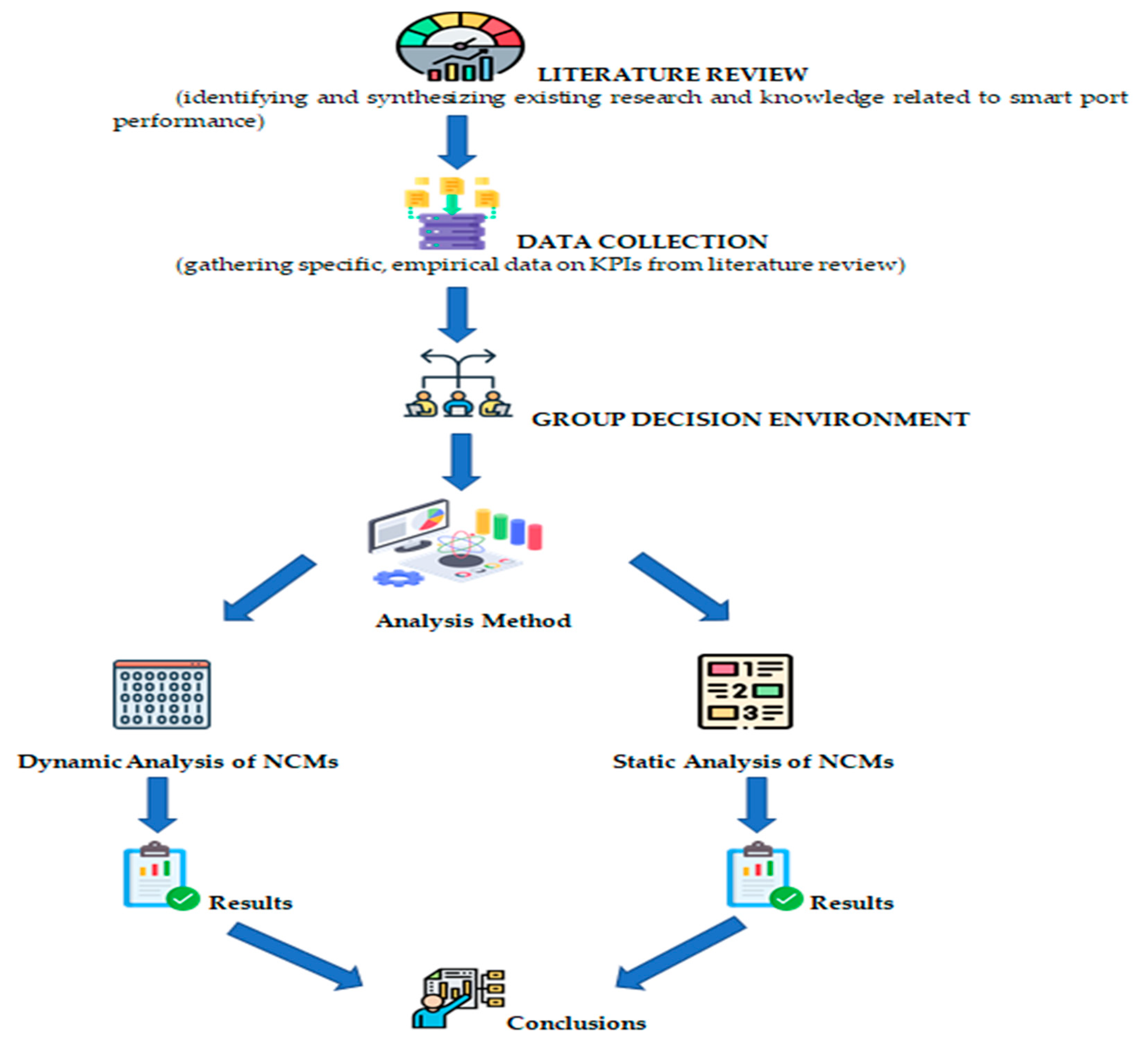
2. Materials and Methods
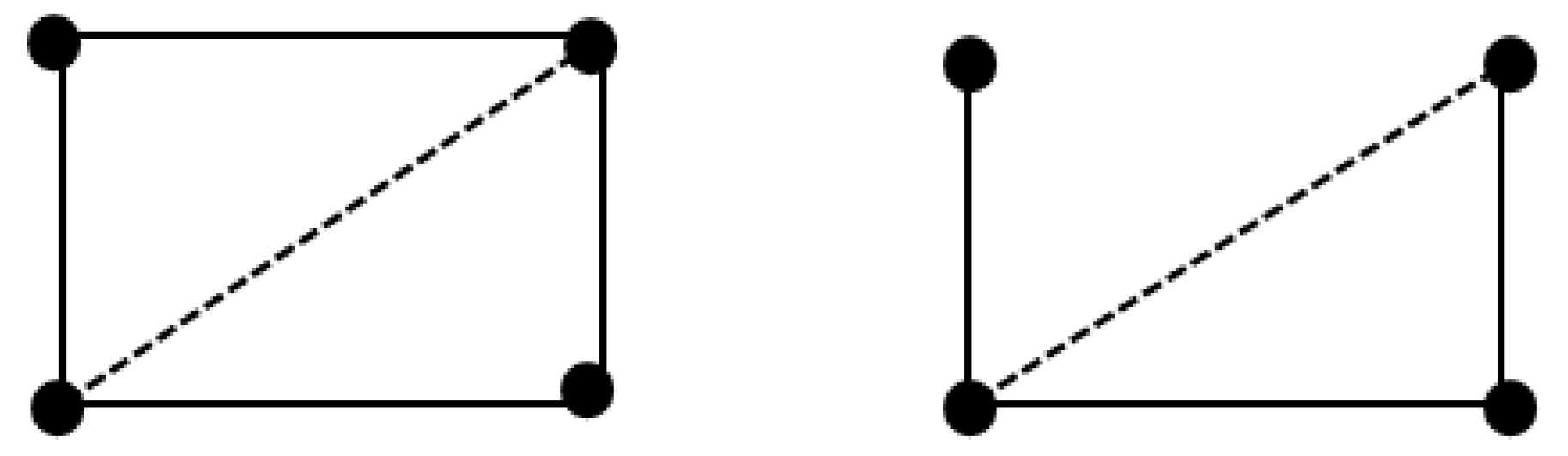
2.1. Basic Definitions
2.2. Analyzing NCMs for Decision Support
2.2.1. Static Analysis of NCMs
- Outdegree is the sum of the row elements in the neutrosophic adjacency matrix and represents the strength of the variable’s outward connections (). It actually indicates the cumulative strengths of connections (Cij). It is a measure of how much a given variable influences other variables.
- Indegree is the sum of the column components in the neutrosophic adjacency matrix, and it represents the strength of the connections () that stem from the variable and shows the cumulative strength of variables entering the unit.
- Total centrality is calculated by summing the variable’s indegree and outdegree.
2.2.2. Dynamic Analysis of NCMs
- = 0 if is off (no effect)
- = 1 if is on (has effect)
- = I if is indeterminate (effect cannot be determined)
- for i = 1, 2, …, n.
- The NCM stabilizes to a stable state (the fixed-point attractor), with certain ideas “on” and others not.
- The NCM repeatedly cycles through the same set of output states (limit cycle).
- The NCM shows unstable behavior (chaotic attractor), shifting states instead of stabilizing as in (1) and (2) above.
2.3. Overview of the Proposed Model
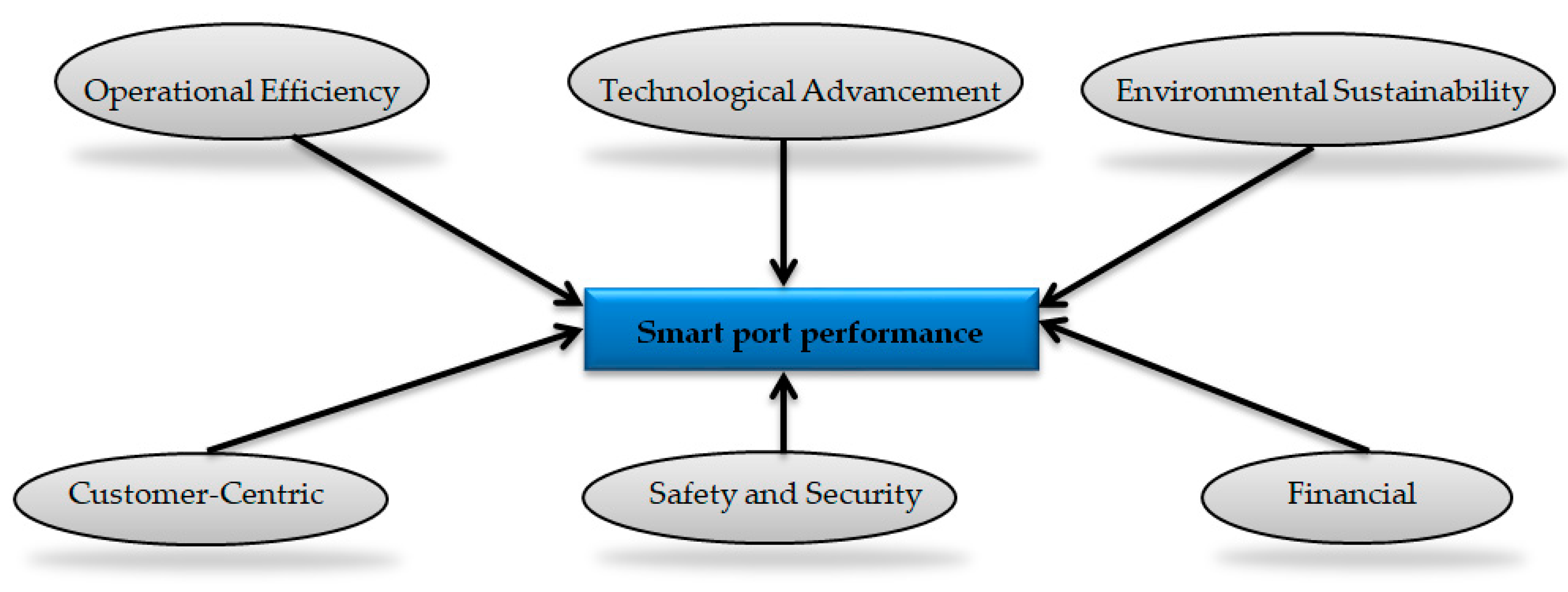
3. Smart Port Performance Indicators
- Operational efficiency [51,52,53,54,55,56,57,58]: Smart ports prioritize operational efficiency by aiming to optimize procedures, decrease costs, and increase productivity through leveraging digital technology and data-driven solutions. In fact, smart ports achieve operational efficiency by combining automation, digitalization, predictive analytics, real-time monitoring, and optimal supply chain integration.
- Financial [54,55,56]: Financial performance metrics are crucial in determining the economic health, efficiency, and profitability of smart ports. These metrics provide information on income growth, expense management, and overall financial sustainability. Financial performance indicators help smart ports monitor their financial health, identify areas for development, make informed investment decisions, and ensure long-term financial growth in a changing marine sector landscape.
- Technological advancement [59,60,61]: Technological advancements play a crucial role in enhancing the performance of smart ports. Ongoing breakthroughs in technology, such as blockchain, 5G connectivity, and self-driving vehicles, create opportunities for innovation and advancement in port operations. An agile and adaptable IT infrastructure enables smart ports to quickly adapt to shifting market demands, regulatory requirements, and emerging technologies, ensuring long-term competitiveness and sustainability. These advancements encompass a range of innovations that revolutionize operations, boost efficiency, and foster sustainability in port settings. Technological breakthroughs facilitate innovation, efficiency, and sustainability in smart port ecosystems, enabling ports to meet the evolving demands of global trade and logistics. Strategic integration of these technologies can enhance port operations, improve competitiveness, and contribute to the development of a more robust and efficient maritime sector.
- Environmental sustainability [62,63,64,65,66,67]: Environmental sustainability is a critical focus for smart ports, as they aim to decrease their ecological impact and help create a more environmentally friendly future. Key performance indicators (KPIs) for environmental sustainability in smart ports help to monitor and measure progress towards sustainability goals. These KPIs also offer valuable data for stakeholders, authorities, and the public to assess a port’s environmental performance and support ongoing improvement efforts.
- Customer-centric orientation [68,69,70]: Customer-centric performance at smart ports focuses on providing excellent services, increasing transparency, and optimizing operations to meet the requirements and expectations of port users, such as shipping firms, cargo owners, and other stakeholders. Metrics such as customer satisfaction, service reliability, transparency, communication, customization, personalization, feedback, and continuous improvement can help focus on customer needs, foster collaboration, leverage technology, and constantly improve services. By aligning key performance indicators (KPIs) with customer-centric goals, smart ports can generate customer satisfaction, loyalty, and a competitive edge in the marine sector.
- Safety and security [71,72,73]: Smart port performance prioritizes safety and security to safeguard assets, staff, and cargo while ensuring seamless operations. By implementing robust safety and security measures, smart ports contribute to a secure and reliable marine ecosystem, protecting assets, maintaining operational continuity, and inspiring trust among stakeholders.
4. Results
4.1. Development Phase
4.2. Application Phase
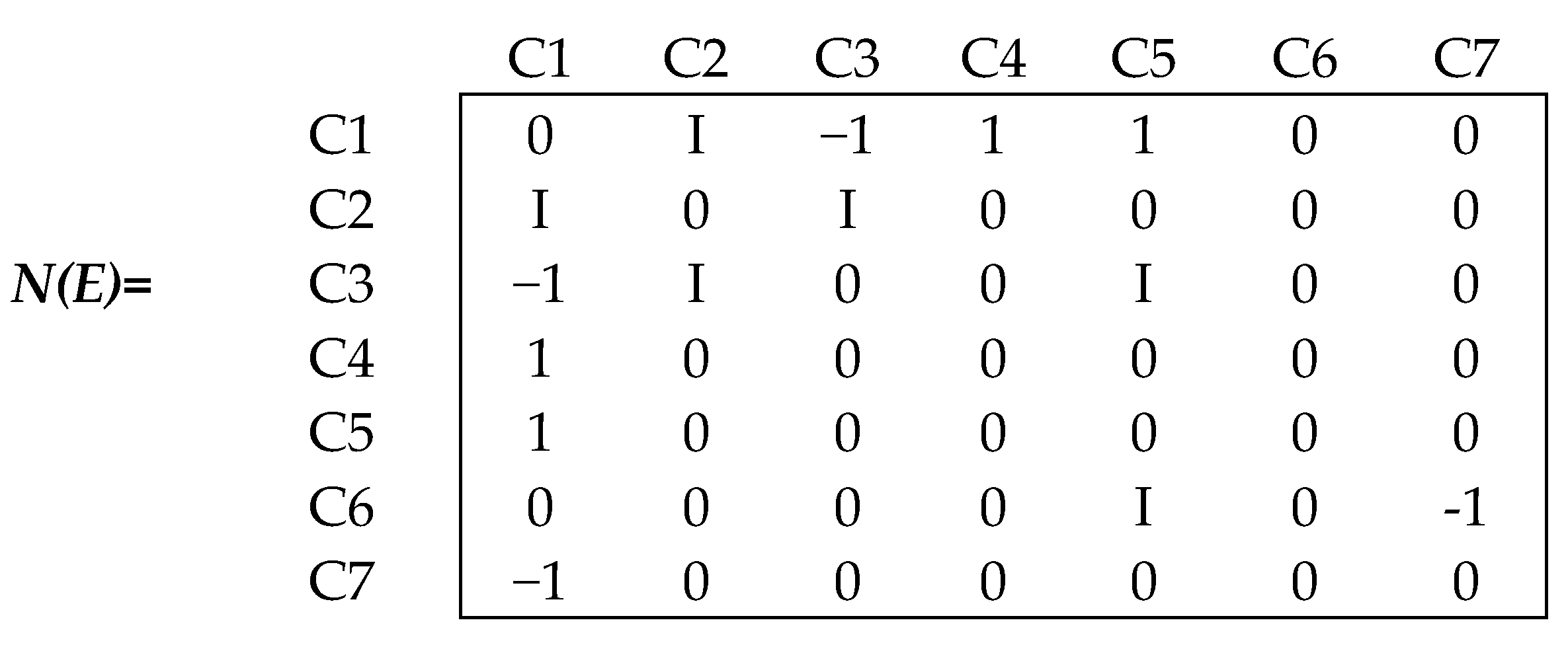
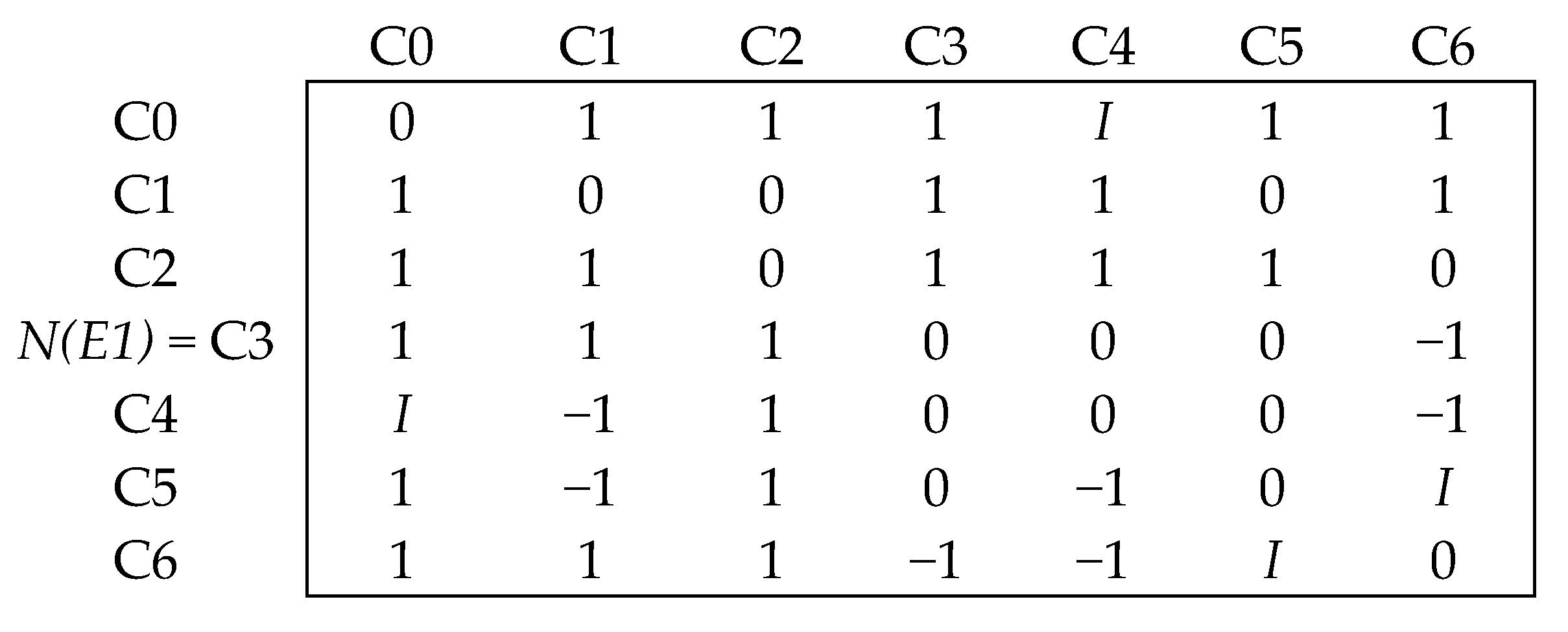
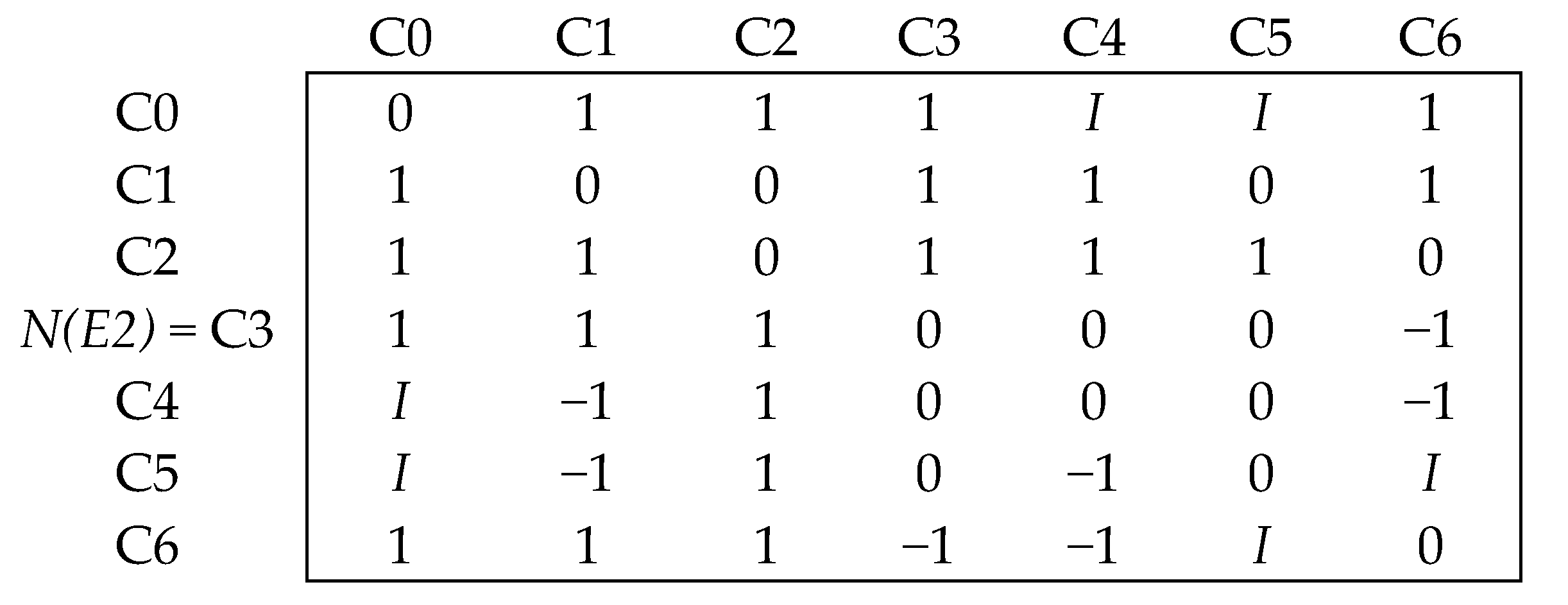
4.2.1. Static Analysis of the NCMs
| C0 → Smart port performance |  | Dimensions/factors |
| C1 → Operational efficiency | ||
| C2 → Technological advancement | ||
| C3 → Environmental sustainability | ||
| C4 → Customer-centric | ||
| C5 → Safety and security | ||
| C6 → Financial |
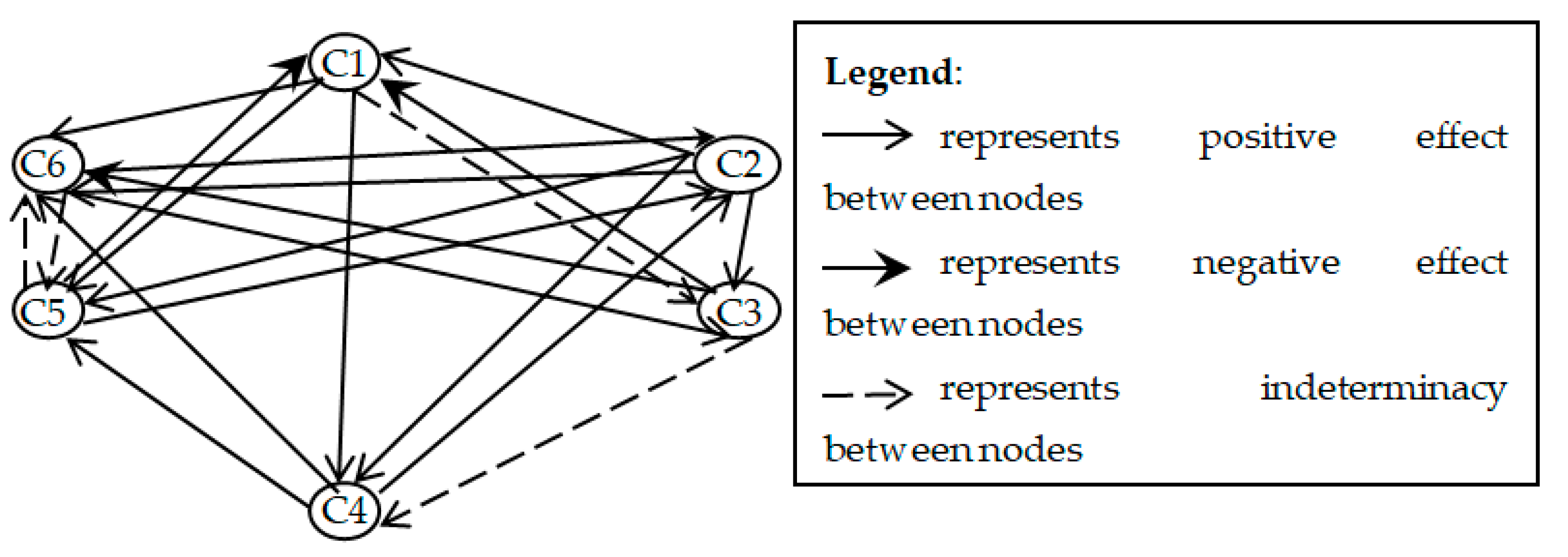
4.2.2. Dynamic Analysis of the NCMs
4.3. Discussion of Results and Implications on Smart Port Management
4.4. Sensitivity Analysis
4.5. Comparison to Other MCDM Methods
5. Conclusions and Future Work
5.1. Concluding Remarks
5.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| DIMENSIONS | OE | TA | ES | CC | SS | F |
|---|---|---|---|---|---|---|
| OE | 0 | |||||
| TA | 0 | |||||
| ES | 0 | |||||
| CC | 0 | |||||
| SS | 0 | |||||
| F | 0 |
| Intensity of Importance | Definition |
|---|---|
| (+) 1.0 | Extreme effect |
| 0.0 | No effect |
| (−) 1.0 | Extremely negative effect |
| I | Not known or not identified effect |
References
- Chiang, C.H.; Hwang, C.C. Competitiveness of container ports in a region with cooperation and integration. J. Soc. Transp. Traffic Stud. 2009, 1, 77–91. [Google Scholar]
- Yau, K.L.A.; Peng, S.; Qadir, J.; Low, Y.C.; Ling, M.H. Towards smart port infrastructures: Enhancing port activities using information and communications technology. IEEE Access 2020, 8, 83387–83404. [Google Scholar] [CrossRef]
- Lin, C.Y.; Dai, G.L.; Wang, S.; Fu, X.M. The evolution of green port research: A knowledge mapping analysis. Sustainability 2022, 14, 11857. [Google Scholar] [CrossRef]
- Douaioui, K.; Fri, M.; Mabrouki, C. Smart port: Design and perspectives. In Proceedings of the 2018 4th International Conference on Logistics Operations Management (GOL), Le Havre, France, 10–12 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Xiao, G.; Pan, L.; Lai, F. Application, opportunities, and challenges of digital technologies in the decarbonizing shipping industry: A bibliometric analysis. Front. Mar. Sci. 2025, 12, 1523267. [Google Scholar] [CrossRef]
- Chen, X.; Wu, H.; Han, B.; Liu, W.; Montewka, J.; Liu, R.W. Orientation-aware ship detection via a rotation feature decoupling supported deep learning approach. Eng. Appl. Artif. Intell. 2023, 125, 106686. [Google Scholar] [CrossRef]
- Rodrigues, T.D.A.; Ojiako, U.; Mota, C.M.D.M.; Marshall, A.; Chipulu, M.; Dweiri, F. Assessing risk dimensions in dry port projects: Prioritization, interdependence and heterogeneity. Marit. Bus. Rev. 2024, 9, 311–330. [Google Scholar] [CrossRef]
- Yang, W.; Bao, X.; Zheng, Y.; Zhang, L.; Zhang, Z.; Li, L. A digital twin framework for large comprehensive ports and a case study of Qingdao Port. Int. J. Adv. Manuf. Technol. 2024, 131, 5571–5588. [Google Scholar] [CrossRef]
- Kaplan, R.; Norton, D. Putting the Balanced Scorecard to Work; Harvard Business Review: Brighton, MA, USA, 1993. [Google Scholar]
- Kaplan, R.; Norton, D. The Balanced Scorecard—Measures that Drive Performance; Harvard Business Review: Brighton, MA, USA, 1992. [Google Scholar]
- Kaplan, R.; Norton, D. Using the Balanced Scorecard as a Strategic Management System; Harvard Business Review: Brighton, MA, USA, 1996. [Google Scholar]
- Tongzon, J. Efficiency measurement of selected Australian and other international ports using data envelopment analysis. Transp. Res. Part A Policy A Pract. 2001, 35, 107–122. [Google Scholar] [CrossRef]
- Niu, B.; Dong, J.; Wang, H. Smart port vs port integration to mitigate congestion: ESG performance and data validation. Transp. Res. Part E: Logist. Transp. Rev. 2024, 191, 103741. [Google Scholar] [CrossRef]
- Cullinane, K.; Song, D.W.; Gray, R. A stochastic frontier model of the efficiency of major container terminals in Asia: Assessing the influence of administrative and ownership structures. Transp. Res. Part A Policy Pract. 2002, 36, 743–762. [Google Scholar] [CrossRef]
- Coto-Millan, P.; Baños-Pino, J.; Rodríguez-Alvarez, A. Economic efficiency in Spanish ports: Some empirical evidence. Marit. Manag. 2000, 27, 169–174. [Google Scholar] [CrossRef]
- Tongzon, J. Systematizing international benchmarking for ports. Marit. Manag. 1995, 22, 171–177. [Google Scholar] [CrossRef]
- Khan, M.S.; Quaddus, M. Group decision support using fuzzy cognitive maps for causal reasoning. Group Decis. Negot. 2004, 13, 463–480. [Google Scholar] [CrossRef]
- Özesmi, U.; Özesmi, S.L. Ecological models based on people’s knowledge: A multi-step fuzzy cognitive mapping approach. Ecol. Model. 2004, 176, 43–64. [Google Scholar] [CrossRef]
- AbdelMouty, A.M. Decision making model for strategy choice in higher education under neutrosophic environment. J. Neutrosophic Fuzzy Syst. 2023, 1, 99–106. [Google Scholar] [CrossRef]
- Mahmood, A.; Abbas, M.; Murtaza, G. Multi-Valued Multi-Polar Neutrosophic Sets with an application in Multi-Criteria Decision-Making. Neutrosophic Sets Syst. 2023, 53, 32. [Google Scholar]
- Zaher, M.A.; Eldakhly, N.M. Integrated multi-criteria decision making via trapezoidal neutrosophic sets to evaluate the risks of failure mode. J. Neutrosophic Fuzzy Syst. 2023, 5, 23–29. [Google Scholar] [CrossRef]
- Hanine, M.; Boutkhoum, O.; Tikniouine, A.; Agouti, T. Application of an integrated multi-criteria decision making AHP-TOPSIS methodology for ETL software selection. SpringerPlus 2016, 5, 263. [Google Scholar] [CrossRef]
- Hanin, N.; Zaria, D.; Dhandio, D.J.; Kusnandar, D. Implementation Of AHP-TOPSIS As A Support For Making Decisions On Micro Business Funding In Sambas Regency. Int. J. Econ. Bus. Account. Res. (IJEBAR) 2023, 7, 394–410. [Google Scholar]
- Paraskevas, A.; Madas, M.; Zeimpekis, V.; Fouskas, K. Smart Ports in Industry 4.0: A Systematic Literature Review. Logistics 2024, 8, 28. [Google Scholar] [CrossRef]
- Kardaras, D.; Mentzas, G. Using fuzzy cognitive maps to model and analyze business performance assessment. Adv. Ind. Eng. Appl. Pract. II 1997, 2, 63–68. [Google Scholar]
- Nápoles, G.; Grau, I.; Bello, R.; Grau, R. Two-steps learning of Fuzzy Cognitive Maps for prediction and knowledge discovery on the HIV-1 drug resistance. Expert Syst. Appl. 2014, 41, 821–830. [Google Scholar] [CrossRef]
- Al Farsi, A.; Petrovic, D.; Doctor, F. A non-iterative reasoning algorithm for fuzzy cognitive maps based on type 2 fuzzy sets. Inf. Sci. 2023, 622, 319–336. [Google Scholar] [CrossRef]
- Mehryar, S.; Schwarz, N.; Sliuzas, R.; van Maarseveen, M. Making use of fuzzy cognitive maps in agent-based modeling. In Advances in Social Simulation: Looking in the Mirror; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 307–313. [Google Scholar]
- Kandasamy, W.V.; Smarandache, F. Fuzzy Cognitive Maps and Neutrosophic Cognitive Maps; Infinite Study: Harlesden, UK, 2003. [Google Scholar]
- Jousselme, A.L.; Maupin, P. Neutrosophy in situation analysis. In Proceedings of Fusion; International Society of Information Fusion: Mountain View, CA, USA, 2004; pp. 400–406. [Google Scholar]
- Zafar, A.; Wajid, M.A. Neutrosophic Cognitive Maps for Situation Analysis; Infinite Study: Harlesden, UK, 2019. [Google Scholar]
- Ramalingam, S.; Govindan, K.; Kandasamy, W.V.; Broumi, S. An Approach for Study of Traffic Congestion Problem Using Fuzzy Cognitive Maps and Neutrosophic Cognitive Maps—The Case of Indian Traffic; Infinite Study: Harlesden, UK, 2019. [Google Scholar]
- Obbineni, J.; Kandasamy, I.; Vasantha, W.B.; Smarandache, F. Combining SWOT analysis and neutrosophic cognitive maps for multi-criteria decision making: A case study of organic agriculture in India. Soft Comput. 2023, 27, 18311–18332. [Google Scholar] [CrossRef]
- Shakil, M.T.A.; Ubaid, S.; Sohail, S.S.; Alam, M.A. A Neutrosophic cognitive map based approach to explore the health deterioration factors. Neutrosophic Sets Syst. 2021, 41, 198. [Google Scholar]
- Murugesan, R.; Parthiban, Y.; Devi, R.; Mohan, K.R.; Kumarave, S.K. A Comparative Study of Fuzzy Cognitive Maps and Neutrosophic Cognitive Maps on Covid Variants. Neutrosophic Sets Syst. 2023, 55, 20. [Google Scholar]
- Paraskevas, A.; Madas, M. Neutrosophic Cognitive Maps: Theoretical and Mathematical Formulations, Literature Review and Applications. In Soft Computing & Machine Learning: A Fuzzy and Neutrosophic View of Reality; Taylor and Francis Group: Boca Raton, FL, USA, in press.
- Chen, J.; Xue, K.; Ye, J.; Huang, T.; Tian, Y.; Hua, C.; Zhu, Y. Simplified neutrosophic exponential similarity measures for evaluation of smart port development. Symmetry 2019, 11, 485. [Google Scholar] [CrossRef]
- Vera, P.J.M.; Delgado, C.F.M.; Vera, S.P.C.; Alava, M.V.; Gónzales, M.P. Static analysis in neutrosophic cognitive maps. Neutrosophic Sets Syst. 2016, 14, 61–64. [Google Scholar]
- Aldous, J.M.; Wilson, R.J. Graphs and Applications: An Introductory Approach; Springer Science & Business Media: New York, NY, USA, 2003. [Google Scholar]
- Kosko, B. Fuzzy Cognitive Maps. Int. J. Man-Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Smarandache, F. Redesigning Decision Matrix Method with an indeterminacy-based inference process. Int. J. Appl. Math. Stat. 2008, 13, 4–11. [Google Scholar]
- Stach, W. Learning and Aggregation of Fuzzy Cognitive Maps. An Evolutionary Approach. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2011. [Google Scholar]
- Smarandache, F. Refined literal indeterminacy and the multiplication law of sub-indeterminacies. Neutrosophic Sets Syst. 2015, 9, 58–63. [Google Scholar]
- De la Rosa, C.B.; Bolaños, B.C.; Echeverría, H.C.; Padilla, R.C.; Ruilova, G.S. PESTEL Analysis with Neutrosophic Cognitive Maps to Determine the Factors That Affect Rural Sustainability. Case Study of the South-Eastern Plain of the Province of Pinar del Río; Infinite Study: Harlesden, UK, 2019. [Google Scholar]
- Kosko, B. Hidden patterns in combined and adaptive knowledge networks. Int. J. Approx. Reason. 1988, 2, 377–393. [Google Scholar] [CrossRef]
- Kosko, B. Bidirectional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18, 49–60. [Google Scholar] [CrossRef]
- Smarandache, F.; Neutrosophic systems and neutrosophic dynamic systems. In Collected Papers. Volume VIII: On Neutrosophic Theory and Applications; 2022; p. 50. Available online: https://books.google.co.jp/books?hl=en&lr=&id=vWOjEAAAQBAJ&oi=fnd&pg=PA50&dq=Neutrosophic+systems+and+neutrosophic+dynamic+systems.+&ots=nJYXMrcOc7&sig=7Xnj2RqjjxRwXcvcs94ttukFtD0#v=onepage&q=Neutrosophic%20systems%20and%20neutrosophic%20dynamic%20systems.&f=false (accessed on 8 February 2025).
- Haezendonck, E.; Dooms, M.; Verbeke, A. A new governance perspective on port–hinterland relationships: The Port Hinterland Impact (PHI) Matrix. Marit. Econ. Logist. 2014, 16, 229–249. [Google Scholar] [CrossRef]
- Burns, M. Port Management and Operations; CRC Press: Boca Raton, FL, USA, 2015; pp. 265–266. [Google Scholar]
- 6 Key Primary Indicators (KPIs) That Port Terminals Should Closely Track. Available online: https://medium.com/@octopi_tos/6-key-primary-indicators-kpis-that-port-terminals-should-closely-track-433cb25e1ac6 (accessed on 20 November 2023).
- Belmoukari, B.; Audy, J.F.; Forget, P. Smart port: A systematic literature review. Eur. Transp. Res. Rev. 2023, 15, 4. [Google Scholar] [CrossRef]
- Pham, T.Y. A smart port development: Systematic literature and bibliometric analysis. Asian J. Shipp. Logist. 2023, 39, 57–62. [Google Scholar] [CrossRef]
- Hsu, C.T.; Chou, M.T.; Ding, J.F. Key factors for the success of smart ports during the post-pandemic era. Ocean. Coast. Manag. 2023, 233, 106455. [Google Scholar] [CrossRef]
- Makkawan, K.; Muangpan, T. Developing Smart Port with Crucial Domains and Indicators in the Thai Port Case: A Confirmatory Factor Analysis. Trans. Marit. Sci. 2023, 12, 7. [Google Scholar] [CrossRef]
- Makkawan, K.; Muangpan, T. A conceptual model of smart port performance and smart port indicators in Thailand. J. Int. Logist. Trade 2021, 19, 133–146. [Google Scholar] [CrossRef]
- Liu, C.; Zhan, S.; Heng, L. Evaluation of smart port development level based on entropy weight TOPSIS method. In International Conference on Frontiers of Traffic and Transportation Engineering; SPIE: Bellingham, WA, USA, 2022; Volume 12340, pp. 368–375. [Google Scholar]
- Molavi, A.; Lim, G.J.; Race, B. A framework for building a smart port and smart port index. Int. J. Sustain. Transp. 2020, 14, 686–700. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, T.; Han, H. Approach towards sustainable and smart coal port development: The case of Huanghua port in China. Sustainability 2020, 12, 3924. [Google Scholar] [CrossRef]
- González, A.R.; González-Cancelas, N.; Serrano, B.M.; Orive, A.C. Smart ports: Ranking of Spanish port system. World Sci. News 2020, 144, 1–12. [Google Scholar]
- Lakhmas, K.; Sedqui, P.A. Toward a smart port congestion optimizing model. In Proceedings of the 2020 IEEE 13th International Colloquium of Logistics and Supply Chain Management (LOGISTIQUA), Fez, Morocco, 2–4 December 2020; pp. 1–5. [Google Scholar]
- Rodrigo González, A.; González-Cancelas, N.; Molina Serrano, B.; Orive, A.C. Preparation of a smart port indicator and calculation of a ranking for the Spanish port system. Logistics 2019, 4, 9. [Google Scholar] [CrossRef]
- Angeloudis, P.; Bell, M.G. An uncertainty-aware AGV assignment algorithm for automated container terminals. Transp. Res. E Logist. Transp. Rev. 2010, 46, 354–366. [Google Scholar] [CrossRef]
- Luo, S.; Ren, B. The Monitoring and Managing Application of Cloud Computing Based on Internet of Things; Elsevier North-Holland, Inc.: New York, NY, USA, 2016. [Google Scholar]
- Gu, S.; Hua, J.; Lv, T. Evaluation of customer satisfaction of “Door-to-Door” whole-process logistic service with interval-valued intuitionistic fuzzy information. J. Intell. Fuzzy Syst. 2016, 30, 2487–2495. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, D.; Zheng, J.; Fang, X.; Luo, H. Formation mechanism of quick emergency response capability for urban rail transit: Inter-organizational collaboration perspective. Adv. Mech. Eng. 2016, 8, 1687814016647881. [Google Scholar] [CrossRef]
- Cho, H.; Choi, H.; Lee, W.; Jung, Y.; Baek, Y. LITeTag: Design and implementation of an RFID system for IT-based port logistics. J. Commun. 2006, 1, 48–57. [Google Scholar] [CrossRef]
- Wang, L. Study on Port Logistics Marketing under the Environment of Supply Chain. Int. J. Bus. Manag. 2011, 6, 267. [Google Scholar] [CrossRef]
- Rudjanakanoknad, J.; Suksirivoraboot, W.; Sukdanont, S. Evaluation of International Ports in Thailand through Trade Facilitation Indices from Freight Forwarders. Procedia—Soc. Behav. Sci. 2014, 111, 1073–1082. [Google Scholar] [CrossRef]
- Lai, G.; Debo, L.G.; Sycara, K. Sharing inventory risk in supply chain: The implication of financial constraint. Omega 2009, 37, 811–825. [Google Scholar] [CrossRef]
- Peris-Mora, E.; Diez Orejas, J.M.; Subirats, A.; Ibáñez, S.; Alvarez, P. Development of a system of indicators for sustainable port management. Mar. Pollut. Bull. 2005, 50, 1649–1660. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Zhang, Y.; Ma, W.; Fu, Q.; Yang, X.; Li, C.; Zhou, B.; Yu, Q.; Chen, L. Characteristics and ship traffic source identification of air pollutants in China’s largest port. Atmos. Environ. 2013, 64, 277–286. [Google Scholar] [CrossRef]
- Chen, J.; Wan, Z.; Zhang, F.; Park, N.-K.; Zheng, A.; Zhao, J. Evaluation and comparison of the development performances of typical free trade port zones in China. Transp. Res. Part A Policy Pract. 2018, 118, 506–526. [Google Scholar] [CrossRef]
- Chen, J.; Huang, T.; Xie, X.; Lee, P.T.-W.; Hua, C. Constructing Governance Framework of a Green and Smart Port. J. Mar. Sci. Eng. 2019, 7, 83. [Google Scholar] [CrossRef]
- Squicciarini, M.; Dernis, H.; Criscuolo, C. Measuring Patent Quality: Indicators of Technological and Economic Value. In OECD Science, Technology and Industry Working Papers; No. 2013/03; OECD Publishing: Paris, France, 2013. [Google Scholar] [CrossRef]
- Bougon, M.; Weick, K.; Binkhorst, D. Cognition in organizations: An analysis of the Utrecht jazz orchestra. Adm. Sci. Q. 1977, 22, 606–639. [Google Scholar] [CrossRef]
- Eden, C.; Ackermann, F.; Cropper, S. The analysis of cause maps. J. Manag. Stud. 1992, 29, 309–324. [Google Scholar] [CrossRef]
- Stach, W.; Kurgan, L.A.; Pedrycz, W. Expert-based and Computational Methods for Developing Fuzzy Cognitive Maps, In Fuzzy Cognitive Maps: Advances in Theory, Methodologies and Applications; Glykas, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN -10: 36-42032-19-2. [Google Scholar]
- Onut, S.; Tuzkaya, U.R.; Torun, E. Selecting container port via a fuzzy ANP-based approach: A case study in the Marmara Region, Turkey. Transp. Policy 2011, 18, 182–193. [Google Scholar] [CrossRef]
- Wang, Y.J.; Han, T.C. Efficiency measurement for international container ports of Taiwan and surrounding areas by fuzzy data envelopment analysis. J. Mar. Sci. Technol. 2018, 26, 6. [Google Scholar]
- Eden, C. Strategic thinking with computers. Long Range Plan. 1990, 23, 35–43. [Google Scholar] [CrossRef]
- Eden, C.; Ackermann, F. Making Strategy: The Journey of Strategic Management; Sage: Newcastle, UK, 1998. [Google Scholar]
- Das, S.; Roy, B.K.; Kar, M.B.; Kar, S.; Pamučar, D. Neutrosophic fuzzy set and its application in decision making. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 5017–5029. [Google Scholar] [CrossRef]
- Betancourt-Vázquez, A.; Leyva-Vázquez, M.; Perez-Teruel, K. Neutrosophic cognitive maps for modeling project portfolio interdependencies. Crit. Rev. 2015, 10, 40–44. [Google Scholar]
- Bieker, T.; Waxenberger, B. Sustainability Balanced Scorecard and Business Ethicas. Developing a Balanced Scorecard for Integrity Management. In Proceedings of the 10th Conference of the Greening of Industry Network, Göteborg, Sweden, 23–26 June 2002. [Google Scholar]
- Figge, F.; Hahn, T.; Schaltegger, S.; Wagner, M. Value-Based Sustainability Management with the Balanced Scorecard; Center for Sustainability Management (CSM): Lüneburg, Germany, 2001. [Google Scholar]
- Figge, F.; Hahn, T.; Schaltegger, S.; Wagner, M. The Sustainability Balanced Scorecard—Linking Sustainability management to Business Strategy. Bus. Strategy Environ. 2002, 11, 269–284. [Google Scholar] [CrossRef]
- Paraskevas, A.; Madas, M. An integrated framework of Sustainability Balanced Scorecard with neutrosophic AHP for smart port performance evaluation. In Proceedings of the 9th International Symposium and 31st National Conference on Operational Research (HELORS 2023), Athens, Greece, 29 June–July 2023. [Google Scholar]
- Papageorgiou, E.I.; Salmeron, J.L. A review of fuzzy cognitive maps research during the last decade. IEEE Trans. Fuzzy Syst. 2012, 21, 66–79. [Google Scholar] [CrossRef]
- Salmeron, J.L. Modelling grey uncertainty with fuzzy grey cognitive maps. Expert Syst. Appl. 2010, 37, 7581–7588. [Google Scholar] [CrossRef]
- Park, K.S.; Kim, S.H. Fuzzy cognitive maps considering time relationships. Int. J. Human-Comput. Stud. 1995, 42, 157–168. [Google Scholar] [CrossRef]
- Zhong, M.; Miao, C.; Shen, Z.; Feng, Y. Temporal fuzzy cognitive maps. In Proceedings of the 2008 IEEE International Conference on Fuzzy Systems (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1831–1840. [Google Scholar]
- Bourgani, E.; Stylios, C.D.; Manis, G.; Georgopoulos, V.C. Integrated approach for developing timed fuzzy cognitive maps. In Proceedings of the 7th IEEE International Conference Intelligent Systems IS’2014; Warsaw, Poland, 24–26 September 2014, Volume 1: Mathematical Foundations, Theory, Analyses; Angelov, K., Atanassov, L., Doukovska, M., Hadjiski, V., Jotsov, J., Kacprzyk, N., Kasabov, S., Sotirov, E., Zadrożny, S., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 193–204. [Google Scholar]
- Hagiwara, M. Extended fuzzy cognitive maps. In 1992 Proceedings IEEE International Conference on Fuzzy Systems; IEEE: Piscataway, NJ, USA, 1992; pp. 795–801. [Google Scholar]
- Nair, A.; Reckien, D.; van Maarseveen, M.F. Generalised fuzzy cognitive maps: Considering the time dynamics between a cause and an effect. Appl. Soft Comput. 2020, 92, 106309. [Google Scholar] [CrossRef]
- Poornima, S.; Pushpalatha, M. A survey on various applications of prescriptive analytics. Int. J. Intell. Netw. 2020, 1, 76–84. [Google Scholar] [CrossRef]
- Lepenioti, K.; Bousdekis, A.; Apostolou, D.; Mentzas, G. Prescriptive analytics: Literature review and research challenges. Int. J. Inf. Manag. 2020, 50, 57–70. [Google Scholar] [CrossRef]
- Forrester, J.W. Principles of Systems; Wright Allen Press: Cambridge, MA, USA, 1968. [Google Scholar]

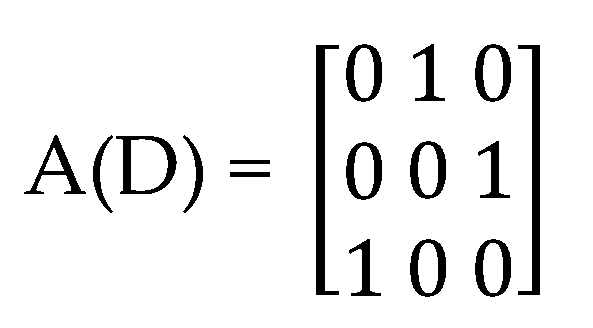









| Perspective | Evaluation Indicator | Reference |
|---|---|---|
| Operational efficiency (OE) | Vessel turnaround time: the time taken for a ship to dock, unload/load cargo, and depart the port | [51,52,53,54,55] |
| Dwell time: the duration cargo spends at the port, including storage and processing times | [54,55] | |
| Berth utilization: the effectiveness of berth allocation and utilization, measured as a percentage of total available time | [56,57,58] | |
| Financial (F) | Revenue and profitability: financial metrics such as revenue, profit, and return on investment, e.g., Total revenue = revenue from port operations + revenue from ancillary services Net profit = total revenue − total expenses ROI = (net profit/total investment) * 100% Profit margin = (net profit/total revenue) * 100% Revenue growth rate = ((current year revenue − previous year revenue)/previous year revenue) * 100% Operating expense ratio = (total operating expenses/total revenue) * 100% | [54,55,56] |
| Cost efficiency: cost per unit of cargo handled or cost per vessel serviced | [55,56,57,58] | |
| Technological advancement (TA) | Digitalization rate: the extent to which digital technologies are integrated into port operations, e.g., Digitalization rate = (number of digitalized processes or operations/total number of processes or operations) * 100% | [59,60] |
| Automation effectiveness: impact and performance of automated systems on efficiency and accuracy, e.g., Automation effectiveness = ((improved efficiency + improved accuracy)/2) * 100% | [61,74] | |
| Technology investment ROI: return on investment for technology upgrades and innovations | [74] | |
| Environmental sustainability (ES) | Carbon emissions: measurement of greenhouse gas emissions from port activities, e.g., Emissions intensity = (total carbon emissions/total cargo handled) * 1000 | [62,63,64,65] |
| Energy efficiency: the efficient use of energy within port operations, e.g., Energy efficiency ratio = total energy consumption/total cargo handled | [66] | |
| Waste management: metrics related to waste reduction, recycling, and proper disposal, e.g., Waste reduction rate = ((initial waste generation rate − final waste generation rate)/initial waste generation rate) * 100% Waste management cost per unit = Total waste management costs/total cargo handled | [66,67] | |
| Customer-centric (CC) | Customer feedback: surveys or feedback mechanisms from port users, reflecting their satisfaction levels | [68] |
| Service quality metrics: timeliness, accuracy, and reliability of port services, e.g., On-time performance (OTP) = (number of services completed on time/total number of services) * 100%, Service reliability index (SRI) = (number of successful service instances/total number of service instances) * 100% | [69,70] | |
| Safety and security (SS) | Safety incident rate: the number of accidents or safety incidents within the port, e.g., Safety incident rate = (number of safety incidents/total hours worked or total operations) * 1,000,000 | [71,72] |
| Security compliance: adherence to security protocols and regulations, e.g., regulatory compliance rate = (number of security regulations adhered to/total number of applicable security regulations) * 100% | [73] |
| Intensity of Importance | Definition |
|---|---|
| (+)1.0 | Extreme effect |
| 0.0 | No effect |
| (−)1.0 | Extremely negative effect |
| I | Not known or not identified effect |
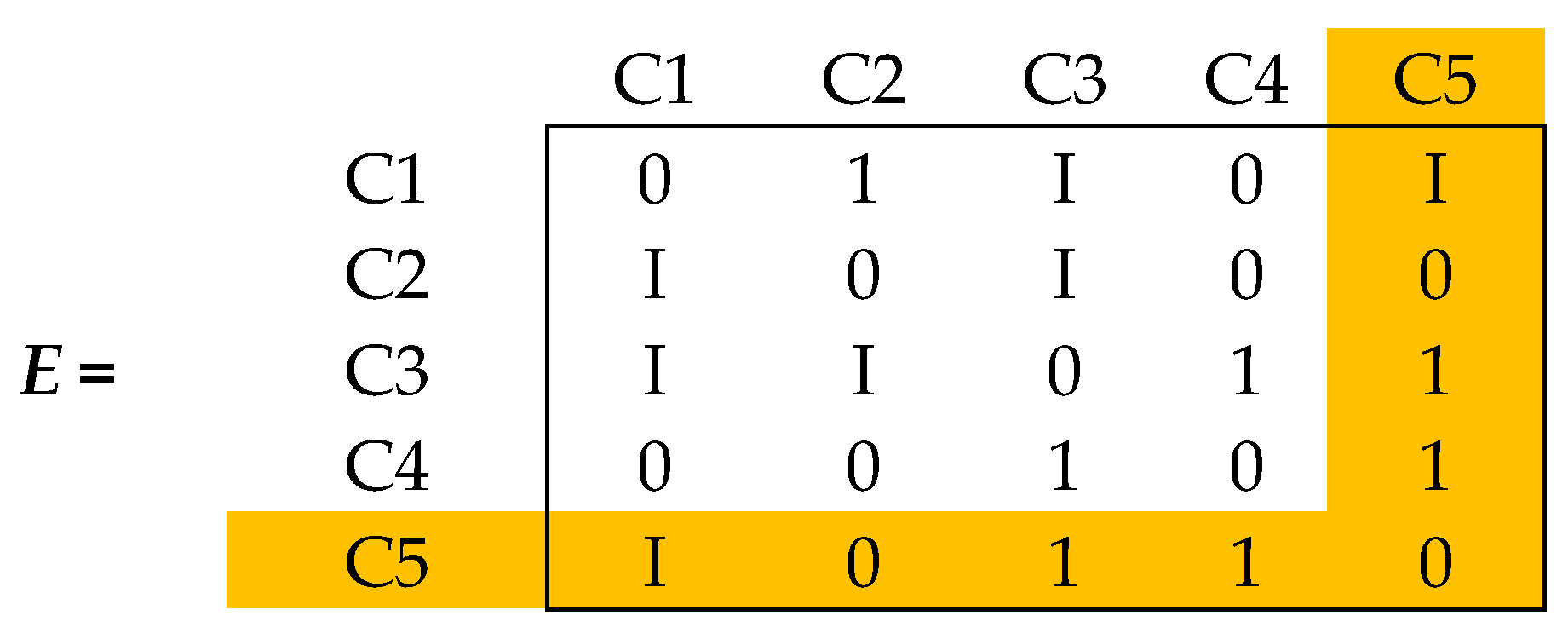
| DIMENSIONS | OE | TA | ES | CC | SS | F |
|---|---|---|---|---|---|---|
| OE | 0 | 0 | 1+I | 2 | I | 2 |
| TA | 2 | 0 | 2 | 2 | 2 | 1 |
| ES | 0 | 1 | 0 | I | 0 | −2 |
| CC | −1 | 2 | 0 | 0 | 1 | 0 |
| SS | −2 | 2 | 0 | −1 | 0 | 2I |
| F | 1 | 2 | 0 | −1 | 2I | 0 |
| Node | Id | Od |
|---|---|---|
| OE | 0 | 5+2I |
| TA | 7 | 9 |
| ES | 3+I | I−1 |
| CC | 2+I | 2 |
| SS | 3+3I | 2I−1 |
| F | 2I+1 | 2+2I |
| Node | Transmitter | Receiver | Ordinary |
|---|---|---|---|
| OE | x | ||
| TA | x | ||
| ES | x | ||
| CC | x | ||
| SS | x | ||
| F | x |
| Node | Total Centrality |
|---|---|
| OE | 5+2I |
| TA | 16 |
| ES | 2+2I |
| CC | 4+I |
| SS | 2+5I |
| F | 3+4I |
| Node | Total Centrality |
|---|---|
| OE | [5, 7] |
| TA | 16 |
| ES | [2, 4] |
| CC | [4, 5] |
| SS | [2, 7] |
| F | [3, 7] |
| Node | Total Centrality |
|---|---|
| OE | 6 |
| TA | 16 |
| ES | 3 |
| CC | 4.5 |
| SS | 4.5 |
| F | 5 |
| Node | Id | Od | Td |
|---|---|---|---|
| OE | 1.2 | 5.4+2I | 6.6+2I |
| TA | 7.4 | 13.2 | 20.6 |
| ES | 4.4+I | I−1.2 | 3.2+2I |
| CC | 3.4+I | 2.4 | 5.8+I |
| SS | 4.4+3I | 3I−0.8 | 3.6+6I |
| F | 3.2I+1.2 | 3.2+3.2I | 4.4+6.4I |
| Node | Total Centrality |
|---|---|
| OE | [6.6, 8.6] |
| TA | 20.6 |
| ES | [3.2, 5.2] |
| CC | [5.8, 6.8] |
| SS | [3.6, 9.6] |
| F | [4.4, 10.8] |
| Node | Total Centrality |
|---|---|
| OE | 7.6 |
| TA | 20.6 |
| ES | 4.2 |
| CC | 6.3 |
| SS | 6.6 |
| F | 7.6 |
| Node | Total Centrality |
|---|---|
| OE | 6.1 |
| TA | 11.4 |
| ES | 2.8 |
| CC | 3.7 |
| SS | 4.4 |
| F | 4.1 |
| Method | Proposed Method-NCM | Fuzzy ANP | Fuzzy DEA | |
|---|---|---|---|---|
| Criteria | ||||
| Ranking of alternatives | Yes | Yes | Yes | |
| Handling of indeterminacy | Yes | No | No | |
| Influence of one factor over other factors | Yes | No | No | |
| Dynamic behavior | Yes | No | No | |
| Stakeholder integration | Yes | Limited | Limited | |
| Flexibility of application | Yes | Limited | Limited | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paraskevas, A.; Madas, M.; Nikolaidis, Y. Using Neutrosophic Cognitive Maps to Support Group Decisions About Modeling and Analyzing Smart Port Performance. Appl. Sci. 2025, 15, 1981. https://doi.org/10.3390/app15041981
Paraskevas A, Madas M, Nikolaidis Y. Using Neutrosophic Cognitive Maps to Support Group Decisions About Modeling and Analyzing Smart Port Performance. Applied Sciences. 2025; 15(4):1981. https://doi.org/10.3390/app15041981
Chicago/Turabian StyleParaskevas, Antonios, Michael Madas, and Yiannis Nikolaidis. 2025. "Using Neutrosophic Cognitive Maps to Support Group Decisions About Modeling and Analyzing Smart Port Performance" Applied Sciences 15, no. 4: 1981. https://doi.org/10.3390/app15041981
APA StyleParaskevas, A., Madas, M., & Nikolaidis, Y. (2025). Using Neutrosophic Cognitive Maps to Support Group Decisions About Modeling and Analyzing Smart Port Performance. Applied Sciences, 15(4), 1981. https://doi.org/10.3390/app15041981








