Abstract
With the explosive growth of information on the internet, personalized recommendation technology has become an important tool for helping users efficiently acquire information. However, existing spreading-based recommendation algorithms only consider user choices and fail to fully leverage the potential relationships between users and items. Additionally, the incomplete utilization of user and item information limits their application potential and applicable scenarios, resulting in suboptimal recommendation performance in practical applications. To address this issue, we propose a Light Graph Convolutional Recommendation Algorithm Based on Hybrid Spreading (LGCNHS). This algorithm first optimizes the embeddings of users and items using their respective feature matrix, then learns the latent embedding representations of users and items through a lightweight graph convolutional network. Finally, the latent embedding representations are incorporated as key parameters into the hybrid spreading recommendation algorithm to generate recommendations. Comparative experiments on two publicly available datasets, MovieLens and Douban, demonstrate that LGCNHS achieves improved accuracy and diversity in recommendations compared to related methods. The algorithm code is available on github.
1. Introduction
With the rapid development of Internet technology, the explosive expansion of information makes users have to face massive data every day. How to effectively filter information from massive data, so that users can efficiently retrieve the information they are interested in, has become an important research topic. Personalized recommendation technology has attracted much attention for its ability to help users recommend the information they are interested in or potentially need, and it can provide accurate recommendation services according to users’ personalized needs and interests, thus greatly improving the efficiency of users’ access to information [1,2].
In recent years, scholars from the fields of computer science, physics, mathematics, etc. have conducted a lot of research on the design of personalized recommendation algorithms, and many classical personalized recommendation algorithms, such as collaborative filtering recommendation algorithms, content-based recommendation algorithms, deep learning recommendation algorithms, etc., are now widely used in various fields. However, each method has its own defects: collaborative filtering recommendation algorithms are based on similarity, so there is a prevalence bias problem; content-based recommendation algorithms rely on item features, and there are limitations in the cold-start problem; deep learning recommendation algorithms are powerful but require a large amount of labeled data, suffer from poor interpretability, and are prone to overfitting [3]. Facing the long-standing challenges of recommendation systems, some scholars have adopted a physics-based approach, modeling user–item interaction data as a bipartite network and leveraging tools like random walk, heat spreading, and heat conduction to design effective recommendation algorithms [4,5,6]. The integration of prior knowledge embedded in physical models with recommendation systems has now emerged as a new paradigm for exploring user recommendations. Among these, spreading-based recommendation algorithms are the most representative. These algorithms generate recommendations by assigning initial resources to items and spreading the resources through physical processes such as random walk and heat spreading [6].
Current research for spreading-based recommendation algorithms focuses on the way resources are updated and allocated during the spreading process [7,8,9,10]. However, the core of this class of algorithms is to utilize the user–item interaction data to set the initial resource value of the item based on whether users have interacted with them. These values are then updated through the spreading process to generate recommendations. This approach ignores auxiliary information, such as user features and item features. Consequently, regardless of how the resource allocation method is modified, this spreading process still interprets user choices as an indication of interest in items and updates resources accordingly, ultimately generating recommendations based on the user’s historical behaviors.
Although this approach reflects the user’s behavior to some extent, it fails to address the limitations of such algorithms, which do not fully exploit the potential relationships between users and items or leverage auxiliary information, such as user features and item features. This restricts their application potential and applicable scenarios, leading to suboptimal recommendation performance in real-world scenarios. Specifically, existing methods suffer from the following key limitations: (1) over-reliance on user behavior while neglecting personalized user features; (2) ineffective integration of latent item information, making it difficult to capture deep semantic associations between items; and (3) insufficient exploration of user–item interaction data, failing to fully account for the complex potential relationships between users and items.
To address these issues, we propose Light Graph Convolutional Recommendation Algorithm Based on Hybrid Spreading (LGCNHS). The algorithm has an optimized embeddings layer based on LightGCN, effectively learning latent embedding representations of users and items through user features and item features. These embeddings are transformed into an allocation weight matrix, which is further incorporated into the second round of the hybrid spreading process. This enables LGCNHS to not only utilize user–item interaction data but also comprehensively consider the semantics of user features and item features. By flexibly adjusting the allocation weight matrix based on users’ historical behaviors and interest preferences, LGCNHS generates more accurate and personalized recommendations for each user. This innovation effectively addresses the shortcomings of traditional spreading-based recommendation algorithms in handling personalized user features and latent item information, thereby improving recommendation accuracy and diversity. More importantly, by introducing the allocation weight matrix into the second round of the hybrid spreading process, LGCNHS captures more complex potential relationships between users and items, fully considering user–item interaction data.
The algorithm proposed in this paper is compared with four other related algorithms in a comparative study, and the effectiveness of the algorithm is verified by quantitative analysis using two real datasets, which illustrates that the combination of spreading-based recommendation algorithms and deep learning has certain potential and provides new ideas and directions for future research.
2. Related Work
2.1. Spreading-Based Recommendation Algorithm
Widely known spreading-based recommendation algorithms include probabilistic spreading algorithms (ProbS) [4], heat spreading algorithms (HeatS) [5], hybrid spreading algorithms (HybridS) [6], etc. These algorithms model user–item interaction data as a bipartite network and, by assigning initial resource value to items and simulating the spreading process, generate recommendations through two rounds of the spreading process: from items to users and from users to items. This approach effectively leverages user–item interaction data. Many scholars have extended these algorithms in various directions. For instance, Qiang Guo et al. considered that users have different preferences for different items, introduced item popularity in the second round of the probabilistic spreading process of the probabilistic spreading algorithm to allocate resources, significantly improving recommendation accuracy and diversity compared to the original probabilistic spreading algorithm [7]. Dacheng Nie et al. proposed a novel hybrid spreading algorithm that assigns equal weight to probabilistic spreading and heat spreading algorithms, achieving higher accuracy and diversity than traditional hybrid spreading-based recommendation algorithms [8]. Guilin Chen et al. proposed a bidirectional spreading algorithm based on probabilistic spreading, which penalizes the weights of popular items during the bidirectional spreading process, effectively improving both accuracy and diversity [9]. Leyang Xue explored the theoretical upper bound of accuracy for spreading-based recommendation algorithms using quantitative methods, highlighting that further improvements in accuracy are still needed [10]. Jinyu Zhou utilized user labels and item labels weight factors to weight the initial user–item interaction matrix, performed bipartite graph spreading on the optimized matrix to derive user similarity based on label weighting, and employed a combination of similarity based on ratings and label-weighted similarity for collaborative filtering recommendations. This method significantly improved accuracy and better reflects user preferences compared to traditional collaborative filtering recommendation algorithms [11].
Although these works have enhanced the accuracy and diversity of recommendations, several issues remain: (1) the focus on modifying resource update configuration during the spreading process overlooks the fact that user interests and preferences influence resource spreading from users to items. This oversight leads to underutilization of potential relationship between the user and the item; and (2) these algorithms rely solely on user–item interaction data and neglect auxiliary information such as user features and item features. This limits their application potential and applicable scenarios.
2.2. Recommendation Algorithm Based on a Graph Convolutional Network
Graph Convolutional Networks (GCNs), a powerful graph-structured data processing method, have been widely adopted in recommendation systems. By incorporating neighborhood information, GCNs enable the propagation and updating of node features through the graph structure, effectively capturing relationships between nodes [12]. In recommendation systems, GCN can model user–item interaction data and capture user interests, thereby improving the accuracy and diversity of recommendations. For instance, NGCF leverages GCNs to learn the latent embedding representations between nodes through graph convolutional networks, extracting higher-order information from user–item interaction data. This demonstrates that graph convolutional embedding propagation improves the quality of embedding for both users and items [13]. To address the limitations of GCN in terms of complexity and computational efficiency, LightGCN simplifies the hierarchical structure of GCNs by removing redundant nonlinear transformations and feature projections, focusing directly using neighborhood information for node embedding updates. This significantly reduces computational complexity [14]. Qihang Liu et al. optimized the loss function of LightGCN based on contrastive learning and proposed a novel filtering loss function that automatically filters out low-information negative samples [15]. Chungan Huang et al. utilized a multi-layer feature fusion strategy in LightGCN to capture the complete feature embedding of nodes, improving recommendation performance [16]. Hui Wang et al. used the adjacency matrix to optimize the embedding of users and items, and introduced layer attenuation coefficients during convolutional layer aggregation to distinguish the importance of different layers. This allows the model to fully utilize historical user–item interaction data for better learning of user preferences [17]. Guang Wang et al. utilized a mapping matrix at the embedding layer to transform initial feature vectors into adaptive embeddings and introduced an attention mechanism to aggregate different aspects of user embeddings, thereby learning latent embedding representations of users and items to enhance recommendation effectiveness [18]. Dong Liao et al. combined user social behavior data, user–item interaction data, and item relationships to explicitly construct a connection between items, enabling better learning of user preferences [19]. Huang Song proposed a cross-design network user identification model based on bidirectional GCN, which utilizes the Jaccard similarity coefficient to calculate user intimacy and constructs an adjacency matrix to represent user relationships in social networks, subsequently extracting user information across social networks [20]. Qiang Guo et al. constructed a feature matrix reflecting user preferences based on ratings, and utilized a breadth-first search to transform the bipartite network into a compact low-dimensional vector. This approach integrates rating behavior into the graph convolutional network while preserving the topological structure and interconnectivity [21].
These works have improved the accuracy of recommendations and demonstrated the effectiveness of using the GCN framework to mine latent embedding representations of users and items in recommendation systems.
3. Model Design
3.1. General Framework
In a spreading-based recommendation algorithm, it is typically assumed that equal resources exist for all the user’s interaction items, and the resources obtained by the user are considered as a weighted linear aggregation of the average resources of the items they have selected. After the spreading process, the more resources an item receives, the higher its likelihood of being selected. However, this assumption is idealized. In reality, this characterization treats the user choice as interest in items, whereas the spreading process should be interpreted as the flow of the user interest, reflecting users’ differentiated preferences for different items.
Our proposed LGCNHS is divided into two parts. The first part is the embedding-optimized LightGCN, which introduces user features and item features to optimize the embedding layer based on LightGCN. Subsequently, through the propagation layer and prediction layer, it deeply explores personalized user features and semantic features of items, learning the latent embedding representations of users and items. It then transforms them into an allocation weight matrix, which is used to adjust the resource allocation process in subsequent steps. This approach addresses the issues of over-reliance on user behavior and insufficient integration of latent item information. The second part integrates an allocation weight matrix into the hybrid spreading. During the second round of the hybrid spreading process, the allocation weight matrix is introduced to adjust resource allocation based on the weights. This ensures that the higher the user’s interest level in items, the more resources are allocated. This method compensates for the limitations of traditional hybrid spreading recommendation algorithms in exploring user–item interaction data and fully considers the complex latent relationships between users and items. Finally, recommendations are generated for target users based on the resource values of each item. The general framework structure of the model is illustrated in Figure 1.
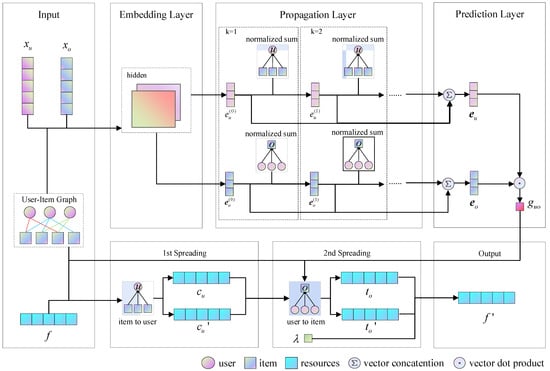
Figure 1.
Diagram of the frame structure. denotes the user features vector, denotes the item features vector, and denote the embedding vector of user and item output from the th propagation layer, denotes the allocation weight, and denote the user resource vector obtained after the first round of probabilistic spreading and heat spreading, and denote the item resource vector obtained after the second round of probabilistic spreading and heat spreading, denotes the initial resource vector of target user, denotes the resource vector of target user after hybrid spreading, denotes the hyperparameter.
Furthermore, to better understand the general framework of the LGCNHS, we have drawn a flowchart of the LGCNHS. The overall process of the model is illustrated in Figure 2. The overall process is as follows:
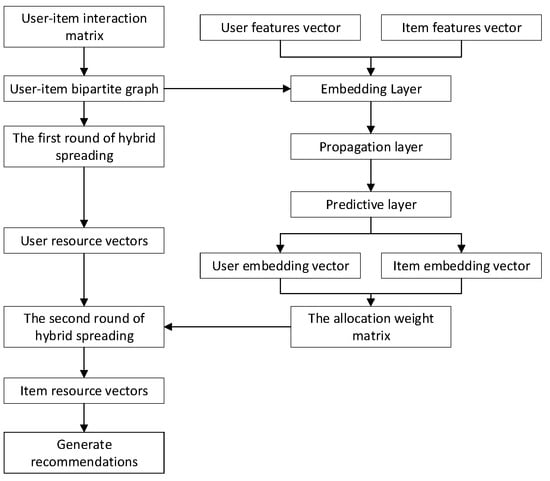
Figure 2.
Diagram of the overall process of the LGCNHS.
- First, user features and item features are input into the optimized embedding layer. The user embedding vector and item embedding vector are learned through the propagation layer and predictive layer, resulting in the allocation weight matrix.
- Additionally, the user–item bipartite graph is constructed using the user–item interaction data, and the first round of the hybrid spreading process is performed to obtain the user resource vector.
- Finally, the allocation weight matrix is combined with the user resource vector for the second round of the hybrid spreading process to generate recommendations.
In the following sections, each model component will be described in detail.
3.2. Embedding-Optimized LightGCN
3.2.1. Embedding Layer
Assuming that there are users in the user set and items in the item set , the user features vector and the item features vector obtained from feature extraction are mapped through the linear layer and converted into the initial embedding vector of the user and the item , respectively, . The computational formula is:
where and are the dimensions of the user features vector and item features vector, is the initial embedding vector dimension, and and are the learnable weight matrix.
3.2.2. Propagation Layer
The embedding vector of users and items generated by the embedding layer are computed by LightGCN. Denote superscript as the index of the th propagation layer, and denotes the embedding vector of user and item output from the th propagation layer. The latent embedding representations of the user–item direction and the item–user direction of each layer are calculated during the updating of the user embedding and the item embedding:
where and denote the neighborhood of user and item .
3.2.3. Predictive Layer
After propagation through layers, the embedding vector set of user and the embedding set of item are obtained. The embedding vector and obtained at each propagation layer are linearly weighted and combined together to obtain the final latent embedding representations of the user and the item:
where is the weighted contribution of the th layer embedding to the final embedding.
After obtaining the final embedding matrix for all users and the final embedding matrix for all items, multiply the two embedding matrices and use them as the allocation weight matrix for the spreading of users to items:
3.2.4. Loss Function
The loss function for model training adopts the widely used Bayesian Personalized Ranking (BPR) loss as the ranking loss [13]. The set of items interacted with by each user is obtained from their historical behaviors, which is treated as the positive sample set. Subsequently, a set of negative samples, consisting of items the user has not interacted with, is generated. The loss is calculated based on the user, positive samples, and negative samples, and the parameters are updated through backpropagation combined with the optimizer. The specific formula is as follows:
where denotes the score of user and positive sample , denotes the score of user and negative sample , and is the hyperparameter controlling the strength of L2 regularization.
3.3. Incorporating the Hybrid Spreading of the Embedding Matrix
The recommendation system is represented as a bipartite network , where , , and denote the users, the items, and the interactions between pairs of users and items, respectively, it can be described using the adjacency matrix , if there is an interaction relationship between user and item , then , otherwise .
Assuming that a user interacts with an item because the user is interested in the item, the basic task of a recommendation system becomes generating an interest list of items that the target user has not interacted with. All spreading-based recommendation algorithms assign a certain amount of initial resource to the items for the target user , and then reallocate the resources by spreading . Where is referred to as the resource transfer matrix, and the transfer matrix elements for ProbS and HeatS are denoted as:
where are the transfer matrix elements for ProbS, are the transfer matrix elements for HeatS, is the degree of item , is the degree of item , it the degree of user .
ProbS has high accuracy but low diversity, and HeatS is designed to meet the challenge of diversity, but its accuracy is low. The spreading process for both is illustrated in Figure 3. It describes the spreading process of ProbS and HeatS, with weights calculated according to Equation (6). The changes in weights during the spreading process will alter the relative influence of items and users. If a certain user’s weight is large, then the weights of other items will be greatly affected by that user, and the recommendation system will tend to recommend items that have a relationship with that user; if a certain item’s weight is large, it indicates that the item has a strong influence on multiple users, likely categorizing it as a popular item, and the recommendation system will make this item more likely to be recommended.
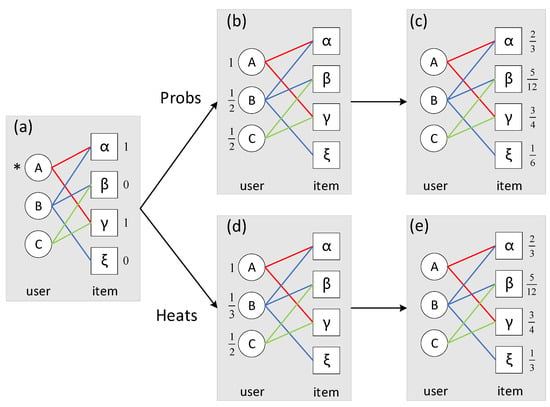
Figure 3.
Diagram of the spreading process in the user–item bipartite network. * a is the target user. (a) The initial resource value of each item for user A; (b) The value of each user’s resource for user A after the first round of the probability spreading process; (c) The value of each item’s resource for user A after the second round of probability spreading process; (d) The value of each user’s resource for user A after the first round of heat spreading process; (e) The value of each item’s resource for user A after the second round of the heat spreading process.
According to the spreading process of ProbS and HeatS, mark the user resource vector obtained after the first round of probabilistic spreading and heat spreading as , and allocate a certain amount of initial resources for the item against the target user , then:
where it the degree of item , is the degree of user .
According to Equations (6) and (7), it can be obtained:
denote , then:
Tao Zhou et al. proposed a HybridS for weighted linear aggregation of ProbS and HeatS by introducing the hyperparameter in the transfer matrix [6]. HybridS degenerates to HeatS when and to ProbS when . By adjusting the hyperparameter , a compromise between diversity and accuracy can be made.
Based on this idea, introduce on top of the item resource vector obtained after the second round of probabilistic spreading and heat spreading mentioned above and mark the item resource vector obtained after hybrid spreading as , then for the item , there are:
denote as the resource transfer matrix with:
using a vectorized representation:
where is the resource matrix after spreading from users, is the initial resource matrix for users, is the resource transfer matrix for items, is the allocation weight matrix for spreading from users to items, and stands for the Hadamard product.
4. Experiments
4.1. Dataset
In this research, two widely used recommendation datasets, MovieLens and Douban, are utilized to evaluate the recommendation performance of the proposed algorithm. The MovieLens dataset is collected by the GroupLens research program at the University of Minnesota, contains movie rating information from the MovieLens website between January 1995 and March 2015. The Douban dataset, obtained from the movie rating website Douban, includes movie rating information from June 2015 to September 2019. The basic statistical properties of these datasets are summarized in Table 1.

Table 1.
Dataset information.
4.2. Evaluation Indicators
Accuracy and diversity are important metrics for evaluating personalized recommendation algorithms. Accuracy is evaluated using Precision, Recall, F1 Score, and Normalized Discounted Cumulative Gain.
Precision (P) evaluates the proportion of items in the recommendation list that are of interest to the user, while Recall (R) evaluates the proportion of items of interest to the user that are included in the recommendation list. The F1 score (F1) is the harmonic mean of Precision and Recall, combining the performance of both metrics. The Normalized Discounted Cumulative Gain (NDCG) considers the ranking of items in the recommendation list and relevance between users and items.
These four metrics range between , with higher values indicating better recommendation accuracy. The formulae are as follows:
where and denotes the number of true positive, false positive and false negative samples, respectively. is the size of the recommendation list, is the recommendation list of user , is the set of items that user has interacted with in the test set, is a list of items sorted by relevance, and is the hierarchical relevance of the recommendation list at position ( if the item is in the test set, otherwise).
For diversity, considering both user diversity and individual diversity, average Hamming distance and average internal similarity are used for assessment.
The average Hamming distance(H) effectively evaluates the differences in recommendation lists between users, with values ranging from . A higher value indicates greater differences in recommendation lists between users, reflecting a higher the degree of user diversity. The formula is as follows:
where is the number of users, is the size of the recommendation list, is the number of overlapping items in the recommendation lists of user and user .
Additionally, recommendation algorithms should exhibit a certain degree of diversity in recommendation lists for individual users, otherwise, users may become fatigued by receiving recommendation on the same topic. Therefore, this research utilizes Intra-similarity (I) to evaluate individual diversity, with values ranging from . A smaller value indicates higher individual diversity. The formula is as follows:
where is the number of users, is the size of the recommendation list, denotes the degree of items , is the preference of user for items , which is usually an interaction matrix indicating whether the user has interactive behavior with the items.
4.3. Experimental Setup
To validate the superiority of the proposed model, we selected ProbS, HeatS, HybridS, and LightGCN as benchmark algorithms for comparative experiments. These algorithms are closely related to the LGCNHS model proposed in this research.
Considering the sparsity of the dataset, we utilized two quantiles to ensure that the recommendation algorithm could identify sufficient overlap between users and items, thereby enhancing the effectiveness of the model. We conducted multiple adjustments to these parameters during the experiments, retaining only users whose rating counts fell within the specified quantile range and the items they interacted with. Based on the adjustment results, we selected a quantile that was relatively excellent in terms of both performance and efficiency, ultimately choosing for the MovieLens dataset and for the Douban dataset.
Subsequently, the datasets were randomly split into a training set, validation set and test set according to . The model was trained and generated recommendations on the training set, evaluated on the validation set, and tested for performance on the test set.
The LGCNHS model proposed in this research was implemented using the PyTorch 1.13.1 framework, and the experimental environment was configured with the Ubuntu 18.04.1 LTS operating system, an Intel(R) Xeon(R) Gold 5318Y CPU, eight RTX 3090 GPUs, and 377 GB of memory (Intel, Santa Clara, CA, USA).
The experimental parameters were adopted from the literature [14]. The embedding dimension was set to , the batch size to , the learning rate set to , the regularization coefficient of the loss function to , the number of propagation layers was set to 3, and the weighted contribution of th layer set to .
4.4. Mixing Spreading Proportionality Constant
To determine the optimal hybrid spreading proportionality constant for the LGCNHS model, experiments were conducted on both datasets with recommendation list lengths set to 30, 50, and 100. The value of was adjusted within the range in increments of .
Based on a comprehensive analysis of the evaluation metrics, it was observed that for different recommendation list lengths, the metrics achieved near-optimal performance on the MovieLens dataset when was set to 0.85,0.88 and 0.91, respectively. Similarly, on the Douban dataset, the metrics reached near-optimal performance when was set to 0.63, 0.71, and 0.87, respectively.
For this purpose, the optimal hybrid spreading proportionality constant was averaged across the different recommendation list lengths, resulting in for the MovieLens dataset and for the Douban dataset. Figure 4 illustrated the variation curve of the hybrid spreading constant against the metrics for a recommendation list length of 30.
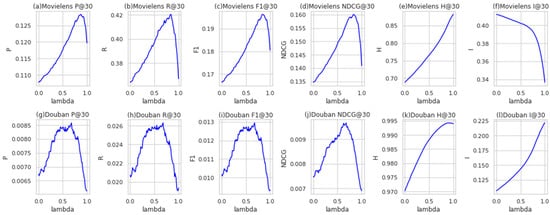
Figure 4.
Hybrid spreading proportionality constant λ vs. the curve of each metrics for a recommendation list length of 30.
4.5. Comparison Experiments
To evaluate the superiority of LGCNHS, we varied the length of the recommendation list () while keeping other parameters fixed and compared its performance with four related algorithms. The results demonstrate that LGCNHS outperforms the four benchmark algorithms in terms of both accuracy and diversity. For detailed results, refer to Table 2, Table 3 and Table 4.

Table 2.
Compare the results of the test (@30).

Table 3.
Compare the results of the test (@50).

Table 4.
Compare the results of the test (@100).
From the comparison of ProbS [4], HeatS [5], and HybridS [6], it is evident that HybridS significantly outperforms both ProbS and HeatS across different recommendation list lengths in terms of accuracy and diversity. This indicates that the linear fusion of these two spreading-based recommendation algorithms can effectively enhance the recommendation performance. Specifically, HybridS achieves a balance between accuracy and diversity in practical recommendation scenarios, demonstrating its advantage in balancing these two aspects. These results validate that HybridS not only accurately captures user preferences but also provides more diverse recommendations, thereby improving the limitations of spreading-based recommendation algorithms to a certain extent.
Compared to ProbS, HeatS, and HybridS, LightGCN performs poorly across various metrics, indicating that LightGCN-based recommendation algorithms are inferior to spreading-based recommendation algorithm on these two datasets. Although LightGCN effectively capture relationships between users and items, spreading-based recommendation algorithms such as ProbS, HeatS, and HybridS demonstrate better performance in terms of recommendation accuracy and diversity when handling information dissemination and user interest modeling. This may be due to LightGCN’s reliance solely on user–item latent embedding representations for recommendations, as well as its susceptibility to data sparsity. Consequently, on these datasets, spreading-based recommendation algorithms outperform LightGCN.
The LGCNHS model, which integrates HybridS and LightGCN, demonstrates outstanding performance across various metrics on the MovieLens dataset, indicating its excellence in both recommendation accuracy and diversity. On the Douban dataset, LGCNHS also performs exceptionally well in accuracy metrics, with its average Hamming distance comparable to other algorithms. Although its intra-similarity dose not reach the minimum value, LGCNHS demonstrates a significant advantage over ProbS, HeatS, and HybridS in this regard, indicating excellent improvement effects.
These results indicates that LGCNHS can achieve excellent recommendation performance in various scenarios, further demonstrating the potential and effectiveness of combining spreading-based recommendation algorithms with deep learning methods. Additionally, the adaptability of LGCNHS is one of its advantages. Unlike traditional spreading-based recommendation algorithms, which are confined to processing user–item interaction data, LGCNHS is capable of effectively handling diverse types of complex data, including user–item interaction data, user features, and item features. This capability makes LGCNHS valuable in applications such as e-commerce recommendations, movie recommendations, and music recommendations, offering new perspectives for both future research and practical applications.
4.6. Ablation Experiments
To validate the effectiveness of embedding optimization in LGCNHS, ablation experiments were conducted on the embedding optimization component with the recommendation list length set to 50. The experimental results are illustrated in Figure 5. where the variant model LGCNHS-e was constructed by removing the embedding optimization module.
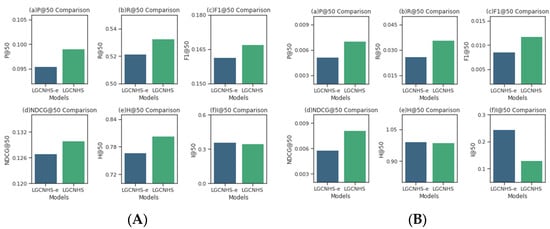
Figure 5.
(A) Ablation experiments in the dataset MovieLens (B) Ablation experiments in the dataset Douban.
As illustrated in the figure, LGCNHS outperforms the variant model across all evaluation metrics compared on both the MovieLens dataset and the Douban dataset, indicating that an embedding optimization module is important for achieving recommendations.
5. Conclusions
In this paper, we first analyze the defects of existing spreading-based recommendation algorithms and discuss the application of graph neural networks in recommendation systems. Building on this foundation, we propose Light Graph Convolutional Hybrid Spreading (LGCNHS), a novel recommendation algorithm that integrates spreading-based recommendation algorithms with LightGCN. First, the model utilizes a features matrix for embedding optimization of users and items; second, the latent embedding representations of users and items are learned through a LightGCN; and finally, the learned embedding matrix is incorporated as a key parameter into a hybrid spreading algorithm for generating recommendation results. Comparative experiments and ablation experiments were conducted on two publicly available datasets, MovieLens, and Douban. The results demonstrate that the recommendation effect of LGCNHS has improved accuracy and diversity over related methods.
While LGCNHS outperforms related algorithms and provides a novel perspective for spreading-based recommendation algorithms, there are still some potential limitations. First, LGCNHS faces challenges regarding computational complexity and resource consumption when handling large-scale datasets, which poses a challenge to its scalability, optimizing computational efficiency in large-scale data environments remains a question worthy of in-depth research. In a large-scale data environment, how to optimize computational efficiency to enhance the practicality of algorithms remains an important issue that urgently needs to be addressed. Future research can focus on algorithm optimization, parallel processing, and other directions to tackle this challenge and improve the performance of LGCNHS in large-scale data scenarios.
Additionally, the interpretability of LGCNHS is relatively weak, which may affect its transparency and user trust in practical applications to a certain extent. To enhance user acceptance and trust in the system, future research could explore ways to improve model interpretability, such as introducing interpretability frameworks, visualization techniques, or combining local model explanation methods, thereby providing users with clearer and more understandable reasons for recommendations.
Finally, LGCNHS still has room for further improvement, particularly in the broader field of recommendation system. Future research could explore more specifically how to enhance the performance and adaptability of the model, for instance, by optimizing the recommendation process through reinforcement learning, allowing the recommendation system to achieve more personalized and precise results by continuously interacting with users and self-adjusting. Furthermore, alternative feature selection strategies are also a worthwhile direction for expansion, investigating how to optimize the model structure of LGCNHS through more efficient feature selection methods to improve its accuracy and generalization ability in specific application scenarios.
We hope these issues can be effectively addressed to propose more innovative and practical recommendation algorithms in subsequent research, and we also hope this paper can provide inspiration for researchers and practitioners in related fields.
Author Contributions
Conceptualization, Y.D.; Methodology, Y.D.; Validation, Y.D.; Investigation, Y.D. and J.L.; Writing—original draft, Y.D.; writing—review and editing, L.Z. and X.L.; Supervision, L.Z. and X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 62202281.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, Z.; Fan, W.; Li, J.; Liu, Y.; Mei, X.; Wang, Y.; Wen, Z.; Wang, F.; Zhao, X.; Tang, J.; et al. Recommender systems in the era of large language models (LLMs). IEEE Trans. Knowl. Data Eng. 2024, 36, 6889–6907. [Google Scholar] [CrossRef]
- Zheng, B.; Hou, Y.; Lu, H.; Chen, Y.; Zhao, W.X.; Chen, M.; Wen, J.R. Adapting large language models by integrating collaborative semantics for recommendation. In Proceedings of the 2024 IEEE 40th International Conference on Data Engineering (ICDE), Utrecht, The Netherlands, 13–17 May 2024; pp. 1435–1448. [Google Scholar]
- Ko, H.; Lee, S.; Park, Y.; Choi, A. A survey of recommendation systems: Recommendation models, techniques, and application fields. Electronics 2022, 11, 141. [Google Scholar] [CrossRef]
- Zhou, T.; Su, R.-Q.; Liu, R.-R.; Jiang, L.-L.; Wang, B.-H.; Zhang, Y.-C. Accurate and diverse recommendations via eliminating redundant correlations. New J. Phys. 2009, 11, 123008. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Blattner, M.; Yu, Y.K. Heat conduction process on community networks as a recommendation model. Phys. Rev. Lett. 2007, 99, 154301. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Kuscsik, Z.; Liu, J.-G.; Medo, M.; Wakeling, J.R.; Zhang, Y.-C. Solving the apparent diversity-accuracy dilemma of recommender systems. Proc. Natl. Acad. Sci. USA 2010, 107, 4511–4515. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Song, W.; Hu, Z.; Hou, L.; Zhang, Y.; Chen, F. Non-equilibrium mass diffusion recommendation algorithm based on popularity. J. Comput. Appl. 2015, 35, 3502–3505. (In Chinese) [Google Scholar]
- Nie, D.-C.; An, Y.-H.; Dong, Q.; Fu, Y.; Zhou, T. Information filtering via balanced diffusion on bipartite networks. Phys. A Stat. Mech. Its Appl. 2015, 421, 44–53. [Google Scholar] [CrossRef]
- Chen, G.; Gao, T.; Zhu, X.; Tian, H.; Yang, Z. Personalized recommendation based on preferential bidirectional mass diffusion. Phys. A Stat. Mech. Its Appl. 2017, 469, 397–404. [Google Scholar] [CrossRef]
- Xu, L.Y. The Predictability of Diffusion-Based Method and Enhancing Its Long-term Performance. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2020. (In Chinese). [Google Scholar]
- Zhou, J.Y. Research on Recommendation Methods Based on Bipartite Graphs and Clustering. Master’s Thesis, North China University Of Technology, Beijing, China, 2024. (In Chinese). [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T.S. Neural graph collaborative filtering. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019; ACM Press: New York, NY, USA, 2019; pp. 165–174. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. LightGCN: Simplifying and powering graph convolution network for recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 639–648. [Google Scholar]
- Liu, Q.H.; Sun, G.; Ma, Z.Y. An improved LightGCN algorithm based on contrast learning. J. Anqing Norm. Univ. (Nat. Sci. Ed.) 2024, 30, 98–103. (In Chinese) [Google Scholar]
- Huang, J.G.; Wang, G.P.; Wu, B.; Xin, B. Diversified recommendation based on light graph convolution networks and implicit feedback enhancement. Comput. Sci. 2024, 51, 681–691. (In Chinese) [Google Scholar]
- Wang, H.; Liang, X.Z.; Zhang, X.; Xia, C. Graph convolutional recommendation based on adjacency matrix optimization and negative sampling. Appl. Res. Comput. 2024; in press. (In Chinese) [Google Scholar]
- Wang, G.; Yin, K. Adaptive graph convolutional recommendation algorithm integrating user social relationship. Appl. Res. Comput. 2024, 41, 482–487. (In Chinese) [Google Scholar]
- Liao, D.; Yu, H.Z. Graph neural network recommendation algorithm based on item relations. Comput. Sci. 2023, 50, 492–500. (In Chinese) [Google Scholar]
- Huang, S.; Xiang, H.; Leng, C.; Xiao, F. Cross-Social-Network User Identification Based on Bidirectional GCN and MNF-UI Models. Electronics 2024, 13, 2351. [Google Scholar] [CrossRef]
- Qiang, G.; Yong, L.; Yang, O. Identification of perceptive users based on the graph convolutional network. Expert Syst. Appl. 2025, 267, 125844. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).