Abstract
As the dual carbon goals are being approached, there has been an increase in the number of energy-saving renovation projects for existing buildings. However, building renovation also brings about environmental impacts and incremental costs, which need to be addressed urgently. This study proposes an integrated artificial intelligence framework to facilitate multi-criteria energy renovation decision making by combining a surrogate-based machine learning (ML) model and an evolutionary generative algorithm to efficiently and accurately identify optimal renovation strategies. To enhance the robustness of the methodology, a comparative analysis of four different ML models—light gradient boosting machine (LightGBM), fast random forest (FRF), multivariate linear regression (MVLR), and artificial neural network (ANN)—was conducted, with LightGBM demonstrating the best performance in terms of accuracy, adaptability, and efficiency. Using the heuristic optimization algorithm and entropy-weighted method, the framework achieved average energy savings of 56.62%, a reduction in carbon emissions of 51.60%, and a 24.27% decrease in life-cycle costs. Compared to local ultra-low-energy building standards, the optimal solutions resulted in a 2.60% reduction in carbon emissions and a 15.85% decrease in life-cycle costs. This integrated framework demonstrates the potential of combining machine learning surrogate models, evolutionary generation, and entropy-weighted methods in building energy retrofitting optimizations, offering a novel, efficient, and adaptable approach for researchers and practitioners seeking to balance energy consumption, carbon emissions, and life-cycle costs in renovation projects.
1. Introduction
The building and construction sector is the largest energy consumer and greenhouse gas emitter, responsible for 39% of global energy-related carbon emissions [1]. In the context of growing global environmental awareness and the implementation of policies to reduce energy consumption and emissions, the significance of energy-saving renovation in the building sector is increasing. As the largest energy consumer and the primary source of carbon dioxide emissions, China plays a pivotal role in the global effort to combat climate change. As China experiences an increase in building energy consumption driven by rising living standards and economic expansion, the importance of the building sector will only grow. This trend poses a considerable challenge to achieving China’s carbon peaking and neutrality objectives. China’s 14th National Five-Year Plan places significant emphasis on the modernization of aging residential areas to enhance living conditions, promote development, and improve local governance. The Plan’s objectives are twofold: first, to renovate more than 350 million square meters of existing buildings by 2025 [2]; and second, to increase energy efficiency while reducing energy consumption and emissions, with a particular focus on regions experiencing seasonal temperature extremes [3].
However, applying retrofitting strategies to existing constructions necessitates the resolution of numerous challenges while offering prospects for advancement, including climate change, financial limitations, changes in human behavior, shifts in governmental policy, and disruptions to operations [4]. Current approaches in China to building retrofitting frequently employ rigorous energy-saving measures, such as those outlined in the Passivhaus standard [5] or the local nearly zero-energy building code [6], which prioritize insulation and, in the case of Passivhaus, emphasize the airtightness of the building envelope, particularly in extremely cold climate zones. A considerable body of research has demonstrated the efficacy of these high-performance energy building standards, indicating a significant reduction in energy usage. Current building retrofitting efforts aim to minimize heat losses through both opaque and transparent components of the building envelope, as well as to eradicate thermal bridges and ensure minimal air leakage. However, studies have identified potential negative impacts, such as the risk of indoor overheating during summer and increased cooling demands due to the building’s airtightness and heavy insulation [7]. Furthermore, difficulties in meeting cooling energy demands during energy-saving retrofits have been observed, even in some severe cold climates [8,9]. Given future climate change and its associated environmental consequences [10], the carbon emissions generated by insulation materials and aluminum used for external shading systems must also be considered. While aluminum shading systems are increasingly popular due to their relatively low cost and adaptability to various forms, their production contributes significantly to carbon emissions [11]. Consequently, implementing excessively stringent energy-saving design standards without holistic evaluation may inadvertently exacerbate climate change [12].
The primary challenge in optimizing building retrofits is selecting and implementing the most effective technologies to enhance energy performance, reduce carbon emissions and environmental impact, and ensure acceptable initial investment and payback periods within realistic constraints. Therefore, selecting appropriate energy-saving renovation strategies is a multi-objective decision-making task, which requires identifying the most effective balance between multiple performance indicators. Simulation software has been frequently employed with optimization algorithms to automate the optimization process [13]. These optimization methods principally comprise those grounded in mathematical programming (e.g., Epsilon-Constraint Method, Weighted-Sum Method, and Tchebycheff), evolutionary algorithms (e.g., SPEA2, MOEA/D, NSGA-II, and NSGA-III), swarm intelligence algorithms (e.g., MOPSO, MOGWO, and MOMFO), hybrid algorithms (e.g., NSGA-II+SA), and so forth [14,15,16,17,18]. Among optimization algorithms, heuristic algorithms, particularly NSGA-II and its variants, are widely employed for multi-objective decision making in energy-saving building renovation [19,20,21,22,23]. For instance, Mostafazadeh et al. proposed an enhanced NSGA-III algorithm, incorporating parallel computing and result-archiving mechanisms, significantly boosting its computational efficiency and potential [14]. Rosso et al. implemented an archive NSGA-II to optimize building retrofits in a Mediterranean climate, significantly reducing optimization time and substantially decreasing energy expenses, use, and greenhouse gas emissions [24]. Penna et al. implemented NSGA-II in order to identify the initial design parameters for optimal retrofit solutions, aiming to reduce energy consumption and maximize economic performance while improving indoor thermal comfort [25]. Wang et al. employed the NSGA-II algorithm for the multi-objective optimization of the energy performance and indoor thermal environment for rural tourism buildings, marking a substantial advancement in scientifically driven passive design strategies [26]. These studies validate the effectiveness of heuristic algorithms (especially the NSGA-II algorithm and its variants) for a wide range of multi-objective problems, demonstrating their widespread application and continued progress in improving building energy performance, economic efficiency, and occupant comfort across various settings.
However, evolutionary algorithms, commonly employed in this context, typically require extensive cost function evaluations to achieve satisfactory outcomes [27]. In recent years, there has been a notable increase in research focusing on the utilization of alternative models for approximating or simulating computationally intensive models, a development precipitated by advancements in artificial intelligence technology [28,29]. Numerous studies have combined surrogate models (e.g., artificial neural networks (ANNs)) with optimization algorithms [30,31,32], particularly NSGA-II [33,34,35] or other randomized algorithms [18,36,37], in what is commonly known as surrogate model-based optimization. This approach expedites building performance evaluations across various retrofit options, significantly accelerating the search for optimal solutions [38]. Surrogate models leverage diverse machine learning (ML) algorithms, such as random forest (RF), support vector machine (SVM), multivariate linear regression (MVLR), gradient boosting machines (GBMs), response surface methods (RSM), and artificial neural networks (ANNs) [39,40,41,42,43]. Compared to conventional optimization methods, these approaches analyze simulation data from various renovation options, construct energy performance prediction models, and integrate metaheuristic algorithms for multi-criteria optimization. By overcoming the constraints of a limited solution space, these methods dramatically enhance optimization efficiency. Among the surrogate models, ANNs have been widely employed in building energy optimization studies [38,44]. However, the reliance on ANNs alone has limitations, including potential inefficiencies, overfitting risks, and a lack of comparative analysis with alternative ML models that may offer better performance. To address this gap, this study incorporates a broader dataset and compares the performance of four different ML models: light gradient boosting machine (LightGBM), fast random forest (FRF), multivariate linear regression (MVLR), and artificial neural network (ANN).
This paper introduces a novel optimization method that combines machine learning with the evolutionary generation algorithm for solving the multi-objective building retrofit optimization problem. The method’s effectiveness is evaluated in terms of efficiency and reliability, thereby contributing to the refinement of tools for building retrofit projects. A multi-objective design scheme for residential building envelope retrofits is proposed, taking into account economic factors, life-cycle carbon emissions, and energy consumption under different energy efficiency design standards for residential buildings.
The primary objectives of this study are as follows:
(1) To propose a novel framework that integrates ML models and heuristic optimization algorithms to address decision-making challenges in the renovation of existing buildings. This framework aims to provide a robust and data-driven approach to optimizing renovation strategies.
(2) To evaluate the effectiveness and efficiency of the proposed method through comprehensive testing and analysis, including assessing its performance in terms of accuracy, adaptability, and scalability for real-world applications.
(3) To provide policymakers with scientific evidence and actionable insights from the study’s results. The findings aim to support informed decision making by enhancing energy performance and reducing life-cycle carbon emissions and costs.
2. Method
As demonstrated in Figure 1, the proposed residential building energy-saving renovation optimization framework consists primarily of the following six stages:
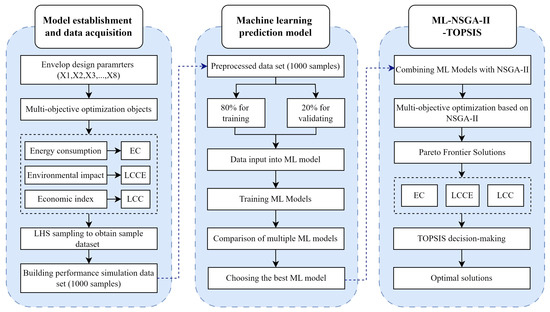
Figure 1.
The overall research framework.
(1) Develop a building energy simulation model for the reference building.
(2) Identify the building envelope design variables and the optimization objectives.
(3) Conduct a sensitivity analysis on the building renovation design variables to determine the impact trends on the optimization objectives.
(4) Apply the Latin Hypercube Sampling (LHS) algorithm to generate a representative database of simulation cases, which is then used to validate the reliability of the ML models.
(5) Integrate ML models with NSGA-II to obtain the Pareto solution set.
(6) Use the entropy-weighted multi-criteria method to determine the weights assigned to different optimization objectives and identify the appropriate retrofit strategy based on stakeholder preferences.
2.1. Design Variables for Optimization
In the field of building renovation, measures oriented toward enhancing energy efficiency in buildings can directly contribute to the mitigation of greenhouse gas emissions and thus merit the highest possible priority [45,46]. Previous studies outlined the potential of residential building envelope renovation for energy savings, pointing out that envelope renovation can substantially enhance the energy efficiency of residential buildings, which is why this area is given higher priority for renovation [22,23,47,48]. Therefore, in order to reduce the solution space and the model’s complexity, this study selects passive energy-saving design strategies explicitly focused on the renovation of building envelopes as decision variables, including airtightness, depth of the south overhang shading system, type of windows, and insulation type and thickness of the walls and roof [49]. For the above decision variables, the depth of the south overhang shading system and the insulation thickness for the walls and roof are continuous variables. In contrast, the window types, airtightness, and insulation type of the walls and roof are regarded as discrete variables.
The outcomes of any optimization process depend heavily on the bounds and probability distribution of the optimized variables. This study conducted a quantitative evaluation to assess the relative importance of the various components of energy, cost, and emissions. The thermal characteristics of the building envelope elements are fully described based on the national and local building codes for conventional design and energy efficiency design [50,51]. This study obtained the financial implications of the components through market research and supplier quotations. Table 1 and Table 2 provide a comprehensive overview of the potential decision variables and their associated ranges of variability and constraints, including material costs and carbon emission factors (CEFs). The balanced optimization model estimates the configuration of the building based on optimization objectives using eight design variables. A comprehensive evaluation yielded 4.32 × combinatorial designs.

Table 1.
Design variables of building retrofit strategies.

Table 2.
Glazing types for retrofit.
2.2. Optimization Objectives
In energy renovation of residential buildings, improving energy performance, reducing environmental impact, and ensuring an acceptable initial investment and payback period under realistic constraints are most important. The following three objective functions are thus addressed for the multi-criteria decision-making model in this paper: energy consumption (EC), life-cycle carbon emissions (LCCE), and life-cycle cost (LCC).
2.2.1. Energy Consumption
In this study, the total energy consumption is mainly composed of annual heating and cooling energy consumption. The mechanical ventilation rate was standardized at one air change per hour across all simulation cases, with supply air temperatures set to 20 °C for heating during winter and 26 °C for cooling during summer. The hourly simulations were conducted throughout the year, with a frequency of six times per hour. This calculation excludes fluctuations in the energy consumption of electronic equipment and domestic hot water, which do not vary significantly during the building’s operation time. The air-conditioning system is regarded as the optimal unit for heating and cooling, with coefficients of performance (COP) of 0.92 and 3, respectively. The energy consumption calculation formula is as follows:
where is the energy consumption; denotes the cooling energy demand; represents the heating energy demand; denotes the lighting energy consumption; is the efficiency of the cooling system; and is the efficiency of the heating system.
2.2.2. Life-Cycle Cost
This study employed the life-cycle cost as the index for evaluating economic indicators, encompassing the present values of both the initial investment and the costs incurred throughout the building’s operational lifespan. In order to evaluate the economic feasibility of a building renovation project, it is essential to consider the initial investment and the life-cycle energy savings achieved once the program is implemented. Given that typical existing residential buildings constructed in severe cold climate regions in China during the 1980s have a typical lifespan of 70 years, it is crucial to consider the remaining operational lifespan when planning a renovation project; a renovated building typically has a lifespan of 20 to 40 years. Consequently, this study uses a 30-year life cycle and employs the net present value method to calculate life-cycle costs, incorporating the time value of money. The calculation formula is as follows:
where is the investment cost for the building retrofitting strategy; denotes the cost of maintenance in the i-th year following the renovation; the annual maintenance cost is hypothesized to be 8% of the initial investment; is the annual cost for energy; is the heating energy to coal conversion factor, with a value of 0.36 in this study; is the local coal price; is the local electricity price; and represents the present value factor.
The net present value (NPV) method was employed to calculate the life-cycle costs, incorporating the time value of money, inflation, and energy price escalation. The following formula was used:
where is the number of years for the operation, assumed to be 30 in this study; is the number of years that have elapsed since the original year; is the rate modified to account for market energy price escalation; is the effective interest rate; is the interest rate, assumed to be 0.07 in this study; is the inflation rate, assumed to be 0.02; and is the cost of total energy escalation during the study period above the rate of inflation, assumed to be 0.012 in this study.
These parameters were chosen to align with typical market trends in the region, aiming to capture both short-term and long-term economic impacts. While this study does not explicitly model material cost volatility, future research could incorporate sensitivity analyses to better understand the impact of fluctuating material prices on life-cycle costs.
2.2.3. Life-Cycle Carbon Emission
The term ‘life-cycle carbon emission’ refers to the total amount of carbon emissions, including the embodied carbon emissions generated during the manufacturing and shipping of retrofit materials, as well as those from total building energy consumption during operational phases, serving as a comprehensive measure of environmental impact. A carbon emission factor (CEF), derived from the national building carbon calculation standard, was used to quantify both the embodied carbon emissions and energy-related emissions of building materials [52]. The objective function is described as follows:
where denotes the material type for renovation; represents the specific material quantity; is the CEF for the particular material; denotes the CEF for coal, which is 2.27 in this study; and represents the CEF for electricity, which is 1.15 in this study.
2.3. Sensitivity Analysis
Sensitivity analysis (SA) has been widely utilized in building performance simulations to determine the pivotal factors that substantially impact optimization objectives, as evidenced by numerous studies [53,54]. Regression techniques are favored among the various global SA methods due to their ease of implementation and relatively moderate sample size requirements [53]. Notably, the standardized rank regression coefficient (SRRC) and partial correlation coefficient (PCC) stand out for their effectiveness in dealing with correlated input variables. These two indices can efficiently isolate the effects of variable correlations, thereby enabling a more precise evaluation of the influence of each variable on the target outcome [55]. Therefore, this study uses SRRC and PCC methods to investigate the influence of building renovation strategies on specified objectives and to uncover the underlying correlations between these strategies and optimization objectives.
2.4. Machine Learning Modeling
For machine learning (ML) training, a larger dataset is needed to enhance the training process and improve model accuracy. Previous studies have demonstrated the benefits of utilizing more extensive datasets [56]. To address this limitation, this study uses the Latin Hypercube Sampling (LHS) method to generate the sample space [57]. LHS is a stratified sampling method commonly applied in Monte Carlo simulations and is recognized as a powerful technique for producing small yet statistically representative samples. Compared to random sampling, LHS achieves the same level of statistical accuracy with a smaller sample size [58]. It has been extensively used to establish simulation case databases for validating machine learning models, particularly in residential building energy optimization [59] and building energy retrofitting [10,60].
For building optimization, the sample size required for LHS is typically ten times the number of design variables, influenced by the complexity of the interactions between these variables [46]. This size is considered sufficient if the probability density function stabilizes toward uniformity, effectively representing the entire building library. This study determined a sample size of 1000 cases based on the number of design variables and their interactions. The LHS method generated a matrix that effectively represents diverse building configurations. These configurations were then simulated to populate the database used in the machine learning model. To train and validate the machine learning model, the dataset was split into two subsets: 80% of the sample was used for training, and 20% was reserved for validation. The training step involved optimizing the model’s weighting biases to improve predictive accuracy, while validation ensured the robustness and reliability of the model’s predictions.
To ensure a comprehensive analysis, four different ML models were compared: fast random forest (FRF), light gradient boosting machine (LightGBM), multivariate linear regression (MVLR), and artificial neural network (ANN). These models were selected due to their widespread use in predictive modeling and optimization tasks, as well as their potential to perform well in energy performance prediction for building retrofits. The performance of each model was evaluated using four statistical indicators: the coefficient of determination (R2), root mean square error (RMSE), mean square error (MSE), and mean absolute error (MAE). These metrics provide insights into the accuracy of predictions from different perspectives.
R2 measures the proportion of variance in the dependent variable explained by the model. Higher values indicate better model performance.
RMSE quantifies the standard deviation of residuals, representing the average distance between the predicted and actual values. Smaller values indicate better predictions.
MSE calculates the average of squared differences between the predicted and actual values, with smaller values reflecting better accuracy.
MAE assesses the average magnitude of prediction errors, with lower values indicating smaller prediction errors.
By combining these indicators, the study ensures a rigorous evaluation of each model’s accuracy, efficiency, and overall performance. The formulas for calculating these metrics are as follows:
where denotes the number of samples, represents the number of case studies in the cluster, denotes the actual value of a sample, represents the predicted value of a sample, and represents the mean of the actual values.
2.5. Multi-Criteria Decision Method
The evolutionary generation algorithm is a fundamental tool for addressing multi-criteria decision-making problems; it generates a set of non-dominated solutions and facilitates subsequent preference-based decision making [61,62]. It is evident that, within the scope of these methodologies, NSGA-II is particularly well suited for resolving optimization problems encompassing three or more objectives. Consequently, it is extensively employed for multi-criteria decision-making processes in the context of building energy renovation [63]. Additionally, TOPSIS has been widely used for multi-objective decision making in building energy-saving renovation projects [64,65,66]. TOPSIS evaluates the closeness of different solutions to an ideal target. Thus, the entropy-weighted TOPSIS ranking model with the Mahalanobis distance method was used in this study [67]. For building renovation decision making, where energy performance, economic considerations, and sustainability are equally important, the weights for the three optimization objectives were set to be equal.
The following equations show the calculation of the decision matrix, the Mahalanobis distance, and the relative closeness.
- (1)
- Normalize the Decision MatrixThe normalized decision matrix element is calculated as
- (2)
- Calculate the Mahalanobis Distance
- a.
- The Mahalanobis distance from solution to the ideal solution is given by
- b.
- The Mahalanobis distance from solution to the negative ideal solution is given by
- (3)
- Compute the Relative ClosenessThe relative closeness for each solution is calculated as
Each solution is ranked by its value of , with higher values indicating a better solution for , and lower values indicating a less desirable solution.
3. Case Study
3.1. Reference Building
The present study constructed a reference model for typical existing residential buildings in Shenyang, China, which has a severely cold climate. The reference building represents a typical residential structure built in the region during the 1980s (Figure 2). It is a typical seven-floor construction with a 3519 total floor area and 63 apartments, each with a ceiling height of 2.7 m (Figure 3). A comprehensive investigation and collation of information on the envelope structures of existing residential buildings were conducted. The investigation indicated that a significant number of local residential buildings constructed in the 1980s were not equipped with insulation layers. Two layers of single-pane glass were used for the windows without broken bridge frames. Since 2022, the government has carried out large-scale renovations of existing residential buildings according to local residential building energy-saving design standards [51]. The renovation added 100 mm EPS to the exterior wall and 200 mm to the roof. The windows remained unchanged, consisting of two layers of single-pane glass. Table 3 presents the calculated heat transfer coefficients of the exterior walls, roofs, floors, and exterior windows, as well as the thermal performance parameters of the residential building envelope in this case.

Figure 2.
Image of the reference building.
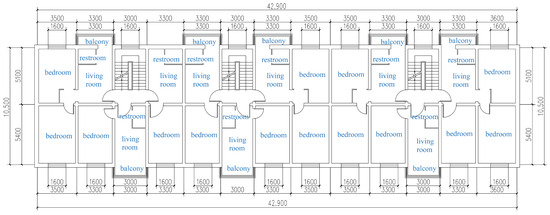
Figure 3.
Floor plan of the reference building.

Table 3.
Building envelope and material properties.
Table 4 presents the internal heat gain from artificial lighting, equipment, and three occupants per unit, along with the typical workday schedule for each residential unit. Despite the absence of shading overhangs in the reference building, their potential inclusion was explored in the subsequent parametric simulations. Specifically, overhangs above south-facing windows were modeled, with their depth being a key design parameter under optimization. Conversely, no external shading devices were considered for north- and east-facing windows.

Table 4.
Internal heat-gain schedule.
3.2. Monitoring and Calibration
Since measuring the actual airtightness of the case study building was not feasible, we referred to former studies on the airtightness of residential buildings [68,69], a parametric analysis was conducted using a building model with varying airtightness values, ranging from 0.0001 to 0.0009 . The impact of these different scenarios on the building’s performance was assessed, and the model’s accuracy was validated by comparing the simulated results with the measured indoor temperatures on-site, allowing us to estimate the building’s actual airtightness. Hourly indoor temperature data were recorded using the Testo 174H temperature testing instrument between 18 April and 26 April 2024 under free-running conditions. The data were collected in a south-facing bedroom, with measurement points situated 1 m from the windows and readings taken at 15 min intervals. NMBE and cv(RMSE) were used to quantify the error between the measurement and simulation data. This study followed the ASHRAE Guideline 14-2002 [70], a standard method for calibrating building models that provides acceptable calibration accuracy limits. For hourly data, the acceptable limits are and , while for monthly data, the limits are and . NMBE and cv(RMSE) were calculated using the following equations:
where denotes the measured data; is the predicted value; i indicates the number of case studies in the cluster; n is the number of samples; and represents the average of the actual values of the sample.
As shown in Table 5 and Figure 4, when the value of airtightness is 0.0006, the NMBE and cv(RMSE) of the measurement points are 1.85% and 4.87%, respectively, which are within ASHRAE’s error tolerance. Therefore, it can be concluded that the model is well calibrated.

Table 5.
Calibration for the airtightness of the case study.
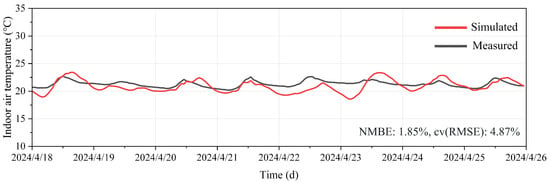
Figure 4.
Comparison of monitored hourly data and simulated results.
4. Results and Discussion
4.1. Sensitivity Analysis of Design Variables
Figure 5 shows the sensitivity coefficients of the three target objectives for each variable. The results provided by the PCC and SRRC methods consistently assessed the positive and negative impacts of the sensitivity coefficients on the target objectives for the reference building. As expected and consistent with experience, the impacts of the design variables on the three objective functions differed. Increasing the thickness of external insulation and improving the external window glass material were negatively correlated with energy consumption but positively associated with life-cycle costs and carbon emissions. The external windows represented a much higher sensitivity to energy consumption and cost than the external insulation thickness and a lower sensitivity to carbon emissions. While external shading, such as overhangs, has been increasingly applied to address cooling energy demand, particularly in the context of climate change, their carbon emissions during production often outweighed their limited energy-saving potential. This trade-off underscores the importance of carefully evaluating shading design choices in building retrofitting projects, especially in severe cold climates where shading may play a less critical role in the overall energy performance.
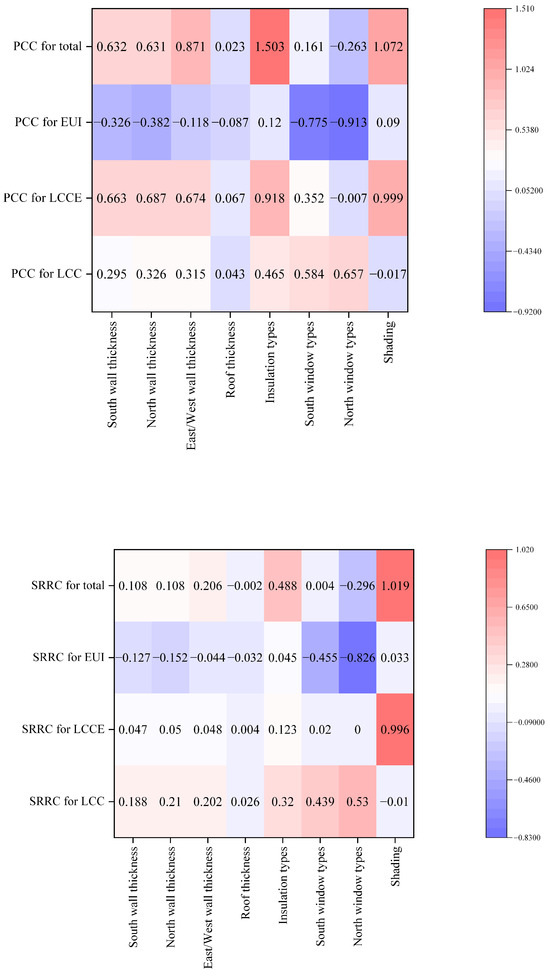
Figure 5.
The Sensitivity index PCC and SRRC of optimization variables.
The sensitivity analysis results also indicate that the insulation thickness of the south and north walls had a significantly greater impact on energy performance than that of the east and west walls in the reference building, primarily because the latter orientations have comparatively smaller surface areas. Additionally, the roof insulation thickness was found to have the least impact in this case. This finding suggests that optimization strategies can prioritize insulation improvements for the larger orientations, such as the south and north walls in this case study, while simplifying considerations for the east and west walls. Additionally, using different external insulation materials had little impact on energy consumption but a significant impact on carbon emissions and costs, warranting careful analysis when applied.
4.2. Machine Learning Model Performance
This section analyzes the performance of four distinct machine learning algorithms in predicting building energy consumption (EC) based on the given dataset. These machine learning algorithms, which have demonstrated exceptional capabilities in energy prediction tasks in previous studies [10,39,42], included fast random forest, LightGBM, MVLR, and ANN. To evaluate the predictive performance of each model, metrics were employed, including the coefficient of determination (), mean absolute error (MAE), mean squared error (MSE), and root mean squared error (cv(RMSE)). A model with MAE, cv(RMSE), and MSE values closer to zero, and an value closer to one, is considered to have superior predictive accuracy. The target feature in this analysis was energy consumption (EC), and the performance of each algorithm was assessed to identify the most reliable and efficient approach for energy prediction. The results of this evaluation provide valuable insights into the comparative strengths and weaknesses of these machine learning models.
Figure 6 illustrates box plots of the performance metrics for the four machine learning models used in energy consumption prediction. The results reveal that the LightGBM model outperformed the other three ML models by demonstrating superior performance across all evaluated metrics. Additionally, the ANN and FRF models exhibited nearly identical predictive performance; however, the FRF box plot indicates a greater number of outliers, suggesting that the FRF algorithm generated a higher proportion of poorly performing predictive models. In contrast, the ANN algorithm displayed fewer outliers, indicating more consistent and stable predictive accuracy compared to the FRF model. Among the four models, MVLR exhibited the poorest performance, highlighting its limited capability to address the complexities of energy consumption prediction tasks.
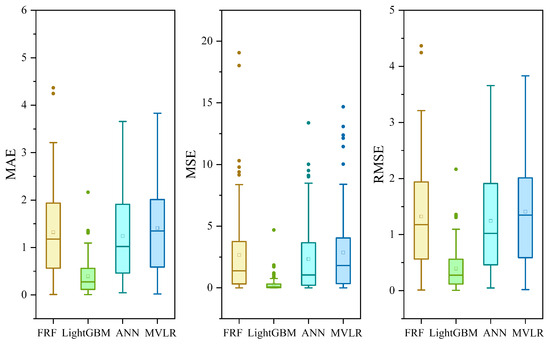
Figure 6.
Optimization results and Pareto front solutions.
Table 6 provides a detailed comparison of the performance metrics for each machine learning model. The LightGBM model achieves significantly lower MAE, MSE, and RMSE values compared to the other three models, indicating its exceptional predictive performance. In contrast, the higher MAE, MSE, and RMSE values observed for the MVLR, FRF, and ANN models suggest relatively lower prediction accuracy. These findings underscore the suitability of gradient boosting models, such as LightGBM, for handling the inherent complexities of building energy consumption prediction tasks. Their superior accuracy and reliability position them as a more effective solution compared to simpler models. Based on this comparative analysis, the LightGBM model was identified as the optimal choice for predicting building energy consumption due to its outstanding stability and accuracy.

Table 6.
Performance comparison of ML models.
Figure 7 illustrates the regression performance of the LightGBM model in predicting energy consumption (EC). The scatterplot compares the tested EC values (x-axis) with the predicted EC values (y-axis) generated by the LightGBM model. The results demonstrate a strong linear relationship between the predicted and true values. This indicates that the LightGBM model achieves high predictive accuracy and effectively captures the relationship between the input features and energy consumption. The clustering of points along the diagonal further supports the model’s stability and reliability in predicting energy consumption across the dataset.
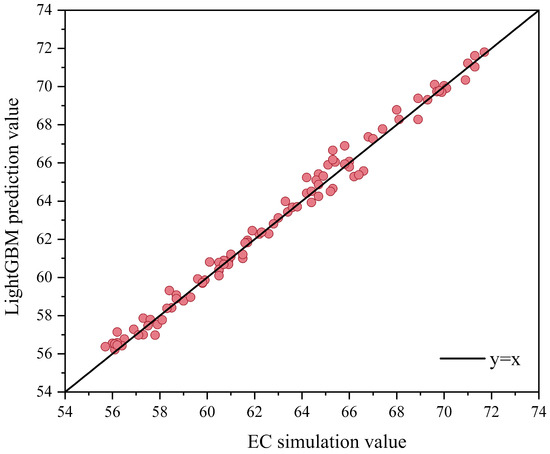
Figure 7.
Optimization results and Pareto front solutions.
4.3. The Optimal Pareto Front Solution Sets
The optimization procedure used to create the model and the run results are described below. Eight design variables and 1.44 × 107 combinatorial designs were evaluated in the case study. After 63 generations, the Pareto solutions successfully converged in less than 3 min. This study used the Intel Core i9-13950HX processor for training. The machine learning surrogate model significantly shortened the required time, making the optimization process a viable approach in the context of engineering practice.
Figure 8 shows the optimization results and Pareto front solutions, illustrating the Pareto front for minimizing energy consumption, carbon emissions, and life-cycle costs. Each solution represents an optimized building envelope design that balances the three objectives. As anticipated, trade-offs are evident between the objectives. The dispersion of solutions is influenced by the case study’s characteristics and the notable differences in the market prices and embodied carbon emissions of building envelope materials.
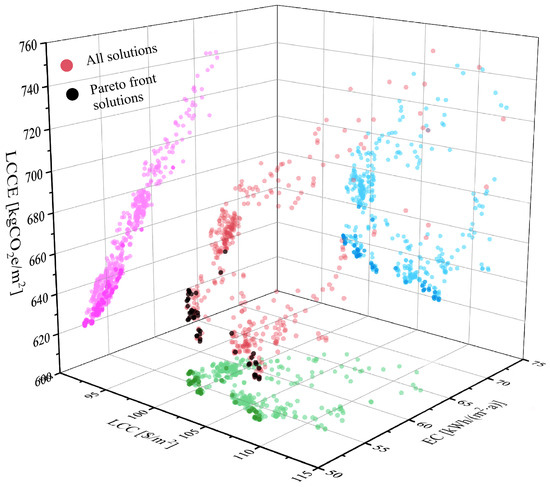
Figure 8.
Optimization results and Pareto front solutions.
As shown in Table 7, a comparative analysis was performed on the design solutions pertaining to the different energy efficiency standards, namely the case study building (CSB) and ultra-low-energy building (ULB), with the solutions corresponding to the three minimal objectives derived from the Pareto solutions. The CSB model represents the original design retrofitted based on the local energy efficiency design standard [51], and the ULB model is derived from the latest local energy efficiency design standard for ultra-low-energy residential buildings [71]. The values of all the design variables for the renovation strategies, as well as the corresponding EC, LCCE, and LCC values, are listed.

Table 7.
Comparison of single-objective solutions with the case study building and ultra-low-energy building.
Table 8 presents a comparison between the minimal single-objective optimization results, case study building, and ultra-low-energy building. Compared with the CSB model, the minimum energy consumption, life-cycle carbon emission, and cost schemes all achieved significant reductions. The three indicators were reduced to varying degrees, reflecting considerable energy savings, emission reductions, and cost advantages. Compared with the ULB model, the minimum energy consumption scheme in the Pareto solution also reduced energy consumption, carbon emissions, and life-cycle costs to varying degrees. The minimum carbon emission and life-cycle cost schemes significantly reduced carbon emissions and life-cycle costs by decreasing the use of building envelope materials, thereby achieving win-win economic and environmental benefits.

Table 8.
Comparison between minimal single-objective optimization results, case study building, and ultra-low-energy building.
Table 9 presents the top five solutions derived using the entropy-weighted TOPSIS method, evaluated against the criteria of minimizing EUI, LCCE, and LCC. With equal weights of 0.33 assigned to each criterion, the analysis identified solutions exhibiting the highest relative closeness values, signifying their proximity to the ideal solution while maintaining substantial separation from the negative ideal solution. The top-ranked solution achieved a relative closeness of 0.7964, followed sequentially by solutions with relative closeness values of 0.4767, 0.4475, 0.4131, and 0.4036. These rankings underscore the balanced integration of all criteria in the evaluation process, demonstrating the method’s ability to prioritize Pareto-optimal solutions effectively. The findings highlight the utility of entropy-weighted TOPSIS as a robust tool for informed decision making in multi-criteria optimization scenarios.

Table 9.
The ranking of optimal solutions and relative closeness values.
As shown in Figure 9 and Table 10, in comparison to the CSB model, all selected optimal solutions resulted in average energy savings of 56.62%, reductions in carbon emissions of 51.60%, and 24.27% decreases in life-cycle costs. In comparison to the ULB model, all selected optimal solutions resulted in a significant reduction in carbon emissions and life-cycle costs by 2.60% and 15.85%, respectively, despite slightly higher energy consumption.
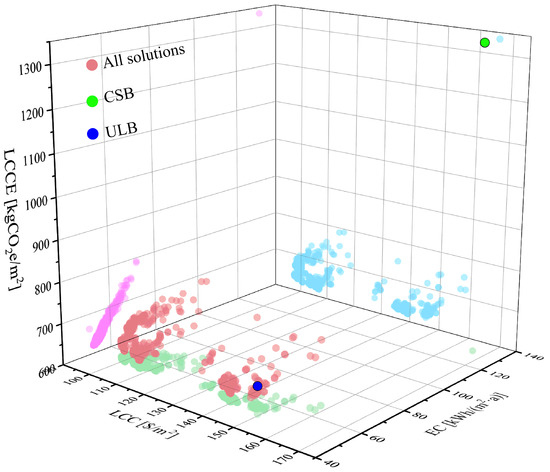
Figure 9.
Optimization results and Pareto front solutions.

Table 10.
Top five multi-objective optimization solutions.
The majority of optimal solutions recommended EPS as the primary insulation material for the building envelope, which is attributed to its relatively low incremental cost and acceptable performance.
Across all selected solutions, the insulation thickness on the south-facing wall was reduced to 160 mm, a noticeable decrease compared to the ULB model. This adjustment reflects the lower energy demand for the south-facing wall, given its higher solar exposure and heat-gain potential. Similarly, the east and west walls were recommended to have a reduced insulation thickness of 260 mm, as these orientations have a minimal overall impact on energy performance. In contrast, the north-facing wall was suggested to maintain a 280–300 mm thickness for enhanced thermal performance. However, reducing the north wall insulation to 220 mm could significantly lower life-cycle carbon emissions (LCCE) at the expense of energy efficiency, leading to higher life-cycle costs (LCC). This trade-off arises because, in this case study, energy costs constitute a substantial portion of the total 30-year life-cycle costs.
The optimization also highlights the importance of window selection. Solutions C, D, and E recommended using high-performance windows (W7 or W8) with triple-glazed, high-transmission Low-E glass. These windows help minimize life-cycle costs and carbon emissions while maintaining energy efficiency. Conversely, solution B recommended using lower-cost windows (W4 or W5, double-glazed), which increase annual energy consumption by 14.90% compared to the ULB benchmark. However, over a 30-year life cycle, this approach significantly reduces life-cycle costs (33.78%) and achieves a marginal reduction in life-cycle carbon emissions (0.66%) while also minimizing the initial investment for renovation materials.
In addition, the overhang depth for south-facing shading was inappropriate, aligning with the findings of the sensitivity analysis. The primary advantage of south-facing shading is that it reduces a minor portion of the summer cooling load. However, the overhang depth is excessive, increasing the energy used for lighting and winter heating. Furthermore, this approach may have a detrimental impact on the environment due to the considerable CEF value of the shading material, which does not contribute to reducing carbon emissions.
Overall, the results illustrate a balanced approach, where selecting insulation materials, thickness, and window types can be tailored to meet specific objectives, such as minimizing lifecycle carbon emissions, reducing costs, or maintaining high energy efficiency.
5. Conclusions
The present study provides a valuable illustration of the efficacy of automated machine learning, in conjunction with the NSGA-II algorithm, in the domain of multi-criteria decision making for the energy-saving retrofitting of residential buildings. The research results reveal that the utilization of a surrogate model can lead to a substantial reduction in optimization time, facilitating rapid and effective analysis and prediction of the effects of diverse energy-saving renovation strategies and identifying the optimal balance among total energy demand, life-cycle carbon emissions, and cost targets. Among the four machine learning algorithms evaluated, the light gradient boosting machine algorithm emerged as the most efficient and accurate model for predicting building energy performance.
Through the metaheuristic algorithm and entropy-weighted decision-making mechanism, the obtained Pareto front results, compared to the original design of the case study building, which followed the national energy efficiency design code, showed significant improvements in all three objectives after optimization. The optimal solutions reduced energy consumption by 56.62%, carbon emissions by 51.60%, and life-cycle cost by 24.27%. This highlights the necessity of further retrofitting existing buildings that have already met the national energy efficiency standard from both an energy-saving and life-cycle environmental perspective. Compared to the ultra-low-energy building energy standard, all selected optimal solutions significantly reduced energy emissions by 2.60% and the life-cycle cost by 15.85%.
The present study contributes significantly to building energy conservation in two respects: Firstly, it proposes a novel framework that integrates a machine learning surrogate model with a heuristic optimization algorithm and entropy-weighted decision-making mechanism. This novel framework introduces original methodologies for the multi-criteria evaluation process in energy-saving renovation for existing residential buildings. The novel methods simplify the steps of model selection and hyperparameter adjustment, enhancing the prediction model’s accuracy. Secondly, the optimal solution can assist residents in optimizing building energy use, facilitating the transition to fossil fuel alternatives, and reducing dependency on traditional energy sources. From economic and environmental viewpoints, these optimal solutions are highly suitable for future renovation strategies that promote sustainable and cost-effective building performance improvements.
This study also has limitations that are worth noting. As climate change progresses, long-term building renovation strategies must incorporate projections of future climatic conditions to ensure the durability and efficacy of implemented solutions. Rising temperatures, changing weather patterns, and shifting heating and cooling demands necessitate a climate-responsive approach to retrofitting. For example, in future climate scenarios (e.g., 2050 and 2080), indoor thermal comfort will likely become a critical factor in colder regions, necessitating a re-evaluation of existing retrofit standards and the integration of renewable energy systems, such as photovoltaic panels, to achieve net-zero-energy performance while mitigating carbon emissions. Future studies will focus on conducting urban-scale building energy analyses for residential neighborhoods under projected climate conditions. This broader scope will allow for the development of optimized retrofit strategies at both the individual building and community levels, ensuring that renovation efforts align with the evolving needs of urban areas in response to climate change. Such efforts will enhance energy efficiency and improve urban resilience and adaptability to long-term environmental challenges.
Author Contributions
Conceptualization, R.S.; methodology, R.S.; software, W.L.; validation, W.L. and H.T.; formal analysis, W.L. and H.T.; investigation, W.L. and H.T.; resources, W.G.; data curation, W.L. and H.T.; writing—original draft preparation, R.S., W.L. and X.L.; writing—review and editing, R.S., X.L. and W.G.; visualization, W.L. and H.T.; supervision, R.S. and W.G.; project administration, W.G.; funding acquisition, R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Liaoning Provincial Natural Science Foundation Joint Fund, 2023-MSBA-102, and the Northeastern University (China) National Project Incubation Fund (Science and Technology), grant number N2311003.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | Artificial neural network |
| CEF | Carbon emission factor |
| GBM | Gradient boosting machine |
| LCC | Life-cycle cost |
| LCCE | Life-cycle carbon emission |
| LHS | Latin hypercube sampling |
| MAE | Mean absolute error |
| MOEA/D | Multi-Objective Evolutionary Algorithm based on Decomposition |
| MSE | Mean square error |
| MVLR | Multivariate linear regression |
| NSGA-II | Non-dominated sorting genetic algorithm II |
| NSGA-III | Non-dominated sorting genetic algorithm III |
| NZEB | Nearly zero-energy building |
| PCC | Partial correlation coefficient |
| PSO | Particle swarm optimization |
| R2 | Coefficient of determination |
| RF | Random forest |
| RMSE | Root mean square error |
| RSM | Response surface method |
| SA | Sensitivity analysis |
| SHGC | Solar heat gain coefficient |
| SPEA2 | Strength Pareto Evolutionary Algorithm 2 |
| SRRC | Standardized rank regression coefficient |
| SVM | Support vector machine |
| TOPSIS | Technique for Order Preference by Similarity to an Ideal Solution |
| ULB | Ultra-low-energy building |
References
- Christopher, S.; Vikram, M.P.; Bakli, C.; Thakur, A.K.; Ma, Y.; Ma, Z.; Xu, H.; Cuce, P.M.; Cuce, E.; Singh, P. Renewable energy potential towards attainment of net-zero energy buildings status—A critical review. J. Clean. Prod. 2023, 405, 136942. [Google Scholar] [CrossRef]
- Xue, S.; Na, J.; Wang, L.; Wang, S.; Xu, X. The Outlook of Green Building Development in China during the ‘Fourteenth Five-Year Plan’ Period. Int. J. Environ. Res. Public Health 2023, 20, 5122. [Google Scholar] [CrossRef]
- Ma, Z.; Cooper, P.; Daly, D.; Ledo, L. Existing building retrofits: Methodology and state-of-the-art. Energy Build. 2012, 55, 889–902. [Google Scholar] [CrossRef]
- Deb, C.; Schlueter, A. Review of data-driven energy modelling techniques for building retrofit. Renew. Sustain. Energy Rev. 2021, 144, 110990. [Google Scholar] [CrossRef]
- Huang, H.; Mohd Nazi, W.I.B.W.; Yu, Y.; Wang, Y. Energy performance of a high-rise residential building retrofitted to passive building standard—A case study. Appl. Therm. Eng. 2020, 181, 115902. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, Q.; Tian, Z.; He, B.; Jin, G. A comprehensive analysis on definitions, development, and policies of nearly zero energy buildings in China. Renew. Sustain. Energy Rev. 2019, 114, 109314. [Google Scholar] [CrossRef]
- Laouadi, A.; Bartko, M.; Lacasse, M.A. A new methodology of evaluation of overheating in buildings. Energy Build. 2020, 226, 110360. [Google Scholar] [CrossRef]
- Guillén-Lambea, S.; Rodríguez-Soria, B.; Marín, J.M. Review of European ventilation strategies to meet the cooling and heating demands of nearly zero energy buildings (nZEB)/Passivhaus. Comparison with the USA. Renew. Sustain. Energy Rev. 2016, 62, 561–574. [Google Scholar] [CrossRef]
- Yu, J.; Dong, Y.; Zhao, Y.; Yu, Y.; Chen, Y.; Guo, H. Using phase change materials to alleviate overheating phenomenon of residential buildings in severe cold and cold regions of China. Case Stud. Therm. Eng. 2023, 49, 103207. [Google Scholar] [CrossRef]
- Shi, Y.; Chen, P. Energy retrofitting of hospital buildings considering climate change: An approach integrating automated machine learning with NSGA-III for multi-objective optimization. Energy Build. 2024, 319, 114571. [Google Scholar] [CrossRef]
- Babaizadeh, H.; Haghighi, N.; Asadi, S.; Broun, R.; Riley, D. Life cycle assessment of exterior window shadings in residential buildings in different climate zones. Build. Environ. 2015, 90, 168–177. [Google Scholar] [CrossRef]
- Toosi, H.A.; Lavagna, M.; Leonforte, F.; Del Pero, C.; Aste, N. Life Cycle Sustainability Assessment in Building Energy Retrofitting; A Review. Sustain. Cities Soc. 2020, 60, 102248. [Google Scholar] [CrossRef]
- Shan, R.; Junghans, L. Multi-Objective Optimization for High-Performance Building Facade Design: A Systematic Literature Review. Sustainability 2023, 15, 15596. [Google Scholar] [CrossRef]
- Mostafazadeh, F.; Eirdmousa, S.J.; Tavakolan, M. Energy, economic and comfort optimization of building retrofits considering climate change: A simulation-based NSGA-III approach. Energy Build. 2023, 280, 112721. [Google Scholar] [CrossRef]
- Gossard, D.; Lartigue, B.; Thellier, F. Multi-objective optimization of a building envelope for thermal performance using genetic algorithms and artificial neural network. Energy Build. 2013, 67, 253–260. [Google Scholar] [CrossRef]
- Delgarm, N.; Sajadi, B.; Kowsary, F.; Delgarm, S. Multi-objective optimization of the building energy performance: A simulation-based approach by means of particle swarm optimization (PSO). Appl. Energy 2016, 170, 293–303. [Google Scholar] [CrossRef]
- Khoroshiltseva, M.; Slanzi, D.; Poli, I. A Pareto-based multi-objective optimization algorithm to design energy-efficient shading devices. Appl. Energy 2016, 184, 1400–1410. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, L.; Zhang, Q.; Sun, X. Multi-objective optimization of building energy performance using a particle swarm optimizer with less control parameters. J. Build. Eng. 2020, 32, 101505. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Protić, M.; Petrović, N. Multi-objective optimization of energy performance for a detached residential building with a sunspace using the NSGA-II genetic algorithm. Sol. Energy 2021, 224, 1426–1444. [Google Scholar] [CrossRef]
- Zhan, X.; Zhang, W.; Chen, R.; Bai, Y.; Wang, J.; Deng, G. Non-dominated sorting genetic algorithm-II: A multi-objective optimization method for building renovations with half-life cycle and economic costs. Build. Environ. 2025, 267, 112155. [Google Scholar] [CrossRef]
- Carlucci, S.; Cattarin, G.; Causone, F.; Pagliano, L. Multi-objective optimization of a nearly zero-energy building based on thermal and visual discomfort minimization using a non-dominated sorting genetic algorithm (NSGA-II). Energy Build. 2015, 104, 378–394. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, G.; Yan, C.; Wang, G.; Jiang, Y.; Zhao, K. A two-stage multi-objective optimization method for envelope and energy generation systems of primary and secondary school teaching buildings in China. Build. Environ. 2021, 204, 108142. [Google Scholar] [CrossRef]
- Semahi, S.; Zemmouri, N.; Hamdy, M.; Attia, S. Passive envelope design optimization of residential buildings using NSGA-II in different Algerian climatic zones. In Proceedings of the Building Simulation Conference Proceedings, Weimar, Germany, 20–22 September 2022; pp. 1287–1294. [Google Scholar] [CrossRef]
- Rosso, F.; Ciancio, V.; Dell’Olmo, J.; Salata, F. Multi-objective optimization of building retrofit in the Mediterranean climate by means of genetic algorithm application. Energy Build. 2020, 216, 109945. [Google Scholar] [CrossRef]
- Penna, P.; Prada, A.; Cappelletti, F.; Gasparella, A. Multi-objectives optimization of Energy Efficiency Measures in existing buildings. Energy Build. 2015, 95, 57–69. [Google Scholar] [CrossRef]
- Wang, M.; Chen, C.; Fan, B.; Yin, Z.; Li, W.; Wang, H.; Chi, F.A. Multi-Objective Optimization of Envelope Design of Rural Tourism Buildings in Southeastern Coastal Areas of China Based on NSGA-II Algorithm and Entropy-Based TOPSIS Method. Sustainability 2023, 15, 7238. [Google Scholar] [CrossRef]
- Costa-Carrapiço, I.; Raslan, R.; González, J.N. A systematic review of genetic algorithm-based multi-objective optimisation for building retrofitting strategies towards energy efficiency. Energy Build. 2020, 210, 109690. [Google Scholar] [CrossRef]
- Ardabili, S.; Abdolalizadeh, L.; Mako, C.; Torok, B.; Mosavi, A. Systematic Review of Deep Learning and Machine Learning for Building Energy. Front. Energy Res. 2022, 10, 786027. [Google Scholar] [CrossRef]
- Roman, N.D.; Bre, F.; Fachinotti, V.D.; Lamberts, R. Application and characterization of metamodels based on artificial neural networks for building performance simulation: A systematic review. Energy Build. 2020, 217, 109972. [Google Scholar] [CrossRef]
- Bre, F.; Roman, N.; Fachinotti, V.D. An efficient metamodel-based method to carry out multi-objective building performance optimizations. Energy Build. 2020, 206, 109576. [Google Scholar] [CrossRef]
- Chen, J.; Gao, X.; Hu, Y.; Zeng, Z.; Liu, Y. A meta-model-based optimization approach for fast and reliable calibration of building energy models. Energy 2019, 188, 116046. [Google Scholar] [CrossRef]
- Prada, A.; Gasparella, A.; Baggio, P. On the performance of meta-models in building design optimization. Appl. Energy 2018, 225, 814–826. [Google Scholar] [CrossRef]
- Bagheri-Esfeh, H.; Dehghan, M.R. Multi-objective optimization of setpoint temperature of thermostats in residential buildings. Energy Build. 2022, 261, 111955. [Google Scholar] [CrossRef]
- Etemad, A.; Shafaat, A.; Bahman, A.M. Data-driven performance analysis of a residential building applying artificial neural network (ANN) and multi-objective genetic algorithm (GA). Build. Environ. 2022, 225, 109633. [Google Scholar] [CrossRef]
- Huo, H.; Deng, X.; Wei, Y.; Liu, Z.; Liu, M.; Tang, L. Optimization of energy-saving renovation technology for existing buildings in a hot summer and cold winter area. J. Build. Eng. 2024, 86, 108597. [Google Scholar] [CrossRef]
- Chegari, B.; Tabaa, M.; Simeu, E.; Moutaouakkil, F.; Medromi, H. Multi-objective optimization of building energy performance and indoor thermal comfort by combining artificial neural networks and metaheuristic algorithms. Energy Build. 2021, 239, 110839. [Google Scholar] [CrossRef]
- Li, K.; Pan, L.; Xue, W.; Jiang, H.; Mao, H. Multi-Objective Optimization for Energy Performance Improvement of Residential Buildings: A Comparative Study. Energies 2017, 10, 245. [Google Scholar] [CrossRef]
- Chegari, B.; Tabaa, M.; Simeu, E.; Moutaouakkil, F.; Medromi, H. An optimal surrogate-model-based approach to support comfortable and nearly zero energy buildings design. Energy 2022, 248, 123584. [Google Scholar] [CrossRef]
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Ayoub, M. A multivariate regression to predict daylighting and energy consumption of residential buildings within hybrid settlements in hot-desert climates. Indoor Built Environ. 2018, 28, 848–866. [Google Scholar] [CrossRef]
- Smarra, F.; Jain, A.; De Rubeis, T.; Ambrosini, D.; D’Innocenzo, A.; Mangharam, R. Data-driven model predictive control using random forests for building energy optimization and climate control. Appl. Energy 2018, 226, 1252–1272. [Google Scholar] [CrossRef]
- Batra, R.; Arora, S.; Sharma, M.M.; Rana, S.; Raheja, K.; Saber, A.; Shah, M.A. Integration of LSTM networks with gradient boosting machines (GBM) for assessing heating and cooling load requirements in building energy efficiency. Energy Explor. Exploit. 2024, 42, 2191–2217. [Google Scholar] [CrossRef]
- Srivastav, A.; Tewari, A.; Dong, B. Baseline building energy modeling and localized uncertainty quantification using Gaussian mixture models. Energy Build. 2013, 65, 438–447. [Google Scholar] [CrossRef]
- Arjomandnia, R.; Ilbeigi, M.; Kazemidemneh, M.; Hashemi, A.N. Renovating buildings by modelling energy—CO2 emissions using particle swarm optimization and artificial neural network (case study: Iran). Indoor Built Environ. 2023, 32, 1621–1637. [Google Scholar] [CrossRef]
- Panagiotidou, M.; Aye, L.; Rismanchi, B. Optimisation of multi-residential building retrofit, cost-optimal and net-zero emission targets. Energy Build. 2021, 252, 111385. [Google Scholar] [CrossRef]
- Xue, Q.; Wang, Z.; Chen, Q. Multi-objective optimization of building design for life cycle cost and CO2 emissions: A case study of a low-energy residential building in a severe cold climate. Build. Simul. 2022, 15, 83–98. [Google Scholar] [CrossRef]
- Jung, Y.; Heo, Y.; Lee, H. Multi-objective optimization of the multi-story residential building with passive design strategy in South Korea. Build. Environ. 2021, 203, 108061. [Google Scholar] [CrossRef]
- Chang, S.; Castro-Lacouture, D.; Yamagata, Y. Decision support for retrofitting building envelopes using multi-objective optimization under uncertainties. J. Build. Eng. 2020, 32, 101413. [Google Scholar] [CrossRef]
- Kheiri, F. A review on optimization methods applied in energy-efficient building geometry and envelope design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- GB 50176-2016; Code for Thermal Design of Civil Building. China Architecture & Building Press Beijing: Beijing, China, 2016.
- JGJ 26-2018; Design Standard for Energy Efficiency of Residential Buildings in Severe Cold and Cold Zones. China Architecture & Building Press Beijing: Beijing, China, 2018.
- GB/T 51366-2019; Standard for Building Carbon Emission Calculation. China Architecture & Building Press Beijing: Beijing, China, 2019.
- Pang, Z.; O’Neill, Z.; Li, Y.; Niu, F. The role of sensitivity analysis in the building performance analysis: A critical review. Energy Build. 2020, 209, 109659. [Google Scholar] [CrossRef]
- Wei, T. A review of sensitivity analysis methods in building energy analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
- Gao, Y.; Luo, S.; Jiang, J.; Rong, Y. Environmental-thermal-economic performance trade-off for rural residence retrofitting in the Beijing–Tianjin–Hebei region, Northern China: A multi-objective optimisation framework under different scenarios. Energy Build. 2023, 286, 112910. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Jankowski, R. Machine learning-based seismic fragility and seismic vulnerability assessment of reinforced concrete structures. Soil Dyn. Earthq. Eng. 2023, 166, 107761. [Google Scholar] [CrossRef]
- Loh, W.L. On Latin Hypercube Sampling. Ann. Stat. 1996, 24, 2058–2080. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef]
- Wu, C.; Pan, H.; Luo, Z.; Liu, C.; Huang, H. Multi-objective optimization of residential building energy consumption, daylighting, and thermal comfort based on BO-XGBoost-NSGA-II. Build. Environ. 2024, 254, 111386. [Google Scholar] [CrossRef]
- Markarian, E.; Qiblawi, S.; Krishnan, S.; Divakaran, A.; Ramalingam, R.O.; Thomas, A.; Azar, E. Informing building retrofits at low computational costs: A multi-objective optimisation using machine learning surrogates of building performance simulation models. J. Build. Perform. Simul. 2024, 1–17. [Google Scholar] [CrossRef]
- Wang, R.; Lu, S.; Feng, W. A three-stage optimization methodology for envelope design of passive house considering energy demand, thermal comfort and cost. Energy 2020, 192, 116723. [Google Scholar] [CrossRef]
- de Weck, O.; Agte, J.; Sobieszczanski-Sobieski, J.; Arendsen, P.; Morris, A.; Spieck, M. State-of-the-art and future trends in multidisciplinary design optimization. In Proceedings of the 48th Aiaa/Asme/Asce/Ahs/Asc Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; Volume 3, pp. 2467–2487. [Google Scholar] [CrossRef]
- Machairas, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for optimization of building design: A review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Song, J.; Wang, W.; Ni, P.; Zheng, H.; Zhang, Z.; Zhou, Y. Framework on low-carbon retrofit of rural residential buildings in arid areas of northwest China: A case study of Turpan residential buildings. Build. Simul. 2023, 16, 279–297. [Google Scholar] [CrossRef]
- Amorocho, J.A.P.; Hartmann, T. A multi-criteria decision-making framework for residential building renovation using pairwise comparison and TOPSIS methods. J. Build. Eng. 2022, 53, 104596. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Wang, X.J. Research on green renovations of existing public buildings based on a cloud model –TOPSIS method. J. Build. Eng. 2021, 34, 101930. [Google Scholar] [CrossRef]
- Zhou, J.; Xiahou, T.; Liu, Y. Multi-objective optimization-based TOPSIS method for sustainable product design under epistemic uncertainty. Appl. Soft Comput. 2021, 98, 106850. [Google Scholar] [CrossRef]
- Wu, Z.; Ding, Y.; Zhang, N.; Gong, X.; Luo, X.; Jin, Y. Feasibility analysis of retrofitting existing residential towards the EnerPHit standard in HSCW zone: A case study in Guilin, China. Energy Build. 2023, 298, 113554. [Google Scholar] [CrossRef]
- Chen, S.; Levine, M.D.; Li, H.; Yowargana, P.; Xie, L. Measured air tightness performance of residential buildings in North China and its influence on district space heating energy use. Energy Build. 2012, 51, 157–164. [Google Scholar] [CrossRef]
- Garrett, A.; New, J.R. Suitability of ASHRAE Guideline 14 Metrics for Calibration; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2016. [Google Scholar]
- DB2101/T 0048-2022; Design Standard or Energy Efficiency of Local Ultra-Low Residential Buildings. Shenyang Urban and Rural Construction Bureau: Shenyang, China, 2022.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).