Numerical Analysis of Friction Reduction of Grouting in Long-Distance Pipe Jacking

Abstract

During pipe jacking construction, in addition to overcoming the resistance at the front, there is also the need to overcome significant frictional resistance. Grouting technology is commonly used in engineering to reduce the frictional resistance exerted on the pipe’s external surface during the jacking process. This paper first reviews the commonly used grouting materials and processes, summarizes their mechanisms for friction reduction, and then establishes a numerical analysis model for grouting in pipe jacking, enhancing the common theoretical methods based on simulation results. The study employs different interface reduction coefficients to simulate the different effects of friction reduction by grouting, focuses on the impact of grouting on friction reduction during long pipe jacking, and compares the results with those calculated using common methods. The results show that the frictional resistance around the pipe is the main source of jacking force in long-distance pipe jacking, and the jacking force increases approximately linearly with the interface reduction coefficient.

1. Introduction

The pipe jacking method is a trenchless underground pipeline installation technique, with advantages, such as a short construction period and minimal environmental impact, leading to significant economic benefits [1]. In recent years, with increasing engineering demands, pipe jacking construction has been evolving towards larger diameters and longer distances. In long-distance pipe jacking, the jacking force is one of the key parameters for the selection of pipe segments, the jacking machine, and the working shaft [2]. Typically, the jacking force comes from the front resistance and the frictional resistance. As the jacking distance increases, the frictional resistance around the pipe also increases, thus increasing the required jacking force [3], particularly in ultra-long-distance pipe jacking [4]. If a precise calculation of the jacking force can be achieved, it will significantly contribute to practical engineering applications.

Currently, many scholars have conducted extensive research on grouting for friction reduction in pipe jacking. In terms of the slurry materials and interaction between slurry and soil, Wei et al. [5] and Namli and Guler [6] analyzed the properties of a thixotropic slurry, the grouting mechanism, and the use of a bentonite slurry to reduce the jacking resistance. Huang et al. [7] conducted experiments showing that the slurry can reduce the friction resistance in saturated sandy soil to 63.1%. Yu et al. [8] analyzed the relationship between the microscopic structure of slurry and friction resistance through laboratory tests, finding that friction resistance increases with time.

The effectiveness of grouting lubrication in pipe jacking largely depends on the selected grouting material. Currently, commonly used grouting materials include a bentonite slurry, cement grout, polymers, and composite slurries. Bentonite slurry is composed of bentonite, CMC (carboxymethyl cellulose), soda ash, and water, characterized by its swelling and thixotropic properties. Bentonite primarily consists of potassium, calcium, and sodium, montmorillonite, with a typical concentration of approximately 5%. When mixed with water and stirred, bentonite forms a suspension. When static, the montmorillonite particles transition from a dispersed state to a gel structure. Upon agitation, the particle structure is disrupted and redistributes, forming a viscous and flowable colloidal liquid. Once the suspension is stationary again, the gel structure re-forms, a property known as thixotropy. Due to its low cost and excellent performance, the bentonite slurry is the preferred material for pipe jacking projects. Cement grout is one of the most basic and commonly used materials in pipe jacking grouting. It has good flowability and strength, enabling it to form a solid structure during the grouting process, effectively reinforcing the soil layer, and improving the bearing capacity and stability of the soil. Polymers primarily consist of materials, such as an epoxy resin slurry and polyurethane slurry and are highly suitable for engineering projects that require excellent reinforcement effects, impermeability, and high durability. The composite slurry mainly includes a cement–sodium silicate slurry and cement–sodium silicate–fly ash slurry. It has a short settling time and high early strength, along with strong fluidity at the beginning, making it suitable for soil layers that require rapid reinforcement and projects with high environmental protection requirements.

In terms of the application of grout in friction reduction for pipe jacking, Zhou et al. [9] studied the variation pattern of the jacking force under grouting conditions in silty strata through model tests. The tests showed that the viscosity and condensation force of the slurry play a major role in reducing the friction resistance and surface settlement. As the slurry settles or consolidates, the liquid phase (usually water) starts to drain or evaporate, causing the solid particles to come closer together. This process results in an increase in density and the development of internal forces within the slurry. These forces can influence the stability, pressure distribution, and overall performance of the slurry in its application. Wang et al. [10] conducted detailed research and discussion on the slurry scheme for large-diameter, long-distance pipe jacking based on the construction of the Hong Kong–Zhuhai–Macau Bridge tunnel at the Gongbei site. Through the research, the engineers significantly reduced the friction resistance in practical engineering and solved the problem of excessive jacking force.

The grouting process is as follows. At the beginning of the grouting, we need to pressurize first, then jack. During the process, we need to pressurize and jack simultaneously and regrout timely. An appropriate amount of friction-reducing slurry is injected into the outer wall of the pipe section through the grouting annular pipe. By using a multi-point symmetrical grouting method, the slurry can be evenly distributed in the gap between the outer wall of the pipe section and the surrounding soil, thereby reducing the friction resistance between the pipe section and the soil and lowering the jacking force.

The main technical parameters of grouting are as follows:

(1)

Grouting Volume: This parameter quantifies the relationship between the pipe jacking length and the thickness of the grout layer. By dynamically monitoring the grouting volume, jacking length, and grout layer thickness, the actual friction-reducing effect of the grouting can be evaluated.

(2)

Grouting Pressure: During the grouting process, it is essential to strictly control the grouting pressure. On the one hand, if the pressure is too low, the grouting effect may not be achieved. On the other hand, if the pressure is too high, it may fail to form an effective grout layer and could cause grout leakage (overflow).

(3)

Grouting Speed: The grouting speed is influenced and controlled by several factors, including the arrangement of the grouting holes, the formation of the slurry sleeve, and the jacking speed.

There are generally two methods for grouting in long-distance pipe jacking:

(1)

Double-layer Grouting Method: The double-layer grouting method effectively reduces friction resistance by forming a protective layer between the slurry and the surrounding soil. This method first injects a consolidation grout behind the jacking head. As the jacking head and pipe advance, the consolidation grout gradually hardens to form a solid shell. Then, an expansion device compresses the consolidation grout, forming a strong protective layer. Finally, grout is injected into the gap between this protective layer and the pipe to ensure the integrity of the grout sheath. This method requires two types of slurry to be stored and injected separately, with consolidation grout primarily used for support and lubrication and supplementary grout used for further lubrication [11].

(2)

Pipe Membrane Pushing Method: This method installs a pipe with a plastic membrane inside at the rear of the tunneling machine. During the jacking process, the plastic membrane is continuously drawn out from the pipe, and grout is injected between the membrane and the pipe to facilitate pipe sliding, avoiding uneven grouting and grout leakage.

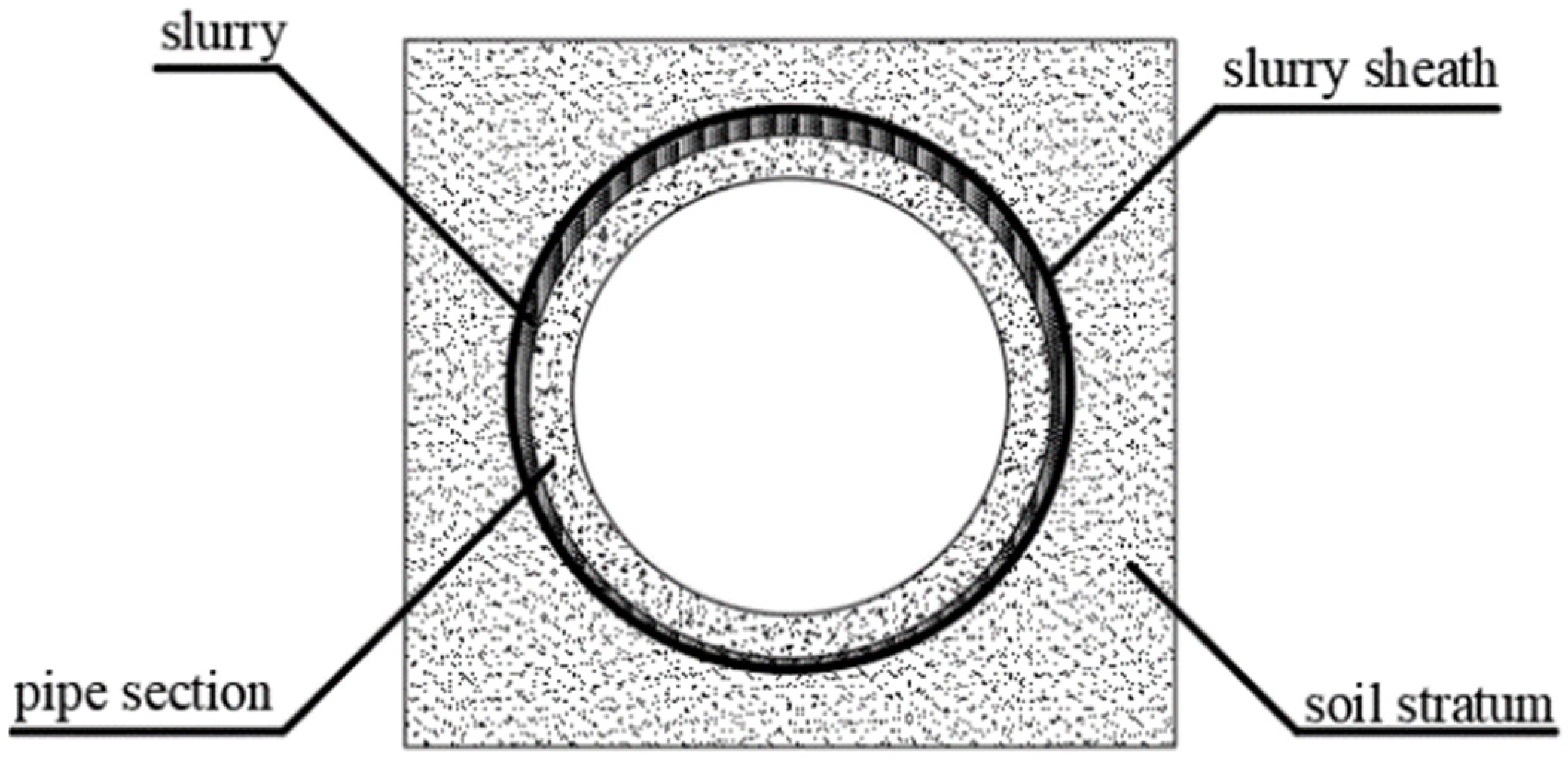
Regardless of the grouting material or method used, the similar grouting-friction-reduction processes work as follows: after the grout comes into contact with the soil, the grouting pressure causes the free water in the grout to permeate into the cracks of the surrounding soil, leading to water loss in the grout [12]. As the permeation process continues, the grout gradually transforms into a gel-like substance, filling the voids in the soil. During this permeation process, a dense permeation layer forms between the grout and the soil, causing the solid particles in the grout to adhere to this layer, forming a low-permeability slurry sheath. This reduces water loss from the grout. The combined structure of the slurry and the permeation layer is referred to as the grout sheath [12], as shown in Figure 1.

The grout sheath transmits the liquid pressure, which exceeds the underground water pressure to the soil particles, and the effective stress generated by this process compacts the soil. Meanwhile, the hydraulic pressure of the grout also supports the borehole wall, maintaining its stability and preventing collapse.

Therefore, the mechanism of grouting mainly involves two aspects: on one hand, the grout provides lubrication between the pipe and the surrounding soil, thereby reducing the frictional resistance during the jacking process; on the other hand, grouting fills the gaps between the pipe and the soil, and the grouting pressure supports the soil, reducing its deformation, thus enhancing the stability of the soil.

In the calculation of jacking force considering grout friction reduction, the most common method is presented in Section 2 [13]. This method assumes that the circumferential friction of the pipe is uniformly distributed and uses an imprecise range of average unit frictional resistance between the pipe’s outer surface and the soil to account for the friction reduction. This method cannot consider the depth at which the pipe is buried, which is a significant parameter that influences the friction values. To address these limitations, some scholars have proposed new methods to enhance the accuracy. Li et al. [14] derived a calculation formula for the additional stress in soil caused by grouting pressure under self-weight conditions based on Terzaghi’s theory of earth pressure. Wang et al. [15] proposed a method to determine the three common slurry ring shapes for a circular pipe and introduced a segmental method to calculate the corresponding friction resistance.

However, in practice, the distribution of friction resistance around the pipe is continuous and more complex, which can affect the calculation results, especially in the analysis of friction resistance for ultra-long pipe jacking, leading to non-negligible errors. The friction is influenced not only by the grouting, but also by the depth. It is necessary to improve the common method through a numerical analysis, especially by accounting for both the grouting and the depth at which the pipe is buried.

This paper first presents the common theoretical calculation method adopted in China. Then, finite element analysis is employed to simulate the jacking force in long-distance pipe jacking, obtaining the jacking force values under different interface friction angles to simulate the effect of the grouting. The common theoretical method about the friction resistance is improved based on the simulation results to take into account both the grouting and the depth. The improved theoretical method evaluates the friction by calculating interface friction angles through the friction-reduction effect of grouting and normal stress distribution. The numerical and improved theoretical results are compared with the common method that assumes an imprecise range of average unit frictional resistance.

2. Theoretical Calculation Methods for the Jacking Force

During the pipe jacking processes, the axial loads primarily include the front resistance of the pipe and the frictional resistance between the pipe and the surrounding soil. The frictional resistance around the pipe is influenced by the soil characteristics, contact conditions, and properties of the grout, which are reflected by the interface friction angle. The forces acting on the pipe are illustrated in Figure 2.

Based on the axial force equilibrium, the total jacking force required can be expressed as

$$F=P_A+P_f$$

(1)

$P_A$ represents the front resistance, which is influenced by factors, such as the soil type, excavation depth, and support pressure.

$P_f$ represents the frictional resistance, which is the circumferential resistance generated by the interaction between the pipe and the surrounding soil.

2.1. The Front Resistance

According to the regulation of China [13], the front resistance can be calculated as

$$P_A={\displaystyle \frac{\pi }{4}}{D}_g^2{\gamma }_s(H_s+D_g)$$

(2)

In the formula,

$D_g$ is the outer diameter of the pipe jacking (m);

${\gamma }_s$ is the unit weight of the soil (kN/m³);

$H_s$ is the thickness of the overlying stratum (m).

2.2. The Friction Resistance

When the circumferential friction of the pipe is uniformly distributed, it can be calculated using Equation (3) according to the regulation of China [13]:

$$P_f=\pi D_{1}L{f}_k$$

(3)

In the formula,

$D_1$ is the outer diameter of the pipe (m);

$L$ is the jacking length of the pipe (m);

$f_k$ is the average unit frictional resistance between the pipe’s outer surface and the soil (kN/m²). The specific values are shown in

Table 1. Average frictional resistance between the pipe and soil for thixotropic grout (kN/m²).

Soil Type	Soft Clay	Silt	Silty Fine Soil	Medium-to-Coarse Sand
Reinforced Concrete Pipe	3.0~5.0	5.0~8.0	8.0~11.0	11.0~16.0
Steel Pipe	2.0~4.0	4.0~7.0	7.0~10.0	10.0~13.0

[13].

3. Case Study

3.1. Example Verification

To ensure the reliability of the proposed numerical model, example verification was performed using a case provided in the article by Cao et al. [16].

The details of the case are provided in the article [16]. The method of processing the numerical simulation is similar to the subsequent simulation process. However, there are two main differences: the length of the pipe is 100 m in this example verification, which is significantly shorter than the following simulation; the bottom burial depth is 9.6 m, which is significantly shallower than the following simulation. The partial results are illustrated in Figure 3 and Figure 4. According to the statistics in the article [16], the soil stratum through which the pipe traverses is silty clay. As shown in Table 1, the average frictional resistance ranges between 5 kN/m and 8 kN/m; these values are used to calculate the theoretical results, determining the minimum and maximum values. Similarly, according to

Table 2. Interface reduction coefficients between the pipe and the surrounding soil.

Soil Type	Wet	Dry
Clay, Silty Clay	0.2~0.3	0.4~0.5
Sand, Silty Sand	0.3~0.4	0.5~0.6

[17], the interface friction angle ranges from 0.2 to 0.3; these two values are used to calculate the numerical results, determining their corresponding minimum and maximum values.

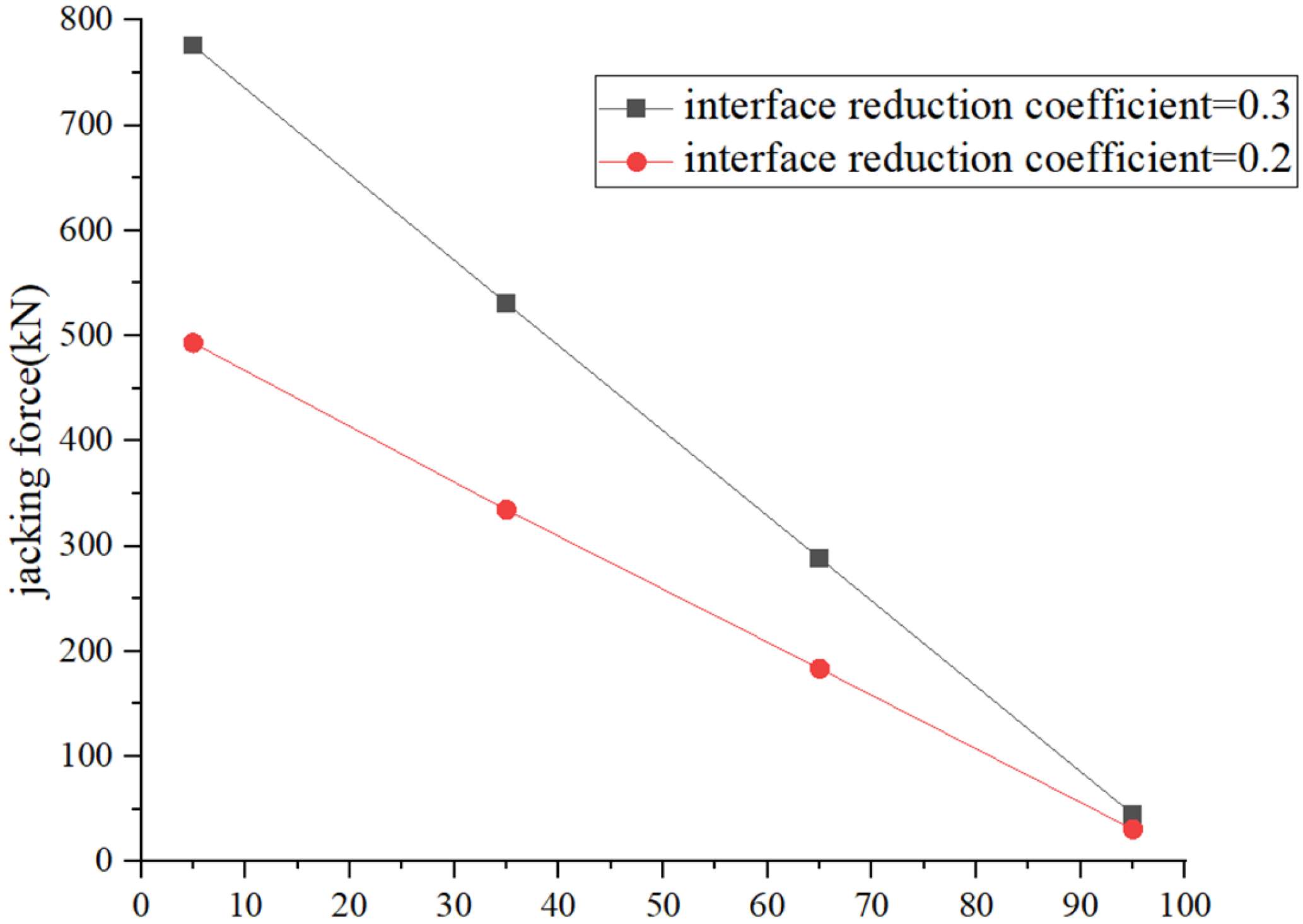
The interface reduction coefficient is set to 0.2 in Figure 3. The numerical result of the distribution is approximately circular and conforms to prevalent viewpoints [18] and Chinese regulations [13]. The distribution of axial force under different reduction coefficients is shown in Figure 4. It can be observed that as the distance from the launch shaft increases, the jacking force decreases approximately linearly, indicating that the distribution of shear stress along the pipe is relatively uniform. Additionally, the jacking force increases by approximately 1.5 times when the interface reduction coefficient is increased by the same factor, which aligns with common sense.

From

Table 3. Contrast between three results.

Calculation Results	Average Frictional Resistance	Interface Reduction Coefficient	Results
Numerical Results	Not used	0.2 and 0.3	5442 kN and 8610 kN
Theoretical Results	5 kN/m and 8 kN/m	Not used	5498 kN and 8796 kN
Field-measured results	7 kN/m	Not used	8000 kN

, the numerical results are compared with the theoretical results introduced in Section 2 and the field-measured results provided in the referenced article. It can be observed that the numerical results closely align with the theoretical results, and the field-measured results fall within both ranges.

From the above example, the numerical results presented below were validated for reliability and trustworthiness. It should be noted that the main differences between the example verification and the subsequent simulation are the length and the depth of the pipe. If the length is significantly increased or the depth is considerably deeper, the theoretical results may lead to significant errors.

3.2. Overview of the Numerical Model

In an electric utility corridor project located in a soft soil area, “F”-type steel reinforced concrete pipes with an outer diameter of 3600 mm and an inner diameter of 3000 mm are planned for use. “F”-type-steel-reinforced concrete pipes are named after the F-type joint that they use. Due to their excellent sealing performance and durability, they are widely used in urban engineering projects [19] as shown in Figure 5. Each pipe section is 2.5 m in length, with a total jacking length of 625 m. The soil layer of the pipe consists of silty clay.

The finite element software PLAXIS 3D (Edition 2017) is used for the calculation. Considering that the impact range of the tunnel construction is 3 to 5 times the larger value between the height and width of the tunnel section, the model’s soil domain is set to a height of 43.6 m (the depth is a boundary between two strata) and a width of 60 m to eliminate boundary effects. The ten-node elements are set. In order to consider the different effect of the grout, the interface reduction coefficients are set to different values.

3.3. Soil Parameter Settings

The soil adopts the Mohr–Coulomb model with a “drained” condition. The groundwater level is located 11 m below the ground surface. The basic parameters of the soil layers are shown in

Table 4. Basic parameters of the soil.

Soil Layer	Thickness/m	Unit Weight (Unsaturation)/ kN·m−3	Unit Weight (Saturation)/ kN·m−3	Elastic Modulus /MPa	Poisson’s Ratio	Internal Friction Angle/°	Cohesion/kPa
Fill Soil	10.2	18.71	19.37	17.52	0.2	15.3	30.6
Silty Clay	1.9	18.57	19.11	14.13	0.3	14.5	26.9
Silty Clay	1.2	18.70	19.30	16.59	0.3	15.5	35.7
clay	2.3	18.77	19.20	21.33	0.35	12.1	43.7
Silty Clay	3.6	18.77	19.50	18.60	0.3	16.7	35.2
Silty Clay	3.4	18.96	19.60	22.14	0.3	16.2	37.5
Silty Clay	3.6	19.16	19.70	23.91	0.3	17.2	37.2
clay	8.2	19.12	19.60	27.96	0.35	14.2	49.7
Silty Clay	3.7	19.40	20.00	29.10	0.3	17.7	38.4
clay	5.5	19.48	19.80	33.51	0.35	14.7	54.4

. The soil model is shown in Figure 6.

3.4. Structure Parameter Settings

The pipe is modeled using linear elastic plate elements. The outer diameter is 3600 mm, the inner diameter is 3000 mm, and the longitudinal length is 625 m. The bottom burial depth is 24.4 m. The structure model is shown in Figure 7.

The unit weight of the pipe (γ) is 24.5 kN/m³, and the thickness is 0.3 m. In order to consider the effect of the grouting, the interface between the pipe and the surrounding soil is set. Typically, the range of the interface reduction coefficient between the pipe and the surrounding soil is listed in Table 2 [17].

Different interface reduction coefficients are set on the interface to simulate different effects of grouting. The relationship between the interface friction angle and the internal friction angle can be calculated as

$${tan\phi }_{inter}=tan\phi \times R_{inter}$$

(4)

In the formula,

${\phi }_{inter}$ is the interface friction angle;

$\phi$ is the internal friction angle;

$R_{inter}$ is interface reduction coefficient;

In this case, the strata through which the pipe traverses consist of silty clay, and the groundwater level is located 11 m below the ground surface, resulting in wet soil conditions. According to Table 2, the Interface reduction coefficients between the pipe and the surrounding soil should be set within the range of 0.2 to 0.3. However, the friction-reduction effect of grouting may not be effective in long-distance pipe jacking. To address potential issues and ensure the safety of practical engineering applications, additional considerations may be required. Therefore, six interface reduction coefficients are set separately by 0.2, 0.24, 0.28, 0.32, 0.36, and 0.4.

To simulate the pressure exerted by the soil on the front surface of the pipe, a force perpendicular to the surface is applied. The magnitude of this force increases along the vertical direction to reflect the rise in the lateral soil pressure with depth.

3.5. Mesh and Phases Settings

The element mesh density is medium. The first phase is the initial phase, the soil elements outside the pipe interior, plate elements, the force implied on the front surface, interface elements are activated, and the calculation type is the $K_0$ procedure. The equilibrium of the forces is not guaranteed, and thus, the second phase is set without any change in the model only to consider the force equilibrium with the “plasticity” calculation mode. There are three modes to select, namely “plasticity”, “consolidation”, and “safety”. The plasticity mode considers an elastoplastic drained or undrained analysis, without considering consolidation. The consolidation mode considers a time-dependent analysis of deformation and excess pore pressure. The safety mode calculates the overall safety factor using the strength-reduction method. The simulation does not consider the effect of the pore pressure and the strength-reduction method; thus, the first mode is selected. In order to exert the frictional resistance, a 10 cm displacement along the longitudinal direction of the whole pipe is applied in the third phase.

3.6. Results Analysis

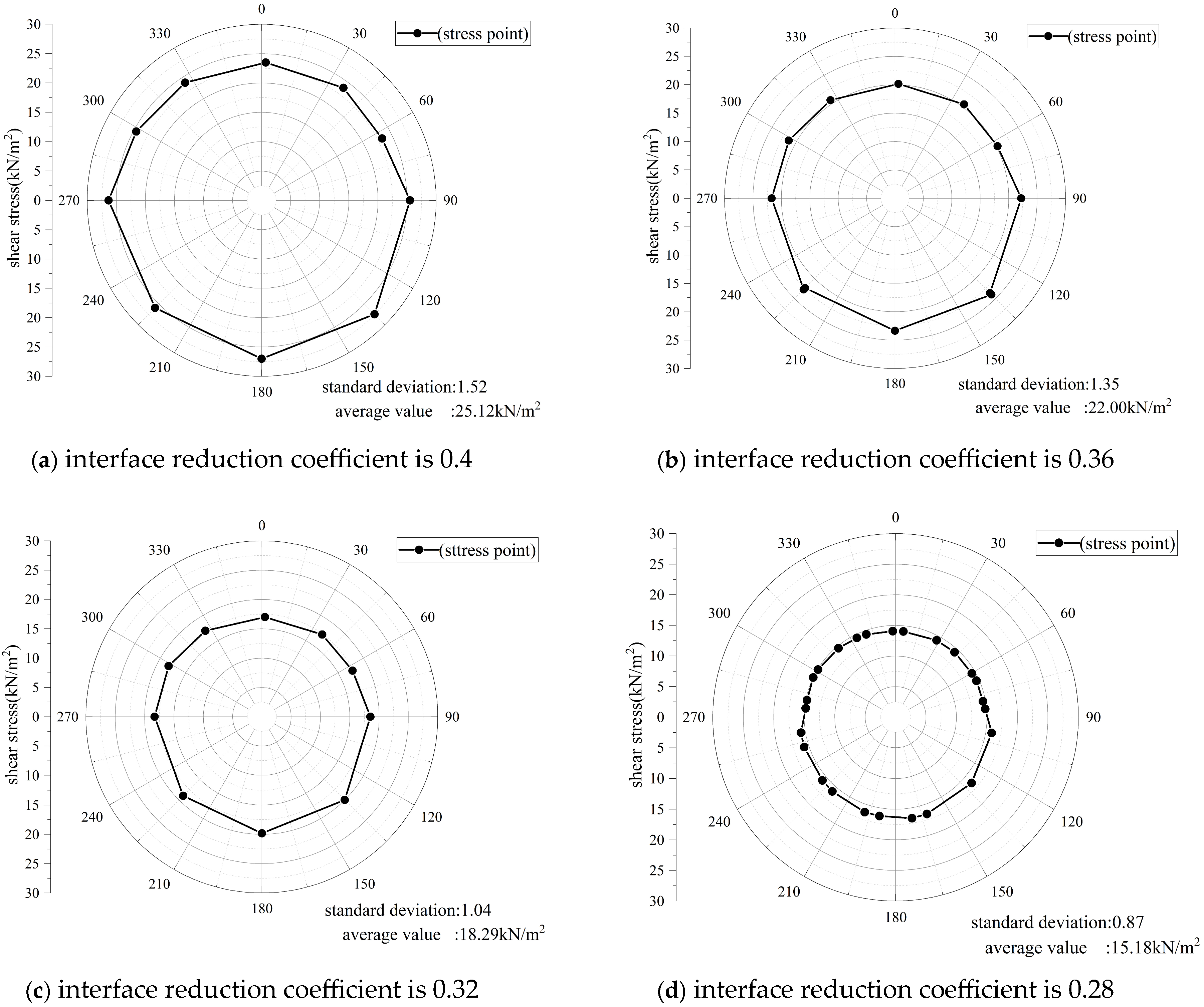
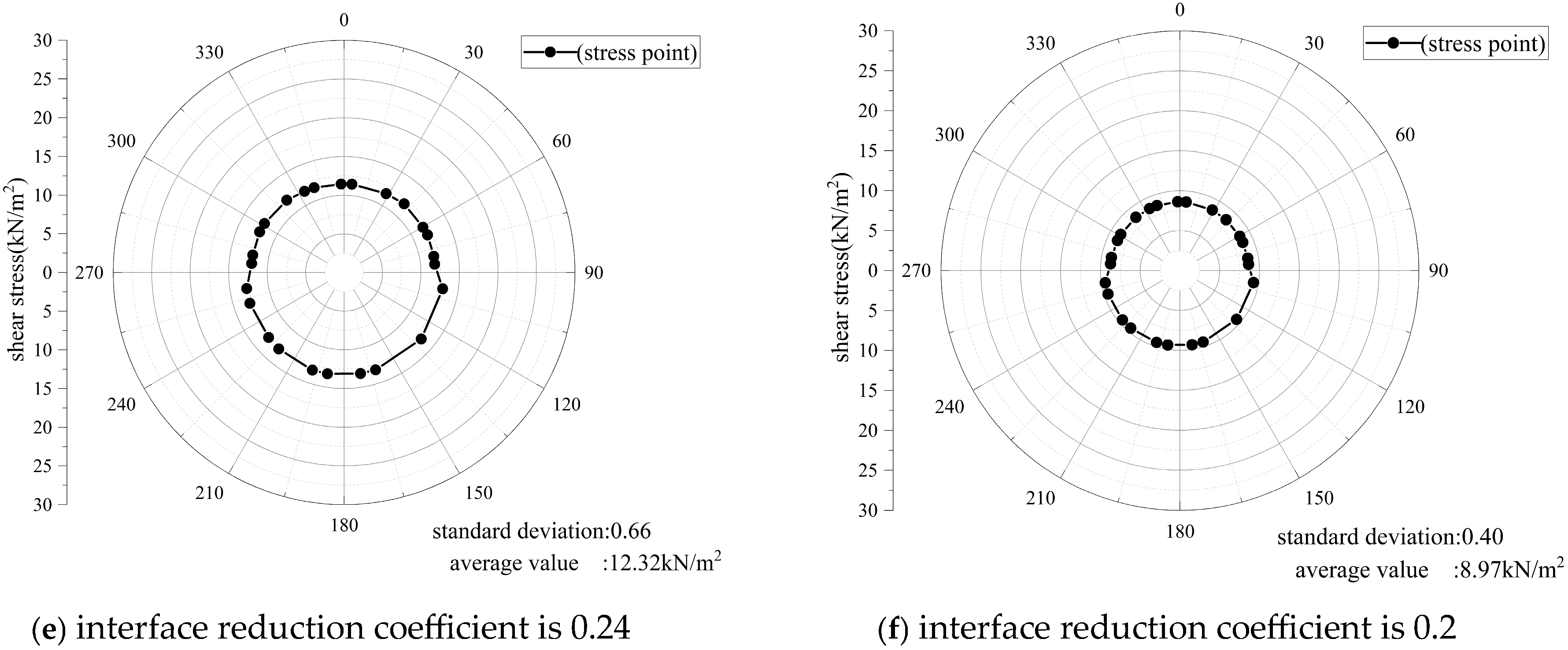
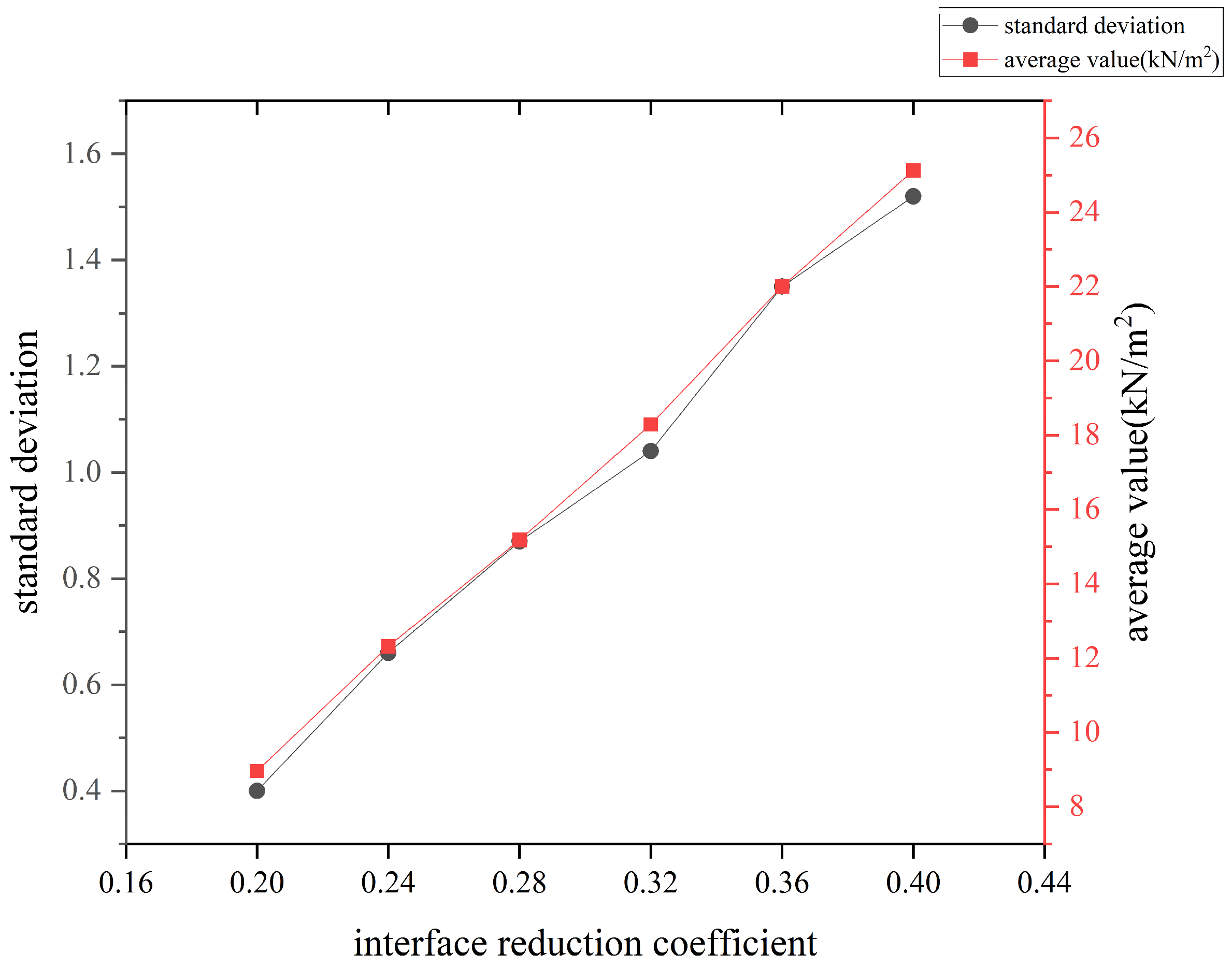
Figure 8 shows the distribution of sectional frictional resistance at the same position (100 m from the launch shaft) under different interface reduction coefficients. Figure 9 illustrates the variation in the standard deviation and average value with respect to different interface reduction coefficients. It can be observed that as the coefficient increases in the range of 0.2 to 0.4, the average frictional resistance around the pipe increases approximately linearly, and the value of the standard deviation of the stress points around the pipe also increases linearly. This reveals that as the interface reduction coefficient increases, the distribution of the stress around the pipe becomes more uneven. Thus, if the interface friction angle is sufficiently large, the variation in shear stress across the same section should be considered.

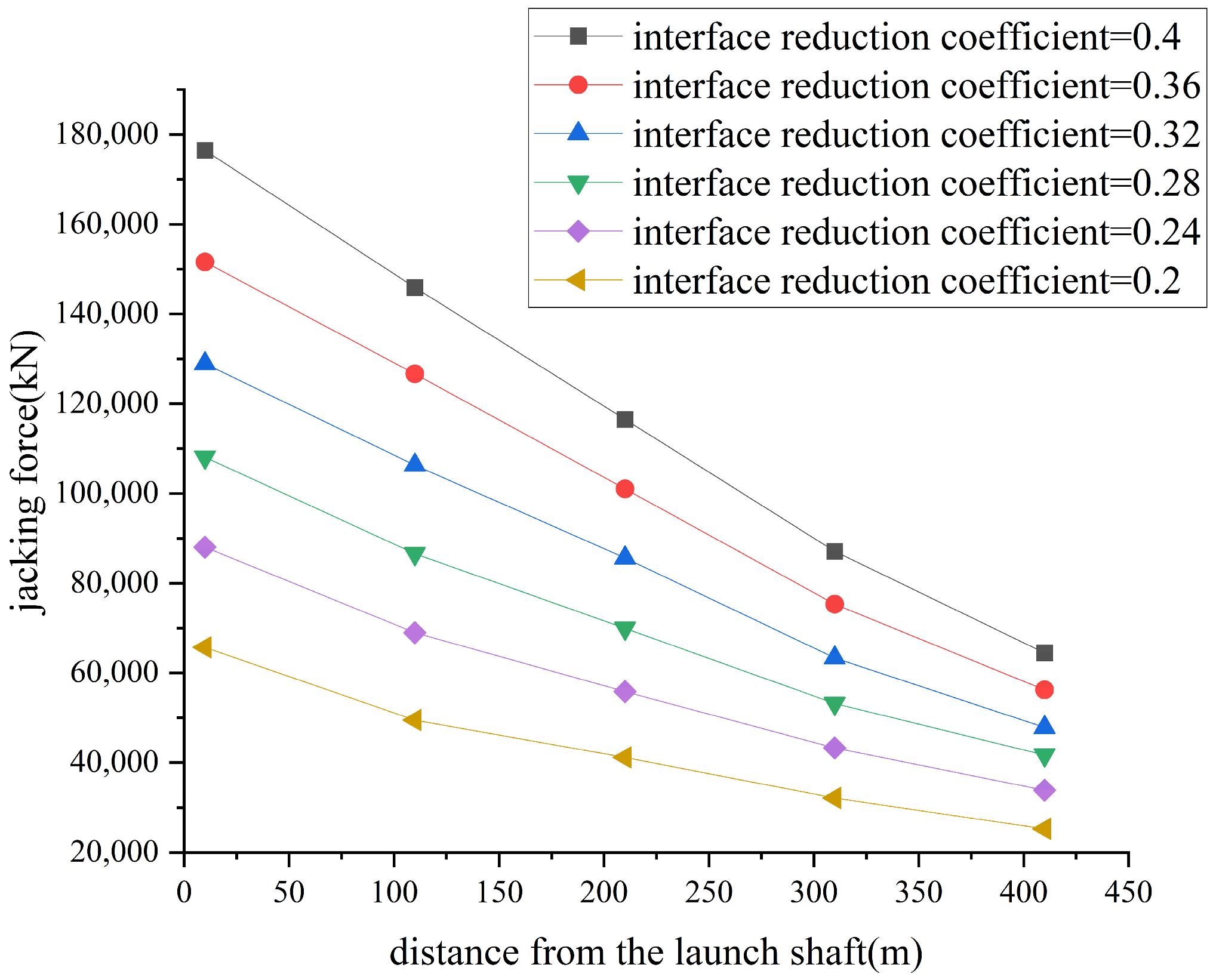
Figure 10 shows the axial jacking force along the length of the pipe under different interface reduction coefficients. It can be observed that as the distance from the launch shaft increases, the reduction in the jacking force slows down, indicating a slight decrease in the frictional resistance around the pipe. The reason may be the difference in displacement between the pipe and the surrounding soil. There should be sufficient relative distance to develop frictional resistance. Since the pipe is not modeled as rigid, the displacement near the launch shaft is greater than that at the pipe’s end, reducing the frictional resistance at the end.

The theoretical and numerical results of the jacking force are summarized in Figure 11. Regarding the numerical results, as the interface friction angle increases, the total jacking force of the pipe increases approximately linearly. It can be inferred that in long-distance pipe jacking projects, the proportion of front resistance is very small, and the main resistance originates from the frictional resistance between the pipe and the surrounding soil.

The theoretical method is presented in Section 2, indicating that the frictional resistance is 10 kN/m², as shown in Table 1. The jacking force remains constant because the frictional resistance is defined as a fixed range. The different values can be applied within this range, but the value is too imprecise to select, so the fixed value is applied here. The simulated jacking force is much larger than the theoretical value because the theoretical value does not consider the increasing trend of frictional resistance with the depth of the pipe. 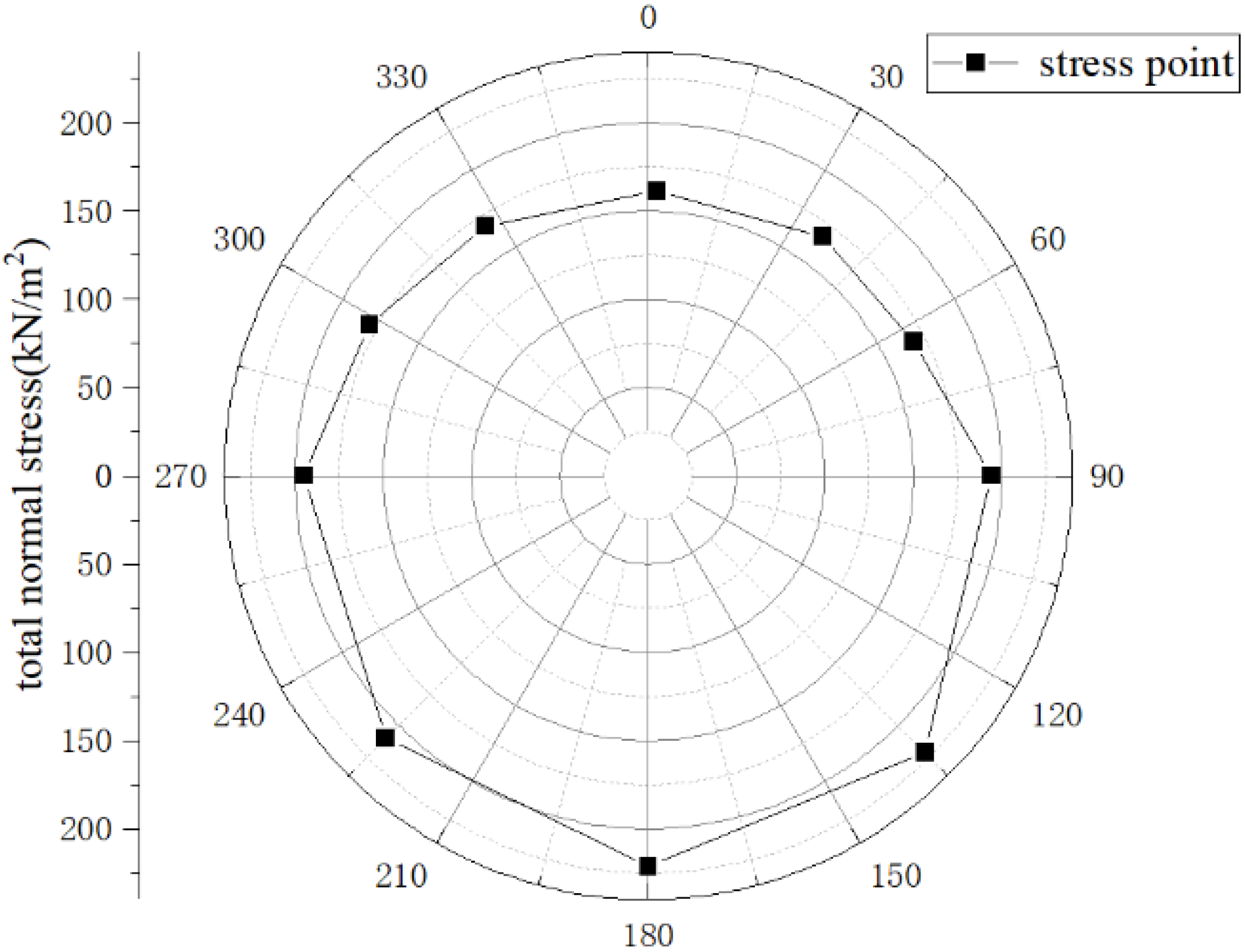In this simulation, the pipe’s bottom end is buried at a depth of 24.4 m, where the normal stress on the interface between the soil and the pipe is quite large, as shown in Figure 12 (100 m from the launch shaft). This results in significantly larger friction resistance around the pipe, much greater than the average friction resistance between the pipe and soil selected in the theoretical method as shown in Table 1.

3.7. Improved Theoretical Method for Calculating Frictional Resistance

In long-distance pipe jacking projects, the proportion of front resistance is very small, so it is suitable only to improve theoretical methods for calculating the frictional resistance by the simulation results.

First, the total normal stress can be calculated based on the data in Table 4. The formula is expressed as

$${\sigma }_z={\sum }_{i=1}^n\gamma \times h$$

(5)

In this formula,

${\sigma }_z$ is the total normal stress in the vertical direction;

$n$ is the number of soil strata;

$\gamma$ is the saturated unit weight of each stratum;

h is the d = thickness of each stratum.

The effective normal stress at both the bottom and the top of the pipe can be calculated. In this case, the effective normal stress is 474 kPa at the bottom and 403 kPa at the top.

Second, the total normal stress can be estimated based on the ${\sigma }_z$. There are many influencing factors here, such as the arching effect of the soil and the difference between the ${\sigma }_z$ and ${\sigma }_x$ (total normal stress in the lateral direction). In this case, the average total normal stress is 160 kPa (according to Figure 12, the average total normal stress is higher than 160 kPa, but the data are obtained from 100 m from the launch shaft, and there is a slight decrease in the frictional resistance along the longitudinal direction).

Third, by using the formula presented later, the relationship between the average total normal stress and the frictional resistance is established.

$$f_k=\sigma \times R_{inter}\times tan\phi =\sigma \times tan{\phi }_{inter}$$

(6)

In this formula,

$\sigma$ is the average total normal stress;

$\phi$ is the internal friction angle of the soil stratum around the pipe.

In this case, the average internal friction angle is 16.7°, and there are six different values of $R_{inter}$ to calculate. The results are shown in

Table 5. Results of the improved theoretical methods.

${\mathit{R}}_{\mathit{i}\mathit{n}\mathit{t}\mathit{e}\mathit{r}}$	${\mathit{f}}_{\mathit{k}}$ /kN·m−2	Friction Resistance/kN	Total Jacking Force/kN
0.2	9.6	67,600	72,400
0.24	11.5	81,100	85,900
0.28	13.4	94,600	99,400
0.32	15.4	108,000	112,800
0.36	17.3	121,700	126,500
0.40	19.2	135,200	140,000

.

Finally, apply the improved $f_k$ to the Formula (4) to obtain the new answer. And the total jacking force is obtained using Formulas (1) and (2) as the previous theoretical methods. The results are shown in Table 5.

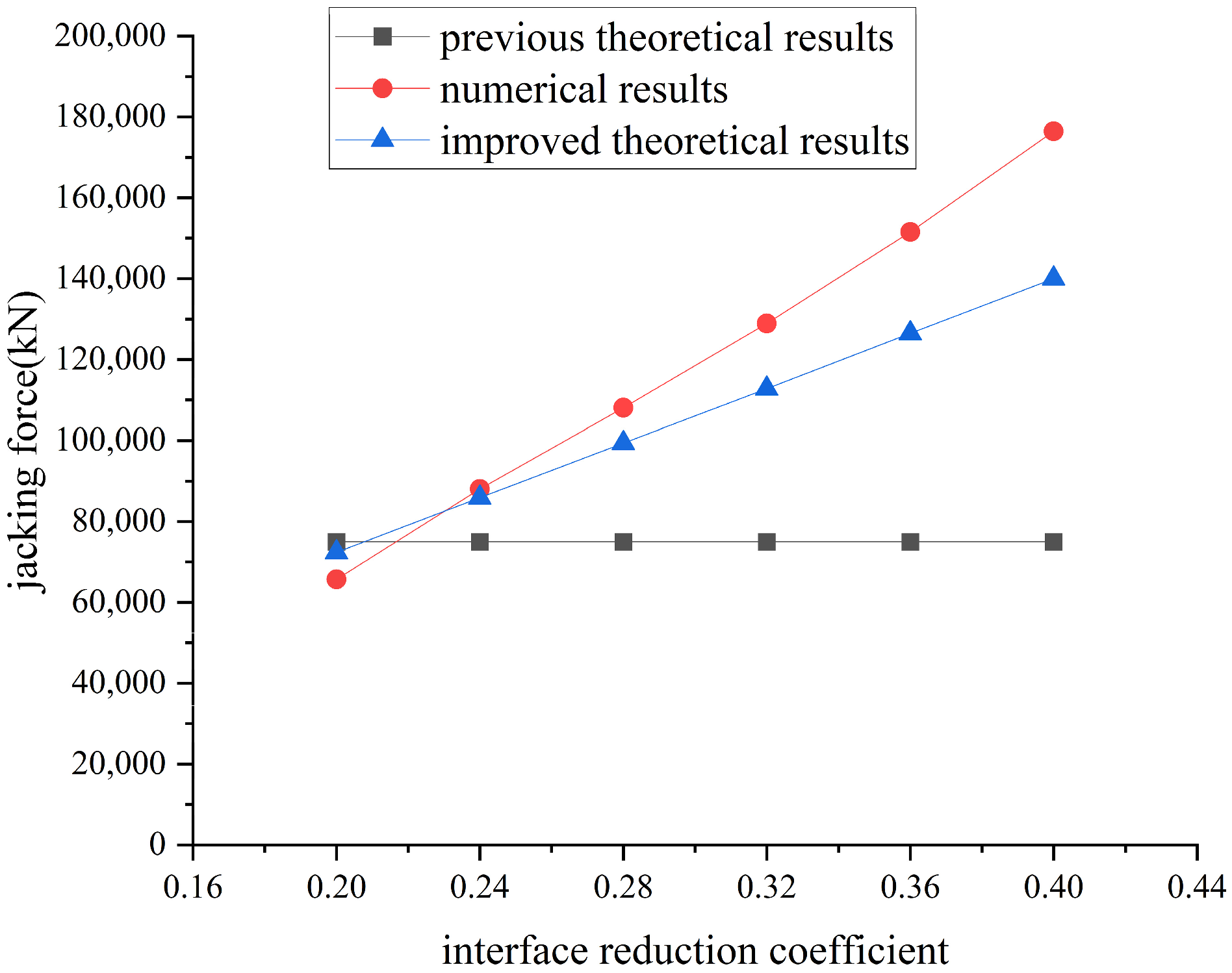
The previous theoretical results, improved theoretical results, and numerical results of the jacking force are summarized in Figure 13.

In Figure 13, it is evident that the improved theoretical results exhibit a linear relationship based on different interface reduction coefficients. This trend aligns better with the numerical results, and the discrepancy between the improved theoretical results and the numerical results is significantly smaller compared to the difference between the previous theoretical results and the numerical results.

4. Conclusions

This paper introduces the grouting materials, grouting process, and grouting-friction-reduction mechanism. To evaluate the effect of friction reduction on the jacking force, the different interface reduction coefficients are simulated via FEM. The improved theoretical method is developed based on the numerical results to achieve relatively more precise outcomes compared to the previous results presented in Section 2. The findings provide valuable references for engineering design. The main conclusions are as follows:

(1)

Grouting-friction-reduction technology can significantly reduce the jacking force. Optimizing the grouting process and preparing a suitable thixotropic slurry can effectively decrease the jacking force for long-distance pipe jacking.

• In long-distance cases, the frictional resistance around the pipe is the main source of jacking force. As the interface reduction coefficient increases, the total jacking force increases approximately linearly, and the distribution of the stress around the pipe becomes more uneven. Thus, if the interface friction angle is sufficiently large, the variation in shear stress across the same section should be considered.

(2)

The simulated jacking force is significantly larger than the theoretical value presented in Section 2, especially when the pipe is buried at a greater depth. Therefore, alternative methods, like the improved theoretical method, should be used in such cases, as the previous theoretical approach may not accurately reflect these conditions.

(3)

In previous theoretical methods, the average unit frictional resistance between the pipe’s outer surface and the soil cannot be precisely selected, leaving only an imprecise range for engineers from which to select. The improved theoretical methods address this issue by providing formulae to estimate the value more accurately.

• There are some limitations in the improved theoretical method, such as its inability to account for the uneven distribution of shear stress across the section, and the unclear correlation between the interface reduction coefficient, and the effect of the grouting. It is recommended that future studies investigate the effect of the shear stress distribution on the friction resistance and a more precise calculation method to assess the friction reduction of the grout.