An Analytical Model for the Steady-State Thermal Analysis of Façade-Integrated PV Modules Cooled by a Solar Chimney

Abstract

This paper proposes a steady-state thermal model for the passive cooling of photovoltaic (PV) modules integrated into a vertical building façade by means of a solar chimney, including an empirical correlation for turbulent free convection from a vertical isothermal plate. The proposed analytical model estimates the air velocities at the inlet and at the outlet of the ventilation channel of such a cooling system and the average temperature of the façade-integrated PV modules. A configuration composed of a maximum of six vertically installed PV modules and one solar chimney is considered. The air velocities at the inlet and at the outlet of the ventilation channel obtained for the case of installing PV modules on the building façade are compared with those calculated for the case where the PV modules are integrated into the roof with a slope of 37°. By comparing each of the solutions with one PV module to the corresponding one with six PV modules, it was found that the increase in the air velocity due to the effects of the solar irradiance and the height difference between the two openings of the ventilation channel ranges between 41.05% in the case of “Roof” and 141.14% in the case of “Façade”. In addition, it was obtained that an increase in the solar chimney height of 1 m leads to a decrease in the average PV section temperature by 1.95–7.21% and 0.65–2.92% in the cases of “Roof” and “Façade”, respectively. Finally, the obtained results confirmed that the use of solar chimneys for passive cooling of façade-integrated PV modules is technically justified.

1. Introduction

The increasing application of various photovoltaic (PV) technologies has led to the exploring new locations for the installation of PV modules, panels, and arrays. In addition to the functional and default locations for installation in urban areas, such as the roofs of residential [1], commercial [2], industrial [3], and other [4] buildings, PV modules can be installed on highway slopes [5], road structures [6], pavements [7], car parks [8], building façades [9], and so on. By installing PV modules, in particular, on building façades, they become integral parts of the buildings, the so-called Building-Integrated Photovoltaics (BIPVs). PV modules intended for installation on buildings can be fully integrated—as a replacement for window walls and roof windows, or ventilated (passively or actively)—in the case of installation on façades and roofs of buildings in combination with air channels [10]. In addition to generating electricity, BIPVs can be used as a construction or architectural solution for the construction or renovation of building façades [11]. By installing BIPVs, the direct exposure of the building walls to solar heating is prevented, which leads to a decrease in the temperature of the building walls and has a positive effect on the energy efficiency of buildings in the summer months [12]. For building façades, as well as for all other locations where PV modules can be integrated with a solar chimney, the velocity of air along the chimney channel and the average temperature of the PV modules can be estimated iteratively by means of steady-state thermal modeling.

Numerous experimental, analytical, and numerical models have already been used in the literature for steady-state thermal analyses. In this view, ventilated air-spaces behind passive and active façades were studied numerically and experimentally in [13]. Reference [14] reviewed and analyzed options to integrate various configurations of a solar chimney with various buildings for the purpose of air ventilation. Air channels of different sizes used for passive ventilation of wall-mounted PV panels were analyzed numerically in [15]. According to [15], the air velocity in any air-cooled channel decreases with increasing channel thickness and increases with increasing channel width. The electrical and thermal performance parameters of a PV wall with different air gaps in unclosed, partially enclosed, and enclosed modes were estimated using a finite element method in [16]. In addition, a BIPV system with enhanced passive ventilation was modeled by computational fluid dynamics in [17]. Performance prediction of a ventilated BIPV system with a crystalline silicon module based on an experimental fitting method was conducted in [18].

The solar chimney effect in a passively ventilated BIPV system was studied experimentally in [19]. This effect has been used for a long time in solar chimney power plants. A solar chimney power plant with various types of heat storage systems was analyzed in [20]. Some methods for improving the performance of such a solar chimney power plant with heat storage were discussed in [21], while a review of existing methods of this kind can be found in [22]. The enhancement of ventilation performance of a roof solar chimney was considered in [23]. The electricity generation and temperature of a roof-integrated PV system in South Korea over a period of 2.5 years were analyzed in [24]. The performance of a combined roof-integrated solar chimney for the natural ventilation of buildings was evaluated in [25]. An assessment of thermal conditioning in a house with a solar chimney using computational fluid dynamics was performed in [26]. A novel method to manufacture power-efficient BIPV modules that are esthetically acceptable for use in zero-energy buildings was suggested in [27]. Two steady-state temperature models for BIPV modules were analyzed in [28]. Moreover, the results of experimental and numerical analyses of the performance of a ventilated energy-productive wall were reported in [29]. The operating performance of PV panels cooled by a natural draft cooling system under typical hot dry conditions was investigated in [30]. The results of the yield analysis of a BIPV façade prototype can be found in [31]. Finally, based on this state-of-the-art review, as well as a few hundred older and newer references reviewed in [32,33,34,35], it was found that there is no analytical thermal model that simultaneously and iteratively determines the air velocities at the inlet and at the outlet of a solar chimney and the average temperature of PV modules integrated with that chimney. In particular, the existing analytical thermal models cannot calculate analytically the air velocities at the inlet and at the outlet of a solar chimney. Therefore, this is recognized as a research gap.

The model proposed here is based on the analytical thermal model developed in [36] for the purpose of analyzing the cooling of PV modules integrated in a roof inclined at an angle of 37°. The model is obtained by replacing empirical correlations for free convection heat transfer from the upper surface of an inclined plate used in [36] with empirical correlations for free convection heat transfer from one surface of a vertical isothermal plate [37]. This represents the main difference in the proposed model, when compared to the model used in [36]. Specifically, the proposed model is a combination of the model from [36], the existing empirical correlations for radiation, laminar free convection, forced convection, sky temperature, and velocity of air along the solar chimney channel, and the proposed empirical correlations for turbulent free convection from a vertical flat plate. The excellent accuracy of the correlations used in the proposed model was previously validated by a large amount of experimental data and the large number of relevant comparisons [37,38,39,40,41,42]. For this reason, the associated validation processes do not have to be repeated. Addressing the research gap identified previously represents another contribution. In addition, the third contribution is the use of empirical correlations for forced convection to model the heat transfer from the back surfaces of PV modules integrated with the solar chimney channel, based on estimated air velocity in it. On the other hand, the limitations of the proposed model refer to the impossibility of taking into account the effects of wind, daily variation in solar irradiance, and daily variation in the ambient air temperature on the heating of the PV modules, as well as wind on the velocity of air along the solar chimney channel.

In this paper, a vertical segment of the façade of a building composed of the top section of a solar chimney, a maximum of six PV modules mounted on the channel of the solar chimney (i.e., PV section), and an absorber section installed above the PV section is considered. It is assumed that the dimensions of these three sections are known. The air velocities at the inlet and at the outlet of the chimney channel and the average temperature of the PV section are estimated iteratively using the proposed steady-state thermal model. For the purpose of comparisons, it is assumed that the dimensions of the chimney channel are identical to the dimensions of the one from [37]. Comparisons are made between the performance parameters calculated for the air velocity along the chimney channels that are inclined at angles of 90° and 37° with regard to the horizontal plane. In addition, the effects of the solar irradiance, the height of the solar chimney, the height difference between the two openings of a ventilation channel, the solar irradiance, the number of PV modules on the air velocities (at the inlet and at the outlet of the solar chimney channel), and the average PV section temperature are quantified.

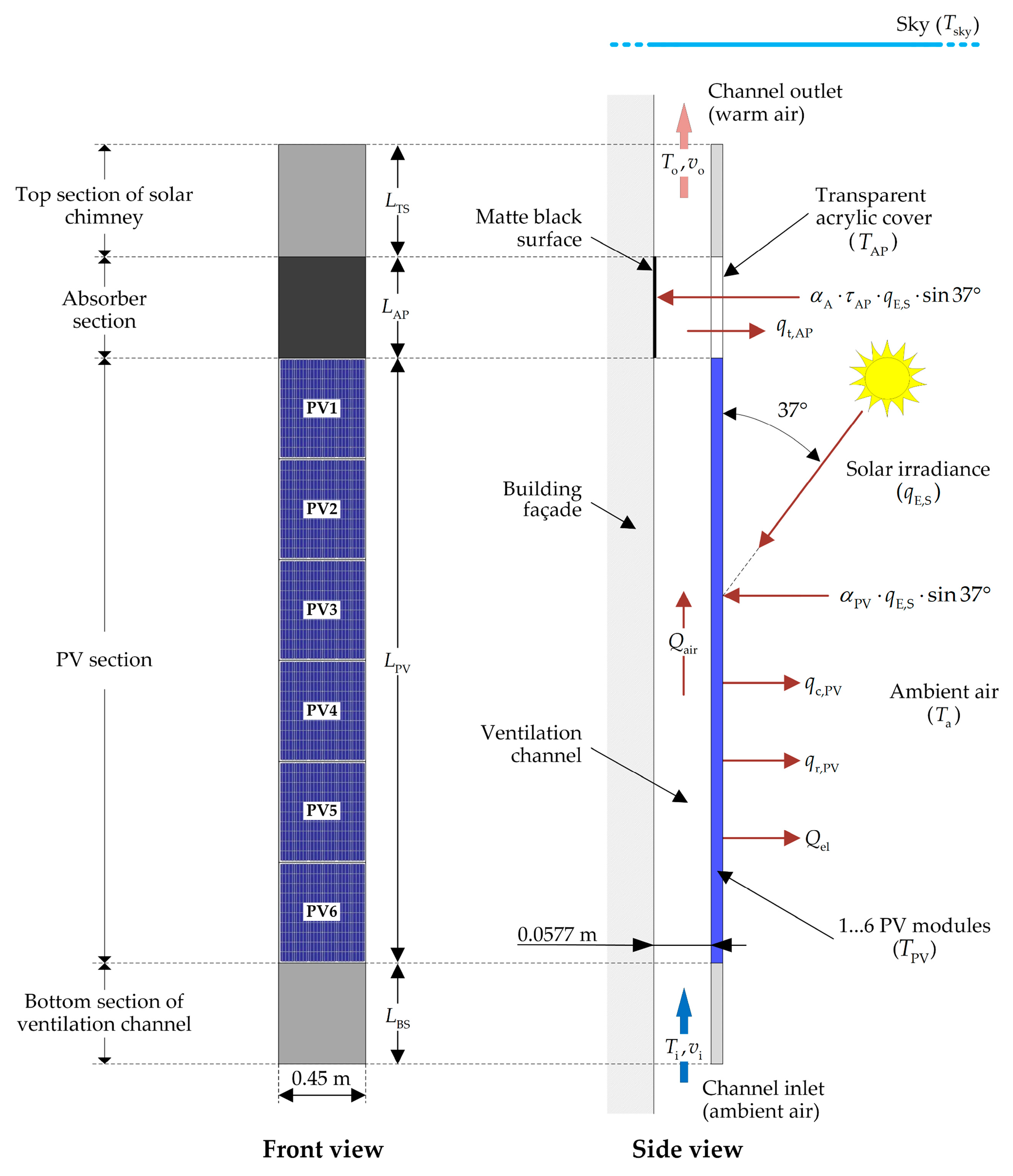
2. Case Study

As the temperature of PV cells increases, the cell voltage and the overall efficiency of any PV module, panel, or array decrease, so it is preferable to install the PV modules so that the heat removal from them is as efficient as possible. By constructing a ventilation channel below or behind the PV modules themselves, it is possible to remove heat from them, where the air velocity and the efficiency of the system depend on the dimensions of that channel, the ambient temperature, and the solar irradiance [12,38]. To improve air circulation in the ventilation channel, the so-called solar chimney effect can usually be utilized.

The solar chimney operates on the basis of creating additional buoyancy force and increasing the air velocity in the channel, which improves the heat removal from the back surfaces of the PV modules [36,39]. The buoyancy force is proportional to the magnitude of the temperature gradient and causes the air to move upward along the channel. This way of cooling the PV modules does not require any additional source of electricity, which is an advantage compared to other cooling systems, by means of cold water circulation or forced ventilation. A solar chimney consists of absorber and top sections. The absorber section is actually an absorber of solar radiation in which additional heating of the air occurs. The absorber is painted in matte black, which intensifies the absorption of solar heat and rises the temperature of air in it. The top section is an extension of the absorber section, and its height affects the buoyancy in the solar chimney, as with a regular chimney. The solar chimney made in this way is then installed as a continuation of the channel that goes under the section with PV modules in order to intensify the air circulation along the back surfaces of the PV modules. Accordingly, Figure 1 shows a segment of the building façade composed of these three sections together with the associated heat transfer processes.

3. Steady-State Thermal Modeling

In this section, an analytical model is given for the steady-state heat transfer from a building PV façade cooled by a solar chimney. In particular, the heat transfer processes taking place along the surfaces of the PV section, the absorber section and the ventilation channel are in accordance with Figure 1. The model is based on the laws of conservation of energy and mass, correlations for sky temperature and heat transfer by radiation between a flat plate and the surroundings, the balance between the total pressure difference due to buoyancy, and the total pressure drop (across the whole ventilation channel), as well as correlations for free and forced convection. The temperature and velocity of the air at the outlet of the ventilation channel, as well as the heat transfer coefficients, are calculated using the proposed model. According to Figure 1, the sky is modeled by an infinite horizontal flat plate of temperature $T_{\mathrm{s}\mathrm{k}\mathrm{y}}\ne T_{\mathrm{a}}$ [36]. In addition, all channel walls are assumed to be adiabatic, except for the PV section and the acrylic plate, which are assumed to be isothermal, and their average temperatures are $T_{\mathrm{P}\mathrm{V}}$ and $T_{\mathrm{A}\mathrm{P}}$, respectively.

The parameters appearing in Figure 1 have the following meanings: $L_{\mathrm{T}\mathrm{S}}$ is the height of the top section of the solar chimney in m; $L_{\mathrm{A}\mathrm{P}}$ is the height of the absorber section (or acrylic plate) in m;$L_{\mathrm{P}\mathrm{V}}$ is the height of the PV section in m; $L_{\mathrm{B}\mathrm{S}}$ is the height of the bottom section of the ventilation channel in m; $T_{\mathrm{i}}=T_{\mathrm{a}}$, $T_{\mathrm{o}}$, $T_{\mathrm{a}}$, and $T_{\mathrm{s}\mathrm{k}\mathrm{y}}$ are the temperatures of the air at the inlet of the ventilation channel, the air at the outlet of the ventilation channel, the ambient air, and the sky in °C, respectively; $T_{\mathrm{P}\mathrm{V}}$, $T_{\mathrm{A}\mathrm{P}}$, and $T_{\mathrm{a},\mathrm{a}\mathrm{v}}$ are the average temperatures of the PV section, the acrylic plate, and the air in the ventilation channel in °C, respectively; $v_{\mathrm{i}}$ and $v_{\mathrm{o}}$ are the air velocities at the inlet of the ventilation channel and at the outlet of the ventilation channel in m/s, respectively; $q_{\mathrm{E},\mathrm{S}}$ is the solar irradiance that can be received by a horizontal surface on Earth in W/m²; ${\alpha }_{\mathrm{P}\mathrm{V}}$ and ${\alpha }_{\mathrm{A}}$ are the solar absorption coefficients for the upper surface of the PV section and the absorption area of the absorber, respectively; ${\tau }_{\mathrm{A}\mathrm{P}}$ is the solar transmittance for the acrylic plate; $q_{\mathrm{c},\mathrm{P}\mathrm{V}}$ is the free convection heat transfer between the upper surface of the PV section and the ambient air in W/m²; $q_{\mathrm{r},\mathrm{P}\mathrm{V}}$ is the radiation heat exchange between the upper surface of the PV section and the surroundings in W/m²; $Q_{\mathrm{e}\mathrm{l}}$ is the power related to the generation of electricity in the PV section in W; $q_{\mathrm{t},\mathrm{A}\mathrm{P}}$ is the heat transfer through the acrylic plate between the air in the ventilation channel and the ambient air in W/m²; and $Q_{\mathrm{a}\mathrm{i}\mathrm{r}}$ is the amount of heat absorbed by the mass of the air in the ventilation channel in W. No SI units are given for the dimensionless parameters in Figure 1.

The free convection and radiation heat transfer coefficients corresponding to the heat transfer processes $q_{\mathrm{c},\mathrm{P}\mathrm{V}}$ and $q_{\mathrm{r},\mathrm{P}\mathrm{V}}$ are $h_{\mathrm{c},\mathrm{P}\mathrm{V}}$ in W/(m²·K) and $h_{\mathrm{r},\mathrm{P}\mathrm{V}}$ in W/(m²·K), respectively. The heat transfer through the acrylic plate is carried out by forced convection between the air in the ventilation channel and the bottom surface of the acrylic plate ($h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{b}}$ in W/(m²·K)), conduction through the acrylic plate, and free convection between the upper surface of the acrylic plate and the ambient air ($h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{u}}$ in W/(m²·K)). Therefore, the heat transfer coefficients $h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{b}}$ and $h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{u}}$ correspond to the heat transfer process $q_{\mathrm{t},\mathrm{A}\mathrm{P}}$. Assuming that some of the parameters from Figure 1 are unknown, it is necessary to estimate the parameters of the air at the outlet of the solar chimney ($T_{\mathrm{o}}$ and $v_{\mathrm{o}}$), as well as energy losses in the considered system.

The iteration procedure for calculating $T_{\mathrm{o}}$, $v_{\mathrm{o}}$, $h_{\mathrm{c},\mathrm{P}\mathrm{V}}$, $h_{\mathrm{r},\mathrm{P}\mathrm{V}}$, $h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{b}}$, and $h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{u}}$ requires knowledge of the temperatures $T_{\mathrm{P}\mathrm{V}}$, $T_{\mathrm{A}\mathrm{P}}$, and $T_{\mathrm{s}\mathrm{k}\mathrm{y}}$, which are also unknown. The initial values for all unknown heat transfer coefficients should be specified so that they correspond to turbulent free convection in air (for instance, 10 W/(m²·K)), while any positive number (for instance, 1 m/s) can be specified for the initial value of the air velocity at the outlet of the solar chimney.

The initial value for $T_{\mathrm{o}}$ can be estimated using the energy balance equation

$${({\alpha }_{\mathrm{P}\mathrm{V}}{S}_{\mathrm{P}\mathrm{V}}+\alpha }_{\mathrm{A}}{\tau }_{\mathrm{A}\mathrm{P}}{S}_{\mathrm{A}\mathrm{P}})q_{\mathrm{E},\mathrm{S}}=Q_{\mathrm{a}\mathrm{i}\mathrm{r}}+q_{\mathrm{t},\mathrm{A}\mathrm{P}}{S}_{\mathrm{A}\mathrm{P}}+\left(q_{\mathrm{c},\mathrm{P}\mathrm{V}}+q_{\mathrm{r},\mathrm{P}\mathrm{V}}\right)S_{\mathrm{P}\mathrm{V}}+Q_{\mathrm{e}\mathrm{l}},$$

(1)

in the following manner

$$T_{\mathrm{o}}=T_{\mathrm{a}}+{\displaystyle \frac{2[{\alpha }_{\mathrm{P}\mathrm{V}}{S}_{\mathrm{P}\mathrm{V}}\left(1-{\eta }_{\mathrm{e}\mathrm{l}}\right)+{\alpha }_{\mathrm{A}}{\tau }_{\mathrm{A}\mathrm{P}}{S}_{\mathrm{A}\mathrm{P}}]q_{\mathrm{E},\mathrm{S}}}{2v_{\mathrm{o}}{\rho }_{\mathrm{o}}{S}_{\mathrm{D}}{c}_{\mathrm{t},\mathrm{i}}+\left(h_{\mathrm{c},\mathrm{P}\mathrm{V}}+h_{\mathrm{r},\mathrm{P}\mathrm{V}}\right)S_{\mathrm{P}\mathrm{V}}+U_{\mathrm{A}\mathrm{P}}{S}_{\mathrm{A}\mathrm{P}}}},$$

(2)

where [36,39]:

$$q_{\mathrm{c},\mathrm{P}\mathrm{V}}=h_{\mathrm{c},\mathrm{P}\mathrm{V}}(T_{\mathrm{P}\mathrm{V}}-T_{\mathrm{a}}),$$

(3)

$$q_{\mathrm{r},\mathrm{P}\mathrm{V}}=h_{\mathrm{r},\mathrm{P}\mathrm{V}}(T_{\mathrm{P}\mathrm{V}}-T_{\mathrm{a}}),$$

(4)

$$h_{\mathrm{r},\mathrm{P}\mathrm{V}}={\epsilon }_{\mathrm{P}\mathrm{V}}{\sigma }_{\mathrm{S}\mathrm{B}}(T_{\mathrm{P}\mathrm{V}}+T_{\mathrm{s}\mathrm{k}\mathrm{y}})(T_{\mathrm{P}\mathrm{V}}^2+T_{\mathrm{s}\mathrm{k}\mathrm{y}}^2){\displaystyle \frac{(T_{\mathrm{P}\mathrm{V}}-T_{\mathrm{s}\mathrm{k}\mathrm{y}})}{(T_{\mathrm{P}\mathrm{V}}-T_{\mathrm{a}})}},$$

(5)

$$Q_{\mathrm{e}\mathrm{l}}={\eta }_{\mathrm{e}\mathrm{l}}{\alpha }_{\mathrm{P}\mathrm{V}}{q}_{\mathrm{E},\mathrm{S}}{S}_{\mathrm{P}\mathrm{V}},$$

(6)

$$q_{\mathrm{t},\mathrm{A}\mathrm{P}}=U_{\mathrm{A}\mathrm{P}}(T_{\mathrm{A}\mathrm{P}}-T_{\mathrm{a}}),$$

(7)

$$U_{\mathrm{A}\mathrm{P}}={\left({\displaystyle \frac{1}{h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{b}}}}+{\displaystyle \frac{{\mathsf{\Delta }}_{\mathrm{A}\mathrm{P}}}{k_{\mathrm{t},\mathrm{A}\mathrm{P}}}}+{\displaystyle \frac{1}{h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{u}}}}\right)}^{-1},$$

(8)

$$Q_{\mathrm{a}\mathrm{i}\mathrm{r}}=v_{\mathrm{o}}{\rho }_{\mathrm{o}}{S}_{\mathrm{D}}{c}_{\mathrm{t},\mathrm{i}}(T_{\mathrm{o}}-T_{\mathrm{a}}),$$

(9)

$$T_{\mathrm{P}\mathrm{V}}=T_{\mathrm{A}\mathrm{P}}\approx T_{\mathrm{a},\mathrm{a}\mathrm{v}}={\displaystyle \frac{(T_{\mathrm{a}}+T_{\mathrm{o}})}{2}},$$

(10)

$$T_{\mathrm{s}\mathrm{k}\mathrm{y}}=0.0552T_{\mathrm{a}}^{1.5},$$

(11)

$S_{\mathrm{A}\mathrm{P}}$ is the area of one side of the acrylic plate in m²; $S_{\mathrm{P}\mathrm{V}}$ is the area of one side of the PV section in m²; ${\eta }_{\mathrm{e}\mathrm{l}}$ is the efficiency of conversion of solar energy into electricity; ${\rho }_{\mathrm{o}}$ is the density of air at temperature $T_{\mathrm{o}}$ in kg/m³; $c_{\mathrm{t},\mathrm{i}}$ is the specific heat of air at temperature $T_{\mathrm{a}}$ in J/(kg·K); $S_{\mathrm{D}}$ is the cross-sectional area of the ventilation channel (or air flow in that channel) in m²; $U_{\mathrm{A}\mathrm{P}}$ is the overall heat transfer coefficient for the acrylic plate in W/(m²·K); ${\epsilon }_{\mathrm{P}\mathrm{V}}$ is the thermal emissivity for the upper surface of the PV section; ${\sigma }_{\mathrm{S}\mathrm{B}}$ = 5.67 × 10⁻⁸ W/(m²·K⁴) is the Stefan–Boltzmann constant; $h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{b}}$ is the forced convection heat transfer coefficient between the air in the ventilation channel and the bottom surface of the acrylic plate in W/(m²·K); ${\mathsf{\Delta }}_{\mathrm{A}\mathrm{P}}$ = 0.003 m is the thickness of the acrylic plate; $k_{\mathrm{t},\mathrm{A}\mathrm{P}}$ = 0.19 W/(m·K) is the thermal conductivity of the acrylic plate; and $h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{u}}$ is the free convection heat transfer coefficient between the upper surface of the acrylic plate and the ambient air in W/(m²·K).

Values of density $\rho$ in kg/m³, specific heat $c_{\mathrm{t}}$ in J/(kg·K), dynamic viscosity $\mu$ in kg/(m·s), thermal conductivity $k_{\mathrm{t}}$ in W/(m·K), and Prandtl number $\mathrm{P}\mathrm{r}$ for air at the film temperature $T_{\mathrm{f}}=(T_{\mathrm{a},\mathrm{a}\mathrm{v}}+T_{\mathrm{a}})/2$ in K were read from corresponding input data files and interpolated using a cubic spline. Thus, the Rayleigh number $\mathrm{R}\mathrm{a}$ can be expressed as [37] follows:

$$\mathrm{R}\mathrm{a}={\displaystyle \frac{\mathrm{g}\beta }{\nu {\alpha }_{\mathrm{t}}}}(T_{\mathrm{a},\mathrm{a}\mathrm{v}}-T_{\mathrm{a}})L_{\mathrm{c}}^3,$$

(12)

where $\mathrm{g}$ = 9.81 m/s² is the acceleration due to gravity; $\nu =\mu /\rho$ is the kinematic viscosity of air in m²/s; ${\alpha }_{\mathrm{t}}=k_{\mathrm{t}}/(\rho ·c_{\mathrm{t}})$ is the thermal diffusivity of air in m²/s; $\beta =1/T_{\mathrm{f}}$ is the thermal expansion coefficient of air in 1/K; and $L_{\mathrm{c}}$ is the characteristic length of the PV section ($L_{\mathrm{c}}=L_{\mathrm{P}\mathrm{V}}$) or acrylic plate ($L_{\mathrm{c}}=L_{\mathrm{A}\mathrm{P}}$) in m.

The Nusselt number for free convection from the upper surface of the PV section or acrylic plate (which are inclined at a right angle) can be calculated by means of the following correlations [36,37,40,41]:

$$\mathrm{N}\mathrm{u}=0.67{\left({\displaystyle \frac{\mathrm{R}\mathrm{a}}{1+\frac{0.492}{\mathrm{P}\mathrm{r}}}}\right)}^{1/4}\mathrm{for}{10}^4\le {\displaystyle \frac{\mathrm{R}\mathrm{a}}{1+\frac{0.492}{\mathrm{P}\mathrm{r}}}}\le {10}^9,$$

(13)

$$\mathrm{N}\mathrm{u}=0.12{\left({\displaystyle \frac{\mathrm{R}\mathrm{a}}{1+\frac{0.492}{\mathrm{P}\mathrm{r}}}}\right)}^{1/3}\mathrm{for}{10}^9<{\displaystyle \frac{\mathrm{R}\mathrm{a}}{1+\frac{0.492}{\mathrm{P}\mathrm{r}}}}\le {10}^{12},$$

(14)

where ${\displaystyle \frac{\mathrm{R}\mathrm{a}}{1+\frac{0.492}{\mathrm{P}\mathrm{r}}}}$ represents the fundamental dimensionless number for free convection. Equation (13) refers to laminar flow caused by air buoyancy along the PV section or acrylic plate, and Equation (14) refers to turbulent flow caused by air buoyancy along the PV section or acrylic plate.

The Nusselt number for the cases of fully developed laminar, partially developed turbulent, and fully developed turbulent air flow regimes, through part of the rectangular channel below the acrylic plate, can be calculated using the following correlations for forced convection [41,42]:

$$\mathrm{N}\mathrm{u}=3.66+{\displaystyle \frac{0.0668\left(\frac{d_{\mathrm{H}}}{L_{\mathrm{A}\mathrm{P}}}\right)\mathrm{R}\mathrm{e}\mathrm{P}\mathrm{r}}{1+0.04{\left[\left(\frac{d_{\mathrm{H}}}{L_{\mathrm{A}\mathrm{P}}}\right)\mathrm{R}\mathrm{e}\mathrm{P}\mathrm{r}\right]}^{2/3}}}\mathrm{for}\mathrm{R}\mathrm{e}\le 2300,$$

(15)

$$\mathrm{N}\mathrm{u}=0.036{\mathrm{R}\mathrm{e}}^{4/5}{\mathrm{P}\mathrm{r}}^{1/3}{\left({\displaystyle \frac{d_{\mathrm{H}}}{L_{\mathrm{A}\mathrm{P}}}}\right)}^{0.055}\mathrm{for}2300<\mathrm{R}\mathrm{e}<4000,$$

(16)

$$\mathrm{N}\mathrm{u}=0.023{\mathrm{R}\mathrm{e}}^{4/5}{\mathrm{P}\mathrm{r}}^{2/5}\mathrm{for}\mathrm{R}\mathrm{e}\ge 4000,$$

(17)

where $d_{\mathrm{H}}=4S_{\mathrm{D}}/{\mathsf{\Pi }}_{\mathrm{D}}$ = 0.2308 m is the hydraulic diameter of the channel; ${\mathsf{\Pi }}_{\mathrm{D}}$ = 0.45 m is the wetted perimeter of the channel (this perimeter equals to the width of the channel because the other walls of the channel are adiabatic); $\mathrm{R}\mathrm{e}=v_{\mathrm{a}\mathrm{i}\mathrm{r}}{d}_{\mathrm{H}}/{\nu }_{\mathrm{a}\mathrm{v}}$ is the Reynolds number; ${\nu }_{\mathrm{a}\mathrm{v}}={\nu (T}_{\mathrm{a},\mathrm{a}\mathrm{v}})$ is the average kinematic viscosity of the air in the channel at the temperature $T_{\mathrm{a},\mathrm{a}\mathrm{v}}$ in m²/s; and $v_{\mathrm{a}\mathrm{i}\mathrm{r}}={(v}_{\mathrm{i}}+v_{\mathrm{o}})/2$ is the average velocity of the air in the ventilation channel in m/s. Heat transfer through the PV section between the air in the ventilation channel and the ambient air does not exist because the temperature of the air in that part of the channel (below the PV section) is approximately equal to the temperature of the ambient air.

By equating the total pressure difference due to buoyancy (natural draft pressure)

$${\mathsf{\Delta }p}_{\mathrm{t},\mathrm{b}\mathrm{u}\mathrm{o}\mathrm{y}}=\mathrm{g}({\rho }_{\mathrm{i}}-{\rho }_{\mathrm{o}})(L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}+L_{\mathrm{P}\mathrm{V}}+L_{\mathrm{B}\mathrm{S}}),$$

(18)

in kg/(m·s²), with the total pressure drop across the ventilation channel (the sum of the pressure losses due to friction of the channel walls, at the inlet and at the outlet)

$${\mathsf{\Delta }p}_{\mathrm{t},\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\displaystyle \frac{f(L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}+L_{\mathrm{P}\mathrm{V}}+L_{\mathrm{B}\mathrm{S}}){\rho }_{\mathrm{o}}{v}_{\mathrm{o}}^2}{2d_{\mathrm{H}}}}+{\displaystyle \frac{K_{\mathrm{i}+\mathrm{o}}{\rho }_{\mathrm{o}}{v}_{\mathrm{o}}^2}{2}},$$

(19)

in kg/(m·s²), the velocity of the air at the outlet of the rectangular channel can be expressed as follows [41,43,44]:

$$v_{\mathrm{o}}={\left\{{\displaystyle \frac{2\mathrm{g}(L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}+L_{\mathrm{P}\mathrm{V}}+L_{\mathrm{B}\mathrm{S}})({\rho }_{\mathrm{i}}-{\rho }_{\mathrm{o}})}{{\rho }_{\mathrm{o}}\left[\frac{f\left(L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}+L_{\mathrm{P}\mathrm{V}}+L_{\mathrm{B}\mathrm{S}}\right)}{d_{\mathrm{H}}}+K_{\mathrm{i}+\mathrm{o}}\right]}}\right\}}^{1/2},$$

(20)

where $f$ is the friction coefficient for flow in a smooth pipe or channel, namely $f=64/\mathrm{R}\mathrm{e}$ for laminar flow, and $f={[1.82{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left(\mathrm{R}\mathrm{e}\right)-1.64]}^{-2}$ for turbulent flow [41]; $L_{\mathrm{T}\mathrm{S}}$, $L_{\mathrm{A}\mathrm{P}}$, $L_{\mathrm{P}\mathrm{V}}$, and $L_{\mathrm{B}\mathrm{S}}$ are the section lengths according to Figure 1 in m; ${\rho }_{\mathrm{i}}$ is the density of air at temperature $T_{\mathrm{a}}$ in kg/m³; $K_{\mathrm{i}}=$ 0.5–1.5 is the pressure loss coefficient for the inlet opening of the rectangular channel; $K_{\mathrm{o}}=$ 1.0–2.4 is the pressure loss coefficient for the outlet opening of the rectangular channel; and $K_{\mathrm{i}+\mathrm{o}}=K_{\mathrm{i}}+K_{\mathrm{o}}$ is the sum of the coefficients $K_{\mathrm{i}}$ and $K_{\mathrm{o}}$ [43,44].

Based on the law of conservation of mass written for the case of a channel with a constant cross-section $S_{\mathrm{D}}$ and openings identical to the cross-section of that channel, the velocity of air at the inlet of any rectangular channel can be expressed as follows [41,43,44]:

$$v_{\mathrm{i}}=v_{\mathrm{o}}{\displaystyle \frac{{\rho }_{\mathrm{o}}}{{\rho }_{\mathrm{i}}}},$$

(21)

The air velocity $v_{\mathrm{i}}$ will be used to calculate the Nusselt number according to one of Equations (15)–(17) and the corresponding heat transfer coefficient for forced convection

$$h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{b}}=\mathrm{N}\mathrm{u}{\displaystyle \frac{k_{\mathrm{t},\mathrm{a}\mathrm{v}}}{d_{\mathrm{H}}}},$$

(22)

in W/(m²·K), where $k_{\mathrm{t},\mathrm{a}\mathrm{v}}$ is the thermal conductivity of air at the temperature $T_{\mathrm{a},\mathrm{a}\mathrm{v}}$ in W/(m·K). The remaining heat transfer coefficients for free and forced convection are determined according to the same principle, where the Nusselt number $\mathrm{N}\mathrm{u}$ should be calculated using the appropriate empirical correlation, and where the hydraulic diameter of the channel $d_{\mathrm{H}}$ should be replaced with the appropriate characteristic length ($L_{\mathrm{P}\mathrm{V}}$ or $L_{\mathrm{A}\mathrm{P}}$). The procedure must be iterated until the difference between two successively calculated values for the temperature $T_{\mathrm{o}}$ becomes negligible small, i.e., until the temperature $T_{\mathrm{o}}$ converges to a finite value. It is expected that finite values of the unknown parameters (air velocity, temperature, and heat transfer coefficients) will be obtained after several iterations. Finally, the proposed analytical model is implemented in the form of a MATLAB R2017a program, which, compared to existing commercial software tools, is unique in its application of empirical correlations for free and forced convection (13)–(17).

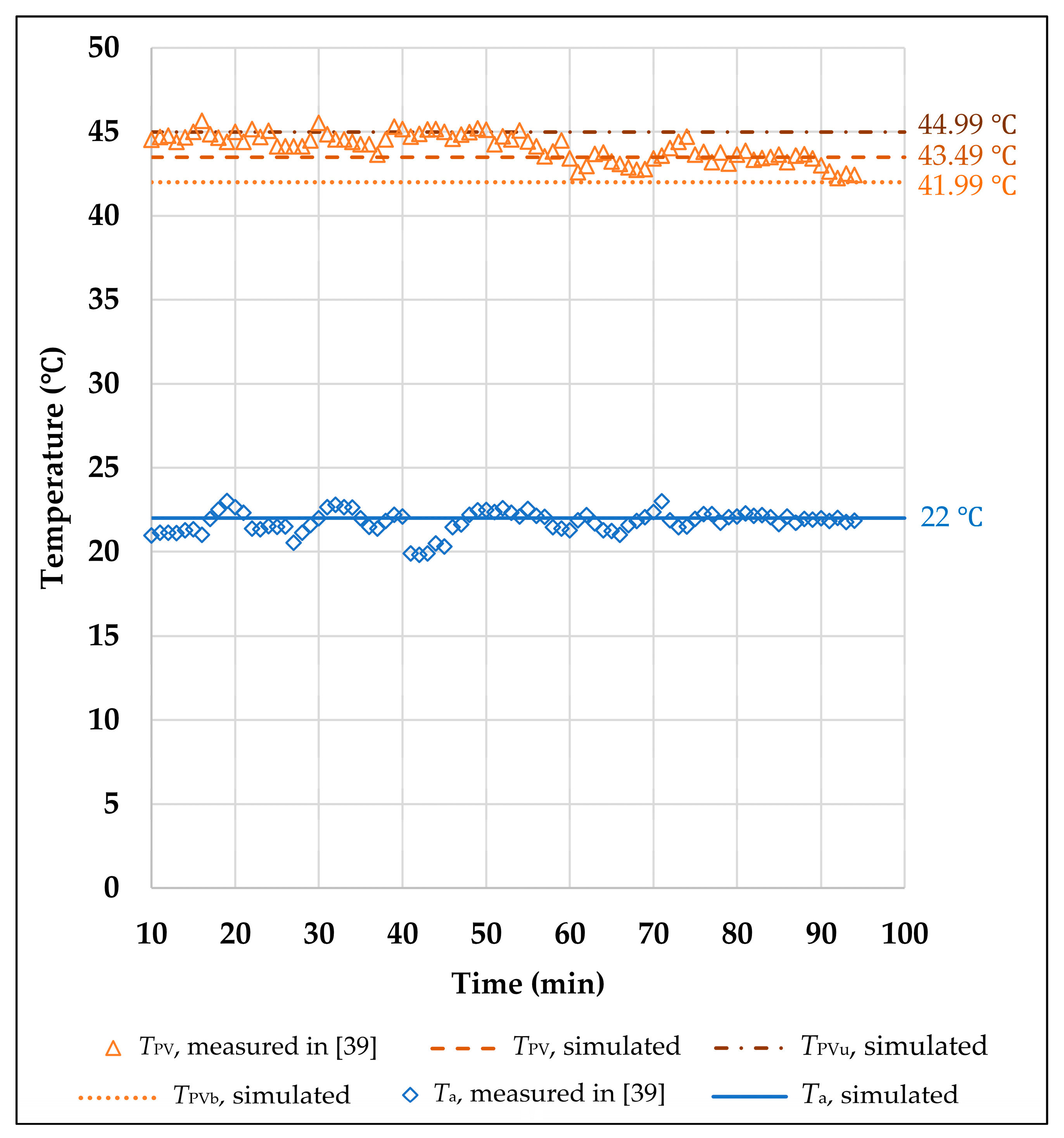
4. Results and Discussion

First of all, the proposed model is validated using experimental data and simulated results from [39]. Two simulation exercises are organized according to the description of the used experimentation [39]. The solar chimney model for cooling one PV module of type BP SX320P was made using a wooden channel that was thermally insulated from the surroundings. BP SX320P is a 20 W module with standard polycrystalline PV cells that can be used efficiently in any climate [45]. The experimental circuit consisted of three sections, as described in Section 2. Two identical PV modules were used in this experimental circuit. The first PV module was mounted on the inclined section of the solar chimney just below the absorber, while the second one was mounted on a separate steel frame next to the solar chimney created. This was carried out to maintain the uniformity of the experimental results for the purpose of comparing them to each other. The experimental circuit was tested on 20 October 2010 in Melbourne (Australia) at 37°47″ south latitude, which roughly corresponds to the northern latitudes where Serbia is located. For this reason, the experiments with PV modules inclined at an angle of $\theta =$ 37° relative to the horizontal are considered. The temperatures of the ambient air and the bottom surfaces of the PV modules with and without the solar chimney were measured with type K thermocouples. These thermocouples are connected to the Data Taker–DT800 for recording and storing data. During the 90 min test, the maximum solar irradiance was 1000 W/m², and there was no wind. The ambient air temperature was around 22 °C. The average difference between temperatures of the bottom surfaces of the PV modules with and without the solar chimney was approximately 7 °C.

Specifically, the same experimental circuit as in [39] is reconsidered, and the analytical model from [36], in which empirical correlations for free convection from a vertical flat plate (13) and (14) were included, is used for verification. The first simulation is performed with the following parameters: an inclination angle of $\theta =$ 37° to the horizontal plane; $L_{\mathrm{T}\mathrm{S}}=$ 0.187 m; $L_{\mathrm{A}\mathrm{P}}=$ 0.313 m; $L_{\mathrm{P}\mathrm{V}}=$ 0.52 m; $S_{\mathrm{A}\mathrm{P}}=S_{\mathrm{P}\mathrm{V}}=$ 0.234 m²; $L_{\mathrm{B}\mathrm{S}}=$ 0 m; $T_{\mathrm{i}}=T_{\mathrm{a}}=$ 22 °C; $q_{\mathrm{E},\mathrm{S}}=$ 1000 W/m²; ${\alpha }_{\mathrm{P}\mathrm{V}}=$ 0.97; ${\epsilon }_{\mathrm{P}\mathrm{V}}=$ 0.91; ${\alpha }_{\mathrm{A}}=$ 0.9; ${\tau }_{\mathrm{A}\mathrm{P}}=$ 0.91; ${\eta }_{\mathrm{e}\mathrm{l}}=$ 0.14; and $K_{\mathrm{i}+\mathrm{o}}=$ 2.7. The required remaining inputs can be found in the previous sections. In addition, it should be emphasized that the sum of $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}$ represents the height of the solar chimney, which should be distinguished from the total length of the ventilation channel.

The results of the first simulation are given in

Table 1. The results of the first and second simulations.

Parameter	Unit	Simulation
		First	Second
$\theta$	Degrees	37	90
$T_{\mathrm{o}}$	°C	44.03	34.3
$T_{\mathrm{a},\mathrm{a}\mathrm{v}}$	°C	33.01	28.15
$v_{\mathrm{i}}$	m/s	0.498	0.524
$v_{\mathrm{o}}$	m/s	0.535	0.545
$v_{\mathrm{a}\mathrm{i}\mathrm{r}}$	m/s	0.517	0.534
${{\alpha }_{\mathrm{P}\mathrm{V}}{S}_{\mathrm{P}\mathrm{V}}q}_{\mathrm{E},\mathrm{S}}$	W	226.98	136.6 1
${\alpha }_{\mathrm{A}}{\tau }_{\mathrm{A}\mathrm{P}}{S}_{\mathrm{A}\mathrm{P}}{q}_{\mathrm{E},\mathrm{S}}$	W	191.65	115.34 2
$Q_{\mathrm{a}\mathrm{i}\mathrm{r}}$	W	342.8	201.05
$q_{\mathrm{t},\mathrm{A}\mathrm{P}}{S}_{\mathrm{A}\mathrm{P}}$	W	3.803	2.031
$q_{\mathrm{c},\mathrm{P}\mathrm{V}}{S}_{\mathrm{P}\mathrm{V}}$	W	17.069	12.23
$q_{\mathrm{r},\mathrm{P}\mathrm{V}}{S}_{\mathrm{P}\mathrm{V}}$	W	32.067	25.42
$Q_{\mathrm{e}\mathrm{l}}$	W	31.777	19.124
$h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{b}}$	W/(m2·K)	2.885	2.972
$h_{\mathrm{c},\mathrm{A}\mathrm{P}\mathrm{u}}$	W/(m2·K)	3.172	2.805
$T_{\mathrm{A}\mathrm{P}}$	°C	27.25	25.16
$h_{\mathrm{c},\mathrm{P}\mathrm{V}}$	W/(m2·K)	3.17	2.805
$h_{\mathrm{r},\mathrm{P}\mathrm{V}}$	W/(m2·K)	12.444	17.66
$T_{\mathrm{P}\mathrm{V}}$	°C	43.49	39.72
$\mathrm{R}\mathrm{a}$	–	1.3257 × 108	7.9744 × 107

¹ This value is obtained from ${{\alpha }_{\mathrm{P}\mathrm{V}}{S}_{\mathrm{P}\mathrm{V}}q}_{\mathrm{E},\mathrm{S}}\mathrm{s}\mathrm{i}\mathrm{n}(37°)$. ² This value is obtained from ${\alpha }_{\mathrm{A}}{\tau }_{\mathrm{A}\mathrm{P}}{S}_{\mathrm{A}\mathrm{P}}{q}_{\mathrm{E},\mathrm{S}}\mathrm{s}\mathrm{i}\mathrm{n}(37°)$.

. According to the Rayleigh number $\mathrm{R}\mathrm{a}=$ 1.3257 × 10⁸, it is obtained that the free convection from the upper surfaces of the PV section and the acrylic plate is laminar. This means that the Nusselt number correlation for an inclined flat plate from [36] reduces to the empirical correlation (13). These results were obtained after the ninth iteration.

The average temperatures of the PV section and the acrylic plate are estimated as follows [36]:

$$T_{\mathrm{P}\mathrm{V}}={\displaystyle \frac{(T_{\mathrm{P}\mathrm{V}\mathrm{b}}+T_{\mathrm{P}\mathrm{V}\mathrm{u}})}{2}},$$

(23)

$$T_{\mathrm{A}\mathrm{P}}={\displaystyle \frac{(T_{\mathrm{A}\mathrm{P}\mathrm{b}}+T_{\mathrm{A}\mathrm{P}\mathrm{u}})}{2}},$$

(24)

respectively; where

$$T_{\mathrm{P}\mathrm{V}\mathrm{b}}=T_{\mathrm{P}\mathrm{V}\mathrm{u}}-{\displaystyle \frac{q_{\mathrm{E},\mathrm{S}}}{1000}}∆T=41.99°\mathrm{C}$$

(25)

is the temperature of the bottom surface of the PV section; $T_{\mathrm{P}\mathrm{V}\mathrm{u}}=$ 44.99 °C is the temperature of the upper surface of the PV section; $∆T=$ 3 K is the temperature difference between the two surfaces of the PV section for the considered mounting method of the PV modules and the assumption that the temperature of the upper surface of the PV section $T_{\mathrm{P}\mathrm{V}\mathrm{u}}$ is equal to the PV cell temperature; $q_{\mathrm{E},\mathrm{S}}=$ 1000 W/m² is the solar irradiance corresponding to the temperature difference $∆T=$ 3 K; $T_{\mathrm{A}\mathrm{P}\mathrm{b}}=$ 27.38 °C is the temperature of the bottom surface of the acrylic plate; and $T_{\mathrm{A}\mathrm{P}\mathrm{u}}=$ 27.12 °C is the temperature of the upper surface of the acrylic plate. In this regard, the temperature $T_{\mathrm{P}\mathrm{V}\mathrm{u}}$ is obtained from the following equation:

$$q_{\mathrm{r},\mathrm{P}\mathrm{V}}={\epsilon }_{\mathrm{P}\mathrm{V}}{\sigma }_{\mathrm{S}\mathrm{B}}F(T_{\mathrm{P}\mathrm{V}\mathrm{u}}^4-T_{\mathrm{a}}^4),$$

(26)

assuming that the appropriate view factor $F$ is equal to 1. Comparisons of the temperatures obtained in this simulation and the corresponding measured values from [39] are shown in Figure 2.

The second simulation is performed with the following parameters: an inclination angle of $\theta =$ 90° to the horizontal plane; $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}=$ 0.52 m; and other parameters as in the first simulation.

The results of the second simulation are listed in Table 1. Based on Table 1, the Rayleigh number is $\mathrm{R}\mathrm{a}=$ 7.9744 × 10⁷. Accordingly, the free convection heat transfer from the upper surfaces of the PV section and the acrylic plate is again laminar. The results of this exercise are also generated after the ninth iteration.

By comparing the results of the first simulation from Table 1 with the experimental and simulated results from Figure 2 and reference [39], one can see that almost identical values are obtained for the velocity of the air at the outlet of the solar chimney $v_{\mathrm{o}}$, the temperature of the bottom surface of the PV section $T_{\mathrm{P}\mathrm{V}\mathrm{b}}$, and the temperature of the upper surface of the PV section $T_{\mathrm{P}\mathrm{V}\mathrm{u}}$. When the inclination with respect to the horizontal plane increases from $\theta =$ 37° to $\theta =$ 90°, the solar irradiance decreases from $q_{\mathrm{E},\mathrm{S}}=$ 1000 W/m² to $q_{\mathrm{E},\mathrm{S}}\mathrm{s}\mathrm{i}\mathrm{n}(37°)=$ 601.815 W/m². This means that the temperatures of the PV section, the acrylic plate, and the air at the outlet of the solar chimney should be significantly reduced. In addition, the height of the solar chimney remained approximately the same (equal to the dimension $L_{\mathrm{A}\mathrm{P}}=$ 0.52 m), so no significant increase in the velocity of air at the outlet of the solar chimney can be expected. Such results are obtained in the second simulation. This was a way to validate and verify the accuracy of the used analytical model based on the available experimental and simulated data.

Figure 3 shows the dependence of the air velocity $v_{\mathrm{o}}$ on the solar irradiance $q_{\mathrm{E},\mathrm{S}}$ for the PV sections consisted of 1 and 6 PV modules (having the lengths $L_{\mathrm{P}\mathrm{V}}=$ 0.52 m and $L_{\mathrm{P}\mathrm{V}}=$ 3.12 m, respectively) and the following heights of the solar chimney: (a) $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}\approx$ 0.5 m; (b) $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}=$ 1 m; and (c) $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}=$ 1.5 m. In this figure, the labels “Roof” and “Façade” refer to the inclination angles of $\theta =$ 37° and $\theta =$ 90° to the horizontal plane, respectively. All curves are obtained assuming that the walls of the ventilation channel are adiabatic (i.e., thermally insulated). The three curves represented with dashed blue lines (and marked as “Roof”) are obtained using the proposed model for the case of the experimental circuit from [39], while the three curves represented with solid red lines (and marked as “Roof”) are generated for the geometry of the roof-integrated PV modules considered in [36]. In addition, the remaining six curves are obtained for the geometry of façade-integrated PV modules from Figure 1.

It can be seen from Figure 3 that the air velocity $v_{\mathrm{o}}$ increases with the increase in the solar irradiance $q_{\mathrm{E},\mathrm{S}}$, as well as with the increase in the height difference between the outlet and the inlet of the ventilation channel. By comparing each curve generated for one PV module with the corresponding curve obtained for six PV modules, it can be noted that the heat transferred from the PV section to the air in the ventilation channel also contributes to the increase in the air velocity $v_{\mathrm{o}}$. For the curves from Figure 3, that increase ranges between 41.05% (for “Roof” in Figure 3c) and 141.14% (for “Façade” in Figure 3a) when $q_{\mathrm{E},\mathrm{S}}$ ranges from 200 W/m² to 1200 W/m², respectively. It can also be noted that the red solid lines or red circles almost coincide with each other, and that there are significant discrepancies between the dashed blue lines or blue squares. This means that the effect of the increase in the height of the solar chimney $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}$ on the air velocity $v_{\mathrm{o}}$ is almost negligible for the case of the PV section composed of a larger number of PV modules, that is, a larger amount of heat transferred between the PV section and the air in the ventilation channel.

The effect of the height of the solar chimney is the same as that of the height difference between the two openings of the ventilation channel. This effect is also presented in Figure 3, and it is of importance only for the cases with one PV module. According to Figure 3a,b, in the range of the considered values for $q_{\mathrm{E},\mathrm{S}}$, an increase in the height difference of 0.5 m leads to an increase in the air velocity $v_{\mathrm{o}}$ by 22.53–23.51% and 12.7–12.93% for the cases of “Roof” and “Façade”, respectively. In addition, according to Figure 3a,c, an increase in the height difference of 1 m leads to an increase in the air velocity $v_{\mathrm{o}}$ by 38.43–39.84% and 23.01–23.46% for the cases of “Roof” and “Façade”, respectively.

Figure 4 illustrates the dependence of the average temperature of the PV section $T_{\mathrm{P}\mathrm{V}}$ on the solar irradiance $q_{\mathrm{E},\mathrm{S}}$ for the PV sections that consisted of 1 and 6 PV modules and the solar chimney heights of (a) $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}\approx$ 0.5 m; (b) $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}=$ 1 m; and (c) $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}=$ 1.5 m. The PV sections with one and six PV modules have the lengths of $L_{\mathrm{P}\mathrm{V}}=$ 0.52 m and $L_{\mathrm{P}\mathrm{V}}=$ 3.12 m, respectively. The labels “Roof” and “Façade”, as well as the marks of the curves, have the same meanings as in the case of Figure 3.

According to Figure 4, the average temperature of the PV section $T_{\mathrm{P}\mathrm{V}}$ increases with the increase in the solar irradiance $q_{\mathrm{E},\mathrm{S}}$ and decreases with the increase in the solar chimney height. The effect of the variation in the height of the solar chimney $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}$ on the average temperature of the PV section $T_{\mathrm{P}\mathrm{V}}$ is almost negligible for the cases of the PV sections composed of six PV modules (the curves represented by solid red lines and red circles). In the cases of the PV sections composed of one PV module, the effect is more pronounced. Furthermore, this decreasing effect is more pronounced in the case of “Roof” than in the case of “Façade”. This is a consequence of the increase in the air velocity $v_{\mathrm{o}}$ with the increase in the solar chimney height from Figure 3. Therefore, the greater the amount of heat transferred between the PV section and the air in the ventilation channel, the smaller the effect of the air velocity $v_{\mathrm{o}}$ on the average temperature of the PV section $T_{\mathrm{P}\mathrm{V}}$. For the curves represented by dashed blue lines and blue squares in Figure 4, in the range of the considered values for $q_{\mathrm{E},\mathrm{S}}$, an increase in the solar chimney height of 0.5 m leads to a decrease in the temperature $T_{\mathrm{P}\mathrm{V}}$ by 1.31–4.71% and 0.37–1.75% for the cases of “Roof” and “Façade”, respectively. In addition to this, an increase in the solar chimney height of 1 m leads to a decrease in the temperature $T_{\mathrm{P}\mathrm{V}}$ by 1.95–7.21% and 0.65–2.92% for the cases of “Roof” and “Façade”, respectively.

In connection with the results shown in Figure 3 and Figure 4, it is interesting to establish the flow types of free convection from the upper surfaces of the PV section and the acrylic plate. This can best be established based on the value of the fundamental dimensionless number for free convection. Accordingly, Figure 5 presents the dependence of the fundamental dimensionless number for free convection on the solar irradiance $q_{\mathrm{E},\mathrm{S}}$ for the PV sections with the lengths $L_{\mathrm{P}\mathrm{V}}=$ 0.52 m (consisting of one PV module) and $L_{\mathrm{P}\mathrm{V}}=$ 3.12 m (consisting of six PV modules) and the solar chimney heights $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}\approx$ 0.5 m, $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}=$ 1 m, and $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}=$ 1.5 m. In Figure 5, the solid blue line, dash–dot red line, and black circles correspond with the PV section consisted of 1 PV module, and the solid green line, dashed red line and black triangles correspond with the PV section that consisted of six PV modules.

According to Figure 5, the fundamental dimensionless number for free convection is lower than 10⁹ for the PV section that consisted of one PV module, which corresponds to laminar flow. In addition, this dimensionless number is greater than 10⁹ for the PV section that consisted of six PV modules, which corresponds to turbulent flow. In particular, turbulent flow corresponds to higher values of the air velocity $v_{\mathrm{o}}$ in accordance with Figure 3, as well as higher values of the average temperature of the PV section $T_{\mathrm{P}\mathrm{V}}$ in accordance with Figure 4. This is also confirmation that the proposed correlation (14) was used for the calculation during the iteration procedure.

Figure 6 shows the air velocity $v_{\mathrm{o}}$ and the average temperature of the PV section $T_{\mathrm{P}\mathrm{V}}$ depending on the height difference between the two openings of the ventilation channel $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}+L_{\mathrm{P}\mathrm{V}}+L_{\mathrm{B}\mathrm{S}}$ for two different numbers of PV modules per section, i.e., the PV sections having the lengths $L_{\mathrm{P}\mathrm{V}}=$ 0.52 m and $L_{\mathrm{P}\mathrm{V}}=$ 3.12 m. The labels “Roof” and “Façade” have the same meanings as in the case of Figure 3. For all the considered cases, it is also assumed that the solar irradiance $q_{\mathrm{E},\mathrm{S}}$ and the solar chimney height $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}$ are 1000 W/m² and 0.5 m (approximately), respectively.

It is evident from Figure 6a that the air velocity $v_{\mathrm{o}}$ increases with the increase in the height difference $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}+L_{\mathrm{P}\mathrm{V}}+L_{\mathrm{B}\mathrm{S}}$, as well as with the increase in the number of PV modules per section. In addition, according to Figure 6b, the average temperature of the PV section $T_{\mathrm{P}\mathrm{V}}$ decreases with the increase in the height difference $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}+L_{\mathrm{P}\mathrm{V}}+L_{\mathrm{B}\mathrm{S}}$, and increases with the increase in the number of PV modules per section. Furthermore, both these dependencies are more pronounced in the case of “Roof” than in the case of “Façade”. Based on the curves from Figure 6a,b, the increases in the air velocity $v_{\mathrm{o}}$ and the average temperature of the PV section $T_{\mathrm{P}\mathrm{V}}$ (due to the increase in the number of PV modules per section) are, respectively, up to 42.79% and 23.24% for the case of “Roof”, as well as 47.63% and 10.47% for the case of “Façade”.

It is now also necessary to demonstrate whether there are specific values of solar irradiance and number of PV modules per section at which laminar-to-turbulent flow transition occurs. For this purpose, Figure 7 is provided. Figure 7 illustrates the fundamental dimensionless number for free convection depending on the solar irradiance $q_{\mathrm{E},\mathrm{S}}$ for the PV sections consisting of one, two, three, four, five, and six PV modules and the solar chimney height of $L_{\mathrm{T}\mathrm{S}}+L_{\mathrm{A}\mathrm{P}}\approx$ 0.5 m.

According to Figure 7, regardless of the value of solar irradiance in an assumed steady-state, for the cases where the PV sections consist of one and two PV modules, the air flow (over the upper surfaces of the PV section and the acrylic plate) is laminar; and for the cases where the PV sections consist of five and six PV modules, the air flow is turbulent. Furthermore, for the cases where the PV sections consist of three and four PV modules, the air flow changes from laminar to turbulent at assumed steady-state solar irradiances of 600 W/m² and 250 W/m², respectively. Therefore, free convection heat transfer from the upper surfaces of the PV section and the acrylic plate is significantly affected under steady-state conditions by the solar irradiance $q_{\mathrm{E},\mathrm{S}}$ and the number of PV modules per section (i.e., the PV section length $L_{\mathrm{P}\mathrm{V}}$).

Finally, it is necessary to compare the powers of different roof- and façade-integrated PV sections cooled by a solar chimney. The power of the PV sections consisting of one, two, three, four, five, and six PV modules (with the lengths $L_{\mathrm{P}\mathrm{V}}=$ 0.52 m, $L_{\mathrm{P}\mathrm{V}}=$ 1.04 m, $L_{\mathrm{P}\mathrm{V}}=$ 1.56 m, $L_{\mathrm{P}\mathrm{V}}=$ 2.08 m, $L_{\mathrm{P}\mathrm{V}}=$ 2.6 m, and $L_{\mathrm{P}\mathrm{V}}=$ 3.12 m, respectively) depending on the solar irradiance $q_{\mathrm{E},\mathrm{S}}$ is shown in Figure 8. For the solar chimney in these simulations, a solar chimney with a height of 0.5 m is chosen. Furthermore, for the purpose of comparing the results, the length of the bottom section is assumed to be $L_{\mathrm{B}\mathrm{S}}=$ 0 m. Figure 8a corresponds with the case of roof-integrated PV modules, while Figure 8b corresponds with façade-integrated PV modules.

According to Figure 8a,b, linear dependences of the PV section power $Q_{\mathrm{e}\mathrm{l}}$ on the solar irradiance $q_{\mathrm{E},\mathrm{S}}$ are obtained for all the cases of the roof- and façade-integrated PV sections cooled by the solar chimney. As could be expected, the PV section power $Q_{\mathrm{e}\mathrm{l}}$ increases with an increase in the solar irradiance $q_{\mathrm{E},\mathrm{S}}$, as well as with an increase in the number of PV modules per section. Since the solar irradiance decreases from $q_{\mathrm{E},\mathrm{S}}=$ 1000 W/m² to $q_{\mathrm{E},\mathrm{S}}\mathrm{s}\mathrm{i}\mathrm{n}(37°)=$ 601.815 W/m² with an increase in the inclination angle $\theta$ from 37° to 90°, this means that the design with façade-integrated PV modules will have a lower power $Q_{\mathrm{e}\mathrm{l}}$ compared to the corresponding design with roof-integrated PV modules. For the considered angles of inclination, this reduction amounts to 39.82% and corresponds to the reduction in the solar irradiance $q_{\mathrm{E},\mathrm{S}}$.

5. Conclusions

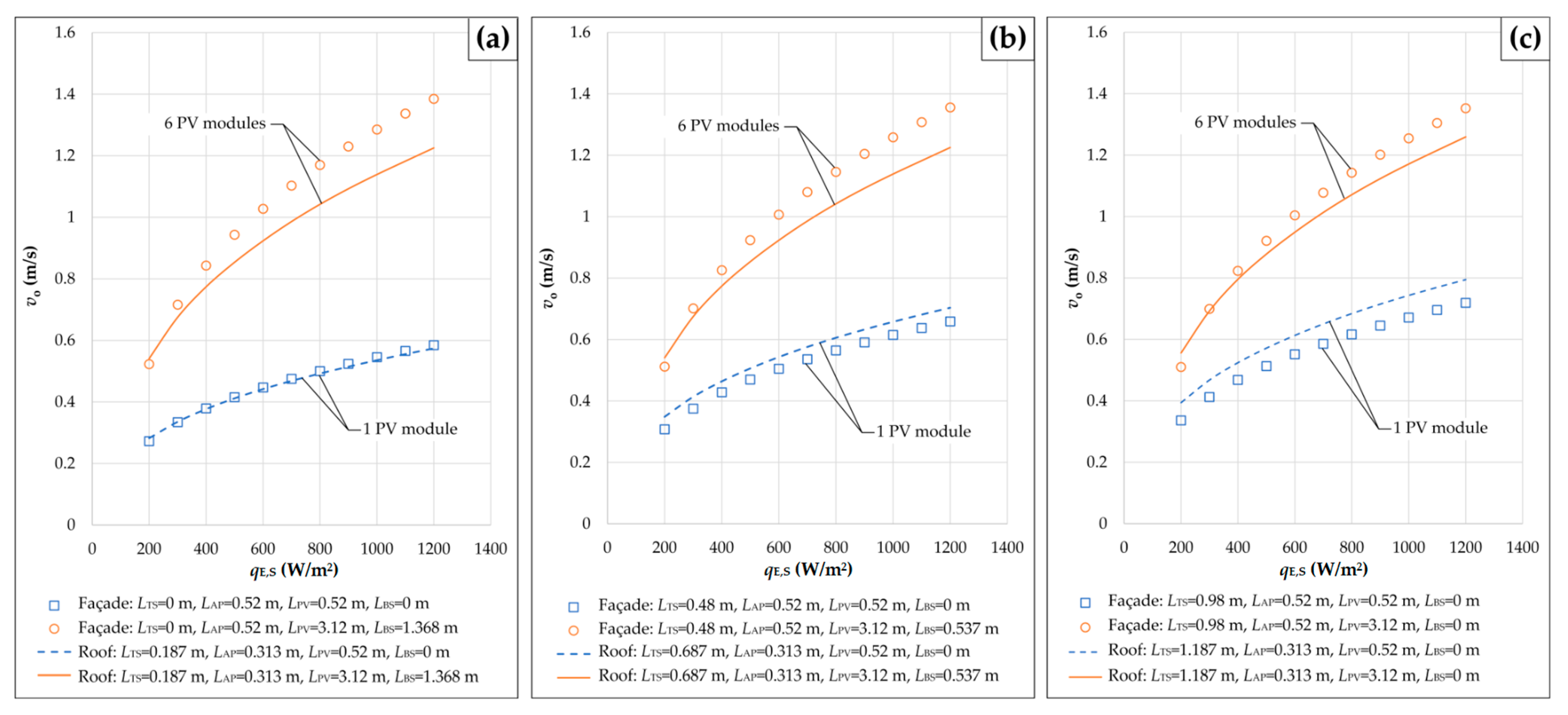
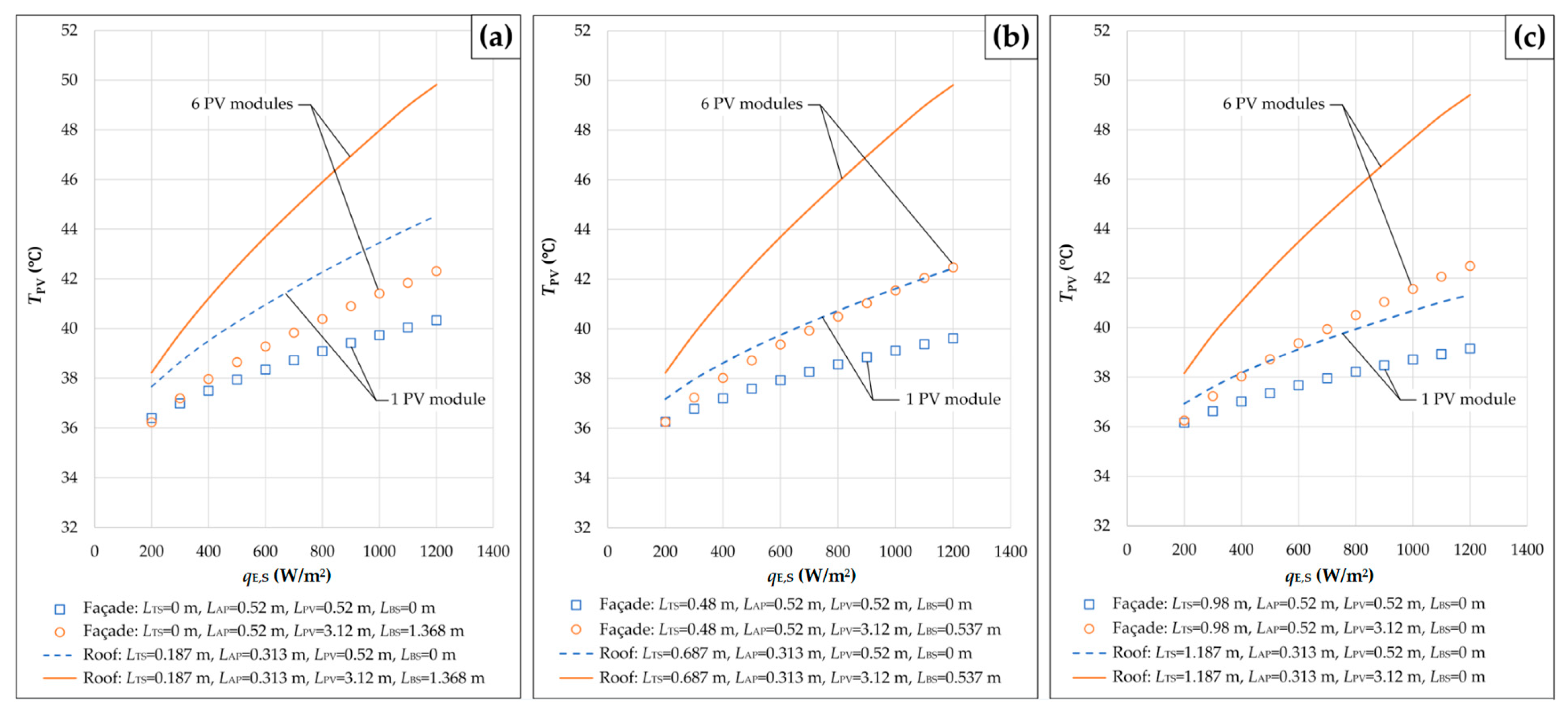
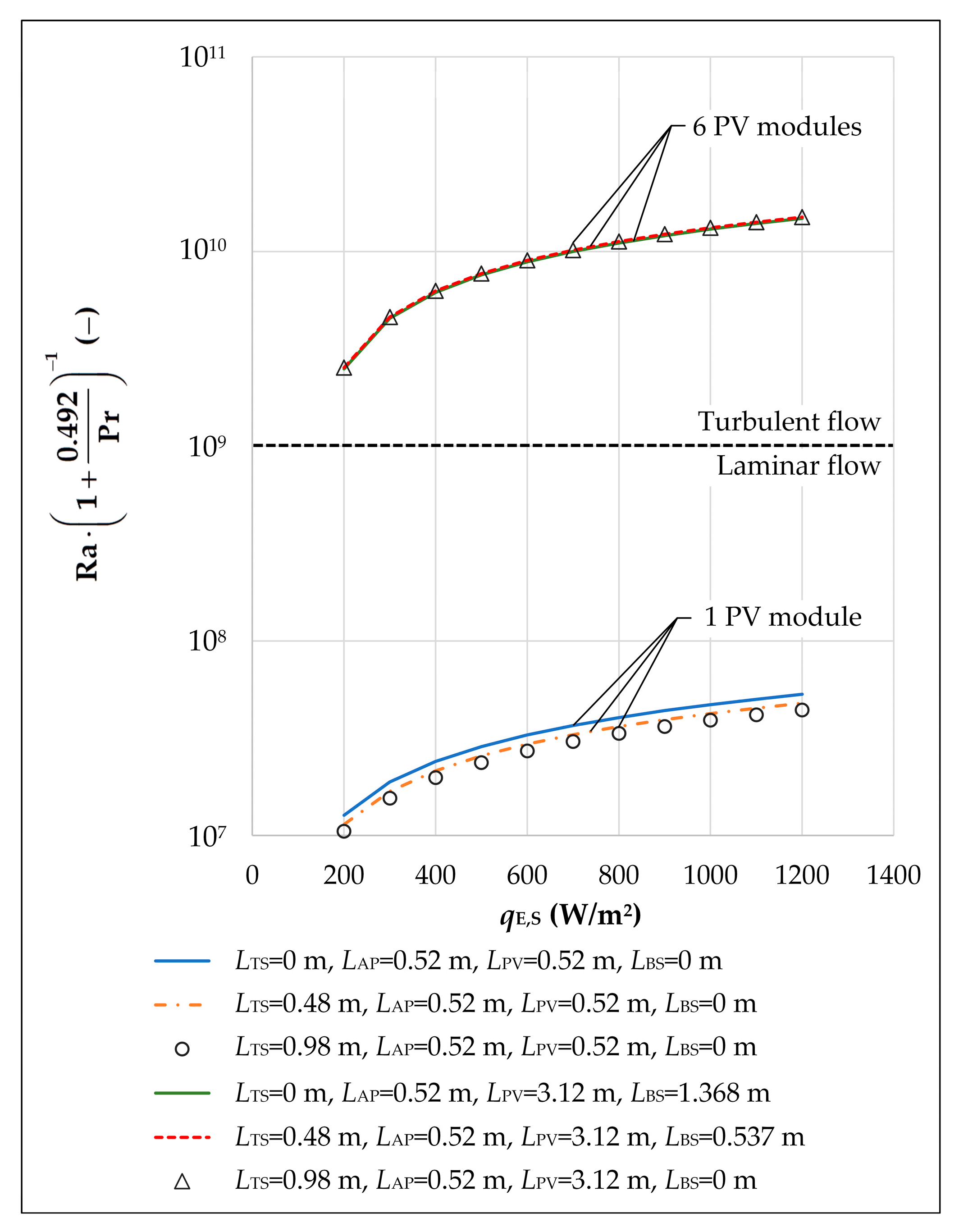
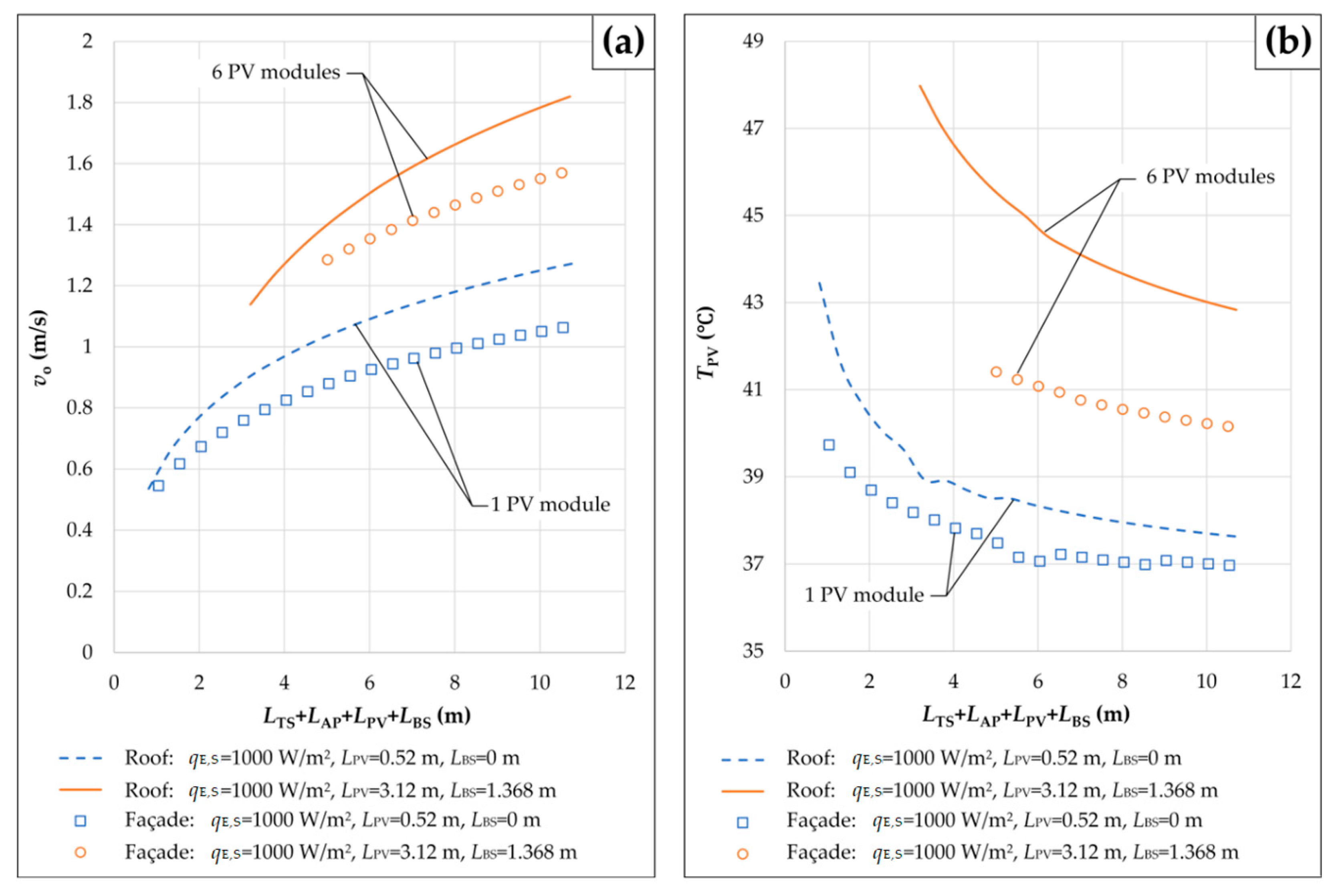
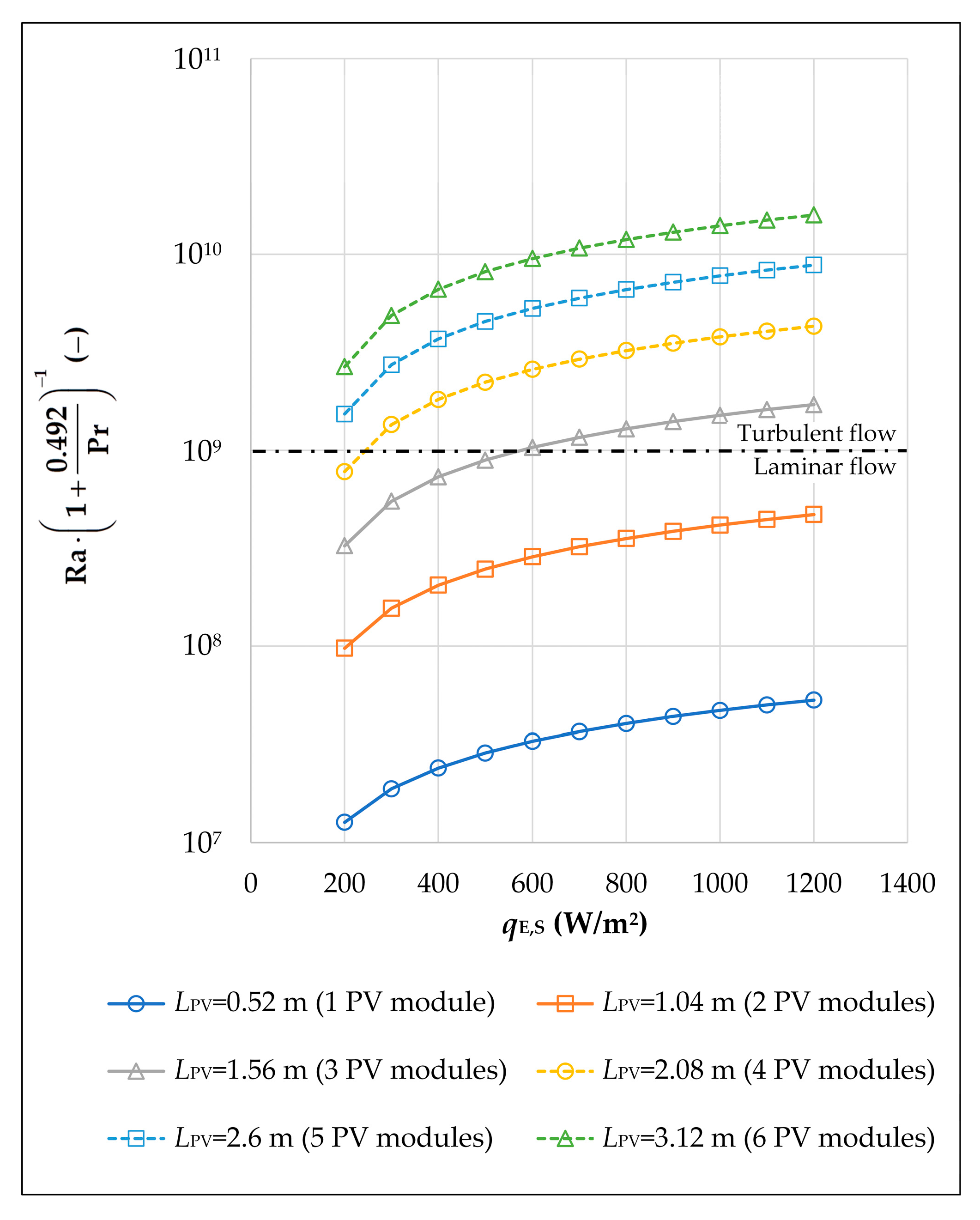
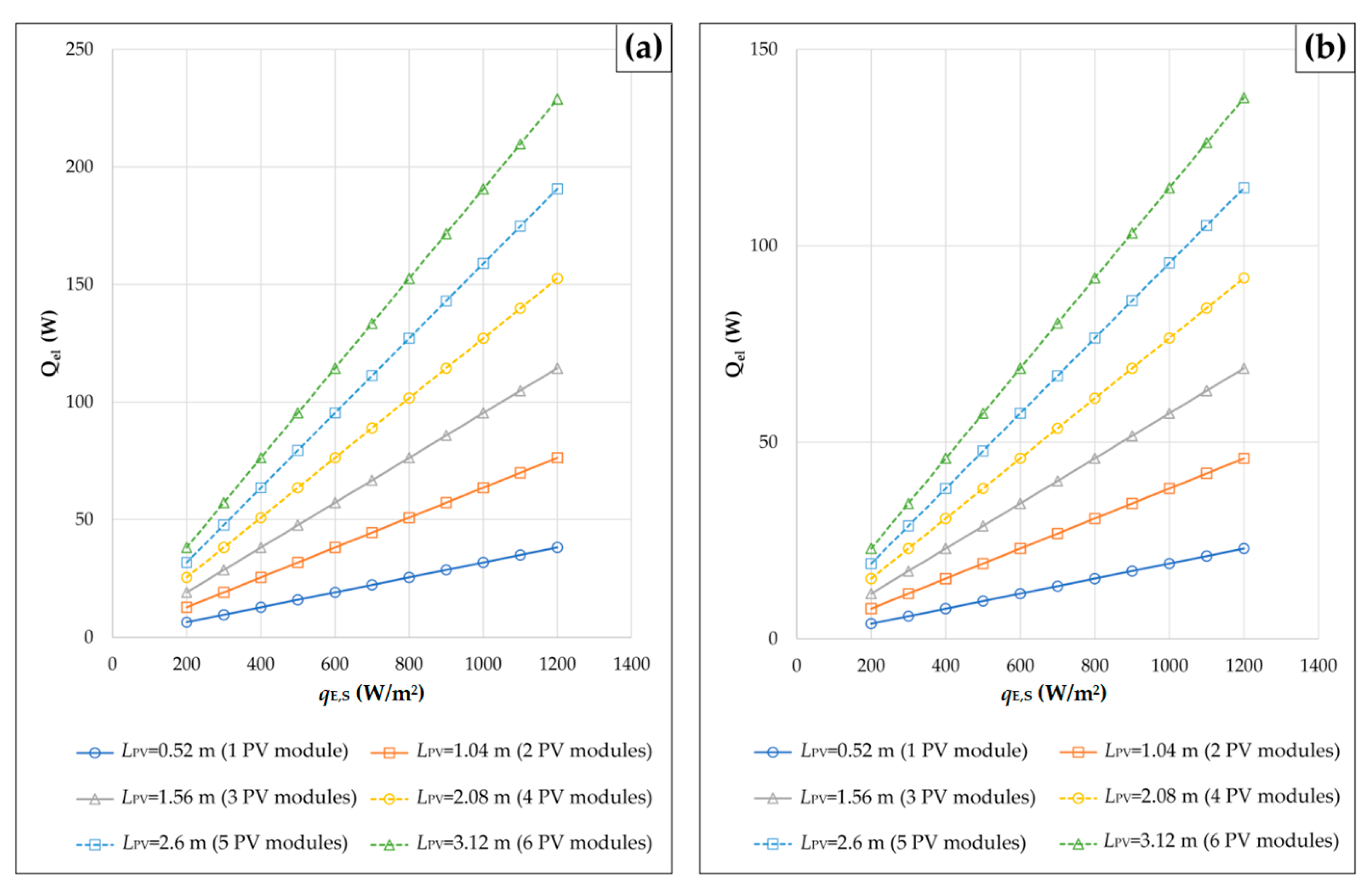
• The velocity of air at the outlet of any solar chimney integrated with PV modules increases with an increase in the solar irradiance and with an increase in the height difference between the outlet and the inlet of the associated ventilation channel. This increase is significantly more pronounced in the case of “Façade” than in the case of “Roof”. In addition, the solar chimney effect on the velocity of air in any ventilation channel is almost negligible for the cases of PV sections with larger numbers of roof- or façade-integrated PV modules. Unlike the air velocity, the average temperature of any PV section increases with increasing solar irradiance and decreases with increasing height of the solar chimney. Moreover, the greater the amount of heat transferred between one PV section and the air in the ventilation channel below it, the smaller the effect of the velocity of air at the outlet of the channel on the average temperature of roof- or façade-integrated PV modules.
• For the cases where PV sections consist of one and two PV modules, the air flow regimes over the upper surfaces of the PV sections and the appropriate acrylic plates are laminar. In addition, the turbulent flow of air along one ventilation channel corresponds to higher values for the velocity of air at the outlet of the channel and the average temperature of roof- or façade-integrated PV modules. Furthermore, for the cases where PV sections consist of four or more PV modules, the air flow is turbulent at solar irradiance greater than 250 W/m² or 200 W/m², respectively. Finally, the use of façade-integrated PV modules in urban areas contributes to the reduction in greenhouse gas emissions, the generation of clean electricity on-site, and the zero carbon transition of cities.
• Future research on this issue should include roof- or façade-integrated PV systems with different ventilation channels, PV sections with seven or more PV modules, and absorbers with larger absorption areas. In addition, future studies should deal with newer PV technologies and include more experiments, as well as appropriate economic and environmental analyses.